强化学习中的随机决策森林

随机森林算法的简要描述

使用了 bagging 的随机森林 (Random Forest, RF) 是最强大的机器学习方法之一, 它略微弱于梯度 boosting。 

随机森林包含了一系列决策树 (也被称为分类数或者 "CART" 回归树，用于解决同名的任务). 它们应用在统计学，数据挖掘和机器学习中。每个单独的树都是一个相对简单的模型，含有分支，节点和叶片，节点包含了所依赖的目标函数的属性，而目标函数的值就通过分支到达叶片。在新案例分类的过程中，有必要通过分支到叶片，根据逻辑原理 "IF-THEN( 如果-那么)" 来遍历所有属性值，根据这些条件，目标变量将会被赋予一个特定数值或者一个类型(目标变量将会归于一个特定叶片)。构建决策树的目的是创建一个模型，可以根据几个输入变量的值来预测目标变量的值。

随机森林就是由使用了 Bagging 算法构建的决策树构成的。Bagging 是一个人造词汇，是由单词组合 bootstrap aggregating（自举汇聚法） 形成的。这个词是由 Leo Breiman 在 1994 年引入的，

Bootstrap（自举或自助法）是统计生成样本的一种方法，其中所选对象的数目与初始对象的数目相同。但是这些对象是使用不同重复数量选择的，换句话说，随机选择的对象被返回并且可以被再次选择。在这种情况下，所选对象的数量将包含约63%的源样本，而其它对象（大约37% ）永远不会落入训练样本中。这样生成的样本用于训练基本算法 (在本例中，即决策树). 这也是随机发生的: 指定长度的随机子集（样本）在随机特性（属性）子集中做训练。剩余的 37% 的样本用于测试所构建模型的泛化能力。

之后，所有训练过的决策树被组合到一起，使用所有用本的平均误差来做简单投票。Bootstrap聚合的使用减少了均方误差，降低了训练分类器的方差。误差在不同的样本间不会相差太大。这样，根据作者的意见，模型将会较少有过度拟合的问题。bagging 方法的效果依赖于基本算法 (决策树) 是在随机变化的样本中训练的，它们的结果可能相差很大，而误差会在投票中大幅抵消。

可以说随机森林是 bagging 的一个特例，在其中决策树是用作基本单元的。同时，与传统的决策树构建方法不同，没有使用修剪（pruning），这种方法是为了整合大量数据样本的时候能够尽可能的快。每个数是使用特定方法创建的，用于构建树节点的特性 (属性) 不是从全部的特性中选择的，而是从它们的随机子集中选择的。当构建回归模型时，特性的数量是 n/3，如果是分类，它就是 √n. 所有这些都是经验的建议，被称为去相关：不同的特征集落入不同的树，并且树被训练在不同的样本上。

图 1. 随机森林运行框架

随机森林算法已被证明非常高效，可以用于解决实际问题，它提供了高质量的训练，在模型的构建过程中引入了大量的随机性。它的超过其他的机器学习模型的优势是一个非线性的时间估计的一方来说，这是不包括在培训样品。因此，对一个单一的样本进行交叉验证或测试对于决策树来说是不必要的。这就足以限制我们对模型的进一步“调整”：选择决策树的数量和正则化组件。 

在标准 MetaTrader 5 开发包里面的 ALGLIB 库就包含了随机决策森林 (Random Decision Forest，RDF) 算法，它是由 Leo Breiman 和 Adele Cutler 所提出的原始随机森林算法的修改版本。该算法结合了两个思想：使用决策树的组合，通过投票获得结果和随机化学习过程的思想。对算法修改的更多详细信息可以在 ALGLIB 网站上找到。

算法的优点

• 学习速度很快
• 非迭代学习 — 算法是完全在确定数量的操作中完成的。
• 可伸缩性（处理大量数据的能力）。
• 取得模型的质量很高 (与 神经网络 和 神经网络集合 相比)。
• 随机抽样对数据尖峰不敏感。
• 配置参数数量不多。
• 由于随机子空间的选择，对特征值的缩放（和一般的单调变换）不敏感。
• 不需要仔细配置参数就可以工作得很好。参数的“调谐”允许根据任务和数据将精度从0.5%提高到3%。
• 即使丢失了大量数据，也能保持良好的精度。
• 模型泛化能力的内部评价。
• 能够在没有预处理的情况下与原始数据一起工作。

算法的缺点

• 构建的模型占用了大量的内存,如果根据 K构造一个基于大小为 N的训练集，则内存需求为 O（K*N）。例如，对于 K=100 并且 N=1000, ALGLIB 所创建的模型要占用大约 1 MB 的内存。但是，当代计算机的内存数量已经足够大了，所以这不是一个大的缺陷。
  
• 经过训练的模型比其他算法工作得慢一些（如果模型中有100棵树，就必须对它们进行迭代以获得结果）。然而，在现代机器上，这一点并不明显。
• 当一组具有许多稀疏特征（文本、词组）或待分类对象可以线性分离时，该算法比大多数线性方法更差。
• 该算法容易出现过度拟合，特别是在噪声较高的任务上。这种问题可以通过调整 r 参数来部分解决，原始随机森林算法也存在类似问题，但是更加明显。然而，作者声称该算法不易过拟合。这种谬论被一些机器学习实践者和理论家所分享。
• 对于包含不同级别的分类变量的数据，随机森林偏向于具有更多级别的特征。树将被更强烈地调整到这样的特征，因为它们允许接收更高值的优化功能（信息增益类型）。
• 与决策树相似，该算法绝对是不能外推（但这可以被认为是一个加号，因为在峰值情况下不会有极值）。

机器学习在交易中的应用特点

在机器学习的新手中，有一种普遍的观点认为，它是某种童话世界，程序为交易者做一切，而他只享受得到的利润。这只是部分正确的，最终的结果将取决于如何解决下面描述的问题。

• 特性的选择

第一个和主要的问题是选择什么样的需要教的模型。代价是受很多因素影响的。只有一种科学方法来研究市场 — 经济学. 主要有三种方法：回归分析法、时间序列分析法和面板分析法。这一领域的一个单独有趣的部分是非参数计量经济学，它仅仅基于可用的数据，而没有对形成它们的原因进行分析。近年来，非参数计量经济学方法在应用研究中得到了广泛的应用：例如，核方法和神经网络。同一部分包括非数值概念的数学分析，例如，模糊集合。如果你打算认真对待机器训练，那么引入经济计量方法将是有益的。本文将重点研究模糊集。

• 模型的选择

第二个问题是对训练模型的选择，有很多线性和非线性模型。例如，在微软站点中可以找到它们的列表和特征比较。

例如，神经网络的种类很多。当使用它们时，必须对网络体系结构进行实验，选择层和神经元的数目。同时，经典的MLP型神经网络训练缓慢（特别是固定步长的梯度下降），实验需要花费大量的时间。现代快速学习的深度学习网络目前无法在终端的标准库中使用，包括DLL形式的第三方库并不十分方便。我还没有充分研究过这样的开发包。

与神经网络不同，线性模型工作速度快，但不总是很好地处理近似。

随机森林没有这些缺点。只需要选择树的数量和负责训练对象中的对象百分比的参数R。在微软Azure机器学习工作室(Microsoft Azure Machine Learning Studio)中的实验表明，在大多数情况下，随机森林对测试数据的预测误差最小。

• 模型测试

一般来说，只有一个严格的建议：训练样本越大，特征越丰富，系统对新数据的稳定性就越高。但是，当解决交易任务时，系统容量不足的情况可能发生，当相互变化的预测者太少，他们是不翔实的。因此，来自预测器的相同信号将产生买卖信号。输出模型将具有较低的泛化能力，因此，在未来的信号质量较差。此外，对大样本的训练将是缓慢的，在优化过程中呈现多次运行是不可能的。尽管如此，也不能保证取得积极的结果。还有一些其它问题，例如报价本身的混乱性质，以及它们的非平稳性，不断变化的市场模式或（更糟），完全没有模式。

选择模型训练方法

随机森林用于解决广泛的回归、分类和聚类问题。

这些方法可以表示如下。

• 无监督学习。聚类、异常检测。这些方法被应用于以编程方式将特征划分为具有自动确定的显著差异的组。
• 有监督学习。分类与回归。一组先前已知的训练实例（标签）被输入作为输入，并且随机森林尝试学习（近似）所有情况。
• 强化学习。这也许是最不寻常和最有前途的机器学习，它与众不同。这里，当虚拟代理与环境交互时，学习发生，而代理试图最大化从该环境中的动作获得的回报。让我们使用这种方法。

在交易系统的开发任务中的强化学习

想象一下创建一个人工智能的交易者，它将与环境交互，并从环境中接收对其行为的某种响应。例如，获利的交易将被鼓励，对无利的交易将被处罚。最后，在经历了几次与市场的互动之后，人工交易者将发展出自己独特的体验，这将被烙印在它的“大脑”上。随机森林将扮演“大脑”的角色。

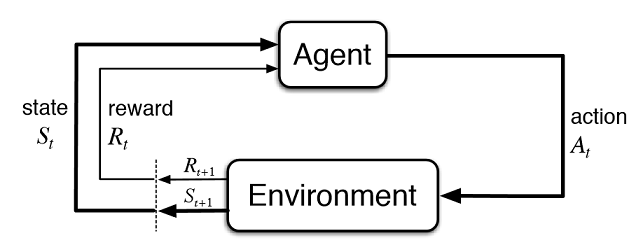
图 2. 虚拟交易者与市场的交互

图2给出了代理（人工交易者）与环境（市场）的交互方案。代理可以在时间 t 执行动作A，同时处于状态 S t。随后，它进入状态 St+1, 根据之前的行为在环境中的成功成都来收到回报 Rt，这些行为可以及许 t+n 次, 知道整个学习序列 (或者代理的游戏情节)完成。这个过程可以进行迭代，使代理学习多次，不断改进结果。

代理的记忆（或经验）应该存储在某处。强化学习的经典实现使用状态动作矩阵。当进入某一状态时，代理被迫为下一个决定来处理矩阵。这种实现适用于具有非常有限的状态集的任务。否则，矩阵可能会变得非常大。因而，表格使用随机森林来替代。

图 3. 深度神经网络还是随机森林用于策略的近似

代理的一个随机参数化策略Π θ 是一组（s，a）对，其中，θ是每个状态的参数向量。最优策略是针对特定任务的最优动作集。让我们同意，代理人寻求制定一个最优的政策。这种方法适用于具有未知状态的连续任务，是一种在强化学习中无模型的演员评论方法。还有许多其他强化学习的方法。它们在 Richard S. Sutton 和 Andrew G. Barto 的 "强化学习: 简介"一书中有所描述。

自主学习EA交易(代理)的软件实现

我在文章中力求连续性，因此模糊逻辑系统将充当代理。在以前的文章中，对Mamdani模糊推理的高斯隶属函数进行了优化。然而，该方法有一个明显的缺点-高斯保持不变的所有情况下，无论当前的环境状况（指标值）。现在的任务是自动选择高斯位置的“中性”项的模糊输出“out”。通过选择值和近似高斯中心的函数，根据三个值的值以及在[0；1 ]的范围内，代理将被开发出最优策略。

在EA交易的全局变量中创建一个指向成员函数的单独指针。这可以使我们在学习过程中可以自由改变它的参数:

CNormalMembershipFunction *updateNeutral=new CNormalMembershipFunction(0.5,0.2);

创建一个随机森林和矩阵类来填充数值:

//RDF 系统. 我们在这里创建所有的 RF 对象.
CDecisionForest      RDF;                                     //随机森林对象
CMatrixDouble        RDFpolicyMatrix;                         //用于随机森林输入和输出的矩阵
CDFReport            RDF_report;                              //RF 在这个对象中返回错误，这样我们可以检查它

随机森林的主要设置被移动到输入参数：树的数量和正则化分量，这使我们可以通过调整这些参数来提高模型:

sinput int number_of_trees=50;
sinput double regularization=0.63;

让我们写一个服务函数来检查模型的状态，如果随机森林已经被训练为当前的时间框架，它将被用于交易信号，如果不是，则用随机值初始化策略（随机交易）。

void checkBeforeLearn()
  {
   if(clear_model)
     {
      int clearRDF=FileOpen("RDFNtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(clearRDF,0);
      FileClose(clearRDF);
      ExpertRemove();
      return;
     }

   int filehnd=FileOpen("RDFNtrees"+ _Symbol + (string)_Period +".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
   int ntrees =  (int)FileReadNumber(filehnd);
   FileClose(filehnd);

   if(ntrees>0)
     {
      random_policy=false;

      int setRDF=FileOpen("RDFBufsize"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      RDF.m_bufsize=(int)FileReadNumber(setRDF);
      FileClose(setRDF);

      setRDF=FileOpen("RDFNclasses"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      RDF.m_nclasses=(int)FileReadNumber(setRDF);
      FileClose(setRDF);

      setRDF=FileOpen("RDFNtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      RDF.m_ntrees=(int)FileReadNumber(setRDF);
      FileClose(setRDF);

      setRDF=FileOpen("RDFNvars"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      RDF.m_nvars=(int)FileReadNumber(setRDF);
      FileClose(setRDF);

      setRDF=FileOpen("RDFMtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_BIN|FILE_ANSI|FILE_COMMON);
      FileReadArray(setRDF,RDF.m_trees);
      FileClose(setRDF);
     }
   else Print("Starting new learn");

   checked_for_learn=true;
  }

您可以从列表中看到，训练过的模型可以从文件中载入，包含:

• 训练样本的大小,
  
• 种类的数量 (如果是回归模型，就是1),
  
• 树的数量,
  
• 特性的数量,
• 以及训练过的树的数组.

训练将在策略测试器的优化模式下进行，在测试的每个通过之后，该模型将被训练在新形成的矩阵上，并存储在上述文件中以供以后使用：

double OnTester()
  {
   if(clear_model) return 0;

   if(MQLInfoInteger(MQL_OPTIMIZATION)==true)
     {
      if(numberOfsamples>0)
        {
         CDForest::DFBuildRandomDecisionForest(RDFpolicyMatrix,numberOfsamples,3,1,number_of_trees,regularization,RDFinfo,RDF,RDF_report);
        }

      int filehnd=FileOpen("RDFBufsize"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(filehnd,RDF.m_bufsize);
      FileClose(filehnd);

      filehnd=FileOpen("RDFNclasses"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(filehnd,RDF.m_nclasses);
      FileClose(filehnd);

      filehnd=FileOpen("RDFNtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(filehnd,RDF.m_ntrees);
      FileClose(filehnd);

      filehnd=FileOpen("RDFNvars"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI|FILE_COMMON);
      FileWrite(filehnd,RDF.m_nvars);
      FileClose(filehnd);

      filehnd=FileOpen("RDFMtrees"+_Symbol+(string)_Period+".txt",FILE_READ|FILE_WRITE|FILE_BIN|FILE_ANSI|FILE_COMMON);
      FileWriteArray(filehnd,RDF.m_trees);
      FileClose(filehnd);
     }

   return 0;
  }

处理上一篇文章的交易信号的功能实际上没有变化，但现在在打开订单后调用以下函数: 

void updatePolicy(double action)
  {
   if(MQLInfoInteger(MQL_OPTIMIZATION)==true)
     {
      numberOfsamples++;
      RDFpolicyMatrix.Resize(numberOfsamples,4);

      RDFpolicyMatrix[numberOfsamples-1].Set(0,arr1[0]);
      RDFpolicyMatrix[numberOfsamples-1].Set(1,arr2[0]);
      RDFpolicyMatrix[numberOfsamples-1].Set(2,arr3[0]);
      RDFpolicyMatrix[numberOfsamples-1].Set(3,action);
     }
  }

它将具有三个指标值的状态向量添加到矩阵中，并用从 Mamdani 模糊推理获得的当前信号填充输出值。

另一个函数:

void updateReward()
  {
   if(MQLInfoInteger(MQL_OPTIMIZATION)==true)
     {
      int unierr;
      if(getLAstProfit()<0) RDFpolicyMatrix[numberOfsamples-1].Set(3,MathRandomUniform(0,1,unierr));
     }
  }

是在每次订单关闭的时候调用的。如果交易结果是无利的，那么代理人的报酬是从一个随机的均匀分布中选择的，否则报酬不变。

图 4. 随机报酬值选择的均匀分布

因此，在当前的实施中，鼓励由代理人做出的有利可图的交易，并且在不盈利的情况下，代理被迫采取随机行动（高斯中心的随机位置）来搜索最优解。

信号处理功能的完整代码如下：

void PlaceOrders(double ts)
  {
   if(CountOrders(0)!=0 || CountOrders(1)!=0)
     {
      for(int b=OrdersTotal()-1; b>=0; b--)
         if(OrderSelect(b,SELECT_BY_POS)==true)
            if(OrderSymbol()==_Symbol && OrderMagicNumber()==OrderMagic)

               switch(OrderType())
                 {
                  case OP_BUY:
                     if(ts>=0.5)
                     if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red))
                       {
                        updateReward();
                        if(ts>0.6)
                          {
                           lots=LotsOptimized();
                           if(OrderSend(Symbol(),OP_SELL,lots,SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,Red)>0)
                             {
                              updatePolicy(ts);
                             };
                          }
                       }
                     break;

                  case OP_SELL:
                     if(ts<=0.5)
                     if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red))
                       {
                        updateReward();
                        if(ts<0.4)
                          {
                           lots=LotsOptimized();
                           if(OrderSend(Symbol(),OP_BUY,lots,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,Green)>0)
                             {
                              updatePolicy(ts);
                             };
                          }
                       }
                     break;
                 }
      return;
     }

   lots=LotsOptimized();

   if((ts<0.4) && (OrderSend(Symbol(),OP_BUY,lots,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN) > 0))
      updatePolicy(ts);
   else if((ts>0.6) && (OrderSend(Symbol(),OP_SELL,lots,SymbolInfoDouble(_Symbol,SYMBOL_BID),0,0,0,NULL,OrderMagic,INT_MIN) > 0))
      updatePolicy(ts);
   return;
  }

计算 Mamdani 模糊推理的功能发生了变化，现在，如果没有随机选择代理的策略，它调用使用训练的随机森林计算沿X轴的高斯位置。随机森林被馈送到当前状态作为具有3个振荡器值的矢量，并且所获得的结果更新高斯的位置。如果EA第一次在优化器中运行，则随机地为每个状态选择高斯的位置。

double CalculateMamdani()
  {
   CopyBuffer(hnd1,0,0,1,arr1);
   NormalizeArrays(arr1);

   CopyBuffer(hnd2,0,0,1,arr2);
   NormalizeArrays(arr2);

   CopyBuffer(hnd3,0,0,1,arr3);
   NormalizeArrays(arr3);

   if(!random_policy)
     {
      vector[0]=arr1[0];
      vector[1]=arr2[0];
      vector[2]=arr3[0];

      CDForest::DFProcess(RDF,vector,RFout);
      updateNeutral.B(RFout[0]);
     }
   else
     {
      int unierr;
      updateNeutral.B(MathRandomUniform(0,1,unierr));
     }
   
   //Print(updateNeutral.B());
   firstTerm.SetAll(firstInput,arr1[0]);
   secondTerm.SetAll(secondInput,arr2[0]);
   thirdTerm.SetAll(thirdInput,arr3[0]);

   Inputs.Clear();
   Inputs.Add(firstTerm);
   Inputs.Add(secondTerm);
   Inputs.Add(thirdTerm);

   CList *FuzzResult=OurFuzzy.Calculate(Inputs);
   Output=FuzzResult.GetNodeAtIndex(0);
   double res=Output.Value();
   delete FuzzResult;

   return(res);
  }

训练和测试模型的过程

代理将在优化器中顺序进行训练，也就是说，前一次训练的结果会写到文件中用于下一次运行，为此，需要禁止所有的测试代理和云服务，只是用一个核心来做。 

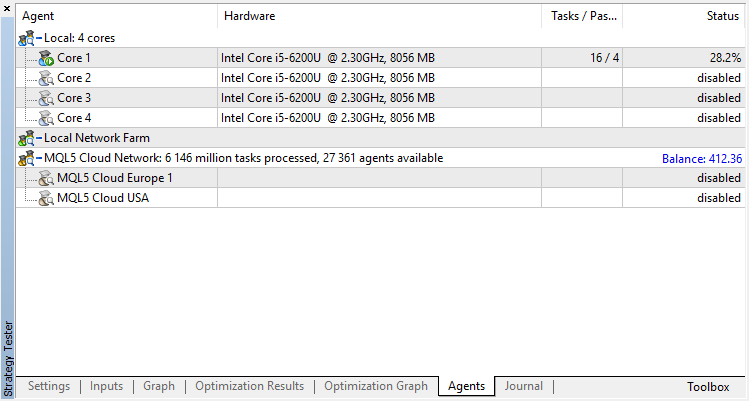
禁用遗传算法 (使用慢速完成算法). 训练/测试是使用开盘价来进行的，因为 EA 明确在新柱开启时进行控制。

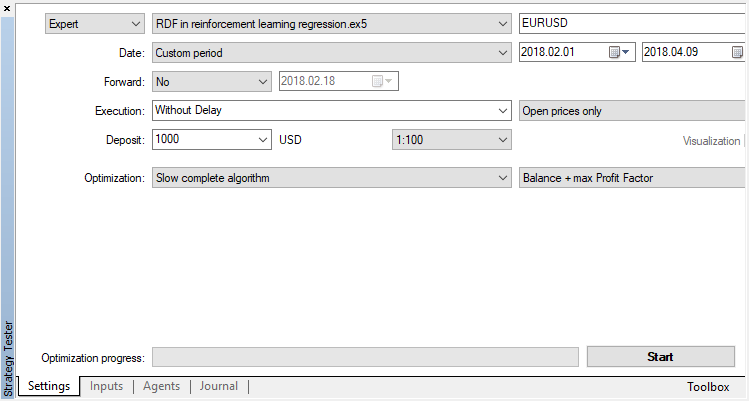
只有一个优化参数 — 在优化器中的通过数量。为了演示算法的运行，设置为15次迭代。

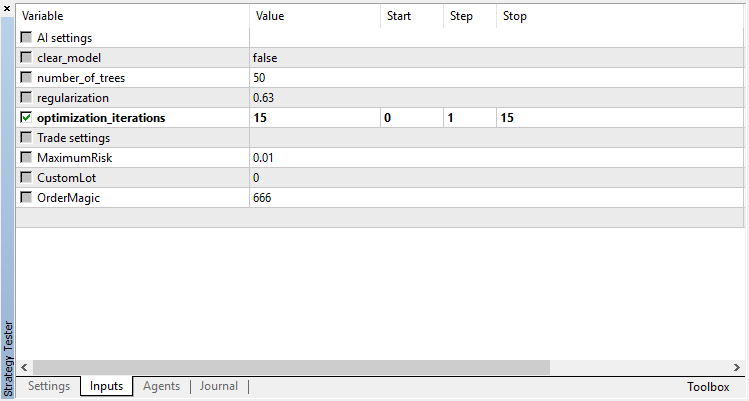
回归模型 (含有一个输出变量) 的优化结果在下面显示。请记住，经过训练的模型保存到文件中，因此只有最后一次运行的结果才会被保存。

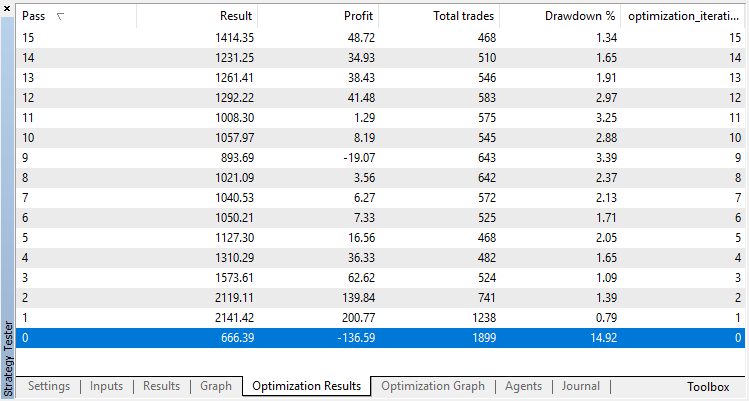
零运行对应于代理的随机策略（第一次运行），因此造成了最大的损失。恰恰相反，第一次运行是最有成效的。随后的运行没有取得任何进展，而是停滞不前。结果，增长图表在第15次运行之后看起来如下:

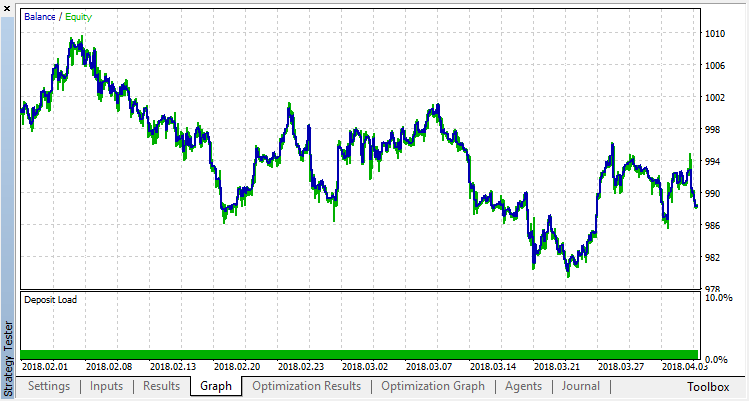
让我们对分类模型进行同样的实验。在这种情况下，奖励分为2类：正面和负面。

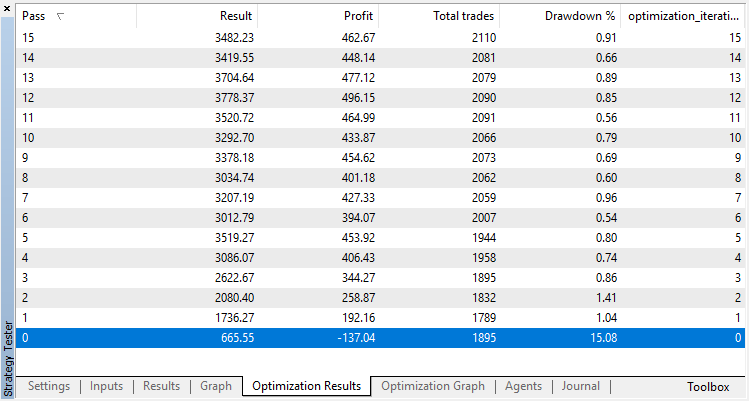
分类执行这项任务要好得多。至少有一个稳定的增长，从零运行，对应于随机政策，直到第十五，增长停止，政策开始波动大约在最佳。

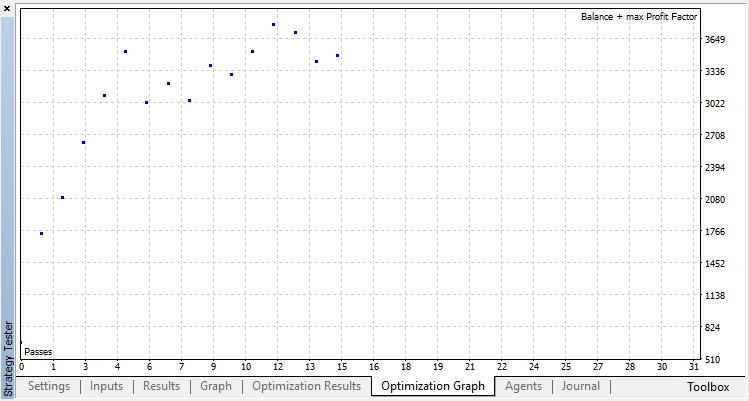
代理运行的最终结果:

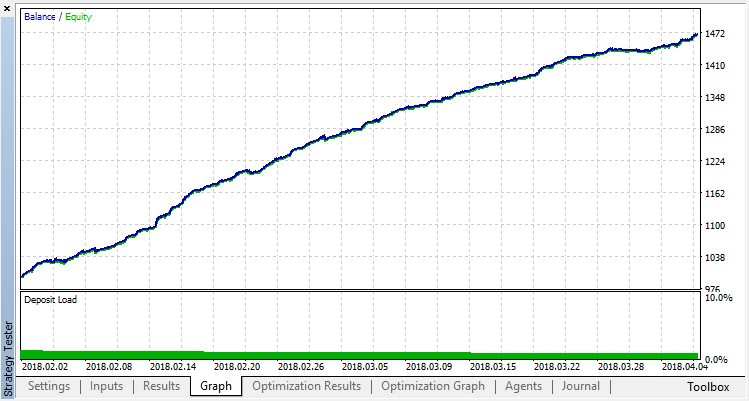
在训练范围以外的样品上检查系统操作的结果. 该模型有很严重的过度拟合:

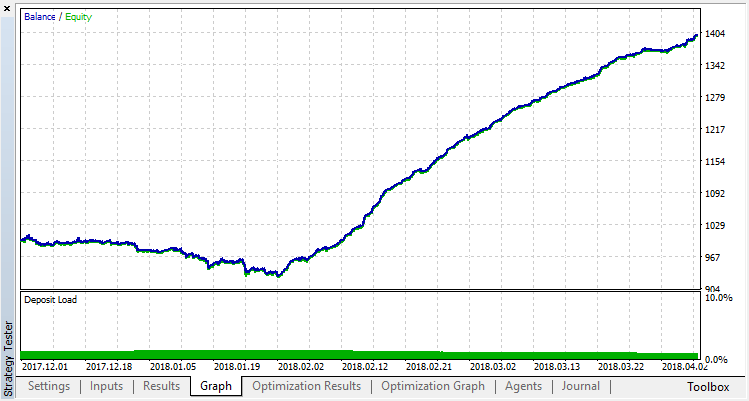
让我们尝试去除过度拟合。将参数 r（正则化）设置为0.25：仅25%的样本将用于训练。使用相同的训练范围.

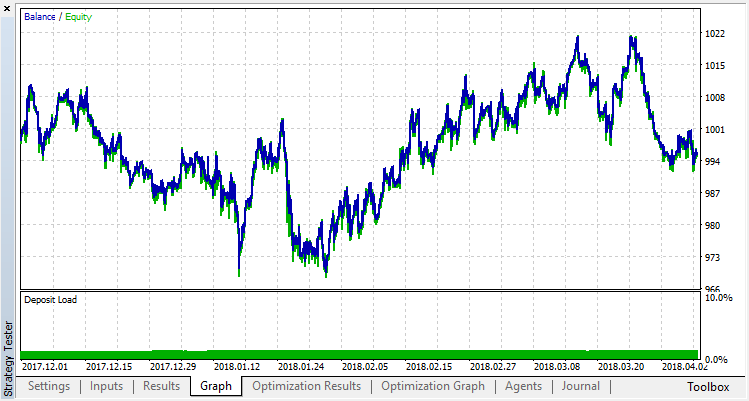
该模型学习得更差（添加了更多的噪声），但是不可能摆脱全局过拟合。这种正则化方法显然只适用于规则不随时间变化的平稳过程。另一个明显的负因素是模型的输入处的3个振荡器，此外，它们相互关联。

文章的总结

目标是展示使用随机森林来近似函数的功能，在本例中，指标函数值是买入或者卖出信号。另外，探讨了两种有监督的学习 - 分类和回归。非标准的方法被应用到学习与先前未知的训练实例，在优化过程中自动选择。一般来说，该过程类似于在测试器（云）中的常规优化，该算法仅在几次迭代中收敛，并且不需要担心优化参数的数目。这就是所应用方法的一个明显优点。该模型的缺点是在不正确地选择策略时过度拟合的趋势，这相当于参数的过度优化。 

按照传统，我将给出改进策略的可能方法（毕竟，目前的实施只是一个粗略的框架）。

• 增加优化参数的数目（多个隶属函数的优化）。
• 添加各种重要的预测因子。
• 采用不同的奖励方法。
• 创建几个竞争对手来增加变体的空间。

自主学习 EA 交易的源代码附加在下面了。

为了使 EA 交易可以正确编译和工作，需要下载 MT4Orders 开发库和更新过的 Fuzzy 开发库。