
CatBoostアルゴリズムを使用した外国為替市場の季節によるパターンの特定
はじめに
季節ごとのパターンの検索に関する記事はすでに他に2つ公開されています(1、2)。機械学習アルゴリズムがパターン検索タスクにどのように対処できるのか疑問に思いました。前述の記事の取引システムは、統計分析に基づいて構築されています。人的要因はモデルに特定の曜日の特定の時間に取引するように指示するだけで排除できるようになっています。パターン検索は、別のアルゴリズムで提供できます。
時間フィルタリング機能
フィルタ機能を追加することで、ライブラリを簡単に拡張できます。
def time_filter(data, count): # filter by hour hours=[15] if data.index[count].hour not in hours: return False # filter by day of week days = [1] if data.index[count].dayofweek not in days: return False return True
この関数は、内部で指定された条件を確認します。他の追加条件(時間フィルタだけでなく)も実装できますが、本稿では季節によるパターンに焦点を当てているため、時間フィルタのみを使用します。すべての条件が満たされると、関数はTrueを返し、適切なサンプルが訓練セットに追加されます。例えば、この特定の場合、火曜日の15:00にのみ取引を開始するようにモデルに指示します。「時間」リストと「日」リストには、他の時間と日を含めることができます。すべての条件をコメントアウトすることで、前の記事のように、条件なしでアルゴリズムを機能させることができます。
add_labels関数は、この条件を入力として受け取るようになりました。Pythonでは、関数は第1レベルのオブジェクトであるため、他の関数に引数として安全に渡すことができます。
def add_labels(dataset, min, max, filter=time_filter): labels = [] for i in range(dataset.shape[0]-max): rand = random.randint(min, max) curr_pr = dataset['close'][i] future_pr = dataset['close'][i + rand] if filter(dataset, i): if future_pr + MARKUP < curr_pr: labels.append(1.0) elif future_pr - MARKUP > curr_pr: labels.append(0.0) else: labels.append(2.0) else: labels.append(2.0) dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop( dataset[dataset.labels == 2].index) return dataset
フィルタが関数に渡されたらすぐに、それを使用して購入または販売取引を指定できます。フィルタは、元のデータセットと現在のバーのインデックスを受け取ります。データセット内のインデックスは、時刻を含む「datetimeindex」として表されます。フィルタは、データフレームの「日時インデックス」でi番目の数値で時間と曜日を検索し、何も見つからない場合はFalseを返します。条件が満たされた場合、取引は1または0として指定され、それ以外の場合は2として指定されます。最後に、2はすべてトレーニングデータセットから削除されるため、フィルタによって決定された特定の曜日と時間の例のみが残ります。
特定の時間に(またはこのフィルタによって設定された他の条件に従って)取引開始を可能にするために、フィルタもカスタムテスターに追加する必要があります。
def tester(dataset, markup=0.0, plot=False, filter=time_filter): last_deal = int(2) last_price = 0.0 report = [0.0] for i in range(dataset.shape[0]): pred = dataset['labels'][i] ind = dataset.index[i].hour if last_deal == 2 and filter(dataset, i): last_price = dataset['close'][i] last_deal = 0 if pred <= 0.5 else 1 continue if last_deal == 0 and pred > 0.5: last_deal = 2 report.append(report[-1] - markup + (dataset['close'][i] - last_price)) continue if last_deal == 1 and pred < 0.5: last_deal = 2 report.append(report[-1] - markup + (last_price - dataset['close'][i])) y = np.array(report).reshape(-1, 1) X = np.arange(len(report)).reshape(-1, 1) lr = LinearRegression() lr.fit(X, y) l = lr.coef_ if l >= 0: l = 1 else: l = -1 if(plot): plt.plot(report) plt.plot(lr.predict(X)) plt.title("Strategy performance") plt.xlabel("the number of trades") plt.ylabel("cumulative profit in pips") plt.show() return lr.score(X, y) * l
これは次のように実装されます。数字「2」は、ポジションがない場合に使用されます(last_deal = 2)。テストを開始する前にはポジションがないため、2を設定します。データセット全体を反復処理し、フィルタ条件が満たされているかどうかを確認します。条件が満たされている場合は、買い取引または売り取引を開きます。別の時間または曜日に決済される可能性があるため、フィルタ条件は取引の決済には適用されません。これらの変更は、さらに正しい訓練とテストを行うのに十分です。
各取引時間の探索的分析
個々の条件ごとに(および時間または日の組み合わせで)モデルを手動でテストするのはあまり便利ではありません。この目的のために特別な関数が作成されており、各条件の要約統計量を個別に高速に取得できます。関数の完了には時間がかかる場合がありますが、モデルのパフォーマンスが向上する時間範囲が出力されます。
def exploratory_analysis(): h = [x for x in range(24)] result = pd.DataFrame() for _h in h: global hours hours = [_h] pr = get_prices(START_DATE, STOP_DATE) pr = add_labels(pr, min=15, max=15, filter=time_filter) gmm = mixture.GaussianMixture( n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) # iterative learning res = [] iterations = 10 for i in range(iterations): res.append(brute_force(10000, gmm)) print('Iteration: ', i, 'R^2: ', res[-1][0], ' hour= ', _h) r = pd.DataFrame(np.array(res)[:, 0], np.full(iterations,_h)) result = result.append(r) plt.scatter(result.index, result, c = result.index) plt.show() return result
確認する時間のリストを関数で設定できます。私の例では、24時間すべてが設定されています。実験を純粋にするために、「min」と「max」(ポジションの最小および最大の地平線)を15に設定して、サンプリングを無効にしました。「iterations」変数は、1時間ごとの再訓練サイクルの数を担当します。このパラメータを増やすと、より信頼性の高い統計を取得できます。操作が完了すると、関数は次のグラフを表示します。
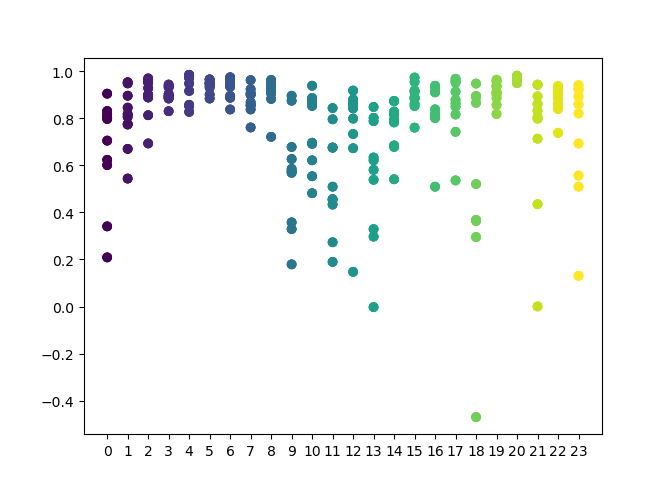
X軸は、時間の序数を示します。Y軸は、各反復の決定係数を表します(10回の反復が使用され、これは1時間ごとのモデルの再訓練を意味します)。ご覧のとおり、4時間、5時間、6時間のパスはより近くに配置されているため、見つかったパターンの品質に対する信頼が高まります。選択の原則は単純です。ポイントの位置と密度が高いほど、モデルは優れています。例えば、9〜15の間隔では、グラフはポイントの大きな分散を示し、モデルの平均品質は0.6に低下します。さらに希望の時間を選択し、モデルを再訓練して、カスタムテスターでその結果を表示できます。
選択したモデルのテスト
探索的分析は、GBPUSD通貨ペアで次のパラメータを使用して実行されました。
SYMBOL = 'GBPUSD' MARKUP = 0.00010 TIMEFRAME = mt5.TIMEFRAME_H1 START_DATE = datetime(2017, 1, 1) TSTART_DATE = datetime(2015, 1, 1) FULL_DATE = datetime(2015, 1, 1) STOP_DATE = datetime(2021, 1, 1)
テストには同じパラメータが使用されます。信頼性を高めるために、FULL_DATE値を変更して、以前の履歴データでモデルがどのように実行されたかを表示できます。
3、4、5、6時間のクラスターを視覚的に区別できます。隣接する時間は同様のパターンを持っていると想定できるため、この時間すべてにわたってモデルを訓練できます。
hours = [3,4,5,6] # make dataset pr = get_prices(START_DATE, STOP_DATE) pr = add_labels(pr, min=15, max=15, filter=time_filter) tester(pr, MARKUP, plot=True, filter=time_filter) # perform GMM clasterizatin over dataset # gmm = mixture.BayesianGaussianMixture(n_components=n_compnents, covariance_type='full').fit(X) gmm = mixture.GaussianMixture( n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) # iterative learning res = [] for i in range(10): res.append(brute_force(10000, gmm)) print('Iteration: ', i, 'R^2: ', res[-1][0]) # test best model res.sort() test_model(res[-1])
残りのコードについては、以前の記事で詳細に説明されているためさらなる説明は必要ありません。唯一の例外は、単純なGMMの代わりにコメント化されているベイズモデルを使用できることですが、これは実験的なアイデアにすぎません。
取引サンプリング後の理想的なモデルは次のようになります。
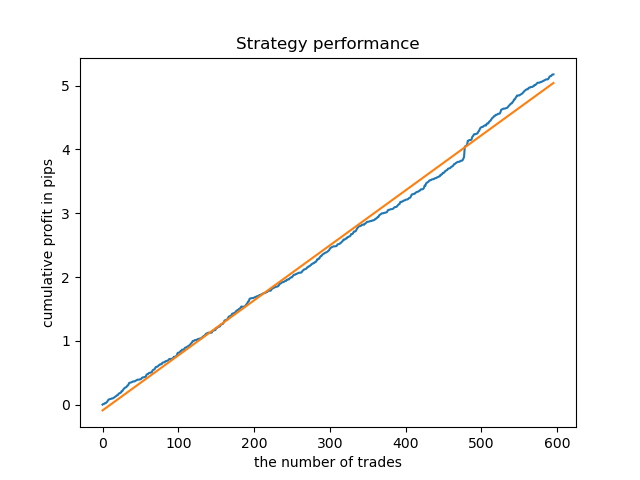
訓練済みモデル(テストデータを含む)は、次のパフォーマンスを示します。
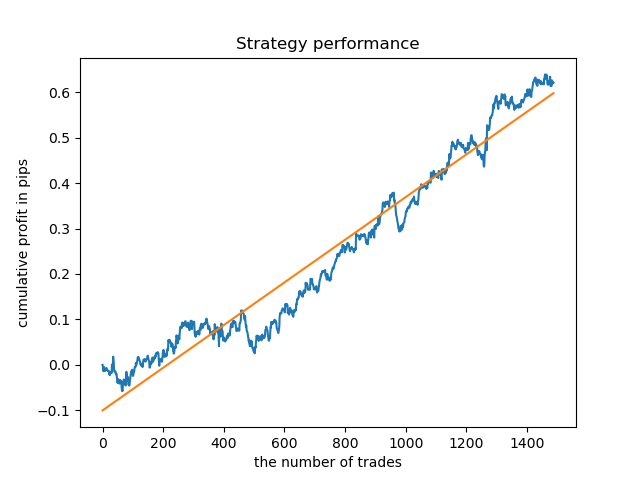
別々のモデルを高密度の時間に訓練できます。以下は、5時間目と20時間目の訓練済みモデルのバランスグラフです。
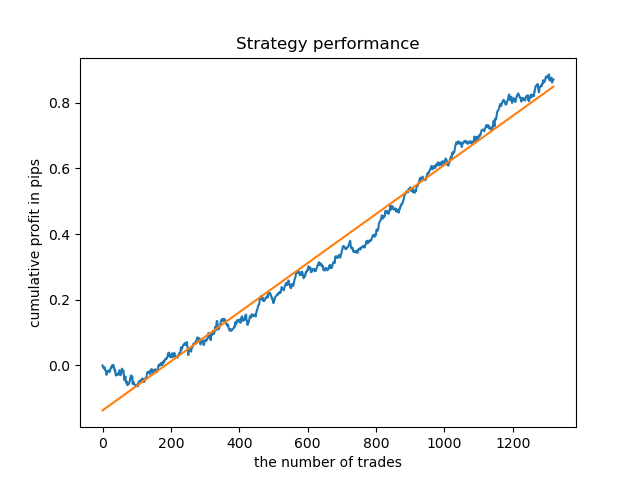
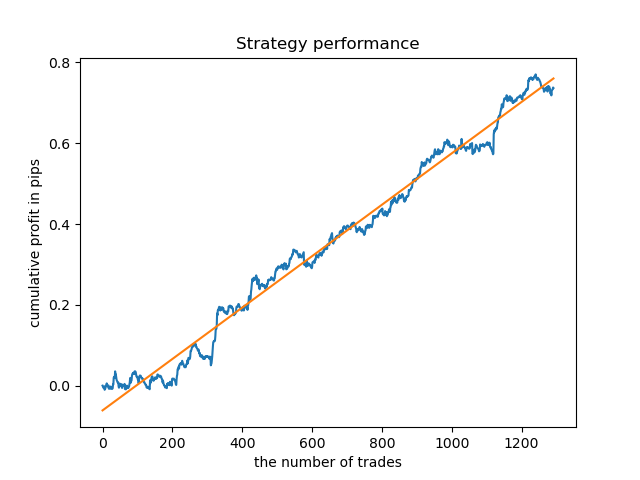
ここで、比較のために、分散が大きい時間で訓練されたモデルを見ることができます。例えば、9時間目と11時間目です。
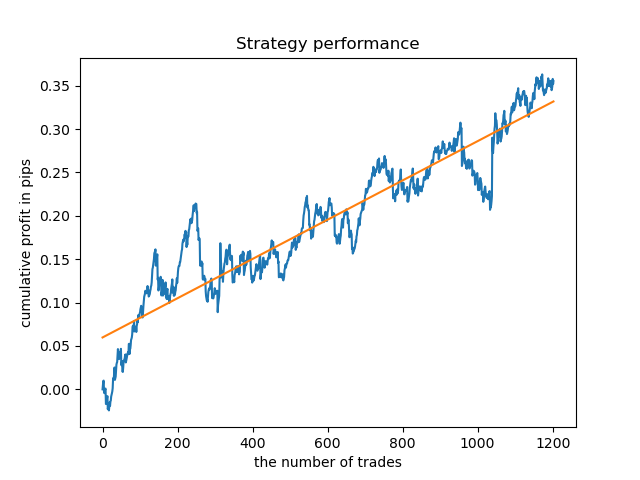

ここでのバランスグラフは、どんなコメントよりも多くを示しています。明らかに、モデルを訓練するときは、タイミングに特別な注意を払う必要があります。
各取引日の探索的分析
フィルタは、例えば曜日など、他の時間間隔に合わせて簡単に変更できます。時間を曜日に置き換えるだけです。
def time_filter(data, count): # filter by day of week global hours if data.index[count].dayofweek not in hours: return False return True
この場合、反復は0から5の範囲で実行する必要があります(土曜日である5番目の序数を除く)。
def exploratory_analysis():
h = [x for x in range(5)]
次に、GBPUSD通貨ペアの探索的分析を実行します。取引の頻度、またはその期間は同じです(15バー)。
pr = add_labels(pr, min=15, max=15, filter=time_filter) 訓練プロセスはコンソールに表示され、現在の期間の決定係数を即座に表示できます。「hour」変数には、時間番号ではなく、曜日の序数が含まれるようになりました。
Iteration: 0 R^2: 0.5297625368835237 hour= 0 Iteration: 1 R^2: 0.8166096906047893 hour= 0 Iteration: 2 R^2: 0.9357674260125702 hour= 0 Iteration: 3 R^2: 0.8913802241811986 hour= 0 Iteration: 4 R^2: 0.8079720208707672 hour= 0 Iteration: 5 R^2: 0.8505663844866759 hour= 0 Iteration: 6 R^2: 0.2736870273207084 hour= 0 Iteration: 7 R^2: 0.9282442121644887 hour= 0 Iteration: 8 R^2: 0.8769775718602929 hour= 0 Iteration: 9 R^2: 0.7046666925774866 hour= 0 Iteration: 0 R^2: 0.7492883761480897 hour= 1 Iteration: 1 R^2: 0.6101962958733655 hour= 1 Iteration: 2 R^2: 0.6877652983219245 hour= 1 Iteration: 3 R^2: 0.8579669286548137 hour= 1 Iteration: 4 R^2: 0.3822441930760343 hour= 1 Iteration: 5 R^2: 0.5207801806491617 hour= 1 Iteration: 6 R^2: 0.6893157850263495 hour= 1 Iteration: 7 R^2: 0.5799059801202937 hour= 1 Iteration: 8 R^2: 0.8228326786957887 hour= 1 Iteration: 9 R^2: 0.8742262956151615 hour= 1 Iteration: 0 R^2: 0.9257707800422799 hour= 2 Iteration: 1 R^2: 0.9413981795880517 hour= 2 Iteration: 2 R^2: 0.9354221623113591 hour= 2 Iteration: 3 R^2: 0.8370429185837882 hour= 2 Iteration: 4 R^2: 0.9142875737195697 hour= 2 Iteration: 5 R^2: 0.9586871067966855 hour= 2 Iteration: 6 R^2: 0.8209392060391961 hour= 2 Iteration: 7 R^2: 0.9457287035542066 hour= 2 Iteration: 8 R^2: 0.9587372191281025 hour= 2 Iteration: 9 R^2: 0.9269140213952402 hour= 2 Iteration: 0 R^2: 0.9001009579436263 hour= 3 Iteration: 1 R^2: 0.8735623527502183 hour= 3 Iteration: 2 R^2: 0.9460714774572146 hour= 3 Iteration: 3 R^2: 0.7221720163838841 hour= 3 Iteration: 4 R^2: 0.9063579778744433 hour= 3 Iteration: 5 R^2: 0.9695391076372475 hour= 3 Iteration: 6 R^2: 0.9297881558889788 hour= 3 Iteration: 7 R^2: 0.9271590681844957 hour= 3 Iteration: 8 R^2: 0.8817985496711311 hour= 3 Iteration: 9 R^2: 0.915205007218742 hour= 3 Iteration: 0 R^2: 0.9378516360378022 hour= 4 Iteration: 1 R^2: 0.9210968481902528 hour= 4 Iteration: 2 R^2: 0.9072205941748894 hour= 4 Iteration: 3 R^2: 0.9408826184927528 hour= 4 Iteration: 4 R^2: 0.9671981453714584 hour= 4 Iteration: 5 R^2: 0.9625144032389237 hour= 4 Iteration: 6 R^2: 0.9759244293257822 hour= 4 Iteration: 7 R^2: 0.9461473783201281 hour= 4 Iteration: 8 R^2: 0.9190627222826241 hour= 4 Iteration: 9 R^2: 0.9130350931314233 hour= 4
すべてのモデルは2017年の初めからのデータを使用して訓練されましたが決定係数にはテスト期間も含まれていることに注意してください(2015年からの追加データ)。毎日一貫して推定値が高いため、さらに信頼性が高まります。最終結果を見てみましょう。
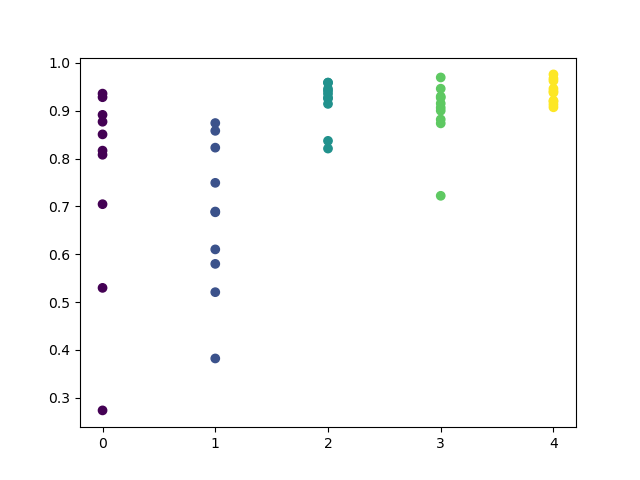
探索的分析によると、水曜日と金曜日が取引に最も適した日であり、特に金曜日です。取引の最悪の日は火曜日です。これは、エラーの分散が大きく、平均値が低いためです。金曜日にのみ取引するようにモデルを訓練でして、結果を確認しましょう。
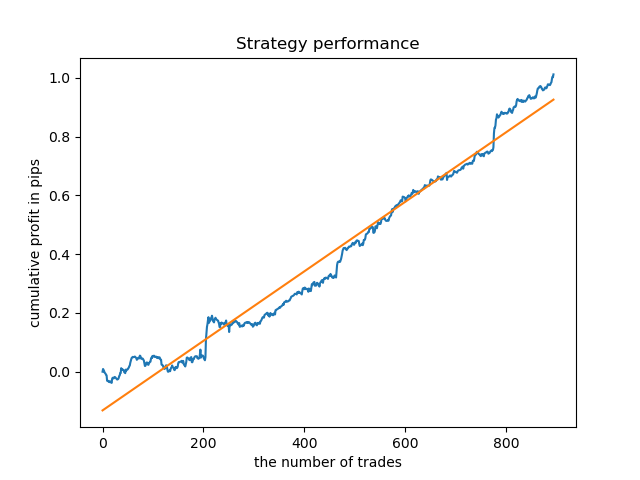
同様に、火曜日に取引されるモデルを取得できます。
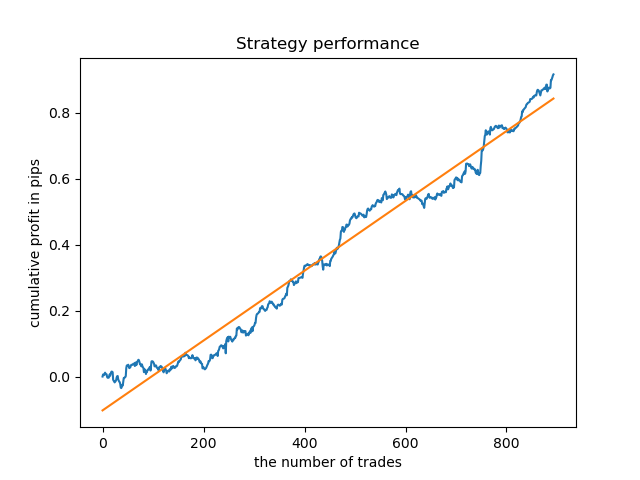
取引の固定期間が常に適切であるとは限らないため、検索ウィンドウを拡大して、探索的分析の反復回数を20回に増やしてみましょう。
pr = add_labels(pr, min=5, max=25, filter=time_filter) gmm = mixture.GaussianMixture( n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) # iterative learning res = [] iterations = 20
値の範囲が広くなり、取引に最適な日は木曜日と金曜日です。
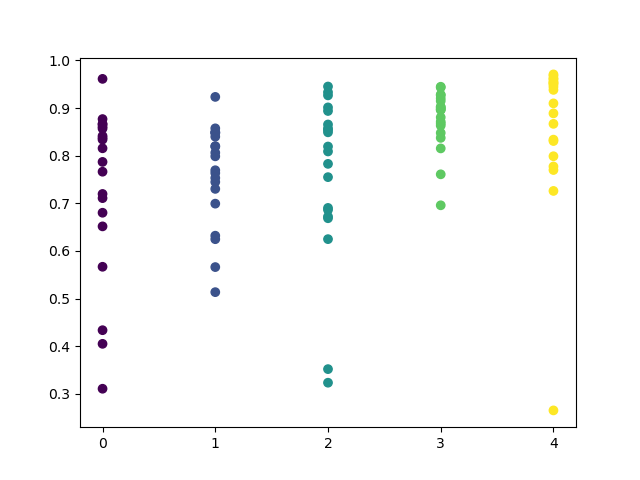
結果を確認するために、木曜日の制御モデルを訓練してみましょう。これは、学習サイクルがどのように見えるかです(以前の記事を読んでいない人のために)。
hours = [3]
# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=5, max=25, filter=time_filter)
tester(pr, MARKUP, plot=True, filter=time_filter)
# perform GMM clasterizatin over dataset
# gmm = mixture.BayesianGaussianMixture(n_components=n_compnents, covariance_type='full').fit(X)
gmm = mixture.GaussianMixture(
n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])
# iterative learning
res = []
for i in range(10):
res.append(brute_force(10000, gmm))
print('Iteration: ', i, 'R^2: ', res[-1][0])
# test best model
res.sort()
test_model(res[-1])
結果は、取引の有効期間が固定されている場合よりもわずかに悪くなります。
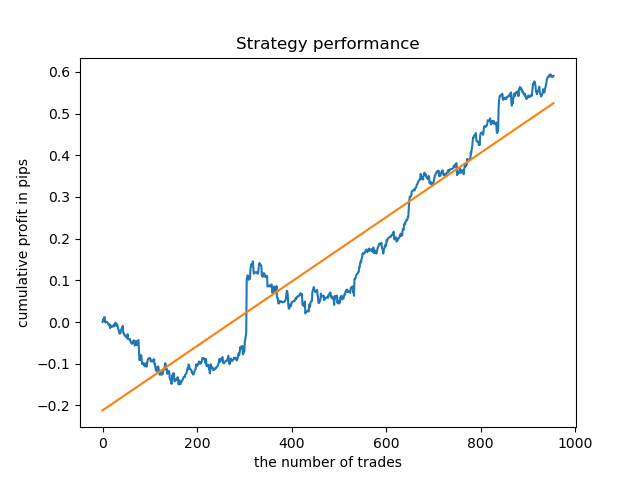
明らかに、特定の期間の頻度(地平線)パラメータは重要です。次に、これらの値を繰り返し処理して、結果にどのように影響するかを確認します。
モデルの品質に対する取引期間の影響の評価
選択した基準(フィルタ)の探索的分析関数と同様に、取引の存続期間に応じてモデルのパフォーマンスを評価する補助関数を作成できます。1〜50バー(またはその他の期間)の間隔で固定取引期間を設定できるとすると、関数は次のようになります。
def deals_frequency_analyzer(): freq = [x for x in range(1, 50)] result = pd.DataFrame() for _h in freq: pr = get_prices(START_DATE, STOP_DATE) pr = add_labels(pr, min=_h, max=_h, filter=time_filter) gmm = mixture.GaussianMixture( n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) # iterative learning res = [] iterations = 5 for i in range(iterations): res.append(brute_force(10000, gmm)) print('Iteration: ', i, 'R^2: ', res[-1][0], ' deal lifetime = ', _h) r = pd.DataFrame(np.array(res)[:, 0], np.full(iterations,_h)) result = result.append(r) plt.scatter(result.index, result, c = result.index) plt.xticks(np.arange(0, len(freq)+1, 1)) plt.title("Performance by deals lifetime") plt.xlabel("deals frequency") plt.ylabel("R^2 estimation") plt.show() return result
「freq」リストには、反復する取引の有効期間の値が含まれています。この反復は、GBPUSDペアの5時間目に実行しました。これが結果です。
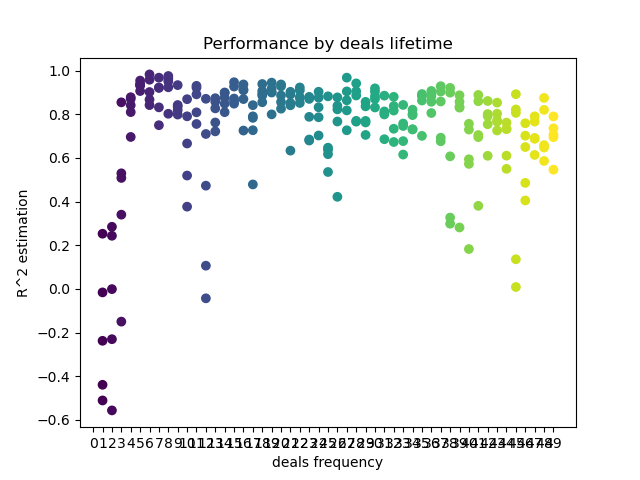
X軸は、取引頻度、つまりその存続期間をバーで示します。Y軸は、各パスの決定係数を表します。ご覧のとおり、0〜5バーの取引は短すぎてモデルのパフォーマンスに悪影響を及ぼしますが、15〜23の寿命が最適です。より長い取引(30バー以上)は結果を悪化させます。取引期間が6〜9バーの小さなクラスターがあり、スコアが最も高くなっています。これらのライフタイム値を使用してモデルを取引し、その結果を他のクラスターと比較してみましょう。
2013年からモデルがテストされた8バーの寿命を選択しました。しかし、バランス曲線は私が望むほど均一ではありません。
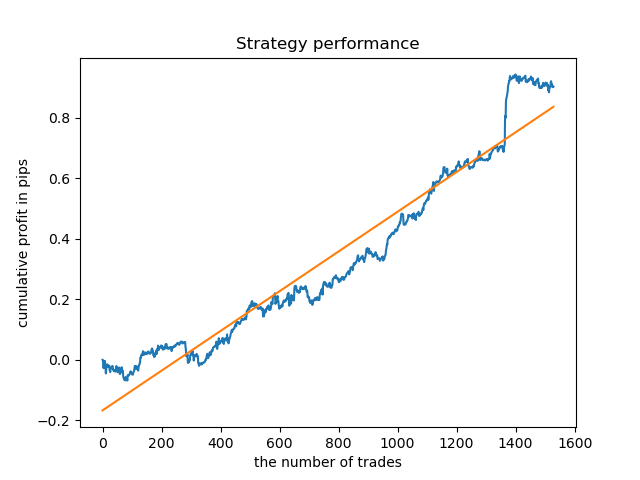
密度が最も高いクラスターの存続期間中、グラフは2015年以降非常に良好に見えますが、モデルは以前の履歴間隔ではパフォーマンスが低下します。
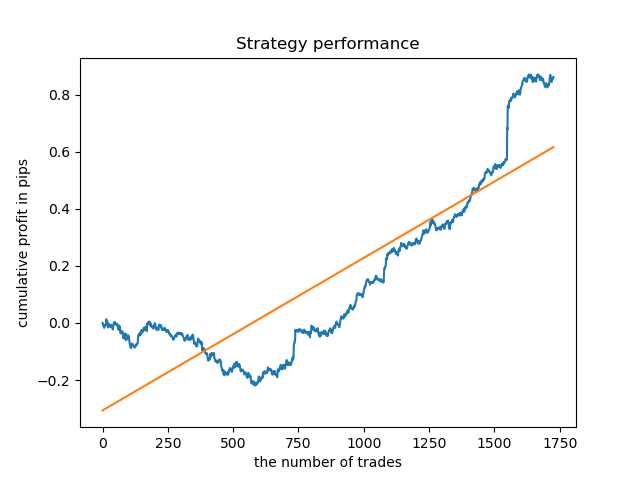
最後に、最適なクラスター15〜23の範囲を選択し、モデルを数回再訓練しました(取引ライフタイムのサンプリングはランダムであるため)。
pr = add_labels(pr, min=15, max=23, filter=time_filter)
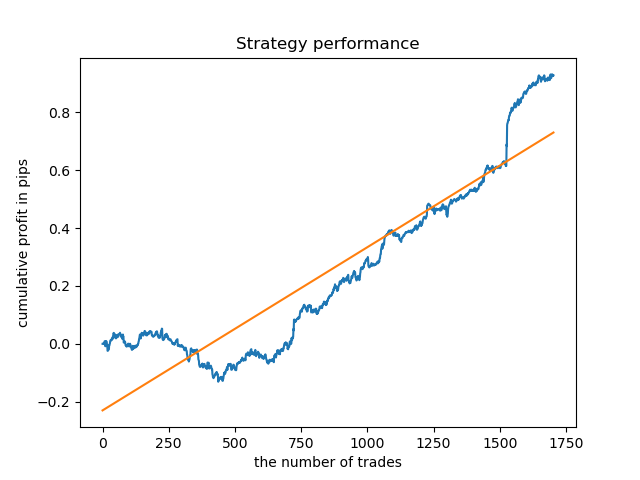
このようなパターンに基づくモデルでは、2015年以前のデータの存続可能性は示されていません。おそらく、市場構造にいくつかの重要な変化があったのでしょう。この状況を分析するには、別の大きな研究が必要です。モデルが選択され、その安定性が特定の時間間隔で証明された後、テストサンプルを含むこの間隔全体で取引を実行できます。その後、このモデルを本番環境に送信できます。
より長い履歴でのテスト
より長い履歴でモデルをチェックするとどうなるでしょうか。モデルは2000年以降のデータで訓練され、1990年以降のデータを使用してテストされました。バランス曲線からわかるように、このような長い履歴期間ではパターンのキャプチャが不十分ですが、結果は依然として良好です。
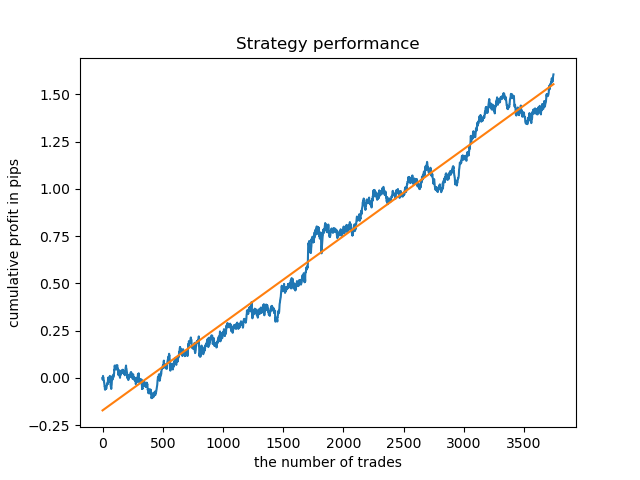
終わりに
本稿では、季節的なパターンを見つけて取引システムを作成するための強力なツールについて説明しています。さまざまな商品(FOREX以外)、さまざまな時間枠、さまざまなフィルタ(時間フィルタだけでなく)での分析が可能です。このアプローチの適用範囲は非常に広いです。その機能を完全に明らかにするには、さまざまなフィルタを使用した複数のテストが必要になります。分析を行った後、前の記事で説明したモデルエクスポート機能を使用して自動売買ロボットを構築できます。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/8863
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 パターン検索への総当たり攻撃アプローチ(第III部): 新しい水平線
パターン検索への総当たり攻撃アプローチ(第III部): 新しい水平線
 市場とそのグローバルパターンの物理学
市場とそのグローバルパターンの物理学
 自己適応アルゴリズムの開発(第II部): 効率の向上
自己適応アルゴリズムの開発(第II部): 効率の向上
 自己適応アルゴリズムの開発(第I部):基本的なパターンの検索
自己適応アルゴリズムの開発(第I部):基本的なパターンの検索
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
このモデルのEAをタイミング付きで公開してもらえますか?
答えは2番目の記事と同じですが、ターミナルに時間による取引開始の制限を追加する必要があります。
曜日や 異なる組み合わせでも同じです。また、MT5では時間のカウントダウンは右に1つずれます。つまり、パイソンで4時間目なら、MTでは5時間目です。
答えは2番目の記事と同じですが、ターミナルに時間による取引開始の制限を追加する必要があります。
曜日や 異なる組み合わせでも同じです。また、MT5では、時間のカウントダウンは右に1つずれます。つまり、Pythonで4時間目なら、MTでは5時間目です。
ありがとうございます。
興味深い身近な話題です。
標準的なMT5テスターの最終的なエクイティを、あなたが選んだFORTS商品で、この方法を適用することによって得られるエクイティを見てみたいと思います。
フィードバックとして、選択した商品における私の季節的アルゴリズムのエクイティを掲載する用意があります。)