
Métodos de otimização da biblioteca Alglib (Parte II)
Conteúdo
- Introdução
- Métodos de otimização da biblioteca ALGLIB:
- BC (Otimização com restrições do tipo caixa)
- NLC (Otimização não linear com restrições utilizando o algoritmo de Lagrange)
- LM (Método de Levenberg-Marquardt)
- Tabela de funções utilizadas nos métodos ALGLIB
- Testes dos métodos
Introdução
Na primeira parte do nosso estudo sobre os algoritmos de otimização da biblioteca ALGLIB incluídos na versão padrão do terminal MetaTrader 5, exploramos em detalhes os algoritmos: BLEIC (restrições lineares de igualdade/desigualdade e limites), L-BFGS (Broyden–Fletcher–Goldfarb–Shanno com memória limitada) e NS (Otimização não suave e não convexa com restrições do tipo caixa, lineares ou não lineares – Restrições não suaves). Não apenas discutimos suas bases teóricas, mas também explicamos uma forma simples de aplicá-los em problemas de otimização.
Neste artigo, daremos continuidade à análise dos métodos restantes do arsenal ALGLIB. A atenção estará voltada principalmente aos testes em funções complexas e multidimensionais, o que nos permitirá formar uma visão completa da eficácia de cada método. Ao final, faremos uma análise abrangente dos resultados obtidos e apresentaremos recomendações práticas para a escolha do algoritmo mais adequado para cada tipo específico de tarefa.
BC (Otimização com restrições do tipo caixa)
A otimização com restrições do tipo caixa é um procedimento que minimiza a função F(x) com N variáveis, considerando restrições do tipo caixa (algumas dessas restrições, na prática, atuam como igualdades). Embora use um algoritmo semelhante ao BLEIC (otimizador com restrições lineares), esse otimizador permite o uso de estratégias mais rápidas de ativação das restrições, pois trabalha apenas com restrições do tipo caixa. Em problemas de grande escala, com várias restrições ativas na solução, esse otimizador pode ser mais rápido que o BLEIC.
Vamos explicar de forma mais simples o que é otimização com restrições do tipo caixa. É um algoritmo de otimização que busca a melhor solução dentro de limites definidos para cada variável – ou seja, cada variável deve permanecer dentro de um intervalo específico – e, basicamente, tenta encontrar o mínimo da função com todas as variáveis respeitando esses intervalos. A principal característica do algoritmo é que ele se parece com o BLEIC, mas é mais rápido, pois foi especialmente otimizado para lidar com restrições do tipo intervalo.
Requisitos: o ponto inicial deve ser viável ou próximo da região viável, e a função deve estar definida em toda a região viável.
Para utilizar o método BC e outros da biblioteca ALGLIB, será necessário incluir o arquivo (a biblioteca já vem com o terminal MetaTrader 5, o usuário não precisa instalar nada adicionalmente).
#include <Math\Alglib\alglib.mqh> Vamos escrever um script para trabalhar de forma eficiente com os métodos da ALGLIB. Não precisamos destacar os passos principais característicos do uso desses métodos, marcando com cores os blocos de código idênticos.
1. Definimos as condições de contorno do problema, como o número de execuções da função de avaliação (função objetivo), os intervalos dos parâmetros a serem otimizados e seu passo. Para os métodos da ALGLIB, é necessário atribuir valores iniciais aos parâmetros "x" que serão otimizados (os métodos são determinísticos e os resultados dependem totalmente dos valores iniciais, por isso usaremos geração de números aleatórios dentro dos intervalos definidos), além do escalonamento "s" (os métodos são sensíveis à escala relativa dos parâmetros, então, neste caso, definimos o escalonamento como "1").
2. Declaramos os objetos necessários para a execução do algoritmo.
3. Definimos os parâmetros externos do algoritmo (as configurações).
4. Realizamos a inicialização do algoritmo, informando os intervalos e passos dos parâmetros a serem otimizados, bem como os parâmetros externos do algoritmo.
5. Executamos a otimização.
6. Obtemos os resultados da otimização para uso posterior.
É importante considerar um aspecto: o usuário não pode interferir no processo de otimização nem interrompê-lo a qualquer momento. O método executa todas as operações de forma autônoma, chamando a função de avaliação dentro do seu próprio processo. Embora o algoritmo leve em consideração o parâmetro definido pelo usuário, ele pode chamar a função de avaliação um número arbitrário de vezes. O usuário pode controlar o número máximo de chamadas permitidas ao repassar ao método um comando de parada.
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Initialization of optimization parameters--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; // Create and initialize arrays for range bounds--------------------- CRowDouble rangeMin, rangeMax; rangeMin.Resize (params); rangeMax.Resize (params); double rangeStep; for (int i = 0; i < params; i++) { rangeMin.Set (i, -10); rangeMax.Set (i, 10); } rangeStep = DBL_EPSILON; CRowDouble x; x.Resize (params); CRowDouble s; s.Resize (params); s.Fill (1); // Generate random initial parameter values in given ranges---- for (int i = 0; i < params; i++) { x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0)); } // Create objects for optimization------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinBCReport rep; // Set the parameters of the BC optimization algorithm------------------------------ double diffStep = 0.00001; double epsg = 1e-16; double epsf = 1e-16; CAlglib::MinBCCreateF (x, diffStep, fFunc.state); CAlglib::MinBCSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinBCSetScale (fFunc.state, s); CAlglib::MinBCSetCond (fFunc.state, epsg, epsf, rangeStep, numbTestFuncRuns); CAlglib::MinBCOptimize (fFunc.state, fFunc, frep, obj); CAlglib::MinBCResults (fFunc.state, x, rep); // Output of optimization results----------------------------------------------- Print ("BC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
Como o método faz chamadas à função de avaliação diretamente (e não por meio do programa do usuário), será necessário encapsular essa função em uma classe que herda de uma classe base da ALGLIB (essas classes base variam de acordo com os métodos). Obtemos a classe encapsuladora como "C_OptimizedFunction" e definir nela os seguintes métodos:
1. Func() — é um método virtual que deve ser sobrescrito nas classes derivadas.2. Init() — inicializa os parâmetros da classe. Dentro do método:
- São inicializadas variáveis relacionadas à contagem de execuções e ao melhor valor encontrado da função.
- São reservados os arrays "c" e "cB" para armazenar coordenadas.
Variáveis:
- state — objeto do tipo CMinBCState, específico do método BC, utilizado na chamada dos métodos estáticos do algoritmo e no acionamento do método de parada.
- numberLaunches — número atual de execuções (necessário para evitar que a função de avaliação execute por tempo indefinido ou de forma descontrolada).
- maxNumbLaunchesAllowed — número máximo permitido de execuções.
- fB — melhor valor encontrado da função de avaliação.
- c[] — array com as coordenadas atuais.
- cB[] — array para armazenar as melhores coordenadas encontradas durante a busca.
//—————————————————————————————————————————————————————————————————————————————— // Class for function optimization, inherits from CNDimensional_Func class C_OptimizedFunction : public CNDimensional_Func { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // A virtual function to contain the function being optimized-------- virtual void Func (CRowDouble &x, double &func, CObject &obj); // Initialization of optimization parameters--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinBCState state; // State int numberLaunches; // Launch counter double fB; // Best found value of the objective function (maximum) double cB []; // Coordinates of the point with the best function value private: //------------------------------------------------------------------- double c []; // Array for storing current coordinates int maxNumbLaunchesAllowed; // Maximum number of function calls allowed }; //——————————————————————————————————————————————————————————————————————————————
O método "Func" da classe "C_OptimizedFunction" é responsável por chamar a função de avaliação definida pelo usuário. Ele recebe como argumentos o vetor "x" (uma das configurações de parâmetros sugerida pelo método de otimização), o argumento "func", no qual o valor calculado da função de avaliação deve ser retornado, e o objeto "obj", cuja finalidade exata não está clara, mas que possivelmente é reservado para a passagem de informações adicionais para/dentro do método. As etapas principais da execução do método são:
- O contador "numberLaunches" é incrementado, controlando o número de vezes que o método "Func" foi chamado.
- Se o número de execuções ultrapassar o valor máximo permitido "maxNumbLaunchesAllowed", o valor de "func" é definido como "DBL_MAX" (o maior valor do tipo "double"; como os métodos ALGLIB minimizam funções, esse valor representa a pior solução possível). Em seguida, a função "MinBCRequestTermination" é chamada para sinalizar ao método BC que o processo de otimização deve ser interrompido.
- Em um laço, os valores do vetor "x" são copiados para o array "c". Isso é necessário para que esses valores possam ser usados ao chamar a função de avaliação do usuário.
- A função "ObjectiveFunction" é chamada para calcular o valor da função objetivo com base nos valores atuais armazenados no array "c". O resultado é guardado na variável "ffVal", e o valor de "func" é definido como o valor negativo de "ffVal" (estamos otimizando um paraboloide invertido que deve ser maximizado, e como o BC minimiza, invertemos o sinal).
- Se o valor atual de "ffVal" for maior do que o melhor valor anterior "fB", então "fB" é atualizado, e o array "cB" recebe uma cópia do estado atual de "c". Isso permite registrar o melhor valor encontrado da função objetivo com os parâmetros correspondentes e acessá-los posteriormente, se necessário.
A função "Func" executa a chamada da função de avaliação do usuário, rastreia o número de execuções e atualiza os melhores resultados encontrados. Ela também gerencia as condições de parada, caso o número de execuções ultrapasse o limite definido.
//—————————————————————————————————————————————————————————————————————————————— // Implementation of the function to be optimized void C_OptimizedFunction::Func (CRowDouble &x, double &func, CObject &obj) { // Increase the function launch counter and limitation control---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { func = DBL_MAX; CAlglib::MinBCRequestTermination (state); return; } // Copy input coordinates to internal array------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Calculate objective function value---------------------------------------- double ffVal = ObjectiveFunction (c); func = -ffVal; // Update the best solution found-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
Após executar o script de teste com o algoritmo BC para otimizar a função de um paraboloide, obtemos o seguinte resultado no print:
Infelizmente, apesar das tentativas de interromper a otimização utilizando o método "MinBCRequestTermination", o algoritmo continuou executando e tentou chamar a função de avaliação além do limite de 10.000 execuções.
Agora vamos deixar o BC sem restrições, permitindo que ele aja livremente. O resultado foi:
Como podemos ver, o BC consegue convergir totalmente na função do paraboloide, porém, nesse caso, não é possível estimar antecipadamente o número necessário de execuções da função objetivo.
No algoritmo, o passo de diferenciação é um fator importante. Por exemplo, se utilizarmos um passo muito pequeno, como 1e-16 em vez de 0.00001, o algoritmo é interrompido precocemente, ou seja, "empaca", e obtemos este resultado:
NLC (Otimização não linear com restrições utilizando o algoritmo de Lagrange aumentado com pré-condicionamento)
Esse algoritmo de otimização não linear com restrições permite minimizar uma função objetivo complexa F(x) com N variáveis, considerando ao mesmo tempo diferentes tipos de restrições: limites nas variáveis (min <= x <= max), desigualdades e igualdades lineares, igualdades não lineares G(x) = 0 e desigualdades não lineares H(x) <= 0.
Imagine que você tem um objetivo complexo que deseja atingir, mas há certas limitações que não podem ser violadas. Por exemplo, você quer maximizar o lucro das vendas, mas sem ultrapassar determinados custos fixos. O algoritmo da ALGLIB ajuda a resolver esse tipo de problema de otimização com restrições. Veja como ele funciona:
1. Você fornece ao algoritmo um ponto inicial — uma suposição de como alcançar esse objetivo. Esse ponto deve ser viável, ou seja, precisa obedecer a todas as restrições.
2. Em seguida, o algoritmo começa a se mover lentamente a partir desse ponto inicial, passo a passo se aproximando da solução ótima. Na cada passo, ele resolve um subproblema auxiliar para determinar em que direção deve seguir.
3. Para acelerar esse processo, o algoritmo utiliza uma técnica especial — o "pré-condicionamento". Isso significa que ele adapta seus "passos" à estrutura do problema para avançar de forma mais eficiente.
4. No final, após algumas iterações, o algoritmo encontra uma solução que minimiza sua função objetivo (por exemplo, minimiza os custos fixos) e ao mesmo tempo satisfaz todas as restrições.
O usuário pode escolher entre três solucionadores diferentes disponíveis na ALGLIB, adequados para problemas de diferentes tamanhos e complexidades:
SQP (programação quadrática sequencial) é recomendado para problemas de tamanho médio com funções objetivo difíceis.
AUL (método de Lagrange aumentado com pré-condicionamento) é recomendado para problemas de grande escala ou com funções objetivo baratas (rápidas de calcular).
SLP (programação linear sequencial) é mais lento, mas mais estável em casos difíceis.
Experimentos com funções de teste demonstraram a eficácia do solucionador AUL, enquanto os demais solucionadores estão comentados no código.
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Initialization of optimization parameters--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; // Create and initialize arrays for range bounds--------------------- CRowDouble rangeMin, rangeMax; rangeMin.Resize (params); rangeMax.Resize (params); double rangeStep; for (int i = 0; i < params; i++) { rangeMin.Set (i, -10); rangeMax.Set (i, 10); } rangeStep = DBL_EPSILON; CRowDouble x; x.Resize (params); CRowDouble s; s.Resize (params); s.Fill (1); // Generate random initial parameter values in given ranges---- for (int i = 0; i < params; i++) { x.Set (i, rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0)); } // Create objects for optimization------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinNLCReport rep; // Setting parameters of the NLC optimization algorithm----------------------------- double diffStep = 0.00001; double rho = 1000.0; int outerits = 5; CAlglib::MinNLCCreateF (x, diffStep, fFunc.state); CAlglib::MinNLCSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinNLCSetScale (fFunc.state, s); CAlglib::MinNLCSetCond (fFunc.state, rangeStep, numbTestFuncRuns); //CAlglib::MinNLCSetAlgoSQP (fFunc.state); CAlglib::MinNLCSetAlgoAUL (fFunc.state, rho, outerits); //CAlglib::MinNLCSetAlgoSLP (fFunc.state); CAlglib::MinNLCOptimize (fFunc.state, fFunc, frep, obj); CAlglib::MinNLCResults (fFunc.state, x, rep); // Output of optimization results----------------------------------------------- Print ("NLC, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
No NLC, o tipo da variável "state" é definido como "CMinNLCState".
//—————————————————————————————————————————————————————————————————————————————— // Class for function optimization, inherits from CNDimensional_FVec class C_OptimizedFunction : public CNDimensional_FVec { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // A virtual function to contain the function being optimized-------- virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj); // Initialization of optimization parameters--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinNLCState state; // State int numberLaunches; // Launch counter double fB; // Best found value of the objective function (maximum) double cB []; // Coordinates of the point with the best function value private: //------------------------------------------------------------------- double c []; // Array for storing current coordinates int maxNumbLaunchesAllowed; // Maximum number of function calls allowed }; //——————————————————————————————————————————————————————————————————————————————
A interrupção do processo de otimização é solicitada com o comando "MinNLCRequestTermination".
//—————————————————————————————————————————————————————————————————————————————— // Implementation of the function to be optimized void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj) { // Increase the function launch counter and limitation control---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { fi.Set (0, DBL_MAX); CAlglib::MinNLCRequestTermination (state); return; } // Copy input coordinates to internal array------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Calculate objective function value---------------------------------------- double ffVal = ObjectiveFunction (c); fi.Set (0, -ffVal); // Update the best solution found-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
Após executar o script de teste com o algoritmo NLC para otimizar a função do paraboloide, obtemos o seguinte resultado no print:
NLC, melhor resultado: 0.8858935739350294, número de execuções da função: 28007
Sem limitar o número de chamadas da função objetivo, o NLC consegue convergir totalmente, mas executa mais de um milhão de iterações:
NLC, melhor resultado: 1.0, número de execuções da função: 1092273
Usando um passo muito pequeno, como 1e-16, o algoritmo não para prematuramente como o método BC, mas apresenta um resultado ligeiramente inferior ao obtido com o passo 0.00001:
NLC, melhor resultado: 0.8543715192632731, número de execuções da função: 20005
LM (Método de Levenberg-Marquardt)
O método de Levenberg-Marquardt (LM) é um algoritmo de otimização amplamente utilizado para resolver problemas de mínimos quadrados não lineares. Esse método é eficaz em tarefas de ajuste de curvas e superfícies.
A ideia principal do LM combina duas técnicas de otimização: o método do gradiente descendente e o método de Gauss-Newton. Isso permite que o algoritmo se adapte à forma da função objetivo. O funcionamento é o seguinte:
- A cada iteração, o algoritmo calcula a direção do passo usando uma combinação entre o gradiente descendente e uma aproximação de segunda ordem.
- O coeficiente de amortecimento (λ) é ajustado automaticamente para controlar o tamanho do passo e o equilíbrio entre os dois métodos.
Imagine que você está tentando encontrar o ponto mais baixo de uma região montanhosa, mas só tem um mapa com contornos pouco definidos. O método de Levenberg-Marquardt funciona como um navegador inteligente que combina duas estratégias para encontrar o caminho:
1. O primeiro modo (método de Gauss-Newton) é rápido, mas arriscado. É como correr ladeira abaixo. Funciona muito bem quando você está perto do objetivo, mas pode "tropeçar" se o terreno for complicado.
2. O segundo modo (gradiente descendente) é mais lento, mas confiável. É como descer com pequenos passos cautelosos — mais devagar, mas mais seguro. Funciona bem mesmo em terrenos difíceis.
O algoritmo alterna de forma inteligente entre esses dois modos. Quando o caminho está claro, ele usa o método rápido, mas quando a situação fica complicada, ele muda automaticamente para o modo cauteloso. O tamanho do passo é ajustado automaticamente.
Esse algoritmo pode ficar preso em um mínimo local. Ele exige uma boa estimativa inicial (é necessário ter uma noção de onde procurar) e não é muito eficiente para problemas com um grande número de parâmetros (mais de 100).
//—————————————————————————————————————————————————————————————————————————————— void OnStart () { // Initialization of optimization parameters--------------------------------------- int numbTestFuncRuns = 10000; int params = 1000; double rangeMin [], rangeMax [], rangeStep; ArrayResize (rangeMin, params); ArrayResize (rangeMax, params); for (int i = 0; i < params; i++) { rangeMin [i] = -10; rangeMax [i] = 10; } rangeStep = DBL_EPSILON; double x []; double s []; ArrayResize (x, params); ArrayResize (s, params); ArrayInitialize (s, 1); // Generate random initial parameter values in given ranges---- for (int i = 0; i < params; i++) { x [i] = rangeMin [i] + ((rangeMax [i] - rangeMin [i]) * rand () / 32767.0); } // Create objects for optimization------------------------------------------ C_OptimizedFunction fFunc; fFunc.Init (params, numbTestFuncRuns); CObject obj; CNDimensional_Rep frep; CMinLMReportShell rep; // Set the parameters of the LM optimization algorithm------------------------------ double diffStep = 1e-16;//0.00001; CAlglib::MinLMCreateV (1, x, diffStep, fFunc.state); CAlglib::MinLMSetBC (fFunc.state, rangeMin, rangeMax); CAlglib::MinLMSetScale (fFunc.state, s); CAlglib::MinLMSetCond (fFunc.state, rangeStep, numbTestFuncRuns); CAlglib::MinLMOptimize (fFunc.state, fFunc, frep, 0, obj); CAlglib::MinLMResults (fFunc.state, x, rep); // Output of optimization results----------------------------------------------- Print ("LM, best result: ", fFunc.fB, ", number of function launches: ", fFunc.numberLaunches); } //——————————————————————————————————————————————————————————————————————————————
No LM, o tipo da variável "state" é definido como "CMinLMStateShell".
//—————————————————————————————————————————————————————————————————————————————— // Class for function optimization, inherits from CNDimensional_FVec class C_OptimizedFunction : public CNDimensional_FVec { public: //-------------------------------------------------------------------- C_OptimizedFunction (void) { } ~C_OptimizedFunction (void) { } // A virtual function to contain the function being optimized-------- virtual void FVec (CRowDouble &x, CRowDouble &fi, CObject &obj); // Initialization of optimization parameters--------------------------------------- void Init (int coords, int maxNumberLaunchesAllowed) { numberLaunches = 0; maxNumbLaunchesAllowed = maxNumberLaunchesAllowed; fB = -DBL_MAX; ArrayResize (c, coords); ArrayResize (cB, coords); } //---------------------------------------------------------------------------- CMinLMStateShell state; // State int numberLaunches; // Launch counter double fB; // Best found value of the objective function (maximum) double cB []; // Coordinates of the point with the best function value private: //------------------------------------------------------------------- double c []; // Array for storing current coordinates int maxNumbLaunchesAllowed; // Maximum number of function calls allowed }; //——————————————————————————————————————————————————————————————————————————————
Assim como nos métodos de otimização anteriores, limitamos a quantidade de chamadas da função objetivo, mas o método LM é o único que não possui suporte para comandos de parada, seria lógico esperar uma função como "MinLMRequestTermination".
//—————————————————————————————————————————————————————————————————————————————— // Implementation of the function to be optimized void C_OptimizedFunction::FVec (CRowDouble &x, CRowDouble &fi, CObject &obj) { // Increase the function launch counter and limitation control---------------- numberLaunches++; if (numberLaunches >= maxNumbLaunchesAllowed) { fi.Set (0, DBL_MAX); //CAlglib::MinLMRequestTermination (state); // such method does not exist return; } // Copy input coordinates to internal array------------------------- for (int i = 0; i < x.Size (); i++) c [i] = x [i]; // Calculate objective function value---------------------------------------- double ffVal = ObjectiveFunction (c); fi.Set (0, -ffVal); // Update the best solution found-------------------------------------- if (ffVal > fB) { fB = ffVal; ArrayCopy (cB, c); } } //——————————————————————————————————————————————————————————————————————————————
Após executar o script de teste com o algoritmo LM para otimizar a função do paraboloide, obtemos o seguinte resultado no print:
LM, melhor resultado: 0.6776047308612422, número de execuções da função: 4003
O método LM parou na 4003ª chamada da função objetivo, ou seja, retirar o limite de iterações não muda o resultado, pois o algoritmo já havia "empacado" antes de atingir o teto de 10.000 iterações:
Com um passo muito pequeno de 1e-16, o algoritmo para ainda mais cedo, na 2001ª execução da função objetivo:
LM, melhor resultado: 0.6670839162547625, número de execuções da função: 2001
Tabela de funções utilizadas nos métodos ALGLIB
Nos métodos de otimização da ALGLIB, são utilizados diferentes tipos de variáveis para os valores iniciais e restrições do tipo caixa, assim como diferentes tipos de classes base da função objetivo, diferentes conjuntos de objetos necessários para a otimização, e listas distintas de funções chamadas. Isso pode tornar a escrita de programas utilizando esses métodos algo pouco intuitivo.
Para facilitar o entendimento e organizar o conhecimento sobre os métodos de otimização da ALGLIB, preparei uma tabela-resumo. Ela ajudará programadores a se situarem rapidamente e iniciarem a otimização corretamente em seus projetos.
| Optimization algorithm | Type FF function | Type of variable | List of objects | List of called methods |
| BLEIC | Func | double | 1) Cobject 2) CNDimensional_Rep 3) CMinBLEICReportShell 4) CminBLEICStateShell | 1) Calglib::MinBLEICCreateF 2) Calglib::MinBLEICSetBC 3) Calglib::MinBLEICSetInnerCond 4) Calglib::MinBLEICSetOuterCond 5) Calglib::MinBLEICOptimize 6) Calglib::MinBLEICResults 7) Calglib::MinBLEICRequestTermination |
| LBFGS | Func | double | 1) Cobject 2) CNDimensional_Rep 3) CminLBFGSReportShell 4) CminLBFGSStateShell | 1) Calglib::MinLBFGSCreateF 2) Calglib::MinLBFGSSetCond 3) Calglib::MinLBFGSSetScale 4) Calglib::MinLBFGSOptimize 5) Calglib::MinLBFGSResults 6) Calglib::MinLBFGSRequestTermination |
| NS | FVec | CRowDouble | 1) CObject 2) CNDimensional_Rep 3) CminNSReport 4) CminNSState | 1) Calglib::MinNSCreateF 2) CAlglib::MinNSSetBC 3) CAlglib::MinNSSetScale 4) CAlglib::MinNSSetCond 5) CAlglib::MinNSSetAlgoAGS 6) CAlglib::MinNSOptimize 7) Calglib::MinNSResults 8) Calglib::MinNSRequestTermination |
| BC | Func | CRowDouble | 1) CObject 2) CNDimensional_Rep 3) CminBCReport 4) CminBCState | 1) CAlglib::MinBCCreateF 2) CAlglib::MinBCSetBC 3) CAlglib::MinBCSetScale 4) CAlglib::MinBCSetCond 5) CAlglib::MinBCOptimize 6) Calglib::MinBCResults 7) Calglib::MinBCRequestTermination |
| NLC | Fvec | CRowDouble | 1) Cobject 2) CNDimensional_Rep 3) CminNLCReport 4) CminNLCState | 1) CAlglib::MinNLCCreateF 2) CAlglib::MinNLCSetBC 3) CAlglib::MinNLCSetScale 4) CAlglib::MinNLCSetCond 5) Calglib::MinNLCSetAlgoAUL 6) Calglib::MinNLCOptimize 7) Calglib::MinNLCResults 8) Calglib::MinNLCRequestTermination |
| LM | FVec | double | 1) Cobject 2) CNDimensional_Rep 3) CminLMReportShell 4) CminLMStateShell | 1) Calglib::MinLMCreateV 2) Calglib::MinLMSetBC 3) Calglib::MinLMSetScale 4) Calglib::MinLMSetCond 5) Calglib::MinLMOptimize 6) Calglib::MinLMResults 7) Calglib::MinLMRequestTermination (does not exist) |
Testes dos métodos
Após estudarmos os métodos de otimização da biblioteca ALGLIB, surge naturalmente a dúvida sobre quais desses métodos escolher para tarefas específicas. Diferentes tipos de problemas de otimização podem ser resolvidos com maior ou menor eficiência dependendo do método utilizado. Para responder a essa questão importante, utilizaremos funções de teste complexas que são reconhecidas por sua semelhança com problemas reais. Essas funções representam casos típicos: funções suaves são representadas pela função de teste Hilly, funções suaves com picos agudos (não diferenciáveis em todo seu domínio) são representadas pela Forest, e uma função puramente discreta é representada pela Megacity.
O teste será realizado com 50 execuções para cada função de teste, com limite de 10.000 chamadas da função objetivo. Prepararemos um script de testes baseado no método BC como exemplo. Essa abordagem nos permitirá obter resultados mais precisos e representativos, facilitando a escolha do método de otimização mais adequado para cada tarefa em particular.
Vamos escrever a função "FuncTests", que executará rodadas de testes de otimização utilizando o respectivo método da ALGLIB. A função permitirá coletar dados sobre o desempenho dos métodos, visualizar seu funcionamento e construir gráficos de convergência.
A seguir, um resumo das funções da "FuncTests":
- Recebe como parâmetros a função objetivo de teste, o número de testes, a cor para visualização e variáveis para os resultados gerais.
- Se a opção de vídeo estiver ativada, constrói o gráfico da função.
- Define os limites de teste e inicializa as variáveis dos resultados.
- Gera dados de entrada aleatórios e executa a otimização utilizando a biblioteca "CAlglib".
- Armazena a quantidade de chamadas à função objetivo e os melhores resultados encontrados.
- Calcula e exibe os resultados médios.
- Atualiza a pontuação geral com base nos testes realizados.
//—————————————————————————————————————————————————————————————————————————————— void FuncTests (C_Function &f, // Reference to the target function object const int funcCount, // Number of functions to test const color clrConv, // Visualization color double &allScore, // Total score of all tests double &allTests) // Total number of tests { if (funcCount <= 0) return; // If the number of functions = 0, exit the function allTests++; // Increase the total number of tests if (Video_P) // If visualization is enabled { ST.DrawFunctionGraph (f); // Draw the function graph ST.SendGraphToCanvas (); // Send the graph to the canvas ST.MaxMinDr (f); // Determine the maximum and minimum of the function ST.Update (); // Update the visualization } //---------------------------------------------------------------------------- C_AO_Utilities Ut; // Utilities for handling numbers int xConv = 0.0; // Variable for converting along the X axis int yConv = 0.0; // Variable for converting along the Y axis double aveResult = 0.0; // Average test result int aveRunsFF = 0; // Average number of function runs int params = funcCount * 2; // Number of parameters (2 for each function) int epochCount = NumbTestFuncRuns_P / PopSize_P; // Number of epochs //---------------------------------------------------------------------------- CRowDouble bndl; bndl.Resize (params); // Array for lower bounds CRowDouble bndu; bndu.Resize (params); // Array for upper bounds for (int i = 0; i < funcCount; i++) // Fill the boundaries for each function { bndu.Set (i * 2, f.GetMaxRangeX ()); // Set the upper boundary by X bndl.Set (i * 2, f.GetMinRangeX ()); // Set the lower boundary by X bndu.Set (i * 2 + 1, f.GetMaxRangeY ()); // Set the upper bound by Y bndl.Set (i * 2 + 1, f.GetMinRangeY ()); // Set the lower boundary by Y } CRowDouble x; x.Resize (params); // Array for parameter values CRowDouble s; s.Resize (params); // Array for scaling s.Fill (1); // Fill the array with ones for (int test = 0; test < NumberRepetTest_P; test++) // Run the tests { for (int i = 0; i < funcCount; i++) // For each function { x.Set (i * 2, Ut.RNDfromCI (bndl [i * 2], bndu [i * 2])); // Generate random values by X x.Set (i * 2 + 1, Ut.RNDfromCI (bndl [i * 2 + 1], bndu [i * 2 + 1])); // Generate random values by Y } //-------------------------------------------------------------------------- CObject obj; // Object for storing results C_OptimizedFunction fFunc; fFunc.Init (params, NumbTestFuncRuns_P, PopSize_P, clrConv); // Initialize the optimization function CNDimensional_Rep frep; // Representation of multidimensional space CMinBCState state; // State of the minimization method CMinBCReport rep; // Minimization report double epsg = 1e-16; // Parameter for gradient stop condition double epsf = 1e-16; // Parameter for the stop condition by function value CAlglib::MinBCCreateF (x, DiffStep_P, state); // Create minimization state CAlglib::MinBCSetBC (state, bndl, bndu); // Set the boundaries CAlglib::MinBCSetScale (state, s); // Set scaling CAlglib::MinBCSetCond (state, epsg, epsf, ArgumentStep_P, NumbTestFuncRuns_P); // Set conditions CAlglib::MinBCOptimize (state, fFunc, frep, obj); // Optimization CAlglib::MinBCResults (state, x, rep); // Get results //-------------------------------------------------------------------------- aveRunsFF += fFunc.numberLaunches; // Sum up the number of function runs aveResult += -fFunc.bestMIN; // Sum up the best minimum found } aveRunsFF /= NumberRepetTest_P; // Calculate the average number of runs aveResult /= NumberRepetTest_P; // Calculate the average result double score = aveResult; // Estimate based on average result Print (funcCount, " ", f.GetFuncName (), "'s; Func runs: ", aveRunsFF, "(", NumbTestFuncRuns_P, "); result: ", aveResult); // Output test results allScore += score; // Update the overall score } //——————————————————————————————————————————————————————————————————————————————
Executaremos o script de testes sequencialmente para todos os métodos de otimização da biblioteca ALGLIB analisados. Abaixo estão vantagens dos resultados dos testes para os respectivos métodos, que devem ser interpretadas da seguinte forma:
BLEIC|bound-constrained limited-memory optimizer with equality and inequality constraints|0.8|: Abreviação do método, nome completo, passo de diferenciação (opcional, parâmetros adicionais dos métodos).
5 Hilly's: Número de funções objetivo de teste do tipo Hilly utilizadas no problema multidimensional.
Func runs: 2178(10000): Número de chamadas da função objetivo — número de tentativas do método de acessar a função objetivo, seguido do limite máximo desejado de chamadas.
result: 0.38483704535107116: Resultado médio obtido após 50 execuções de teste.
Saída da execução do método BLEIC nas funções objetivo de teste:
BLEIC|bound-constrained limited-memory optimizer with equality and inequality constraints|0.8|
=============================
5 Hilly's; Func runs: 2178(10000); result: 0.38483704535107116
25 Hilly's; Func runs: 10130(10000); result: 0.3572376879336238
500 Hilly's; Func runs: 11989(10000); result: 0.2676346390264618
=============================
5 Forest's; Func runs: 1757(10000); result: 0.28835869530001046
25 Forest's; Func runs: 9383(10000); result: 0.22629722977214342
500 Forest's; Func runs: 14978(10000); result: 0.16606494305819486
=============================
5 Megacity's; Func runs: 1211(10000); result: 0.13815384615384615
25 Megacity's; Func runs: 9363(10000); result: 0.12640000000000004
500 Megacity's; Func runs: 15147(10000); result: 0.09791692307692391
=============================
All score: 2.05290 (22.81%)
Saída da execução do método L-BFGS nas funções objetivo de teste:
L-BFGS|limited memory BFGS method for large scale optimization|0.9|
=============================
5 Hilly's; Func runs: 5625(10000); result: 0.38480050402327626
25 Hilly's; Func runs: 10391(10000); result: 0.2944296786579764
500 Hilly's; Func runs: 41530(10000); result: 0.25091140645623417
=============================
5 Forest's; Func runs: 3514(10000); result: 0.2508946897150378
25 Forest's; Func runs: 9105(10000); result: 0.19753907736098766
500 Forest's; Func runs: 40010(10000); result: 0.1483916309143011
=============================
5 Megacity's; Func runs: 916(10000); result: 0.12430769230769222
25 Megacity's; Func runs: 4639(10000); result: 0.10633846153846153
500 Megacity's; Func runs: 39369(10000); result: 0.09022461538461606
=============================
All score: 1.84784 (20.53%)
Saída da execução do método NS nas funções objetivo de teste:
NS|nonsmooth nonconvex optimization|0.5|0.8|50.0|
=============================
5 Hilly's; Func runs: 10171(10000); result: 0.3716823351189392
25 Hilly's; Func runs: 11152(10000); result: 0.30271115043870767
500 Hilly's; Func runs: 1006503(10000); result: 0.2481831526729561
=============================
5 Forest's; Func runs: 10167(10000); result: 0.4432983184931045
25 Forest's; Func runs: 11221(10000); result: 0.20891527876847327
500 Forest's; Func runs: 1006503(10000); result: 0.15071828612481414
=============================
5 Megacity's; Func runs: 7530(10000); result: 0.15076923076923068
25 Megacity's; Func runs: 11069(10000); result: 0.12480000000000002
500 Megacity's; Func runs: 1006503(10000); result: 0.09143076923076995
=============================
All score: 2.09251 (23.25%)
Saída da execução do método BC nas funções objetivo de teste:
BC|box constrained optimization with fast activation of multiple box constraints|0.9|
=============================
5 Hilly's; Func runs: 1732(10000); result: 0.37512809463286956
25 Hilly's; Func runs: 9763(10000); result: 0.3542591015005374
500 Hilly's; Func runs: 22312(10000); result: 0.26434986025328294
=============================
5 Forest's; Func runs: 1564(10000); result: 0.28431712294752914
25 Forest's; Func runs: 8844(10000); result: 0.23891148588644037
500 Forest's; Func runs: 15202(10000); result: 0.16925473100070892
=============================
5 Megacity's; Func runs: 1052(10000); result: 0.12307692307692313
25 Megacity's; Func runs: 9095(10000); result: 0.12787692307692308
500 Megacity's; Func runs: 20002(10000); result: 0.09740000000000082
=============================
All score: 2.03457 (22.61%)
Saída da execução do método NLC nas funções objetivo de teste:
NLC|nonlinearly constrained optimization with preconditioned augmented lagrangian algorithm|0.8|1000.0|5|
=============================
5 Hilly's; Func runs: 8956(10000); result: 0.4270442612182801
25 Hilly's; Func runs: 10628(10000); result: 0.3222093696838907
500 Hilly's; Func runs: 48172(10000); result: 0.24687323917487405
=============================
5 Forest's; Func runs: 8357(10000); result: 0.3230697968403923
25 Forest's; Func runs: 10584(10000); result: 0.2340843463074393
500 Forest's; Func runs: 48572(10000); result: 0.14792910131023018
=============================
5 Megacity's; Func runs: 5673(10000); result: 0.13599999999999995
25 Megacity's; Func runs: 10560(10000); result: 0.1168615384615385
500 Megacity's; Func runs: 47611(10000); result: 0.09196923076923148
=============================
All score: 2.04604 (22.73%)
Saída da execução do método LM nas funções objetivo de teste:
LM|improved levenberg-marquardt algorithm|0.0001|
=============================
5 Hilly's; Func runs: 496(10000); result: 0.2779179366819541
25 Hilly's; Func runs: 4383(10000); result: 0.26680986645907423
500 Hilly's; Func runs: 10045(10000); result: 0.27253276065962373
=============================
5 Forest's; Func runs: 516(10000); result: 0.1549127879839302
25 Forest's; Func runs: 3727(10000); result: 0.14964009375922901
500 Forest's; Func runs: 10051(10000); result: 0.1481206726095718
=============================
5 Megacity's; Func runs: 21(10000); result: 0.0926153846153846
25 Megacity's; Func runs: 101(10000); result: 0.09040000000000001
500 Megacity's; Func runs: 2081(10000); result: 0.08909230769230835
=============================
All score: 1.54204 (17.13%)
Agora podemos analisar visualmente o comportamento dos algoritmos nas funções de teste. Para a maioria dos métodos apresenta parada prematura antes de atingir o limite de chamadas da função objetivo (definimos esse limite como 10.000 iterações nos parâmetros). Por exemplo, o método de Levenberg-Marquardt (LM), na tarefa discreta "Megacity" com 1.000 parâmetros, parava em média após 2.081 iterações; já com apenas 10 parâmetros, parava após apenas 21 iterações. Por outro lado, em funções suaves como "Hilly", esse método fazia significativamente mais iterações na tentativa de encontrar o mínimo. Outros métodos, em contrapartida, realizavam mais de um milhão de chamadas à função objetivo.
Abaixo estão as visualizações da execução dos métodos NS (que obteve a maior pontuação) e LM (que obteve a menor pontuação):

NS na função de teste Hilly

NS na função de teste Forest

NS na função de teste Megacity
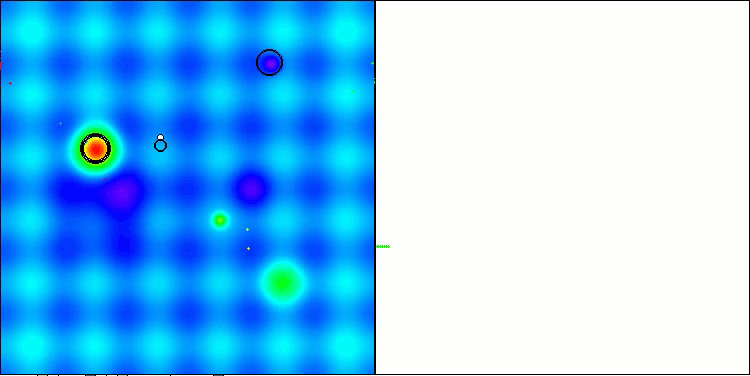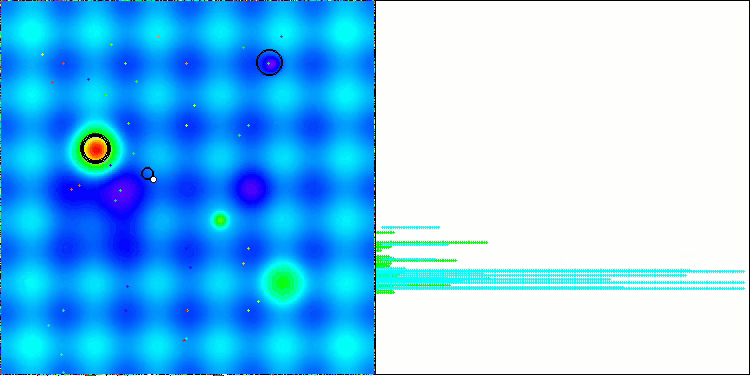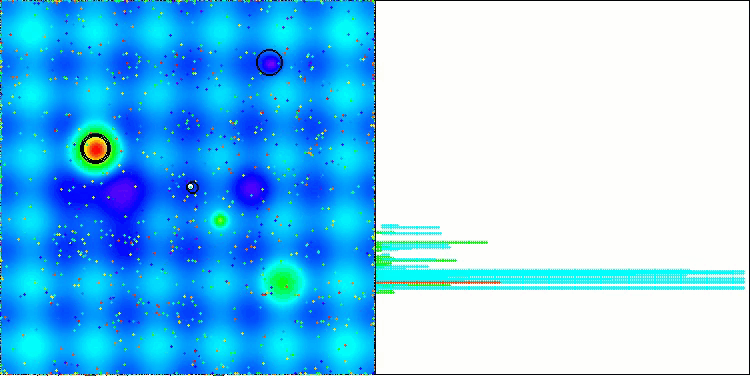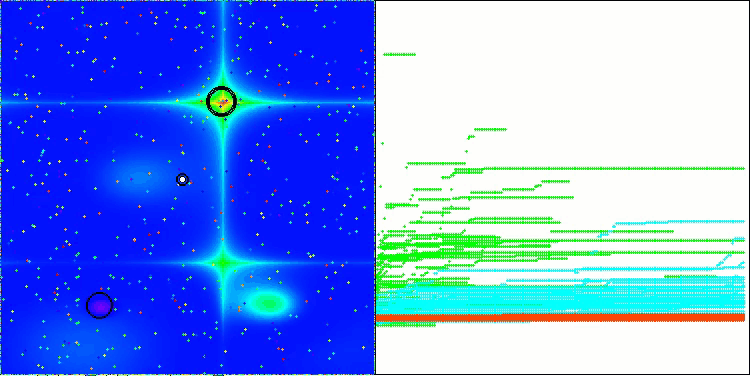
LM na função de teste Hilly
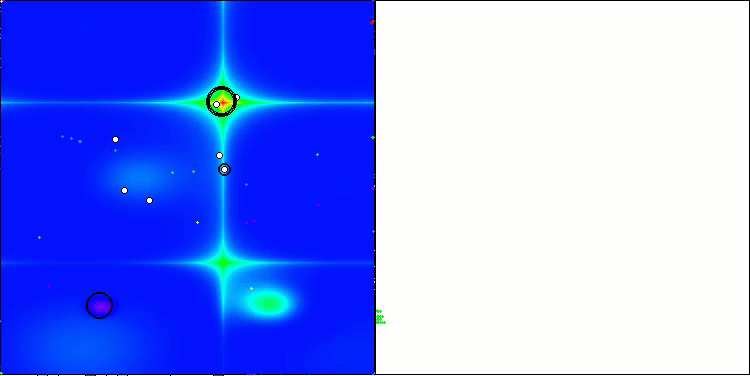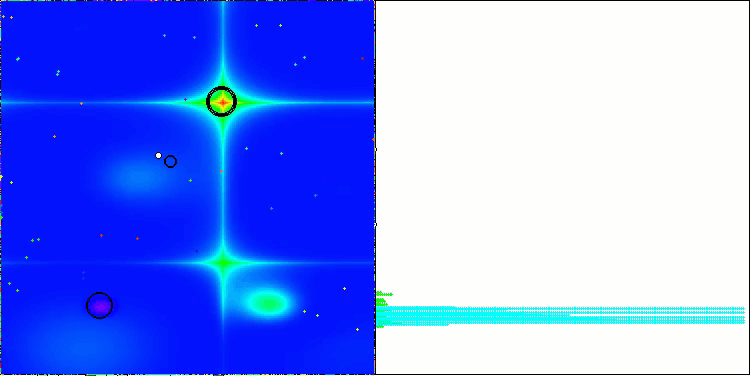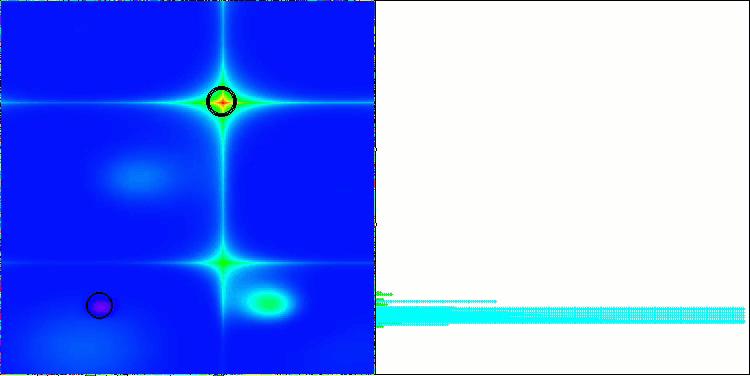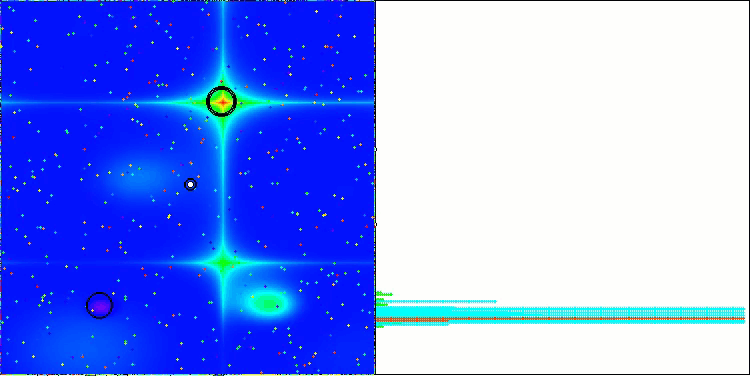
LM na função de teste Forest

LM na função de teste Megacity
Vamos organizar os resultados obtidos em uma tabela.

Graduação de cores dos algoritmos conforme os testes correspondentes
Considerações finais
Ao longo dos dois artigos, analisamos os métodos de otimização da biblioteca ALGLIB, exploramos formas de integrá-los em programas do usuário, e estudamos as particularidades de interação com as funções desses métodos. Além disso, realizamos testes para identificar os pontos fortes e fracos dos algoritmos. Vamos resumir brevemente os principais resultados:
- Em funções suaves (Hilly) com baixa dimensionalidade, o melhor desempenho foi do método NLC, enquanto em alta dimensionalidade, o método LM se destacou.
- Em funções suaves com picos acentuados (Forest), o método NS obteve os melhores resultados na baixa dimensionalidade, enquanto o método BC foi superior na alta dimensionalidade.
- Na tarefa discreta "Megacity", o método NS foi o mais eficaz em baixa dimensionalidade, enquanto o método BLEIC liderou nos testes com alta dimensionalidade.
As diferenças nos resultados entre os métodos não são muito expressivas — os desvios estão dentro da variação normal de seus próprios desempenhos. No entanto, o método NS se mostra mais versátil. Vale ressaltar que ele não pode ser interrompido manualmente durante a execução.
Os códigos anexados ao artigo incluem tudo o que é necessário para começar a utilizar os métodos de otimização em seus próprios projetos, além de permitir visualizar e avaliar seu funcionamento.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Simple test ALGLIB BLEIC.mq5 | Script | Script de teste para uso com o BLEIC |
| 2 | Simple test ALGLIB LBFGS.mq5 | Script | Script de teste para uso com o L-BFGS |
| 3 | Simple test ALGLIB NS.mq5 | Script | Script de teste para uso com o NS |
| 4 | Simple test ALGLIB BC.mq5 | Script | Script de teste para uso com o BC |
| 5 | Simple test ALGLIB NLC.mq5 | Script | Script de teste para uso com o NLC |
| 6 | Simple test ALGLIB LM.mq5 | Script | Script de teste para uso com o LM |
| 7 | Test_minBLEIC.mq5 | Script | Banco de testes para o BLEIC |
| 8 | Test_minLBFGS.mq5 | Script | Banco de testes para o L-BFGS |
| 9 | Test_minNS.mq5 | Script | Banco de testes para o NS |
| 10 | Test_minBC.mq5 | Script | Banco de testes para o BC |
| 11 | Test_minNLC.mq5 | Script | Banco de testes para o NLC |
| 12 | Test_minLM.mq5 | Script | Banco de testes para o LM |
| 13 | CalculationTestResults.mq5 | Script | Script para cálculo dos resultados na tabela comparativa |
| 14 | TestFunctions.mqh | Arquivo incluído | Biblioteca de funções de teste |
| 15 | TestStandFunctions.mqh | Arquivo incluído | Biblioteca de funções do banco de testes |
| 16 | Utilities.mqh | Arquivo incluído | Biblioteca de funções auxiliares |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16164
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Técnicas do MQL5 Wizard que você deve conhecer (Parte 35): Regressão por Vetores de Suporte
Técnicas do MQL5 Wizard que você deve conhecer (Parte 35): Regressão por Vetores de Suporte
 Recursos do SQLite em MQL5: Exemplo de painel interativo com estatísticas de trading por símbolo e magic
Recursos do SQLite em MQL5: Exemplo de painel interativo com estatísticas de trading por símbolo e magic
 Implementando uma Estratégia de Trading Rápido com Parabolic SAR e Média Móvel Simples (SMA) em MQL5
Implementando uma Estratégia de Trading Rápido com Parabolic SAR e Média Móvel Simples (SMA) em MQL5
 Treinamento de perceptron multicamadas com o algoritmo de Levenberg-Marquardt
Treinamento de perceptron multicamadas com o algoritmo de Levenberg-Marquardt
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
1. Ainda não é um fato que os otimizadores da alglib sejam usados corretamente.
1. Você pode questionar qualquer coisa, mas é sempre muito mais construtivo falar a partir da posição de códigos-fonte completos e testes corretos e reproduzíveis.
2) É possível obter um resultado ideal em uma megacidade bidimensional se você pedir a 9 bilhões de pessoas que enfiem os dedos aleatoriamente em uma folha de papel em branco, atrás da qual a superfície da função está oculta (uma delas certamente acabará muito próxima do global e dirá que foi ela quem resolveu o problema com sucesso). Mas precisamos encontrar a solução ideal não em 9 bilhões de tentativas por meio de tentativas aleatórias, mas em 10.000 usando uma estratégia.
Quanto mais alto for o resultado médio de uma série de testes independentes (estabilidade, repetibilidade dos resultados), mais alto será o método testado em comparação com o método de busca aleatória para um tipo específico de problema (para alguns problemas, alguns métodos não são muito diferentes do método de busca aleatória e, para outros, são muito eficazes).
Esse é o objetivo do teste e da comparação de diferentes algoritmos, para os quais não apenas uma função de teste, mas três diferentes com propriedades diferentes são tomadas como benchmarks, para que se possa ver claramente a aplicabilidade de diferentes algoritmos em diferentes tarefas, suas limitações e capacidades em diferentes tarefas. Isso permite que você aborde a solução de problemas de otimização de forma significativa.
No futuro, prefiro responder a perguntas específicas sobre o conteúdo do artigo e sobre os códigos.
Pegamos os métodos de otimização local, aplicamos ao problema global e os comparamos com os métodos de otimização global. É sobre isso que estou falando.
Estou falando sobre como podemos adaptar esses métodos para a otimização global. A opção mais simples é aumentar o número de inicializações.
Se eu entendi corretamente, o Adam etc. é aperfeiçoado para velocidade, não para qualidade.
Seria interessante ver a classificação quando limitada pelo tempo em vez do número de iterações.
Se eu entendi corretamente, Adam etc. está focado na velocidade, não na qualidade.
Seria interessante ver a classificação quando limitada pelo tempo em vez do número de iterações.
A família de algoritmos ADAM (AdamW, RAdam, AdaBelief e outros), bem como SGD, SGRAD e outros (há muitos deles) foram desenvolvidos como um substituto moderno para os métodos clássicos de gradiente e foram projetados para resolver problemas de grandes dimensões sem o conhecimento da fórmula analítica, geralmente para treinar redes neurais (todos eles têm suas vantagens e desvantagens). Há também métodos Lion interessantes do Google (2023) e alguns outros muito recentes. É muito interessante estudar esse tópico, especialmente no contexto do treinamento de redes neurais, em que será útil e informativo criar uma superfície de destino em algum exemplo simples (ou talvez complexo) e realizar experimentos (com análise de suas entranhas, com estudo profundo das propriedades dos métodos, avaliação cuidadosa de seus recursos - tudo como quisermos).
Com restrições de tempo, não há nada a que se prender. Um usuário fará 1 milhão de acessos ao alvo em 1 minuto e outro fará 1 bilhão. Como podemos comparar os algoritmos nessas condições? É por isso que usamos um limite para o número de acessos e comparamos a eficiência dentro desse limite.
Com restrições de tempo, não há nada a que se vincular. Um usuário fará 1 milhão de acessos ao alvo em 1 minuto, enquanto outro fará 1 bilhão. Como podemos comparar os algoritmos entre eles nessas condições? É por isso que usamos um limite para o número de acessos e comparamos a eficiência dentro desse limite.
Vinculação ao PC do autor. Tome como base o tempo de 10.000 iterações de ANS.
Meus resultados no código do fxsaber:
Tamanho do código PS como uma métrica adicional (quão complexa é a implementação do algoritmo)