私の理解が正しければ、我々は1に等しいヒル関数の最大値を求めたい。
double Core (double x, double y) { double res = 20.0 + x * x + y * y - 10.0 * cos (2.0 * M_PI * x) - 10.0 * cos (2.0 * M_PI * y) - 30.0 * exp (-(pow (x - 1.0, 2) + y * y) / 0.1) + 200.0 * exp (-(pow (x + M_PI * 0.47, 2) + pow (y - M_PI * 0.2, 2)) / 0.1) //グローバル・マックス + 100.0 * exp (-(pow (x - 0.5, 2) + pow (y + 0.5, 2)) / 0.01) - 60.0 * exp (-(pow (x - 1.33, 2) + pow (y - 2.0, 2)) / 0.02) //グローバル・ミニッツ - 40.0 * exp (-(pow (x + 1.3, 2) + pow (y + 0.2, 2)) / 0.5) + 60.0 * exp (-(pow (x - 1.5, 2) + pow (y + 1.5, 2)) / 0.1); return Scale (res, -39.701816104859866, 229.91931214214105, 0.0, 1.0); }
この関数には2つのパラメータしかありません。
MinBleicを接続しました。
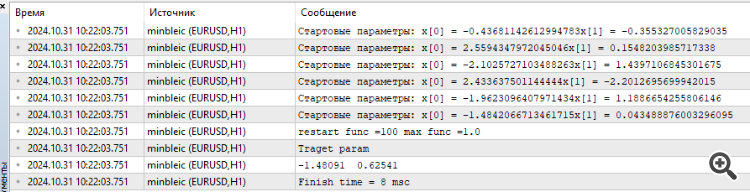
オプティマイザが与える結果の平均値ではなく、最大値をカウントする必要があるようだ。 そしてもちろん、驚異的な8ミリ秒という時間を見ることができる。
1.私の理解が正しければ、私たちは1に等しいヒル関数の最大値を見つけたいのです。
2.この関数には2つのパラメータしかない。
3.接続されたMinBleic
オプティマイザが生成する結果の平均ではなく、最大値を数えるべきだと思う。 もちろん、8ミリ秒という驚異的な時間もわかるだろう。
コメントありがとう。
1.はい、その通りです。すべてのテスト関数は統一されており、その値は[0.0; 1.0]の範囲にあります。
2.すべてのテスト関数は2つのパラメータしか持っていません。しかし、アルゴリズムをテストする際には、2次元の関数を繰り返し複製することで、多次元の探索空間(AOのスケール能力を評価するために、5*2=10、25*2=50、500*2=1000の3種類のテスト)を使用する。
3.パラメータが2つの問題は、アルゴリズム同士を適切に比較するには単純すぎる。アルゴリズムは多次元空間を扱うのが難しい。
最大結果を取るべきか?ポイントは、アルゴリズムの別々の実行における結果のばらつきが重要だということである。すべてのアルゴリズムにおいて、最初の反復では、点の播種のランダムな値は、グローバルな極限の値に非常に近い完全にランダムにすることができ、この場合、アルゴリズムは不合理に迅速に最良の結果を見つけるので、実行結果の平均値は、より良いアルゴリズムの「成功」のランダムな依存性を除外するために、アルゴリズムの特性を反映しています。
これは確率論と関連している。対象とする関数がどんなに複雑であっても、パラメータが1つしかなければ、10個のランダムな値を生成しても、そのうちの1個は大域的極値に非常に近くなる。ALGLIB(勾配降下のバリエーション)法は、空間における点の初期位置に敏感であり、そのため決定論的な性質を持つ。探索空間の次元が大きくなり、空間の複雑さが指数関数的に増大すると、乱数を発生させても大域的極限に到達する方法はない。
その証拠に、問題の次元が大きくなると、単調で滑らかな単峰放物線上にさえ収束するのが難しくなる。
AOが探索空間の初期値に関係なく安定した結果を示せば示すほど、この方法は問題を解く上で信頼できると考えることができる。テストにおいて、AOを複数回実行した平均値を選択するのはそのためである。
今日の現実は、多くのタスクが何百万、何十億ものパラメーターの最適化を必要とし(AI、LLM、生成ネットワーク、生産やビジネスにおける複雑な複合制御タスク)、タスクの滑らかさや単峰性を語ることはできない。
コメントありがとう。
1.はい、その通りです。すべてのテスト関数は統一されており、その値は[0.0; 1.0]の範囲にあります。
2.すべてのテスト関数は2つのパラメータしか持たない。しかし、アルゴリズムをテストする際には、2次元の関数を繰り返し複製することで、多次元の探索空間(AOのスケール能力を評価するために、5*2=10、25*2=50、500*2=1000の3種類のテスト)を使用する。
3.パラメータが2つの問題は、アルゴリズム同士を適切に比較するには単純すぎる。アルゴリズムは多次元空間を扱うのが難しい。
最大結果を取るべきか?ポイントは、アルゴリズムの別々の実行における結果のばらつきが重要だということである。すべてのアルゴリズムでは、最初の反復で、播種点のランダムな値は、完全にランダムに非常にグローバルな極限の値に近いことができ、その場合には、アルゴリズムが不合理に迅速に最良の結果を見つけるので、実行の結果から平均値は、より良いアルゴリズムの "成功 "のランダムな依存性を除外するために、アルゴリズムの特性を反映しています。
これは確率論と関連している。対象関数がどんなに複雑であっても、パラメータが1つしかなければ、10個のランダムな値を生成しても、そのうちの1個は大域的極値に非常に近くなる。ALGLIB(勾配降下のバリエーション)法は、空間における点の初期位置に敏感であり、そのため決定論的な性質を持つ。探索空間の次元が大きくなり、空間の複雑さが指数関数的に増大すると、乱数を発生させても大域的極値に到達する方法はない。
その証拠に、問題の次元が大きくなると、単調で滑らかな一峰性の放物線にさえ収束するのが難しくなる。
AOが探索空間の初期値に関係なく安定した結果を示せば示すほど、この方法は問題を解く上で信頼できると考えることができる。テストにおいて、AOを複数回実行した平均値を選択するのはそのためである。
今日の現実は、多くのタスクが何百万、何十億ものパラメーターの最適化を必要とし(AI、LLM、生成ネットワーク、生産やビジネスにおける複雑な複合制御タスク)、タスクの平滑性や単峰性を語ることはできない。
非常に複雑な関数を取り上げているのだから。パラメータの数が増えるにつれて、このような関数の和の最適なパラメータを見つけることは、純粋に理論的な興味に過ぎないと私は思う。トレーディングの場合、予測数学モデルは多くのパラメータを持つかもしれないが、損失関数自体は非常に単純なので、探索ははるかに簡単だ。もちろん、クルヴァフィッティングに興味がなければ、10億ものパラメーターはありえないが、10~100程度のささやかなものである。
もちろん、クルヴァフィッティングに興味がないのであれば、10~100個程度のささやかなパラメータでいいだろう。私は関数の最大値を求めるパラメータに興味がある。私が興味があるのは、最適値とその最適値に到達するまでの時間である。この時間が許容できるものであれば、コンピュータがパラメータの開始ベクトルを選択するためにどれだけの労力を費やしたかは気にしない。
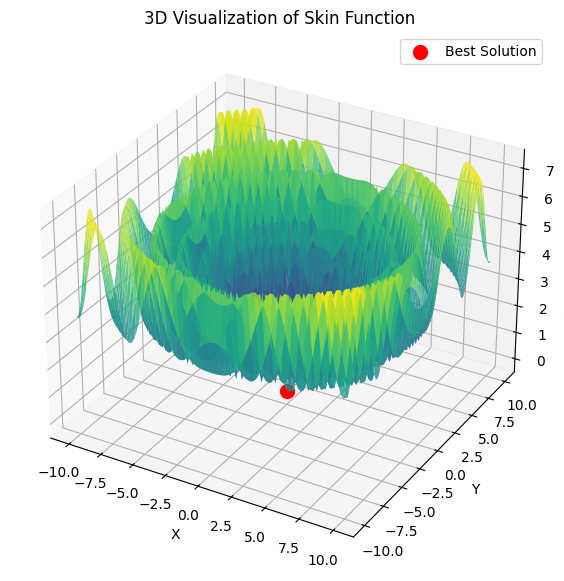
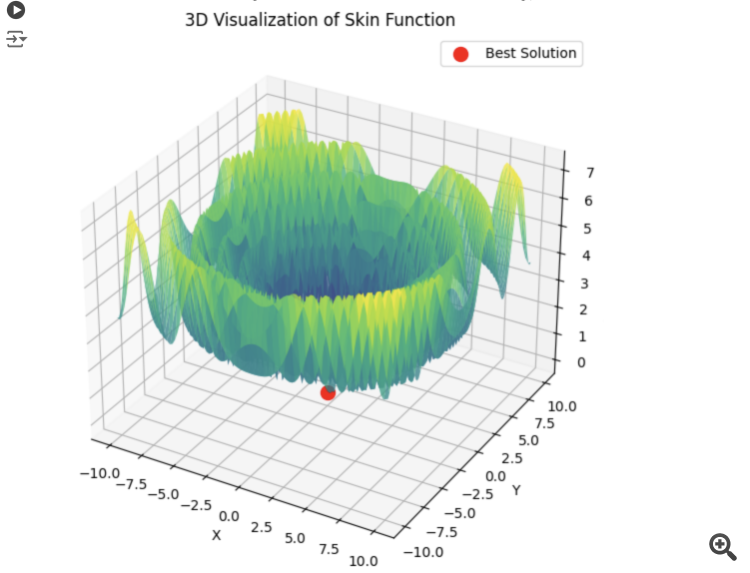
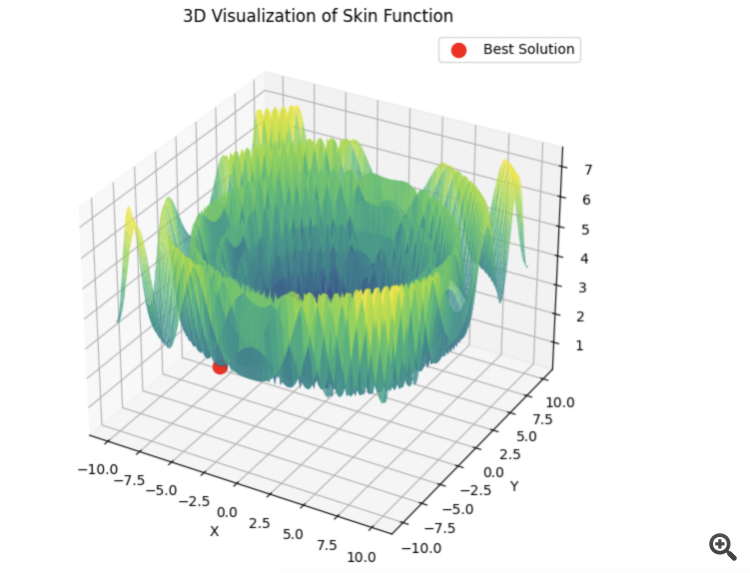
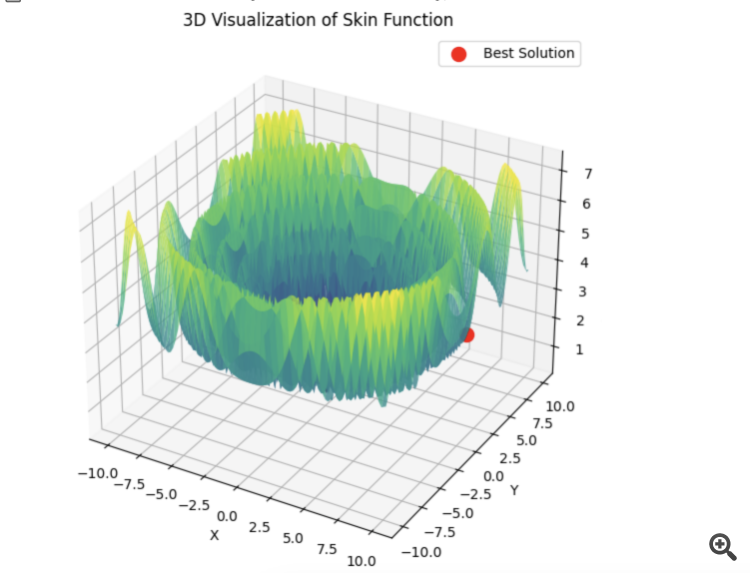
以下は、5つのHilly関数の合計の例である。
15秒の時間で結果は0.76。悪くないと思う。特にトレーディングというテーマを考えると、全体最適が何なのか分からないし、今後も分からないだろう。
とにかく、この記事には感謝している。ここには考えるべきことがたくさんある。後で他のアルゴリズムもテストして、結果を投稿するつもりだ。
1) 非常に複雑な関数を取り上げている。パラメーターの数が増えるにつれて、このような関数の和に最適なパラメーターを見つけることは、純粋に理論的な興味に過ぎないと私は思う。
2) トレーディングの場合、予測数学モデルは多くのパラメータを持つかもしれないが、損失関数自体は非常に単純であるため、探索ははるかに簡単である。もちろん、クルヴァフィッティングに興味がなければ、10億ものパラメータはありえないが、10~100程度のささやかなものである。
3) 結果の観点から見た場合。私は関数の最大値を見つけるパラメータに興味がある。私が興味があるのは、最適値とその最適値に到達するまでの時間である。この時間が許容できるものであれば、コンピュータがパラメータの開始ベクトルを選択するためにどれだけの労力を費やしたかは気にしない。
4) 以下は5つのHilly関数の和の例である。
15秒の時間で結果は0.76。悪くないと思う。特にトレーディングというテーマを考えると、全体最適が何なのかわからないし、これからもわからないだろう。
5) とにかく、記事をありがとう。考えるべきことがたくさんある。後日、残りのアルゴリズムをテストして、結果を投稿するつもりだ。
1) 記事では、AOをそれ単体で真空中の馬のように考えるのではなく(例:PSOは非常に有名で、それゆえ人気があるが、強力ではない、同じAEOは誰にも全く知られていないが、チップが飛ぶように速く滑らかで離散的な空間を切り刻む)、その論理と装置の分析とともに、それらの探索能力を互いに比較して考える。そうすることで、実用的な課題における可能性を深く理解することができる。そして、真の可能性が明らかになるのは、次元の増加とともにであり、それはアルゴリズム同士の比較においてである。もちろん、解析的に解くことができるタスクの話をするのであれば話は別だが。
ランダムな成功」の影響を排除し、アルゴリズムの検索能力を直接明らかにするためです。
そして、AOの実用的な応用に関しては(AOの比較ではなく)、最適化を何度か実行して最良の結果を選択することが推奨されます。しかし、ある弱いアルゴリズムが何度もリスタートしなければならず、ターゲット関数の貴重な実行回数を無駄にするのであれば、別のアルゴリズムの方がはるかに少ない実行回数で同じ結果を得ることができます。同じ結果が得られるのに、なぜ高いお金を払うのでしょうか?弱いアルゴリズムは行き詰まり、探索空間で泥沼にはまり込み、何度も再スタートが必要になる。実際には、このような状況に興味を持つ人はいないでしょう。
2) Expert Advisorを使って、少なくとも2つのパラメータを持つ実際的な問題で損失関数を視覚化しようとすると、表面は滑らかではなく、一峰性でもないことがわかります。トレーディング・タスクは離散的であるため、単純で滑らかなターゲットは存在しない。従って、平滑な放物線上でさえ困難な手法は、トレーディングでは効果がない。
3) 平均結果はアルゴ同士の比較に使われるのであって、実際には使われない(ポイント1参照)。探索に費やされる時間とエネルギーを気にしないのであれば、完全な探索を行えばよいのであって、AOを使う意味はまったくない。しかし、実際にはこのようなことは非常に稀であり、我々は常に時間と計算資源に限りがある。
4) 提示された結果には、指定された結果を得るために必要なターゲット関数の実行回数に関する情報が欠けている。 この指標は、AOの有効性を評価する鍵である。AOの選択は、効率を最大化し(実行回数を最小化し)、特に実用的な取引タスクにおいて、行き詰まる確率を最小化することに基づくべきである。
5) ありがとうございます。記事が推論の根拠となることをうれしく思います。すべてのコードはすでに記事の中で提供されていますが、実行したテストのコードを提供していただけると助かります(どうやら、独自のテスト方法を使用しているようです)。それを見て、解決したいと思います。
この議論で提起された問題については、別の記事を執筆中です。
いろいろなアルゴリズムを試してみてください。Alglib法は非常に高速で、解析的に定式化された問題(これは別のトピックです)を解くのに非常に適していると思いますが、解析式がわからない場合は、他の選択肢もあります。
解析的に定式化された問題を解く必要がある人にとっても、ALGLIBメソッドを使う原理が書かれているこの記事は非常に役に立つでしょう。
メタエバーとグラディエントソルバーをこのように比較するのは正しくない。両者を同じ条件に置くべきだ。
Metaevr.はすでにシードされた点を持っているが、勾配ソルバーは1点から始める。
等しい条件を作るには、後者に対してバッチ処理を行う必要がある。あるいは複数回の初期化が必要だ。
そのため、勾配ソルバーは平均結果ではなく最良の結果で評価する必要がある。そしてそれが、より高速に実行される理由でもある。これにより、ニューラルネットワークのトレーニングにおけるスピードと精度のバランスが取れる。
もしPSOがすぐに正しい最小値を選ぶとしたら:
その場合、lbfgsはロケールからロケールへとジャンプする。しかしPSOは高速で、最適化された関数をバッチに分割して、設定可能な回数だけジャンプすることができる。
# Оптимизация с использованием L-BFGS и батчей def optimize_with_lbfgs_batches(initial_guesses, bounds, batch_size): best_solution = None best_value = float('inf') for batch in generate_batches(initial_guesses, batch_size): for initial_guess in batch: result = minimize(skin_function, initial_guess, method='L-BFGS-B', bounds=bounds) if result.fun < best_value: best_value = result.fun best_solution = result.x return best_solution, best_value # Параметры оптимизации dim = 2 # Размерность пространства решений lower_bound = -10 upper_bound = 10 num_initial_guesses = 100 # Количество начальных приближений batch_size = 10 # Размер батча
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索

新しい記事「ALGLIBライブラリの最適化手法(第2回):」はパブリッシュされました:
本研究の第1回では、MetaTrader 5に標準搭載されているALGLIBライブラリの最適化アルゴリズムについて検討し、アルゴリズム BLEIC (Boundary, Linear Equality-Inequality Constraints)、L-BFGS (Limited-memory Broyden–Fletcher–Goldfarb–Shanno)、NS(箱制約・線形制約・非線形制約付き非滑らか非凸最適化)を詳しく取り上げました。これらのアルゴリズムの理論的基礎を確認しただけでなく、最適化問題への適用方法についても簡単に解説しました。
この記事では、ALGLIBが提供する残りの手法を引き続き探究していきます。特に、複雑な多次元関数に対するテストに重点を置くことで、各手法の効率性を包括的に把握することを目指します。最後に、得られた結果に基づいて総合的な分析を行い、特定のタスクに対して最適なアルゴリズムを選ぶための実践的な推奨事項を提示します。
作者: Andrey Dik