Distribuciones estadísticas en forma de histogramas sin búferes de indicador y matrices

Introducción

Un histograma es un instrumento que permite valorar de forma visual la distribución de los datos estadísticos, agrupados según la frecuencia con la que entran en un intervalo determinado (definido de antemano).

La construcción de histogramas y su uso en el análisis de datos estadísticos es un tema bastante estudiado, al que se han dedicado multitud de artículos [1, 2, 3, 4, 5, 6, 7] y sobre el que se ha creado una considerable cantidad de ejemplos en CodeBase [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]. Sin embargo, los algoritmos utilizados se basan en el uso de búferes de indicador o matrices. En este artículo se analiza la posibilidad de construir distribuciones estadísticas de diferentes características del mercado sin usar cálculos complejos, clasificaciones, muestras, etcétera. Para ello, usaremos la memoria "gráfica", el apartado donde se guardan las propiedades gráficas de los objetos. La cuestión aquí es que al construir los histogramas personalizados, de una forma u otra, se usan objetos gráficos, entonces, ¿por qué no utilizar sus posibilidades "ocultas" en todo potencial y usar esta funcionalidad tan variada?

El objetivo de este artículo es proponer soluciones sencillas a tareas estadísticas estándar. Se hará especial hincapié en la visualización de las distribuciones estadísticas y sus características principales. No nos vamos a detener en la interpretación de los histogramas ni su utilidad.

Principio de construcción de los histogramas

El histograma supone un diagrama de frecuencias en columnas. En uno de los ejes se muestran los valores de la variable, y en el otro, la frecuencia de aparición (surgimiento, etcétera) de estos valores. La altura de cada columna muestra la frecuencia (número) de los valores que pertenecen al intervalo correspondiente, igual a la anchura de la columna. Con mayor frecuencia, estos diagramas se muestran horizontalmente, es decir, los valores de la variable están ubicados en el eje horizontal, y las frecuencias, en el vertical. El uso de histogramas para representar la información investigada permite dotar a los datos estadísticos de un carácter visual y expresivo, facilita la percepción de los mismos, y en muchos casos, también su análisis.

En este artículo vamos a detenernos en los histogramas verticales de las series de variación: los valores de precio de las características estadísticas se encontrarán en el eje vertical en orden creciente, y las frecuencias, en el horizontal (Fig. 1). Los datos de precio que llegan al terminal se distribuyen y agrupan en la barra actual y pueden ser representados con respecto a su eje: a la izquierda, a la derecha, o simultáneamente en ambos lados.

 

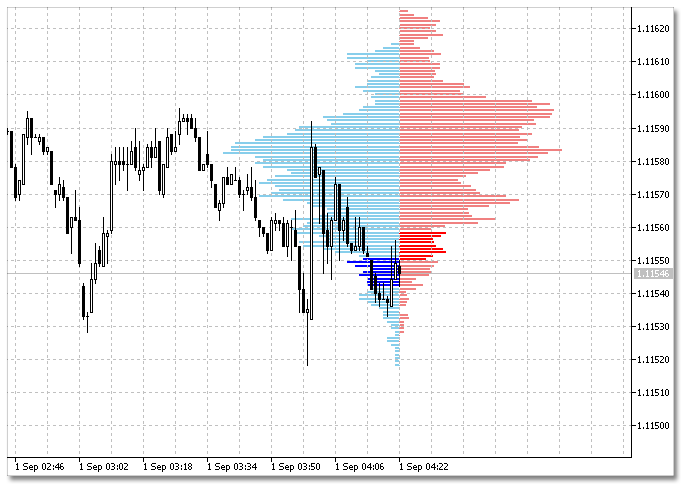
Fig. 1 Histograma vertical de distribución de los precios Bid y Ask.

Veamos una tarea concreta:

• construir el histograma de distribución de los precios Bid y Ask; 
• los datos del precio Ask los ubicaremos a la derecha de la barra actual, y los del precio Bid, a la izquierda;
• al llegar un nuevo tick, calcularemos la frecuencia para cada valor entrante del precio, es decir, el intervalo del histograma es igual al tamaño del punto del instrumento actual.

Ahora vamos a complicar las condiciones: no está permitido usar búferes de indicador, matrices o estructuras.

¿Cómo resolver este problema? 

En primer lugar, hay que pensar dónde guardar las frecuencias acumuladas para cada columna del histograma. Incluso en la fig. 1 se ve que pueden existir tantas columnas como sean necesarias, y lo primero que viene a la cabeza es usar una matriz. Además, dinámica, puesto que el rango posible precios (número de columnas) se conoce de antemano en el segmento elegido del gráfico de precio. Pero las condiciones de la tarea lo prohíben.

En segundo lugar, hay que resolver la tarea de la búsqueda y clasificación: dónde y cómo buscar los datos para recalcular y redibujar el histograma.

Resulta que los desarrolladores de MQL5 ya crearon hace mucho la funcionalidad necesaria para resolver la tarea planteada, además, es bastante potente. Sí, querido lector, nos proponen usar las posibilidades "ocultas" (no obvias) del grupo de funciones de los objetos gráficos. Cada objeto tiene propiedades, son las variables que se crean junto con el objeto y sirven para guardar multitud de diferentes parámetros. Algunos ajustes se pueden usar con otros cometidos, conservando aun así la funcionalidad. Llamaremos a estas propiedades memoria "gráfica". En otras palabras, si necesitamos guardar cierta variable pero no tenemos necesidad de obtener su valor, crearemos un objeto gráfico y asignaremos el valor de la variable a cierta propiedad.

Las propiedades gráficas de los objetos son en cierta forma un análogo de las variables globales del terminal, pero mejores. Las variables globales existen en el terminal de cliente 4 semanas a partir del momento en que se recurrió a ellas por última vez, y después se eliminan automáticamente. La memoria gráfica existe hasta que el objeto gráfico sea eliminado. ¿Imagina las posibilidades que nos proporciona esto? 

¿Qué propiedades de los objetos gráficos se pueden usar en la memoria gráfica?

Al crear cualquier objeto gráfico, debemos asignarle un nombre único, una línea de texto. La línea puede constar de sublíneas, y las sublíneas pueden contener tipos principales de datos formateados: enteros, lógicos, con punto flotante, color, fecha y hora. Por consiguiente, la propiedad OBJPROP_NAME es conveniente para guardar variables, aunque bien es cierto, principalmente para la lectura de datos.

La siguiente propiedad que se puede usar es la descripción del objeto OBJPROP_TEXT. Se trata también de una línea de texto, cuyas posibilidades están por encima que las de la propiedad anterior. En este campo de propiedades, es posible la lectura y el registro de variables.

Cualquier objeto gráfico tiene coordenadas: el precio OBJPROP_PRICE y el tiempo OBJPROP_TIME. También se las puede utilizar en la memoria gráfica.

Volvamos a nuestra tarea. Guardaremos las frecuencias en la propiedad OBJPROP_TEXT, y los valores de los precios Bid y Ask, en la propiedad OBJPROP_NAME. Más abajo mostramos el código de la función que crea los objetos y acumula las frecuencias:

void DrawHistogram(bool draw,     // dibujamos el histograma a la izquierda o a la derecha
                   string h_name, // prefijo único para el nombre del objeto
                   double price,  // precio (parámetro investigado)
                   datetime time, // anclaje del histograma a la barra actual
                   int span,      // número de dígitos del parámetro analizado
                   int swin=0)    // ventana del histograma
  {
   double y=NormalizeDouble(price,span);
   string pfx=DoubleToString(y,span);
// si draw=true, dibujamos el histograma a la derecha
   if(draw)
     {
      string name="+ "+h_name+pfx;                   // nombre del objeto: prefijo+precio
      ObjectCreate(0,name,OBJ_TREND,swin,time,y);    // creamos el objeto
      ObjectSetInteger(0,name,OBJPROP_COLOR,color_R_active); // creamos el color del objeto
      ObjSet;                                                // macro para acortar el código
      if(StringFind(ObjectGetString(0,name,OBJPROP_TEXT),"*",0)<0)
        {// si el precio obtenido ha entrado en la muestra por primera vez
         ObjectSetString(0,name,OBJPROP_TEXT,"*1");          // la frecuencia para este precio es igual a 1
         ObjectSetInteger(0,name,OBJPROP_TIME,1,time+hsize); // hemos determinado la coordenada del tiempo
        }
      else
        {// si el precio obtenido ha entrado en la muestra, pero no por primera vez
         string str=ObjectGetString(0,name,OBJPROP_TEXT);    // obtenemos el valor de la propiedad
         string strint=StringSubstr(str,1);                  // seleccionamos una sublínea
         long n=StringToInteger(strint);                     // obtenemos la frecuencia para cálculos posteriores
         n++;                                                // aumentamos el valor a 1
         ObjectSetString(0,name,OBJPROP_TEXT,"*"+(string)n); // registramos el nuevo valor en la propiedad
         ObjectSetInteger(0,name,OBJPROP_TIME,1,time+hsize*n);//definimos la coordenada del tiempo
        }
     }
// si draw=false, dibujamos el histograma a la izquierda
   if(!draw)
     {
      string name="- "+h_name+pfx;
      ObjectCreate(0,name,OBJ_TREND,swin,time,y);
      ObjectSetInteger(0,name,OBJPROP_COLOR,color_L_active);
      ObjSet;
      if(StringFind(ObjectGetString(0,name,OBJPROP_TEXT),"*",0)<0)
        {
         ObjectSetString(0,name,OBJPROP_TEXT,"*1");
         ObjectSetInteger(0,name,OBJPROP_TIME,1,time-hsize);
        }
      else
        {
         string str=ObjectGetString(0,name,OBJPROP_TEXT);
         string strint=StringSubstr(str,1);
         long n=StringToInteger(strint);
         n++;
         ObjectSetString(0,name,OBJPROP_TEXT,"*"+(string)n);
         ObjectSetInteger(0,name,OBJPROP_TIME,1,time-hsize*n);
        }
     }
   ChartRedraw();
  }

La función consta de dos bloques análogos: para Bid y Ask por separado. Por eso solo hay comentarios en el primer bloque.

Es probable que al lector atento le haya surgido esta pregunta, del todo razonable: ¿para qué doblar el precio, si ya está disponible en la propiedad OBJPROP_PRICE? ¿Qué sentido tiene este trabajo?

Nos detendremos en esta peculiaridad con mayor detalle. Al llegar el precio es necesario determinar en qué columna entra, y allí, por consiguiente, aumentar el valor de la frecuencia. Si se usara la coordenada del precio directamente desde su propiedad, entonces deberíamos iterar todos los objetos gráficos, solicitar el valor de esta propiedad, comparar con el precio entrante y solo después de ello, registrar el nuevo valor de la frecuencia en la columna necesaria. Y comparar las cifras reales del tipo double es una "emboscada" de las buenas. En general, es un algoritmo muy inefectivo. Otra cosa distinta es cuando al llegar un valor nuevo de precio, registramos de inmediato la frecuencia cambiada en el lugar adecuado. ¿De qué forma? La cosa es que al crear un nuevo objeto gráfico con un nombre ya existente, el nuevo objeto no se crea y los campos de propiedades no se resetean. En otras palabras, creamos objetos sin detenernos a pensar si se verán duplicados. No es necesario realizar comprobaciones adicionales, porque no se crearán copias ni clones. De esto se encargará la funcionalidad del terminal y los objetos gráficos. Solo queda determinar si el precio ha entrado por primera vez en la muestra o no. Para ello, en la función analizada DrawHistogram(), se usa el prefijo "asterisco" (*) en la propiedad del objeto OBJPROP_TEXT. Si no hay "asterisco", ese precio ha entrado por primera vez. Cuando creamos un objeto en vano, este campo permanece en blanco. En las llamadas posterioes, allí se guardará el valor de la frecuencia con el prefijo establecido.

El siguiente paso que realizaremos es desplazar el histograma a la derecha. Al aparecer una nueva barra, el gráfico se desplaza a la izquierda, y necesitamos que el histograma suempre se represente en la barra actual, es decir, que se desplace en la dirección opuesta. Veamo cómo hacer esto:

//--- Desplazamiento del diagrama a una nueva barra
   if(time[0]>prevTimeBar) // determinamos la aparición de una nueva barra
     {
      prevTimeBar=time[0];
      // iteramos todos los objetos gráficos
      for(int obj=ObjectsTotal(0,-1,-1)-1;obj>=0;obj--)
        {
         string obj_name=ObjectName(0,obj,-1,-1);               // obtenemos el nombre del objeto encontrado
         if(obj_name[0]==R)                                     // buscamos el prefijo del elemento del histograma
           {                                                    // si encontramos el elemento del histograma
            ObjectSetInteger(0,obj_name,OBJPROP_TIME,           // establecemos un nuevo valor de la coordenada
                             0,time[0]);                        // para el "0" punto de anclaje
            string str=ObjectGetString(0,obj_name,OBJPROP_TEXT);// leemos la variable de la propiedad del objeto
            string strint=StringSubstr(str,1);                  // seleccionamos la sublínea de la variable obtenida
            long n=StringToInteger(strint);                     // transformamos la línea en la variable long
            ObjectSetInteger(0,obj_name,OBJPROP_TIME,           // calculamos el nuevo valor de la coordenada
                             1,time[0]+hsize*n);                // para el "1" punto de anclaje
            ObjectSetInteger(0,obj_name,OBJPROP_COLOR,
                             color_R_passive);                  // cambiamos el color del elemento desplazado
           }
         if(obj_name[0]==L)
           {
            ObjectSetInteger(0,obj_name,OBJPROP_TIME,0,time[0]);
            string str=ObjectGetString(0,obj_name,OBJPROP_TEXT);
            string strint=StringSubstr(str,1);
            long n=StringToInteger(strint);
            ObjectSetInteger(0,obj_name,OBJPROP_TIME,1,time[0]-hsize*n);
            ObjectSetInteger(0,obj_name,OBJPROP_COLOR,color_L_passive);
           }
        }
      ChartRedraw();
     }

Esto es todo. El histograma de los precios Bid y Ask se construye en el gráfico, y el programa no usa ni una matriz o búfer de indicador. El código completo de esta solución se encuentra en los anexos al artículo.

En el vídeo se muestra la solución lista para una tarea análoga usando la memoria gráfica. El propio código se puede encontrar en CodeBase: indicador "Histogram bid and ask prices".

Ejemplos de construcción de histogramas en la ventana principal

La tecnología de programación de la funcionalidad con el uso de la memoria gráfica ya ha sido analizada, vamos a construir ahora varios histogramas para los indicadores estándar. El principio de construcción es análogo al analizado, solo que en lugar de los precios Bid y Ask, utilizaremos los valores de los indicadores en la barra actual.

     1 Indicador iMA. Vamos a tomar dos indicadores con diferentes periodos de promediación y construiremos los histogramas. Este es el aspecto del código:

input int               period_MA1=20;       // Averaging period of iMA1 
input int               period_MA2=14;       // Averaging period of iMA2 
//---- indicator buffers
double      MA1[];
double      MA2[];
//---- handles for indicators
int         iMA1_handle;
int         iMA2_handle;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   ObjectsDeleteAll(0,-1,-1);
   ChartRedraw();
   iMA1_handle=iMA(_Symbol,_Period,period_MA1,0,MODE_SMA,PRICE_CLOSE);
   iMA2_handle=iMA(_Symbol,_Period,period_MA2,0,MODE_SMA,PRICE_CLOSE);
   ArraySetAsSeries(MA1,true);
   ArraySetAsSeries(MA2,true);
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
   ArraySetAsSeries(time,true);
   
   CopyBuffer(iMA1_handle,0,0,1,MA1);
   CopyBuffer(iMA2_handle,0,0,1,MA2);

   DrawHistogram(true,"iMA("+(string)period_MA1+")=",MA1[0],time[0],_Digits);
   DrawHistogram(false,"iMA("+(string)period_MA2+")=",MA2[0],time[0],_Digits);

//--- Desplazamiento del diagrama a una nueva barra
   if(time[0]>prevTimeBar) // determinamos la aparición de una nueva barra
     {
      prevTimeBar=time[0];
      // iteramos todos los objetos gráficos
      for(int obj=ObjectsTotal(0,-1,-1)-1;obj>=0;obj--)
        {
         string obj_name=ObjectName(0,obj,-1,-1);               // obtenemos el nombre del objeto encontrado
         if(obj_name[0]==R)                                     // buscamos el prefijo del elemento del histograma
           {                                                    // si encontramos el elemento del histograma
            ObjectSetInteger(0,obj_name,OBJPROP_TIME,           // establecemos un nuevo valor de la coordenada
                             0,time[0]);                        // para el "0" punto de anclaje
            string str=ObjectGetString(0,obj_name,OBJPROP_TEXT);// leemos la variable de la propiedad del objeto
            string strint=StringSubstr(str,1);                  // seleccionamos la sublínea de la variable obtenida
            long n=StringToInteger(strint);                     // transformamos la línea en la variable long
            ObjectSetInteger(0,obj_name,OBJPROP_TIME,           // calculamos el nuevo valor de la coordenada
                             1,time[0]+hsize*n);                // para el "1" punto de anclaje
            ObjectSetInteger(0,obj_name,OBJPROP_COLOR,
                             color_R_passive);                  // cambiamos el color del elemento desplazado
           }
         if(obj_name[0]==L)
           {
            ObjectSetInteger(0,obj_name,OBJPROP_TIME,0,time[0]);
            string str=ObjectGetString(0,obj_name,OBJPROP_TEXT);
            string strint=StringSubstr(str,1);
            long n=StringToInteger(strint);
            ObjectSetInteger(0,obj_name,OBJPROP_TIME,1,time[0]-hsize*n);
            ObjectSetInteger(0,obj_name,OBJPROP_COLOR,color_L_passive);
           }
        }
      ChartRedraw();
     }
   return(rates_total);
  }

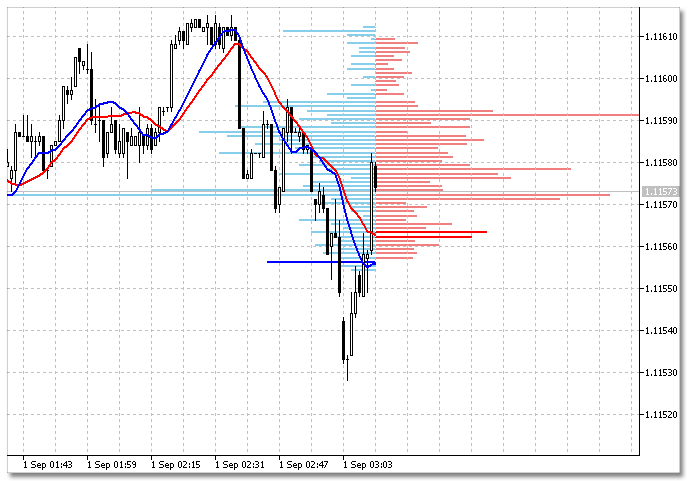
Fig. 2. Histograma de 2 indicadores iMA. 

     2. Indicador iBands. Para este indicador vamos a construir histogramas para los limites superior (UPPER_BAND) e inferior (LOWER_BAND) . El código abreviado se muestra más abajo.

input int   period_Bands=14;           // Averaging period of iBands 
//---- indicator buffers
double      UPPER[];
double      LOWER[];
//---- handles for indicators
int         iBands_handle;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   ObjectsDeleteAll(0,-1,-1);
   ChartRedraw();
   iBands_handle=iBands(_Symbol,_Period,period_Bands,0,5.00,PRICE_CLOSE);
   ArraySetAsSeries(UPPER,true);
   ArraySetAsSeries(LOWER,true);
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   ArraySetAsSeries(time,true);
   
   CopyBuffer(iBands_handle,1,0,1,UPPER);
   CopyBuffer(iBands_handle,2,0,1,LOWER);

   DrawHistogram(true,"iBands(UPPER)=",UPPER[0],time[0],_Digits);
   DrawHistogram(false,"iBands(LOWER)=",LOWER[0],time[0],_Digits);

//--- Desplazamiento del diagrama a una nueva barra
   if(time[0]>prevTimeBar)
     {
     ...
     }
   return(rates_total);
  }

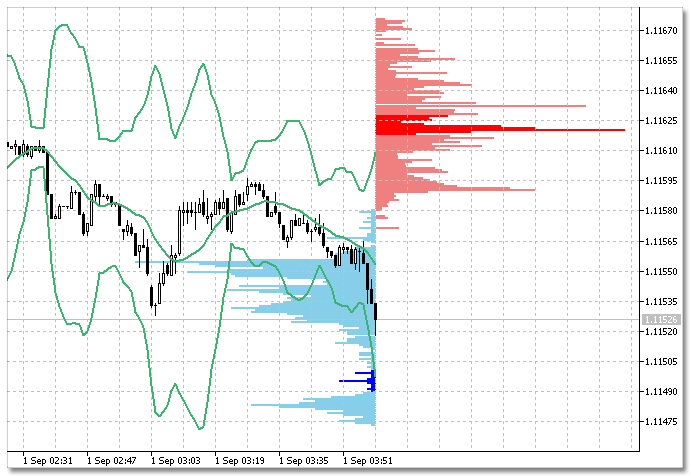
Fig. 3. Histograma de las franjas de Bollinger del indicador iBands. 

Para el indicador Bollinger, resultan histogramas curiosos, si usamos los 3 búferes de indicador (0 - BASE_LINE, 1 - UPPER_BAND, 2 - LOWER_BAND). Ubicaremos el histograma de las franjas inferior y superior a la derecha de la barra actual, y el histograma de la línea básica a la izquierda de la barra cero. El resultado se muestra en el siguiente dibujo:

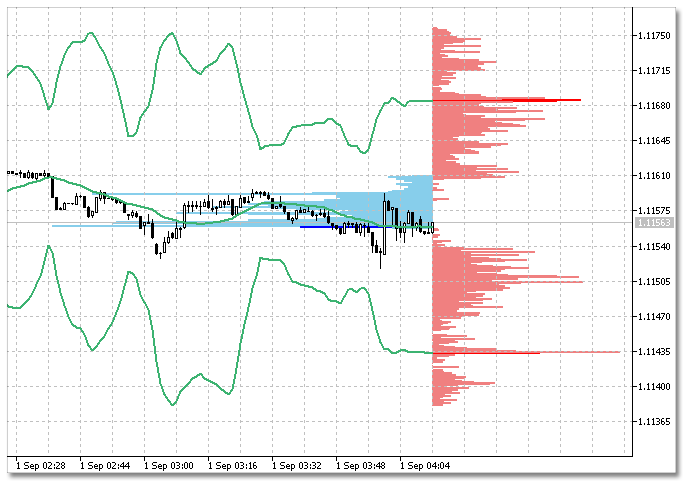
Fig. 4. Histograma de las franjas de Bollinger en 3 búferes de indicador.  

El código de esta variante de los histogramas se muestra más abajo. Preste atención a que a la derecha se representan de hecho dos histogramas: para los límites superior e inferior del indicador. Además, se perciben visualmente como un diagrama único.

input int   period_Bands=20;       // Averaging period of iBands 
//---- indicator buffers
double      BASE[];
double      UPPER[];
double      LOWER[];
//---- handles for indicators
int         iBands_handle;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   ObjectsDeleteAll(0,-1,-1);
   ChartRedraw();
   iBands_handle=iBands(_Symbol,_Period,period_Bands,0,10.00,PRICE_CLOSE);
   ArraySetAsSeries(BASE,true);
   ArraySetAsSeries(UPPER,true);
   ArraySetAsSeries(LOWER,true);
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   ArraySetAsSeries(time,true);
   
   CopyBuffer(iBands_handle,0,0,1,BASE);
   CopyBuffer(iBands_handle,1,0,1,UPPER);
   CopyBuffer(iBands_handle,2,0,1,LOWER);

   DrawHistogram(true,"iBands(UPPER)=",UPPER[0],time[0],_Digits);
   DrawHistogram(true,"iBands(LOWER)=",LOWER[0],time[0],_Digits);
   DrawHistogram(false,"iBands(LOWER)=",BASE[0],time[0],_Digits);

//--- Desplazamiento del diagrama a una nueva barra
   if(time[0]>prevTimeBar)
     {
     ...
     }
   return(rates_total);
  }

Hasta ahora se han analizado ejemplos de las series de variación en las que el intervalo de los valores de la magnitud investigada (variantes) se igualaba al tamaño del punto del instrumento actual _Point. Con otras palabras, todos los valores de precio se han dibujado con una columna del histograma aparte.

Hay que subrayar lo claramente que han sido clasificadas para el lector las series de variación incorporadas en la funcionalidad del terminal. Para ello, no hemos tenido que escribir ni una línea de código.

Ahora veremos cómo cambiar el intervalo de distribución en el que habrá varios valores de variante, usando solo una variable y el potencial de la funcionalidad de los objetos gráficos. En la función analizada más arriba DrawHistogram() tenemos el parámetro de entrada span , el número de dígitos del parámetro investigado. Así, variando el número de dígitos, podremos cambiar el intervalo para el cálculo de las frecuencias del histograma. Puesto que en el nombre del objeto gráfico se incluye el precio, la selección tiene lugar automáticamente en la etapa de creación y corrección de las propiedades de los objetos. Vea con cuánta facilidad se resuleven las tareas de clasificación y agrupación con el uso de la memoria gráfica sin programación.

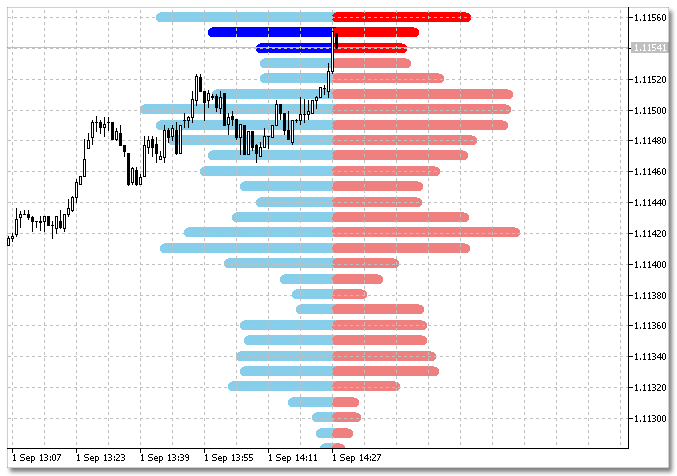
Fig. 5. Histograma de los precios Bid y Ask con intervalo de columnas aumentado. 

Así, construir histogramas en la ventana principal del gráfico ha resultado muy sencillo. Ahora vamos a aclarar cómo hacer diagramas semejantes en las ventanas adicionales del gráfico.

Histogramas en las ventanas adicionales

El principio de creación de las distribuciones estadísticas en las ventanas adicionales es el mismo que en la principal. La diferencia está en que los valores de las magnitudes analizadas pueden tener magnitudes negativas y un número de dígitos aleatorio. Así, en la ventana principal, la escala de precio tiene un número de dígitos conocido de antemano, que se puede obtener con la ayuda de la variable _Digits. En las ventanas adicionales, las variables pueden adoptar tanto valores positivos, como negativos. Además, el número de cifras significativas tras la coma puede ser cualquiera. Por eso, hay que tener en cuenta esta peculiaridad al establecer los parámetros de entrada de la función DrawHistogram() para construir histogramas, así como indicar el número de la ventana adicional. Por defecto, en la función se usa la ventana principal, que es igual a cero.

Ejemplos de construcción de histogramas en las ventanas adicionales

La mejor forma de asimilar la información es con ejemplos. Vamos a dedicarnos a ellos. Veamos varios ejemplos de construcción de histogramas en las ventanas adicionales para los indicadores técnicos estándar.

     1 Indicador iChaikin.

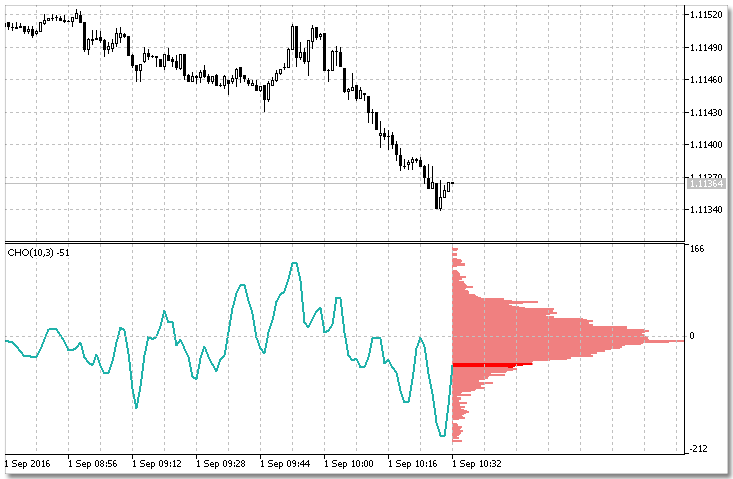
Fig. 6. Histograma del indicador Chaikin Oscillator.

Código abreviado para este indicador:

input int   period_fast=3;       // Averaging period fast of iChaikin 
input int   period_slow=10;      // Averaging period of slow iChaikin 
//---- indicator buffers
double      CHO[];
//---- handles for indicators
int         iChaikin_handle;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   ObjectsDeleteAll(0,-1,-1);
   ChartRedraw();
   iChaikin_handle=iChaikin(_Symbol,_Period,period_fast,period_slow,MODE_SMA,VOLUME_TICK);
   ArraySetAsSeries(CHO,true);
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   ArraySetAsSeries(time,true);
   
   CopyBuffer(iChaikin_handle,0,0,2,CHO);

   DrawHistogram(true,"iChaikin=",CHO[0],time[0],0,1);
   
//--- Desplazamiento del diagrama a una nueva barra
   if(time[0]>prevTimeBar)
     {
     ...
     }
   return(rates_total);
  }

     2. Indicador iCCI.

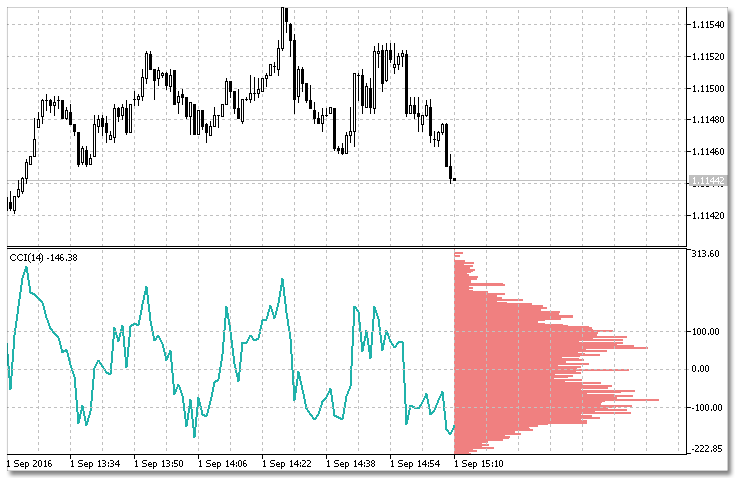
Fig. 7. Histograma del indicador Commodity Channel Index.

Código abreviado:

input int   period_CCI=14;             // Averaging period of iCCI 
//---- indicator buffers
double      CCI[];
//---- handles for indicators
int         iCCI_handle;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   ObjectsDeleteAll(0,-1,-1);
   ChartRedraw();
   iCCI_handle=iCCI(_Symbol,_Period,period_CCI,PRICE_CLOSE);
   ArraySetAsSeries(CCI,true);
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   ArraySetAsSeries(time,true);
   
   CopyBuffer(iCCI_handle,0,0,2,CCI);

   DrawHistogram(true,"iCCI=",CCI[0],time[0],0,1);
   
//--- Desplazamiento del diagrama a una nueva barra
   if(time[0]>prevTimeBar)
     {
     ...
     }
   return(rates_total);
  }

     3. Indicadores: iEnvelopes, iATR, iMACD. Combinación de los histogramas para tres indicadores, cada uno de los cuales se representará en su propia ventana.

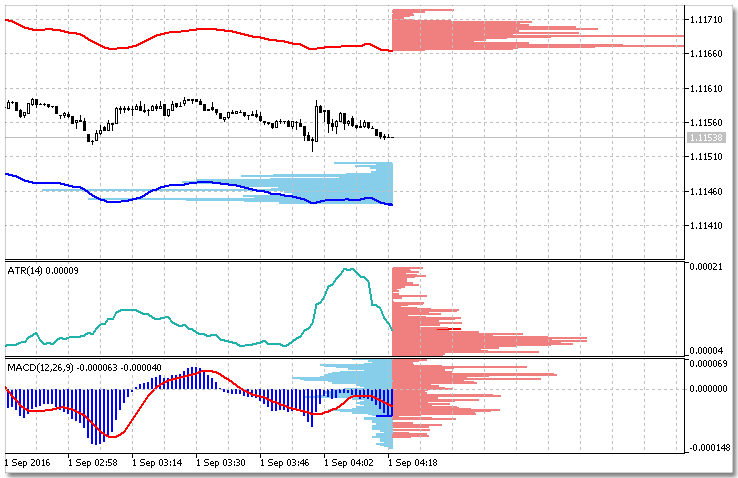
Fig. 8. Histograma de 3 indicadores: iEnvelopes, iATR and iMACD. 

El código abreviado que implementa el conjunto de histogramas, se representa en la fig. 8.

input int   period_Envelopes=14;       // Averaging period of iEnvelopes 
input int   period_ATR=14;             // Averaging period of iATR 
input int   period_fast=12;            // Averaging period fast of iMACD 
input int   period_slow=26;            // Averaging period of slow iMACD 
//---- indicator buffers
double      UPPER[];
double      LOWER[];
double      ATR[];
double      MAIN[];
double      SIGNAL[];
//---- handles for indicators
int         iEnvelopes_handle;
int         iATR_handle;
int         iMACD_handle;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
   ObjectsDeleteAll(0,-1,-1);
   ChartRedraw();
   iEnvelopes_handle=iEnvelopes(_Symbol,_Period,period_Envelopes,0,MODE_SMA,PRICE_CLOSE,0.1);
   iATR_handle=iATR(_Symbol,_Period,period_ATR);
   iMACD_handle=iMACD(_Symbol,_Period,period_fast,period_slow,9,PRICE_CLOSE);
   ArraySetAsSeries(UPPER,true);
   ArraySetAsSeries(LOWER,true);
   ArraySetAsSeries(ATR,true);
   ArraySetAsSeries(MAIN,true);
   ArraySetAsSeries(SIGNAL,true);
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
   ArraySetAsSeries(time,true);
   
   CopyBuffer(iEnvelopes_handle,0,0,1,UPPER);
   CopyBuffer(iEnvelopes_handle,1,0,1,LOWER);
   CopyBuffer(iATR_handle,0,0,1,ATR);
   CopyBuffer(iMACD_handle,0,0,1,MAIN);
   CopyBuffer(iMACD_handle,1,0,1,SIGNAL);

   DrawHistogram(true,"iEnvelopes.UPPER=",UPPER[0],time[0],_Digits);
   DrawHistogram(false,"iEnvelopes.LOWER=",LOWER[0],time[0],_Digits);
   DrawHistogram(true,"iATR=",ATR[0],time[0],_Digits+1,1);
   DrawHistogram(true,"iMACD.SIGNAL=",SIGNAL[0],time[0],_Digits+1,2);
   DrawHistogram(false,"iMACD.MAIN=",MAIN[0],time[0],_Digits+1,2);

//--- Desplazamiento del diagrama a una nueva barra
   if(time[0]>prevTimeBar)
     {
     ...
     }
   return(rates_total);
  }

Así, tras analizar la tecnología de construcción de los diferentes histogramas de las distribuciones estadísticas de las características del mercado, podemos afirmar que:

• la funcionalidad del terminal comercial МТ5;
• las posibilidades de los objetos gráficos MQL5;
• la memoria gráfica (posibilidades poco conocidas de los objetos gráficos);
• la sencillísima función DrawHistogram()

permiten calcular y visualizar los histogramas acumulados de multitud de indicadores, desde estándar hasta personalizados. Sin ebmargo, esto no es suficiente para realizar un análisis más detallado de las caracterísitcas de mercado.

Características numéricas de las distribuciones estadísticas

En la primera parte del artículo se ha mostrado el método de construcción de histogramas para programadores principiantes. Los ejemplos adjuntos se proyectan de forma sencilla a una gran clase de tareas relacionadas con la investigación de las distribuciones estadísticas y su visualización. Para analizar en mayor profundidad los histogramas, son necesarios métodos más universales y progresivos de programación, más concretamente, la POO. Así, veremos qué parámetros de las distribuciones estadísticas serán de interés para el lector.

En primer lugar, nos interesan las características numéricas de las series de variación:

• la media aritmética (frecuencia media);
• la media aritmética ponderada;
• la varianza;
• la desviación media cuadrática.

En segundo lugar, es necesario visualizar las características enumeradas. Por supuesto, todo esto se puede implementar también en un estilo procesal, pero en este artículo solucionaremos las tareas establecidas con el uso de programación orientada a objetos.

Clase CHistogram

La funcionalidad de esta clase permite representar en el gráfico histogramas y las principales características estadísticas de las distribuciones. Vamos a ver los principales métodos.

Método: constructor de clase CHistogram.

Inicializa el ejemplar de la clase. 

void CHistogram(
   string name,                     // prefijo único del nombre
   int    hsize,                    // escala del diagrama
   int    width,                    // grosor de las líneas de las columnas del histograma
   color  active,                   // color de las líneas activas
   color  passive,                  // color de las líneas pasivas
   bool   Left_Right=true,          // left=false or right=true
   bool   relative_frequency=false, // histograma relativo o absoluto
   int    sub_win=0                 // índice de la ventana de construcción del histograma
   );

Parámetros:

 name

    [in] Prefijo único del nombre para todas las columnas del histograma. 

 hsize

    [in] Escala de representación del histograma.

 width

    [in] Grosor de las líneas de las columnas del histograma.

 active

    [in] Color de las columnas del histograma actualizadas en la barra actual.

 passive

    [in] Color de las columnas del histograma que no se han actualizado en la barra actual.

 Left_Right=true

    [in] Dirección de representación del histograma. false — el histograma está colocado a la izquierda de la barra actual, true — a la derecha.

 relative_frequency=false

    [in] Método de registro de los valores de las frecuencias. false — valores absolutos de las frecuencias, true — valores relativos de las frecuencias.

 sub_win=0

    [in] Índice de la ventana para la construcción del histograma. 0 — ventana principal del gráfico. 

Valor retornado:

 No hay valor retornado. En caso de éxito, se crea un ejemplar de clase con los parámetros establecidos.

 

Método: representación del histograma DrawHistogram.

Representa las columnas del histograma: crea nuevas, redacta las ya disponibles, guarda los valores de las frecuencias en la memoria gráfica. representa el histograma en la barra actual.

void DrawHistogram(
   double price,  // valor de la variante
   datetime time  // hora de la barra actual
   );

Parámetros:

 price

    [in] Valor de la variante de la característica de mercado investigada.

 time

    [in] Tiempo de la barra actual. En esta barra estará el eje del histograma.  

Valor retornado:

 No hay valor retornado. En caso de éxito, se creará una columna nueva del histograma o se corregirá una ya existente. Si aparece una nueva barra, el histograma se desplaza de tal forma que el eje se encuentre en la barra actual. 

 

Método: cálculo de las características del histograma HistogramCharacteristics. 

Retorna las características calculadas de la serie de variación en una variable del tipo sVseries.

sVseries HistogramCharacteristics();

Parámetros:

 No hay parámetros de entrada.

Valor retornado:

 En caso de éxito, retorna el valor de una variable del tipo sVseries.

 

Estructura para obtener los valores actuales de las características del histograma (sVseries).

Estructura para guardar los últimos valores de las características de la distribución estadística. Pensada para recibir la información más demandada sobre la serie de variación. 

struct sVseries
  {
   long     N;    // número total de observaciones
   double   Na;   // valor medio de las frecuencias
   double   Vmax; // valor medio de las variantes
   double   Vmin; // valor mínimo de las variantes
   double   A;    // amplitud de la serie
   double   Mean; // media aritmética ponderada
   double   D;    // varianza
   double   SD;   // desviación media cuadrática
  };

La variable del tipo sVseries permite con una llamada de la función HistogramCharacteristics() obtener los valores de todas las características principales de una serie de variación en forma de histograma.

 

Método: visualización del valor de la media DrawMean. 

Representa el valor de la media aritmética ponderada de la serie de variación en el gráfico. 

void DrawMean(
   double coord,     // valor de la media aritmética ponderada
   datetime time,    // tiempo de la barra actual
   bool marker=false,// representar el marcador o no
   bool save=false   // guardar el valor en la historia o no
   );

Parámetros:

 coord

    [in] Valor de la media aritmética ponderada.

 time

    [in] Tiempo de la barra actual. En esta barra se fijará el valor de la media aritmética ponderada.

 marker=false

    [in] Representar el marcador en el gráfico o no. false — el marcador no se representa, true — el marcador se representa en el gráfico.

 save=false

    [in]  Guardar el valor de la media aritmética ponderada en la historia. false — no representar, true — representar en el gráfico.

Valor retornado:

En caso de éxito, en el gráfico se representará una línea horizontal que se corresponde con el valor de la media aritmética ponderada. 

 

Método: visualización de la desviación media cuadrática DrawSD.

Representa el valor de la desviación media cuadrática en forma de rectángulo, cuya anchura coincide con la frecuencia media, y cuya altura es igual a la desviación estándar, dispuesto encima y debajo del valor de la media aritmética ponderada.

void DrawSD(
   sVseries &coord,        // variable del tipo sVseries
   datetime time,          // tiempo de la barra actual
   double deviation=1.0,   // desviación
   color clr=clrYellow     // color de la representación
   );

Parámetros:

 coord

    [in] Valor de variable del tipo sVseries.

 time

    [in] Tiempo de la barra actual.

 deviation=1.0

    [in] Coeficiente por el que se aumentará el valor de la desviación media cuadrática.

 clr=clrYellow

    [in] Color del rectángulo de la desviación media cuadrática visualizada.

Valor retornado: 

 En caso de éxito, en el gráfico se representará un rectángulo que caracteriza la desviación media cuadrática partiendo del valor de la media aritmética ponderada.

  

Ejemplo de construcción de histogramas con uso de la clase CHistogram

Como ejemplo, construiremos histogramas de las distribuciones estadísticas de los precios Bid y Ask, así como de los dos indicadores ATR y MACD (fig. 9). A diferencia de los ejemplos anteriores, con la ayuda de la clase analizada, se pueden crear diagramas relativos. Para los precios del propio histograma, crearemos una representación gráfica de la media aritmética ponderada y de la desviación media cuadrática. Y además, guardaremos la media con la ayuda de búferes de indicador. En el dibujo, las desviaciones medias cuadráticas se representan en forma de rectángulos, cuya anchura corresponde a la frecuencia media, y cuya altura es igual a las dos desviaciones aumentadas varias veces, para una mayor visibilidad. 

 

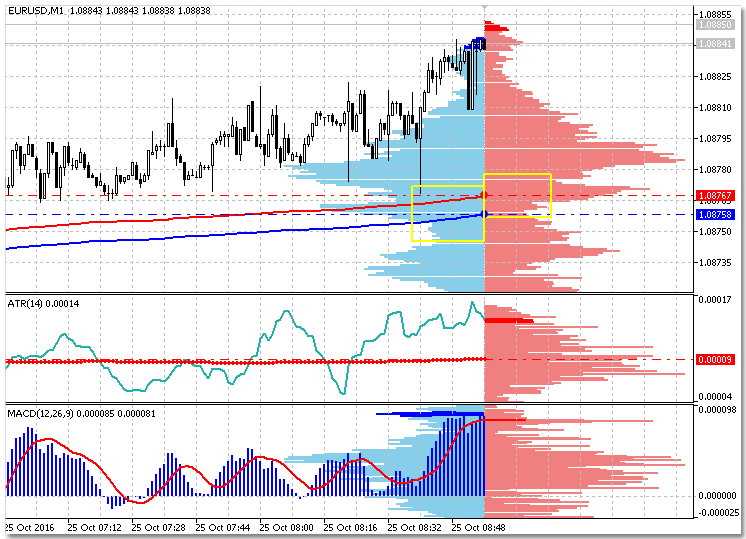
Fig. 9. Histogramas de los 2 indicadores: iATR, iMACD y de los precios Bid y Ask.

El código de este ejemplo se encuentra en los anexos al artículo. El uso de búferes de indicador en este programa está propiciado por el deseo de demostrar la conexión de la clase analizada con la funcionalidad del indicador.

Conclusión

• Las distribuciones estadísticas de las series de variación en forma de histograma sin utilizar matrices y búferes de indicador se pueden implementar tranquilamente con el uso de memoria "gráfica".
• En aquellas tareas donde se usan construcciones gráficas (objetos), en la mayoría de los casos está justificado el uso de las propiedades de los objetos gráficos para economizar memoria. Además, obtenemos acceso a las amplias posibilidades de la funcionalidad del terminal y el lenguaje MQL5: tales como la clasificación, la agrupación, la búsqueda, el muestreo, el acceso directo a los elementos  y otros.
• Hemos analizado los métodos básicos y primitivos de uso de la memoria "gráfica". En realidad, podemos guardar pequeñas matrices y estructuras en las propiedades de los objetos gráficos.