MetaTrader 5 / Ejemplos
English Русский 中文 Deutsch 日本語 Português 한국어 Français Italiano Türkçe
Cálculo de Características Integrales de Emisiones de Indicador

Cálculo de Características Integrales de Emisiones de Indicador

MetaTrader 5 — Ejemplos | 28 mayo 2014, 10:06
989 0
Sergey Pavlov
Sergey Pavlov

Introducción

Las emisiones de indicador representan una dirección nueva y bastante prometedora en el estudio de series cronológicas. Se caracteriza por el hecho de que el análisis no se centra en los indicadores como tal, sino en sus emisiones en el futuro o pasado, en las cuales nos podemos basar para hacer un pronóstico de entorno de mercado:

  • niveles de soporte y resistencia en el futuro;
  • dirección de tendencia (movimiento de precio);
  • fuerza del movimiento acumulado durante el pasado.

Mi artículo anterior llamado "Drawing Indicator's Emissions in MQL5" (“Dibujar emisiones de indicador en MQL5”) trataba sobre el algoritmo de dibujo de emisión y especificaba sus cualidades clave. Recordémoslas:

Una emisión es un conjunto de puntos localizados en las intersecciones de líneas peculiares de los indicadores que se están estudiando.

Los puntos de emisión, a su vez, tienen algunas peculiaridades:

  • Los puntos de emisión del mismo tipo tienden agruparse.
  • Los grupos de punto denso pueden atraer o, por el contrario, repeler al precio.

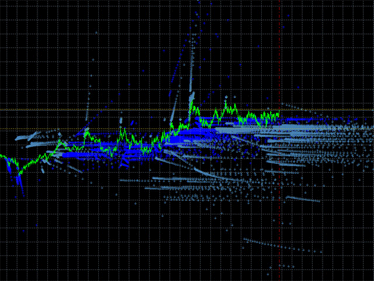
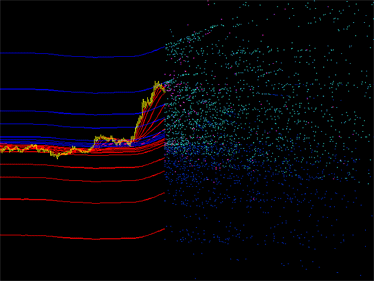
Galería de emisión:

Emisión de DCMV Emisión de iMA y iEnvelopes
Emisión de DCMV Emisión de iMA y iEnvelopes

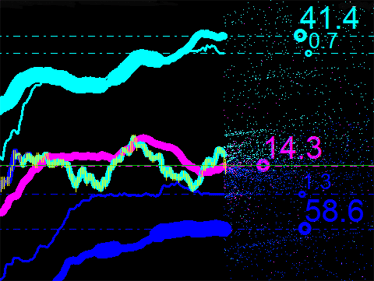Fig. 1. Ejemplos de dibujos de emisión de indicador. Izquierda: emisión del indicador DCMV. Derecha: emisión de los indicadores iMA y iEnvelopes.

En la ilustración del cálculo de características integrales de emisiones, tomaremos envolturas de media móvil (Envelopes) y las medias móviles (Moving Average, o MA) mismas con parámetros de entrada, tal y como se muestra a continuación:

//--- external variable for storing averaging period of the iEnvelopes indicator
input int   ma_period=140; // averaging period of the iEnvelopes indicator
//--- array for storing deviations of the iEnvelopes indicator
double      ENV[]={0.01,0.0165,0.0273,0.0452,0.0747,01234,0.204,0.3373,0.5576,0.9217,1.5237};
//--- array for storing iMA indicator periods
int         MA[]={4,7,11,19,31,51,85};

Ahora buscaremos intersecciones de líneas peculiares con los indicadores seleccionados. El número de líneas y sus características (períodos y desviaciones medias) se eligen aleatoriamente. Una emisión, de hecho, se puede dibujar usando cualquier conjunto de parámetros para estos indicadores (mientras se crucen en el espacio).

Ahora que ya hemos elegido los indicadores, procedamos a crear un Asesor Experto que servirá como programa base para el análisis de emisiones. obtener los datos calculados de los indicadores técnicos iMA y iEnvelopes. Yo propongo usar un mercado descrito en la guía Guide to Using Technical Indicators in Expert Advisors (Guía para el uso de indicadores técnicos en Asesores Expertos).

Para adecuar las líneas cuyas intersecciones es debemos encontrar solo necesitamos configurar dos puntos para cada una de las líneas. tanto, es suficiente obtener valores de indicador para dos barras (por ejemplo la barra actual y la anterior). El precio en la barra anterior es estático, mientras que el precio la barra actual es dinámico, y por tanto se siguen generando nuevos puntos con cada nuevo tick. Aquí está el código: 

//+------------------------------------------------------------------+
//|                                      emission_of_MA_envelope.mq5 |
//|                                           Copyright 2013, DC2008 |
//|                           https://www.mql5.com/es/users/DC2008 |
//+------------------------------------------------------------------+
#property copyright "Copyright 2013, DC2008"
#property link      "https://www.mql5.com/es/users/DC2008"
#property version   "1.00"
//---
#include <GetIndicatorBuffers.mqh>
#include <Emission.mqh>
//--- external variable for storing averaging period of the iEnvelopes indicator
input int   ma_period=140;      // averaging period of the iEnvelopes indicator
//--- array for storing deviations of the iEnvelopes indicator
double      ENV[]={0.01,0.0165,0.0273,0.0452,0.0747,01234,0.204,0.3373,0.5576,0.9217,1.5237};
//--- array for storing the iMA indicator periods
int         MA[]={4,7,11,19,31,51,85};
//--- array for storing pointers to the iMA and iEnvelopes indicators
int         handle_MA[];
int         handle_Envelopes[];
//--- market data
datetime    T[],prevTimeBar=0;
double      H[],L[];
#define     HL(a, b) (a+b)/2
//--- class instances
CEmission      EnvMa(0,300);
PointEmission  pEmission;
//--- drawing styles for points of emission
#define     COLOR_UPPER  C'51,255,255'
#define     COLOR_LOWER  C'0,51,255'
#define     COLOR_MA     C'255,51,255'
color       colorPoint[]={COLOR_UPPER,COLOR_LOWER,COLOR_MA};
CodeColor   styleUpper={158,COLOR_UPPER,SMALL};
CodeColor   styleLower={158,COLOR_LOWER,SMALL};
CodeColor   styleMA={158,COLOR_MA,SMALL};
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   ArraySetAsSeries(T,true);
   ArraySetAsSeries(H,true);
   ArraySetAsSeries(L,true);
//---
   int size=ArraySize(MA);
   ArrayResize(handle_MA,size);
//--- create a pointer to the object - the iMA indicator
   for(int i=0; i<size; i++)
     {
      handle_MA[i]=iMA(NULL,0,MA[i],0,MODE_SMA,PRICE_MEDIAN);
      //--- if an error occurs when creating the object, print the message
      if(handle_MA[i]<0)
        {
         Print("The iMA object[",MA[i],"] has not been created: Error = ",GetLastError());
         //--- forced program termination
         return(-1);
        }
     }
//---
   size=ArraySize(ENV);
   ArrayResize(handle_Envelopes,size);
//--- create a pointer to the object - the iEnvelopes indicator
   for(int i=0; i<size; i++)
     {
      handle_Envelopes[i]=iEnvelopes(NULL,0,ma_period,0,MODE_SMA,PRICE_MEDIAN,ENV[i]);
      //--- if an error occurs when creating the object, print the message
      if(handle_Envelopes[i]<0)
        {
         Print("The iEnvelopes object[",ENV[i],"] has not been created: Error = ",GetLastError());
         //--- forced program termination
         return(-1);
        }
     }
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- market data
   CopyTime(NULL,0,0,2,T);
   CopyHigh(NULL,0,0,2,H);
   CopyLow(NULL,0,0,2,L);
//--- fill the declared arrays with current values from all indicator buffers
   string name;
   uint GTC=GetTickCount();
//---- indicator buffers
   double   ibMA[],ibMA1[];      // arrays for the iMA indicator
   double   ibEnvelopesUpper[];  // array for the iEnvelopes indicator (UPPER_LINE)
   double   ibEnvelopesLower[];  // array for the iEnvelopes indicator (LOWER_LINE)
   for(int i=ArraySize(handle_MA)-1; i>=0; i--)
     {
      if(!CopyBufferAsSeries(handle_MA[i],0,0,2,true,ibMA))
         return;
      //---
      for(int j=ArraySize(handle_Envelopes)-1; j>=0; j--)
        {
         if(!GetEnvelopesBuffers(handle_Envelopes[j],0,2,ibEnvelopesUpper,ibEnvelopesLower,true))
            return;
         //--- find the intersection point of the iEnvelopes(UPPER_LINE) and iMA indicators
         pEmission=EnvMa.CalcPoint(ibEnvelopesUpper[1],ibEnvelopesUpper[0],ibMA[1],ibMA[0],T[0]);
         if(pEmission.real) // if the intersection point is found, draw it in the chart
           {
            name="iEnvelopes(UPPER_LINE)"+(string)j+"=iMA"+(string)i+(string)GTC;
            EnvMa.CreatePoint(name,pEmission,styleUpper);
           }
         //--- find the intersection point of the iEnvelopes(LOWER_LINE) and iMA indicators
         pEmission=EnvMa.CalcPoint(ibEnvelopesLower[1],ibEnvelopesLower[0],ibMA[1],ibMA[0],T[0]);
         if(pEmission.real) // if the intersection point is found, draw it in the chart
           {
            name="iEnvelopes(LOWER_LINE)"+(string)j+"=iMA"+(string)i+(string)GTC;
            EnvMa.CreatePoint(name,pEmission,styleLower);
           }
        }
      //---
      for(int j=ArraySize(handle_MA)-1; j>=0; j--)
        {
         if(i!=j)
           {
            if(!CopyBufferAsSeries(handle_MA[j],0,0,2,true,ibMA1))
               return;
            //--- find the intersection point of the iMA and iMA indicators
            pEmission=EnvMa.CalcPoint(ibMA1[1],ibMA1[0],ibMA[1],ibMA[0],T[0]);
            if(pEmission.real) // if the intersection point is found, draw it in the chart
              {
               name="iMA"+(string)j+"=iMA"+(string)i+(string)GTC;
               EnvMa.CreatePoint(name,pEmission,styleMA);
              }
           }
        }
     }
//--- deletion of the graphical objects of emission not to stuff the chart
   if(T[0]>prevTimeBar) // delete once per bar
     {
      int  total=ObjectsTotal(0,0,-1);
      prevTimeBar=T[0];
      for(int obj=total-1;obj>=0;obj--)
        {
         string obj_name=ObjectName(0,obj,0,OBJ_TEXT);
         datetime obj_time=(datetime)ObjectGetInteger(0,obj_name,OBJPROP_TIME);
         if(obj_time<T[0])
            ObjectDelete(0,obj_name);
        }
      Comment("Emission © DC2008       Objects = ",total);
     }
//---
  }

No insistiré en cada detalle de este Asesor Experto. Lo más notable aquí es que, para dibujar la emisión, hemos usado una instancia de clase CEmission, responsable de los cálculos y visualización de puntos de intersección de cualquier par de líneas.

//+------------------------------------------------------------------+
//|                                                     Emission.mqh |
//|                                           Copyright 2013, DC2008 |
//|                           https://www.mql5.com/es/users/DC2008 |
//+------------------------------------------------------------------+
#property copyright "Copyright 2013, DC2008"
#property link      "https://www.mql5.com/es/users/DC2008"
#property version   "1.00"
#define  BIG   7    // point size
#define  SMALL 3    // point size
//+------------------------------------------------------------------+
//| pMABB structure                                                  |
//+------------------------------------------------------------------+
struct PointEmission
  {
   double            x;       // X-coordinate of the time point
   double            y;       // Y-coordinate of the price point
   datetime          t;       // t-coordinate of the point's time
   bool              real;    // whether the point exists
  };
//+------------------------------------------------------------------+
//| CodeColor structure                                              |
//+------------------------------------------------------------------+
struct CodeColor
  {
   long              Code;    // point symbol code 
   color             Color;   // point color
   int               Width;   // point size
  };
//+------------------------------------------------------------------+
//| Base class for emissions                                         |
//+------------------------------------------------------------------+
class CEmission
  {
private:
   int               sec;
   int               lim_Left;   // limiting range of visibility in bars
   int               lim_Right;  // limiting range of visibility in bars

public:
   PointEmission     CalcPoint(double   y1,  // Y-coordinate of straight line 1 on bar [1]
                               double   y0,  // Y-coordinate of straight line 1 on bar [0]
                               double   yy1, // Y-coordinate of straight line 2 on bar [1] 
                               double   yy0, // Y-coordinate of straight line 2 on bar [0]
                               datetime t0   // t-coordinate of the current bar Time[0]
                               );
   bool              CreatePoint(string name,            // point name
                                 PointEmission &point,   // coordinates of the point
                                 CodeColor &style);      // point drawing style
                                 CEmission(int limitLeft,int limitRight);
                    ~CEmission();
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CEmission::CEmission(int limitLeft,int limitRight)
  {
   sec=PeriodSeconds();
   lim_Left=limitLeft;
   lim_Right=limitRight;
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CEmission::~CEmission()
  {
  }
//+------------------------------------------------------------------+
//| The CalcPoint method of the CEmission class                      |
//+------------------------------------------------------------------+
PointEmission CEmission::CalcPoint(double   y1, // Y-coordinate of straight line 1 on bar [1]
                                   double   y0, // Y-coordinate of straight line 1 on bar [0]
                                   double   yy1,// Y-coordinate of straight line 2 on bar [1]
                                   double   yy0,// Y-coordinate of straight line 2 on bar [0]
                                   datetime t0  // t-coordinate of the current bar Time[0]
                                   )
  {
   PointEmission point={NULL,NULL,NULL,false};
   double y0y1=y0-y1;
   double y1yy1=y1-yy1;
   double yy0yy1=yy0-yy1;
   double del0=yy0yy1-y0y1;
   if(MathAbs(del0)>0)
     {
      point.x=y1yy1/del0;
      if(point.x<lim_Left || point.x>lim_Right) return(point);
      point.y=y1+y0y1*y1yy1/del0;
      if(point.y<0) return(point);
      point.t=t0+(int)(point.x*sec);
      point.real=true;
      return(point);
     }
   return(point);
  }
//+------------------------------------------------------------------+
//| The CreatePoint method of the CEmission class                    |
//+------------------------------------------------------------------+
bool CEmission::CreatePoint(string name,            // point name
                            PointEmission &point,  // coordinates of the point
                            CodeColor &style)      // point drawing style
  {
   if(ObjectCreate(0,name,OBJ_TEXT,0,0,0))
     {
      ObjectSetString(0,name,OBJPROP_FONT,"Wingdings");
      ObjectSetInteger(0,name,OBJPROP_ANCHOR,ANCHOR_CENTER);
      ObjectSetInteger(0,name,OBJPROP_FONTSIZE,style.Width);
      ObjectSetString(0,name,OBJPROP_TEXT,CharToString((uchar)style.Code));
      ObjectSetDouble(0,name,OBJPROP_PRICE,point.y);
      ObjectSetInteger(0,name,OBJPROP_TIME,point.t);
      ObjectSetInteger(0,name,OBJPROP_COLOR,style.Color);
      return(true);
     }
   return(false);
  }

Debemos señalar que los puntos de emisión se muestran por medio de objetos gráficos tales como Texto. En primer lugar, viene del hecho de que las anclas de objetos deberían estar alineadas en el centro del símbolo. En segundo lugar, el tamaño del objeto puede variar ampliamente. Estas propiedades de punto ofrecen un gran potencial para obtener emisiones complejas.

Fig. 2. Emisión original de los indicadores iMA y iEnvelopes

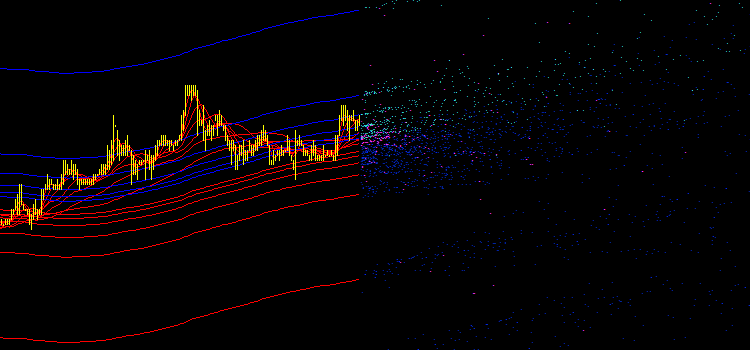
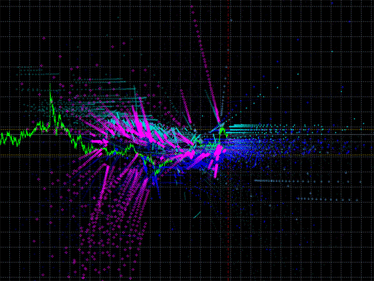
Fig. 2. Emisión original de los indicadores iMA y iEnvelopes

 

Características Integrales de Emisiones

Tras colocar el Asesor Experto en el tráfico, obtendremos muchos puntos en diferentes colores (vea la Fig. 2):

  • Aguamarina: intersecciones de los indicadores iMA y iEnvelopes, buffer UPPER_LINE.
  • Azul - intersecciones de los indicadores iMA y iEnvelopes, buffer LOWER_LINE.
  • Magenta - intersecciones de los indicadores iMA y iMA.

Este caos no se puede usar en trading automatizado. Necesitamos señales, niveles y otras características cuantitativas de mercado. Aquí solo obtendremos imágenes visuales para la meditación y la quiromancia, pero ningún número.

Las características integrales de las emisiones sirven para generalizar datos obtenidos como resultado de emisiones de indicador. 

La necesidad de características integrales de emisiones también se debe al hecho de que ofrecen oportunidades para investigar el mercado usando tipos nuevos de indicador: canales integrales, líneas, niveles, señales, etcétera. Para determinar los valores de emisión más típicos, empezaremos poco a poco y calcularemos el precio medio para cada tipo de punto con el fin de seguir dibujando líneas horizontales a través de ellos, tal y como se muestra a continuación:

Fig. 3. Líneas horizontales del precio medio para cada tipo de punto

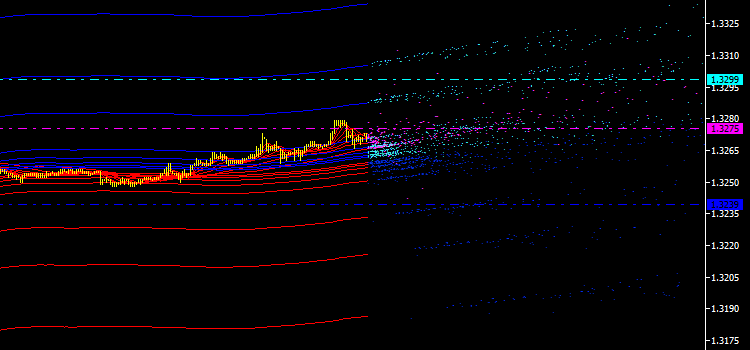
Fig. 3. Líneas horizontales del precio medio para cada tipo de punto

Para ello, añadiremos unos cuantos bloques de código adicionales al código ya existente. En la sección de datos:

//--- arrays for calculation and display of integral characteristics of emissions
#define     NUMBER_TYPES_POINT   3
double      sum[NUMBER_TYPES_POINT],sumprev[NUMBER_TYPES_POINT];
datetime    sum_time[NUMBER_TYPES_POINT];
int         n[NUMBER_TYPES_POINT],W[NUMBER_TYPES_POINT];
color       colorLine[]={clrAqua,clrBlue,clrMagenta};

En el módulo OnTick():

//--- calculation of integral characteristics of emissions
   ArrayInitialize(n,0);
   ArrayInitialize(sum,0.0);
   ArrayInitialize(sum_time,0.0);
   for(int obj=total-1;obj>=0;obj--)
     {
      string   obj_name=ObjectName(0,obj,0,OBJ_TEXT);
      datetime obj_time=(datetime)ObjectGetInteger(0,obj_name,OBJPROP_TIME);
      if(obj_time>T[0])
        {
         color    obj_color=(color)ObjectGetInteger(0,obj_name,OBJPROP_COLOR);
         double   obj_price=ObjectGetDouble(0,obj_name,OBJPROP_PRICE);
         for(int i=ArraySize(n)-1; i>=0; i--)
            if(obj_color==colorPoint[i])
              {
               n[i]++;
               sum[i]+=obj_price;
               sum_time[i]+=obj_time;
              }
        }
     }
//--- displaying integral characteristics of emissions
   for(int i=ArraySize(n)-1; i>=0; i--)
     {
      if(n[i]>0)
        {
         name="H.line."+(string)i;
         ObjectCreate(0,name,OBJ_HLINE,0,0,0,0);
         ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]);
         ObjectSetInteger(0,name,OBJPROP_STYLE,STYLE_DASHDOT);
         ObjectSetInteger(0,name,OBJPROP_WIDTH,1);
         ObjectSetDouble(0,name,OBJPROP_PRICE,sum[i]/n[i]);
        }
     }

Continuemos. Ahora debemos calcular el valor de tiempo medio para cada conjunto de puntos y marcarlo en la línea correspondiente del precio medio (vea la Fig. 4). Así obtendremos las primeras características cuantitativas de emisiones que nunca son estáticas, siempre están en movimiento en el espacio.

El gráfico solo muestra sus posiciones en este momento. Debemos mantenerlas fijas en el historial de algún modo para poder estudiarlas después. Hasta el momento, todavía no está claro cómo se puede hacer esto, y debemos considerarlo con cuidado... Por ahora, seguiremos adelante y mostraremos el número de puntos involucrados en el cálculo al lado de los marcadores en el gráfico. Estos son una especie de pesos de las características obtenidas que también serán útiles conforme sigamos con el análisis.

Fig. 4. Marcadores en puntos de intersección del precio medio y tiempo medio.

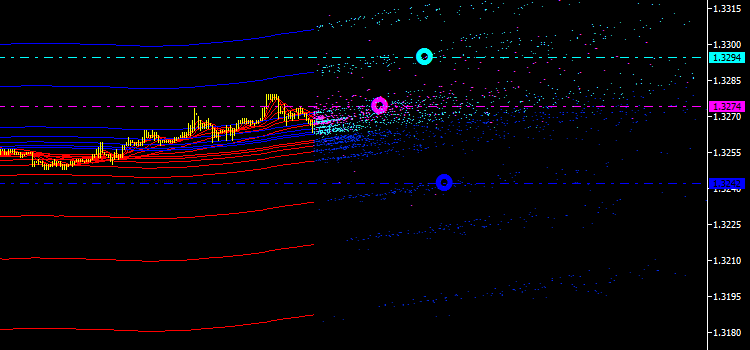
Fig. 4. Marcadores en puntos de intersección del precio medio y tiempo medio.

Sin embargo, por motivos de conveniencia del análisis, usaremos sus proporciones porcentuales. Puesto que los puntos de emisión principales son el resultado de las intersecciones de los indicadores iMA y iEnvelopes, consideraremos que su suma es igual a 100%. Veamos qué tenemos hasta el momento:

Fig. 5. Proporción porcentual de cada tipo de puntos de emisión.

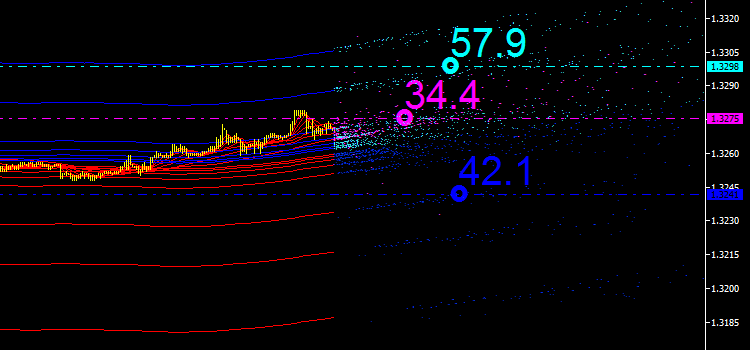
Fig. 5. Proporción porcentual de cada tipo de puntos de emisión.

Si añadimos los tres valores, darán un total superior al 100%. El valor de 34,4 que se muestra en magenta es la propiedad de los puntos de intersección de iMA e iMA en un determinado punto en el tiempo; es decir, el indicador se ha cruzado consigo mismo, pero con diferentes datos de entrada. En este caso, se trata de un valor de referencia, y más tarde quizás pensaremos sobre cómo se puede usar en el análisis del mercado.

Sin embargo, ahora surge otro problema al obtener proporciones porcentuales del número de puntos: ¿cómo podemos arreglar también los valores porcentuales de las características de emisión en el historial, especialmente teniendo en cuenta que también son variables?

 

Análisis Gráfico

Aunque ahora ya tenemos las características integrales de emisiones, todavía no estamos lo suficientemente próximos al análisis y desarrollo de una estrategia de trading basada en los datos obtenidos. Sin embargo, cualquier lector minucioso seguramente ya habrá encontrado una solución a este problema (vea la Fig. 1). Mi solución es la siguiente: propongo dibujar curvas integrales usando grosores diferentes que serían proporcionales a la proporción porcentual de los principales puntos de emisión.

La porción actual de la curva se dibujará a través de la línea del precio medio entre la barra actual y la anterior, teniendo en cuenta que estas coordenadas se toman, de hecho, del futuro. Es una especie de canal integral guía de emisiones de indicador. Sé que suena muy complicado... Y que se debe de estar preguntando si merece la pena seguir leyendo o no. Pero espero que esto se vaya tornando más interesante conforme vayamos avanzando.

Fig. 6. Canal integral de emisiones de indicador.

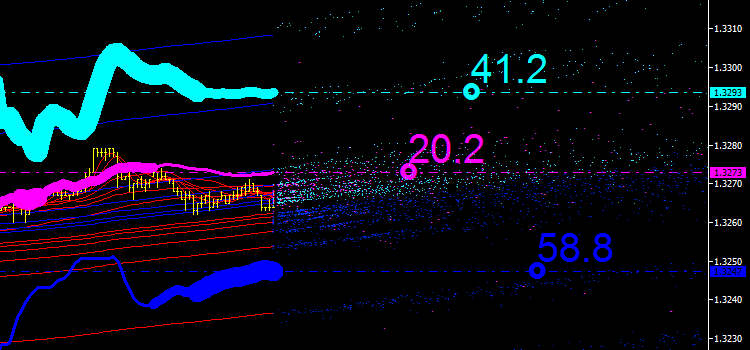
Fig. 6. Canal integral de emisiones de indicador.

Al parecer, hemos encontrado un uso para la emisión de "iMA & iMA" (que se muestra en magenta en el gráfico). Y hemos obtenido un nuevo indicador: la media móvil integrada.

Ahora volvamos al código del Asesor Experto para ver qué cambios han tenido lugar en el módulo OnTick():

//--- displaying integral characteristics of emissions
   ArrayInitialize(W,10);
   W[ArrayMaximum(n)]=20;
   W[ArrayMinimum(n)]=3;
   for(int i=ArraySize(n)-1; i>=0; i--)
     {
      if(n[i]>0)
        {
         //--- horizontal lines of mean prices
         name="H.line."+(string)i;
         ObjectCreate(0,name,OBJ_HLINE,0,0,0,0);
         ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]);
         ObjectSetInteger(0,name,OBJPROP_STYLE,STYLE_DASHDOT);
         ObjectSetInteger(0,name,OBJPROP_WIDTH,1);
         ObjectSetDouble(0,name,OBJPROP_PRICE,sum[i]/n[i]);
         //--- markers
         name="P."+(string)i;
         ObjectCreate(0,name,OBJ_TEXT,0,0,0);
         ObjectSetString(0,name,OBJPROP_FONT,"Wingdings");
         ObjectSetInteger(0,name,OBJPROP_ANCHOR,ANCHOR_CENTER);
         ObjectSetInteger(0,name,OBJPROP_FONTSIZE,17);
         ObjectSetString(0,name,OBJPROP_TEXT,CharToString(163));
         ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]);
         ObjectSetDouble(0,name,OBJPROP_PRICE,sum[i]/n[i]);
         ObjectSetInteger(0,name,OBJPROP_TIME,sum_time[i]/n[i]);
         //--- integral curves
         name="T"+(string)i+".line"+(string)T[1];
         ObjectCreate(0,name,OBJ_TREND,0,0,0);
         ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]);
         ObjectSetInteger(0,name,OBJPROP_WIDTH,W[i]);
         if(sumprev[i]>0)
           {
            ObjectSetDouble(0,name,OBJPROP_PRICE,0,sumprev[i]);
            ObjectSetInteger(0,name,OBJPROP_TIME,0,T[1]);
            ObjectSetDouble(0,name,OBJPROP_PRICE,1,(sum[i]/n[i]));
            ObjectSetInteger(0,name,OBJPROP_TIME,1,T[0]);
           }
         //--- numerical values of integral characteristics
         name="Text"+(string)i+".control";
         ObjectCreate(0,name,OBJ_TEXT,0,0,0);
         ObjectSetInteger(0,name,OBJPROP_ANCHOR,ANCHOR_LEFT_LOWER);
         ObjectSetInteger(0,name,OBJPROP_FONTSIZE,30);
         ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]);
         string str=DoubleToString((double)n[i]/(double)(n[0]+n[1])*100,1);
         ObjectSetString(0,name,OBJPROP_TEXT,str);
         ObjectSetDouble(0,name,OBJPROP_PRICE,0,(sum[i]/n[i]));
         ObjectSetInteger(0,name,OBJPROP_TIME,0,sum_time[i]/n[i]);
        }
     }

Continuemos con nuestro análisis gráfico. Pero nos falta algo... Parece que nos hemos saltado otra característica importante de la emisión. Las curvas integrales se dibujaron basándose solo en los precios medios. Sin embargo, nosotros debemos considerar la coordenada de tiempo medio. Eche un vistazo a la figura de abajo y preste especial atención a los límites del canal:

  • La línea aguamarina es el límite superior del canal.
  • La línea azul es el límite inferior del canal.

Ahora debemos identificar el marcador más cercano temporalmente a la barra cero.

Límite superior guía del canal
 Límite inferior guía del canal

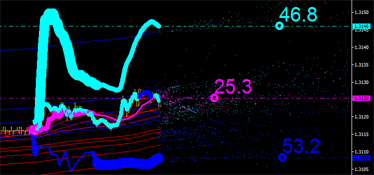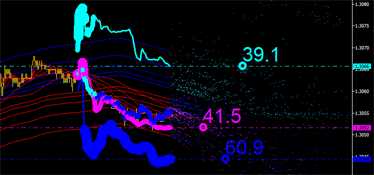Fig. 7. Características integrales guía en el tiempo. Izquierda:: límite superior guía del canal. Derecha: límite inferior guía del canal.

Este problema se puede solucionar de la siguiente manera: añadimos la línea de precio (PRICE_MEDIAN) l gráfico de precios y hacemos que la línea cambie de color dependiendo del color del marcador (aguamarina o azul) que esté más cercano a la última barra (vea la Fig. 7). Además, insertaremos el siguiente bloque de código en el código ya existente:

//---
   if(n[ArrayMinimum(n)]>0)
     {
      datetime d[2];
      for(int j=0;j<2;j++)
        {
         d[j]=sum_time[j]/n[j];
        }
      int i=ArrayMinimum(d);

      name="Price.line"+(string)T[1];
      ObjectCreate(0,name,OBJ_TREND,0,0,0);
      ObjectSetInteger(0,name,OBJPROP_WIDTH,8);
      ObjectSetDouble(0,name,OBJPROP_PRICE,0,HL(H[1],L[1]));
      ObjectSetInteger(0,name,OBJPROP_TIME,0,T[1]);
      ObjectSetDouble(0,name,OBJPROP_PRICE,1,HL(H[0],L[0]));
      ObjectSetInteger(0,name,OBJPROP_TIME,1,T[0]);
      ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine1[i]);
     }
//---

Ahora prepárese para el siguiente paso. ¿Qué pasaría si intentáramos dibujar emisiones basadas en características integrales de emisiones originales, algo así como emisiones de segunda orden? Después de todo, esas líneas también se cruzan, y deberían, por tanto, tener puntos de emisión. Veamos qué sale de ello. Refuerce el anterior bloque de código añadiendo las siguientes líneas de código:

      //--- emissions of integral characteristics of the original emissions
      pEmission=EnvMa.CalcPoint(sumprev[0],sum[0]/n[0],sumprev[2],sum[2]/n[2],T[0]);
      if(pEmission.real) // if the intersection point is found, draw it in the chart
        {
         name="test/up"+(string)GTC;
         EnvMa.CreatePoint(name,pEmission,styleUpper2);
        }
      pEmission=EnvMa.CalcPoint(sumprev[1],sum[1]/n[1],sumprev[2],sum[2]/n[2],T[0]);
      if(pEmission.real) // if the intersection point is found, draw it in the chart
        {
         name="test/dn"+(string)GTC;
         EnvMa.CreatePoint(name,pEmission,styleLower2);
        }

E inserte las siguientes líneas en la sección de datos:

#define     COLOR_2_UPPER  C'102,255,255'
#define     COLOR_2_LOWER  C'51,102,255'
CodeColor   styleUpper2={178,COLOR_2_UPPER,BIG};
CodeColor   styleLower2={178,COLOR_2_LOWER,BIG};

Puede comprobar los resultados en la figura de abajo. Podemos ver nuevos puntos que no nos sugieren nada por ahora.

Fig. 8. Emisiones de líneas integrales

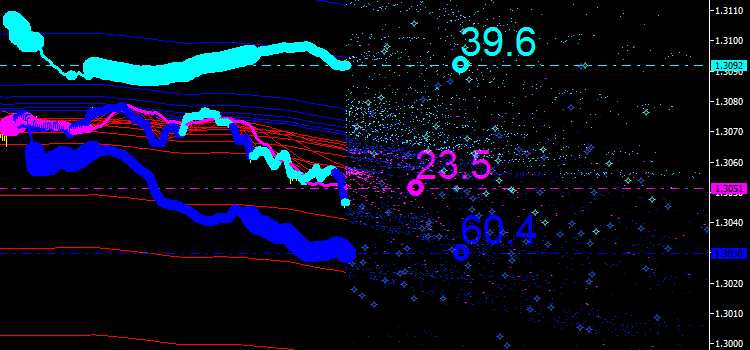
Fig. 8. Emisiones de líneas integrales

Las características integrales, evidentemente, también se pueden calcular para nuevos puntos (vea la Fig. 9) con sus emisiones dibujadas en el tráfico, ¡y así sucesivamente hasta que se vuelva inviable!

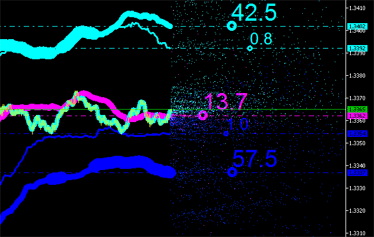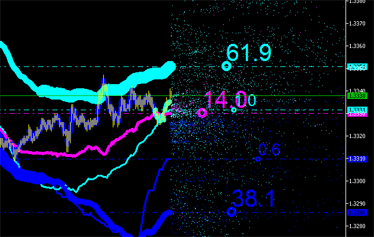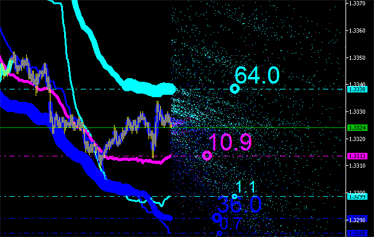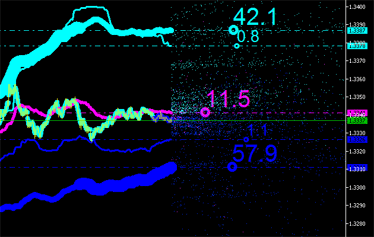Emisión Emisión
Emisión Emisión

Fig. 9. Características integrales de emisiones

De modo que hemos dibujado todo lo que necesitábamos y hemos obtenido las características integrales de emisiones. Ahora podemos proceder a su análisis y al desarrollo de una estrategia de trading. ¡Pero parece imposible! ¿Qué es lo que nos detiene ahora?

 

Series Cronológicas de Emisiones

El análisis gráfico nos permite estudiar características integrales de emisiones, pero hace uso de demasiados recursos. Si tratamos de ejecutar el código propuesto en el modo visual del Probador de Estrategias, ¡la velocidad de simulación caerá a cero! Esto se debe al gran número de objetos gráficos en el gráfico.

De modo que lo más natural es que deseemos deshacernos de toda esa abundancia de puntos y dejar solo las curvas integrales. Para resolver este problema usaremos arrays especiales (buffers).

Las series cronológicas de emisiones son arrays especialmente distribuidos donde se acumula la información sobre las emisiones.

Se diferencian de las series cronológicas estándar en el hecho de que los datos que contienen no siguen una secuencia temporal, a pesar de que el tiempo es el elemento clave.

Series Cronológicas de Emisiones

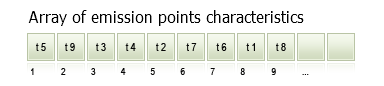
Fig. 10. Series cronológicas de características de emisiones

Estos arrays se distribuyen de manera que los nuevos elementos se almacenan en celdas vacías o en celdas llenas con valores antiguos. Por ello, usaremos la clase CTimeEmission. Aquí puede ver cómo se implementa en el código:

//+------------------------------------------------------------------+
//|                                                 TimeEmission.mqh |
//|                                           Copyright 2013, DC2008 |
//|                           https://www.mql5.com/es/users/DC2008 |
//+------------------------------------------------------------------+
#property copyright "Copyright 2013, DC2008"
#property link      "https://www.mql5.com/es/users/DC2008"
#property version   "1.00"
//---
#include <Emission.mqh>
#define ARRMAX       64
#define ARRDELTA     8
//+------------------------------------------------------------------+
//| pIntegral structure                                              |
//+------------------------------------------------------------------+
struct pIntegral
  {
   double            y;       // Y-coordinate of the price point (mean price of the points with the same time)
   datetime          t;       // t-coordinate of the point's time
   int               n;       // n-number of points with the same time
  };
//+------------------------------------------------------------------+
//| Base class for time series of emissions                          |
//+------------------------------------------------------------------+
class CTimeEmission
  {
private:
   pIntegral         time_series_Emission[]; // time series of emission
   int               size_ts; // number of elements in time series 
   datetime           t[1];
public:
   //--- method of writing new elements to time series of emission
   void              Write(PointEmission &point);
   //--- method of reading integral characteristics of emissions
   pIntegral         Read();
                     CTimeEmission();
                    ~CTimeEmission();
  };

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CTimeEmission::CTimeEmission()
  {
   ArrayResize(time_series_Emission,ARRMAX,ARRMAX);
   size_ts=ArraySize(time_series_Emission);
   for(int i=size_ts-1; i>=0; i--)
      time_series_Emission[i].t=0;
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CTimeEmission::~CTimeEmission()
  {
  }
//+------------------------------------------------------------------+
//| The Write method of the CTimeEmission class                      |
//+------------------------------------------------------------------+
void CTimeEmission::Write(PointEmission &point)
  {
   CopyTime(NULL,0,0,1,t);
   size_ts=ArraySize(time_series_Emission);
   for(int k=0;k<size_ts;k++)
     {
      if(time_series_Emission[k].t<t[0]) // find the first empty cell
        {
         if(k>size_ts-ARRDELTA)
           {   // increase the array size, if necessary
            int narr=ArrayResize(time_series_Emission,size_ts+ARRMAX,ARRMAX);
            for(int l=size_ts-1;l<narr;l++)
               time_series_Emission[l].t=0;
           }
         time_series_Emission[k].y=point.y;
         time_series_Emission[k].t=point.t;
         time_series_Emission[k].n=1;
         return;
        }
      if(time_series_Emission[k].t==point.t) // find the first similar cell
        {
         time_series_Emission[k].y=(time_series_Emission[k].y*time_series_Emission[k].n+point.y)/(time_series_Emission[k].n+1);
         time_series_Emission[k].n++;
         return;
        }
     }
  }
//+------------------------------------------------------------------+
//| The Read method of the CTimeEmission class                       |
//+------------------------------------------------------------------+
pIntegral CTimeEmission::Read()
  {
   CopyTime(NULL,0,0,1,t);
   pIntegral property_Emission={0.0,0,0};
   size_ts=ArraySize(time_series_Emission);
   for(int k=0;k<size_ts;k++)
     {
      if(time_series_Emission[k].t>=t[0])
        {
         property_Emission.y+=time_series_Emission[k].y*time_series_Emission[k].n;
         property_Emission.t+=(time_series_Emission[k].t-t[0])*time_series_Emission[k].n;
         property_Emission.n+=time_series_Emission[k].n;
        }
     }
   if(property_Emission.n>0)
     {
      property_Emission.y=property_Emission.y/property_Emission.n;
      property_Emission.t=property_Emission.t/property_Emission.n+t[0];
     }
   return(property_Emission);
  }

Aquí podemos observar la implementación de dos métodos de clase: escribir puntos de emisión a series cronológicas y leer valores de características integrales de emisiones.

 

Cálculo Parsimonioso de Características Integrales

Ahora que ya tenemos las series cronológicas de emisiones, podemos empezar a crear un algoritmo parsimonioso para el cálculo de características integrales con el fin de seguir desarrollando una estrategia de trading. Actualicemos el Asesor Experto original: 

//+------------------------------------------------------------------+
//|                                   emission_of_MA_envelope_ts.mq5 |
//|                                           Copyright 2013, DC2008 |
//|                           https://www.mql5.com/es/users/DC2008 |
//+------------------------------------------------------------------+
#property copyright "Copyright 2013, DC2008"
#property link      "https://www.mql5.com/es/users/DC2008"
#property version   "1.00"
//---
#include <GetIndicatorBuffers.mqh>
#include <Emission.mqh>
#include <TimeEmission.mqh>
//--- number of point types
#define     NUMBER_TYPES_POINT   3
//--- array for storing the iMA indicator periods
int      MA[]={4,7,11,19,31,51,85};
//--- external variable for storing averaging period of the iEnvelopes indicator
input int ma_period=140; // averaging period of the iEnvelopes indicator
//--- array for storing deviations of the iEnvelopes indicator
double   ENV[]={0.01,0.0165,0.0273,0.0452,0.0747,01234,0.204,0.3373,0.5576,0.9217,1.5237};
//--- array for storing pointers to the iMA indicator
int      handle_MA[];
//--- array for storing pointers to the iEnvelopes indicator
int      handle_Envelopes[];
//--- market data
datetime    T[],prevTimeBar=0;
double      H[],L[];
#define     HL(a, b) (a+b)/2
//--- class instances
CEmission      EnvMa(0,200);
PointEmission  pEmission;
CTimeEmission  tsMA[NUMBER_TYPES_POINT];
pIntegral      integral[NUMBER_TYPES_POINT];
//--- drawing styles for points of emission
#define     DEL            500
//--- arrays for calculation and display of integral characteristics of emissions
double      sumprev[NUMBER_TYPES_POINT];
int         n[NUMBER_TYPES_POINT],W[NUMBER_TYPES_POINT];
color       colorLine[]={clrAqua,clrBlue,clrMagenta};
int         fontPoint[]={30,30,30};
int         fontMarker[]={16,16,16};
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   ArraySetAsSeries(T,true);
   ArraySetAsSeries(H,true);
   ArraySetAsSeries(L,true);
   ArrayInitialize(sumprev,0.0);
//---
   int size=ArraySize(MA);
   ArrayResize(handle_MA,size);
//--- create a pointer to the object - the iMA indicator
   for(int i=0; i<size; i++)
     {
      handle_MA[i]=iMA(NULL,0,MA[i],0,MODE_SMA,PRICE_MEDIAN);
      //--- if an error occurs when creating the object, print the message
      if(handle_MA[i]<0)
        {
         Print("The iMA object[",MA[i],"] has not been created: Error = ",GetLastError());
         //--- forced program termination
         return(-1);
        }
     }
//+------------------------------------------------------------------+
   size=ArraySize(ENV);
   ArrayResize(handle_Envelopes,size);
//--- create a pointer to the object - the iEnvelopes indicator
   for(int i=0; i<size; i++)
     {
      handle_Envelopes[i]=iEnvelopes(NULL,0,ma_period,0,MODE_SMA,PRICE_MEDIAN,ENV[i]);
      //--- if an error occurs when creating the object, print the message
      if(handle_Envelopes[i]<0)
        {
         Print("The iEnvelopes object[",ENV[i],"] has not been created: Error = ",GetLastError());
         //--- forced program termination
         return(-1);
        }
     }
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---

  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- market data
   CopyTime(NULL,0,0,2,T);
   CopyHigh(NULL,0,0,2,H);
   CopyLow(NULL,0,0,2,L);
//--- fill the declared arrays with current values from all indicator buffers
   string name;
   uint GTC=GetTickCount();
//---- indicator buffers
   double   ibMA[],ibMA1[];      // arrays for the iMA indicator
   double   ibEnvelopesUpper[];  // array for the iEnvelopes indicator (UPPER_LINE)
   double   ibEnvelopesLower[];  // array for the iEnvelopes indicator (LOWER_LINE)
   for(int i=ArraySize(handle_MA)-1; i>=0; i--)
     {
      if(!CopyBufferAsSeries(handle_MA[i],0,0,2,true,ibMA))
         return;
      //---
      for(int j=ArraySize(handle_Envelopes)-1; j>=0; j--)
        {
         if(!GetEnvelopesBuffers(handle_Envelopes[j],0,2,ibEnvelopesUpper,ibEnvelopesLower,true))
            return;
         //--- find the intersection point of the iEnvelopes(UPPER_LINE) and iMA indicators
         pEmission=EnvMa.CalcPoint(ibEnvelopesUpper[1],ibEnvelopesUpper[0],ibMA[1],ibMA[0],T[0]);
         if(pEmission.real) // if the intersection point is found, add it to the time series of emission
            tsMA[0].Write(pEmission);
         //--- find the intersection point of the iEnvelopes(LOWER_LINE) and iMA indicators
         pEmission=EnvMa.CalcPoint(ibEnvelopesLower[1],ibEnvelopesLower[0],ibMA[1],ibMA[0],T[0]);
         if(pEmission.real) // if the intersection point is found, add it to the time series of emission
            tsMA[1].Write(pEmission);
        }
      //---
      for(int j=ArraySize(handle_MA)-1; j>=0; j--)
        {
         if(i!=j)
           {
            if(!CopyBufferAsSeries(handle_MA[j],0,0,2,true,ibMA1))
               return;
            //--- find the intersection point of the iMA and iMA indicators
            pEmission=EnvMa.CalcPoint(ibMA1[1],ibMA1[0],ibMA[1],ibMA[0],T[0]);
            if(pEmission.real) // if the intersection point is found, add it to the time series of emission
               tsMA[2].Write(pEmission);
           }
        }
     }
//--- deletion of the graphical objects of emission not to stuff the chart
   if(T[0]>prevTimeBar)
     {
      prevTimeBar=T[0];
      //---
      for(int i=ArraySize(n)-1; i>=0; i--)
         sumprev[i]=integral[i].y;
      //---
      for(int obj=ObjectsTotal(0,0,-1)-1;obj>=0;obj--)
        {
         string obj_name=ObjectName(0,obj,0,OBJ_TREND);
         datetime obj_time=(datetime)ObjectGetInteger(0,obj_name,OBJPROP_TIME);
         if(obj_time<T[0]-DEL*PeriodSeconds())
            ObjectDelete(0,obj_name);
        }
      Comment("Emission © DC2008   Graphical objects = ",ObjectsTotal(0,0,-1));
     }
//--- calculation of integral characteristics of emission
   for(int i=ArraySize(n)-1; i>=0; i--)
      integral[i]=tsMA[i].Read();
//--- displaying integral characteristics of emission
   ArrayInitialize(W,5);
   if(integral[0].n>integral[1].n)
     {
      W[0]=20;
      W[1]=10;
     }
   else
     {
      W[0]=10;
      W[1]=20;
     }
   for(int i=ArraySize(n)-1; i>=0; i--)
     {
      //--- horizontal lines of mean prices
      name="H.line."+(string)i;
      ObjectCreate(0,name,OBJ_HLINE,0,0,0,0);
      ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]);
      ObjectSetInteger(0,name,OBJPROP_STYLE,STYLE_DASHDOT);
      ObjectSetInteger(0,name,OBJPROP_WIDTH,1);
      ObjectSetDouble(0,name,OBJPROP_PRICE,integral[i].y);
      //--- markers
      name="P."+(string)i;
      ObjectCreate(0,name,OBJ_TEXT,0,0,0);
      ObjectSetString(0,name,OBJPROP_FONT,"Wingdings");
      ObjectSetInteger(0,name,OBJPROP_ANCHOR,ANCHOR_CENTER);
      ObjectSetInteger(0,name,OBJPROP_FONTSIZE,fontMarker[i]);
      ObjectSetString(0,name,OBJPROP_TEXT,CharToString(163));
      ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]);
      ObjectSetDouble(0,name,OBJPROP_PRICE,integral[i].y);
      ObjectSetInteger(0,name,OBJPROP_TIME,integral[i].t);
      //--- integral curves
      name="T"+(string)i+".line"+(string)T[1];
      ObjectCreate(0,name,OBJ_TREND,0,0,0);
      ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]);
      ObjectSetInteger(0,name,OBJPROP_WIDTH,W[i]);
      if(sumprev[i]>0)
        {
         ObjectSetDouble(0,name,OBJPROP_PRICE,0,sumprev[i]);
         ObjectSetInteger(0,name,OBJPROP_TIME,0,T[1]);
         ObjectSetDouble(0,name,OBJPROP_PRICE,1,integral[i].y);
         ObjectSetInteger(0,name,OBJPROP_TIME,1,T[0]);
        }
      //--- numerical values of integral characteristics
      if(integral[0].n+integral[1].n>0)
        {
         name="Text"+(string)i+".control";
         ObjectCreate(0,name,OBJ_TEXT,0,0,0);
         ObjectSetInteger(0,name,OBJPROP_ANCHOR,ANCHOR_LEFT_LOWER);
         ObjectSetInteger(0,name,OBJPROP_FONTSIZE,fontPoint[i]);
         ObjectSetInteger(0,name,OBJPROP_COLOR,colorLine[i]);
         string str=DoubleToString((double)integral[i].n/(double)(integral[0].n+integral[1].n)*100,1);
         ObjectSetString(0,name,OBJPROP_TEXT,str);
         ObjectSetDouble(0,name,OBJPROP_PRICE,0,integral[i].y);
         ObjectSetInteger(0,name,OBJPROP_TIME,0,integral[i].t);
        }
     }
  }

El código ahora es más corto, mientras que la velocidad de cálculo ha aumentado. ¡Ahora puede simular y optimizar sus robots de trading sin visualización alguna! 

 

Uso de Características Integrales en Trading

Las características integrales se pueden usar como generadores de señales para:

  • ruptura de canal,
  • intersección entre ellas o con el precio,
  • cambio en la dirección.
Por ejemplo, la figura de abajo muestra cómo las características integrales de emisiones se pueden usar hipotéticamente en intersecciones con el precio. Las señales de venta se generan cuando el precio se cruza hacia arriba con la curva azul, y las señales de compra se generan en el cruce hacia abajo del precio con la curva aguamarina.

Fig. 11. Señales de trading en la intersección de características integrales de emisiones.

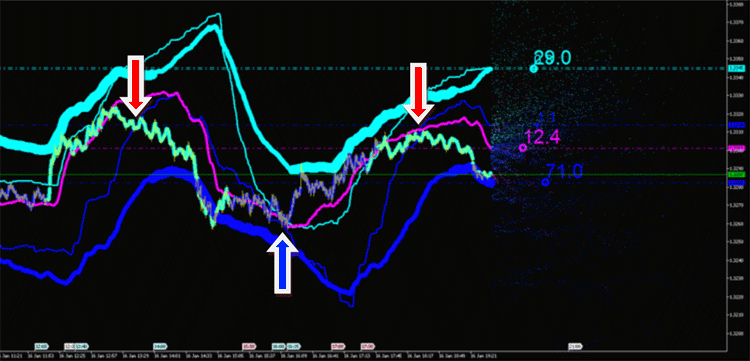
Fig.  11. Señales de trading en la intersección de características integrales de emisiones.

 

Conclusión

  1. El cálculo de características integrales de emisiones de indicador facilita nuevas herramientas y métodos para el análisis de mercado (series cronológicas).
  2. Usando series cronológicas, hemos conseguido aumentar la velocidad de cálculo de características integrales.
  3. Y nos da la posibilidad de desarrollar estrategias de trading automatizado que usan emisiones.

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/610

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores
MQL5 Market Cumple Un Año MQL5 Market Cumple Un Año
Ha pasado un año desde el lanzamiento de ventas en el Mercado de MQL5 (MQL5 Market). Ha sido un año de trabajo duro que ha resultado en el nuevo servicio de la mayor tienda de robots de trading e indicadores técnicos para la plataforma MetaTrader 5.
Cómo Poner a Prueba un Robot de Trading antes de Comprarlo Cómo Poner a Prueba un Robot de Trading antes de Comprarlo
Comprar un robot de trading en el Mercado de MQL5 (Market) tiene un beneficio distintivo sobre todas las demás opciones similares: un sistema automatizado que se puede poner a prueba en profundidad en el terminal de MetaTrader 5. Antes de comprar un Asesor Experto (EA, por sus siglas en inglés) debería simularlo en todos sus modos poco favorables en el Probador de Estrategias incorporado para obtener un control absoluto del sistema.
Libro de Recetas MQL5: Usar Diferentes Modos de Impresión Libro de Recetas MQL5: Usar Diferentes Modos de Impresión
Este es el primer artículo de la serie de Libros de Recetas MQL5. Comenzaré con ejemplos sencillos para permitir a aquellos que están dando sus primeros pasos en programación que se familiaricen poco a poco con el nuevo lenguaje. Recuerdo mis primeros esfuerzos para diseñar y programar sistemas de trading. Debo decir que fue bastante complicado, teniendo en cuenta el hecho de que fue el primer lenguaje de programación en mi vida. No obstante, resultó ser más fácil de lo que pensaba, y solo me costó unos pocos meses desarrollar un programa con una cierta complejidad.
Aprendizaje Automático: Cómo usar las Máquinas de Vectores de Soporte en Trading Aprendizaje Automático: Cómo usar las Máquinas de Vectores de Soporte en Trading
Las máquinas de vectores de soporte se usan desde hace mucho tiempo en campos como la bioinformática y matemáticas aplicadas para estudiar conjuntos de datos complejos y extraer patrones que se pueden usar para clasificar datos. Este artículo examina qué es una máquina de vectores de soporte, cómo funciona y por qué puede resultar muy útil a la hora de extraer patrones complejos. Después investigaremos cómo se puede aplicar al mercado y usar potencialmente para tomar decisiones de trading. Usando la Herramienta de Aprendizaje de Máquina de Vectores de Soporte, el artículo facilitará ejemplos listos que permitirán a los lectores experimentar con sus propias operaciones de trading.