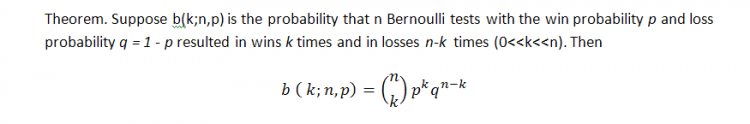Falacias, Parte 2. La estadística es una pseudociencia o la "crónica de la caída en picado de cada día"
Introducción
La primera parte del encabezado de este artículo es una cita de la publicación de SergNF de 17 de abril de 2008, 14:04, https://www.mql5.com/ru/forum/108164. Bueno, incluso las matemáticas más estrictas resultan una pseudociencia cuando son usadas por un "investigador" que decide utilizar atractivas fórmulas sin ninguna aplicación práctica.
Es escepticismo del autor de la cita, incluso moderado con tres "emoticonos", es obvio. La razón de esto es bastante evidente: muchos intentos de aplicar los métodos estadísticos a la realidad objetiva, como las series financieras, fracasan cuando se encuentran con los procesos no estacionarios, "colas gruesas" de las distribuciones probabilísticas que los acompañan y el insuficiente volumen de la información financiera. Ninguno de los modelos del mercado existentes se ajustan adecuadamente a la realidad. E incluso si logramos encontrar regularidades estadísticas, los resultados de su utilización parecen ser desproporcionados en relación con los esfuerzos invertidos en su educción.
En este artículo intentaré referirme no a las series financieras como tales, sino a su presentación subjetiva, en este caso a la forma en que un trader intenta dominar las series, como el sistema de trading. La educción de las regularidades estadísticas de los resultados del trading es una tarea muy apasionante. En algunos casos, pueden sacarse verdaderas conclusiones sobre el modelo de este proceso y estas pueden aplicarse al sistema de trading.
Pido disculpas a los lectores que no conocen las matemáticas por la complejidad de la exposición, pero obviamente es una serie inevitable de contenidos en el artículo. Parece que la promesa mencionada al final de mi artículo anterior, no se ha cumplido. Por tanto, vamos a comenzar nuestra búsqueda.
En el artículo logramos elaborar un ejemplo artificial que nos muestra claramente una estrategia rentable con la regla de gestión del dinero (MM) "lot=0.1" que resulta ser perdedora en una MM geométrica. Se ha usado una serie muy regular de transacciones rentables y perdedoras que difícilmente pueden encontrarse en la realidad: P L P L P L P L P L P L ... La primera pregunta es: ¿Por qué analizo exactamente dichas series "regulares"?
Series perdedoras: Resumen breve
La razón es simple: se indica en el artículo Mi primer "Grial":
Al mismo tiempo, nunca se puede predecir cómo se distribuirán las órdenes con pérdidas entre las órdenes con beneficios. Esta distribución tiene, en general, una naturaleza aleatoria.
P P P L P P P L P P P L P P P L P P P L P P P L P P P L ...
B. A continuación se indica un ejemplo de las situaciones más probables de distribución no uniforme de las transacciones con beneficios y pérdidas durante trading real:
P P P P P P P P P P P P P P P L L L L P P P L P P P L ...
Se muestra una serie de 5 pérdidas consecutivas, aunque estas series pueden ser incluso más largas. Tiene que tener en cuenta que, en este caso, la proporción entre pedidos con beneficios y con pérdidas se ha mantenido en 3: 1.
De esta forma, la alternancia "regular" de transacciones rentables y perdedoras es ideal en términos de reducciones mínimas (y del factor de recuperación máxima). Y si, al igual que en el artículo anterior, logramos mostrar ese evento en este caso ideal (cuando se alternan transacciones rentables y perdedoras) el sistema se convierte en uno perdedor en una MM geométrica, con los mismos valores de esperanza matemática de las transacciones rentables y perdedoras, y luego es seguro que es incluso pero en una distribución no regular de resultados de las transacciones.
Nota: Suponemos que la relación entre las transacciones rentables y perdedoras es igual a 14:9. ¿Cómo distribuiríamos las transacciones en series para tener las mínimas reducciones? Esta no es una cuestión fácil, incluso si tenemos en cuenta la regla de la MM "lot=0.1" e intentamos probar que las series serán óptimas. Queda casi claro que las pérdidas deben estar distribuidas "uniformemente" en las series, digamos, de esta forma:
P L P L P P L P P L P P L P L P L P P L P P L...
Estas son "series elementales" que están compuestas por 23 transacciones, 14 de las cuales son rentables. Después de esto, estas series se repiten. Está claro que dichas series tienen muchas menos reducciones en ambos tipos de MM, por ejemplo, esta:
P P P P P P P P P P P P P P L L L L L L L L L…
Queda especialmente claro con las MM geométricas (las razones se explicaron en el artículo). No obstante, incluso dichas series de pérdidas ("clúster perdedor") no suponen un límite. Para comprender esto, vamos a recordar los fundamentos de la teoría de la probabilidad. Pero antes vamos a definir algunos términos.
Terminología
Este artículo contienen muchos términos relacionados con las series e histogramas de Bernoulli y que representan varias distribuciones de probabilidad. Para no confundirlas, vamos a definir la terminología. Por tanto:
- Todas las series de transacciones se llamarán aquí simplemente una serie. Este término hace referencia tanto a las series obtenidas durante el procesamiento de los resultados de una prueba real única como a las series obtenidas sintéticamente durante la generación de la serie de Bernoulli correspondiente. Si la longitud de la serie debe ser indicada, la llamaremos de esta forma: serie 3457 (una serie que contiene 3457 transacciones).
- Un sucesión de transacciones consecutivas del mismo signo dentro de una serie (transacciones rentables o perdedoras o "éxitos" o "fracasos") se llamará aquí un clúster. Si debe indicarse la longitud, se llamará, por ejemplo un clúster 7 (un clúster de longitud 7).
- Un gran número de series (en este contexto hablaremos principalmente de las series sintéticas) se llamarán una matriz de series. También puede indicarse el número: matriz de 65000 de la serie 5049 (serie de Bernoulli 65000, cada una de 5049 transacciones).
- Cuando elaboramos los histogramas, algunas veces necesitamos tener en cuenta los clúster que pertenecen no solo a algunas series específicas, sino también a toda la matriz de series. El nombre del histograma se corresponde con el parámetro cuya distribución se visualiza. En lugar de escribir "Histograma de distribución de los clúster de longitud 4 en una matriz de series 5000 cada una de 3174" la llamaremos de esta forma: "clúster de 4 en una matriz 5000 de series 3174"..
Sistema Bernoulli: Fundamentos
Con mucha frecuencia, muchas tareas prácticas en las que se tiene en cuenta una serie de eventos, pueden reducirse al sistema siguiente:
- Cada evento tiene solo dos resultados: "éxitos" y "fracasos" ("ganar" y "perder"). La probabilidad de "éxito" es p y la de "fallo" es q=1-p.
- La probabilidad del resultado del evento no depende del historial de eventos que lo precede.
Esto se llama el sistema Bernoulli (o pruebas Bernoulli). Nuestra sucesión coloreada y codificada podría considerarse un sistema Bernoulli si estuviéramos seguros en el segundo criterio de la definición dada anteriormente.
El autor cree que es cierto para la mayoría de sistemas de trading. Estas son algunas de las pruebas indirectas:
- Cualquier información sobre un sistema de cuenta Z según la opinión de aquellos que intentaron aplicarlo para la optimización MM, parece ser inútil cuando se intenta calcular la probabilidad de una cierta transacción, incluso si la probabilidad de ganar es superior al 90 %;
- La eficiencia de varios sistemas martingale, en todas las apariciones, es también igual a cero o incluso negativa, aunque conduce a reducciones inadmisibles.
Por esta razón ahora podría tener sentido aceptar esto en la mayoría de sistemas de trading, ya que una serie de transacciones sucesivas se corresponde con el criterio del sistema de Bernoulli. Dicha hipótesis conduce a consecuencias muy profundas.
La fórmula clásica de la probabilidad de k ganadoras (nos podemos referir aquí a las transacciones perdedoras, a propósito) en la serie de n pruebas en el sistema de Bernoulli es la siguiente (la probabilidad de ganar es igual a p):
Esta fórmula muestra algunos parámetros propios de la serie y el número de ganadoras pero no nos dice nada sobre cómo se distribuyen estas ganadoras uniformemente, es decir, no sabemos nada sobre la longitud de los clúster posibles. La búsqueda de la longitud de los clúster de pérdida probables en la serie de Bernoulli es una tarea mucho más compleja y su solución es descrita por Feller [1]. A continuación se indican las fórmulas para la esperanza matemática de una longitud de una serie de prueba y su distribución con los parámetros p (probabilidad de una ganadora), q (probabilidad de una perdedora) y r (longitud del clúster ganador), siempre que tengamos una serie de pruebas que coincidan con el sistema de Bernoulli: la esperanza y la distribución matemática del tiempo de retorno para la serie ganadora de longitud r son respectivamente iguales a
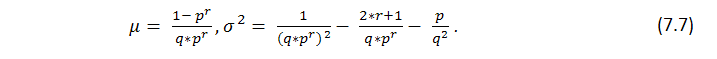
Se deduce del teorema que con un valor grande de n, el número ![]() de series de longitud r obtenido en n pruebas tiene aproximadamente una distribución normal, es decir con un
de series de longitud r obtenido en n pruebas tiene aproximadamente una distribución normal, es decir con un ![]() fijo, la probabilidad de la inecuación
fijo, la probabilidad de la inecuación
tiende a
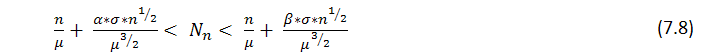
La tabla contiene las esperanzas matemáticas de una serie de tiempos de retorno típicos.
| Longitud de la serie, r | p = 0.6 | p=0.5 (moneda) | p=1/6 (dado) |
|---|---|---|---|
| 5 | 30,7 seg. | 1 min. | 2,6 horas |
| 10 | 6,9 min. | 34,1 min. | 28 meses |
| 15 | 1,5 horas | 18,2 horas | 18.098 años |
| 20 | 19 horas | 25,3 días | 140,7 años |
Tabla 1. Tiempo de retorno medio para la serie ganadora (se realiza una prueba por segundo).
Consecuencia 2: Limitación, considerable desaceleración o, al contrario, el exceso del clúster perdedor que depende de la longitud de la serie de prueba apunta al hecho de que el sistema de trading no satisface el sistema de Bernoulli. Por ejemplo, si en los asignados previamente
Consecuencia 3: si la hipótesis del "sistema de Bernoulli" no es verdadera, dicha estrategia no es muy distinta al sistema de lanzar una moneda asimétrica con las probabilidades correspondientes iguales a p, q = 1-p (o lanzar un sándwich con mantequilla).
Ahora vamos a analizar un par de estrategias "interesantes" desde este punto de vista.
Reventa especulativa: "Afortunado (Lucky)", Parte 1.
Todos o casi todos los sistemas de reventa especulativa poseen un cierto número de características en común:
- SL es mucho más que TP (valores típicos – 20 and 2; los valores de punto corresponden a las cotizaciones de 4 dígitos de EURUSD);
- p es mucho más que q (la posibilidad de una transacción rentable es superior al 80 %, algunas veces hasta el 99 %);
- el número de transacciones es muy grande y no puede alcanzar las decenas de miles para el periodo de un año.
No profundizaremos en el tercer punto: si esto es posible en centros de transacciones o no. Este tema se discute en el artículo mencionado anteriormente de SK., así como en el foro. Debemos asumir que un centro de transacciones no entorpece a nuestro trader mediante las recotizaciones, deslizamiento MODE incrementado_STOPLEVEL y demás.
Un trader que haya creado un sistema de trading de reventa especulativa (TS) cae en el error sobre la frecuencia de las transacciones perdedoras. Las causas de esta ilusión se remontan a la idea del carácter de Wiener sobre los procesos del precio de cierre y el carácter verdadero de la fórmula de Einstein para el movimiento browniano: "si hacemos SL=20, TP=2, la probabilidad de iniciar una stop-loss es (20/2)^2=100 veces inferior que la probabilidad de alcanzar TP, por tanto dicha TS debe ser rentable". Lo engañoso de este concepto está en el hecho de que este proceso no es un proceso de Wiener y las posibilidades correspondientes difieren en una cuantía mucho menor que 100 veces.
En este caso exactamente, la hipótesis del "sistema Bernoulli" es bastante probable, debido a que las estrategias de trading de reventa especulativa suelen intentar usar las peculiaridades aleatorias del proceso y debido a que su filtración es aceptada en algunos centros de transacciones.
Ahora vamos a tomar los parámetros de la estrategia de trading que conocemos con el nombre de"Lucky" (https://www.mql5.com/en/code/7464). En su forma original (en la misma sección, Lucky_new.mq4) este asesor experto es solo un juguete, ya que difícilmente puede ser un centro de transacciones que acepte la apertura de varios centenares de transacciones al día con la esperanza matemática de una rentable en torno a uno-dos puntos. No obstante, es posible modificar el código y establecer requisitos más rigurosos en el nivel TP y aún así, algunas veces obtener curvas de balance/equidad bastante satisfactorias. El código del asesor experto modificado (teniendo en cuenta las restricciones sobre el número de transacciones abiertas al mismo tiempo, que en este caso es igual a 1, puede consultar las explicaciones más adelante) está adjunto a este artículo.
La principal ventaja de este asesor experto es que ejecuta una gran cantidad de transacciones y proporciona un valioso material para la estadística. Esto se demostrará más adelante. Ahora solo tenemos como objetivo encontrar evidencias que confirmen o refuten la hipótesis: "los resultados de la transacción son acordes con el sistema de Bernoulli". Para aquellos que les guste discutir sobre el carácter no aleatorio de los movimientos del mercado, indicaré que: No dudo que los movimientos de las cotizaciones no siempre son aleatorios. No asimilaré el mercado (exactamente el mercado) con el lanzamiento de una moneda a la Bachelier. Solo me interesa para las estadísticas de los resultados de la transacción, nada más. Más adelante verá que algunos conjuntos de parámetros externos se eligen intencionadamente como "perdedores", solo para comprobar la hipótesis establecida.
Estos son los resultados de la primera prueba:
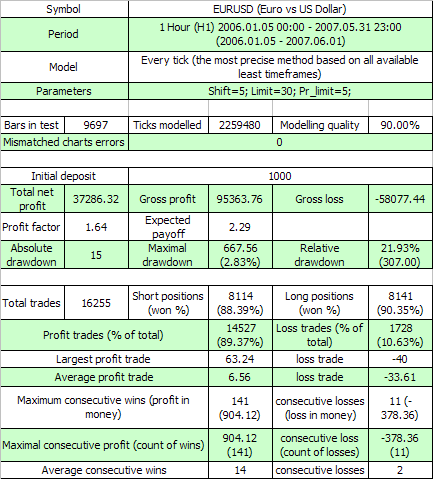
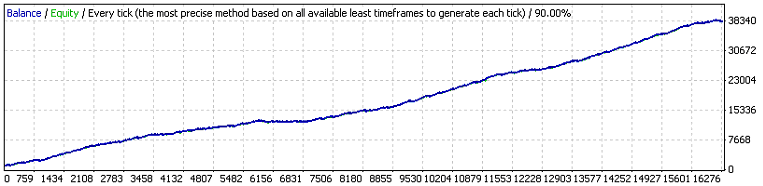
Las dos primeras variables externas tienen el mismo significado que en el código original, mientras que la tercera es el valor del beneficio en puntos que una orden debe superar para iniciar el evento take profit. Vamos a estimar, de acuerdo con 7,7, la esperanza matemática de las series de prueba mínimas necesarias para coincidir con el clúster de 11 de la pérdidas (p=0.8937, q=0.1063, r_loss=11):
N_loss = 1 / (p * q^r_loss) – 1 / p ~ 57 140 275 804
Esta es la estimación análoga para la esperanza matemática de la longitud de la serie de prueba para coincidir con el clúster de 141 rentable.
N_profit = 1 / (q * p^r_profit) – 1 / q ~ 71 685 085
Bueno... Como sabemos, la longitud real de la serie es igual a solo 16255 transacciones, y no a decenas de miles de millones o millones. Dicho exceso tan grande en la longitud de la serie real es signo de que para esta TS, la hipótesis del sistema de Bernoulli es difícil que funcione directamente. ¿Es posible que haya aquí una influencia de un factor que no hayamos tenido en cuenta?
Sistema Bernoulli: Un resultado interesante
Existe dicho factor: un asesor experto puede abrir muchas más que una transacción al mismo tiempo: en el segundo centenar de transacciones (órdenes 158...163) abrió 6 transacciones sucesivamente (y las cierra en grandes cantidades también). Este "factor de multiplicación" es probablemente el responsable del considerable incremento de las longitudes del clúster cuando se compara con las esperadas: si el mercado está plano con un volumen considerable, el asesor experto comienza a abrir muchas transacciones casi en cada tick. No obstante, debido a su carácter, como consecuencia del mercado plano y del pequeño tamaño de take-profit comparado con el de stop-loss, la mayoría de ellas, si no todas, se cerrarán con rentabilidad. Por otro lado, si se inicia un fuerte movimiento dirigido, el asesor experto abrirá muchas transacciones unidireccionales en dirección opuesta al movimiento del mercado y finalmente, la mayoría de ellas se cerrarán, perdiendo incluso "masivamente".
Vamos a realizar unos simples cálculos. Tomamos ambas fórmulas para la esperanza matemática de toda la longitud de la serie de prueba del apartado anterior. Aquí r_loss_real, r_profit_real son las longitudes reales de los clústeres de pérdidas y ganancias máximas respectivamente. Aunque los valores obtenidos de N_xxxx son bastante elevados, al truncar los segundos términos (1/p y 1/q) no se producirá prácticamente ningún error si dividimos estas igualdades por cada uno de los términos:
N_loss / N_profit = q * p ^ r_profit_real / ( p * q ^ r_loss_real ) =
p ^ ( r_profit_real – 1) / q ^ (r_loss_real – 1)
Vamos a encontrar el logaritmo y a simplificar:
ln( N_loss / N_profit ) = ( r_profit_real – 1 ) * ln( p ) - ( r_loss_real – 1 ) * ln( q )
Ahora vamos a marcar que si las pruebas están gobernadas por el sistema de Bernoulli y las longitudes de los clústeres más largos y ambas posibilidades p y q no son muy pequeñas, entonces los valores N_loss y N_profit deben ser aproximadamente iguales. Por tanto, obtenemos una correlación aproximada interesante:
( r_profit_real – 1 ) / ( r_loss_real – 1 ) * ln( p ) / ln( q ) ~ 1 (*)
Y si volvemos a escribirlo de otra forma:
p ^ ( r_profit_real – 1 ) ~ q ^ ( r_loss_real – 1 )
el significado de la correlación (*) es claro: en la TS de Bernoulli (con una serie de prueba bastante larga y unas probabilidades p y q no demasiado pequeñas) las probabilidades de dos clústeres de longitud máxima ("ganadores" y "perdedores") son prácticamente iguales. En realidad, este principio puede ser aplicado a cualquier otra TS que tampoco sea de Bernoulli, aunque la forma de correlación (*) es específica del sistema Bernoulli. Esta correlación puede considerarse una prueba aproximada de una TS respecto a su semejanza a una Bernoulli.
Reventa especulativa: "Afortunado (Lucky)", Parte 2.
Vamos a excluir el factor de multiplicación: establecemos la limitación del número de órdenes abiertas al mismo tiempo en 1. Aunque el número de órdenes ha disminuido varias veces para el mismo periodo de tiempo, ampliaremos el rango de la prueba y lo estableceremos desde el 1 de enero de 2004 hasta el 4 de abril de 2008. A continuación se muestra la tabla de resultados y algunos cálculos (BS es una forma abreviada del "sistema Bernoulli" (ver el análisis siguiente). El primer "+" indica una buena correspondencia con el sistema Bernoulli para los clústeres rentables, el segundo para los clústeres perdedores, "-" es una hipótesis refutada "El sistema satisface BS" y "0" significa dudas sobre si es correcta):
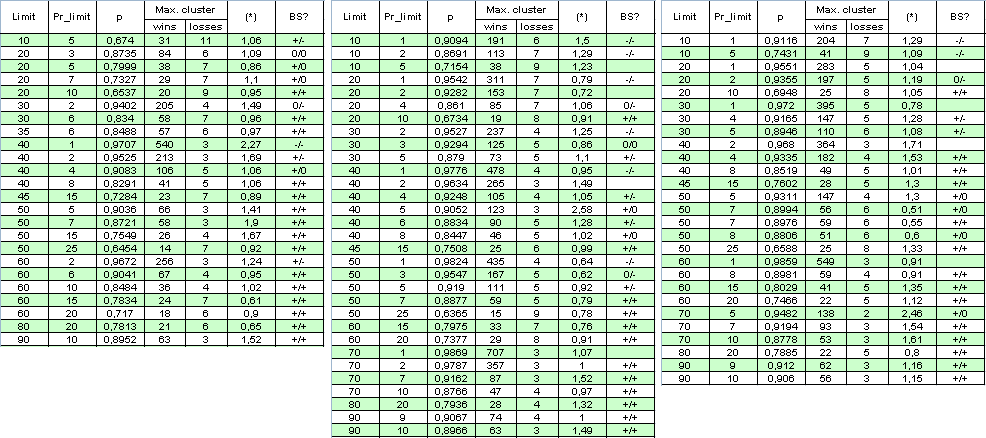
El autor pide disculpas por el gran tamaño de la tabla para tener una idea general. El parámetro (*) parece ser insuficiente para decidir sobre si el sistema es de Bernoulli, ya que algunas veces incluso cuando es cercano a 1, el sistema tiene dificultades para adecuarse a un sistema Bernoulli.
Nota final Incluso a pesar del hecho de que los multiplicadores en (*) se apartan algunas veces bastante de 1, los valores (*) siguen siendo aún cercanos a 1. Por ejemplo, si Limit = 40 y Pr_limit = 1 en la segunda columna, tenemos:
( * ) = ( 478 - 1 ) / ( 4 - 1 ) * ln( 0.9776 ) / ln( 0.0224 ) ~
477 / 3 * ( -0.02265 ) / ( - 3.7987 ) ~ 0.95
A propósito, este hecho reconoce otra hipótesis: incluso si se pospone la hipótesis del sistema Bernoulli, la dependencia de las transacciones aquí es "casi la misma" para las rentables y las perdedoras.
Criterio de correspondencia de un sistema de trading con el sistema Bernoulli.
Descripción del funcionamiento del script
¿Cómo podemos dividir de forma más fiable los resultados de las pruebas en dos grupos: sistemas Bernoulli y "sistemas no Bernoulli"? Podemos probar varios métodos, aunque el más simple, en mi opinión, es el siguiente: si creamos muchas series Bernoulli con parámetros que se correspondan con aquellas realmente detectadas durante las pruebas, en el caso de un sistema Bernoulli la función de distribución de probabilidad de la longitud del clúster debería quedar prácticamente sin cambios. El hecho se deduce obviamente de la suposición de invariabilidad de la probabilidad de ganar y de la independencia de las transacciones.
Por desgracia, la función teórica de distribución de los clústeres ganar/perder según su longitud la desconozco. Más arriba, he incluido algunas fórmulas que permiten estimar la expresión matemática del número de clústeres ganadores en las series de prueba en función de su longitud y probabilidad de ganar (véase el apartado 7.8 anterior). Para esta finalidad, Feller ([1]) ofrece un método especial a partir de la teoría de los eventos recurrentes a la que pertenecen los clústeres. A primera vista, este método no se ajusta completamente al conocimiento de un trader sobre el término "series ganadoras", aunque este método simplifica considerablemente la propia teoría, de forma que la identificación del "registro del clúster r" no depende del futuro ([1], página 302):
Series ganadoras en las pruebas Bernoulli. El término "series ganadoras de longitud r" fue definido a través de varios métodos. La cuestión sobre si la secuencia de tres ganadoras consecutivas debe suponerse que contiene 0, 1 o 2 series de longitud 2 es principalmente cuestión de comodidad y para distintos propósitos aceptamos distintas denotaciones. No obstante, si queremos aplicar la teoría de los eventos recurrentes, el significado de las series de longitud r debe definirse de forma que tras el final de las series el proceso comience de nuevo. Esto significa que deberíamos aceptar la siguiente definición: La serie n de letras W y L contiene tantas series de longitud r como subseries, cada una de las cuales contiene r letras W que permanecen juntas. Si en la serie de las pruebas de Bernoulli aparece una nueva serie como resultado de una prueba enésima (n), diremos que esta serie aparece en la prueba con el número n.
De este modo, en la serie WWW|WL|WWW|WWW hay tres series de longitud 3 que aparecieron en las pruebas tercera, octava y onceava y la misma serie contiene cinco series de longitud 2. Estas aparecen en las pruebas segunda, cuarta, séptima, novena y onceava. Esta definición simplifica considerablemente la teoría, ya que las series de longitud fija se convierten en eventos recurrentes. Esto es equivalente al recuento de series compuesto por al menos r ganadoras consecutivas con la reserva de que 2*r de las ganadoras consecutivas se consideran dos series, y así sucesivamente.
Por otro lado, para un trader, el número de clústeres ganadores ("series ganadoras" según Feller) en la fila indicada (WWWWLWWWWWW) será el siguiente: primer clúster de 4 de ganadoras, luego, después de una perdedoras, clúster de 6 de ganadoras. No hay clústeres "completos" de longitud 1, 2, 3 y 5 para un trader, aunque sí los hay según Feller. Este extracto de [1] se publica aquí solo para indicar la dificultad del problema. De este modo, solo generaremos un gran número de series de Bernoulli y detectaremos las series en ellas que se correspondan con el conocimiento de las mismas por parte de un trader (15 ganadoras en una fila que termine en una perdedora no son 15 registros de un clúster de 1, ni 5 registros de un clúster de 3, según Feller, sino que solo es un registro de un clúster de 15 "auténtico"). Para comprobar si las series son de Bernoulli, son suficientes 1.000 series de Bernoulli.
De acuerdo con esta idea, primero se escribió un script que permite cargar la serie de resultados de las transacciones reales en una matriz y luego obtener los datos para trazar un histograma de la longitud del clúster en MS Excel. Este script también contiene las funciones que generan las series Bernoulli y prepara los datos para elaborar histogramas en MS Excel. No me gustaría insertar el código del script en el artículo. En su lugar, daré unos comentarios generales sobre el código. El script se ajunta a continuación. El informe del probador debe colocarse primero en el directorio experts\files\Sequences\, y su nombre debe trasladarse a los parámetros de un script externo.
Al principio, en base al archivo del informe del probador, con la ayuda de la función readIntoArray() se introducen en una matriz global los resultados de las transacciones (1 o -1) _res[]. Para comprender el funcionamiento vamos a ilustrar nuestras explicaciones usando una pequeña matriz. El funcionamiento de esta función al final da como resultado, por ejemplo, la siguiente matriz _res[] (el número de transacciones, es decir, la longitud de las series, es 50):
1,1,-1,-1,1,1,1,1,1,-1,1,1,1,1,1,1,1,-1,1,1,-1,-1,-1,-1,1,1,1,-1,1,1,1,1,-1,1,-1,1,-1,-1,-1,1, 1,-1,1,1,1,1,1,1,1,1
Después de esto, la función formClustersArray( int results[], int& sequences[], int& h, int nr ) calcula las longitudes de los clústeres y luego, dependiendo del parámetro global _what, que define aquello que nos interesa, beneficios o pérdidas, escribe las longitudes de las series en la matriz sequences[] (realmente en la matriz global _seq[]). Vamos a contar los clústeres en esta matriz:
2,-2,5,-1,7,-1,2,-4,3,-1,4,-1,1,-1,1,-3,2,-1,8
Los valores negativos se refieren a los clústeres perdedores. Está claro que la suma de todos los valores absolutos de los números es igual a la longitud de la serie, 50. Supongamos que estamos interesados en las pérdidas, es decir, _what = -1. Entonces la matriz _seq[] contendrá solo los valores negativos, aunque con el signo "más":
2,1,1,4,1,1,1,3,1
Después de esto, se procesa la matriz _seq[] con la finalidad de crear la matriz _histogramReal[]. Ahora solo necesitamos calcular las cantidades de 1-, 2-, 3- etc., clústeres y escribirlas en una serie en la matriz. Como resultado, la matriz _histogramReal[] contendrá los siguientes valores:
6,1,1,1
Esto significa que nuestra serie contiene 6 clústeres de 1 perdedores, 1 clúster de 2 perdedor, 1 clúster de 3 perdedor y 1 clúster de 4 perdedor. Posteriormente la matriz se escribe en el archivo de salida. El archivo no está cerrado, ya que necesitamos escribir en él "histogramas" análogos de las series sintéticas de pruebas según el sistema Bernoulli.
Al formar los "sintéticos", la función clave es el generador de una única prueba según el sistema Bernoulli. A pesar de este código simple, funciona bastante bien: no se observó ningún "efecto de borde" responsable de la distorsión de la distribución regular de resultados en el segmento [0, 32767].
// genera una única prueba Bernoulli (+-1 con distintas probabilidades) int genBernTest( double probab ) { int rnd = MathRand(); if( rnd < probab * 32767 ) return( _what ); else return( -_what ); }
Después de una única llamada a MathSrand( GetTickCount() ), esta función es llamada tantas veces como transacciones reales hay en el periodo de prueba (_testsTotal). Luego, cuando hemos generado las series de Bernoulli, los resultados se procesan por el recuento de clúster y las funciones de construcción del "histograma". Estas acciones son responsables de la creación de un histograma correspondiente a una prueba (la función genSynthHistogr( int& h, int nr ) ). Y finalmente se llama a la última función en el bucle, de forma que en el resultado, se genera la matriz de las series Bernoulli, cuyos histogramas se crean y se escriben en un archivo de salida.
Ahora podemos abrir este archivo en MS Excel, crear los diagramas necesarios y extraer conclusiones sobre la correspondencia del sistema con el sistema Bernoulli. Los números en las líneas del archivo tienen el siguiente significado (la tabla está cortada, y no mostramos aquí los datos en los clústeres de 5 y siguientes):
1 9 1639 1058 724 440
Número de series de prueba
Longitud máx. del clúster
Número de clústeres de 1
Número de clústeres de 2
Número de clústeres de 3
Número de clústeres de 4
0
11
1649
1044
688
478
1
8
1681
1093
675
458
2
13
1628
1067
701
461
3
7
1616
1039
726
474
4
12
1601
1054
699
465
La primera línea del archivo (verde) muestra el resultado de la prueba real, y las líneas siguientes corresponden a las series de pruebas sintéticas con el número comenzando por 0.
Y, finalmente, la última etapa: la estimación de los resultados de las pruebas reales para la correspondencia con el sistema Bernoulli, donde se eligen las columnas correspondientes de las series de Bernoulli sintéticas para construir un histograma de los clústeres de longitud necesaria. Por ejemplo, para construir un histograma de una distribución de cantidad de clúster 1 ganadora, debemos tomar la tercera columna (1649, 1681, 1628, 1616, 1601….) y la cantidad total de dichos números es igual a la cantidad de series de Bernoulli sintéticas). Para clústeres de 2 ganadores tomamos la cuarta columna (1044, 1093, 1067, 1039, 1054…), y así sucesivamente.
Dichos histogramas se construyen de acuerdo con el método descrito por Bulashev [7] y luego comprobamos la hipótesis cero sobre la igualdad del número en la prueba real con la estimación de la media en las series sintéticas. El nivel aceptado previamente de significatividad para la hipótesis cero, "el número real es igual a una media para las sintéticas", es igual a 0,05 (se refiere a, aproximadamente, dos desviaciones estándar).
Primeros resultados
Vamos a iniciar el script sobre los resultados de las pruebas de Lucky en los parámetros 3, 20, 10. Los parámetros del script: _what = 1 (clústeres rentables), _globalSeriesQty = 5000. El parámetro (*) en la tabla grande es igual a 1, es decir, podemos esperar que los resultados de la operación del script muestren la correspondencia con el sistema de Bernoulli. Mostraremos aquí los registros de archivo correspondientes a la comprobación directa de la hipótesis cero para longitudes de clúster 1-6 (se modifican ligeramente en forma de tabla para una mejor apreciación):
// La primera línea del archivo son los resultados de la prueba real realizada en el probador. Las dos primeras cifras son el número de series y la longitud de un clúster máximo.
,20,1639,1058,724.440.271.212.137,91,62,30,26,22,5,7,1,4,1,0,1,1
…
// Final del archivo (parcialmente):

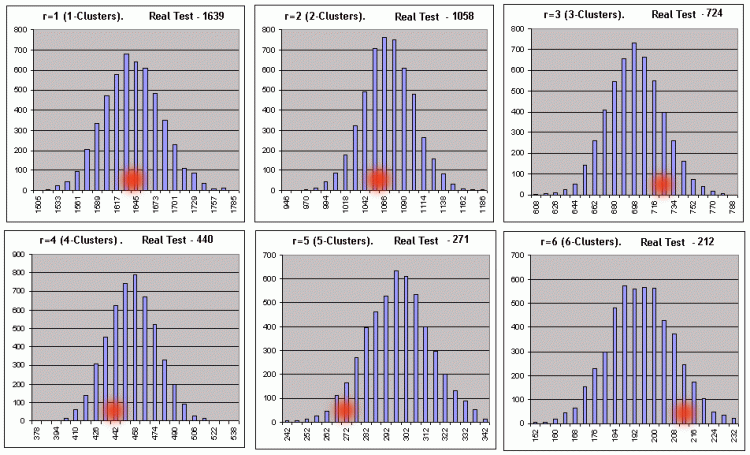
En cada una de las 6 tablas de dos líneas, la línea superior corresponde a los valores de la izquierda en los intervalos del histograma, y la inferior al número de series Bernoulli (de las 5000) en las que los números de los clústeres de longitud dada estaban dentro de estos intervalos. A continuación se visualizan gráficamente (el número de clústeres r rentables en las series Bernoulli siempre que el número total de series sea igual a 5000):
Las abscisas de puntos rojos corresponden a los números de clústeres obtenidos en la prueba real. El mismo script para los clústeres perdedores (_what = -1) en los mismos parámetros también da una buena imagen, con el descuento para la longitud razonable de clústeres perdedores: tan pronto como el número de intervalos calculados de acuerdo con las recomendaciones de [7] comienza a sobrepasar la distribución de los datos en las sintéticas, la construcción de histogramas con el número establecido de intervalos se hace imposible. No obstante, los ceros formales en el informe del script no deben preocuparnos, ya que todos los parámetros necesarios pueden calcularse sin un histograma. En los parámetros establecidos, solo se rechazó la hipótesis cero para los clústeres de 3 y de 7. Como criterio principal para hacer referencia a un sistema probado con respecto a un sistema Bernoulli, se eligió un criterio muy dudoso del tipo impreciso. Vamos a considerar el principio de toma de decisiones sobre el ejemplo de los resultados de la operación del script para los clústeres perdedores:
La diferencia de una prueba real con la estimación de una media = -0.37 SD (desviación estándar)
La diferencia de una prueba real con la estimación de una media = 0.95 SD
La diferencia de una prueba real con la estimación de una media = -2.04 SD
La diferencia de una prueba real con la estimación de una media = -0.45 SD
La diferencia de una prueba real con la estimación de una media = 0.36 SD
La diferencia de una prueba real con la estimación de una media = 1.13 SD
La diferencia de una prueba real con la estimación de una media = 3.27 SD
La diferencia de una prueba real con la estimación de una media = 0.11 SD
La diferencia de una prueba real con la estimación de una media = 0.46 SD
La diferencia de una prueba real con la estimación de una media = -0.47 SD
Por tanto, este es el criterio principal:
- Si la media de los módulos de las cifras no supera 1.5 (aquí es 0.96),
- la media de las cifras no es superior a 1.2 en módulo,
- el número de valores atípicos (aquí estos están en negrita y corresponden a la diferencia que excede de 2 SD) no supera el 20 % de su cantidad total,
un sistema se considera "con seguridad de Bernoulli". Si las cifras "críticas" correspondientes son 2, 1.5 y 30 %, el sistema es "dudosamente de Bernoulli". Si las cifras superan estos límites, la hipótesis es rechazada. Creo que el segundo punto es razonable, ya que las desviaciones no deberían ser principalmente de un signo.
Los criterios estadísticos de la correspondencia con el sistema de Bernoulli me son desconocidos, y por esa razón tuve que inventar tale criterio. Los resultados de este criterio decisivo improvisado se encuentran en el archivo de informe de la operación del script. Un lector interesado puede ofrecer un criterio decisivo más razonable.
Para este caso, podemos "concluir con seguridad" que el sistema Lucky_ con los parámetros 3, 20, 10 cumple realmente el sistema Bernoulli, es decir, con el sistema cotidiano lanzando aleatoriamente.
Ahora vamos a tomar uno de los "peores" casos y a realizar los mismos cálculos en el número de series de Bernoulli igual a 1000; los parámetros de Lucky son 5, 10, 1. Vamos a considerar los clústeres de 1 rentables:
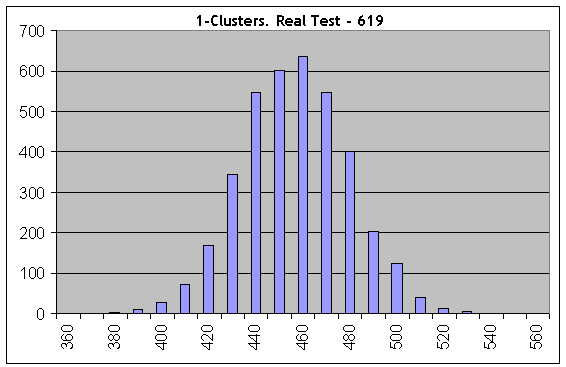
Incluso en el primer histograma, todo es completamente distinto: los resultados de la prueba real (619 clústeres de 1) no se ajustan con los "sintéticos" con la misma longitud de las series de prueba y la misma probabilidad de ganar. Por tanto, las transacciones no son independientes.
Recordemos que las pruebas de estimación similares con muchos conjuntos de parámetros de una tabla grande permiten concluir que el sistema Bernoulli ("lanzando un cotidiano") es más una regla que una excepción. Además, hay casos en los que para algún grupo de transacciones (como las "transacciones rentables") se satisface el sistema de Bernoulli, y para otro grupo no. Esto no afecta al uso de este modelo, al menos parcialmente, para obtener información útil, que se discutirá posteriormente en este artículo. Y la última cosa: el criterio decisivo no es tan fiable en los clústeres perdedores debido a la insuficiente cantidad de datos estadísticos, pero he aplicado el script para ellos también para obtener una imagen completa.
Sistema "Universo": De nuevo el sistema Bernoulli
Ahora vamos a tomar un sistema absolutamente distinto para el estudio: "Universo"; su código fuente está publicado en https://www.mql5.com/en/code/7999. El autor señala que el sistema funciona en las barras formadas, y por esta razón las pruebas de "todos los ticks" no son necesarias. El balance inicial en el que el sistema puede recopilar las estadísticas de las transacciones para el periodo 2000.01.01 - 2008.04.04, se estableció igual a cerca de $10M. El primer lote abierto es 0.1. En realidad, los tres parámetros cambiados son p, tp, sl. No se aprecia ninguna multiplicación, por lo que el estudio es fácil:
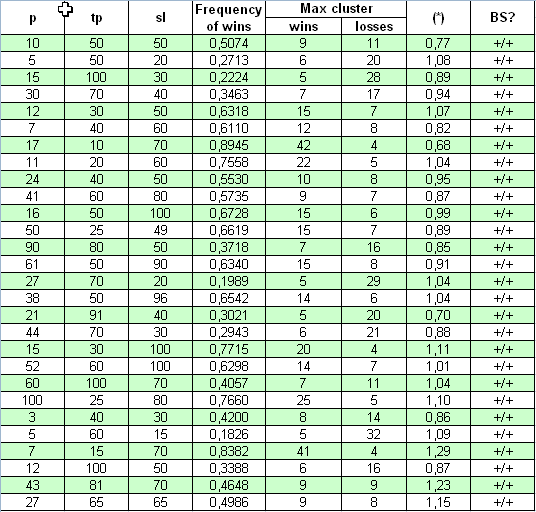
Vemos aquí que la conformidad del parámetro (*) con 1 es mucho mejor que en el caso anterior: los valores (*) se diferencian ligeramente de uno. La comprobación con un criterio decisivo también muestra que en todos los casos, en un rango de parámetros bastante amplio, este TS cumple el sistema de Bernoulli.
Conclusiones preliminares
Ralph Vince en [4] ofrece otro procedimiento de series de prueba para comprobar la correspondencia con el sistema Bernoulli. Este es el cálculo de la puntuación Z y la prueba de los resultados de la transacción para una correlación especial (autocorrelación de una fila fuente y un fila cambiada por otra). No creo que este procedimiento de resultados mucho más significativos que los descritos anteriormente (donde la desviación del número de clústeres con distinta longitud en series reales se comprueba frente a las series del modelo). Es cierto, el criterio decisivo ofrecido es bastante libre y requiere alguna fundamentación. Además, como he indicado anteriormente, la fiabilidad de esta comprobación en una longitud corta del clúster máximo no es alta (para Lucky_ estas son normalmente pruebas de series perdedoras). No obstante, en mi opinión este criterio decisivo requiere más cálculos y es mejor cubrir el carácter específico de las series de prueba en el contexto de su conformidad con el sistema Bernoulli. Esta cuestión requiere estudios adicionales y, por supuesto, aún no está cerrada.
No obstante, las expectativas han sido probadas: en la mayoría de casos, en conjuntos muy distintos de parámetros externos, las series de transacciones se corresponden con el sistema Bernoulli, y las desviaciones del sistema Bernoulli casi siempre proceden de la explotación sistemática de regularidades que son características del proceso de filtrado de las cotizaciones y con más frecuencia inherentes a los sistemas con el valor pequeño de Pr_limit. Esto es especialmente evidente en la tabla grande con los resultados de la comprobación de Lucky_.
Vince señala que si la comprobación empírica de la correlación serial de la prueba de puntuación Z reveló la dependencia entre las transacciones, el sistema es subóptimo, y la dependencia debe incluirse explícitamente en TS, para reducirla en los resultados de la prueba e incrementar la cualidad óptima de TS. De este modo, al posponer los resultados de las pruebas de los dos sistemas, debemos admitir que el sistema "Universo" es generalmente más óptimo que el sistema "Lucky". No obstante, esto no justifica el MM usado en Universo.
¿Cómo usar la cualidad Bernoulli del sistema?
1. ¿Qué sabemos ahora?
Al saber de antemano que al menos en algunos casos la serie de resultados de transacciones expresada por 1 ("éxito", es decir, beneficio) y -1 ("fracaso", es decir, pérdida) es de tipo Bernoulli, podemos obtener un modelo adecuado de este proceso. Ahora sabemos lo suficiente sobre este proceso, ya que en realidad es una modificación de un movimiento browniano con una derivación. P. Samuelson introdujo el movimiento browniano geométrico (o, como él lo llamó, económico) en la teoría y práctica financiera ([6]):
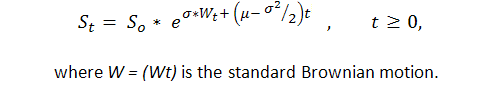
De este modo, podemos aplicar resultados sólidos de los estudios teóricos del movimiento browniano estándar (las leyes del arcoseno, por ejemplo) a la curva de balance. No obstante, la teoría del movimiento browniano es bastante compleja y solo puede ser entendida por un número de personas que tengan una educación matemática sólida en la integración estocástica.
El segundo enfoque es refutar los cálculos altamente teóricos, realizar una generación directa del programa de series de Bernoulli largas y luego transformarlas en curvas de balance para "lote 0.1 MM de prueba". Aquí necesitamos saber solo los valores medios de las transacciones rentables y perdedoras y la frecuencia de ganadoras p. Incluso varios centenares de dichas series (por ejemplo, la matriz de 1000 de la serie Bernoulli) puede darnos una idea bastante buena de qué puede lograr una estrategia que cumpla con el sistema Bernoulli.
Es importante comprender claramente que dicha prueba sintética es una buena alternativa a una prueba Pardo aburrida ([5]): si podemos realmente validar la hipótesis cero ("la sucesión de transacciones es de tipo Bernoulli" no es refutada), esto puede proporcionarnos información suficiente sobre el sistema sustancialmente distinta de la proporcionada por el análisis hacia adelante descrito en [5]. Por supuesto, las curvas de balance puede diferir mucho de la curva obtenida por la prueba real.
***********
En general, nada afecta a la implementación de dicho enfoque ya que dicha prueba se realiza en un ordenador durante varios minutos. Como resultado, obtenemos una cantidad importante de información que puede ser analizada en profundidad. Por desgracia, el volumen del artículo no permite publicar todos los resultados. Estos son algunos gráficos de Lucky_ con los parámetros 4, 70, 10 en el mismo periodo de prueba de la tabla. La tarea de generar sistema de Bernoulli sintéticos es mucho más sencilla que las tareas realizadas por el script descrito anteriormente, por lo que los medios que proporciona MS Excel son sobradamente suficientes.
Prueba real en 0.1:
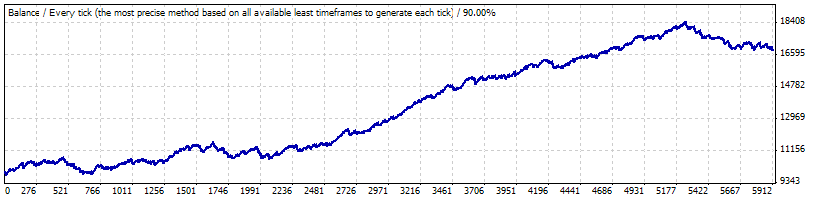
Para nosotros son importantes los siguientes parámetros del informe. Los usaremos al generar las series de Bernoulli y al transformar las series en curvas de cambio de balance:
Frecuencia de transacciones rentables (P)
0,8765
Transacción ganadora promedio
11,71
Transacción perdedora promedio
-73,73
Cantidad total de transacciones
5904
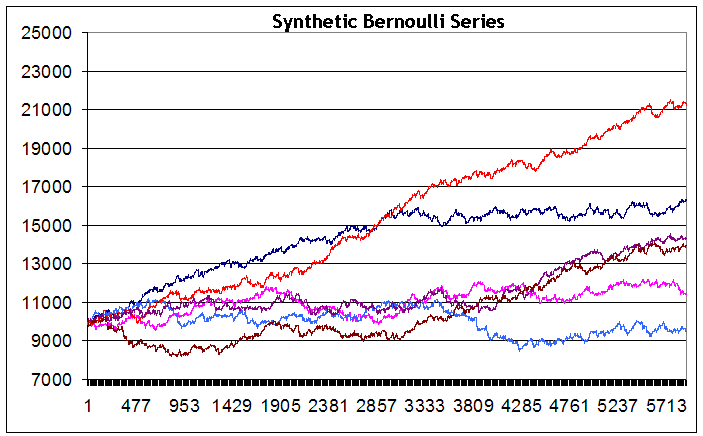
Vemos que, a pesar del hecho de que las series se generaron en datos de entrada idénticos, los resultados del balance integral al final del periodo de prueba son considerablemente distintos entre una serie y otra: desde una pequeña pérdida (línea azul) a un gran beneficio (línea roja) Debo admitir que no he logrado generar una serie con un balance claramente descendente (aunque quería lograr dicho gráfico y realicé cerca de 200 intentos). Quizás podría haberlo logrado con un gran número de series. Pero parece que dicho caso no es típico de esta estrategia. Además, en ninguna de las series vi una reducción de más de 2.500 puntos.
Ahora vamos a considerar un par de resultados aislados relacionados con la estimación de algunos parámetros de una estrategia que cumple el sistema de Bernoulli.
2. Estimación de un clúster perdedor máximo que excede los valores del informe ("cisne negro")
Al haber recibido pruebas de que es un sistema de tipo Bernoulli, podemos estimar en términos reales la longitud máxima de un clúster perdedor que pueda esperarnos en la misma cantidad de transacciones que en la prueba real. Aquí solo podemos generar un lote de series Bernoulli y luego estimar las opciones de un "cisne negro" real (ver [2, 3 ]), es decir, el evento para el que nunca podríamos estimar la probabilidad únicamente en base a los resultados de la prueba, ya que este simplemente no ha ocurrido en el periodo de la prueba. Es este modelo de probabilidad teórico el que puede recoger las estadísticas necesarias en cualquier volumen que necesitemos.
Vamos a usar los resultados del trading de todos los sistemas Lucky_ iguales con los parámetros 4, 50, 7:

Según el informe, la longitud del clúster perdedor máximo es igual a 5. Ahora vamos a establecer un número muy grande de series de Bernoulli, 65000, con el parámetro _what igual a -1 (clústeres perdedores), y luego aplicar nuestro script al informe del probador. Vamos a encontrar la línea más larga (el primer número es un número de la serie Bernoulli, el segundo es la longitud del clúster máximo y luego van los números de clústeres de cada longitud):
26001 9 1030 136 13 4 0 0 0 0 1
Vemos que la longitud del clúster perdedor máximo puede ser mucho mayor que 5 (aquí es 9). ¿Puede que sea este un evento muy raro? Cierto, es muy raro: solo se cumplió una vez entre 65.000 series, por lo que su aparición en una prueba real puede considerarse casi inexistente, teniendo en cuenta la "hipótesis de ergodicidad" (ver algo más adelante). No obstante, este estimación de la frecuencia es muy poco fiable, por lo que no podemos confiar en ella: esta serie puede ocurrir, por ejemplo, entre solo 20 series de Bernoulli. Como resultado, si no conocíamos el criterio estadístico de la estimación de la fiabilidad, consideraríamos erróneamente que esta estimación tenía una alta probabilidad.
En la versión que yo ofrezco, la "hipótesis de ergodicidad" es la siguiente: la probabilidad de un evento en el "espacio de pruebas sintéticas" (en base al modelo adecuado del evento) es aproximadamente igual a la probabilidad del mismo evento en el espacio de tiempo, es decir, para el trading real, siempre que el número de transacciones en la prueba real sea igual al correspondiente en las pruebas del modelo. Se considera, por supuesto, que la serie de resultados de las transacciones en las pruebas reales es estacionaria, como el sistema Bernoulli. Con una gran cantidad de transacciones, esta afirmación no se aleja tanto de la realidad, ya que la única fuente de no estacionaridad aquí puede ser, probablemente, la llamada "deriva ganadora" distribuida según la ley normal y descrita a continuación.
A continuación se muestra la tabla de números de clústeres perdedores en la matriz de 65.000 de la serie Bernoulli:
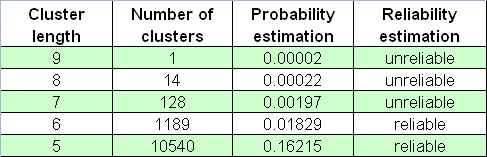
No deberíamos olvidar tampoco los "cisnes negros" que vienen exactamente cuando no los esperamos.
Contrastando con los cálculos anteriores, podemos usar estimaciones para los "cisnes negros" de un tipo distinto, a saber, clústeres rentables de longitud mayor. Recordamos que las pruebas reales muestran que la longitud del clúster rentable máximo es igual a 59. Usando el modelado análogo para 65.000 series modelo, de nuevo encontramos la línea más larga en el informe del script:
44118 153 115 117 111 87 70 71 52 51 50 40 36 42 42 34 20 32 15 20 20 13 10 11 12 8 5 7 3 5 4 2 2 6 7 0 2 1 2 1 1 5 0 0 1 0 0 0 0 0 0 1 0 0 2 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
Esta es una serie del modelo #44118, con una longitud de clúster rentable máximo igual a 153 transacciones (segunda cifra en la lista), aproximadamente 2,6 veces más larga que el clúster máximo en la prueba real. No obstante, las estimaciones significativas estadísticas de frecuencias de clústeres pueden ser obtenidas en su longitud comenzando por cerca de 80 (la estimación de probabilidad de la serie es 0,0088) e inferior, y 80 es mucho más que 59. El cuantil de orden ½ (el valor de la longitud del clúster en que la función de distribución integral toma el valor de 0,5, es decir, un valor por el que la distribución se divide en dos áreas iguales bajo la función de distribución de densidad de probabilidad) para clústeres rentables es de unos 62, es decir, algo más de 59. El histograma de distribución de longitud de clúster máximo en la matriz de series de Bernoulli se incluye aquí para su referencia:
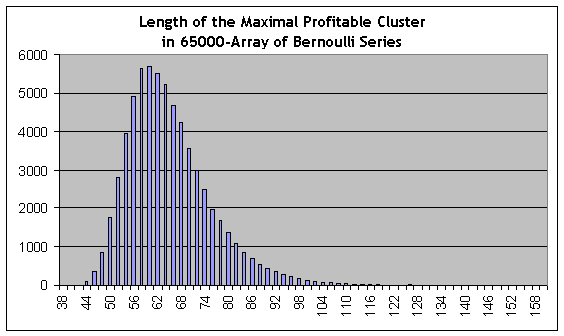
Por supuesto, el término "cisne negro" se usa aquí sin mucho cuidado, ya que desde Taleb esto parece ser un evento cuya probabilidad no es computable. No obstante, podemos decir que, juzgando solo por los datos empíricos (informe de pruebas) y sin usar los modelos teóricos, difícilmente podríamos sacar conclusiones fiables sobre las probabilidades de clústeres de 6 perdedores o clústeres de 80 rentables, es decir, para los eventos que no cumplimos en el informe.
3. "Deriva de fracaso": Una desviación desfavorable de la probabilidad de fracaso a partir de la frecuencia empírica.
Sistema de tratamiento, intento nº 1
En una gran cantidad de pruebas en la serie por el sistema Bernoulli (unas siete mil aproximadamente) la frecuencia de fracaso f difiere ligeramente de la probabilidad de fallo q y obedece a la distribución normal "correcta" con algo de varianza: la ley de los grandes números (aquí el teorema de Laplace) sigue siendo efectiva. No obstante, f puede también variar y para las estrategias de reventa especulativa con una esperanza matemática muy pequeña de una transacción, dicha deriva puede ser crítica y es capaz de convertir el sistema en uno perdedor para todo el intervalo de prueba. Ahora tenemos herramientas suficientes para la estimación estadística de opciones de dicha deriva, si hay una evidencia que pruebe que el sistema Bernoulli "funciona" en este caso.
Por desgracia, el asesor experto Lucky_ incluso limitado en sus posibilidades hasta una transacción para un tiempo establecido, proporciona demasiadas estadísticas.
Esta información es incorrecta, pero me quedó claro solo después de la publicación del artículo original en ruso. No obstante, decidí dejarlo "tal cual estaba" en esta traducción para que fuera auténtico. - Matemáticas
Para un desarrollador de estrategias serio, esto es más una excepción que una regla, ya que uno tiene normalmente que sacar conclusiones retorcidas en base a los resultados de la pruebas que contienen varios centenares o incluso docenas de transacciones (ver la explicación más adelante). El incremento en el volumen de las estadísticas lleva convenientemente al descenso correspondiente del ancho de la distribución de Gauss y reduce considerablemente las opciones de grandes desviaciones de su valor central.
Como ejemplo, vamos a considerar Lucky_ con los parámetros alejados del valor favorable para el asesor experto: 4, 80, 20, en el lote 0.1. Primero vamos a realizar su prueba para todo el intervalo de tiempo ("intervalo A") – desde el 1 de enero de 2004 al 4 de abril de 2008 (EURUSD H1). Aquí el gráfico de balance dado por el informe:
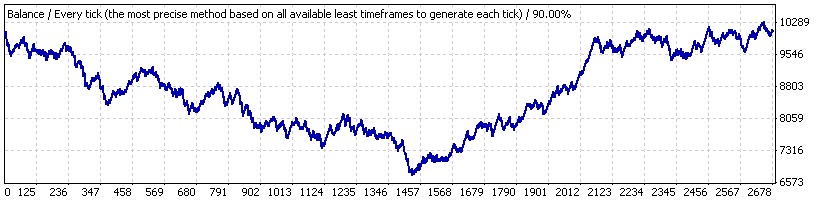
Vemos que queda alejado de ser sorprendente. Después de comprobar la secuencia de transacciones con nuestro script (en 1000 series Bernoulli modelo) encontramos que la serie de transacción completa puede considerarse que corresponde al sistema Bernoulli, tanto para los clústeres rentables como para los perdedores.
Vemos los parámetros de las transacciones promedio:
Transacción rentable promedio
21,71
Operación de pérdidas
-83,32
Ahora, supongamos que probamos el asesor experto solo para un corto periodo desde el 21-10-2005 al 07-06-2007 ("intervalo B"), donde la estrategia muestra un crecimiento estable. El gráfico es el siguiente:
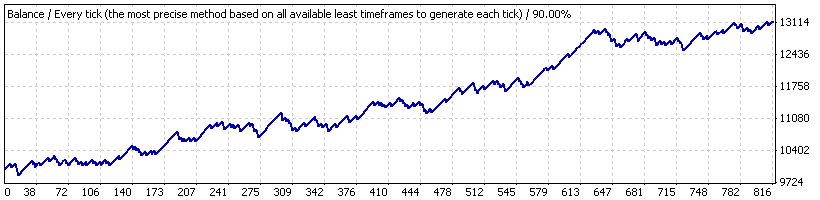
Estos son los resultados de las transacciones promedio:
| Transacción rentable promedio | 21,69 | Operación de pérdidas | -82,94 |
De media, las transacciones han cambiado muy ligeramente, por lo que pueden considerarse aproximadamente invariantes, con independencia de la rentabilidad de la estrategia para el periodo de prueba. En realidad, podríamos haber visto esto antes, teniendo en cuenta que las transacciones se cierran solo después de que estas alcancen cierto nivel de beneficio/pérdida establecido por los estrictos parámetros externos.
La segunda comprobación de tipo Bernoulli (1000 serie modelo) de nuevo confirma su adecuación con el sistema Bernoulli. Ahora vamos a aplicar nuestro script con un gran número de series Bernoulli (65000) a los resultados del periodo de tiempo corto (intervalo B) y luego importaremos los resultados de las 65000 series del modelo Bernoulli a MS Excel para construir el histograma de la distribución del coeficiente de transacciones rentables:
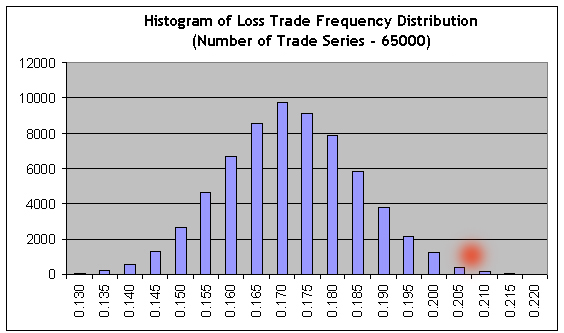
Es obvio que para lorgrar la ausencia de beneficio, las frecuencias de beneficios y pérdidas debe estar relacionadas inversamente con el coeficiente de sus valores medios: r = 21.69/82.94 = 0.2615. Por tanto, la frecuencia de las transacciones perdedoras debe ser igual a f = r / ( 1+r ) = 0.2073. Vemos que este valor (ver el punto rojo) se sitúa lejos del área de la cola de la derecha, donde la suma de las barras a la derecha es cercana al 0,3 % de la suma de todas las barras del histograma, es decir, la probabilidad de la opción sin beneficio/pérdida es en torno al 0,003. Aproximadamente, se obtiene el mismo valor en el uso directo del teorema de Laplace.
Algo está mal en el reino de Dinamarca: los datos del informe en el intervalo A nos dicen que en la primera mitad de A, antes de este intervalo de crecimiento, el balance calló casi con la misma rapidez y el periodo de descenso no es más corto que B en lo que respecta al número de transacciones. Si estimamos la probabilidad de aproximadamente el mismo intervalo de balance descendente (pérdida estable) sobre la base de nuestros datos de prueba en el intervalo B, se desvanecerá (ya que la frecuencia límite f cambiará incluso más a la derecha), y esto parece ser contrario a los datos experimentales.
Probablemente, el problema sea que dicha serie larga de transacciones con la rentabilidad correspondiente al intervalo B es una desviación muy grande: la prueba desde enero de 1999 hasta comienzos de mayo de 2008 muestra que esta estrategia no es rentable ni perdedora:
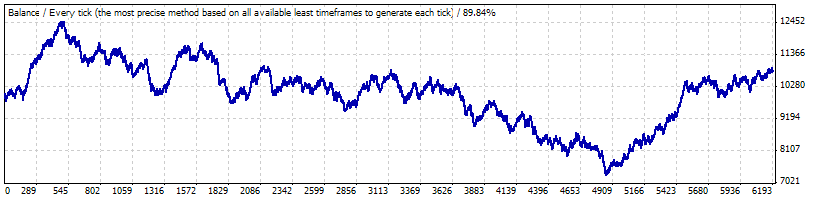
La esperanza matemática de una transacción es solo 0,17 y la frecuencia "natural" de las transacciones perdedoras es aproximadamente igual a la calculada anteriormentef (0.2073) y llega a ser 0.2054.
Está claro que las estimaciones de probabilidades basadas en las estadísticas de eventos atípicos (la frecuencia de transacciones perdedoras en el intervalo B es igual a 0,1706 y se diferencia de la "natural" en 2,8 "sigmas" en la dirección favorable) no es lo suficientemente fiable. Pero no podemos saber con seguridad la "verdadera" frecuencia. ¿Puede el concepto de "deriva de fracaso sernos de utilidad?
4. "Deriva de fracaso": Estimación de probabilidad de reducciones de "choque" a corto plazo.
Sistema de tratamiento, intento nº 2
Aparentemente, podemos, si establecemos objetivos razonables y no extremos correspondientes a las "colas" de las distribuciones. Vamos a ver esta tarea de esta forma: supongamos que tenemos los resultados de la prueba para el intervalo B. Estamos seguros de que este es el sistema Bernoulli y la esperanza matemática de las transacciones rentables y perdedoras prácticamente no dependen de lo que le está ocurriendo al balance. En base a estimaciones muy optimistas (realmente falsas) sobre la probabilidad de pérdidas, vamos a intentar estimar nuestras opciones para las reducciones de "choque" cortas pero profundas. Dichas reducciones tienen exactamente el efecto más devastador sobre la psicología de un trader, ya que después de esto, un trader comienza a hablar sobre frases místicas como "el mercado ha cambiado" o incluso "se ha convertido en uno dirigido".
Debo añadir aquí que el teorema de Laplace no sería de gran ayuda en este caso, ya que el valor n*p*q contenido en su fórmula será pequeño, en torno a 10 e inferior (esto se corresponde a varias docenas de transacciones, aproximadamente. La idea principal en la base de este cálculo es que en series de transacciones muy cortas, la frecuencia de las pérdidas puede diferir lo suficiente de la "verdadera", es decir, de la probabilidad: la distribución de la frecuencia de pérdida se distribuye ampliamente debido a pequeño número de pruebas.
Recordemos que la estimación de una reducción a corto plazo es una tarea que se diferencia mucho del problema de estimar la longitud máxima de un clúster perdedor, ya que una reducción no está compuesta necesariamente solo de transacciones perdedoras. Vamos a usar nuestro script para generar 65.000 series de longitud 40 a una "muy favorable" frecuencia de pérdidas 0,1706 ("intervalo B"), y luego construir el histograma como el del apartado Sistema de tratamiento, intento nº 1:
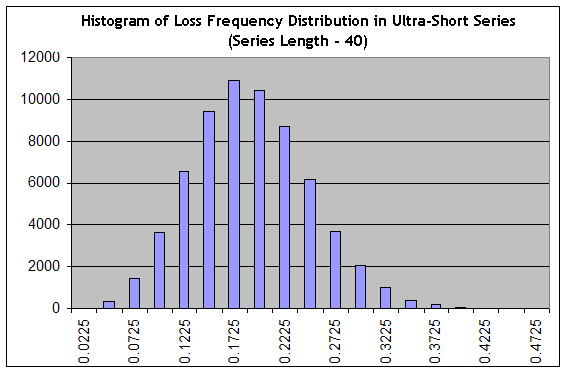
Vemos que la configuración ha cambiado de forma drástica: desde una pronunciada, la distribución cambió a una suave, es decir, ha aumentado el "ancho relativo". La probabilidad de que en series de longitud 40 obtengamos algo en el rango a partir de un trading prácticamente sin beneficio (en la frecuencia de transacciones perdedoras igual a 0,1975 una transacción media alcanza 0,25 puntos) hasta un trading perdedor pronunciado (en la frecuencia de transacciones perdedoras 0,3, la estimación de la esperanza matemática de una transacción en esta serie es igual a 0.7*20-0.3*80=-10 puntos), es igual a la suma de las columnas desde la columna "0,2225" y hasta la derecha de esta, que es cerca del 34 % de la suma total de las columnas (65.000). De todos modos, esta estimación es optimista, ya que el pico de la distribución está en la frecuencia "optimista" de 0,1706.
Teniendo presenta la hipótesis de ergodicidad, que es poner un puente entre la distribución de probabilidad y el espacio de trading, es decir, el espacio del tiempo real, obtenemos al menos un 34 % del tiempo de trading en el que el sistema no logrará ningún beneficio ni pérdida de media. Esta cifra está muy bien correlacionada con los datos de [4], según los cuales un sistema Bernoulli sigue en reducción aproximadamente desde el 35 al 55 % de todo el tiempo de trading.
Preste atención al hecho de que la probabilidad real para encontrar una reducción de choque no depende fuertemente de la frecuencia inicial "favorable", sin que importe lo atractivo que parezca. Esta es la función característica del sistema, que está relacionada con su cualidad de Bernoulli, y este evento puede suavizarse solo mediante el coeficiente mejorado de resultados de transacciones rentables y perdedoras medio.
A propósito, estas estimaciones exactamente basadas en la generación de series ultracortas permite a menudo con mucha fiabilidad seleccionar los resultados de la prueba de un sistema bastante "rentable" con solo docenas de transacciones en el intervalo de pruebas: a pesar de que la muy positiva "esperanza matemática" de una transacción, en tan pequeño número de transacciones las reducciones de "choque" son inevitables en caso de que el sistema sea de tipo Bernoulli.
Conclusión
A pesar del hecho de que nos gusta crear construcciones lógicas orgullosamente llamadas "Sistemas de trading mecánicos", con frecuencia no nos damos cuenta de cuánta aleatoriedad contienen, incluyendo las que no encontramos en los resultados de las pruebas ("cisnes negros").
Como los resultados de las transacciones sucesivas expresadas en la notación binaria ("éxito" o "fracaso") muy a menudo cumplen el sistema Bernoulli, estos no tienen ninguna diferencia con el lanzamiento de una moneda cotidiano. Por supuesto, esto no significa que los sistemas rentables sean imposibles: una estrategia puede ser rentable y robusta, incluso si cumple idealmente con el sistema de Bernoulli. Esto se deriva claramente de la idea de que si la rentabilidad de una transacción rentable y su esperanza matemática son establemente más elevadas que las de una transacción perdedora, la estrategia es obviamente rentable.
Un lector que al menos en algunas ocasiones sea capaz de "comunicarse" con las matemáticas como un "familiar" debe comprender el beneficio de los modelos bastante bien, incluso si estos están lejos de ser determinísticos. El principal valor de los modelos que son adecuados para el fenómeno estadístico real es que permiten obtener un valioso conocimiento sobre el universo , es decir, la información que no puede obtenerse de los escasos datos experimentales. En este caso, el valor del sistema Bernoulli es considerablemente mayor debido a la extrema simplicidad de su generación y la ausencia de "colas anchas" en distribuciones de probabilidad claves.
Vamos a finalizar este artículo con una pregunta bastante dura: probablemente, la parte analítica de la mayoría de TS es inútil, y los principales esfuerzos deben destinarse a los métodos de gestión del dinero eficientes y bien fundamentados ("La analítica no es nada pero la gestión del dinero lo es todo") ¿verdad?
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/1530
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 El espectáculo debe continuar, o una vez más sobre el ZigZag
El espectáculo debe continuar, o una vez más sobre el ZigZag
 Modificación en dos etapas de posiciones abiertas
Modificación en dos etapas de posiciones abiertas
 Integración del terminal de cliente de MetaTrader 4 con MS SQL Server
Integración del terminal de cliente de MetaTrader 4 con MS SQL Server
 Una plantilla para una orden trailing stop y de salida del mercado
Una plantilla para una orden trailing stop y de salida del mercado
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso