Obtenga una ventaja sobre cualquier mercado (Parte V): Datos alternativos de FRED (Federal Reserve Economic Data) sobre el EURUSD
En esta serie de artículos, nuestro objetivo es ayudarlo a navegar por el panorama cada vez mayor de datos financieros alternativos. El inversor moderno, que vive en la era del big data, puede no poseer recursos suficientes para decidir cuidadosamente qué conjuntos de datos alternativos debería incluir en su proceso de negociación. Nuestro objetivo es brindarle la información que necesita para que pueda tomar una decisión informada sobre qué conjuntos de datos alternativos debería considerar y cuáles serían mejores si no los tuviera.
Descripción general de la estrategia comercial
La correlación es un principio fundamental de un enfoque analítico de las finanzas. Si dos activos están correlacionados, entonces los inversores que buscan diversificar sus carteras o maximizar su exposición a cambios de precios anticipados, pueden usar esta métrica de manera inteligente para construir su cartera.
El Sistema de la Reserva Federal mantiene una colección de índices que sirven como medidas resumidas del valor del tipo de cambio del dólar. De todos los índices que teníamos disponibles, nos interesaba especialmente el Nominal Broad Dollar Daily Index (NBDD). El índice se estableció en enero de 2006 con un valor de 100 puntos. Al momento de escribir este artículo, el índice alcanzó mínimos históricos de aproximadamente 86 puntos durante la recesión de 2008 y alcanzó su máximo histórico de aproximadamente 128 puntos en 2022. El índice ha estado en una tendencia alcista desde finales de 2011 y actualmente ronda los 121 puntos. Este nivel se sitúa muy cerca de su máximo histórico.
En el gráfico a continuación, hemos superpuesto el índice Broad Dollar y el tipo de cambio del par EURUSD. Es casi imposible ver alguna relación material entre los datos de dos series de tiempo. El tipo de cambio del dólar estadounidense está casi oculto como la línea plana en la parte inferior del gráfico en azul, mientras que el índice Broad Dollar es la línea roja claramente visible.
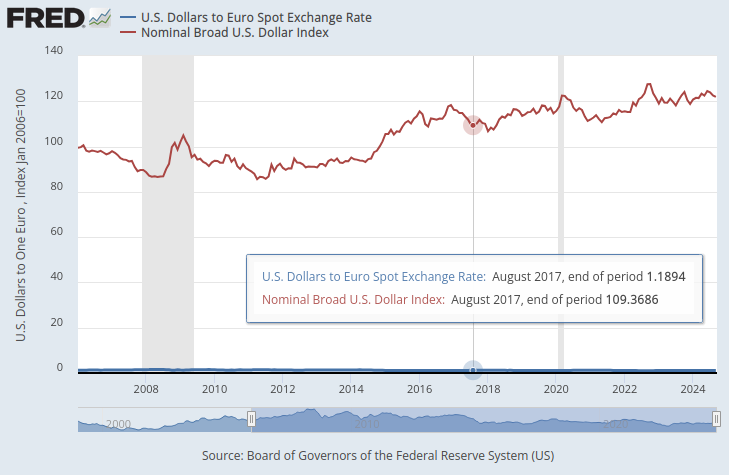
Figura 1: El tipo de cambio al contado del dólar al euro y el índice Broad Dollar.
Si nos aseguráramos de que ambos datos de series temporales estuvieran en la misma escala, surgiría un patrón obvio. Cambiaremos nuestro eje y para que registre el cambio porcentual en los datos de series de tiempo durante 1 año. Cuando realizamos este paso, podemos observar claramente que el índice muestra una correlación negativa casi perfecta con el tipo de cambio EURUSD.
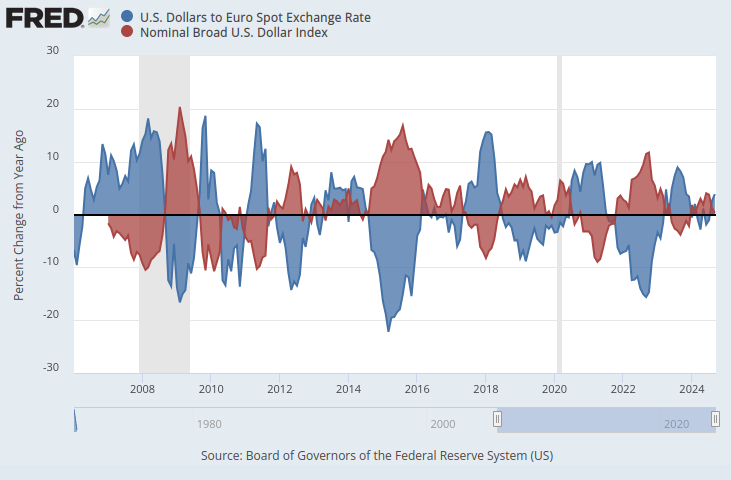
Figura 2: El tipo de cambio al contado del dólar al euro y el índice Broad Dollar en una escala porcentual.
Exploraremos la viabilidad de aprender algorítmicamente una estrategia comercial que emplee estos conjuntos de datos para predecir el tipo de cambio futuro del EURUSD. Dada la correlación negativa perfecta, potencialmente podría haber alguna información que nuestro modelo podría aprender sobre el tipo de cambio, dados los indicadores macroeconómicos de la Base de Datos Económica de la Reserva Federal (Federal Reserve Economic Database, FRED).
Descripción general de la metodología
Para probar la validez de nuestra propuesta, comenzamos obteniendo los tipos de cambio históricos diarios del EURUSD desde nuestro terminal MetaTrader 5 y fusionamos los datos con tres conjuntos de datos macroeconómicos que recuperamos de la API Python de FRED. Se registraron los 3 conjuntos de datos de series temporales de FRED:
- Tipos de interés de los bonos estadounidenses
- Tasas de inflación previstas en EE.UU.
- Índice Broad Dollar
Esto nos permitió crear 3 conjuntos de datos para construir nuestro modelo de IA:
- Cotizaciones ordinarias de mercado OHLC.
- Datos FRED alternativos
- Un superconjunto de los 2 primeros.
Tras fusionar todos los conjuntos de datos en cuestión y convertir las escalas para replicar lo que hicimos en el sitio web del FRED, observamos que los niveles de correlación entre los precios del tipo de cambio EURUSD y el índice Broad Dollar eran de casi -0,9. ¡Ésta es una puntuación casi perfecta! Not only that, but we also observed the correlation between the current value of the Broad Dollar Index and the future value, 20 days into the future, of the EURUSD close was -0.7.
Tras la visualización, pudimos separar los datos de las series temporales notablemente bien, con un nivel de delicadeza que dudo que hayamos demostrado antes en esta serie de artículos. Parece que utilizar el cambio porcentual de los datos en ventanas relativamente más largas nos permite separar los datos extremadamente bien. Nuestros gráficos de dispersión 3D validaron aún más lo bien que estaban separados los datos y pudimos identificar zonas alcistas y bajistas aparentes. Además, cuando realizamos diagramas de dispersión de los datos en el sitio web oficial de FRED, pudimos observar claramente una tendencia en los datos. La tendencia en el diagrama de dispersión estaba bien definida, incluso sin tener que utilizar nuestra bolsa habitual de herramientas analíticas avanzadas en Python. Esto nos dio confianza de que podría haber cierta información potencial compartida por los dos conjuntos de datos de series de tiempo que esperamos que nuestro modelo pueda aprender.
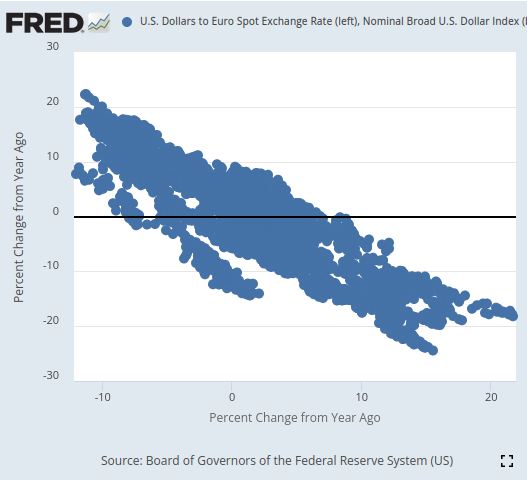
Figura 3: Visualización de un diagrama de dispersión de los 2 conjuntos de datos que nos interesan.
Por muy prometedor que pueda parecer todo esto hasta ahora, nada de esto se tradujo en un mejor desempeño en nuestra capacidad de predecir el valor futuro del tipo de cambio EURUSD. De hecho, nuestro desempeño solo empeoró y parece que nos fue mejor usar el primer conjunto de datos que solo contenía cotizaciones de mercado ordinarias.
Entrenamos 3 regresores de redes neuronales profundas (Deep Neural Network, DNN) idénticos para aprender la relación entre nuestros 3 conjuntos de datos y el objetivo común que todos compartían. El primer modelo DNN produjo la tasa de error más baja. Además, ninguno de nuestros algoritmos de selección de características pareció impresionado por ninguno de los conjuntos de datos FRED que seleccionamos para nuestro análisis. Sin dejarnos intimidar, logramos ajustar con éxito los parámetros de nuestro modelo DNN usando el conjunto de datos de entrenamiento, sin sobreajustarlos. Esto nos lo sugiere el hecho de que superamos el modelo DNN predeterminado en datos de validación no vistos. Utilizamos la validación cruzada de series de tiempo sin mezcla aleatoria para llegar a estas decisiones durante el entrenamiento y la validación.
Antes de exportar nuestro modelo al formato ONNX, inspeccionamos los residuos de nuestro modelo para asegurarnos de que esté en buenas condiciones. Lamentablemente, los residuos que observamos de nuestro modelo se comportaron incorrectamente, lo que puede sugerir que nuestro modelo no ha logrado aprender de manera efectiva.
Finalmente, exportamos nuestro modelo al formato ONNX y construimos un asesor experto integrado impulsado por IA utilizando Python y MQL5.
Obteniendo los datos
Para comenzar, primero importamos las bibliotecas de Python que necesitamos.
#Import the libraries we need from fredapi import Fred import seaborn as sns import numpy as np import pandas as pd import MetaTrader5 as mt5 import matplotlib.pyplot as plt
Luego definimos nuestras credenciales y qué series de tiempo nos gustaría obtener de FRED.
#Define important variables fred_api = "ENTER YOUR API KEY" fred_broad_dollar_index = "DTWEXBGS" fred_us_10y = "DGS10" fred_us_5y_inflation = "T5YIFR"
Iniciar sesión en FRED.
#Login to fred
fred = Fred(api_key=fred_api)Obtengamos los datos que necesitamos.
#Fetch the data
dollar_index = fred.get_series(fred_broad_dollar_index)
us_10y = fred.get_series(fred_us_10y)
us_5y_inflation = fred.get_series(fred_us_5y_inflation)Nombrar la serie nos permitirá fusionarlas más adelante.
#Name the series so we can merge the data dollar_index.name = "Dollar Index" us_10y.name = "Bond Interest" us_5y_inflation.name = "Inflation"
Rellene los valores que falten con la media móvil.
#Fill in any missing values dollar_index.fillna(dollar_index.rolling(window=5,min_periods=1).mean(),inplace=True) us_10y.fillna(us_10y.rolling(window=5,min_periods=1).mean(),inplace=True) us_5y_inflation.fillna(dollar_index.rolling(window=5,min_periods=1).mean(),inplace=True)
Antes de que podamos obtener datos de nuestro terminal MetaTrader 5, primero tenemos que inicializarlo.
#Initialize the terminal
mt5.initialize()Nos gustaría obtener 4 años de datos históricos.
#Define how much data to fetch amount = 365 * 4 #Fetch data eur_usd = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",mt5.TIMEFRAME_D1,0,amount)) eur_usd
Convierte la columna de tiempo del formato de segundos a fechas reales.
#Convert the time column eur_usd['time'] = pd.to_datetime(eur_usd.loc[:,'time'],unit='s')
Asegúrese de que la columna de tiempo sea el índice de nuestros datos.
#Set the column as the index
eur_usd.set_index('time',inplace=True)Definir hasta qué punto en el futuro nos gustaría realizar el pronóstico.
#Define the forecast horizon look_ahead = 20
Especificaremos ahora nuestros predictores y objetivos.
#Define the predictors predictors = ["open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"] ohlc_predictors = ["open","high","low","close","tick_volume"] fred_predictors = ["Dollar Index","Bond Interest","Inflation"] target = "Target" all_data = ["Target","open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"] all_data_binary = ["Binary Target","open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"]
Fusionar los datos.
#Merge our data
merged_data = eur_usd.merge(dollar_index,right_index=True,left_index=True)
merged_data = merged_data.merge(us_10y,right_index=True,left_index=True)
merged_data = merged_data.merge(us_5y_inflation,right_index=True,left_index=True)Etiqueta los datos.
#Define the target target = merged_data.loc[:,"close"].shift(-look_ahead) target.name = "Target"
Formatee los datos para que nos muestren el cambio porcentual anual, tal como los datos que analizamos en el sitio web de FRED.
#Convert the data to yearly percent changes merged_data = merged_data.loc[:,predictors].pct_change(periods = 365) * 100 merged_data = merged_data.merge(target,right_index=True,left_index=True) merged_data.dropna(inplace=True) merged_data
Agregue un objetivo binario para fines de trazado.
#Add binary targets for plotting purposes merged_data["Binary Target"] = 0 merged_data.loc[merged_data["close"] < merged_data["Target"],"Binary Target"] = 1
Restablecer el índice de los datos.
#Reset the index
merged_data.reset_index(inplace=True,drop=True)
merged_dataAnálisis exploratorio de datos
Comenzaremos recreando el gráfico que generamos en el sitio web de la Reserva Federal de St. Louis; esto validará que hemos realizado nuestros pasos de preprocesamiento según lo previsto.
#Plotting our data set plt.title("EURUSD Close Against FRED Broad Dollar Index") plt.plot(merged_data.loc[:,"close"]) plt.plot(merged_data.loc[:,"Dollar Index"])
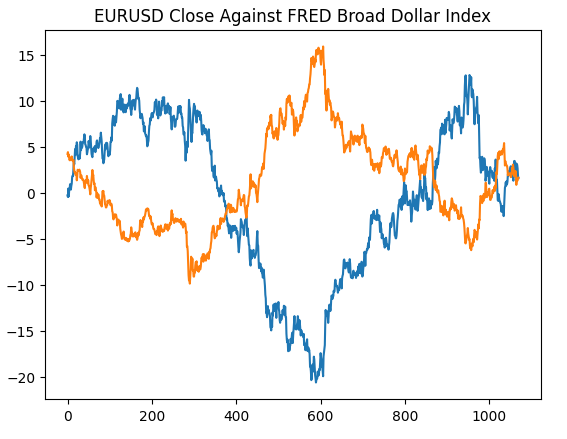
Figura 4: Recreación de nuestra observación en el sitio web de FRED en Python.
Analicemos ahora los niveles de correlación dentro de nuestro conjunto de datos. Como podemos observar, el conjunto de datos de inflación tiene los niveles de correlación más débiles de los tres conjuntos de datos FRED alternativos que hemos obtenido. Sin embargo, no obtuvimos ninguna mejora en el rendimiento a pesar de que nuestros dos conjuntos de datos alternativos restantes parecían tener mucho potencial.
#Exploratory data analysis
sns.heatmap(merged_data.loc[:,all_data].corr(),annot=True)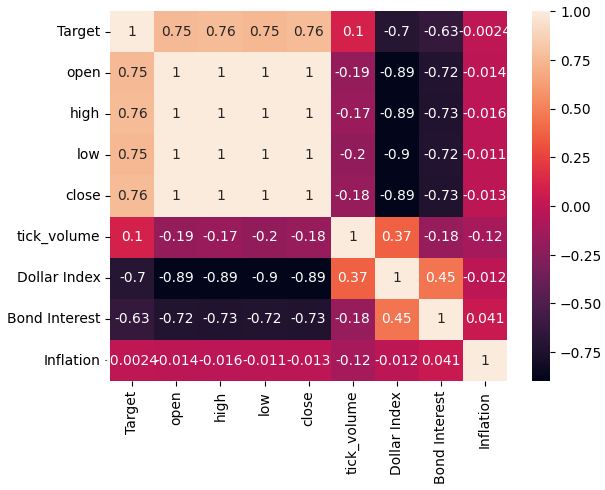
Figura 5: Nuestro mapa de calor de correlación.
Al visualizar muchos conjuntos de datos a la vez, los gráficos de pares pueden ayudarnos a ver rápidamente las relaciones que pueden existir entre todos los datos que tenemos disponibles. Podemos ver claramente que los puntos naranjas y azules parecen estar notablemente bien separados. Además, tenemos gráficos de estimación de densidad de kernel (Kernel-Density Estimation, KDE) que recorren la diagonal principal de este gráfico. Los gráficos KDE nos ayudan a visualizar la distribución de los datos dentro de cada columna. El hecho de que observemos lo que parecen ser dos formas similares a colinas que se superponen en una pequeña sección, implica que los datos están en su mayor parte bien separados.
sns.pairplot(merged_data.loc[:,all_data_binary],hue="Binary Target")
Figura 6: Visualización de nuestros datos mediante gráficos de pares.
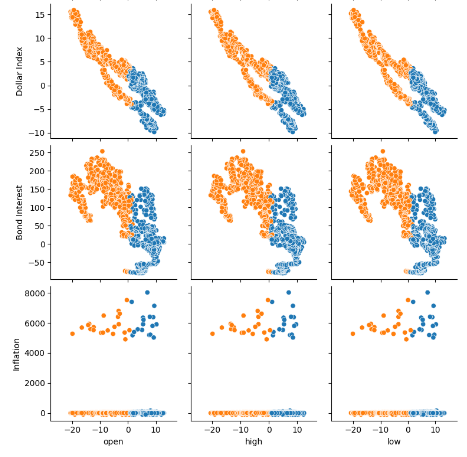
Figura 7: Visualización de nuestros datos alternativos FRED y su relación con nuestro par EURUSD.
Ahora realizaremos gráficos de dispersión 3D utilizando el índice amplio del dólar y la tasa de interés de los bonos en los ejes 'x' e 'y', y el cierre del EURUSD en el eje 'z'. Los datos parecen estar en dos grupos distintos, con poca superposición. Esto naturalmente implicaría que podría haber un límite de decisión que nuestro modelo podría aprender de los datos. Lamentablemente, creo que no logramos exponer esto de manera efectiva a nuestro modelo.
#Define the 3D Plot fig = plt.figure(figsize=(7,7)) ax = plt.axes(projection="3d") ax.scatter(merged_data["Dollar Index"],merged_data["Bond Interest"],merged_data["close"],c=merged_data["Binary Target"]) ax.set_xlabel("Dollar Index") ax.set_ylabel("Bond Interest") ax.set_zlabel("EURUSD close")
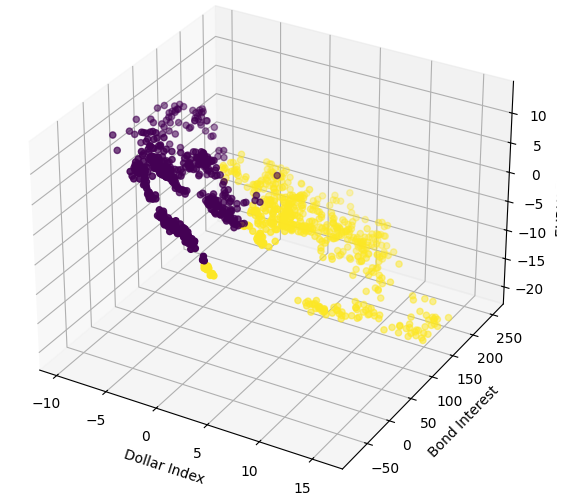
Figura 8: Visualización de nuestros datos de mercado en 3D.
Preparación para modelar los datos
Ahora preparémonos para modelar los datos financieros que tenemos, comenzaremos por definir las entradas y el objetivo de nuestro modelo.
#Let's define our set of predictors X = merged_data.loc[:,predictors] y = merged_data.loc[:,"Target"]
Importando la librería que necesitamos.
#Import the libraries we need
from sklearn.model_selection import train_test_splitAhora dividiremos nuestros datos en los tres grupos que describimos anteriormente.
#Partition the data ohlc_train_X,ohlc_test_X,train_y,test_y = train_test_split(X.loc[:,ohlc_predictors],y,test_size=0.5,shuffle=False) fred_train_X,fred_test_X,_,_ = train_test_split(X.loc[:,fred_predictors],y,test_size=0.5,shuffle=False) train_X,test_X,_,_ = train_test_split(X.loc[:,predictors],y,test_size=0.5,shuffle=False)
Cree un marco de datos para almacenar la precisión de validación cruzada de nuestro modelo.
#Prepare the dataframe to store our validation error validation_error = pd.DataFrame(columns=["MT5 Data","FRED Data","ALL Data"],index=np.arange(0,5))
Modelado de datos
Importemos las bibliotecas que necesitamos para modelar los datos.
#Let's cross validate our models from sklearn.neural_network import MLPRegressor from sklearn.model_selection import cross_val_score
Defina las tres redes neuronales que describimos anteriormente.
#Define the neural networks ohlc_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500) fred_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500) all_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
Pruebe cada modelo.
#Let's obtain our cv score ohlc_score = cross_val_score(ohlc_nn,ohlc_train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) fred_score = cross_val_score(fred_nn,fred_train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) all_score = cross_val_score(all_nn,train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)
Almacene nuestras puntuaciones de validación cruzada.
for i in np.arange(0,5): validation_error.iloc[i,0] = ohlc_score[i] validation_error.iloc[i,1] = fred_score[i] validation_error.iloc[i,2] = all_score[i]
Visualizar el error de validación.
#Our validation error
validation_error| Datos de MetaTrader 5 | Datos alternativos de FRED | Todos los datos |
|---|---|---|
| -0.147973 | -0.79131 | -4.816608 |
| -0.103913 | -2.073764 | -0.655701 |
| -0.211833 | -0.276794 | -0.838832 |
| -0.094998 | -1.954753 | -0.259959 |
| -1.233912 | -2.152471 | -3.677273 |
El análisis de nuestro rendimiento medio en los 5 pliegues muestra que nuestros datos de mercado ordinarios de MetaTrader 5 pueden ser nuestra mejor apuesta.
#Our mean performane across all groups
validation_error.mean()| Datos de entrada | Error medio de 5 pliegues |
|---|---|
| MetaTrader 5 | -0.358526 |
| FRED | -1.449818 |
| TODO | -2.049675 |
Cuando graficamos el rendimiento de nuestros modelos, podemos observar que los datos de MetaTrader 5 produjeron niveles de error más consistentes.
#Plotting our performance
validation_error.plot()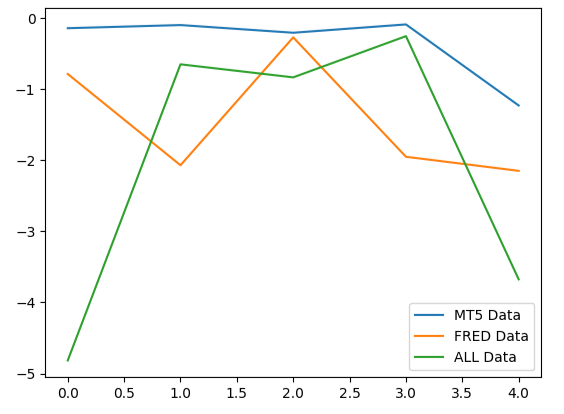
Figura 9: Visualización de los 3 niveles de error diferentes producidos por los 3 conjuntos de datos que teníamos para elegir.
La forma aplastada del gráfico de caja de errores de MetaTrader 5 es deseable porque muestra que el modelo está demostrando habilidad a través de su rendimiento constante.
#Creating box-plots of our performance
sns.boxplot(validation_error)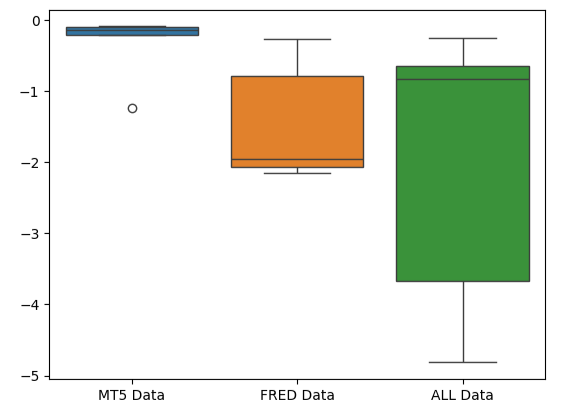
Figura 10: Visualización de las métricas de error de nuestro modelo como diagramas de caja.
Importancia de las características
Razonemos qué características pueden ser más importantes para nuestro modelo DNN. Con suerte, los datos alternativos que hemos seleccionado serán útiles y, por lo tanto, nuestros algoritmos de importancia de características así lo considerarán. Lamentablemente, nuestro análisis sugiere que la variación de los datos de mercado de MetaTrader 5 parece explicar el objetivo razonablemente bien por sí sola. Por lo tanto, no había información adicional contenida en la serie temporal FRED que nuestro modelo no pudiera haber deducido a partir de los datos que tenía.
Para comenzar, importemos las bibliotecas que necesitamos.
#Feature importance
from alibi.explainers import ALE, plot_aleLos gráficos de efectos locales acumulados (Accumulated Local Effects, ALE) nos ayudan a visualizar el efecto que tiene cada entrada del modelo sobre el objetivo. Los gráficos ALE son populares por su sólida capacidad para explicar modelos que han sido entrenados con datos muy correlacionados, como los nuestros. Los métodos académicos clásicos, como los gráficos de dependencia parcial (Partial Dependency, DP), simplemente no eran fiables a la hora de explicar predictores con fuertes niveles de correlación. La especificación original del algoritmo puede leerse en el trabajo de investigación completo de 2016 de Daniel W. Apley y Jingyu Zhu enlazado, aquí.

Figura 11: Daniel W. Apley, cocreador del algoritmo ALE.
Adaptemos ALE a nuestro DNN regresor.
#Explaining our deep neural network model = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500) model.fit(train_X,train_y) dnn_ale = ALE(model.predict,feature_names=predictors,target_names=["Target"])
Ahora podemos obtener una explicación de cada uno de los efectos del predictor sobre el objetivo. Las gráficas ALE tienen una interpretación visual intuitiva que las convierte en un buen punto de partida. En pocas palabras, si el gráfico ALE que obtenemos es una línea plana, entonces, desde la perspectiva de nuestro modelo DNN, el predictor bajo observación tiene poco o ningún efecto sobre el objetivo. En la misma línea, cuanto más se aleja el gráfico ALE de la linealidad, más lejos ha aprendido nuestro modelo que puede estar la relación entre el objetivo y el predictor de una relación lineal simple.
El gráfico ALE del precio de apertura y el objetivo, la esquina superior izquierda de la figura 12, nos sugiere que a medida que aumenta el precio de apertura del EURUSD, el modelo ha aprendido que el precio de cierre futuro también aumentará. Observe cómo los gráficos ALE del precio de apertura y cierre varían en direcciones opuestas. Esto puede sugerirnos que esos dos predictores por sí solos podrían explicar una variación significativa en el objetivo.
#Obtaining the explanation
ale_X = X.to_numpy()
dnn_explanations = dnn_ale.explain(ale_X)
#Plotting feature importance
plot_ale(dnn_explanations,n_cols=3,fig_kw={'figwidth':8,'figheight':8},sharey=None)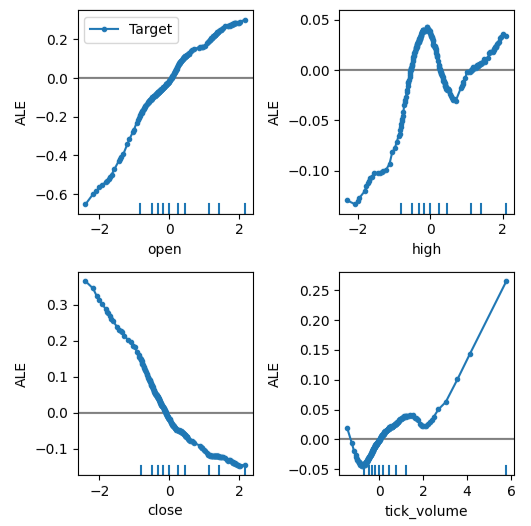
Figura 12: Visualización de nuestros gráficos ALE en nuestros datos de mercado de MetaTrader 5.
Ahora realizaremos la selección hacia adelante. El algoritmo comienza con un modelo nulo y agrega iterativamente 1 característica que mejorará al máximo el rendimiento del modelo, hasta que ya no se pueda aumentar más.
#Forward selection from mlxtend.feature_selection import SequentialFeatureSelector as SFS from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs
Inicializar el modelo.
#Reinitialize the model all_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
Ahora necesitamos especificar el objeto de selección avanzada que queremos. Daremos instrucciones a esta instancia del algoritmo para que seleccione tantas variables como considere importantes.
#Define the feature selector sfs1 = SFS(all_nn, k_features=(1,X.shape[1]), forward=True, scoring='neg_mean_squared_error', cv=5, n_jobs=-1 )
Ninguna de las series temporales FRED fue seleccionada por el algoritmo.
#Best features we identified
sfs1.k_feature_names_Podemos visualizar el proceso de selección del algoritmo. Nuestro gráfico muestra claramente que el rendimiento de nuestro modelo disminuyó a medida que aumentamos los parámetros del modelo.
#Fit the forward selection algorithm fig1 = plot_sfs(sfs1.get_metric_dict(), kind='std_dev')
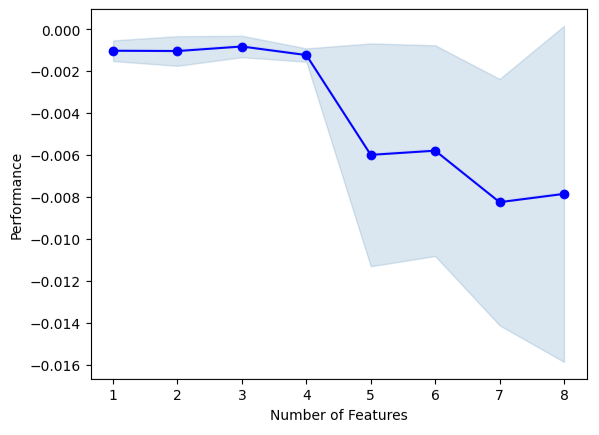
Figura 13: Visualización del rendimiento de nuestro modelo a medida que agregamos iterativamente más predictores.
Ajuste de parámetros
Realicemos un ajuste de parámetros en nuestro modelo DNN usando una búsqueda aleatoria. Primero necesitamos inicializar nuestro modelo.
#Reinitialize the model model = MLPRegressor(max_iter=500)
Ahora definiremos nuestros parámetros de ajuste.
#Define the tuner
tuner = RandomizedSearchCV(
model,
{
"activation" : ["relu","logistic","tanh","identity"],
"solver":["adam","sgd","lbfgs"],
"alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
"tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"learning_rate":['constant','adaptive','invscaling'],
"learning_rate_init":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"hidden_layer_sizes":[(10,20,40),(10,20,40,80),(5,10,20,100),(100,50,10),(20,20,10),(1,5,10,20),(20,10,5,1)],
"early_stopping":[True,False],
"warm_start":[True,False],
"shuffle": [True,False]
},
n_iter=500,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
)Ajustar el objeto de afinación.
#Fit the tuner
tuner.fit(train_X,train_y)Veamos los mejores parámetros que hemos encontrado.
#The best parameters we found
tuner.best_params_'tol': 1e-05,
'solver': 'lbfgs',
'shuffle': True,
'learning_rate_init': 0.01,
'learning_rate': 'invscaling',
'hidden_layer_sizes': (10, 20, 40, 80),
'early_stopping': True,
'alpha': 0.1,
'activation': 'relu'}
Optimización más profunda de parámetros
Busquemos mejores parámetros del modelo utilizando la biblioteca SciPy. Podemos imaginar los procesos de optimización como problemas de búsqueda, casi como el juego infantil del escondite. Verás, los parámetros ideales para nuestro modelo que producirán la mejor tasa de error en datos que el modelo no ha visto antes están ocultos en el espacio infinito de valores posibles que podríamos asignar a cada uno de nuestros parámetros continuos.
Importemos las bibliotecas que necesitamos.
#Deeper optimization from scipy.optimize import minimize from sklearn.metrics import mean_squared_error from sklearn.model_selection import TimeSeriesSplit
Define un objeto dividido en series de tiempo.
#Define the time series split object tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
Cree un marco de datos para devolver el costo actual y cree una lista para almacenar el progreso de nuestro modelo para su visualización.
#Create a dataframe to store our accuracy current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"]) algorithm_progress = []
Ahora definiremos nuestra función de costes. La biblioteca de SciPy nos ofrece varios algoritmos para encontrar las entradas de cualquier función, que darán como resultado la salida mínima de la función. Utilizaremos la media del nivel de error quíntuple del modelo en los datos de entrenamiento como cantidad a minimizar, manteniendo constantes todos los demás parámetros de la DNN.
#Define the objective function def objective(x): #The parameter x represents a new value for our neural network's settings model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=x[0], tol=x[1], learning_rate_init=x[2] ) #Now we will cross validate the model for i,(train,test) in enumerate(tscv.split(train_X)): #Train the model model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]]) #Measure the RMSE current_error_rate.iloc[i,0] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:])) #Store the algorithm's progress algorithm_progress.append(current_error_rate.iloc[:,0].mean()) #Return the Mean CV RMSE return(current_error_rate.iloc[:,0].mean())
Definamos los puntos de partida de la rutina y especifiquemos también los límites de los parámetros. Para este problema, nuestros únicos límites son que todos los parámetros del modelo deben ser positivos.
#Define the starting point pt = [tuner.best_params_["alpha"],tuner.best_params_["tol"],tuner.best_params_["learning_rate_init"]] bnds = ((10.00 ** -100,10.00 ** 100), (10.00 ** -100,10.00 ** 100), (10.00 ** -100,10.00 ** 100))
Utilizaremos el algoritmo Truncated Newton Constrained (TNC) para optimizar los parámetros de nuestro modelo. Los métodos de Newton truncados son una familia de métodos adecuados para resolver grandes problemas de optimización no lineal sujetos a límites. La biblioteca SciPy nos proporciona un contenedor para una implementación en C del algoritmo.
#Searching deeper for parameters result = minimize(objective,pt,method="TNC",bounds=bnds)
Veamos si hemos completado la finalización con éxito.
#The result of our optimization
resultsuccess: False
status: 4
fun: 0.001911232280110637
x: [ 1.000e-100 1.000e-100 1.000e-100]
nit: 0
jac: [ 2.689e+06 9.227e+04 1.124e+05]
nfev: 116
Parece que tuvimos dificultades para encontrar entradas óptimas, visualicemos el rendimiento de nuestro procedimiento de optimización.
#Store the optimal coefficients optimal_weights = result.x optima_y = min(algorithm_progress) optima_x = algorithm_progress.index(optima_y) inputs = np.arange(0,len(algorithm_progress)) #Plot the performance of our optimization procedure plt.scatter(inputs,algorithm_progress) plt.plot(optima_x,optima_y,'ro',color='r') plt.axvline(x=optima_x,ls='--',color='red') plt.axhline(y=optima_y,ls='--',color='red') plt.xlabel("Iterations") plt.ylabel("Training MSE") plt.title("Minimizing Training Error")
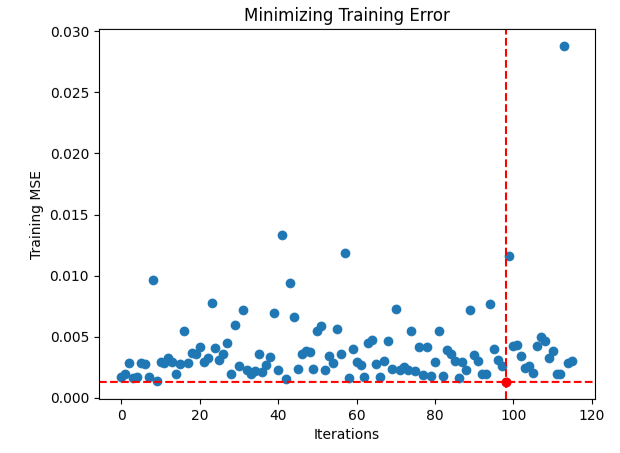
Figura 14: El punto rojo representa los valores de entrada óptimos estimados por nuestro optimizador TNC.
Prueba de sobreajuste
Inicialicemos nuestros tres modelos y veamos si podemos entrenarlos en el conjunto de entrenamiento y superar al modelo predeterminado en los datos de prueba. Recordemos que hasta ahora no hemos utilizado los datos de prueba en nuestro proceso de toma de decisiones.
#Testing for overfitting default_nn = MLPRegressor(max_iter=500) #Randomized NN random_search_nn = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"] ) #TNC NN tnc_nn = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=result.x[0], tol=result.x[1], learning_rate_init=result.x[2] )
Ajuste cada uno de los modelos en el conjunto de entrenamiento.
#Store the models in a list models = [default_nn,random_search_nn,tnc_nn] #Fit the models for model in models: model.fit(train_X,train_y)
Cree un marco de datos para almacenar nuestros niveles de error de validación.
#Create a dataframe to store our validation error validation_error = pd.DataFrame(columns=["Default","Randomized","TNC"],index=np.arange(0,5))
Pruebe cada modelo y registre su puntuación.
#Let's obtain our cv score default_score = cross_val_score(default_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) random_score = cross_val_score(random_search_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) tnc_score = cross_val_score(tnc_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) #Store the model error in a dataframe for i in np.arange(0,5): validation_error.iloc[i,0] = default_score[i] validation_error.iloc[i,1] = random_score[i] validation_error.iloc[i,2] = tnc_score[i]
Veamos el error de validación.
#Let's see the validation error validation_error
| Modelo predeterminado | Búsqueda aleatoria | TNC |
|---|---|---|
| -0.362851 | -0.029476 | -0.054709 |
| -0.323601 | -0.053967 | -0.087707 |
| -0.064432 | -0.024282 | -0.026481 |
| -0.121226 | -0.019693 | -0.017709 |
| -0.064801 | -0.012812 | -0.016125 |
El cálculo de nuestro rendimiento promedio en los cinco aspectos muestra claramente que nuestro modelo de búsqueda aleatoria es nuestra mejor opción.
#Our best performing model
validation_error.mean()| Modelo | Error medio de validación |
|---|---|
| Modelo predeterminado | -0.187382 |
| Búsqueda aleatoria | -0.028046 |
| TNC | -0.040546 |
La creación de gráficos de caja nos muestra rápidamente hasta qué punto varió el rendimiento del modelo por defecto. Nuestros modelos personalizados consiguieron funcionar dentro de una banda estrecha de niveles de error, lo que nos dio más confianza en nuestras elecciones de ajuste de parámetros.
#Let's create box-plots sns.boxplot(validation_error)

Figura 15: Visualización del rendimiento de nuestro modelo como diagramas de caja.
La creación de gráficos lineales de los datos de validación cruzada resalta la disparidad entre el modelo predeterminado y nuestros modelos ajustados. Podemos ver que hay una cantidad significativa de error entre la línea azul que representa el rendimiento del modelo predeterminado y los gráficos de colores restantes.
#We can also visualize model performance through a line plot
validation_error.plot()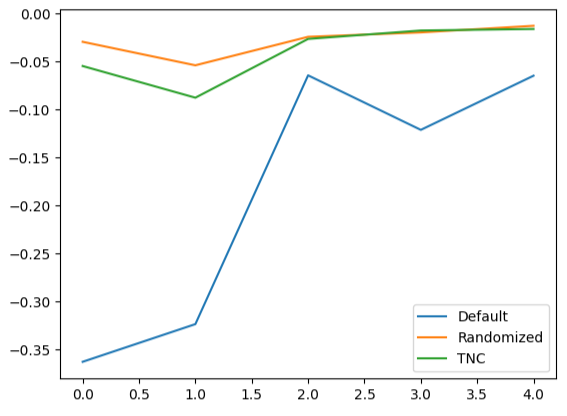
Figura 16: Representación gráfica del rendimiento quíntuple de nuestros diferentes modelos en datos de prueba.
Análisis de residuos
No podemos confiar ciegamente en nuestro modelo e implementarlo en producción. Intentemos asegurarnos de que nuestro modelo realmente ha aprendido de manera efectiva inspeccionando los residuos de nuestro modelo. Idealmente, un modelo que ha aproximado perfectamente una función tendrá residuos que sean una línea plana. Lo que significa que no hay ningún error en la predicción del modelo. Además, esto también implica que la cantidad de error en la predicción del modelo no cambia.
En consecuencia, cuanto más se aleje el rendimiento de nuestro modelo del ideal, mayor distorsión observaremos en el gráfico de residuos lineales y estacionarios ideal. Los residuos de nuestro modelo mostraron una cantidad variable de error, que a veces estaba correlacionada con la cantidad de error anterior. Esto probablemente es motivo de preocupación y podría solucionarse transformando el predictor o el objetivo.
Inicialicemos el modelo.
#Resdiuals analysis model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"] )
Ajuste el modelo a los datos de entrenamiento y luego registre los residuos utilizando los datos de prueba.
#Fit the model model.fit(train_X,train_y) #Record the residuals residuals = test_y - model.predict(test_X)
Nuestro gráfico de residuos estaba lejos de ser ideal, y es posible que necesitemos explorar otros pasos de preprocesamiento para abordar esto.
#Residuals analysis
residuals.plot()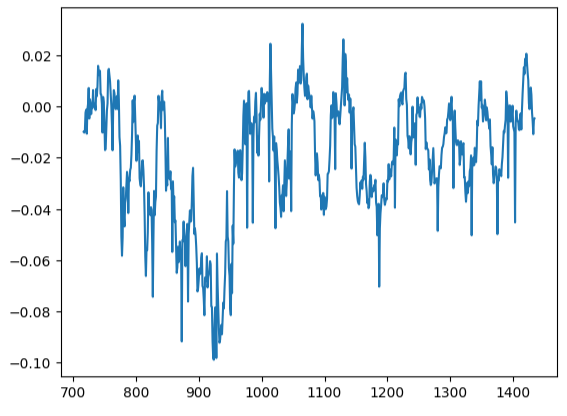
Figura 17: Visualización de los residuos de nuestro modelo en datos de prueba.
Medir la autocorrelación es un enfoque sólido para detectar posibles regresiones espurias. Lamentablemente, los residuos de nuestro modelo también fallaron en esta prueba y posiblemente podrían servir como indicador de que podemos obtener mejoras adicionales si transformamos mejor nuestros predictores u objetivos.
#Autocorrelation plot from statsmodels.graphics.tsaplots import plot_acf acf = plot_acf(residuals,lags=40)
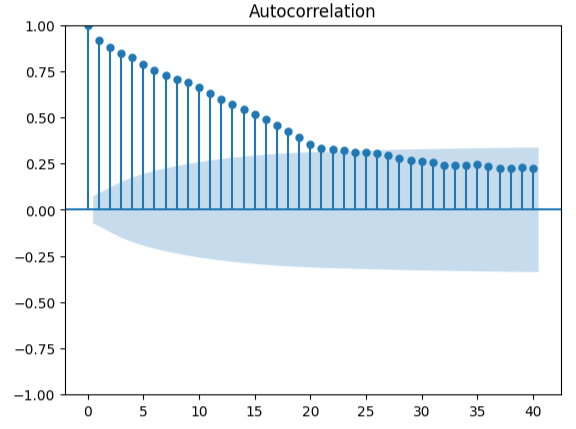
Figura 18: Visualización de los residuos de nuestro modelo.
Preparándose para exportar a ONNX
Antes de poder exportar nuestros datos al formato ONNX, primero almacenemos los valores medios y las desviaciones estándar de cada columna en un marco de datos. Tenga en cuenta que, dado que no obtuvimos ninguna mejora al transformar los datos en cambios porcentuales, utilizaremos los datos en su forma original y los usaremos para nuestros cálculos de puntuación 'z'.
#Prepare to convert the model to ONNX format scale_factors = pd.DataFrame(columns=X.columns,index=["mean","std"]) for i in X.columns: scale_factors.loc["mean",i] = merged_data.loc[:,i].mean() scale_factors.loc["std",i] = merged_data.loc[:,i].std() merged_data.loc[:,i] = (merged_data.loc[:,i] - scale_factors.loc["mean",i]) / scale_factors.loc["std",i] scale_factors

Figura 19: Nuestro marco de datos con nuestras puntuaciones 'z'.
Escriba los datos en formato CSV.
#Save the scale factors to CSV format scale_factors.to_csv("FRED EURUSD D1 scale factors.csv")
Exportando a ONNX
ONNX es un protocolo de código abierto que permite a los desarrolladores crear e implementar modelos de aprendizaje automático en cualquier lenguaje de programación que admita la API ONNX. Primero importaremos las bibliotecas que necesitamos.
# Import the libraries we need
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorTypeInicializar el modelo, por última vez.
#Initialize the model model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"] )
Ajuste el modelo a todos los datos que tenemos.
# Fit the model on all the data we have
model.fit(merged_data.loc[:,predictors],merged_data.loc[:,target])Define la forma de salida de nuestro modelo.
# Define the input type initial_types = [("float_input",FloatTensorType([1,X.shape[1]]))]
Cree una representación gráfica ONNX de nuestro modelo.
# Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
Guarde el modelo ONNX.
# Save the ONNX model onnx.save_model(onnx_model,"FRED EURUSD D1.onnx")
Visualizando nuestro modelo en Netron
Visualizar nuestro modelo nos ayudará a validar que ha sido creado según nuestras especificaciones. Queremos validar que las formas de entrada y salida estén en línea con nuestras expectativas. Netron es una biblioteca de código abierto para visualizar modelos de aprendizaje automático. Importemos la biblioteca para comenzar.
import netron
Ahora podemos visualizar fácilmente nuestro regresor DNN.
netron.start("FRED EURUSD D1.onnx")
Figura 20: Visualización de nuestro regresor DNN.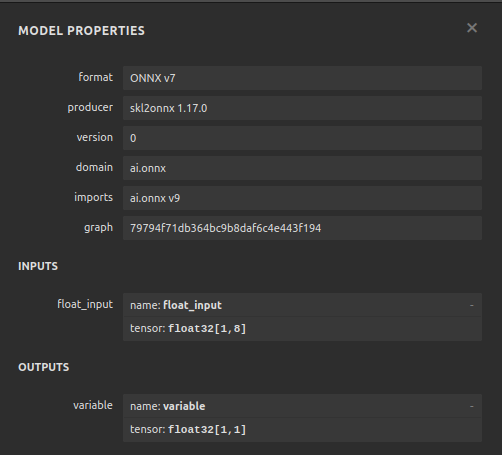
Figura 21: Visualización de las formas de entrada y salida de nuestro modelo.
Implementación en MQL5
El primer componente que necesitaremos integrar en nuestro Asesor Experto será el modelo ONNX. Simplemente incluiremos el archivo ONNX como recurso para nuestro Asesor Experto.
//+------------------------------------------------------------------+ //| FRED EURUSD AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Require the ONNX file | //+------------------------------------------------------------------+ #resource "\\Files\\FRED EURUSD D1.onnx" as const uchar onnx_buffer[];
Ahora carguemos la biblioteca comercial que necesitamos para administrar nuestras posiciones.
//+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
Creando variables globales que necesitaremos a lo largo de nuestro programa.
//+------------------------------------------------------------------+ //| Define global variables | //+------------------------------------------------------------------+ long model; double mean_values[5] = {1.1113568153310105,1.1152603484320558,1.1078179790940768,1.1114909337979093,65505.27177700349}; double std_values[5] = {0.05467420688685988,0.05413287747761819,0.05505429755411189,0.054630920048519924,26512.506288360997}; vectorf model_output = vectorf::Zeros(1); vectorf model_inputs = vectorf::Zeros(8); int model_sate = 0; int system_sate = 0; double bid,ask;
Siempre que nuestro modelo se cargue por primera vez, primero intentemos cargar nuestro modelo ONNX y luego probemos si funciona.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX model if(!load_onnx_model()) { //--- We failed to load the ONNX model return(INIT_FAILED); } //--- Test if we can get a prediction from our model model_predict(); //--- Eveything went fine return(INIT_SUCCEEDED); }
Si eliminamos nuestro modelo del gráfico, también liberaremos los recursos que ya no utilizamos.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we no longer need release_resources(); }
Cada vez que recibamos nuevos precios, actualizaremos las variables que hemos asignado para almacenar los precios actuales del mercado. Del mismo modo, si no tenemos posiciones abiertas, seguiremos la directiva de nuestro modelo. Por otro lado, si ya tenemos posiciones abiertas, entonces permitiremos que nuestro modelo nos advierta sobre posibles reversiones y cerraremos nuestras posiciones en consecuencia.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update our bid and ask prices update_market_prices(); //--- Fetch an updated prediction from our model model_predict(); //--- If we have no trades, follow our model's directions. if(PositionsTotal() == 0) { //--- Our model is predicting price levels will appreciate if(model_sate == 1) { Trade.Buy(0.3,"EURUSD",ask,0,0,"FRED EURUSD AI"); system_sate = 1; } //--- Our model is predicting price levels will deppreciate if(model_sate == -1) { Trade.Sell(0.3,"EURUSD",ask,0,0,"FRED EURUSD AI"); system_sate = -1; } } //--- Otherwise Manage our open positions else { if(system_sate != model_sate) { Alert("AI System Detected A Reversal! Closing All Positions on EURUSD"); Trade.PositionClose("EURUSD"); } } } //+------------------------------------------------------------------+
Esta función actualizará nuestras variables que registran los precios actuales del mercado.
//+------------------------------------------------------------------+ //| Update market prices | //+------------------------------------------------------------------+ void update_market_prices(void) { bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); }
Ahora definiremos la forma en que deben liberarse nuestros recursos.
//+------------------------------------------------------------------+ //| Release the resources we no longer need | //+------------------------------------------------------------------+ void release_resources(void) { OnnxRelease(model); ExpertRemove(); }
Definamos la función responsable de crear nuestro modelo ONNX a partir del buffer que creamos anteriormente. Si esta función falla en algún momento, devolverá falso (false), lo que interrumpirá nuestro procedimiento de inicialización.
//+------------------------------------------------------------------+ //| Create our ONNX model from the buffer we defined above | //+------------------------------------------------------------------+ bool load_onnx_model(void) { //--- Create the ONNX model from the buffer we defined model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); //--- Validate the model was not illdefined if(model == INVALID_HANDLE) { //--- We failed to define our model Comment("We failed to create our ONNX model: ",GetLastError()); return false; } //---- Define the model I/O shape ulong input_shape[] = {1,8}; ulong output_shape[] = {1,1}; //--- Validate our model's I/O shapes if(!OnnxSetInputShape(model,0,input_shape) || !OnnxSetOutputShape(model,0,output_shape)) { Comment("Failed to define our model I/O shape: ",GetLastError()); return(false); } //--- Everything went fine! return(true); }
Esta es la función responsable de obtener una predicción de nuestro modelo. La función primero buscará y normalizará las cotizaciones de los datos del mercado EURUSD, antes de llamar a una rutina responsable de leer nuestros datos alternativos FRED actuales.
//+------------------------------------------------------------------+ //| This function will fetch a prediction from our model | //+------------------------------------------------------------------+ void model_predict(void) { //--- Get the input data ready for(int i =0; i < 6; i++) { //--- The first 5 inputs will be fetched from the market matrix eur_usd_ohlc = matrix::Zeros(1,5); eur_usd_ohlc[0,0] = iOpen(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,1] = iHigh(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,2] = iLow(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,3] = iClose(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,4] = iTickVolume(Symbol(),PERIOD_D1,0); //--- Fill in the data if(i<4) { model_inputs[i] = (float)((eur_usd_ohlc[0,i] - mean_values[i])/ std_values[i]); } //--- We have to read in the fred alternative data else { read_fred_data(); } } } //+------------------------------------------------------------------+
Esta función leerá nuestros datos alternativos FRED desde nuestro directorio MQL5\Files. Recuerde que el archivo CSV se actualizará todos los días mediante nuestro script Python.
//+------------------------------------------------------------------+ //| This function will read in our FRED data | //+------------------------------------------------------------------+ bool read_fred_data(void) { //--- Read in the file string file_name = "FRED EURUSD ALT DATA.csv"; //--- Try open the file int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols). //--- Check the result if(result != INVALID_HANDLE) { Print("Opened the file"); //--- Store the values of the file int counter = 0; string value = ""; while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end { if(counter > 20) //if you aim to read 10 values set a break point after 10 elements have been read break; //stop the reading progress value = FileReadString(result); Print("Counter: "); Print(counter); Print("Trying to read string: ",value); if(counter == 3) { model_inputs[5] = (float) value; } if(counter == 5) { model_inputs[6] = (float) value; } if(counter == 7) { model_inputs[7] = (float) value; } if(FileIsLineEnding(result)) { Print("row++"); } counter++; } //--- Show the input and Fred data Print("Input Data: "); Print(model_inputs); //---Close the file FileClose(result); //--- Store the model prediction OnnxRun(model,ONNX_DEFAULT,model_inputs,model_output); Comment("Model Forecast: ",model_output[0]); if(model_output[0] > iClose(Symbol(),PERIOD_D1,0)) { model_sate = 1; } else { model_sate = -1; } //--- Everything went fine return(true); } //--- We failed to find the file else { //--- Give the user feedback Print("We failed to find the file with the FRED data"); return false; } //--- Something went wrong return false; }
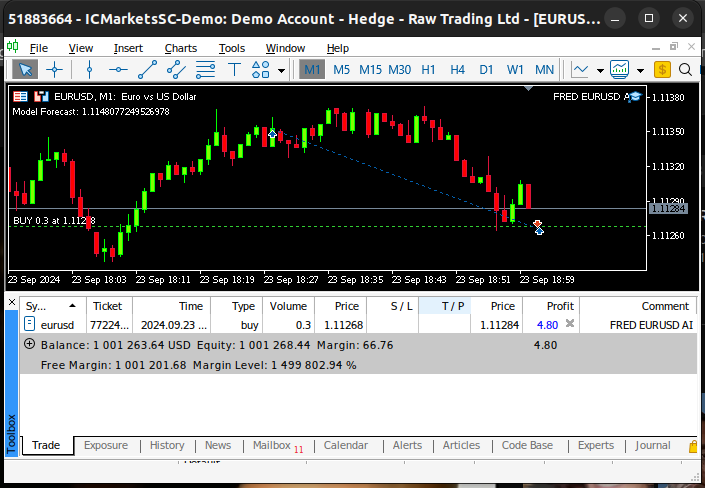
Figura 22: Pruebas futuras de nuestro algoritmo.
Conclusión
En este artículo, hemos demostrado que el Índice Diario Amplio Nominal (Nominal Broad Daily Index, NBDI) puede no ser de mucha ayuda a la hora de intentar pronosticar el par EURUSD o, alternativamente, el símbolo puede requerir más transformaciones antes de que se pueda aprender efectivamente la verdadera relación. Alternativamente, también podemos considerar probar una variedad más amplia de modelos para maximizar nuestra probabilidad de capturar bien la relación. Los modelos como las máquinas de vectores de soporte tienden a funcionar bien en problemas que requieren aprender un límite de decisión en un espacio de alta dimensión. Hay cientos de miles de conjuntos de datos que aún debemos explorar. Pero desafortunadamente no obtuvimos ventaja sobre el resto del mercado hoy.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/15949
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Redes neuronales en el trading: Transformador contrastivo de patrones (Final)
Redes neuronales en el trading: Transformador contrastivo de patrones (Final)
 Métodos de optimización de la biblioteca ALGLIB (Parte I)
Métodos de optimización de la biblioteca ALGLIB (Parte I)
 Creación de un modelo de restricción de tendencia de velas (Parte 9): Asesor Experto de múltiples estrategias (I)
Creación de un modelo de restricción de tendencia de velas (Parte 9): Asesor Experto de múltiples estrategias (I)
 Ejemplo de nuevo Indicador y LSTM condicional
Ejemplo de nuevo Indicador y LSTM condicional
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso