El Papel de las Distribuciones Estadísticas en el Trabajo del Trader
1 738
0
Las regularidades hacen nuestra vida más fácil, pero es importante beneficiarse de la aleatoriedad también.
(Georgiy Aleksandrov)
Introducción
Este artículo es una continuación lógica de mi artículo "Distribuciones de Probabilidad Estadísticas en MQL5", que presentó las clases para trabajar con algunas distribuciones estadísticas teóricas. Me pareció necesario exponer primero la base en forma de clases de distribución para que al usuario le resultara más conveniente su uso en la práctica más adelante.
Ahora que ya tenemos una base teórica, sugiero proceder directamente a conjuntos de datos reales para darle un uso a esta base. Al mismo tiempo, explicaremos algunos asuntos relativos a las estadísticas matemáticas.
1. Generación de Números Aleatorios con una Distribución Especificada
Pero antes de considerar conjuntos de datos reales, es muy importante ser capaz de obtener grupos de valores estrechamente relacionados con la distribución teórica deseada.
En otras palabras, un usuario solo debería configurar parámetros de la distribucio y tamaño de muestra deseados. Un programa (en nuestro caso, una jerarquía de clases) debería generar y dar como resultado estas muestras de valores para trabajar con ellas más adelante.
Otro detalle significativo es que las muestras generadas por una ley especificada se usan para comprobar varias pruebas estadísticas. El área de las estadísticas matemáticas - la generación de variables aleatorias con diferentes leyes de distribución - es muy interesante, y todo un desafío.
Para mis propósitos, usé un generador de alta calidad descrito en el libro Numerical Recipes: The Art of Scientific Computing ("Recetas Numéricas: el Arte de la Computación Científica") [2]. Su período es aproximadamente igual a 3.138*1057. El código C se pasó fácilmente a MQL5.
Y así, creé la clase Random tal y como se muestra a continuación:
//+------------------------------------------------------------------+ //| Random class definition | //+------------------------------------------------------------------+ class Random { private: ulong u, //unsigned 64-bit integers v, w; public: //+------------------------------------------------------------------+ //| The Random class constructor | //+------------------------------------------------------------------+ void Random() { randomSet(184467440737095516); } //+------------------------------------------------------------------+ //| The Random class set-method | //+------------------------------------------------------------------+ void randomSet(ulong j) { v=4101842887655102017; w=1; u=14757395258967641292; u=j^v; int64(); v = u; int64(); w = v; int64(); } //+------------------------------------------------------------------+ //| Return 64-bit random integer | //+------------------------------------------------------------------+ ulong int64() { uint k=4294957665; u=u*2862933555777941757+7046029254386353087; v^= v>> 17; v ^= v<< 31; v ^= v>> 8; w = k*(w & 0xffffffff) +(w>> 32); ulong x=u^(u<<21); x^=x>>35; x^=x<<4; return(x+v)^w; }; //+------------------------------------------------------------------+ //| Return random double-precision value in the range 0. to 1. | //+------------------------------------------------------------------+ double doub() { return 5.42101086242752217e-20*int64(); } //+------------------------------------------------------------------+ //| Return 32-bit random integer | //+------------------------------------------------------------------+ uint int32() { return(uint)int64(); } };
Ahora podemos crear clases para valores de muestra de una distribución.
Como ejemplo, echemos un vistazo a una variable aleatoria de la distribución normal. La clase CNormaldev es como se muestra a continuación:
//+------------------------------------------------------------------+ //| CNormaldev class definition | //+------------------------------------------------------------------+ class CNormaldev : public Random { public: CNormaldist N; //Normal Distribution instance //+------------------------------------------------------------------+ //| The CNormaldev class constructor | //+------------------------------------------------------------------+ void CNormaldev() { CNormaldist Nn; setNormaldev(Nn,18446744073709); } //+------------------------------------------------------------------+ //| The CNormaldev class set-method | //+------------------------------------------------------------------+ void setNormaldev(CNormaldist &Nn,ulong j) { N.mu=Nn.mu; N.sig=Nn.sig; randomSet(j); } //+------------------------------------------------------------------+ //| Return Normal deviate | //+------------------------------------------------------------------+ double dev() { double u,v,x,y,q; do { u = doub(); v = 1.7156*(doub()-0.5); x = u - 0.449871; y = fabs(v) + 0.386595; q = pow(x,2) + y*(0.19600*y-0.25472*x); } while(q>0.27597 && (q>0.27846 || pow(v,2)>-4.*log(u)*pow(u,2))); return N.mu+N.sig*v/u; } }; //+------------------------------------------------------------------+
Como puede ver, la clase tiene un miembro de datos N del tipo CNormaldist. El código C original no tenía esta conexión con la distribución. Yo consideré necesario que una variable aleatoria generada por la clase (en este caso, por la clase CNormaldev) tuvera una conexión lógica y programática con su distribución.
En la versión original, el tipo Normaldev se definió tal y como se muestra a continuación:
typedef double Doub; typedef unsigned __int64 Ullong; struct Normaldev : Ran { Doub mu,sig; Normaldev(Doub mmu, Doub ssig, Ullong i) ... }
Los números aleatorios se generan aquí desde la distribución normal usando el método de proporción de uniformes de Leva.
Todas las demás clases que asisten en el cálculo de variables aleatorias de distribuciones diversas se encuentran en el artículo incluido Random_class.mqh.
Ahora terminaremos con la generación y veremos, en la parte práctica del artículo, cómo crear un array de valores y simular una muestra.
2. Cálculo de Parámetros de Distribución, Hipótesis Estadísticas
Queda claro que trabajaremos con variables discretas. En la práctica, no obstante, si el número de variables discretas es significativo, es más conveniente considerar el conjunto de estas variables discretas como un grupo de variables continuas. Este es un enfoque estándar en estadísticas matemáticas. Por tanto, para su análisis, podemos usar distribuciones definidas por fórmulas analíticas que estén relacionadas a variables continuas.
De modo que vayamos al análisis de la distribución empírica.
Se da por hecho que estamos estudiando una muestra de una población general cuyos miembros cumplen con los criterios de representación. Además, también se cumplen con los requisitos de los cálculos especificados en la Sección 8.3 [9]. Lps parámetros de distribución numérica se pueden encontrar por medio de métodos de cálculo de punto e intervalo.
2.1 Gestión de Muestras Usando la Clase CExpStatistics
Primero se deberían eliminar los llamados outliers, o "valores atípicos", de la muestra; estas serían observaciones que se desviarían mucho de las observaciones de la mayor parte de la muestra (tanto hacia arriba como hacia abajo). No hay un método universal para eliminar outliers.
Sugiero usar la descrita por S.V. Bulashev en la Sección 6.3 [5]. En el foro de MQL4 se creó una biblioteca de funciones estadístcas en la base en la que el problema especificado se puede resolver fácilmente. Dicho esto, seguramente aplicaremos OOP y lo actualizaremos un poco.
Yo llamé a la clase creada de cálculos de características estadísticas CExpStatistics (Clase de Estadísticas Esperadas).
Es más o menos así:
//+------------------------------------------------------------------+ //| Expected Statistics class definition | //+------------------------------------------------------------------+ class CExpStatistics { private: double arr[]; //initial array int N; //initial array size double Parr[]; //processed array int pN; //processed array size void stdz(double &outArr_st[],bool A); //standardization public: void setArrays(bool A,double &Arr[],int &n); //set array for processing bool isProcessed; //array processed? void CExpStatistics(){}; //constructor void setCExpStatistics(double &Arr[]); //set the initial array for the class void ZeroCheckArray(bool A); //check the input array for zero elements int get_arr_N(); //get the initial array length double median(bool A); //median double median50(bool A); //median of 50% interquantile range (midquartile range) double mean(bool A); //mean of the entire initial sample double mean50(bool A); //mean of 50% interquantile range double interqtlRange(bool A); //interquartile range double RangeCenter(bool A); //range center double meanCenter(bool A); //mean of the top five estimates double expVariance(bool A); //estimated variance double expSampleVariance(bool A); //shifted estimate of sample variance double expStddev(bool A); //estimated standard deviation double Moment(int index,bool A,int sw,double xm); //moment of distribution double expKurtosis(bool A,double &Skewness); ////estimated kurtosis and skewness double censorR(bool A); //censoring coefficient int outlierDelete(); //deletion of outliers from the sample int pArrOutput(double &outArr[],bool St); //processed array output void ~CExpStatistics(){};//destructor }; //+------------------------------------------------------------------+
La implementación de cada método se puede estudiar en detalle en el archivo incluido ExpStatistics_class.mqh, de modo que no seguiré con ello aquí.
Lo importante es que esta clase devuelve el array sin outliers (Parr[]), en caso de que los hubiera. Además, ayuda a obtener algunas estadísticas descriptivas de muestreo y sus cálculos.
2.2 Crear un Histograma de Muestra Procesado
Ahora que el array está libre de outliers, se puede dibujar un histograma (de distribución de frecuencia) basado en sus datos. Nos ayudará a calcular visualmente la ley de distribucion de variables aleatorias. Hay un proceso paso a paso para crear un historgrama.
Primero se debe calcular el número de clases requeridas. En este contexto, el término "clase" significa agrupación, intervalo. El número de clases se calcula con la fórmula de Sturges:
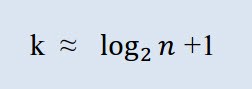
Donde k es el número de clases, y n es el número de observaciones.
En MQL5, la fórmula se puede representar tal y como se muestra a continuación:
int Sturges(int n) /* Function for determining the number of class intervals using Sturges' rule. Variables: y is the number of sampling observations. Returned value: number of class intervals. */ { double s; // Returned value s=1.+log2(y); if(s>15) // Empirical rule s=15; return(int) floor(s); }
Cuando se ha recibido el número de clases (intervalos) requerido usando la fórmula de Sturges, es el momento de dividir los datos del array en clases. Estos datos se llaman observaciones (en singular, observación). Lo haremos usando la función Allocate, tal y como se muestra a continuación:
void Allocate(double &data[],int n,double &f[],double &b[],int k) /* Function for allocating observations to classes. Variables: 1) data — initial sample (array) 2) n — sample size 3) f — calculated array of observations allocated to classes 4) b — array of class midpoints 5) k — number of classes */ { int i,j; // Loop counter double t,c; // Auxiliary variable t=data[ArrayMinimum(data)]; // Sample minimum t=t>0 ? t*0.99 : t*1.01; c=data[ArrayMaximum(data)]; // Sample maximum c=c>0 ? c*1.01 : c*0.99; c=(c-t)/k/2; // Half of the class interval b[0]=t+c; // Array of class interval midpoints f[0]= 0; for(i=1; i<k; i++) { b[i] = b[i - 1] + c + c; f[i] = 0; } // Grouping for(i=0; i<n; i++) for(j=0; j<k; j++) if(data[i]>b[j]-c && data[i]<=b[j]+c) { f[j]++; break; } }
Como puede ver, la función toma el array de observaciones iniciales (data), su longitud (n), número de clases (k) y distribuye las observaciones en una determinada clase f[i] del array f, donde b[i] es el punto medio de la clase f[i]. Los datos del histograma ya están listos.
Mostraremos el histograma usando las herramientas descritas en el artículo previamente mencionado. Para ello, escribí la función histogramSave, que mostrará el histograma para las series que estamos estudiando en HTML. La función toma dos parámetros: array de clases (f) y array de puntos medios de clase (b).
Como ejemplo, creé un histograma para diferencias absolutas entre máximos y mínimos de 500 barras del par EURUSD en un marco temporal de cuatro horas en puntos usando el scriptvolatilityTest.mq5.
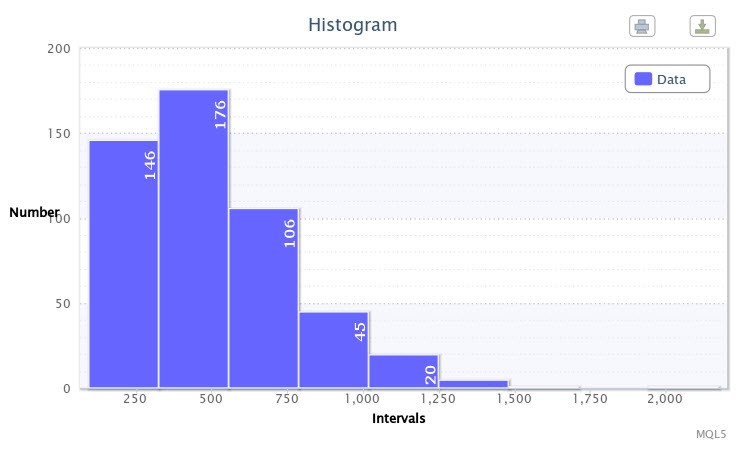
Figura 1. Histograma de datos (volatilidad absoluta de EURUSD H4)
Como se muestra en el histograma (Fig. 1), la primera clase tiene 146 observaciones, la segunda clase tiene 176 observaciones, etc. La función del histograma sirve para dar una idea visual de la distribución empírica de la muestra que estudiamos.
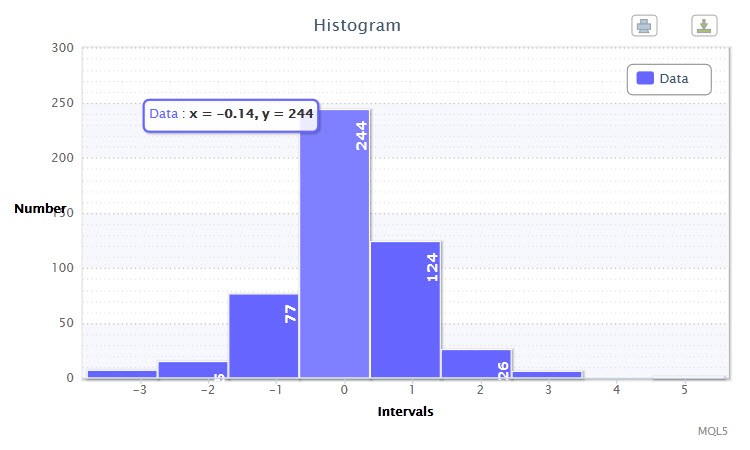
Figura 2. Histograma de datos (retornos estandarizados de EURUSD H4)
En el otro histograma (Fig.2) se muestran retornos logarítmicos estandarizados de 500 barras del par EURUSD en el marco temporal H4. Como puede observar, la cuarta y quinta clase son las más impresionantes, puesto que cuentan con 244 y 124 observaciones, respectivamente. Este histograma se creó con el script returnsTest.mq5.
Por tanto, el histograma nos permite elegir la ley de distribución, cuyos parámetros se seguirán calculando. Aunque no resulte visualmente evidente qué distribución es mejor, puede calcular parámetros de varias distribuciones teóricas.
Ninguna de las distribuciones que hemos visto se parecen a las normales en apariencia, especialmente la primera. No obstante, no confiemos solo en la representación visual, y procedamos a las figuras.
2.3 Hipótesis de Normalidad
Es costumbre primero resolver y simular la suposición (hipótesis) de si la la distribución en cuestión es normal. Esta hipótesis se llama la hipótesis principal. Uno de los métodos más populares para simular la normalidad de una muestra es el test Jarque-Bera.
Su algoritmo, aunque no es el más complejo, es bastante extenso debido a la aproximación. Hay varias versiones del algoritmo en C++ y otros lenguajes. Una de las versiones más exitosas y usadas es la versión situada en una biblioteca de análisis numérico de plataforma multimedia ALGLIB. Su autor [S.A. Bochkanov] hizo un enorme trabajo, particularmente en la compilación de la tabla cuantil de prueba. Yo simplemente la actualicé un poco de acuerdo con las necesidades de MQL5.
La función principal, jarqueberatest, es tal y como se muestra a continuación:
//+------------------------------------------------------------------+ // the Jarque-Bera Test | //+------------------------------------------------------------------+ void jarqueberatest(double &x[],double &p) /* The Jarque-Bera test is used to check hypothesis about the fact that a given sample xS is a sample of normal random variable with unknown mean and variance. Variables: x - sample Xs; p - p-value; */ { int n=ArraySize(x); double s; p=0.; if(n<5)//N is too small { p=1.0; return; } //N is large enough jarquebera_jarqueberastatistic(x,n,s); p=jarquebera_jarqueberaapprox(n,s); } //+------------------------------------------------------------------+
Trata la muestra de datos inicial (x) y devuelve el р-value, es decir, un valor que caracteriza la probabilidad de rechazo de una hipótesis nula si la hipótesis nula es, en realidad, cierta.
Hay dos funciones auxiliares en el cuerpo de la función. La primera función - jarquebera_jarqueberastatistic - calcula la estadística Jarque-Bera, y la segunda - jarquebera_jarqueberaapprox - calcula el p-value. Debo señalar que la última, a su vez, pone en acción funciones auxiliares relativas a la aproximación, que son casi 30 en el algoritmo.
De modo que tratemos de poner a prueba nuestras muestras para ver su normalidad. Usaremos el script returnsTest.mq5 que tratará la muestra de retornos estandarizados de EURUSD H4.
Tal y como esperábamos, la prueba demostró que la probabilidad de rechazo de una hopótesis nula cierta es 0.0000. En otras palabras, la distribución de esta muestra no pertenece a la familia de distribuciones normales. Para tratar la muestra de volatilidad absoluta del par EURUSD, ejecute el script volatilityTest.mq5. El resultado será similar: la distribución no es normal.
3. Ajuste de Distribución
Hay unos cuantos métodos en estadísticas matemáticas que permiten la comparación de la distribución empírica con la distribución normal. El mayor problema es que los parámetros de distribución normal son desconocidos para nosotros, y se asume que los datos que se estudian no reflejan la normalidad de una distribución.
Por tanto, debemos usar tests no paramétricos y llenar los parámetros desconocidos con los cálculos obtenidos de la distribución empírica.
3.1 Cálculo y Pruebas
Una de las pruebas más populares y, lo más importante, adecuadas en esta situación es la prueba χ2. Se basa en la medida de ajustamiento de Pearson (Pearson's goodness of fit measure).
Llevaremos a cabo la prueba usando la función chsone:
void chsone(double &f[],double &ebins[],double &df, double &chsq,double &prob,const int knstrn=1) /* 1) f — array of observations allocated to classes 2) ebins - array of expected frequencies 3) df - number of degrees of freedom 3) chsq — chi-square statistics 4) prob - probability of accepting a true null hypothesis 5) knstrn — constraint */ { CGamma gam; int j,nbins=ArraySize(bins),q,g; double temp; df=nbins-knstrn; chsq=0.0; q=nbins/2; g=nbins-1; for(j=0;j<nbins/2;j++) //passing through the left side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j+1]+=ebins[j]; bins[j+1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } for(j=nbins-1;j>nbins/2-1;j--) //passing through the right side of the distribution { if(ebins[j]<0.0 || (ebins[j]==0. && bins[j]>0.)) Alert("Bad expected number in chsone!"); if(ebins[j]<=5.0) { --df; ebins[j-1]+=ebins[j]; //starting with the last class bins[j-1]+=bins[j]; } else { temp=bins[j]-ebins[j]; chsq+=pow(temp,2)/ebins[j]; } } if(df<1)df=1; //compensate prob=gam.gammq(0.5*df,0.5*chsq); //Chi-square probability function }
Como puede observar en el listado, se usa un ejemplo de la clase CGamma en representación de la función gamma incompleta, que se incluye en el archivo Distribution_class.mqh, así como en las distribuciones mencionadas. También se debería señalar que el array de frecuencias esperadas (ebins) se obtendrá usando las funciones estimateDistribution y expFrequency.
Ahora deberemos seleccionar los parámetros numéricos que están incluidos en la fórmula analítica para la distribución teórica. El número de parámetros depende de la distribución particular. Por ejemplo, hay dos parámetros en la distribución normal, y un parámetro en la distribución exponencial, etc.
Al determinar los parámetros de distribución, normalmente usamos métodos de cálculo como el método de momentos, método cuantil y método de máxima similitud. El primero es más sencillo, puesto que implica que los cálculos de muestreo (expectativa, diferencia, oblicuidad, etc.) deberían coincidir con los cálculos generales.
Tratemos de seleccionar una distribución teórica para nuestra muestra usando un ejemplo. Vamos a tomar una serie de retornos estandarizados deEURUSD H4 para los que ya hemos dibujado un histograma.
La primera impresión es que la distribución normal no es apropiada para la serie, puesto que se observa un exceso de coeficiente de kurtosis. Como comparación, apliquemos otra distribución.
Así, al iniciar el ya conocido script returnsTest.mq5, intentaremos seleccionar distribuciones como Hypersec. Además, el script calculará y dará como resultado los parámetros de distribución seleccionados usando la función estimateDistribution, y ejecutará inmediatamente la prueba χ2. Los parámetros de distribución seleccionados serán tal y como se muestra a continuación:
Hyperbolic Secant distribution: X~HS(-0.00, 1.00);
y los resultados de la prueba fueron:
"Chi-square statistic: 1.89; probability of rejecting a true null hypothesis: 0.8648"
Note que la distribución seleccionada es un buen ajuste, puesto que el valor de la estadística χ2 es bastante pequeño.
Además, usando la función histogramSaveE se dibujará un histograma doble para las proporciones de frecuencia observadas y esperadas (la proporción de frecuencia es una frecuencia expresada en fracción o porcentaje) de retornos estandarizados (Fig. 3). Puede ver que las barras casi se duplican mutuamente. Esto es prueba de que el ajuste tuvo éxito.
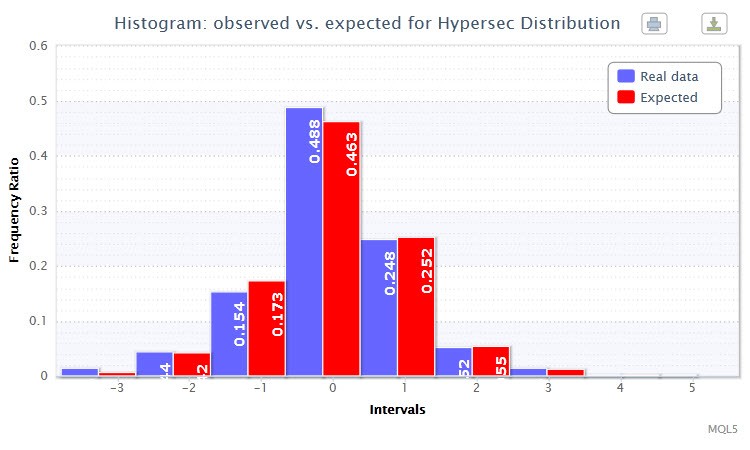
Figura 3. Histograma de las proporciones de frecuencia observadas y esperadas (retornos estandarizados de EURUSD H4)
Llevemos a cabo un procedimiento similar para datos de volatilidad usando el ya conocido volatilityTest.mq5.
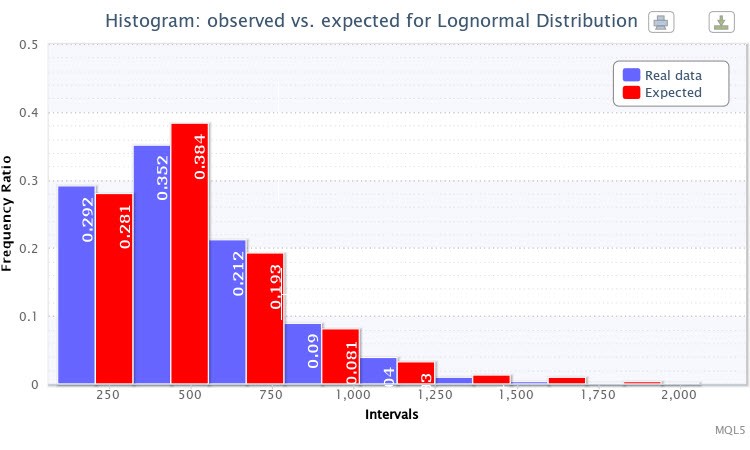
Figura 4. Histograma de las proporciones de frecuencia observadas y esperadas (volatilidad absoluta de EURUSD H4)
Seleccioné la distribución Lognormal para hacer la prueba. Como resultado, se recibió el siguiente cálculo de los parámetros:
Distribución Lognormal: X~Logn(6.09, 0.53);
y los resultados de la prueba fueron:
"Chi-square statistic: 6.17; probability of rejecting a true null hypothesis: 0.4040"
La distribución teórica para esta distribución empírica se seleccionó con bastante éxito. Por tanto, se puede considerar que la hipótesis nula no se puede rechazar (en el nivel de confianza estándar p=0,05). Se puede ver en la Fig. 4 que las barras de las proporciones de frecuencia observadas y esperadas se parecen mucho.
Permítame recordarle que tenemos otra posibilidad para generar una muestra de variables aleatorias desde una distribución con parámetros establecidos. Para usar una jerarquía de clases relacionada con esta operación, yo escribí el script randomTest.mq5.
En su inicio, debemos introducir los parámetros tal y como se muestra en la Fig. 5.
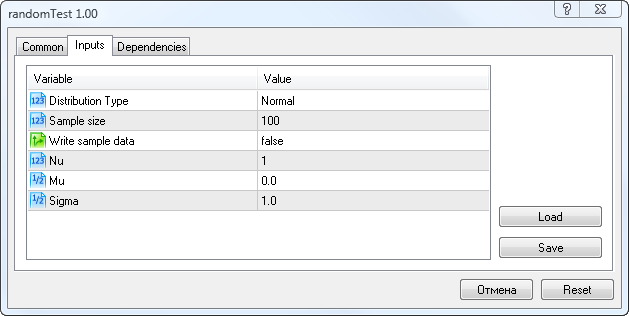
Figura 5. Parámetros de entrada del script randomTest.mq5
Aquí puede seleccionar el tipo de distribución (Distribution Type), el número de variables aleatorias en una muestra (Sample Size), la opción de guardar muestra (Write sample data), el parámetro Nu (para la distribución Student's t), y los parámetros Mu y Sigma.
Si en Write sample data configura el valor como true, el script guardará la muestra de variables aleatorias con parámetros personalizados en el archivo Randoms.csv. De lo contrario, leerá los datos de muestra de este archivo, y después llevará a cabo pruebas estadísticas.
Para algunas distribuciones que no tengan parámetros Mu ni Sigma, aquí les facilito una tabla de correlación de parámetros con los cambios en la ventana de inicio de script.
| Distribución | Primer parámetro de distribución | Segundo parámetro de distribución |
|---|---|---|
| Logistic | alph --> Mu | bet --> Sigma |
| Exponential | lambda --> Mu | -- |
| Gamma | alph --> Mu | bet --> Sigma |
| Beta | alph --> Mu | bet --> Sigma |
| Laplace | alph --> Mu | bet --> Sigma |
| Binomial | n --> Mu | pe --> Sigma |
| Poisson | lambda --> Mu | -- |
Por ejemplo, si se selecciona la distribución Poisson, se introducirá el parámetro lambda a través del campo Mu, etc.
El script no calcula los parámetros de la distribución Student's t porque en la mayoría absoluta de los casos solo se usa en unos pocos procedimientos estadísticos: cálculo de punto, construcción de intervalos de confianza y pruebas de hipótesis que se refieren al medio desconocido de una muestra estadística de la distribución normal.
Como ejemplo, ejecuté el script para la distribución normal con los parámetros X~Nor(3,50, 2,77), donde Write sample data=true. El script generó primero una muestra. Durante la segunda ejecución en Write sample data=false, se dibujó un histograma, tal y como se muestra en la Fig. 6.
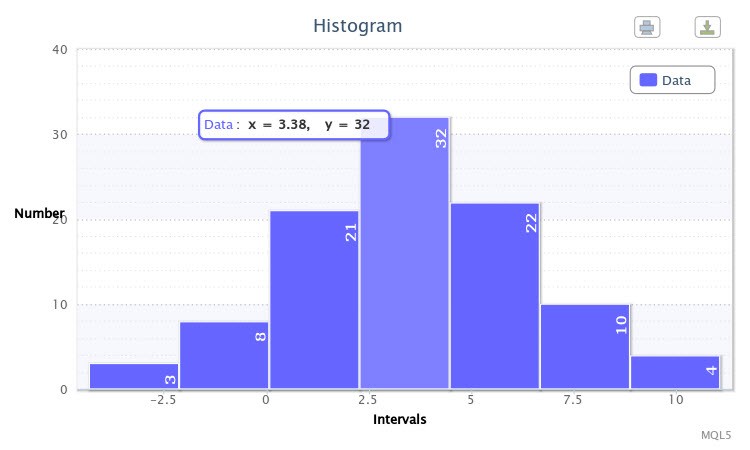
Figura 6. La muestra de variables aleatorias X~Nor(3,50,2,77)
El resto de la información mostrada en la ventana del terminal es tal y como se muestra a continuación:
El test Jarque-Bera: "The Jarque-Bera test: probability of rejecting a true null hypothesis is 0,9381";
Cálculo de parámetro: Normal distribution: X~Nor(3,58, 2,94);
Resultados del test Chi-square: "Chi-square statistic: 0,38; probability of rejecting a true null hypothesis: 0,9843".
Y, finalmente, se mostró otro histograma doble de las proporciones de frecuencia observadas y esperadas para la muestra (Fig. 7).
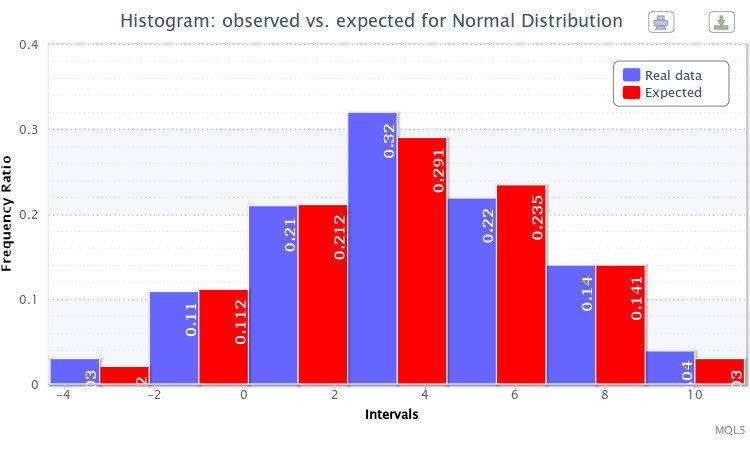
Figura 7. Histograma de las proporciones de frecuencia observadas y esperadas para X~Nor(3,50,2,77)
En general, la generación de la distribución especificada tuvo éxito.
También escribí el script fitAll.mq5, que funciona de forma similar al script randomTest.mq5. La única diferencia es que el primero tiene la función fitDistributions. Configuré la siguiente tarea: ajustar todas las distribuciones disponibles a una muestra de variables aleatorias y ejecutar una prueba estadística.
No siempre será posible ajustar una distribución a una muestra a causa del conflicto entre parámetros que lleva a la apariencia de líneas en el terminal informando de que el cálculo no es posible: "Beta distribution cannot be estimated!"
Además, decidí que este script debería mostrar resultados estadísticos en forma de pequeño informe HTML. Se puede encontrar un ejemplo de ello en el artículo "Charts and Diagrams in HTML" ("Gráficos y Diagramas en HTM") (Fig. 8).
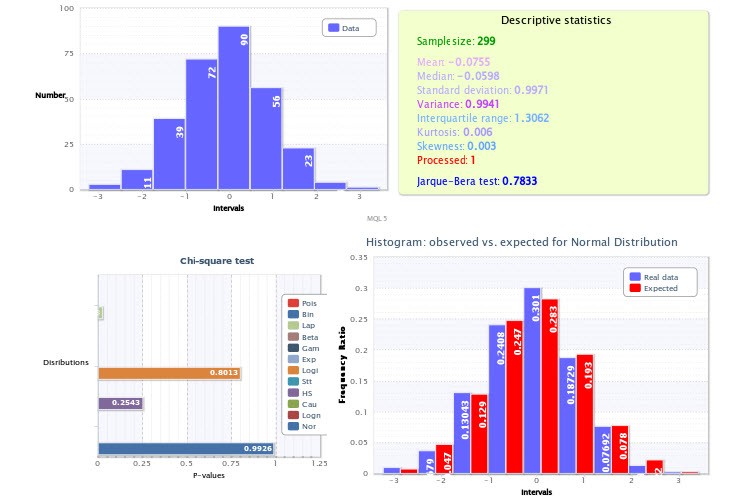
Figura 8. Informe estadístico en cálculo de muestra
Puede observar un histograma estándar de la muestra en la esquina superior izquierda; la esquina superior izquierda representa las estadísticas descriptivas y el resultado del test Jarque-Bera, en el que si el resultado de la variable Processed es igual a 1, significa que los outliers se eliminaron, mientras que un valor de 0 significa que no habían outliers.
Los valores P del test χ2 para cada distribución seleccionada se muestran en la esquina inferior izquierda. Aquí, la distribución normal resultó ser la mejor en términos de ajuste (p=0,9926). Por tanto, se dibujó un histograma de las proporciones de frecuencia observadas y esperadas en la esquina inferior derecha.
No hay tantas distribuciones en mi galería todavía. Pero este script le ahorrará mucho tiempo si hay un gran número de distribuciones.
Ahora que ya sabemos exactamente los parámetros de distribución de muestras que estamos estudiando, podemos proceder al razonamiento estadístico.
3.2 Probabilidades de Valores de Variables Aleatorias
En el artículo sobre distribuciones teóricas ya facilité el script continuousDistribution.mq5 como ejemplo. Usándolo, trataremos de mostrar cualquier ley de distribución con parámetros conocidos que puedan ser de interés para nosotros.
De modo que, para los datos de volatilidad, introduciremos los parámetros de distribución lognormales que obtuvimos antes (Mu=6,09, Sigma=0,53), seleccionaremos el tipo de distribución Lognormal y el modo cdf (Fig. 9).
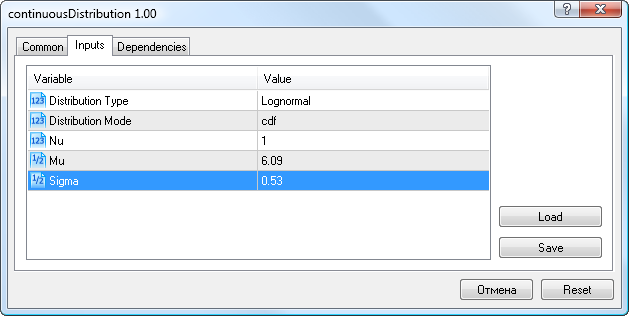
Figura 9. Parámetros de distribución lognormal X~Logn(6.09,0.53)
Con ello, el script mostrará la función de distribución para nuestra muestra. Aparecerá tal y como se muestra en la Fig. 10.
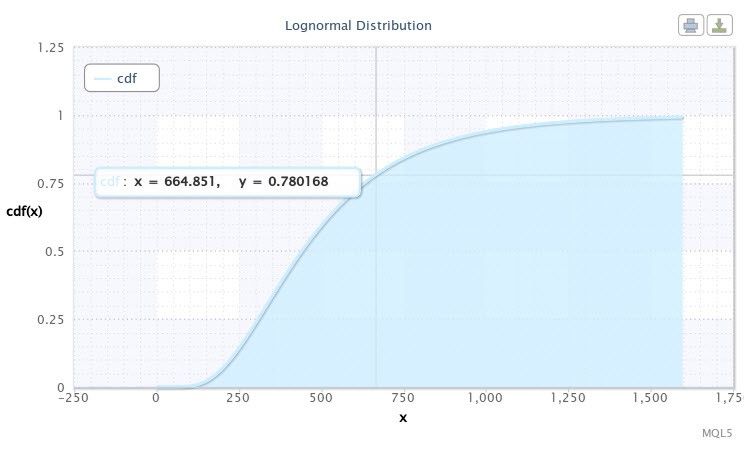
Figura 10. Función de distribución para X~Logn(6,09,0,53)
Podemos ver en el gráfico que el cursor señala un punto en las coordenadas, aproximadamente [665;0,78]. Esto significa que hay una probabilidad del 78% de que la volatilidad de EURUSD H4 no sobrepasará los 665 puntos. Esta información puede ser muy útil para un desarrollador de un Asesor Experto (EA, por sus siglas en inglés). Y seguramente se pueden tomar otros valores de la curva moviendo el cursor.
Supongamos que estamos interesados en la probabilidad del evento en el que el valor de volatilidad permanecerá en el intervalo entre 500 y 750 puntos. Para ello, deberemos realizar la siguiente operación:
cdf(750) - cdf(500) = 0.84 - 0.59 = 0.25.
Por tanto, en una serie de eventos, la volatilidad del par fluctuará en el intervalo entre 500 y 750 puntos.
Ejecutemos el script con los mismos parámetros de distribución de nuevo, seleccionando solo sf como modo de ley de distribución. La función de fiabillidad (supervivencia) aparecerá tal y como se muestra a continuación (Fig. 11).
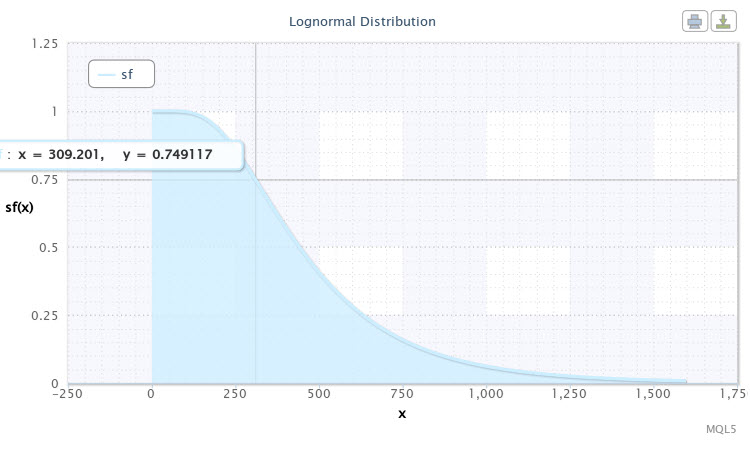
Figura 11. La función de supervivencia para X~Logn(6,09,0,53)
El punto marcado en el gráfico de curva se puede interpretar de la siguiente forma: podemos esperar con una probabilidad de casi un 75% que la volatilidad del par será de 310 puntos. Cuanto más abajo vayamos en la curva, menor será la probabilidad de que aumente la volatilidad. Por tanto, una volatilidad de más de 1.000 puntos ya se puede considerar un evento raro, puesto que la probabilidad de que esto ocurra es de menos del 5%.
Se pueden construir curvas de distribución similares para la muestra de retornos estandarizados, así como para otras muestras. Supongo que la metodología queda clara en general.
Conclusión
Debemos señalar que las derivaciones analíticas propuestas no siempre tienen éxito, puesto que las series tienen a variar. Aunque, por ejemplo, no concierte a series de retornos logarítmicos. No obstante, no me propuse la tarea de evaluar los métodos en este artículo. Sugiero que los lectores interesados en ello hagan comentarios sobre este tema.
Es importante destacar la necesidad de considerar el mercado, los instrumentos de mercado y los expertos en trade desde la perspectiva de probabilidad. Este es el enfoque que he tratado de demostrar. Espero que este tema despierte el interés del lector y lleve a una discusión constructiva.
Localización de los archivos:
| # | Archivo | Ruta | Descripción |
|---|---|---|---|
| 1 | Distribution_class.mqh | %MetaTrader%\MQL5\Include | Galería de clases de distribución |
| 2 | DistributionFigure_class.mqh | %MetaTrader%\MQL5\Include | Clases para la visualización gráfica de distribuciones |
| 3 | Random_class.mqh | %MetaTrader%\MQL5\Include | Clases para la generación de una muestra de número aleatorio |
| 4 | ExpStatistics_class.mqh | %MetaTrader%\MQL5\Include | Clase y funciones de cálculo de características estadísticas |
| 5 | volatilityTest.mq5 | %MetaTrader%\MQL5\Scripts | Script para el cálculo de la muestra de volatilidad de EURUSD H4 |
| 6 | returnsTest.mq5 | %MetaTrader%\MQL5\Scripts | Script para el cálculo de la muestra de retornos de EURUSD H4 |
| 7 | randomTest.mq5 | %MetaTrader%\MQL5\Scripts | Script para el cálculo de la muestra de variable aleatoria |
| 8 | fitAll.mq5 | %MetaTrader%\MQL5\Scripts | Script para el ajuste de cálculo de todas las distribuciones |
| 9 | Volat.csv | %MetaTrader%\MQL5\Files | Archivo de datos de muestra de volatilidad de EURUSD H4 |
| 10 | Returns_std.csv | %MetaTrader%\MQL5\Files | Archivo de datos de muestra de retornos de EURUSD H4 |
| 11 | Randoms.csv | %MetaTrader%\MQL5\Files | Archivo de datos de muestra de variable aleatoria |
| 12 | Histogram.htm | %MetaTrader%\MQL5\Files | Histograma de la muestra en HTML |
| 13 | Histogram2.htm | %MetaTrader%\MQL5\Files | Histograma doble de la muestra en HTML |
| 14 | chi_test.htm | %MetaTrader%\MQL5\Files | Informe estadístico HTML del cálculo de la muestra |
| 15 | dataHist.txt | %MetaTrader%\MQL5\Files | Datos para la visualización de un histograma de muestras |
| 16 | dataHist2.txt | %MetaTrader%\MQL5\Files | Datos para la visualización de un histograma doble de muestras |
| 17 | dataFitAll.txt | %MetaTrader%\MQL5\Files | Datos para la visualización de un informe HTML |
| 18 | highcharts.js | %MetaTrader%\MQL5\Files | Biblioteca JavaScript de gráficos interactivos |
| 19 | jquery.min.js | %MetaTrader%\MQL5\Files | Biblioteca JavaScript |
| 20 | ReturnsIndicator.mq5 | %MetaTrader%\MQL5\Indicators | Indicador de retornos logarítmicos |
Material de referencia:
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/257
Filtrar Señales Basadas en Datos Estadísticos de Correlación de Precios
Usar Pseudo-Plantillas como Alternativa a Plantillas C++
3 Métodos de Aceleración de Indicadores según el Ejemplo de Regresión Lineal
La implementación del análisis automático de las Ondas de Elliott en MQL5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso