
Modelado 3D en MQL5
Aplicado a los mercados financieros, el modelado 3-D se usa, por ejemplo, para representar en tres dimensiones las series temporales. Una serie temporal es un sistema dinámico en el que los valores de una cierta magnitud aleatoria llegan de forma consecutiva: ininterrumpidamente o tras un cierto intervalo temporal (ticks, barras, fractales, etcétera). En este artículo estudiaremos el tema de la visualización de la representación en tres dimensiones de las series temporales, tales como TimeSeries e indicadores (ver la fig. 1).
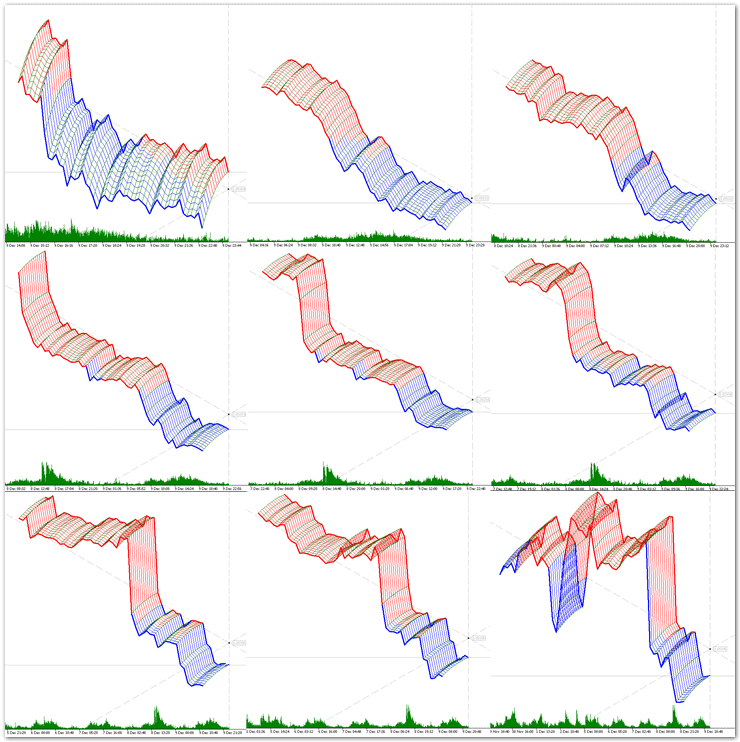
Fig. 1 Ejemplos de representación de series temporales en tres dimensiones.
Una imagen en tres dimensiones se diferencia de otra en dos dimensiones en que incluye la construcción de la proyección geométrica de un modelo tridimensional en una superficie con la ayuda de funciones especiales. Para obtener una imagen tridimensional en un plano necesitamos seguir los siguientes pasos:
- modelado: creación de un modelo matemático tridemensional de una serie temporal;
- renderización (visualización): construcción de una proyección de acuerdo con un modelo elegido;
- exhibición de la imagen obtenida en la pantalla.
El objetivo es mostrar los gráficos habituales en un espacio tridimensional. Puesto que en este momento no hay aún soluciones listas para el modelado 3D en MQL5, comenzaremos con los principios y métodos básicos, concretamente con los objetos 3-D y los sistemas de coordenadas. Es posible que los lectores se muestren excépticos con este tema y lo lean por encima, pero aun así, algunos algoritmos y métodos pueden resultarles útiles en otras tareas no relacionadas con la visualización en 3-D.
Objeto gráfico interactivo
Comenzaremos por los objetos 3-D. La rica funcionalidad de MQL5 permite operar con objetos bidimensionales y crear construcciones gráficas complejas. Basta con añadir varias funciones y en el terminal МТ5 también estarán disponibles gráficos en tres dimensiones.
Para comenzar, enumeraremos qué requisitos deberán cumplirse al proyectarse las clases básicas de los objetos 3D.
- Sencillez de uso.
- Gran vitalidad.
- Independiencia.
- Interactividad.
Sencillez de uso.
Para el desarrollador y el usuario deberá crearse un conjunto mínimo de funciones, pero lo suficientemente amplio para resolver la mayoría de las tareas de los gráficos tridimensionales.
Gran vitalidad.
El objeto 3D debe ser "inmortal" durante todo el tiempo de vida útil del programa del ejemplar de clase creado. Debe estar protegido contra la eliminación casual o consciente y el cambio de las propiedades básicas.
Independiencia.
El objeto debe estar dotado de "inteligencia" y adaptarse de forma independiente a las condiciones cambiantes (rotación del sistema de coordenadas, cambio de los puntos de anclaje básicos, etcétera). Estará obligado a filtrar la información necesaria del flujo entrante de eventos y a reaccionar de la forma correspondiente.
Interactividad.
La visualización 3D propone la posibilidad de cambiar el punto de vista sobre el modelo tridimensional (rotación del sistema de coordenadas). Por eso hay que crear una funcionalidad tal que no necesite del uso de paneles de control adicionales, ni nada por el estilo. Hablando estrictamente, los objetos gráficos en el lenguaje MQL5 ya poseen la propiedad de la interactividad: el objeto se puede seleccionar, reubicar, ver sus propiedades modificadas, etcétera. Basta con perfeccionar esta capacidad hasta el nivel de control e interacción colectivos. Por ejemplo, nosotros modificamos el centro de coordenadas y todos los objetos interrelacionados se reubican independientemente, además, sin errores.
Si cumplimos todos estos requisitos, el objeto 3D se transformará en un objeto gráfico interactivo (IGO). El objeto gráfico interactivo se encuentra obligatoriamente vinculado a un objeto gráfico del lenguaje MQL5. Procedemos al análisis de la clase básica CIGO de los objetos gráficos interactivos.
{
protected:
bool on_event; // bandera de procesamiento de eventos
int m_layer; // capa a la que pertenece el IGO
//---
double SetPrice(double def,int prop_modifier=0);
public:
string m_name; // nombre del objeto IGO
double m_price; // punto básico de anclaje del IGO [precio]
double m_angle; // valor del ángulo de anclaje del IGO [grado]
CIGO();
~CIGO();
//---
virtual // Método: crear el IGO
void Create(string name) {on_event=true;}
virtual // Método: redibujar el IGO
void Redraw() {ChartRedraw();}
virtual // Método de procesamiento del evento OnChartEvent
bool OnEvent(const int id, // identificador del evento
const long &lparam, // parámetro de evento del tipo long
const double &dparam, // parámetro de evento del tipo double
const string &sparam, // parámetro de evento del tipo string
int iparamemr=0, // identificador de evento del IGO
double dparametr=0.0);// parámetro de evento del IGO del tipo double
};
La clase básica contiene un mínimo de campos y métodos que se puede redefinir en lo sucesivo, o también ser complementado en las clases herederas. Veremos con detalle solo dos métodos de la clase: el método virtual OnEvent() de procesamiento de eventos OnChartEvent y el método de definición del punto básico de anclaje SetPrice(). Nos detenedremos en ellos, puesto que precisamente en ellos se implementan los principios esenciales de los objetos gráficos interactivos.
Método: procesamiento de eventos entrantes OnEvent.
Procesa los eventos que llegan desde el terminal de cliente al trabajar con el gráfico. El método reacciona solo a los 4 eventosestándar: eliminar un objeto gráfico, cambiar los tamaños o las propiedades del gráfico, arrastrar el objeto y pulsar el ratón sobre el mismo. Vamos a analizar con cuidado cada uno de ellos.
- Eliminar un objeto gráfico. Al aparecer este evento, el objeto en el gráfico deja de existir, es eliminado. Dado que necesitamos cumplir la condición de la vitalidad, habrá que restablecerlo de inmediato, es decir, crearlo de nuevo, además, con las mismas propiedades que poseía antes de ser eliminado. Preste atención: se elimina el objeto gráfico, pero no el ejemplar de la clase CIGO relacionado con él. El ejemplar de la clase sigue existiendo, y además recuerda la información sobre el objeto gráfico eliminado, por eso se puede restablecer fácilmente con la ayuda del método Create().
- Cambio de las dimensiones o las propiedadesdel gráfico. Hay muchos eventos de este tipo: la aparición de una nueva barra, el cambio de la escala del gráfico, el paso a otro marco temporal y otros. La reacción al evento deberá ser la misma: redibujar el objeto teniendo en cuenta las modificiones del entorno, usando el método Redraw(). Es importante destacar que al pasar a otro marco temporal, el ejemplar de la clase se inicializa de nuevo y pierde los datos sobre el objeto gráfico creado, que se han guardado en los campos de la clase, aunque el propio objeto gráfico ha permanecido en el gráfico. Por eso, los campos del ejemplar de la clase se restablecen con los valores de las propiedades del objeto gráfico, lo que sin duda aumenta la vitalidad del IGO.
- Arrastrar un objeto gráfico. En este evento se construye la interactividad del objeto gráfico. Al arrastrarlo, cambian los puntos básicos de anclaje. Antes de arrastrar un objeto, hay que seleccionarlo (con un doble click del ratón). Si ha tenido lugar este evento, el método retorna true, en caso contrario, false. Este valor nos será necesario cuando organicemos el trabajo colectivo de los objetos gráficos interactivos. Debemos destacar que si necesitáramos un objeto gráfico que no se pudiese arrastrar, bastaría prohibir la posibilidad de seleccionarlo cuando lo creemos.
- Pulsar el ratón en un objeto gráfico. Si la pulsación del ratón ha tenido lugar en cualquier otro objeto distinto a este, entonces quitaremos la selección del objeto, para evitar su desplazamiento por casualidad. De esta forma, en el gráfico se podrá seleccionar solo un objeto IGO. bool CIGO::OnEvent(const int id,
const long &lparam,
const double &dparam,
const string &sparam,
int iparamemr=0,
double dparametr=0.0)
{
bool res=false;
if(on_event) // el procesamiento de eventos está permitido
{
// Eliminar un objeto gráfico
if((ENUM_CHART_EVENT)id==CHARTEVENT_OBJECT_DELETE && sparam==m_name)
{
Create(m_name);
}
// Modificación de las dimensiones del gráfico o cambio de sus propiedades a través de la ventana de diálogo de propiedades
if((ENUM_CHART_EVENT)id==CHARTEVENT_CHART_CHANGE)
{
Redraw();
}
// Arrastrar el objeto gráfico
if((ENUM_CHART_EVENT)id==CHARTEVENT_OBJECT_DRAG)
if(ObjectGetInteger(0,sparam,OBJPROP_SELECTED)==1 && sparam==m_name)
{
m_price=ObjectGetDouble(0,m_name,OBJPROP_PRICE);
Redraw();
res=true; // anunciamos que ha cambiado el punto básico de anclaje
}
// pulsar el ratón en un objeto gráfico distinto a este
if((ENUM_CHART_EVENT)id==CHARTEVENT_OBJECT_CLICK && sparam!=m_name)
{
ObjectSetInteger(0,m_name,OBJPROP_SELECTED,0);
ChartRedraw();
}
}
return(res);
}
Parámetros:
id
[in] Identificador del evento. Existen 9 tipos de evento que pueden ser procesados con la ayuda de este método.
lparam
[in] Parámetro de evento del tipo long.
dparam
[in] Parámetro de evento del tipo double.
sparam
[in] Parámetro de evento del tipo string.
iparametr
[in] Identificador de evento de usuario.
dparametr
[in] Parámetro de evento de usuario del tipo double.
Valor retornado:
Retorna true, si ha sucedido un cambio en las coordenadas del punto básico de anclaje del objeto. En caso contrario, false.
Método: establecer las coordenadas del punto básico de anclaje SetPrice.
Establece el valor "price" en el sistema de coordenadas "Gráfico" para el campo m_price del ejemplar de la clase.
Aclararemos lo que sucede cuando se solicita la coordenada de un punto básico de anclaje con este método.
- Al inicializar el ejemplar de la clase, el campo m_price (coordenada del punto básico de anclaje) no contiene valor de entrada, por eso m_price=NULL. La incialización tiene lugar o bien al crear un ejemplar de clase, o al cambiar el gráfico a otro marco temporal. Sin embargo, el propio objeto gráfico puede existir en el gráfico. Es posible que permanezca desde la anterior llamada del programa o al cambiar de marco temporal. Por consiguiente, al campo m_price le asignamos el valor de la propiedad gráfica correspondiente.
- Si el objeto gráfico con el nombre m_name no existe, entonces tras el primer paso, la coordenada del punto básico de anclaje seguirá sin definirse: m_price=NULL. En este caso, al valor del campo m_price se le asigna por defecto def.
{
if(m_price==NULL) // si no hay valor de la variable
m_price=ObjectGetDouble(0,m_name,OBJPROP_PRICE,prop_modifier);
if(m_price==NULL) // si no hay coordenadas
m_price=def; // valor por defecto
return(m_price);
}
Parámetros:
def
[in] Valor de la variable por defecto.
prop_modifier
[in] Modificador de la propiedad solicitada del objeto gráfico.
Valor retornado:
Valor de la coordenada del punto básico de anclaje.
Ahora vamos a ver los herederos directos de la clase básica de los objtos interactivos. En primer lugar, nos interesan los objetos 3-D para crear el entorno imprescindible de modelado en tres dimensiones.
Clase C_OBJ_ARROW_RIGHT_PRICE: objeto "Etiqueta de precio a la derecha"
Descendiente directo de la clase básica CIGO.
//| Clase OBJ_ARROW_RIGHT_PRICE: objeto "Etiqueta de precio a la derecha" |
//+------------------------------------------------------------------+
class C_OBJ_ARROW_RIGHT_PRICE:public CIGO
{
public:
virtual // Método: crear objeto
void Create(string name);
virtual // Método: redibujar objeto
void Redraw();
};
//+------------------------------------------------------------------+
//| Método: crear objeto |
//+------------------------------------------------------------------+
void C_OBJ_ARROW_RIGHT_PRICE::Create(string name)
{
m_name=name;
m_price=SetPrice((ChartGetDouble(0,CHART_PRICE_MAX)+ChartGetDouble(0,CHART_PRICE_MIN))/2);
ObjectCreate(0,m_name,OBJ_ARROW_RIGHT_PRICE,0,0,0);
ObjectSetInteger(0,m_name,OBJPROP_SELECTABLE,true);
ObjectSetInteger(0,m_name,OBJPROP_WIDTH,1);
ObjectSetInteger(0,m_name,OBJPROP_COLOR,clrISO);
//---
ObjectSetInteger(0,m_name,OBJPROP_TIME,0,T(0));
ObjectSetDouble(0,m_name,OBJPROP_PRICE,0,m_price);
//---
ChartRedraw();
on_event=true; // permitimos el procesamiento de eventos
}
//+------------------------------------------------------------------+
//| Método: redibujar objeto |
//+------------------------------------------------------------------+
void C_OBJ_ARROW_RIGHT_PRICE::Redraw()
{
ObjectSetInteger(0,m_name,OBJPROP_TIME,0,T(0));
ChartRedraw();
}
Esta clase es la que más conviene para organizar el centro de un sistema de coordenadas en tres dimensiones. El ejemplar de la clase está vinculado a la barra actual y en realidad se encuentra en el eje Z.
Clase C_OBJ_TREND: objeto "Línea de tendencia"
Descendiente directo de la clase básica CIGO.
//| Clase C_OBJ_TREND: objeto "Línea de tendencia" |
//+------------------------------------------------------------------+
class C_OBJ_TREND:public CIGO
{
public:
virtual // Método: crear objeto
void Create(string name);
virtual // Método: redibujar objeto
void Redraw();
};
//+------------------------------------------------------------------+
//| Método: crear objeto |
//+------------------------------------------------------------------+
void C_OBJ_TREND::Create(string name)
{
m_name=name;
m_price=(ChartGetDouble(0,CHART_PRICE_MAX)+ChartGetDouble(0,CHART_PRICE_MIN))/2;
ObjectCreate(0,m_name,OBJ_TREND,0,0,0);
ObjectSetInteger(0,m_name,OBJPROP_COLOR,clrISO);
ObjectSetInteger(0,m_name,OBJPROP_WIDTH,0);
ObjectSetInteger(0,m_name,OBJPROP_STYLE,styleISO);
ObjectSetDouble(0,m_name,OBJPROP_PRICE,0,m_price);
ObjectSetInteger(0,m_name,OBJPROP_TIME,0,T(0));
ObjectSetDouble(0,m_name,OBJPROP_PRICE,1,m_price+1);
ObjectSetInteger(0,m_name,OBJPROP_TIME,1,T(0));
ObjectSetInteger(0,m_name,OBJPROP_RAY_RIGHT,true);
ObjectSetInteger(0,m_name,OBJPROP_RAY_LEFT,true);
ObjectSetInteger(0,m_name,OBJPROP_BACK,true);
ObjectSetInteger(0,m_name,OBJPROP_SELECTABLE,false);
//---
ChartRedraw();
on_event=true; // permitimos el procesamiento de eventos
}
//+------------------------------------------------------------------+
//| Método: redibujar objeto |
//+------------------------------------------------------------------+
void C_OBJ_TREND::Redraw()
{
ObjectSetInteger(0,m_name,OBJPROP_TIME,0,T(0));
ObjectSetInteger(0,m_name,OBJPROP_TIME,1,T(0));
ChartRedraw();
}
Lo más lógico es crear el eje Z con la ayuda de esta clase. Las posibilidades son mínimas, pero suficientes para el modelado en 3D.
Clase C_OBJ_TRENDBYANGLE: objeto "Línea de tendencia en ángulo"
Descendiente directo de la clase básica CIGO.
//| Clase C_OBJ_TRENDBYANGLE: objeto "Línea de tendencia en ángulo" |
//+------------------------------------------------------------------+
class C_OBJ_TRENDBYANGLE:public CIGO
{
protected:
int m_bar; // número de la barra para el anclaje del segundo punto básico
//---
double SetAngle(double def)
{
if(m_angle==NULL) // si no hay valor de la variable
m_angle=ObjectGetDouble(0,m_name,OBJPROP_ANGLE);
if(m_angle==NULL) // si no hay coordenadas
m_angle=def; // valor por defecto
return(m_angle);
}
public:
C_OBJ_TRENDBYANGLE();
virtual // Método: crear objeto
void Create(string name,double price,double angle);
virtual // Método: redibujar objeto
void Redraw();
virtual // Método de procesamiento del evento OnChartEvent
bool OnEvent(const int id,
const long &lparam,
const double &dparam,
const string &sparam,
int iparamemr=0,
double dparametr=0.0);
};
//+------------------------------------------------------------------+
//| Constructor |
//+------------------------------------------------------------------+
C_OBJ_TRENDBYANGLE::C_OBJ_TRENDBYANGLE()
{
m_bar=c_bar;
}
//+------------------------------------------------------------------+
//| Método: crear objeto |
//+------------------------------------------------------------------+
void C_OBJ_TRENDBYANGLE::Create(string name,double price,double angle)
{
datetime time=T(0);
datetime deltaT=T(m_bar)-time;
m_name=name;
m_price=SetPrice(price);
m_angle=SetAngle(angle);
ObjectCreate(0,m_name,OBJ_TRENDBYANGLE,0,time,m_price,time+deltaT,m_price);
ObjectSetInteger(0,m_name,OBJPROP_COLOR,clrISO);
ObjectSetInteger(0,m_name,OBJPROP_WIDTH,0);
ObjectSetInteger(0,m_name,OBJPROP_STYLE,styleISO);
ObjectSetInteger(0,m_name,OBJPROP_RAY_RIGHT,true);
ObjectSetInteger(0,m_name,OBJPROP_RAY_LEFT,true);
ObjectSetInteger(0,m_name,OBJPROP_BACK,true);
ObjectSetInteger(0,m_name,OBJPROP_SELECTABLE,true);
//--- medimos el ángulo de inclinación de la línea de tendencia; en el proceso de alteración del ángulo, la coordenada del segundo
//--- punto de la línea se redefine de forma automática de acuerdo con el nuevo valor del ángulo
ObjectSetDouble(0,m_name,OBJPROP_ANGLE,m_angle);
ChartRedraw();
//---
on_event=true; // permitimos el procesamiento de eventos
}
//+------------------------------------------------------------------+
//| Método: redibujar objeto |
//+------------------------------------------------------------------+
void C_OBJ_TRENDBYANGLE::Redraw()
{
ObjectSetInteger(0,m_name,OBJPROP_TIME,T(0));
ObjectSetInteger(0,m_name,OBJPROP_TIME,1,T(0)+T(m_bar)-T(0));
ObjectSetDouble(0,m_name,OBJPROP_PRICE,m_price);
ObjectSetDouble(0,m_name,OBJPROP_ANGLE,m_angle);
ChartRedraw();
}
//+------------------------------------------------------------------+
//| Método de procesamiento del evento OnChartEvent |
//+------------------------------------------------------------------+
bool C_OBJ_TRENDBYANGLE::OnEvent(const int id,
const long &lparam,
const double &dparam,
const string &sparam,
int iparamemr=0,
double dparametr=0.0)
{
//---
bool res=false;
if(on_event) // el procesamiento de eventos está permitido
{
// Eliminación del objeto gráfico
if((ENUM_CHART_EVENT)id==CHARTEVENT_OBJECT_DELETE && sparam==m_name)
{
Create(m_name,m_price,m_angle);
}
// Modificación de las dimensiones del gráfico o cambio de sus propiedades a través de la ventana de diálogo de propiedades
if((ENUM_CHART_EVENT)id==CHARTEVENT_CHART_CHANGE)
{
Redraw();
}
// Arrastrar el objeto gráfico
if((ENUM_CHART_EVENT)id==CHARTEVENT_OBJECT_DRAG)
{
//---
if(ObjectGetInteger(0,sparam,OBJPROP_SELECTED)==1 && sparam==m_name)
{
m_angle=ObjectGetDouble(0,m_name,OBJPROP_ANGLE);
Create(m_name,m_price,m_angle);
res=true; // anunciamos que ha cambiado el punto básico de anclaje
}
if(iparamemr==Event_1)// recibido mensaje sobre el cambio del punto básico
{
m_price=dparametr;
Create(m_name,m_price,m_angle);
}
if(iparamemr==Event_2)// recibido mensaje sobre el cambio del ángulo básico
{
m_angle=dparametr;
Create(m_name,m_price,m_angle);
}
}
// pulsar el ratón en un objeto gráfico distinto a este
if((ENUM_CHART_EVENT)id==CHARTEVENT_OBJECT_CLICK && sparam!=m_name)
{
ObjectSetInteger(0,m_name,OBJPROP_SELECTED,0);
ChartRedraw();
}
}
return(res);
}
En principio se planeaba utilizar para el eje X e Y los herederos de la clase "línea de tendencia", pero durante el proceso quedó claro que para estos objetivos es ideal la "línea de tendencia en ángulo". Tras releer la documentación de MQL5, he descubierto este potente instrumento: después de construir la línea de tendencia en ángulo, al cambiar de marco temporal o de escala, permanecía como enterrada, es decir, el ángulo no cambiaba.
Conclusión: Relea la documentación y descubrirá multitud de funciones e instrumentos necesarios.
Memoria gráfica (GM)
Ya se ha hablado de algunos aspectos de la memoria gráfica usando ejemplos en el artículo "Distribuciones estadísticas en forma de histogramas sin búferes de indicador y matrices". Aquí solo voy a repetir el principio principal: en las propiedades de los objetos gráficos se puede guardar la información necesaria para usarla posteriormente en otros objetos o funciones del programa.
Para que sea más cómodo programar y resulte más práctico aplicar la memoria gráfica se ha creado una clase especial:
{
private:
public:
string m_name; // nombre del objeto gráfico
CGM(){}
~CGM(){}
void Create(string name) {m_name=name;}
// lectura de la propiedad OBJPROP_PRICE
double R_OBJPROP_PRICE(int prop_modifier=0)
{
return(ObjectGetDouble(0,m_name,OBJPROP_PRICE,prop_modifier));
}
// lectura de la propiedad OBJPROP_TIME
datetime R_OBJPROP_TIME(int prop_modifier=0)
{
return((datetime)ObjectGetInteger(0,m_name,OBJPROP_TIME,prop_modifier));
}
// lectura de la propiedad OBJPROP_ANGLE
double R_OBJPROP_ANGLE()
{
return(ObjectGetDouble(0,m_name,OBJPROP_ANGLE));
}
// lectura de la porpiedad OBJPROP_TEXT
string R_OBJPROP_TEXT()
{
return(ObjectGetString(0,m_name,OBJPROP_TEXT));
}
// retorna el valor del precio para el tiempo especificado
double R_ValueByTime(datetime time)
{
return(ObjectGetValueByTime(0,m_name,time));
}
// registrar la propiedad OBJPROP_TEXT
void W_OBJPROP_TEXT(string text)
{
ObjectSetString(0,m_name,OBJPROP_TEXT,text);
}
};
Como se puede ver en el código, aquí tenemos los métodos de lectura y registro de las propiedades de los objetos gráficos. La comodidad de esta clase consiste en que se vincula a un objeto gráfico al crearse y permite recibir/transmitir de forma operativa la información necesaria para cualquier objeto gráfico interactivo que esté intersesado en estos mensajes. Por ejemplo,
- se ha creado el objeto 3D А y se ha vinculado al mismo el ejemplar de clase de la memoria gráfica AA;
- ahora se crea el objeto gráfico 3D B, que puede recibir a través de AA la información necesaria sobre el objeto A. No existe una relación directa entre los objetos A y B, pero a través del ejemplar de clase AA se ha organizado la transmisión de datos de A a B;
- al crear el objeto B, se crea el ejemplar de clase de la memoria gráfica BB. Ahora el objeto A tiene acceso a la información necesaria del objeto B;
- etcétera. El número de objetos puede ser cualquiera, pero cada uno de ellos tiene la posibilidad de recibir y transmitir la información necesaria a través de los ejemplares de clase de la memoria gráfica.
Podemos imaginar la memoria gráfica como un tablón de anuncios en el que se ubican aplicaciones, así como la demanda de cierta información. De esta forma, tiene lugar el intercambio de datos entre objetos gráficos interactivos. Qué datos precisamente son necesarios para que funcione correctamente un objeto 3D es algo que se programa en la etapa de proyecto del modelo 3D. La información más valiosa la poseen los objetos del sistema de coordenadas, puesto que al rotarlo o trasladar el centro de coordenadas, toda la "manada" de objetos 3D deberá cambiar sus propiedades y su ubucación dentro del espacio en tres dimensiones.
Vea cómo se usa la memoria gráfica en la clase del sistema interactivo de coordenadas CUSC.
Sistema de coordenadas
El análisis visual en tres dimensiones permite analizar los datos en un espacio 3D: por ejemplo, constuir una imagen en tres dimensiones de las secuencias de datos originales (observaciones) para una o varias variables elegidas. Las variables elegidas se presentan en el eje Y, las observaciones consecutivas, en el X, y el valor de las variables (para esta observación) se muestran en el eje Z.
Estos gráficos tridimensionales se usan para visualizar la secuencia de los valores de varias variables.
La principal ventaja de las representaciones en tres dimensiones con respecto al componente bidimensional de los gráficos lineales es que para ciertos conjuntos de datos, al darse una representación con volumen, es más sencillo reconocer ciertas secuencias de valores. Al elegir el ángulo de visión correcto con la ayuda, por ejemplo, de la rotación interactiva de las líneas del gráfico, no se taparán ni solaparán las unas con las otras, como sucede con frecuencia en los gráficos lineales compuestos en dos dimensiones.
Antes de pasar al modelado en 3-D, vamos a analizar aquellos sistemas de coordenadas con los que tendremos que tratar. Los dos sistemas de coordenadas "Gráfico" e "Imagen" han sido creados por los desarrolladores de MQL5, y el sistema de tres dimensiones (axionometría) lo implementaremos por nosotros mismos. Bien, veamos cuál es la diferencia y el objetivo meta de cada uno de ellos.
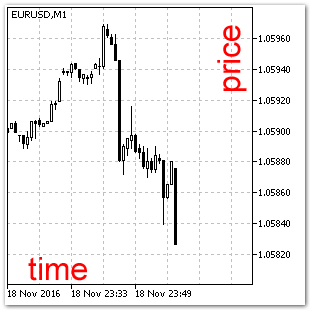
Fig. 2. Sistema de coordenadas "Gráfico".
Sistema de coordenadas "Gráfico" (fig. 2).Se trata de un sistema bidimensional de coordenadas para representar datos de precio, series temporales e indicadores. En el eje horizontal se ubica la escala de tiempo (time), dirigida de izquierda a derecha, y en el eje vertical, el precio (price) del instrumetno financiero. Precisamente en este sistema de coordenadas funciona la mayoría de los objetos gráficos de MQL5. La peculiaridad reside en que el precio y la barra actual se encuentran en el eje vertical, y al aparecer una nueva barra, el gráfico se desplaza automáticamente a la izquierda.
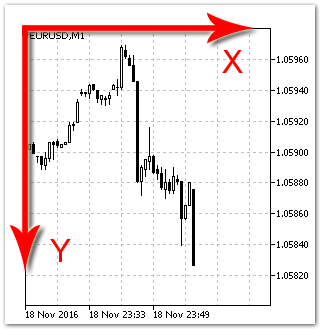
Fig. 3. Sistema de coordenadas "Imagen".
Sistema de coordenadas "Imagen" (fig. 3).A cada punto de la pantalla le corresponde un píxel. Las coordenadas de los puntos se calculan a partir del ángulo superior izquierdo del gráfico. Ella, igual que el "Gráfico", es bidimensional y se usa con los objetos no vinculados a las series temporales. Este sistema de coordenadas no será necesario en este artículo.
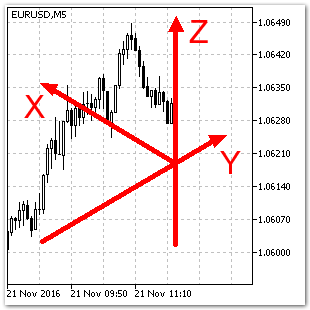
Fig. 4. Sistema de coordenadas tridimensional.
Sistema de coordenadas tridimensional (fig. 4). En este sistema de coordenadas los tres ejes son perpendiculares entre sí. Sin embargo, visualmente, en el sistema de coordenadas "Imagen" los ángulos entre los ejes XYZ no son iguales a 90 grados. Por ejemplo, el eje X y el eje Y forman entre sí un ángulo de 120 grados. Este ángulo también puede ser diferente, pero en el marco del artículo lo tomaremos así.
El eje Z está vinculado a la barra actual, y la escala del eje coincide con la escala "price" en el sistema de coordenadas "Gráfico". Esto es muy cómodo, puesto que no es necesario crear una escala aparte para el eje Z, y se puede utilizar la escala "price", en este caso, Z=price.
El eje X está orientado hacia la izquierda, es decir, en dirección contraria a la escala "time" en el sistema de coordenadas "Gráfico". En este eje vamos a postergar el valor de la variable Bar; es decir, la proyección de cualquier barra en el eje X coincidirá con su valor (X=Bar).
El eje Y está concebido para las series de datos bidimensionales XZ. Por ejemplo, podemos desplazar la línea de la series temporales Open, Close, High, Low por este eje, y ellas se ubicarán cada una en su superficie. Si unimos todos los puntos de estas líneas en superficies que sean paralelas a la superficie YZ, obtendremos una cuadrícula de superficie, es decir, el objeto tridimensional de la serie temporal (ver la fig. 5).
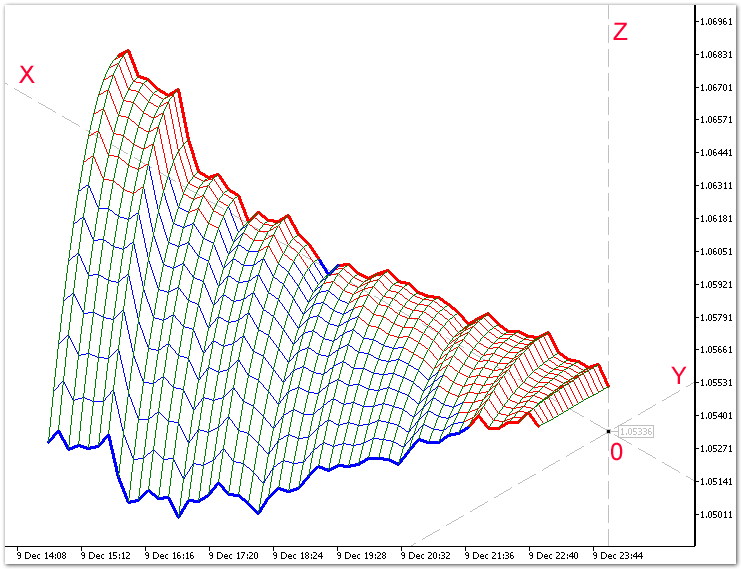
Fig. 5. Objeto 3D en el sistema tridimensional de coordenadas.
Sistema de coordenadas interactivo: Clase CUSC
Descendiente directo de la clase básica CIGO.
{
private:
datetime m_prev_bar;
datetime m_next_bar;
//---
C_OBJ_ARROW_RIGHT_PRICE Centr; // declaración del ejemplar de la clase C_OBJ_ARROW_RIGHT_PRICE
C_OBJ_TREND AxisZ; // declaración del ejemplar de la clase C_OBJ_TREND
C_OBJ_TRENDBYANGLE AxisY,AxisX; // declaración de los ejemplares de la clase C_OBJ_TRENDBYANGLE
//---
CGM gCentr; // declaración del ejemplar de la clase CGM
CGM gAxisY,gAxisX; // declaración de los ejemplares de la clase CGM
public:
CUSC();
~CUSC();
//--- Cálculo de la coordenada Z
sPointCoordinates Z(double price, // precio en el sistema de coordenadas "Gráfico"
int barX, // desplazamiento por el eje X
int barY); // desplazamiento por el eje Y
//--- nueva barra
bool on_bar()
{
m_next_bar=T(0);
if(m_next_bar>m_prev_bar)
{
m_prev_bar=m_next_bar;
return(true);
}
return(false);
}
//---
virtual // Método: crear objeto IGO
void Create(string name);
virtual // Método de procesamiento del evento OnChartEvent
void OnEvent(const int id,
const long &lparam,
const double &dparam,
const string &sparam);
};
Veamos con detalle solo tres métodos de esta clase: Create(), OnEvent(), Z().
Método Create: crear un sistema de coordenadas tridimensional
Crea el objeto 3D del sistema de coordenadas interactivo. La interactividad incluye: la rotación del sistema de coordenadas alrededor del eje Z y el desplazamiento del punto de comienzo de las coordenadas.
{
//--- Centro del sistema tridimensional de coordenadas
Centr.Create("Axis XYZ"); // creamos el centro del sistema de coordenadas
gCentr.Create(Centr.m_name); // creamos el objeto de la memoria gráfica
m_price=gCentr.R_OBJPROP_PRICE();
//--- Eje Z
AxisZ.Create("Axis Z"); // creamos el eje Z del sistema de coordenadas
//--- Eje Y
AxisY.Create("Axis Y", // creamos el eje Y del sistema de coordenadas
gCentr.R_OBJPROP_PRICE(), // obtenemos el valor a partir de GM
30); // establecemos el ángulo de inclinación del eje a 30 grados
gAxisY.Create(AxisY.m_name); // creamos el objeto de memoria gráfica
m_angle=gAxisY.R_OBJPROP_ANGLE();
//--- Eje X
AxisX.Create("Axis X", // creamos el eje X del sistema de coordenadas
gCentr.R_OBJPROP_PRICE(), // obtenemos el valor a partir de GM
gAxisY.R_OBJPROP_ANGLE()+ISO); // obtenemos el valor a partir de GM y lo aumentamos por ISO grados
gAxisX.Create(AxisX.m_name); // creamos el objeto de memoria gráfica
//---
ChartRedraw();
on_event=true; // permitimos el procesamiento de eventos
}
Parámetros:
name
[in] Nombre del sistema de coordenadas.
Valor retornado:
No hay valor retornado. En caso de éxito, se crea el sistema de coordenadas.
Método OnEvent: procesamiento de mensajes entrantes
Procesa los eventos que llegan desde el terminal de cliente al trabajar con el gráfico. El método reacciona solo a un evento estándar: arrastrar un objeto gráfico. El resto de eventos se transmiten más adelante por todos los ejemplares de las clases creados al programar el sistema de coordenadas.
const long &lparam,
const double &dparam,
const string &sparam)
{
if(on_event) // el procesamiento de eventos está permitido
{
//--- transmisión de eventos OnChartEvent
AxisZ.OnEvent(id,lparam,dparam,sparam);
//---
if(Centr.OnEvent(id,lparam,dparam,sparam))
{// Arrastrar un objeto gráfico
AxisY.OnEvent(id,lparam,dparam,sparam,Event_1,gCentr.R_OBJPROP_PRICE());
AxisX.OnEvent(id,lparam,dparam,sparam,Event_1,gCentr.R_OBJPROP_PRICE());
}
else
{
if(AxisY.OnEvent(id,lparam,dparam,sparam))
{// Cambio de ángulo del objeto gráfico
AxisX.OnEvent(id,lparam,dparam,sparam,Event_2,gAxisY.R_OBJPROP_ANGLE()+ISO);
}
else
{
if(AxisX.OnEvent(id,lparam,dparam,sparam))
{// Cambio de ángulo del objeto gráfico
AxisY.OnEvent(id,lparam,dparam,sparam,Event_2,gAxisX.R_OBJPROP_ANGLE()-ISO);
}
}
}
ChartRedraw();
m_price=gCentr.R_OBJPROP_PRICE();
m_angle=gAxisY.R_OBJPROP_ANGLE();
}
}
Parámetros:
id
[in] Identificador del evento. Existen 9 tipos de evento que pueden ser procesados con la ayuda de este método.
lparam
[in] Parámetro de evento del tipo long.
dparam
[in] Parámetro de evento del tipo double.
sparam
[in] Parámetro de evento del tipo string.
iparametr
[in] Identificador de evento de usuario.
dparametr
[in] Parámetro de evento de usuario del tipo double.
Valor retornado:
No hay valor retornado.
Estructura para obtener los valores de las coordenadas (sPointCoordinates).
Estructura para guardar los valores de las coordenadas en el sistema de coordenadas "Gráfico". Está concebido para obtener las coordenadas de un punto 3D.
{
datetime time; // coordenada en el sistema "Gráfico"
double price; // coordenada en el sistema "Gráfico"
};
La variable del tipo sPointCoordinates permite con solo una llamada de la función Z() obtener los valores de las coordenadas de un punto 3D en el sistema de coordenadas "Gráfico".
Método Z: cálculo de la coordenada Z.
El método calcula la coordenada Z.
{
sPointCoordinates res;
res.price=0;
res.time=0;
double dX,dY;
dX=0;
dX=gAxisX.R_ValueByTime(T(barX))-m_price;
dY=0;
dY=gAxisY.R_ValueByTime(T(-barY))-m_price;
res.price=price+dX-dY;
res.time=T(barX-barY);
return(res);
}
Parámetros:
price
[in] Coordenada Z del objeto 3D.
barX
[in] Coordenada X del objeto 3D. El valor se indica en barras.
barY
[in] Coordenada Y del objeto 3D. El valor se indica en barras.
Valor retornado:
En caso de éxito, retorna el valor de una variable del tipo sPointCoordinates.
Ejemplo de creación de una superficie 3D en forma de cuadrícula
Como ejemplo, analizaremos la construcción de una superficie tridimensional según la función:
#define StepX 10 // salto de incremento a lo largo del eje Х [bar]
#define StepY 5 // salto de incremento a lo largo del eje Y [bar]
#define _X 50 // número de puntos en el eje Х
#define _Y 15 // número de puntos en el eje Y
#define W1 1 // grosor de las líneas
#define W2 3 // grosor de las líneas exteriores
//--- Incluimos los archivos de las clases
#include <3D\USC.mqh>
//---
#property indicator_chart_window
//--- Número de búferes para el cálculo del indicador
#property indicator_buffers 0
//--- Número de series gráficas en el indicador
#property indicator_plots 0
//---
CUSC USC;
double fun[_X][_Y];
//+------------------------------------------------------------------+
//| Custom indicator initialization function |
//+------------------------------------------------------------------+
int OnInit()
{
USC.Create("3D");
//---
return(INIT_SUCCEEDED);
}
//+------------------------------------------------------------------+
//| Custom indicator iteration function |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
const int prev_calculated,
const datetime &time[],
const double &open[],
const double &high[],
const double &low[],
const double &close[],
const long &tick_volume[],
const long &volume[],
const int &spread[])
{
ArraySetAsSeries(close,true);
//--- función de la superficie 3D
for(int i=0;i<_X;i++)
for(int j=0;j<_Y;j++)
{
fun[i][j]=close[i*StepX]-_Point*j*j;
//fun[i][j]=close[i*StepX]-_Point*j*j*i/7;
}
////--- líneas X
for(int i=1;i<_X;i++)
for(int j=0;j<_Y;j++)
{
sPointCoordinates a0=USC.Z(fun[(i-1)][j], // función
(i-1)*StepX, // X
-j*StepY); // Y
sPointCoordinates a1=USC.Z(fun[i][j], // función
i*StepX, // X
-j*StepY); // Y
string name="line x "+"x"+(string)i+"y"+(string)+j;
ObjectCreate(0,name,OBJ_TREND,0,a0.time,a0.price,a1.time,a1.price);
if(fun[i][j]>USC.m_price && fun[i-1][j]>USC.m_price)
ObjectSetInteger(0,name,OBJPROP_COLOR,clrRed);
else
ObjectSetInteger(0,name,OBJPROP_COLOR,clrBlue);
ObjectSetInteger(0,name,OBJPROP_WIDTH,W1);
if(j==0 || j==_Y-1)
ObjectSetInteger(0,name,OBJPROP_WIDTH,W2);
ObjectSetInteger(0,name,OBJPROP_STYLE,STYLE_SOLID);
ObjectSetInteger(0,name,OBJPROP_RAY_RIGHT,false);
ObjectSetInteger(0,name,OBJPROP_RAY_LEFT,false);
ObjectSetInteger(0,name,OBJPROP_BACK,true);
ObjectSetInteger(0,name,OBJPROP_SELECTABLE,false);
}
////--- líneas Y
for(int i=0;i<_X;i++)
for(int j=1;j<_Y;j++)
{
sPointCoordinates a0=USC.Z(fun[i][j-1], // función
i*StepX, // X
-(j-1)*StepY); // Y
sPointCoordinates a1=USC.Z(fun[i][j], // función
i*StepX, // X
-j*StepY); // Y
string name="line y "+"x"+(string)i+"y"+(string)+j;
ObjectCreate(0,name,OBJ_TREND,0,a0.time,a0.price,a1.time,a1.price);
ObjectSetInteger(0,name,OBJPROP_COLOR,clrGreen);
ObjectSetInteger(0,name,OBJPROP_WIDTH,1);
ObjectSetInteger(0,name,OBJPROP_STYLE,STYLE_SOLID);
ObjectSetInteger(0,name,OBJPROP_RAY_RIGHT,false);
ObjectSetInteger(0,name,OBJPROP_RAY_LEFT,false);
ObjectSetInteger(0,name,OBJPROP_BACK,true);
ObjectSetInteger(0,name,OBJPROP_SELECTABLE,false);
}
//--- return value of prev_calculated for next call
return(rates_total);
}
//+------------------------------------------------------------------+
//| ChartEvent function |
//+------------------------------------------------------------------+
void OnChartEvent(const int id,
const long &lparam,
const double &dparam,
const string &sparam)
{
USC.OnEvent(id,lparam,dparam,sparam);
}
Las líneas en las superficies paralelas a las superficies XZ e YZ se dibujan por separado. Es posible variar el número de nodos en cada eje y también en la propia función.
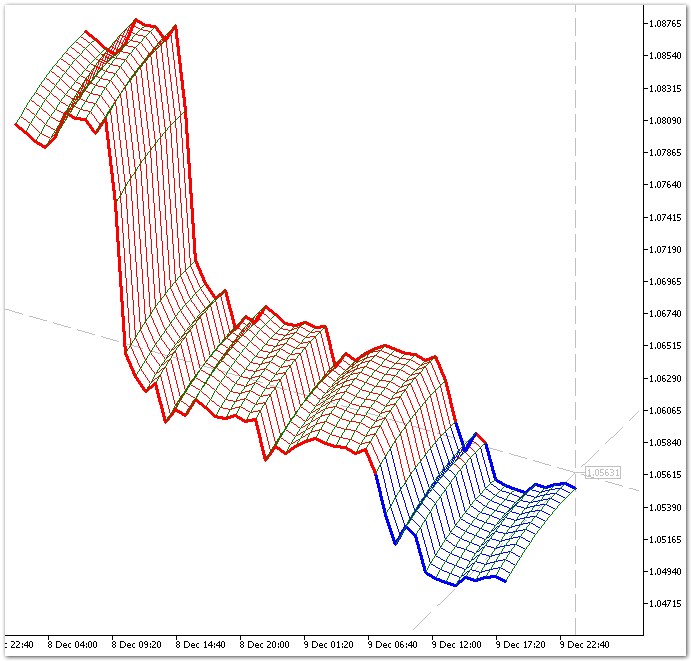
Fig. 6. Ejemplo de construcción de una superficie 3D.
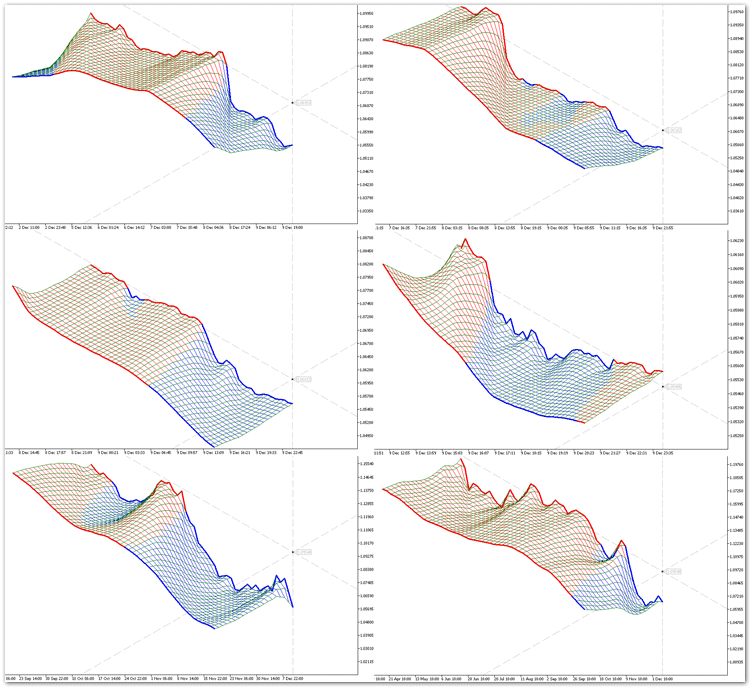
Fig. 7. Ejemplo de construcción del indicador 3D Moving Average.
Y ahora, la respuesta a la pregunta de muchos escépticos: ¿Para qué sirve el modelado en 3D y cómo puede ayudar a la hora de comerciar?
Está claro que el terminal MetaTrader 5 ha sido concebido para comerciar en los mercados financieros. Los tráders y desarrolladores de sistemas de comercio automatizado se interesan en primer lugar por los algoritmos comerciales y la construcción de estrategias comerciales. Por el momento, el enfoque analizado se encuentra en su estado de desarrollo inicial y no dará resultados concretos en el comercio, pero el modelado en 3D puede ser utilizado en la presentación de ideas y estrategias comerciales para inversores potenciales. Además, en el terminal se crean modelos 3D dinámicos que reaccionan a la llegada de la información de mercado y se deforman en el tiempo (reconstruyen su cuerpo), y este hecho hace posible crear indicadores 3D.
Mostraré como argumento una analogía con Windows: las primeras versiones del sistema eran torpes y lentas. Los defensores de Norton Commander percibían con mucho escepticismo la idea de las interfaces gráficas. ¿Y dónde está ahora NC?
Conclusión
- El modelado en 3D es una tarea bastante compleja en cualquier entorno de programación, pero los desarrolladores del lenguaje MQL5 se han anticipado a los usuarios, proporcionándoles una funcionalidad lo suficientemente potente para implementar la visualización en tres dimensiones en el terminal comercial.
- Por el momento, solo hemos logrado los primeros resultados en la programación de la biblioteca de clases de los objetos 3D. El tema del modelado en 3D es tan amplio que con un solo artículo resulta imposible abarcar todas sus posibilidades y perspectivas. Espero que haya seguidores para esta corriente y que propongan caminos para desarrollar nuevos enfoques de trading en 3D y en la programación con el lenguaje MQL5.
- El instrumento de modelado en 3D creado puede influir notablemente en la creación de una nueva tendencia en el análisis técnico: los indicadores en 3D y su análisis.
- Existen ciertos problemas con la velocidad de procesamiento de la renderización, pero en esta etapa de desarrollo de la biblioteca, no se trata por el momento de un problema crítico.
- El principio de construcción de objetos 3D propuesto en el artículo probablemente sea apropiado para su traslado a OpenCL.
Nota:
Los archivos de la biblioteca deberán ubicarse en la carpeta ..\Include\3D.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/2828
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Corregido un poco el ejemplo del artículo.
Estupendo.
Acabo de tener una necesidad de modelado 3D.
¿Podrías decirme cómo atornillarlo todo a MT4?
Aunque ya lo tengo. Lo más destacado del modelado 3D es el uso de la línea de tendencia por ángulo.
Estupendo.
Acabo de tener una necesidad de modelado 3D.
¿Podrías decirme cómo atornillarlo todo a MT4?
Aunque ya lo tengo. Lo más destacado del modelado 3D es el uso de la línea de tendencia por ángulo.
Se puede añadir para MT4 también, pero no veo el punto todavía. Incluso en MT5 las coordenadas en la función ObjectGetValueByTime() no se calculan con suficiente precisión.
Análisis de Volumen 3D y Tick
MachineLearning EA
Todo el código no cabe en los Archivos
aquí hay un enlace a github
Ejemplos de Indicadores
https://github.com/zephyrrr/MLEA/tree/master/MQL5/Indicators/Examples
Ejemplos de Expertos
https://github.com/zephyrrr/MLEA/tree/master/MQL5/Experts
Exportar a MySQL
https://github.com/xenu256/MT4toMySQL
Sobre el "milagro" de los Premios Nobel de Economía
https://www.youtube.com/watch?v=OmDhTUYkkdE& t=388s