
Localización automática de extremos basada en un salto de precio establecido
Introducción
Muchas estrategias comerciales populares se basan en el uso de diferentes modelos gráficos: "cabeza y hombros", "pico doble/valle doble" y otros. En algunas estrategias se analiza la divergencia de los extremos en los gráficos. Al automatizar estos sistemas comerciales, surge la necesidad de encontrar los picos y los valles en el gráfico, y a continuación su efectividad en cuanto a procesamiento e interpretación. Los instrumentos existentes dan la posibilidad de encontrar extremos de acuerdo con los criterios establecidos. En el artículo se presentan algoritmos efectivos y soluciones programáticas para encontrar y procesar los extremos en los gráficos de precio dependiendo de los saltos de precio.
1 Instrumentos existentes para la búsqueda de extremos
1.1. Fractales e instrumentos semejantesLos fractales son un instrumento popular para encontrar extremos. Permiten encontrar el mínimo y el máximo del precio para una serie de 5 barras (fig. 1). Los extremos se definen tanto en los movimientos fuertes, como en los débiles. Si elegimos correctamente el marco temporal, los fractales pueden mostrar resultados bastante buenos, pero su eficacia depende fuertemente de las condiciones de mercado.

Fig. 1 Resultados del uso de fractales: los extremos con un tamaño relativo de 140 a 420 pips, en caso de que haya tendencia (a), los extremos en caso de ausencia de movimientos de precio respecto a un tamaño no superior a 50 pips (b)
En el segundo caso, el tamaño relativo de los extremos (cambio del precio de un extremo a otro) puede no superar varios pips. Estos picos y valles tan insignificantes, en la mayoría de los casos, no se tienen en cuenta a la hora de comerciar manualmente. El cambio de marco temporal no permitirá filtrar los extremos poco significativos, en caso de un movimiento lateral prolongado, se los definirá de todas formas.
Puede surgir otra complejidad, esta vez opuesta: que no se determinen todos los extremos. Si en un pequeño periodo de tiempo no se observan oscilaciones de precio con una gran cantidad de picos y valles, estos no serán detectados. Los fractales permiten detectar solos 2 extremos en el intervalo temporal que se define con 5 barras del marco temporal actual. Partiendo de lo dicho más arriba, no podemos recomendar los fractales para detectar todos o la mayoría de los extremos importantes al comerciar de forma automática.
Los instrumentos presentados en el artículo "La contribución de Thomas DeMark al análisis técnico" tienen los mismos defectos que los fractales. Si elegimos una ventana grande para buscar los extremos, muchos de ellos podrían ser omitidos. Si la ventana tiene un tamaño no muy grande, se definirán los extremos poco significativos. En cualquier caso, al procesar los resultados habrá que o bien optimizar los parámetros permanentemente de forma manual y descartar los mínimos y máximos poco significativos, o bien desarrollar para ello un algioritmo especial.
1.2. Uso de medias móviles a la hora de buscar extremos
Al automatizar la búsqueda de extremos, resultará muy tentadora la idea de usar una cierta línea media, por ejemplo, la media móvil. La búsqueda del extremo se realiza en el número de barras establecido con la condición de que el precio se aparte de la línea media en una cantidad determinada de puntos. Este instrumento permite filtrar los picos y valles poco significativos, por lo que su aspecto es mejor que el de los fractales. Sin embargo, sigue sin resolver el problema de localización de los máximos y mínimos próximos (fig.2, а).

Fig. 2. Uso de medias móviles a la hora de buscar extremos: los 2 extremos se determinan como uno (a), omisión de un extremo situado en una cercanía inmediata de la media móvil (b).
Podemos intentar usar la media móvil y los fractales de forma conjunta. La media móvil se usa para filtrar extremos poco significativos, mientras que los fractales se utilizarán para su consecuente búsqueda en el intervalo deseado. No obstante, este esquema tampoco resuelve todos los problemas. Aun así, surge la necesidad de elegir la ventana de forma óptima. Como resultado, sea cual sea el método que usemos para encontrar el máximo o el mínimo, de todas formas será necesario elegir los parámetros en la ventana de búsqueda. En caso de no seleccionarlos de manera óptima, solo se podrá determinar uno de cada dos picos que se encuentren situados demasiado cerca (fig.2, а).
Vamos a ver otro problema propio de este método de definición de extremos. Si surge una situación de mercado con oscilaciones bruscas de precio, la media móvil, independientemente del periodo, podría no reaccionar de forma significativa a esta señal. En esta situación (fig.2, b) un valle situado entre dos picos y que se encuentre cerca de la media móvil no será determinado. Estas situaciones son bastante raras en el mercado, pero nos hacen reflexionar sobre la elección correcta de la ventana de la media móvil.
Bien, los métodos de definición de extremos presentados más arriba, así como los derivados de los mismos, tienen defectos y necesitan de soluciones programáticas adicionales. Veamos más en profundidad las complicaciones que surgen al definir los extremos, así como los algoritmos que permiten superarlas.
2. Problemas y ambigüedades que surgen al buscar los extremos
2.1. Elección de la amplitud del salto para localizar picos y vallesEn las estrategias y tácticas existentes, el uso de extremos puede ser explícito o no explícito. Además, la tarea de definición de extremos es con frecuencia subjetiva: en el mismo gráfico una persona verá solo picos y valles, y otra destacará otras cosas diferentes. Vamos a ver uno de los modelos gráficos más famosos, «El pico doble».
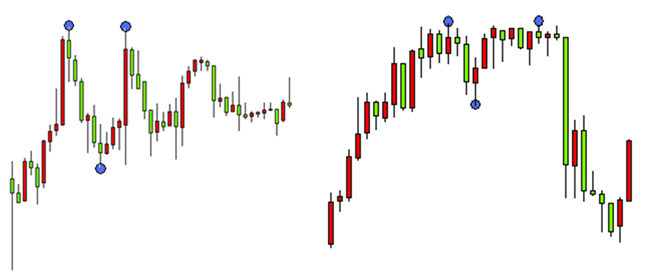
Fig. 3. Modelo gráfico de "Pico doble"
En los dos gráficos (fig. 3) se presenta el mismo modelo, pero dependiendo de la amplitud del salto entre extremos, podemos definirlo o no. Así, en el primer gráfico, después del primer pico va un valle, y después se ubica un segundo valle. Por consiguiente, si no hubiera valles entre picos, no podríamos definir el modelo gráfico «Pico doble». El modelo sería definido como un extremo normal. Una situación análoga surge cuando el valle se ha expresado de forma no explícita, entonces, dependiendo de un punto de vista subjetivo, el «Pico doble» puede ser definido o no. En este caso, es más probable que encontremos este modelo en el primer gráfico que en el segundo, además, la diferencia entre ambos solo consistirá en la amplitud del salto entre extremos contiguos.
Veamos otro ejemplo: en algunas estrategias, la tendencia se define como ascendente si los extremos consecutivos (tanto los picos, como los valles) se ubican por encima de los anteriores. La tendencia descendente se define de forma análoga. En el ejemplo analizado (fig. 4) se puede determinar la dirección de la tendencia, y en ese caso, se usan claramente los extremos.

Fig. 4. Detección del movimiento de precio en el mismo gráfico: tendencia ascendente (a), tendencia descendente (b)
Resulta que en el mismo gráfico se puede encontrar una tendencia tanto ascendente como descendete. En el pirmer caso (fig. 4, a) los extremos determinados 1,2,3,4 indican de forma explícita una tendencia ascendente. Definiendo en el mismo gráfico como extremos los puntos 2,5,6,3 (fig. 4, b), podemos llegar a la conclusión de que hay una tendencia descendente. Usando otros extremos completamente distintos, podemos obtener al final cualquiera de las dos variantes. Partiendo de ello, sacamos la conclusión de que es precisamente la amplitud del salto lo que influirá en mayor medida en la posición de los extremos.
2.2. Separación efectiva de picos o valles contiguosExiste un segundo problema a la hora de definir los extremos. Para definir y separar con efectividad dos o más picos, entre los mismos deberá haber un valle. Esta observación es adecuada tanto para el primer ejemplo, la localización del pico doble, como para el segundo, pero aquí la situación es aún más interesante. En los gráficos presentados (fig. 5,6), de acuerdo con la estrategia mencionada arriba, solo se puede definir la tendencia después de encontrar los extremos.
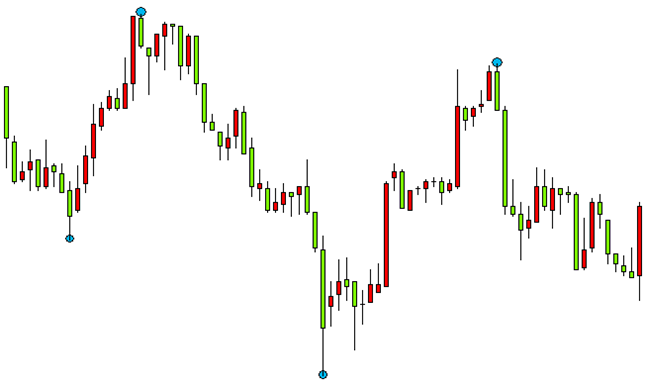
Fig. 5. Definiendo picos y valles en la inversión a largo plazo
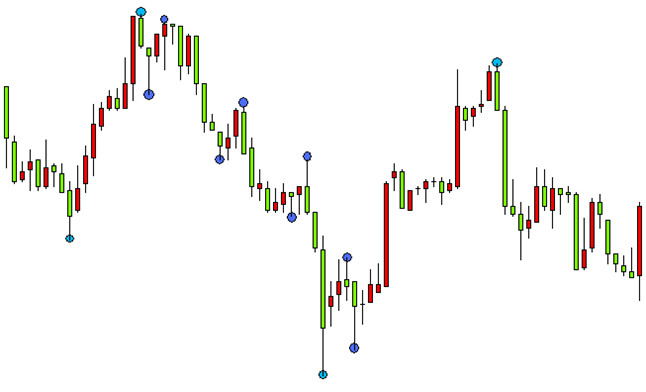
Fig. 6. Definiendo picos y valles poco significativos
Si no encontramos los valles que separan a los picos, y, de forma análoga, los picos que separan a los valles, la estrategia no podrá funcionar de aucerdo con los criterios establecidos, aunque en el gráfico se defina de forma visual la tendencia ascendente. Vamos a ver un ejemplo característico. Cuando se da un movimiento ascendente del precio, se forma un pico, y tras él, el siguiente, más alto. Si no existe valle entre ellos o se muestra débilmente, en calidad de extremo se definirá solo el pico más alto. En el caso cuando los extremos se definen con respecto a una cierta línea, por ejemplo, una media móvil, la tarea de separación de dos picos o valles contiguos es también muy actual. Y en este caso, para separar los dos picos también hay que usar un extremo entre ellos.
Generalizando lo dicho más arriba, para todas las estrategias que usen de forma explícita o no explícita los extremos, se puede usar la siguiente suposición: el precio se mueve desde el pico al valle y desde el valle al pico, tanto en las situaciones de movimiento del pasado al futuro, como en la dirección contraria. Si no nos valemos de esa suposición, entonces dos picos en el gráfico de precio, dependiendo de un punto de vista subjetivo:
- o bien serán detectados,
- o bien solo se definirá el más alto,
- o bien ninguno de los dos extremos será detectado.
Lo mismo sucede con los valles. Basándonos en esta suposición, podemos desarrollar un algoritmo para encontrar los extremos de forma unívoca usando una amplitud de salto especifica.
2.3. Definiendo el primer extremoEl tercer problema que surge está también relacionado con los saltos de precio, y consiste en la definición del primer extremo. Para cualquier táctica o estrategia comercial, los extremos más nuevos serán más importantes que los más antiguos. Y como ya hemos aclarado, de la definición de un extremo depende la ubicación de los picos y valles contiguos. Por eso, si elegimos un extremo a una cierta distacnia del momento actual, los resultados obtenidos dependerán más de los datos históricos alejados, mientras que dependerán débilmente de las oscilaciones de precio más recientes. Este problema existe al usar el indicador ZigZag. La posición de los últimos extremos depende muy poco de las últimas oscilaciones de precio.
Otra situación completamente distinta surge cuando buscamos los extremos desde el final del gráfico. En este caso, al principio se encontrarán los picos más cercanos al final, o bien el valle tras el cual se definen con seguridad el resto. Dependiendo de la estrategia usada y de la amplitud de salto elegida, se pueden aplicar 3 variantes:
- se localiza el pico más cercano,
- se localiza el valle más cercano,
- se localiza el extremo más cercano (o bien pico, o bien valle).
Veamos el caso en el que se busca el extremo más crecano. Eligiendo una amplitud de salto determinada, es posible definir de forma inequívoca el primer extremo más cercano. Sin embargo, esta definición tendrá lugar con cierto retraso, lo que podría repercutir de forma negativa en el funcionamiento de la estrategia. Y es que para «ver» un extremo, deberemos registrar el cambio de precio - establecido por la amplitud del salto - con respecto a dicho extremo. Para el cambio de precio se necesita un cierto tiempo, eso es precisamente lo que provoca el retraso. Asimismo, es posible usar como extremo el último valor de precio conocido, pero es poco probable que precisamente este punto resulte en consecuencia un pico o valle.
En este caso, lo más eficaz es encontrar el primer extremo con la ayuda de un coeficiente adicional. Lo eficaz es presentarlo como parte fraccionada de la amplitud del salto que se usa para encontrar el resto de los extremos. Por ejemplo, podemos elegir el valor 0.5.
El valor elegido del coeficiente adicional determinará el cambio mínimo de precio del valor actual hasta el valor del precio mínimo para el valle más cercano (valor máximo del precio del pico más próximo) que permita determinar este valle (pico) en calidad de extremo. Si el salto entre el valor actual del precio y el valor extremo para el valle o pico más cercano es menor a la magnitud establecida, este extremo no se determinará. En este caso, tendremos una cierta certeza de que el primer extremo localizado será realmente un pico o un valle en lo sucesivo. Al mismo tiempo, se resuelve la tarea de definir lo más pronto posible los extremos, su análisis posterior y, en caso necesario, la apertura de transacciones.
Veamos un ejemplo para el que la magnitud del salto se ha establecido a un nivel de 140 pips. Para determinar el primer extremo, se usará un coeficiente adicional. En el primer caso, su valor es 0.9 (fig. 7, a) y en el segundo, 0.7 (fig. 7, b). Entonces el valor del coeficiente adicional determinará el salto mínimo de precio en pips que permita detectar el primer extremo. Para el primer caso, se tratará de un salto de 126 pips, y para el segundo, de 98 pips. En ambos casos, se analiza el mismo gráfico. La línea vertical muestra de forma convencional el momento actual, para el que se realiza el cálculo. Con puntos, se muestran los extremos localizados en este segmento.

Fig. 7. Influencia del coeficiente adicional en la definición de los extremos: para el valor 0.9 (126 pips) el primer extremo se determina con un salto de 205 pips (a), con el valor 0,7 (98 pips), el primer extremo se define ya con un salto de 120 pips, la definición de los otros dos se realiza de acuerdo con la magnitud de salto establecida (b)
El valor elegido del coeficiente adicional para el primer caso ha permitido determinar el valle solo con un salto de 205 pips, mientras que el salto mínimo de precio es igual a un valor de 126 pips. Para el segundo caso, si elegimos un coeficiente adicional igual a 0,7 (98 pips), el primer valle se definirá con un salto de 120 pips con respecto al valor actual del precio. Los dos extremos tras él se han determinado de acuerdo con una magnitud de salto establecida, igual a 140 pips. Por consiguiente, el salto de precio entre el primer valle y el pico que lo sigue es ligeramente superior a los 140 pips. El segundo valle también se ha definido por un salto de precio superior a los 140 pips, pero ya con respecto al pico encontrado.
Como podemos ver, el valor del coficiente adicional influye notablemente en la posición del primer extremo localizado, y puede influir en su tipo. Para diferentes valores (entre 0 y 1) se podrá determinar en primer lugar o bien un pico, o bien un valle para el mismo gráfico. Los dos primeros extremos que se han detectado para el segundo caso (fig. 7, b) en el primer caso no se han definido en absoluto.
Asimismo, merece la pena destacar que, en caso de establecer un valor de coeficiente aún más bajo, el primer extremo se determinará un poco más rápido. Así, para el segundo caso (fig. 7, b) con un valor del coeficiente adicional 0.4, el primer extremo encontrado se ha podido determinar 5 barras antes (5 minutos antes, según la escala temporal del marco temporal actual).
3. Soluciones algorítmicas de las tareas de localización de los extrmos y su implementación programática
Vamos a comenzar por la elección del salto de precio para construir los extremos. Resulta obvio que dependiendo del marco temporal, el tamaño de las barras y los parámetros de los extremos se diferenciarán sustancialmente. La presencia o ausencia de picos y valles dependerá también de la existencia de una tendencia, del momento del día y otros factores. Usando los indicadores correspondientes, por ejemplo fractales e instrumentos semejantes, podremos encontrar los extremos en cualquier marco temporal, tanto con la presencia de tendencias, como en su ausencia. Si usamos la media móvil al buscar picos y valles, el tamaño de los extremos con respecto a la media móvil puede ser de 2 puntos, e incluso de 100. ¿Nos resultarán interesantes los extremos de 2 puntos al practicar comercio intradía? Seguramente, no. En la inversión a largo plazo, no prestamos atención a los extremos menores a 20 puntos, independientemente del marco temporal analizado.
Por eso precisamente es necesario introducir la amplitud del salto: la entenderemos como un cierto valor medio del tamaño de los extremos. Como punto de referencia podemos usar la media móvil, con su ayuda determinaremos la distancia hasta el extremo y limitaremos su tamaño desde abajo. Pero en este caso, el periodo de la media móvil influirá sustancialmente en la posición de los picos y valles encontrados, y elegir algún pico como patrón de referencia será muy complicado.
Por eso, en lo sucesivo usaremos la suposición de que el precio se mueve de un pico hacia un valle, y a partir de la distancia del valle al pico y la amplitud del salto, determinaremos el valor mínimo del precio en puntos entre dos extremos vecinos: un pico y un valle. Si alguno de los extremos ya ha sido definido, entonces el contiguo debe encontrarse a una distancia no inferior a la distancia establecida en la magnitud del salto. Usando este criterio, tendremos la posibilidad de determinar los extremos independientemente del marco temporal y la presencia de tendencia. Este instrumento vendrá muy bien tanto para el comercio intradía, como para la inversión a largo plazo.
Vamos a ver su algoritmo de trabajo. Para comenzar, determinaremos visualmente los extremos usando el mismo gráfico, pero en el primer caso, la magnitud del salto será de 60 pips (fig. 8), y en el segundo, de 30 pips (fig. 9). Asimismo, supondremos que el primer extremo ya ha sido localizado (punto 1), y que estamos buscando los que le han precedido.
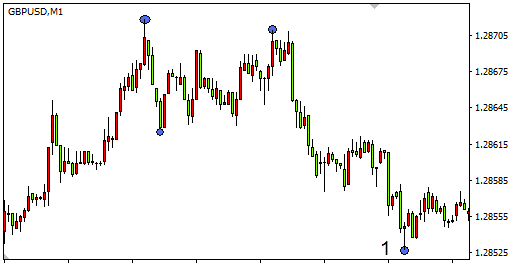
Fig. 8. Uso de la amplitud de salto de 60 pips
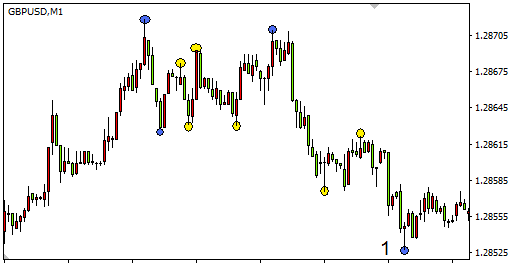
Fig. 9. Uso de la amplitud de salto de 30 pips
La búsqueda de los extremos se realiza desde el final del gráfico (a partir del punto 1). En el primer caso, en la ventana se han encontrado 4 extremos, en el segundo caso, en el mismo segmento se han encontrado 10. Al aumentar la amplitud del salto en la parte indicada del gráfico, los extremos no se definirán en absoluto. Por eso, partiendo de la volatilidad del mercado y del marco temporal indicado, hay que afrontar de forma realista la elección de la ventana de búsqueda de los extremos. Como ventana, en este caso entenderemos el número de barras en el que se realiza la búsqueda.
Aunando todo lo dicho anteriormente, propondremos para la búsqueda de extremos un algoritmo de iteración. ¿Por qué de iteración? Porque después del primer pico deberá haber obligatoriamente un valle, y después del mismo, un segundo pico etcétera. Si no localizamos el segundo pico (el gráfico se empeña en no ir hacia arriba), se redefinen las posiciones del valle, y en la nueva serie se mueve más y más lejos. De esta forma, podemos corregir la posición del primer pico y de cualquier extremo. También hay que descartar aquellas variantes donde se defina la misma barra como pico y como valle.
Por supuesto, este enfoque necesita de una gran cantidad de cálculos. Resulta eficaz usarlo para determinar varios extremos, y cuanto menos sean, a mayor velocidad funcionará el programa. La velocidad de cálculo dependerá también de la ventana en la que se realiza la búsqueda. Pero este enfoque está justificado, puesto que permite encontrar de forma unívoca simultáneamente los picos y valles con la influencia de las oscilaciones de precio más reciente. Si tenemos que definir muchos extremos, yo recomendaría usar el indicador ZigZag.
3.2 Implementación programática del indicadorEl código del algoritmo de iteración se muestra más abajo, para lograr la mayor velocidad de acción posible, utiliza un pequeño número de iteraciones. Esta simplificación no conllevará una pérdida significativa de calidad a la hora de detectar extremos. Los principales parámetros de entrada se relacionan con la búsqueda de extremos y con la magnitud del salto.
input double delta_points=160; // amplitud del salto que define la distancia mínima entre un pico y un valle en puntos
input double first_extrem=0.9; // coeficiente adicional para buscar el primer extremo
input double reload_time=5; // valor del intervalo temporal con el que se recalculan los valores del indicador en segundos
El cuerpo del programa contiene 3 ciclos incorporados para determinar cuatro extremos. En esta parte del programa, se definen solo el primer valle y los extremos relacionados con él. La definición del primer pico y los extremos relacionados con él se realiza de forma semejante.
datetime Time[];
ArraySetAsSeries(Low,true);
int copied1=CopyLow(Symbol(),0,0,bars+2,Low);
ArraySetAsSeries(High,true);
int copied2=CopyHigh(Symbol(),0,0,bars+2,High);
ArraySetAsSeries(Time,true);
int copied3=CopyTime(Symbol(),0,0,bars+2,Time);
double delta=delta_points*Point(); // amplitud del salto entre extremos en magnitudes absolutas
int j,k,l;
int j2,k2,l2;
double j1,k1,l1;
int min[6]; // matriz para definir los valles, el valor se corresponde con el número de la barra para el extremo localizado
int max[6]; // matriz para definir los picos, el valor se corresponde con el número de la barra para el extremo localizado
int mag1=bars;
int mag2=bars;
int mag3=bars;
int mag4=bars;
j1=SymbolInfoDouble(Symbol(),SYMBOL_BID)+(1-first_extrem)*delta_points*Point();
// al buscar el primer extremo, el coeficiente adicional determina el precio mínimo por debajo del cual deberá ubicarse el primer valle
j2=0; // en la primera iteración, la búsqueda se realiza comenzando por la última barra de la historia
for(j=0;j<=15;j++) // ciclo que determina el primer valle - min[1]
{
min[1]=minimum(j2,bars,j1);
//se define el valle más próximo en el intervalo indicado
j2=min[1]+1; // en la próxima iteración, la búsqueda se realizará a partir del valle encontrado min[1]
j1=Low[min[1]]+delta;
//el precio mínimo para el valle localizado en la siguiente iteración deberá ser inferior al precio mínimo para el valle localizado en la iteración actual
k1=Low[min[1]];
//el precio mínimo para un valle al buscar el pico siguiente define el precio máximo por encima del cual se deberá ubicar este pico
k2=min[1]; //la búsqueda del pico ubicado tras un valle se realiza a partir del valle encontrado min[1]
for(k=0;k<=12;k++) // ciclo que determina el primer pico - max[1]
{
max[1]=maximum(k2,bars,k1);
//--- se determina el pico más próximo en el intervalo indicado
k1=High[max[1]]-delta;
//el precio máximo para el pico localizado en la siguiente iteración deberá ser superior al precio máximo para el pico localizado en la iteración actual
k2=max[1]+1; // en la próxima iteración, la búsqueda se realizará a partir del pico encontrado max[1]
l1=High[max[1]];
//el precio máximo para un pico al buscar el valle siguiente define el precio mínimo por debajo del cual se deberá ubicar este valle
l2=max[1]; // la búsqueda del valle ubicado tras el pico se realiza a partir del pico encontrado max[1]
for(l=0;l<=10;l++) // ciclo que determina el segundo valle - min[2], y el segundo pico max[2]
{
min[2]=minimum(l2,bars,l1);
//---se determina el valle más próximo en el intervalo indicado
l1=Low[min[2]]+delta;
//el precio mínimo para el valle localizado en la siguiente iteración deberá ser inferior al precio mínimo para el valle localizado en la iteración actual
l2=min[2]+1; // en la próxima iteración, la búsqueda se realizará a partir del valle encontrado min[2]
max[2]=maximum(min[2],bars,Low[min[2]]);
//se determina el pico más próximo en el intervalo indicado
if(max[1]>min[1] && min[1]>0 && min[2]>max[1] && min[2]<max[2] && max[2]<mag4)
//se filtran los extremos coincidentes y los casos especiales
{
mag1=min[1]; // en cada iteración, en caso de que se cumplan las condiciones, la ubicación de los extremos encontrados se registra
mag2=max[1];
mag3=min[2];
mag4=max[2];
}
}
}
}
min[1]=mag1; // los extremos están definidos, en caso contrario, a todas las variables se les asigna el valor bars
max[1]=mag2;
min[2]=mag3;
max[2]=mag4;
La tarea de encontrar la barra más cercana, cuyo precio mínimo sea menor a la magnitud indicada (o cuyo precio máximo sea superior a la magnitud indicada) es bastante más sencilla, y se muestra en una función aparte.
//la función define el valle más próximo en el intervalo establecido, y que además se encuentre por debajo del precio price0 a una distancia superior que la magnitud del salto
{
double High[],Low[];
ArraySetAsSeries(Low,true);
int copied4=CopyLow(Symbol(),0,0,bars+2,Low);
int i,e;
e=bars;
double pr=price0-delta_points*Point(); // valor del precio por debajo del cual deberá ubicarse el valle con la amplitud del salto ya añadida
for(i=a;i<=b;i++) // búsqueda del valle en la ventana establecida con los parámetros a y b
{
if(Low[i]<pr && Low[i]<Low[i+1]) // se define el valle más cercano tras el cual comienza el crecimiento del precio
{
e=i;
break;
}
}
return(e);
}
int maximum(int a,int b,double price1)
//--- la función define el pico más próximo en el intervalo establecido, que además se encuentre por encima del precio price1 a una distancia superior que la amplitud del salto
{
double High[],Low[];
ArraySetAsSeries(High,true);
int copied5=CopyHigh(Symbol(),0,0,bars+2,High);
int i,e;
e=bars;
double pr1=price1+delta_points*Point(); // valor del precio por encima del cual se debe encontrar el pico con la amplitud del salto ya añadida
for(i=a;i<=b;i++) // búsqueda del pico en la ventana establecida con los parámetros a y b
{
if(High[i]>pr1 && High[i]>High[i+1]) // se define el pico más cercano tras el cual comienza la caída del precio
{
e=i;
break;
}
}
return(e);
}
La tarea de localización de los extremos ya ha sido solucionada, pero solo en una primera aproximación. Deberemos tener en cuenta que un pico localizado con este algoritmo y que se encuentre entre dos valles, podría no se el más alto en el intervalo indicado. Como la búsqueda ha comenzado desde el final del gráfico, también la especificación de las posiciones de los picos y los valles se realiza desde el final para el primer extremo, el segundo, el tercero y los siguientes. La comprobación y corrección de la posición para los picos y para los valles se han introducido en funciones aparte. La implementación programática para la especificación de la posición tiene el aspecto que sigue:
min[1]=check_min(min[1],max[1]); // comprobación y corrección de la posición del primer valle en el intervalo indicado
max[1]=check_max(max[1],min[2]); // comprobación y corrección de la posición del primer pico en el intervalo indicado
min[2]=check_min(min[2],max[2]); // comprobación y corrección de la posición del segundo valle en el intervalo indicado
int check_min(int a,int b)
// función para la comprobación y corrección de la posición del valle en el intervalo indicado
{
double High[],Low[];
ArraySetAsSeries(Low,true);
int copied6=CopyLow(Symbol(),0,0,bars+1,Low);
int i,c;
c=a;
for(i=a+1;i<b;i++) // al buscar el valle, se comprueban todas las barras que han sido establecidas por la ventana
{
if(Low[i]<Low[a] && Low[i]<Low[c]) // si se ha encontrado un valle que se ubique por debajo
c=i; // la posición del valle se determina de nuevo
}
return(c);
}
//--- función para la comprobación y corrección de un pico en el intervalo indicado
{
double High[],Low[];
ArraySetAsSeries(High,true);
int copied7=CopyHigh(Symbol(),0,0,bars+1,High);
int i,d;
d=a;
for(i=(a+1);i<b;i++) // al buscar el valle, se comprueban todas las barras que han sido establecidas por la ventana
{
if(High[i]>High[a] && High[i]>High[d]) // si se ha encontrado un pico que se ubique por encima
d=i; // la posición del pico se determina de nuevo
}
return(d);
}
Si se han encontrado 4 extremos, podemos limitarnos a especificar solo la posición de los tres primeros. El asunto es que esta función para comprobar y corregir la posición funciona en un diapasón definido para el extremo actual por su propia posición y la posición del extremo que las sigue. Después de la especificación podremos estar seguros de que los extremos encontrados se corresponden con los criterios establecidos.
A continuación, se realiza la búsqueda del primer pico desde el final del gráfico, después de lo cual se comparan las posiciones del primer valle y el primer pico. Como resultado de los cálculos realizados, en la salida obtenemos el primer extremo más cercano al final del gráfico, así como el resto de extremos relacionados con él.
Vamos a detenernos de nuevo en la definición del primer extremo. Más arriba se ha propuesto introducir un coeficiente adicional para localizarlo, una fracción de la amplitud del salto, por ejemplo 0.7. Además, sus valores altos (0.8…0.9) permiten definir con un alto nivel de precisión el primer extremo, pero con retraso, y los valores pequeños (0.1…0.25) permiten reducir el retraso al mínimo, pero en este caso, se difumina la precisión de la definición. Por consiguiente, el valor del coeficiente adicional se debe elegir dependiendo de la estrategia usada.
Los picos y valles localizados se marcan con flechas. Las flechas representan las coordenadas de los extremos (una coordenada representa la posición en la serie temporal, la otra, el valor del precio máximo/mínimo para el pico/valle encontrado). Puesto que al realizar los cálculos se ejecutan muchas operaciones, en el programa se ha incorporado un parámetro de entrada que establece el valor del intervalo con el cual se recalculan los valores del indicador. Si en la ventana elegida no se han encontrado picos o valles, el indicador emitirá el mensaje correspondiente. La implementación programática de la representación gráfica de los extremos tiene el aspecto siguiente:
if(min[1]<Max[1]) // en el caso de que el valle se ubique más cerca, se marca su posición y la posición de los extremos relacionados con él
{
ObjectDelete(0,"id_1"); // eliminación de las marcas realizadas en el paso anterior
ObjectDelete(0,"id_2");
ObjectDelete(0,"id_3");
ObjectDelete(0,"id_4");
ObjectDelete(0,"id_5");
ObjectDelete(0,"id_6");
ObjectCreate(0,"id_1",OBJ_ARROW_UP,0,Time[min[1]],Low[min[1]]); // marcamos el primer valle
ObjectSetInteger(0,"id_1",OBJPROP_ANCHOR,ANCHOR_TOP);
//--- para el primer valle localizado, el anclaje se realiza según la posición en la serie temporal y el valor del precio mínimo
ObjectCreate(0,"id_2",OBJ_ARROW_DOWN,0,Time[max[1]],High[max[1]]); // marcamos el primer pico
ObjectSetInteger(0,"id_2",OBJPROP_ANCHOR,ANCHOR_BOTTOM);
//--- para el pico localizado, el anclaje se realiza según la posición en la serie temporal y el valor del precio mínimo
ObjectCreate(0,"id_3",OBJ_ARROW_UP,0,Time[min[2]],Low[min[2]]); // marcamos el primer valle
ObjectSetInteger(0,"id_3",OBJPROP_ANCHOR,ANCHOR_TOP);
//--- para el primer valle localizado, el anclaje se realiza según la posición en la serie temporal y el valor del precio mínimo
}
if(min[1]>Max[1]) // en el caso de que el pico se ubique más cerca , se marca su posición y la posición de los extremos relacionados con él
{
ObjectDelete(0,"id_1"); // eliminación de las marcas realizadas en el paso anterior
ObjectDelete(0,"id_2");
ObjectDelete(0,"id_3");
ObjectDelete(0,"id_4");
ObjectDelete(0,"id_5");
ObjectDelete(0,"id_6");
ObjectCreate(0,"id_4",OBJ_ARROW_DOWN,0,Time[Max[1]],High[Max[1]]); // marcamos el primer pico
ObjectSetInteger(0,"id_4",OBJPROP_ANCHOR,ANCHOR_BOTTOM);
//para el primer pico localizado, el anclaje se realiza según la posición en la serie temporal y el valor del precio máximo
ObjectCreate(0,"id_5",OBJ_ARROW_UP,0,Time[Min[1]],Low[Min[1]]); // marcamos el primer valle
ObjectSetInteger(0,"id_5",OBJPROP_ANCHOR,ANCHOR_TOP);
//para el valle localizado, el anclaje se realiza según la posición en la serie temporal y el valor del precio mínimo
ObjectCreate(0,"id_6",OBJ_ARROW_DOWN,0,Time[Max[2]],High[Max[2]]); // marcamos el segundo pico
ObjectSetInteger(0,"id_6",OBJPROP_ANCHOR,ANCHOR_BOTTOM);
//para el segundo pico localizado, el anclaje se realiza según la posición en la serie temporal y el valor del precio máximo
}
if(min[1]==Max[1]) Alert("En la ventana establecida, ",bars," barras, no se ha encontrado ningún extremo");
// en caso de que no se haya encontrado ningún extremo, se muestra el mensaje correspondiente
En el proceso de desinicialización del indicador, los objetos que designen picos y valles se eliminan.
Según los algoritmos presentados, se ha desarrollado un indicador de usuario que busca los extremos y los marca en el gráfico (fig. 10).

Fig. 10. Resultados del funcionamiento del indicador: amplitud del salto 120 pips (a), amplitud del salto 160 pips (b)
Los resultados obtenidos son definidos por la amplitud del salto. Para el valor 120 pips e inferior (fig. 10, a) los extremos se ubican bastante cerca el uno del otro, y el tamaño de la ventana no es tan importante. Para el valor 160 pips y superior (fig. 10, b) los extremos se ubican bastante lejos. Es imprescindible tenerlo en cuenta al elegir la ventana para la búsqueda. En el caso de que el mercado se estanque, una ventana elegida óptimamente permitirá, no solo encontrar los picos y valles de forma automática cuando aparezca un pequeño movimiento, sino también filtrar (omitir) los extremos separados por intervalos temporales demasiado grandes.
3.3 Asesor que implementa la estrategia de divergencia entre el histograma MACD y los preciosEs posible aplicar los algoritmos presentados para implementar diferentes estrategias. Los resultados del funcionamiento del indicador scale_factor vienen bien para trabajar con modelos gráficos tales como «cabeza y hombros», «pico doble», «fondo doble» y otros. También se los puede utilizar en las estrategias que usen la divergencia de los picos y valles para los gráficos de precio y los indicadores. Uno de los ejemplos es un experto que funciona según la estrategia de divergencia entre el gráfico de precios y el histograma MACD. Esta estrategia ha sido bastante investigada en la literatura, como en el libro de Alexander Elder "Cómo jugar y ganar en la bolsa".
De acuerdo con esta estrategia, si el precio forma al subir un nuevo pico que se ubica por encima del anterior, pero al mismo tiempo el pico formado por el histograma es inferior al anterior, tendremos una señal de venta.
Cuando el precio se mueve hacia abajo, si se forma un nuevo valle que se ubica por debajo del valle más cercano, pero al mismo tiempo el valle formado en el histograma MACD se ubica por encima del anterior valle del histograma, aparecerá la señal que indica el viraje y la necesidad de comprar.
El experto que implementa el algoritmo mostrado más arriba encuentra de forma inequívoca los picos y valles necesarios para trabajar, de acuerdo con la amplitud del salto indicada, en primer lugar se orienta por los últimos cambios sucedidos en el gráfico de precio.
Parámetros de entrada: la ventana de búsqueda de los extremos y la amplitud del salto. Asimismo, es necesario establecer la desviación mínima de los precios para los 2 últimos picos durante el crecimiento (para los 2 últimos valles cuando el precio cae), la divergencia mínima del histograma MACD para los extremos. Se establece el riesgo de cada transacción en la divisa del depósito y el coeficiente adicional. El parámetro guard_points define el desplazamiento adicional del stop-loss con respecto al valor mínimo del precio para el valle más cercano, si se abre una posición larga. Por consiguiente, el stop-loss se desplaza hacia arriba al abrirse una posición corta. Asimismo, existe la posibilidad de mostrar los parámetros de los extremos localizados en el caso de apertura de transacciones (show_info=1).
input double delta_points=160; // amplitud del salto que define la distancia mínima entre un pico y un valle en puntos
input double first_extrem=0.9; // coeficiente adicional para buscar el primer extremo
input int orderr_size=10; // riesgo en cada transacción
input double macd_t=0.00002; // divergencia mínima del histograma MACD
input double trend=100; // divergencia mínima del precio para los 2 picos/valles más cercanos
input double guard_points=30; // desplazamiento del stop-loss
input int time=0; // retraso en segundos
input int show_info=0; // mostrar la información sobre los extremos
Los cálculos pueden ejecutarse en cada tick, al igual que las operaciones comerciales. Pero la estrategia también funcionará bien al introducir un retraso temporal. Después de determinar los parámetros básicos en magnitudes absolutas, pasaremos a la localización de extremos. La primera parte del programa permite detectar los extremos si el primero de ellos es un valle, después de lo cual se concretan sus posiciones. La segunda parte permite encontrar los extremos en el caso de que sea un pico el primero en ubicarse a partir del final del gráfico. En el siguiente paso se precisan los parámetros de los picos y los valles.
{
Sleep(1000*time); // introducimos la variable de retraso
double High[],Low[];
ArraySetAsSeries(Low,true);
int copied1=CopyLow(Symbol(),0,0,bars+2,Low);
ArraySetAsSeries(High,true);
int copied2=CopyHigh(Symbol(),0,0,bars+2,High);
ArraySetAsSeries(Time,true);
int copied3=CopyTime(Symbol(),0,0,bars+2,Time);
MqlTick last_tick;
double Bid=last_tick.bid;
double Ask=last_tick.ask;
double delta=delta_points*Point(); // amplitud del salto en magnitudes absolutas
double trendd=trend*Point(); // divergencia mínima de los precios de los 2 picos/valles más cercanos en magnitudes absolutas
double guard=guard_points*Point(); // desplazamiento del stop-loss en magnitudes absolutas
int j,k,l;
int j2,k2,l2;
double j1,k1,l1;
int min[6]; // matriz que define los valles en caso de que el primer extremo en encontrado sea un valle, el valor corresponde al número de la barra para el extremo localizado
int max[6]; // matriz que define los picos en caso de que el primer extremo en encontrado sea un valle, el valor corresponde al número de la barra para el extremo localizado
int Min[6]; // matriz que define los valles en caso de que el primer extremo en encontrado sea un pico, el valor corresponde al número de la barra para el extremo localizado
int Max[6]; // matriz que define los picos en caso de que el primer extremo en encontrado sea un pico, el valor corresponde al número de la barra para el extremo localizado
int mag1=bars;
int mag2=bars;
int mag3=bars;
int mag4=bars;
j1=SymbolInfoDouble(Symbol(),SYMBOL_BID)+(1-first_extrem)*delta_points*Point();
// al buscar el primer extremo, el coeficiente adicional define el precio mínimo por debajo del cual deberá ubicarse el primer valle
j2=0; // en la primera iteración, la búsqueda se realiza comenzando desde la última barra de la historia
for(j=0;j<=15;j++) // ciclo que determina el primer valle - min[1]
{
min[1]=minimum(j2,bars,j1);
//se define el valle más próximo en el intervalo indicado
j2=min[1]+1; //en la próxima iteración, la búsqueda se realizará a partir del valle encontrado min[1]
j1=Low[min[1]]+delta;
//--- el precio mínimo para el valle localizado en la siguiente iteración deberá ser inferior al precio mínimo para el valle localizado en la iteración actual
k1=Low[min[1]];
//el precio mínimo para un valle al buscar el pico siguiente define el precio máximo por encima del cual se deberá ubicar este pico
k2=min[1]; // la búsqueda del pico ubicado tras un valle se realiza a partir del valle encontrado min[1]
for(k=0;k<=12;k++) // ciclo que determina el primer pico - max[1]
{
max[1]=maximum(k2,bars,k1);
//--- se determina el pico más próximo en el intervalo indicado
k1=High[max[1]]-delta;
//--- el precio máximo para el pico localizado en la siguiente iteración deberá ser superior al precio máximo para el pico localizado en la iteración actual
k2=max[1]+1; // en la próxima iteración, la búsqueda se realizará a partir del pico encontrado max[1]
l1=High[max[1]];
//--- el precio máximo para un pico al buscar el valle siguiente define el precio mínimo por debajo del cual se deberá ubicar este valle
l2=max[1]; // la búsqueda del valle ubicado tras el pico se realiza a partir del pico encontrado max[1]
for(l=0;l<=10;l++) // ciclo que determina el segundo valle - min[2], y el segundo pico max[2]
{
min[2]=minimum(l2,bars,l1);
//--- se determina el valle más próximo en el intervalo indicado
l1=Low[min[2]]+delta;
//el precio mínimo para el valle localizado en la siguiente iteración deberá ser inferior al precio mínimo para el valle localizado en la iteración actual
l2=min[2]+1; //en la próxima iteración, la búsqueda se realizará a partir del valle encontrado min[2]
max[2]=maximum(min[2],bars,Low[min[2]]);
//se determina el pico más próximo en el intervalo indicado
if(max[1]>min[1] && min[1]>0 && min[2]>max[1] && min[2]<max[2] && max[2]<mag4)
//--- se filtran los extremos coincidentes y los casos especiales
{
mag1=min[1]; // en cada iteración, en caso de que se cumplan las condiciones, la ubicación de los extremos encontrados se registra
mag2=max[1];
mag3=min[2];
mag4=max[2];
}
}
}
}
//--- los extremos están definidos, en caso contrario, a todas las variables se les asigna el valor bars
min[1]=mag1;
max[1]=mag2;
min[2]=mag3;
max[2]=mag4;
//--- comprobamos y corregimos la posición de los extremos en el intervalo indicado
max[1]=check_max(max[1],min[2]);
min[2]=check_min(min[2],max[2]);
//---------------------------------------------------------------------------------------------------------------
mag1=bars;
mag2=bars;
mag3=bars;
mag4=bars;
j1=SymbolInfoDouble(Symbol(),SYMBOL_BID)-(1-first_extrem)*delta_points*Point();
// al buscar el primer extremo, el coeficiente adicional define el precio máximo por encima del cual deberá ubicarse el primer pico
j2=0; // en la primera iteración, la búsqueda se realiza comenzando desde la última barra de la historia
for(j=0;j<=15;j++) // ciclo que determina el primer valle - Max[1]
{
Max[1]=maximum(j2,bars,j1);
//se define el pico más próximo en el intervalo indicado
j1=High[Max[1]]-delta;
//el precio máximo para el pico localizado en la siguiente iteración deberá ser superior al precio máximo para el pico localizado en la iteración actual
j2=Max[1]+1; // en la próxima iteración, la búsqueda se realizará a partir del pico encontrado Max[1]
k1=High[Max[1]];
//el precio máximo para un pico al buscar el valle siguiente define el precio mínimo por debajo del cual se deberá ubicar este valle
k2=Max[1]; // la búsqueda del valle ubicado tras el pico se realiza a partir del pico encontrado Max[1]
for(k=0;k<=12;k++) //ciclo que determina el primer pico - Min[1]
{
Min[1]=minimum(k2,bars,k1);
//--- se determina el valle más próximo en el intervalo indicado
k1=Low[Min[1]]+delta;
//el precio mínimo para el valle localizado en la siguiente iteración deberá ser inferior al precio mínimo para el valle localizado en la iteración actual
k2=Min[1]+1; // en la próxima iteración, la búsqueda se realizará a partir del valle encontrado Min[1]
l1=Low[Min[1]];
//---el precio mínimo para un valle al buscar el pico siguiente define el precio máximo por encima del cual se deberá ubicar este pico
l2=Min[1]; // la búsqueda del pico ubicado tras un valle se realiza a partir del valle encontrado Min[1]
for(l=0;l<=10;l++)//ciclo que determina el segundo pico - Max[2], y el segundo valle Min[2]
{
Max[2]=maximum(l2,bars,l1);
//se define el pico más próximo en el intervalo indicado
l1=High[Max[2]]-delta;
//el precio máximo para el pico localizado en la siguiente iteración deberá ser superior al precio máximo para el pico localizado en la iteración actual
l2=Max[2]+1; //en la próxima iteración, la búsqueda se realizará a partir del pico encontrado Max[2]
Min[2]=minimum(Max[2],bars,High[Max[2]]);
//---se determina el valle más próximo en el intervalo indicado
if(Max[2]>Min[1] && Min[1]>Max[1] && Max[1]>0 && Max[2]<Min[2] && Min[2]<bars)
//--- se filtran los extremos coincidentes y los casos especiales
{
mag1=Max[1]; // en cada iteración, en caso de que se cumplan las condiciones, la posición de los extremos encontrados se registra
mag2=Min[1];
mag3=Max[2];
mag4=Min[2];
}
}
}
}
Max[1]=mag1; // los extremos están definidos, en caso contrario, a todas las variables se les asigna el valor bars
Min[1]=mag2;
Max[2]=mag3;
Min[2]=mag4;
Max[1]=check_max(Max[1],Min[1]); // comprobación y corrección de la posición de los extremos en el intervalo indicado
Min[1]=check_min(Min[1],Max[2]);
Max[2]=check_max(Max[2],Min[2]);
En lo sucesivo, se podrán usar tanto el primer pico encontrado, como el primer valle encontrado, pero lo más efectivo es utilizar el extremo situado más cerca, así como los picos y valles obtenidos sobre su base.
Para ambas variantes se calcula el valor del lote, así como los valores del indicador que correspondan a las posiciones de los extremos. Se comprueba la condición sobre la correcta detección de los extremos y la ausencia de posiciones abiertas.
Si se observa una divergencia de los valores de los precios para los extremos y el histograma MACD, y esta divergencia no es menor a los valores establecidos con los parámetros de entrada, se abre la posición correspondiente. Las divergencias, además, deberán tener direcciones diferentes.
//se calcula el valor del lote al comprar
double lot_sell=NormalizeDouble(0.1*orderr_size/(NormalizeDouble(((High[Max[1]]-SymbolInfoDouble(Symbol(),SYMBOL_ASK)+guard)*10000),0)+0.00001),2);
//--- se calcula el valor del lote al vender
int index_handle=iMACD(NULL,PERIOD_CURRENT,12,26,9,PRICE_MEDIAN);
double MACD_all[];
ArraySetAsSeries(MACD_all,true);
int copied4=CopyBuffer(index_handle,0,0,bars+2,MACD_all);
double index_min1=MACD_all[min[1]];
double index_min2=MACD_all[min[2]];
//--- se calculan los valores del indicador que correspondan a las posiciones de los extremos, en caso de que el primer extremo sea un valle
double index_Max1=MACD_all[Max[1]];
double index_Max2=MACD_all[Max[2]];
//se calculan los valores del indicador que correspondan a las posiciones de los extremos, en caso de que el primer extremo sea un pico
bool flag_1=(min[2]<bars && min[2]!=0 && max[1]<bars && max[1]!=0 && max[2]<bars && max[2]!=0); //Se comprueba la condición de la correcta detección de los extremos
bool flag_2=(Min[1]<bars && Min[1]!=0 && Max[2]<bars && Max[2]!=0 && Min[2]<bars && Min[2]!=0);
bool trend_down=(Low[min[1]]<(Low[min[2]]-trendd));
bool trend_up=(High[Max[1]]>(High[Max[2]]+trendd));
//---la diferencia de los valores de los precios para los extremos deberá ser no inferior a la magnitud establecida
openedorder=PositionSelect(Symbol()); //comprobamos la condición de la ausencia de posiciones abiertas
if(min[1]<Max[1] && trend_down && flag_1 && !openedorder && (index_min1>(index_min2+macd_t)))
//en el caso de que el primer extremo sea un valle, se abrirá una transacción de compra
//la diferencia de los valores del indicador MACD para los extremos no es menor al valor establecido por el parámetro de entrada macd_t
// la transacción se abre en caso de que tengan dirección opuesta el precio y el indicador calculados según los valores de los extremos
{
if(show_info==1) Alert("En las últimas",bars," barras, la distancia en barras hasta el valle y los extremos más próximos",min[1]," ",max[1]," ",min[2]);
//--- mostramos la información sobre los extremos
MqlTradeResult result={0};
MqlTradeRequest request={0};
request.action=TRADE_ACTION_DEAL;
request.magic=123456;
request.symbol=_Symbol;
request.volume=lot_buy;
request.price=SymbolInfoDouble(Symbol(),SYMBOL_ASK);
request.sl=Low[min[1]]-guard;
request.tp=MathAbs(2*SymbolInfoDouble(Symbol(),SYMBOL_BID)-Low[min[1]])+guard;
request.type=ORDER_TYPE_BUY;
request.deviation=50;
request.type_filling=ORDER_FILLING_FOK;
OrderSend(request,result);
}
if(min[1]>Max[1] && trend_up && flag_2 && !openedorder && (index_Max1<(index_Max2-macd_t)))
//en el caso de que el primer extremo sea un pico, se abrirá una transacción de venta
//la diferencia de los valores del indicador MACD para los extremos no es menor al valor establecido por el parámetro de entrada macd_t
// la transacción se abre en caso de que tengan dirección opuesta el precio y el indicador calculados según los valores de los extremos
{
if(show_info==1) Alert("En las últimas ",bars," barras, la distancia en barras hasta el pico y los extremos más próximos",Max[1]," ",Min[1]," ",Max[2]);
//---mostrando la información de los extremos
MqlTradeResult result={0};
MqlTradeRequest request={0};
request.action=TRADE_ACTION_DEAL;
request.magic=123456;
request.symbol=_Symbol;
request.volume=lot_sell;
request.price=SymbolInfoDouble(Symbol(),SYMBOL_BID);
request.sl=High[Max[1]]+guard;
request.tp=MathAbs(High[Max[1]]-2*(High[Max[1]]-SymbolInfoDouble(Symbol(),SYMBOL_ASK)))-guard;
request.type=ORDER_TYPE_SELL;
request.deviation=50;
request.type_filling=ORDER_FILLING_FOK;
OrderSend(request,result);
}
Al abrir una posición corta, el stop-loss se coloca según la posición del pico más cercano, al abrir una posición larga, según la posición del valle más cercano, lo que permite colocar precios realistas tanto en el caso de oscilaciones fuertes de precio, como en el caso de que el mercado esté tranquilo. En ambas situaciones, el take-profit se coloca de forma simétrica al stop-loss del valor actual del precio. Al comerciar en intradía, se elige una amplitud pequeña de salto, mientras que en la inversión a largo plazo, será conveniente elegir una amplitud de salto varias veces mayor.
Vamos a ver el funcionamiento del experto en el ejemplo (fig. 11). Parámetros básicos utilizados: amplitud del salto — 160 pips, divergencia mínima del histograma MACD – 0,0004; divergencia mínima de los precios para los 2 picos/valles más cercanos – 120 pips y coeficiente adicional – 0.9.
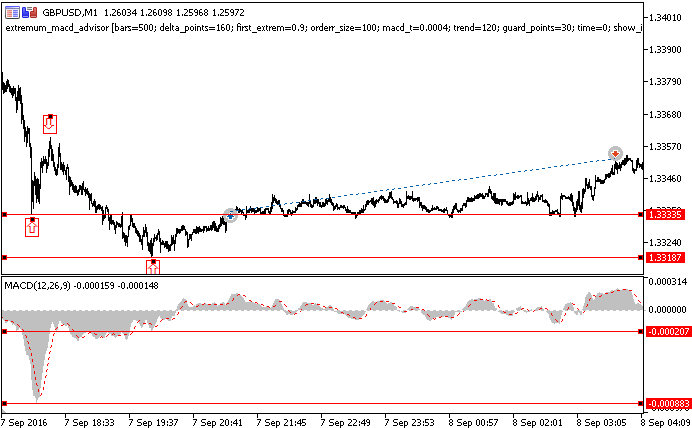
Fig. 11. Resultados del funcionamiento del experto
Al principio se ha realizado la búsqueda de los 3 extremos. En el momento en el que se tomó la decisión de abrir una posición larga, se encontraron un pico y dos valles (marcados con flechas). El experto, a diferencia del indicador, no marca la posición de los extremos, pero en caso necesario, usando el parámetro show_info y asignándole el valor 1, podemos obtener información sobre la posición de los extremos al abrir transacciones.
La divergencia de los precios para los 2 valles más cercanos ha sido de 148 pips. Un valor mayor al indicado. La divergencia del histograma MACD para estos mismos extremos es de 0.00062, y esta magnitud es también superior al valor establecido. Teniendo en cuenta el cambio en direcciones opuestas del precio y de los valores del indicador encontrado en los 2 últimos valles, en el punto determinado por el coeficiente adicional (su valor es de 150 pips) se ha abierto una posición larga. Al usar valores menores en el coeficiente adicional, la posición podría haberse abierto antes, por consiguiente, el beneficio se podría haber fijado con anterioridad.
En último lugar, presentamos los resultados de la simualación del experto (fig. 12). En el proceso de simulación se ha establecido la influencia máxima de los parámetros macd_t y trend en el beneficio. Cuanto mayor sea el valor de estos parámetros, mayor será el número de transacciones con beneficio en tanto por ciento. Pero con el aumento del beneficio, tendrá lugar de forma simultánea la reducción del número total de transacciones.
Bien, para los parámetros macd_t = 0,0006 y trend=160 (fig. 12), de 44 transacciones, el 56% han sido rentables. Al usar los valores macd_t = 0,0004 y trend=120, se han realizado 84 transacciones, de ellas, el 51% han sido rentables.

Fig. 12. Resultados de la simulación del experto
Al optimizar la estrategia, en primer lugar hay que elegir de forma óptima los parámetros macd_t y trend. Y por supuesto, en los parámetros de las transacciones influirá el valor de la amplitud del salto y el coeficiente adicional. La amplitud del salto determinará el número de extremos añadidos, y por consiguiente, de transacciones. El coeficiente adicional determina lo estrechamente que se ubicarán el take-profit y el stop-loss al abrir posiciones.
Esta estrategia y varias otras pueden funcionar con el máximo de corrección solo si se usan los instrumentos propuestos. En otro caso, pueden surgir situaciones en las que una transacción con un take-profit y un stop-loss a 200 puntos del valor actual del precio puede abrirse basándose en señales recibidas al usar extremos con tamaños de 5 puntos y menos. La relevancia de estos extremos en este caso es muy pequeña. Tanto en estas como en otras muchas situaciones, los instrumentos tradicionales o bien definen demasiados extremos poco significativos, o bien no permiten detectar en general picos y valles. Asimismo, otro problema de los instrumentos tradicionales está relacionado con la definición de los extremos ubicados al final de la serie temporal.
Conclusión
Los algoritmos y soluciones programáticas presentados en el artículo dan la posibilidad de encontrar de forma unívoca los extremos en los gráficos de precio dependiendo de los saltos de precio. Los resultados obtenidos se pueden aplicar tanto en la definición de modelos gráficos, como a la hora de implementar estrategias comerciales que usen modelos gráficos e indicadores. Los instrumentos desarrollados tienen una serie de ventajas en comparación con las soluciones más conocidas. Solo se determinan los extremos importantes, y estos deben ser sometidos a observación independientemente de la situación en el mercado; se definen igualmente bien tanto en presencia de tendencia, como con movimiento lateral. Solo se localizan los extremos cuyo tamaño sea mayor a la magnitud establecida, el resto de los picos y valles se ignorarán. La búsqueda de extremos se realiza desde el final del gráfico, lo que permite obtener resultados que dependan al máximo de las oscilaciones de precio más recientes. Los datos obtenidos dependen en poca medida del marco temporal elegido, y se definen solo por el salto de precio establecido.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/2817
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Patrones disponibles al comerciar con cestas de divisas
Patrones disponibles al comerciar con cestas de divisas
 Interfaces gráficas X: Gestión ampliada de las listas y tablas. Optimización de código (build 7)
Interfaces gráficas X: Gestión ampliada de las listas y tablas. Optimización de código (build 7)
 Distribuciones estadísticas en forma de histogramas sin búferes de indicador y matrices
Distribuciones estadísticas en forma de histogramas sin búferes de indicador y matrices
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Se ha publicado un nuevo artículo Detección automática de puntos extremos basada en cambios específicos de precios:
Autor: Sergey Strutinskiy
¡Buena idea!
¿Tiene algún código en mt4?
Se ha publicado un nuevo artículo Detección automática de puntos extremos a partir de una variación de precios determinada:
Autor: Sergey Strutinskiy
¿Cómo puedo utilizar este indicador en mi EA? No he visto un Buffer para su uso en ICustom.