
Neuronale Netze im Handel: Verallgemeinerte 3D-Segmentierung von referenzierten Ausdrücken
Einführung
3D Referring Expression Segmentation (3D-RES) ist ein aufstrebendes Gebiet im multimodalen Bereich, das bei Forschern großes Interesse geweckt hat. Diese Aufgabe konzentriert sich auf die Segmentierung von Zielinstanzen auf der Grundlage gegebener natürlichsprachlicher Ausdrücke. Herkömmliche Ansätze von 3D-RES sind jedoch auf Szenarien mit einem einzigen Ziel beschränkt, was ihre praktische Anwendbarkeit erheblich einschränkt. In der Praxis führen Anweisungen oft zu Situationen, in denen das Ziel nicht gefunden werden kann oder in denen mehrere Ziele gleichzeitig identifiziert werden müssen. Diese Realität stellt ein Problem dar, mit dem die bestehenden Modelle von 3D-RES nicht umgehen können. Um diese Lücke zu schließen, haben die Autoren von „3D-GRES: Generalized 3D Referring Expression Segmentation“ eine neuartige Methode unter dem Namen Generalized 3D Referring Expression Segmentation (3D-GRES) vorgeschlagen, die dazu dient, Anweisungen zu interpretieren, die auf eine beliebige Anzahl von Zielen verweisen.
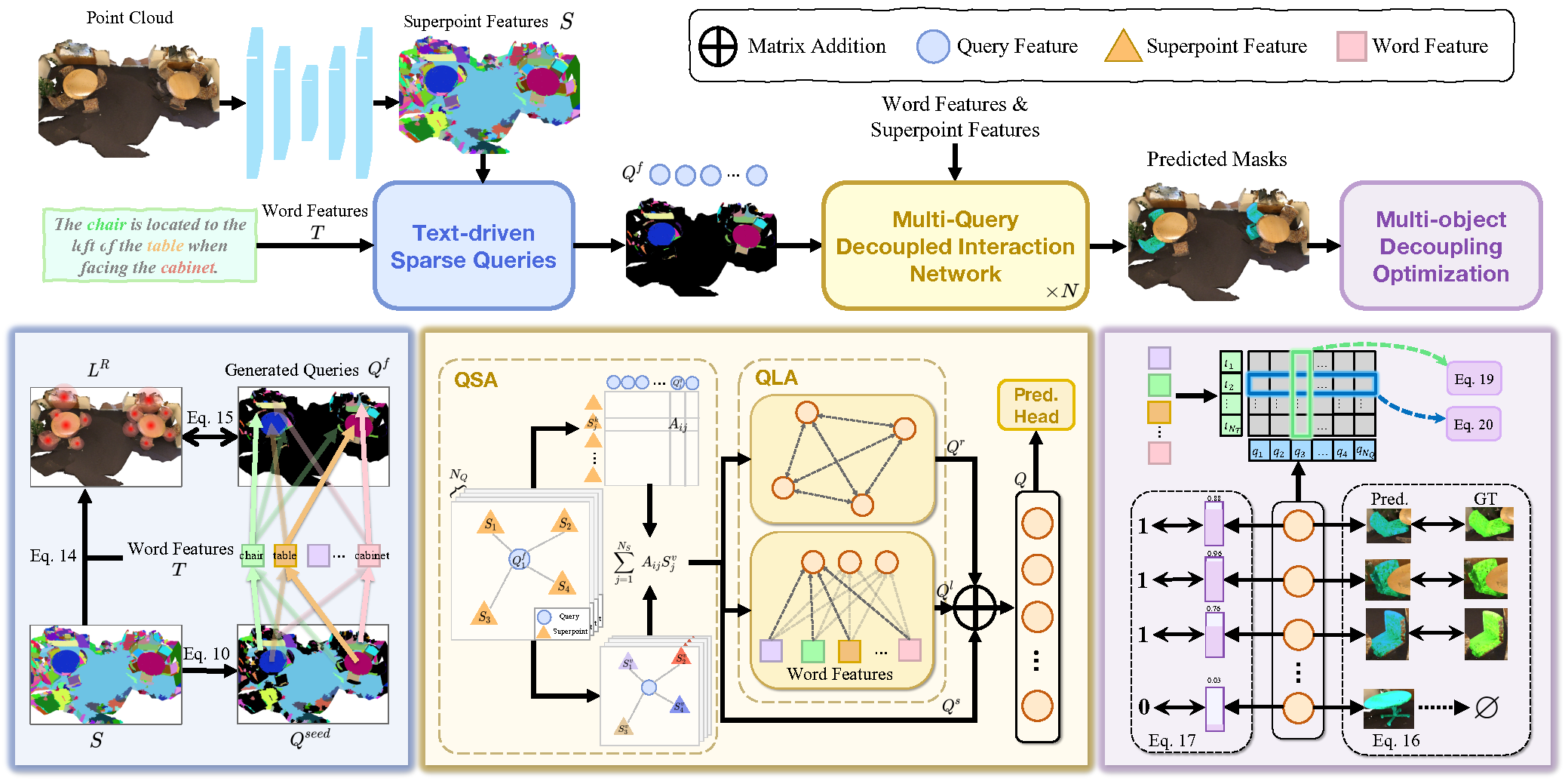
Das Hauptziel von 3D-GRES ist die genaue Identifizierung mehrerer Ziele innerhalb einer Gruppe ähnlicher Objekte. Der Schlüssel zur Lösung solcher Aufgaben liegt darin, das Problem so zu zerlegen, dass mehrere Abfragen gleichzeitig die Lokalisierung von Sprachbefehlen mit mehreren Objekten verarbeiten können. Jede Abfrage (Query) ist für eine einzelne Instanz in einer Szene mit mehreren Objekten zuständig. Die Autoren von 3D-GRES haben das Multi-Query Decoupled Interaction Network (MDIN) eingeführt, ein Modul, das die Interaktion zwischen Abfragen, Superpunkten und Text optimieren soll. Um eine beliebige Anzahl von Zielen effektiv verwalten zu können, wurde ein Mechanismus eingeführt, der es ermöglicht, dass mehrere Abfragen unabhängig voneinander funktionieren und gleichzeitig gemeinsame Ausgaben für mehrere Objekte erzeugen. Jede Abfrage ist dabei für ein einzelnes Ziel innerhalb des Multi-Instanz-Kontextes zuständig.
Um die wichtigsten Ziele in der Punktwolke durch die lernfähigen Abfragen gleichmäßig abzudecken, haben die Autoren ein neues Modul für textgeleitete spärliche Abfragen (TSQ) vorgeschlagen, das textbezogene Ausdrücke verwendet. Um gleichzeitig die Unterscheidbarkeit von Abfragen zu erreichen und die semantische Konsistenz zu wahren, entwickelten die Autoren eine Optimierungsstrategie namens Multi-Object Decoupling Optimization (MDO). Bei dieser Strategie wird eine Multi-Objekt-Maske in einzelne Einzel-Objekt-Überwachungen zerlegt, wobei die Trennschärfe der einzelnen Abfragen erhalten bleibt. Der Abgleich zwischen Abfragefunktionen und den Superpunktmerkmalen in der Punktwolke mit textueller Semantik gewährleistet semantische Konsistenz über mehrere Ziele hinweg.
1. Der Algorithmus von 3D-GRES
Die klassische Aufgabe von 3D-RES konzentriert sich auf die Generierung einer 3D-Maske für ein einzelnes Zielobjekt in einer Punktwolkenszene, die durch einen verweisenden Ausdruck gesteuert wird. Diese traditionelle Formulierung weist erhebliche Einschränkungen auf. Erstens ist es nicht für Szenarien geeignet, in denen kein Objekt in der Punktwolke dem gegebenen Ausdruck entspricht. Zweitens berücksichtigt es nicht die Fälle, in denen mehrere Objekte die beschriebenen Kriterien erfüllen. Diese beträchtliche Lücke zwischen den Modellfähigkeiten und der realen Anwendbarkeit schränkt den praktischen Einsatz der Technologien von 3D-RES ein.
Um diese Einschränkungen zu überwinden, wurde die Methode Generalized 3D Referring Expression Segmentation (3D-GRES) vorgeschlagen, mit der eine beliebige Anzahl von Objekten aus Textbeschreibungen identifiziert werden kann. 3D-GRES analysiert eine 3D-Punktwolkenszene P und einen referenzierenden Ausdruck E. Daraus entstehen entsprechende 3D-Masken M, die leer sein oder ein oder mehrere Objekte enthalten können. Die vorgestellte Methode ermöglicht es, mehrere Objekte mit Hilfe von Ausdrücken mit mehrfachen Zielen zu finden und das Vorhandensein bestimmter Objekte in einer Szene mit Hilfe von „nothing“-Ausdrücken zu verifizieren, wodurch die Flexibilität und Robustheit bei der Objektsuche und Interaktion erhöht wird.
3D-GRES verarbeitet zunächst den eingegebenen verweisenden Ausdruck, indem es ihn mit Hilfe eines vortrainierten Modells RoBERTa in Text-Token 𝒯 kodiert. Um den multimodalen Abgleich zu erleichtern, werden die kodierten Token in einen multimodalen Raum der Dimension D projiziert. Auf die resultierenden Darstellungen wird eine positionsbezogene Kodierung angewendet.
Für die Eingabepunktwolke mit Positionen P und Merkmalen F werden Superpunkte mit Hilfe eines spärlichen 3D-U-Netzes extrahiert und in denselben D-dimensionalen, multimodalen Raum projiziert.
Das Multi-Query Decoupled Interaction Network (MDIN) nutzt mehrere Abfragen, um einzelne Instanzen innerhalb von Szenen mit mehreren Objekten zu behandeln und sie zu einem Endergebnis zu aggregieren. In Szenen ohne Zielobjekte stützen sich die Vorhersagen auf die Konfidenzwerte der einzelnen Abfragen - wenn alle Abfragen eine niedrige Konfidenz aufweisen, wird eine Nullausgabe vorhergesagt.
MDIN besteht aus mehreren identischen Modulen, die jeweils ein Query-SuperpointAggregation (QSA)-Modul und ein Query-Language Aggregation (QLA)-Modul umfassen, die die Interaktion zwischen Query, Superpoints und dem Text erleichtern. Im Gegensatz zu früheren Modellen, die eine zufällige Abfrageinitialisierung verwenden, nutzt MDIN ein textgeleitetes Sparse Query (TSQ)-Modul, um eine textgesteuerte spärliche Query zu generieren, die eine effiziente Szenenabdeckung gewährleisten. Darüber hinaus unterstützt die Strategie der Multi-Object Decoupling Optimization (MDO) mehrere Abfragen.
Die Query kann als Anker im Punktwolkenraum verwendet werden. Durch die Interaktion mit Superpunkten erfassen die Abfragen den globalen Kontext der Punktwolke. Insbesondere fungieren ausgewählte Superpunkte während des Interaktionsprozesses als Abfragen, wodurch die lokale Aggregation verbessert wird. Dieser lokalisierte Fokus unterstützt die effektive Entkopplung von Abfragen.
Zunächst wird eine Ähnlichkeitsverteilung zwischen den Superpoint-Merkmalen S und den Query Embeddings Qf berechnet. Anschließend werden die Abfragen anhand von Ähnlichkeitsverteilungen die entsprechenden verwandten Superpunkte aggregieren. Die aktualisierte Szenendarstellung, die nun durch Qs informiert ist, wird an das QLA-Modul weitergegeben, um die Interaktionen zwischen Query-Query und Query-Language zu modellieren. QLA umfasst einen Selbstaufmerksamkeits-Block für Abfragemerkmale Qs und einen multimodalen Kreuzaufmerksamkeits-Block zur Erfassung von Abhängigkeiten zwischen jedem Wort und jeder Abfrage.
Die Abfragemerkmale mit Beziehungskontext Qr, sprachbezogenen Merkmalen Ql und szeneinformierten Merkmalen Qs werden dann summiert und mit Hilfe eines MLP fusioniert.
Um eine spärliche Verteilung der initialisierten Abfragen über die Punktwolkenszene zu gewährleisten und gleichzeitig die wesentlichen geometrischen und semantischen Informationen zu erhalten, wenden die Autoren von 3D-GRES das Furthest Point Sampling (Stichprobe der entferntesten Punkte) direkt auf die Superpunkte an.
Um die Trennung von Abfragen und die Zuordnung zu bestimmten Objekten weiter zu verbessern, nutzt die Methode die intrinsischen Attribute der von TSQ generierten Abfragen. Jede Abfrage geht von einem bestimmten Superpunkt in der Punktwolke aus und ist somit mit einem entsprechenden Objekt verknüpft. Abfragen, die mit Zielinstanzen verbunden sind, übernehmen die Segmentierung für diese Instanzen, während nicht verwandte Objekte der nächstgelegenen Abfrage zugewiesen werden. Bei diesem Ansatz werden vorläufige visuelle Beschränkungen verwendet, um Abfragen zu entflechten und sie verschiedenen Zielen zuzuordnen.
Eine visuelle Darstellung der Methode 3D-GRES, wie sie von den Autoren vorgestellt wurde, ist unten abgebildet.
2. Die Implementation in MQL5
Nach der Betrachtung der theoretischen Aspekte der Methode 3D-GRES gehen wir zum praktischen Teil unseres Artikels über, in dem wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umsetzen. Betrachten wir zunächst, was den 3D-GRES-Algorithmus von den zuvor untersuchten Methoden unterscheidet und welche Gemeinsamkeiten sie haben.
In erster Linie ist es die Multimodalität der 3D-GRES-Methode. Dies ist das erste Mal, dass wir auf Ausdrücke stoßen, die darauf abzielen, die Analyse gezielter zu gestalten. Und wir werden diese Idee mit Sicherheit nutzen. Statt ein Sprachmodell zu verwenden, werden wir jedoch den Kontostand und die offenen Positionen als Input für das Modell kodieren. Je nach Einbettung des Kontostandes wird das Modell also dazu angehalten, nach Einstiegs- oder Ausstiegspunkten zu suchen.
Ein weiterer wichtiger Punkt, der hervorzuheben ist, ist die Art und Weise, wie trainierbare Abfragen behandelt werden. Wie die zuvor untersuchten Modelle verwendet auch 3D-GRES eine Reihe von trainierbaren Abfragen. Es gibt einen Unterschied im Prinzip ihrer Bildung. SPFormer und MAFT verwenden statische Abfragen, die während des Trainings optimiert und während der Inferenz festgelegt werden. So lernte das Modell einige Muster und handelte dann nach einem „vorbereiteten Schema“. Die Autoren von 3D-GRES schlagen vor, Abfragen auf der Grundlage der Eingabedaten zu generieren, um sie lokalisierter und dynamischer zu gestalten. Um eine optimale Abdeckung des analysierten Szenenraums zu gewährleisten, werden verschiedene Heuristiken angewendet. Wir werden diese Idee auch bei unserer Umsetzung anwenden.
Außerdem wird in 3D-GRES eine Positionskodierung von Token verwendet. Dies ist ähnlich wie bei der MAFT-Methode und dient als Grundlage für die Wahl der übergeordneten Klasse in der Implementierung. Auf dieser Grundlage beginnen wir mit der Erweiterung unseres OpenCL-Programms.
2.1 Diversifizierung der Abfrage
Um eine maximale räumliche Abdeckung der Szene durch trainierbare Abfragen zu gewährleisten, führen wir einen Diversitätsverlust ein, der dazu dient, Abfragen von ihren Nachbarn „weg drängt“:
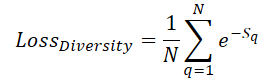
Hier bezeichnet Sq die Entfernung zur Anfrage q. Wenn S=0 ist, ist der Verlust natürlich gleich 1. Wenn der durchschnittliche Abstand zwischen den Abfragen zunimmt, tendiert der Verlust gegen 0. Folglich wird das Modell beim Training die Abfragen gleichmäßiger verteilen.
Unser Schwerpunkt liegt jedoch nicht auf dem Wert des Verlustes selbst, sondern auf der Richtung des Gradienten, der die Abfrageparameter so anpasst, dass sie möglichst weit voneinander entfernt sind. In unserer Implementierung berechnen wir sofort den Fehlergradienten und fügen ihn dem Haupt-Backpropagation-Flow hinzu, sodass die Parameter entsprechend optimiert werden können. Dieser Algorithmus ist im Kernel DiversityLoss implementiert.
Dieser Kernel benötigt zwei globale Datenpuffer und zwei skalare Variablen als Parameter. Der erste Puffer enthält die aktuellen Abfragemerkmale, und der zweite Puffer speichert die berechneten Gradienten des Diversitätsverlustes.
__kernel void DiversityLoss(__global const float *data, __global float *grad, const int activation, const int add ) { const size_t main = get_global_id(0); const size_t slave = get_local_id(1); const size_t dim = get_local_id(2); const size_t total = get_local_size(1); const size_t dimension = get_local_size(2);
Unser Kernel wird in einem dreidimensionalen Arbeitsraum arbeiten. Die ersten beiden Dimensionen entsprechen der Anzahl der zu analysierenden Abfragen, während die dritte Dimension die Größe des Merkmalsvektors für jede Abfrage darstellt. Um den Zugriff auf den langsameren, globalen Speicher zu minimieren, gruppieren wir Threads in Arbeitsgruppen entlang der letzten beiden Dimensionen des Aufgabenraums.
Innerhalb des Kernelkörpers beginnen wir wie üblich mit der Identifizierung des aktuellen Threads in allen drei Dimensionen des globalen Aufgabenraums. Als Nächstes deklarieren wir ein lokales Speicherarray, um die gemeinsame Nutzung von Daten durch die Threads innerhalb einer Arbeitsgruppe zu erleichtern.
__local float Temp[LOCAL_ARRAY_SIZE];
Wir bestimmen auch den Offset in den globalen Datenpuffern zu den analysierten Werten.
const int shift_main = main * dimension + dim; const int shift_slave = slave * dimension + dim;
Danach laden wir die Werte aus den globalen Datenpuffern und ermitteln die Abweichung zwischen ihnen.
const int value_main = data[shift_main]; const int value_slave = data[shift_slave]; float delt = value_main - value_slave;
Beachten Sie, dass der Aufgabenbereich und die Arbeitsgruppen so organisiert sind, dass jeder Thread nur 2 Werte aus dem globalen Speicher liest. Als Nächstes müssen wir die Summe der Entfernungen von allen Strömen erfassen. Zu diesem Zweck organisieren wir zunächst eine Schleife, um die Summe der einzelnen Werte in den Elementen des lokalen Arrays zu sammeln.
for(int d = 0; d < dimension; d++) { for(int i = 0; i < total; i += LOCAL_ARRAY_SIZE) { if(d == dim) { if(i <= slave && (i + LOCAL_ARRAY_SIZE) > slave) { int k = i % LOCAL_ARRAY_SIZE; float val = pow(delt, 2.0f) / total; if(isinf(val) || isnan(val)) val = 0; Temp[k] = ((d == 0 && i == 0) ? 0 : Temp[k]) + val; } } barrier(CLK_LOCAL_MEM_FENCE); } }
Es ist erwähnenswert, dass wir zunächst die einfache Differenz zwischen zwei Werten in einer Variablen namens delt speichern. Erst kurz vor dem Hinzufügen der Entfernung zum lokalen Array wird dieser Wert quadriert. Dies ist eine bewusste Entscheidung: Die Ableitung unserer Verlustfunktion beinhaltet die Rohdifferenz selbst. Wir bewahren sie also in ihrer ursprünglichen Form, um spätere redundante Neuberechnungen zu vermeiden.
Im nächsten Schritt addieren wir die Summe aller Werte in unserem lokalen Array.
const int ls = min((int)total, (int)LOCAL_ARRAY_SIZE); int count = ls; do { count = (count + 1) / 2; if(slave < count) { Temp[slave] += ((slave + count) < ls ? Temp[slave + count] : 0); if(slave + count < ls) Temp[slave + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Erst dann berechnen wir den Wert des Diversifikationsfehlers der analysierten Abfrage und den Fehlergradienten des entsprechenden Elements.
float loss = exp(-Temp[0]); float gr = 2 * pow(loss, 2.0f) * delt / total; if(isnan(gr) || isinf(gr)) gr = 0;
Danach haben wir einen spannenden Weg vor uns: die Erfassung von Fehlergradienten in Bezug auf einzelne Merkmale der analysierten Abfrage. Der Algorithmus für die Summierung der Fehlergradienten ähnelt dem oben beschriebenen für die Summierung der Abstände.
for(int d = 0; d < dimension; d++) { for(int i = 0; i < total; i += LOCAL_ARRAY_SIZE) { if(d == dim) { if(i <= slave && (i + LOCAL_ARRAY_SIZE) > slave) { int k = i % LOCAL_ARRAY_SIZE; Temp[k] = ((d == 0 && i == 0) ? 0 : Temp[k]) + gr; } } barrier(CLK_LOCAL_MEM_FENCE); } //--- int count = ls; do { count = (count + 1) / 2; if(slave < count && d == dim) { Temp[slave] += ((slave + count) < ls ? Temp[slave + count] : 0); if(slave + count < ls) Temp[slave + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1); if(slave == 0 && d == dim) { if(isnan(Temp[0]) || isinf(Temp[0])) Temp[0] = 0; if(add > 0) grad[shift_main] += Deactivation(Temp[0],value_main,activation); else grad[shift_main] = Deactivation(Temp[0],value_main,activation); } barrier(CLK_LOCAL_MEM_FENCE); } }
Es ist wichtig zu beachten, dass der oben beschriebene Algorithmus die Iterationen sowohl des Vorwärts- als auch des Rückwärtsdurchlaufs kombiniert. Diese Integration ermöglicht es uns, den Algorithmus ausschließlich während des Modelltrainings zu verwenden und diese Operationen während der Inferenz zu eliminieren. Diese Optimierung wirkt sich somit positiv auf die Entscheidungszeit in Produktionsszenarien aus.
Damit schließen wir unsere Arbeit am OpenCL-Programm ab und gehen zur Konstruktion der Klasse über, die die Kernideen der Methode von 3D-GRES implementieren wird.
2.2 Die Methodenklasse 3D-GRES
Um die in der 3D-GRES-Methode vorgeschlagenen Ansätze zu implementieren, erstellen wir ein neues Objekt im Hauptprogramm: CNeuronGRES. Wie bereits erwähnt, wird die Kernfunktionalität von der CNeuronMAFT Klasse abgeleitet. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronGRES : public CNeuronMAFT { protected: CLayer cReference; CLayer cRefKey; CLayer cRefValue; CLayer cMHRefAttentionOut; CLayer cRefAttentionOut; //--- virtual bool CreateBuffers(void); virtual bool DiversityLoss(CNeuronBaseOCL *neuron, const int units, const int dimension, const bool add = false); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; public: CNeuronGRES(void) {}; ~CNeuronGRES(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint window_sp, uint units_sp, uint heads_sp, uint ref_size, uint layers, uint layers_to_sp, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronGRES; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Neben der Kernfunktionalität erben wir auch eine breite Palette interner Objekte von der übergeordneten Klasse, die die meisten unserer Anforderungen abdecken werden. Die meisten, aber nicht alle. Um den verbleibenden Bedarf zu decken, führen wir zusätzliche Objekte für den Umgang mit verweisenden Ausdrücken ein. Alle Objekte in dieser Klasse sind als statisch deklariert, sodass wir sowohl den Konstruktor als auch den Destruktor leer lassen können. Die Initialisierung aller deklarierten und geerbten Komponenten erfolgt in der Init-Methode, die die wichtigsten Konstanten erhält, die zur eindeutigen Definition der Architektur des konstruierten Objekts erforderlich sind.
bool CNeuronGRES::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint window_sp, uint units_sp, uint heads_sp, uint ref_size, uint layers, uint layers_to_sp, ENUM_OPTIMIZATION optimization_type, uint batch ) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
Leider unterscheidet sich die Struktur unserer neuen Klasse erheblich von der übergeordneten Klasse, was die vollständige Wiederverwendung aller geerbten Methoden verhindert. Dies spiegelt sich auch in der Logik der Initialisierungsmethode wider. Hier müssen wir nicht nur die hinzugefügten, sondern auch die geerbten Komponenten manuell initialisieren.
Im Hauptteil der Methode Init wird zunächst die gleichnamige Initialisierungsmethode der Basisklasse aufgerufen, die die anfängliche Validierung der Eingabeparameter durchführt und die Datenaustauschschnittstellen zwischen den neuronalen Schichten für den Modellbetrieb aktiviert.
Danach speichern wir die erhaltenen Parameter in den internen Variablen unserer Klasse.
iWindow = window; iUnits = units_count; iHeads = heads; iSPUnits = units_sp; iSPWindow = window_sp; iSPHeads = heads_sp; iWindowKey = window_key; iLayers = MathMax(layers, 1); iLayersSP = MathMax(layers_to_sp, 1);
Hier werden wir auch mehrere Variablen für die temporäre Speicherung von Zeigern auf Objekte verschiedener neuronaler Schichten deklarieren, die wir innerhalb unserer Methode initialisieren werden.
CNeuronBaseOCL *base = NULL; CNeuronTransposeOCL *transp = NULL; CNeuronConvOCL *conv = NULL; CNeuronLearnabledPE *pe = NULL;
Als Nächstes gehen wir zur Konstruktion der trainierbaren Abfragegenerierungsmodule über. Es sei daran erinnert, dass die Autoren von 3D-GRES vorgeschlagen haben, dynamische Abfragen auf der Grundlage der eingegebenen Punktwolke zu erstellen. Die analysierte Punktwolke kann sich jedoch von der Menge der trainierbaren Abfragen sowohl in der Anzahl der Elemente als auch in der Dimensionalität der Merkmalsvektoren pro Element unterscheiden. Wir gehen diese Herausforderung in zwei Schritten an. Zunächst transponieren wir den ursprünglichen Datentensor und verwenden eine Faltungsschicht, um die Anzahl der Elemente in der Sequenz zu ändern. Die Verwendung einer Faltungsschicht ermöglicht es uns, diese Operation innerhalb unabhängiger univariater Sequenzen durchzuführen.
//--- Init Querys cQuery.Clear(); transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, 0, OpenCL, iSPUnits, iSPWindow, optimization, iBatch) || !cQuery.Add(transp)) return false; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, 1, OpenCL, iSPUnits, iSPUnits, iUnits, 1, iSPWindow, optimization, iBatch) || !cQuery.Add(conv)) return false; conv.SetActivationFunction(SIGMOID);
In der zweiten Stufe führen wir die inverse Transposition des Tensors durch und projizieren ihn in den multimodalen Raum.
transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, 2, OpenCL, iSPWindow, iUnits, optimization, iBatch) || !cQuery.Add(transp)) return false; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, 3, OpenCL, iSPWindow, iSPWindow, iWindow, iUnits, 1, optimization, iBatch) || !cQuery.Add(conv)) return false; conv.SetActivationFunction(SIGMOID);
Jetzt müssen wir nur noch eine vollständig trainierbare Positionskodierung hinzufügen.
pe = new CNeuronLearnabledPE(); if(!pe || !pe.Init(0, 4, OpenCL, iWindow * iUnits, optimization, iBatch) || !cQuery.Add(pe)) return false;
Ähnlich wie beim Algorithmus der übergeordneten Klasse werden wir die Positionskodierungsdaten von Anfragen in einem separaten Informationsfluss unterbringen.
base = new CNeuronBaseOCL(); if(!base || !base.Init(0, 5, OpenCL, pe.Neurons(), optimization, iBatch) || !base.SetOutput(pe.GetPE()) || !cQPosition.Add(base)) return false;
Der Algorithmus zur Erzeugung der Modellarchitektur der Superpoints wurde vollständig und ohne Änderungen von der übergeordneten Klasse übernommen.
//--- Init SuperPoints int layer_id = 6; cSuperPoints.Clear(); for(int r = 0; r < 4; r++) { if(iSPUnits % 2 == 0) { iSPUnits /= 2; CResidualConv *residual = new CResidualConv(); if(!residual || !residual.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPUnits, optimization, iBatch) || !cSuperPoints.Add(residual)) return false; } else { iSPUnits--; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPWindow, iSPUnits, 1, optimization, iBatch) || !cSuperPoints.Add(conv)) return false; conv.SetActivationFunction(SIGMOID); } layer_id++; } conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iSPWindow, iSPWindow, iWindow, iSPUnits, 1, optimization, iBatch) || !cSuperPoints.Add(conv)) return false; conv.SetActivationFunction(SIGMOID); layer_id++; pe = new CNeuronLearnabledPE(); if(!pe || !pe.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch) || !cSuperPoints.Add(pe)) return false; layer_id++;
Und um die Einbettung des verweisenden Ausdrucks zu generieren, verwenden wir einen vollständig verknüpften MLP mit einer zusätzlichen Positionskodierungsschicht.
//--- Reference cReference.Clear(); base = new CNeuronBaseOCL(); if(!base || !base.Init(iWindow * iUnits, layer_id, OpenCL, ref_size, optimization, iBatch) || !cReference.Add(base)) return false; layer_id++; base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch) || !cReference.Add(base)) return false; base.SetActivationFunction(SIGMOID); layer_id++; pe = new CNeuronLearnabledPE(); if(!pe || !pe.Init(0, layer_id, OpenCL, base.Neurons(), optimization, iBatch) || !cReference.Add(pe)) return false; layer_id++;
Es ist wichtig zu beachten, dass die Ausgabe des MLP einen Tensor erzeugt, der dimensional an den trainierbaren Abfragesensor angepasst ist. Diese Konstruktion ermöglicht es uns, den verweisenden Ausdruck in mehrere semantische Komponenten zu zerlegen, was eine umfassendere Analyse der aktuellen Marktsituation ermöglicht.
Die Initialisierung der Objekte, die für die primäre Verarbeitung der Eingabedaten zuständig sind, ist damit abgeschlossen. Als Nächstes gehen wir zur Initialisierungsschleife für die internen Objekte der neuronalen Schicht über. Zuvor werden jedoch die internen Arrays der Objektsammlung gelöscht, um eine saubere Einrichtung zu gewährleisten.
//--- Inside layers cQKey.Clear(); cQValue.Clear(); cSPKey.Clear(); cSPValue.Clear(); cSelfAttentionOut.Clear(); cCrossAttentionOut.Clear(); cMHCrossAttentionOut.Clear(); cMHSelfAttentionOut.Clear(); cMHRefAttentionOut.Clear(); cRefAttentionOut.Clear(); cRefKey.Clear(); cRefValue.Clear(); cResidual.Clear(); for(uint l = 0; l < iLayers; l++) { //--- Cross-Attention //--- Query conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1,optimization, iBatch) || !cQuery.Add(conv)) return false; layer_id++;
Im Schleifenkörper wird zunächst die Kreuzaufmerksamkeit der Query-Superpoint-Objekte initialisiert. Hier erstellen wir ein Objekt zur Generierung der Query-Entität für den Aufmerksamkeitsblock. Und dann fügen wir, falls erforderlich, Objekte für die Erzeugung der Entitäten vonKey und Value hinzu.
if(l % iLayersSP == 0) { //--- Key conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1, optimization, iBatch) || !cSPKey.Add(conv)) return false; layer_id++; //--- Value conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1, optimization, iBatch) || !cSPValue.Add(conv)) return false; layer_id++; }
Wir fügen eine Ebene hinzu, um die Ergebnisse der mehrköpfigen Aufmerksamkeit zu erfassen.
//--- Multy-Heads Attention Out base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cMHCrossAttentionOut.Add(base)) return false; layer_id++;
Und eine Skalierungsebene des Ergebnisses.
//--- Cross-Attention Out conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1, optimization, iBatch) || !cCrossAttentionOut.Add(conv)) return false; layer_id++;
Der Kreuzaufmerksamkeits-Block endet mit einer Schicht von Residual-Verbindungen.
//--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch) || !cResidual.Add(base)) return false; layer_id++;
Im nächsten Schritt initialisieren wir den Block der Selbstaufmerksamkeit, um die Abhängigkeiten von Query-Query zu analysieren. Hier werden alle Entitäten auf der Grundlage der Ergebnisse des vorangegangenen Kreuzaufmerksamkeits-Blocks generiert.
//--- Self-Attention //--- Query conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) || !cQuery.Add(conv)) return false; layer_id++; //--- Key conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) || !cQKey.Add(conv)) return false; layer_id++; //--- Value conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) || !cQValue.Add(conv)) return false; layer_id++;
In diesem Fall erzeugen wir für jede interne Schicht alle Entitäten mit der gleichen Anzahl von Aufmerksamkeitsköpfen.
Wir fügen eine Ebene hinzu, auf der die Ergebnisse der mehrköpfigen Aufmerksamkeit aufgezeichnet werden.
//--- Multy-Heads Attention Out base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cMHSelfAttentionOut.Add(base)) return false; layer_id++;
Und eine Skalierungsebene des Ergebnisses.
//--- Self-Attention Out conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, 1, optimization, iBatch) || !cSelfAttentionOut.Add(conv)) return false; layer_id++;
Parallel zum Selbstaufmerksamkeits-Block gibt es den Kreuzaufmerksamkeits-Block von Query zu semantisch verweisenden Ausdrücken. Die Query-Entität wird hier auf der Grundlage der Ergebnisse des vorangegangenen Kreuzaufmerksamkeits-Blocks erstellt.
//--- Reference Cross-Attention //--- Query conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) || !cQuery.Add(conv)) return false; layer_id++;
Der Tensor von Key-Value wird aus den zuvor erstellten semantischen Einbettungen gebildet.
//--- Key conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) || !cRefKey.Add(conv)) return false; layer_id++; //--- Value conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindow, iWindow, iWindowKey*iHeads, iUnits, 1, optimization, iBatch) || !cRefValue.Add(conv)) return false; layer_id++;
Ähnlich wie beim Block der Selbstaufmerksamkeit erzeugen wir alle Entitäten auf jeder neuen Ebene mit der gleichen Anzahl von Aufmerksamkeitsköpfen.
Als Nächstes fügen wir Schichten von mehrköpfigen Aufmerksamkeitsergebnissen und Ergebnisskalierung hinzu.
//--- Multy-Heads Attention Out base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cMHRefAttentionOut.Add(base)) return false; layer_id++; //--- Cross-Attention Out conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0,layer_id, OpenCL, iWindowKey*iHeads, iWindowKey*iHeads, iWindow, iUnits, 1, optimization, iBatch) || !cRefAttentionOut.Add(conv)) return false; layer_id++; if(!conv.SetGradient(((CNeuronBaseOCL*)cSelfAttentionOut[cSelfAttentionOut.Total() - 1]).getGradient(), true)) return false;
Dieser Block wird durch eine Schicht von Residuen-Verbindungen vervollständigt, die die Ergebnisse aller drei Aufmerksamkeitsblöcke kombiniert.
//--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch)) return false; if(!cResidual.Add(base)) return false; layer_id++;
Die abschließende Verarbeitung angereicherter Abfragen wird im Block von FeedForward mit Residuen-Verbindungen durchgeführt. Seine Struktur ist ähnlich wie die des reinen Transformers.
//--- Feed Forward conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, 4*iWindow, iUnits, 1, optimization, iBatch)) return false; conv.SetActivationFunction(LReLU); if(!cFeedForward.Add(conv)) return false; layer_id++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; if(!cFeedForward.Add(conv)) return false; layer_id++; //--- Residual base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch)) return false; if(!base.SetGradient(conv.getGradient())) return false; if(!cResidual.Add(base)) return false; layer_id++;
Außerdem übernehmen wir von der übergeordneten Klasse den Algorithmus zur Korrektur der Objektzentren. Beachten Sie, dass dieses Objekt von den Autoren der Methode 3D-GRES zur Verfügung gestellt wurde.
//--- Delta position conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch)) return false; conv.SetActivationFunction(SIGMOID); if(!cQPosition.Add(conv)) return false; layer_id++; base = new CNeuronBaseOCL(); if(!base || !base.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch)) return false; if(!base.SetGradient(conv.getGradient())) return false; if(!cQPosition.Add(base)) return false; layer_id++; }
Wir gehen nun zur nächsten Iteration der Schleife über, in der die Objekte der inneren Ebene erstellt werden. Nachdem alle Iterationen der Schleife erfolgreich abgeschlossen wurden, ersetzen wir die Zeiger auf die Datenpuffer, wodurch wir die Anzahl der Datenkopiervorgänge reduzieren und den Lernprozess beschleunigen können.
base = cResidual[iLayers * 3 - 1]; if(!SetGradient(base.getGradient())) return false; //--- SetOpenCL(OpenCL); //--- return true; }
Am Ende der Methodenoperationen geben wir ein boolesches Ergebnis an das aufrufende Programm zurück, das den Erfolg oder Misserfolg der ausgeführten Schritte angibt.
Es ist erwähnenswert, dass wir, genau wie in unserem vorherigen Artikel, die Erstellung von Hilfsdatenpuffern in eine separate Methode namens CreateBuffers ausgelagert haben. Ich möchte Sie ermutigen, diese Methode unabhängig zu prüfen. Der vollständige Quellcode ist im Anhang zu finden.
Nachdem das Objekt unserer neuen Klasse initialisiert wurde, fahren wir mit der Konstruktion des Algorithmus des Vorwärtsdurchlauf fort, der in der Methode feedForward implementiert ist. Diesmal nimmt die Methode zwei Zeiger auf Eingabedatenobjekte entgegen. Eine davon enthält die analysierte Punktwolke, die andere den zugehörigen Ausdruck.
bool CNeuronGRES::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) { //--- Superpoints CNeuronBaseOCL *superpoints = NeuronOCL; int total_sp = cSuperPoints.Total(); for(int i = 0; i < total_sp; i++) { if(!cSuperPoints[i] || !((CNeuronBaseOCL*)cSuperPoints[i]).FeedForward(superpoints)) return false; superpoints = cSuperPoints[i]; }
Im Hauptteil der Methode organisieren wir sofort eine Vorwärtsschleife unseres Modells zur Erzeugung kleiner Superpunkte. In ähnlicher Weise erstellen wir Abfragen.
//--- Query CNeuronBaseOCL *query = NeuronOCL; for(int i = 0; i < 5; i++) { if(!cQuery[i] || !((CNeuronBaseOCL*)cQuery[i]).FeedForward(query)) return false; query = cQuery[i]; }
Die Generierung des Tensors der semantischen Einbettungen für den verweisenden Ausdruck erfordert etwas mehr Arbeit. Der verweisende Ausdruck wird als Rohdatenpuffer empfangen. Die internen Module im Vorwärtsdurchlauf erwarten jedoch ein Objekt der neuronalen Schicht als Eingabe. Daher verwenden wir die erste Schicht des internen semantischen Einbettungsgeneratormodells als Platzhalter, um die Eingabedaten zu empfangen, ähnlich wie wir die Eingaben im Hauptmodell behandeln. In diesem Fall wird jedoch nicht der gesamte Pufferinhalt kopiert, sondern die zugrunde liegenden Datenzeiger werden durch die aus dem Puffer ersetzt.
//--- Reference CNeuronBaseOCL *reference = cReference[0]; if(!SecondInput) return false; if(reference.getOutput() != SecondInput) if(!reference.SetOutput(SecondInput, true)) return false;
Als Nächstes führen wir eine Vorwärtsschleife für das interne Modell durch.
for(int i = 1; i < cReference.Total(); i++) { if(!cReference[i] || !((CNeuronBaseOCL*)cReference[i]).FeedForward(reference)) return false; reference = cReference[i]; }
Damit ist die vorläufige Verarbeitung der Quelldaten abgeschlossen, und wir können mit dem Hauptalgorithmus zur Datendekodierung fortfahren. Zu diesem Zweck organisieren wir eine Schleife durch die internen Schichten des Decoders.
CNeuronBaseOCL *inputs = query, *key = NULL, *value = NULL, *base = NULL, *cross = NULL, *self = NULL; //--- Inside layers for(uint l = 0; l < iLayers; l++) { //--- Calc Position bias cross = cQPosition[l * 2]; if(!cross || !CalcPositionBias(cross.getOutput(), ((CNeuronLearnabledPE*)superpoints).GetPE(), cPositionBias[l], iUnits, iSPUnits, iWindow)) return false;
Wir beginnen mit der Definition der Abstandskoeffizienten der Positionen und folgen dabei dem Ansatz, der in der MAFT-Methode verwendet wird. Dies stellt eine Abweichung vom ursprünglichen Algorithmus 3D-GRES dar, bei dem die Autoren ein MLP zur Erzeugung der Aufmerksamkeitsmaske verwendeten.
Als Nächstes gehen wir zum Kreuzaufmerksamkeits-Block QSA über, der für die Modellierung der Abhängigkeiten von Query-Superpoint zuständig ist. In diesem Block erzeugen wir zunächst die Tensoren für die Entitäten Query, Key und Value. Die beiden letzteren werden nur bei Bedarf erstellt.
//--- Cross-Attention query = cQuery[l * 3 + 5]; if(!query || !query.FeedForward(inputs)) return false; key = cSPKey[l / iLayersSP]; value = cSPValue[l / iLayersSP]; if(l % iLayersSP == 0) { if(!key || !key.FeedForward(superpoints)) return false; if(!value || !value.FeedForward(cSuperPoints[total_sp - 2])) return false; }
Dann analysieren wir die Abhängigkeiten unter Berücksichtigung der Koeffizienten für die Positionsverzerrung.
if(!AttentionOut(query, key, value, cScores[l * 3], cMHCrossAttentionOut[l], cPositionBias[l], iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey, true)) return false;
Wir skalieren die Ergebnisse der mehrköpfigen Aufmerksamkeit und fügen die restlichen Verbindungswerte hinzu, gefolgt von einer Normalisierung der Daten.
base = cCrossAttentionOut[l]; if(!base || !base.FeedForward(cMHCrossAttentionOut[l])) return false; value = cResidual[l * 3]; if(!value || !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, false, 0, 0, 0, 1)|| !SumAndNormilize(cross.getOutput(), value.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1)) return false; inputs = value;
Im nächsten Schritt organisieren wir den Betrieb des Moduls QLA. Hier müssen wir einen Vorwärtsdurchlauf zwischen zwei Aufmerksamkeitsblöcken organisieren:
- Selbstaufmerksamkeit → Query-Query;
- Kreuzaufmerksamkeit → Query-Referenz.
Zunächst implementieren wir die Operationen des Selbstaufmerksamkeits-Blocks. Hier werden auf der Grundlage der vom vorangegangenen Decoder-Block erhaltenen Daten die Tensoren der Entitäten Query, Key und Value vollständig erzeugt.
//--- Self-Atention query = cQuery[l * 3 + 6]; if(!query || !query.FeedForward(inputs)) return false; key = cQKey[l]; if(!key || !key.FeedForward(inputs)) return false; value = cQValue[l]; if(!value || !value.FeedForward(inputs)) return false;
Dann analysieren wir die Abhängigkeiten im reinen, mehrköpfigen Aufmerksamkeitsmodul.
if(!AttentionOut(query, key, value, cScores[l * 3 + 1], cMHSelfAttentionOut[l], -1, iUnits, iHeads, iUnits, iHeads, iWindowKey, false)) return false; self = cSelfAttentionOut[l]; if(!self || !self.FeedForward(cMHSelfAttentionOut[l])) return false;
Danach skalieren wir die erzielten Ergebnisse.
Der Kreuzaufmerksamkeits-Block ist in ähnlicher Weise aufgebaut. Der einzige Unterschied besteht darin, dass die Entitäten Key und Value aus den semantischen Einbettungen des verweisenden Ausdrucks generiert werden.
//--- Reference Cross-Attention query = cQuery[l * 3 + 7]; if(!query || !query.FeedForward(inputs)) return false; key = cRefKey[l]; if(!key || !key.FeedForward(reference)) return false; value = cRefValue[l]; if(!value || !value.FeedForward(reference)) return false; if(!AttentionOut(query, key, value, cScores[l * 3 + 2], cMHRefAttentionOut[l], -1, iUnits, iHeads, iUnits, iHeads, iWindowKey, false)) return false; cross = cRefAttentionOut[l]; if(!cross || !cross.FeedForward(cMHRefAttentionOut[l])) return false;
Anschließend werden die Ergebnisse aller drei Aufmerksamkeitsblöcke summiert und die erhaltenen Daten normalisiert.
value = cResidual[l * 3 + 1]; if(!value || !SumAndNormilize(cross.getOutput(), self.getOutput(), value.getOutput(), iWindow, false, 0, 0, 0, 1) || !SumAndNormilize(inputs.getOutput(), value.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1)) return false; inputs = value;
Es folgt der Block FeedForward des einfachen Transformers mit Residuen-Verbindung und Datennormalisierung.
//--- Feed Forward base = cFeedForward[l * 2]; if(!base || !base.FeedForward(inputs)) return false; base = cFeedForward[l * 2 + 1]; if(!base || !base.FeedForward(cFeedForward[l * 2])) return false; value = cResidual[l * 3 + 2]; if(!value || !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1)) return false; inputs = value;
Sie haben vielleicht bemerkt, dass der konstruierte Algorithmus des Vorwärtsdurchlaufs eine Art Symbiose aus 3D-GRES und MAFT ist. Bleibt noch der letzte Schliff der Methode MAFT - die Anpassung der Abfragepositionen.
//--- Delta Query position base = cQPosition[l * 2 + 1]; if(!base || !base.FeedForward(inputs)) return false; value = cQPosition[(l + 1) * 2]; query = cQPosition[l * 2]; if(!value || !SumAndNormilize(query.getOutput(), base.getOutput(), value.getOutput(), iWindow, false, 0, 0, 0,0.5f)) return false; }
Danach geht es weiter zur nächsten Decoderschicht. Nach Abschluss der Iterationen durch alle internen Schichten des Decoders fassen wir die angereicherten Abfragewerte mit ihrer Positionskodierung zusammen. Wir übergeben die Ergebnisse über grundlegende Schnittstellen an die nächste Schicht unseres Modells.
value = cQPosition[iLayers * 2]; if(!value || !SumAndNormilize(inputs.getOutput(), value.getOutput(), Output, iWindow, true, 0, 0, 0, 1)) return false; //--- return true; }
An dieser Stelle geben wir einfach ein boolesches Ergebnis an das aufrufende Programm zurück, das angibt, ob die Operationen erfolgreich abgeschlossen wurden.
Damit schließen wir die Implementierung der Methoden der Vorwärtsdurchläufe ab und gehen zum Algorithmus des Rückwärtsdurchlauf über. Wie üblich ist dieser Prozess in zwei Phasen unterteilt:
- Gradientenverteilung (calcInputGradients);
- Optimierung der Modellparameter (updateInputWeights).
In der ersten Phase folgen wir den Operationen des Vorwärtsdurchlaufs in umgekehrter Reihenfolge, um die Fehlergradienten rückwärts zu verteilen. In der zweiten Stufe rufen wir die entsprechenden Aktualisierungsmethoden der internen Schichten auf, die trainierbare Parameter enthalten. Auf den ersten Blick sieht das ziemlich normal aus. Es gibt jedoch ein besonderes Detail im Zusammenhang mit der Diversifizierung von Abfragen. Betrachten wir daher die Implementierung der Methode calcInputGradients genauer, da sie für die Verteilung der Fehlergradienten zuständig ist.
Diese Methode erhält als die Parameter Zeiger auf drei Datenobjekte sowie eine Konstante, die die Aktivierungsfunktion für die zweite Eingabequelle angibt.
bool CNeuronGRES::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1) { if(!NeuronOCL || !SecondGradient) return false;
Im Hauptteil der Methode werden nur zwei der Zeiger validiert. Während des Vorwärtsdurchlaufs haben wir den Zeiger auf die zweite Eingangsquelle gespeichert. Daher ist das Fehlen eines gültigen Zeigers in den Parametern in diesem Stadium für uns nicht entscheidend. Dies gilt jedoch nicht für den Puffer, der zur Speicherung der Fehlergradienten verwendet wird. Deshalb überprüfen wir ausdrücklich ihre Gültigkeit, bevor wir fortfahren.
An dieser Stelle deklarieren wir auch eine Reihe von Variablen, um temporär Zeiger auf relevante Objekte zu speichern. Damit ist die Vorbereitungsphase unserer Umsetzung abgeschlossen.
CNeuronBaseOCL *residual = GetPointer(this), *query = NULL, *key = NULL, *value = NULL, *key_sp = NULL, *value_sp = NULL, *base = NULL;
Als Nächstes organisieren wir eine Rückwärtsschleife durch die internen Schichten des Decoders.
//--- Inside layers for(int l = (int)iLayers - 1; l >= 0; l--) { //--- Feed Forward base = cFeedForward[l * 2]; if(!base || !base.calcHiddenGradients(cFeedForward[l * 2 + 1])) return false; base = cResidual[l * 3 + 1]; if(!base || !base.calcHiddenGradients(cFeedForward[l * 2])) return false;
Dank der gut durchdachten Ersetzung von Pufferzeigern innerhalb interner Objekte vermeiden wir unnötige Datenkopiervorgänge und beginnen mit der Weitergabe des Fehlergradienten durch den FeedForward-Block.
Der auf der Eingangsebene des FeedForward-Blocks ermittelte Fehlergradient wird mit den entsprechenden Werten auf der Ausgangsebene unserer Klasse summiert, die mit dem Residuen-Datenfluss in diesem Block übereinstimmt. Das Ergebnis dieser Operationen wird dann an den Ergebnispuffer des Selbstaufmerksamkeits-Blocks übergeben.
//--- Residual value = cSelfAttentionOut[l]; if(!value || !SumAndNormilize(base.getGradient(), residual.getGradient(), value.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; residual = value;
Die Eingabe für den FeedForward-Block bestand aus der Summe der Ausgaben von drei Aufmerksamkeitsblöcken. Dementsprechend muss der resultierende Fehlergradient auf alle Quellen zurückgeführt werden. Bei der Summierung der Daten wird der gesamte Gradient auf jede Komponente übertragen. Die Ausgänge des QSA-Blocks wurden auch als Eingänge für andere Module innerhalb unseres Decoders verwendet. Daher werden wir seinen Fehlergradienten später sammeln, ähnlich wie bei den Datenströmen der Restglieder. Um das unnötige Kopieren von Fehlergradienten in den Kreuzaufmerksamkeits-Block der Query-Reference zu vermeiden, haben wir während der Objektinitialisierung präventiv eine Zeigertausch organisiert. Wenn wir also Daten in den Selbstaufmerksamkeits-Block eingeben, geben wir gleichzeitig dieselben Daten in den Query-Reference des Kreuzaufmerksamkeits-Block ein. Diese kleine Optimierung trägt dazu bei, den Speicherverbrauch und die Trainingszeit zu reduzieren, indem redundante Operationen eliminiert werden.
Wir gehen nun dazu über, den Fehlergradienten durch den Query-Reference-Kreuzaufmerksamkeits-Block zu propagieren.
//--- Reference Cross-Attention base = cMHRefAttentionOut[l]; if(!base || !base.calcHiddenGradients(cRefAttentionOut[l], NULL)) return false; query = cQuery[l * 3 + 7]; key = cRefKey[l]; value = cRefValue[l]; if(!AttentionInsideGradients(query, key, value, cScores[l * 3 + 2], base, iUnits, iHeads, iUnits, iHeads, iWindowKey)) return false;
Wir geben den Fehlergradienten von der Query-Entität an das QSA-Modul weiter, nachdem wir ihm zuvor den Fehlergradienten aus dem FeedForward-Block (Fluss der Restglieder) hinzugefügt haben.
base = cResidual[l * 3]; if(!base || !base.calcHiddenGradients(query, NULL)) return false; value = cCrossAttentionOut[l]; if(!SumAndNormilize(base.getGradient(), residual.getGradient(),value.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; residual = value;
In ähnlicher Weise leiten wir den Fehlergradienten durch den Selbstaufmerksamkeits-Block.
//--- Self-Attention base = cMHSelfAttentionOut[l]; if(!base || !base.calcHiddenGradients(cSelfAttentionOut[l], NULL)) return false; query = cQuery[l * 3 + 6]; key = cQKey[l]; value = cQValue[l]; if(!AttentionInsideGradients(query, key, value, cScores[l * 2 + 1], base, iUnits, iHeads, iUnits, iHeads, iWindowKey)) return false;
Nun müssen wir aber den Fehlergradienten von allen drei Einheiten in das QSA-Modul einfügen. Zu diesem Zweck wird der Fehlergradient sequentiell auf die Ebene der Verbindungsschicht der Restglieder verteilt und die erhaltenen Werte werden zur zuvor akkumulierten Summe der QSA-Modulgradienten addiert.
base = cResidual[l * 3 + 1]; if(!base.calcHiddenGradients(query, NULL)) return false; if(!SumAndNormilize(base.getGradient(), residual.getGradient(), residual.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; if(!base.calcHiddenGradients(key, NULL)) return false; if(!SumAndNormilize(base.getGradient(), residual.getGradient(), residual.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; if(!base.calcHiddenGradients(value, NULL)) return false; if(!SumAndNormilize(base.getGradient(), residual.getGradient(), residual.getGradient(), iWindow, false, 0, 0, 0, 1)) return false;
Wir werden auch die Summe der akkumulierten Gradientenwerte aus der Positionskodierung von Abfragen an den parallelen Informationsfluss weitergeben und sie zu den Gradienten aus einem anderen Informationsfluss hinzufügen.
//--- Qeury position base = cQPosition[l * 2]; value = cQPosition[(l + 1) * 2]; if(!base || !SumAndNormilize(value.getGradient(), residual.getGradient(), base.getGradient(), iWindow, false, 0, 0, 0, 1)) return false;
Jetzt müssen wir nur noch den Fehlergradienten durch das QSA-Modul propagieren. Hier verwenden wir denselben Algorithmus für die Ausbreitung des Fehlergradienten durch den Aufmerksamkeitsblock, nehmen aber eine Anpassung für die Fehlergradienten der Entitäten von von Schlüssel (Key) und Wert (Value) aus mehreren Decoderschichten vor. Wir sammeln zunächst die Fehlergradienten in temporären Datenpuffern und speichern dann die resultierenden Werte in den Puffern der entsprechenden Objekte.
//--- Cross-Attention base = cMHCrossAttentionOut[l]; if(!base || !base.calcHiddenGradients(residual, NULL)) return false; query = cQuery[l * 3 + 5]; if(((l + 1) % iLayersSP) == 0 || (l + 1) == iLayers) { key_sp = cSPKey[l / iLayersSP]; value_sp = cSPValue[l / iLayersSP]; if(!key_sp || !value_sp || !cTempCrossK.Fill(0) || !cTempCrossV.Fill(0)) return false; } if(!AttentionInsideGradients(query, key_sp, value_sp, cScores[l * 2], base, iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey)) return false; if(iLayersSP > 1) { if((l % iLayersSP) == 0) { if(!SumAndNormilize(key_sp.getGradient(), GetPointer(cTempCrossK), key_sp.getGradient(), iWindowKey, false, 0, 0, 0, 1)) return false; if(!SumAndNormilize(value_sp.getGradient(), GetPointer(cTempCrossV), value_sp.getGradient(), iWindowKey, false, 0, 0, 0, 1)) return false; } else { if(!SumAndNormilize(key_sp.getGradient(), GetPointer(cTempCrossK), GetPointer(cTempCrossK), iWindowKey, false, 0, 0, 0, 1)) return false; if(!SumAndNormilize(value_sp.getGradient(), GetPointer(cTempCrossV), GetPointer(cTempCrossV), iWindowKey, false, 0, 0, 0, 1)) return false; } }
Der Fehlergradient von der Entität der Query wird auf die Ebene der Ausgangsdaten übertragen. Hier fügen wir auch Daten über den Informationsfluss von Residual-Verbindungen hinzu. Danach geht es weiter mit der nächsten Iteration der Umkehrschleife durch die Decoderschichten.
if(l == 0) base = cQuery[4]; else base = cResidual[l * 3 - 1]; if(!base || !base.calcHiddenGradients(query, NULL)) return false; //--- Residual if(!SumAndNormilize(base.getGradient(), residual.getGradient(), base.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; residual = base; }
Nachdem der Fehlergradient erfolgreich durch alle Schichten des Decoders verteilt wurde, müssen wir ihn über die Operationen des Datenvorverarbeitungsmoduls auf die Quelldatenebene übertragen. Zunächst verteilen wir den Fehlergradienten aus unseren trainierbaren Abfragen. Zu diesem Zweck wird der Fehlergradient durch eine Positionskodierungsschicht geleitet.
//--- Qeury query = cQuery[3]; if(!query || !query.calcHiddenGradients(cQuery[4])) return false;
In diesem Stadium wird der Gradient des Positionskodierungsfehlers aus dem entsprechenden Informationsfluss eingespeist.
base = cQPosition[0]; if(!DeActivation(base.getOutput(), base.getGradient(), base.getGradient(), SIGMOID) || !(((CNeuronLearnabledPE*)cQuery[4]).AddPEGradient(base.getGradient()))) return false;
Dann fügen wir den Gradienten des Abfrage-Diversifikationsfehlers hinzu, aber hier arbeiten wir bereits ohne Informationen über die Positionskodierung. Dieser Schritt wird absichtlich durchgeführt, damit der Diversifizierungsfehler die Positionskodierung nicht beeinträchtigt.
if(!DiversityLoss(query, iUnits, iWindow, true)) return false;
Dann folgt eine einfache Schleife der umgekehrten Iteration über die Schichten unseres Abfragegenerierungsmodells, wobei der Fehlergradient auf die Ebene der Eingabedaten übertragen wird.
for(int i = 2; i >= 0; i--) { query = cQuery[i]; if(!query || !query.calcHiddenGradients(cQuery[i + 1])) return false; } if(!NeuronOCL.calcHiddenGradients(query, NULL)) return false;
Dabei ist zu beachten, dass der Fehlergradient auch auf die Eingangsebene des internen Superpoint-Generierungsmodells propagiert werden muss. Um Datenverluste zu vermeiden, speichern wir einen Zeiger auf den Gradientenpuffer des Eingabedatenobjekts in einer lokalen Variablen. Dann ersetzen wir sie im Eingabedatenobjekt durch den Gradientenpuffer aus der Transpositionsebene des Abfragegenerierungsmodells.
Die Transpositionsschicht enthält keine trainierbaren Parameter, sodass der Verlust ihrer Fehlergradienten kein Risiko darstellt.
CBufferFloat *inputs_gr = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(query.getGradient(), false)) return false;
Der nächste Schritt besteht darin, den Fehlergradienten durch das Superpoint-Generierungsmodell zu propagieren. Es ist jedoch wichtig zu beachten, dass wir während des Rückwärtsdurchlaufs durch die Decoder-Schichten keinen Gradienten an dieses Modell weitergegeben haben. Daher müssen wir zunächst die Fehlergradienten aus den entsprechenden Entitäten von Key und Value sammeln. Wir wissen, dass wir mindestens einen Tensor für jede dieser Entitäten haben. Aber es gibt noch ein weiteres wichtiges Detail: Die Entität Key wurde aus der Ausgabe der letzten Schicht des Superpoint-Modells mit Positionskodierung erzeugt, während die Entität Value aus der vorletzten Schicht ohne Positionskodierung stammt. Die Fehlergradienten müssen sich also entlang dieser spezifischen Datenpfade ausbreiten.
Zu Beginn berechnen wir den Fehlergradienten für die erste Schicht der Entität Key und leiten ihn in die letzte Schicht des internen Modells ein.
//--- Superpoints //--- From Key int total_sp = cSuperPoints.Total(); CNeuronBaseOCL *superpoints = cSuperPoints[total_sp - 1]; if(!superpoints || !superpoints.calcHiddenGradients(cSPKey[0])) return false;
Dann überprüfen wir die Anzahl der Schichten der Entität Key und ersetzen gegebenenfalls die Datenpuffer, um den Verlust des zuvor erhaltenen Fehlergradienten zu verhindern.
if(cSPKey.Total() > 1) { CBufferFloat *grad = superpoints.getGradient(); if(!superpoints.SetGradient(GetPointer(cTempSP), false)) return false;
Anschließend durchlaufen wir eine Schleife durch die übrigen Schichten dieser Einheit, berechnen den Fehlergradienten und summieren dann das Ergebnis mit den zuvor akkumulierten Werten.
for(int i = 1; i < cSPKey.Total(); i++) { if(!superpoints.calcHiddenGradients(cSPKey[i]) || !SumAndNormilize(superpoints.getGradient(), grad, grad, iWindow, false, 0, 0, 0, 1)) return false; }
Nachdem alle Schleifeniterationen erfolgreich abgeschlossen wurden, geben wir einen Zeiger auf einen Puffer mit der akkumulierten Fehlergradientensumme zurück.
if(!superpoints.SetGradient(grad, false)) return false; }
Auf der letzten Ebene des Superpoint-Modells haben wir also den Fehlergradienten aus allen Ebenen der Entität Key gesammelt und können ihn nun eine Ebene unter dem angegebenen Modell weitergeben.
superpoints = cSuperPoints[total_sp - 2]; if(!superpoints || !superpoints.calcHiddenGradients(cSuperPoints[total_sp - 1])) return false;
Und nun müssen wir auf derselben Ebene den Fehlergradienten von der Entität Value erfassen. Hier verwenden wir denselben Algorithmus. Aber in diesem Fall haben wir im Fehlergradientenpuffer bereits Daten von der nachfolgenden Schicht erhalten. Deshalb ersetzen wir sofort Datenpuffer und sammeln dann in einer Schleife Informationen aus parallelen Datenströmen.
//--- From Value CBufferFloat *grad = superpoints.getGradient(); if(!superpoints.SetGradient(GetPointer(cTempSP), false)) return false; for(int i = 0; i < cSPValue.Total(); i++) { if(!superpoints.calcHiddenGradients(cSPValue[i]) || !SumAndNormilize(superpoints.getGradient(), grad, grad, iWindow, false, 0, 0, 0, 1)) return false; } if(!superpoints.SetGradient(grad, false)) return false;
Dann fügen wir noch Diversifikationsfehler hinzu, die es uns ermöglichen, die Superpunkte so weit wie möglich zu diversifizieren.
if(!DiversityLoss(superpoints, iSPUnits, iSPWindow, true)) return false;
Anschließend wird in der umgekehrten Schleife durch die Modellschichten von Superpoints der Fehlergradient auf die Ebene der Eingabedaten verteilt.
for(int i = total_sp - 3; i >= 0; i--) { superpoints = cSuperPoints[i]; if(!superpoints || !superpoints.calcHiddenGradients(cSuperPoints[i + 1])) return false; } //--- Inputs if(!NeuronOCL.calcHiddenGradients(cSuperPoints[0])) return false;
An dieser Stelle sei daran erinnert, dass wir einen Teil des Fehlergradienten auf der Eingabeebene nach der Verarbeitung des Informationsflusses der Abfrage beibehalten haben. Dabei haben wir einen Austausch von Datenpuffern vorgenommen. Und nun summieren wir den Fehlergradienten beider Informationsflüsse. Dann geben wir den Zeiger auf den Datenpuffer zurück.
if(!SumAndNormilize(NeuronOCL.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1)) return false; if(!NeuronOCL.SetGradient(inputs_gr, false)) return false;
Auf diese Weise haben wir den Fehlergradienten aus zwei Informationsflüssen für die erste Quelle von Eingangsdaten gesammelt. Wir müssen den Fehlergradienten jedoch noch auf das zweite Quelldatenobjekt übertragen. Dazu synchronisieren wir zunächst die Zeiger auf die Fehlergradientenpuffer des zweiten Quelldatenobjekts und der ersten Schicht des Referenzmodells.
base = cReference[0]; if(base.getGradient() != SecondGradient) { if(!base.SetGradient(SecondGradient)) return false; base.SetActivationFunction(SecondActivation); }
In der letzten Schicht des spezifizierten Modells wird dann der Fehlergradient aus allen Tensoren der entsprechenden Entitäten von Key und Value gesammelt. Der Algorithmus ist ähnlich wie der oben beschriebene.
base = cReference[2]; if(!base || !base.calcHiddenGradients(cRefKey[0])) return false; inputs_gr = base.getGradient(); if(!base.SetGradient(GetPointer(cTempQ), false)) return false; if(!base.calcHiddenGradients(cRefValue[0])) return false; if(!SumAndNormilize(base.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1)) return false; for(uint i = 1; i < iLayers; i++) { if(!base.calcHiddenGradients(cRefKey[i])) return false; if(!SumAndNormilize(base.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1)) return false; if(!base.calcHiddenGradients(cRefValue[i])) return false; if(!SumAndNormilize(base.getGradient(), inputs_gr, inputs_gr, 1, false, 0, 0, 0, 1)) return false; } if(!base.SetGradient(inputs_gr, false)) return false;
Wir propagieren den Fehlergradienten durch eine Positionskodierungsschicht.
base = cReference[1]; if(!base.calcHiddenGradients(cReference[2])) return false;
Und wir fügen einen Vektor-Diversifikationsfehler hinzu, um eine maximale Vielfalt der semantischen Komponenten zu gewährleisten.
if(!DiversityLoss(base, iUnits, iWindow, true)) return false;
Danach propagieren wir den Fehlergradienten auf die Ebene der Eingangsdaten.
base = cReference[0]; if(!base.calcHiddenGradients(cReference[1])) return false; //--- return true; }
Am Ende der Ausführung der Methode geben wir einfach das logische Ergebnis der Operationen an das aufrufende Programm zurück.
Damit ist unsere Untersuchung der in der neuen Klasse implementierten algorithmischen Methoden abgeschlossen. Den vollständigen Quellcode für diese Klasse und alle ihre Methoden finden Sie im Anhang. Dort finden Sie auch eine ausführliche Beschreibung der Modellarchitekturen und aller bei der Erstellung dieses Artikels verwendeten Programme.
Die Architektur der trainierbaren Modelle wurde fast vollständig aus früheren Arbeiten übernommen. Die einzige Änderung, die vorgenommen wurde, betraf eine einzelne Schicht des Encoders, die für die Beschreibung des Umweltzustands zuständig ist.
Darüber hinaus wurden die Trainingsprogramme für das Modell und die Interaktionslogik mit der Umwelt geringfügig aktualisiert. Diese Änderungen wurden vorgenommen, weil wir eine zweite Datenquelle in den Kodierer des Umweltzustands einspeisen mussten. Diese Änderungen sind jedoch gezielt und minimal. Wie bereits erwähnt, haben wir den Kontostandsvektor als Referenzausdruck verwendet. Die Vorbereitung dieses Vektors war bereits implementiert, da er von unserem Actor-Modell verwendet wurde.
3. Tests
Wir haben viel Arbeit geleistet und mit MQL5 ein hybrides System entwickelt, das die Ansätze der 3D-GRES- und MAFT-Methoden kombiniert. Nun ist es an der Zeit, die Ergebnisse zu bewerten. Unsere Aufgabe ist es, das Modell mit Hilfe der vorgeschlagenen Technologie auf realen historischen Daten zu trainieren und die Leistung der trainierten Actor-Politik zu bewerten.
Wie immer verwenden wir zum Trainieren der Modelle reale historische Daten des Instruments EURUSD mit dem Zeitrahmen H1 für das gesamte Jahr 2023. Alle Indikatorparameter wurden auf ihre Standardwerte gesetzt.
Für das Training haben wir einen Algorithmus verwendet, der bereits in früheren Studien validiert wurde.
Die trainierte Akteurs-Politik wurde im Strategietester des MetaTrader 5 mit historischen Daten vom Januar 2024 getestet. Alle anderen Parameter blieben unverändert. Die Testergebnisse sind wie folgt:
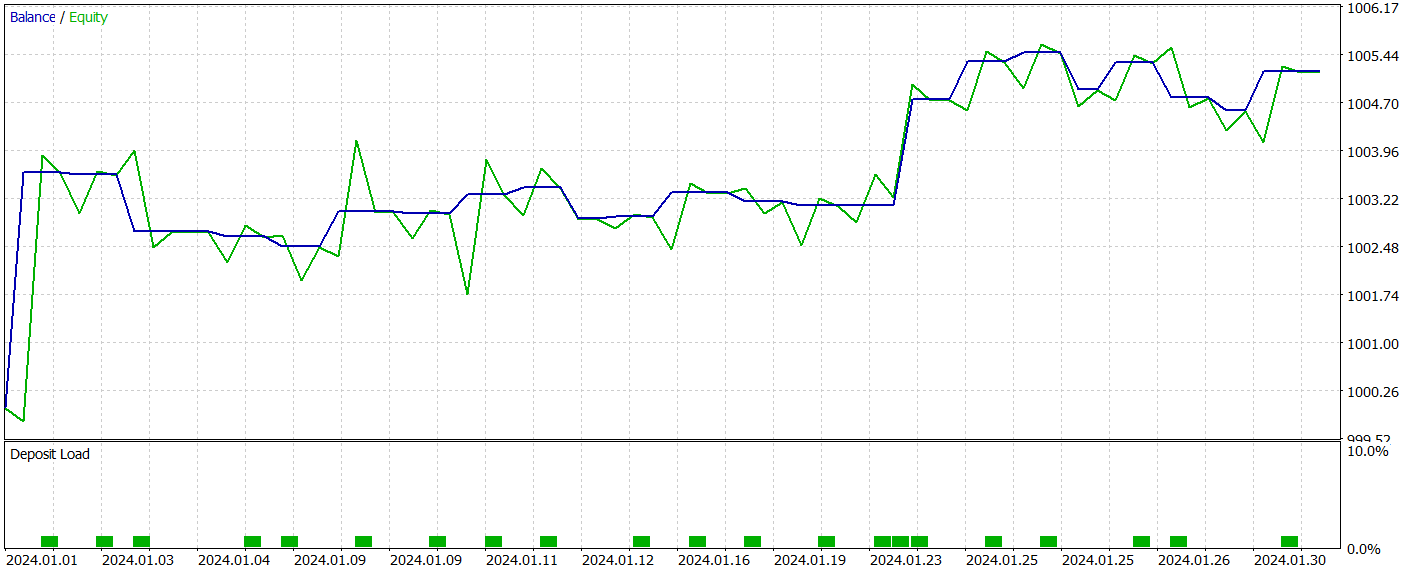

Während des Testzeitraums führte das Modell 22 Handelsgeschäfte aus, von denen genau die Hälfte mit Gewinn abgeschlossen wurde. Bemerkenswert ist, dass der durchschnittliche Gewinn pro Gewinngeschäft mehr als doppelt so hoch war wie der durchschnittliche Verlust pro Verlustgeschäft. Der größte Gewinn überstieg den größten Verlust um das Vierfache. Im Ergebnis erreichte das Modell einen Gewinnfaktor von 2,63. Aufgrund der geringen Anzahl von Handelsgeschäften und des kurzen Testzeitraums lassen sich jedoch keine endgültigen Schlussfolgerungen über die langfristige Wirksamkeit der Methode ziehen. Bevor das Modell in einer realen Umgebung eingesetzt wird, sollte es auf einem längeren historischen Datensatz trainiert und einem umfassenden Test unterzogen werden.
Schlussfolgerung
Die in der Methode Generalized 3D Referring Expression Segmentation (3D-GRES) vorgeschlagenen Ansätze zeigen eine vielversprechende Anwendbarkeit im Bereich des Handels, indem sie eine tiefere Analyse von Marktdaten ermöglichen. Diese Methode kann für die Segmentierung und Analyse mehrerer Marktsignale angepasst werden, was zu präziseren Interpretationen komplexer Marktbedingungen führt und letztlich die Vorhersagegenauigkeit und Entscheidungsfindung verbessert.
Im praktischen Teil dieses Artikels haben wir unsere Vision der vorgeschlagenen Ansätze mit MQL5 umgesetzt. Unsere Experimente zeigen das Potenzial der vorgeschlagenen Lösungen für den Einsatz in realen Handelsszenarien.
Referenzen
Programme, die im diesem Artikel verwendet werden| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA zum Sammeln von Beispielen |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | Test.mq5 | Expert Advisor | Modelltraining EA |
| 5 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 6 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 7 | NeuroNet.cl | Bibliothek | OpenCL-Programmcode-Bibliothek |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15997
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Entwicklung eines Replay-Systems (Teil 69): Das richtige Bestimmen der Zeit (II)
Entwicklung eines Replay-Systems (Teil 69): Das richtige Bestimmen der Zeit (II)
 Von der Grundstufe bis zur Mittelstufe: Arrays und Zeichenketten (III)
Von der Grundstufe bis zur Mittelstufe: Arrays und Zeichenketten (III)
 Neuronale Netze im Handel: Kontrollierte Segmentierung (letzter Teil)
Neuronale Netze im Handel: Kontrollierte Segmentierung (letzter Teil)
 Entwicklung eines Replay-Systems (Teil 68): Das richtige Bestimmen der Zeit (I)
Entwicklung eines Replay-Systems (Teil 68): Das richtige Bestimmen der Zeit (I)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.