Neuronale Netze im Handel: Maskenfreier Ansatz zur Vorhersage von Preisentwicklungen

MetaTrader 5 — Handelssysteme | 21 Mai 2025, 14:24

Einführung

Wir setzen unsere Erkundung mit der Methode der Punktwolkenverarbeitung fort. Im vorigen Artikel haben wir die Methode SPFormer vorgestellt. Die Autoren entwickelten einen umfassenden Algorithmus auf der Grundlage der Architektur des Transformers. Mehrere Schichten des Transformer-Decoders verwenden eine feste Anzahl von Objektabfragen, die eine iterative Verarbeitung von globalen Merkmalen und eine direkte Objektvorhersage ermöglichen. Der SPFormer benötigt keine Nachbearbeitung, um Duplikate zu eliminieren, da während des Trainings eine Strategie zum Abgleich einer Eins-zu-Eins-Bipartite angewendet wird. Darüber hinaus werden die in der letzten Ebene erzeugten Objektmasken zur Lenkung der Kreuzaufmerksamkeit verwendet.

Allerdings weisen die Autoren der Studie „Mask-Attention-Free Transformer for 3D Instance Segmentation“ darauf hin, dass aktuelle Methoden aus der Basis eines Transformers unter langsamer Konvergenz leiden. Bei der Analyse der Basismethode wurde festgestellt, dass dieses Problem möglicherweise auf die geringe Qualität der ursprünglichen Masken zurückzuführen ist. Konkret werden die anfänglichen Objektmasken generiert, indem die Ähnlichkeit zwischen anfänglichen Objektabfragen und punktuellen Maskenmerkmalen abgebildet wird. Qualitativ minderwertige Ausgangsmasken erhöhen die Komplexität des Trainings und verlangsamen so die Konvergenz.

Um die geringe Vollständigkeit der anfänglichen Masken zu beheben, schlagen die Autoren einen neuartigen Algorithmus vor, den „Mask-Attention-Free Transformer“ (MATF), der auf das Design der Maskenaufmerksamkeit verzichtet und stattdessen eine zusätzliche zentrale Regressionsaufgabe zur Steuerung der Kreuzaufmerksamkeit einführt. Um eine Zentrumsregression zu ermöglichen, haben die Autoren eine Reihe von Komponenten entwickelt, die die Position der Punkte berücksichtigen. Zunächst fügen sie eine Reihe von erlernbaren Positionsabfragen hinzu, die jeweils die Position einer entsprechenden Inhaltsabfrage darstellen. Diese Abfragepositionen sind dicht über den Lernraum verteilt. Außerdem wird eine Einschränkung eingeführt, um sicherzustellen, dass sich jede Abfrage auf ihre lokale Region konzentriert. Infolgedessen können Abfragen Objekte in der Szene mit höherer Unterscheidungskraft effektiv erfassen, was für die Reduzierung der Trainingskomplexität und die Beschleunigung der Konvergenz entscheidend ist.

Darüber hinaus schlagen die Autoren von MATF eine kontextbezogene Kodierung der relativen Position für Kreuzaufmerksamkeit vor. Im Vergleich zur Aufmerksamkeitsmaske, die in früheren Arbeiten verwendet wurde, ist diese Lösung flexibler, da die Aufmerksamkeitsgewichte auf der Grundlage der relativen Positionen und nicht auf der Grundlage einer starren Maske angepasst werden. Die Abfragepositionen werden iterativ aktualisiert, um genauere Darstellungen zu erhalten.

Die in dem Papier vorgestellten experimentellen Ergebnisse zeigen, dass MATF bei verschiedenen Datensätzen eine überragende Leistung erbringt.

1. Der MATF-Algorithmus

Der SPFormer-Algorithmus stellt eine vollständige Ende-zu-Ende-Pipeline dar, mit der Objektabfragen direkt Instanzvorhersagen erzeugen können. Mit Hilfe von Transformer-Decodern werden durch eine feste Anzahl von Objektabfragen globale Objektinformationen aus der analysierten Punktwolke aggregiert. Darüber hinaus nutzt SPFormer Objektmasken, um die Kreuzaufmerksamkeit zu steuern, sodass die Abfragen nur auf maskierte Merkmale ausgerichtet sind. In der Anfangsphase der Ausbildung sind diese Masken jedoch von geringer Qualität. Dies beeinträchtigt die Leistung in den nachfolgenden Schichten und erhöht die Gesamtkomplexität des Trainings.

Um dieses Problem zu lösen, führen die Autoren der Methode MAFT eine Hilfsaufgabe zur Zentrumsregression ein, um die Segmentierung der Instanzen zu steuern. Zunächst werden globale Positionen 𝒫 aus der Rohpunktwolke ausgewählt und globale Objektmerkmale ℱ über ein Backbone-Netzwerk extrahiert. Dies können Voxel oder Superpunkte sein. Zusätzlich zu den Inhaltsabfragen 𝒬0c führen die Autoren von MAFT eine feste Anzahl von Positionsabfragen 𝒬0p ein, die normalisierte Objektzentren darstellen. Während 𝒬0p zufällig initialisiert wird, beginnt 𝒬0c mit Nullwerten. Das Hauptziel besteht darin, dass die Positionsabfragen die entsprechenden kontextuellen Abfragen bei der Kreuzaufmerksamkeit leiten, gefolgt von einer iterativen Verfeinerung beider Abfragesätze, um Objektzentren, Klassen und Masken vorherzusagen.

Um die Aufgabe der Regression des Objektzentrums effektiv zu lösen und die Erstellung der anfänglichen Objektmasken zu verbessern, schlagen die Autoren von MAFT eine Reihe von architektonischen Komponenten vor, die die Punktpositionen berücksichtigen.

Im Gegensatz zu früheren Ansätzen wird ein zusätzlicher Satz von Positionsabfragen 𝒬0p eingeführt. Da die Punktbereiche in verschiedenen Szenen stark variieren, werden die anfänglichen Positionsabfragen in normalisierter Form als lernbare Parameter gespeichert, gefolgt von einer Sigmoid-Aktivierungsfunktion.

Es ist bemerkenswert, dass diese anfänglichen Positionsabfragen dicht über den Zielraum verteilt sind. Außerdem aggregiert jede Abfrage Objekte aus der entsprechenden lokalen Region. Dieses Design erleichtert die Fähigkeit der anfänglichen Abfragen, Szenenobjekte mit hoher Wiedererkennung zu erfassen. Damit wird das Problem der geringen Einprägsamkeit gelöst, das durch die schlechte Qualität der anfänglichen Instanzmasken verursacht wird, und die Komplexität des Trainings in den nachfolgenden Schichten verringert.

Zusätzlich zur absoluten Positionskodierung verwendet MAFT eine kontextbezogene relative Positionskodierung im Kreuzaufmerksamkeit-Mechanismus. Um dies zu erreichen, werden die relativen Positionen 𝐫 zwischen den Positionsabfragen 𝒬tp und globalen Positionen 𝒫 werden zunächst berechnet und dann in diskrete ganze Zahlen 𝐫' quantisiert. Diese diskreten relativen Positionen werden als Indizes verwendet, um die entsprechenden Werte aus einer Positionskodierungstabelle abzurufen.

Anschließend wird die relative Positionskodierung 𝐟pos mit der Query 𝐟q oder den Merkmalen von Key 𝐟k im Kreuzaufmerksamkeits-Modul multipliziert. Das Ergebnis wird dann zu den Gewichten der Kreuzaufmerksamkeit addiert, gefolgt von einer Softmax-Funktion.

Es ist erwähnenswert, dass die relative Positionskodierung im Vergleich zur maskierten Aufmerksamkeit mehr Flexibilität und Robustheit gegenüber Fehlern bietet. Sie funktioniert im Wesentlichen wie eine weiche Maske, die die Aufmerksamkeitsgewichtung flexibel anpasst, anstatt eine starre Maskierung vorzunehmen. Ein weiterer Vorteil ist, dass semantische Informationen integriert werden und der lokale Kontext selektiv erfasst werden kann. Dies wird durch die Interaktion zwischen relativen Positionen und semantischen Merkmalen erreicht.

Da die kontextbezogenen Abfragen in den Decoderschichten ständig aktualisiert werden, ist die Beibehaltung fester Positionsabfragen während der gesamten Dekodierung suboptimal. Da die anfänglichen Positionsabfragen statisch sind, ist es von Vorteil, sie in den nachfolgenden Schichten an die spezifische Eingangsszene anzupassen. Um dies zu erreichen, verfeinern die Autoren iterativ die Positionsabfragen auf der Grundlage der Inhaltsabfragen. Konkret wird ein MLP zur Vorhersage des mittleren Versatzes Δpt aus der aktualisierten, kontextuellen Abfrage 𝒬t+1c. Dieser Versatz wird dann zur vorherigen Positionsabfrage 𝒬tp addiert.

Die ursprüngliche Visualisierung der Methode MAFT aus dem oben genannten Artikel ist unten dargestellt.

2. Die Implementation in MQL5

Nachdem wir die theoretischen Grundlagen der Methode Mask-Attention-Free Transformer untersucht haben, gehen wir nun zum praktischen Teil unseres Artikels über, in dem wir unsere Interpretation der vorgeschlagenen Ansätze mit MQL5 umsetzen. Wir beginnen mit der Erweiterung des OpenCL-Programms.

2.1 Erweitern des OpenCL-Programms

Wir beginnen mit der Konstruktion des Algorithmus für die relative Positionskodierung. Einerseits ist der Algorithmus relativ einfach. Wir müssen nur den Abstand zwischen zwei Punkten berechnen. Außerdem berechnen die Autoren den Abstand entlang jeder Koordinatenachse einzeln. Andererseits führen die Autoren von MAFT eine Quantisierung der resultierenden Offsets durch, die dann zur Indizierung einer lernfähigen Parametertabelle verwendet werden. Wir haben uns für eine leichte Optimierung der ursprünglichen Lösung entschieden. Unsere Implementierung basiert auf der Annahme, dass der größte Einfluss von Punkten ausgeht, die sich in unmittelbarer Nähe der zu analysierenden Anfrage befinden. Dieser Logik folgend, berechnen wir zunächst den Abstand S zwischen zwei Punkten in einem N-dimensionalen Raum. Dann berechnen wir den Positionskoeffizienten kpb nach der folgenden Formel:

Es ist klar, dass der Abstand zwischen zwei beliebigen Punkten immer größer oder gleich 0 ist. Wenn die Punkte übereinstimmen, ist der Koeffizient gleich 1. Mit zunehmender Entfernung nähert sich der relative Positionskodierungskoeffizient dem Wert 0.

Die Implementierung des vorgeschlagenen Algorithmus ist in CalcPositionBias enthalten. Die Parameter enthalten Zeiger auf drei globale Datenpuffer: 2 davon enthalten die Eingabedaten. Der dritte ist für die Speicherung der Ergebnisse vorgesehen. Zusätzlich geben wir die Dimensionalität des Merkmalsvektors für ein einzelnes Element an.

Um den Abstand zwischen zwei Vektoren korrekt zu berechnen, müssen sie auf denselben Unterraum projiziert werden. Dies bedeutet, dass die Merkmalsvektoren in beiden Eingabetensoren die gleiche Dimensionalität haben müssen.

__kernel void CalcPositionBias(__global const float *data1,
                               __global const float *data2,
                               __global float *result,
                               const int dimension
                              )
  {
   const size_t idx1 = get_global_id(0);
   const size_t idx2 = get_global_id(1);
   const size_t total1 = get_global_size(0);
   const size_t total2 = get_global_size(1);

Wir planen, den Kernel in einem zweidimensionalen Raum von Aufgaben zu starten, von denen jede gleich der Anzahl der Elemente im entsprechenden Tensor der Originaldaten ist. Im Hauptteil des Kernels identifizieren wir sofort den aktuellen Thread in beiden Dimensionen des Aufgabenraums.

Im nächsten Schritt bestimmen wir den Offset in den Datenpuffern.

   const int shift1 = idx1 * dimension;
   const int shift2 = idx2 * dimension;
   const int shift_out = idx1 * total2 + idx2;

Nach Abschluss der Vorbereitungsphase gehen wir zur Durchführung der Berechnungen über. Hier organisieren wir zunächst eine Schleife zur Berechnung des Abstands zwischen den analysierten Vektoren.

   float res = 0;
   for(int i = 0; i < dimension; i++)
      res = pow(data1[shift1 + i] - data2[shift2 + i], 2.0f);
   res = sqrt(res);

Und dann berechnen wir den relativen Verzerrungskoeffizienten.

   res = 1.0f / exp(res);
   if(isnan(res) || isinf(res))
      res = 0;
//---
   result[shift_out] = res;
  }

Anschließend schreiben wir den berechneten Wert in das entsprechende Element im Ergebnispuffer.

Es ist zu beachten, dass keiner der ermittelten Koeffizienten negativ ist. Das bedeutet, dass wir keine Elemente in der Eingabesequenz ausblenden. Im Gegenteil, unsere Implementierung hebt die Elemente hervor, die der Abfrage räumlich am nächsten sind.

In diesem Stadium haben wir die relativen Koeffizienten für die Positionsverzerrung berechnet. Der nächste Schritt besteht darin, sie in unseren Kreuzaufmerksamkeit-Mechanismus zu integrieren. Bevor wir jedoch mit der Umsetzung beginnen, möchte ich Ihre Aufmerksamkeit auf ein wichtiges Detail lenken. Schauen Sie sich die oben gezeigte Visualisierung der Methode MAFT durch die Autoren genauer an. Achten Sie besonders auf den Informationsfluss der Szenendarstellung. Besonders hervorzuheben ist der Ansatz der Autoren zur Positionskodierung innerhalb der Szenendarstellung. Insbesondere wird die Positionskodierung nur auf die Entitäten von Key angewendet. Die Elemente von Value bleiben von der Positionskodierung unberührt. Dies scheint eine bewusste Entscheidung zu sein, um sicherzustellen, dass die Aufmerksamkeitsgewichte unter Berücksichtigung der Positionskodierung berechnet werden. Gleichzeitig verzerren sie aber nicht die eigentlichen Merkmalsbeschreibungen der Szenenelemente. Folglich müssen die Tensoren Key und Value aus unterschiedlichen Quellen generiert werden. In der Praxis müssen wir zunächst den Tender der Values aus der rohen Eingabedarstellung erzeugen. Dann fügen wir den Originaldaten eine Positionskodierung hinzu. Nur so können wir den Tensor Key erhalten.

Warum hebe ich das jetzt hervor? Die obige Argumentation impliziert, dass wir die Entitäten Key und Value in verschiedene Tensoren aufteilen müssen. Wir können einen neuen Aufmerksamkeitskern entwickeln, der dieser architektonischen Nuance Rechnung trägt. Mit diesem Ansatz können wir auch die Verkettung von zwei Tensoren vermeiden, die wir bisher durchführen mussten.

Um den Aufmerksamkeitsalgorithmus zu implementieren, erstellen wir einen Kernel namens MHPosBiasAttentionOut. Dieser Kernel akzeptiert eine umfangreiche Liste von globalen Datenpuffern, von denen viele aus unseren früheren Implementierungen des Aufmerksamkeitsmechanismus bekannt sind. Zusätzlich übergeben wir einen Zeiger auf den Puffer der relativen Positionsverzerrungsindizes pos_bias. Wir haben diesen Kernel auch so konzipiert, dass er optional die Berechnung der Standardaufmerksamkeit ohne Positionsverzerrung unterstützt. Diese Funktion kann mit dem Parameter use_pos_bias aktiviert und deaktiviert werden.

__kernel void MHPosBiasAttentionOut(__global const float *q,         ///<[in] Matrix of Querys
                                    __global const float *k,         ///<[in] Matrix of Keys
                                    __global const float *v,         ///<[in] Matrix of Values
                                    __global float *score,           ///<[out] Matrix of Scores
                                    __global const float *pos_bias,  ///<[in] Position Bias
                                    __global float *out,             ///<[out] Matrix of attention
                                    const int dimension,             ///< Dimension of Key
                                    const int heads_kv,
                                    const int use_pos_bias
                                   )
  {
//---
   const int q_id = get_global_id(0);
   const int k_id = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_global_size(1);
   const int heads = get_global_size(2);

Wie bisher wollen wir diesen Kernel in einem dreidimensionalen Aufgabenraum betreiben. Die ersten beiden geben die Anzahl der Elemente in den zu analysierenden Sequenzen an, und die dritte Dimension des Aufgabenraums gibt die Anzahl der verwendeten Aufmerksamkeitsköpfe an. Der Kernel-Algorithmus beginnt mit der Identifizierung des aktuellen Threads in allen drei Dimensionen des Aufgabenraums.

Als Nächstes definieren wir alle notwendigen Konstanten.

   const int h_kv = h % heads_kv;
   const int shift_q = dimension * (q_id * heads + h);
   const int shift_kv = dimension * (heads_kv * k_id + h_kv);
   const int shift_s = kunits * (q_id *  heads + h) + k_id;
   const int shift_pb = q_id * kunits + k_id;
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;

Dann erstellen wir ein Array mit Daten im lokalen Speicher, um Daten zwischen den Threads der lokalen Gruppe auszutauschen.

   __local float temp[LOCAL_ARRAY_SIZE];

Damit sind die vorbereitenden Arbeiten abgeschlossen, und wir können direkt mit den Berechnungen beginnen. Der Berechnungsprozess wiederholt weitgehend den klassischen Algorithmus. Wir fügen nur dort, wo es notwendig ist, eine relative Positionsverzerrung hinzu. Die Notwendigkeit ihrer Verwendung wird durch den Wert des Parameters use_pos_bias gesteuert.

Zunächst wird die Summe der Exponentialwerte der Aufmerksamkeitskoeffizienten berechnet. In der ersten Phase berechnet jeder Thread der lokalen Gruppe seinen Anteil. Dann wird das Ergebnis im entsprechenden Element des lokalen Datenarrays gespeichert.

//--- sum of exp
   uint count = 0;
   if(k_id < ls)
     {
      temp[k_id] = 0;
      do
        {
         if(q_id >= (count * ls + k_id))
            if((count * ls) < (kunits - k_id))
              {
               float sum = 0;
               int sh_k = dimension * heads_kv * count * ls;
               for(int d = 0; d < dimension; d++)
                  sum = q[shift_q + d] * k[shift_kv + d + sh_k];
               sum = exp(sum / koef);
               if(isnan(sum))
                  sum = 0;
               temp[k_id] = temp[k_id] + sum + (use_pos_bias > 0 ? pos_bias[shift_pb + count * ls] : 0);
              }
         count++;
        }
      while((count * ls + k_id) < kunits);
     }
   barrier(CLK_LOCAL_MEM_FENCE);

Bitte beachten Sie, dass die Summe, die wir berechnen, die Summe der Positionskoeffizienten enthalten muss.

Als Nächstes summieren wir den Wert der Elemente des lokalen Arrays.

   count = min(ls, (uint)kunits);
//---
   do
     {
      count = (count + 1) / 2;
      if(k_id < ls)
         temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0);
      if(k_id + count < ls)
         temp[k_id + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Nach der Berechnung der Gesamtsumme werden die normierten Werte der Abhängigkeitskoeffizienten unter Berücksichtigung der Lagekoeffizienten ermittelt und gespeichert.

//--- score
   float sum = temp[0];
   float sc = 0;
   if(q_id >= (count * ls + k_id))
      if(sum != 0)
        {
         for(int d = 0; d < dimension; d++)
            sc = q[shift_q + d] * k[shift_kv + d];
         sc = (exp(sc / koef) + (use_pos_bias > 0 ? pos_bias[shift_pb] : 0)) / sum;
         if(isnan(sc))
            sc = 0;
        }
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

Die erhaltenen Aufmerksamkeitskoeffizienten ermöglichen die Berechnung der endgültigen Werte der mehrköpfigen Aufmerksamkeit für jedes Element der analysierten Sequenz.

//--- out
   for(int d = 0; d < dimension; d++)
     {
      uint count = 0;
      if(k_id < ls)
         do
           {
            if((count * ls) < (kunits - k_id))
              {
               int sh_v = 2 * dimension * heads_kv * count * ls;
               float sum =
                  v[shift_kv + d + sh_v] * (count == 0 ? sc : score[shift_s + count * ls]);
               if(isnan(sum))
                  sum = 0;
               temp[k_id] = (count > 0 ? temp[k_id] : 0) + sum;
              }
            count++;
           }
         while((count * ls + k_id) < kunits);
      barrier(CLK_LOCAL_MEM_FENCE);
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k_id < ls)
            temp[k_id] += (k_id < count && (k_id + count) < kunits ? temp[k_id + count] : 0);
         if(k_id + count < ls)
            temp[k_id + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      out[shift_q + d] = temp[0];
     }
  }

Als Nächstes implementieren wir den Rückwärtsdurchlauf-Algorithmus in MHPosBiasAttentionInsideGradients. Es sei daran erinnert, dass bei der Verteilung von Fehlergradienten durch eine Summationsoperation der Gradient normalerweise vollständig auf beide Summanden übertragen wird. Die Verwendung einer Lernrate, die deutlich unter 1 liegt, gleicht die mögliche Überzähligkeit des Fehlers mehr als aus. Ein weiterer wichtiger Punkt ist, dass die Berechnung der relativen Lagekoeffizienten ausschließlich auf der tatsächlichen räumlichen Anordnung der Punkte beruht. Diese stellen eigentlich die rohen Eingabedaten dar. Diese Berechnungen werden also nicht durch Modellparameter beeinflusst. Der Berechnungsprozess selbst enthält keine lernbaren Parameter. Folglich ist die Übertragung von Gradienten auf den Tensor der relativen Positionskoeffizienten unlogisch. Daher schließen wir diesen Schritt aus dem Backpropagation-Verfahren aus.

Unter Berücksichtigung dieser Überlegungen kommen wir zu einem klassischen Gradientenverteilungsansatz für den Aufmerksamkeitsblock. Wir haben jedoch einen neuen Kernel entwickelt, da wir, wie bereits erwähnt, die Entitäten Key und Value in verschiedene Datenpuffer aufgeteilt haben. Die Implementierung des Kern des Rückwärtsdurchlaufs, MHPosBiasAttentionInsideGradients, können Sie in der angehängten Datei einsehen. Damit schließen wir unsere Arbeit an OpenCL ab.

2.2 Erstellen der Klasse MAFT

Der nächste Schritt unserer Arbeit besteht darin, ein neues Objekt zu erstellen, in dessen Code wir unsere Vision der von den Autoren der Mask-Attention-Free-Transformer-Methode vorgeschlagenen Ansätze umsetzen. Zu diesem Zweck führen wir eine neue Klasse namens CNeuronMAFT ein.

Der MAFT-Algorithmus basiert auf der zuvor diskutierten SPFormer Architektur. In ähnlicher Weise wird unsere Implementierung die Grundlagen nutzen, die in der Klasse CNeuronSPFormer gelegt wurden. Aufgrund des Umfangs und der Tragweite der Änderungen ist die Vererbung von dieser Klasse jedoch nicht praktikabel. Daher erbt unser neues Objekt direkt von der Basisklasse CNeuronBaseOCL, der vollständig verbundene Schicht abgeleitet. Die Struktur der neuen Klasse ist unten dargestellt.

class CNeuronMAFT   : public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iUnits;
   uint              iHeads;
   uint              iSPWindow;
   uint              iSPUnits;
   uint              iSPHeads;
   uint              iWindowKey;
   uint              iLayers;
   uint              iLayersSP;
   //---
   CLayer            cSuperPoints;
   CLayer            cQuery;
   CLayer            cQPosition;
   CLayer            cQKey;
   CLayer            cQValue;
   CLayer            cMHSelfAttentionOut;
   CLayer            cSelfAttentionOut;
   CLayer            cSPKey;
   CLayer            cSPValue;
   CArrayInt         cScores;
   CArrayInt         cPositionBias;
   CLayer            cMHCrossAttentionOut;
   CLayer            cCrossAttentionOut;
   CLayer            cResidual;
   CLayer            cFeedForward;
   CBufferFloat      cTempSP;
   CBufferFloat      cTempQ;
   CBufferFloat      cTempCrossK;
   CBufferFloat      cTempCrossV;
   //---
   virtual bool      CreateBuffers(void);
   virtual bool      CalcPositionBias(CBufferFloat *pos_q, CBufferFloat *pos_k, const int pos_bias,
                                      const int units,
                                      const int units_kv,
                                      const int dimension);
   virtual bool      AttentionOut(CNeuronBaseOCL *q, CNeuronBaseOCL *k, CNeuronBaseOCL *v,
                                  const int scores, CNeuronBaseOCL *out, const int pos_bias,
                                  const int units,
                                  const int heads,
                                  const int units_kv,
                                  const int heads_kv,
                                  const int dimension,
                                  const bool use_pos_bias);
   virtual bool      AttentionInsideGradients(CNeuronBaseOCL *q, CNeuronBaseOCL *k, CNeuronBaseOCL *v,
         const int scores, CNeuronBaseOCL *out,
         const int units, const int heads,
         const int units_kv, const int heads_kv,
         const int dimension);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMAFT(void) {};
                    ~CNeuronMAFT(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, uint heads,
                          uint window_sp, uint units_sp, uint heads_sp,
                          uint layers, uint layers_to_sp,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMAFT; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

In der vorgestellten Struktur sehen wir die bekannte Reihe von überschreibbaren, virtuellen Methoden zusammen mit einer großen Anzahl von internen Objekten. Einige dieser internen Komponenten wiederholen die bereits verwendeten, während andere völlig neu sind. Wir werden uns mit der Funktionsweise der einzelnen Funktionen vertraut machen, wenn wir mit der Implementierung der Methoden der Klasse CNeuronMAFT fortfahren.

Wie zuvor werden alle internen Objekte statisch deklariert, sodass wir den Konstruktor und Destruktor der Klasse leer lassen können. Die Initialisierung sowohl von geerbten als auch von neu deklarierten Komponenten wird in der Methode Init durchgeführt.

bool CNeuronMAFT::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint window, uint window_key, uint units_count,
                       uint heads, uint window_sp, uint units_sp, uint heads_sp,
                       uint layers, uint layers_to_sp,
                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Die Parameter dieser Methode umfassen Schlüsselkonstanten, die die Architektur des zu erstellenden Objekts definieren. Dabei fällt auf, dass die Parameter dieser Methode vollständig aus der entsprechenden Methode der Klasse CNeuronSPFormer entlehnt sind. Dies steht im Einklang mit der auf Vererbung basierenden Designphilosophie, die wir verfolgen. Die eigentliche Logik der Methode hat sich jedoch nicht wesentlich geändert.

Im Hauptteil der Methode rufen wir zunächst dieselbe Methode der übergeordneten Klasse auf, die die Primärkontrolle über die empfangenen Parameter implementiert und die geerbten Objekte initialisiert. Danach speichern wir die resultierenden Konstanten in den internen Variablen der Klasse.

   iWindow = window;
   iUnits = units_count;
   iHeads = heads;
   iSPUnits = units_sp;
   iSPWindow = window_sp;
   iSPHeads = heads_sp;
   iWindowKey = window_key;
   iLayers = MathMax(layers, 1);
   iLayersSP = MathMax(layers_to_sp, 1);

Der nächste Schritt besteht darin, die Objekte zu initialisieren, um lernfähige Abfragen von Objekten und deren Positionskodierung zu erzeugen. Die Autoren der MAFT-Methode haben vorgeschlagen, die Abfragen mit Nullwerten zu initialisieren. Wir können dasselbe tun. Zu diesem Zweck setzen wir die Parameter für die Abfragegenerierung zurück.

   CNeuronBaseOCL *base = new CNeuronBaseOCL();
   if(!base)
      return false;
   if(!base.Init(iWindow * iUnits, 0, OpenCL, 1, optimization, iBatch))
      return false;
   CBufferFloat *buf = base.getOutput();
   if(!buf || !buf.BufferInit(1, 1) || !buf.BufferWrite())
      return false;
   buf = base.getWeights();
   if(!buf || !buf.BufferInit(buf.Total(), 0) ||
      !buf.BufferWrite())
      return false;
   if(!cQuery.Add(base))
      return false;
   base = new CNeuronBaseOCL();
   if(!base || !base.Init(0, 1, OpenCL, iWindow * iUnits, optimization, iBatch))
      return false;
   if(!cQuery.Add(base))
      return false;

Wir fügen auch eine lernfähige Positionskodierung hinzu, die mit Zufallswerten initialisiert wird.

   CNeuronLearnabledPE *pe = new CNeuronLearnabledPE();
   if(!pe || !pe.Init(0, 2, OpenCL, base.Neurons(), optimization, iBatch))
      return false;
   if(!cQuery.Add(pe))
      return false;

Es sei darauf hingewiesen, dass die Positionskodierung als separater Informationsfluss durch den gesamten MAFT-Algorithmus verläuft. Daher werden wir sie als separate Objekte bereitstellen.

   if(!base || !base.Init(0, 3, OpenCL, pe.Neurons(), optimization, iBatch))
      return false;
   if(!base.SetOutput(pe.getOutput()))
      return false;
   if(!cQPosition.Add(base))
      return false;

Die nächste Stufe ist die Primärdatenverarbeitung. Und hier leihen wir uns den Superpoint-Ansatz, der in der SPFormer-Methode vorgestellt wurde.

//--- Init SuperPoints
   int layer_id = 4;
   for(int r = 0; r < 4; r++)
     {
      if(iSPUnits % 2 == 0)
        {
         iSPUnits /= 2;
         CResidualConv *residual = new CResidualConv();
         if(!residual)
            return false;
         if(!residual.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPUnits, optimization, iBatch))
            return false;
         if(!cSuperPoints.Add(residual))
            return false;
        }
      else
        {
         iSPUnits--;
         CNeuronConvOCL *conv = new CNeuronConvOCL();
         if(!conv.Init(0, layer_id, OpenCL, 2 * iSPWindow, iSPWindow, iSPWindow, iSPUnits, 1,
                                                                        optimization, iBatch))
            return false;
         if(!cSuperPoints.Add(conv))
            return false;
        }
      layer_id++;
     }

Bitte beachten Sie, dass die hier vorgestellte Implementierung die Verwendung von Tensoren verschiedener Dimensionen für die Kreuzaufmerksamkeit erlaubt. Dies ist jedoch für den vorgeschlagenen Algorithmus der relativen Positionsoffsetkoeffizienten nicht akzeptabel. Daher fügen wir dem lernbaren Abfrageraum eine Superpunktprojektionsschicht hinzu.

   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv.Init(0, layer_id, OpenCL, iSPWindow, iSPWindow, iWindow, iSPUnits, 1, optimization, iBatch))
      return false;
   if(!cSuperPoints.Add(conv))
      return false;
   layer_id++;

Und wir fügen eine Ebene der Positionskodierung hinzu.

   pe = new CNeuronLearnabledPE();
   if(!pe || !pe.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch))
      return false;
   if(!cSuperPoints.Add(pe))
      return false;
   layer_id++;

Bitte beachten Sie, dass wir an dieser Stelle ein wenig von dem ursprünglichen Algorithmus abweichen, den die Autoren der MAFT-Methode vorgeschlagen haben. In ihrer Arbeit verwendeten sie die Zerstückelung einer Punktwolke auf der Grundlage der ursprünglichen Koordinaten. Stattdessen haben wir eine vollständig erlernbare Positionskodierung verwendet, die es dem Modell ermöglicht, die optimalen Positionen der einzelnen Elemente der Eingabesequenz zu erlernen.

Nach Abschluss der Arbeit an der primären Verarbeitung der Quelldaten organisieren wir eine Schleife durch die internen Schichten des Decoders.

//--- Inside layers
   for(uint l = 0; l < iLayers; l++)
     {
      //--- Self-Attention
      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, 
                                                                              optimization, iBatch))
         return false;
      if(!cQuery.Add(conv))
         return false;
      layer_id++;

Hier ist zu beachten, dass die Autoren von MAFT ein klassisches Layout verwenden: Selbstaufmerksamkeit -> Kreuzaufmerksamkeit -> Weiterleitung. Die Autoren der SPFormer-Methode haben jedoch Selbstaufmerksamkeit und Fremdaufmerksamkeit vertauscht.

Zunächst erzeugen wir die Entitäten der Query. Dann fügen wir Key und Value hinzu.

      //--- Key
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, 
                                                                              optimization, iBatch))
         return false;
      if(!cQKey.Add(conv))
         return false;
      layer_id++;
      //--- Value
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, 
                                                                               optimization, iBatch))
         return false;
      if(!cQValue.Add(conv))
         return false;
      layer_id++;

In diesem Fall erwarten wir, dass wir eine kleine Anzahl von lernfähigen Abfragen verwenden. Daher reduzieren wir die Anzahl der Köpfe für Key-Value nicht und erzeugen neue Entitäten auf jeder internen Ebene.

Wir leiten die generierten Entitäten an den mehrköpfigen Aufmerksamkeitsblock weiter, ohne Positionskoeffizienten zu verwenden.

      //--- Multy-Heads Attention Out
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch))
         return false;
      if(!cMHSelfAttentionOut.Add(base))
         return false;
      layer_id++;

Wir fügen eine Ebene der Skalierung der Ergebnisse der mehrköpfigen Aufmerksamkeit hinzu.

      //--- Self-Attention Out
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow,
                                                                     iUnits, 1, optimization, iBatch))
         return false;
      if(!cSelfAttentionOut.Add(conv))
         return false;
      layer_id++;

Am Ende des Selbstaufmerksamkeits-Blocks fügen wir nach dem klassischen Transformer-Algorithmus eine Schicht von Residual-Verbindungen hinzu.

      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!cResidual.Add(base))
         return false;
      layer_id++;

Als Nächstes bauen wir die Objekte des Kreuzaufmerksamkeit-Blocks. Wir beginnen mit dem Entitäts-Tensor von Query.

      //--- Cross-Attention
      //--- Query
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1,
                                                                              optimization, iBatch))
         return false;
      if(!cQuery.Add(conv))
         return false;
      layer_id++;

Dann fügen wir Tensoren für die Entitäten Key und Value hinzu. Diesmal lassen wir uns von den Anweisungen des Nutzers leiten, die Aufmerksamkeitsköpfe zu senken und die Ebenen zu wechseln.

      if(l % iLayersSP == 0)
        {
         //--- Key
         conv = new CNeuronConvOCL();
         if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1,
                                                                                     optimization, iBatch))
            return false;
         if(!cSPKey.Add(conv))
            return false;
         layer_id++;
         //--- Value
         conv = new CNeuronConvOCL();
         if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindowKey * iSPHeads, iSPUnits, 1, 
                                                                                     optimization, iBatch))
            return false;
         if(!cSPValue.Add(conv))
            return false;
         layer_id++;
        }

Wir fügen eine Ebene von Ergebnissen aus mehrköpfiger Aufmerksamkeit hinzu.

      //--- Multy-Heads Attention Out
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch))
         return false;
      if(!cMHCrossAttentionOut.Add(base))
         return false;
      layer_id++;

Die Skalierung erfolgt dann durch Addition der restlichen Verbindungen.

      //--- Cross-Attention Out
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow,
                                                                    iUnits, 1, optimization, iBatch))
         return false;
      if(!cCrossAttentionOut.Add(conv))
         return false;
      layer_id++;
      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!cResidual.Add(base))
         return false;
      layer_id++;

Der Decoder wird durch den FeedForward-Block vervollständigt, zu dem wir auch Restverbindungen hinzufügen.

      //--- Feed Forward
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, 4 * iWindow, iUnits, 1, 
                                                                         optimization, iBatch))
         return false;
      conv.SetActivationFunction(LReLU);
      if(!cFeedForward.Add(conv))
         return false;
      layer_id++;
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, 
                                                                         optimization, iBatch))
         return false;
      if(!cFeedForward.Add(conv))
         return false;
      layer_id++;
      //--- Residual
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, iWindow * iUnits, optimization, iBatch))
         return false;
      if(!base.SetGradient(conv.getGradient()))
         return false;
      if(!cResidual.Add(base))
         return false;
      layer_id++;

Jetzt müssen wir nur noch MLP-Korrekturen für die Positionskodierung von lernbaren Abfragen hinzufügen.

      //--- Delta position
      conv = new CNeuronConvOCL();
      if(!conv || !conv.Init(0, layer_id, OpenCL, iWindow, iWindow, iWindow, iUnits, 1, optimization, iBatch))
         return false;
      conv.SetActivationFunction(SIGMOID);
      if(!cQPosition.Add(conv))
         return false;
      layer_id++;
      base = new CNeuronBaseOCL();
      if(!base || !base.Init(0, layer_id, OpenCL, conv.Neurons(), optimization, iBatch))
         return false;
      if(!base.SetGradient(conv.getGradient()))
         return false;
      if(!cQPosition.Add(base))
         return false;
      layer_id++;
     }

Dann gehen wir zur nächsten Iteration der Schleife über und erstellen Objekte der neuen internen Schicht des Decoders.

Nach erfolgreicher Initialisierung der Objekte aller internen Schichten des Decoders ersetzen wir Zeiger auf Fehlergradientenpuffer und geben das boolesche Ergebnis, das den Erfolg anzeigt, an das aufrufende Programm zurück.

   base = cResidual[iLayers * 3 - 1];
   if(!SetGradient(base.getGradient()))
      return false;
//---
   SetOpenCL(OpenCL);
//---
   return true;
  }

Es sollte hinzugefügt werden, dass die Initialisierung von Hilfsdatenpuffern in eine separate Methode CreateBuffers verlagert wurde, die Sie selbst studieren sollten.

Die vollständige Implementierung dieser Klasse und aller ihrer Methoden finden Sie im Anhang.

Nach der Initialisierung der internen Objekte wird in der Methode feedForward ein Vorwärtsdurchlaufs-Algorithmus konstruiert. In den Parametern dieser Methode erhalten wir einen Zeiger auf das Quelldatenobjekt.

bool CNeuronMAFT::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- Superpoints
   CNeuronBaseOCL *superpoints = NeuronOCL;
   int total_sp = cSuperPoints.Total();
   for(int i = 0; i < total_sp; i++)
     {
      if(!cSuperPoints[i] ||
         !((CNeuronBaseOCL*)cSuperPoints[i]).FeedForward(superpoints))
         return false;
      superpoints = cSuperPoints[i];
     }

Wir verwenden das resultierende Objekt sofort bei der Erstellung von Superpunktmerkmalen. Hierfür wird ein verschachteltes Modell cSuperPoints verwendet.

Die letzte Ebene dieses Modells ist die Ebene der Positionskodierung.

Als Nächstes generieren wir lernfähige Abfragen mit Positionskodierung.

//--- Query
   CNeuronBaseOCL *inputs = NULL;
   for(int i = 0; i < 2; i++)
     {
      inputs = cQuery[i + 1];
      if(!inputs ||
         !inputs.FeedForward(cQuery[i]))
         return false;
     }

Dann erstellen wir lokale Variablen, um vorübergehend Zeiger auf Objekte zu speichern.

   CNeuronBaseOCL *query = NULL, *key = NULL, *value = NULL, *base = NULL;

Wir organisieren eine Schleife durch die internen Schichten des Decoders.

//--- Inside layers
   for(uint l = 0; l < iLayers; l++)
     {
      //--- Self-Atention
      query = cQuery[l * 2 + 3];
      if(!query || !query.FeedForward(inputs))
         return false;
      key = cQKey[l];
      if(!key || !key.FeedForward(inputs))
         return false;
      value = cQValue[l];
      if(!value || !value.FeedForward(inputs))
         return false;

Hier organisieren wir zunächst die Operationen des Selbstaufmerksamkeits-Blocks für die lernfähigen Abfragen mit positioneller Kodierung. Dazu erzeugen wir zunächst die notwendigen Entitäten, die wir an den mehrköpfigen Aufmerksamkeitsblock übergeben.

      if(!AttentionOut(query, key, value, cScores[l * 2], cMHSelfAttentionOut[l], -1, 
                                   iUnits, iHeads, iUnits, iHeads, iWindowKey, false))
         return false;

Dann skalieren wir die erzielten Ergebnisse und fügen die restlichen Verbindungen hinzu.

      base = cSelfAttentionOut[l];
      if(!base || !base.FeedForward(cMHSelfAttentionOut[l]))
         return false;
      value = cResidual[l * 3];
      if(!value ||
         !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
      inputs = value;

In einem separaten Thema fügen wir die Positionskodierung hinzu.

      value = cQPosition[l * 2];
      if(!value ||
         !SumAndNormilize(inputs.getOutput(), value.getOutput(),inputs.getOutput(), iWindow, false, 0, 0, 0, 1))
         return false;

Danach geht es weiter mit dem Kreuzaufmerksamkeit-Block. Definieren wir aber zunächst die Koeffizienten der relativen Positionsverzerrung.

      //--- Calc Position bias
      if(!CalcPositionBias(value.getOutput(),
                           ((CNeuronLearnabledPE*)superpoints).GetPE(), cPositionBias[l],
                           iUnits, iSPUnits, iWindow))
         return false;

Als Nächstes generieren wir eine Query-Entität aus dem positionalen Query-Tensor unter Berücksichtigung der positionalen Kodierung.

      //--- Cross-Attention
      query = cQuery[l * 2 + 4];
      if(!query || !query.FeedForward(inputs))
         return false;

Was die Operationen der Entitäten von Key und Value betrifft, so sind diese voller Nuancen. Erstens werden neue Tensoren nur bei Bedarf erzeugt.

      key = cSPKey[l / iLayersSP];
      value = cSPValue[l / iLayersSP];
      if(l % iLayersSP == 0)
        {
         if(!key || !key.FeedForward(superpoints))
            return false;
         if(!value || !value.FeedForward(cSuperPoints[total_sp - 2]))
            return false;
        }

Zweitens wird die Entität Key aus den Daten der letzten cSuperPoints-Ebene erzeugt, die eine Positionskodierung enthält. Zur Erzeugung von Value verwenden wir die vorletzte Ebene, die keine Positionskodierung hat.

Wir leiten die resultierenden Entitäten an den mehrköpfigen Aufmerksamkeitsblock weiter, ohne Positionskoeffizienten zu verwenden.

      if(!AttentionOut(query, key, value, cScores[l * 2 + 1], cMHCrossAttentionOut[l], cPositionBias[l], 
                                                  iUnits, iHeads, iSPUnits, iSPHeads, iWindowKey, true))
         return false;

Danach skalieren wir die erhaltenen Daten und fügen Restverbindungen hinzu.

      base = cCrossAttentionOut[l];
      if(!base || !base.FeedForward(cMHCrossAttentionOut[l]))
         return false;
      value = cResidual[l * 3 + 1];
      if(!value ||
         !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
      inputs = value;

Am Ende des Decoders leiten wir die Daten durch einen FeedForward-Block, gefolgt von Residual-Verbindungen.

      //--- Feed Forward
      base = cFeedForward[l * 2];
      if(!base || !base.FeedForward(inputs))
         return false;
      base = cFeedForward[l * 2 + 1];
      if(!base || !base.FeedForward(cFeedForward[l * 2]))
         return false;
      value = cResidual[l * 3 + 2];
      if(!value ||
         !SumAndNormilize(inputs.getOutput(), base.getOutput(), value.getOutput(), iWindow, true, 0, 0, 0, 1))
         return false;
      inputs = value;

In diesem Stadium haben wir die Operationen einer Decoderschicht abgeschlossen, aber wir müssen noch die Positionskodierungsdaten der lernfähigen Abfragen anpassen. Zu diesem Zweck wird auf der Grundlage der empfangenen Daten eine Positionsabweichung generiert und zu den vorhandenen Werten addiert.

      //--- Delta Query position
      base = cQPosition[l * 2 + 1];
      if(!base ||
         !base.FeedForward(inputs))
         return false;
      value = cQPosition[(l + 1) * 2];
      query = cQPosition[l * 2];
      if(!value ||
         !SumAndNormilize(query.getOutput(), base.getOutput(), value.getOutput(), iWindow, false, 0,0,0,0.5f))
         return false;
     }

Nun können wir mit den Operationen der nächsten inneren Schicht des Decoders fortfahren.

Nach erfolgreicher Ausführung der Operationen aller internen Schichten des Decoders erhalten wir das Ergebnis in Form von angereicherten Abfragen und deren verfeinerten Positionen. Die beiden resultierenden Tensoren werden addiert und an den Vorhersagekopf weitergeleitet.

   value = cQPosition[iLayers * 2];
   if(!value ||
      !SumAndNormilize(inputs.getOutput(), value.getOutput(), Output, iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Die Methode gibt einen booleschen Wert zurück, der den Erfolg oder Misserfolg des Initialisierungsprozesses anzeigt.

Damit ist die Implementierung des Vorwärtsdurchlauf abgeschlossen. Wir fahren nun fort mit der Entwicklung der Backpropagation-Algorithmen, die in den Methoden calcInputGradients und updateInputWeights implementiert sind. Erstere ist für die Verteilung der Fehlergradienten auf alle internen Komponenten entsprechend ihrem Beitrag zum Endergebnis verantwortlich. Letztere aktualisiert die Modellparameter.

Wie Sie wissen, erfolgt die Gradientenverteilung in streng umgekehrter Reihenfolge zum Informationsfluss des Vorwärtsdurchlaufs. Ich möchte Sie ermutigen, die Umsetzung dieser Methoden auf eigene Faust zu erkunden.

Die vollständige Implementierung dieser Klasse und aller ihrer Methoden finden Sie im Anhang.

Die Architektur der Modelle, die in diesem Artikel verwendet werden, sowie alle Programme für das Training und die Interaktion mit der Umgebung sind vollständig aus unserer früheren Arbeit entlehnt. Die einzige Änderung, die wir am Encoder für den Umweltzustand vorgenommen haben, war die Änderung der Kennung einer einzelnen Schicht. Daher werden wir sie hier nicht im Detail untersuchen. Der vollständige Code für alle Programmklassen, die bei der Erstellung dieses Artikels verwendet wurden, ist ebenfalls im Anhang enthalten.

3. Tests

In diesem Artikel haben wir uns mit der Methode MAFT vertraut gemacht und unsere Vision der vorgeschlagenen Ansätze in MQL5 umgesetzt. Wir fahren nun fort, die Ergebnisse unserer Arbeit zu bewerten. Das Modell wird anhand realer historischer Daten unter Verwendung des MAFT-Rahmens trainiert, gefolgt von einem Test der trainierten Akteurs-Politik.

Wie immer verwenden wir zum Trainieren der Modelle reale historische Daten des Instruments EURUSD mit dem Zeitrahmen H1 für das gesamte Jahr 2023. Alle Indikatorparameter wurden auf ihre Standardwerte gesetzt.

Das Verfahren zur Ausbildung des Modells und die entsprechenden Instrumente wurden aus unseren früheren Artikeln übernommen.

Die trainierte Akteurs-Politik wurde im Strategietester des MetaTrader 5 mit historischen Daten vom Januar 2024 getestet. Alle anderen Parameter blieben unverändert. Die Testergebnisse werden im Folgenden vorgestellt.

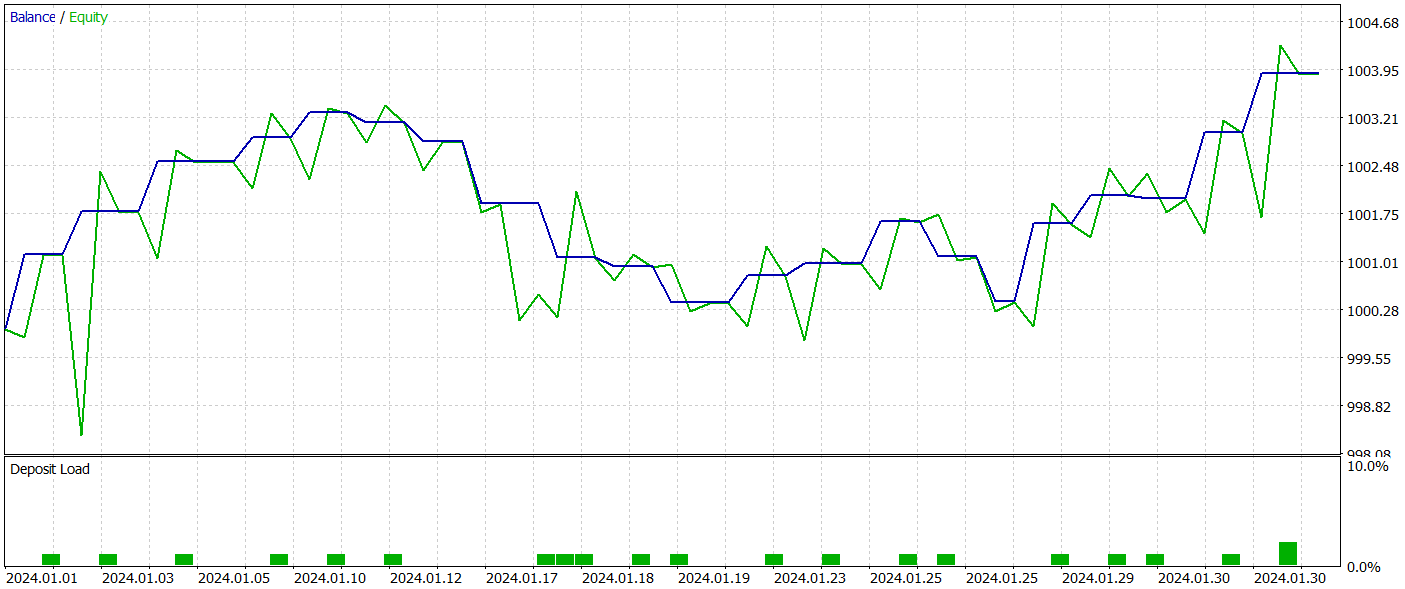
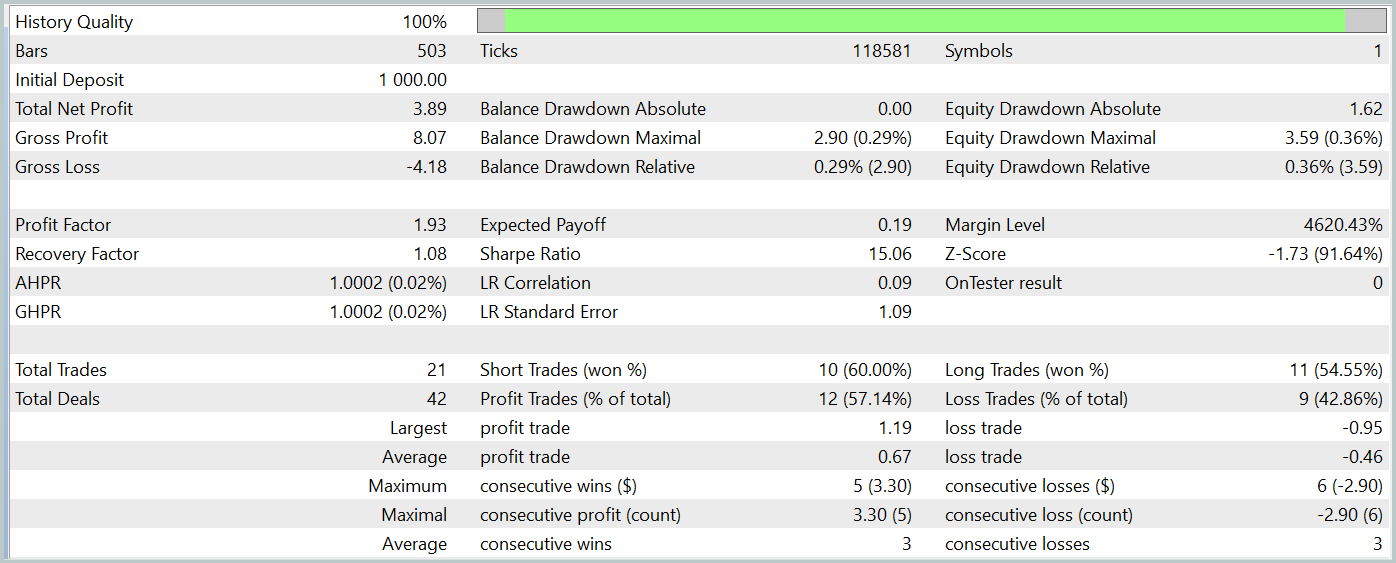
Das Saldendiagramm während des Testzeitraums zeigt einen Aufwärtstrend, was eindeutig ein positives Ergebnis ist. Allerdings führte das Modell während des gesamten Testzeitraums nur 21 Handelsgeschäfte aus, von denen 12 profitabel waren. Leider lässt diese begrenzte Anzahl von Geschäften keine abschließende Bewertung der Wirksamkeit des Modells über längere Zeiträume zu.

Schlussfolgerung

In diesem Artikel befassen wir uns mit der Methode des Mask-Attention-Free Transformer (MAFT) und ihrer Anwendung im algorithmischen Handel. Im Gegensatz zu herkömmlichen Transformer-Architekturen bietet MAFT eine höhere Recheneffizienz, da die Notwendigkeit der Datenmaskierung entfällt und die Sequenzverarbeitung beschleunigt wird.

Die Testergebnisse bestätigten, dass MAFT die Vorhersagegenauigkeit verbessern und gleichzeitig die Trainingszeit des Modells reduzieren kann.

Referenzen

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	EA zum Sammeln von Beispielen
2	ResearchRealORL.mq5	Expert Advisor	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modelltraining EA
4	Test.mq5	Expert Advisor	Modelltraining EA
5	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
6	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
7	NeuroNet.cl	Bibliothek	OpenCL-Programmcode-Bibliothek

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15973

Beigefügte Dateien |

ZIP herunterladen

MQL5.zip (1878.59 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum

Vorhersage von Wechselkursen mit klassischen Methoden des maschinellen Lernens: Logit- und Probit-Modelle

In diesem Artikel wird der Versuch unternommen, einen Handels-EA zur Vorhersage von Wechselkursen zu erstellen. Der Algorithmus basiert auf klassischen Klassifikationsmodellen - logistische und Probit-Regression. Das Kriterium des Wahrscheinlichkeitsquotienten wird als Filter für Handelssignale verwendet.

Von der Grundstufe bis zur Mittelstufe: Arrays und Zeichenketten (II)

In diesem Artikel werde ich zeigen, dass wir, obwohl wir uns noch in einem sehr grundlegenden Stadium der Programmierung befinden, bereits einige interessante Anwendungen realisieren können. In diesem Fall werden wir einen recht einfachen Passwortgenerator erstellen. Auf diese Weise werden wir in der Lage sein, einige der bisher erläuterten Konzepte anzuwenden. Darüber hinaus werden wir uns ansehen, wie Lösungen für einige spezifische Probleme entwickelt werden können.

Eine alternative Log-datei mit der Verwendung der HTML und CSS

In diesem Artikel werden wir eine sehr einfache, aber leistungsfähige Bibliothek zur Erstellung der HTML-Dateien schreiben, dabei lernen wir auch, wie man eine ihre Darstellung einstellen kann (nach seinem Geschmack) und sehen wir, wie man es leicht in seinem Expert Advisor oder Skript hinzufügen oder verwenden kann.

Wirtschaftsprognosen: Erkunden des Potenzials von Python

Wie kann man die Wirtschaftsdaten der Weltbank für Prognosen nutzen? Was passiert, wenn man KI-Modelle und Wirtschaft kombiniert?