Neuronale Netze im Handel: Leichtgewichtige Modelle für die Zeitreihenprognose
Einführung
Die Prognose zukünftiger Preisbewegungen ist für die Entwicklung einer effektiven Handelsstrategie von entscheidender Bedeutung. Um genaue Prognosen zu erzielen, ist normalerweise der Einsatz leistungsstarker und komplexer Deep-Learning-Modelle erforderlich.
Die Grundlage präziser langfristiger Zeitreihenprognosen liegt in der inhärenten Periodizität und den Trends der Daten. Darüber hinaus ist seit langem bekannt, dass die Preisbewegungen von Währungspaaren eng mit bestimmten Handelssitzungen zusammenhängen. Wenn beispielsweise eine Zeitreihe täglicher Sequenzen zu einer bestimmten Tageszeit diskretisiert wird, weist jede Teilsequenz ähnliche oder sequenzielle Trends auf. Dabei werden Periodizität und Trend der ursprünglichen Abfolge zerlegt und transformiert. Periodische Muster werden in Inter-Subsequenz-Dynamik umgewandelt, während Trendmuster als Intra-Subsequenz-Charakteristiken neu interpretiert werden. Diese Zerlegung eröffnet neue Möglichkeiten für die Entwicklung leichter Modelle für die Prognose langfristiger Zeitreihen, ein Ansatz, der in dem Artikel „ SparseTSF: Modellierung langfristiger Zeitreihenprognosen mit 1.000 Parametern" erklärt wurde.
In ihrer Arbeit untersuchen die Autoren möglicherweise zum ersten Mal, wie Periodizität und Datenzerlegung genutzt werden können, um spezialisierte, leichtgewichtige Zeitreihenprognosemodelle zu erstellen. Dieser Ansatz ermöglicht es ihnen, SparseTSF vorzuschlagen, ein extrem leichtgewichtiges Modell für die Prognose langfristiger Zeitreihen.
Die Autoren stellen eine technische Methode zur zeitraumübergreifenden spärlichen (sparse) Prognose vor. Zunächst werden die Eingabedaten in Sequenzen mit konstanter Periodizität aufgeteilt. Anschließend wird für jede heruntergesampelte Teilfolge eine Vorhersage durchgeführt. Somit vereinfacht sich das ursprüngliche Problem der Prognose von Zeitreihen auf das Problem der Prognose des Trends zwischen den Perioden.
Dieser Ansatz bietet zwei Vorteile:
- Effiziente Trennung von Datenperiodizität und Trend, sodass das Modell periodische Merkmale stabil identifizieren und erfassen kann, während es sich gleichzeitig auf die Vorhersage von Trendänderungen konzentriert.
- Extreme Komprimierung der Modellparametergröße, wodurch der Bedarf an Rechenressourcen deutlich reduziert wird.
1. Der Algorithmus SparseSTF
Das Ziel der langfristigen Zeitreihenprognose (LTSF) besteht darin, anhand zuvor beobachteter, multivariater Zeitreihendaten zukünftige Werte über einen längeren Zeitraum vorherzusagen. Das primäre Ziel von LTSF ist die Erweiterung des Prognosehorizonts H, da dadurch umfassendere und erweiterte Erkenntnisse für praktische Anwendungen bereitgestellt werden. Allerdings erhöht eine Erweiterung des Prognosehorizonts häufig die Komplexität des trainierten Modells. Um dieses Problem zu lösen, konzentrierten sich die Autoren von SparseTSF auf die Entwicklung von Modellen, die nicht nur außergewöhnlich leicht, sondern auch robust und effizient sind.
Jüngste Fortschritte bei LTSF haben bei der Verarbeitung multivariater Zeitreihendaten zu einer Verlagerung hin zur unabhängigen Kanalprognose geführt. Diese Strategie vereinfacht den Prognoseprozess, indem sie sich auf einzelne univariate Zeitreihen innerhalb des Datensatzes konzentriert und so die Komplexität der Abhängigkeiten zwischen den Kanälen reduziert. Infolgedessen hat sich der Hauptschwerpunkt moderner Modelle in den letzten Jahren in Richtung effizienter Prognosen durch die Modellierung langfristiger Abhängigkeiten, einschließlich Periodizität und Trends, in univariaten Sequenzen verlagert.
Angesichts der Tatsache, dass prognostizierte Daten häufig eine konsistente, a priori Periodizität aufweisen, schlagen die Autoren von SparseTSF eine spärliche Prognose zwischen den Perioden vor, um die Extraktion langfristiger sequentieller Abhängigkeiten zu verbessern und gleichzeitig die Komplexität der Modellparameter zu reduzieren. Die vorgeschlagene Lösung verwendet eine einzelne lineare Schicht zur Modellierung von LTSF.
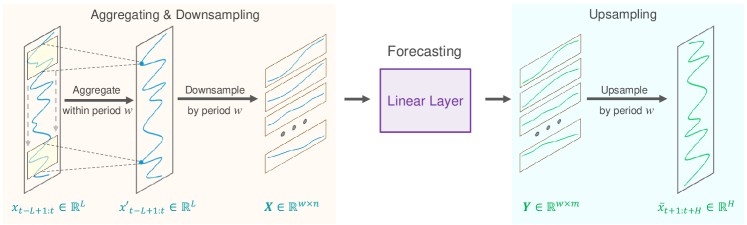
Es wird angenommen, dass eine Zeitreihe X t der Länge L eine bekannte Periodizität w hat. Der erste Schritt des vorgeschlagenen Algorithmus besteht darin, die ursprüngliche Sequenz in w Teilsequenzen der Länge n (n=L/w) herunterzusampeln. Auf diese Teilsequenzen wird dann ein Prognosemodell mit gemeinsamen Parametern angewendet. Durch diese Operation entstehen w vorhergesagte Teilfolgen, jede mit einer Länge von m (m=H/w), die zusammen die vollständige vorhergesagte Folge der Länge H bilden.
Intuitiv ähnelt dieser Prognoseprozess einer gleitenden Prognose mit einem spärlichen Intervall w, die von einer vollständig verbundenen Schicht mit Parameterfreigabe über einen festen Zeitraum w durchgeführt wird. Dies kann als ein Modell interpretiert werden, das spärliche gleitende Prognosen über Zeiträume hinweg durchführt.
Aus technischer Sicht entspricht der Downsampling-Prozess der Umformung des Tensors der Originaldaten X t in eine n*w-Matrix und anschließender Transposition in eine w*n-Matrix. Die Prognose einer spärlichen Gleittrajektorie entspricht dann dem Anwenden einer linearen Schicht der Größe n*m auf die endgültige Dimension der Matrix. Das Ergebnis der Operation ist eine w*m-Matrix.
Beim Upsampling führen wir die inversen Operationen aus: Wir transponieren die w*m-Matrix und formatieren sie dann neu in die vollständige vorhergesagte Sequenz der Länge H.
Der vorgeschlagene Ansatz weist jedoch zwei Problemen auf:
- Informationsverlust, da pro Zeitraum nur ein Datenpunkt zur Prognose verwendet wird, während andere ignoriert werden.
- Erhöhte Empfindlichkeit gegenüber Ausreißern, da Extremwerte innerhalb heruntergesampelter Teilsequenzen die Prognose direkt beeinflussen können.
Um diese Probleme zu mildern, führen die Autoren von SparseTSF einen gleitenden Aggregationsschritt ein, bevor sie die spärliche Prognose durchführen. Jeder aggregierte Datenpunkt enthält Informationen von umgebenden Punkten innerhalb des Zeitraums und befasst sich mit dem ersten Problem. Da der aggregierte Wert im Wesentlichen einen gewichteten Durchschnitt der umliegenden Punkte darstellt, mildert er zudem die Auswirkungen von Ausreißern und löst so das zweite Problem.
Technisch kann diese gleitende Datenaggregation mithilfe einer Faltungsschicht mit Null-Padding implementiert werden.
Zeitreihendaten weisen häufig Verteilungsverschiebungen zwischen Trainings- und Testdatensätzen auf. Einfache Normalisierungsstrategien zwischen den Originaldaten und den vorhergesagten Sequenzen können dazu beitragen, dieses Problem zu mildern. Im Algorithmus SparseTSF wird eine einfache Normalisierungsstrategie verwendet: Der Mittelwert der Sequenz wird von den Eingabedaten abgezogen, bevor er in das Modell eingespeist wird, und dann wieder zu den resultierenden Prognosen hinzugefügt.
Die Visualisierung der Methode SparseTSF durch die Autoren wird unten dargestellt.
2. Implementierung in MQL5
Nachdem wir die theoretischen Aspekte von SparseTSF betrachtet haben, fahren wir mit der Implementierung der vorgeschlagenen Ansätze mithilfe von MQL5 fort. Als Teil unserer Bibliothek erstellen wir eine neue Klasse, CNeuronSparseTSF.
2.1 Erstellen der KLasse SparseTSF
Unsere neue Klasse erbt die Kernfunktionalität von der Basisklasse CNeuronBaseOCL. Die Struktur der Klasse CNeuronSparseTSF wird unten dargestellt.
class CNeuronSparseTSF : public CNeuronBaseOCL { protected: CNeuronConvOCL cConvolution; CNeuronTransposeOCL acTranspose[4]; CNeuronConvOCL cForecast; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSparseTSF(void) {}; ~CNeuronSparseTSF(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint sequence, uint variables, uint period, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSparseTSF; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
In der Struktur der neuen Klasse werden wir zwei Faltungsschichten hinzufügen. Einer von ihnen übernimmt die Aufgabe der Datenaggregation und der zweite sagt nachfolgende Sequenzen voraus. Darüber hinaus werden wir eine ganze Reihe von Transpositionen verwenden, um die Daten neu zu formatieren. Alle hinzugefügten internen Objekte werden statisch deklariert, wodurch der Klassenkonstruktor und -destruktor „leer“ bleiben können. Die Initialisierung eines Klassenobjekts wird in Init durchgeführt.
In den Parametern der Initialisierungsmethode übergeben wir die Hauptparameter des erstellten Objekts:
- sequence — Länge der Sequenz der Anfangsdaten
- variables — die Anzahl der univariaten Sequenzen innerhalb der analysierten multimodalen Zeitreihe
- period — Periodizität der Eingabedaten
- forecast – Tiefe der Prognose.
bool CNeuronSparseTSF::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint sequence, uint variables, uint period, uint forecast, ENUM_OPTIMIZATION optimization_type, uint batch ) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, forecast * variables, optimization_type, batch)) return false;
Im Hauptteil der Methode rufen wir wie üblich die gleichnamige Methode der übergeordneten Klasse auf. Diese Methode implementiert bereits den Prozess der Initialisierung geerbter Objekte und Variablen.
Beachten Sie, dass wir beim Aufrufen der Initialisierungsmethode der übergeordneten Klasse die Schichtgröße gleich dem Produkt aus der Prognosetiefe und der Anzahl der Einheitssequenzen in den multimodalen Daten angeben.
Nach der erfolgreichen Initialisierung der abgeleiteten Objekte und Variablen fahren wir mit der Phase der Initialisierung der hinzugefügten internen Objekte fort. Wir werden sie in der Reihenfolge des Vorwärtsdurchgangs initialisieren. Achten Sie nun besonders auf die Dimension des Datentensors, den wir verarbeiten.
Am Eingang der Schicht erwarten wir einen Eingabedatentensor der Dimension L*v, wobei L die Länge der Eingabesequenz und v die Anzahl der unitären Reihen in den multimodalen Quelldaten ist. Wie im ersten Teil dieses Artikels erwähnt, arbeitet SparseTSF nach dem Paradigma der Vorhersage unabhängiger unitärer Sequenzen. Um einen solchen Prozess zu implementieren, transponieren wir die Eingabedatenmatrix in eine v*L-Matrix.
if(!acTranspose[0].Init(0, 0, OpenCL, sequence, variables, optimization, iBatch)) return false;
Als Nächstes planen wir, die Eingabedaten mithilfe einer Faltungsschicht zu aggregieren. Bei dieser Operation führen wir eine Faltung innerhalb von 2 Perioden der Originaldaten mit einem Schritt von 1 Periode durch. Um die Dimensionalität zu bewahren, ist die Anzahl der Faltungsfilter gleich der Periodengröße.
if(!cConvolution.Init(0, 1, OpenCL, 2 * period, period, period, sequence / period, variables, optimization, iBatch)) return false; cConvolution.SetActivationFunction(None);
Bitte beachten Sie, dass wir die Datenaggregation innerhalb unabhängiger Einheitssequenzen durchführen.
Der nächste Schritt des Algorithmus SparseTSF ist die Diskretisierung der Originaldaten. In dieser Phase schlagen die Autoren der Methode vor, die Dimensionalität zu ändern und den Tensor der Originaldaten zu transponieren. In unserem Fall arbeiten wir mit eindimensionalen Datenpuffern. Das Ändern der Dimensionalität der Originaldaten ist rein deklarativ; es ist keine Neuanordnung der Daten im Speicher erforderlich. Das Gleiche lässt sich allerdings von der Umsetzung nicht behaupten. Daher fahren wir mit der Initialisierung der nächsten Schicht zur Datentransposition fort.
if(!acTranspose[1].Init(0, 2, OpenCL, variables * sequence / period, period, optimization, iBatch)) return false;
Die Verwendung einer zweiten Datentranspositionsebene mag etwas seltsam erscheinen. Auf den ersten Blick führt es eine Operation aus, die die Umkehrung der vorherigen Transposition der Originaldaten ist. Aber das stimmt nicht ganz. Es hat die Dimensionen der oben genannten Daten hervorgehoben. Die Gesamtgröße unseres Datenpuffers bleibt unverändert: L*v. Erst wenn wir die Dimension der Datenmatrix deklarativ ändern, können wir sagen, dass ihre Größe gleich (v * L/w) * w ist, wobei w die Periodizität der Anfangsdaten ist. Wir transponieren es in w * (L/w * v). Nach dieser Operation zeigt unser Datenpuffer eine Abfolge einzelner Phasen der Periodizität der Originaldaten an, wobei die Unabhängigkeit der einheitlichen Reihe der Originaldaten berücksichtigt wird.
Grafisch lässt sich das Ergebnis der beiden Datentranspositionsschritte wie folgt darstellen:
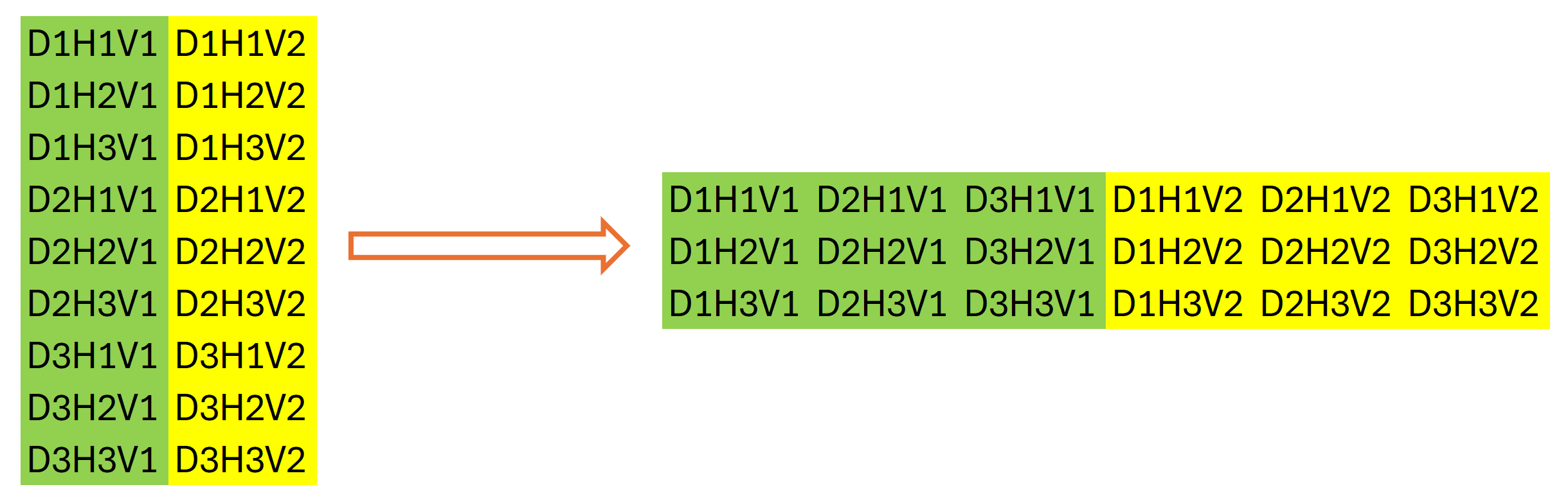
Wir verwenden dann eine Faltungsschicht, um einzelne Schritte innerhalb der Periodizität der Eingabedaten für einheitliche Sequenzen über einen bestimmten Planungshorizont unabhängig vorherzusagen.
if(!cForecast.Init(0, 3, OpenCL, sequence / period, sequence / period, forecast / period, variables, period, optimization, iBatch)) return false; cForecast.SetActivationFunction(TANH);
Beachten Sie, dass die Größe des analysierten Quelldatenfensters und sein Schritt „Sequenz/Periode“ und die Anzahl der Faltungsfilter „Prognose/Periode“ beträgt. Dadurch erhalten wir in einem Durchgang Prognosewerte für den gesamten Planungshorizont. In diesem Fall verwenden wir für jeden Schritt des Zeitraums der analysierten Daten separate Filter.
Da wir mit normalisierten Daten arbeiten möchten, verwenden wir den Tangens Hyperbolicus als Aktivierungsfunktion für die vorhergesagten Werte. Dadurch können wir die Prognoseergebnisse auf den Bereich [-1, 1] beschränken.
Als Nächstes müssen wir die vorhergesagten Werte in die erforderliche Sequenz konvertieren. Wir führen diese Operation mithilfe von zwei aufeinanderfolgenden Datentranspositionsebenen durch, die die inversen Permutationsoperationen der Werte durchführen.
if(!acTranspose[2].Init(0, 4, OpenCL, period, variables * forecast / period, optimization, iBatch)) return false; if(!acTranspose[3].Init(0, 5, OpenCL, variables, forecast, optimization, iBatch)) return false;
Um unnötiges Kopieren von Daten zu vermeiden, organisieren wir den Austausch der Ergebnispuffer und Fehlergradienten der aktuellen Schicht.
if(!SetOutput(acTranspose[3].getOutput()) || !SetGradient(acTranspose[3].getGradient()) ) return false; //--- return true; }
Bei jeder Iteration überprüfen wir die Ergebnisse der Operationen. Das endgültige logische Ergebnis der Methodenoperation wird an den Anrufer zurückgegeben.
Bitte beachten Sie, dass wir während des Objektinitialisierungsprozesses die Architekturparameter der von uns erstellten Ebene nicht gespeichert haben. In diesem Fall müssen wir nur die entsprechenden Parameter an die vernetzen Objekte übergeben. Ihre Architektur definiert die Funktionsweise der Klasse eindeutig, sodass die empfangenen Parameter nicht zusätzlich gespeichert werden müssen.
Nach der Initialisierung des Klassenobjekts fahren wir mit der Erstellung der Methode des Vorwärtsdurchgangs CNeuronSparseTSF::feedForward fort, in der wir den Algorithmus der Methode SparseTSF mit der Datenübertragung zwischen internen Objekten konstruieren.
In den Parametern der Vorwärts-Methode erhalten wir einen Zeiger auf das Objekt der vorherigen Schicht, das die Originaldaten enthält.
bool CNeuronSparseTSF::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!acTranspose[0].FeedForward(NeuronOCL)) return false;
Da wir den Algorithmus mithilfe zuvor erstellter Methoden vernetzen Objekte neu erstellen, fügen wir die Validierung des empfangenen Zeigers nicht hinzu. Wir übergeben es einfach an die Vorwärts-Methode der ersten Datentranspositionsschicht, in der neben den Operationen der Hauptfunktionalität im Zusammenhang mit der Datenpermutation im Datenpuffer bereits eine ähnliche Prüfung implementiert ist. Wir überprüfen nur das logische Ergebnis der Ausführung der Operationen der aufgerufenen Methode.
Als Nächstes führen wir eine Datenaggregation durch, indem wir die Feedforward-Methode der Faltungsschicht aufrufen.
if(!cConvolution.FeedForward(acTranspose[0].AsObject())) return false;
Gemäß dem Algorithmus SparseTSF werden die aggregierten Daten mit den Originaldaten summiert. Um jedoch die Konsistenz der Daten zu wahren, summieren wir die transponierte Version der Originaldaten mit den Aggregationsergebnissen.
if(!SumAndNormilize(cConvolution.getOutput(), acTranspose[0].getOutput(), cConvolution.getOutput(), 1, false)) return false;
Im nächsten Schritt rufen wir die Vorwärts-Methode der nächsten Datentranspositionsschicht auf, die den Diskretisierungsprozess der ursprünglichen Sequenz abschließt.
if(!acTranspose[1].FeedForward(cConvolution.AsObject())) return false;
Anschließend prognostizieren wir mithilfe der zweiten, verbundenen Faltungsschicht die wahrscheinlichste Fortsetzung der analysierten Zeitreihe.
if(!cForecast.FeedForward(acTranspose[1].AsObject())) return false;
Ich möchte Sie daran erinnern, dass die Prognose von Teilfolgen auf der Grundlage der Analyse einzelner Schritte innerhalb der gegebenen Periodizität der Ausgangsdaten erfolgt. In diesem Fall erstellen wir unabhängige Prognosen für jede einheitliche Sequenz der multimodalen Eingabezeitreihe. Für jeden Schritt des geschlossenen Zyklus der Eingabedatenperiodizität verwenden wir individuelle Trainingsparameter.
Die Neuanordnung der vorhergesagten Werte in die erforderliche Reihenfolge der erwarteten Ausgabesequenz wird mithilfe von zwei aufeinanderfolgenden Datentranspositionsebenen durchgeführt.
if(!acTranspose[2].FeedForward(cForecast.AsObject())) return false; if(!acTranspose[3].FeedForward(acTranspose[2].AsObject())) return false; //--- return true; }
Natürlich könnten wir für den Schritt der Neuanordnung der vorhergesagten Werte im Datenpuffer einen neuen Kernel erstellen und die beiden Transpositionsebenen durch einen einzigen Kernel-Aufruf ersetzen. Dies würde zu einer gewissen Leistungsverbesserung führen, da unnötige Datenübertragungsvorgänge eliminiert würden. Angesichts der Größe des Modells ist der erwartete Leistungsgewinn jedoch vernachlässigbar. In diesem Experiment haben wir uns dafür entschieden, den Programmcode zu vereinfachen und den Arbeitsaufwand des Programmierers zu reduzieren.
Es ist wichtig zu beachten, dass die Operationen der Vorwärts-Methode mit der Ausführung der Vorwärts-Methoden der vernetzen Objekte abschließen. Gleichzeitig übertragen wir keine Werte in den Ergebnispuffer der aktuellen Ebene, der von der übergeordneten Klasse abgeleitet wird. Nachfolgende Schichten unseres Modells haben jedoch keinen Zugriff auf die vernetzen Objekte und arbeiten mit dem Ergebnispuffer unserer Schicht. Um diese offensichtliche Lücke im Datenfluss auszugleichen, haben wir während der Initialisierung unserer Klasse die Ergebnis- und Fehlergradientenpuffer ersetzt. Als Ergebnis erhielt der Ergebnispuffer unserer Schicht einen Zeiger auf den Ergebnispuffer der letzten Transpositionsschicht. Indem wir die letzte Transpositionsoperation durchführen, schreiben wir Daten effektiv in den Ergebnispuffer unserer Ebene und vermeiden so unnötige Datenübertragungsoperationen zwischen Objekten.
Wie immer überprüfen wir in jeder Phase das Ergebnis der Operationen und geben das endgültige logische Ergebnis an das aufrufende Programm zurück.
Damit schließen wir die Implementierung des Vorwärtsdurchgangs der Methode SparseTSF ab und fahren mit der Konstruktion der Backpropagation-Algorithmen fort. Dabei gilt es, den Fehlergradienten auf alle Prozessteilnehmer entsprechend ihres Einflusses auf das Ergebnis zu verteilen und die Modellparameter so anzupassen, dass der Prognosefehler der analysierten multimodalen Zeitreihe möglichst gering bleibt.
Der erste Schritt besteht darin, eine Methode zur Verteilung des Fehlergradienten zu entwickeln: CNeuronSparseTSF::calcInputGradients. Wie beim Vorwärtsdurchgang enthalten die Methodenparameter einen Zeiger auf das Objekt der vorherigen Ebene, wo wir den Fehlergradienten basierend auf dem Einfluss der Originaldaten auf die Modellausgabe aufzeichnen.
bool CNeuronSparseTSF::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!acTranspose[2].calcHiddenGradients(acTranspose[3].AsObject())) return false;
Wir verteilen den Fehlergradienten entsprechend den Vorwärts-Operationen, jedoch in umgekehrter Reihenfolge. Wie Sie wissen, landet der von der nächsten Modellschicht empfangene Fehlergradient aufgrund der Zeigersubstitution für Datenpuffer im Puffer der letzten internen Transpositionsschicht. Dadurch können wir direkt mit internen Objekten fortfahren, ohne zusätzliche Datenübertragungsvorgänge.
Zuerst leiten wir den Fehlergradienten durch die beiden Transpositionsschichten, um die erforderliche Diskretisierung der Gradienten zu erreichen.
if(!cForecast.calcHiddenGradients(acTranspose[2].AsObject())) return false;
Bei Bedarf passen wir den erhaltenen Gradienten durch die Ableitung der Aktivierungsfunktion der Datenvorhersageschicht an.
if(cForecast.Activation() != None && !DeActivation(cForecast.getOutput(), cForecast.getGradient(), cForecast.getGradient(), cForecast.Activation())) return false;
Anschließend propagieren wir den Fehlergradienten auf die Ebene der aggregierten Daten.
if(!acTranspose[1].calcHiddenGradients(cForecast.AsObject())) return false; if(!cConvolution.calcHiddenGradients(acTranspose[1].AsObject())) return false;
Dann leiten wir den Fehlergradienten durch die Aggregationsschicht weiter.
if(!acTranspose[0].calcHiddenGradients(cConvolution.AsObject())) return false;
Beim Aggregieren der Daten nutzten wir Residualbeziehungen, indem wir die aggregierten Daten und die ursprüngliche Sequenz summierten. Daher durchläuft der Fehlergradient auch zwei Datenströme und wir summieren die Werte der beiden Fehlergradientenpuffer.
if(!SumAndNormilize(cConvolution.getGradient(), acTranspose[0].getGradient(), acTranspose[0].getGradient(), 1, false)) return false;
Anschließend übertragen wir den erhaltenen Fehlergradienten auf die vorherige Schicht und passen ihn, falls erforderlich, an die Ableitung der Aktivierungsfunktion an.
if(!NeuronOCL || !NeuronOCL.calcHiddenGradients(acTranspose[0].AsObject())) return false; if(NeuronOCL.Activation() != None && !DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(), NeuronOCL.Activation())) //--- return true; }
Am Ende der Methode geben wir das logische Ergebnis der durchgeführten Operationen an das aufrufende Programm zurück.
Nachdem wir den Fehlergradienten entsprechend ihrem Einfluss auf das Endergebnis auf alle Objekte unseres Modells verteilt haben, müssen wir die Modellparameter anpassen, um den Datenprognosefehler zu minimieren. Diese Funktionalität wird in der Methode CNeuronSparseTSF::updateInputWeights ausgeführt. Hier ist alles ganz unkompliziert. Unsere neue Klasse enthält nur 2 interne Faltungsschichten, die die trainierbaren Parameter enthalten. Wie Sie wissen, werden bei der Datentransposition keine trainierbaren Parameter verwendet. Daher müssen wir im Rahmen des Prozesses zur Anpassung der Modellparameter nur die Methoden der verbundenen Faltungsschichten mit demselben Namen aufrufen und den logischen Wert der Ausführung der Operationen der aufgerufenen Methoden überprüfen. Der gesamte Prozess der Parameteranpassung ist bereits in interne Objekte integriert.
bool CNeuronSparseTSF::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cConvolution.UpdateInputWeights(acTranspose[0].AsObject())) return false; if(!cForecast.UpdateInputWeights(acTranspose[1].AsObject())) return false; //--- return true; }
Damit ist die Beschreibung der Methoden der Hauptfunktionalität unserer neuen Klasse CNeuronSparseTSF abgeschlossen. Alle Hilfsmethoden dieser Klasse folgen der Ihnen aus den vorherigen Artikeln dieser Serie bekannten Logik. Deshalb werden wir in diesem Artikel nicht näher darauf eingehen. Den vollständigen Code aller Methoden der neuen Klasse finden Sie im Anhang.
2.2 Die Architektur trainierbarer Modelle
Wir haben die wichtigsten Ansätze des Algorithmus von SparseTSF in MQL5 in der neuen Klasse CNeuronSparseTSF implementiert. Jetzt müssen wir ein Objekt der neuen Klasse in unser Modell implementieren. Ich denke, es ist offensichtlich, dass wir den Algorithmus zur Zeitreihenprognose im Encoder-Modell verwenden werden, wenn der Umgebungszustand … Die Architektur dieses Modells wird in der Methode CreateEncoderDescriptions dargestellt. In seinen Parametern übergeben wir einen Zeiger auf ein dynamisches Array-Objekt zum Schreiben der Architektur des Modells.
bool CreateEncoderDescriptions(CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
Im Methodenkörper validieren wir die Relevanz des empfangenen Zeigers und erstellen bei Bedarf ein neues dynamisches Array-Objekt.
Als Nächstes verwenden wir wie üblich eine grundlegende, vollständig verbundene Schicht, um die Anfangsdaten zu schreiben.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM_MINI; if(!encoder.Add(descr)) { delete descr; return false; }
Wir speisen „rohe“, unverarbeitete Eingabedaten in das Modell ein. Eine aufwändige Aufbereitung der Ausgangsdaten auf Seiten des Hauptprogramms entfällt dadurch. Die empfangenen Daten werden dann in der Batch-Normalisierungsschicht vorverarbeitet.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Nach dieser Schicht folgt die neue Schicht der Methode SparseTSF.
if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSparseTSF; descr.count = HistoryBars; descr.window = BarDescr;
Ich möchte Sie daran erinnern, dass wir in dieser Reihe unsere Modelle mithilfe historischer Daten aus dem Zeitrahmen H1 trainieren und testen. Unter diesen Bedingungen legen wir die Größe des anfänglichen Datenzeitraums auf 24 fest, welches einem Kalendertag entspricht.
descr.step = 24; descr.window_out = NForecast; descr.activation = None; descr.optimization = ADAM_MINI; if(!encoder.Add(descr)) { delete descr; return false; }
Dabei ist zu beachten, dass die Anwendung der hier betrachteten Modelle nicht auf den Zeitrahmen von H1 beschränkt ist. Durch das Testen und Trainieren verschiedener Modelle unter denselben Bedingungen können wir jedoch die Leistung der Modelle bewerten und gleichzeitig den Einfluss externer Faktoren minimieren.
Trotz ihrer scheinbaren Einfachheit ist die Methode SparseTSF ziemlich komplex und autark. Um die gewünschte Prognose der bevorstehenden Preisbewegung zu erhalten, müssen wir nur die Verteilungsindikatoren der Originaldaten hinzufügen, die in der Batch-Normalisierungsebene extrahiert wurden.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = BarDescr * NForecast; descr.activation = None; descr.optimization = ADAM; descr.layers = 1; if(!encoder.Add(descr)) { delete descr; return false; }
Um die Häufigkeitscharakteristika der vorhergesagten Werte anzugleichen, verwenden wir die Ansätze der Methode FreDF.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronFreDFOCL; descr.window = BarDescr; descr.count = NForecast; descr.step = int(true); descr.probability = 0.7f; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- return true; }
Wie Sie sehen, ist die Architektur des Umgebungszustands des Encoder-Modells recht kurz. Dies steht im Einklang mit der von den Autoren von SparseTSF angegebenen Leichtgewichtigkeit.
Wir kopieren Akteur (Actor) und Kritiker (Critic) aus dem vorherigen Artikel ohne Änderungen. Gleiches gilt für Programme zum Training von Modellen und zur Interaktion mit der Umgebung. Deshalb werden wir im Rahmen dieses Artikels nicht näher darauf eingehen. Der vollständige Code für alle in diesem Artikel verwendeten Programme ist im Anhang enthalten.
3. Tests
In den vorherigen Abschnitten dieses Artikels haben wir die theoretischen Aspekte der Methode SparseTSF betrachtet und die von den Autoren der Methode vorgeschlagenen Ansätze mit MQL5 implementiert. Jetzt ist es an der Zeit, die Wirksamkeit der vorgeschlagenen Ansätze im Hinblick auf ihre Fähigkeit zu bewerten, künftige Preisbewegungen anhand realer historischer Daten vorherzusagen. Wir müssen auch die Möglichkeit prüfen, die erhaltenen Prognosen für die Entwicklung einer wirksamen Handlungspolitik für die Akteure zu nutzen.
Beim Aufbau des neuen Modells haben wir keine Änderungen an der Struktur der Eingabedaten und den erwarteten Prognoseergebnissen vorgenommen. Daher können wir die Umgebungsinteraktions- und Modelltrainingsprogramme aus früheren Arbeiten ohne Änderungen verwenden. Außerdem können wir zuvor gesammelte Trainingsdatensätze für das anfängliche Training von Modellen verwenden. Daher trainieren wir den Umgebungszustands des Encoders mithilfe des Erfahrungswiedergabepuffers zuvor trainierter Modelle.
Wie Sie sich erinnern, arbeitet der Umgebungszustands des Encoders nur mit Preisbewegungen und Werten der analysierten Indikatoren, die nicht von den Aktionen des Akteurs abhängen. Dementsprechend nimmt der Encoder alle Durchläufe im Trainingsdatensatz in einem historischen Intervall als identisch wahr. Das bedeutet, dass wir den Encoder trainieren können, ohne den Trainingsdatensatz aktualisieren zu müssen. Und die Leichtgewichtigkeit des vorgeschlagenen Modells ermöglicht es, den für das Training des Encoders erforderlichen Ressourcen- und Zeitaufwand erheblich zu reduzieren.
Wir können nicht sagen, dass der Modelltrainingsprozess hochpräzise Vorhersagen nachfolgender Zustände hervorgebracht hat. Aber insgesamt ist die Qualität der Prognosen mit der komplexeren Modellen vergleichbar, die mehr Ressourcen und Zeit zum Trainieren erfordern. Wir können also sagen, dass wir das gewünschte Ergebnis teilweise erreicht haben.
Die zweite Phase besteht darin, die Akteurs-Richtlinie basierend auf den erhaltenen vorhergesagten Werten zu trainieren. In dieser Phase führen wir ein iteratives Training der Modelle mit regelmäßiger Aktualisierung des Trainingsdatensatzes durch, wodurch wir über einen aktuellen Trainingsdatensatz mit einer echten Belohnung für die Verteilung von Aktionen verfügen, die der aktuellen Richtlinie des Akteurs nahe kommen. Ich muss zugeben, dass ich in diesem Stadium positiv überrascht war – die auf den ersten Blick wenig beeindruckenden Vorhersagen zukünftiger Preisbewegungen erwiesen sich als recht aufschlussreich für die Konstruktion der Strategien des Akteurs, die sowohl mit den Trainings- als auch mit den Testdatensätzen Gewinne erzielen konnten.
Zum Trainieren der Modelle haben wir historische Daten für das Instrument EURUSD im Zeitrahmen von H1 für das gesamte Jahr 2023 verwendet. Die Parameter aller analysierten Indikatoren werden auf Standardwerte gesetzt. Die trainierten Modelle wurden dann anhand historischer Daten ab Januar 2024 getestet, wobei alle anderen Parameter unverändert gelassen wurden. Daher haben wir die Modelltests eng an realen Bedingungen ausgerichtet.
Die Testergebnisse des trainierten Modells werden unten dargestellt.
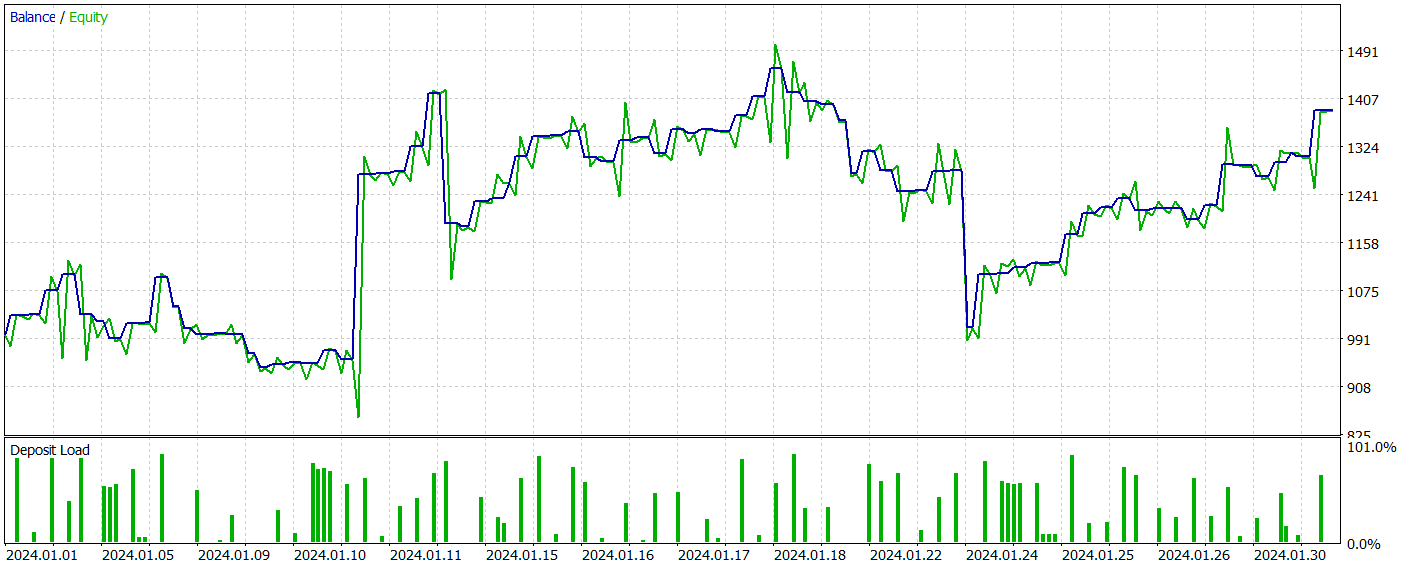
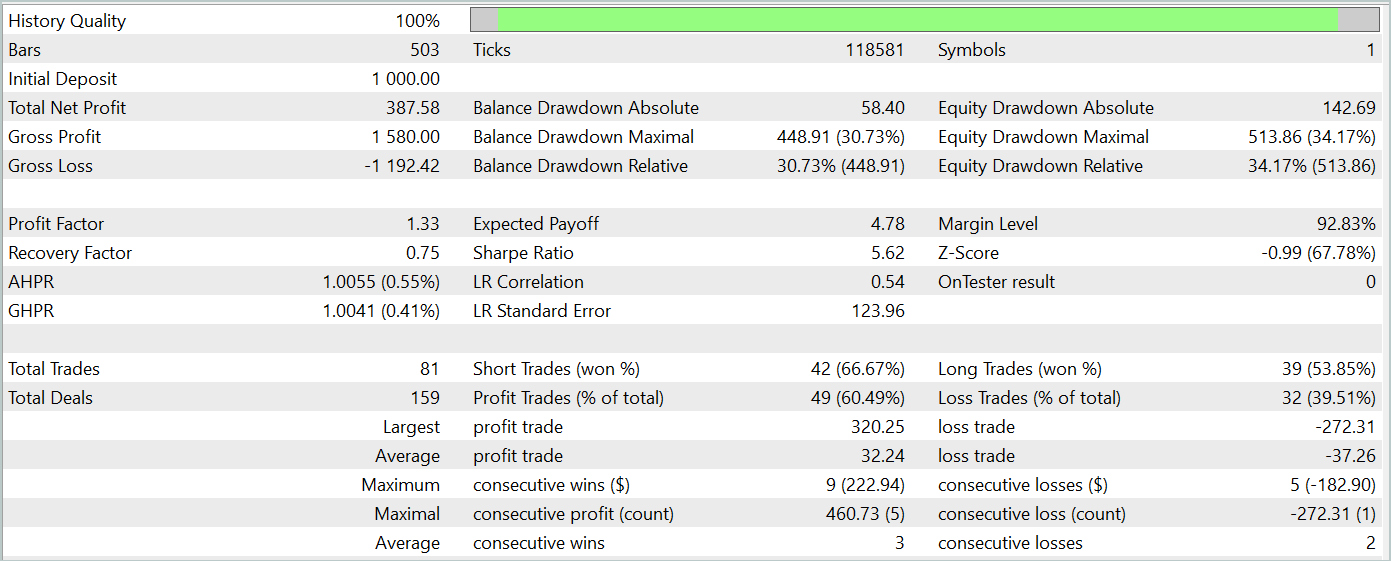
Während des Testzeitraums führte das Modell 81 Handelsgeschäfte aus. Das Verhältnis von Kauf- und Verkaufs-Positionen war nahezu gleich: 42 gegenüber 39. Mehr als 60 % der Handelsgeschäfte wurden mit Gewinn abgeschlossen, was zu einem Gewinnfaktor von 1,33 führte.
Eine Besonderheit von SparseTSF besteht darin, dass sie Daten in Form einzelner Schritte innerhalb des Zyklizitätszeitraums der Originaldaten prognostiziert. Zur Erinnerung: Im trainierten Umgebungszustand des Encoders haben wir H1-Daten mit einer Zykluszeit von 24 Stunden analysiert. Dieser Aspekt macht die Rentabilität des Modells bei einer Betrachtung auf Stundenbasis besonders interessant.
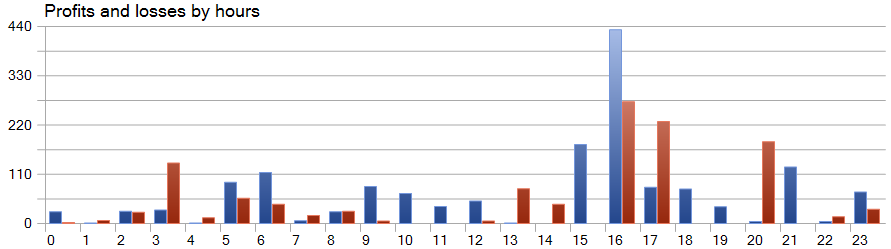
In der dargestellten Grafik stellen wir fest, dass es in der ersten Hälfte der europäischen Sitzung von 9:00 bis 12:00 Uhr praktisch keine Verluste gab. Die durchschnittliche Dauer eines Handelsgeschäfts von 1 Stunde und 6 Minuten weist auf eine minimale Verzögerung zwischen dem Handelsbeginn und der Realisierung des Gewinns/Verlusts hin. Die höchste Rentabilität tritt zu Beginn der amerikanischen Sitzung (15:00 - 16:00 Uhr) auf.
Schlussfolgerung
In diesem Artikel haben wir SparseTSF vorgestellt, die aufgrund ihrer leichtgewichtigen Architektur und effizienten Ressourcennutzung Vorteile bei der Zeitreihenprognose aufweist. Aufgrund der minimalen Parameteranzahl ist das vorgeschlagene Modell besonders nützlich für Anwendungen mit begrenzten Rechenressourcen und kurzer Entscheidungszeit.
SparseTSF ermöglicht die Analyse einzelner Schritte in Zeitreihen mit einer bestimmten Periodizität und erstellt unabhängige Prognosen für jede einheitliche Sequenz. Dies verleiht dem Modell eine hohe Flexibilität und Anpassungsfähigkeit.
Im praktischen Teil des Artikels haben wir die vorgeschlagenen Ansätze mit MQL5 implementiert, das Modell trainiert und es anhand realer historischer Daten getestet. Als Ergebnis erhielten wir ein Modell, das sowohl mit Trainings- als auch mit Testdatensätzen Gewinne erzielen kann, was die Wirksamkeit der vorgeschlagenen Ansätze belegt.
Ich möchte Sie jedoch noch einmal daran erinnern, dass die in diesem Artikel vorgestellten Programme lediglich dazu gedacht sind, eine Variante der Implementierung der vorgeschlagenen Ansätze und ihrer Verwendung zu demonstrieren. Die vorgestellten Programme sind nicht für den Einsatz auf realen Finanzmärkten bereit.
Referenzen
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Beispielsammlung EA |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | StudyEncoder.mq5 | Expert Advisor | Trainings-EA des Encoders |
| 5 | Test.mq5 | Expert Advisor | Trainings-EA für das Model |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/15392
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Von der Grundstufe bis zur Mittelstufe: Variablen (III)
Von der Grundstufe bis zur Mittelstufe: Variablen (III)
 Künstlicher Bienenstock-Algorithmus (ABHA): Tests und Ergebnisse
Künstlicher Bienenstock-Algorithmus (ABHA): Tests und Ergebnisse
 Neuronale Netze im Handel: Verwenden von Sprachmodellen für die Zeitreihenprognose
Neuronale Netze im Handel: Verwenden von Sprachmodellen für die Zeitreihenprognose
 Neuronale Netze im Handel: Verringerung des Speicherverbrauchs mit der Adam-mini-Optimierung
Neuronale Netze im Handel: Verringerung des Speicherverbrauchs mit der Adam-mini-Optimierung
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.