Neuronale Netze im Handel: Räumlich-zeitliches neuronales Netz (STNN)

Einführung

Zeitreihenprognosen spielen in verschiedenen Bereichen, darunter auch im Finanzwesen, eine wichtige Rolle. Wir haben uns bereits daran gewöhnt, dass viele reale Systeme es uns ermöglichen, multidimensionale Daten zu messen, die umfangreiche Informationen über die Dynamik der Zielvariablen enthalten. Eine effektive Analyse und Vorhersage multivariater Zeitreihen wird jedoch häufig durch den „Fluch der Dimensionen“ behindert. Dies macht die Wahl des historischen Datenfensters für die Analyse zu einem kritischen Faktor. Wenn ein unzureichendes Fenster analysierter Daten verwendet wird, zeigt das Prognosemodell häufig eine unbefriedigende Leistung und versagt. 

Um der Komplexität multivariater Daten gerecht zu werden, wurde die Transformationsgleichung der „Spatio-Temporal Information“ (STI) entwickelt, die auf dem Delay Embedding Theorem basiert. Die STI-Gleichung transformiert die räumliche Information multivariater Variablen in die zeitliche Dynamik der Zielvariablen. Auf diese Weise wird die Stichprobengröße effektiv erhöht und die Probleme, die sich durch kurzfristige Daten ergeben, gemildert.

Transformer-basierte Modelle, die bereits mit der Handhabung von Datensequenzen vertraut sind, nutzen den Selbtaufmerksamkeit-Mechanismus, um Beziehungen zwischen Variablen zu analysieren, wobei ihre relativen Abstände außer Acht gelassen werden. Diese Aufmerksamkeitsmechanismen erfassen globale Informationen und konzentrieren sich auf die wichtigsten Merkmale, wodurch der Fluch der Dimensionalität gemildert wird.

In der Studie „Spatiotemporal Transformer Neural Network for Time-Series Forecasting“ wurde ein Spatiotemporal Transformer Neural Network (STNN) vorgeschlagen, das eine effiziente mehrstufige Vorhersage von multivariaten Kurzzeit-Zeitreihen ermöglicht. Dieser Ansatz macht sich die Vorteile der STI-Gleichung und des Transformer-Rahmens zunutze.

Die Autoren heben mehrere wesentliche Vorteile der von ihnen vorgeschlagenen Methoden hervor:

1. STNN verwendet die STI-Gleichung, um die räumlichen Informationen der multivariaten Variablen in die zeitliche Entwicklung der Zielvariablen umzuwandeln, wodurch sich der Stichprobenumfang effektiv erhöht.
2. Es wird ein kontinuierlicher Aufmerksamkeitsmechanismus vorgeschlagen, um die Genauigkeit der numerischen Vorhersage zu verbessern.
3. Die räumliche Selbtaufmerksamkeit-Struktur im STNN sammelt effizient räumliche Informationen aus multivariaten Variablen, während die zeitliche Selbtaufmerksamkeit-Struktur Informationen über die zeitliche Entwicklung sammelt. Die Transformer-Struktur kombiniert räumliche und zeitliche Informationen.
4. Das STNN-Modell kann den Phasenraum eines dynamischen Systems für Zeitreihenprognosen rekonstruieren.

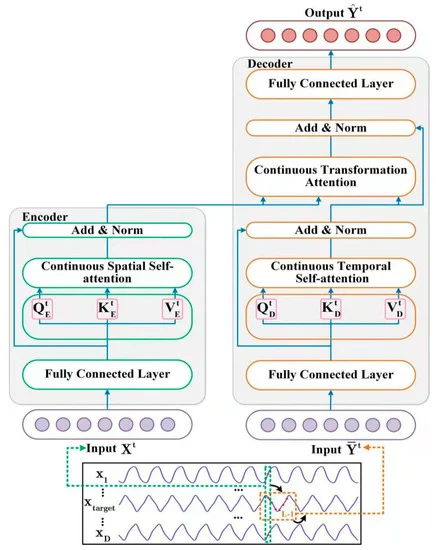
1. STNN-Algorithmus

Der Zweck des STNN-Modells ist die effektive Lösung der nichtlinearen Transformationsgleichung STI durch Transformer-Training.

Das STNN-Modell nutzt die Transformationsgleichung STI und umfasst zwei spezielle Aufmerksamkeitsmodule zur Durchführung von Vorhersagen in mehreren Schritten. Wie Sie aus der obigen Gleichung ersehen können, werden die D-dimensionalen Eingangsdaten zum Zeitpunkt t (Xt) in den Encoder eingespeist, der aus den Eingangsvariablen effektive räumliche Informationen extrahiert.

Danach wird die effektive räumliche Information an den Decoder übertragen, der eine Zeitreihe der Länge L-1 aus der Zielvariablen Y (𝐘t) einführt. Der Decoder extrahiert Informationen über die zeitliche Entwicklung der Zielvariablen. Anschließend werden die zukünftigen Werte der Zielvariablen vorhergesagt, indem die räumlichen Informationen der Eingangsvariablen (𝐗t) und die zeitlichen Informationen der Zielvariablen (𝐘t) kombiniert werden.

Beachten Sie, dass die Zielvariable eine der Variablen in den multivariaten Eingabedaten X ist.

Die nichtlineare Transformation von STI wird durch das Encoder-Decoder-Paar gelöst. Der Encoder besteht aus 2 Schichten. Bei der ersten handelt es sich um eine vollständig vernetzte Schicht, bei der zweiten um eine kontinuierliche räumliche Selbtaufmerksamkeit-Schicht. Die Autoren der STNN-Methode verwenden eine kontinuierliche räumliche Selbtaufmerksamkeit-Schicht, um effektive räumliche Informationen aus multivariaten Eingabedaten 𝐗t zu extrahieren.

Eine vollständig verknüpfte Schicht wird verwendet, um die multivariaten Zeitreihendaten 𝐗t zu glätten und Rauschen herauszufiltern. Ein einschichtiges neuronales Netz ist in der folgenden Abbildung dargestellt.

Dabei ist WFFN die Matrix der Koeffizienten
      bFFN ist die Verzerrung
      ELU ist die Aktivierungsfunktion.

Die kontinuierliche räumliche Selbtaufmerksamkeit-Schicht akzeptiert 𝐗t,FFN als Eingangsdaten. Da die Selbtaufmerksamkeit-Schicht eine multivariate Zeitreihe akzeptiert, kann der Encoder räumliche Informationen aus den Eingabedaten extrahieren. Um effektive räumliche Informationen (SSAt) zu erhalten, wird ein Mechanismus der kontinuierlichen Aufmerksamkeit der räumlichen Selbstaufmerksamkeitsschicht vorgeschlagen. Seine Funktionsweise kann wie folgt beschrieben werden.

Zunächst werden drei Matrizen mit trainierbaren Parametern (WQE, WKE and WVE) erstellt, die in der kontinuierlichen räumlichen Selbstbeobachtungsschicht verwendet werden.

Durch Multiplikation der Eingabedaten 𝐗t,FFN mit den oben genannten Gewichtungsmatrizen werden dann die Einheiten von Query, Key und Value (Anfrage, Schlüssel, Wert) der kontinuierlichen räumlichen Selbtaufmerksamkeit-Schicht erzeugt.

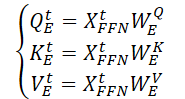
Mit Hilfe des Skalarprodukts der Matrix erhalten wir einen Ausdruck für die räumliche Schlüsselinformation (SSAt) für die Eingabedaten 𝐗t.

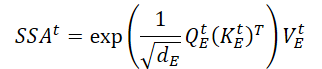
Dabei ist ddE die Dimension der Matizen von Query, Key und Value.

Die Autoren der STNN-Methode betonen, dass im Gegensatz zum klassischen Mechanismus der diskreten probabilistischen Aufmerksamkeit der vorgeschlagene Mechanismus der kontinuierlichen Aufmerksamkeit eine ununterbrochene Übertragung der Encoder-Daten gewährleisten kann.

Am Ausgang des Encoders summieren wir den zentralen räumlichen Informationstensor mit den geglätteten Eingabedaten, gefolgt von einer Datennormalisierung, die das schnelle Verschwinden des Gradienten verhindert und die Konvergenzrate des Modells beschleunigt.

Der Decoder kombiniert effektive räumliche Informationen und zeitliche evolutionäre Zielvariablen. Seine Architektur umfasst 2 vollständig verknüpfte Schichten, eine kontinuierliche zeitliche Selbstaufmerksamkeitsschicht und eine Schicht der Transformationsaufmerksamkeit.

Wir füttern den Decoder mit den Eingangsdaten der historischen Sequenz der Zielvariablen. Wie beim Encoder werden die Eingangsdaten (𝐘t,FFN) nach dem Herausfiltern des Rauschens mit einer vollständig verbundenen Schicht effizient dargestellt.

Die empfangenen Daten werden dann an die kontinuierliche zeitliche Selbtaufmerksamkeit-Schicht weitergeleitet, die sich auf historische Informationen über die zeitliche Entwicklung zwischen verschiedenen Zeitschritten der Zielvariablen konzentriert. Da der Einfluss der Zeit unumkehrbar ist, bestimmen wir den aktuellen Zustand der Zeitreihe anhand historischer Informationen, aber nicht anhand zukünftiger Informationen. Die kontinuierliche zeitliche Aufmerksamkeitsschicht nutzt also den Mechanismus der maskierten Aufmerksamkeit, um zukünftige Informationen herauszufiltern. Schauen wir uns diesen Vorgang einmal genauer an.

Zunächst erstellen wir 3 Matrizen mit trainierbaren Parameter (WQD, WKD und WVD) für die räumlich-zeitliche Selbstaufmerksamkeitsschicht. Dann werden wir die entsprechenden Matrizen von Query, Key und Value berechnen.

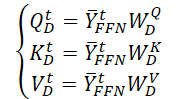
Wir führen ein Matrix-Skalarprodukt durch, um Informationen über die zeitliche Entwicklung der Zielvariablen über den analysierten Zeitraum zu erhalten.

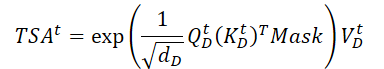
Im Gegensatz zum Encoder fügen wir hier eine Maske hinzu, die den Einfluss der nachfolgenden Elemente der analysierten Daten entfernt. Auf diese Weise erlauben wir dem Modell nicht, bei der Konstruktion der zeitlichen Entwicklungsfunktion der Zielvariablen „in die Zukunft zu schauen“.

Als Nächstes verwenden wir die Residualverbindung und normalisieren die Informationen über die zeitliche Entwicklung der Zielvariablen.

Die kontinuierliche Transformationsaufmerksamkeitsschicht zur Vorhersage zukünftiger Werte der Zielvariablen integriert Informationen über die räumliche Abhängigkeit (SSAt) mit Daten über die zeitliche Entwicklung der Zielvariablen (TSAt).

Auch hier werden Restbeziehungen und Datennormalisierung verwendet.

Am Ausgang des Decoders verwenden die Autoren der Methode eine zweite voll verknüpfte Schicht, um die Werte der Zielvariablen vorherzusagen

Beim Training des STNN-Modells verwendeten die Autoren der Methode MSE als Verlustfunktion und L2-Regularisierung der Parameter.

Im Folgenden wird die Visualisierung der Methode durch den Autor vorgestellt.

2. Implementierung in MQL5

Nach der Betrachtung der theoretischen Aspekte der STNN-Methode gehen wir zum praktischen Teil unseres Artikels über, in dem wir die vorgeschlagenen Ansätze in MQL5 implementieren.

In diesem Artikel stellen wir unsere eigene Vorstellung von der Umsetzung vor, die von der Umsetzung der Methode durch den Autor abweichen kann. Außerdem haben wir im Rahmen dieser Umsetzung versucht, unsere bestehenden Entwicklungen optimal zu nutzen, was sich ebenfalls auf das Ergebnis ausgewirkt hat. Darüber werden wir bei der Umsetzung der vorgeschlagenen Ansätze sprechen.

Wie Sie vielleicht aus der theoretischen Beschreibung des oben vorgestellten STNN-Algorithmus ersehen haben, umfasst er 2 Hauptblöcke: Kodierer und Dekodierer. Wir werden unsere Arbeit auch in die Implementierung von 2 entsprechenden Klassen unterteilen. Beginnen wir mit der Implementierung des Encoders.

2.1 STNN-Kodierer

Wir werden den Encoder-Algorithmus innerhalb der Klasse CNeuronSTNNEncoder implementieren. Die Autoren der Methode haben einige Anpassungen am Selbtaufmerksamkeit-Algorithmus vorgenommen. Er ist jedoch nach wie vor gut erkennbar und enthält die grundlegenden Komponenten des klassischen Ansatzes. Um eine neue Klasse zu implementieren, werden wir daher bestehende Entwicklungen nutzen und die Hauptfunktionalität des grundlegenden Selbstaufmerksamkeitsalgorithmus von der Klasse CNeuronMLMHAttentionMLKV erben. Die allgemeine Struktur der neuen Klasse wird im Folgenden dargestellt.

class CNeuronSTNNEncoder  :  public CNeuronMLMHAttentionMLKV
  {
protected:
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronSTNNEncoder(void)  {};
                    ~CNeuronSTNNEncoder(void)  {};
   //---
   virtual int       Type(void)   override const   {  return defNeuronSTNNEncoder;   }
  };

Wie Sie sehen können, gibt es keine Deklarationen neuer Variablen und Objekte innerhalb der neuen Klasse. Außerdem enthält die vorgestellte Struktur nicht einmal eine Überschreibung der Objektinitialisierungsmethoden. Hierfür gibt es Gründe. Wie bereits erwähnt, nutzen wir unsere bestehenden Entwicklungen optimal aus.

Betrachten wir zunächst die Unterschiede zwischen den vorgeschlagenen Ansätzen und denen, die wir bisher umgesetzt haben. Zunächst einmal haben die Autoren der STNN-Methode eine vollständig verknüpfte Schicht vor den Block Selbstaufmerksamkeit gesetzt. Technisch gesehen gibt es kein Problem mit der Objektdeklaration, da sie nur die Implementierung der Algorithmen für den Vorwärts- und Rückwärtsdruchgang betrifft. Dies bedeutet, dass die Implementierung dieses Moments den Algorithmus der Initialisierungsmethode nicht beeinflusst.

Der zweite Punkt ist, dass die Autoren der STNN-Methode nur eine vollständig verbundene Schicht vorgesehen haben. Beim klassischen Ansatz wird jedoch ein Block aus 2 vollständig verbundenen Schichten erstellt. Ich persönlich bin der Meinung, dass die Verwendung eines Blocks von 2 vollständig verknüpften Schichten zwar den Rechenaufwand erhöht, aber die Qualität des Modells nicht beeinträchtigt. Versuchsweise können wir, um die Erhaltung bestehender Entwicklungen zu maximieren, 2 Schichten anstelle von 1 verwenden.

Darüber hinaus haben die Autoren der Methode die SoftMax-Funktion aus dem Schritt der Normalisierung der Aufmerksamkeitskoeffizienten entfernt. Stattdessen verwenden sie einfache Matrixproduktexponenten für Query und Key. Meiner Meinung nach liegt der Unterschied von SoftMax nur in der Datennormalisierung und den komplexeren Berechnungen. Daher werde ich bei meiner Implementierung den zuvor mit SoftMax umgesetzten Ansatz verwenden.   

Als Nächstes werden wir uns mit der Implementierung der Algorithmen der Vorwärtsdurchgänge befassen. Hier ist mir aufgefallen, dass die Autoren der Methode die Maskierung der nachfolgenden Elemente nur im Decoder implementiert haben. Wir erinnern uns, dass die Zielvariable in der Menge der Ausgangsdaten des Encoders enthalten sein kann. Ich dachte, es gäbe eine gewisse Unlogik. Aber alles wird klar, wenn man die Visualisierung der Methode durch den Autor genau studiert.

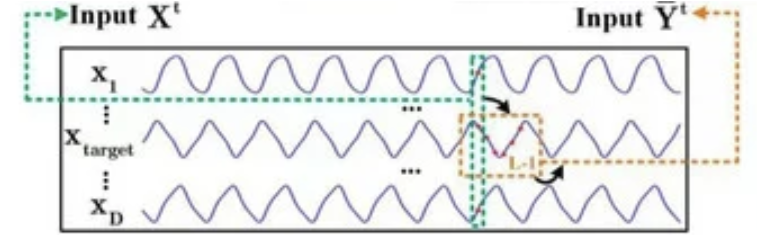
Die Eingänge des Encoders befinden sich in einiger Entfernung vom analysierten Zustand. Ich kann nicht beurteilen, warum die Autoren der Methode diese Umsetzung gewählt haben. Ich persönlich bin jedoch der Meinung, dass wir durch die Verwendung aller zum Zeitpunkt der Datenanalyse verfügbaren Informationen mehr Informationen erhalten und die Qualität unserer Prognosen möglicherweise verbessern können. In meiner Implementierung verschiebe ich also die Eingaben des Encoders auf den aktuellen Zeitpunkt und füge eine Maske der Ausgangsdaten hinzu, die es uns ermöglicht, Abhängigkeiten nur mit früheren Daten zu analysieren.

Um die Datenmaskierung zu implementieren, müssen wir Änderungen am OpenCL-Programm vornehmen. Hier werden wir nur kleine Änderungen an der MH2AttentionOut Kernel vornehmen. Wir werden keinen zusätzlichen Maskierungspuffer verwenden. Wir werden es auf eine einfachere Weise tun. Fügen wir nur eine Konstante hinzu, die bestimmt, ob wir eine Maske verwenden müssen. Die Maskierung wird direkt im Kernel-Algorithmus organisiert. 

__kernel void MH2AttentionOut(__global float *q,
                              __global float *kv,
                              __global float *score,
                              __global float *out,
                              int dimension,
                              int heads_kv,
                              int mask ///< 1 - calc only previous units, 0 - calc all
                             )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_global_size(1);
   const int heads = get_global_size(2);
   const int h_kv = h % heads_kv;
   const int shift_q = dimension * (q_id * heads + h);
   const int shift_k = dimension * (2 *  heads_kv * k + h_kv);
   const int shift_v = dimension * (2 *  heads_kv * k + heads_kv + h_kv);
   const int shift_s = kunits * (q_id *  heads + h) + k;
   const uint ls = min((uint)get_local_size(1), (uint)LOCAL_ARRAY_SIZE);
   float koef = sqrt((float)dimension);
   if(koef < 1)
      koef = 1;
   __local float temp[LOCAL_ARRAY_SIZE];

Im Hauptteil des Kernels werden wir bei der Berechnung der Summe der Exponenten nur geringfügige Anpassungen vornehmen. 

//--- sum of exp
   uint count = 0;
   if(k < ls)
     {
      temp[k] = 0;
      do
        {
         if(mask == 0 || q_id <= (count * ls + k))
            if((count * ls) < (kunits - k))
              {
               float sum = 0;
               int sh_k = 2 * dimension * heads_kv * count * ls;
               for(int d = 0; d < dimension; d++)
                  sum = q[shift_q + d] * kv[shift_k + d + sh_k];
               sum = exp(sum / koef);
               if(isnan(sum))
                  sum = 0;
               temp[k] = temp[k] + sum;
              }
         count++;
        }
      while((count * ls + k) < kunits);
     }
   barrier(CLK_LOCAL_MEM_FENCE);
   count = min(ls, (uint)kunits);

Hier fügen wir Bedingungen hinzu und berechnen die Exponenten nur für die vorangehenden Elemente. Bitte beachten Sie, dass wir bei der Erstellung der Inputs für das Modell diese aus Zeitreihen historischer Preisdaten und Indikatoren bilden. In Zeitreihen hat der aktuelle Balken den Index „0“. Um Elemente in der historischen Chronologie zu maskieren, setzen wir daher die Abhängigkeitskoeffizienten aller Elemente zurück, deren Index kleiner ist als die analysierte Query. Dies zeigt sich bei der Berechnung der Summe der Exponenten und der Abhängigkeitskoeffizienten (im Codeunterstrichen).

//---
   do
     {
      count = (count + 1) / 2;
      if(k < ls)
         temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0);
      if(k + count < ls)
         temp[k + count] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);
//--- score
   float sum = temp[0];
   float sc = 0;
   if(mask == 0 || q_id >= (count * ls + k))
      if(sum != 0)
        {
         for(int d = 0; d < dimension; d++)
            sc = q[shift_q + d] * kv[shift_k + d];
         sc = exp(sc / koef) / sum;
         if(isnan(sc))
            sc = 0;
        }
   score[shift_s] = sc;
   barrier(CLK_LOCAL_MEM_FENCE);

Der Rest des Kernel-Codes bleibt unverändert.

//--- out
   for(int d = 0; d < dimension; d++)
     {
      uint count = 0;
      if(k < ls)
         do
           {
            if((count * ls) < (kunits - k))
              {
               float sum =
                  kv[shift_v + d] * (count == 0 ? sc : score[shift_s + count * ls]);
               if(isnan(sum))
                  sum = 0;
               temp[k] = (count > 0 ? temp[k] : 0) + sum;
              }
            count++;
           }
         while((count * ls + k) < kunits);
      barrier(CLK_LOCAL_MEM_FENCE);
      //---
      count = min(ls, (uint)kunits);
      do
        {
         count = (count + 1) / 2;
         if(k < ls)
            temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : 0);
         if(k + count < ls)
            temp[k + count] = 0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);
      //---
      out[shift_q + d] = temp[0];
     }
  }

Beachten Sie, dass wir bei dieser Implementierung einfach die Abhängigkeitskoeffizienten der nächsten Elemente auf Null gesetzt haben. Dadurch konnten wir die Maskierung mit minimalen Änderungen am Kernel des Vorwärtsdurchgangs implementieren. Außerdem erfordert dieser Ansatz keine Anpassung der Kernel des Rückwärtsdurchgangs. Da „0“ im Abhängigkeitskoeffizienten den Fehlergradienten auf solchen Elementen der Sequenz einfach auf Null setzt.

Damit sind die Anpassungen auf der OpenCL-Programmseite abgeschlossen. Jetzt können wir mit dem Hauptprogramm weiterarbeiten.

Hier fügen wir zunächst den Aufruf des obigen Kernels in die Methode CNeuronSTNNEncoder::AttentionOut ein. Der Algorithmus der Methode zur Platzierung des Kernels in der Ausführungswarteschlange hat sich nicht geändert. Sie können den Code im Anhang selbst studieren. Ich möchte nur auf die Angabe „1“ im Parameter def_k_mh2ao_mask zur Durchführung der Datenmaskierung aufmerksam machen.

Als Nächstes implementieren wir die Vorwärtsdurchgangs-Methode unserer neuen Klasse. Wir müssen die Methode überschreiben, um den Vorwärtsdurchgangs-Block vor die Selbtaufmerksamkeit zu verschieben. Es sei auch darauf hingewiesen, dass der Vorwärtsdurchgangs-Block im Gegensatz zum klassischen Transformer keine Restbeziehungen und keine Datennormalisierung aufweist.

Vor der Implementierung des Algorithmus ist es wichtig, daran zu erinnern, dass wir, um unnötiges Kopieren von Daten während der Initialisierung der übergeordneten Klasse zu vermeiden, die Ergebnis- und Fehlergradienten-Pufferzeiger unserer Schicht durch analoge Puffer aus der letzten Schicht des Vorwärtsdurchgangs-Blocks ersetzt haben. Dieser Ansatz macht sich die Tatsache zunutze, dass die Ergebnispuffergrößen des Aufmerksamkeitsblocks und des Vorwärtsdurchgangs-Blocks identisch sind. Daher können wir die Indizierung beim Zugriff auf die jeweiligen Datenpuffer einfach anpassen.

Schauen wir uns nun unsere Implementierung an. Wie zuvor enthalten die Methodenparameter einen Zeiger auf das Objekt der vorangehenden Schicht, das die Eingabedaten liefert.

bool CNeuronSTNNEncoder::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(CheckPointer(NeuronOCL) == POINTER_INVALID)
      return false;

Gleich zu Beginn der Methode wird die Gültigkeit des empfangenen Zeigers überprüft. Sobald dies geschehen ist, gehen wir direkt zur Konstruktion des Vorwärtsdurchgangs-Algorithmus über. An dieser Stelle ist es wichtig, einen weiteren Unterschied in unserer Umsetzung hervorzuheben. Die Autoren der STNN-Methode geben weder die Anzahl der Encoder-Schichten noch die Anzahl der Aufmerksamkeitsköpfe an. Ausgehend von der zuvor beschriebenen Visualisierung und Methode könnte man erwarten, dass nur ein einziger Aufmerksamkeitskopf in einer einzigen Encoder-Schicht vorhanden ist. In unserer Implementierung halten wir uns jedoch an den klassischen Ansatz, indem wir die Aufmerksamkeit mehrerer Köpfe in einer mehrschichtigen Architektur nutzen. Dann organisieren wir eine Schleife, um durch die verschachtelten Encoder-Ebenen zu iterieren.

Innerhalb der Schleife durchlaufen die Eingabedaten, wie bereits erwähnt, zunächst den Vorwärtsdurchgangs-Block, in dem eine Glättung und Filterung der Daten erfolgt.

   CBufferFloat *kv = NULL;
   for(uint i = 0; (i < iLayers && !IsStopped()); i++)
     {
      //--- Feed Forward
      CBufferFloat *inputs = (i == 0 ? NeuronOCL.getOutput() : FF_Tensors.At(6 * i - 4));
      CBufferFloat *temp = FF_Tensors.At(i * 6 + 1);
      if(IsStopped() || 
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), inputs, temp, 
                                                                      iWindow, 4 * iWindow, LReLU))
         return false;
      inputs = FF_Tensors.At(i * 6);
      if(IsStopped() ||
         !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), temp, inputs, 
                                                                       4 * iWindow, iWindow, None))
         return false;

Danach definieren wir die Matrizen der Entitäten Query, Key und Value.

      //--- Calculate Queries, Keys, Values
      CBufferFloat *q = QKV_Tensors.At(i * 2);
      if(IsStopped() || 
        !ConvolutionForward(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), inputs, q, 
                                                          iWindow, iWindowKey * iHeads, None))
         return false;
      if((i % iLayersToOneKV) == 0)
        {
         uint i_kv = i / iLayersToOneKV;
         kv = KV_Tensors.At(i_kv * 2);
         if(IsStopped() || 
           !ConvolutionForward(KV_Weights.At(i_kv * (optimization == SGD ? 2 : 3)), inputs, kv, 
                                                      iWindow, 2 * iWindowKey * iHeadsKV, None))
            return false;
        }

Bitte beachten Sie, dass wir in diesem Fall die Ansätze der Methode MLKV verwenden, die von der übergeordneten Klasse geerbt wurde. Auf diese Weise können wir einen Puffer Key-Value für mehrere Aufmerksamkeitsköpfe und Selbstaufmerksamkeitsebenen verwenden.

Auf der Grundlage der erhaltenen Einheiten werden wir die Abhängigkeitskoeffizienten unter Berücksichtigung der Datenmaskierung bestimmen.

      //--- Score calculation and Multi-heads attention calculation
      temp = S_Tensors.At(i * 2);
      CBufferFloat *out = AO_Tensors.At(i * 2);
      if(IsStopped() || !AttentionOut(q, kv, temp, out))
         return false;

Anschließend wird das Ergebnis der Aufmerksamkeitsschicht unter Berücksichtigung der Restverbindungen und der Datennormalisierung berechnet.

      //--- Attention out calculation
      temp = FF_Tensors.At(i * 6 + 2);
      if(IsStopped() || 
        !ConvolutionForward(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out, temp, 
                                                      iWindowKey * iHeads, iWindow, None))
         return false;
      //--- Sum and normilize attention
      if(IsStopped() || !SumAndNormilize(temp, inputs, temp, iWindow, true))
         return false;
     }
//---
   return true;
  }

Dann geht es weiter mit der nächsten verschachtelten Ebene. Sobald alle Ebenen abgearbeitet sind, beenden wir die Methode.

In ähnlicher Weise, aber in umgekehrter Reihenfolge, konstruieren wir den Algorithmus für die Methode der Fehlergradientenverteilung CNeuronSTNNEncoder::calcInputGradients. In den Parametern erhält die Methode auch einen Zeiger auf das Objekt der vorherigen Ebene. Diesmal müssen wir ihm jedoch den Fehlergradienten übergeben, der dem Einfluss der Eingaben auf die Modellausgabe entspricht.

bool CNeuronSTNNEncoder::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(CheckPointer(prevLayer) == POINTER_INVALID)
      return false;
//---
   CBufferFloat *out_grad = Gradient;
   CBufferFloat *kv_g = KV_Tensors.At(KV_Tensors.Total() - 1);

Im Hauptteil der Methode wird wie zuvor die Korrektheit des empfangenen Zeigers überprüft. Wir deklarieren auch lokale Variablen für die vorübergehende Speicherung von Zeigern auf Objekte unserer Datenpuffer.

Als Nächstes deklarieren wir eine Schleife, die die verschachtelten Ebenen des Encoders durchläuft.

   for(int i = int(iLayers - 1); (i >= 0 && !IsStopped()); i--)
     {
      if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0)
         kv_g = KV_Tensors.At((i / iLayersToOneKV) * 2 + 1);
      //--- Split gradient to multi-heads
      if(IsStopped() ||
        !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9)), out_grad, 
                                   AO_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1), iWindowKey * iHeads, iWindow, None))
         return false;

Im Schleifenkörper verteilen wir zunächst den aus der nachfolgenden Schicht gewonnenen Fehlergradienten auf die Aufmerksamkeitsköpfe. Danach werden wir den Fehler auf der Ebene von Query, Key und Value der Entität ermitteln.

      //--- Passing gradient to query, key and value
      if(i == int(iLayers - 1) || (i + 1) % iLayersToOneKV == 0)
        {
         if(IsStopped() ||
           !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), 
                                     KV_Tensors.At((i / iLayersToOneKV) * 2), kv_g, 
                                     S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1)))
            return false;
        }
      else
        {
         if(IsStopped() || 
           !AttentionInsideGradients(QKV_Tensors.At(i * 2), QKV_Tensors.At(i * 2 + 1), 
                                     KV_Tensors.At((i / iLayersToOneKV) * 2), GetPointer(Temp), 
                                     S_Tensors.At(i * 2), AO_Tensors.At(i * 2 + 1)))
            return false;
         if(IsStopped() || !SumAndNormilize(kv_g, GetPointer(Temp), kv_g, iWindowKey, false, 0, 0, 0, 1))
            return false;
        }

Man beachte die Verzweigung des Algorithmus, die mit unterschiedlichen Ansätzen zur Verteilung des Fehlergradienten auf den Tensor von Key-Value je nach aktueller Schicht verbunden ist.

Als Nächstes propagieren wir den Fehlergradienten von Query zum Vorwärtsdurchgangs-Block, wobei wir die verbleibenden Verbindungen berücksichtigen.

      CBufferFloat *inp = FF_Tensors.At(i * 6);
      CBufferFloat *temp = FF_Tensors.At(i * 6 + 3);
      if(IsStopped() || 
        !ConvolutionInputGradients(QKV_Weights.At(i * (optimization == SGD ? 2 : 3)), QKV_Tensors.At(i * 2 + 1), 
                                                                  inp, temp, iWindow, iWindowKey * iHeads, None))
         return false;
      //--- Sum and normilize gradients
      if(IsStopped() || !SumAndNormilize(out_grad, temp, temp, iWindow, false, 0, 0, 0, 1))
         return false;

Falls erforderlich, fügen wir einen Einflussfehler bei den Entitäten Key und Value hinzu.

      if((i % iLayersToOneKV) == 0)
        {
         if(IsStopped() || 
           !ConvolutionInputGradients(KV_Weights.At(i / iLayersToOneKV * (optimization == SGD ? 2 : 3)), kv_g, inp, 
                                                         GetPointer(Temp), iWindow, 2 * iWindowKey * iHeadsKV, None))
            return false;
         if(IsStopped() || !SumAndNormilize(GetPointer(Temp), temp, temp, iWindow, false, 0, 0, 0, 1))
            return false;
        }

Dann propagieren wir den Fehlergradienten durch den Vorwärtsdurchgangs-Block.

      //--- Passing gradient through feed forward layers
      if(IsStopped() ||
        !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 2), out_grad, 
                                   FF_Tensors.At(i * 6 + 1), FF_Tensors.At(i * 6 + 4), 4 * iWindow, iWindow, None))
         return false;
      inp = (i > 0 ? FF_Tensors.At(i * 6 - 4) : prevLayer.getOutput());
      temp = (i > 0 ? FF_Tensors.At(i * 6 - 1) : prevLayer.getGradient());
      if(IsStopped() || 
        !ConvolutionInputGradients(FF_Weights.At(i * (optimization == SGD ? 6 : 9) + 1), FF_Tensors.At(i * 6 + 4), 
                                                                           inp, temp, iWindow, 4 * iWindow, LReLU))
         return false;
      out_grad = temp;
     }
//---
   return true;
  }

Die Iterationen der Schleife werden fortgesetzt, bis alle verschachtelten Schichten abgearbeitet sind, und enden mit der Weitergabe des Fehlergradienten an die vorhergehende Schicht.

Sobald der Fehlergradient verteilt ist, besteht der nächste Schritt darin, die Modellparameter zu optimieren, um den Gesamtvorhersagefehler zu minimieren. Diese Operationen sind in der Methode CNeuronSTNNEncoder::updateInputWeights implementiert. Ihr Algorithmus entspricht vollständig der analogen Methode der übergeordneten Klasse, wobei der einzige Unterschied in der Angabe von Datenpuffern besteht. Daher werden wir an dieser Stelle nicht auf die Einzelheiten eingehen, und ich möchte Sie ermutigen, sie in den beigefügten Unterlagen selbst nachzulesen. Der vollständige Code für die Klasse Encoder und alle ihre Methoden sind ebenfalls dort zu finden.

2.2 STNN-Decoder

Nach der Implementierung des Encoders gehen wir zum zweiten Teil unserer Arbeit über, der die Entwicklung des Decoder-Algorithmus für die STNN-Methode beinhaltet. Hier werden wir uns an die gleichen Prinzipien halten, die bei der Konstruktion des Encoders verwendet wurden. Insbesondere werden wir versuchen, so viel wie möglich von dem bereits entwickelten Code zu verwenden.

Wenn wir mit der Implementierung der Decoder-Algorithmen beginnen, ist es wichtig, einen wesentlichen Unterschied zum Encoder zu beachten: Die neue Klasse erbt von den Objekten der Kreuzaufmerksamkeit (cross-attention). Dies ist notwendig, da diese Ebene räumliche und zeitliche Informationen abbilden wird. Die vollständige Struktur der neuen Klasse wird im Folgenden dargestellt.

class CNeuronSTNNDecoder   :  public CNeuronMLCrossAttentionMLKV
  {
protected:
   CNeuronSTNNEncoder      cEncoder;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context) override;
   virtual bool      AttentionOut(CBufferFloat *q, CBufferFloat *kv, CBufferFloat *scores, CBufferFloat *out) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, 
                                       CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context) override;

public:
                     CNeuronSTNNDecoder(void) {};
                    ~CNeuronSTNNDecoder(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, 
                          uint window_kv, uint heads_kv, uint units_count, uint units_count_kv, uint layers, 
                          uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronSTNNDecoder;   }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
  };

Beachten Sie, dass wir in dieser Klasse ein verschachteltes Objekt des zuvor erstellten Encoders deklarieren. Ich sollte jedoch klarstellen, dass sie in diesem Fall einem etwas anderen Zweck dient.

Wenn man sich die theoretische Beschreibung der Methode aus Teil 1 dieses Artikels vergegenwärtigt, kann man Ähnlichkeiten zwischen den Blöcken erkennen, die für die Identifizierung räumlicher und zeitlicher Abhängigkeiten zuständig sind. Der Unterschied liegt in der Art der zu analysierenden Eingangsdaten. Im Block für die räumliche Abhängigkeit wird eine große Anzahl von Parametern über ein kurzes Zeitintervall analysiert, während im Block für die zeitliche Abhängigkeit die Zielvariable über einen bestimmten historischen Abschnitt analysiert wird. Trotz dieser Unterschiede sind die Algorithmen recht ähnlich. Daher verwenden wir in diesem Fall den verschachtelten Encoder, um zeitliche Abhängigkeiten der Zielvariablen zu identifizieren.

Kehren wir zur Beschreibung der Algorithmen unserer Methode zurück. Die Deklaration eines zusätzlichen verschachtelten Objekts, auch wenn es statisch ist, erfordert, dass wir die Initialisierungsmethode Init der Klasse überschreiben. Dennoch hat unser Engagement für die Wiederverwendung bereits entwickelter Komponenten zu Ergebnissen geführt: Die neue Initialisierungsmethode ist sehr einfach.

bool CNeuronSTNNDecoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, 
                              uint heads, uint window_kv, uint heads_kv, uint units_count, uint units_count_kv, 
                              uint layers, uint layers_to_one_kv, ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!cEncoder.Init(0, 0, open_cl, window, window_key, heads, heads_kv, units_count, layers, layers_to_one_kv, 
                                                                                        optimization_type, batch))
      return false;
   if(!CNeuronMLCrossAttentionMLKV::Init(numOutputs, myIndex, open_cl, window, window_key, heads, window_kv, heads_kv, 
                                        units_count, units_count_kv, layers, layers_to_one_kv, optimization_type, batch))
      return false;
//---
   return true;
  }

Hier rufen wir einfach die Methoden des verschachtelten Encoders und der übergeordneten Klasse mit denselben Parameterwerten für die entsprechenden Argumente auf. Unsere Aufgabe beschränkt sich dann darauf, die Ergebnisse der Operation zu überprüfen und den erhaltenen booleschen Wert an das aufrufende Programm zurückzugeben.

Ein ähnlicher Ansatz ist bei den Vorwärts- und Rückwärtsdurchgangs-Methoden zu beobachten. Bei der Vorwärtsdurchgangsmethode zum Beispiel rufen wir zunächst die entsprechende Encoder-Methode auf, um zeitliche Abhängigkeiten zwischen den Werten der Zielvariablen zu ermitteln. Anschließend gleichen wir diese identifizierten zeitlichen Abhängigkeiten mit den räumlichen Abhängigkeiten ab, die wir über die Kontextparameter dieser Methode vom Encoder des STNN-Modells erhalten. Dieser Vorgang wird mit Hilfe des von der übergeordneten Klasse geerbten Vorwärtsdurchgangs-Mechanismus durchgeführt.

bool CNeuronSTNNDecoder::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *Context)
  {
   if(!cEncoder.FeedForward(NeuronOCL, Context))
      return false;
   if(!CNeuronMLCrossAttentionMLKV::feedForward(cEncoder.AsObject(), Context))
      return false;
//---
   return true;
  }

Es lohnt sich, einige Momente hervorzuheben, in denen wir von dem von den Autoren der STNN-Methode vorgeschlagenen Algorithmus abgewichen sind. Während wir das Gesamtkonzept beibehalten haben, haben wir uns bei der Umsetzung der vorgeschlagenen Ansätze erhebliche Freiheiten genommen.

Die Teile, die wir erhalten haben:

• Identifizierung von zeitlichen Abhängigkeiten.
• Abgleich von zeitlichen und räumlichen Abhängigkeiten zur Vorhersage von Zielvariablenwerten.

Wie beim Encoder verwenden wir jedoch einen Vorwärtsdurchgangs-Block, der aus zwei vollständig verknüpften Schichten besteht, anstatt der von den Autoren vorgeschlagenen einzelnen Schicht. Dies gilt sowohl für die Datenfilterung vor der Identifizierung zeitlicher Abhängigkeiten als auch für die Vorhersage von Zielvariablenwerten am Decoderausgang.

Zur Implementierung der Kreuzaufmerksamkeit haben wir außerdem den Vorwärtsdurchgang der Elternklasse verwendet, der den klassischen mehrschichtigen Kreuzaufmerksamkeits-Algorithmus mit Restverbindungen zwischen Aufmerksamkeitsblöcken und Vorwärtsdurchgang implementiert. Dies unterscheidet sich von dem von den Autoren der STNN-Methode vorgeschlagenen Kreuzaufmerksamkeits-Algorithmus.

Nichtsdestotrotz glaube ich, dass diese Implementierung gerechtfertigt ist, vor allem wenn man bedenkt, dass das Ziel unseres Experiments darin besteht, die Wiederverwendung von bereits entwickelten Komponenten zu maximieren.

Ich möchte auch darauf hinweisen, dass trotz der Verwendung einer mehrschichtigen Struktur in den Blöcken für die zeitliche Abhängigkeit und die gegenseitige Aufmerksamkeit die Gesamtarchitektur des Decoders einschichtiger Natur ist. Mit anderen Worten, wir identifizieren zunächst zeitliche Abhängigkeiten im mehrschichtigen verschachtelten Encoder. Ein mehrschichtiger Kreuzaufmerksamkeits-Block vergleicht dann zeitliche und räumliche Abhängigkeiten, bevor er die Werte der Zielvariablen vorhersagt.

Die Rückwärtsdurchgangs-Methoden sind auf ähnliche Weise aufgebaut. Aber wir wollen uns jetzt nicht damit aufhalten. Ich schlage vor, dass Sie sich anhand der Codes in der Anlage mit ihnen vertraut machen.

Damit ist unsere Diskussion über die Architektur und die Algorithmen für die neuen Objekte abgeschlossen. Der vollständige Code für diese Komponenten ist in den Anhängen verfügbar.

2.3 Modellarchitektur

Nachdem wir die Implementierungsalgorithmen der vorgeschlagenen STNN-Methode untersucht haben, gehen wir nun zu ihrer praktischen Anwendung in trainierbaren Modellen über. Es ist wichtig zu beachten, dass der Encoder und der Decoder im vorgeschlagenen Algorithmus mit unterschiedlichen Eingangsdaten arbeiten. Diese Unterscheidung veranlasste uns, sie als separate Modelle zu implementieren, deren Architektur in der Methode CreateStateDescriptions definiert ist.

Die Parameter dieser Methode umfassen zwei Zeiger auf dynamische Arrays, die zur Definition der Architektur der jeweiligen Modelle verwendet werden.

bool CreateStateDescriptions(CArrayObj *&encoder, CArrayObj *&decoder)
  {
//---
   CLayerDescription *descr;
//---
   if(!encoder)
     {
      encoder = new CArrayObj();
      if(!encoder)
         return false;
     }
//---
   if(!decoder)
     {
      decoder = new CArrayObj();
      if(!decoder)
         return false;
     }

Im Hauptteil der Methode werden die empfangenen Zeiger überprüft und gegebenenfalls neue Objektinstanzen erstellt.

Wir füttern den Encoder mit dem Rohdatensatz, der uns bereits bekannt ist.

//--- Encoder
   encoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Die Daten werden in der Batch-Normalisierungsschicht vorverarbeitet.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Als Nächstes folgt die Schicht des STNN-Encoder.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSTNNEncoder;
   descr.count = HistoryBars;
   descr.window = BarDescr;
   descr.window_out = 32;
   descr.layers   =  4;
   descr.step = 2;
     {
      int ar[] = {8, 4};
      if(ArrayCopy(descr.heads, ar) < (int)ar.Size())
         return false;
     }
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Hier verwenden wir 4 verschachtelte Encoder-Schichten, von denen jede 8 Aufmerksamkeitsköpfe für Abfrageentitäten und 4 für den Schlüssel-Wert-Tensor verwendet. Außerdem wird ein Key-Value-Tensor für 2 verschachtelte Encoder-Schichten verwendet.

Damit ist die Architektur des Encoder-Modells abgeschlossen. Wir werden seine Ausgabe im Decoder verwenden.

Wir füttern den Decoder mit den historischen Werten der Zielvariablen. Die Tiefe der analysierten Historie entspricht unserem Planungshorizont.

//--- Decoder
   decoder.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = (NForecast * ForecastBarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

Auch hier verwenden wir Rohdaten, die in eine Batch-Daten-Normalisierungsschicht eingespeist werden.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

Danach folgt die STNN-Decoder-Schicht. Dann folgt die STNN-Decoder-Schicht, deren Architektur ebenfalls 4 verschachtelte Schichten mit Zeitbeziehungen und Kreuzaufmerksamkeit umfasst.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronSTNNDecoder;
     {
      int ar[] = {NForecast, HistoryBars};
      if(ArrayCopy(descr.units, ar) < (int)ar.Size())
         return false;
     }
     {
      int ar[] = {ForecastBarDescr, BarDescr};
      if(ArrayCopy(descr.windows, ar) < (int)ar.Size())
         return false;
     }
     {
      int ar[] = {8, 4};
      if(ArrayCopy(descr.heads, ar) < (int)ar.Size())
         return false;
     }
   descr.window_out = 32;
   descr.layers   =  4;
   descr.step = 2;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

Am Ausgang des Decoders erwarten wir die vorhergesagten Werte der Zielvariablen. Wir fügen ihnen die statistischen Variablen hinzu, die in der Batch-Normalisierungsschicht extrahiert wurden.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronRevInDenormOCL;
   descr.count = ForecastBarDescr * NForecast;
   descr.activation = None;
   descr.optimization = ADAM;
   descr.layers = 1;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }

Dann gleichen wir die Frequenzmerkmale der prognostizierten Zeitreihen an.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronFreDFOCL;
   descr.window = ForecastBarDescr;
   descr.count =  NForecast;
   descr.step = int(true);
   descr.probability = 0.7f;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!decoder.Add(descr))
     {
      delete descr;
      return false;
     }
//---
   return true;
  }

Die Architekturen der Akteur- und Kritiker-Modelle bleiben gegenüber früheren Artikeln unverändert und werden in der Methode CreateDescriptions vorgestellt, die sich im Anhang zu diesem Artikel befindet (Datei“...\Experts\STNN\Trajectory.mqh“).

2.4 Modellhafte Trainingsprogramme

Die Aufteilung des Environment State Encoders in zwei Modelle erforderte Änderungen an den Trainingsprogrammen für diese Modelle. Neben der Aufteilung des Algorithmus in zwei Modelle wurden auch Änderungen bei der Aufbereitung der Eingabedaten und der Zielwerte vorgenommen. Diese Anpassungen werden am Beispiel der Trainings-EA für den Umgebungszustand Encoder“...\Experts\STNN\StudyEncoder.mq5“ diskutiert.

Im Rahmen dieses EA trainieren wir ein Modell zur Vorhersage der bevorstehenden Kursentwicklung für einen bestimmten Planungshorizont, das ausreicht, um zu einem bestimmten Zeitpunkt eine Handelsentscheidung zu treffen.

In diesem Artikel werden wir nicht auf alle Verfahren des Programms eingehen, sondern nur die Modellbildungsmethode Train betrachten. Hier bestimmen wir zunächst die Wahrscheinlichkeiten für die Auswahl von Trajektorien aus dem Erfahrungswiedergabepuffer entsprechend ihrer tatsächlichen Leistung bei realen historischen Daten.

void Train(void)
  {
//---
   vector<float> probability = GetProbTrajectories(Buffer, 0.9);
//---
   vector<float> result, target, state;
   matrix<float> mstate = matrix<float>::Zeros(1, NForecast * ForecastBarDescr);
   bool Stop = false;

Wir deklarieren auch das notwendige Minimum an lokalen Variablen. Danach organisieren wir eine Schleife für das Training der Modelle. Die Anzahl der Iterationen der Schleife wird vom Nutzer in den externen Parametern des EA festgelegt.

   uint ticks = GetTickCount();
//---
   for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++)
     {
      int tr = SampleTrajectory(probability);
      int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - NForecast));
      if(i <= 0)
        {
         iter--;
         continue;
        }
      state.Assign(Buffer[tr].States[i].state);
      if(MathAbs(state).Sum() == 0)
        {
         iter--;
         continue;
        }

Im Schleifenkörper werden die Trajektorie und der Zustand abgetastet, um Iterationen der Modelloptimierung durchzuführen. Wir führen zunächst die Erkennung von räumlichen Abhängigkeiten zwischen den analysierten Variablen durch, indem wir die Vorwärtsdurchgangsmethode unseres Encoders aufrufen.

      bStateE.AssignArray(state);
      //--- State Encoder
      if(!Encoder.feedForward((CBufferFloat*)GetPointer(bStateE), 1, false, (CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Als Nächstes bereiten wir die Eingänge für den Decoder vor. Im Allgemeinen gehen wir davon aus, dass der Planungshorizont kleiner ist als die Tiefe der analysierten Geschichte. Daher übertragen wir zunächst die historischen Daten des analysierten Umweltzustands in die Matrix. Die Größe wird so angepasst, dass jede Zeile der Matrix die Daten eines Balkens der historischen Daten repräsentiert. Und wir trimmen die Matrix. Die Anzahl der Zeilen der resultierenden Matrix sollte dem Planungshorizont entsprechen, während die Anzahl der Spalten den Zielvariablen entsprechen sollte.

      mstate.Assign(state);
      mstate.Reshape(HistoryBars, BarDescr);
      mstate.Resize(NForecast, ForecastBarDescr);
      bStateD.AssignArray(mstate);

An dieser Stelle sei angemerkt, dass wir bei der Erstellung des Trainingsdatensatzes zunächst die Parameter der Kursbewegung für jeden Balken erfasst haben. Das sind die Werte, für die wir planen werden. Wir nehmen also die ersten Spalten der Matrix.

Die Werte aus der resultierenden Matrix werden dann in den Datenpuffer übertragen, und wir führen einen Vorwärtsdurchlauf durch den Decoder durch.

      if(!Decoder.feedForward((CBufferFloat*)GetPointer(bStateD), 1, false, GetPointer(Encoder)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Nach der Durchführung des Vorwärtsdurchgangs müssen wir die Modellparameter optimieren. Zu diesem Zweck müssen wir Zielwerte für die vorhergesagten Variablen vorbereiten. Dieser Vorgang ist ähnlich wie die Vorbereitung der Eingänge für den Decoder. Diese Operationen werden jedoch über die nachfolgenden historischen Werte ausgeführt.

      //--- Collect target data
      mstate.Assign(Buffer[tr].States[i + NForecast].state);
      mstate.Reshape(HistoryBars, BarDescr);
      mstate.Resize(NForecast, ForecastBarDescr);
      if(!Result.AssignArray(mstate))
         continue;

Führen wir den Rückwärtsdurchgang des Decoders durch. Hier optimieren wir die Decoder-Parameter und geben den Fehlergradienten an den Encoder weiter.

      if(!Decoder.backProp(Result, GetPointer(Encoder)))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Danach optimieren wir die Encoder-Parameter.

      if(!Encoder.backPropGradient((CBufferFloat*)NULL))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         Stop = true;
         break;
        }

Dann müssen wir den Nutzer nur noch über den Lernfortschritt informieren und mit der nächsten Iteration des Lernzyklus fortfahren.

      if(GetTickCount() - ticks > 500)
        {
         double percent = double(iter) * 100.0 / (Iterations);
         string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Decoder", 
                                       percent, Decoder.getRecentAverageError());
         Comment(str);
         ticks = GetTickCount();
        }
     }

Nachdem alle Trainingsiterationen erfolgreich abgeschlossen wurden, protokollieren wir die Ergebnisse des Modelltrainings und initialisieren den Prozess der Programmabschaltung.

   Comment("");
//---
   PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Decoder", Decoder.getRecentAverageError());
   ExpertRemove();
//---
  }

Damit ist das Thema Modellbildungsalgorithmen abgeschlossen. Und im Anhang finden Sie den vollständigen Code aller hier verwendeten Programme.

3. Tests

In diesem Artikel haben wir eine neue Methode zur Vorhersage von Zeitreihen auf der Grundlage von raumzeitlichen Informationen STNN eingeführt. Wir haben unsere Vision der vorgeschlagenen Ansätze mit MQL5 umgesetzt. Jetzt ist es an der Zeit, die Ergebnisse unserer Bemühungen zu bewerten.

Wie üblich trainieren wir unsere Modelle anhand historischer Daten des EURUSD-Instruments im H1-Zeitrahmen für das gesamte Jahr 2023. Anschließend testen wir die trainierten Modelle im MetaTrader 5 Strategie-Tester mit Daten vom Januar 2024. Es ist leicht zu erkennen, dass die Testphase direkt auf die Ausbildungsphase folgt. Dieser Ansatz simuliert die realen Bedingungen für den Betrieb der Modelle sehr genau.

Für das Training des Modells zur Vorhersage der späteren Kursentwicklung verwenden wir den Trainingsdatensatz, der bei der Vorbereitung früherer Artikel dieser Reihe gesammelt wurde. Wie Sie wissen, beruht die Ausbildung dieses Modells ausschließlich auf der Analyse historischer Kursbewegungen und der analysierten Indikatoren. Die Aktionen des Agenten wirken sich nicht auf die analysierten Daten aus, sodass wir das Umgebungszustand-Encoder-Modell ohne regelmäßige Aktualisierungen des Trainingsdatensatzes trainieren können.

Wir setzen den Trainingsprozess fort, bis sich der Vorhersagefehler stabilisiert. Leider sind wir in dieser Phase enttäuscht worden. Unser Modell lieferte nicht die gewünschte Vorhersage für die bevorstehende Kursbewegung, sondern gab nur die allgemeine Richtung des Trends an.

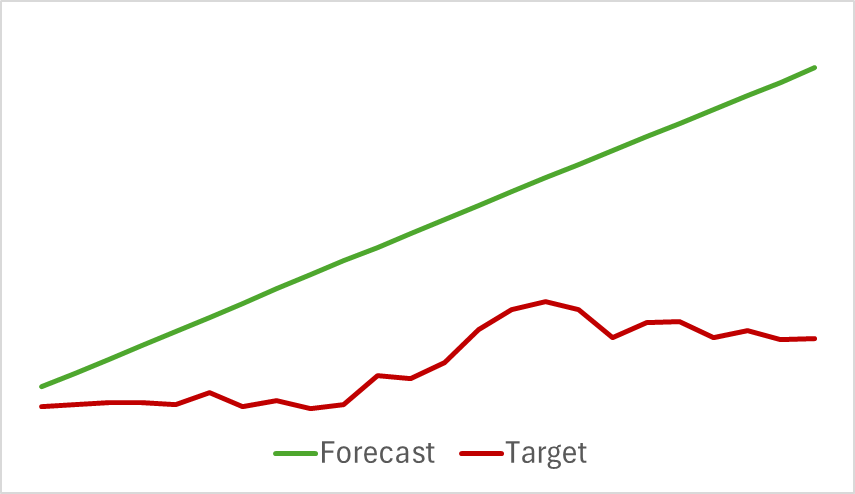
Obwohl die vorhergesagte Bewegung linear erschien, zeigten die digitalisierten Werte immer noch kleine Schwankungen. Diese Schwankungen waren jedoch so gering, dass sie in der Grafik nicht sichtbar wurden. Das wirft die Frage auf: Reichen diese Schwankungen aus, um eine rentable Strategie für unseren Akteur zu entwickeln?

Wir trainieren die Modelle Akteur und Kritiker iterativ mit regelmäßigen Aktualisierungen des Trainingsdatensatzes. Wie Sie wissen, sind regelmäßige Aktualisierungen erforderlich, um die Maßnahmen des Akteurs genauer zu bewerten, wenn sich seine Politik während der Ausbildung ändert.

Leider war es uns nicht möglich, die Politik des Akteurs so zu trainieren, dass sie auf dem Testdatensatz konsistente Gewinne erzielt.

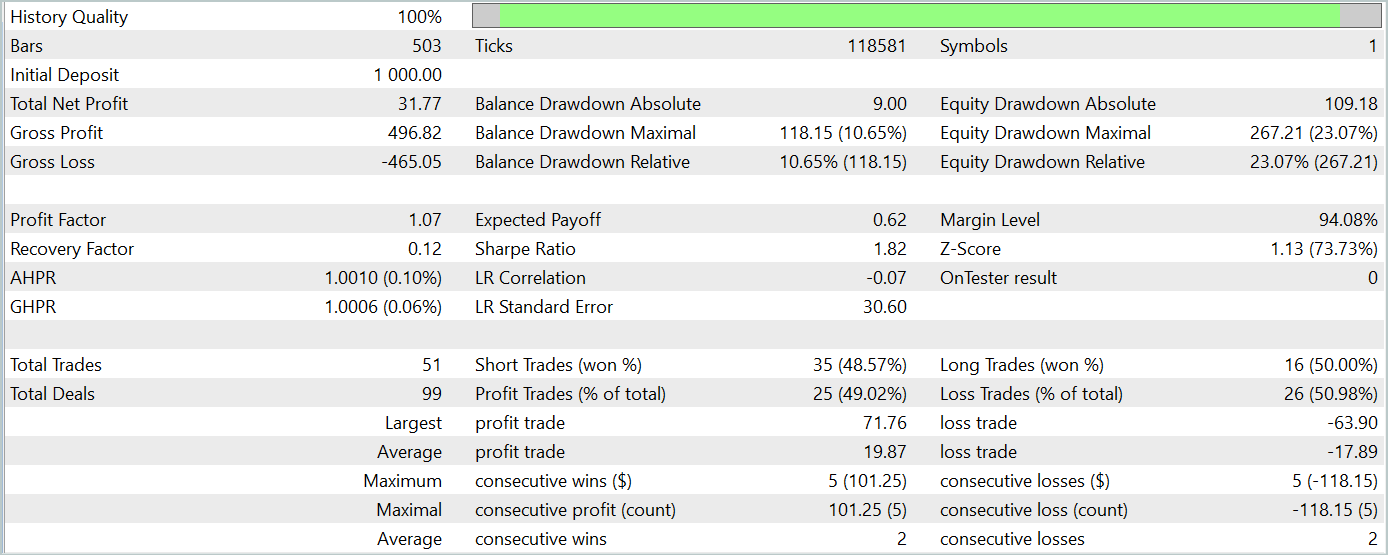
Dennoch räumen wir ein, dass während unserer Arbeit erhebliche Abweichungen von der ursprünglichen Methode vorgenommen wurden, die sich auf die erzielten Ergebnisse ausgewirkt haben könnten.

Schlussfolgerung

In diesem Artikel haben wir einen anderen Ansatz für die Zeitreihenprognose auf der Grundlage des räumlich-zeitlichen neuronalen NetzesSTNN ( Spatial-Transformer Neural Network) untersucht. Dieses Modell kombiniert die Vorteile der Gleichung für die räumlich-zeitliche Informationstransformation (STI) und der Transformer-Struktur, um eine effektive mehrstufige Vorhersage kurzfristiger Zeitreihen zu ermöglichen.

STNN verwendet die STI-Gleichung, die die räumliche Information von mehrdimensionalen Variablen in die zeitliche Information der Zielvariablen umwandelt. Dies kommt einer Vergrößerung der Stichprobe gleich und trägt dazu bei, das Problem der unzureichenden kurzfristigen Daten zu lösen.

Um die Genauigkeit der numerischen Vorhersage zu verbessern, enthält STNN einen kontinuierlichen Aufmerksamkeitsmechanismus, der es dem Modell ermöglicht, sich besser auf wichtige Aspekte der Daten zu konzentrieren.

Im praktischen Teil des Artikels haben wir unsere Vision der vorgeschlagenen Ansätze in der Sprache MQL5 umgesetzt. Wir haben jedoch erhebliche Abweichungen von dem ursprünglichen Algorithmus vorgenommen, was die Ergebnisse unserer Experimente beeinflusst haben könnte.

Referenzen

Spatiotemporal Transformer Neural Network for Time-Series Forecasting

Predicting future dynamics from short-term time series using an Anticipated Learning Machine

Weitere Artikel aus dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	Beispielsammlung EA
2	ResearchRealORL.mq5	Expert Advisor	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modelltraining EA
4	StudyEncoder.mq5	Expert Advisor	Trainings-EA des Encoders
5	Test.mq5	Expert Advisor	Trainings-EA für das Model
6	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
7	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
8	NeuroNet.cl	Code Base	Die Bibliothek des Programmcodes von OpenCL