Datenwissenschaft und maschinelles Lernen — Neuronales Netzwerk (Teil 02): Entwurf von Feed Forward NN-Architekturen
232
0
„Ich will damit nicht sagen, dass neuronale Netze einfach sind. Man muss schon ein Experte sein, damit diese Dinge funktionieren. Aber dieses Fachwissen kommt Ihnen bei einem breiteren Spektrum von Anwendungen zugute. In gewissem Sinne fließt der gesamte Aufwand, der zuvor in die Entwicklung von Merkmalen floss, nun in die Entwicklung von Architekturen, Verlustfunktionen und Optimierungsverfahren. Die manuelle Arbeit ist auf eine höhere Abstraktionsebene gehoben worden“.
--Stefano Soatto
Einführung
Im vorigen Artikel haben wir die Grundlagen eines neuronalen Netzes besprochen und ein sehr einfaches und statisches MLP gebaut, aber wir wissen, dass wir in realen Anwendungen keine einfachen 2 Eingänge und 2 verborgene Schichten im Netz bis zum Ausgang benötigen, wie wir es beim letzten Mal gebaut haben.
Manchmal ist ein Netzwerk, das für Ihr Problem am besten geeignet ist, eines mit 10 Knoten in der Eingabeschicht, 13 Knoten/Neuronen in der verborgenen Schicht und etwa vier oder so in der Ausgabeschicht, ganz zu schweigen davon, dass Sie die Anzahl der verborgenen Schichten im gesamten Netzwerk abstimmen müssen.
Ich will damit sagen, dass wir etwas Dynamisches brauchen. Ein dynamischer Code, bei dem wir die Parameter ändern und optimieren können, ohne das Programm zu zerstören. Wenn Sie die Bibliothek zum Aufbau eines neuronalen Netzes verwenden, müssen Sie weniger Arbeit mit der Konfiguration und Kompilierung selbst komplexer Architekturen aufwenden. Das ist etwas, das wir in MQL5 erreichen wollen.
Genau wie in Teil 3 der linearen Regression, der zu den Pflichtlektüren dieser Artikelserie gehört, habe ich die Matrix-/Vektorform von Modellen eingeführt, um flexible Modelle mit einer unbegrenzten Anzahl von Eingaben erstellen zu können.
Matrizen als Retter in der Not
Wir alle wissen, dass hart kodierte Modelle scheitern, wenn es darum geht, die neuen Parameter zu optimieren, das ganze Verfahren ist zeitaufwendig, verursacht Kopfschmerzen, Rückenschmerzen usw. (Das ist es nicht wert)
Wenn wir uns die Vorgänge in einem neuronalen Netz genauer ansehen, werden Sie feststellen, dass jede Eingabe mit der ihr zugewiesenen Gewichtung multipliziert wird und ihre Ausgabe dann zum Bias addiert wird. Dies kann mit den Matrixoperationen gut bewältigt werden.
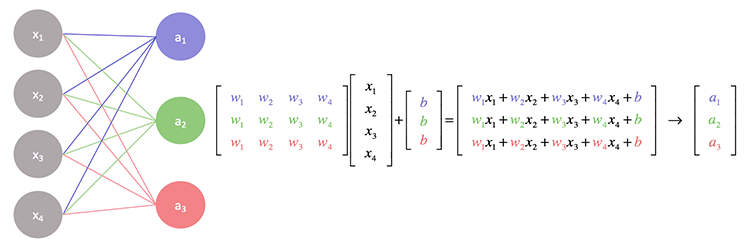
Im Grunde genommen ermitteln wir das Punktprodukt der Input- und der Gewichtsmatrix und addieren es schließlich zum Bias.
Um ein flexibles neuronales Netz aufzubauen, werde ich eine ungerade Architektur mit 2 Knoten in der Eingabeschicht, 4 in der ersten verborgenen Schicht, 6 in der zweiten verborgenen Schicht und 1 in der dritten verborgenen Schicht und schließlich einem Knoten in der Ausgabeschicht versuchen.
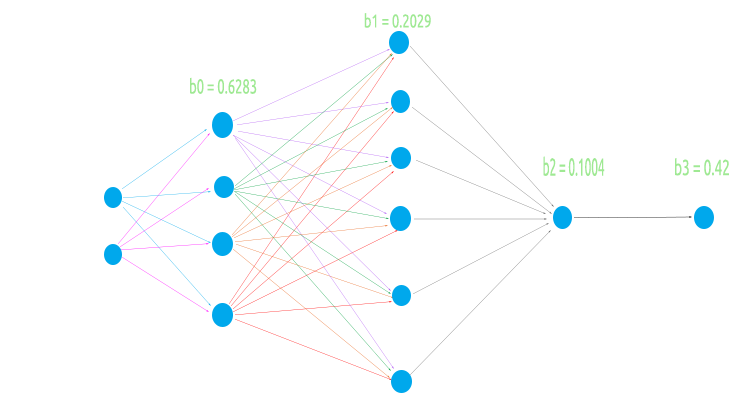
Dies dient dazu, zu testen, ob unsere Matrixlogik in allen Fällen reibungslos funktionieren wird.
- Wenn die vorherige Schicht (Eingabeschicht) weniger Knoten hat als die nächste Schicht (Ausgabeschicht).
- Wenn die vorherige (Eingabe-) Schicht viel mehr Knoten hat als die nächste Schicht.
- Bei gleicher Anzahl von Knoten in der Eingabeschicht und in der nächsten Schicht (Ausgabeschicht).
Bevor wir die Matrixoperationen codieren und die Werte berechnen, müssen wir die grundlegenden Dinge tun, die die gesamte Operation ermöglichen.
Generierung der Zufallsgewichte und Verzerrungswerte.
//Generate random bias for(int i=0; i<m_hiddenLayers; i++) bias[i] = MathRandom(0,1); //generate weights int sum_weights=0, L_inputs=inputs; double L_weights[]; for (int i=0; i<m_hiddenLayers; i++) { sum_weights += L_inputs * m_hiddenLayerNodes[i]; ArrayResize(Weights,sum_weights); L_inputs = m_hiddenLayerNodes[i]; } for (int j=0; j<sum_weights; j++) Weights[j] = MathRandom(0,1);
Wir haben diesen Vorgang im vorigen Teil gesehen, aber es ist zu beachten, dass diese Gewichtswert und das Bias einmalig generiert werden sollen, um im Epochenzyklus verwendet zu werden.
Was ist eine Epoche?
Eine Epoche ist ein vollständiger Durchlauf aller Daten im neuronalen Netz, in einem Feedforward-Netzwerk ein vollständiger Vorwärtsdurchlauf aller Eingänge, in einem Backpropagation-Netzwerk ein vollständiger Vorwärts- und Rückwärtsdurchlauf. Einfach ausgedrückt, wenn ein neuronales Netz alle Daten gesehen hat.
Anders als bei der MLP, die wir im vorigen Artikel gesehen haben, kommen wir diesmal mit einer Implementierung, die die Aktivierungsfunktion in der Ausgabeschicht berücksichtigt - etwas, mit dem diejenigen, die keras verwenden, wahrscheinlich vertraut sind. Im Grunde können wir verschiedene Aktivierungsfunktionen in der verborgenen Schicht und derjenigen, die zur Ausgabe in der Ausgabeschicht führt, haben.
CNeuralNets(fx HActivationFx,fx OActivationFx,int &NodesHL[],int outputs=NULL, bool SoftMax=false);
Achten Sie auf die Eingaben. HActivationFx steht für die Aktivierungsfunktion in den verborgenen Schichten, OActivationFx für die Aktivierungsfunktion in der Ausgabeschicht und NodesHL[] für die Anzahl der Knoten in der verborgenen Schicht. Wenn dieses Array, sagen wir, 3 Elemente hat, bedeutet das, dass wir 3 verborgen Schichten haben werden und die Anzahl der Knoten in diesen Schichten wird durch die Elemente innerhalb des Arrays bestimmt, siehe den folgenden Code.
int hlnodes[3] = {4,6,1}; int outputs = 1; neuralnet = new CNeuralNets(SIGMOID,RELU,hlnodes,outputs);
Dies ist die Architektur auf dem Bild, das wir gerade oben gesehen haben. Das Ausgabe-Argument ist optional, wenn Sie es auf NULL setzen, wird die folgende Konfiguration auf die Output-Schicht angewendet:
if (m_outputLayers == NULL) { if (A_fx == RELU) m_outputLayers = 1; else m_outputLayers = ArraySize(MLPInputs); }
Wenn wir RELU als Aktivierungsfunktion in der verborgen Schicht gewählt haben, hat die Ausgabeschicht einen Knoten, andernfalls ist die Anzahl der Ausgänge in der letzten Schicht gleich der Anzahl der Eingänge in der ersten Schicht. Die Wahrscheinlichkeit ist groß, dass Sie ein neuronales Klassifizierungsnetz verwenden, wenn Sie eine andere Aktivierungsfunktion als RELU in der verwenden Schicht verwenden, sodass die Standardausgabeschicht der Anzahl der Spalten entspricht. Dies ist unzuverlässig, obwohl die Ausgaben die Anzahl der gezielten Merkmale aus Ihrem Datensatz sein müssen, wenn Sie versuchen, ein Klassifizierungsproblem zu lösen, ich werde einen Weg finden, dies in den weiteren Updates zu ändern, im Moment müssen Sie manuell die Anzahl der Ausgabe-Neuronen wählen.
Rufen wir nun die vollständige Funktion MLP auf und sehen wir uns die Ausgabe an, dann werde ich erklären, was getan wurde, um die Operationen zu ermöglichen.
LI 0 10:10:29.995 NNTestScript (#NQ100,H1) CNeural Nets Initialized activation = SIGMOID UseSoftMax = No IF 0 10:10:29.995 NNTestScript (#NQ100,H1) biases EI 0 10:10:29.995 NNTestScript (#NQ100,H1) 0.6283 0.2029 0.1004 IQ 0 10:10:29.995 NNTestScript (#NQ100,H1) Hidden Layer 1 | Nodes 4 | Bias 0.6283 NS 0 10:10:29.995 NNTestScript (#NQ100,H1) Inputs 2 Weights 8 JD 0 10:10:29.995 NNTestScript (#NQ100,H1) 4.00000 6.00000 FL 0 10:10:29.995 NNTestScript (#NQ100,H1) 0.954 0.026 0.599 0.952 0.864 0.161 0.818 0.765 EJ 0 10:10:29.995 NNTestScript (#NQ100,H1) Arr size A 2 EM 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[0] = 3.81519 X A[0] = 4.000 B[0] = 0.954 NI 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[0] = 9.00110 X A[1] = 6.000 B[4] = 0.864 IE 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[1] = 0.10486 X A[0] = 4.000 B[1] = 0.026 DQ 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[1] = 1.06927 X A[1] = 6.000 B[5] = 0.161 MM 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[2] = 2.39417 X A[0] = 4.000 B[2] = 0.599 JI 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[2] = 7.29974 X A[1] = 6.000 B[6] = 0.818 GE 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[3] = 3.80725 X A[0] = 4.000 B[3] = 0.952 KQ 0 10:10:29.995 NNTestScript (#NQ100,H1) AxBMatrix[3] = 8.39569 X A[1] = 6.000 B[7] = 0.765 DL 0 10:10:29.995 NNTestScript (#NQ100,H1) before rows 1 cols 4 GI 0 10:10:29.995 NNTestScript (#NQ100,H1) IxWMatrix QM 0 10:10:29.995 NNTestScript (#NQ100,H1) Matrix CH 0 10:10:29.995 NNTestScript (#NQ100,H1) [ HK 0 10:10:29.995 NNTestScript (#NQ100,H1) 9.00110 1.06927 7.29974 8.39569 OO 0 10:10:29.995 NNTestScript (#NQ100,H1) ] CH 0 10:10:29.995 NNTestScript (#NQ100,H1) rows = 1 cols = 4 <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< End of the first Hidden Layer >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> NS 0 10:10:29.995 NNTestScript (#NQ100,H1) Hidden Layer 2 | Nodes 6 | Bias 0.2029 HF 0 10:10:29.995 NNTestScript (#NQ100,H1) Inputs 4 Weights 24 LR 0 10:10:29.995 NNTestScript (#NQ100,H1) 0.99993 0.84522 0.99964 0.99988 EL 0 10:10:29.996 NNTestScript (#NQ100,H1) 0.002 0.061 0.056 0.600 0.737 0.454 0.113 0.622 0.387 0.456 0.938 0.587 0.379 0.207 0.356 0.784 0.046 0.597 0.511 0.838 0.848 0.748 0.047 0.282 FF 0 10:10:29.996 NNTestScript (#NQ100,H1) Arr size A 4 EI 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 0.00168 X A[0] = 1.000 B[0] = 0.002 QE 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 0.09745 X A[1] = 0.845 B[6] = 0.113 MR 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 0.47622 X A[2] = 1.000 B[12] = 0.379 NN 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 0.98699 X A[3] = 1.000 B[18] = 0.511 MI 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[1] = 0.06109 X A[0] = 1.000 B[1] = 0.061 ME 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[1] = 0.58690 X A[1] = 0.845 B[7] = 0.622 PR 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[1] = 0.79347 X A[2] = 1.000 B[13] = 0.207 KN 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[1] = 1.63147 X A[3] = 1.000 B[19] = 0.838 GI 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[2] = 0.05603 X A[0] = 1.000 B[2] = 0.056 GE 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[2] = 0.38353 X A[1] = 0.845 B[8] = 0.387 GS 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[2] = 0.73961 X A[2] = 1.000 B[14] = 0.356 CO 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[2] = 1.58725 X A[3] = 1.000 B[20] = 0.848 KH 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[3] = 0.59988 X A[0] = 1.000 B[3] = 0.600 OD 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[3] = 0.98514 X A[1] = 0.845 B[9] = 0.456 LS 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[3] = 1.76888 X A[2] = 1.000 B[15] = 0.784 KO 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[3] = 2.51696 X A[3] = 1.000 B[21] = 0.748 PH 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[4] = 0.73713 X A[0] = 1.000 B[4] = 0.737 FG 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[4] = 1.53007 X A[1] = 0.845 B[10] = 0.938 RS 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[4] = 1.57626 X A[2] = 1.000 B[16] = 0.046 OO 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[4] = 1.62374 X A[3] = 1.000 B[22] = 0.047 EH 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[5] = 0.45380 X A[0] = 1.000 B[5] = 0.454 DG 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[5] = 0.95008 X A[1] = 0.845 B[11] = 0.587 PS 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[5] = 1.54675 X A[2] = 1.000 B[17] = 0.597 EO 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[5] = 1.82885 X A[3] = 1.000 B[23] = 0.282 KH 0 10:10:29.996 NNTestScript (#NQ100,H1) before rows 1 cols 6 RL 0 10:10:29.996 NNTestScript (#NQ100,H1) IxWMatrix HI 0 10:10:29.996 NNTestScript (#NQ100,H1) Matrix NS 0 10:10:29.996 NNTestScript (#NQ100,H1) [ ND 0 10:10:29.996 NNTestScript (#NQ100,H1) 0.98699 1.63147 1.58725 2.51696 1.62374 1.82885 JM 0 10:10:29.996 NNTestScript (#NQ100,H1) ] LG 0 10:10:29.996 NNTestScript (#NQ100,H1) rows = 1 cols = 6 <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< End of second Hidden Layer >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> ML 0 10:10:29.996 NNTestScript (#NQ100,H1) Hidden Layer 3 | Nodes 1 | Bias 0.1004 OG 0 10:10:29.996 NNTestScript (#NQ100,H1) Inputs 6 Weights 6 NQ 0 10:10:29.996 NNTestScript (#NQ100,H1) 0.76671 0.86228 0.85694 0.93819 0.86135 0.88409 QM 0 10:10:29.996 NNTestScript (#NQ100,H1) 0.278 0.401 0.574 0.301 0.256 0.870 RD 0 10:10:29.996 NNTestScript (#NQ100,H1) Arr size A 6 NO 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 0.21285 X A[0] = 0.767 B[0] = 0.278 QK 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 0.55894 X A[1] = 0.862 B[1] = 0.401 CG 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 1.05080 X A[2] = 0.857 B[2] = 0.574 DS 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 1.33314 X A[3] = 0.938 B[3] = 0.301 HO 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 1.55394 X A[4] = 0.861 B[4] = 0.256 CJ 0 10:10:29.996 NNTestScript (#NQ100,H1) AxBMatrix[0] = 2.32266 X A[5] = 0.884 B[5] = 0.870 HF 0 10:10:29.996 NNTestScript (#NQ100,H1) before rows 1 cols 1 LR 0 10:10:29.996 NNTestScript (#NQ100,H1) IxWMatrix NS 0 10:10:29.996 NNTestScript (#NQ100,H1) Matrix DF 0 10:10:29.996 NNTestScript (#NQ100,H1) [ NN 0 10:10:29.996 NNTestScript (#NQ100,H1) 2.32266 DJ 0 10:10:29.996 NNTestScript (#NQ100,H1) ] GM 0 10:10:29.996 NNTestScript (#NQ100,H1) rows = 1 cols = 1
Lassen Sie mich das Netzwerk visualisieren, damit wir sehen können, was nur auf der ersten Schicht getan wurde, der Rest ist nur eine Iteration des exakt gleichen Verfahrens.
Die Matrixmultiplikation war in der Lage, die Gewichte der ersten Schicht genau so mit den Eingaben zu multiplizieren, wie sie es tun sollte, aber die Kodierung der Logik ist nicht so einfach, wie es sich anhört, die Dinge können etwas verwirrend werden, siehe den folgenden Code. Ignorieren Sie den Rest des Codes und konzentrieren Sie sich auf die Funktion MatrixMultiply.
void CNeuralNets::FeedForwardMLP( double &MLPInputs[], double &MLPOutput[]) { //--- m_hiddenLayers = m_hiddenLayers+1; ArrayResize(m_hiddenLayerNodes,m_hiddenLayers); m_hiddenLayerNodes[m_hiddenLayers-1] = m_outputLayers; int HLnodes = ArraySize(MLPInputs); int weight_start = 0; double Weights[], bias[]; ArrayResize(bias,m_hiddenLayers); //--- int inputs=ArraySize(MLPInputs); int w_size = 0; //size of weights int cols = inputs, rows=1; double IxWMatrix[]; //dot product matrix //Generate random bias for(int i=0; i<m_hiddenLayers; i++) bias[i] = MathRandom(0,1); //generate weights int sum_weights=0, L_inputs=inputs; double L_weights[]; for (int i=0; i<m_hiddenLayers; i++) { sum_weights += L_inputs * m_hiddenLayerNodes[i]; ArrayResize(Weights,sum_weights); L_inputs = m_hiddenLayerNodes[i]; } for (int j=0; j<sum_weights; j++) Weights[j] = MathRandom(0,1); for (int i=0; i<m_hiddenLayers; i++) { w_size = (inputs*m_hiddenLayerNodes[i]); ArrayResize(L_weights,w_size); ArrayCopy(L_weights,Weights,0,0,w_size); ArrayRemove(Weights,0,w_size); MatrixMultiply(MLPInputs,L_weights,IxWMatrix,cols,cols,rows,cols); ArrayFree(MLPInputs); ArrayResize(MLPInputs,m_hiddenLayerNodes[i]); inputs = ArraySize(MLPInputs); for(int k=0; k<ArraySize(IxWMatrix); k++) MLPInputs[k] = ActivationFx(IxWMatrix[k]+bias[i]); } }
Die allererste Eingabe in das Netz in der Eingabeschicht ist eine 1xn-Matrix, d. h. sie besteht aus 1 Zeile und unbekannten Spalten (n). Wir initialisieren diese Logik außerhalb vor der 'for'-Schleife in der Zeile
int cols = inputs, rows=1;
Um die Gesamtzahl der Gewichte zu ermitteln, die für die Multiplikation benötigt werden, multiplizieren wir die Anzahl der Eingänge der vorherigen Schicht mit der Anzahl der Ausgänge der nächsten Schicht. In diesem Fall haben wir 2 Eingänge und 4 Knoten in der ersten verborgenen Schicht, so dass wir schließlich 2x4 = 8, also acht (8) Gewichtungswerte benötigen. Der wichtigste Trick von allen ist hier zu finden:
MatrixMultiply(MLPInputs,L_weights,IxWMatrix,cols,cols,rows,cols);
Um dies besser zu verstehen, wollen wir uns ansehen, was die Matrixmultiplikation bewirkt:
void MatrixMultiply(double &A[],double &B[],double &AxBMatrix[], int colsA,int rowsB,int &new_rows,int &new_cols)
Die letzten Eingänge new_rows, new_cols nehmen die neuen aktualisierten Werte für Zeilen und Spalten für die neue Matrix auf und werden dann als Anzahl der Zeilen und Spalten für die nächste Matrix wiederverwendet. Erinnern Sie sich? Die Eingabe der nächsten Schicht ist die Ausgabe der vorherigen Schicht.
Dies ist für die Matrix umso wichtiger, da
- in der ersten Schicht ist die Eingabematrix 1x2, die Gewichtungsmatrix = 2x4 : Ausgabematrix = 1x4.
- in der zweiten Schicht ist die Eingangsmatrix 1x4 Gewichtungsmatrix = 4x6 : Ausgangsmatrix = 1x6
- die dritte Schicht ist der Eingang 1x6 Gewichtsmatrix 6x1 Ausgangsmatrix = 1x1
Wir wissen, dass zur Matrixmultiplikation die Anzahl der Spalten der ersten Matrix gleich der Anzahl der Zeilen der zweiten Matrix sein muss. Die resultierende Matrix hat die Dimensionen der Anzahl der Zeilen der ersten Matrix und die Anzahl der Spalten der zweiten Matrix.
Aus den oben genannten Vorgängen
Die allererste Eingabe ist diejenige, deren Dimensionen bekannt sind, aber die Gewichtungsmatrix hat 8 Elemente, die durch Multiplikation der Eingaben und der Anzahl der Knoten in der verborgenen Schicht gefunden wurden, so dass wir schließlich feststellen können, dass die Zeilen gleich der Anzahl der Spalten in der vorherigen Schicht/der Eingabe sind, und das war's auch schon. Der Prozess der Anpassung der Werte der neuen Zeilen und neuen Spalten an die alten ermöglicht diese Logik (innerhalb der Funktion Matrix Multiply)
new_rows = rowsA; new_cols = colsB;
Weitere Informationen über Matrizen finden Sie in der Standardbibliothek für Matrizen oder in der Bibliothek, die am Ende des Artikels verlinkt ist.
Nachdem wir nun eine flexible Architektur haben, wollen wir sehen, wie das Training des Netzes und das Training und Testen für dieses Feedforward-MLP aussehen könnten.
Beteiligter Prozess
- Wir trainieren das Netz x Epochen und finden das Modell mit den geringsten Fehlern.
- Wir speichern die Parameter des Modells in einer Binärdatei, die wir in anderen Programmen lesen können, zum Beispiel in einem Expert Advisor.
Moment mal, habe ich gerade gesagt, dass wir das Modell mit den geringsten Fehlern finden? Nun, das tun wir nicht, das ist nur ein Feedforward.
Einige Leute in der MQL5.community bevorzugen es, den EA mit diesen Parametern an den Eingängen zu optimieren, das funktioniert auch, aber in diesem Fall erzeugen wir die Gewichte und die Bias nur einmal und verwenden sie für den Rest der Epochen, so wie wir es bei der Backpropagation machen, aber das Einzige hier ist, dass wir diese Werte nicht aktualisieren, sobald sie einmal festgelegt sind, sie werden nicht aktualisiert - Punkt.
Verwenden Sie die Standardanzahl von Epochen, die auf 1 (Eins) eingestellt ist.
void CNeuralNets::train_feedforwardMLP(double &XMatrix[],int epochs=1)
Sie können einen Weg finden, den Code zu modifizieren und die Gewichte auf die Eingänge des Skripts zu legen, von dort aus können Sie die Anzahl der Epochen auf beliebige Werte setzen, Sie sind jedoch nicht auf diesen Weg beschränkt. Dies ist übrigens eine Demonstration.
Testen oder Anwenden des Modells auf nie gesehene Daten
Um das von uns trainierte Modell verwenden zu können, müssen wir in der Lage sein, seine Parameter mit anderen Programmen auszutauschen. Dies könnte mit Hilfe von Dateien möglich sein. Da unsere Modellparameter reelle Werte der Arrays sind, benötigen wir binäre Dateien, Wir lesen die Binärdateien, in denen wir unsere Gewichte und die Bias gespeichert haben, und tragen sie in den entsprechenden Arrays ein.
Hier ist also die Funktion, die für das Training des neuronalen Netzes verantwortlich ist.
void CNeuralNets::train_feedforwardMLP(double &XMatrix[],int epochs=1) { double MLPInputs[]; ArrayResize(MLPInputs,m_inputs); double MLPOutputs[]; ArrayResize(MLPOutputs,m_outputLayers); double Weights[], bias[]; setmodelParams(Weights,bias); //Generating random weights and bias for (int i=0; i<epochs; i++) { int start = 0; int rows = ArraySize(XMatrix)/m_inputs; { if (m_debug) printf("<<<< %d >>>",j+1); ArrayCopy(MLPInputs,XMatrix,0,start,m_inputs); FeedForwardMLP(MLPInputs,MLPOutputs,Weights,bias); start+=m_inputs; } } WriteBin(Weights,bias); }
Die Funktion setmodelParams() ist eine Funktion, die zufällige Werte für Gewichte und Bias erzeugt. Nach dem Training des Modells erhalten wir die Werte der Gewichte und Bias und speichern sie in einer Binärdatei.
WriteBin(Weights,bias);
Um zu demonstrieren, wie alles in der MLP funktioniert, werden wir den realen Beispieldatensatz von hier verwenden.
Das Argument XMatrix[] ist eine Matrix aller Eingabewerte, mit denen wir unser Modell trainieren wollen. In diesem Fall müssen wir eine CSV-Datei in eine Matrix importieren.
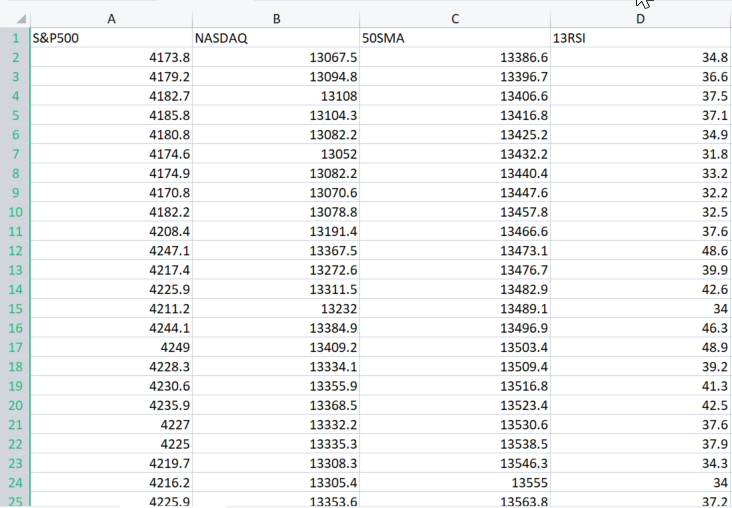
Importieren wir den Datensatz
Nun, ich habe das für Sie gemacht.
double XMatrix[]; int rows,cols; CSVToMatrix(XMatrix,rows,cols,"NASDAQ_DATA.csv"); MatrixPrint(XMatrix,cols,3);
Die Ausgabe des obigen Codes:
MN 0 12:02:13.339 NNTestScript (#NQ100,H1) Matrix MI 0 12:02:13.340 NNTestScript (#NQ100,H1) [ MJ 0 12:02:13.340 NNTestScript (#NQ100,H1) 4173.800 13067.500 13386.600 34.800 RD 0 12:02:13.340 NNTestScript (#NQ100,H1) 4179.200 13094.800 13396.700 36.600 JQ 0 12:02:13.340 NNTestScript (#NQ100,H1) 4182.700 13108.000 13406.600 37.500 FK 0 12:02:13.340 NNTestScript (#NQ100,H1) 4185.800 13104.300 13416.800 37.100 ..... ..... ..... DK 0 12:02:13.353 NNTestScript (#NQ100,H1) 4332.700 14090.200 14224.600 43.700 GD 0 12:02:13.353 NNTestScript (#NQ100,H1) 4352.500 14162.000 14225.000 47.300 IN 0 12:02:13.353 NNTestScript (#NQ100,H1) 4401.900 14310.300 14226.200 56.100 DK 0 12:02:13.353 NNTestScript (#NQ100,H1) 4405.200 14312.700 14224.500 56.200 EE 0 12:02:13.353 NNTestScript (#NQ100,H1) 4415.800 14370.400 14223.200 60.000 OS 0 12:02:13.353 NNTestScript (#NQ100,H1) ] IE 0 12:02:13.353 NNTestScript (#NQ100,H1) rows = 744 cols = 4
Jetzt wird die gesamte CSV-Datei in XMatrix[] eingetragen. Zum Wohl!
Das Gute an dieser resultierenden Matrix ist, dass man sich nicht mehr um die Eingaben eines neuronalen Netzes kümmern muss, da die Variable cols die Anzahl der Spalten aus einer Csv-Datei erhält. Diese werden die Eingaben eines neuronalen Netzes sein. Und so sieht das gesamte Skript aus:
//+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ #include "NeuralNets.mqh"; CNeuralNets *neuralnet; //+------------------------------------------------------------------+ void OnStart() { int hlnodes[3] = {4,6,1}; int outputs = 1; int inputs_=2; double XMatrix[]; int rows,cols; CSVToMatrix(XMatrix,rows,cols,"NASDAQ_DATA.csv"); MatrixPrint(XMatrix,cols,3); neuralnet = new CNeuralNets(SIGMOID,RELU,cols,hlnodes,outputs); neuralnet.train_feedforwardMLP(XMatrix); delete(neuralnet); }
Einfach, oder? In train_feedforwardMLP müssen wir die Iterationen des gesamten Datensatzes zu einer einzigen Epocheniteration hinzufügen, um die Bedeutung einer Epoche vollständig zu erfassen.
for (int i=0; i<epochs; i++) { int start = 0; int rows = ArraySize(XMatrix)/m_inputs; for (int j=0; j<rows; j++) //iterate the entire dataset in a single epoch { if (m_debug) printf("<<<< %d >>>",j+1); ArrayCopy(MLPInputs,XMatrix,0,start,m_inputs); FeedForwardMLP(MLPInputs,MLPOutputs,Weights,bias); start+=m_inputs; } }
Schauen wir uns nun die Protokolle an, wenn wir das Programm im Debug-Modus ausführen.
bool m_debug = true;
Der Debug-Modus kann den Speicherplatz auf Ihrer Festplatte füllen, es sei denn, Sie debuggen das neuronale Netzwerk. Setzen Sie ihn bitte auf „false“. Ich habe das Programm einmal laufen lassen und hatte Protokolle, die bis zu 21Mb Speicherplatz beanspruchten.
Ein kurzer Überblick über die beiden Iterationen:
MR 0 12:23:16.485 NNTestScript (#NQ100,H1) <<<< 1 >>> DE 0 12:23:16.485 NNTestScript (#NQ100,H1) Hidden layer nodes plus the output FS 0 12:23:16.485 NNTestScript (#NQ100,H1) 4 6 1 1 KK 0 12:23:16.485 NNTestScript (#NQ100,H1) Hidden Layer 1 | Nodes 4 | Bias 0.3903 IN 0 12:23:16.485 NNTestScript (#NQ100,H1) Inputs 4 Weights 16 MJ 0 12:23:16.485 NNTestScript (#NQ100,H1) 4173.80000 13067.50000 13386.60000 34.80000 DF 0 12:23:16.485 NNTestScript (#NQ100,H1) 0.060 0.549 0.797 0.670 0.420 0.914 0.146 0.968 0.464 0.031 0.855 0.240 0.717 0.288 0.372 0.805 .... PD 0 12:23:16.485 NNTestScript (#NQ100,H1) MLP Final Output LM 0 12:23:16.485 NNTestScript (#NQ100,H1) 1.333 HP 0 12:23:16.485 NNTestScript (#NQ100,H1) <<<< 2 >>> PG 0 12:23:16.485 NNTestScript (#NQ100,H1) Hidden layer nodes plus the output JR 0 12:23:16.485 NNTestScript (#NQ100,H1) 4 6 1 1 OH 0 12:23:16.485 NNTestScript (#NQ100,H1) Hidden Layer 1 | Nodes 4 | Bias 0.3903 EI 0 12:23:16.485 NNTestScript (#NQ100,H1) Inputs 4 Weights 16 FM 0 12:23:16.485 NNTestScript (#NQ100,H1) 4179.20000 13094.80000 13396.70000 36.60000 II 0 12:23:16.486 NNTestScript (#NQ100,H1) 0.060 0.549 0.797 0.670 0.420 0.914 0.146 0.968 0.464 0.031 0.855 0.240 0.717 0.288 0.372 0.805 GJ 0 12:23:16.486 NNTestScript (#NQ100,H1)
Alles ist wie erwartet eingerichtet und funktioniert gut. Lassen Sie uns nun die Modellparameter in den Binärdateien speichern.
Speichern der Parameter des Modells in einer Binärdatei
bool CNeuralNets::WriteBin(double &w[], double &b[]) { string file_name_w = NULL, file_name_b= NULL; int handle_w, handle_b; file_name_w = MQLInfoString(MQL_PROGRAM_NAME)+"\\"+"model_w.bin"; file_name_b = MQLInfoString(MQL_PROGRAM_NAME)+"\\"+"model_b.bin"; FileDelete(file_name_w); FileDelete(file_name_b); handle_w = FileOpen(file_name_w,FILE_WRITE|FILE_BIN); if (handle_w == INVALID_HANDLE) { printf("Invalid %s Handle err %d",file_name_w,GetLastError()); } else FileWriteArray(handle_w,w); FileClose(handle_w); handle_b = FileOpen(file_name_b,FILE_WRITE|FILE_BIN); if (handle_b == INVALID_HANDLE) { printf("Invalid %s Handle err %d",file_name_b,GetLastError()); } else FileWriteArray(handle_b,b); FileClose(handle_b); return(true); }
Dieser Schritt ist sehr wichtig. Wie bereits erwähnt, hilft es, die Modellparameter mit anderen Programmen zu teilen, die dieselbe Bibliothek verwenden. Die Binärdateien werden in einem Unterverzeichnis mit dem Namen Ihrer Skriptdatei gespeichert:
Ein Beispiel dafür, wie man in anderen Programmen auf die Modellparameter zugreifen kann:
double weights[], bias[]; int handlew = FileOpen("NNTestScript\\model_w.bin",FILE_READ|FILE_BIN); FileReadArray(handlew,weights); FileClose(handlew); int handleb = FileOpen("NNTestScript\\model_b.bin",FILE_READ|FILE_BIN); FileReadArray(handleb,bias); FileClose(handleb); Print("bias"); ArrayPrint(bias,4); Print("Weights"); ArrayPrint(weights,4);
Ausgänge:
HR 0 14:14:02.380 NNTestScript (#NQ100,H1) bias DG 0 14:14:02.385 NNTestScript (#NQ100,H1) 0.0063 0.2737 0.9216 0.4435 OQ 0 14:14:02.385 NNTestScript (#NQ100,H1) Weights GG 0 14:14:02.385 NNTestScript (#NQ100,H1) [ 0] 0.5338 0.6378 0.6710 0.6256 0.8313 0.8093 0.1779 0.4027 0.5229 0.9181 0.5449 0.4888 0.9003 0.2870 0.7107 0.8477 NJ 0 14:14:02.385 NNTestScript (#NQ100,H1) [16] 0.2328 0.1257 0.4917 0.1930 0.3924 0.2824 0.4536 0.9975 0.9484 0.5822 0.0198 0.7951 0.3904 0.7858 0.7213 0.0529 EN 0 14:14:02.385 NNTestScript (#NQ100,H1) [32] 0.6332 0.6975 0.9969 0.3987 0.4623 0.4558 0.4474 0.4821 0.0742 0.5364 0.9512 0.2517 0.3690 0.4989 0.5482Toll, jetzt können Sie von überall auf diese Datei zugreifen, solange Sie die Namen kennen und wissen, wo sie zu finden sind.
Verwendung des Modells
Das ist der einfache Teil. Die Feed-Forward-MLP-Funktion wurde modifiziert, neue Eingangsgewichte und Bias wurden hinzugefügt, was bei der Ausführung des Modells für z. B. aktuelle Preisdaten oder ähnliches hilfreich sein wird.
void CNeuralNets::FeedForwardMLP(double &MLPInputs[],double &MLPOutput[],double &Weights[], double &bias[])
Vollständiger Code zum Extrahieren der Gewichte und Bias und zur Live-Nutzung des Modells. Zuerst lesen wir die Parameter, dann geben wir die Eingabewerte ein , nicht eine Eingabematrix, denn diesmal verwenden wir das trainierte Modell, um das Ergebnis der Eingabewerte vorherzusagen. MLPOutput[] liefert Ihnen das Ausgabe-Array:
double weights[], bias[]; int handlew = FileOpen("NNTestScript\\model_w.bin",FILE_READ|FILE_BIN); FileReadArray(handlew,weights); FileClose(handlew); int handleb = FileOpen("NNTestScript\\model_b.bin",FILE_READ|FILE_BIN); FileReadArray(handleb,bias); FileClose(handleb); double Inputs[]; ArrayCopy(Inputs,XMatrix,0,0,cols); //copy the four first columns from this matrix double Output[]; neuralnet = new CNeuralNets(SIGMOID,RELU,cols,hlnodes,outputs); neuralnet.FeedForwardMLP(Inputs,Output,weights,bias); Print("Outputs"); ArrayPrint(Output); delete(neuralnet);
Das sollte gut funktionieren.
Jetzt können Sie sich frei fühlen, verschiedene Arten von Architektur zu erkunden und verschiedene Optionen zu erforschen, um zu sehen, was für Sie am besten funktioniert.
Das neuronale Feedforward-Netz war der erste und einfachste Typ eines künstlichen neuronalen Netzes. In diesem Netz bewegen sich die Informationen nur in eine Richtung - von den Eingangsknoten über die verborgenen Knoten (falls vorhanden) zu den Ausgangsknoten. Es gibt keine Zyklen oder Schleifen im Netz
Dieses Modell, das wir gerade kodiert haben, ist ein einfaches Modell und liefert nicht unbedingt die gewünschten Ergebnisse, es sei denn, es wird optimiert (da bin ich mir 100%ig sicher), aber hoffentlich werden Sie kreativ sein und etwas daraus machen.
Abschließende Überlegungen
Es ist wichtig, die Theorie und alles, was sich hinter den verschlossenen Türen der einzelnen maschinellen Lerntechniken verbirgt, zu verstehen, da wir in MQL5 keine Data Science-Pakete haben. Wenigstens haben wir die Python-Frameworks, aber es gibt Zeiten, in denen wir uns in MetaTrader zurechtfinden müssen. Ohne ein solides Verständnis der Theorie, die hinter diesen Dingen steckt, wird es schwierig sein, die Dinge herauszufinden und das Beste aus dem maschinellen Lernen zu machen, denn je weiter wir gehen, desto wichtiger werden die Theorie und die Dinge, die wir zuvor in der Artikelserie besprochen haben.
Mit freundlichen Grüßen.
GitHub repo: https://github.com/MegaJoctan/NeuralNetworks-MQL5
Lesen Sie mehr über meine Bibliothek für Matrizen und Vektoren
Weiterführende Literatur | Bücher | Referenzen
- Neural Networks for Pattern Recognition (Advanced Texts in Econometrics)
- Neural Networks: Tricks of the Trade (Lecture Notes in Computer Science, 7700)
- Deep Learning (Adaptive Computation and Machine Learning series)
Artikel Referenzen:
- Datenwissenschaft und maschinelles Lernen (Teil 01): Lineare Regression
- Datenwissenschaft und maschinelles Lernen (Teil 02): Logistische Regression
- Datenwissenschaft und maschinelles Lernen (Teil 03): Matrix-Regressionen
- Datenwissenschaft und maschinelles Lernen (Teil 06): Gradientenverfahren
- Datenwissenschaft und maschinelles Lernen — Neuronales Netzwerk (Teil 01): Entmystifizierte Feed Forward Neurale Netzwerke
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/11334
Lernen Sie, wie man ein Handelssystem mit dem VIDYA entwickelt
Neuronale Netze leicht gemacht (Teil 18): Assoziationsregeln
Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 21): Neues Auftragssystem (IV)
Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 20): Neues Auftragssystem (III)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.