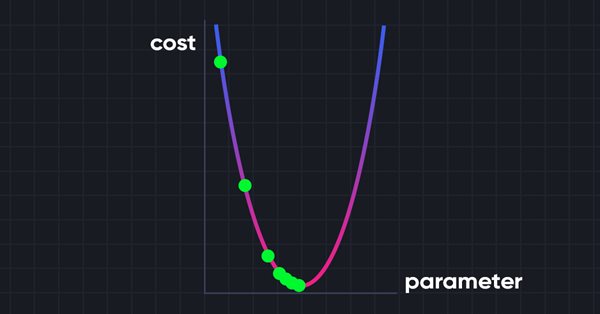
Datenwissenschaft und maschinelles Lernen (Teil 06): Gradientenverfahren
Verfrühte Optimierung ist die Wurzel allen Übels in der Programmierung
-Donald Knuth
Einführung
Nach Wikipedia ist das Gradientenverfahren (oft auch genannt steilster Abstieg) ist ein iterativer Optimierungsalgorithmus erster Ordnung zum Auffinden eines lokalen Minnimums einer differenzierbaren Funktion. Die Idee ist, wiederholte Schritte in die entgegengesetzte Richtung des Gradienten (oder ungefähren Gradienten) der Funktion am aktuellen Punkt zu machen, da dies die Richtung des steilsten Abstiegs ist. Umgekehrt führt ein Schritt in Richtung des Gradienten zu einem lokalen Maximum dieser Funktion; das Verfahren wird dann als Gradientenanstieg bezeichnet. Grundsätzlich ist der Gradientenverfahren (Gradientenabstieg) ein Optimierungsalgorithmus, der dazu dient, das Minimum einer Funktion zu finden:
Das Gradientenverfahren ist ein sehr wichtiger Algorithmus beim maschinellen Lernen, da er uns hilft, die Parameter für das beste Modell für unseren Datensatz zu finden.
Kostenfunktion
Manche nennen dies Verlustfunktion, eine Metrik zur Berechnung, wie gut oder schlecht unser Modell die Beziehung zwischen den Werten von x und y vorhersagen kann.
Es gibt eine Vielzahl von Metriken, die verwendet werden können, um festzustellen, wie gut das Modell Vorhersagen trifft. Im Gegensatz zu all diesen Metriken ermittelt die Kostenfunktion den durchschnittlichen Verlust über den gesamten Datensatz, und je größer die Kostenfunktion ist, desto schlechter ist unser Modell beim Auffinden der Beziehungen in unserem Datensatz.
Das Gradientenverfahren zielt darauf ab, die Kostenfunktion zu minimieren, da das Modell mit der niedrigsten Kostenfunktion das beste Modell ist. Um zu verstehen, was ich gerade erklärt habe, sehen wir uns das folgende Beispiel an;Angenommen, unsere Kostenfunktion hat die Gleichung
Wenn wir ein Diagramm dieser Funktion mit Python erstellen, sieht es folgendermaßen aus
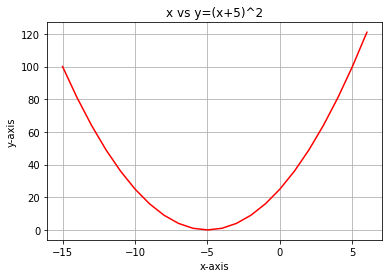
Der allererste Schritt, den wir für unsere Kostenfunktion tun müssen, ist die Differenzierung der Kostenfunktion unter Verwendung der Kettenregel:
Die Gleichung y= (x+5)^2 ist eine zusammengesetzte Funktion (eine Funktion steckt in einer anderen), wobei die äußere Funktion (x+5)^2 und die innere Funktion (x+5) ist. Um dies zu differenzieren, wenden wir die Kettenregel an, siehe Abbildung

Am Ende ist ein Video verlinkt, in dem ich die Mathematik von Hand ausführe, falls Sie das schwer zu verstehen finden. OK, also diese Funktion, die wir gerade erhalten haben, ist der Gradient. Der Prozess, den Gradienten einer Gleichung zu finden, ist der wichtigste Schritt von allen, und ich wünschte, meine Mathematiklehrer hätten mir damals gesagt, dass der Zweck der Differenzierung der Funktion darin besteht, den Gradienten einer Funktion zu erhalten.
Dies ist der erste und wichtigste Schritt, der zweite Schritt ist
Schritt 02:
Wir bewegen uns in die negative Richtung des Gradienten, hier stellt sich die Frage, wie weit wir uns bewegen sollten. An dieser Stelle kommt die Lernrate ins Spiel.
Lernrate
Per Definition ist dies die Schrittgröße bei jeder Iteration, während man sich auf ein Minimum einer Verlustfunktion zubewegt. Nehmen wir das Beispiel einer Person, die den Berg hinuntersteigt, ihre Schritte sind die Lernrate, je kleiner die Schritte sind, desto länger wird sie brauchen, um den Fuß des Berges zu erreichen und umgekehrt.Halten Sie die Lernrate des Algorithmus bei kleineren Werten, aber nicht bei sehr kleinen wie 0,0001. Dadurch erhöhen Sie die Ausführungszeit des Programms, da es länger dauern kann, bis der Algorithmus die Mindestwerte erreicht; im Gegensatz dazu führt die Verwendung großer Zahlen für die Lernrate dazu, dass der Algorithmus die Mindestwerte überspringt, was letztendlich dazu führen kann, dass Sie den Mindestwert nicht erreichen
Die Standard-Lernrate beträgt 0,01
Führen wir die Iteration durch, um zu sehen, wie der Algorithmus funktioniert
Erste Iteration: Wir wählen einen beliebigen Punkt als Startpunkt für unseren Algorithmus, ich habe 0 als ersten Wert von x gewählt, um die Werte von x zu aktualisieren, lautet die Formel
Mit jeder Iteration nähern wir uns dem Minimalwert der Funktion an, daher der Name Gradientenabstieg, Macht das jetzt Sinn?
Lassen Sie uns sehen, wie das im Detail funktioniert. Lassen Sie uns nun die Werte für 2 Iterationen manuell berechnen, damit Sie ein solides Verständnis dafür bekommen, was passiert:
1. Iteration:
Formel: x1 = x0 - Lernrate * ( 2*(x+5) )
x1 = 0 - 0.01 * 0.01 * 2*(0+5)
x1 = -0.01 * 10
x1 = -0,1 (endgültig)
Nun aktualisieren wir die Werte, indem wir den neuen Wert dem alten Wert zuordnen und den Vorgang so lange wiederholen, bis wir das Minimum einer Funktion erreichen:
x0 = x1
2. Iteration:
x1 = -0.1 - 0.01 * 2*(-0.1+5)
x1 = -0.198
Dann gilt: x0 = x1
Wenn wir diesen Vorgang mehrmals wiederholen, ergibt sich für die ersten 10 Iterationen folgendes Ergebnis:
RS 0 17:15:16.793 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction CUSTOM QQ 0 17:15:16.793 gradient-descent test (EURUSD,M1) 1 x0 = 0.0000000000 x1 = -0.1000000000 CostFunction = 10.0000000000 ES 0 17:15:16.793 gradient-descent test (EURUSD,M1) 2 x0 = -0.1000000000 x1 = -0.1980000000 CostFunction = 9.8000000000 PR 0 17:15:16.793 gradient-descent test (EURUSD,M1) 3 x0 = -0.1980000000 x1 = -0.2940400000 CostFunction = 9.6040000000 LE 0 17:15:16.793 gradient-descent test (EURUSD,M1) 4 x0 = -0.2940400000 x1 = -0.3881592000 CostFunction = 9.4119200000 JD 0 17:15:16.793 gradient-descent test (EURUSD,M1) 5 x0 = -0.3881592000 x1 = -0.4803960160 CostFunction = 9.2236816000 IG 0 17:15:16.793 gradient-descent test (EURUSD,M1) 6 x0 = -0.4803960160 x1 = -0.5707880957 CostFunction = 9.0392079680 IG 0 17:15:16.793 gradient-descent test (EURUSD,M1) 7 x0 = -0.5707880957 x1 = -0.6593723338 CostFunction = 8.8584238086 JF 0 17:15:16.793 gradient-descent test (EURUSD,M1) 8 x0 = -0.6593723338 x1 = -0.7461848871 CostFunction = 8.6812553325 NI 0 17:15:16.793 gradient-descent test (EURUSD,M1) 9 x0 = -0.7461848871 x1 = -0.8312611893 CostFunction = 8.5076302258 CK 0 17:15:16.793 gradient-descent test (EURUSD,M1) 10 x0 = -0.8312611893 x1 = -0.9146359656 CostFunction = 8.3374776213
Schauen wir uns auch die anderen zehn Werte des Algorithmus an, wenn er sich sehr nahe am Minimum der Funktion befindet:
GK 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1052 x0 = -4.9999999970 x1 = -4.9999999971 CostFunction = 0.0000000060 IH 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1053 x0 = -4.9999999971 x1 = -4.9999999971 CostFunction = 0.0000000059 NH 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1054 x0 = -4.9999999971 x1 = -4.9999999972 CostFunction = 0.0000000058 QI 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1055 x0 = -4.9999999972 x1 = -4.9999999972 CostFunction = 0.0000000057 II 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1056 x0 = -4.9999999972 x1 = -4.9999999973 CostFunction = 0.0000000055 RN 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1057 x0 = -4.9999999973 x1 = -4.9999999973 CostFunction = 0.0000000054 KN 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1058 x0 = -4.9999999973 x1 = -4.9999999974 CostFunction = 0.0000000053 JO 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1059 x0 = -4.9999999974 x1 = -4.9999999974 CostFunction = 0.0000000052 JO 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1060 x0 = -4.9999999974 x1 = -4.9999999975 CostFunction = 0.0000000051 QL 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1061 x0 = -4.9999999975 x1 = -4.9999999975 CostFunction = 0.0000000050 QL 0 17:15:16.800 gradient-descent test (EURUSD,M1) 1062 x0 = -4.9999999975 x1 = -4.9999999976 CostFunction = 0.0000000049 HP 0 17:15:16.800 gradient-descent test (EURUSD,M1) Local miminum found =-4.999999997546217
Nach 1062 (eintausendzweiundsechzig) Iterationen konnte der Algorithmus das lokale Minimum dieser Funktion erreichen B A M
Bei diesem Algorithmus ist Folgendes zu beachten
Wenn Sie sich die Werte der Kostenfunktion ansehen, werden Sie feststellen, dass sich die Werte zu Beginn stark ändern, die letzten Werte einer Kostenfunktion jedoch nur sehr geringfügig.
Das Gradientenverfahren macht größere Schritte, wenn er sich nicht in der Nähe des Minimums einer Funktion befindet, aber er macht kleine Schritte, wenn er sich in der Nähe des Minimums der Funktion befindet, das Gleiche, was Sie tun werden, wenn Sie sich in der Nähe des Fußes des Berges befinden, also wissen Sie jetzt, dass das Gradientenverfahren ziemlich schlau ist !!!
Das lokale Minimum ist schließlich:
HP 0 17:15:16.800 gradient-descent test (EURUSD,M1) Local miminum found =-4.999999997546217
Das ist der genaue Wert, denn das Minimum dieser Funktion ist -5,0 - B A M
Die eigentliche Frage
Woher weiß der Gradient, wann er aufhören muss? Wir können den Algorithmus bis ins Unendliche iterieren lassen oder zumindest bis zum Ende der Rechenkapazität eines Computers.
Wenn die Kostenfunktion gleich Null ist, wissen wir, dass der Gradientenabstieg seine Aufgabe erfüllt hat
Lassen Sie uns nun diesen ganzen Vorgang in MQL5 codieren
while (true) { iterations++; x1 = x0 - m_learning_rate * CustomCostFunction(x0); printf("%d x0 = %.10f x1 = %.10f CostFunction = %.10f",iterations,x0,x1,CustomCostFunction(x0)); if (NormalizeDouble(CustomCostFunction(x0),8) == 0) { Print("Local miminum found =",x0); break; } x0 = x1; }
Der obige Codeblock ist derjenige, der uns die gewünschten Ergebnisse liefert, aber er ist nicht der einzige in der Klasse CGradientDescent. Die Funktion CustomCostFunction ist der Ort, an dem unsere differenzierte Gleichung aufbewahrt und berechnet wurde
double CGradientDescent::CustomCostFunction(double x) { return(2 * ( x + 5 )); }
Was ist der Zweck?
Man könnte sich fragen, wozu all diese Berechnungen, wenn man einfach das lineare Standardmodell verwenden kann, das von den vorhergehenden Bibliotheken erstellt wurde, die wir in dieser Artikelserie besprochen haben. Das mit den Standardwerten erstellte Modell ist nicht unbedingt das beste Modell. Sie müssen den Computer die besten Parameter für das Modell mit den wenigsten Fehlern lernen lassen (bestes Modell).
Wir sind dem Aufbau künstlicher neuronaler Netze ein paar Artikel näher gekommen, und damit jeder verstehen kann, wie neuronale Netze lernen (sich selbst die Muster beibringen), ist das Gradientenverfahren der beliebteste Algorithmus, der all das möglich gemacht hat. Ohne ein solides Verständnis davon werden Sie den Prozess vielleicht nie verstehen, denn die Dinge werden kompliziert werden.
Das Gradientenverfahren für ein Regressionsmodell
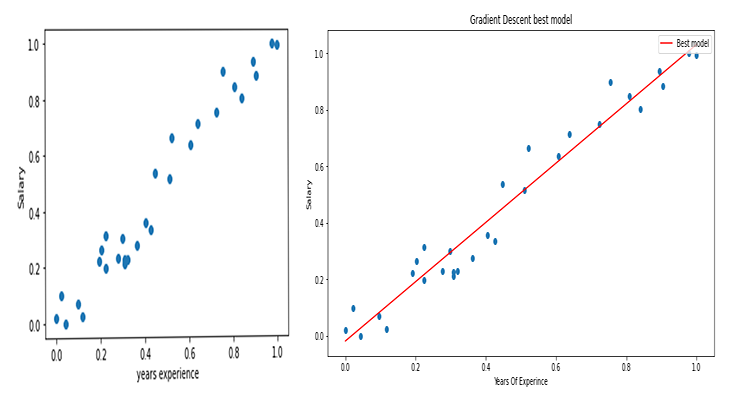
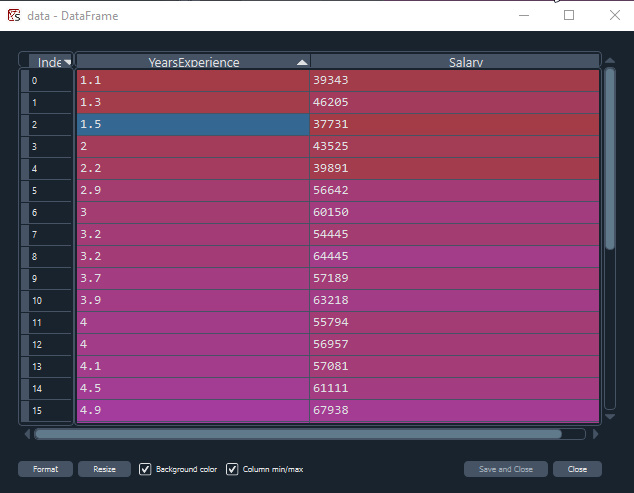
Mit Hilfe des Gehaltsdatensatzes wollen wir das beste Modell mit Hilfe des Gradientenverfahren erstellen,
Datenvisualisierung, In python
import pandas as pd import numpy as np import matplotlib.pyplot as plt data = pd.read_csv(r"C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\Salary_Data.csv") print(data.head(10)) x = data["YearsExperience"] y = data["Salary"] plt.figure(figsize=(16,9)) plt.title("Experience vs Salary") plt.scatter(x,y,c="green") plt.xlabel(xlabel="Years of Experience") plt.ylabel(ylabel="Salary") plt.show()
Dies wird unser Graph sein
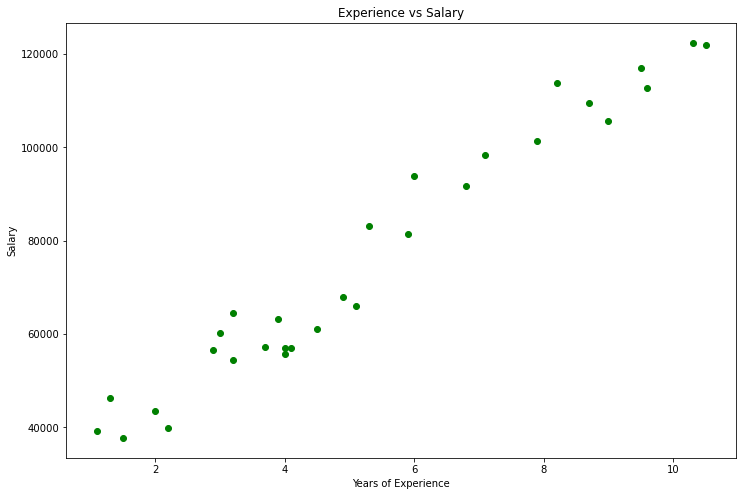
Wenn Sie sich unseren Datensatz ansehen, werden Sie feststellen, dass es sich um ein Regressionsproblem handelt, aber wir können eine Million Modelle haben, die uns bei der Vorhersage helfen, oder was auch immer wir erreichen wollen.
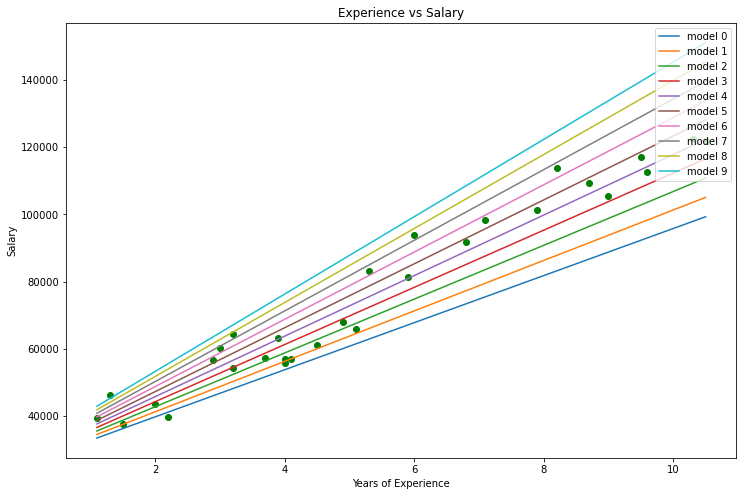
Welches Modell am besten geeignet ist, um Vorhersagen über die Erfahrung einer Person und ihr Gehalt zu treffen, werden wir herausfinden. Aber zuerst wollen wir die Kostenfunktion für unser Regressionsmodell ableiten.
Theorie
Lassen Sie mich auf die lineare Regression zurückkommen.
Wir wissen mit Sicherheit, dass jedes lineare Modell mit Fehlern behaftet ist. Wir wissen auch, dass wir eine Million Linien in diesem Diagramm erstellen können und dass die Linie mit der besten Anpassung immer die Linie mit den geringsten Fehlern ist.
Die Kostenfunktion stellt den Fehler zwischen unseren tatsächlichen Werten und den vorhergesagten Werten dar, wir können die Formel für die Kostenfunktion so schreiben, dass sie gleich ist:
Kosten = Y Tatsächliche - Y Voraussichtliche. Da wir die Größenordnung der Fehler sehen, die wir in das Quadrat setzen, lautet unsere Formel nun
![]()
Da wir aber nach Fehlern in unserem gesamten Datensatz suchen, müssen wir die Summierung vornehmen
![]()
Schließlich teilen wir die Summe der Fehler durch m, das ist die Anzahl der Elemente im Datensatz:
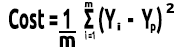
Hier ist das Video über die gesamten mathematischen Verfahren, die von Hand durchgeführt werden.
Da wir nun die Kostenfunktion haben, können wir das Gradientenverfahren und die besten Parameter für beide finden, den Koeffizienten von X (Steigung), bezeichnet als B0 , und den Y-Achsenabschnitt, bezeichnet als B1.
double cost_B0=0, cost_B1=0; if (costFunction == MSE) { int iterations=0; for (int i=0; i<m_iterations; i++, iterations++) { cost_B0 = Mse(b0,b1,Intercept); cost_B1 = Mse(b0,b1,Slope); b0 = b0 - m_learning_rate * cost_B0; b1 = b1 - m_learning_rate * cost_B1; printf("%d b0 = %.8f cost_B0 = %.8f B1 = %.8f cost_B1 = %.8f",iterations,b0,cost_B0,b1,cost_B1); DBL_MAX_MIN(b0); DBL_MAX_MIN(cost_B0); DBL_MAX_MIN(cost_B1); if (NormalizeDouble(cost_B0,8) == 0 && NormalizeDouble(cost_B1,8) == 0) break; } printf("%d Iterations Local Minima are\nB0(Intercept) = %.5f || B1(Coefficient) = %.5f",iterations,b0,b1); }
Beachten Sie ein paar Dinge aus dem Code für das Gradientenverfahren,
- Der Prozess ist immer noch derselbe wie zuvor, aber dieses Mal werden die Werte zweimal auf einmal ermittelt und aktualisiert: B0 und B1.
- Es gibt eine begrenzte Anzahl von Iterationen. Jemand hat einmal gesagt, der beste Weg, eine Endlosschleife zu machen, sei die Verwendung einer while-Schleife . Wir verwenden dieses Mal nicht die while-Schleife, sondern wollen die Anzahl der Durchläufe des Algorithmus begrenzen, um die Koeffizienten für das beste Modell zu finden.
- DBL_MAX_MIN ist eine Funktion für Debugging-Zwecke, die überprüft, ob die mathematischen Grenzen eines Computers erreicht sind und uns darüber informiert.
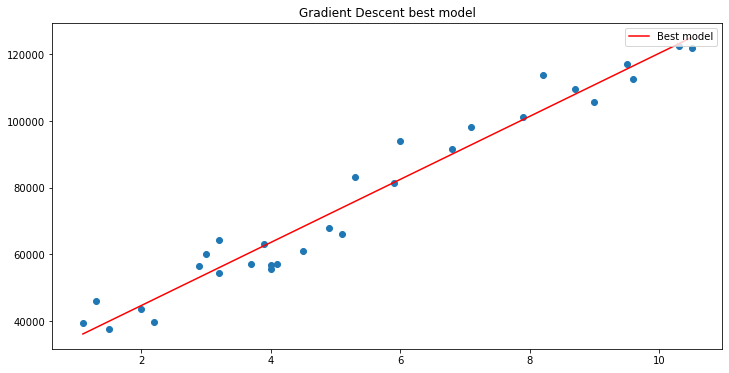
Dies ist die Ausgabe der Operationen des Algorithmus, Lernrate = 0,01 Iterationen = 10000.
PD 0 17:29:17.999 gradient-descent test (EURUSD,M1) [20] 91738.0000 98273.0000 101302.0000 113812.0000 109431.0000 105582.0000 116969.0000 112635.0000 122391.0000 121872.0000 JS 0 17:29:17.999 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction MSE RF 0 17:29:17.999 gradient-descent test (EURUSD,M1) 0 b0 = 1520.06000000 cost_B0 = -152006.00000000 B1 = 9547.97400000 cost_B1 = -954797.40000000 OP 0 17:29:17.999 gradient-descent test (EURUSD,M1) 1 b0 = 1995.08742960 cost_B0 = -47502.74296000 B1 = 12056.69235267 cost_B1 = -250871.83526667 LP 0 17:29:17.999 gradient-descent test (EURUSD,M1) 2 b0 = 2194.02117366 cost_B0 = -19893.37440646 B1 = 12707.81767044 cost_B1 = -65112.53177770 QN 0 17:29:17.999 gradient-descent test (EURUSD,M1) 3 b0 = 2319.78332575 cost_B0 = -12576.21520809 B1 = 12868.77569178 cost_B1 = -16095.80213357 LO 0 17:29:17.999 gradient-descent test (EURUSD,M1) 4 b0 = 2425.92576238 cost_B0 = -10614.24366387 B1 = 12900.42596039 cost_B1 = -3165.02686058 GH 0 17:29:17.999 gradient-descent test (EURUSD,M1) 5 b0 = 2526.58198175 cost_B0 = -10065.62193621 B1 = 12897.99808257 cost_B1 = 242.78778134 CJ 0 17:29:17.999 gradient-descent test (EURUSD,M1) 6 b0 = 2625.48307920 cost_B0 = -9890.10974571 B1 = 12886.62268517 cost_B1 = 1137.53974060 DD 0 17:29:17.999 gradient-descent test (EURUSD,M1) 7 b0 = 2723.61498028 cost_B0 = -9813.19010723 B1 = 12872.93147573 cost_B1 = 1369.12094310 HF 0 17:29:17.999 gradient-descent test (EURUSD,M1) 8 b0 = 2821.23916252 cost_B0 = -9762.41822398 B1 = 12858.67435081 cost_B1 = 1425.71249248 <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< Last Iterations >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> EI 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6672 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 NG 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6673 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 GD 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6674 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 PR 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6675 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 IS 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6676 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 RQ 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6677 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 KN 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6678 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 DL 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6679 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 RM 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6680 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 IK 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6681 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 PH 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6682 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 GF 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6683 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000 MG 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6684 b0 = 25792.20019866 cost_B0 = -0.00000000 B1 = 9449.96232146 cost_B1 = 0.00000000 LE 0 17:29:48.247 gradient-descent test (EURUSD,M1) 6684 Iterations Local Minima are OJ 0 17:29:48.247 gradient-descent test (EURUSD,M1) B0(Intercept) = 25792.20020 || B1(Coefficient) = 9449.96232
Wenn wir das Diagramm mit zeichnen.
B A M, Das Gradientenverfahren hat erfolgreich das beste Modell von 10000 Modellen, die wir ausprobiert haben, gefunden. Das ist großartig, aber es gibt einen entscheidenden Schritt, den wir auslassen, der dazu führen kann, dass sich unser Modell seltsam verhält und wir die Ergebnisse bekommen, die wir nicht wollen.
Normalisierung der Eingabedaten der linearen Regression
Wir wissen, dass für verschiedene Datensätze die besten Modelle nach verschiedenen Iterationen gefunden werden können, wobei einige 100 Iterationen benötigen, um die besten Modelle zu erreichen, und andere 10000 oder bis zu einer Million Iterationen, um die Kostenfunktion auf Null zu bringen, ganz zu schweigen davon, dass wir bei falschen Werten für die Lernrate am Ende die lokalen Minima verpassen können, und wenn wir dieses Ziel verfehlen, stoßen wir am Ende an die mathematischen Grenzen eines Computers, sehen wir uns das in der Praxis an.
Lernrate = 0,1 Iterationen 1000
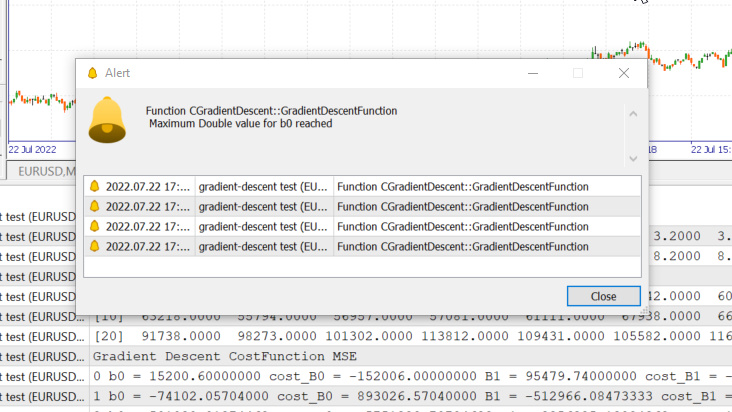
Wir haben soeben den vom System erlaubten Höchstwert für ‚double‘ Zahlen erreicht, hier unsere Protokolle:
GM 0 17:28:14.819 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction MSE OP 0 17:28:14.819 gradient-descent test (EURUSD,M1) 0 b0 = 15200.60000000 cost_B0 = -152006.00000000 B1 = 95479.74000000 cost_B1 = -954797.40000000 GR 0 17:28:14.819 gradient-descent test (EURUSD,M1) 1 b0 = -74102.05704000 cost_B0 = 893026.57040000 B1 = -512966.08473333 cost_B1 = 6084458.24733333 NM 0 17:28:14.819 gradient-descent test (EURUSD,M1) 2 b0 = 501030.91374462 cost_B0 = -5751329.70784622 B1 = 3356325.13824362 cost_B1 = -38692912.22976952 LH 0 17:28:14.819 gradient-descent test (EURUSD,M1) 3 b0 = -3150629.51591119 cost_B0 = 36516604.29655810 B1 = -21257352.71857720 cost_B1 = 246136778.56820822 KD 0 17:28:14.819 gradient-descent test (EURUSD,M1) 4 b0 = 20084177.14287909 cost_B0 = -232348066.58790281 B1 = 135309993.40314889 cost_B1 = -1565673461.21726084 OQ 0 17:28:14.819 gradient-descent test (EURUSD,M1) 5 b0 = -127706877.34210962 cost_B0 = 1477910544.84988713 B1 = -860620298.24803317 cost_B1 = 9959302916.51181984 FM 0 17:28:14.819 gradient-descent test (EURUSD,M1) 6 b0 = 812402202.33122230 cost_B0 = -9401090796.73331833 B1 = 5474519904.86084747 cost_B1 = -63351402031.08880615 JJ 0 17:28:14.819 gradient-descent test (EURUSD,M1) 7 b0 = -5167652856.43381691 cost_B0 = 59800550587.65039062 B1 = -34823489070.42410278 cost_B1 = 402980089752.84948730 MP 0 17:28:14.819 gradient-descent test (EURUSD,M1) 8 b0 = 32871653967.62362671 cost_B0 = -380393068240.57440186 B1 = 221513298448.70788574 cost_B1 = -2563367875191.31982422 MM 0 17:28:14.819 gradient-descent test (EURUSD,M1) 9 b0 = -209097460110.12799072 cost_B0 = 2419691140777.51611328 B1 = -1409052343513.33935547 cost_B1 = 16305656419620.47265625 HD 0 17:28:14.819 gradient-descent test (EURUSD,M1) 10 b0 = 1330075004152.67309570 cost_B0 = -15391724642628.00976562 B1 = 8963022367351.18359375 cost_B1 = -103720747108645.23437500 DP 0 17:28:14.819 gradient-descent test (EURUSD,M1) 11 b0 = -8460645083849.12207031 cost_B0 = 97907200880017.93750000 B1 = -57014041694401.67187500 cost_B1 = 659770640617528.50000000
Das bedeutet, dass wir, wenn wir die Lernrate falsch gewählt haben, nur eine geringe bis gar keine Chance haben, das beste Modell zu finden, und die Wahrscheinlichkeit hoch ist, dass wir am Ende an die mathematischen Grenzen eines Computers stoßen, wie Sie gerade gesehen haben.
Wenn ich aber 0,01 für die Lernrate in diesem Datensatz ausprobiere, werden wir am Ende keine Probleme haben, obwohl der Trainingsprozess viel langsamer wird, aber wenn ich diese Lernrate für diesen dataset verwende, werde ich am Ende an mathematische Grenzen stoßen. Sie wissen also, dass jeder Datensatz seine eigene Lernrate hat, aber wir haben vielleicht nicht die Möglichkeit, die Lernrate zu optimieren, weil wir manchmal komplexe Datensätze mit mehreren Variablen haben und dies auch eine ineffektive Art ist, diesen ganzen Prozess durchzuführen.
Die Lösung für all diese Probleme ist die Normalisierung des gesamten Datensatzes, so dass er auf der gleichen Skala liegen kann. Dies verbessert die Lesbarkeit , wenn wir die Werte auf der gleichen Achse darstellen, und es verbessert die Trainingszeit, da die normalisierten Werte normalerweise im Bereich von 0 bis 1 liegen .01 Lesen Sie mehr über die Normalisierung hier.
Zu guter Letzt
Wir wissen auch, dass die Werte unserer Gehaltsdaten zwischen 39.343 und 121.782 liegen, während die Erfahrungsjahre zwischen 1,1 und 10,5 liegen, wenn wir die Daten so belassen, sind die Werte für das Gehalt so groß, dass sie das Modell glauben lassen können, dass sie wichtiger sind als alle anderen Werte, sodass sie eine große Auswirkung im Vergleich zu den Erfahrungsjahren haben, wir brauchen alle unabhängigen Variablen, um die gleichen Auswirkungen wie alle anderen Variablen zu haben, jetzt sehen Sie, wie wichtig es ist, Werte zu normalisieren.
(Normalisierung) Min-Max Skalar
Bei diesem Ansatz werden die Daten so normalisiert, dass sie im Bereich von 0 und 1 liegen. Die Formel lautet wie unten angegeben:
Wenn Sie diese Formel in Codezeilen in MQL5 umwandeln, wird daraus:
void CGradientDescent::MinMaxScaler(double &Array[]) { double mean = Mean(Array); double max,min; double Norm[]; ArrayResize(Norm,ArraySize(Array)); max = Array[ArrayMaximum(Array)]; min = Array[ArrayMinimum(Array)]; for (int i=0; i<ArraySize(Array); i++) Norm[i] = (Array[i] - min) / (max - min); printf("Scaled data Mean = %.5f Std = %.5f",Mean(Norm),std(Norm)); ArrayFree(Array); ArrayCopy(Array,Norm); }
Die Funktion std() dient nur dazu, uns die Standardabweichung mitzuteilen, nachdem die Daten normalisiert wurden, hier ist ihr Code:
double CGradientDescent::std(double &data[]) { double mean = Mean(data); double sum = 0; for (int i=0; i<ArraySize(data); i++) sum += MathPow(data[i] - mean,2); return(MathSqrt(sum/ArraySize(data))); }
Rufen wir nun all dies auf und drucken die Ausgabe, um zu sehen, was passiert:
void OnStart() { //--- string filename = "Salary_Data.csv"; double XMatrix[]; double YMatrix[]; grad = new CGradientDescent(1, 0.01,1000); grad.ReadCsvCol(filename,1,XMatrix); grad.ReadCsvCol(filename,2,YMatrix); grad.MinMaxScaler(XMatrix); grad.MinMaxScaler(YMatrix); ArrayPrint("Normalized X",XMatrix); ArrayPrint("Normalized Y",YMatrix); grad.GradientDescentFunction(XMatrix,YMatrix,MSE); delete (grad); }
Ausgabe:
OK 0 18:50:53.387 gradient-descent test (EURUSD,M1) Scaled data Mean = 0.44823 Std = 0.29683 MG 0 18:50:53.387 gradient-descent test (EURUSD,M1) Scaled data Mean = 0.45207 Std = 0.31838 MP 0 18:50:53.387 gradient-descent test (EURUSD,M1) Normalized X JG 0 18:50:53.387 gradient-descent test (EURUSD,M1) [ 0] 0.0000 0.0213 0.0426 0.0957 0.1170 0.1915 0.2021 0.2234 0.2234 0.2766 0.2979 0.3085 0.3085 0.3191 0.3617 ER 0 18:50:53.387 gradient-descent test (EURUSD,M1) [15] 0.4043 0.4255 0.4468 0.5106 0.5213 0.6064 0.6383 0.7234 0.7553 0.8085 0.8404 0.8936 0.9043 0.9787 1.0000 NQ 0 18:50:53.387 gradient-descent test (EURUSD,M1) Normalized Y IF 0 18:50:53.387 gradient-descent test (EURUSD,M1) [ 0] 0.0190 0.1001 0.0000 0.0684 0.0255 0.2234 0.2648 0.1974 0.3155 0.2298 0.3011 0.2134 0.2271 0.2286 0.2762 IS 0 18:50:53.387 gradient-descent test (EURUSD,M1) [15] 0.3568 0.3343 0.5358 0.5154 0.6639 0.6379 0.7151 0.7509 0.8987 0.8469 0.8015 0.9360 0.8848 1.0000 0.9939
Die Diagramme sehen nun wie folgt aus:
Gradientenverfahren für logistische Regression
Wir haben gesehen, wie die lineare Seite des Gradientenverfahrens funktioniert, nun wollen wir uns die logistische Seite ansehen.
Hier führen wir die gleichen Prozesse durch wie bei der linearen Regression, da die beteiligten Prozesse genau die gleichen sind, nur dass der Prozess der Differenzierung der logistischen Regression komplexer ist als der eines linearen Modells, lassen Sie uns zuerst die Kostenfunktion betrachten.
Wie im zweiten Artikel der Serie über die logistische Regression erläutert, ist die Kostenfunktion eines logistischen Regressionsmodells die unten angegebene binäre Kreuzentropie, auch bekannt als Log Loss.
Jetzt kommt der schwierige Teil, nämlich die Differenzierung dieser Funktion, um ihre Steigung zu erhalten.
Nach der Ermittlung der Ableitungen:
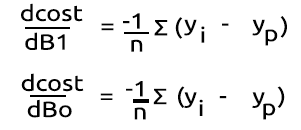
Lassen Sie uns die Formeln in MQL5-Code innerhalb der Funktion Bce umwandeln, die für Binary Cross Entropy steht .
double CGradientDescent::Bce(double Bo,double B1,Beta wrt) { double sum_sqr=0; double m = ArraySize(Y); double x[]; MatrixColumn(m_XMatrix,x,2); if (wrt == Slope) for (int i=0; i<ArraySize(Y); i++) { double Yp = Sigmoid(Bo+B1*x[i]); sum_sqr += (Y[i] - Yp) * x[i]; } if (wrt == Intercept) for (int i=0; i<ArraySize(Y); i++) { double Yp = Sigmoid(Bo+B1*x[i]); sum_sqr += (Y[i] - Yp); } return((-1/m)*sum_sqr); }
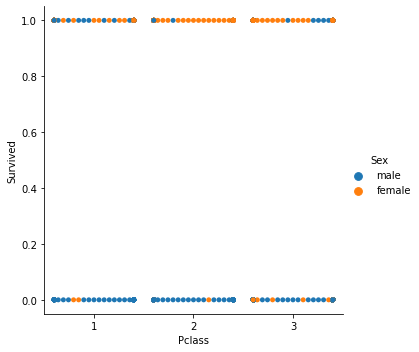
Da es sich um ein Klassifizierungsmodell handelt, ist unser Datensatz der Titanic-Datensatz, den wir in der logistischen Regression verwendet haben. Unsere unabhängige Variable ist Pclass (Passagierklasse), unsere abhängige Variable hingegen ist Survived (Überlebt).
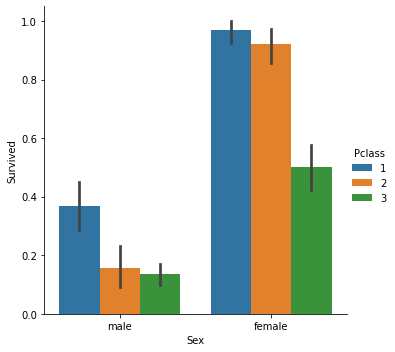
klassifiziertes Streudiagramm
Jetzt werden wir die Klasse des Gradientenverfahrens aufrufen, aber dieses Mal mit der BCE (Binary Cross Entropy) als Kostenfunktion.
filename = "titanic.csv"; ZeroMemory(XMatrix); ZeroMemory(YMatrix); grad.ReadCsvCol(filename,3,XMatrix); grad.ReadCsvCol(filename,2,YMatrix); grad.GradientDescentFunction(XMatrix,YMatrix,BCE); delete (grad);
Warten wir das Ergebnis ab:
CP 0 07:19:08.906 gradient-descent test (EURUSD,M1) Gradient Descent CostFunction BCE KD 0 07:19:08.906 gradient-descent test (EURUSD,M1) 0 b0 = -0.01161616 cost_B0 = 0.11616162 B1 = -0.04057239 cost_B1 = 0.40572391 FD 0 07:19:08.906 gradient-descent test (EURUSD,M1) 1 b0 = -0.02060337 cost_B0 = 0.08987211 B1 = -0.07436893 cost_B1 = 0.33796541 KE 0 07:19:08.906 gradient-descent test (EURUSD,M1) 2 b0 = -0.02743120 cost_B0 = 0.06827832 B1 = -0.10259883 cost_B1 = 0.28229898 QE 0 07:19:08.906 gradient-descent test (EURUSD,M1) 3 b0 = -0.03248925 cost_B0 = 0.05058047 B1 = -0.12626640 cost_B1 = 0.23667566 EE 0 07:19:08.907 gradient-descent test (EURUSD,M1) 4 b0 = -0.03609603 cost_B0 = 0.03606775 B1 = -0.14619252 cost_B1 = 0.19926123 CF 0 07:19:08.907 gradient-descent test (EURUSD,M1) 5 b0 = -0.03851035 cost_B0 = 0.02414322 B1 = -0.16304363 cost_B1 = 0.16851108 MF 0 07:19:08.907 gradient-descent test (EURUSD,M1) 6 b0 = -0.03994229 cost_B0 = 0.01431946 B1 = -0.17735996 cost_B1 = 0.14316329 JG 0 07:19:08.907 gradient-descent test (EURUSD,M1) 7 b0 = -0.04056266 cost_B0 = 0.00620364 B1 = -0.18958010 cost_B1 = 0.12220146 HE 0 07:19:08.907 gradient-descent test (EURUSD,M1) 8 b0 = -0.04051073 cost_B0 = -0.00051932 B1 = -0.20006123 cost_B1 = 0.10481129 ME 0 07:19:08.907 gradient-descent test (EURUSD,M1) 9 b0 = -0.03990051 cost_B0 = -0.00610216 B1 = -0.20909530 cost_B1 = 0.09034065 JQ 0 07:19:08.907 gradient-descent test (EURUSD,M1) 10 b0 = -0.03882570 cost_B0 = -0.01074812 B1 = -0.21692190 cost_B1 = 0.07826600 <<<<<< Last 10 iterations >>>>>> FN 0 07:19:09.725 gradient-descent test (EURUSD,M1) 6935 b0 = 1.44678930 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 PN 0 07:19:09.725 gradient-descent test (EURUSD,M1) 6936 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 NM 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6937 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 KL 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6938 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 PK 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6939 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 RK 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6940 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 MJ 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6941 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 HI 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6942 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 CH 0 07:19:09.726 gradient-descent test (EURUSD,M1) 6943 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 MH 0 07:19:09.727 gradient-descent test (EURUSD,M1) 6944 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000 QG 0 07:19:09.727 gradient-descent test (EURUSD,M1) 6945 b0 = 1.44678931 cost_B0 = -0.00000000 B1 = -0.85010666 cost_B1 = 0.00000000 NG 0 07:19:09.727 gradient-descent test (EURUSD,M1) 6945 Iterations Local Minima are MJ 0 07:19:09.727 gradient-descent test (EURUSD,M1) B0(Intercept) = 1.44679 || B1(Coefficient) = -0.85011
Bei der logistischen Regression werden die klassifizierten Daten nicht normalisiert oder skaliert, wie dies bei der linearen Regression der Fall ist.
B A M, Da haben Sie es, das Gradientenverfahren für die beiden und wichtigsten Machine Learning Modelle. Ich hoffe, es war leicht zu verstehen und der in diesem Artikel verwendet hilfreich. Der Datensatz ist zu diesen Daten repo bei GitHub verlinkt.
Schlussfolgerung
Wir haben den Gradientenabstieg für eine unabhängige und eine abhängige Variable gesehen. Für mehrere unabhängige Variablen müssen Sie die Vektor-/Matrizenform der Gleichungen verwenden. Ich denke, dieses Mal wird es für jeden einfach werden, es selbst zu versuchen und herauszufinden, jetzt, da wir die Bibliothek für Matrizen haben, die kürzlich von MQL5 veröffentlicht wurde. Für jede Hilfe zu den Matrizen können Sie mich gerne erreichen, ich werde mehr als glücklich sein zu helfen.
Mit besten Grüßen
Erfahren Sie mehr über Calculus:
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/11200
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 18): Neues Auftragssystems (I)
Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 18): Neues Auftragssystems (I)
 Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 17): Zugang zu Daten im Internet (III)
Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 17): Zugang zu Daten im Internet (III)
 Lernen Sie, wie man ein Handelssystem mit dem Chaikin Oscillator entwickelt
Lernen Sie, wie man ein Handelssystem mit dem Chaikin Oscillator entwickelt
 Automatisierter Grid-Handel mit Limit-Orders an der Moskauer Börse (MOEX)
Automatisierter Grid-Handel mit Limit-Orders an der Moskauer Börse (MOEX)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
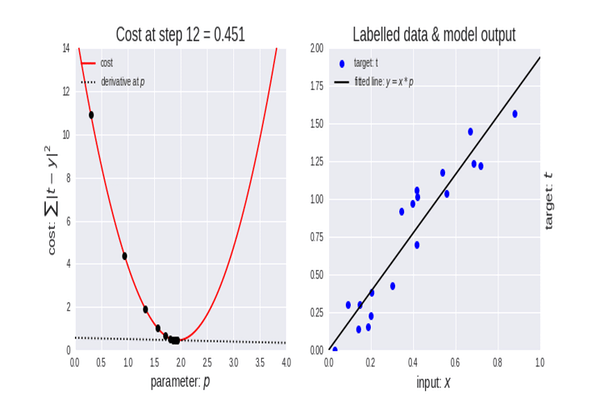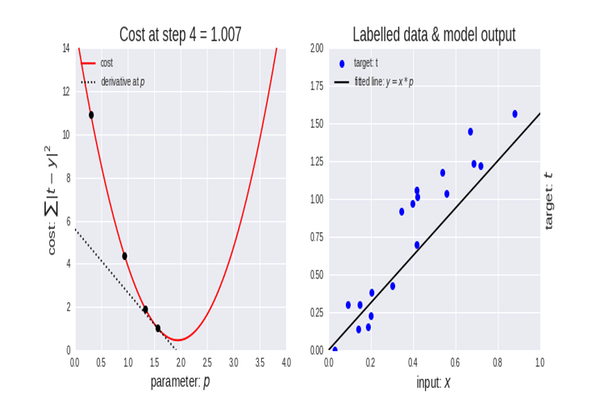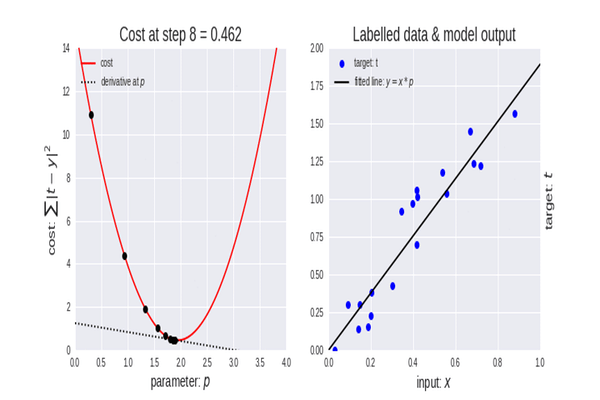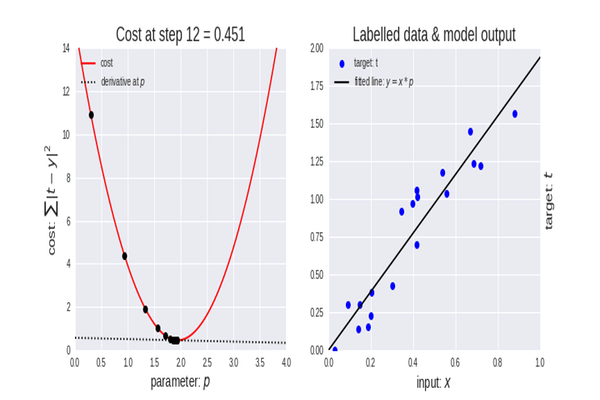


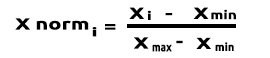

Erste Iteration
Formel: x1 = x0 - Lernrate * ( 2*(x+5) ) )
x1 = 0 - 0.01 * 0.01 * 2*(0+5)
x1 = -0.01 * 10
x1 = -0.1.
Hier steht zweimal 0,01.Sie verwirren die Leute.