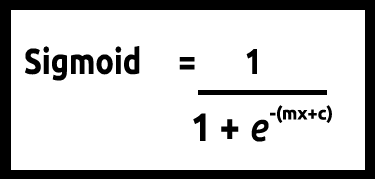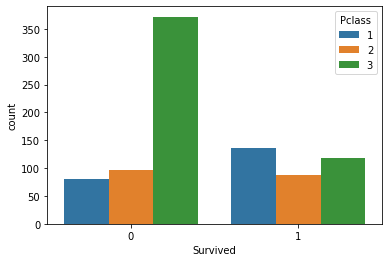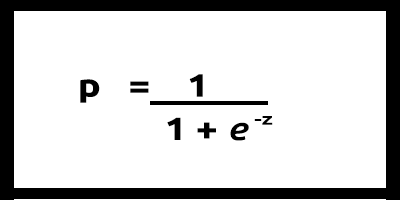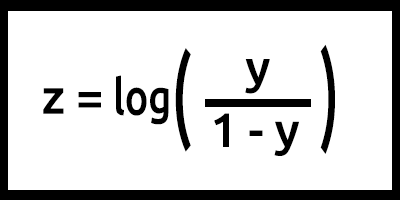
Datenwissenschaft und maschinelles Lernen (Teil 02): Logistische Regression
325
0
Im Gegensatz zur linearen Regression, die wir in Teil 01 besprochen haben, ist die logistische Regression ein Klassifikationsverfahren, das auf der linearen Regression basiert.
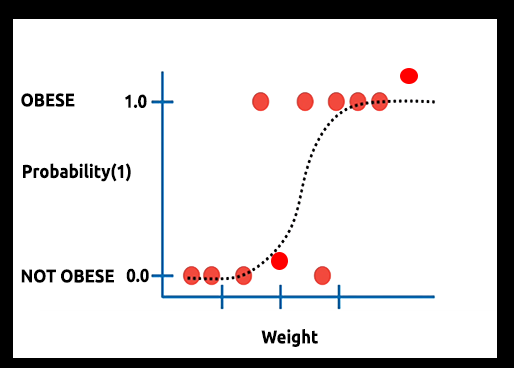
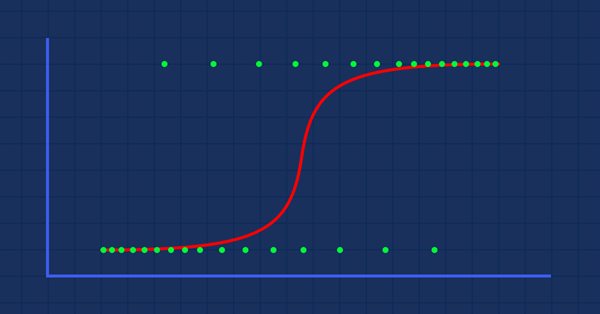
Theorie: Angenommen, wir zeichnen ein Diagramm der Wahrscheinlichkeit, dass jemand fettleibig ist, gegen sein Gewicht.
In diesem Fall können wir kein lineares Modell verwenden, sondern müssen eine andere Technik anwenden, um diese Linie in eine S-Kurve zu verwandeln, die als Sigmoid bekannt ist.
Da die logistische Regression Ergebnisse in einem binären Format liefert, das zur Vorhersage des Ergebnisses der kategorialen abhängigen Variablen verwendet wird, sollte das Ergebnis diskret/kategorial sein, wie z. B.:
- 0 oder 1
- Ja oder Nein
- Wahr oder Falsch
- Hoch oder Tief
- Kaufen oder Verkaufen
In unserer Bibliothek, die wir erstellen werden, werden wir andere diskrete Werte ignorieren. Wir konzentrieren uns auf die nur binären (0,1).
Da unsere Werte für y zwischen 0 und 1 liegen sollen, muss unsere Linie bei 0 und 1 abgeschnitten werden. Dies kann durch die Formel erreicht werden:
Damit erhalten wir dieses Diagramm:
Das lineare Modell wird an eine logistische Funktion (sigmoid/p) =1/1+e^t übergeben, wobei t das lineare Modell ist, dessen Ergebnis Werte zwischen 0 und 1 sind. Dies stellt die Wahrscheinlichkeit dar, dass ein Datenpunkt zu einer Klasse gehört.
Anstatt y eines linearen Modells als abhängig zu verwenden, wird seine Funktion als "p" als abhängig verwendet:
p = 1/1+e^-(c+m1x1+m2x2+....+mnxn) ,bei mehrfachen Werten
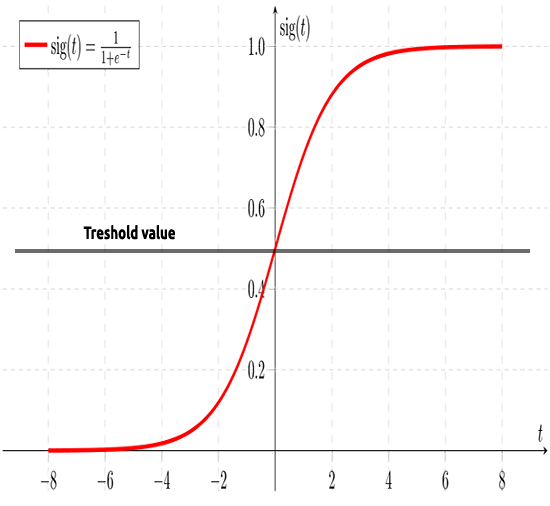
Wie bereits erwähnt, zielt die Sigmoidkurve darauf ab, Unendlichkeitswerte in eine binäre Ausgabe (0 oder 1) umzuwandeln. Aber was ist, wenn ein Datenpunkt bei 0,8 liegt? Wie kann man dann entscheiden, ob der Wert Null oder Eins ist? An dieser Stelle kommen die Schwellenwerte ins Spiel.
Der Schwellenwert gibt die Wahrscheinlichkeit an, entweder zu gewinnen oder zu verlieren. Er liegt bei 0,5 (die Mitte zwischen 0 und 1).
Jeder Wert, der größer oder gleich 0,5 ist, wird auf 1 aufgerundet und gilt somit als Gewinner, während jeder Wert unter 0,5 auf 0 aufgerundet wird und somit als Verlierer gilt. An dieser Stelle ist es an der Zeit, den Unterschied zwischen linearer und logistischer Regression zu erkennen.
Lineare vs. logistische Regression
| Linear | Logistische Regression |
|---|---|
| Kontinuierliche Variable | Kategoriale Variable |
| Löst Regressionsprobleme | Löst Klassifikationsprobleme |
| Das Modell hat eine lineare Gleichung | Das Modell hat eine logistische Gleichung |
Bevor wir uns mit dem Kodierungsteil und den Algorithmen zur Klassifizierung der Daten befassen, können uns mehrere Schritte helfen, die Daten zu verstehen und die Erstellung unseres Modells zu erleichtern:
- Sammeln und Analysieren von Daten
- Bereinigung Ihrer Daten
- Prüfen der Genauigkeit
01:Sammeln und Analysieren von Daten
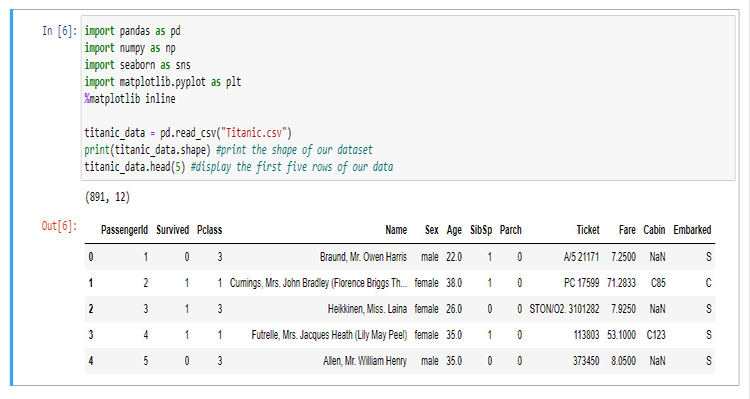
In diesem Abschnitt werden wir eine Menge Python-Code schreiben, um unsere Daten zu visualisieren. Beginnen wir mit dem Import der Bibliotheken, die wir für die Extraktion und Visualisierung der Daten im Jupyter-Notebook verwenden werden.
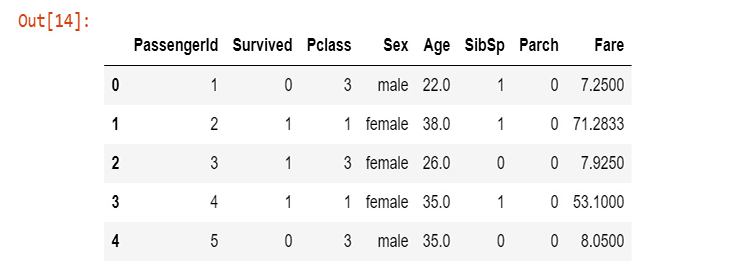
Für den Aufbau unserer Bibliothek werden wir die Titanic-Daten verwenden, für diejenigen, die damit nicht vertraut sind, es sind die Daten über das Unglück der Titanic, die am 15. April 1912 im Nordatlantik sank, nachdem sie einen Eisberg gerammt hatte, Wikipedia. Alle Python-Codes und der Datensatz sind auf meinem GitHub zu finden, das am Ende des Artikels verlinkt ist.
Die Spalten stehen für
survival - Überlebt (0 = Nein; 1 = Ja)
class - Passagierklasse (1 = 1; 2 = 2; 3 = 3)
name - Name
sex - Geschlecht
age - Alter
sibsp - Anzahl der Geschwister/Ehegatten an Bord
parch - Anzahl der Eltern/Kinder an Bord
ticket - Ticketnummer
fare - Preis der Überfahrt
cabin - Kabine
embarked - Hafen der Einschiffung (C = Cherbourg; Q = Queenstown; S = Southampton)
Nun, da wir unsere Daten gesammelt und in einer Variablen titanic_data gespeichert haben, können wir mit der Visualisierung der Daten in Spalten beginnen, beginnend mit der Überlebensspalte.
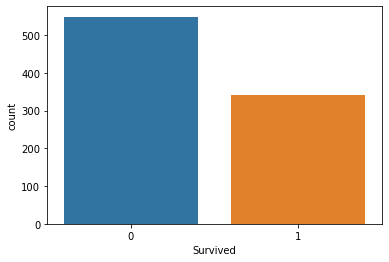
sns.countplot(x="Survived", data = titanic_data)
Ausgabe
Daraus geht hervor, dass nur eine Minderheit der Passagiere den Unfall überlebt hat, weniger als die Hälfte der Passagiere auf dem Schiff hat den Unfall überlebt.
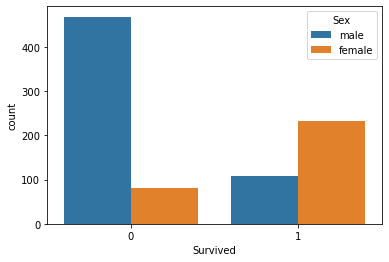
Lassen Sie uns die Überlebenszahlen nach Geschlecht visualisieren
sns.countplot(x='Survived', hue='Sex', data=titanic_data)
Ich weiß nicht, was mit den Männern an diesem Tag geschah, aber von den Frauen überlebten mehr als doppelt so viele wie die Männer
Lassen Sie uns die Überlebenszahlen nach Klassengruppen visualisieren
sns.countplot(x='Survived', hue='Pclass', data=titanic_data)
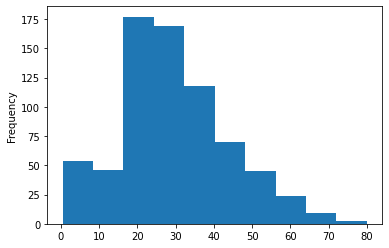
Zeichnen wir das Histogramm der Altersgruppen der Passagiere, die sich auf dem Schiff befanden. Hier können wir nicht die Count-plots verwenden, um unsere Daten zu visualisieren, da es viele verschiedene Werte für das Alter in unserem Datensatz gibt, die nicht organisiert sind.
titanic_data['Age'].plot.hist()Ausgabe:
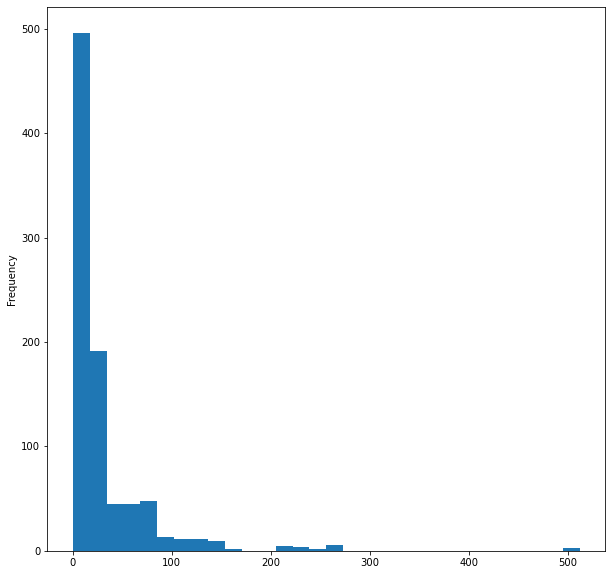
Als Letztes wollen wir das Histogramm des Fahrpreises des Schiffes visualisieren
titanic_data['Fare'].plot.hist(bins=30, figsize=(10,10))
Das war's mit der Visualisierung der Daten, obwohl wir nur 5 von 12 Spalten visualisiert haben, weil ich denke, dass dies die wichtigen Spalten sind.
02: Bereinigung unserer Daten
Hier bereinigen wir unsere Daten, indem wir die NaN-Werte (fehlende Werte) entfernen und gleichzeitig unnötige Spalten im Datensatz vermeiden/entfernen.
Bei der logistischen Regression werden reelle und ganzzahlige Werte benötigt, sodass nicht aussagekräftige Zeichenketten-Werte vermieden werden müssen; in diesem Fall werden wir die folgenden Spalten ignorieren:
- Spalte "Name" (sie enthält keine aussagekräftigen Informationen)
- Ticketspalte (macht keinen Sinn für das Überleben des Unfalls)
- Kabinen-Spalte (sie hat zu viele fehlende Werte, das zeigen schon die ersten 5 Zeilen)
- Eingeschifft (ich denke, es ist irrelevant)
Dazu öffne ich die CSV-Datei in WPS office und entferne die Spalten manuell, Sie können ein beliebiges Tabellenkalkulationsprogramm Ihrer Wahl verwenden.
Nach dem Entfernen der Spalten mit einem Tabellenkalkulationsprogramm wollen wir die neuen Daten visualisieren.
new_data = pd.read_csv(r'C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\titanic.csv') new_data.head(5)
Ausgabe:
Wir haben jetzt bereinigte Daten, obwohl wir immer noch fehlende Werte in der Spalte Alter haben, ganz zu schweigen von den Zeichenketten-Werten in der Spalte sex (Geschlecht). Lassen Sie uns das Problem mit etwas Code beheben. Erstellen wir einen Label-Codierer, um die Zeichenketten "male" (männlich) und "female" (weiblich) in 0 bzw. 1 zu konvertieren.
void CLogisticRegression::LabelEncoder(string &src[],int &EncodeTo[],string members="male,female") { string MembersArray[]; ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(members,separator,MembersArray); //convert members list to an array ArrayResize(EncodeTo,ArraySize(src)); //make the EncodeTo array same size as the source array int binary=0; for(int i=0;i<ArraySize(MembersArray);i++) // loop the members array { string val = MembersArray[i]; binary = i; //binary to assign to a member int label_counter = 0; for (int j=0; j<ArraySize(src); j++) { string source_val = src[j]; if (val == source_val) { EncodeTo[j] = binary; label_counter++; } } Print(MembersArray[binary]," total =",label_counter," Encoded To = ",binary); } }
Um das Quell-Array mit dem Namen src[] zu erhalten, habe ich auch eine Funktion programmiert, die Daten aus einer bestimmten Spalte in einer CSV-Datei abruft und sie dann in ein Array von String-Werten MembersArray[] einfügt, sehen Sie sich das an:
void CLogisticRegression::GetDatatoArray(int from_column_number, string &toArr[]) { int handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI,m_delimiter); int counter=0; if (handle == INVALID_HANDLE) Print(__FUNCTION__," Invalid csv handle err=",GetLastError()); else { int column = 0, rows=0; while (!FileIsEnding(handle)) { string data = FileReadString(handle); column++; //--- if (column==from_column_number) //if column in the loop is the same as the desired column { if (rows>=1) //Avoid the first column which contains the column's header { counter++; ArrayResize(toArr,counter); toArr[counter-1]=data; } } //--- if (FileIsLineEnding(handle)) { rows++; column=0; } } } FileClose(handle); }
In unserem testscript.mq5 werden die Funktionen korrekt aufgerufen und die Bibliothek initialisiert:
#include "LogisticRegressionLib.mqh"; CLogisticRegression Logreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- Logreg.Init("titanic.csv",","); string Sex[]; int SexEncoded[]; Logreg.GetDatatoArray(4,Sex); Logreg.LabelEncoder(Sex,SexEncoded,"male,female"); ArrayPrint(SexEncoded); }
Die Ausgabe wird nach erfolgreicher Ausführung des Skripts ausgedruckt,
male total =577 Encoded To = 0
female total =314 Encoded To = 1
[ 0] 0 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 0 1 1 0 0 1 0 0 1 1 0 0 0 0 0 1 1 1 1 0 1 1 0 0 1 0 1 0 0 1 1 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0
[ 75] 0 0 0 0 1 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 1 1 0 0 0 0 1 0 0
... ... ... ...
... ... ... ...
[750] 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0
[825] 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 0 0 0 1 1 0 1 1 0 0 0 0 1 0 0 1 1 0 0 0 1 1 0 1 0 0 1 0 1 1 0 0
Bevor Sie Ihre Werte kodieren, achten Sie auf die members="male,female" auf Ihrem Funktionsargument, der erste Wert, der in Ihrer Zeichenkette erscheint, wird als 0 kodiert, wie Sie sehen können, erscheint die männliche Spalte zuerst, daher werden alle männlichen Werte als 0 kodiert, die weiblichen als 1. Diese Funktion ist nicht auf zwei Werte beschränkt, Sie können so viele Werte kodieren, wie Sie wollen, solange die Zeichenkette einen Sinn für Ihre Daten ergibt.
Fehlende Werte
Wenn Sie auf die Spalte Alter achten, werden Sie feststellen, dass es fehlende Werte gibt. Die fehlenden Werte können hauptsächlich auf einen Grund zurückzuführen sein... den Tod, der es uns in unserem Datensatz unmöglich macht, das Alter einer Person zu identifizieren. Sie können diese Lücken identifizieren, indem Sie sich den Datensatz ansehen, was vor allem bei großen Datensätzen zeitaufwendig sein kann, da wir auch pandas zur Visualisierung unserer Daten verwenden.
titanic_data.isnull().sum()
Der Ausdruck ist:
PassengerId 0
Survived 0
Pclass 0
Sex 0
Age 177
SibSp 0
Parch 0
Fare 0
dtype: int64
Von den 891 Zeilen in unserer Spalte Alter haben 177 Zeilen fehlende Werte (NAN).
Wir werden nun die fehlenden Werte in unserer Spalte ersetzen, indem wir die Werte durch den Mittelwert aller Werte ersetzen.
void CLogisticRegression::FixMissingValues(double &Arr[]) { int counter=0; double mean=0, total=0; for (int i=0; i<ArraySize(Arr); i++) //first step is to find the mean of the non zero values { if (Arr[i]!=0) { counter++; total += Arr[i]; } } mean = total/counter; //all the values divided by their total number Print("mean ",MathRound(mean)," before Arr"); ArrayPrint(Arr); for (int i=0; i<ArraySize(Arr); i++) { if (Arr[i]==0) { Arr[i] = MathRound(mean); //replace zero values in array } } Print("After Arr"); ArrayPrint(Arr); }
Diese Funktion findet den Mittelwert aller Nicht-Null-Werte und ersetzt dann alle Nullwerte im Array durch den Mittelwert.
Die Ausgabe nach erfolgreicher Ausführung der Funktion. Wie Sie sehen können, wurden alle Nullwerte durch 30.0 ersetzt, was das durchschnittliche Alter der Passagiere der Titanic war.
mean 30.0 before Arr
[ 0] 22.0 38.0 26.0 35.0 35.0 0.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 0.0 31.0 0.0 35.0 34.0 15.0 28.0 8.0 38.0 0.0 19.0 0.0 0.0
… … … … … … … … …
[840] 20.0 16.0 30.0 34.5 17.0 42.0 0.0 35.0 28.0 0.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 0.0 41.0 21.0 48.0 0.0 24.0 42.0 27.0 31.0 0.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 0.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 0.0 26.0 32.0
After Arr
[ 0] 22.0 38.0 26.0 35.0 35.0 30.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 30.0 31.0 30.0 35.0 34.0 15.0 28.0 8.0 38.0 30.0 19.0 30.0 30.0
… … … … … … … … …
[840] 20.0 16.0 30.0 34.5 17.0 42.0 30.0 35.0 28.0 30.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 30.0 41.0 21.0 48.0 30.0 24.0 42.0 27.0 31.0 30.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 30.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 30.0 26.0 32.0
Aufbau des logistischen Regressionsmodells
Zunächst erstellen wir unsere logistische Regression mit einer unabhängigen und einer abhängigen Variable. Später werden wir dann zu einem vollständigen Lösungsmodell für unser Problem übergehen.
Lassen Sie uns das Modell auf zwei Variablen aufbauen: Überlebt versus Alter. Wir wollen herausfinden, wie hoch die Überlebenschancen einer Person in Abhängigkeit von ihrem Alter sind.
Bisher wissen wir, dass in einem logistischen Modell ein lineares Modell enthalten ist. Beginnen wir mit der Codierung der Funktionen, die ein lineares Modell möglich machen.
Die Funktionen Coefficient_of_X() und y_intercept() sind nicht neu. Wir haben sie im ersten Artikel dieser Serie entwickelt, den Sie lesen sollten, um weitere Informationen über diese Funktionen und die lineare Regression im Allgemeinen zu erhalten.
double CLogisticRegression::y_intercept() { // c = y - mx return (y_mean-coefficient_of_X()*x_mean); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CLogisticRegression::coefficient_of_X() { double m=0; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<ArraySize(m_xvalues); i++) { x__x = m_xvalues[i] - x_mean; //right side of the numerator (x-side) y__y = m_yvalues[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
Programmieren wir nun das logistische Modell anhand der Formel.
Man beachte, dass z auch als log-odds bezeichnet wird, da die Umkehrung des Sigmoid besagt, dass z als der Logarithmus der Wahrscheinlichkeit der Kennzeichnung 1 (z. B. "überlebt") geteilt durch die Wahrscheinlichkeit der Bezeichnung 0 (z. B. "hat nicht überlebt") definiert werden kann:
In diesem Fall ist y = mx+c (erinnern Sie sich an das lineare Modell?).
In Code umgewandelt lautet das Ergebnis dann,
double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1);
Achten Sie darauf, was hier mit der Variablen z gemacht wurde, die Formel ist log(y/1-y), aber der Code ist geschrieben als log(y_)-log(1-y_); erinnern Sie sich an die Logarithmengesetze in Mathematik!!! Die Division von Logarithmen mit der gleichen Basis führt zur Subtraktion der Exponenten, nachlesen.
Das ist im Grunde unser Modell, wenn die Formel programmiert ist, aber in unserer Funktion LogistischenRegression() geht eine Menge vor sich, hier ist alles, was sich in der Funktion befindet:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { int arrsize = ArraySize(x); //the input array size double p_hat =0; //store the probability //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Training our model in the background double c = y_intercept(), m = coefficient_of_X(); //--- Here comes the logistic regression model int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //resize the array to match the train size Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } //--- Testing our model if (train_size_split<1.0) //if there is room for testing { ArrayRemove(m_xvalues,0,train_size); //clear our array ArrayRemove(m_yvalues,0,train_size); //clear our array from train data ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended ArrayCopy(m_yvalues,y,0,train_size,test_size); //new values of y, starts from where the testing ended Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //resize the array to match the test size for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } }
Nun trainieren und testen wir unser Modell in unserem TestScript.mq5
double Age[]; Logreg.GetDatatoArray(5,Age); Logreg.FixMissingValues(Age); double y_survival[]; int Predicted[]; Logreg.GetDatatoArray(2,y_survival); Logreg.LogisticRegression(Age,y_survival,Predicted);
Die Ausgabe eines erfolgreichen Skriptlaufs lautet:
Training starting..., train size=624
0 Age =22.00 survival_Predicted =0
1 Age =38.00 survival_Predicted =0
... .... ....
622 Age =20.00 survival_Predicted =0
623 Age =21.00 survival_Predicted =0
start testing...., test size=267
0 Age =21.00 survival_Predicted =0
1 Age =61.00 survival_Predicted =1
.... .... ....
265 Age =26.00 survival_Predicted =0
266 Age =32.00 survival_Predicted =0
Großartig. Unser Modell funktioniert jetzt und wir können zumindest die Ergebnisse erhalten, aber macht das Modell auch gute Vorhersagen?
Wir müssen seine Genauigkeit überprüfen.
Die Konfusionsmatrix
Wie wir alle wissen, kann jedes gute oder schlechte Modell Vorhersagen machen. Ich habe eine CSV-Datei für die Vorhersagen erstellt, die unser Modell gemacht hat, zusammen mit den Originalwerten aus den Testdaten zum Überleben der Passagiere. 1 bedeutet wieder überlebt, 0 bedeutet hat nicht überlebt.
Hier sind nur ein paar 10 Spalten:
| Original | prognostiziert | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 0 |
| 6 | 1 | 1 |
| 7 | 0 | 1 |
| 8 | 1 | 0 |
| 9 | 0 | 0 |
Wir berechnen die Konfusionsmatrix mit:
- TP - Wahr Positiv
- TN - Wahr Negativ
- FP - Falsch Positiv
- FN - Falsch Negativ
Wie lauten nun diese Werte?
TP ( Wahr Positiv )
ist, wenn der Originalwert positiv (1) ist und Ihr Modell ebenfalls positiv (1) vorhersagt.
TN ( Wahr Negativ )
ist, wenn der ursprüngliche Wert negativ (0) ist und Ihr Modell auch negativ (0) vorhersagt.
FP ( Falsch Positiv )
ist, wenn der Originalwert negativ (0) ist, aber Ihr Modell ein Positiv (1) vorhersagt
FN ( Falsch Negativ )
Ist, wenn der ursprüngliche Wert positiv (1) ist, Ihr Modell aber ein Negativ (0) vorhersagt.
Da Sie nun die Werte kennen, lassen Sie uns als Beispiel die Konfusionsmatrix für das obige Beispiel berechnen
| Original | prognostiziert | TP/TN/FP/FN | |
|---|---|---|---|
| 0 | 0 | 0 | TN |
| 1 | 0 | 1 | FP |
| 2 | 0 | 1 | FP |
| 3 | 1 | 0 | FN |
| 4 | 0 | 0 | TN |
| 5 | 0 | 0 | TN |
| 6 | 1 | 1 | TP |
| 7 | 0 | 1 | FP |
| 8 | 1 | 0 | FN |
| 9 | 0 | 0 | TN |
Die Konfusionsmatrix kann verwendet werden, um die Genauigkeit unseres Modells mit dieser Formel zu berechnen.
Aus unserer Tabelle:
- TN = 4
- TP = 1
- FN = 2
- FP = 3
Genauigkeit = (1 + 5) / (4 + 1 + 2 + 3)
Gemauigkeit = 0.5
In diesem Fall beträgt unsere Genauigkeit 50% ( 0.5*100%, um es in Prozent umzurechnen)
Nun, da Sie verstehen, wie die 1x1 Konfusionsmatrix funktioniert. Es ist an der Zeit, sie in Code umzuwandeln und die Genauigkeit unseres Modells für den gesamten Datensatz zu analysieren
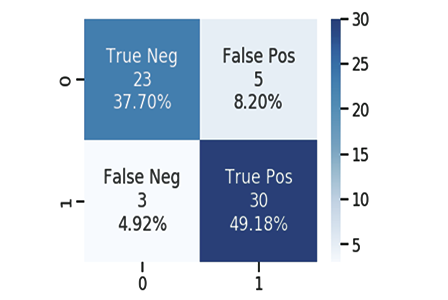
void CLogisticRegression::ConfusionMatrix(double &y[], int &Predicted_y[], double& accuracy) { int TP=0, TN=0, FP=0, FN=0; for (int i=0; i<ArraySize(y); i++) { if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==1) TP++; if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==0) TN++; if (Predicted_y[i]==1 && (int)y[i]==0) FP++; if (Predicted_y[i]==0 && (int)y[i]==1) FN++; } Print("Confusion Matrix \n ","[ ",TN," ",FP," ]","\n"," [ ",FN," ",TP," ] "); accuracy = (double)(TN+TP) / (double)(TP+TN+FP+FN); }
Gehen wir nun zurück zu unserer Hauptfunktion in unserer Klasse, bekannt als LogisticRegression(), dieses Mal werden wir sie in eine Doppelfunktion umwandeln, die die Genauigkeit des Modells zurückgibt. Ich werde auch die Anzahl der Print()-Methoden reduzieren, aber sie zu einer if-Anweisung hinzufügen, da wir die Werte nicht jedes Mal ausgeben wollen, es sei denn, wir wollen unsere Klasse debuggen. Alle Änderungen sind Blau hervorgehoben:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { double accuracy =0; //Accuracy of our Train/Testmodel int arrsize = ArraySize(x); //the input array size double p_hat =0; //store the probability //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Training our model in the background double c = y_intercept(), m = coefficient_of_X(); //--- Here comes the logistic regression model int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //resize the array to match the train size Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } ConfusionMatrix(m_yvalues,TrainPredicted,accuracy); //be careful not to confuse the train predict values arrays printf("Train Model Accuracy =%.5f",accuracy); //--- Testing our model if (train_size_split<1.0) //if there is room for testing { ArrayRemove(m_xvalues,0,train_size); //clear our array ArrayRemove(m_yvalues,0,train_size); //clear our array from train data ArrayCopy(m_xvalues,x,0,train_size,test_size); //new values of x, starts from where the training ended ArrayCopy(m_yvalues,y,0,train_size,test_size); //new values of y, starts from where the testing ended Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //resize the array to match the test size for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //round the values to give us the actual 0 or 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } ConfusionMatrix(m_yvalues,Predicted,accuracy); printf("Testing Model Accuracy =%.5f",accuracy); } return (accuracy); //Lastly, the testing Accuracy will be returned }
Wenn das Skript erfolgreich ausgeführt wurde, wird Folgendes ausgegeben:
Training starting..., train size=624
Confusion Matrix
[ 378 0 ]
[ 246 0 ]
Train Model Accuracy =0.60577
start testing...., test size=267
Confusion Matrix
[ 171 0 ]
[ 96 0 ]
Testing Model Accuracy =0.64045
Hurra! Wir können nun anhand von Zahlen erkennen, wie gut unser Modell ist. Obwohl die Genauigkeit von 64,045 % bei den Testdaten nicht gut genug ist, um das Modell für Vorhersagen zu verwenden (meiner Meinung nach), haben wir zumindest jetzt eine Bibliothek, die uns bei der Klassifizierung der Daten mithilfe der logistischen Regression helfen kann.
Weitere Erläuterungen zur Hauptfunktion:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7)
Der Eingabeparameter train_size_split ist für die Aufteilung der Daten in Training und Testen. Standardmäßig ist die Aufteilung 0,7, was bedeutet, dass 70% der Daten für das Training sind, während die restlichen 30% für Testzwecke sind, das Referenz-Array Predicted[] gibt die vorhergesagten Testdaten zurück.
Binäre Kreuzentropie alias Verlustfunktion
So wie der mittlere quadratische Fehler die Fehlerfunktion für die lineare Regression ist, ist die binäre Kreuzentropie die Kostenfunktion für die logistische Regression.
Theorie:
Schauen wir uns an, wie sie in zwei Anwendungsfällen für logistische Regression funktioniert, d. h. wenn die tatsächliche Ausgabe 0 und 1 ist.
01: Wenn der tatsächliche Ausgabewert 1 ist
Betrachten wir das Modell für zwei Eingabeproben p1 = 0,4 und p2 = 0,6. Es wird erwartet, dass p1 stärker bestraft werden sollte als p2, da es im Vergleich zu p1 weit von 1 entfernt ist.
Aus mathematischer Sicht ist der negative Logarithmus einer kleinen Zahl eine große Zahl und umgekehrt.
Um die Eingaben zu bestrafen (penalty), verwenden wir die folgende Formel
penalty = -log(p)
Für diese beiden Fälle:
- Penalty = -log(0.4)=0.4 d.h. die Strafe für p1 ist 0.4
- Penalty = -log(0.6)=0.2 d.h. die Strafe für p2 ist 0.2
02: Wenn der tatsächliche Ausgabewert 0 ist
Betrachten Sie die Modellausgabe für zwei Eingabeproben, p1 = 0,4 und p2= 0,6 (wie im vorherigen Fall). Es ist zu erwarten, dass p2 stärker bestraft werden sollte als p1, da es weit von 0 entfernt ist, aber bedenken Sie, dass die Ausgabe des logistischen Modells die Wahrscheinlichkeit ist, dass eine Stichprobe positiv ist. Um die Eingabewahrscheinlichkeiten zu bestrafen, müssen wir die Wahrscheinlichkeit finden, dass eine Stichprobe negativ ist, das ist einfach, hier ist die Formel.
Wahrscheinlichkeit, dass eine Probe negativ ist = 1-Wahrscheinlichkeit, dass eine Probe positiv ist.
Um die Strafe in diesem Fall zu ermitteln, lautet die Formel für die Strafe also:
penalty = -log(1-p)
Für diese beiden Fälle:
- penalty = -log(1-p) = -log(1-0.4) = 0.2 d.h. die Strafe ist 0.2
- penalty = -log(1-p) = -log(1-0.6) = 0.4 d.h. die Strafe ist 0.4
Die Strafe für p2 ist größer als für p1 (funktioniert wie erwartet) - cool!
Nun kann die Strafe für eine einzelne Eingabeprobe, deren Modellausgabe p und der wahre Ausgabewert y ist, wie folgt berechnet werden.
wenn die Eingabeprobe positiv ist y=1:
penalty = -log(p)
sonst:
penalty = -log(1-p)
Eine einzeilige Gleichung, die der obigen if-else-Blockanweisung entspricht, kann wie folgt geschrieben werden:
penalty = -( y*log(p) + (1-y)*log(1-p) )
wobei
y = tatsächliche Werte aus unserem Datensatz
p = rohe Vorhersagewahrscheinlichkeit des Modells (vor Abrundung)
Beweisen wir, dass diese Gleichung mit der obigen if-else-Anweisung äquivalent ist
01: wenn die Ausgangswerte y = 1
penalty = -( 1*log(p) + (1-1)*log(1-p) ) = -log(p) also bewiesen
02: wenn der Ausgangswert y = 0
penalty = -( 0*log(p) + (1-0)* log(1-p) ) = log(1-p) also bewiesen
Schließlich sieht die logarithmische Verlustfunktion (log loss) für N Eingangsstichproben wie folgt aus:
log loss ist ein Indikator dafür, wie nahe die Vorhersagewahrscheinlichkeit am entsprechenden tatsächlichen/echten Wert liegt (0 oder 1 im Falle einer binären Klassifizierung). Je mehr die Vorhersagewahrscheinlichkeit vom tatsächlichen Wert abweicht, desto höher ist der Wert der logarithmische Verlustfunktion log loss.
Kostenfunktionen wie log loss und viele andere können als Maßstab dafür verwendet werden, wie gut das Modell ist, aber der größte Nutzen liegt in der Optimierung des Modells für die besten Parameter mit Hilfe von Gradientenabstieg oder anderen Optimierungsalgorithmen(wir werden das in einer späteren Serie diskutieren, bleiben Sie dran).
Wenn man es messen kann, kann man es auch verbessern. Das ist der Hauptzweck der Kostenfunktionen.
Aus unserem Test- und Trainingsdatensatz geht hervor, dass unser log loss zwischen 0,64 und 0,68 liegt, was (grob gesagt) nicht ideal ist.
Trainingsdatensatz
Logloss =0.6858006105398738
Test-Datensatz
Logloss =0.6599503403665642
So können wir unsere logarithmische Verlustfunktion in einen Programmcode umwandeln:
double CLogisticRegression::LogLoss(double &rawpredicted[]) { double log_loss =0; double penalty=0; for (int i=0; i<ArraySize(rawpredicted); i++ ) { penalty += -((m_yvalues[i]*log(rawpredicted[i])) + (1-m_yvalues[i]) * log(1-rawpredicted[i])); //sum all the penalties if (m_debug) printf("penalty =%.5f",penalty); } log_loss = penalty/ArraySize(rawpredicted); //all the penalties divided by their total number Print("Logloss =",log_loss); return(log_loss); }
Um die rohe vorhergesagte Ausgabe zu erhalten, müssen wir zu den Hauptschleifen für Testen und Trainieren zurückkehren und die Daten im rohen, vorhergesagten Array direkt vor dem Prozess des Abrundens der Wahrscheinlichkeiten speichern.
Mehrere dynamische logistische Regressionen als Herausforderung
Die größte Herausforderung, der ich mich beim Aufbau der linearen und logistischen Regressionsbibliotheken in diesem und dem vorhergehenden Artikel gegenübersah, ist die Entwicklung mehrerer dynamischer Regressionsfunktionen, die für mehrere Datenspalten verwendet werden können, ohne dass wir für alle Daten, die unserem Modell hinzugefügt werden, einen Hardcode erstellen müssen. Im vorhergehenden Artikel habe ich zwei Funktionen mit demselben Namen hartcodiert, der einzige Unterschied zwischen ihnen war die Anzahl der Daten, mit denen jedes Modell arbeiten konnte:
void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]);
Aber diese Methode ist unbequem und fühlt sich an wie eine verfrühte Art, Dinge zu kodieren, und sie verletzt die Regeln des sauberen Codes und der DRY-Prinzipien (wiederhole dich nicht), die OOP uns zu erreichen helfen soll.
Im Gegensatz zu Python mit seinen flexiblen Funktionen, die mit Hilfe von *args und **kwargs eine große Anzahl von funktionalen Argumenten annehmen können, kann dies in MQL5, soweit ich denken kann, das nur durch die Verwendung von Zeichenketten erreicht werden, damit wird das zu unserem Ausgangspunkt.
void CMultipleLogisticRegression::MLRInit(string x_columns="3,4,5,6,7,8")
Die Eingabe x_columns repräsentiert alle unabhängigen Variablenspalten, die wir in unserer Bibliothek verwenden werden. Diese Spalten erfordern, dass wir mehrere unabhängige Arrays für jede der Spalten haben, aber es gibt keine Möglichkeit, Arrays dynamisch zu erstellen, also fällt die Verwendung von Arrays hier flach.
Wir können mehrere CSV-Dateien dynamisch erstellen und sie als Arrays verwenden, aber das wird unsere Programme teurer machen, wenn es um die Nutzung von Computerressourcen geht, verglichen mit der Verwendung von Arrays, vor allem, wenn wir mit mehreren Daten arbeiten, ganz zu schweigen von den while-Schleifen, die wir häufig verwenden werden, um die Dateien zu öffnen, was den gesamten Prozess verlangsamen wird, ich bin mir nicht 100% sicher, also korrigieren Sie mich, wenn ich falsch liege.
Wir können aber immer noch die erwähnte Methode verwenden.
Ich habe den Weg nach vorne entdeckt. Um Arrays zu verwenden, werden wir alle Daten aus allen Spalten in einem Array speichern und dann die Daten separat von einem einzigen Array verwenden.
int start = 0; if (m_debug) //if we are on debug mode print Each Array vs its row for (int i=0; i<x_columns_total; i++) { ArrayCopy(EachXDataArray,m_AllDataArray,0,start,rows_total); start += rows_total; Print("Array Number =",i," From column number ",m_XColsArray[i]); ArrayPrint(EachXDataArray); }
Innerhalb der for-Schleife können wir die Daten in den Arrays manipulieren und alle Berechnungen für das Modell auf die gewünschte Weise für alle Spalten durchführen. Ich habe diese Methode ausprobiert, bin aber immer noch bei erfolglosen Versuchen. Der Grund, warum ich diese Hypothese erkläre, ist, damit jeder, der diesen Artikel liest, diese Herausforderung versteht, und ich begrüße alle Ihre Meinungen im Kommentarabschnitt, wie wir diese mehrfache dynamische logistische Regressionsfunktion kodieren können. Mein vollständiger Versuch, diese Bibliothek zu erstellen, ist auf diesem Link https://www.mql5.com/en/code/38894 zu finden.
Dieser Versuch war nicht erfolgreich, aber er lässt hoffen und ich glaube, dass er es wert ist, geteilt zu werden.
Vorteile der logistischen Regression
- Keine Annahmen über die Verteilung der Klassen im Merkmalsraum
- Leichte Erweiterung auf mehrere Klassen (multinomiale Regression)
- Natürliche probabilistische Ansicht der Klassenvorhersagen
- Schnell zu trainieren
- Sehr schnelle Klassifizierung unbekannter Datensätze
- Gute Genauigkeit für viele einfache Datensätze
- Widerstandsfähig gegen Überanpassung
- Modellkoeffizienten können als Indikator für die Bedeutung von Merkmalen interpretiert werden
Nachteile
- Konstruiert lineare Grenzen
Abschließende Überlegungen
Das war's für diesen Artikel. Die logistische Regression wird in vielen Bereichen des realen Lebens eingesetzt, z. B. bei der Klassifizierung von E-Mails als Spam und Nicht-Spam, bei der Erkennung von Handschriften und bei vielen anderen interessanten Dingen.
Ich weiß, dass wir keine logistischen Regressionsalgorithmen verwenden werden, um Titanic-Daten oder eines der erwähnten Felder zu klassifizieren, vor allem nicht auf der MetaTrader 5-Plattform. Wie bereits gesagt, wurde der Datensatz nur zum Zweck des Aufbaus der Bibliothek im Vergleich mit dem Ergebnis verwendet, das in dem hier verlinkten Python erreicht wurde > https://github.com/MegaJoctan/LogisticRegression-MQL5-and-python. Im nächsten Artikel werden wir sehen, wie wir die logistischen Modelle nutzen können, um den Börsencrash vorherzusagen.
Da dieser Artikel zu lang geworden ist, überlasse ich die Aufgabe der multiplen Regression allen Lesern als Hausaufgabe.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/10626
Lernen Sie, wie Sie ein Handelssystem mit Hilfe des MACD entwickelt
Lernen Sie, wie man ein Handelssystem mit dem CCI entwickelt
DirectX-Tutorial (Teil I): Zeichnen des ersten Dreiecks
Verwendung der Klasse CCanvas in MQL-Anwendungen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.