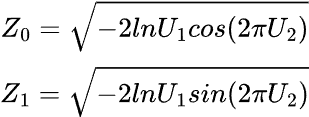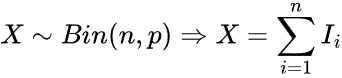MetaTrader 5 / Experten
English 日本語
preview
Datenwissenschaft und ML (Teil 35): NumPy in MQL5 - Die Kunst, komplexe Algorithmen mit weniger Code zu erstellen

Datenwissenschaft und ML (Teil 35): NumPy in MQL5 - Die Kunst, komplexe Algorithmen mit weniger Code zu erstellen

MetaTrader 5 — Experten |
82 0
Omega J Msigwa
Omega J Msigwa

Inhalt

Glaube daran, dass du es kannst, und du hast schon die Hälfte geschafft.

-- Theodore Roosevelt.

Einführung

Keine Programmiersprache ist völlig autark für jede denkbare Aufgabe, die wir mit Hilfe von Code lösen können. Jede Programmiersprache hängt von gut ausgearbeiteten Werkzeugen ab, bei denen es sich um Bibliotheken, Frameworks und Module handelt, die dabei helfen, bestimmte Probleme zu lösen und bestimmte Ideen in die Realität umzusetzen.

MQL5 ist da keine Ausnahme. Da es in erster Linie für den algorithmischen Handel entwickelt wurde, beschränkte sich seine Funktionalität anfangs hauptsächlich auf Handelsoperationen. Im Gegensatz zu seinem Vorgänger MQL4, das als schwächere Sprache gilt, ist MQL5 weitaus leistungsfähiger und fähiger. Der Aufbau eines voll funktionsfähigen Handelsroboters erfordert jedoch mehr als nur den Aufruf von Funktionen zum Platzieren von Kauf- und Verkaufstransaktionen.

Um sich in der Komplexität der Finanzmärkte zurechtzufinden, setzen Händler häufig ausgeklügelte mathematische Verfahren ein, darunter maschinelles Lernen und künstliche Intelligenz (KI). Dies hat zu einer wachsenden Nachfrage nach optimierten Codebasen und spezialisierten Frameworks geführt, die komplexe Berechnungen effizient durchführen können.

Bildquelle: pexels.com

Um den Inhalt dieses Artikels vollständig zu verstehen, sind Grundkenntnisse über Python und NumPy erforderlich.



Warum NumPy?

Wenn es um den Umgang mit komplexen Berechnungen in MQL5 geht, haben wir viele gute Bibliotheken, die von MetaQuotes zur Verfügung gestellt werden, wie z.B. Fuzzy, Stat und die mächtige Alglib (zu finden in MetaEditor unter MQL5\Include\Math).

Diese Bibliotheken verfügen über viele Funktionen, die sich für die Programmierung komplexer Expertenberater mit minimalem Aufwand eignen. Allerdings sind die meisten Funktionen in diesen Bibliotheken aufgrund der übermäßigen Verwendung von Arrays und Objektzeigern nicht sehr flexibel, ganz zu schweigen davon, dass einige mathematische Kenntnisse erfordern, um sie richtig zu nutzen.

Seit der Einführung von Matrizen und Vektoren ist die Sprache MQL5 vielseitiger und flexibler geworden, wenn es um Datenspeicherung und Berechnungen geht. Diese Arrays haben die Form von Objekten, die von vielen eingebauten mathematischen Funktionen begleitet werden, die früher manuelle Implementierungen erforderten.

Aufgrund der Flexibilität von Matrizen und Vektoren können wir sie zu etwas Größerem ausbauen und eine Sammlung verschiedener mathematischer Funktionen erstellen, die denen in NumPy (Numerical Python, eine Python-Bibliothek, die eine Sammlung mathematischer Funktionen auf hohem Niveau bietet, einschließlich Unterstützung für mehrdimensionale Arrays, maskierte Arrays und Matrizen) ähneln.

Man kann mit Fug und Recht behaupten, dass die meisten Funktionen, die Matrizen und Vektoren in MQL5 bieten, von NumPy inspiriert wurden, da die Syntax sehr ähnlich ist, wie aus der Dokumentation hervorgeht.


MQL5

 Python 
vector::Zeros(3);
vector::Full(10);
 
numpy.zeros(3)
numpy.full(10)

Laut der Dokumentation wurde diese ähnliche Syntax auf eingeführt, um „die Übersetzung von Algorithmen und Codes von Python nach MQL5 mit minimalem Aufwand zu erleichtern. Viele Datenverarbeitungsaufgaben, mathematische Gleichungen, neuronale Netze und Aufgaben des maschinellen Lernens können mit vorgefertigten Python-Methoden und -Bibliotheken gelöst werden.“

Das ist richtig, aber die Funktionen von Matrizen und Vektoren reichen nicht aus. In diesem Artikel werden wir einige der nützlichsten Funktionen und Methoden von NumPy in MQL5 implementieren und dabei eine sehr enge Syntax verwenden, um die Übersetzung von Algorithmen aus der Programmiersprache Python zu erleichtern.

Um die Syntax ähnlich der von Python zu halten, werden wir die Namen der Funktionen in Kleinbuchstaben implementieren. Beginnend mit Methoden zur Initialisierung von Vektoren und Matrizen.


Initialisierung von Vektoren und Matrizen

Um mit Vektoren und Matrizen arbeiten zu können, brauchen wir Methoden, um sie zu initialisieren, indem wir sie mit einigen Werten füllen. Im Folgenden finden Sie einige der Funktionen für die Aufgabe.


Methode

 Beschreibung 
template <typename T>
vector CNumpy::full(uint size, T fill_value) { return vector::Full(size, fill_value); }
template <typename T>
matrix CNumpy::full(uint rows, uint cols, T fill_value) { return matrix::Full(rows, cols, fill_value); }
  Konstruieren eines neuen Vektors/einer neuen Matrix mit gegebener Größe/Zeilen und Spalten, gefüllt mit einem Wert. 
vector CNumpy::ones(uint size) { return vector::Ones(size); }
matrix CNumpy::ones(uint rows, uint cols) { return matrix::Ones(rows, cols); }
  Konstruieren eines neuen Vektors einer bestimmten Größe/Matrix mit bestimmten Zeilen und Spalten, gefüllt mit Einsen 
vector CNumpy::zeros(uint size) { return vector::Zeros(size); }
matrix CNumpy::zeros(uint rows, uint cols) { return matrix::Zeros(rows, cols); }
  Konstruieren eines Vektors einer bestimmten Größe/Matrix mit bestimmten Zeilen und Spalten, gefüllt mit Nullen 
matrix CNumpy::eye(const uint rows, const uint cols, const int ndiag=0) { return matrix::Eye(rows, cols, ndiag); }
  Konstruieren einer Matrix mit Einsen auf der Diagonalen und Nullen an anderen Stellen. 
matrix CNumpy::identity(uint rows) { return matrix::Identity(rows, rows); }
  Konstruieren einer quadratischen Matrix mit Einsen auf der Hauptdiagonalen.

Trotz ihrer Einfachheit sind diese Methoden von entscheidender Bedeutung für die Erstellung von Platzhaltermatrizen und -vektoren, die häufig bei Transformationen, Auffüllungen und Augmentierungen verwendet werden. 

Beispiel für die Verwendung:

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Initialization
    
    // Vectors One-dimensional
    
    Print("numpy.full: ",np.full(10, 2));
    Print("numpy.ones: ",np.ones(10));
    Print("numpy.zeros: ",np.zeros(10));
    
    // Matrices Two-Dimensional
    
    Print("numpy.full:\n",np.full(3,3, 2));
    Print("numpy.ones:\n",np.ones(3,3));
    Print("numpy.zeros:\n",np.zeros(3,3));
    Print("numpy.eye:\n",np.eye(3,3));
    Print("numpy.identity:\n",np.identity(3));
 }


Mathematische Funktionen

Dieses Thema ist sehr umfangreich, da es viele mathematische Funktionen gibt, die sowohl für Vektoren als auch für Matrizen zu implementieren und zu beschreiben sind, und wir werden nur einige davon besprechen. Wir beginnen mit mathematischen Konstanten.

Konstanten

Mathematische Konstanten sind ebenso nützlich wie die Funktionen.


Konstante

 Beschreibung

numpy.e

  Eulersche Konstante, Basis der natürlichen Logarithmen, Napiersche Konstante.

numpy.euler_gamma  

  Definiert als die begrenzte Differenz zwischen der harmonischen Reihe und dem natürlichen Logarithmus.

np.inf

  

 IEEE 754 Gleitkommadarstellung der (positiven) Unendlichkeit.

np.nan


 IEEE 754 Gleitkommadarstellung von Not a Number (NaN).
np.pi
 Das ist das Verhältnis von Kreisumfang zu Kreisdurchmesser und entspricht ungefähr 3,14159. 

Beispiel für die Verwendung.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Mathematical functions
   
    Print("numpy.e: ",np.e);
    Print("numpy.euler_gamma: ",np.euler_gamma);
    Print("numpy.inf: ",np.inf);
    Print("numpy.nan: ",np.nan);
    Print("numpy.pi: ",np.pi);
 }

Funktionen

Im Folgenden sind einige der Funktionen der Klasse CNumpy aufgeführt.

Methode
Beschreibung

 
vector CNumpy::add(const vector&a, const vector&b) { return a+b; };
matrix CNumpy::add(const matrix&a, const matrix&b) { return a+b; };
 Addiert zwei Vektoren/Matrizen. 
vector CNumpy::subtract(const vector&a, const vector&b) { return a-b; };
matrix CNumpy::subtract(const matrix&a, const matrix&b) { return a-b; };
 Subtrahiert zwei Vektoren/Matrizen. 
vector CNumpy::multiply(const vector&a, const vector&b) { return a*b; };
matrix CNumpy::multiply(const matrix&a, const matrix&b) { return a*b; };
 Multipliziert zwei Vektoren/Matrizen. 
vector CNumpy::divide(const vector&a, const vector&b) { return a/b; };
matrix CNumpy::divide(const matrix&a, const matrix&b) { return a/b; };
 Teilt zwei Vektoren/Matrizen 
vector CNumpy::power(const vector&a, double n) { return MathPow(a, n); };
matrix CNumpy::power(const matrix&a, double n) { return MathPow(a, n); };
 Potenziert alle Elemente der Matrix/des Vektors a mit n. 
vector CNumpy::sqrt(const vector&a) { return MathSqrt(a); }; 
matrix CNumpy::sqrt(const matrix&a) { return MathSqrt(a); };
 Berechnet die Quadratwurzel aus jedem Element des Vektors/der Matrix a.

Beispiel für die Verwendung.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Mathematical functions
   
    vector a = {1,2,3,4,5};
    vector b = {1,2,3,4,5};  
    
    Print("np.add: ",np.add(a, b));
    Print("np.subtract: ",np.subtract(a, b));
    Print("np.multiply: ",np.multiply(a, b));
    Print("np.divide: ",np.divide(a, b));  
    Print("np.power: ",np.power(a, 2));
    Print("np.sqrt: ",np.sqrt(a));
    Print("np.log: ",np.log(a));
    Print("np.log1p: ",np.log1p(a));
 }


Statistische Funktionen

Diese können auch als mathematische Funktionen klassifiziert werden, aber im Gegensatz zu den grundlegenden mathematischen Operationen helfen diese Funktionen bei der Bereitstellung analytischer Metriken aus den gegebenen Daten. Beim maschinellen Lernen werden sie vor allem bei der Merkmalstechnik und Normalisierung verwendet.

Die folgende Tabelle zeigt einige der Funktionen, die in der Klasse MQL5-Numpy implementiert sind.


Methode

 Beschreibungen 
double sum(const vector& v) { return v.Sum(); }
double sum(const matrix& m) { return m.Sum(); };
vector sum(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Sum(axis); };
  Berechnet die Summe der Vektor-/Matrixelemente, was auch für die angegebene Achse (Achsen) durchgeführt werden kann. 
double mean(const vector& v) { return v.Mean(); }
double mean(const matrix& m) { return m.Mean(); };
vector mean(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Mean(axis); };


 Berechnet das arithmetische Mittel von Elementwerten in einem Vektor/einer Matrix.

 
double var(const vector& v) { return v.Var(); }
double var(const matrix& m) { return m.Var(); };
vector var(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Var(axis); };


 Berechnet die Varianz der Werte von Matrix/Vektor-Elementen.

 
double std(const vector& v) { return v.Std(); }
double std(const matrix& m) { return m.Std(); };
vector std(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Std(axis); };


 Gibt die Standardabweichung der Werte von Vektor-/Matrixelementen oder von Elementen entlang der angegebenen Achse zurück.

 
double median(const vector& v) { return v.Median(); }
double median(const matrix& m) { return m.Median(); };
vector median(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Median(axis); };
  

 Berechnet den Median der Vektor-/Matrixelemente.

 
double percentile(const vector &v, int value) { return v.Percentile(value); }
double percentile(const matrix &m, int value) { return m.Percentile(value); }
vector percentile(const matrix &m, int value, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Percentile(value, axis); }

 Diese Funktionen berechnen das angegebene Perzentil der Werte eines Vektor-/Matrixelements oder von Elementen entlang der angegebenen Achse.

 
double quantile(const vector &v, int quantile_) { return v.Quantile(quantile_); } 
double quantile(const matrix &m, int quantile_) { return m.Quantile(quantile_); }
vector quantile(const matrix &m, int quantile_, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Quantile(quantile_, axis); }
  

Sie berechnen das angegebene Quantil der Werte von Matrix-/Vektorelementen oder Elementen entlang der angegebenen Achse.

 
vector cumsum(const vector& v) { return v.CumSum(); };
vector cumsum(const matrix& m) { return m.CumSum(); };
matrix cumsum(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.CumSum(axis); };

Diese Funktionen berechnen die kumulative Summe der Matrix-/Vektor-Elemente, einschließlich derer entlang der angegebenen Achse.

 
vector cumprod(const vector& v) { return v.CumProd(); }
vector cumprod(const matrix& m) { return m.CumProd(); };
matrix cumprod(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.CumProd(axis); };
  

Sie geben das kumulative Produkt der Matrix-/Vektor-Elemente zurück, einschließlich derer entlang der angegebenen Achse.

 
double average(const vector &v, const vector &weights) { return v.Average(weights); }
double average(const matrix &m, const matrix &weights) { return m.Average(weights); }
vector average(const matrix &m, const matrix &weights, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Average(weights, axis); }


Berechnung des gewichteten Mittelwerts von Matrix-/Vektorwerten.

 
ulong argmax(const vector& v) { return v.ArgMax(); }
ulong argmax(const matrix& m) { return m.ArgMax(); }
vector argmax(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.ArgMax(axis); };
  

Sie geben den Index des Höchstwertes zurück.


 
ulong argmin(const vector& v) { return v.ArgMin(); }
ulong argmin(const matrix& m) { return m.ArgMin(); }
vector argmin(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.ArgMin(axis); };
 Sie geben den Index des Mindestwertes zurück. 
double min(const vector& v) { return v.Min(); }
double min(const matrix& m) { return m.Min(); }
vector min(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Min(axis); };
 Sie geben den kleinsten Wert in einem Vektor/einer Matrix zurück, einschließlich der Werte entlang der angegebenen Achse. 
double max(const vector& v) { return v.Max(); }
double max(const matrix& m) { return m.Max(); }
vector max(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Max(axis); };
  Sie geben den Maximalwert in einem Vektor/einer Matrix zurück, einschließlich der Werte entlang der angegebenen Achse. 
double prod(const vector &v, double initial=1.0) { return v.Prod(initial); }
double prod(const matrix &m, double initial) { return m.Prod(initial); }
vector prod(const matrix &m, double initial, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Prod(axis, initial); }
  

Sie geben das Produkt der Matrix-/Vektorelemente zurück, das auch für die angegebene Achse durchgeführt werden kann.

 
double ptp(const vector &v) { return v.Ptp(); }
double ptp(const matrix &m) { return m.Ptp(); }
vector ptp(const matrix &m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Ptp(axis); }
  

Sie geben den Wertebereich einer Matrix/eines Vektors oder der angegebenen Matrixachse zurück, was der Funktion Max() - Min() entspricht. Ptp - Spitze zu Spitze (peak to peak).

Diese Funktionen werden von eingebauten statistischen Funktionen für Vektoren und Matrizen angetrieben, wie in den Dokumenten zu sehen ist, alles, was ich tat, war eine NumPy ähnliche Syntax zu erstellen und diese Funktionen zu verpacken.

Nachfolgend finden Sie ein Beispiel für die Verwendung dieser Funktionen.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {    
//--- Statistical functions
   
     vector z = {1,2,3,4,5};
    
     Print("np.sum: ", np.sum(z));
     Print("np.mean: ", np.mean(z));
     Print("np.var: ", np.var(z));
     Print("np.std: ", np.std(z));
     Print("np.median: ", np.median(z));
     Print("np.percentile: ", np.percentile(z, 75));
     Print("np.quantile: ", np.quantile(z, 75));
     Print("np.argmax: ", np.argmax(z));
     Print("np.argmin: ", np.argmin(z));
     Print("np.max: ", np.max(z));
     Print("np.min: ", np.min(z));
     Print("np.cumsum: ", np.cumsum(z));
     Print("np.cumprod: ", np.cumprod(z));
     Print("np.prod: ", np.prod(z));
     
     vector weights = {0.2,0.1,0.5,0.2,0.01};
     Print("np.average: ", np.average(z, weights));
     Print("np.ptp: ", np.ptp(z));
}


Zufallszahlen-Generatoren

NumPy hat eine Vielzahl von praktischen Submodulen, eines davon ist das random submodule. 

Das Submodul numpy.random stellt verschiedene Funktionen zur Erzeugung von Zufallszahlen zur Verfügung, die auf dem PCG64-Zufallszahlengenerator (aus NumPy 1.17+) basieren. Die meisten dieser Methoden beruhen auf mathematischen Prinzipien aus der Wahrscheinlichkeitstheorie und statistischen Verteilungen.

Beim maschinellen Lernen werden häufig Zufallszahlen für viele Anwendungsfälle generiert. Wir generieren Zufallszahlen als anfängliche Startgewichte für neuronale Netze und viele Modelle, die iterative, auf Gradientenabstieg basierende Methoden für das Training verwenden, manchmal generieren wir sogar Zufallsmerkmale, die einer statistischen Verteilung folgen, um Testdaten für unsere Modelle zu erhalten.

Es ist sehr wichtig, dass die Zufallszahlen, die wir erzeugen, einer statistischen Verteilung folgen, was wir mit den nativen/eingebauten Zufallszahlengenerierungsfunktionen in MQL5 nicht erreichen können.

Zunächst wird hier beschrieben, wie Sie den Zufallswert für das Submodul CNumpy.random festlegen können.

np.random.seed(42);


Uniform Distribution #

Wir generieren Zufallszahlen aus einer gleichmäßigen Verteilung zwischen einigen niedrigen und hohen Werten.

Formel:

Dabei ist R eine Zufallszahl aus [0,1].

 template <typename T>
 vector uniform(T low, T high, uint size=1)
  { 
    vector res = vector::Zeros(size);
    for (uint i=0; i<size; i++)
       res[i] = low + (high - low) * (rand() / double(RAND_MAX));  // Normalize rand()
    
    return res;
  }

Verwendung:

In der Datei Numpy.mqh wurde eine separate Struktur mit dem Namen CRandom erstellt, die dann innerhalb der Klasse CNumpy aufgerufen wird. Dies ermöglicht es uns, eine Struktur innerhalb einer Klasse aufzurufen, was uns eine Python-ähnliche Syntax bietet.

class CNumpy
  {
protected:
    
public:
                     CNumpy(void);
                    ~CNumpy(void);
                    
                    CRandom random;
  }
Print("np.random.uniform: ",np.random.uniform(1,10,10));

Ausgabe:

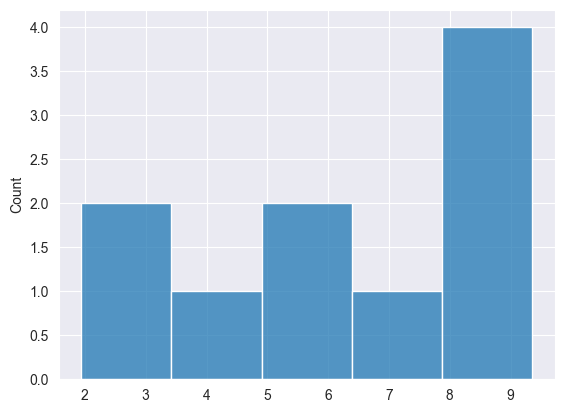
2025.03.16 15:03:15.102 Numpy  np.random.uniform: [8.906552323984496,9.274605548265022,7.828760643330179,9.355082857753228,2.218420972319712,5.772331919309061,3.76067384868923,6.096438489944151,1.93908505508591,8.107272560808131]

Wir können die Ergebnisse visualisieren, um zu sehen, ob die Daten gleichmäßig verteilt sind.



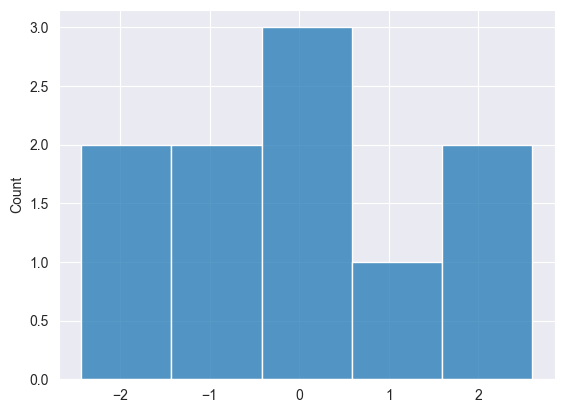
Normalverteilung #

Diese Methode wird in vielen ML-Modellen verwendet, z. B. bei der Initialisierung von Gewichten in neuronalen Netzen.

Wir können dies mit transformieren.

Formel:

wobei:

 sind Zufallszahlen aus [0,1].

 vector normal(uint size, double mean=0, double std=1)
   {
       vector results = {};  // Declare the results vector
       
       // We generate two random values in each iteration of the loop
       uint n = size / 2 + size % 2;  // If the size is odd, we need one extra iteration
   
       // Loop to generate pairs of normal numbers
       for (uint i = 0; i < n; i++)
       {
           // Generate two random uniform variables
           double u1 = MathRand() / 32768.0;  // Uniform [0,1] -> (MathRand() generates values from 0 to 32767)
           double u2 = MathRand() / 32768.0;  // Uniform [0,1]
   
           // Apply the Box-Muller transform to get two normal variables
           double z1 = MathSqrt(-2 * MathLog(u1)) * MathCos(2 * M_PI * u2);
           double z2 = MathSqrt(-2 * MathLog(u1)) * MathSin(2 * M_PI * u2);
   
           // Scale to the desired mean and standard deviation, and add them to the results
           results = push_back(results, mean + std * z1);
           if ((uint)results.Size() < size)  // Only add z2 if the size is not reached yet
               results = push_back(results, mean + std * z2);
       }
       
       // Return only the exact size of the results (if it's odd, we cut off one value)
       
       results.Resize(size);
       return results;
   }

Verwendung:

Print("np.random.normal: ",np.random.normal(10,0,1));

Ausgabe:

2025.03.16 15:33:08.791 Numpy test (US Tech 100,H1)     np.random.normal: [-1.550635379340936,0.963285267506685,0.4587699653416977,-0.4813064556591148,-0.6919587880027229,1.649030932484221,-2.433415738330552,2.598464400400878,-0.2363726420659525,-0.1131299501178828]



Exponentialverteilung #

Die Exponentialverteilung ist eine Wahrscheinlichkeitsverteilung, die die Zeit zwischen Ereignissen in einem Poisson-Prozess beschreibt, in dem Ereignisse kontinuierlich und unabhängig voneinander mit einer konstanten durchschnittlichen Rate auftreten.

Er ist gegeben durch die Formel:

Um exponentiell verteilte Zufallszahlen zu erzeugen, verwenden wir die Methode der inversen Transformationsstichprobe. Die Formel lautet.

wobei:

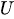  •  ist eine gleichmäßige Zufallszahl zwischen 0 und 1.
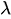  •  ist der Ratenparameter.

 vector  exponential(uint size, double lmbda=1.0)
   {
      vector res = vector::Zeros(size);
      for (uint i=0; i<size; i++)
         res[i] = -log((rand()/RAND_MAX)) / lmbda;
          
      return res;
   }

Verwendung:

Print("np.random.exponential: ",np.random.exponential(10));

Ausgabe:

2025.03.16 15:57:36.124 Numpy test (US Tech 100,H1)     np.random.exponential: [0.4850272647406031,0.7617651806321184,1.09800210467871,2.658253432915927,0.5814831387699247,0.9920104404467721,0.7427922283035616,0.09323707153463576,0.2963563234048633,1.790326127008611]



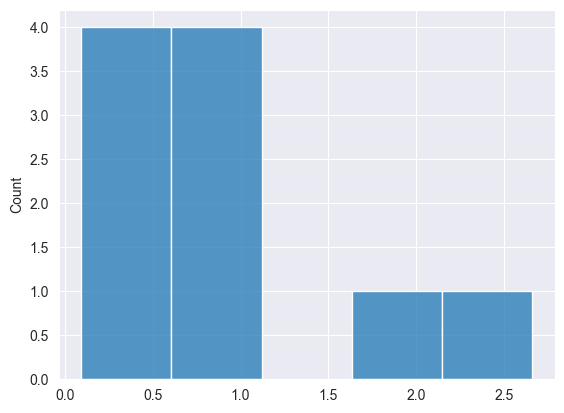
Binomialverteilung #

Dabei handelt es sich um eine diskrete Wahrscheinlichkeitsverteilung, die die Anzahl der Erfolge bei einer festen Anzahl unabhängiger Versuche modelliert, die jeweils die gleiche Erfolgswahrscheinlichkeit haben.

Gegeben durch die Formel.

Wir können dies wie folgt umsetzen.

// Function to generate a single Bernoulli(p) trial
int bernoulli(double p)
  {
    return (double)rand() / RAND_MAX < p ? 1 : 0;
  }
// Function to generate Binomial(n, p) samples
vector binomial(uint size, uint n, double p)
  {
    vector res = vector::Zeros(size);
    
    for (uint i = 0; i < size; i++)
      {
        int count = 0;
        for (uint j = 0; j < n; j++)
          count += bernoulli(p); // Sum of Bernoulli trials

        res[i] = count;
      }
    
    return res;
}

Verwendung:

Print("np.random.binomial: ",np.random.binomial(10, 5, 0.5));

Ausgabe:

2025.03.16 19:35:20.346 Numpy test (US Tech 100,H1)     np.random.binomial: [2,1,2,3,2,1,1,4,0,3]



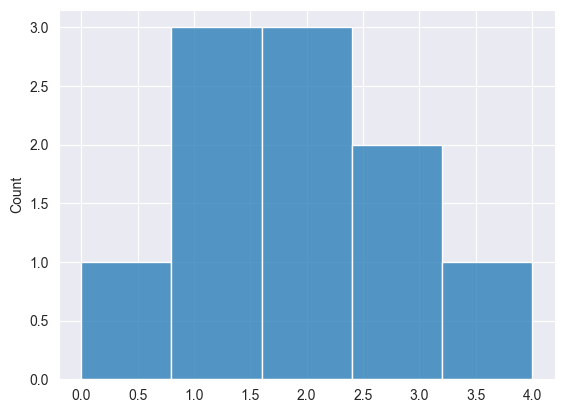
Poisson-Verteilung #

Dies ist eine Wahrscheinlichkeitsverteilung, die die Wahrscheinlichkeit ausdrückt, dass eine bestimmte Anzahl von Ereignissen in einem festen Zeit- oder Raumintervall eintritt, wenn diese Ereignisse mit einer konstanten durchschnittlichen Rate und unabhängig von der Zeit seit dem letzten Ereignis eintreten.

Die Formel:

wobei:

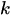  •  ist die Anzahl der Vorkommen (0,1,2...).
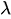  •  (lambda) ist die durchschnittliche Häufigkeit des Auftretens.
  • e ist die Eulersche Zahl.

int poisson(double lambda)
   {
       double L = exp(-lambda);
       double p = 1.0;
       int k = 0;
   
       while (p > L)
       {
           k++;
           p *= MathRand() / 32767.0; // Normalize MathRand() to (0,1)
       }
       
       return k - 1; // Since we increment k before checking the condition
   }
// We generate a vector of Poisson-distributed values
vector poisson(double lambda, int size)
{
    vector result = vector::Zeros(size);
    for (int i = 0; i < size; i++)
        result[i] = poisson(lambda);
    
    return result;
}

Verwendung:

Print("np.random.poisson: ",np.random.poisson(4, 10));

Ausgabe:

2025.03.16 18:39:56.058 Numpy test (US Tech 100,H1)     np.random.poisson: [6,6,5,1,3,1,1,3,6,7]




Shuffle #

Wenn wir versuchen, Modelle für maschinelles Lernen zu trainieren, um Muster in den Daten zu verstehen, mischen wir oft die Stichproben, damit die Modelle die in den Daten vorhandenen Muster und nicht die Anordnung der Daten verstehen.

Die Zufallswiedergabe ist in einer solchen Situation sehr praktisch.

Beispiel für die Verwendung.

vector data = {1,2,3,4,5,6,7,8,9,10};
np.random.shuffle(data);

Print("Shuffled: ",data);

Ausgabe:

2025.03.16 18:55:36.763 Numpy test (US Tech 100,H1)     Shuffled: [6,4,9,2,3,10,1,7,8,5]


Zufallsauswahl #

Ähnlich wie shuffle, nimmt diese Funktion eine Zufallsstichprobe aus dem gegebenen 1-dimensionalen Bereich, jedoch mit der Option, mit oder ohne Ersetzung zu mischen.

template<typename T>
vector<T> choice(const vector<T> &v, uint size, bool replace=false)

Mit Ersetzung.

Die Werte sind nicht eindeutig, dieselben Elemente können in dem resultierenden gemischten Vektor/Array wiederholt werden.

vector data = {1,2,3,4,5,6,7,8,9,10};

Print("np.random.choice replace=True: ",np.random.choice(data, (uint)data.Size(), true));

Ausgabe:

2025.03.16 19:11:53.520 Numpy test (US Tech 100,H1)     np.random.choice replace=True: [5,3,9,2,1,3,4,7,8,3]

Ohne Ersetzung.

Der daraus resultierende gemischte Vektor enthält die gleichen eindeutigen Elemente wie der ursprüngliche Vektor, nur ihre Reihenfolge wird geändert.

Print("np.random.choice replace=False: ",np.random.choice(data, (uint)data.Size(), false));

Ausgabe:

2025.03.16 19:11:53.520 Numpy test (US Tech 100,H1)     np.random.choice replace=False: [8,4,3,10,5,7,1,9,6,2]

Alle Funktionen an einem Ort.

Beispiel für die Verwendung.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Random numbers generating
    
    np.random.seed(42);
    
    Print("---------------------------------------:");  
    Print("np.random.uniform: ",np.random.uniform(1,10,10));
    Print("np.random.normal: ",np.random.normal(10,0,1));
    Print("np.random.exponential: ",np.random.exponential(10));
    Print("np.random.binomial: ",np.random.binomial(10, 5, 0.5));
    Print("np.random.poisson: ",np.random.poisson(4, 10));
    
    vector data = {1,2,3,4,5,6,7,8,9,10};
    //np.random.shuffle(data);
    //Print("Shuffled: ",data);
    
    Print("np.random.choice replace=True: ",np.random.choice(data, (uint)data.Size(), true));
    Print("np.random.choice replace=False: ",np.random.choice(data, (uint)data.Size(), false));
 }


Fast Fourier Transform (FFT) #

Eine schnelle Fourier-Transformation (FFT) ist ein Algorithmus, der die diskrete Fourier-Transformation (DFT) einer Sequenz oder ihre Umkehrung (IDFT) berechnet. Eine Fourier-Transformation wandelt ein Signal von seinem ursprünglichen Bereich (oft Zeit oder Raum) in eine Darstellung im Frequenzbereich um und umgekehrt. Die DFT wird durch Zerlegung einer Folge von Werten in Komponenten verschiedener Frequenzen ermittelt, weiter lesen ...

Dieser Vorgang ist in vielen Bereichen nützlich, z. B.:

  1. In der Signal- und Audioverarbeitung wird sie zur Umwandlung von Schallwellen im Zeitbereich in Frequenzspektren verwendet. Bei der Kodierung der Audioformate und der Filterung des Rauschens.
  2. Sie wird auch bei der Bildkomprimierung und bei der Erkennung von Mustern in Bildern eingesetzt.
  3. Datenwissenschaftler verwenden FFT häufig, um Merkmale aus Zeitreihendaten zu extrahieren.

Das Submodul numpy.fft ist für die FFT zuständig.

In unserem aktuellen CNumpy habe ich nur die eindimensionalen FFT-Standardfunktionen implementiert.

Bevor wir uns mit den in der Klasse implementierten Methoden der „Standard-FFT“ beschäftigen, wollen wir die Funktion zur Erzeugung von DFT-Frequenzen verstehen.

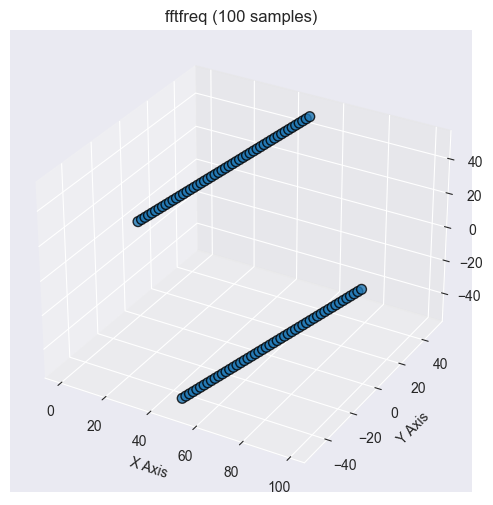
FFT-Frequenz

Bei der FFT von Signalen oder Daten liegt das Ergebnis im Frequenzbereich. Um es zu interpretieren, müssen wir wissen, welcher Frequenz jedes Element der FFT entspricht. Hier setzt diese Methode an.

Diese Funktion gibt die Abtastfrequenzen der Diskreten Fourier-Transformation (DFT) zurück, die mit einer FFT einer bestimmten Größe verbunden sind. Sie hilft bei der Bestimmung der entsprechenden Frequenzen für jeden FFT-Koeffizienten.

vector fft_freq(int n, double d)

Beispiel für die Verwendung.

2025.03.17 11:11:10.165 Numpy test (US Tech 100,H1)     np.fft.fftfreq: [0,0.1,0.2,0.3,0.4,-0.5,-0.4,-0.3,-0.2,-0.1]



Standard-Fast-Fourier-Transformationen #

FFT

Diese Funktion berechnet die FFT eines Eingangssignals und wandelt es vom Zeitbereich in den Frequenzbereich um. Es ist ein effizienter Algorithmus zur Berechnung der diskreten Fourier-Transformation (DFT).

vector<complex> fft(const vector &x)

Diese Funktion basiert auf CFastFourierTransform::FFTR1D, einer von ALGLIB bereitgestellten Funktion. Weitere Informationen finden Sie unter ALGLIB.

Beispiel für die Verwendung.

vector signal = {0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9};
Print("np.fft.fft: ",np.fft.fft(signal));

Ausgabe:

2025.03.17 11:28:16.739 Numpy test (US Tech 100,H1)     np.fft.fft: [(4.5,0),(-0.4999999999999999,1.538841768587627),(-0.4999999999999999,0.6881909602355869),(-0.5000000000000002,0.3632712640026804),(-0.5000000000000002,0.1624598481164532),(-0.5,-3.061616997868383E-16),(-0.5000000000000002,-0.1624598481164532),(-0.5000000000000002,-0.3632712640026804),(-0.4999999999999999,-0.6881909602355869),(-0.4999999999999999,-1.538841768587627)]

Inverse FFT

Diese Funktion berechnet die inverse schnelle Fourier-Transformation (IFFT), die Daten aus dem Frequenzbereich zurück in den Zeitbereich konvertiert. Sie macht im Wesentlichen die Wirkung der vorherigen Methode np.fft.fft rückgängig.

vector ifft(const vectorc &fft_values)

Beispiel für die Verwendung.

vector signal = {0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9};

vectorc fft_res = np.fft.fft(signal); //perform fft
Print("np.fft.fft: ",fft_res); //fft results
Print("np.fft.ifft: ",np.fft.ifft(fft_res)); //Original signal

Ausgabe:

2025.03.17 11:45:04.537 Numpy test     np.fft.fft: [(4.5,0),(-0.4999999999999999,1.538841768587627),(-0.4999999999999999,0.6881909602355869),(-0.5000000000000002,0.3632712640026804),(-0.5000000000000002,0.1624598481164532),(-0.5,-3.061616997868383E-16),(-0.5000000000000002,-0.1624598481164532),(-0.5000000000000002,-0.3632712640026804),(-0.4999999999999999,-0.6881909602355869),(-0.4999999999999999,-1.538841768587627)]
2025.03.17 11:45:04.537 Numpy test     np.fft.ifft: [-4.440892098500626e-17,0.09999999999999991,0.1999999999999999,0.2999999999999999,0.4,0.5,0.6,0.7,0.8000000000000002,0.9]


Lineare Algebra #

Lineare Algebra ist ein Teilgebiet der Mathematik, das sich mit Vektoren, Matrizen und linearen Transformationen befasst. Sie ist die Grundlage für viele Bereiche wie Physik, Technik, Datenwissenschaft usw.

NumPy bietet das Modul np.linalg, ein Untermodul, das sich mit Funktionen der linearen Algebra beschäftigt. Es bietet fast alle Funktionen der linearen Algebra, wie z. B. das Lösen linearer Systeme, die Berechnung von Eigenwerten/Eigenvektoren und vieles mehr.

Im Folgenden werden einige der in der Klasse CNumpy implementierten Funktionen der linearen Algebra vorgestellt.


Methode

 Beschreibung 
matrix inv(const matrix &m)  {  return m.Inv();  }

Berechnet die multiplikative Inverse einer quadratischen invertierbaren Matrix nach der Jordan-Gauss-Methode.

 
double det(const matrix &m)  {  return m.Det();  }

Berechnet die Determinante einer quadratischen invertierbaren Matrix.

 
matrix kron(const matrix &a, const matrix &b) { return a.Kron(b); }
matrix kron(const vector &a, const vector &b) { return a.Kron(b); }
matrix kron(const vector &a, const matrix &b) { return a.Kron(b); }
matrix kron(const matrix &a, const vector &b) { return a.Kron(b); }

Sie berechnen das Kronecker-Produkt von zwei Matrizen, einer Matrix und einem Vektor, einem Vektor und einer Matrix oder zwei Vektoren.

 
struct eigen_results_struct
  {
   vector eigenvalues;
   matrix eigenvectors;
  };

eigen_results_struct eig(const matrix &m) 
 {
   eigen_results_struct res;
   if (!m.Eig(res.eigenvectors, res.eigenvalues))
      printf("%s failed to calculate eigen vectors and values, error = %d",__FUNCTION__,GetLastError());
   
   return res;
 }

Diese Funktion berechnet die Eigenwerte und rechten Eigenvektoren einer quadratischen Matrix.


 
double norm(const matrix &m, ENUM_MATRIX_NORM norm) {  return m.Norm(norm); }
double norm(const vector &v, ENUM_VECTOR_NORM norm) {  return v.Norm(norm); }

Rückgabe der Matrix- oder Vektornorm, mehr lesen.

 
svd_results_struct svd(const matrix &m)
  {
    svd_results_struct res;
    if (!m.SVD(res.U, res.V, res.singular_vectors))
      printf("%s failed to calculate the SVD");
    
    return res;
  }
 Berechnet die Singulärwert-Zerlegung (SVD).

 
vector solve(const matrix &a, const vector &b) { return a.Solve(b); }

Löst eine lineare Matrixgleichung oder ein System von linearen algebraischen Gleichungen.

 
vector lstsq(const matrix &a, const vector &b) { return a.LstSq(b); }

Berechnet die Lösung der kleinsten Quadrate von linearen algebraischen Gleichungen (für nicht quadratische oder entartete Matrizen).

 
ulong matrix_rank(const matrix &m) { return m.Rank(); }
 Diese Funktion berechnet den Rang einer Matrix, d. h. die Anzahl der linear unabhängigen Zeilen oder Spalten in der Matrix. Es ist ein Schlüsselkonzept für das Verständnis des Lösungsraums eines Systems linearer Gleichungen. 
matrix cholesky(const matrix &m)
{
  vector values = eig(m).eigenvalues;
  
  for (ulong i=0; i<values.Size(); i++)
   {
    if (values[i]<=0)
       {
          printf("%s Failed Matrix is not positive definite",__FUNCTION__);
          return matrix::Zeros(0,0);
       }
   }
   
   matrix L;   
   if (!m.Cholesky(L))
      printf("%s Failed, Error = %d",__FUNCTION__, GetLastError());
      
   return L;
} 
 Die Cholesky-Zerlegung wird verwendet, um eine positiv-definite Matrix in das Produkt aus einer unteren Dreiecksmatrix und ihrer Transponierten zu zerlegen. 
matrix matrix_power(const matrix &m, uint exponent) { return m.Power(exponent); }
 Berechnet die auf eine bestimmte ganzzahlige Potenz angehobene Matrix. Genauer gesagt berechnet es , wobei eine Matrix und eine nichtnegative ganze Zahl ist.

Beispiel für die Verwendung.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {    
    //--- Linear algebra
    
    
    matrix m = {{1,1,10},
                {1,0.5,1},
                {1.5,1,0.78}};
                
    Print("np.linalg.inv:\n",np.linalg.inv(m));
    Print("np.linalg.det: ",np.linalg.det(m));
    Print("np.linalg.det: ",np.linalg.kron(m, m));
    Print("np.linalg.eigenvalues:",np.linalg.eig(m).eigenvalues," eigenvectors: ",np.linalg.eig(m).eigenvectors);
    Print("np.linalg.norm: ",np.linalg.norm(m, MATRIX_NORM_P2));
    Print("np.linalg.svd u:\n",np.linalg.svd(m).U, "\nv:\n",np.linalg.svd(m).V);
        
    
    matrix a = {{1,1,10},
                {1,0.5,1},
                {1.5,1,0.78}};
                
    vector b = {1,2,3};
    
    Print("np.linalg.solve ",np.linalg.solve(a, b));
    Print("np.linalg.lstsq: ", np.linalg.lstsq(a, b));
    Print("np.linalg.matrix_rank: ", np.linalg.matrix_rank(a));
    Print("cholesky: ", np.linalg.cholesky(a));
    Print("matrix_power:\n", np.linalg.matrix_power(a, 2));
 }


Polynome (Potenzreihen) #

Das Submodul numpy.polynomial bietet eine Reihe von leistungsfähigen Werkzeugen zum Erstellen, Auswerten, Differenzieren, Integrieren und Manipulieren von Polynomen. Sie ist numerisch stabiler als die Verwendung von numpy.poly1d für polynomielle Operationen.

Es gibt verschiedene Arten von Polynomen in der Bibliothek NumPy in der Programmiersprache Python, aber in unserer Klasse CNumpy-MQL5 habe ich derzeit eine Standard-Potenzbasis (Polynom) implementiert.

class CPolynomial: protected CNumpy
  {
protected:
   vector m_coeff;
      
   matrix vector21DMatrix(const vector &v)
    {
      matrix res = matrix::Zeros(v.Size(), 1);
      for (ulong r=0; r<v.Size(); r++)
         res[r][0] = v[r];
         
      return res;
    }
    
public:
                     CPolynomial(void);
                     CPolynomial(vector &coefficients); //for loading pre-trained model
                    ~CPolynomial(void);
                    
                     vector fit(const vector &x, const vector &y, int degree);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPolynomial::CPolynomial(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPolynomial::~CPolynomial(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPolynomial::CPolynomial(vector &coefficients):
m_coeff(coefficients)
 {
   
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CPolynomial::fit(const vector &x, const vector &y, int degree)
 {
   //Constructing the vandermonde matrix
   matrix X = vander(x, degree+1, true);
   
   matrix temp1 =  X.Transpose().MatMul(X);
   matrix temp2 = X.Transpose().MatMul(vector21DMatrix(y));
   
   matrix coef_m = linalg.inv(temp1).MatMul(temp2);
   
   return (this.m_coeff = flatten(coef_m));
 }

Beispiel für die Verwendung.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {     
    //--- Polynomial
    
    vector X = {0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9};
    vector y = MathPow(X, 3) + 0.2 * np.random.randn(10);  // Cubic function with noise
    
    CPolynomial poly;
    
    Print("coef: ", poly.fit(X, y, 3));
 }

Ausgabe:

2025.03.17 14:01:43.026 Numpy test (US Tech 100,H1)     coef: [-0.1905916844269999,2.3719065699851,-5.625684489899982,4.749058310806731]

Zusätzlich gibt es Hilfsfunktionen, die bei der Bearbeitung von Polynomen helfen. Diese Funktionen befinden sich in der Hauptklasse CNumpy.


Funktion

 Beschreibung 
vector polyadd(const vector &p, const vector &q);
 Addiert zwei Polynome, indem es sie auf der Grundlage ihres Grades (Länge der Koeffizienten) ausrichtet. Wenn ein Polynom kürzer ist, wird es vor der Addition mit Nullen aufgefüllt. 
vector polysub(const vector &p, const vector &q);
 Subtrahiert zwei Polynome. 
vector polymul(const vector &p, const vector &q);
 Multipliziert zwei Polynome mit Hilfe der distributiven Eigenschaft, wobei jeder Term von p mit jedem Term von q multipliziert wird und die Ergebnisse addiert werden.
 
vector polyder(const vector &p, int m=1);
 Berechnet die Ableitungen des Polynoms p, die Ableitung wird durch Anwendung der Standardregel für Ableitungen berechnet. Jeder Begriff wird zu . 
vector polyint(const vector &p, int m=1, double k=0.0)
 Berechnet das Integral des Polynoms p, das Integral jedes Terms wird . Die Methode ermöglicht die Berechnung des m-ten Integrals mit einer Integrationskonstante k, die nach der Integration hinzugefügt wird. 
double polyval(const vector &p, double x);
 Bewertet das Polynom bei einem bestimmten Wert x durch Summierung der Terme des Polynoms, wobei jeder Term als berechnet wird.   
struct polydiv_struct
  {
     vector quotient, 
            remainder;
  };

polydiv_struct polydiv(const vector &p, const vector &q);
 Diese Funktion dividiert zwei Polynome und gibt den Quotienten und den Rest zurück.

Beispiel für die Verwendung.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Polynomial utils
    
    vector p = {1,-3, 2};
    vector q = {2,-4, 1};
    
    Print("polyadd: ",np.polyadd(p, q));
    Print("polysub: ",np.polysub(p, q));
    Print("polymul: ",np.polymul(p, q));
    Print("polyder:", np.polyder(p));
    Print("polyint:", np.polyint(p)); // Integral of polynomial
    Print("plyval x=2: ", np.polyval(p, 2)); // Evaluate polynomial at x = 2
    Print("polydiv:", np.polydiv(p, q).quotient," ",np.polydiv(p, q).remainder);
 }


Andere häufig verwendete NumPy-Methoden

Es ist schwierig, alle NumPy-Methoden zu klassifizieren. Im Folgenden finden Sie einige der nützlichsten Funktionen der Klasse, die wir noch nicht besprochen haben.


Methode

 Beschreibung 
vector CNumpy::arange(uint stop)
vector CNumpy::arange(int start, int stop, int step)
 Die erste Funktion erzeugt einen Vektor mit einer Reihe von Werten in einem bestimmten Intervall.

Die zweite Variante tut das Gleiche, berücksichtigt aber den Schritt für die Inkrementierung der Werte. Diese beiden Funktionen sind nützlich, um einen Vektor mit einer bestimmten Zahl in aufsteigender Reihenfolge zu erzeugen.
 
vector CNumpy::flatten(const matrix &m)
vector CNumpy::ravel(const matrix &m) { return flatten(m); };
 Sie wandeln eine 2D-Matrix in einen 1D-Vektor um.

Oft haben wir eine Matrix mit vielleicht einer Zeile und einer Spalte, die wir der Einfachheit halber in einen Vektor umwandeln müssen.		 
matrix CNumpy::reshape(const vector &v,uint rows,uint cols)
  Formt einen 1D-Vektor in eine Matrix aus Zeilen und Spalten (cols) um. 
matrix CNumpy::reshape(const matrix &m,uint rows,uint cols)
  Formt eine 2D-Matrix in eine neue Form (rows und cols) um. 
matrix CNumpy::expand_dims(const vector &v, uint axis)
  Fügt dem 1D-Vektor eine neue Achse hinzu und wandelt ihn damit in eine Matrix um. 
vector CNumpy::clip(const vector &v,double min,double max)
  Beschneidet die Werte eines Vektors so, dass sie innerhalb eines bestimmten Bereichs (zwischen Minimum und Maximum) liegen. Dies ist nützlich, um extreme Werte zu reduzieren und den Vektor innerhalb eines gewünschten Bereichs zu halten. 
vector CNumpy::argsort(const vector<T> &v)
  Gibt Indizes zurück, die ein Array sortieren würden. 
vector CNumpy::sort(const vector<T> &v)
  Sortiert ein Array in aufsteigender Reihenfolge. 
vector CNumpy::concat(const vector &v1, const vector &v2);
vector CNumpy::concat(const vector &v1, const vector &v2, const vector &v3);
  Verkettet mehrere Vektoren zu einem einzigen großen Vektor. 
matrix CNumpy::concat(const matrix &m1, const matrix &m2, ENUM_MATRIX_AXIS axis = AXIS_VERT)
Bei Achse=0 wird die Matrix entlang der Zeilen verkettet (stapelt die Matrizen m1 und m2 horizontal).

Bei Achse=1 wird die Matrix entlang der Spalten verkettet (stapelt die Matrizen m1 und m2 vertikal).		 
matrix CNumpy::concat(const matrix &m, const vector &v, ENUM_MATRIX_AXIS axis = AXIS_VERT)
 Ist axis = 0, wird der Vektor als neue Zeile angehängt (nur wenn seine Größe der Anzahl der Spalten in der Matrix entspricht).

Wenn axis = 1, wird der Vektor als neue Spalte angehängt (nur wenn seine Größe der Anzahl der Zeilen in der Matrix entspricht).		 
matrix CNumpy::dot(const matrix& a, const matrix& b);
double CNumpy::dot(const vector& a, const vector& b);
matrix CNumpy::dot(const matrix& a, const vector& b);
 Sie berechnen das Punktprodukt (auch als inneres Produkt bezeichnet) von zwei Matrizen, Vektoren oder einer Matrix und einem Vektor. 
vector CNumpy::linspace(int start,int stop,uint num,bool endpoint=true)
  Es wird ein Array aus gleichmäßig verteilten Zahlen über einen bestimmten Bereich (Start, Stop) erstellt. num = die Anzahl der zu erzeugenden Stichproben.
Endpunkt (Standardwert=true), wird stop einbezogen, bei false wird stop ausgeschlossen.		 
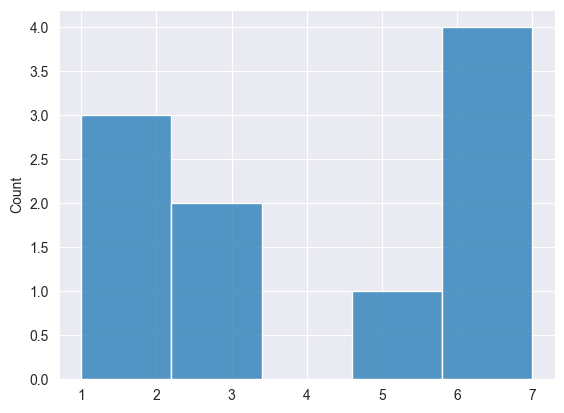
struct unique_struct
 {
   vector unique, count;
 };

unique_struct CNumpy::unique(const vector &v)
  Gibt die eindeutigen (unique) Elemente in einem Vektor und deren gezählte Anzahl des Vorhandenseins (count) zurück.

Beispiel für die Verwendung.

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
    //--- Common methods
    
    vector v = {1,2,3,4,5,6,7,8,9,10};  
    
    Print("------------------------------------");  
    Print("np.arange: ",np.arange(10));
    Print("np.arange: ",np.arange(1, 10, 2));
    
    matrix m = {
      {1,2,3,4,5},
      {6,7,8,9,10}
    };
      
    Print("np.flatten: ",np.flatten(m));
    Print("np.ravel: ",np.ravel(m));
    Print("np.reshape: ",np.reshape(v, 5, 2));
    Print("np.reshape: ",np.reshape(m, 2, 3));
   
    Print("np.expnad_dims: ",np.expand_dims(v, 1));
    Print("np.clip: ", np.clip(v, 3, 8));
   
    //--- Sorting
   
    Print("np.argsort: ",np.argsort(v));
    Print("np.sort: ",np.sort(v));
   
    //--- Others
    
    matrix z = {
      {1,2,3},
      {4,5,6},
      {7,8,9},
    };
      
    Print("np.concatenate: ",np.concat(v,  v));
    Print("np.concatenate:\n",np.concat(z,  z, AXIS_HORZ));
    
    vector y = {1,1,1};
    
    Print("np.concatenate:\n",np.concat(z,  y, AXIS_VERT));
    Print("np.dot: ",np.dot(v, v));
    Print("np.dot:\n",np.dot(z, z));
    Print("np.linspace: ",np.linspace(1, 10, 10, true));
    
    Print("np.unique: ",np.unique(v).unique, " count: ",np.unique(v).count);
 }

Ausgabe:

NJ      0       16:34:01.702    Numpy test (US Tech 100,H1)     ------------------------------------
PL      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.arange: [0,1,2,3,4,5,6,7,8,9]
LG      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.arange: [1,3,5,7,9]
QR      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.flatten: [1,2,3,4,5,6,7,8,9,10]
QO      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.ravel: [1,2,3,4,5,6,7,8,9,10]
EF      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.reshape: [[1,2]
NL      0       16:34:01.703    Numpy test (US Tech 100,H1)      [3,4]
NK      0       16:34:01.703    Numpy test (US Tech 100,H1)      [5,6]
NQ      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8]
HF      0       16:34:01.703    Numpy test (US Tech 100,H1)      [9,10]]
HD      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.reshape: [[1,2,3]
QD      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6]]
OH      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.expnad_dims: [[1,2,3,4,5,6,7,8,9,10]]
PK      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.clip: [3,3,3,4,5,6,7,8,8,8]
FM      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.argsort: [0,1,2,3,4,5,6,7,8,9]
KD      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.sort: [1,2,3,4,5,6,7,8,9,10]
FQ      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.concatenate: [1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6,7,8,9,10]
FS      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.concatenate:
PK      0       16:34:01.703    Numpy test (US Tech 100,H1)     [[1,2,3]
DM      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6]
CJ      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8,9]
IS      0       16:34:01.703    Numpy test (US Tech 100,H1)      [1,2,3]
DH      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6]
PL      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8,9]]
FQ      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.concatenate:
CH      0       16:34:01.703    Numpy test (US Tech 100,H1)     [[1,2,3,1]
KN      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6,1]
KH      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8,9,1]]
JR      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.dot: 385.0
PK      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.dot:
JN      0       16:34:01.703    Numpy test (US Tech 100,H1)     [[30,36,42]
OH      0       16:34:01.703    Numpy test (US Tech 100,H1)      [66,81,96]
RN      0       16:34:01.703    Numpy test (US Tech 100,H1)      [102,126,150]]
RI      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.linspace: [1,2,3,4,5,6,7,8,9,10]
MQ      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.unique: [1,2,3,4,5,6,7,8,9,10] count: [1,1,1,1,1,1,1,1,1,1]


Kodierung von Modellen für maschinelles Lernen von Grund auf mit MQL5-NumPy

Wie ich bereits erklärt habe, ist die NumPy-Bibliothek das Rückgrat vieler Modelle für maschinelles Lernen, die in der Programmiersprache Python implementiert sind, da sie eine große Anzahl von Methoden enthält, die bei Arrays, Matrizen, grundlegender Mathematik und sogar linearer Algebra helfen. Da wir nun einen ähnlichen Abschluss in MQL5 haben, wollen wir versuchen, damit ein einfaches maschinelles Lernmodell von Grund auf zu implementieren.

Am Beispiel eines linearen Regressionsmodells.

Ich habe diesen Code online gefunden. Es handelt sich um ein lineares Regressionsmodell, das in seiner Trainingsfunktion den Gradientenabstieg verwendet.

import numpy as np
from sklearn.metrics import mean_squared_error, r2_score

class LinearRegression:
    def __init__(self, learning_rate=0.01, epochs=1000):
        self.learning_rate = learning_rate
        self.epochs = epochs
        self.weights = None
        self.bias = None

    def fit(self, X, y):
        """
        Train the Linear Regression model using Gradient Descent.
        X: Input features (numpy array of shape [n_samples, n_features])
        y: Target values (numpy array of shape [n_samples,])
        """
        n_samples, n_features = X.shape
        self.weights = np.zeros(n_features)
        self.bias = 0

        for _ in range(self.epochs):
            y_pred = np.dot(X, self.weights) + self.bias  # Predictions
            
            # Compute Gradients
            dw = (1 / n_samples) * np.dot(X.T, (y_pred - y))
            db = (1 / n_samples) * np.sum(y_pred - y)
            
            # Update Parameters
            self.weights -= self.learning_rate * dw
            self.bias -= self.learning_rate * db

    def predict(self, X):
        """
        Predict output for the given input X.
        """
        return np.dot(X, self.weights) + self.bias

# Example Usage
if __name__ == "__main__":
    # Sample Data (X: Input features, y: Target values)
    X = np.array([[1], [2], [3], [4], [5]])  # Feature
    y = np.array([2, 4, 6, 8, 10])           # Target (y = 2x)

    # Create and Train Model
    model = LinearRegression(learning_rate=0.01, epochs=1000)
    model.fit(X, y)

    # Predictions
    y_pred = model.predict(X)

    # Evaluate Model
    print("Predictions:", y_pred)
    print("MSE:", mean_squared_error(y, y_pred))
    print("R² Score:", r2_score(y, y_pred))

Leistung der Zelle.

Predictions: [2.06850809 4.04226297 6.01601785 7.98977273 9.96352761]
MSE: 0.0016341843485627612
R² Score: 0.9997957269564297

Achten Sie auf die Fit-Funktion, wir haben ein paar NumPy-Methoden in der Trainingsfunktion. Da wir die gleichen Funktionen auch in CNumpy haben, sollten wir die gleiche Implementierung in MQL5 vornehmen.

#include <MALE5\Numpy\Numpy.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
    // Sample Data (X: Input features, y: Target values)
    matrix X = {{1}, {2}, {3}, {4}, {5}};
    vector y = {2, 4, 6, 8, 10};

    // Create and Train Model
    CLinearRegression model(0.01, 1000);
    model.fit(X, y);

    // Predictions
    vector y_pred = model.predict(X);

    // Evaluate Model
    Print("Predictions: ", y_pred);
    Print("MSE: ", y_pred.RegressionMetric(y, REGRESSION_MSE));
    Print("R² Score: ", y_pred.RegressionMetric(y_pred, REGRESSION_R2));
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CLinearRegression
  {
protected:

   CNumpy np;
   double m_learning_rate;
   uint m_epochs;
   vector weights;
   double bias;
   
public:
                     CLinearRegression(double learning_rate=0.01, uint epochs=1000);
                    ~CLinearRegression(void);
                    
                    void fit(const matrix &x, const vector &y);
                    vector predict(const matrix &X);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CLinearRegression::CLinearRegression(double learning_rate=0.01, uint epochs=1000):
 m_learning_rate(learning_rate),
 m_epochs(epochs)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CLinearRegression::~CLinearRegression(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CLinearRegression::fit(const matrix &x, const vector &y)
 {
   ulong n_samples = x.Rows(), n_features = x.Cols();
   this.weights = np.zeros((uint)n_features);
   this.bias = 0.0;

//---
   
   for (uint i=0; i<m_epochs; i++)
      {
        matrix temp = np.dot(x, this.weights);
        vector y_pred = np.flatten(temp) + bias;
        
        // Compute Gradients
        
        temp = np.dot(x.Transpose(), (y_pred - y));
                
        vector dw = (1.0 / (double)n_samples) * np.flatten(temp);
        double db = (1.0 / (double)n_samples) * np.sum(y_pred - y);

        // Update Parameters
        
        this.weights -= this.m_learning_rate * dw;
        this.bias -= this.m_learning_rate * db;
      }
   
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CLinearRegression::predict(const matrix &X)
 {
   matrix temp = np.dot(X, this.weights);
   
   return np.flatten(temp) + this.bias;
 }

Ausgabe:

RD      0       18:15:22.911    Linear regression from scratch (US Tech 100,H1) Predictions: [2.068508094061713,4.042262972785917,6.01601785151012,7.989772730234324,9.963527608958529]
KH      0       18:15:22.911    Linear regression from scratch (US Tech 100,H1) MSE: 0.0016341843485627612
RQ      0       18:15:22.911    Linear regression from scratch (US Tech 100,H1) R² Score: 1.0

Großartig, wir haben mit diesem Modell die gleichen Ergebnisse erzielt wie mit dem Python-Code.


Was nun?

Sie verfügen über eine leistungsstarke Bibliothek und eine Sammlung wertvoller Methoden, die zur Erstellung unzähliger maschineller Lern- und statistischer Algorithmen in der Programmiersprache Python verwendet wurden. Nichts hält Sie davon ab, ausgefeilte Handelsroboter zu programmieren, die mit komplexen Berechnungen ausgestattet sind, wie man sie häufig in Python sieht.

Wie es steht derzeit die Bibliothek fehlt noch die meisten Funktionen, wie es würde mich Monate dauern, um alles zu schreiben, so fühlen Sie sich frei, eine Ihrer eigenen hinzufügen, die Funktionen darin vorhanden sind diejenigen, die ich oft verwenden oder finden mich verwenden wollen, wie ich mit ML-Algorithmen in MQL5 arbeiten.

Die Python-Syntax in MQL5 kann manchmal verwirrend sein. Zögern Sie daher nicht, die Funktionsnamen so zu ändern, wie es für Sie am besten passt.

Peace out.

Bleiben Sie dran und tragen Sie zur Entwicklung von Algorithmen für maschinelles Lernen für die Sprache MQL5 in diesem GitHub repository bei.


Tabelle der Anhänge

Dateiname Beschreibung
Include\Numpy.mqh NumPy MQL5 Klon, alle NumPy Methoden für MQL5 können in dieser Datei gefunden werden.
Scripts\Linear regression from scratch.mq5 Ein Skript, in dem das Beispiel der linearen Regression mit CNumpy implementiert wird.
Scripts\Numpy test.mq5  Dieses Skript ruft alle Methoden von Numpy.mqh zu Testzwecken auf.

Es ist eine Spielwiese für alle in diesem Artikel besprochenen Methoden.

Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/17469

Beigefügte Dateien |
ZIP herunterladen
attachments.zip (16 KB)

Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum
Automatisieren von Handelsstrategien in MQL5 (Teil 14): Stapelstrategie für den Handel mit statistischen MACD-RSI-Methoden Automatisieren von Handelsstrategien in MQL5 (Teil 14): Stapelstrategie für den Handel mit statistischen MACD-RSI-Methoden
In diesem Artikel stellen wir die Stapelstrategie des Handels (Trading-Layering) vor, die MACD- und RSI-Indikatoren mit statistischen Methoden kombiniert, um den dynamischen Handel in MQL5 zu automatisieren. Wir untersuchen die Architektur dieses kaskadierenden Ansatzes, erläutern seine Implementierung anhand wichtiger Codesegmente und geben dem Leser eine Anleitung für die Backtests, um die Leistung zu optimieren. Abschließend wird das Potenzial der Strategie hervorgehoben und die Voraussetzungen für weitere Verbesserungen im automatisierten Handel geschaffen.
Vom Neuling zum Experten: Support and Resistance Strength Indicator (SRSI) Vom Neuling zum Experten: Support and Resistance Strength Indicator (SRSI)
In diesem Artikel erfahren Sie, wie Sie die MQL5-Programmierung nutzen können, um Marktniveaus zu bestimmen und zwischen schwächeren und stärkeren Kursniveaus zu unterscheiden. Wir werden einen funktionierenden Support and Resistance Strength Indicator (SRSI) entwickeln.
MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 57): Überwachtes Lernen mit gleitendem Durchschnitt und dem stochastischen Oszillator MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 57): Überwachtes Lernen mit gleitendem Durchschnitt und dem stochastischen Oszillator
Der gleitende Durchschnitt und der Stochastik-Oszillator sind sehr gängige Indikatoren, die von manchen Händlern aufgrund ihres verzögerten Charakters nicht oft verwendet werden. In einer dreiteiligen Miniserie, die sich mit den drei wichtigsten Formen des maschinellen Lernens befasst, gehen wir der Frage nach, ob die Voreingenommenheit gegenüber diesen Indikatoren gerechtfertigt ist, oder ob sie vielleicht einen Vorteil haben. Wir führen unsere Untersuchung mit Hilfe eines Assistenten durch, der Expert Advisors zusammenstellt.
Erstellen eines Handelsadministrator-Panels in MQL5 (Teil IX): Code Organisation (V): Die Klasse AnalyticsPanel Erstellen eines Handelsadministrator-Panels in MQL5 (Teil IX): Code Organisation (V): Die Klasse AnalyticsPanel
In dieser Diskussion wird untersucht, wie man Echtzeit-Marktdaten und Handelskontoinformationen abruft, verschiedene Berechnungen durchführt und die Ergebnisse in einem nutzerdefinierten Panel anzeigt. Um dies zu erreichen, werden wir die Entwicklung der Klasse AnalyticsPanel vertiefen, die all diese Funktionen, einschließlich der Panel-Erstellung, kapselt. Dieser Aufwand ist Teil unserer kontinuierlichen Erweiterung des New Admin Panel EA, mit der wir fortschrittliche Funktionalitäten unter Verwendung modularer Designprinzipien und Best Practices für die Codeorganisation einführen.