Datenwissenschaft und maschinelles Lernen - Neuronales Netzwerk (Teil 01): Entmystifizierte Feed Forward Neurale Netzwerke
„...müde, zu viel zu wissen und zu wenig zu verstehen.“
- Jan Karon, Aufruhr in Holly Springs
Einführung
Neuronale Netze klingen wie diese schicken neuen Dinger, die einen Weg zu einem perfekten Handelssystem, oder einem heiligen Gral, zu bauen scheinen. Viele Händler sind von den Programmen der neuronalen Netzen wie betäubt. Sie scheinen gut, Marktbewegungen vorhersagen zu können und im Grunde für jede beliebige Aufgabe.
Auch ich glaube, dass sie ein enormes Potenzial haben, wenn es darum geht, Vorhersagen oder Klassifizierungen auf der Grundlage von untrainierten /noch nie gesehenen Daten zu treffen.
So gut sie auch sein mögen, sie müssen von jemandem konstruiert werden, der sich damit auskennt, und manchmal müssen sie optimiert werden, um sicherzustellen, dass nicht nur das mehrschichtige Perzeptron die richtige Architektur hat, sondern auch die Art des Problems diejenige ist, für die ein neuronales Netzwerk benötigt wird und nicht nur ein lineares oder logistisches Regressionsmodell oder eine andere maschinelle Lerntechnik.
Neuronale Netze sind ein umfassenderes Thema, ebenso wie das maschinelle Lernen im Allgemeinen. Deshalb habe ich mich entschlossen, eine Unterüberschrift für neuronale Netze hinzuzufügen, da ich andere Aspekte des maschinellen Lernens in der anderen Unterüberschrift der Serie behandeln werde.
In diesem Artikel werden wir uns die Grundlagen eines neuronalen Netzwerks ansehen und einige der grundlegenden Fragen beantworten, die meiner Meinung nach für einen ML-Enthusiasten wichtig sind, damit er dieses Thema beherrscht.
Was ist ein künstliches neuronales Netz?
Künstliche neuronale Netze (KNN), gewöhnlich als neuronale Netze bezeichnet, sind Computersysteme, die sich an den biologischen neuronalen Netzen orientieren, die das Gehirn von Tieren bilden.
Mehrschichtiges Perzeptron vs. Tiefes Neuronales Netz
Wenn von neuronalen Netzen die Rede ist, hört man oft den Begriff Mehrschicht-Perzeptron (multi-layer perceptron, MLP). Dabei handelt es sich um die gängigste Form eines neuronalen Netzes, das aus einer Eingabeschicht, einer verborgenen Schicht und weniger als drei verborgenen Schichten besteht.
Aufgrund ihrer Einfachheit benötigen sie kurze Trainingszeiten, um die Präsentationen in den Daten zu lernen und eine Ausgabe zu erzeugen.
Anwendungen:
MLPs werden in der Regel für Daten verwendet, die nicht linear trennbar sind, wie z. B. bei der Regressionsanalyse.
Aufgrund ihrer Einfachheit eignen sie sich am besten für komplexe Klassifizierungsaufgaben und prädiktive Modellierung. Sie wurden bereits für maschinelle Übersetzungen, Wettervorhersagen, Betrugserkennung, Börsenprognosen, Bonitätsprognosen und viele andere denkbare Aspekte eingesetzt.
Tiefe neuronale Netze hingegen haben eine gemeinsame Struktur, der einzige Unterschied besteht darin, dass sie zu viele verborgene Schichten umfassen. Wenn Ihr Netz mehr als drei (3) verborgene Schichten hat, gilt es als tiefes neuronales Netz.
Aufgrund ihrer Komplexität benötigen sie lange Zeiträume, um das Netz auf den Eingabedaten zu trainieren. Außerdem erfordern sie leistungsstarke Computer mit speziellen Verarbeitungseinheiten wie Tensor Processing Units (TPU) und Neural Processing Units (NPU).
Anwendungen:
DNNs sind aufgrund ihrer tiefen Schichten leistungsstarke Algorithmen und werden daher in der Regel für die Bearbeitung komplexer Rechenaufgaben eingesetzt, zu denen auch das Computersehen gehört.
Tabelle der Unterschiede:
| MLP | DNN |
|---|---|
| Geringe Anzahl von verborgenen Schichten | Hohe Anzahl von verborgenen Schichten |
| Kurze Trainingszeiten | Längere Trainingszeiten |
| GPU-fähiges Gerät ist ausreichend | TPU-Freigabegerät ist ausreichend |
Schauen wir uns nun die Arten von neuronalen Netzen an.
Es gibt viele Arten von neuronalen Netzen, aber grob lassen sie sich in drei (3) Hauptklassen einteilen;
- Neuronale Netze mit Feed Forward
- Convolutional Neuronale Netze
- Rekurrente Neuronale Netze
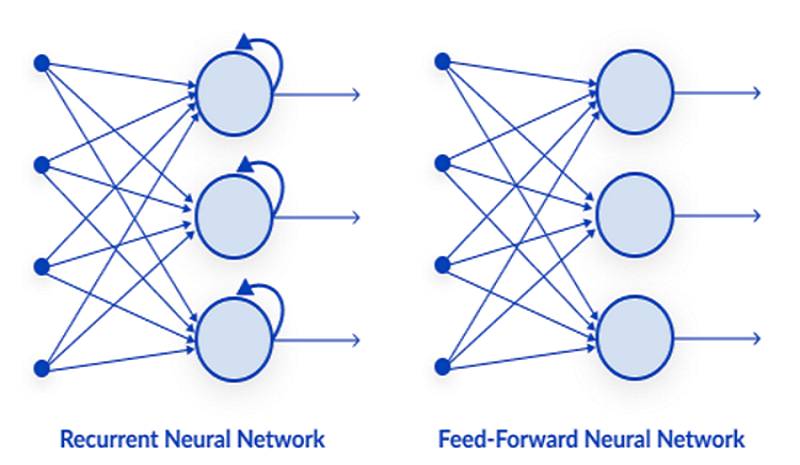
01: Neuronales Netz mit Feed Forward:
Dies ist eine der einfachsten Arten von neuronalen Netzen. In einem neuronalen Feed-Forward-Netzwerk durchlaufen die Daten die verschiedenen Eingangsknoten, bis sie einen Ausgangsknoten erreichen.
Im Gegensatz zur Backpropagation, bei der sich die Daten nur in eine Richtung bewegen.
Backpropagation führt im neuronalen Netz die gleichen Prozesse aus wie Feed Forward, bei dem Daten von der Eingabeschicht an die Ausgabeschicht weitergeleitet werden, mit der Ausnahme, dass es bei Backpropagation, nachdem die Ausgabe des Netzes die Ausgabeschicht erreicht hat, den tatsächlichen Wert einer Klasse zu sehen bekommt und ihn mit dem Wert vergleicht, den es vorhergesagt hat. Dieser Algorithmus ist selbstlernend.
02: Rekurrentes neuronales Netz
Ein rekurrentes neuronales Netz ist eine Art künstliches neuronales Netz, bei dem die Ausgabe einer bestimmten Schicht gespeichert und in die Eingabeschicht zurückgeführt wird, was die Vorhersage des Ergebnisses der Schicht erleichtert.
Rekurrente neuronale Netze werden verwendet, um Probleme zu lösen, die mit folgenden Themen zusammenhängen
- Zeitreihendaten
- Textdaten
- Audio-Daten
Der häufigste Verwendungszweck von Textdaten ist beispielsweise die Empfehlung der nächsten Wörter, die eine KI sprechen soll: Wie + geht + es + Ihnen +?
03: Convolution Neural Network (CNN)
CNNs sind in der Deep-Learning-Community in aller Munde und werden vor allem in Projekten zur Bild- und Videoverarbeitung eingesetzt.
Zum Beispiel:
Die KI zur Bilderkennung und -klassifizierung besteht aus neuronalen Faltungsnetzen.
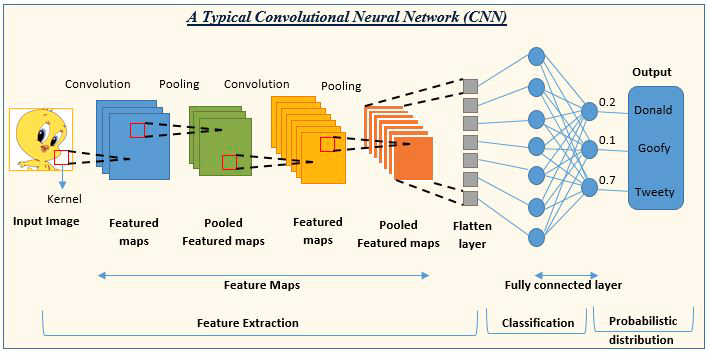
Bildquelle: analyticsvidhya.com
Nachdem wir nun die Arten von neuronalen Netzen kennengelernt haben, wollen wir uns nun dem Hauptthema dieses Artikels widmen, den Feed Forward Neural Networks.
Feed Forward Neural Networks
Im Gegensatz zu anderen, komplexeren Arten von neuronalen Netzen gibt es keine Backpropagation, d. h. die Daten fließen bei dieser Art von neuronalem Netz nur in eine Richtung. Ein neuronales Netz mit Feed Forward kann eine einzelne oder mehrere verborgene Schichten haben.
Sehen wir uns an, was dieses Netzwerk ausmacht
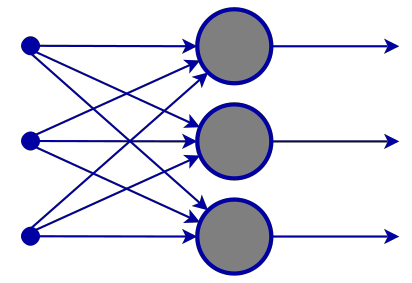
Eingabeschicht
Auf den Bildern eines neuronalen Netzes sieht es so aus, als gäbe es eine Eingabeschicht, aber tief im Inneren ist eine Eingabeschicht nur eine Präsentation. In der Eingabeschicht werden keine Berechnungen durchgeführt.
Verborgene Schicht
Die verborgene Schicht ist der Ort, an dem der Großteil der Arbeit im Netz geleistet wird.
Um die Dinge zu verdeutlichen, lassen Sie uns den zweiten verborgenen Schichtknoten zerlegen.
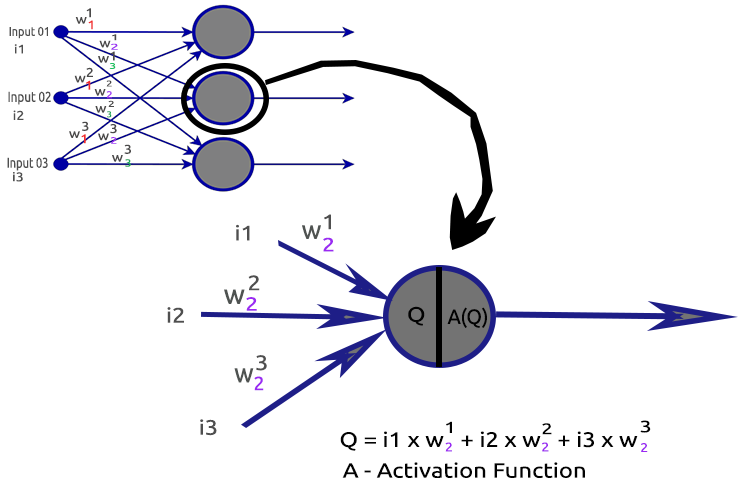
Beteiligte Prozesse:
- Ermitteln des Punktprodukts der Eingaben und ihrer jeweiligen Gewichte
- Addition des erhaltenen Punktprodukts mit der Verzerrung
- Das Ergebnis der zweiten Prozedur wird an die Aktivierungsfunktion übergeben
Was ist Bias (Voreingenommenheit)?
Mit der Verzerrung können Sie die lineare Regression nach oben und unten verschieben, um die Vorhersagelinie besser an die Daten anzupassen. Dies entspricht dem Achsenabschnitt in einer linearen Regressionslinie.
Sie werden diesen Parameter unter dem Abschnitt MLP mit einem einzelnen Knoten in einer verborgenen Schicht ist ein lineares Regressionsmodell gut verstehen.
Die Bedeutung der Voreingenommenheit wird in dieser Website Stack gut erklärt.
Was sind die Gewichte?
Die Gewichte spiegeln wider, wie wichtig die Eingabe ist, sie sind die Koeffizienten der Gleichung, die Sie zu lösen versuchen. Negative Gewichte verringern den Wert der Ausgabe und umgekehrt.
Wenn ein neuronales Netz auf einem Trainingsdatensatz trainiert wird, wird es mit einem Satz von Gewichten initialisiert. Diese Gewichte werden dann während des Trainingszeitraums optimiert und der optimale Wert der Gewichte wird ermittelt.
Was ist eine Aktivierungsfunktion?
Eine Aktivierungsfunktion ist nichts anderes als eine mathematische Funktion, die eine Eingabe annimmt und eine Ausgabe erzeugt.
Arten von Aktivierungsfunktionen
Es gibt viele Aktivierungsfunktionen und ihre Varianten, aber hier sind die am häufigsten verwendeten;
- Relu
- Sigmoid
- TanH
- Softmax
Es ist sehr wichtig zu wissen, welche Aktivierungsfunktion an welcher Stelle zu verwenden ist. Ich kann Ihnen nicht sagen, wie oft ich im Internet Artikel gesehen habe, in denen vorgeschlagen wurde, eine Aktivierungsfunktion an einer Stelle zu verwenden, an der sie irrelevant war.
01: RELU
RELU steht für Rektifizierte Lineare Aktivierungsfunktion.
Dies ist die am häufigsten verwendete Aktivierungsfunktion in neuronalen Netzen. Sie ist die einfachste von allen, leicht zu kodieren und die Ausgabe leicht zu interpretieren, deshalb ist sie so beliebt.
> Diese Funktion gibt die Eingabe direkt aus, wenn die Eingabe eine positive Zahl ist, andernfalls gibt sie Null aus.
Hier ist die Logik
if x < 0 : return 0
else return x
Diese Funktion kann besser zur Lösung von Regressionsproblemen verwendet werden
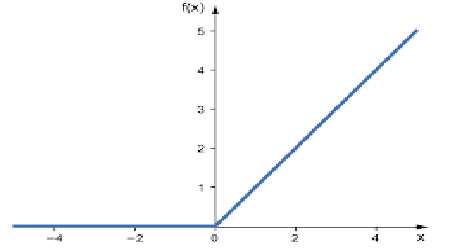
Seine Leistung reicht von Null bis zum plus Unendlich.
der MQL5-Code ist:
double CNeuralNets::Relu(double z) { if (z < 0) return(0); else return(z); }
RELU löst das Problem des verschwindenden Gradienten, unter dem Sigmoid und TanH leiden (wir werden im Artikel über Backpropagation sehen, was es damit auf sich hat).
02: Sigmoid
Kommt Ihnen das bekannt vor? Erinnern Sie sich an die logistische Regression!
Ihre Formel lautet wie folgt.
![]()
Diese Funktion ist besser für Klassifizierungsprobleme geeignet, insbesondere für die Klassifizierung von nur einer oder zwei Klassen.
> Seine Ausgabe reicht von Null bis Eins (Wahrscheinlichkeitsterme).
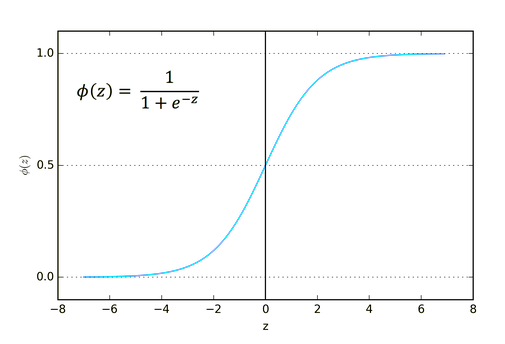
Ihr Netzwerk hat zum Beispiel zwei Knoten in der Ausgabe; der erste Knoten ist für eine Katze und der andere für einen Hund. Sie könnten die Ausgabe wählen, wenn die Ausgabe des ersten Knotens größer als 0,5 ist, um anzuzeigen, dass es sich um eine Katze handelt, und das Gleiche aber umgekehrt für einen Hund.
Sein MQL5-Code lautet:
double CNeuralNets::Sigmoid(double z) { return(1.0/(1.0+MathPow(e,-z))); }
03: TanH
Die hyperbolische Tangensfunktion.
Sie entspricht durch folgender Formel:
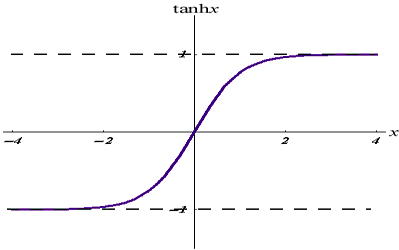
Der Graph sieht wie folgt aus,
Diese Aktivierungsfunktion ist ähnlich wie die Sigmoidfunktion, aber besser.
> Seine Ausgabe reicht von -1 bis 1.
Diese Funktion sollte besser in neuronalen Netzen zur Klassifizierung in mehreren Klassen verwendet werden.
Der MQL5-Code ist unten angegeben:
double CNeuralNets::tanh(double z) { return((MathPow(e,z) - MathPow(e,-z))/(MathPow(e,z) + MathPow(e,-z))); }
04: SoftMax
Jemand fragte einmal, warum es für die SoftMax-Funktion keinen Graphen gibt. Im Gegensatz zu anderen Aktivierungsfunktionen wird SoftMax nicht in den verborgenen Schichten, sondern nur in der Ausgabeschicht verwendet und sollte nur dann eingesetzt werden, wenn Sie die Ausgabe eines neuronalen Netzes mit mehreren Klassen in Wahrscheinlichkeitsterme umwandeln möchten.
Der SoftMax sagt eine multinomiale Wahrscheinlichkeitsverteilung voraus.
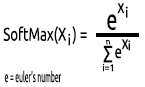
Beispiel: Die Ausgaben eines neuronalen Regressionsnetzes lauten [1,3,2]. Wendet man die SoftMax-Funktion auf diese Ausgabe an, so erhält man die Ausgabe [0,09003, 0,665240, 0,244728].
> Die Ausgabe dieser Funktion reicht von 0 bis 1
Sein MQL5-Code wird sein,
void CNeuralNets::SoftMax(double &Nodes[]) { double TempArr[]; ArrayCopy(TempArr,Nodes); ArrayFree(Nodes); double proba = 0, sum=0; for (int j=0; j<ArraySize(TempArr); j++) sum += MathPow(e,TempArr[j]); for (int i=0; i<ArraySize(TempArr); i++) { proba = MathPow(e,TempArr[i])/sum; Nodes[i] = proba; } ArrayFree(TempArr); }
Da wir nun wissen, woraus ein einzelnes Neuron einer verborgenen Schicht besteht, wollen wir es codieren:
void CNeuralNets::Neuron(int HLnodes, double bias, double &Weights[], double &Inputs[], double &Outputs[] ) { ArrayResize(Outputs,HLnodes); for (int i=0, w=0; i<HLnodes; i++) { double dot_prod = 0; for(int j=0; j<ArraySize(Inputs); j++, w++) { if (m_debug) printf("i %d w %d = input %.2f x weight %.2f",i,w,Inputs[j],Weights[w]); dot_prod += Inputs[j]*Weights[w]; } Outputs[i] = ActivationFx(dot_prod+bias); } }
Innerhalb von ActivationFx() haben wir die Wahl, welche Aktivierungsfunktion beim Aufruf des NeuralNets-Konstruktors gewählt wurde
double CNeuralNets::ActivationFx(double Q) { switch(A_fx) { case SIGMOID: return(Sigmoid(Q)); break; case TANH: return(tanh(Q)); break; case RELU: return(Relu(Q)); break; default: Print("Unknown Activation Function"); break; } return(0); }
Weitere Erläuterungen zum Code:
Die Funktion Neuron() ist nicht nur ein einzelner Knoten innerhalb der verborgenen Schicht, sondern alle Operationen einer verborgenen Schicht werden innerhalb dieser einen Funktion durchgeführt. Die Knoten in allen verborgenen Schichten haben die gleiche Größe wie der Eingabeknoten bis hin zum endgültigen Ausgabeknoten. Ich habe diese Struktur gewählt, weil ich im Begriff bin, eine Klassifizierung mit diesem neuronalen Netzwerk auf einem zufällig generierten Datensatz durchzuführen.
Die untenstehende Funktion FeedForwardMLP() ist eine NxN-Struktur, d.h. wenn Sie 3 Eingabeknoten haben und sich für 3 verborgene Schichten entschieden haben, haben Sie 3 verborgene Knoten auf jeder verborgenen Schicht (siehe Abbildung).
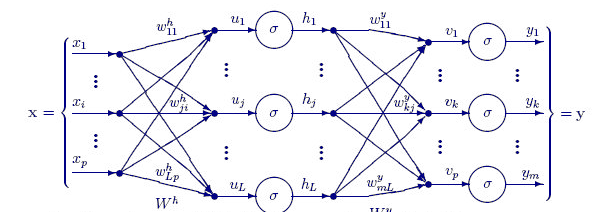
Hier ist die Funktion FeedForwardMLP();
void CNeuralNets::FeedForwardMLP(int HiddenLayers, double &MLPInputs[], double &MLPWeights[], double &bias[], double &MLPOutput[]) { double L_weights[], L_inputs[], L_Out[]; ArrayCopy(L_inputs,MLPInputs); int HLnodes = ArraySize(MLPInputs); int no_weights = HLnodes*ArraySize(L_inputs); int weight_start = 0; for (int i=0; i<HiddenLayers; i++) { if (m_debug) printf("<< Hidden Layer %d >>",i+1); ArrayCopy(L_weights,MLPWeights,0,weight_start,no_weights); Neuron(HLnodes,bias[i],L_weights,L_inputs,L_Out); ArrayCopy(L_inputs,L_Out); ArrayFree(L_Out); ArrayFree(L_weights); weight_start += no_weights; } if (use_softmax) SoftMax(L_inputs); ArrayCopy(MLPOutput,L_inputs); if (m_debug) { Print("\nFinal MLP output(s)"); ArrayPrint(MLPOutput,5); } }
Die Operationen zur Ermittlung des Punktprodukts in einem neuronalen Netz könnten mit Matrixoperationen durchgeführt werden, aber um die Dinge in diesem ersten Artikel übersichtlich und für jeden verständlich zu halten, habe ich mich für die Schleifenmethode entschieden, die wir beim nächsten Mal für die Matrixmultiplikation verwenden werden.
Nachdem Sie nun die Architektur gesehen haben, die ich für den Aufbau der Bibliothek standardmäßig gewählt habe, stellt sich nun die Frage nach der Architektur neuronaler Netze.
Wenn Sie bei Google nach Bildern eines neuronalen Netzes suchen, werden Sie mit Tausenden, wenn nicht Zehntausenden von Bildern bombardiert, die verschiedene Strukturen neuronaler Netze zeigen, wie zum Beispiel diese,

Eine Millionen-Dollar-Frage lautet: Was ist die beste Architektur für ein neuronales Netz?
„Niemand liegt so falsch wie der Mann, der alle Antworten kennt“ - Thomas Merton.
Lassen Sie uns die Sache aufschlüsseln, um zu verstehen, was notwendig ist und was nicht.
Die EingabeschichtDie Anzahl der Eingänge, aus denen diese Schicht besteht, sollte der Anzahl der Merkmale (Spalten im Datensatz) entsprechen.
Die Ausgabeschicht
Die Größe (die Anzahl der Neuronen) wird bei einem neuronalen Klassifizierungsnetz durch die Klassen in Ihrem Datensatz bestimmt, bei einem Regressionsproblem wird die Anzahl der Neuronen durch die gewählte Modellkonfiguration bestimmt, eine Ausgabeschicht für einen Regressor ist oft mehr als genug.
Verborgene Schichten
Wenn Ihr Problem nicht so komplex ist, sind ein oder zwei verborgene Schichten mehr als genug, in der Tat sind zwei verborgene Schichten für die meisten Probleme ausreichend.
Aber wie viele Knoten braucht man in jeder verborgenen Schicht?
Ich bin mir nicht sicher, aber ich denke, es hängt von der Leistung ab. Sie als Entwickler sollten verschiedene Knoten ausprobieren, um zu sehen, was für eine bestimmte Art von Problem am besten funktioniert.
Auf stats.stackexchange.com gibt es hier eine großartige Diskussion zu diesem Thema.
Ich denke, dass die gleiche Anzahl von Knoten wie die Eingabeschicht für alle verborgenen Schichten ideal für ein neuronales Feed-Forward-Netz ist, das ist die Konfiguration, die ich meistens verwende.
MLP mit einem einzigen Knoten und einer einzigen verborgenen Schicht ist ein lineares Modell.
Wenn Sie auf die Operationen innerhalb eines einzelnen Knotens einer verborgenen Schicht eines neuronalen Netzes achten, werden Sie dies feststellen;
Q = wi * Ii + b
In der Zwischenzeit lautet die lineare Regressionsgleichung;
Y = mi * xi + c
Fällt Ihnen eine Ähnlichkeit auf? Theoretisch handelt es sich dabei um den gleichen Vorgang, nämlich den linearen Regressor, womit wir wieder bei der Bedeutung des Bias einer verborgenen Schicht wären. Der Bias ist eine Konstante für das lineare Modell mit der Aufgabe, die Flexibilität unseres Modells zur Anpassung an den gegebenen Datensatz zu erhöhen; ohne diesen Bias gehen alle Modelle zwischen der x- und y-Achse bei Null (0) durch.

Beim Training des neuronalen Netzes werden die Gewichte und die Verzerrungen aktualisiert. Die Parameter, die die geringsten Fehler für unser Modell ergeben, werden beibehalten und im Testdatensatz gespeichert.
Lassen Sie mich nun ein MLP für die Klassifizierung in zwei Klassen erstellen, um die Punkte zu verdeutlichen.
Zuvor möchte ich einen Zufallsdatensatz mit gekennzeichneten Stichproben generieren, die wir durch unser neuronales Netz sehen werden. Die folgende Funktion erstellt einen Zufallsdatensatz, wobei die zweite Stichprobe mit 5 und die erste mit 2 multipliziert wird, um Daten in verschiedenen Größenordnungen zu erhalten
void MakeBlobs(int size=10) { ArrayResize(data_blobs,size); for (int i=0; i<size; i++) { data_blobs[i].sample_1 = (i+1)*(2); data_blobs[i].sample_2 = (i+1)*(5); data_blobs[i].class_ = (int)round(nn.MathRandom(0,1)); } }
Wenn ich den Datensatz drucke, wird folgendes ausgegeben,
QK 0 18:27:57.298 TestScript (EURUSD,M1) CNeural Nets Initialized activation = SIGMOID UseSoftMax = No IR 0 18:27:57.298 TestScript (EURUSD,M1) [sample_1] [sample_2] [class_] LH 0 18:27:57.298 TestScript (EURUSD,M1) [0] 2.0000 5.0000 0 GG 0 18:27:57.298 TestScript (EURUSD,M1) [1] 4.0000 10.0000 0 NL 0 18:27:57.298 TestScript (EURUSD,M1) [2] 6.0000 15.0000 1 HJ 0 18:27:57.298 TestScript (EURUSD,M1) [3] 8.0000 20.0000 0 HQ 0 18:27:57.298 TestScript (EURUSD,M1) [4] 10.0000 25.0000 1 OH 0 18:27:57.298 TestScript (EURUSD,M1) [5] 12.0000 30.0000 1 JF 0 18:27:57.298 TestScript (EURUSD,M1) [6] 14.0000 35.0000 0 DL 0 18:27:57.298 TestScript (EURUSD,M1) [7] 16.0000 40.0000 1 QK 0 18:27:57.298 TestScript (EURUSD,M1) [8] 18.0000 45.0000 0 QQ 0 18:27:57.298 TestScript (EURUSD,M1) [9] 20.0000 50.0000 0
Als Nächstes werden zufällige Gewichtswerte und der Bias generiert,
generate_weights(weights,ArraySize(Inputs));
generate_bias(biases);
Hier ist die Ausgabe,
RG 0 18:27:57.298 TestScript (EURUSD,M1) weights QS 0 18:27:57.298 TestScript (EURUSD,M1) 0.7084 -0.3984 0.6182 0.6655 -0.3276 0.8846 0.5137 0.9371 NL 0 18:27:57.298 TestScript (EURUSD,M1) biases DD 0 18:27:57.298 TestScript (EURUSD,M1) -0.5902 0.7384
Schauen wir uns nun die gesamten Vorgänge in der Hauptfunktion unseres Skripts an,
#include "NeuralNets.mqh"; CNeuralNets *nn; input int batch_size =10; input int hidden_layers =2; data data_blobs[]; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- nn = new CNeuralNets(SIGMOID); MakeBlobs(batch_size); ArrayPrint(data_blobs); double Inputs[],OutPuts[]; ArrayResize(Inputs,2); ArrayResize(OutPuts,2); double weights[], biases[]; generate_weights(weights,ArraySize(Inputs)); generate_bias(biases); Print("weights"); ArrayPrint(weights); Print("biases"); ArrayPrint(biases); for (int i=0; i<batch_size; i++) { Print("Dataset Iteration ",i); Inputs[0] = data_blobs[i].sample_1; Inputs[1]= data_blobs[i].sample_2; nn.FeedForwardMLP(hidden_layers,Inputs,weights,biases,OutPuts); } delete(nn); }
Dinge, die man beachten sollte:
- Die Anzahl der Bias ist gleich der Anzahl der verborgenen Schichten.
- Gesamtzahl der Gewichte = Anzahl der Eingänge zum Quadrat multipliziert mit der Anzahl der verborgenen Schichten. Dies wurde dadurch möglich, dass unser Netz die gleiche Anzahl von Knoten hat wie die Eingabeschicht/vorherige Schicht des Netzes (alle Schichten haben die gleiche Anzahl von Knoten von der Eingabe bis zur Ausgabe).
- Es gilt das gleiche Prinzip: Wenn Sie 3 Eingangsknoten haben, haben alle verborgenen Schichten 3 Knoten, mit Ausnahme der letzten Schicht, deren Handhabung wir gleich sehen werden.
Wenn Sie sich den nach dem Zufallsprinzip generierten Datensatz ansehen, werden Sie feststellen, dass es zwei Eingabemerkmale/Spalten im Datensatz gibt und ich mich für 2 verborgene Schichten entschieden habe. Hier ist der kurze Überblick in unseren Protokollen, wie unser Modell die Berechnungen durchführt (unterdrücken Sie diese Protokolle, indem Sie den Debug-Modus im Code auf false setzen).
NL 0 18:27:57.298 TestScript (EURUSD,M1) Dataset Iteration 0 EJ 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 1 >> GO 0 18:27:57.298 TestScript (EURUSD,M1) NS 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 EI 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 2.00000 x weight 0.70837 FQ 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 5.00000 x weight -0.39838 QP 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product -0.57513 + bias -0.590 = -1.16534 RH 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.23770 CQ 0 18:27:57.298 TestScript (EURUSD,M1) OE 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 CO 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 2.00000 x weight 0.61823 FI 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 5.00000 x weight 0.66553 PN 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 4.56409 + bias -0.590 = 3.97388 GM 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.98155 DI 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 2 >> GL 0 18:27:57.298 TestScript (EURUSD,M1) NF 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 FH 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 0.23770 x weight -0.32764 ID 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 0.98155 x weight 0.88464 QO 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 0.79044 + bias 0.738 = 1.52884 RK 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.82184 QG 0 18:27:57.298 TestScript (EURUSD,M1) IH 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 DQ 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 0.23770 x weight 0.51367 CJ 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 0.98155 x weight 0.93713 QJ 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 1.04194 + bias 0.738 = 1.78034 JP 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.85574 EI 0 18:27:57.298 TestScript (EURUSD,M1) GS 0 18:27:57.298 TestScript (EURUSD,M1) Final MLP output(s) OF 0 18:27:57.298 TestScript (EURUSD,M1) 0.82184 0.85574 CN 0 18:27:57.298 TestScript (EURUSD,M1) Dataset Iteration 1 KH 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 1 >> EM 0 18:27:57.298 TestScript (EURUSD,M1) DQ 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 QH 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 4.00000 x weight 0.70837 PD 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 10.00000 x weight -0.39838 HR 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product -1.15027 + bias -0.590 = -1.74048 DJ 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.14925 OP 0 18:27:57.298 TestScript (EURUSD,M1) CK 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 MN 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 4.00000 x weight 0.61823 NH 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 10.00000 x weight 0.66553 HI 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 9.12817 + bias -0.590 = 8.53796 FO 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.99980 RG 0 18:27:57.298 TestScript (EURUSD,M1) << Hidden Layer 2 >> IR 0 18:27:57.298 TestScript (EURUSD,M1) PD 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 1 RN 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 0 = input 0.14925 x weight -0.32764 HF 0 18:27:57.298 TestScript (EURUSD,M1) i 0 w 1 = input 0.99980 x weight 0.88464 EM 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 0.83557 + bias 0.738 = 1.57397 EL 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.82835 KE 0 18:27:57.298 TestScript (EURUSD,M1) GN 0 18:27:57.298 TestScript (EURUSD,M1) HLNode 2 LS 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 2 = input 0.14925 x weight 0.51367 FL 0 18:27:57.298 TestScript (EURUSD,M1) i 1 w 3 = input 0.99980 x weight 0.93713 KH 0 18:27:57.298 TestScript (EURUSD,M1) dot_Product 1.01362 + bias 0.738 = 1.75202 IR 0 18:27:57.298 TestScript (EURUSD,M1) Activation function Output =0.85221 OH 0 18:27:57.298 TestScript (EURUSD,M1) IM 0 18:27:57.298 TestScript (EURUSD,M1) Final MLP output(s) MH 0 18:27:57.298 TestScript (EURUSD,M1) 0.82835 0.85221
Achten Sie nun auf die endgültige(n) MLP-Ausgabe(n) für alle Iterationen. Sie werden feststellen, dass die Ausgänge dazu neigen, genau die gleichen Werte zu haben. Dieses Problem hat mehrere Ursachen, wie hier besprochen. Eine davon ist die Verwendung der falschen Aktivierungsfunktion in der Ausgabeschicht, hier kommt die SoftMax-Aktivierungsfunktion ins Spiel,
Nach meinem Verständnis gibt die Sigmoid-Funktion nur dann Wahrscheinlichkeiten zurück, wenn es einen einzigen Knoten in der Ausgabeschicht gibt, der eine Klasse klassifizieren muss. In diesem Fall würden Sie die Ausgabe von Sigmoid benötigen, um zu wissen, ob etwas zu einer bestimmten Klasse gehört oder nicht, aber bei mehreren Klassen ist es eine andere Geschichte. Wenn wir die Ausgänge unserer Endknoten addieren, übersteigt der Wert in den meisten Fällen den Wert 1. Sie wissen also, dass es sich nicht um Wahrscheinlichkeiten handelt, da eine Wahrscheinlichkeit den Wert 1 nicht überschreiten kann.
Wenn wir SoftMax auf die letzte Schicht anwenden, werden die Ausgaben sein;
Ergebnisse der ersten Iteration [0,4915 0,5085], Ergebnisse der zweiten Iteration [0,4940 0,5060]
Sie können die Ergebnisse als [Wahrscheinlichkeit der Zugehörigkeit zu Klasse 0, Wahrscheinlichkeit der Zugehörigkeit zu Klasse 1] interpretieren .
Nun, zumindest haben wir jetzt Wahrscheinlichkeiten, auf die wir uns verlassen können, um etwas Sinnvolles aus unserem Netzwerk zu interpretieren.
Abschließende Überlegungen
Wir sind noch nicht fertig mit dem neuronalen Feed Forward-Netzwerk, aber zumindest haben Sie jetzt ein Verständnis der Theorie und der wichtigsten Dinge, die für Sie hilfreich sein werden, um neuronale Netze in MQL5 zu meistern. Das entworfene neuronale Feedforward-Netzwerk ist dasjenige für Klassifizierungszwecke, was bedeutet, dass die geeigneten Aktivierungsfunktionen sigmoid und tanh sind, je nach den Proben und Klassen, die Sie in Ihrem Datensatz klassifizieren möchten. Die Einführung von Matrizen wird dazu beitragen, dass all diese Operationen dynamisch werden, sodass wir ein sehr standardisiertes neuronales Netz für jede Aufgabe aufbauen können. Das ist das Ziel dieser Artikelserie. Bleiben Sie dran für mehr.
Es ist auch wichtig zu wissen, wann ein neuronales Netz eingesetzt werden sollte, denn nicht alle Aufgaben müssen durch neuronale Netze gelöst werden. Wenn eine Aufgabe durch lineare Regression gelöst werden kann, kann ein lineares Modell das neuronale Netz übertreffen.
GitHub Repo: https://github.com/MegaJoctan/NeuralNetworks-MQL5
Weiterführende Literatur | Bücher | Referenzen
-
Neural Networks for Pattern Recognition (Advanced Texts in Econometrics)
-
Neural Networks: Tricks des Handwerks (Vorlesungsnotizen in Informatik, 7700)
-
Deep Learning (Adaptive Computation and Machine Learning series)
Artikel Referenzen:
-
Datenwissenschaft und maschinelles Lernen (Teil 01): Lineare Regression
-
Datenwissenschaft und maschinelles Lernen (Teil 02): Logistische Regression
-
Datenwissenschaft und maschinelles Lernen (Teil 03): Matrix-Regressionen
-
Datenwissenschaft und maschinelles Lernen (Teil 06): Gradientenverfahren
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/11275
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Lernen Sie, wie man ein Handelssystem mit Bears Power entwirft
Lernen Sie, wie man ein Handelssystem mit Bears Power entwirft
 Metamodelle für maschinelles Lernen und Handel: Ursprünglicher Zeitpunkt der Handelsaufträge
Metamodelle für maschinelles Lernen und Handel: Ursprünglicher Zeitpunkt der Handelsaufträge
 Lernen Sie, wie man ein Handelssystem mit Bulls Power entwirft
Lernen Sie, wie man ein Handelssystem mit Bulls Power entwirft
 Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 19): Neues Auftragssystem (II)
Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 19): Neues Auftragssystem (II)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.

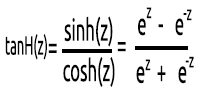
...
Können Sie das erklären? Oder einige Beispiele nennen?
Der Unterschied zwischen der Optimierung mit dem Strategietester und der Optimierung der Parameter des neuronalen Netzes ist das Ziel. Beim Strategietester konzentrieren wir uns auf die Parameter, die die profitabelsten Ergebnisse oder zumindest die gewünschten Handelsergebnisse liefern, was nicht unbedingt bedeutet, dass das neuronale Netz ein gutes Modell hat, das zu diesen Ergebnissen geführt hat.
Einige Leute bevorzugen es, die Gewichte und den Bias als Eingangsparameter von auf neuronalen Netzen basierenden Systemen zu verwenden(grob gesagt Feed Forward), aber ich denke, dass die Optimierung mit dem Strategietester im Grunde genommen das Finden der zufälligen Werte der besten Ergebnisse ist(das Finden der optimalen Ergebnisse hört sich an, als wäre man vom Glück abhängig), während wir uns bei der Optimierung mit Hilfe des stochastischen Gradientenabstiegs auf das Modell mit den geringsten Fehlern in den Vorhersagen bei jedem Schritt zubewegen
Der Unterschied zwischen der Optimierung auf dem Strategietester und der Optimierung der Parameter des neuronalen Netzes ist das Ziel. Auf dem Strategietester konzentrieren wir uns auf die Parameter, die die profitabelsten Ergebnisse oder zumindest die gewünschten Handelsergebnisse liefern, was nicht unbedingt bedeutet, dass das neuronale Netz ein gutes Modell hat, das zu diesen Ergebnissen geführt hat.
Einige Leute bevorzugen es, die Gewichte und den Bias als Eingangsparameter von auf neuronalen Netzen basierenden Systemen zu verwenden(grob gesagt Feed Forward), aber ich denke, dass die Optimierung mit dem Strategietester im Grunde genommen das Finden der zufälligen Werte der besten Ergebnisse ist(das Finden der optimalen Ergebnisse hört sich an, als wäre man vom Glück abhängig), während wir uns bei der Optimierung mit Hilfe des stochastischen Gradientenabstiegs auf das Modell mit den geringsten Fehlern in den Vorhersagen bei jedem Schritt zubewegen
Ich danke Ihnen für Ihre Antwort.
Ich habe Ihren Standpunkt verstanden.
Warum haben Sie mit dem ersten Teil begonnen?
alter Artikel:
DATENWISSENSCHAFT UND MASCHINELLES LERNEN (TEIL 01): LINEARE REGRESSION
https://www.mql5.com/de/articles/10459
Warum haben Sie mit dem ersten Teil begonnen?
alter Artikel:
DATENWISSENSCHAFT UND MASCHINELLES LERNEN (TEIL 01): LINEARE REGRESSION
https://www.mql5.com/de/articles/10459
Was meinen Sie?
Warum haben Sie mit dem ersten Teil begonnen?
alter Artikel:
DATENWISSENSCHAFT UND MASCHINELLES LERNEN (TEIL 01): LINEARE REGRESSION
https://www.mql5.com/de/articles/10459