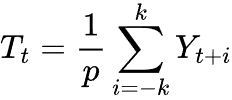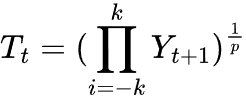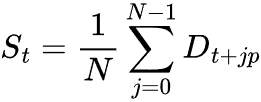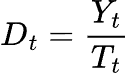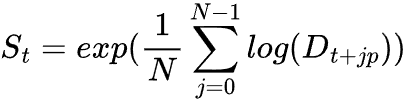
Datenwissenschaft und ML (Teil 34): Zeitreihenzerlegung, den Aktienmarkt auf den Kern herunterbrechen.

Einführung

Die Vorhersage von Zeitreihendaten war noch nie einfach. Muster sind oft versteckt und mit Rauschen und Unsicherheiten behaftet, und Charts sind oft irreführend, da sie einen Überblick über die Marktentwicklung geben, der nicht dazu gedacht ist, Ihnen tiefe Einblicke in das Geschehen zu geben.

Bei der statistischen Vorhersage und dem maschinellen Lernen versuchen wir, die Zeitreihendaten, bei denen es sich um Marktpreise handelt (Eröffnungs-, Höchst-, Tiefst- und Schlusswerte), in mehrere Komponenten aufzuschlüsseln, die aufschlussreicher sein könnten als eine einzelne Zeitreihenreihe.

In diesem Artikel befassen wir uns mit der statistischen Technik, die als saisonale Dekomposition oder Zerlegung bekannt ist. Wir wollen damit die Aktienmärkte analysieren, um Trends, saisonale Muster und vieles mehr zu erkennen.

Was ist saisonale Zerlegung?

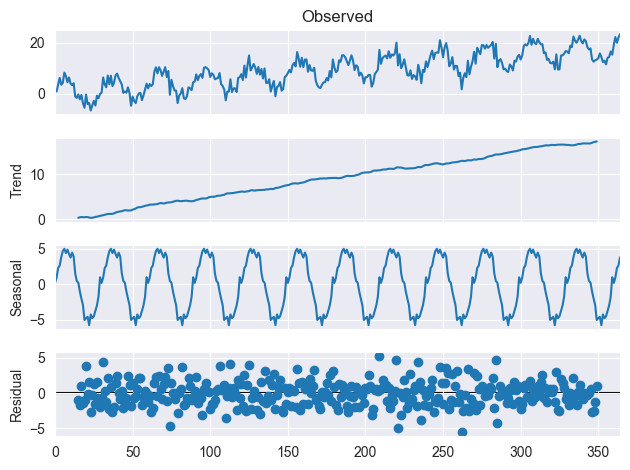
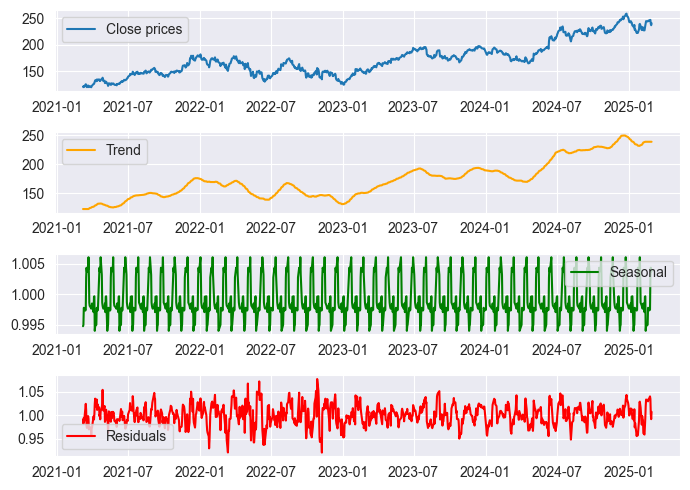
Die saisonale Zerlegung ist ein statistisches Verfahren, mit dem die Daten der Zeitreihen in mehrere Komponenten zerlegt werden können: Trend, Saisonalität und Residuen. Diese Komponenten lassen sich wie folgt erläutern.

Trend

Die Trendkomponente der Zeitreihendaten bezieht sich auf die langfristigen Veränderungen oder Muster, die im Laufe der Zeit beobachtet werden.

Sie gibt die allgemeine Richtung an, in die sich die Daten bewegen. Wenn beispielsweise die Daten im Laufe der Zeit zunehmen, ist die Trendkomponente aufwärts gerichtet, und wenn die Daten im Laufe der Zeit abnehmen, ist die Trendkomponente abwärts gerichtet.

Dies ist fast allen Händlern bekannt, denn der Trend ist am einfachsten am Markt zu erkennen, wenn man sich nur das Chart ansieht.

Saisonalität

Die saisonale Komponente von Zeitreihendaten bezieht sich auf die zyklischen Muster, die innerhalb eines bestimmten Zeitraums beobachtet werden. Wenn wir beispielsweise die monatlichen Umsatzdaten eines Einzelhändlers analysieren, der sich auf Dekoration und Geschenke spezialisiert hat, würde die saisonale Komponente die Tatsache erfassen, dass der Umsatz im Dezember aufgrund der Weihnachtseinkäufe seinen Höhepunkt erreicht, während er nach der Urlaubssaison in den Monaten Januar, Februar usw. abflacht.

Residuen

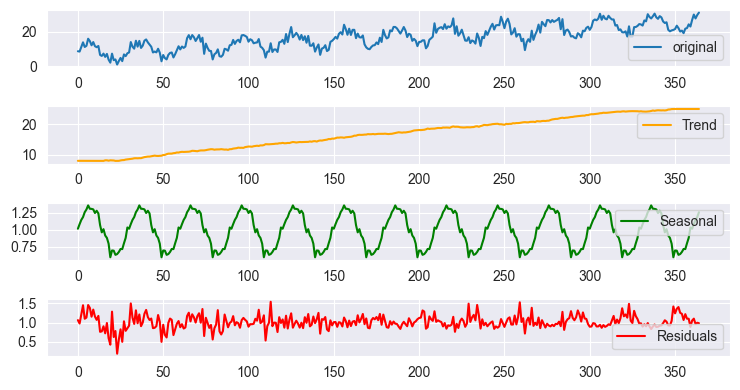
Die Residualkomponente einer Zeitreihe stellt die zufällige Schwankung dar, die übrig bleibt, nachdem die Trend- und Saisonkomponenten berücksichtigt wurden. Er stellt das Rauschen oder den Fehler in den Daten dar, der nicht durch den Trend oder saisonale Muster erklärt werden kann.

Um dies besser zu verstehen, sehen Sie sich das folgende Bild an.

Warum machen wir die saisonale Zerlegung?

Bevor wir in die mathematischen Details gehen und die saisonale Zerlegung in MQL5 implementieren, sollten wir zunächst die Gründe verstehen, warum wir die saisonale Komposition in Zeitreihendaten durchführen.

1. Erkennen von zugrunde liegenden Mustern und Trends in den Daten
   
   Die saisonale Zerlegung kann uns dabei helfen, Trends und Muster in den Daten zu erkennen, die bei der Untersuchung der Rohdaten nicht sofort ersichtlich sind. Durch die Zerlegung der Daten in ihre einzelnen Komponenten (Trend, Saisonalität und Residuen) erhalten wir ein besseres Verständnis dafür, wie diese Komponenten zum Gesamtverhalten der Daten beitragen.
   
   
2. Um die Auswirkungen der Saisonalität zu beseitigen
   
   Die saisonale Zerlegung kann verwendet werden, um die Auswirkungen der Saisonalität aus den Daten zu entfernen, sodass wir uns auf den zugrundeliegenden Trend konzentrieren können, oder umgekehrt, wenn wir zum Beispiel nur mit saisonalen Mustern arbeiten wollen: Bei der Arbeit mit Wetterdaten, die starke saisonale Muster aufweisen.
   
   
3. Um genaue Vorhersagen zu treffen
   
   Wenn Sie die Daten in Komponenten aufschlüsseln, hilft dies, unnötige Informationen herauszufiltern, die je nach Problem weniger erforderlich sein könnten. Wenn Sie beispielsweise versuchen, einen Trend vorherzusagen, ist es klüger, nur die Trendinformationen und nicht die saisonalen Daten zu haben.
   
   
4. Vergleich von Trends über verschiedene Zeiträume oder Regionen hinweg
   
   Mit Hilfe der saisonalen Zerlegung lassen sich Trends über verschiedene Zeiträume oder Regionen hinweg vergleichen, was Aufschluss darüber gibt, wie sich verschiedene Faktoren auf die Daten auswirken. Wenn wir beispielsweise Einzelhandelsumsatzdaten zwischen verschiedenen Regionen vergleichen, kann uns die saisonale Zerlegung helfen, regionale Unterschiede in den saisonalen Mustern zu erkennen und unsere Analysen entsprechend anzupassen.

Implementierung der saisonalen Zerlegung in MQL5

Um diesen analytischen Algorithmus zu implementieren, generieren wir zunächst einige einfache Zufallsdaten mit Trendmerkmalen, saisonalen Mustern und etwas Rauschen. Dies ist etwas, das in realen Datenszenarien vorkommt, insbesondere auf den Devisen- und Aktienmärkten, wo die Daten nicht einfach und reib sind.

Wir werden für diese Aufgabe die Programmiersprache Python verwenden.

Datei: seasonal_decomposition_visualization.ipynb

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import os

sns.set_style("darkgrid")

# Create synthetic time-series data
np.random.seed(42)
time = np.arange(0, 365)  # 1 year (daily data)
trend = 0.05 * time  # Linear upward trend
seasonality = 5 * np.sin(2 * np.pi * time / 30)  # 30-day periodic seasonality
noise = np.random.normal(scale=2, size=len(time))  # Random noise

# Combine components to form the time-series
time_series = trend + seasonality + noise

# Plot the original time-series
plt.figure(figsize=(10, 4))
plt.plot(time, time_series, label="Original Time-Series", color="blue")
plt.xlabel("Time (Days)")
plt.ylabel("Value")
plt.title("Synthetic Time-Series with Trend and Seasonality")
plt.legend()
plt.show()

Ergebnis:

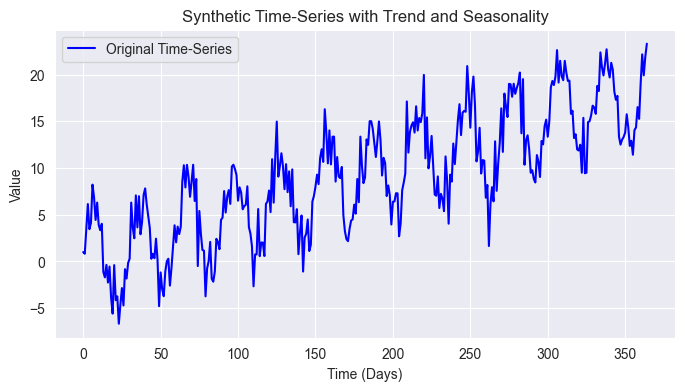
Wir wissen, dass der Aktienmarkt komplexer ist als das, aber angesichts dieser einfachen Daten wollen wir versuchen, die 30-tägigen saisonalen Muster, die wir der Zeitreihe hinzugefügt haben, sowie den allgemeinen Trend aufzudecken und einige Störungen aus den Daten herauszufiltern.

Trend-Extraktion

Um die Trendmerkmale zu extrahieren, können wir den gleitenden Durchschnitt (MA) verwenden, da er eine Zeitreihe glättet, indem er die Werte über ein festes Fenster mittelt. Dies hilft, kurzfristige Schwankungen herauszufiltern und den zugrunde liegenden Trend zu erkennen.

Bei der additiven Zerlegung wird der Trend anhand eines gleitenden Durchschnitts über ein Fenster geschätzt, das dem saisonalen Zeitraum p entspricht.

wobei:

 = Trendkomponente zum Zeitpunkt t.

 = Fenstergröße oder saisonaler Zeitraum.

 = Die Hälfte des saisonalen Zeitraums.

 = Beobachtete Zeitreihenwerte.

Für die multiplikative Zerlegung nehmen wir stattdessen das geometrische Mittel.

wobei:

 = Produkt-Operator, wobei statt der Summe alle Werte innerhalb des Fensters multipliziert werden, da bei der multiplikativen Zerlegung davon ausgegangen wird, dass saisonale Effekte die Daten skalieren, anstatt sie zu addieren.

Dies mag wie komplexe Mathematik erscheinen, aber es kann in ein paar Zeilen MQL5-Code heruntergebrochen werden.

vector moving_average(const vector &v, uint k, ENUM_VECTOR_CONVOLVE mode=VECTOR_CONVOLVE_VALID)
 {
   vector kernel = vector::Ones(k) /  k;
   vector ma = v.Convolve(kernel, mode);
    
   return ma;  
 }

Wir berechnen den gleitenden Durchschnitt auf der Grundlage der Faltungsmethode, da sie flexibel und effizient ist und im Gegensatz zur Berechnung des gleitenden Durchschnitts mit Hilfe der Methode rolling() auch fehlende Werte an den Rändern des Arrays berücksichtigt.

Wir können die Formel wie folgt abschließen.

//--- compute the trend

   int n = (int)timeseries.Size();  
   res.trend = moving_average(timeseries, period);
   
   // We align trend array with the original series length
   
   int pad = (int)MathFloor((n - res.trend.Size()) / 2.0);
   int pad_array[] = {pad, n-(int)res.trend.Size()-pad};
   
   res.trend = Pad(res.trend, pad_array, edge);

Extraktion von saisonalen Bestandteilen

Die Extraktion saisonaler Komponenten bezieht sich auf die Isolierung der sich wiederholenden Muster in einer Zeitreihe, die in einem bestimmten Intervall auftreten, z. B. täglich, monatlich, jährlich usw.

Diese Komponente wird berechnet, nachdem der Trend aus den ursprünglichen Zeitreihendaten entfernt wurde. Sie kann unterschiedlich extrahiert werden, je nachdem, ob das Modell additiv oder multiplikativ ist.

Additives Modell

Nach der Schätzung des Trends wird die trendbereinigte Zeitreihe ohne Trend wie folgt berechnet.

wobei:

 = ein trendbereinigter Wert zum Zeitpunkt t.

 = Zeitreihenwert zum Zeitpunkt t.

 = Trendkomponente zum Zeitpunkt t.

Zur Berechnung der saisonalen Komponente wird der Durchschnitt der trendbereinigten Werte über alle vollständigen Zyklen der saisonalen Periode p gebildet.

wobei:

 = Anzahl der vollständigen saisonalen Zyklen im Datensatz.

 = der saisonale Zeitraum (z. B. 30 für tägliche Daten in einem monatlichen Zyklus).

 = Extrahierte saisonale Komponente.

Multiplikatives Modell

Beim multiplikativen Modell dividieren wir, anstatt zu subtrahieren, um eine trendbereinigte Zeitreihe zu erhalten.

Die saisonale Komponente wird extrahiert, indem das geometrische Mittel anstelle des arithmetischen Mittels verwendet wird.

Dies trägt dazu bei, Verzerrungen aufgrund der multiplikativen Natur des Modells zu vermeiden.

Wir können diese Funktion in MQL5 wie folgt implementieren.

//--- compute the seasonal component
   
   if (model == multiplicative)
     {
       for (ulong i=0; i<timeseries.Size(); i++)
         if (timeseries[i]<=0)
            {
               printf("Error, Multiplicative seasonality is not appropriate for zero and negative values");
               return res;
            }
     }
   
   vector detrended = {};
   vector seasonal = {};
   
   switch(model)
     {
      case  additive:
        {
          detrended = timeseries - res.trend;
          seasonal = vector::Zeros(period);
         
          for (uint i = 0; i < period; i++)
            seasonal[i] = SliceStep(detrended, i, period).Mean(); //Arithmetic mean over cycles
        }    
        break;
      case  multiplicative:
        {
          detrended = timeseries / res.trend;
          seasonal = vector::Zeros(period);
         
          for (uint i = 0; i < period; i++)
            seasonal[i] = MathExp(MathLog(SliceStep(detrended, i, period)).Mean()); //Geometric mean
        }    
        break;
      default:
        printf("Unknown model for seasonal component calculations");
        break;
     }

    
    vector seasonal_repeated = Tile(seasonal, (int)MathFloor(n/period)+1);
    res.seasonal = Slice(seasonal_repeated, 0, n);

Die Pad-Funktion fügt Auffüllungen (zusätzliche Werte) um einen Vektor hinzu, ähnlich wie Numpy.pad in diesem Szenario hilft sie, die gleitenden Durchschnittswerte zu zentrieren.

Aufgrund des Vorhandenseins einer logarithmischen Transformationsfunktion MathLog, die nicht für Null- und Negativwerte verwendet werden kann, sollte das multiplikative Modell auf positive Zeitreihen beschränkt werden; diese Bedingung muss überprüft und verstärkt werden.

   if (model == multiplicative)
     {
       for (ulong i=0; i<timeseries.Size(); i++)
         if (timeseries[i]<=0)
            {
               printf("Error, Multiplicative seasonality is not appropriate for zero and negative values");
               return res;
            }
     }

Die Funktion Tile konstruiert einen großen Vektor, indem sie den saisonalen Vektor mehrmals wiederholt. Dieser Prozess ist entscheidend für die Erfassung der wiederkehrenden saisonalen Muster in einer Zeitreihe.

Berechnung der Residuen

Schließlich berechnen wir die Residuen, indem wir den Trend und die Saisonalität abziehen.

Für das additive Modell:

Für das multiplikative Modell:

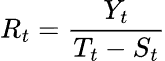
wobei:

 = ursprünglicher Zeitreihenwert zum Zeitpunkt t.

 = Trendwert zum Zeitpunkt t.

 = saisonaler Wert zum Zeitpunkt t.

Alles in einer Funktion zusammenfassen

Ähnlich wie bei der Funktion seasonal_decompose, von der ich mich inspirieren ließ, musste ich alle Berechnungen in eine Funktion namens seasonal_decompose packen, die eine Struktur mit Trend-, Saison- und Residualvektoren zurückgibt.

enum seasonal_model
 {
   additive,
   multiplicative
 };

struct seasonal_decompose_results
 {
   vector trend;
   vector seasonal;
   vector residuals;
 };
 
seasonal_decompose_results seasonal_decompose(const vector &timeseries, uint period, seasonal_model model=additive)
 {
   seasonal_decompose_results res;
   
   if (timeseries.Size() < period)
    {
      printf("%s Error: Time series length is smaller than the period. Cannot compute seasonal decomposition.",__FUNCTION__);
      return res;
    }
   
//--- compute the trend

   int n = (int)timeseries.Size();  
   res.trend = moving_average(timeseries, period);
   
   // We align trend array with the original series length
   
   int pad = (int)MathFloor((n - res.trend.Size()) / 2.0);
   int pad_array[] = {pad, n-(int)res.trend.Size()-pad};
   
   res.trend = Pad(res.trend, pad_array, edge);

//--- compute the seasonal component
   
   if (model == multiplicative)
     {
       for (ulong i=0; i<timeseries.Size(); i++)
         if (timeseries[i]<=0)
            {
               printf("Error, Multiplicative seasonality is not appropriate for zero and negative values");
               return res;
            }
     }
   
   vector detrended = {};
   vector seasonal = {};
   
   switch(model)
     {
      case  additive:
        {
          detrended = timeseries - res.trend;
          seasonal = vector::Zeros(period);
         
          for (uint i = 0; i < period; i++)
            seasonal[i] = SliceStep(detrended, i, period).Mean(); //Arithmetic mean over cycles
        }    
        break;
      case  multiplicative:
        {
          detrended = timeseries / res.trend;
          seasonal = vector::Zeros(period);
         
          for (uint i = 0; i < period; i++)
            seasonal[i] = MathExp(MathLog(SliceStep(detrended, i, period)).Mean()); //Geometric mean
        }    
        break;
      default:
        printf("Unknown model for seasonal component calculations");
        break;
     }


    
    vector seasonal_repeated = Tile(seasonal, (int)MathFloor(n/period)+1);
    res.seasonal = Slice(seasonal_repeated, 0, n);

//--- Compute Residuals

    if (model == additive)
        res.residuals = timeseries - res.trend - res.seasonal;
    else  // Multiplicative
        res.residuals = timeseries / (res.trend * res.seasonal);
        
   return res;
 }

Nun können wir diese Funktion testen.

Ich musste auch positive Werte erzeugen und sie in einer CSV-Datei speichern, um die saisonale Zerlegung mit dem multiplikativen Modell zu testen.

Datei: seasonal_decomposition_visualization.ipynb

# Create synthetic time-series data
np.random.seed(42)
time = np.arange(0, 365)  # 1 year (daily data)
trend = 0.05 * time  # Linear upward trend
seasonality = 5 * np.sin(2 * np.pi * time / 30)  # 30-day periodic seasonality
noise = np.random.normal(scale=2, size=len(time))  # Random noise

# Combine components to form the time-series
time_series = trend + seasonality + noise

# Fix for multiplicative decomposition: Shift the series to make all values positive
min_value = np.min(time_series)
if min_value <= 0:
    shift_value = abs(min_value) + 1  # Ensure strictly positive values
    time_series_shifted = time_series + shift_value
else:
    time_series_shifted = time_series

ts_pos_df = pd.DataFrame({
    "timeseries": time_series_shifted
})

ts_pos_df.to_csv(os.path.join(files_path,"pos_ts_df.csv"), index=False)

In unserem MQL5-Skript laden wir beide Zeitreihendatensätze mit Hilfe der Bibliothek der Datenrahmen, die wir in diesem Artikel besprochen haben. Nach dem Laden der Daten führen wir die Algorithmen zur saisonalen Zerlegung aus.

Datei: seasonal_decompose test.mq5

#include <MALE5\Stats Models\Tsa\Seasonal Decompose.mqh>
#include <MALE5\pandas.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Additive model
   
   CDataFrame df;
   df.FromCSV("ts_df.csv");
   
   vector time_series = df["timeseries"];
   
//---
    
    seasonal_decompose_results res_ad = seasonal_decompose(time_series, 30, additive);
    
    df.Insert("original", time_series);
    df.Insert("trend",res_ad.trend);
    df.Insert("seasonal",res_ad.seasonal);
    df.Insert("residuals",res_ad.residuals);
    
    df.ToCSV("seasonal_decomposed_additive.csv");

//--- Multiplicative model

   CDataFrame pos_df;
   pos_df.FromCSV("pos_ts_df.csv");
   
   time_series = pos_df["timeseries"];
   
//---
    
    seasonal_decompose_results res_mp = seasonal_decompose(time_series, 30, multiplicative);
    
    pos_df.Insert("original", time_series);
    pos_df.Insert("trend",res_mp.trend);
    pos_df.Insert("seasonal",res_mp.seasonal);
    pos_df.Insert("residuals",res_mp.residuals);
    
    pos_df.ToCSV("seasonal_decomposed_multiplicative.csv");
  }

Ich musste die Ergebnisse wieder in neue CSV-Dateien speichern, um sie mit Python zu visualisieren.

Saisonale Zerlegung unter Verwendung des additiven Modells Ergebnisdarstellung

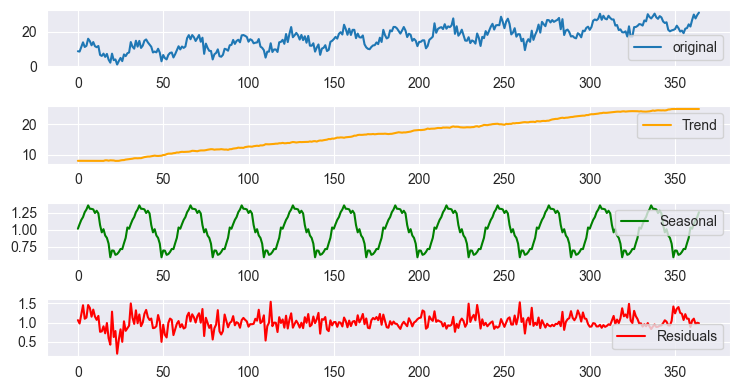
Saisonale Zerlegung unter Verwendung des multiplikativen Modells der Ergebnisdarstellung

Die Diagramme sehen aufgrund des Maßstabs fast gleich aus, aber die Ergebnisse unterscheiden sich, wenn man sich die Daten ansieht. Dies ist das gleiche Ergebnis, das Sie mit tsa.seasonal.seasonal_decompose erhalten würden, das von stats models in Python bereitgestellt wird.

Nachdem wir nun die Funktion zur saisonalen Zerlegung kennen, wollen wir sie zur Analyse der Aktienmärkte verwenden.

Beobachtung von Mustern auf dem Aktienmarkt

Bei der Analyse des Aktienmarktes ist es oft einfach, den Trend zu erkennen, insbesondere bei gut etablierten und fundamental starken Unternehmen. Viele große, finanziell stabile Unternehmen tendieren dazu, im Laufe der Zeit aufgrund von beständigem Wachstum, Innovation und Marktnachfrage einen Aufwärtstrend zu verfolgen.

Die Erkennung von saisonalen Mustern in Aktienkursen kann jedoch sehr viel schwieriger sein. Im Gegensatz zu Trends bezieht sich die Saisonalität auf wiederkehrende Kursbewegungen in festen Intervallen, die nicht immer offensichtlich sind; diese Muster können in verschiedenen Zeitrahmen auftreten.

Intraday-Saisonalität

Bestimmte Stunden eines Handelstages können ein sich wiederholendes Kursverhalten aufweisen (z. B. erhöhte Volatilität bei Markteröffnung oder -schluss).

Monatliche oder vierteljährliche Saisonalität

Aktienkurse können Zyklen folgen, die auf Gewinnmeldungen, wirtschaftlichen Bedingungen oder der Stimmung der Anleger beruhen.

Langfristige Saisonalität

Einige Aktien weisen im Laufe der Jahre aufgrund von Konjunkturzyklen oder unternehmensspezifischen Faktoren immer wiederkehrende Trends auf.

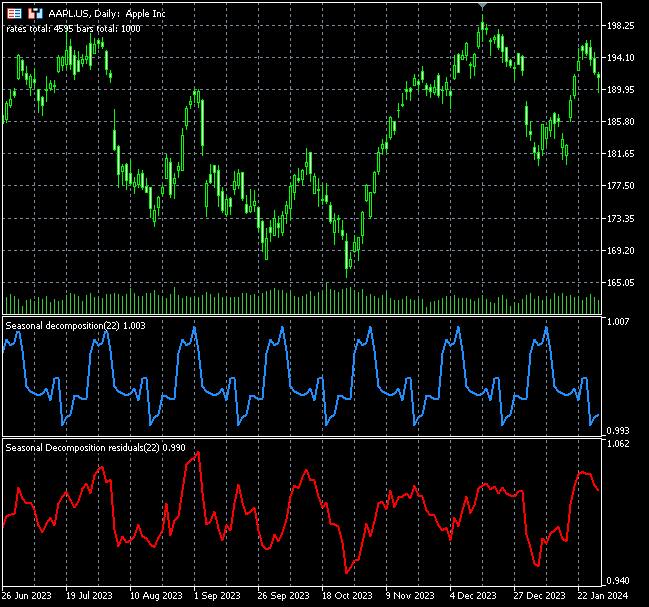
Fallstudie, Die Apple (AAPL) Aktie

Am Beispiel der Apple-Aktie können wir die Hypothese aufstellen, dass saisonale Muster alle 22 Handelstage auftreten, was bei einem jährlichen Datensatz etwa einem Handelsmonat entspricht. Diese Annahme beruht auf der Tatsache, dass es ungefähr 22 Handelstage pro Monat gibt (ohne Wochenenden und Feiertage).

Durch die Anwendung saisonaler Zerlegungstechniken können wir analysieren, ob die Apple-Aktie alle 22 Tage wiederkehrende Kursbewegungen aufweist. Wenn eine starke saisonale Komponente vorhanden ist, deutet dies darauf hin, dass die Preisschwankungen vorhersehbaren Zyklen folgen, was für Händler und Analysten nützlich sein kann. Wenn jedoch keine signifikante Saisonalität festgestellt wird, können die Preisbewegungen weitgehend durch externe Faktoren, Rauschen oder einen vorherrschenden Trend bestimmt werden.

Wir sammeln die täglichen Schlusskurse für 1000 Balken und führen eine multiplikative saisonale Zerlegung für einen Zeitraum von 22 Tagen durch.

#include <MALE5\Stats Models\Tsa\Seasonal Decompose.mqh>
#include <MALE5\pandas.mqh>

input uint bars_total = 1000;
input uint period_ = 22;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   
    vector close, time;
    close.CopyRates(Symbol(), PERIOD_D1, COPY_RATES_CLOSE, 1, bars_total); //closing prices
    time.CopyRates(Symbol(), PERIOD_D1, COPY_RATES_TIME, 1, bars_total); //time
   
    seasonal_decompose_results res_ad = seasonal_decompose(close, period_, multiplicative);
    
    CDataFrame df; //A dataframe object for storing the seasonal decomposition outcome
    
    df.Insert("time", time);
    df.Insert("close", close);
    df.Insert("trend",res_ad.trend);
    df.Insert("seasonal",res_ad.seasonal);
    df.Insert("residuals",res_ad.residuals);
    
    df.ToCSV(StringFormat("%s.%s.period=%d.seasonal_dec.csv",Symbol(), EnumToString(PERIOD_D1), period_));
  }

Das Ergebnis wurde dann in einem Jupyter-Notebook namens stock_market seasonal dec.ipynb dargestellt.

Okay, wir können einige saisonale Muster im obigen Diagramm erkennen, aber wir können uns der saisonalen Muster nicht zu 100 % sicher sein, da es immer einige Fehler gibt. Die Herausforderung besteht darin, die Fehlerwerte zu interpretieren und Ihre Analyse entsprechend durchzuführen.

Anhand des Residualdiagramms können wir sehen, dass es in den Jahren 2020 bis 2022 Spitzen bei den Residualwerten gibt. Wir alle wissen, dass dies der Zeitraum war, in dem es eine globale Pandemie gab, sodass die saisonalen Muster vielleicht gestört und inkonsistent waren, was darauf hindeutet, dass wir den saisonalen Mustern, die wir in diesem Zeitraum sehen, nicht trauen können.

Faustformel.

Gute Zerlegung:  Die Residuen sollten wie zufälliges Rauschen (weißes Rauschen) aussehen.

Schlechte Zerlegung: Die Residuen zeigen immer noch eine sichtbare Struktur (Trends oder saisonale Effekte, die nicht entfernt wurden).

Wir können verschiedene mathematische Techniken verwenden, um die Residuen zu visualisieren, z. B;

Das Verteilungsdiagramm

Wir haben ein normalverteiltes Residuen-Diagramm, was ein gutes Zeichen dafür sein könnte, dass es einige monatliche Muster in der Apple-Aktie geben könnte.

Der Mittelwert und die Standardabweichung

Beim additiven Modell sollte der Mittelwert der Residuen nahe bei 0 liegen, was bedeutet, dass die meisten Abweichungen durch den Trend und die Saisonalität erklärt werden.

Beim multiplikativen Modell liegt der Restmittelwert idealerweise nahe bei 1, was bedeutet, dass die ursprüngliche Reihe durch den Trend und die Saisonalität gut erklärt wird.

Der Wert der Standardabweichung muss klein sein

print("Residual Mean:", residuals.mean())  # Should be close to 0
print("Residual Std Dev:", residuals.std())  # Should be small

Ausgabe:

Residual Mean: 1.0002367590572043
Residual Std Dev: 0.021749969975933727

Schließlich können wir das alles in einen Indikator einbauen.

#property indicator_separate_window
#property indicator_buffers 2
#property indicator_plots 1

#property indicator_color1 clrDodgerBlue
#property indicator_style1 STYLE_SOLID
#property indicator_type1 DRAW_LINE
#property indicator_width1 2

//+------------------------------------------------------------------+

double trend_buff[];
double seasonal_buff[];

#include <MALE5\Stats Models\Tsa\Seasonal Decompose.mqh>
#include <MALE5\pandas.mqh>

input uint bars_total = 10000;
input uint period_ = 22;
input ENUM_COPY_RATES price = COPY_RATES_CLOSE;

//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   
   SetIndexBuffer(0, seasonal_buff, INDICATOR_DATA);
   SetIndexBuffer(1, trend_buff, INDICATOR_CALCULATIONS);
   
//---
   
   IndicatorSetString(INDICATOR_SHORTNAME, "Seasonal decomposition("+string(period_)+")");
   PlotIndexSetString(1, PLOT_LABEL, "seasonal ("+string(period_)+")");
   
   PlotIndexSetDouble(0, PLOT_EMPTY_VALUE, 0.0);
   
   ArrayInitialize(seasonal_buff, EMPTY_VALUE);
   ArrayInitialize(trend_buff, EMPTY_VALUE);
    
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
    
    if (prev_calculated==rates_total) //not on a new bar, calculate the indicator on the opening of a new bar  
      return rates_total;
    
    ArrayInitialize(seasonal_buff, EMPTY_VALUE);
    ArrayInitialize(trend_buff, EMPTY_VALUE);

//---

    Comment("rates total: ",rates_total," bars total: ",bars_total);
    
    //if (rates_total<(int)bars_total)
    //  return rates_total;
          
    vector close_v;
    close_v.CopyRates(Symbol(), Period(), price, 0, bars_total); //closing prices
      
    seasonal_decompose_results res = seasonal_decompose(close_v, period_, multiplicative);
    
    for (int i=MathAbs(rates_total-(int)bars_total), count=0; i<rates_total; i++, count++) //calculate only the chosen number of bars
      {
         trend_buff[i] = res.trend[count];
         seasonal_buff[i] = res.seasonal[count];
      }
    
//--- return value of prev_calculated for next call
   return(rates_total);
  }

Da die Berechnung der saisonalen Zerlegung sehr rechenintensiv sein kann, wenn alle im Chart verfügbaren Kurse zur Berechnung herangezogen werden, müssen wir die Anzahl der für die Berechnung und Darstellung zu verwendenden Balken begrenzen, sobald neue Kurse im Chart erscheinen.

Ich musste zwei separate Indikatoren erstellen, einen für die Darstellung der saisonalen Muster und einen für die Darstellung der Residuen, wobei ich dieselbe Logik verwendete.

Nachfolgend sind die Indikatoren für das Apple-Symbol abgebildet. 

Die saisonalen Muster des Indikators können auch als Handelssignale oder als überverkaufte und überkaufte Bedingungen interpretiert werden, wie im obigen Chart zu sehen ist. Im Moment ist es schwierig zu sagen, da ich den Indikator noch nicht auf der Handelsseite erforscht habe. Ich möchte Sie ermutigen, dies als Hausaufgabe zu tun.

Abschließende Überlegungen

Die saisonale Zerlegung ist eine nützliche Technik, die Sie in Ihrem Werkzeugkasten für den algorithmischen Handel haben sollten. Einige Datenwissenschaftler verwenden sie, um neue Merkmale auf der Grundlage der ihnen vorliegenden Zeitreihendaten zu erstellen, während andere sie verwenden, um die Art der Daten zu analysieren und dann zu entscheiden, welche maschinellen Lerntechniken für das jeweilige Problem am besten geeignet sind? 

Einige Datenwissenschaftler beginnen mit einer saisonalen Zerlegung, um die Zeitreihe in ihre zugrunde liegenden Komponenten zu zerlegen: Trend, Saisonalität und Residuen. Wenn die Daten ein eindeutiges saisonales Muster aufweisen, wird die saisonale, exponentielle Glättung (auch bekannt als saisonale Holt-Winters-Methode) eingesetzt, um zu versuchen, die Daten zu prognostizieren. Gibt es jedoch kein eindeutiges saisonales Muster oder ist das saisonale Muster schwach oder unregelmäßig, werden ARIMA-Modelle und andere Standardmodelle des maschinellen Lernens eingesetzt, um zu versuchen, die Muster in den Zeitreihendaten zu entschlüsseln und Vorhersagen zu treffen.

Tabelle der Anhänge

Dateiname & Pfad	Beschreibung und Verwendung
Include\pandas.mqh	Besteht aus der Dataframe-Klasse für die Speicherung und Bearbeitung von Daten in einem Pandas-ähnlichen Format.
Include\Seasonal Decompose.mqh	Enthält alle Funktionen und Codezeilen, die die saisonale Zerlegung in MQL5 ermöglichen.
Indicators\Seasonal Decomposition.mq5	Dieser Indikator stellt die saisonale Komponente dar.
Indicators\Seasonal Decomposition residuals.mq5	Dieser Indikator stellt die Residualkomponente dar.
Scripts\seasonal_decompose test.mq5	Ein einfaches Skript, das zur Implementierung und Fehlersuche in der Funktion „Saisonale Zerlegung“ und ihren Bestandteilen dient.
Scripts\stock market seasonal dec.mq5	Ein Skript zum Analysieren des Schlusskurses eines Symbols und zum Speichern des Ergebnisses in einer CSV-Datei zu Analysezwecken.
Python\seasonal_decomposition_visualization.ipynb	Jupyter-Notebook zur Visualisierung von saisonalen Zersetzungsergebnissen in CSV-Dateien.
Python\stock_market seasonal dec.ipynb	Jupyter-Notebook zur Visualisierung der saisonalen Zerlegungsergebnisse einer Aktie.
Files\*.csv	CSV-Dateien mit saisonalen Zerlegungsergebnissen und Daten aus Python-Code und MQL5.