
Datenwissenschaft und maschinelles Lernen (Teil 03): Matrix-Regression
Nach einer langen Periode von Versuchen und Fehlern ist das Rätsel der multiplen dynamischen Regression endlich gelöst... Lesen Sie weiter.
Wenn Sie die beiden vorangegangenen Artikel aufmerksam gelesen haben, werden Sie feststellen, dass das große Problem, das ich hatte, darin bestand, Modelle zu programmieren, die mit mehr unabhängigen Variablen umgehen können. Damit meine ich, dass sie dynamisch mit mehr Eingaben umgehen können, denn wenn es um die Erstellung von Strategien geht, werden wir mit Hunderten von Daten zu tun haben.
Matrix
Für diejenigen, die den Mathematikunterricht übersprungen haben: Eine Matrix ist eine rechteckige Anordnung oder Tabelle von Zahlen oder anderen mathematischen Objekten, die in Zeilen und Spalten angeordnet sind und zur Darstellung eines mathematischen Objekts oder einer Eigenschaft eines solchen Objekts verwendet werden.
Zum Beispiel
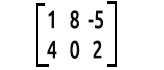
Der Elefant im Raum,
wir lesen Matrizen wie folgt: Zeilenx Spalten. Die obige Matrix ist eine 2x3-Matrix, was 2 Zeilen und 3 Spalten bedeutet.
Es besteht kein Zweifel daran, dass Matrizen eine große Rolle dabei spielen, wie moderne Computer Informationen verarbeiten und große Zahlen berechnen. Der Hauptgrund dafür, dass sie so etwas erreichen können, ist, dass die Daten in einer Matrix in Form eines Arrays gespeichert werden, das Computer lesen und manipulieren können. Schauen wir uns also ihre Anwendung beim maschinellen Lernen an,
Lineare Regression
Matrizen ermöglichen Berechnungen in der linearen Algebra. Daher ist das Studium von Matrizen ein großer Teil der linearen Algebra, so dass wir Matrizen verwenden können, um unsere linearen Regressionsmodelle zu erstellen.
Wie wir alle wissen, ist die Gleichung einer Geraden
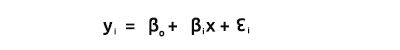
wobei ∈ der Fehlerterm, ßo und ßi die Koeffizienten y-Achsenabschnitt bzw. Steigungskoeffizient sind.
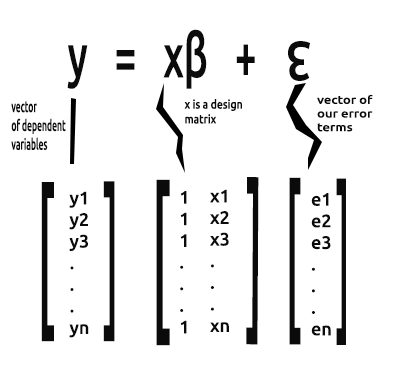
Was uns in diesen Artikelserien von nun an interessiert, ist die Vektorform einer Gleichung, hier ist sie:
Dies ist die Form einer einfachen linearen Regression in einer Matrixform.
Für ein einfaches lineares Modell (und andere Regressionsmodelle) sind wir in der Regel daran interessiert, die Steigungskoeffizienten bzw. die Schätzer der gewöhnlichen kleinsten Quadrate zu finden.
Der Vektor Beta ist ein Vektor, der die Betas enthält.
ßo und ß1, wie aus der folgenden Gleichung hervorgeht:
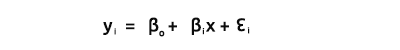
Wir sind daran interessiert, die Koeffizienten zu finden, da sie für die Erstellung eines Modells sehr wichtig sind.
Die Formel für die Schätzer der Modelle in Vektorform lautet:
Dies ist eine sehr wichtige Formel, die alle Nerds da draußen auswendig lernen sollten.
Wir werden in Kürze besprechen, wie man die Elemente der Formel findet.
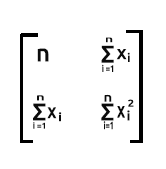
Das Produkt von xTx ergibt die symmetrische Matrix, da die Anzahl der Spalten in xT die gleiche ist wie die Anzahl der Zeilen in x, wir werden das später in Aktion sehen.
Wie bereits gesagt,
x wird auch als Entwurfsmatrix bezeichnet, und so sieht die Matrix aus:
Entwurfsmatrix
Wie Sie sehen können, haben wir in der allerersten Spalte nur die Werte von 1 bis zum Ende unserer Zeilen in ein Matrix-Array eingefügt. Dies ist der erste Schritt zur Vorbereitung unserer Daten für die Matrix-Regression, und Sie werden die Vorteile einer solchen Vorgehensweise sehen, wenn wir uns weiter mit den Berechnungen beschäftigen.
Wir behandeln diesen Prozess in der Funktion Init() unserer Bibliothek
void CSimpleMatLinearRegression::Init(double &x[],double &y[], bool debugmode=true) { ArrayResize(Betas,2); //since it is simple linear Regression we only have two variables x and y if (ArraySize(x) != ArraySize(y)) Alert("There is variance in the number of independent variables and dependent variables \n Calculations may fall short"); m_rowsize = ArraySize(x); ArrayResize(m_xvalues,m_rowsize+m_rowsize); //add one row size space for the filled values ArrayFill(m_xvalues,0,m_rowsize,1); //fill the first row with one(s) here is where the operation is performed ArrayCopy(m_xvalues,x,m_rowsize,0,WHOLE_ARRAY); //add x values to the array starting where the filled values ended ArrayCopy(m_yvalues,y); m_debug=debugmode; }
Wenn wir die Werte der Entwurfsmatrix ausdrucken, sehen Sie hier unsere Ausgabe. Wie Sie sehen können, endet der gefüllte Wert einer Zeile dort, wo der Wert von x beginnt:
[ 0] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 21] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
........
........
[ 693] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 714] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 735] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 4173.8 4179.2 4182.7 4185.8 4180.8 4174.6 4174.9 4170.8 4182.2 4208.4 4247.1 4217.4
[ 756] 4225.9 4211.2 4244.1 4249.0 4228.3 4230.6 4235.9 4227.0 4225.0 4219.7 4216.2 4225.9 4229.9 4232.8 4226.4 4206.9 4204.6 4234.7 4240.7 4243.4 4247.7
........
........
[1449] 4436.4 4442.2 4439.5 4442.5 4436.2 4423.6 4416.8 4419.6 4427.0 4431.7 4372.7 4374.6 4357.9 4381.6 4345.8 4296.8 4321.0 4284.6 4310.9 4318.1 4328.0
[1470] 4334.0 4352.3 4350.6 4354.0 4340.1 4347.5 4361.3 4345.9 4346.5 4342.8 4351.7 4326.0 4323.2 4332.7 4352.5 4401.9 4405.2 4415.8
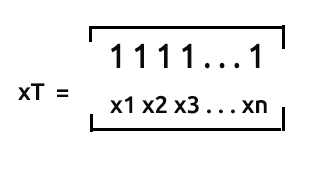
xT oder x transponieren ist der Prozess in einer Matrix, bei dem die Zeilen mit den Spalten vertauscht werden.
Das bedeutet, dass die Multiplikation dieser beiden Matrizen
Wir werden den Prozess der Transposition einer Matrix überspringen, da die Art und Weise, wie wir unsere Daten gesammelt haben, bereits in transponierter Form vorliegt, obwohl wir auf der anderen Seite die x-Werte 'untransponieren' müssen, damit wir sie mit der bereits transponierten x-Matrix multiplizieren können.
Nur ein kleiner Hinweis: Die Matrix nx2 , die nicht transponiert ist, sieht aus wie [1 x1 1 x2 1 ... 1 xn]. Sehen wir uns das in Aktion an:
Untransponieren der X-Matrix
Unsere Matrix in transponierter Form, die aus einer csv-Datei gewonnen wurde, sieht wie folgt aus, wenn sie ausgedruckt wird
Transposed Matrix
[
[ 0] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
...
...
[ 0] 4174 4179 4183 4186 4181 4175 4175 4171 4182 4208 4247 4217 4226 4211 4244 4249 4228 4231 4236 4227 4225 4220 4216 4226
...
...
[720] 4297 4321 4285 4311 4318 4328 4334 4352 4351 4354 4340 4348 4361 4346 4346 4343 4352 4326 4323 4333 4352 4402 4405 4416
]
Beim Untransponieren müssen wir nur die Zeilen mit den Spalten vertauschen, das ist der umgekehrte Vorgang wie beim Transponieren der Matrix:
int tr_rows = m_rowsize, tr_cols = 1+1; //since we have one independent variable we add one for the space created by those values of one MatrixUnTranspose(m_xvalues,tr_cols,tr_rows); Print("UnTransposed Matrix"); MatrixPrint(m_xvalues,tr_cols,tr_rows);
Hier wird's knifflig
Wenn wir die Spalten einer transponierten Matrix an die Stelle setzen, an der die Zeilen sein sollen, und die Zeilen an die Stelle, an der die Spalten benötigt werden, wird die Ausgabe bei der Ausführung dieses Codeschnipsels folgendermaßen aussehen:
UnTransposed Matrix [ 1 4248 1 4201 1 4352 1 4402 ... ... 1 4405 1 4416 ]
xT ist eine 2xn Matrix, x ist eine nx2 und die resultierende Matrix ist eine 2x2 Matrix.
Rechnen wir also aus, wie das Produkt ihrer Multiplikation aussehen wird.
Achtung: Damit eine Matrixmultiplikation möglich ist, muss die Anzahl der Spalten in der ersten Matrix gleich der Anzahl der Zeilen in der zweiten Matrix sein.
Siehe Regeln für die Matrixmultiplikation unter diesem Link https://de.wikipedia.org/wiki/Matrizenmultiplikation.
Die Multiplikation wird in dieser Matrix wie folgt durchgeführt:
- Zeile 1 mal Spalte 1
- Zeile 1 mal Spalte 2
- Zeile 2 mal Spalte 1
- Zeile 2 mal Spalte 2
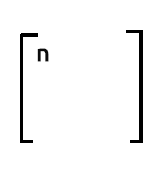
Aus unseren Matrizen Zeile 1 mal Spalte1 wird das Ergebnis
die Summe des Produkts von Zeile1, das die Werte von eins enthält, und des Produkts von Spalte1, das ebenfalls die Werte von eins enthält. Das ist nichts anderes, als wenn man den Wert von eins bei jeder Iteration um eins erhöht.
Anmerkung:
Wenn Sie die Anzahl der Beobachtungen in Ihrem Datensatz wissen möchten, können Sie sich auf die Zahl in der ersten Zeile und der ersten Spalte in der Ausgabe von xTx verlassen.
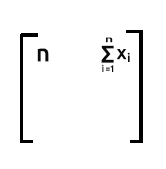
Zeile 1 mal Spalte 2. Da Zeile 1 die Werte von Einsen enthält, wird bei der Addition des Produkts von Zeile1 (das sind die Werte von Eins) und Spalte2(das sind die Werte von x) die Ausgabe die Summe von x Elementen sein, da Eins keine Auswirkung auf die Multiplikation haben wird.
Zeile2 mal Spalte1, Die Ausgabe wird die Summierung von x sein, da die Werte von eins aus Zeile2 keine Auswirkung haben, wenn sie die x-Werte multiplizieren, die auf der Säule1 sind:
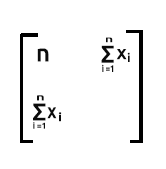
Der letzte Teil ist die Summierung der x-Werte, wenn sie quadriert werden,
da es sich um die Summierung des Produkts aus Zeile2, die x-Werte enthält, und Spalte2, die ebenfalls x-Werte enthält, handelt:
Wie Sie sehen können, ist die Ausgabe der Matrix in diesem Fall eine 2x2-Matrix
Lassen Sie uns sehen, wie dies in der realen Welt funktioniert, indem wir den Datensatz aus unserem allerersten Artikel über lineare Regression https://www.mql5.com/de/articles/10459
verwenden.Extrahieren wir die Daten und legen sie in ein Array x für die unabhängige Variable und y für die abhängige Variable
//inside MatrixRegTest.mq5 script #include "MatrixRegression.mqh"; #include "LinearRegressionLib.mqh"; CSimpleMatLinearRegression matlr; CSimpleLinearRegression lr; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //double x[] = {651,762,856,1063,1190,1298,1421,1440,1518}; //stands for sales //double y[] = {23,26,30,34,43,48,52,57,58}; //money spent on ads //--- double x[], y[]; string file_name = "NASDAQ_DATA.csv", delimiter = ","; lr.GetDataToArray(x,file_name,delimiter,1); lr.GetDataToArray(y,file_name,delimiter,2); }
Ich habe die Bibliothek CsimpleLinearRegression, die wir im ersten Artikel erstellt haben, hier importiert:
CSimpleLinearRegression lr;
weil es bestimmte Funktionen gibt, die wir vielleicht verwenden wollen, z. B. um Daten in Arrays zu erhalten.
Finden wir xTx
MatrixMultiply(xT,m_xvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols); Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5); //remember?? the output of the matrix will be the row1 and col2 marked in red
Wenn Sie auf das Array xT[] achten, können Sie sehen, dass wir die x-Werte einfach kopiert und in diesem xT[]-Array gespeichert haben. Nur zur Klarstellung: Wie ich bereits sagte, haben wir mit der Funktion GetDataToArray() Daten aus unserer CSV-Datei in einem Array gesammelt, das bereits transponiert ist.
Wir haben dann das Array xT[] mit m_xvalues[] multipliziert, das nun untranponiert ist, m_xvalues ist das global definierte Array für unsere x-Werte in dieser Bibliothek, dies ist das Innere unserer Funktion MatrixMultiply():
void CSimpleMatLinearRegression::MatrixMultiply(double &A[],double &B[],double &output_arr[],int row1,int col1,int row2,int col2) { //--- double MultPl_Mat[]; //where the multiplications will be stored if (col1 != row2) Alert("Matrix Multiplication Error, \n The number of columns in the first matrix is not equal to the number of rows in second matrix"); else { ArrayResize(MultPl_Mat,row1*col2); int mat1_index, mat2_index; if (col1==1) //Multiplication for 1D Array { for (int i=0; i<row1; i++) for(int k=0; k<row1; k++) { int index = k + (i*row1); MultPl_Mat[index] = A[i] * B[k]; } //Print("Matrix Multiplication output"); //ArrayPrint(MultPl_Mat); } else { //if the matrix has more than 2 dimensionals for (int i=0; i<row1; i++) for (int j=0; j<col2; j++) { int index = j + (i*col2); MultPl_Mat[index] = 0; for (int k=0; k<col1; k++) { mat1_index = k + (i*row2); //k + (i*row2) mat2_index = j + (k*col2); //j + (k*col2) //Print("index out ",index," index a ",mat1_index," index b ",mat2_index); MultPl_Mat[index] += A[mat1_index] * B[mat2_index]; DBL_MAX_MIN(MultPl_Mat[index]); } //Print(index," ",MultPl_Mat[index]); } ArrayCopy(output_arr,MultPl_Mat); ArrayFree(MultPl_Mat); } } }
Um ehrlich zu sein, sieht diese Multiplikation verwirrend und hässlich aus, vor allem wenn Dinge wie:
k + (i*row2); j + (k*col2);
verwendet werden, entspann Dich Bruder !! Die Art und Weise, wie ich diese Indizes manipuliert habe, ist so, dass sie uns den Index in einer bestimmten Zeile und Spalte geben können. Dies könnte leicht verständlich sein, wenn ich z.B. Matrix[Zeilen][Spalten] verwendet hätte, was in diesem Fall Matrix[i][k] wäre, aber ich habe mich dagegen entschieden, weil mehrdimensionale Arrays Einschränkungen haben, also musste ich einen Weg finden. Ich habe einfachen c++ Code am Ende des Artikels verlinkt, der Ihnen helfen würde zu verstehen, wie ich das gemacht habe, oder Sie können diesen Blog lesen, um mehr darüber zu erfahren: https://www.programiz.com/cpp-programming/examples/matrix-multiplication
Die Ausgabe der erfolgreichen Funktion xTx unter Verwendung einer Funktion MatrixPrint() wird sein:
Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5);
xTx [ 744.00000 3257845.70000 3257845.70000 14275586746.32998 ]
Wie Sie sehen, enthält das erste Element in unserem xTx-Array die Anzahl der Beobachtungen für die einzelnen Daten in unserem Datensatz, weshalb es sehr wichtig ist, die Entwurfsmatrix zunächst in der allerersten Spalte mit Werten von eins zu füllen.
Lassen Sie uns nun die Inverse der xTx-Matrix ermitteln.
Inverse der xTx-Matrix
Um die Inverse einer 2x2-Matrix zu finden,
vertauschen wir zunächst das erste und das letzte Element der Diagonale, dann fügen wir negative Vorzeichen zu den beiden anderen Werten hinzu.
Die Formel ist in der folgenden Abbildung dargestellt:
Ermitteln wir die Determinante einer Matrix det(xTx) = Produkt der ersten Diagonale - Produkt der zweiten Diagonale:
Hier ist, wie wir die Inverse in mql5 Code finden können,
void CSimpleMatLinearRegression::MatrixInverse(double &Matrix[],double &output_mat[]) { // According to Matrix Rules the Inverse of a matrix can only be found when the // Matrix is Identical Starting from a 2x2 matrix so this is our starting point int matrix_size = ArraySize(Matrix); if (matrix_size > 4) Print("Matrix allowed using this method is a 2x2 matrix Only"); if (matrix_size==4) { MatrixtypeSquare(matrix_size); //first step is we swap the first and the last value of the matrix //so far we know that the last value is equal to arraysize minus one int last_mat = matrix_size-1; ArrayCopy(output_mat,Matrix); // first diagonal output_mat[0] = Matrix[last_mat]; //swap first array with last one output_mat[last_mat] = Matrix[0]; //swap the last array with the first one double first_diagonal = output_mat[0]*output_mat[last_mat]; // second diagonal //adiing negative signs >>> output_mat[1] = - Matrix[1]; output_mat[2] = - Matrix[2]; double second_diagonal = output_mat[1]*output_mat[2]; if (m_debug) { Print("Diagonal already Swapped Matrix"); MatrixPrint(output_mat,2,2); } //formula for inverse is 1/det(xTx) * (xtx)-1 //determinant equals the product of the first diagonal minus the product of the second diagonal double det = first_diagonal-second_diagonal; if (m_debug) Print("determinant =",det); for (int i=0; i<matrix_size; i++) { output_mat[i] = output_mat[i]*(1/det); DBL_MAX_MIN(output_mat[i]); } } }
Die Ausgabe der Ausführung dieses Codeblocks lautet:
Diagonal already Swapped Matrix
[
14275586746 -3257846
-3257846 744
]
determinant =7477934261.0234375 Drucken wir auch die Inverse der Matrix, um zu sehen, wie sie aussieht:
Print("inverse xtx"); MatrixPrint(inverse_xTx,2,2,_digits); //inverse of simple lr will always be a 2x2 matrix
Die Ausgabe schaut sicher so aus:
[
1.9090281 -0.0004357
-0.0004357 0.0000001
]
Jetzt haben wir die Inverse von xTx, und wir können weitermachen.
Finden von xTy
Hier multiplizieren wir xT[] mit den Werten y[]:
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //1 at the end is because the y values matrix will always have one column which is it Print("xTy"); MatrixPrint(xTy,tr_rows,1,_digits); //remember again??? how we find the output of our matrix row1 x column2
Die Ausgabe schaut sicher so aus:
xTy
[
10550016.7000000 46241904488.2699585
]
Siehe dazu die Formel:
Jetzt, da wir xTx invers und xTy haben, können wir die Sache abschließen:
MatrixMultiply(inverse_xTx,xTy,Betas,2,2,2,1); //inverse is a square 2x2 matrix while xty is a 2x1 Print("coefficients"); MatrixPrint(Betas,2,1,5); // for simple lr our betas matrix will be a 2x1
Mehr Details über den Aufruf der Funktion.
Die Ausgabe dieses Codeschnipsels wird sein:
coefficients
[
-5524.40278 4.49996
]
B A M !!! Dies ist das gleiche Ergebnis für die Koeffizienten, das wir mit unserem Modell in skalarer Form in Teil o1 dieser Artikelserie erhalten konnten.
Die Zahl am ersten Index des Arrays Betas wird immer die Konstante/der Y-Achsenabschnitt sein. Der Grund, warum wir in der Lage sind, sie anfangs zu erhalten, ist, dass wir die Entwurfsmatrix mit den Werten von eins in der ersten Spalte gefüllt haben.
Nun sind wir mit der einfachen linearen Regression fertig. Schauen wir uns an, wie die multiple Regression aussehen wird. Passen Sie gut auf, denn die Dinge können manchmal kompliziert werden.
Das Rätsel der multiplen dynamischen Regression ist gelöst.
Das Gute daran, unsere Modelle auf der Grundlage einer Matrix zu erstellen, ist, dass man sie leicht skalieren kann, ohne den Code großartig ändern zu müssen, wenn es um die Erstellung des Modells geht. Die wesentliche Änderung, die Sie bei der multiplen Regression bemerken werden, ist die Art und Weise, wie die Inverse einer Matrix gefunden wird, denn das ist der schwierigste Teil, den ich lange Zeit versucht habe herauszufinden. Ich werde später im Detail darauf eingehen, wenn wir zu diesem Abschnitt kommen, aber jetzt lassen Sie uns erst einmal die Dinge codieren, die wir in unserer Bibliothek MultipleMatrixRegression benötigen.
Wir könnten nur eine Bibliothek haben, die einfache und mehrfache Regression behandelt, indem sie uns nur die Funktionsargumente eingeben lässt, aber ich habe beschlossen, eine weitere Datei zu erstellen, um die Dinge zu verdeutlichen, da der Prozess fast derselbe ist, solange Sie die Berechnungen verstanden haben, die wir in unserem Abschnitt über einfache lineare Regression durchgeführt haben, den ich gerade erklärt habe.
Lassen Sie uns zunächst die grundlegenden Dinge codieren, die wir in unserer Bibliothek benötigen könnten:
class CMultipleMatLinearReg { private: int m_handle; string m_filename; string DataColumnNames[]; //store the column names from csv file int rows_total; int x_columns_chosen; //Number of x columns chosen bool m_debug; double m_yvalues[]; //y values or dependent values matrix double m_allxvalues[]; //All x values design matrix string m_XColsArray[]; //store the x columns chosen on the Init string m_delimiter; double Betas[]; //Array for storing the coefficients protected: bool fileopen(); void GetAllDataToArray(double& array[]); void GetColumnDatatoArray(int from_column_number, double &toArr[]); public: CMultipleMatLinearReg(void); ~CMultipleMatLinearReg(void); void Init(int y_column, string x_columns="", string filename = NULL, string delimiter = ",", bool debugmode=true); };
Dies geschieht innerhalb der Methode Init()
void CMultipleMatLinearReg::Init(int y_column,string x_columns="",string filename=NULL,string delimiter=",",bool debugmode=true) { //--- pass some inputs to the global inputs since they are reusable m_filename = filename; m_debug = debugmode; m_delimiter = delimiter; //--- ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen); //--- if (m_debug) { Print("Init, number of X columns chosen =",x_columns_chosen); ArrayPrint(m_XColsArray); } //--- GetAllDataToArray(m_allxvalues); GetColumnDatatoArray(y_column,m_yvalues); // check for variance in the data set by dividing the rows total size by the number of x columns selected, there shouldn't be a reminder if (rows_total % x_columns_chosen != 0) Alert("There are variance(s) in your dataset columns sizes, This may Lead to Incorrect calculations"); else { //--- Refill the first row of a design matrix with the values of 1 int single_rowsize = rows_total/x_columns_chosen; double Temp_x[]; //Temporary x array ArrayResize(Temp_x,single_rowsize); ArrayFill(Temp_x,0,single_rowsize,1); ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //after filling the values of one fill the remaining space with values of x //Print("Temp x arr size =",ArraySize(Temp_x)); ArrayCopy(m_allxvalues,Temp_x); ArrayFree(Temp_x); //we no longer need this array int tr_cols = x_columns_chosen+1, tr_rows = single_rowsize; ArrayCopy(xT,m_allxvalues); //store the transposed values to their global array before we untranspose them MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //we add one to leave the space for the values of one if (m_debug) { Print("Design matrix"); MatrixPrint(m_allxvalues,tr_cols,tr_rows); } } }
Weitere Einzelheiten zu den durchgeführten Maßnahmen:
ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen);
Hier erhalten wir die x-Spalten, die man ausgewählt hat (die unabhängigen Variablen), wenn man die Init-Funktion im TestScript aufruft, dann speichern wir diese Spalten in einem globalen Array m_XColsArray. Die Spalten in einem Array zu haben, hat Vorteile, da wir sie schnell erkennen können, sodass wir sie in der richtigen Reihenfolge in das Array aller x-Werte (unabhängige Variablen Matrix)/Designmatrix speichern können.
Wir müssen auch sicherstellen, dass alle Zeilen in unseren Datensätzen gleich sind, denn sobald es nur in einer Zeile oder Spalte einen Unterschied gibt, werden alle Berechnungen fehlschlagen.
if (rows_total % x_columns_chosen != 0) Alert("There are variances in your dataset columns sizes, This may Lead to Incorrect calculations");
Dann holen wir uns alle Daten der x-Spalten einer Matrix / Design-Matrix / Array aller unabhängigen Variablen (Sie können einen dieser Namen wählen).
GetAllDataToArray(m_allxvalues);
Wir wollen auch alle abhängigen Variablen in ihrer Matrix speichern.
GetColumnDatatoArray(y_column,m_yvalues);
Dies ist der entscheidende Schritt, um die Entwurfs-Matrix für die Berechnungen vorzubereiten, indem wir die Werte von eins in die erste Spalte unserer x-Werte-Matrix einfügen, wie bereits hier erwähnt:
{
//--- Refill the first row of a design matrix with the values of 1
int single_rowsize = rows_total/x_columns_chosen;
double Temp_x[]; //Temporary x array
ArrayResize(Temp_x,single_rowsize);
ArrayFill(Temp_x,0,single_rowsize,1);
ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //after filling the values of one fill the remaining space with values of x
//Print("Temp x arr size =",ArraySize(Temp_x));
ArrayCopy(m_allxvalues,Temp_x);
ArrayFree(Temp_x); //we no longer need this array
int tr_cols = x_columns_chosen+1,
tr_rows = single_rowsize;
MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //we add one to leave the space for the values of one
if (m_debug)
{
Print("Design matrix");
MatrixPrint(m_allxvalues,tr_cols,tr_rows);
}
} Diesmal geben wir die untransponierte Matrix beim Initialisieren der Bibliothek aus.
Das ist alles, was wir für Init() brauchen. Rufen wir sie in unserem multipleMatRegTestScript.mq5 (verlinkt am Ende des Artikels) auf.
#include "multipleMatLinearReg.mqh"; CMultipleMatLinearReg matreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string filename= "NASDAQ_DATA.csv"; matreg.Init(2,"1,3,4",filename); }
Die Ausgabe nach erfolgreichem Skriptlauf ist (dies ist nur ein Überblick):
Init, number of X columns chosen =3 "1" "3" "4" All data Array Size 2232 consuming 52 bytes of memory Design matrix Array [ 1 4174 13387 35 1 4179 13397 37 1 4183 13407 38 1 4186 13417 37 ...... ...... 1 4352 14225 47 1 4402 14226 56 1 4405 14224 56 1 4416 14223 60 ]
Ermitteln von xTx
Genau wie bei der einfachen Regression ist es hier derselbe Prozess, wir nehmen die Werte von xT, die die Rohdaten aus einer CSV-Datei sind, und multiplizieren sie mit der nicht transponierten Matrix:
MatrixMultiply(xT,m_allxvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols);
Die Ausgabe, wenn die xTx-Matrix ausgedruckt wird, lautet:
xTx [ 744.00 3257845.70 10572577.80 36252.20 3257845.70 14275586746.33 46332484402.07 159174265.78 10572577.80 46332484402.07 150405691938.78 515152629.66 36252.20 159174265.78 515152629.66 1910130.22 ]
Cool, es funktioniert wie erwartet.
Die Inverse von xTx
Dies ist der wichtigste Teil der multiplen Regression, Sie sollten gut aufpassen, denn die Dinge werden jetzt kompliziert, wir werden jetzt tief in die Mathematik einsteigen
Als wir im vorherigen Teil die Inverse unserer xTx gefunden haben, haben wir die Inverse einer 2x2-Matrix gefunden. Aber jetzt sind wir nicht mehr an diesem Punkt, sondern wir finden die Inverse einer 4x4-Matrix, weil wir 3 Spalten als unsere unabhängigen Variablen ausgewählt haben. Wenn wir die Werte einer Spalte addieren, haben wir 4 Spalten, die uns zu einer 4x4-Matrix führen, wenn wir versuchen, die Inverse zu finden,
Wir können die Methode, die wir vorher benutzt haben, diesmal nicht mehr verwenden, um die Inverse zu finden. Die eigentliche Frage ist Warum?
Hier steht, wie man die Inverse einer Matrix mit der Determinanten-Methode finden kann. Die, die wir vorher verwendet haben, funktioniert nicht, wenn die Matrizen riesig sind, man kann sie nicht einmal benutzen, um die Inverse einer 3x3-Matrix zu finden.
Viele Methoden wurden von verschiedenen Mathematikern erfunden, um die Inverse einer Matrix zu finden, eine davon ist die klassische Adjunkte-Methode, aber nach meinen Recherchen sind die meisten dieser Methoden schwer zu kodieren und können manchmal verwirrend sein. Wenn Sie mehr Details über die Methoden erfahren wollen und wie sie kodiert werden können, schauen Sie sich diesen Blogbeitrag an: https://www.geertarien.com/blog/2017/05/15/different-methods-for-matrix-inversion/.
Von allen Methoden habe ich mich für die Gauß-Jordan-Elimination entschieden, weil ich herausgefunden habe, dass sie zuverlässig, einfach zu kodieren und leicht skalierbar ist. Es gibt ein großartiges Video https://www.youtube.com/watch?v=YcP_KOB6KpQ, das die Gauß-Jordan-Elimination gut erklärt, ich hoffe, es hilft dir, das Konzept zu verstehen.
Ok, also lasst uns den Gauß-Jordan codieren, wenn der Code schwer zu verstehen ist, habe ich einen C++ Code für den gleichen Code unten verlinkt und auf meinem GitHub auch unten verlinkt, das könnte helfen zu verstehen, wie die Dinge gemacht wurden.
void CMultipleMatLinearReg::Gauss_JordanInverse(double &Matrix[],double &output_Mat[],int mat_order) { int rowsCols = mat_order; //--- Print("row cols ",rowsCols); if (mat_order <= 2) Alert("To find the Inverse of a matrix Using this method, it order has to be greater that 2 ie more than 2x2 matrix"); else { int size = (int)MathPow(mat_order,2); //since the array has to be a square // Create a multiplicative identity matrix int start = 0; double Identity_Mat[]; ArrayResize(Identity_Mat,size); for (int i=0; i<size; i++) { if (i==start) { Identity_Mat[i] = 1; start += rowsCols+1; } else Identity_Mat[i] = 0; } //Print("Multiplicative Indentity Matrix"); //ArrayPrint(Identity_Mat); //--- double MatnIdent[]; //original matrix sided with identity matrix start = 0; for (int i=0; i<rowsCols; i++) //operation to append Identical matrix to an original one { ArrayCopy(MatnIdent,Matrix,ArraySize(MatnIdent),start,rowsCols); //add the identity matrix to the end ArrayCopy(MatnIdent,Identity_Mat,ArraySize(MatnIdent),start,rowsCols); start += rowsCols; } //--- int diagonal_index = 0, index =0; start = 0; double ratio = 0; for (int i=0; i<rowsCols; i++) { if (MatnIdent[diagonal_index] == 0) Print("Mathematical Error, Diagonal has zero value"); for (int j=0; j<rowsCols; j++) if (i != j) //if we are not on the diagonal { /* i stands for rows while j for columns, In finding the ratio we keep the rows constant while incrementing the columns that are not on the diagonal on the above if statement this helps us to Access array value based on both rows and columns */ int i__i = i + (i*rowsCols*2); diagonal_index = i__i; int mat_ind = (i)+(j*rowsCols*2); //row number + (column number) AKA i__j ratio = MatnIdent[mat_ind] / MatnIdent[diagonal_index]; DBL_MAX_MIN(MatnIdent[mat_ind]); DBL_MAX_MIN(MatnIdent[diagonal_index]); //printf("Numerator = %.4f denominator =%.4f ratio =%.4f ",MatnIdent[mat_ind],MatnIdent[diagonal_index],ratio); for (int k=0; k<rowsCols*2; k++) { int j_k, i_k; //first element for column second for row j_k = k + (j*(rowsCols*2)); i_k = k + (i*(rowsCols*2)); //Print("val =",MatnIdent[j_k]," val = ",MatnIdent[i_k]); //printf("\n jk val =%.4f, ratio = %.4f , ik val =%.4f ",MatnIdent[j_k], ratio, MatnIdent[i_k]); MatnIdent[j_k] = MatnIdent[j_k] - ratio*MatnIdent[i_k]; DBL_MAX_MIN(MatnIdent[j_k]); DBL_MAX_MIN(ratio*MatnIdent[i_k]); } } } // Row Operation to make Principal diagonal to 1 /*back to our MatrixandIdentical Matrix Array then we'll perform operations to make its principal diagonal to 1 */ ArrayResize(output_Mat,size); int counter=0; for (int i=0; i<rowsCols; i++) for (int j=rowsCols; j<2*rowsCols; j++) { int i_j, i_i; i_j = j + (i*(rowsCols*2)); i_i = i + (i*(rowsCols*2)); //Print("i_j ",i_j," val = ",MatnIdent[i_j]," i_i =",i_i," val =",MatnIdent[i_i]); MatnIdent[i_j] = MatnIdent[i_j] / MatnIdent[i_i]; //printf("%d Mathematical operation =%.4f",i_j, MatnIdent[i_j]); output_Mat[counter]= MatnIdent[i_j]; //store the Inverse of Matrix in the output Array counter++; } } //--- }
Rufen wir also die Funktion auf und drucken wir die Inverse einer Matrix aus.
double inverse_xTx[]; Gauss_JordanInverse(xTx,inverse_xTx,tr_cols); if (m_debug) { Print("xtx Inverse"); MatrixPrint(inverse_xTx,tr_cols,tr_cols,7); }
Die Ausgabe schaut sicher so aus:
xtx Inverse [ 3.8264763 -0.0024984 0.0004760 0.0072008 -0.0024984 0.0000024 -0.0000005 -0.0000073 0.0004760 -0.0000005 0.0000001 0.0000016 0.0072008 -0.0000073 0.0000016 0.0000290 ]
Nicht vergessen!! Um die Inverse einer Matrix zu finden, muss es sich um eine quadratische Matrix handeln. Aus diesem Grund haben wir in den Funktionsargumenten das Argument mat_order, das der Anzahl der Zeilen und Spalten entspricht.
Finden von xTy
Jetzt wollen wir das Matrixprodukt von x transponiert und Y finden, das gleiche Verfahren wie vorher:
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //remember!! the value of 1 at the end is because we have only one dependent variable y
Wenn die Ausgabe ausgedruckt wird, sieht sie wie folgt aus:
xTy [ 10550016.70000 46241904488.26996 150084914994.69019 516408161.98000 ]
Cool, eine 1x4-Matrix wie erwartet.
Siehe dazu die Formel:
Nun, da wir alles haben, was wir brauchen, um die Koeffizienten zu finden, können wir das Ganze abschließen:
MatrixMultiply(inverse_xTx,xTy,Betas,tr_cols,tr_cols,tr_cols,1); Das Ergebnis ist (noch einmal zur Erinnerung: Das erste Element unserer Koeffizienten/Beta-Matrix ist die Konstante oder, anders ausgedrückt, der y-Achsenabschnitt:
Coefficients Matrix [ -3670.97167 2.75527 0.37952 8.06681 ]
Großartig, jetzt möchte ich mit Python beweisen, dass ich falsch liege:
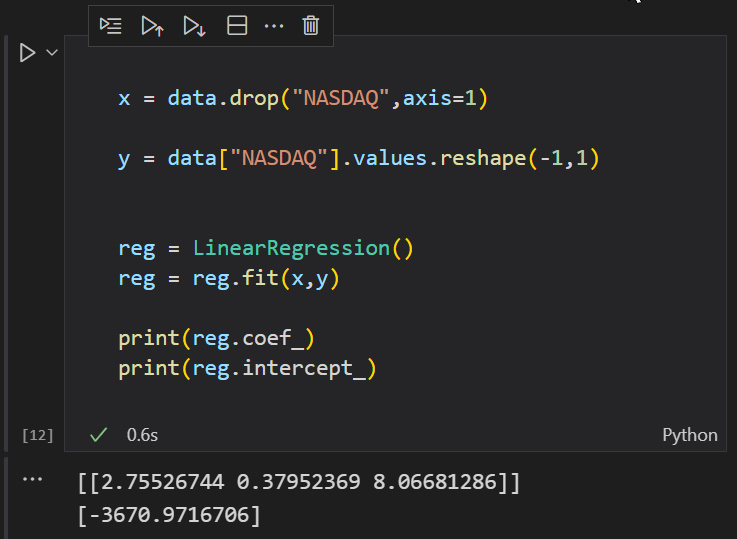
double B A M ! ! ! Diesmal
Jetzt ist es endlich möglich, multiple dynamische Regressionsmodelle in mql5 zu erstellen. Lassen Sie uns sehen, wo alles angefangen hat.
Alles begann hier:
matreg.Init(2,"1,3,4",filename);
Die Idee war, eine Zeichenketteneingabe zu haben, die uns helfen könnte, eine unbegrenzte Anzahl von unabhängigen Variablen zu setzen, und es scheint, dass es in mql5 keine Möglichkeit gibt, *args und *kwargs von Sprachen wie Python zu haben, die uns zu viele Argumente eingeben lassen könnten. Also war unsere einzige Möglichkeit, dies zu tun, eine Zeichenkette zu verwenden und dann einen Weg zu finden, wie wir das Array manipulieren können, damit nur ein einziges Array alle unsere Daten enthält. Später können wir dann einen Weg finden, sie zu manipulieren, siehe meinen ersten erfolglosen Versuch für weitere Informationen https://www. mql5.com/en/code/38894. Der Grund, warum ich das alles sage, ist, weil ich glaube, dass jemand den gleichen Weg bei diesem oder einem anderen Projekt gehen könnte, ich erkläre nur, was bei mir funktioniert hat und was nicht.
Abschließende Überlegungen
So cool es auch klingen mag, dass Sie jetzt so viele unabhängige Variablen haben können, wie Sie wollen, denken Sie daran, dass es eine Grenze gibt, wenn Sie zu viele unabhängige Variablen oder sehr lange Datensatzspalten haben, die zu Berechnungsbeschränkungen durch einen Computer führen könnten, wie Sie gerade gesehen haben, könnten die Matrixberechnungen auch zu einer großen Zahl während der Berechnungen kommen.
Das Hinzufügen von unabhängigen Variablen zu einem multiplen linearen Regressionsmodell erhöht immer die Varianz der abhängigen Variable, die typischerweise als r-Quadrat ausgedrückt wird; daher kann das Hinzufügen zu vieler unabhängiger Variablen ohne theoretische Begründung zu einem überangepassten Modell führen.
Wenn wir zum Beispiel ein Modell wie im ersten Artikel dieser Serieauf der Grundlage von nur zwei abhängigen Variablen (NASDAQ) und unabhängigen Variablen (S&P500) erstellt hätten, hätte unsere Genauigkeit mehr als 95 % betragen können, aber das ist in diesem Fall vielleicht nicht der Fall, weil wir jetzt drei unabhängige Variablen haben.
Es ist immer eine gute Idee, die Genauigkeit Ihres Modells zu überprüfen, nachdem es erstellt wurde. Außerdem sollten Sie vor der Erstellung eines Modells überprüfen, ob es eine Korrelation zwischen jeder unabhängigen Variable und dem Ziel gibt.
Bauen Sie das Modell immer auf Daten auf, die nachweislich eine starke lineare Beziehung zu Ihrer Zielvariablen aufweisen.
Danke fürs Lesen, mein GitHub Repository ist hier zu finden https://github.com/MegaJoctan/MatrixRegressionMQL5.git
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/10928
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Lernen Sie, wie man ein Handelssystem mit Hilfe von Parabolic SAR entwickelt
Lernen Sie, wie man ein Handelssystem mit Hilfe von Parabolic SAR entwickelt
 Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 7): Hinzufügen des Volumens zum Preis (I)
Einen handelnden Expert Advisor von Grund auf neu entwickeln (Teil 7): Hinzufügen des Volumens zum Preis (I)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.

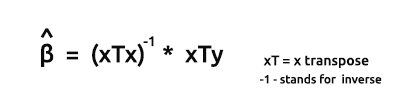
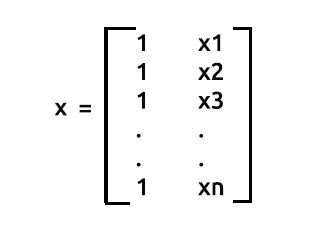
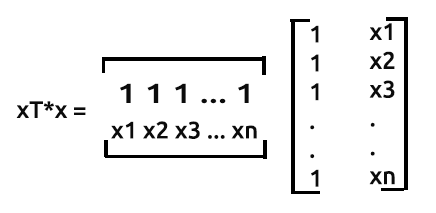

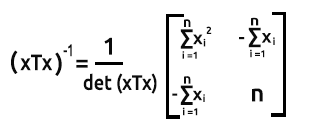
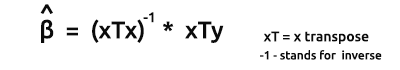
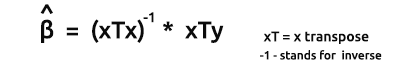
Der neue Artikel Data Science und Maschinelles Lernen Teil 03: Matrixregressionen wurde veröffentlicht:
Autor: Omega J Msigwa