MetaTrader 5 / 交易
English Русский Deutsch 日本語
preview
基于隐马尔可夫模型的趋势跟踪波动率预测

基于隐马尔可夫模型的趋势跟踪波动率预测

MetaTrader 5 — 交易 |
55 0
Zhuo Kai Chen
Zhuo Kai Chen

概述

隐马尔可夫模型（HMMs）是强大的统计工具，可通过分析可观测的价格波动来识别潜在的市场状态。在交易领域，隐马尔可夫模型通过建模和预测市场状态的转变，可提升波动率预测的准确性，并为趋势跟踪策略提供依据。 

在本文中，我们将完整介绍一种趋势跟踪策略的开发流程，该策略利用隐马尔可夫模型预测波动率，并将其作为交易信号的过滤条件。该流程包括：在MetaTrader 5平台上使用MQL5开发核心策略框架，在Python环境中获取数据并训练隐马尔可夫模型，最后将训练好的模型重新集成到MetaTrader 5中，通过回测验证策略有效性。


契机

在戴夫·阿伦森（Dave Aronson）所著的《基于证据的技术分析》（Evidence-Based Technical Analysis）一书中，他建议交易者采用科学的方法开发交易策略。这一过程始于基于直觉形成假设，并通过严格测试来避免数据监测偏差。在本文中，我们将尝试采用同样的方法。首先，我们必须尝试理解什么是隐马尔可夫模型，以及它为何有助于我们的策略开发。

隐马尔可夫模型是一种无监督机器学习模型，用于描述系统底层状态不可观测但可通过可观测事件或数据推断的场景。该模型基于马尔可夫假设，即系统的未来状态仅取决于当前的状态，而与过去的状态无关。在隐马尔可夫模型中，系统被建模为一组离散状态，每个状态都有一定的概率转移到其他状态。这些转移由一组称为转移概率的概率所控制。系统会生成可观测数据（如资产价格或市场收益率），但状态本身无法直接观测，因此得名“隐含”。

隐马尔可夫模型的组成部分包括：

  1. 状态：指系统的不可观测条件或市场状态。在金融市场中，这些状态可能代表不同的市场环境，例如牛市、熊市，或高波动率与低波动率时期。这些状态根据特定的概率规则演变。

  2. 转移概率：定义从一个状态转移到另一个状态的可能性。根据马尔可夫性质，系统在时间t的状态仅取决于时间t-1的状态。转移矩阵用于量化这些概率。

  3. 发生概率：描述在给定底层状态的情况下，观测到特定数据（如股票价格或收益率）的可能性。每个状态都有一个概率分布，用于确定在该状态下观察到特定市场条件或价格变动的可能性。

  4. 初始概率：表示系统从特定状态开始的概率，为模型分析提供起点。

基于这些组成部分，模型利用贝叶斯推断（Bayesian inference）根据观测数据推断出最可能的隐含状态序列。通常通过前向-后向算法（Forward-Backward algorithm）或维特比算法（Viterbi algorithm）实现，这些算法用于估计给定隐含状态序列下观测数据的可能性。

在交易中，波动率是影响资产价格和市场动态的关键因素。隐马尔可夫模型在预测波动率方面尤为有效，因为它能够识别出不可直接观测但对市场行为有重大影响的底层市场状态。

  1. 识别市场状态：通过将市场条件划分为不同状态（如高波动率或低波动率），隐马尔可夫模型能够捕捉市场状态的转变。这有助于交易者了解市场何时可能经历高波动率或稳定时期，这些都会直接影响资产价格。

  2. 波动率聚集：金融市场表现出波动率聚集现象，即高波动率时期之后往往跟随高波动率，低波动率时期之后往往跟随低波动率。隐马尔可夫模型可以通过为高波动率或低波动率状态分配长期保持的高概率，来模拟这一特征，从而提供对未来市场走势更准确的预测。

  3. 波动率预测：通过观察不同市场状态之间的转移，隐马尔可夫模型可以提供对未来波动率的预测性见解。例如，如果模型识别出市场处于高波动率状态，交易者可以预期价格波动将更大，并相应调整策略。此外，如果市场正在向低波动率状态转变，模型可以帮助交易者调整风险敞口或调整交易策略。

  4. 适应性：隐马尔可夫模型能够根据新数据持续更新其概率分布和状态转移，使其能够适应不断变化的市场条件。这种实时调整能力使交易者能够预见波动率的变化，并动态调整策略，从而获得优势。

正如众多学者所研究的那样，我们的假设是：在高波动率环境下，我们的趋势跟踪策略往往表现更优，因为更大的市场波动会推动价格形成趋势。我们计划使用隐马尔可夫模型对波动率进行聚类，并定义高波动率和低波动率状态。然后，我们将训练一个模型来预测下一个波动率状态是高还是低。如果策略发出交易信号的同时，模型预测为高波动率状态，我们将入场交易；否则，我们将不参与市场。


核心策略框架

我们将采用的趋势跟踪策略与我在此前一篇机器学习相关文章中实现的一致。其基本逻辑基于两条移动平均线：一条快速线和一条慢速线。当两条移动平均线交叉时产生交易信号，交易方向跟随快速移动平均线，因此称为“趋势跟踪”。当价格穿越慢速移动平均线时触发离场信号，为跟踪止损留出更大空间。完整代码如下：

#include <Trade/Trade.mqh>
//XAU - 1h.
CTrade trade;

input ENUM_TIMEFRAMES TF = PERIOD_CURRENT;
input ENUM_MA_METHOD MaMethod = MODE_SMA;
input ENUM_APPLIED_PRICE MaAppPrice = PRICE_CLOSE;
input int MaPeriodsFast = 15;
input int MaPeriodsSlow = 25;
input int MaPeriods = 200;
input double lott = 0.01;
ulong buypos = 0, sellpos = 0;
input int Magic = 0;
int barsTotal = 0;
int handleMaFast;
int handleMaSlow;
int handleMa;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
   trade.SetExpertMagicNumber(Magic);
   handleMaFast =iMA(_Symbol,TF,MaPeriodsFast,0,MaMethod,MaAppPrice);
   handleMaSlow =iMA(_Symbol,TF,MaPeriodsSlow,0,MaMethod,MaAppPrice);  
   handleMa = iMA(_Symbol,TF,MaPeriods,0,MaMethod,MaAppPrice); 
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {

  }  

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  //Beware, the last element of the buffer list is the most recent data, not [0]
  if (barsTotal!= bars){
     barsTotal = bars;
     double maFast[];
     double maSlow[];
     double ma[];
     CopyBuffer(handleMaFast,BASE_LINE,1,2,maFast);
     CopyBuffer(handleMaSlow,BASE_LINE,1,2,maSlow);
     CopyBuffer(handleMa,0,1,1,ma);
     double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
     double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
     double lastClose = iClose(_Symbol, PERIOD_CURRENT, 1);
     //The order below matters
     if(buypos>0&& lastClose<maSlow[1]) trade.PositionClose(buypos);
     if(sellpos>0 &&lastClose>maSlow[1])trade.PositionClose(sellpos);   
     if (maFast[1]>maSlow[1]&&maFast[0]<maSlow[0]&&buypos ==sellpos)executeBuy(); 
     if(maFast[1]<maSlow[1]&&maFast[0]>maSlow[0]&&sellpos ==buypos) executeSell();
     if(buypos>0&&(!PositionSelectByTicket(buypos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      buypos = 0;
      }
     if(sellpos>0&&(!PositionSelectByTicket(sellpos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      sellpos = 0;
      }
    }
 }

//+------------------------------------------------------------------+
//| Expert trade transaction handling function                       |
//+------------------------------------------------------------------+
void OnTradeTransaction(const MqlTradeTransaction& trans, const MqlTradeRequest& request, const MqlTradeResult& result) {
    if (trans.type == TRADE_TRANSACTION_ORDER_ADD) {
        COrderInfo order;
        if (order.Select(trans.order)) {
            if (order.Magic() == Magic) {
                if (order.OrderType() == ORDER_TYPE_BUY) {
                    buypos = order.Ticket();
                } else if (order.OrderType() == ORDER_TYPE_SELL) {
                    sellpos = order.Ticket();
                }
            }
        }
    }
}

//+------------------------------------------------------------------+
//| Execute sell trade function                                      |
//+------------------------------------------------------------------+
void executeSell() {      
       double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
       bid = NormalizeDouble(bid,_Digits);
       trade.Sell(lott,_Symbol,bid);  
       sellpos = trade.ResultOrder();  
       }   

//+------------------------------------------------------------------+
//| Execute buy trade function                                       |
//+------------------------------------------------------------------+
void executeBuy() {
       double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
       ask = NormalizeDouble(ask,_Digits);
       trade.Buy(lott,_Symbol,ask);
       buypos = trade.ResultOrder();
}

我不会再就核心策略的验证及选择建议展开赘述。更多详细内容可参阅我此前发布的机器学习相关文章，链接已附此处。


获取数据

在本文中，我们将定义两种状态：高波动率（用1表示）和低波动率（用0表示）。波动率将根据最近50根K线的收益率标准差来定义，具体公式如下：

波动率计算公式

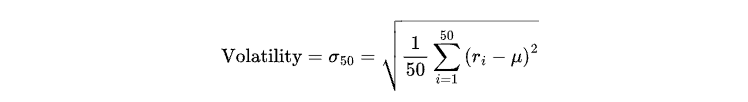
其中：

  • ri表示第i根K线的收益率（根据相邻两根收盘K线的价格变动百分比计算得出）。

  • μ是最近50根收盘K线的平均收益率，计算公式如下：

平均收益率

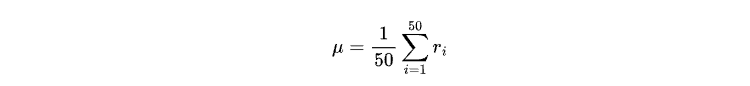
在训练模型时，我们仅需收盘价数据和日期时间信息。尽管可以直接从MetaTrader 5终端获取数据，但该终端提供的大部分数据仅限于实时tick数据。若要从经纪商处获取更长时间周期的OHLC（开盘价、最高价、最低价、收盘价）数据，我们可以创建一个获取OHLC数据的EA来处理此任务。

#include <FileCSV.mqh>

int barsTotal = 0;
CFileCSV csvFile;

input string fileName = "Name.csv";
string headers[] = {
    "time",
    "close"
};

string data[100000][2];
int indexx = 0;
vector xx;

input bool SaveData = true;

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {//Initialize model
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   if (!SaveData) return;
   if(csvFile.Open(fileName, FILE_WRITE|FILE_ANSI))
     {
      //Write the header
      csvFile.WriteHeader(headers);
      //Write data rows
      csvFile.WriteLine(data);
      //Close the file
      csvFile.Close();
     }
   else
     {
      Print("File opening error!");
     }

  }
  
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  
  if (barsTotal!= bars){
     barsTotal = bars;
   data[indexx][0] =(string)TimeTradeServer() ;
   data[indexx][1] = DoubleToString(iClose(_Symbol,PERIOD_CURRENT,1), 8); 
   indexx++;
   }
 }

此代码用于将金融数据（时间戳和收盘价）读写至CSV文件。在每个tick数据到达时，程序会检测K线数量是否发生变化。如果检测到变化，则将当前交易品种的服务器时间和收盘价更新至数据数组。当脚本反初始化时，会将收集到的数据写入CSV文件，包含表头和多行数据记录。文件操作采用 CFileCSV类实现。

在策略测试器中以指定时间周期运行该EA，生成的CSV文件将自动保存至/Tester/Agent-sth000目录中。

获取设置

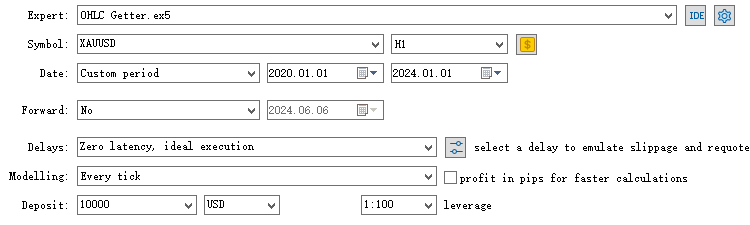
我们将使用2020年1月1日至2024年1月1日的样本内数据进行模型训练。2024年1月1日至2025年1月1日的数据将用于样本外测试。


训练模型

现在，打开任意Python编辑器，并确保按照本节要求通过pip安装所需的库。

初始CSV文件仅包含一列数据，其中时间戳和收盘价以分号分隔混合存储。为优化存储效率，这些值均以字符串的形式保存。处理时需按以下方式读取CSV文件，将两列数据分离，并将字符串转换为datetime和float类型：

import pandas as pd
data = pd.read_csv("XAU_test.csv",sep=";")
data = data.dropna()
data["close"] = data["close"].astype(float)
data['time'] = pd.to_datetime(data['time'])
data.set_index('time', inplace=True)

波动率可通过以下代码轻松计算：

data['volatility'] = data['returns'].rolling(window=50).std()

接下来，我们可视化波动率分布以更好理解其特征。从图中可以清晰看出，波动率近似服从正态分布。

波动率数值


波动率分布

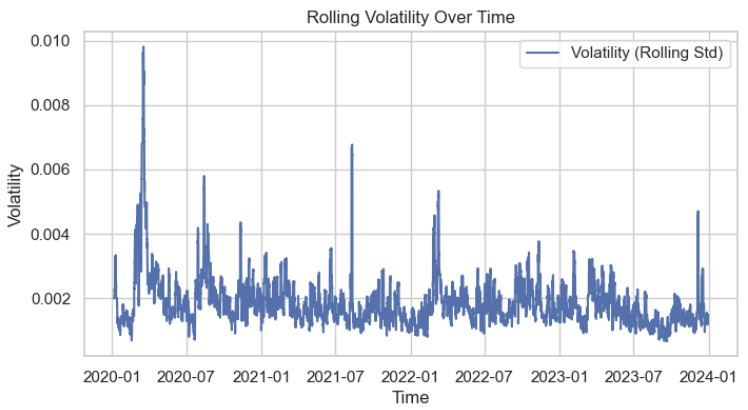
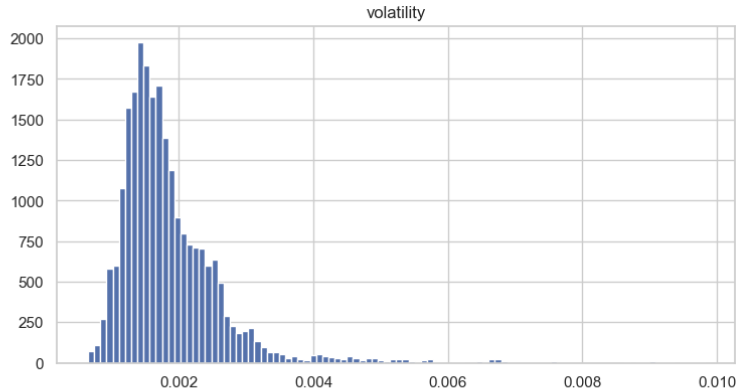
我们采用增广迪基-富勒检验（Augmented Dickey-Fuller, ADF）来验证波动率数据的平稳性。该检验最有可能得出以下结果：

Augmented Dickey-Fuller Test: Volatility
ADF Statistic: -13.120552520156329
p-value: 1.5664189630119278e-24
# Lags Used: 46
Number of Observations Used: 23516
=> The series is likely stationary.

尽管隐马尔可夫模型因具备滚动更新特性，对平稳数据并非严格必需，但使用平稳数据能显著优化聚类效果并提升模型精度。

尽管波动率数据可能已呈现平稳且服从正态分布的特征，我们仍需将其标准化为标准正态分布，使得数据范围更易于处理。 

在统计学中，这一过程称为数据标准化（scaling），通过以下公式可将任意正态分布的随机变量x转换为标准正态分布（N(0,1) ）：

数据标准化

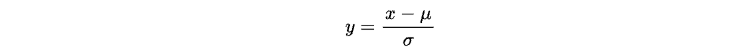
其中，μ表示变量x的均值，σ表示其标准差。

需要特别注意的是，后续将标准化流程集成至MetaTrader 5编辑器时，必须执行完全相同的标准化操作。因此，我们需同时保存均值μ和标准差σ的计算结果。

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled_volatility = scaler.fit_transform(data[['volatility']])
scaled_volatility = scaled_volatility.reshape(-1, 1)
scaler_mean = scaler.mean_[0]  # Mean of the volatility feature
scaler_std = scaler.scale_[0]  # Standard deviation of the volatility feature

随后，我们使用标准化后的波动率数据按如下方式训练模型：

from hmmlearn import hmm
import numpy as np
# Define the number of hidden states
n_states = 2
# Initialize the Gaussian HMM
model = hmm.GaussianHMM(n_components=n_states, covariance_type="full", n_iter=100, random_state=42, verbose = True)
# Fit the model to the scaled volatility data
model.fit(scaled_volatility)

在对每个训练数据点的隐含状态进行预测时，聚类分布呈现出高度合理性，仅存在微小误差。

# Predict the hidden states
hidden_states = model.predict(scaled_volatility)

# Add the hidden states to your dataframe
data['hidden_state'] = hidden_states
plt.figure(figsize=(14, 6))
for state in range(n_states):
    state_mask = data['hidden_state'] == state
    plt.plot(data.index[state_mask], data['volatility'][state_mask], 'o', label=f'State {state}')
plt.title('Hidden States and Rolling Volatility')
plt.xlabel('Time')
plt.ylabel('Volatility')
plt.legend()
plt.show()

隐马尔可夫模型数据标准化

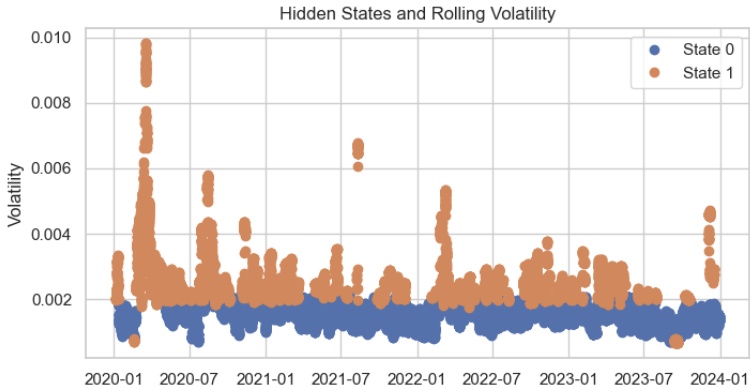
最后，我们将所需的输出结果格式化为MQL5语言，并将其保存至JSON头文件，以便将对应的矩阵数值直接复制粘贴到MetaTrader 5编辑器中。

import json

# Your HMM model parameters
transition_matrix = model.transmat_
means = model.means_
covars = model.covars_

# Construct the data in the required format
data = {
    "A": [
        [transition_matrix[0, 0], transition_matrix[0, 1]],
        [transition_matrix[1, 0], transition_matrix[1, 1]]
    ],
    "mu": [means[0, 0], means[1, 0]],
    "sigma_sq": [covars[0, 0], covars[1, 0]],
    "scaler_mean": scaler_mean,
    "scaler_std": scaler_std
}

# Create the output content in the desired format
output_str = """
const double A[2][2] = { 
    {%.16f, %.16f}, 
    {%.16f, %.16f}
};
const double mu[2] = {%.16f, %.16f};
const double sigma_sq[2] = {%.16f, %.16f};
const double scaler_mean = %.16f;
const double scaler_std = %.16f;
""" % (
    data["A"][0][0], data["A"][0][1], data["A"][1][0], data["A"][1][1],
    data["mu"][0], data["mu"][1],
    data["sigma_sq"][0], data["sigma_sq"][1],
    data["scaler_mean"], data["scaler_std"]
)

# Write to a file
with open('model_parameters.h', 'w') as f:
    f.write(output_str)

print("Parameters saved to model_parameters.h")

结果文件大致如下：

const double A[2][2] = { 
    {0.9941485184089348, 0.0058514815910651}, 
    {0.0123877225858242, 0.9876122774141759}
};
const double mu[2] = {-0.4677410059727503, 0.9797900996225393};
const double sigma_sq[2] = {0.1073520489683212, 1.4515804806463273};
const double scaler_mean = 0.0018685496675093;
const double scaler_std = 0.0008350190448735;

我们需将这些矩阵数值以全局变量的形式粘贴到EA的代码中。


系统集成

现在，我们返回MetaTrader 5代码编辑器，在原有策略代码的基础上进行扩展开发。

首先需要创建用于计算滚动更新波动率的函数模块。

//+------------------------------------------------------------------+
//| Get volatility Function                                          |
//+------------------------------------------------------------------+
void GetVolatility(){
// Step 1: Get the last two close prices to compute the latest percent change
        double close_prices[2];
        int copied = CopyClose(_Symbol, PERIOD_CURRENT, 1, 2, close_prices);
        if(copied != 2){
            Print("Failed to copy close prices. Copied: ", copied);
            return;
        }
        
        // Step 2: Compute the latest percent change
        double latest_close = close_prices[0];
        double previous_close = close_prices[1];
        double percent_change = 0.0;
        if(previous_close != 0){
            percent_change = (latest_close - previous_close) / previous_close;
        }
        else{
            Print("Previous close price is zero. Percent change set to 0.");
        }
        
        // Step 3: Update the percent_changes buffer
        percent_changes[percent_change_index] = percent_change;
        percent_change_index++;
        if(percent_change_index >= 50){
            percent_change_index = 0;
            percent_change_filled = true;
        }
        
        // Step 4: Once the buffer is filled, compute the rolling std dev
        if(percent_change_filled){
            double current_stddev = ComputeStdDev(percent_changes, 50);
            // Step 5: Scale the std dev
            double scaled_stddev = (current_stddev - scaler_mean) / scaler_std;
            
            // Step 6: Update the volatility array (ring buffer for Viterbi)
            // Shift the volatility array to make room for the new std dev
            for(int i = 0; i < 49; i++){
                volatility[i] = volatility[i+1];
            }
            volatility[49] = scaled_stddev; // Insert the latest std dev
       }
}

//+------------------------------------------------------------------+
//| Compute Standard Deviation Function                              |
//+------------------------------------------------------------------+
double ComputeStdDev(double &data[], int size)
{
    if(size <= 1)
        return 0.0;
    
    double sum = 0.0;
    double sum_sq = 0.0;
    for(int i = 0; i < size; i++)
    {
        sum += data[i];
        sum_sq += data[i] * data[i];
    }
    double mean = sum / size;
    double variance = (sum_sq - (sum * sum) / size) / (size - 1);
    return MathSqrt(variance);
}
  • GetVolatility()函数通过计算标准化后的价格百分比变动标准差，实现滚动波动率的动态追踪与存储。
  • ComputeDtsDev()作为辅助函数，用于计算指定数据数组的标准差。 

随后，我们编写两个核心函数，基于预计算的矩阵参数与当前滚动波动率，实时推断当前的隐含状态。

//+------------------------------------------------------------------+
//| Viterbi Algorithm Implementation in MQL5                         |
//+------------------------------------------------------------------+
int Viterbi(double &obs[], int &states[])
{
    // Initialize dynamic programming tables
    double T1[2][50];
    int T2[2][50];

    // Initialize first column
    for(int s = 0; s < 2; s++)
    {
         double emission_prob = (1.0 / MathSqrt(2 * M_PI * sigma_sq[s])) * MathExp(-MathPow(obs[0] - mu[s], 2) / (2 * sigma_sq[s])) + 1e-10;

        T1[s][0] = MathLog(pi[s]) + MathLog(emission_prob);
        T2[s][0] = 0;
    }

    // Fill the tables
    for(int t = 1; t < 50; t++)
    {
        for(int s = 0; s < 2; s++)
        {
            double max_prob = -DBL_MAX; // Initialize to negative infinity
            int max_state = 0;
            for(int s_prev = 0; s_prev < 2; s_prev++)
            {
                double transition_prob = A[s_prev][s];
                if(transition_prob <= 0) transition_prob = 1e-10; // Prevent log(0)
                double prob = T1[s_prev][t-1] + MathLog(transition_prob);
                if(prob > max_prob)
                {
                    max_prob = prob;
                    max_state = s_prev;
                }
            }
            // Calculate emission probability with epsilon
            double emission_prob = (1.0 / MathSqrt(2 * M_PI * sigma_sq[s])) * MathExp(-MathPow(obs[t] - mu[s], 2) / (2 * sigma_sq[s])) + 1e-10;
            T1[s][t] = max_prob + MathLog(emission_prob);
            T2[s][t] = max_state;
        }
    }

    // Backtrack to find the optimal state sequence
    // Find the state with the highest probability in the last column
    double max_final_prob = -DBL_MAX;
    int last_state = 0;
    for(int s = 0; s < 2; s++)
    {
        if(T1[s][49] > max_final_prob)
        {
            max_final_prob = T1[s][49];
            last_state = s;
        }
    }    
    // Initialize the states array
    ArrayResize(states, 50);
    states[49] = last_state;
    // Backtrack
    for(int t = 48; t >= 0; t--)
    {
        states[t] = T2[states[t+1]][t+1];
    }
    return 0; // Success
}

//+------------------------------------------------------------------+
//| Predict Current Hidden State                                     |
//+------------------------------------------------------------------+
int PredictCurrentState(double &obs[])
{   
    // Define states array
    int states[50];
    
    // Apply Viterbi
    int ret = Viterbi(obs, states);
    if(ret != 0)
        return -1; // Error
    
    // Return the most probable current state
    return states[49];
}

Viterbi()函数实现了维特比算法——一种基于动态规划的方法，用于在给定观测序列（obs[]）的情况下，求解隐马尔可夫模型中最可能的隐含状态序列。

1. 初始化：

  • 动态规划表定义：

    • T1[s][t]：记录在时刻t结束于状态s的最优路径对数概率。
    • T2[s][t]：指针表，存储在时刻t转移到状态s时概率最大的前驱状态。

  • 初始时刻（t = 0）：

    • 根据各状态的先验概率（π[s]）和首个观测值（obs[0]）的发射概率，计算初始概率。

2. 递推计算阶段：

对每个时刻t（从1到49）：

  1. 对于每个状态s：

      通过以下公式计算从任意前驱状态s_prev转移到s的最大概率：               

      最大状态转移方程

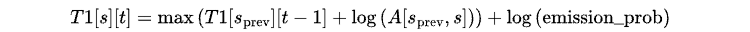
      此处将状态转移概率A[s_prev, s]转换为对数空间计算，以避免数值下溢问题。

  2. 将使概率最大化的前驱状态s_prev存储于指针表T2[s][t]中。

3. 回溯检索最优路径：

  1. 从最后一个时刻（t=49）概率最大的状态开始，
  2. 通过指针表T2逆向追溯，重建最可能的隐含状态序列，并将结果存入states[] 数组。

    最终输出为states[]，即全局最优的隐含状态序列。

    PredictCurrentState()函数调用Viterbi()算法，基于观测序列预测当前隐含状态：

    1. 初始化长度为50的数组states[]，用于存储维特比算法的输出结果。
    2. 将观测序列obs[]传入Viterbi()，计算最优隐含状态序列。
    3. 返回最后一个时刻的状态states[49]，作为当前最可能的隐含状态估计。

    如果您对相关的数学原理有疑问，强烈建议您查阅网络上的直观图解从而辅助理解。我通过以下示意图简要说明算法流程。

    图表

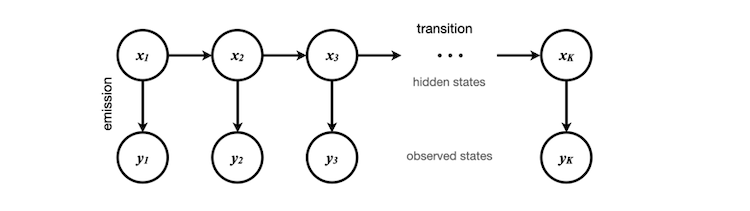
    观测状态为标准化后的波动率数据，通过预处理后存储于长度为50的 obs[] 数组中。这些元素对应示意图中的y₁、y₂、…、y₅₀。隐含状态仅取0或1，分别表示当前波动率的抽象状态（高或低）。

    这些状态标签通过前期Python模型训练中的聚类分析自动生成。需要注意的是，Python代码仅执行数据聚类和状态转移特征提取，不涉及具体业务含义的解读。

    初始阶段，我们随机为x₁赋予一个状态，并假设每个状态的权重相等。如果不想做此假设，也可利用训练数据计算初始状态的平稳分布，即转移矩阵的特征向量。为简化起见，这里我们把平稳分布向量设为 [0.5, 0.5]。

    通过训练隐马尔可夫模型，我们得到从当前隐含状态转移到下一隐含状态以及生成不同观测值的概率。基于贝叶斯定理，可计算每条马尔可夫链中所有可能路径的概率。从而确定序列最终隐含状态x₅₀的最优估计。

    最后，我们调整原始OnTick()逻辑，为每根收盘K线计算隐含状态，并且增加隐含状态为1的入场条件。

    //+------------------------------------------------------------------+
//| Check Volatility is filled Function                              |
//+------------------------------------------------------------------+
bool IsVolatilityFilled(){
     bool volatility_filled = true;
     for(int i = 0; i < 50; i++){
         if(volatility[i] == 0){
             volatility_filled = false;
             break;
         }
     }
     if(!volatility_filled){
         Print("Volatility buffer not yet filled.");
         return false;
     }
     else return true;
}  

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
  int bars = iBars(_Symbol,PERIOD_CURRENT);
  if (barsTotal!= bars){
     barsTotal = bars;
     double maFast[];
     double maSlow[];
     double ma[];  
     
     GetVolatility();
     if(!IsVolatilityFilled()) return;
     int currentState = PredictCurrentState(volatility);
     
     CopyBuffer(handleMaFast,BASE_LINE,1,2,maFast);
     CopyBuffer(handleMaSlow,BASE_LINE,1,2,maSlow);
     CopyBuffer(handleMa,0,1,1,ma);

     double bid = SymbolInfoDouble(_Symbol, SYMBOL_BID);
     double ask = SymbolInfoDouble(_Symbol, SYMBOL_ASK);
     double lastClose = iClose(_Symbol, PERIOD_CURRENT, 1);
     //The order below matters
     if(buypos>0&& lastClose<maSlow[1]) trade.PositionClose(buypos);
     if(sellpos>0 &&lastClose>maSlow[1])trade.PositionClose(sellpos);        
     if (maFast[1]>maSlow[1]&&maFast[0]<maSlow[0]&&buypos ==sellpos&&currentState==1)executeBuy(); 
     if(maFast[1]<maSlow[1]&&maFast[0]>maSlow[0]&&sellpos ==buypos&&currentState==1) executeSell();
     
     if(buypos>0&&(!PositionSelectByTicket(buypos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      buypos = 0;
      }
     if(sellpos>0&&(!PositionSelectByTicket(sellpos)|| PositionGetInteger(POSITION_MAGIC) != Magic)){
      sellpos = 0;
      }
    }
 }


    回测

    我们使用2020年1月1日至2024年1月1日的样本内数据训练模型。现计划在2024年1月1日至2025年1月1日时间段内，黄金兑美元（XAUUS）1小时（H1）周期上测试。

    首先，我们会与基准策略（未整合HMM的原始策略）的表现进行对比。

    基准设置

    参数

    基准资金曲线

    基准结果

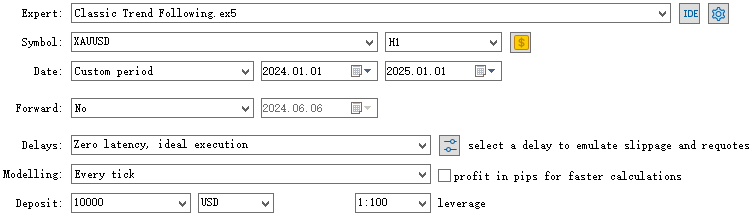
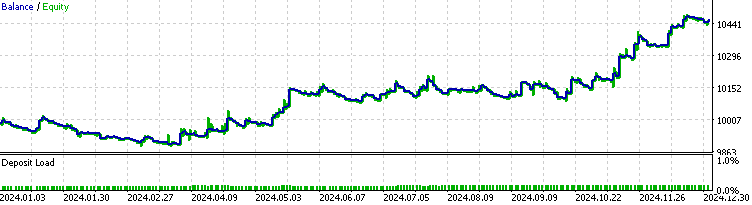
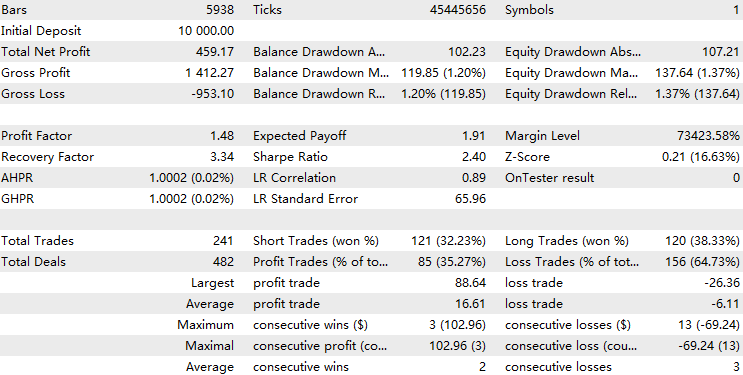
    现对集成了HMM模型过滤器的EA进行回测。

    HMM参数设置

    参数

    HMM资金曲线

    HMM结果

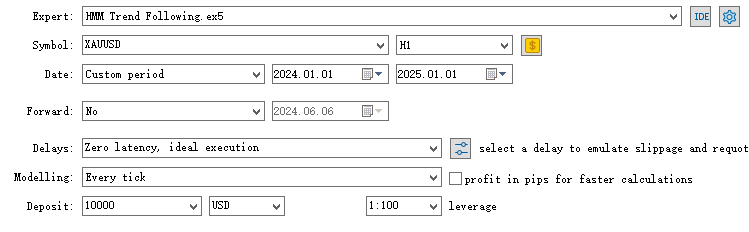
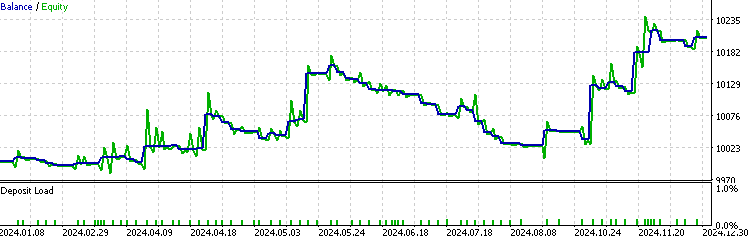
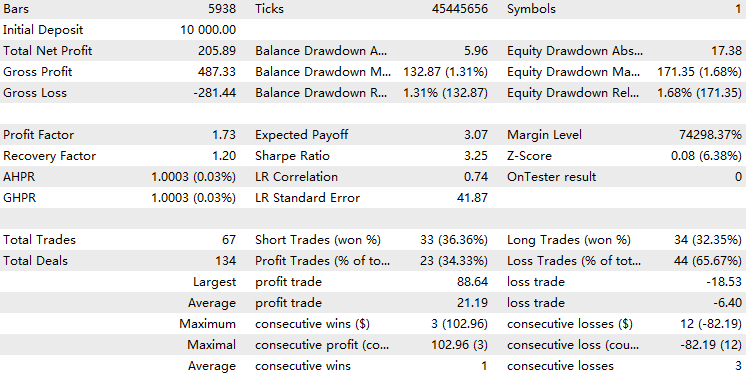
    由此可见，集成HMM过滤器的EA过滤了约70%的交易信号，其表现显著优于基准策略。利润因子达到1.73，高于基准策略的1.48，同时夏普比率也更高。这表明我们训练的HMM模型具备一定预测能力。

    如果采用滚动回测方法（自2004年起，每年重新训练4年数据并测试1年，将所有结果合并为资金曲线），可获得如下结果：

    滚动资金曲线

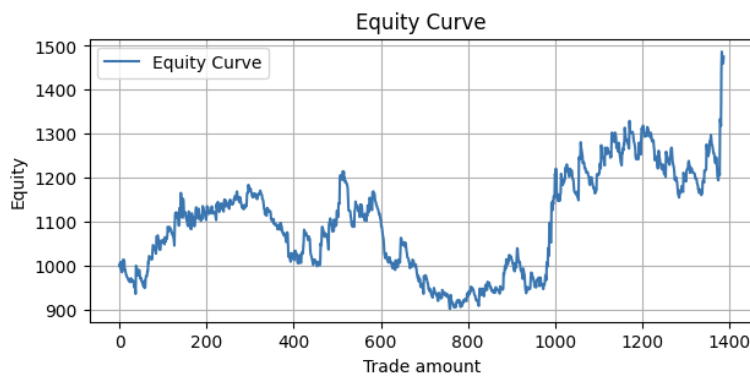
    度量指标：

    Profit Factor: 1.10
Maximum Drawdown: -313.17
Average Win: 11.41
Average Loss: -5.01
Win Rate: 32.56%

    当前策略已实现盈利，但仍存在优化空间。


    反思

    在机器学习主导的量化交易领域，关于模型复杂度的争议持续存在：是采用循环神经网络（RNN）等复杂模型，还是坚持使用隐马尔可夫模型（HMM）等简单架构？

    优点：

    1. 简洁性：实现与解释成本显著低于RNN，避免参数含义模糊导致的"黑箱"问题。
    2. 低数据依赖：仅需少量训练样本即可完成参数估计，计算资源消耗更低。
    3. 参数更少：对过拟合问题更具鲁棒性。

    缺点：

    1. 复杂度受限：难以捕捉RNN可建模的波动数据中的复杂非线性模式。
    2. 马尔可夫假设缺陷：假设波动率转移无记忆性，与真实市场存在的路径依赖特征矛盾。
    3. 过拟合风险：当隐含状态数量过多时，HMM仍可能陷入过拟合困境。

    学术界普遍认为，机器学习在波动率预测（而非价格预测）领域更具可靠性。然而，本文策略的局限在于使用50周期滚动波动率均值作为每根新K线的观测值，以及与所定义的隐藏状态（高/低波动状态）存在天然相关性，导致预测显著性下降。仅用观测数据作为交易过滤器或许也能得到类似结果。

    针对后续优化，建议读者尝试探索隐含状态的不同定义方式，并且扩展隐含状态数量以增强模型的预测能力和鲁棒性。


    结论

    本文首先阐述了将隐马尔可夫模型（HMM）应用于趋势跟踪策略波动率状态预测的契机，并介绍了HMM的基础理论框架。随后，我们系统梳理了策略开发全流程：先在MetaTrader 5中用MQL5搭建核心策略，再获取数据并在 Python内训练HMM，最后将训练好的模型集成回MetaTrader 5。随后，我们进行了回测并分析其表现，还通过示意图简要解释了HMM背后的数学逻辑。最后，我分享了对该策略的实践反思，并在此框架基础上提出了对未来开发的展望。


    File Table

    文件名 用途
    HMM Test.mq5 交易EA的实现
    Classic Trend Following.mq5 基准策略EA
    OHLC Getter.mq5 用于获取数据的EA
    FileCSV.mqh 用于将数据存储为CSV格式的Include文件
    rollingBacktest.ipynb 用于训练模型和获取矩阵

    本文由MetaQuotes Ltd译自英文
    原文地址： https://www.mql5.com/en/articles/16830

    附加的文件 |
    下载ZIP
    HMM-TF.zip (45.1 KB)

    注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

    本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

    该作者的其他文章

    前往讨论
    交易策略 交易策略
    各种交易策略的分类都是任意的，下面这种分类强调从交易的基本概念上分类。
    交易中的神经网络：多智代自适应模型（MASA） 交易中的神经网络：多智代自适应模型（MASA）
    我邀您领略多智代自适应（MASA）框架，其结合了强化学习和自适应策略，在动荡市场条件下提供盈利能力、及风险管理之间的和谐均衡。
    新手在交易中的10个基本错误 新手在交易中的10个基本错误
    新手在交易中会犯的10个基本错误: 在市场刚开始时交易, 获利时不适当地仓促, 在损失的时候追加投资, 从最好的仓位开始平仓, 翻本心理, 最优越的仓位, 用永远买进的规则进行交易, 在第一天就平掉获利的仓位,当发出建一个相反的仓位警示时平仓, 犹豫。
    从基础到中级：联合（二） 从基础到中级：联合（二）
    今天我们有一篇非常有趣的文章。我们将研究联合并尝试解决之前讨论的问题。我们还将探讨在应用程序中使用联合时可能出现的一些不寻常的情况。此处提供的材料仅用于教学目的。在任何情况下，除了学习和掌握所提出的概念外，都不应出于任何目的使用此应用程序。