数据科学和机器学习（第 27 部分）：MetaTrader 5 中训练卷积神经网络（CNN）交易机器人 — 值得吗？

MetaTrader 5 — EA交易 | 31 三月 2025, 07:57

543

Omega J Msigwa

卷积神经网络中用到的池化操作是一个大错误，且事实上它运行得如此之好是一场灾难。

杰弗里·辛顿（Geoffrey Hinton）

内容

为了完全理解本文的内容，需要对 MQL5 中的 Python 编程语言、人工神经网络、机器学习、和 ONNX 有基本的了解。

什么是卷积神经网络（CNNS）？

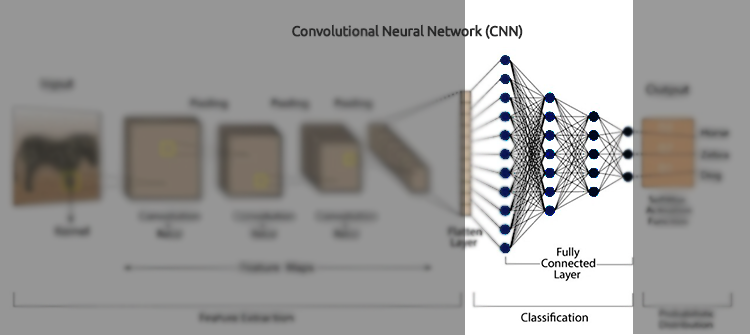
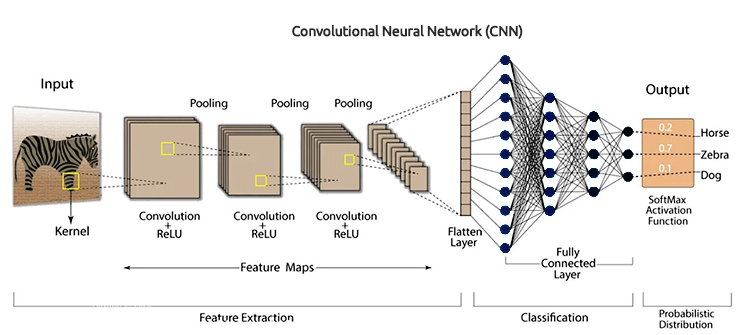
卷积神经网络（CNN）是一类深度学习算法，专门设计用于处理结构化网格状数据，例如图像、音频频谱图、和时间序列数据。它们特别适合视觉数据任务，因为它们可以从输入数据中自动、且自适应地学习特征的空间层次。

CNN 是人工神经网络（ANN）的扩展版本。它们主要用于从网格状矩阵数据集中提取特征。例如，像是图像或视频等视觉数据集，其中数据形态扮演广泛角色。

卷积神经网络有若干关键组件，例如：卷积层、激活函数、池化层、全连接层、和舍弃层。为了深入理解 CNN，我们剖析每个组件，并查看它的全部内容。

卷积层

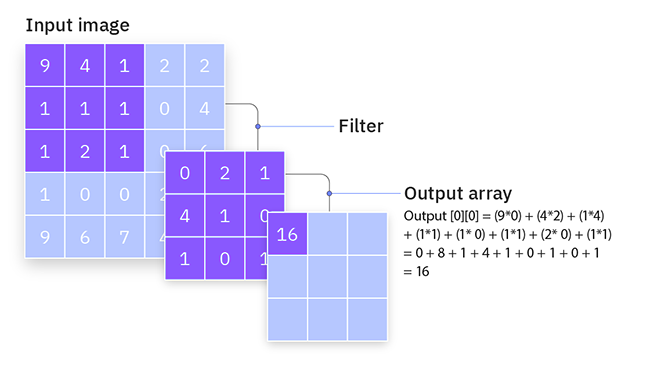
这些是 CNN 的核心构建模块，其所在会产生主要计算。卷积层负责检测输入数据中的局部形态，例如图像中的边缘。这可以通过使用过滤器（或内核）来达成，其在输入数据上滑动，从而生成特征映射。

卷积层是一个隐藏层，在卷积神经网络中包含多个卷积单元，用于特征提取。

from tensorflow.keras.layers import Conv1D

model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2])))

过滤器/内核

过滤器（或内核）是小型可学习的方形矩阵（通常大小为 3x3、5x5、等等），可在输入数据上滑动，从而检测局部形态。

它们是如何工作的？

它们通过在输入数据之间移动来操作，然后在过滤器值与过滤器当前感知域内的输入值之间执行元素级乘法，随后汇总结果。该操作称为卷积。

在训练期间，网络学习过滤器的最优值。在早期层中，过滤器典型情况下学习检测简单特征，譬如边缘和纹理，而在较深的层中，过滤器能够检测更复杂的形态，例如形状和对象。

研究一个简单的 3x3 过滤器，和一个 5x5 输入图像。过滤器在图像上滑动，计算卷积运算，从而生成特征映射。

卷积网内核

跨距

这是卷积层中发现的另一个特征。跨距是过滤器在输入数据中移动的步长。它判定过滤器在卷积过程中每一步的偏移量。

它们是如何工作的？

跨距为 1，则过滤器一次移动一个单位，成果则是高度重叠、且详细的特征映射。这将生成较大的输出特征映射。

跨距为 2 或更大，则过滤器会跳过一些单位，从而导致输出特征映射不太详细、但更小。这降低了输出空间维度，有效地进行输入降级采样。

例如，如果您有一个 3x3 过滤器，和一个跨距为 1 的 5x5 输入图像，则过滤器将一次移动一个像素，生成 3x3 输出特征映射。跨距为 2 时，过滤器将一次移动两个像素，生成 2x2 输出特征映射。

填充

填充涉及在输入数据的边界周围加入额外的像素（通常为 0）。这可确保过滤器正确拟合，并控制输出特征映射的空间维度。

填充的类型

根据 Keras 的说法，有三种填充类型。（大小写敏感)

valid - 无需应用填充，
same - 输入填充，以便在 strides=1 时输出大小与输入大小匹配。
causal - 用于时态数据，以便确保时间步 t 的输出不依赖于未来的输入。

填充有助于保留输入数据的空间维度。若无填充，输出特征映射会随着每个卷积层缩水，结果也许会丢失重要的边缘信息。

通过添加填充，网络能够有效地学习边缘特征，并维护输入的空间分辨率。

研究一个 3x3 过滤器，和一个 5x5 输入图像。配以有效的填充（无填充），输出特征映射将为 3x3。配以相同的填充，您或许会在输入周围加上一个零值边界，令其达到 7x7。然后，输出特征映射将是 5x5，保留了输入维度。

以下是卷积层的 Python 代码。

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv1D

model = Sequential()
model.add(Conv1D(filters=64, 
                 kernel_size=3, 
                 activation='relu', 
                 strides=2,
                 padding='causal',
                 input_shape=(window_size, X_train.shape[2])
                )
         )

激活函数

正如《神经网络揭秘》一文中所讨论的，激活函数是接受输入，并处理输出的数学函数。

应用的激活函数按元素级，将非线性引入模型。CNN 中常用的激活函数包括 ReLU（整流线性单元）、Sigmoid、和 TanH。

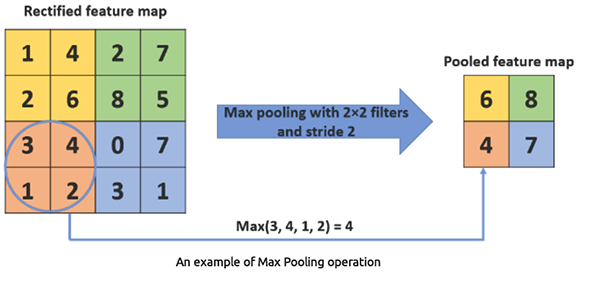
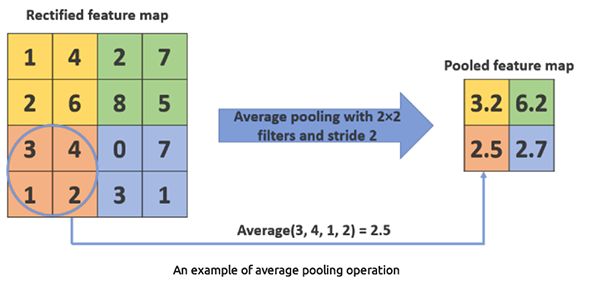
池化层

已知也称为逆采样层，这些层是 CNN 的基础部分，它们负责从宽度和高度方面降低输入数据的空间维度，同时保留最重要的信息。

它们是如何工作的？

首先，它们将输入数据切分为重叠的区域或窗口，然后在每个窗口上应用聚合函数（如最大池化、或平均池化），从而获得单一数值。

最大池化从过滤器区域内的一组值中获取最大值。它降低了数据的空间维度，这有助于降低计算负载、和参数量。

Python

from tensorflow.keras.layers import Conv1D, MaxPooling1D

model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2])))
model.add(MaxPooling1D(pool_size=2))

MaxPooling1D(pool_size=2)

该层从每两个元素窗口中获取最大值。

最大池化

更多信息。

平均池化从过滤器区域内的一组值中获取平均值。比最大池化所用更少。

Python

from tensorflow.keras.layers import Conv1D, AveragePooling1D

model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2])))
model.add(AveragePooling1D(pool_size=2))

AveragePooling1D(pool_size=2)

该层从每两元素窗口中获取平均值。

平均池化

更多信息。

为什么要用一维卷积层？

CNN 有 Conv1D、Conv2D 和 Conv3D 层。一维卷积层适合这种类型问题，因为它是为一维数据设计的，令其适用于顺序、或时间序列数据。其它卷积层，例如 Conv2D 和 Conv3D，对于此类问题来说太复杂了。

全连接层

全连接层中的神经元、与前一层中的所有激活都有连接。这些层典型情况下偏向用在网络末尾，以便基于卷积层和池化层提取的特征执行分类或回归。

from tensorflow.keras.layers import Conv1D, MaxPooling1D, Flatten, Dense, Dropout

model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2])))
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())
model.add(Dense(100, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=len(np.unique(y)), activation='sigmoid'))  # For binary classification (e.g., buy/sell signal)

model.summary()

偏平层将一维池化特征映射转换为一维向量，如此就能将其投喂到完全连接（密集）层之中。

密集层（Dense）是完全连接的层，用于基于卷积层和池化层提取的特征制定最终决策。密集层本质上是传统人工神经网络（ANN）的核心组件。

在 CNN 上高亮的密集层

舍弃层

舍弃层充当掩码，剔除一些神经元对后续层的贡献，同时维护所有其它神经元的功能。如果我们将舍弃层应用于输入向量，则它的一些特征会被消除；不过，如果我们将其应用于隐藏层，则一些隐藏神经元会被消除。

由于它们避免了过度拟合训练数据，因此舍弃层在 CNN 的训练中至关重要。如果它们缺失，则第一组训练样本对学习的影响过大。结果就是，仅在后续样本或批次中展现出的特征将不会被学习。

from tensorflow.keras.layers import Conv1D, MaxPooling1D, Flatten, Dense, Dropout

model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(window_size, X_train.shape[2])))
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())
model.add(Dense(100, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=len(np.unique(y)), activation='sigmoid'))  # For binary classification (e.g., buy/sell signal)

model.summary()

为什么要用卷积神经网络（CNN）进行金融分析和交易应用？

CNN 广泛用于图像和视频处理应用，因为这就是它们的设计初衷。如果您看一下上面的解释，您或许会注意到，我指的是在处理图像分类和原材料时用到 CNN。

与其它类型神经网络，譬如前馈神经网络（FFNN）、递归神经网络（RNN）、长-短期记忆（LSTM）、和门控递归单元（GRU）相比，运用卷积神经网络（CNN）处理表格数据，譬如财经分析，似乎不合常规。不过，在这种背景下任用 CNN 有若干原因和潜在益处概括如下。

01. CNN 专长从数据中自动提取局部形态

财经数据往往表现出局部时态=间形态，例如趋势和季节性。将数据作为时间序列处置。CNN 能学习这些局部依赖关系，以及特征之间的交互，而传统方法则或许会错过这些。

02. 它们能学习层次特征

CNN 中的多层令它们能够学习复杂的特征层次结构。早期层可以检测简单形态，而较深的层能将这些简单形态组合成更复杂和抽象的表示形式。这种层次特征学习有助于捕获财经数据中的复杂形态。

03. 它们能应对噪声和冗余特征时保持稳健

众所周知，金融数据集包含噪音和冗余的数据。CNN 中的池化层有助于模型应对微小变化和噪声时保持稳健，因为它们对特征映射降级采样，并减少微小波动的影响。

04 CNN 能很好地处理多元时间序列

财经数据通常涉及多个相关的时间序列，譬如不同的股票价格和交易量。CNN 能有效地捕获这些多时间序列之间的交互和依赖关系，令其适用于多变量时间序列预测。

05. 它们对于高维数据的计算很高效

财经数据可以拥有高维度（许多特征）。通过权重分享和局部连接，CNN 的计算效率比完全连接神经网络更高，令其能够定标到高维数据。

06. CNN 启用端到端学习

CNN 能直接从原生数据中学习、并生成预测，无需手工特征工程。这种端到端学习方式能简化建模过程，并让模型发现最相关的特征，潜在地提供更佳性能。

07. CNN 应用卷积运算，对于某些数据类型颇具优势。

卷积运算能检测和强化数据内的重要信号，例如突然变化、或特定形态。这在财经分析中特别实用，其中检测突发市场变化或形态至关重要。

现在我们有充分的理由在交易应用中运用 CNN，我们来创建一个并训练它，然后我们将看到如何在 Meta Trader 5 智能系统（EA）中使用 CNN。

利用 Python 打造卷积神经网络（CNN）

这涉及若干步骤。

收集数据
为 CNN 模型准备数据
训练 CNN 模型
将 CNN 模型保存为 ONNX 格式

01：收集数据

使用我们在前几篇文章中用过的时间序列预测数据。

时间序列预测数据集

现在我们知道卷积神经网络（CNN）擅长检测高维数据内的形态，无需令模型复杂化，我们可以选择一些特征，我相信有大量形态能被 CNN 模型检测到。

Python 代码

open_price = df['TARGET_OPEN']
close_price = df['TARGET_CLOSE']

# making the target variable

target_var = []
for i in range(len(open_price)):
    if close_price[i] > open_price[i]: # if the price closed above where it opened
        target_var.append(1) # bullish signal
    else:
        target_var.append(0) # bearish signal

        
new_df = pd.DataFrame({
    'OPEN': df['OPEN'],
    'HIGH': df['HIGH'],
    'LOW': df['LOW'],
    'CLOSE': df['CLOSE'],
    'TARGET_VAR': target_var
})

print(new_df.shape)

基于 TARGET_OPEN 和 TARGET_CLOSE 准备目标变量后不久，其分别对应开盘值和收盘值，收集一根前向柱线。我们创建了一个名为 new_df 的迷你数据集版本，其只有 4 个自变量 OPEN、HIGH 和 LOW 值，以及一个名为 TARGET_VAR 的因变量。

02：为 CNN 模型准备数据

首先，我们必须预处理输入数据，经重塑，并对齐到窗口之中。在 CNN 中与表格数据打交道时，这一点至关重要，此处是为什么。

由于交易数据是顺序的，出现形态往往覆盖一连串时间步骤，而非单一时间点。通过创建重叠的数据窗口，我们可以捕获时间依赖关系，并为 CNN 模型提供上下文。

此外，CNN 期望输入数据处于特定形状。对于一维卷积层，输入形状典型需要为（窗口数、窗口大小、特征数）。这种形状类似于我们在上一篇文章中使用递归神经网络（RNN）分析时间序列时所用的那个。我们将要做的预处理过程，是确保数据采用这种格式，令其适于 CNN 模型输入。

# Example data preprocessing function

def preprocess_data(df, window_size):
    X, y = [], []
    for i in range(len(df) - window_size):
        X.append(df.iloc[i:i+window_size, :-1].values)
        y.append(df.iloc[i+window_size, -1])
    return np.array(X), np.array(y)


window_size = 10


X, y = preprocess_data(new_df, window_size)
print(f"x_shape = {X.shape}\ny_shape = {y.shape}")

输出

x_shape = (990, 10, 4)
y_shape = (990,)

由于我们的数据是按日线时间帧收集的，窗口大小为 10 表示我们将在 10 天内训练 CNN 模型来理解形态。

然后我们必须将数据拆分为训练样本和测试样本。

# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False)

# Standardize the data
scaler = StandardScaler()

X_train = scaler.fit_transform(X_train.reshape(-1, X_train.shape[-1])).reshape(X_train.shape)
X_test = scaler.transform(X_test.reshape(-1, X_test.shape[-1])).reshape(X_test.shape)

print(f"x_train\n{X_train.shape}\nx_test\n{X_test.shape}\n\ny_train {y_train.shape} y_test {y_test.shape}")

输出

x_train
(792, 10, 4)
x_test
(198, 10, 4)

y_train (792,) y_test (198,)

最后，我们必须针对这个分类问题任务，为目标变量进行独热编码。

from tensorflow.keras.utils import to_categorical

y_train_encoded = to_categorical(y_train)
y_test_encoded = to_categorical(y_test)

print(f"One hot encoded\n\ny_train {y_train_encoded.shape}\ny_test {y_test_encoded.shape}")

输出

One hot encoded

y_train (792, 2)
y_test (198, 2)

03：训练 CNN 模型

这是大多数工作完成的所在。

# Defining the CNN model

model = Sequential()
model.add(Conv1D(filters=64, 
                 kernel_size=3, 
                 activation='relu', 
                 strides=2,
                 padding='causal',
                 input_shape=(window_size, X_train.shape[2])
                )
         )

model.add(MaxPooling1D(pool_size=2))
model.add(Flatten()) 
model.add(Dense(100, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(units=len(np.unique(y)), activation='softmax'))  # For binary classification (buy/sell signal)

model.summary()

# Compiling the model

optimizer = Adam(learning_rate=0.001)

model.compile(optimizer=optimizer, loss='categorical_crossentropy', metrics=['accuracy'])

# Training the model

early_stopping = EarlyStopping(monitor='val_loss', patience=10, restore_best_weights=True)

history = model.fit(X_train, y_train_encoded, epochs=100, batch_size=16, validation_split=0.2, callbacks=[early_stopping])

plt.figure(figsize=(7.5, 6))
plt.plot(history.history['loss'], label='Training Loss')
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Training Loss Curve')
plt.legend()
plt.savefig("training loss cuver-cnn-clf.png")
plt.show()

输出

Model: "sequential_2"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape           ┃       Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
│ conv1d_2 (Conv1D)               │ (None, 5, 64)          │           832 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ max_pooling1d_2 (MaxPooling1D)  │ (None, 2, 64)          │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ flatten_2 (Flatten)             │ (None, 128)            │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_4 (Dense)                 │ (None, 100)            │        12,900 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dropout_2 (Dropout)             │ (None, 100)            │             0 │
├─────────────────────────────────┼────────────────────────┼───────────────┤
│ dense_5 (Dense)                 │ (None, 2)              │           202 │
└─────────────────────────────────┴────────────────────────┴───────────────┘

训练停止在第 34 局次

40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.5105 - loss: 0.6875 - val_accuracy: 0.4843 - val_loss: 0.6955
Epoch 32/100
40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.5099 - loss: 0.6888 - val_accuracy: 0.5283 - val_loss: 0.6933
Epoch 33/100
40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.4636 - loss: 0.6933 - val_accuracy: 0.5283 - val_loss: 0.6926
Epoch 34/100
40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - accuracy: 0.5070 - loss: 0.6876 - val_accuracy: 0.5346 - val_loss: 0.6963

CNN 训练验证亏损曲线

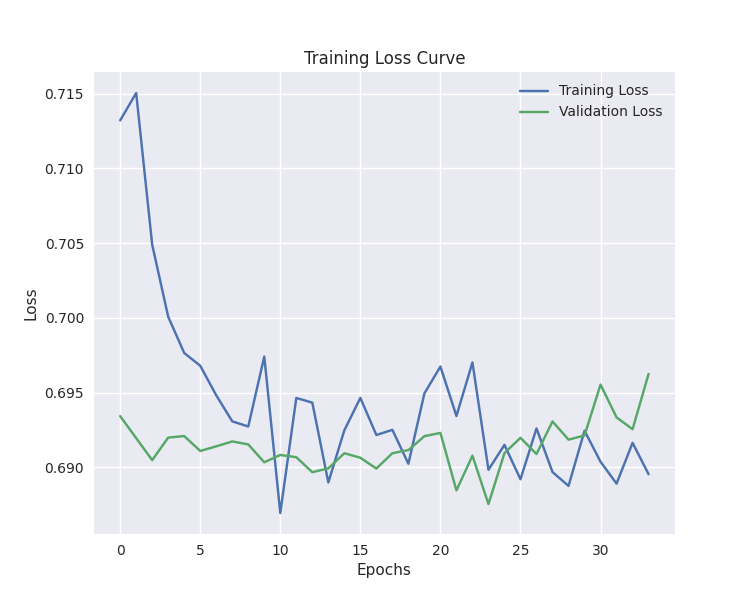
该模型在样本外的预测准确率约为 57%。

y_pred = model.predict(X_test) 

classes_in_y = np.unique(y)
y_pred_binary = classes_in_y[np.argmax(y_pred, axis=1)]

# Confusion Matrix
cm = confusion_matrix(y_test, y_pred_binary)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues')
plt.xlabel("Predicted Label")
plt.ylabel("True Label")
plt.title("Confusion Matrix")
plt.savefig("confusion-matrix CNN")  # Display the heatmap


print("Classification Report\n",
      classification_report(y_test, y_pred_binary))

输出

7/7 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step
Classification Report
               precision    recall  f1-score   support

           0       0.53      0.24      0.33        88
           1       0.58      0.83      0.68       110

    accuracy                           0.57       198
   macro avg       0.55      0.53      0.50       198
weighted avg       0.55      0.57      0.52       198

我们的 CNN 模型对于智能系统来说已经足够好了。但是，在我们开始编写 EA 之前，我们以 ONNX 格式保存我们训练的 CNN 模型。

04：将 CNN 模型保存为 ONNX 格式。

该过程相当简单，我们必须将 CNN 模型保存为 .onnx 格式，并将定标技术参数保存在二进制文件中。

import tf2onnx

onnx_file_name = "cnn.EURUSD.D1.onnx"

spec = (tf.TensorSpec((None, window_size, X_train.shape[2]), tf.float16, name="input"),)
model.output_names = ['outputs']

onnx_model, _ = tf2onnx.convert.from_keras(model, input_signature=spec, opset=13)

# Save the ONNX model to a file
with open(onnx_file_name, "wb") as f:
    f.write(onnx_model.SerializeToString())
    
    
# Save the mean and scale parameters to binary files
scaler.mean_.tofile(f"{onnx_file_name.replace('.onnx','')}.standard_scaler_mean.bin")
scaler.scale_.tofile(f"{onnx_file_name.replace('.onnx','')}.standard_scaler_scale.bin")

创建基于卷积神经网络（CNN）的交易机器人

在智能系统内，我们要做的第一件事是将 ONNX 格式的模型和标准定标二进制文件作为资源包含在内。

MQL5 格式 | ConvNet EA.mq5

#resource "\\Files\\cnn.EURUSD.D1.onnx" as uchar onnx_model[]
#resource "\\Files\\cnn.EURUSD.D1.standard_scaler_scale.bin" as double scaler_stddev[]
#resource "\\Files\\cnn.EURUSD.D1.standard_scaler_mean.bin" as double scaler_mean[]

我们必须初始化定标和 onnx 模型两者。

#include <MALE5\Convolutioal Neural Networks(CNNs)\Convnet.mqh>
#include <MALE5\preprocessing.mqh>

CConvNet cnn;
StandardizationScaler scaler;
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+

input group "cnn";
input uint cnn_data_window = 10; 
//this value must be the same as the one used during training in a python script

vector classes_in_y = {0,1}; //we have to assign the classes manually | it is essential that their order is preserved as they can be seen in python code, HINT: They are usually in ascending order
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   
   if (!cnn.Init(onnx_model)) //Initialize the ONNX model
     return INIT_FAILED;
     
//--- Initializing the scaler with values loaded from binary files 

   scaler = new StandardizationScaler(scaler_mean, scaler_stddev); //load the scaler
      
   return(INIT_SUCCEEDED);
  }

这足以启动并运行模型。我们制作函数来提取数据，类似于在训练期间所用的自变量方式。我们用到了四个变量，从前一根收盘柱线到往前的 10 根柱线，这是必须保留的时间帧的窗口大小（日线时间帧）。

input group "cnn";
input uint cnn_data_window = 10; 
//this value must be the same as the one used during training in a python script

input ENUM_TIMEFRAMES timeframe = PERIOD_D1;
input int magic_number = 1945;
input int slippage = 50;

matrix GetXVars(int bars, int start_bar=1)
 {
   vector open(bars), 
          high(bars),
          low(bars), 
          close(bars);

//--- Getting OHLC values
   
   open.CopyRates(Symbol(), timeframe, COPY_RATES_OPEN, start_bar, bars);
   high.CopyRates(Symbol(), timeframe, COPY_RATES_HIGH, start_bar, bars);
   low.CopyRates(Symbol(), timeframe, COPY_RATES_LOW, start_bar, bars);
   close.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar, bars);
   
//---

   matrix data(bars, 4); //we have 10 inputs from cnn | this value is fixed
   
//--- adding the features into a data matrix
   
   data.Col(open, 0);
   data.Col(high, 1);
   data.Col(low, 2);
   data.Col(close, 3);
   
   return data;
 }

现在我们得到一个收集自变量的函数，我们能定案我们的交易策略。

void OnTick()
  {
//---
   
   if (NewBar()) //Trade at the opening of a new candle
    {
      matrix input_data_matrix = GetXVars(cnn_data_window); //get data for the past 10 days(default)
      input_data_matrix = scaler.transform(input_data_matrix); //applying StandardSCaler to the input data
      
      int signal = cnn.predict_bin(input_data_matrix, classes_in_y); //getting trade signal from the RNN model
     
      Comment("Signal==",signal);
     
   //---
     
      MqlTick ticks;
      SymbolInfoTick(Symbol(), ticks);
      
      if (signal==1) //if the signal is bullish
       {
          if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions
           {
             if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, 0, 0)) //Open a buy trade
               printf("Failed to open a buy position err=%d",GetLastError());

             ClosePosition(POSITION_TYPE_SELL); //close opposite trade
           }
       }
      else if (signal==0) //Bearish signal
        {
          if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions
            if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, 0, 0)) //open a sell trade
               printf("Failed to open a sell position err=%d",GetLastError());
               
               ClosePosition(POSITION_TYPE_BUY); 
        }
      else //There was an error
        return;
    }
  }

策略很简单。在收到特定信号之时，假设买入信号，我们开立一笔无止损和止盈值的买入交易，然后我们按相反信号平仓，反之亦然，以获得卖出信号。

最后，我依据品种 EURUSD ，训练它，为期十年，并测试该策略。从 2014.01.01 至 2024.05.27，每根柱线的开盘价，H4 时间帧。

convNet EA 策略测试器配置

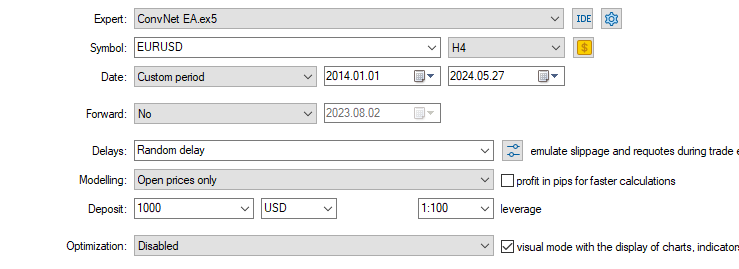
策略测试器的结果非常出色。

ConvNet EA 策略测试器报告

ConvNet EA 测试器图形

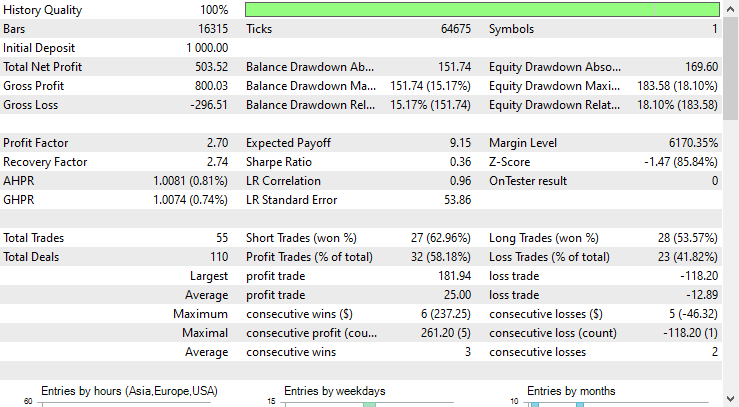
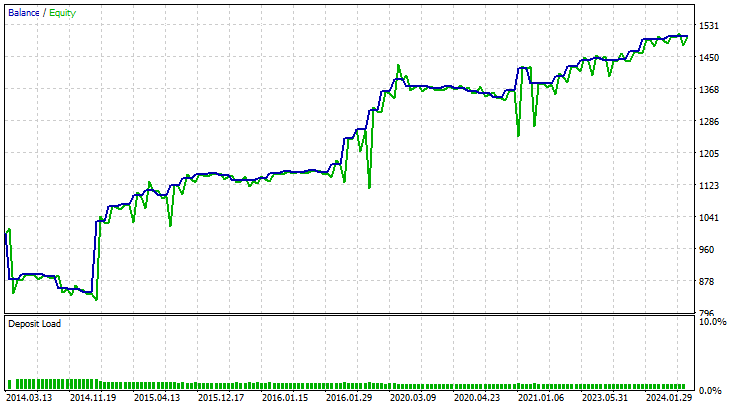
基于 CNN 的 EA 在全部时间里做出了 58% 的准确预测，由此 EA 赚取了 503 美元的净盈利。

底线

尽管是专为图像和视频处理而设计的，但当用于处理表格数据（例如我们提供给它的外汇数据）时，卷积神经网络（CNN）亦可完成检测形态的适宜工作，并用它们来预测外汇市场。

如策略测试器报告中所见，基于 CNN 的 EA 做出了适宜的预测。我敢打赌，考虑到 CNN 模型仅有 4 个自变量（OHLC），许多为表格数据设计的传统模型，如线性回归、支持向量机、朴素贝叶斯、等等，都无法达成这样的预测准确性。据我的经验，在给定少量变量的情况下，没有多少模型能够变得如此出色。

此致敬意。

跟踪机器学习模型的开发，在 GitHub 存储库上有更多本系列文章的讨论内容。

附件表

文件名	文件类型	说明/用法
ConvNet EA.mq5	智能系统	交易机器人，加载 ONNX 格式 CNN 模型，并在 MetaTrader 5 中测试最终交易策略。
cnn.EURUSD.D1.onnx	ONNX	ONNX 格式的 CNN 模型。
cnn.EURUSD.D1.standard_scaler_mean.bin cnn.EURUSD.D1.standard_scaler_scale.bin	二进制文件	标准化定标器的二进制文件
preprocessing.mqh	包含文件	由标准化定标器组成的函数库
ConvNet.mqh	包含文件	ONNX 格式的加载和部署 CNN 模型的函数库
cnn-for-trading-applications-tutorial.ipynb	Python 脚本/Jupyter 笔记簿	包含本文讨论的所有 python 代码