MetaTrader 5 / 交易系统
English Русский Español Deutsch 日本語 Português
preview
数据科学和机器学习（第 13 部分）：配合主成分分析（PCA）改善您的金融市场分析

数据科学和机器学习（第 13 部分）：配合主成分分析（PCA）改善您的金融市场分析

MetaTrader 5 — 交易系统 | 11 八月 2023, 07:56
942 0
Omega J Msigwa
Omega J Msigwa

“PCA 是数据分析和机器学习的基础技术，广泛用于从图像和信号处理到金融和社会科学的各种应用。“ 

大卫·谢斯金（David J. Sheskin）

概述

主成分分析（PCA）是一种降维方法，通常用于降低大型数据集的维数，具体就是将大型变量集转换为仍然包含大型数据集中大部分信息的较小变量集。

减少数据集中变量的数量通常以牺牲准确度为代价，但降维的诀窍就是牺牲很少的准确度来换取简单性。 您我都知道，数据集中的一些变量更容易探索、可视化，并令机器学习算法的分析数据变得更加容易和快捷。 我个人并不认为牺牲准确度来换取交易简单是一件坏事，因为我们身处交易领域。 准确度并不一定意味着盈利。

pca 文章图片

PCA 的主要思想在核心上非常简单：减少数据集中的变量数量，同时保留尽可能多的信息。 我们来看一下主成分分析算法中涉及的步骤。


主成分分析算法涉及的步骤

  1. 标准化数据
  2. 查找矩阵的协方差
  3. 查找特征向量和特征值
  4. 查找 PCA 得分并对其进行标准化
  5. 获取成分

事不宜迟，我们从标准化数据开始。


01：标准化数据

标准化数据的目的是将所有变量带到相同的尺度上，以便将它们平等地进行比较和分析。 在分析数据时，变量通常具有不同的测量单位或尺度，这可能会导致结果有偏差或结论不正确。 例如，移动平均线指标的价格范围与市场价值相同，而 RSI 指标的值通常介于 0 和 100 之间。 当在任何模型中配和使用时，这两个变量都是无可比拟的。 它们不能以有意义的方式配合使用。

数据标准化涉及转换每个变量，令其均值为 0，且标准偏差为 1。这确保了每个变量具有相同的尺度和分布，令它们直接具有可比性。 标准化数据还有助于提高机器学习模型的准确度和稳定性，尤其是当变量具有不同的量级或方差时。

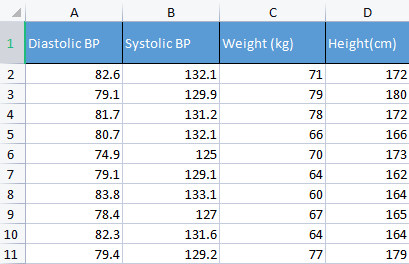
为了演示这一点，我将采用血压数据。 我通常选取不同种类的不相关数据来构建东西，因为这种数据是与人类相关的，因此它更容易理解，并作为调试材料。

   matrix Matrix = matrix_utiils.ReadCsv("bp data.csv");

   pre_processing = new CPreprocessing(Matrix, NORM_STANDARDIZATION);

之前和之后：

CS      0       10:17:31.956    PCA Test (NAS100,H1)    Non-Standardized data
CS      0       10:17:31.956    PCA Test (NAS100,H1)    [[82.59999999999999,132.1,71,172]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [79.09999999999999,129.9,79,180]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [81.7,131.2,78,172]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [80.7,132.1,66,166]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [74.90000000000001,125,70,173]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [79.09999999999999,129.1,64,162]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [83.8,133.1,60,164]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [78.40000000000001,127,67,165]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [82.3,131.6,64,164]
CS      0       10:17:31.956    PCA Test (NAS100,H1)     [79.40000000000001,129.2,77,179]]
CS      0       10:17:31.956    PCA Test (NAS100,H1)    Standardized data
CS      0       10:17:31.956    PCA Test (NAS100,H1)    [[0.979632638610581,0.8604038253411385,0.2240645398825688,0.3760399462363875]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.4489982926965129,-0.0540350228475094,1.504433339211528,1.684004976623816]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.6122703991316175,0.4863152056275964,1.344387239295408,0.3760399462363875]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.2040901330438764,0.8604038253411385,-0.5761659596980309,-0.6049338265541837]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-2.163355410265021,-2.090739730176784,0.06401843996644889,0.539535575034816]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.4489982926965129,-0.3865582403706605,-0.8962581595302708,-1.258916341747898]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.469448957915872,1.276057847245071,-1.536442559194751,-0.9319250841510407]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.7347244789579271,-1.259431686368917,-0.416119859781911,-0.7684294553526122]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.8571785587842599,0.6525768143891719,-0.8962581595302708,-0.9319250841510407]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.326544212870186,-0.3449928381802696,1.184341139379288,1.520509347825387]]

在主成分分析（PCA）的上下文中，标准化数据是必不可少的步骤，因为 PCA 基于协方差矩阵，该矩阵对变量之间的尺度和方差差值很敏感。 在运行 PCA 之前对数据进行标准化可确保生成的主成分不受具有较大量级或方差的变量的支配，因其可能会扭曲分析，并导致错误的结论。


02：查找矩阵的协方差

协方差矩阵是一个矩阵，其中包含对随机变量共同变化的影响程度的衡量值。 它用于计算数据矩阵的每一列之间的协方差。 具有有限秒矩的两个联合分布的实数型值随机变量 X 和 Y 之间的协方差定义为：

但您不必担心理解此公式，因为标准库具有此函数。 

   matrix Cova = Matrix.Cov(false);

   Print("Covariances\n", Cova);  

输出:

CS      0       10:17:31.957    PCA Test (NAS100,H1)    Covariances
CS      0       10:17:31.957    PCA Test (NAS100,H1)    [[1.111111111111111,1.05661579634328,-0.2881675653452953,-0.3314539233600543]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.05661579634328,1.111111111111111,-0.2164241126576326,-0.2333966556085017]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.2881675653452953,-0.2164241126576326,1.111111111111111,1.002480628180182]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.3314539233600543,-0.2333966556085017,1.002480628180182,1.111111111111111]]

请注意，协方差是对角线上值为 1 的方阵。 当调用该协方差矩阵方法时，必须将 rowval 输入设置为 false。

matrix matrix::Cov( 
  const bool    rowvar=true  // rows or cols vectors of observations 
);

因为我们希望我们的方阵是一个单位矩阵，基于我们给出的该函数列，因为我们有 4 列。 输出将是 4x4 矩阵，否则它将是 8x8 矩阵。


03：查找特征向量和特征值

特征向量，是与方阵关联的特殊向量。 矩阵的特征向量是一个非零向量，当乘以矩阵时，会产生自身的标量倍数，称为特征值。

更正式地说，如果 A 是方阵，则非零向量 v 是 A 的特征向量，如果存在标量 λ，称为特征值，如此 Av = λv。 有关更多细节，请参阅。

无需担心理解公式，它也在标准库中。

   if (!Cova.Eig(component_matrix, eigen_vectors))
      Print("Failed to get the Component matrix matrix & Eigen vectors");

如果您仔细看看这个 Eig 方法。

bool matrix::Eig( 
  matrix&  eigen_vectors,     // matrix of eigenvectors  
  vector&  eigen_values       // vector of eigenvalues  
   );

您可能会注意到第一个输入矩阵 eigen_vectors 返回特征向量，就像所标记的那样。 但这个特征向量也可以称为分量矩阵。 故此，我将这个特征向量存储在成分矩阵中，因为我发现根据 MQL5 语言标准，称其为特征向量令人困惑，而实际上它是一个矩阵。

Print("\nComponent matrix\n",component_matrix,"\nEigen Vectors\n",eigen_vectors);

输出:

CS      0       10:17:31.957    PCA Test (NAS100,H1)    Component matrix
CS      0       10:17:31.957    PCA Test (NAS100,H1)    [[-0.5276049902734494,0.459884739531444,0.6993704635263588,-0.1449826035480651]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.4959779194731578,0.5155907011803843,-0.679399121133044,0.1630612352922813]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.4815459137666799,0.520677926282417,-0.1230090303369406,-0.6941734714553853]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.4937128827246101,0.5015643052337933,0.184842006606018,0.6859404272536788]]
CS      0       10:17:31.957    PCA Test (NAS100,H1)    Eigen Vectors
CS      0       10:17:31.957    PCA Test (NAS100,H1)    [2.677561590453738,1.607960239905343,0.04775016337426833,0.1111724507110918]


05：查找 PCA 得分

查找主成分分析分数非常容易，只需一行代码。

 pca_scores = Matrix.MatMul(component_matrix);

可以通过将归一化矩阵乘以成分矩阵来寻找 PCA 分数。

输出:

CS      0       10:17:31.957    PCA Test (NAS100,H1)    PCA SCORES
CS      0       10:17:31.957    PCA Test (NAS100,H1)    [[-0.6500472384886967,1.199407986803537,0.1425145462368588,0.1006701620494091]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.819562596624738,1.393614599196321,-0.1510888243020112,0.1670753033981925]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.2688014256048517,1.420914385142756,0.001937917070391801,-0.6847663538666366]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-1.110534258768705,-0.06593596223641518,-0.4827665581567511,0.09571954869438426]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [2.475561333978323,-1.768915328424386,-0.0006861487484489809,0.2983796568520111]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.6245145789301378,-1.503882637300733,-0.1738415909335406,-0.2393186981373224]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-2.608156175249579,0.0662886285379769,0.1774740257067155,0.4223436077935874]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.4325302694103054,-1.589321053467977,0.2509606394263523,-0.337079680008286]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-1.667608250048573,-0.2034163217366656,0.09411419638842802,-0.03495245015036286]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.664404875867474,1.051245703485609,0.1413817973120564,0.2119289033750197]]

一旦我们得到 PCA 分数，我们需要对它们进行标准化。

   pre_processing = new CPreprocessing(pca_scores_standardized, NORM_STANDARDIZATION);

输出:

CS      0       10:17:31.957    PCA Test (NAS100,H1)    PCA SCORES | STANDARDIZED
CS      0       10:17:31.957    PCA Test (NAS100,H1)    [[-0.4187491401035159,0.9970295470975233,0.68746486754918,0.3182591681100855]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.172130620033975,1.15846730049564,-0.7288256625700642,0.528192723531639]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.1731572094549987,1.181160740523977,0.009348167869829477,-2.164823873278453]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.715386880184365,-0.05481045923432144,-2.328780161211247,0.3026082735855334]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.594713612332284,-1.470442808583469,-0.003309859736641006,0.9432989819176616]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-0.4023014443028848,-1.250129598312728,-0.8385809690405054,-0.7565833632510734]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-1.68012890598631,0.05510361946569121,0.8561031894464458,1.335199254045385]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [0.2786284867625921,-1.321151824538665,1.210589566461227,-1.06564543418136]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [-1.074244269325531,-0.1690934905926844,0.4539901733759543,-0.1104988556867913]
CS      0       10:17:31.957    PCA Test (NAS100,H1)     [1.072180711318756,0.8738669736790375,0.6820006878558206,0.6699931252073736]]


06：获取 PCA 成分

最后但不可或缺，我们需要获得主成分，这是我们所做的所有这些步骤的目的。

为了能够获得成分，我们需要找到非标准化 PCA 分数的系数，请记住！！ 我们现在有两个 PCA 分数，标准化的和非标准化的。

每个 PCA 分数的系数只是 PCA 分数列中每列的方差。

   pca_scores_coefficients.Resize(cols);
   vector v_row;
   
   for (ulong i=0; i<cols; i++)
     {
       v_row = pca_scores.Col(i);
       
       pca_scores_coefficients[i] = v_row.Var(); //variance of the pca scores
     }  

输出:

2023.02.25 10:17:31.957 PCA Test (NAS100,H1)    SCORES COEFF [2.409805431408367,1.447164215914809,0.04297514703684173,0.1000552056399828]

为了提取主成分，我们需要考虑许多准则：

  1. 特征值（Eigenvalues_and_eigenvectors）准则：该准则涉及选择具有最大特征值的主成分。 该思路是，最大的特征值对应于捕获数据中最大方差的主成分。
  2. 方差比例（The Proportion of Variance）准则：此准则涉及选择解释数据中总方差一定比例的主成分。 在此函数库中，我将它设置为大于 90%。
  3. 碎石图（Scree Plot）准则：该准则涉及检查碎石图，该碎石图按降序显示每个主成分的特征值。 曲线开始趋于平稳的点位用作选择要保留的主成分的阈值。
  4. 凯撒（Kaiser）准则：此标准涉及仅保留特征值大于系数平均值的主分量。 换言之，系数大于 1 的主成分。
  5. 交叉验证（Cross-validation）准则：此准则涉及评估验证集上 PCA 模型的性能，并选择产生最佳预测准确性的主成分。

在这个函数库中，我已为三个准则进行了编码，我认为这些准则更好，且计算效率更高。 它们是方差比例、凯撒图和碎石图。 您可以从以下枚举中选择它们中的每一个；

enum criterion
  {
    CRITERION_VARIANCE,
    CRITERION_KAISER,
    CRITERION_SCREE_PLOT
  };

以下是提取主成分的完整函数：

matrix Cpca::ExtractComponents(criterion CRITERION_)
 {

  vector vars = pca_scores_coefficients;   
  vector vars_percents = (vars/(double)vars.Sum())*100.0;
  
//--- for Kaiser
  double vars_mean = pca_scores_coefficients.Mean();

//--- for scree 
   double x[], y[];
   
//---
  matrix PCAS = {};
  
  double sum=0;
  ulong  max;
  vector v_cols = {};
   
   switch(CRITERION_)
     {
      case  CRITERION_VARIANCE:       
       #ifdef DEBUG_MODE
        Print("vars percentages ",vars_percents);       
       #endif  
     
         for (int i=0, count=0; i<(int)cols; i++)
           { 
             count++;
             
              max = vars_percents.ArgMax();
              sum += vars_percents[max];
              
              vars_percents[max] = 0; 
              
              v_cols.Resize(count);
              v_cols[count-1] = (int)max;
                   
              if (sum >= 90.0)
		 break;
           }
         
         PCAS.Resize(rows, v_cols.Size());
         
         for (ulong i=0; i<v_cols.Size(); i++)
            PCAS.Col(pca_scores.Col((ulong)v_cols[i]), i);
         
        break;
      case  CRITERION_KAISER:
      
      #ifdef DEBUG_MODE
         Print("var ",vars," scores mean ",vars_mean);
      #endif 
      
       vars = pca_scores_coefficients;
        for (ulong i=0, count=0; i<cols; i++)
           if (vars[i] > vars_mean)
             {
               count++;
       
               PCAS.Resize(rows, count);
               
               PCAS.Col(pca_scores.Col(i), count-1);
             }           
           
        break;
      case  CRITERION_SCREE_PLOT:        
         v_cols.Resize(cols);     
         for (ulong i=0; i<v_cols.Size(); i++)
             v_cols[i] = (int)i+1;
             
         
          vars = pca_scores_coefficients;          
          SortAscending(vars); //Make sure they are in ascending first order
          ReverseOrder(vars);  //Set them to descending order
          
          VectorToArray(v_cols, x);
          VectorToArray(vars, y);
          
          plt.ScatterCurvePlots("Scree plot",x,y,"variance","PCA","Variance");

//---
       vars = pca_scores_coefficients;
        for (ulong i=0, count=0; i<cols; i++)
           if (vars[i] > vars_mean)
             {
               count++;       
               PCAS.Resize(rows, count);       
               PCAS.Col(pca_scores.Col(i), count-1);
             }    
             
        break;
     } 
   return (PCAS);
 }

由于设置凯撒准则来选择含系数主成分，其可解释所有方差的 90% 以上。 我不得不将方差转换为百分比：

  vector vars = pca_scores_coefficients;   
  vector vars_percents = (vars/(double)vars.Sum())*100.0;

以下是使用每种方法的输出。

凯撒准则：

CS      0       12:03:49.579    PCA Test (NAS100,H1)    PCA'S
CS      0       12:03:49.579    PCA Test (NAS100,H1)    [[-0.6500472384886967,1.199407986803537]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [1.819562596624738,1.393614599196321]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [0.2688014256048517,1.420914385142756]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-1.110534258768705,-0.06593596223641518]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [2.475561333978323,-1.768915328424386]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-0.6245145789301378,-1.503882637300733]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-2.608156175249579,0.0662886285379769]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [0.4325302694103054,-1.589321053467977]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-1.667608250048573,-0.2034163217366656]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [1.664404875867474,1.051245703485609]]

方差准则：

CS      0       12:03:49.579    PCA Test (NAS100,H1)    PCA'S
CS      0       12:03:49.579    PCA Test (NAS100,H1)    [[-0.6500472384886967,1.199407986803537]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [1.819562596624738,1.393614599196321]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [0.2688014256048517,1.420914385142756]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-1.110534258768705,-0.06593596223641518]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [2.475561333978323,-1.768915328424386]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-0.6245145789301378,-1.503882637300733]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-2.608156175249579,0.0662886285379769]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [0.4325302694103054,-1.589321053467977]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [-1.667608250048573,-0.2034163217366656]
CS      0       12:03:49.579    PCA Test (NAS100,H1)     [1.664404875867474,1.051245703485609]]

碎石图准则：

碎石图

太棒了，如此我们现在就有两个主成分。 按简单的语言，数据集从 4 个变量减少到只有 2 个变量。 然后，您可于正在处理的任何项目中使用这些变量。


MetaTrader 中的主成分分析

现在，是时候在您想要见识的领域里运用主成分分析了，譬如交易环境。

为此，我选取了 10 个振荡器。 由于它们都是振荡指标，在尝试证明一个观点时，我决定给它们一点机会，如果您有 10 个相同类型的指标，您可以靠 PCA 来减少它们，如此您最终会得到一些易于操控的变量。

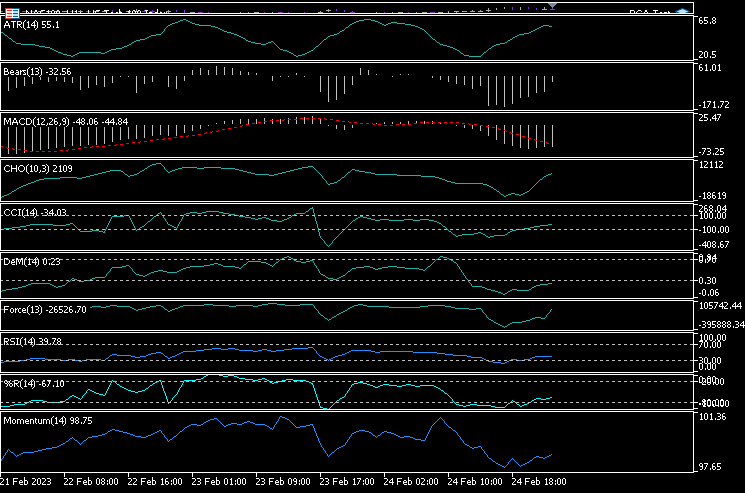
我在单个图表中添加了 10 个指标，分别是：ATR、熊市力量、MACD、柴金振荡器、商品通道指数、DeMarker、推动力指数、动量、RSI、威廉姆斯百分比范围。

   handles[0] = iATR(Symbol(),PERIOD_CURRENT, period);
   handles[1] = iBearsPower(Symbol(), PERIOD_CURRENT, period);
   handles[2] = iMACD(Symbol(),PERIOD_CURRENT,12, 26,9,PRICE_CLOSE);
   handles[3] = iChaikin(Symbol(), PERIOD_CURRENT,12,26,MODE_SMMA,VOLUME_TICK);
   handles[4] = iCCI(Symbol(),PERIOD_CURRENT,period, PRICE_CLOSE);
   handles[5] = iDeMarker(Symbol(),PERIOD_CURRENT,period);
   handles[6] = iForce(Symbol(),PERIOD_CURRENT,period,MODE_EMA,VOLUME_TICK);
   handles[7] = iMomentum(Symbol(),PERIOD_CURRENT,period, PRICE_CLOSE);
   handles[8] = iRSI(Symbol(),PERIOD_CURRENT,period,PRICE_CLOSE);
   handles[9] = iWPR(Symbol(),PERIOD_CURRENT,period);
   
   
   for (int i=0; i<10; i++)
    {
      matrix_utiils.CopyBufferVector(handles[i],0,0,bars,buff_v);
      ind_Matrix.Col(buff_v, i); //store each indicator in ind_matrix columns
    }

我决定在同一张图表中看到所有这些指标。 以下是它们的样子：

振荡器

它们到底是怎么做到看起来几乎一样的，我们来看看它们的相关矩阵：

    Print("Oscillators Correlation Matrix\n",ind_Matrix.CorrCoef(false));  

输出:

CS      0       18:03:44.405    PCA Test (NAS100,H1)    Oscillators Correlation Matrix
CS      0       18:03:44.405    PCA Test (NAS100,H1)    [[1,0.01772984879133655,-0.01650305145071043,0.03046861668248528,0.2933315924162302,0.09724971519249033,-0.054459564042778,-0.0441397473782667,0.2171969726706487,0.3071254662907512]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [0.01772984879133655,1,0.6291675928958272,0.2432064602541826,0.7433991440764224,0.7857575973967624,0.8482060554701495,0.8438879842180333,0.8287766948950483,0.7510097635884428]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [-0.01650305145071043,0.6291675928958272,1,0.80889919514547,0.3583185473647767,0.79950773673123,0.4295059398014639,0.7482107564439531,0.8205910850439753,0.5941794310595322]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [0.03046861668248528,0.2432064602541826,0.80889919514547,1,0.03576792595345671,0.436675349452699,0.08175026884450357,0.3082792264724234,0.5314362133025707,0.2271361556104472]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [0.2933315924162302,0.7433991440764224,0.3583185473647767,0.03576792595345671,1,0.6368513319457978,0.701918992559641,0.6677393692960837,0.7952832674277922,0.8844891719743937]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [0.09724971519249033,0.7857575973967624,0.79950773673123,0.436675349452699,0.6368513319457978,1,0.6425071357003039,0.9239712092224102,0.8809179254503203,0.7999862160768584]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [-0.054459564042778,0.8482060554701495,0.4295059398014639,0.08175026884450357,0.701918992559641,0.6425071357003039,1,0.7573281438252102,0.7142333470379938,0.6534102287503526]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [-0.0441397473782667,0.8438879842180333,0.7482107564439531,0.3082792264724234,0.6677393692960837,0.9239712092224102,0.7573281438252102,1,0.8565660350098397,0.8221821793990941]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [0.2171969726706487,0.8287766948950483,0.8205910850439753,0.5314362133025707,0.7952832674277922,0.8809179254503203,0.7142333470379938,0.8565660350098397,1,0.8866871375902136]
CS      0       18:03:44.405    PCA Test (NAS100,H1)     [0.3071254662907512,0.7510097635884428,0.5941794310595322,0.2271361556104472,0.8844891719743937,0.7999862160768584,0.6534102287503526,0.8221821793990941,0.8866871375902136,1]]

查看相关矩阵，您可能会注意到只有少数指标与其它少量指标相关，但它们微不足道，如此它们看起来毕竟有所区别。 我们将 PCA 应用于这个矩阵，看看该算法为我们带来了什么。

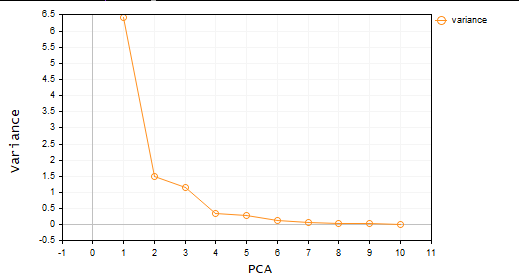
    pca = new Cpca(ind_Matrix);
    matrix pca_matrix = pca.ExtractComponents(ENUM_CRITERION);

下图我选择的是碎石图准则：

振荡器碎石图

查看碎石图，不可否认的是，仅选择了 3 个 PCA，以下是它们的样子；

CS      0       15:03:30.992    PCA Test (NAS100,H1)    PCA'S
CS      0       15:03:30.992    PCA Test (NAS100,H1)    [[-2.297373513063062,0.8489493134565058,0.02832445955171548]
CS      0       15:03:30.992    PCA Test (NAS100,H1)     [-2.370488225540198,0.9122356709081817,-0.1170316144060158]
CS      0       15:03:30.992    PCA Test (NAS100,H1)     [-2.728297784013197,1.066014896296926,-0.2859442064697605]
CS      0       15:03:30.992    PCA Test (NAS100,H1)     [-1.818906988827231,1.177846546204641,-0.748128826146959]
...
...
CS      0       15:03:30.992    PCA Test (NAS100,H1)     [-3.26602969252589,0.4816995789189212,-0.7408982990360158]
CS      0       15:03:30.992    PCA Test (NAS100,H1)     [-3.810781495417407,0.4426824869307094,-0.5737277071364888…]

从 10 个变量减到只有 3 个变量，呵呵！！

这就是为什么成为数据分析师非常重要的原因，因为我看到许多交易者在图表上加了很多指标，有时在智能系统里，我认为使用这种方式来减少变量是值得的，顺便说一下，尽可能降低我们程序的计算成本，这不是一条交易建议，如果您一直在做的事情对您有用并且您满意，那么就没有什么可担心的了。

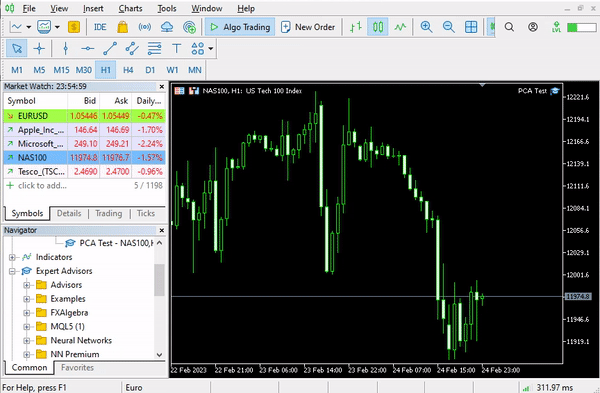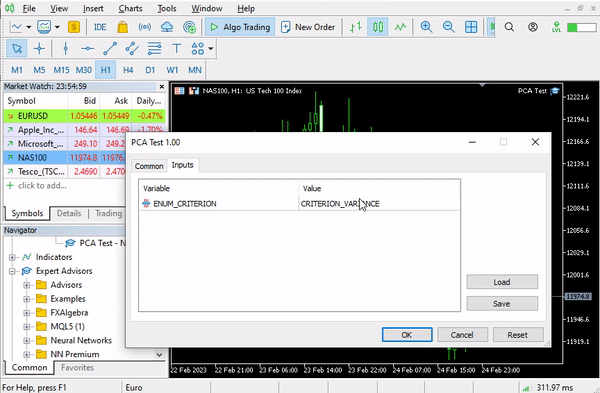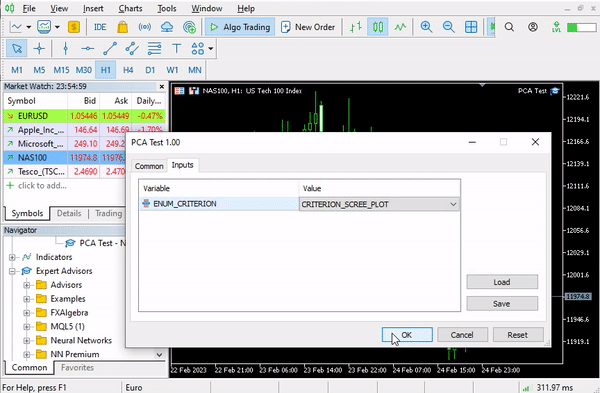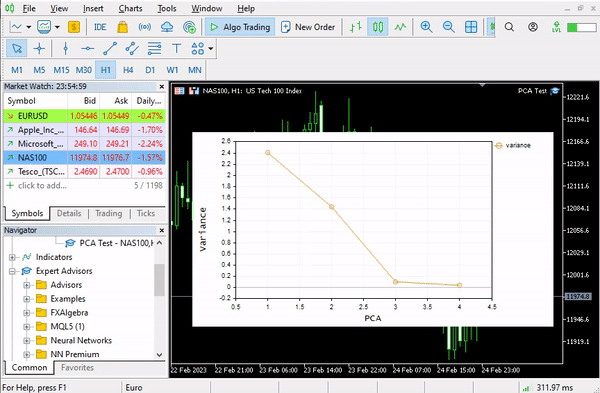
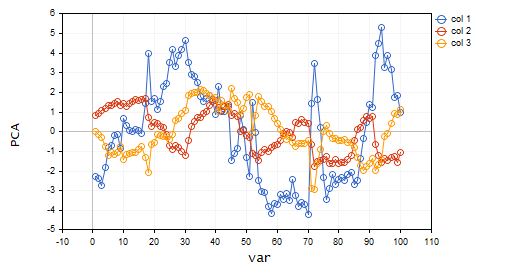
我们来可视化这些主成分，看看它们在同一轴上的外观。

       plt.ScatterCurvePlotsMatrix("pca's ",pca_matrix,"var","PCA");

输出:

主成分


主成分分析的优势

  1. 降维：PCA 可以有效地减少数据集中的变量数量，同时保留最重要的信息。 这可以简化数据分析和可视化，降低计算复杂性，并提高模型性能。
  2. 数据压缩：PCA 可以有效地将大型数据集压缩成较少数量的主成分，可以节省存储空间，并减少数据传输时间。
  3. 降噪：PCA 可以通过关注最重要的形态，或趋势来消除数据中的噪声或随机变化。 正如您刚刚看到的，10 个振荡器里有很多噪声。
  4. 可解释的结果：PCA 产生易于解释和可视化的主成分，这有助于理解数据的结构。 
  5. 数据规范化：PCA 通过缩放到单位方差来标准化数据，可以减少变量尺度差异的影响，提高统计模型的准确性。

    主成分分析的缺点。

    1. 信息丢失：如果丢弃了太多主成分，或者保留的成分未能捕获数据中的所有相关变化，则 PCA 可能导致信息丢失。
    2. 解释结果可能很烦人：解释主成分可能很困难，因为它们只是变量，您不知道具体线索，尤其是当原始变量高度相关，或主成分数量很大时。
    3. 对异常值敏感：就像许多 ML 技术一样，异常值令该算法失真，并导致结果的偏差。
    4. 计算密集型：在大型数据集中，PCA 算法在试图求解时也许会产生相同的问题。
    5. 模型假设：该算法假设数据线性相关，主成分不相关，这在实践中并不总是正确的。 违反这些假设可能会导致糟糕的结果。


    后记

    总之，主成分分析（PCA）是一种强大的技术，可用于降低数据的维度，同时保留最重要的信息。 通过辨别数据集的主要成分，我们可以深入了解市场的底层结构。 PCA 在工程和生物学等交易领域之外具有广泛的应用，尽管它是一种数学密集型技术，但它的好处令其值得一试。 依据正确的方式和数据，PCA 可以帮助我们解锁新的见解，并根据我们可能拥有的数据做出明智的交易决策。

    在我的 GitHub 存储库上跟踪该算法的发展和更新：https://github.com/MegaJoctan/MALE5

    文件 说明
    matrix_utils.mqh  包含其它矩阵操作函数
    pca.mqh  主成分分析函数库
    plots.mqh   包含有助于绘制向量的类
    preprocessing.mqh  为 ML 算法准备和扩展数据的函数库
     PCA Test.mqh  测试算法的 EA 以及本文中讨论的所有内容 

    参考文章：




    本文由MetaQuotes Ltd译自英文
    原文地址： https://www.mql5.com/en/articles/12229

    附加的文件 |
    下载ZIP
    PCA_Attachments.zip (12.8 KB)
    注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

    该作者的其他文章

    前往讨论
    种群优化算法：树苗播种和成长（SSG）算法 种群优化算法：树苗播种和成长（SSG）算法
    树苗播种和成长（SSG）算法的灵感来自星球上最具韧性的生物之一，在各种条件下都表现出杰出的生存能力。
    开发回放系统 — 市场模拟（第 02 部分）：首次实验（II） 开发回放系统 — 市场模拟（第 02 部分）：首次实验（II）
    这一次，我们尝试换一种不同的方式来实现 1 分钟的目标。 然而，这项任务并非如人们想象的那么简单。
    学习如何基于斐波那契（Fibonacci）设计交易系统 学习如何基于斐波那契（Fibonacci）设计交易系统
    在本文中，我们将继续如何基于最流行的技术指标创建交易系统的系列文章。 这次一个新的技术工具，即斐波那契（Fibonacci），我们将学习如何基于该技术指标设计交易系统。
    数据科学和机器学习（第 12 部分）：自训练神经网络能否帮助您跑赢股市？ 数据科学和机器学习（第 12 部分）：自训练神经网络能否帮助您跑赢股市？
    您是否厌倦了持续尝试预测股市？ 您是否希望有一个水晶球来帮助您做出更明智的投资决策？ 自训练神经网络可能是您一直在寻找的解决方案。 在本文中，我们将探讨这些强大的算法是否可以帮助您“乘风破浪”，并跑赢股市。 通过分析大量数据和识别形态，自训练神经网络通常可以做出比人类交易者更准确的预测。 发现如何使用这项尖端技术来最大化您的盈利，并制定更明智的投资决策。