数据科学和机器学习(第 29 部分):为 AI 训练目的而选择最佳外汇数据的基本技巧
内容
- 概述
- 什么是特征选择
- 为什么特征选择对于 AI 模型是必需的?
- 过滤方法
相关矩阵
统计测试
— 卡方测试
— ANOVA 测试 - 包装方法
递归特征消除(RFE)
顺序特征选择(SFS) - 嵌入式方法
套索回归
基于决策树的方法 - 降维技术
- 结束语
概述
所有交易数据和信息,诸如指标(MetaTrader 5 中有超过 36 个内置指标)、品种对(有 100 多个品种),都能够当作关联策略的数据,还有对交易者颇具价值的新闻等。我试图提出的一点是,交易者在手工交易、或尝试构建人工智能模型时有充裕的信息可供使用,从而帮助我们在交易机器人中制定明智的交易决策。
在我们手头的所有信息当中,肯定有一些坏信息(这只是常识)。并非所有指标、数据、策略、等都对特定的交易品种、策略、或情况有用。我们如何判定可供交易和机器学习模型所用的正确信息,以便实现最大的效率和盈利能力?这就是特征选择发挥作用之处。
什么是特征选择
特征选择是从原始数据集中识别和选择相关特征子集,用于模型构造的过程。这是一个判定最实用信息,以供机器学习模型,并丢弃垃圾(不太重要的特征/信息)的过程。
特征选择是构建有效机器学习模型的关键步骤之一,以下是原因。
为什么特征选择对于 AI 模型是必需的?
- 降低维度
通过剔除不相关或冗余的特征,特征选择简化了模型,并降低了计算成本。 - 提高性能
专注于信息量最大的特征,可以提升模型的准确性、和预测能力。 - 提升高可解释性
特征较少的模型往往更容易理解和解释。 - 通过删除噪声或不相关的数据来处理噪音
通过删除不重要的特征,特征选择能够帮助防止过度拟合,这往往是由太多不相关的数据而导致。
现在我们知道特征选择如此重要,那么我们来探索一些数据科学家和机器学习智能系统用到的不同技术,以便为其 AI 模型找到最佳特征。
使用我们在这篇文章(必读)中所用的相同数据集,该数据集有 28 个变量。
在 28 个变量中,我们想找到与 “TARGET_OPEN”(持有下一根蜡烛的开盘价)和 “TARGET_CLOSE” (持有下一根蜡烛的收盘价)列最相关的变量,并留下不太不相关的数据。
特征选择技术和方法能分为三种主要类型;筛选方法、包装方法、和嵌入方法。我们来一个接一个地剖析每种方法,看看它们都和什么有关。
筛选方法
筛选方法评估特征与机器学习模型或算法的独立性。这些方法包括使用相关矩阵和执行统计测试。
相关矩阵
相关矩阵是一张表格,显示不同变量之间相关系数。
相关系数是一种统计度量,指示两个变量之间的关系强度和方向。其范围从 -1 到 1。
值 1 示意完全正相关(当一个变量增加时,另一个变量按比例增加)。
值 0 示意没有相关性(两个变量之间没有关系)。
值 -1 示意完全负相关(当一个变量增加时,另一个变量按比例减少)。
我们从使用 Python 计算相关矩阵开始。
计算相关矩阵
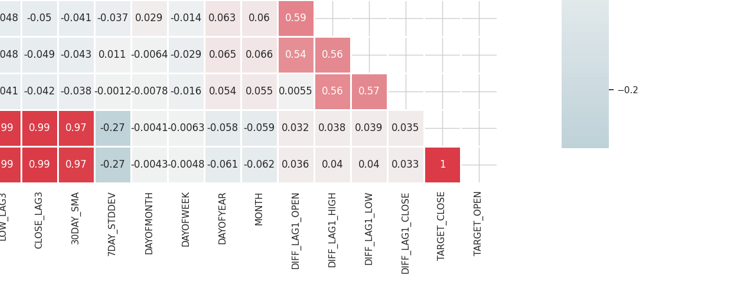
# Compute the correlation matrix corr_matrix = df.corr() # We generate a mask for the upper triangle mask = np.triu(np.ones_like(corr_matrix, dtype=bool)) cmap = sns.diverging_palette(220, 10, as_cmap=True) # Custom colormap plt.figure(figsize=(28, 28)) # 28 columns to fit better # Draw the heatmap with the mask and correct aspect ratio sns.heatmap(corr_matrix, mask=mask, cmap=cmap, vmax=1.0, center=0, annot=True, square=True, linewidths=1, cbar_kws={"shrink": .75}) plt.title('Correlation Matrix') plt.savefig("correlation matrix.png") plt.show()
输出
矩阵太大不好显示,以下是一些非常有用的部分。
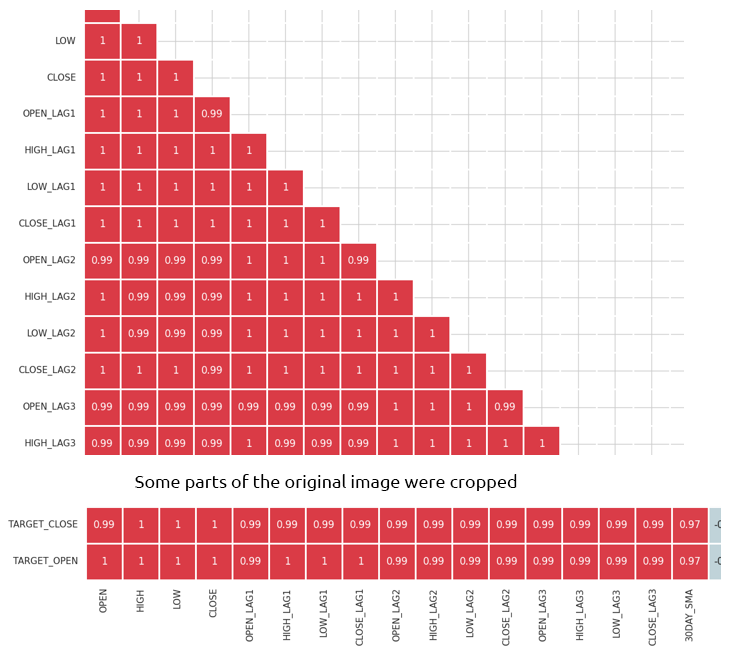
识别并消除高度相关的特征
当两个或多个特征彼此高度相关时,会出现高度多重共线性,这就会导致许多机器学习算法出问题,尤其是线性模型,这种状态会导致系数估算不稳定。
自变量本身之间的相关性
通过组合或删除高度相关特征,您可简化模型而不会丢失太多信息。例如,在上面的相关矩阵图片中,开盘价、最高价、和最低价是 100% 相关。它们的相关性为 99.x%(这些最终值是四舍五入)。 我们可以决定删除这些变量,并仅保留一个变量,或用技术来降低我们将要讨论的数据维度。
自变量(特征)与目标变量之间的相关性
与目标变量具有强相关性的特征通常信息量更大,并且可以提高模型的预测性能。
统计测试
我们可以运行统计测试来选择与目标变量具有显著关系的特征。
— 卡方测试
卡方测试衡量预期计数与列联表格中所观察计数的比较情况。它有助于判定两个类别变量之间是否存在显著关联。
列联表是一种矩阵格式的表格,显示变量的频率分布,它可用于检查两个类别变量之间的关系。在卡方测试中,使用列联表将类别变量的观测到频率与预期频率进行比较。
卡方测试仅应用于类别变量。
在我们的数据集中,我们有几个类别变量(DAYOFMONTH、DAYOFWEEK、DAYOFYEAR 和 MONTH)。我们还必须创建一个目标变量来衡量它与特征之间的关系。
Python 代码from sklearn.feature_selection import chi2 from sklearn.feature_selection import SelectKBest target = [] # Loop through each row in the DataFrame to create the target variable for i in range(len(df)): if df.loc[i, 'TARGET_CLOSE'] > df.loc[i, 'TARGET_OPEN']: target.append(1) else: target.append(0) X = pd.DataFrame({ 'DAYOFMONTH': df['DAYOFMONTH'], 'DAYOFWEEK': df['DAYOFWEEK'], 'DAYOFYEAR': df['DAYOFYEAR'], 'MONTH': df['MONTH'] }) chi2_selector = SelectKBest(chi2, k='all') chi2_selector.fit(X, target) chi2_scores = chi2_selector.scores_ # Output scores for each feature feature_scores = pd.DataFrame({'Feature': X.columns, 'Chi2 Score': chi2_scores}) print(feature_scores)
输出
Feature Chi2 Score 0 DAYOFMONTH 0.622628 1 DAYOFWEEK 0.047481 2 DAYOFYEAR 14.618057 3 MONTH 0.489713
从上面的输出中,我们看到 DAYOFYEAR 的 Chi2 分数最高,这表明与其它变量相比,它是对目标变量影响最大的变量。这是有道理的,因为数据收集是来自日线时间帧,且日线唯一地对应于一年中的某一天。数据集中 DAYOFYEAR 变量的强势表现可能会增加其频率和重要性,令其成为预测目标变量的关键特征。
ANOVA(方差分析)测试
ANOVA 是一种统计方法,用于比较三个或更多组的均值,以便查看是否至少有一组均值与其它组的均值存在统计差异。它有助于判定连续特征与类别目标变量之间关系的强度。
它的工作不仅分析每组内和各组之间的方差,还要衡量每组内观察到的变异性,以及不同组均值之间的变异性。
该测试计算 F-统计量,即组间方差与组内方差的比值。F-统计量越高,表示各组具有不同的均值。
我们使用 Scikit-learn 中的 “f_classif” 来执行特征选择的方差分析测试。
Python 代码
from sklearn.feature_selection import f_classif
# We start by dropping the categorical variables in the dataset
X = df.drop(columns=[
"DAYOFMONTH",
"DAYOFWEEK",
"DAYOFYEAR",
"MONTH",
"TARGET_CLOSE",
"TARGET_OPEN"
])
# Perform ANOVA test
selector = SelectKBest(score_func=f_classif, k='all')
selector.fit(X, target)
# Get the F-scores and p-values
anova_scores = selector.scores_
anova_pvalues = selector.pvalues_
# Create a DataFrame to display results
anova_results = pd.DataFrame({'Feature': X.columns, 'F-Score': anova_scores, 'p-Value': anova_pvalues})
print(anova_results) 输出
Feature F-Score p-Value 0 OPEN 3.483736 0.062268 1 HIGH 3.627995 0.057103 2 LOW 3.400320 0.065480 3 CLOSE 3.666813 0.055792 4 OPEN_LAG1 3.160177 0.075759 5 HIGH_LAG1 3.363306 0.066962 6 LOW_LAG1 3.309483 0.069181 7 CLOSE_LAG1 3.529789 0.060567 8 OPEN_LAG2 3.015757 0.082767 9 HIGH_LAG2 3.034694 0.081810 10 LOW_LAG2 3.259887 0.071295 11 CLOSE_LAG2 3.206956 0.073629 12 OPEN_LAG3 3.236211 0.072329 13 HIGH_LAG3 3.022234 0.082439 14 LOW_LAG3 3.020219 0.082541 15 CLOSE_LAG3 3.075698 0.079777 16 30DAY_SMA 2.665990 0.102829 17 7DAY_STDDEV 0.639071 0.424238 18 DIFF_LAG1_OPEN 1.237127 0.266293 19 DIFF_LAG1_HIGH 0.991862 0.319529 20 DIFF_LAG1_LOW 0.131002 0.717472 21 DIFF_LAG1_CLOSE 0.198001 0.656435
F-分数越高,表明该特征与目标变量的关系越强。
P-值小于显著水平(例如 0.05)则被视为统计显著。
我们还可以选择 F-分数最高、或 P-值最低的特征,这些特征是最重要的特征,而其它特征抛之于后。我们选择 10 个顶级特征。
Python 代码
selector = SelectKBest(score_func=f_classif, k=10) X_selected = selector.fit_transform(X, target) # print the selected feature names selected_features = X.columns[selector.get_support()] print("Selected Features:", selected_features)
输出
Selected Features: Index(['OPEN', 'HIGH', 'LOW', 'CLOSE', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1', 'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3'], dtype='object')
包装方法
这些方法涉及使用不同的子集或特征评估模型的性能。在包装器方法下,我们将讨论递归特征消除(RFE),和顺序特征选择(SFS)。
递归特征消除(RFE)
这是一种特征选择技术,旨在通过递归参考越来越小的特征集来选择最相关的特征。它的工作是拟合模型,并删除最不重要的特征,直至达到所需的特征数量。
RFE 如何工作
我们从训练任意机器学习模型开始。在该示例中,我们使用逻辑回归。
Python 代码
from sklearn.feature_selection import RFE from sklearn.linear_model import LogisticRegression # Prepare the target variable, again y = [] # Loop through each row in the DataFrame to create the target variable for i in range(len(df)): if df.loc[i, 'TARGET_CLOSE'] > df.loc[i, 'TARGET_OPEN']: y.append(1) else: y.append(0) # Drop future variables from the feature set X = df.drop(columns=["TARGET_CLOSE", "TARGET_OPEN"]) # Initialize the model model = LogisticRegression(max_iter=10000)
然后,我们根据想从数据中选择的模型、及最具影响力的特征数量来初始化 RFE。
# Initialize RFE with the model and number of features to select rfe = RFE(estimator=model, n_features_to_select=10) # Fit RFE rfe.fit(X, y) selected_features_mask = rfe.support_
最后,我们判定最不重要的特征,并消除它们。
Python 代码
# Getting the names of the selected features feature_names = X.columns selected_feature_names = feature_names[selected_features_mask] selected_features = pd.DataFrame({ "Name": feature_names, "Mask": selected_features_mask }) selected_features.head(-1)
输出
Name Mask 0 OPEN True 1 HIGH True 2 LOW True 3 CLOSE True 4 OPEN_LAG1 False 5 HIGH_LAG1 True 6 LOW_LAG1 True 7 CLOSE_LAG1 True 8 OPEN_LAG2 False 9 HIGH_LAG2 False 10 LOW_LAG2 True 11 CLOSE_LAG2 True 12 OPEN_LAG3 True 13 HIGH_LAG3 False 14 LOW_LAG3 False 15 CLOSE_LAG3 False 16 30DAY_SMA False 17 7DAY_STDDEV False 18 DAYOFMONTH False 19 DAYOFWEEK False 20 DAYOFYEAR False 21 MONTH False 22 DIFF_LAG1_OPEN False 23 DIFF_LAG1_HIGH False 24 DIFF_LAG1_LOW False
所有赋予了 True 值的特征都是最重要的值。为了获得它们,我们可以从原始 X 矩阵中对它们进行切片。
# Filter the dataset to keep only the selected features X_selected = X.loc[:, selected_features_mask] #for better readability, we convert this into pandas dataframe X_selected_df = pd.DataFrame(X_selected, columns=selected_feature_names) print("Selected Features") X_selected_df.head()
输出
- RFE 能与任何可按重要性进行特征排名的模型搭配使用。
- 通过消除不相关的特征,RFE 能提升模型的性能。
- 通过删除不必要的特征,它能帮助降低过度拟合
- 当给定大型数据集和复杂模型(如神经网络)时,计算成本可能会很高,因为它需要多次重新训练模型。
- RFE 是一种贪婪算法,或许并不总能找到特征的最佳子集。
顺序特征选择(SFS)
这是一种特征选择的包装方法,它基于特征对模型性能的贡献增减特征,来逐步构建特征集。顺序特征选择有两种主要类型:前向和后向消除。
在前向选择中,从空集开始逐个添加特征,直至达到所需的特征数量,或者添加更多不会提升模型性能的特征。
在向后选择中,其与前向选择相反。我们从所有特征开始,然后逐个删除它们,每次删除最不重要的特征,直到留下所需数量的特征。
前向选择
from sklearn.feature_selection import SequentialFeatureSelector # Create a logistic regression model model = LogisticRegression(max_iter=10000) # Create a SequentialFeatureSelector object sfs = SequentialFeatureSelector(model, n_features_to_select=10, direction='forward') # Fit the SFS object to the training data sfs.fit(X, target) # Get the selected feature indices selected_features = sfs.get_support(indices=True) selected_features_names = X.columns[selected_features] # get the feature names # Print the selected features print("Selected feature indices:", selected_features) print("Selected feature names:", selected_feature_names)
输出
Selected feature indices: [ 1 7 8 12 17 19 22 23 24 25] Selected feature names: Index(['OPEN', 'HIGH', 'LOW', 'CLOSE', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1', 'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3'], dtype='object')
后向选择
# Create a logistic regression model model = LogisticRegression(max_iter=10000) # Create a SequentialFeatureSelector object sfs = SequentialFeatureSelector(model, n_features_to_select=10, direction='backward') # Fit the SFS object to the training data sfs.fit(X, target) # Get the selected feature indices selected_features = sfs.get_support(indices=True) selected_features_names = X.columns[selected_features] # get the feature names # Print the selected features print("Selected feature indices:", selected_features) print("Selected feature names:", selected_feature_names)
输出
Selected feature indices: [ 2 3 7 10 11 12 13 14 15 16] Selected feature names: Index(['OPEN', 'HIGH', 'LOW', 'CLOSE', 'HIGH_LAG1', 'LOW_LAG1', 'CLOSE_LAG1', 'LOW_LAG2', 'CLOSE_LAG2', 'OPEN_LAG3'], dtype='object')
尽管采取了不同的方式,但后向和前向方法都收敛到相同的解。生成相同数量的特征。
- 易于理解和实现。
- 它可与任意机器学习算法配合使用。
- 通过选择最相关的特征,往往能导致模型性能更佳。
- 该方法配以大型数据集、或许多特征,速度会很慢。
- 或许无法找到最优特征集,因为它会基于局部改进做出决策。
嵌入式方法
这些方法涉及在模型训练过程中执行特征选择。嵌入式特征选择工作流程涉及,
- 训练机器学习模型
- 衍生特征重要性
- 选择排名靠前的预测变量
Lasso 回归
线性回归模型基于特征空间的线性组合预测成果。系数是通过实际值和预测的目标值之间的最小平方差来判定的。有三个主要的正则化过程:Ridge、Lasso 和 Elastic Net 正则化,后者结合了前两者。在 Lasso 回归中,使用 L1 正则化将系数按给定常数缩小。在 Ridge 回归中,使用 L2 正则化将系数的平方按常数进行惩罚。缩小系数旨在降低方差,并防止过度拟合。最佳常量(正则化参数)需要通过超参数优化来估算。Lasso 正则化可以将某些系数精确设置为零。这样特征选择的结果,令我们能够安全地从数据中删除这些特征。
Python 代码
from sklearn.model_selection import train_test_split from sklearn.linear_model import Lasso from sklearn.metrics import r2_score from sklearn.preprocessing import MinMaxScaler y = df["TARGET_CLOSE"] # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # A scaling technique scaler = MinMaxScaler() # Initialize and fit the lasso model lasso = Lasso(alpha=0.001) # You need tune for the best penalty value # Train the scaler and transfrom data X_train = scaler.fit_transform(X_train) lasso.fit(X_train, y_train) print(f'Coefficients: {lasso.coef_}') #print coefficients # Predict on the test set X_test = scaler.transform(X_test) y_pred = lasso.predict(X_test) # Calculate mean squared error mse = r2_score(y_test, y_pred) print(f'Lasso regression test accuracy = {mse}') # select all features with coefficents not equal to zero selected_features = X.columns[lasso.coef_ != 0] print(f'Selected Features: {selected_features}')
输出
Coefficients: [ 0. 0.02575516 0.05720178 0.1453415 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.0228085 -0. 0. -0. 0. 0. 0. 0. 0. 0. ] Lasso regression test accuracy = 0.9894539761500866 Selected Features: Index(['HIGH', 'LOW', 'CLOSE', '30DAY_SMA'], dtype='object')
该模型的准确率为 98%,因为它只选择了 4 个特征。
- Lasso 会自动选择最重要的特征,这简化了模型,并提升了可解释性。
- 通过添加惩罚项,lasso 降低了过度拟合的风险。
- 由于消除了不相关的特征,Lasso 可以生成更易于解释的模型。
- 当特征高度相关时,lasso 回归技术可能会导致系数估算不稳定。
- 如果特征数量超过观测值数量,lasso 或许难以正常运行。
基于决策树的方法
决策树算法通过递归分区数据来预测成果。在每个节点,算法选择一个特征、及一个值来拆分数据,旨在最大限度地减少杂质。
决策树中的特征重要性,按照每个特征达成的降低整棵树的杂质总量来判定。例如,如果用一个特征在多个节点处切分数据,则其重要性的计算,是所有这些节点处的杂质减少量之和。随机森林并行生长出众多决策树。最终预测是单棵树预测的均值(或多数投票)。随机森林中的特征重要性是所有树中每个特征的平均重要性。
梯度提升机(GBM),例如 XGBoost,按顺序构建树。每棵树都旨在纠正前一棵树的误差(容错)。在 GBM 中,特征重要性是所有树的重要性之和。
通过分析决策树生成的特征重要性数值,我们可以识别和选择模型最重要的特征。
from sklearn.ensemble import RandomForestClassifier y = [] # Loop through each row in the DataFrame to create the target variable for i in range(len(df)): if df.loc[i, 'TARGET_CLOSE'] > df.loc[i, 'TARGET_OPEN']: y.append(1) else: y.append(0) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) model = RandomForestClassifier(n_estimators=50, min_samples_split=10, max_depth=5, min_samples_leaf=5) model.fit(X_train, y_train) importances = model.feature_importances_ print(importances) selected_features = importances > 0.04 selected_feature_names = X.columns[selected_features] print("selected features\n",selected_feature_names)
输出
[0.02691807 0.05334113 0.03780997 0.0563491 0.03162462 0.03486413 0.02652285 0.0237652 0.03398946 0.02822157 0.01794172 0.02818283 0.04052433 0.02821834 0.0386661 0.03921218 0.04406372 0.06162133 0.03103843 0.02206782 0.05104613 0.01700301 0.05191551 0.07251801 选择的特征 Index(['HIGH', 'CLOSE', 'OPEN_LAG3', '30DAY_SMA', '7DAY_STDDEV', 'DAYOFYEAR', 'DIFF_LAG1_OPEN', 'DIFF_LAG1_HIGH', 'DIFF_LAG1_LOW', 'DIFF_LAG1_CLOSE'], dtype='object')
在我们急于使用所选特征之前,我们必须衡量这些所选特征对于随机森林分类器的准确性。确保在测试数据上,按模型获取的选择特征表现良好。
from sklearn.metrics import accuracy_score
test_pred = model.predict(X_test)
print(f"Random forest test accuracy = ",accuracy_score(y_test, test_pred)) - 随机森林会创建一片树的融汇,与单棵决策树相比,这降低了过度拟合的风险。这种稳健性令特征重要性分数更加可靠。
- 它们能管理拥有大量特征的数据集,而不会显著降低性能,这令其适合在高维空间中进行特征选择。
- 它们能捕获特征之间复杂的非线互动,从而更细致地了解特征重要性。
- 对于大型数据集和大量特征,训练随机森林的计算成本可能很昂贵。
- 随机森林或许会为相关要素分配相似的重要性分数,令其难以区分哪些因素真正重要。
- 随机森林有时可能偏爱连续特征、或那些拥有多个级别的特征,多过级别较少的类别特征,潜在地会令特征重要性分数产生偏差。
降维技术
降维技术也可添加到特征选择技术的组合之中。主成分分析(PCA)、线性判别分析(LDA)、非负矩阵分解(NMF)、截断 SVD、等降维技术旨在将数据转换到低维空间。
如从相关矩阵中可见,开盘价、最高价、最低价、和收盘价特征高度相关。我们将这些变量合并为一个变量,以便简化模型的特征,同时在 PCA 生成的这个变量中保留必要的信息。使用线性回归模型,我们将衡量 PCA 的降维数据与原始数据相比,如何有效保持准确性。
from sklearn.decomposition import PCA from sklearn.linear_model import LinearRegression pca = PCA(n_components=1) ohlc = pd.DataFrame({ "OPEN": df["OPEN"], "HIGH": df["HIGH"], "LOW": df["LOW"], "CLOSE": df["CLOSE"] }) y = df["TARGET_CLOSE"] # let us use the linear regression model model = LinearRegression() # for OHLC original data model.fit(ohlc, y) preds = model.predict(ohlc) print("ohlc_original data LR accuracy = ",r2_score(y, preds)) # For data reduced in dimension ohlc_reduced = pca.fit_transform(ohlc) print(ohlc_reduced[:10]) # print 10 rows of the reduced data model.fit(ohlc_reduced, y) preds = model.predict(ohlc_reduced) print("ohlc_reduced data LR accuracy = ",r2_score(y, preds))
输出
ohlc_original data LR accuracy = 0.9937597843724363 [[-0.14447016] [-0.14997874] [-0.14129409] [-0.1293209 ] [-0.12659902] [-0.12895961] [-0.13831287] [-0.14061213] [-0.14719862] [-0.15752861]] ohlc_reduced data LR accuracy = 0.9921387699876517
两种模型产生的准确度值大致相同,约为 0.99。一个使用原始数据(拥有 4 个特征),另一个使用降维数据(拥有 1 个特征)。
最后,我们可以通过删除开盘价、最高价、最低价、和收盘价特征,并添加一个名为 OHLC 的新特征来修改原始数据,该特征结合了前面的四个特征。
new_df = df.drop(columns=["OPEN", "HIGH", "LOW", "CLOSE"]) # new_df["OHLC"] = ohlc_reduced # Reorder the columns to make "ohlc" the first column cols = ["OHLC"] + [col for col in new_df.columns if col != "OHLC"] new_df = new_df[cols] new_df.head(10)
输出
降维技术在特征选择中的优点
- 降低特征数量能通过消除噪音和冗余信息,来提高机器学习模型的性能。
- 通过减少特征空间,在与更有可能发生过拟合的高维数据打交道时,降维技术有助于减轻过拟合。
- 这些技术能从数据集中过滤掉噪音,导致获得更清晰的数据,从而提升模型的准确性和可靠性。
- 特征较少的模型更简单,且更易于解释。
降维技术在特征选择中的缺点
- 降维通常会导致重要信息丢失,这或许会对模型的性能产生负面影响。
- 像 PCA 这样的技术需要选择要保留的分量数量,这或许并不直截了当,且可能涉及反复试验、或交叉验证。
- 与原始特征相比,由降维技术创建的新特征可能难以解释。
- 降低维度可能会过度简化数据,导致模型错失特征之间微妙、但重要的关系。
后记
知晓如何提取最有价值的信息,对于优化机器学习模型至关重要。有效的特征选择可以显著降低训练时间,并提升模型准确性,从而在 MetaTrader 5 中实现更高效的 AI 驱动的交易机器人。通过仔细选择最相关特征,您能强化实时交易和策略测试期间的性能,最终令您的交易算法达成更佳结果。
此致敬意。
附件表
| 文件 | 说明/用法 |
|---|---|
| feature_selection.ipynb | 本文中讨论的所有 Python 代码都可以在此 Jupyter 笔记簿中找到 |
| Timeseries OHLC.csv | 本文中用到的数据集 |
源
- 一种基于卡方统计的文本分类特征选择方法 (https://www.researchgate.net/publication/331850396_A_Chi-Square_Statistics_Based_Feature_Selection_Method_in_Text_Classification)
- 特征选择 (https://en.wikipedia.org/wiki/Feature_selection)
- 嵌入式方法 (https://www.blog.trainindata.com/feature-selection-with-embedded-methods/)
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/15482
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 神经网络实践:绘制神经元
神经网络实践:绘制神经元
 Connexus入门(第一部分):如何使用WebRequest函数?
Connexus入门(第一部分):如何使用WebRequest函数?
 随机优化和最优控制示例
随机优化和最优控制示例