神经网络实验（第 4 部分）：模板

MetaTrader 5 — 交易系统 | 7 八月 2023, 10:20

1 014

Roman Poshtar

我想更频繁地与您分享我的经验，但如您所知，这样的活动需要时间和计算机资源，不幸的是，与设定的任务相比，这些资源非常稀缺。

在前面的文章（第 1 部分、第 2 部分、第 3 部分）中，我们尝试了造型和角度，其值被传递给感知器和基于 DeepNeuralNetwork.mqh 函数库构建的神经网络。我们还在策略测试器中对优化方法进行了实验。我对基于 DeepNeuralNetwork.mqh 函数库的神经网络的成果，以及第 3 部分中讲述的智能优化算法的低效工作并不完全满意。在一个简单感知器上的结果揭示其比神经网络更好。也许，我们正在把不恰当的数据传递给神经网络来完成此任务，并且其散射范围无法产生稳定的结果。此外，对以前文章的反馈包含对止盈与止损比率的质疑。所有这些都在下面的实验中被考虑在内。

在我的搜索过程中，我在大家最喜欢的 MQL5 论坛上遇到了一个有趣的形态跟踪算法。它的本质是将价格带至某种形态，以便判定入场开仓，而不关心其在神经网络中的使用。

我称之为“技术”模板。我不知道这是否正确，但这对我来说似乎是最合适的词汇。

当前实验中的一项重要任务就是跟踪传输数据量的影响，以及我们从中获取这些数据的历史深度。此外，我们需要揭示形态、是做空亦或做多效果更佳，以及我们是否应该传递或少或多的参数。

现在我正在撰写这个介绍，坦率地说，我不知道我最终会得到什么结果。与往常一样，我只会用到 MetaTrader 5 工具，而不使用任何第三方软件。本文很可能类似于分步指导。我将尝试尽可能清晰和简单地解释一切。

1. 货币对。优化和前瞻测试范围。设置

在此，我将提供优化和前向验证测试的所有参数，以免在文本中重复：

外汇；
EURUSD;
时间帧：H1；
模板：扇形、平行四边形、三角形；
在报价为 5 位小数的品种上，止损和止盈相应修改为 600 和 60，余额为 200 和 230，考虑到点差，为止盈加上 30 点，200 点和 430 点，止盈是止损的 2 倍，余额·的止盈为 30 点；
“仅开盘价”和“最复杂准则”优化和测试模式。常重要的是使用“最大复杂准则”模式，与“最大盈利能力”相比，它展示出更稳定和有利可图的结果；
优化范围 3 年。 2019.02.18 - 2022.02.18. 3 年并非是一个可靠的准则。您可以自行试验此参数;
前向验证测试范围为 1 年。 2022.02.18 - 2023.02.18. 参考我的文章（神经网络实验（第 3 部分）：实际应用）中讲述的算法检查所有内容。这意味着若干个最佳优化同时交易结果；
我们现在将执行 20 次优化。与之前的测试相比，我们将其增加 2 倍并查看结果。
在所有前向验证测试中，同时使用了 40 个优化结果。与之前的测试相比，该值增加了 2 倍；
EA 优化采用“快速（基于遗传算法）”感知器；
依据 DeepNeuralNetwork.mqh “快速（基于遗传算法）” 函数库的 EA 优化。由于（第 2 部分）中研究的算法优化缓慢，因此决定直接使用 MetaTrader 5 进行优化；
初始本金 10000 单位；
杠杆 1:500。

我差点忘了告诉您，我如何在“快速（遗传算法）”模式下优化 20、40 或更多次。为此，我使用了一个用 Delphi 编写的小型自动点击器程序。我不能在这里发布它，但我会在私人消息中将其发送给任何需要它的人。它的工作原理如下：

输入所需的优化次数。
将鼠标光标悬停在策略优化器中的“开始”按钮上。
等待。

优化在指定的循环后结束，且程序关闭。自动点击器响应“开始”按钮颜色的变化。该程序显示在下面的屏幕截图中。

Autoclicker

2. 模板

模板是一种类似于“浮动形态”的结构。它的值会根据市场情况不断变化，但每个值都在一定的范围内，而这恰是我们实验所需要的。由于我们已知我们传输到神经网络的数据应该在一定范围内，因此模板中的数值会被四舍五入为整数，以便感知器和神经网络能更好地理解。因此，我们得到了更多的触发条件，并大幅降低了感知器和神经网络上的负载。以下您会遇到我脑海里的第一个模板。我称它为扇形。我认为，相似的形状显而易见。在本文中，我们不会使用指标，而是操控烛条。

以下是使用历史记录缩放的示例，如此我们便可分析更短或更深的历史。

在模板中使用相同数量的蜡烛不是先决条件，这为反映先前价格值的相关性提供了一个额外的字段。在我们的例子中，这些是蜡烛的收盘价。

重要的是要理解，在使用 DeepNeuralNetwork.mqh 库处理 24 根蜡烛的示例中，我们所用的函数库与我在前面文章中讲述的不同。它们拥有不同的输入设置。即，有 4 个和 8 个参数用于神经网络的输入。您不必担心这个。我已经在附件中添加了 EA 和必要的库文件。

2.1 四个值的扇形模板在 24 根蜡烛上延伸。它等于 H1 上的一天。

扇形 4 24

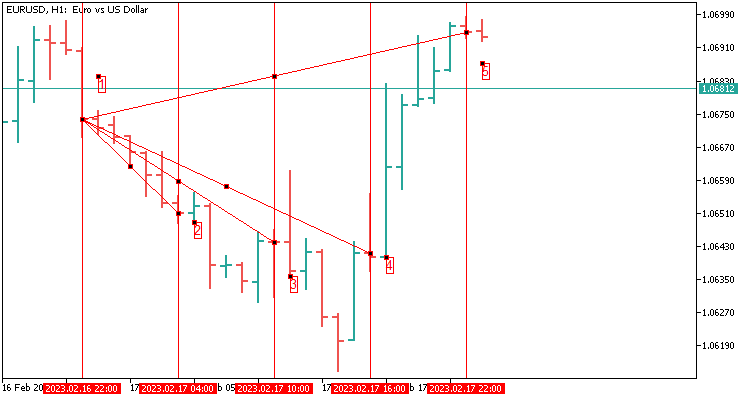
我们来讲述一下我们将转移到感知器和神经网络的内容，以便更好地理解：

从端点 1 到端点 2 的四舍五入距离（以点数为单位）；
从端点 1 到端点 3 的四舍五入距离（以点数为单位）；
从端点 1 到端点 4 的四舍五入距离（以点数为单位）；
从端点 1 到端点 5 的四舍五入距离（以点数为单位）；

这是它在感知器 EA 代码中的样子：

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   a1 = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point()));
   a2 = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   a3 = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point()));
   a4 = (int)(a4/100)*100;
   
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

这是它在基于 DeepNeuralNetwork.mqh 函数库的 EA 代码中的样子：

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point()));
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point()));
   xInputs[3] = (int)(a4/100)*100;  
   
   return(1);

  }

2.2 八个值的扇形模板在 24 根蜡烛上延伸。它等于 H1 上的一天。

模板 8 24

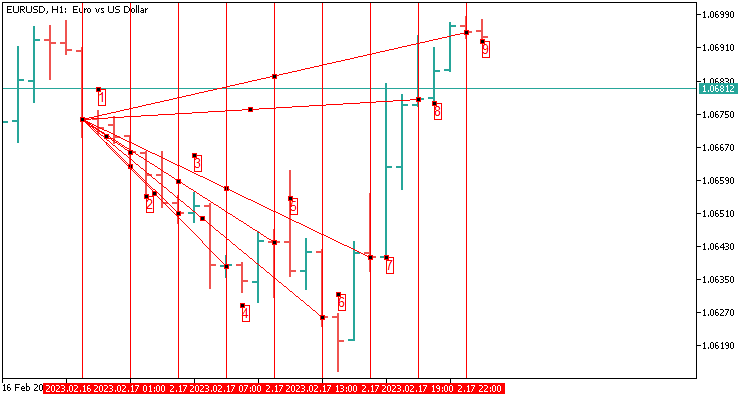
我们看看我们传递给感知器和神经网络的内容，以便更好地理解：

从端点 1 到端点 2 的四舍五入距离（以点数为单位）；
从端点 1 到端点 3 的四舍五入距离（以点数为单位）；
从端点 1 到端点 4 的四舍五入距离（以点数为单位）；
从端点 1 到端点 5 的四舍五入距离（以点数为单位）；
从端点 1 到端点 6 的四舍五入距离（以点数为单位）；
从端点 1 到端点 7 的四舍五入距离（以点数为单位）；
从端点 1 到端点 8 的四舍五入距离（以点数为单位）；
从端点 1 到端点 9 的四舍五入距离（以点数为单位）；

这是它在感知器 EA 代码中的样子：

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   double v1 = y1 - 10.0;
   double v2 = y2 - 10.0;
   double v3 = y3 - 10.0;
   double v4 = y4 - 10.0;
   
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   a1 = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,4))/Point()));
   a2 = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point()));
   a3 = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,10))/Point()));
   a4 = (int)(a4/100)*100;
   
   int b1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   b1 = (int)(b1/100)*100;
   int b2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,16))/Point()));
   b2 = (int)(b2/100)*100;
   int b3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point()));
   b3 = (int)(b3/100)*100;
   int b4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,22))/Point()));
   b4 = (int)(b4/100)*100;
   
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4   +   v1 * b1 + v2 * b2 + v3 * b3 + v4 * b4);
  }

这是它在基于 DeepNeuralNetwork.mqh 函数库的 EA 代码中的样子：

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,4))/Point()));
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point()));
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,10))/Point()));
   xInputs[3] = (int)(a4/100)*100;
   
   int g1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   xInputs[4] = (int)(g1/100)*100;
   int g2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,16))/Point()));
   xInputs[5] = (int)(g2/100)*100;
   int g3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point()));
   xInputs[6] = (int)(g3/100)*100;
   int g4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,22))/Point()));
   xInputs[7] = (int)(g4/100)*100;
   
   return(1);

  }

2.3 四个值的扇形模板在 48 根蜡烛上延伸。它等于 H1 上的两天。

扇形 48

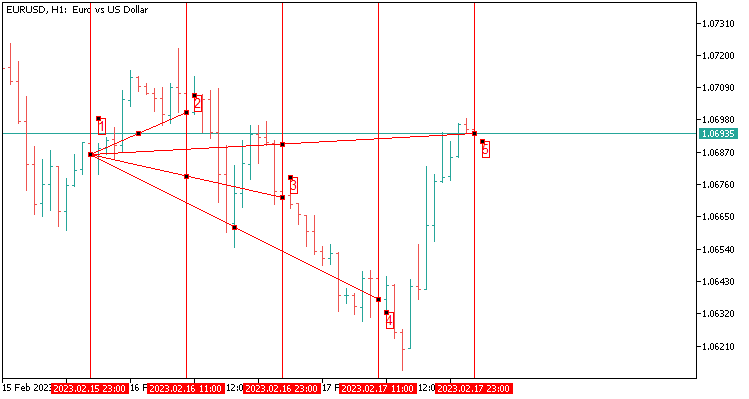
我们提供一个描述，以便更好地理解：

从端点 1 到端点 2 的四舍五入距离（以点数为单位）；
从端点 1 到端点 3 的四舍五入距离（以点数为单位）；
从端点 1 到端点 4 的四舍五入距离（以点数为单位）；
从端点 1 到端点 5 的四舍五入距离（以点数为单位）；

这就是它在感知器 EA 代码中的样子。我们看到前面的示例在时间上延伸了 2 天：

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   a1 = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   a2 = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point()));
   a3 = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point()));
   a4 = (int)(a4/100)*100;
   
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

这就是它依据 DeepNeuralNetwork.mqh 函数库代码的样子。我们看到前面的示例在时间上延伸了 2 天：

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point()));
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point()));
   xInputs[3] = (int)(a4/100)*100;  
   
   return(1);

  }

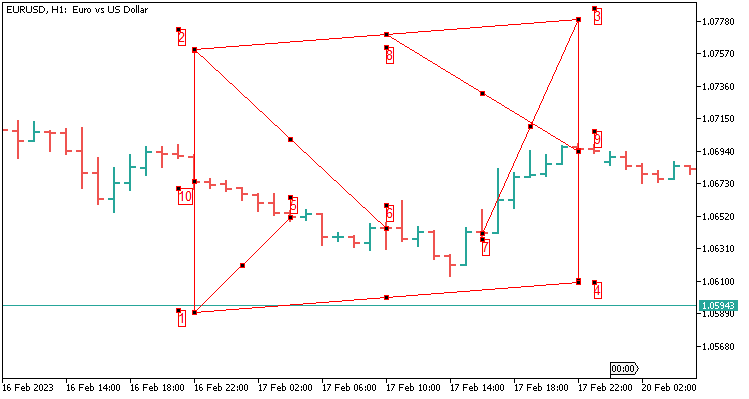
2.4 八个值的扇形模板在 48 根蜡烛上延伸。它等于 H1 上的两天。

扇形 8 48

参考点移动了相同数量的蜡烛：

从端点 1 到端点 2 的四舍五入距离（以点数为单位）；
从端点 1 到端点 3 的四舍五入距离（以点数为单位）；
从端点 1 到端点 4 的四舍五入距离（以点数为单位）；
从端点 1 到端点 5 的四舍五入距离（以点数为单位）；
从端点 1 到端点 6 的四舍五入距离（以点数为单位）；
从端点 1 到端点 7 的四舍五入距离（以点数为单位）；
从端点 1 到端点 8 的四舍五入距离（以点数为单位）；
从端点 1 到端点 9 的四舍五入距离（以点数为单位）；

在感知器 EA 代码中的样子：

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   double v1 = y1 - 10.0;
   double v2 = y2 - 10.0;
   double v3 = y3 - 10.0;
   double v4 = y4 - 10.0;
   
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   a1 = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point()));
   a2 = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   a3 = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point()));
   a4 = (int)(a4/100)*100;
   
   int b1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point()));
   b1 = (int)(b1/100)*100;
   int b2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,31))/Point()));
   b2 = (int)(b2/100)*100;
   int b3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point()));
   b3 = (int)(b3/100)*100;
   int b4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,43))/Point()));
   b4 = (int)(b4/100)*100;
   
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4   +   v1 * b1 + v2 * b2 + v3 * b3 + v4 * b4);
  }

基于 DeepNeuralNetwork.mqh 函数库的 EA 代码样子：

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point()));
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point()));
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point()));
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point()));
   xInputs[3] = (int)(a4/100)*100;
   
   int g1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point()));
   xInputs[4] = (int)(g1/100)*100;
   int g2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,31))/Point()));
   xInputs[5] = (int)(g2/100)*100;
   int g3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point()));
   xInputs[6] = (int)(g3/100)*100;
   int g4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,43))/Point()));
   xInputs[7] = (int)(g4/100)*100;
   
   return(1);

  }

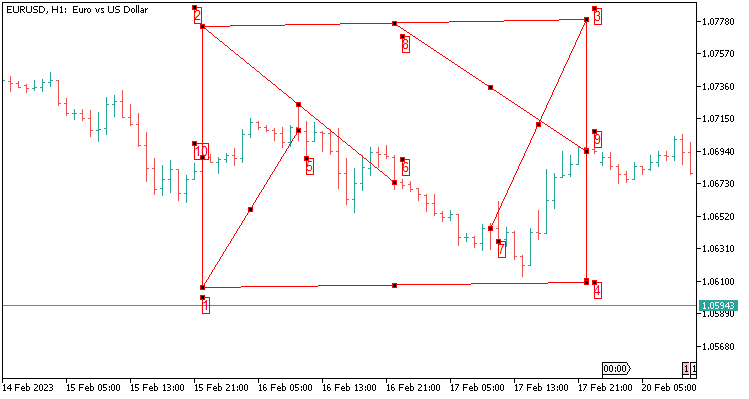
2.5 四个值的平行四边形模板在 24 根蜡烛上延伸。更复杂的构造需要传递的参数。等于 H1 上的一天。

平行四边形

以下是我们所需传递数值的描述：

就我的例子而言，对于 5 位小数报价品种，从端点 10 加上 800 点，得到端点 2；
从端点 10 减去 800 点，得到端点 1；
从端点 9 加上 800 点，得到端点 3；
从端点 9 减去 800 点，得到端点 4；
从端点 8 到端点 9 的舍入（端点 2 和端点 3 之间的差值是 8 点）;
从端点 1 到端点 7 的舍入值；
从端点 2 到端点 8 的舍入值；
从端点 1 到端点 5 的舍入值；

在感知器 EA 代码中的样子：

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,7)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point());
   a4 = (int)(a4/100)*100;
   
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

基于 DeepNeuralNetwork.mqh 的 EA 代码：

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,7)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point());
   xInputs[3] = (int)(a4/100)*100;
   
   return(1);

  }

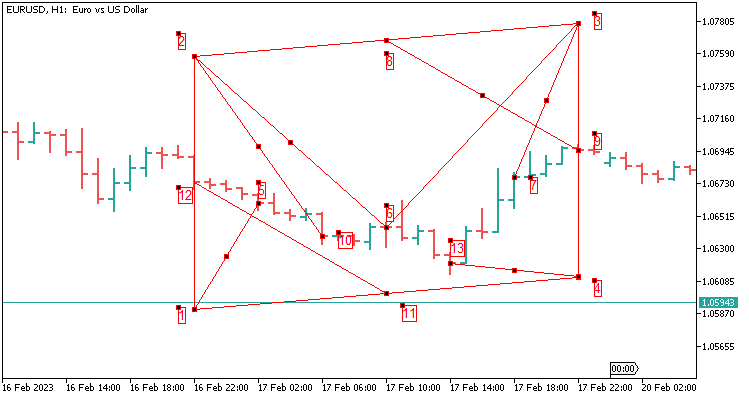
2.6 四个值的平行四边形模板在 48 根蜡烛上延伸。随着时间的推移，覆盖范围会更大。它等于 H1 上的两天。

平行四边形

以下是我们所需传递数值的描述：

就我的例子而言，对于 5 位小数报价品种，从端点 10 加上 1200 点，得到端点 2，因为价格在两天内可能差异会很大。这样，我们的构造就保持无碍；
从端点 10 到端点 1 减去 10 点；
从端点 9 加上 1200 点，得到端点 3；
从端点 9 减去 1200 点，得到端点 4；
从端点 8 到端点 9 的舍入（端点 2 和端点 3 之间的差值是 8 点）;
从端点 1 到端点 7 的舍入值；
从端点 2 到端点 8 的舍入值；
从端点 1 到端点 5 的舍入值；

在感知器 EA 代码中的样子：

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,13)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point());
   a4 = (int)(a4/100)*100;
   
   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

基于 DeepNeuralNetwork.mqh 的 EA 代码：

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,13)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point());
   xInputs[3] = (int)(a4/100)*100;
   
   return(1);

  }

2.7 平行四边形模板的八个值在 24 根蜡烛上延伸。它等于 H1 上的一天。

平行四边形

以下是我们所需传递数值的描述：

就我的例子而言，对于 5 位小数报价品种，从端点 10 加上 800 点；
从端点 9 减去 800 点，得到端点 4；
从端点 12 加上 800 点，得到端点 2；
从端点 12 减去 800 点，得到端点 1；
从端点 8 到端点 9 的舍入（端点 2 和端点 3 之间的差值是 8 点）;
从端点 7 到端点 3 的舍入值；
从端点 13 到端点 4 的舍入值；
从端点 6 到端点 3 的舍入值；
从端点 2 到端点 8 的舍入值；
从端点 2 到端点 10 的舍入值；
从端点 12 到端点 11 的舍入（端点 4 和端点 1 之间的差值 1 点）；
从端点 1 到端点 5 的舍入值；

在感知器 EA 代码中的样子：

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   double v1 = y1 - 10.0;
   double v2 = y2 - 10.0;
   double v3 = y3 - 10.0;
   double v4 = y4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,5)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,9)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,13)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())))/Point());
   a4 = (int)(a4/100)*100;

   int b1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   b1 = (int)(b1/100)*100;
   int b2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,17))/Point());
   b2 = (int)(b2/100)*100;
   int b3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,21))/Point());
   b3 = (int)(b3/100)*100;
   int b4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,24)-(800*Point()))/2))/Point()) ;
   b4 = (int)(b4/100)*100;

   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4   +   v1 * b1 + v2 * b2 + v3 * b3 + v4 * b4);
  }

这是它在基于 DeepNeuralNetwork.mqh 函数库的 EA 代码中的样子：

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,5)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,9)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,13)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())))/Point());
   xInputs[3] = (int)(a4/100)*100;

   int g1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   xInputs[4] = (int)(g1/100)*100;
   int g2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)+(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,17))/Point());
   xInputs[5] = (int)(g2/100)*100;
   int g3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-(800*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,21))/Point());
   xInputs[6] = (int)(g3/100)*100;
   int b4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,24)-(800*Point()))/2))/Point()) ;
   xInputs[7] = (int)(g4/100)*100;
   
   return(1);

  }

2.8 八个值的平行四边形模板在 48 根蜡烛上延伸，以便获得更大的历史覆盖范围。它等于 H1 上的两天。

平行四边形

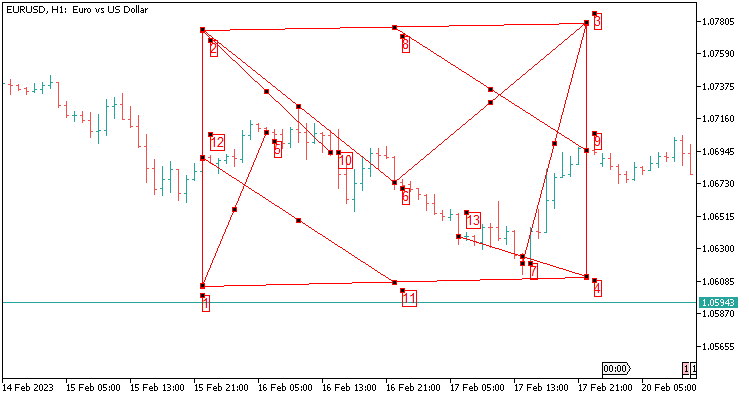
以下是我们所需传递数值的描述：

就我的例子而言，对于 5 位小数报价品种，从端点 8 加上 1200 点；
从端点 9 减去 800 点，得到端点 4；
从端点 12 加上 1200 点，得到端点 2；
从端点 12 减去 800 点，得到端点 1；
从端点 8 到端点 9 的舍入（端点 2 和端点 3 之间的差值是 8 点）;
从端点 7 到端点 3 的舍入值；
从端点 13 到端点 4 的舍入值；
从端点 6 到端点 3 的舍入值；
从端点 2 到端点 8 的舍入值；
从端点 2 到端点 10 的舍入值；
从端点 12 到端点 11 的舍入（端点 4 和端点 1 之间的差值 1 点）；
从端点 1 到端点 5 的舍入值；

在感知器 EA 代码中的样子：

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   double v1 = y1 - 10.0;
   double v2 = y2 - 10.0;
   double v3 = y3 - 10.0;
   double v4 = y4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,9)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,17)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,25)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())))/Point());
   a4 = (int)(a4/100)*100;

   int b1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   b1 = (int)(b1/100)*100;
   int b2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,33))/Point());
   b2 = (int)(b2/100)*100;
   int b3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,41))/Point());
   b3 = (int)(b3/100)*100;
   int b4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,48)-(1200*Point()))/2))/Point()) ;
   b4 = (int)(b4/100)*100;

   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4   +   v1 * b1 + v2 * b2 + v3 * b3 + v4 * b4);
  }

基于 DeepNeuralNetwork.mqh 的 EA 代码：

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,9)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())))/Point());
   xInputs[0] = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,17)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())))/Point());
   xInputs[0] = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,25)-(iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())))/Point());
   xInputs[0] = (int)(a4/100)*100;

   int g1 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   xInputs[0] = (int)(g1/100)*100;
   int g2 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)+(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,33))/Point());
   xInputs[0] = (int)(g2/100)*100;
   int g3 = (int)(((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-(1200*Point()))-iClose(symbolS1.Name(),PERIOD_CURRENT,41))/Point());
   xInputs[0] = (int)(g3/100)*100;
   int g4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point()))+(iClose(symbolS1.Name(),PERIOD_CURRENT,48)-(1200*Point()))/2))/Point()) ;
   xInputs[0] = (int)(g4/100)*100;
   
   return(1);

  }

2.9 四个值的三角形模板在 24 根蜡烛上延伸。它等于 H1 上的一天。

三角形

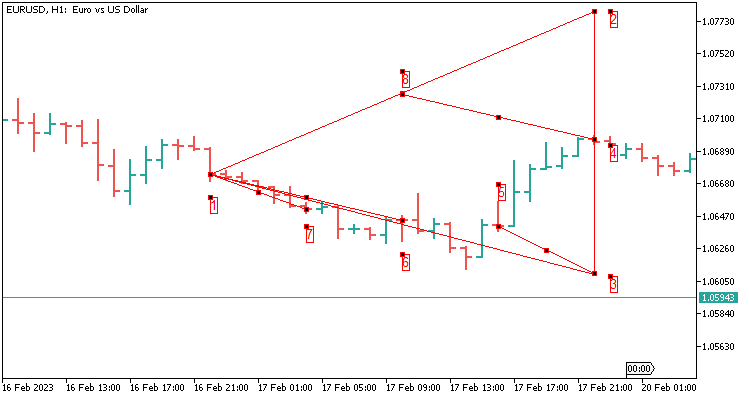
以下是我们所需传递数值的描述：

就我的例子而言，对于 5 位小数报价品种，从端点 4 加上 800 点，得到端点 2；
从端点 4 减去 800 点，得到端点 3；
从端点 8 到端点 4 的舍入（端点 2 和端点 1 之间的差值是 8 点）;
从端点 3 到端点 5 的舍入值；
从端点 1 到端点 6 的舍入值；
从端点 1 到端点 7 的舍入值；

在感知器 EA 代码中的样子：

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point());
   a4 = (int)(a4/100)*100;

   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

基于 DeepNeuralNetwork.mqh 的 EA 代码：

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point());
   xInputs[3] = (int)(a4/100)*100;
   
   return(1);

  }

2.10 四个值的三角形模板，历史覆盖 48 根蜡烛。在 H1 上是两天。

三角形

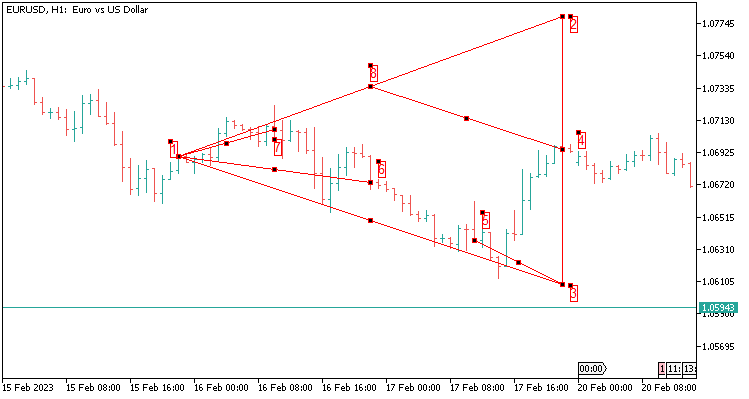
以下是传递给感知器和神经网络的值：

就我的例子而言，对于 5 位小数报价品种，从端点 4 加上 1200 点，得到端点 2；
从端点 4 减去 1200 点，得到端点 3；
从端点 8 到端点 4 的舍入（端点 2 和端点 1 之间的差值是 8 点）;
从端点 3 到端点 5 的舍入值；
从端点 1 到端点 6 的舍入值；
从端点 1 到端点 7 的舍入值；

感知器 EA 中的模板代码：

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point());
   a4 = (int)(a4/100)*100;

   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4);
  }

基于 DeepNeuralNetwork.mqh 的 EA 模板代码：

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
  
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point());
   xInputs[3] = (int)(a4/100)*100;
   
   return(1);

  }

2.11 八个值的三角形模板，在 24 根蜡烛上延伸。在 H1 上分析一天的历史记录覆盖。

三角形

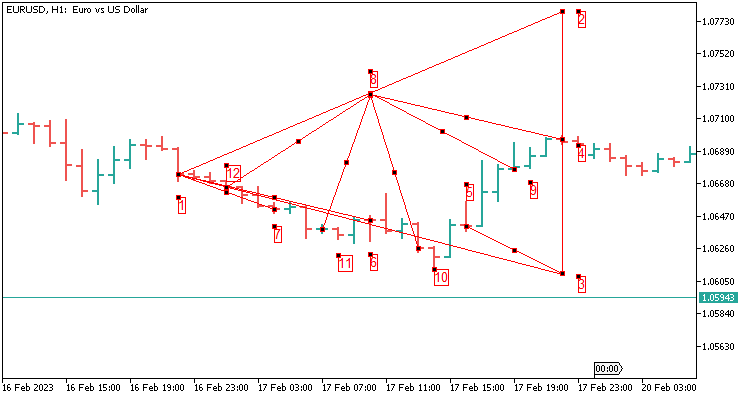
传递的值如下所述：

就我的例子而言，对于 5 位小数报价品种，从端点 4 加上 800 点，得到端点 2；
从端点 4 减去 800 点，得到端点 3；
从端点 8 到端点 4 的舍入（端点 2 和端点 1 之间的差值是 8 点）;
从端点 3 到端点 5 的舍入值；
从端点 1 到端点 6 的舍入值；
从端点 1 到端点 7 的舍入值；
从端点 8 到端点 9 的舍入（端点 2 和端点 1 之间的差值是 8 点）;
从端点 8 到端点 10 的舍入（端点 2 和端点 1 之间的差值是 8 点）;
从端点 8 到端点 11 的舍入（端点 2 和端点 1 之间的差值是 8 点）;
从端点 8 到端点 12 的舍入（端点 2 和端点 1 之间的差值是 8 点）;

感知器 EA 中的模板代码：

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   double v1 = y1 - 10.0;
   double v2 = y2 - 10.0;
   double v3 = y3 - 10.0;
   double v4 = y4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point());
   a4 = (int)(a4/100)*100;
   
   int b1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,4))/Point());
   b1 = (int)(b1/100)*100;
   int b2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,10))/Point());
   b2 = (int)(b2/100)*100;
   int b3 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,16))/Point());
   b3 = (int)(b3/100)*100;
   int b4 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,22))/Point());
   b4 = (int)(b4/100)*100;

   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4   +   v1 * b1 + v2 * b2 + v3 * b3 + v4 * b4);
  }

基于 DeepNeuralNetwork.mqh 的 EA 模板代码：

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,7))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,24)-iClose(symbolS1.Name(),PERIOD_CURRENT,19))/Point());
   xInputs[3] = (int)(a4/100)*100;
   
   int g1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,4))/Point());
   xInputs[4] = (int)(g1/100)*100;
   int g2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,10))/Point());
   xInputs[5] = (int)(g2/100)*100;
   int g3 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,16))/Point());
   xInputs[6] = (int)(g3/100)*100;
   int g4 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(800*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,24))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,22))/Point());
   xInputs[7] = (int)(g4/100)*100;
   
   return(1);

  }

2.12 八个值的三角形模板在 48 根蜡烛上延伸。在 H1 上分析两天的历史记录覆盖。

三角形

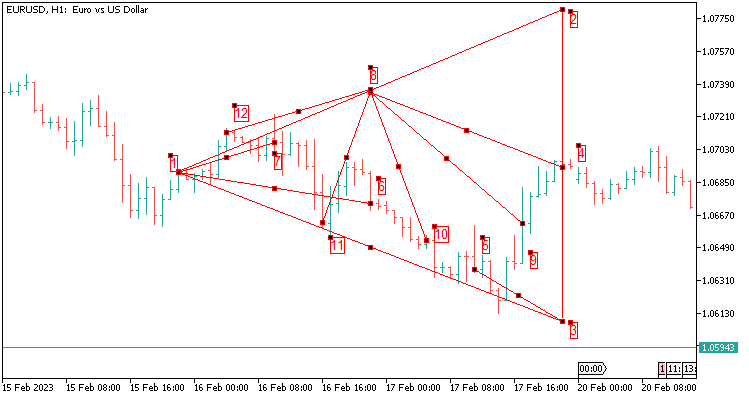
传递的值如下所述：

就我的例子而言，对于 5 位小数报价品种，从端点 4 加上 1200 点，得到端点 2，提升的加数是依据 48 根蜡烛得来；
从端点 4 减去 1200 点，得到端点 3；
从端点 8 到端点 4 的舍入（端点 2 和端点 1 之间的差值是 8 点）;
从端点 3 到端点 5 的舍入值；
从端点 1 到端点 6 的舍入值；
从端点 1 到端点 7 的舍入值；
从端点 8 到端点 9 的舍入（端点 2 和端点 1 之间的差值是 8 点）;
从端点 8 到端点 10 的舍入（端点 2 和端点 1 之间的差值是 8 点）;
从端点 8 到端点 11 的舍入（端点 2 和端点 1 之间的差值是 8 点）;
从端点 8 到端点 12 的舍入（端点 2 和端点 1 之间的差值是 8 点）;

感知器 EA 中的模板代码：

//+------------------------------------------------------------------+
//|  The PERCEPRRON - a perceiving and recognizing function          |
//+------------------------------------------------------------------+
double perceptron1() 
  {
   double w1 = x1 - 10.0;
   double w2 = x2 - 10.0;
   double w3 = x3 - 10.0;
   double w4 = x4 - 10.0;
   
   double v1 = y1 - 10.0;
   double v2 = y2 - 10.0;
   double v3 = y3 - 10.0;
   double v4 = y4 - 10.0;
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   a1 = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   a2 = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   a3 = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point());
   a4 = (int)(a4/100)*100;
   
   int b1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,6))/Point());
   b1 = (int)(b1/100)*100;
   int b2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,18))/Point());
   b2 = (int)(b2/100)*100;
   int b3 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,31))/Point());
   b3 = (int)(b3/100)*100;
   int b4 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,43))/Point());
   b4 = (int)(b4/100)*100;

   return (w1 * a1 + w2 * a2 + w3 * a3 + w4 * a4   +   v1 * b1 + v2 * b2 + v3 * b3 + v4 * b4);
  }

基于 DeepNeuralNetwork.mqh 的三角形模板 EA 代码：

//+------------------------------------------------------------------+
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double &xInputs[])
  {
   
   int a1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,1))/Point());
   xInputs[0] = (int)(a1/100)*100;
   int a2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,13))/Point());
   xInputs[1] = (int)(a2/100)*100;
   int a3 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,25))/Point());
   xInputs[2] = (int)(a3/100)*100;
   int a4 = (int)((iClose(symbolS1.Name(),PERIOD_CURRENT,48)-iClose(symbolS1.Name(),PERIOD_CURRENT,37))/Point());
   xInputs[3] = (int)(a4/100)*100;
   
   int g1 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)+(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,6))/Point());
   xInputs[4] = (int)(g1/100)*100;
   int g2 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,18))/Point());
   xInputs[5] = (int)(g2/100)*100;
   int g3 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,31))/Point());
   xInputs[6] = (int)(g3/100)*100;
   int g4 = (int)((((iClose(symbolS1.Name(),PERIOD_CURRENT,1)-(1200*Point())+iClose(symbolS1.Name(),PERIOD_CURRENT,48))/2)-iClose(symbolS1.Name(),PERIOD_CURRENT,43))/Point());
   xInputs[7] = (int)(g4/100)*100;
   
   return(1);

  }

3. 智能系统

好了，我们进入最有趣的部分，即模板的优化和测试。您也许还记得，基于 DeepNeuralNetwork.mqh 函数库构建的智能系统的优化和测试是使用标准 MQL5 工具进行的，并未用到（文章 2）中讲述的优化技术。还注意到，对于这些 EA 来说，20 次的验算有点不够。我建议您自行进行更多的迭代优化。我相信这将改善结果。大量需要优化的参数需要更多时间来判定最佳结果。在本文中，我只想展示在神经网络中传输数据的非标准方法。

基于 DeepNeuralNetwork.mqh 函数库的智能系统具有四个参数，在模板中包含 4-4-3 神经网络逻辑流程，而在有八个参数的情况下，该逻辑流程为 8-4-3。

我尝试根据其策略和所分析模板来为每个 EA 命名。如此我认为很难迷失。无论如何，您可随时在论坛上、或通过私人消息与我联系。

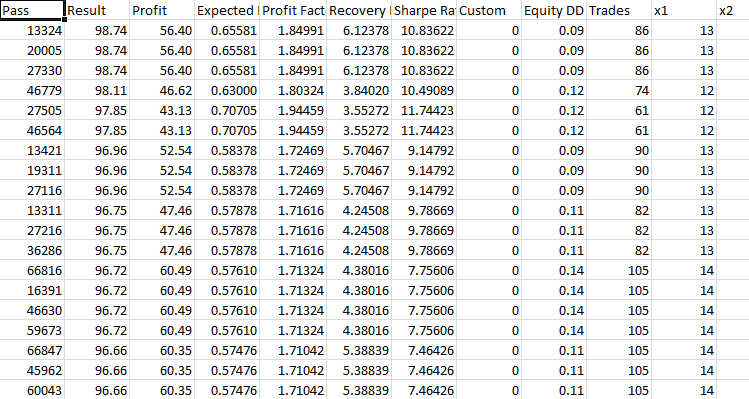
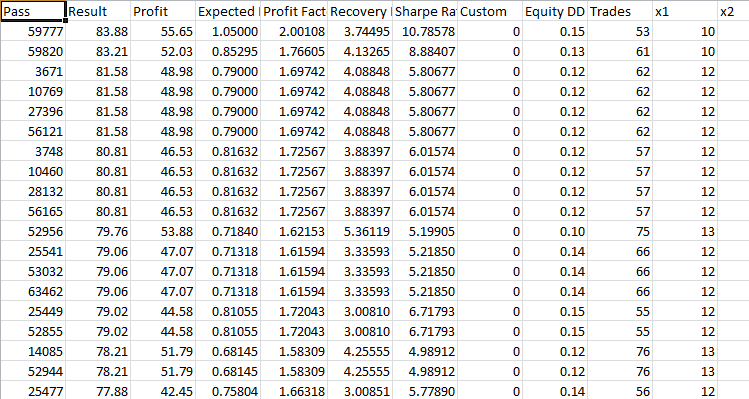
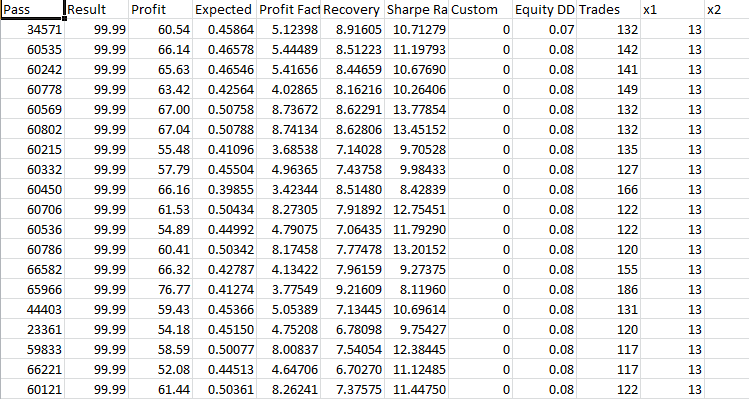
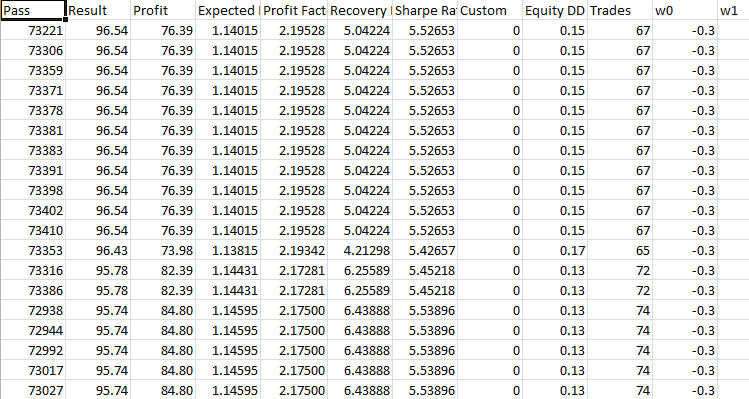
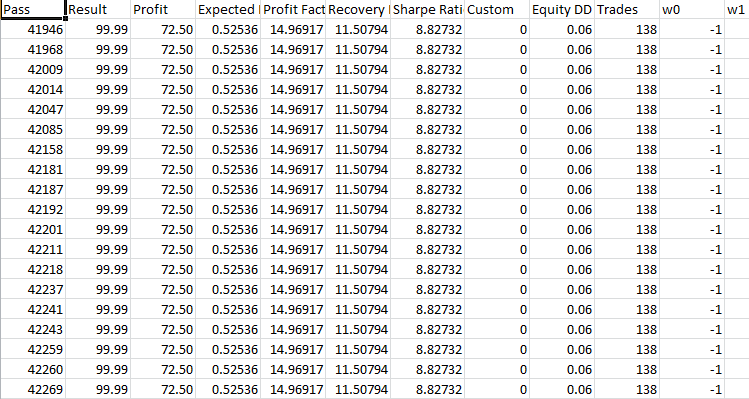
取“最大复杂准则”模式下优化期间获得的前 40 个最佳结果，并将其用于每个 EA 的前向验证测试。我将以优化结果的格式发布结果，下面是前向验证测试的结果。

在本文中，我将基于扇形模板测试 EA，并得出有关所呈现的“技术”的结论。如果有兴趣，您可以自行测试其余模板。我以现成代码的形式发布了上述所有模板的技术部分，因此我认为您在替换文章末尾发布的 EA 中的模板代码，并进行优化和测试时不会有问题。

如果您在理解测试时遇到困难，请阅读本系列的第 3 部分。那里详细讲述了所有内容。

3.1 基于感知器的 EA

感知器扇形 4 SL TP 24 - 交易 — 基于 24 根蜡烛的四个参数，扇形模板：

止盈 60 止损 600：

前向验证

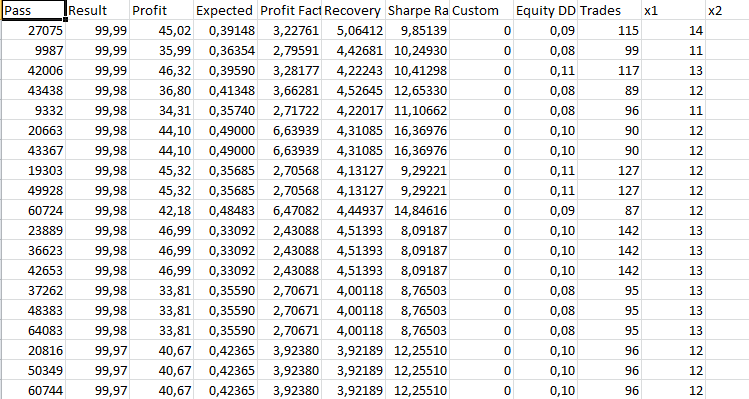
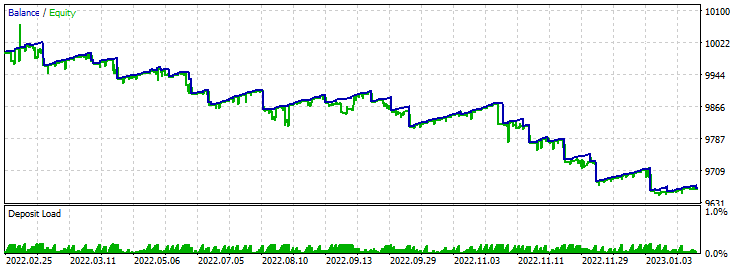
前向验证测试的结果并不令人鼓舞。我们可以看到贯穿整个历史阶段，资金平滑地流失。测试结果的盈利因子处于较高水平。这可能与止损与止盈的比率有关。

止盈 230 止损 200：

前向验证

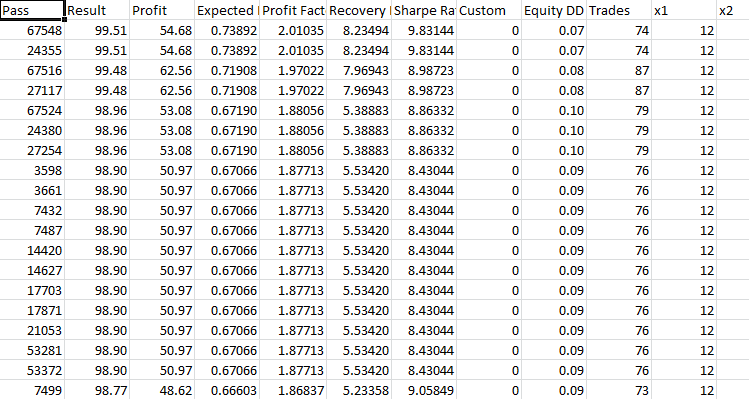
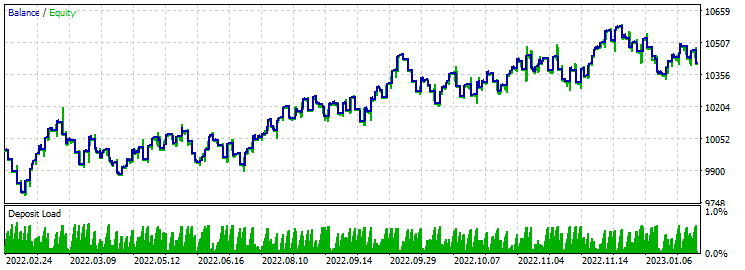
盈利因子勉强超过 1.8。在整个年度历史中可以看到大规模的资金回撤。最低资金增长。我们只是在原地踏步。

止盈 430 止损 200：

前向验证

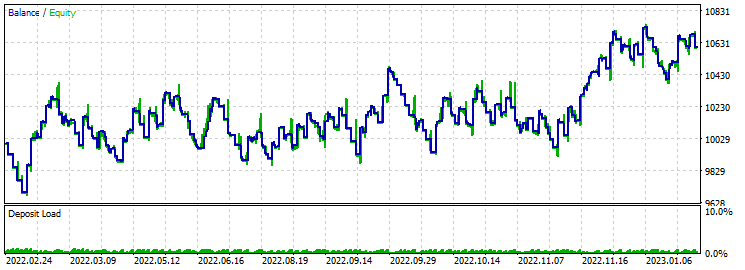
资金的波动在前向验证测试的整个范围内可见。盈利与亏损相匹配，结果不稳定。优化期间的盈利因子约为 2。

感知器扇形 4 SL TP 48 - 交易 — 基于 48 根蜡烛的四个参数，扇形模板：

止盈 60 止损 600：

前向验证

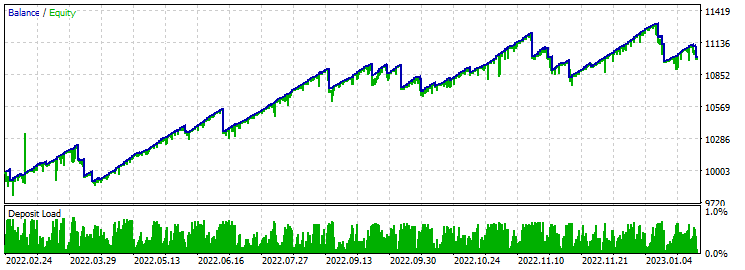
前六个月资金稳定增长后会出现一定的下降。我相信，发生这种情况是由于在如此长的一段时间内缺乏额外的优化。通过增加传递参数中的时间，可以观察到更稳定的结果。盈利因子远高于 24 根蜡烛的结果。没有与止损止盈率绑定的迹象。

止盈 230 止损 200：

前向验证

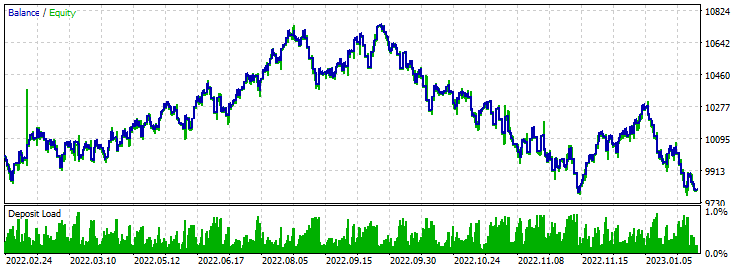
资金在前五个月稳定增长，然后下降。大概，与感知器中的选定条件相比，市场已经发生了变化。前五个月不均匀的图表仍然表明系统的不稳定性。

止盈 430 止损 200：

前向验证

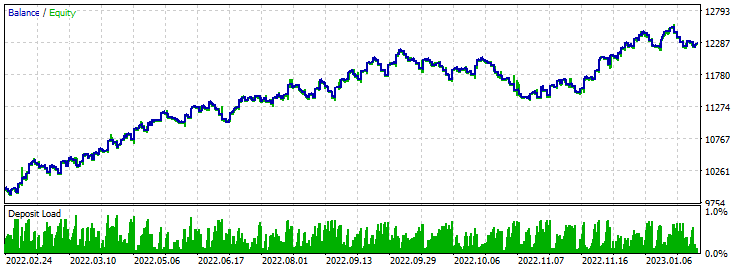
使用扇形模板在感知器上进行测试时最稳定的结果。前六个月稳步增长。然后，由于缺乏重新优化而略有下降。根据基本交易规则，止盈超过两倍止损，给出了良好的结果。盈利大于亏损。优化后，盈利因子处于 1.6 的水平，考虑到止损与止盈的比率，我认为这是很自然的。

感知器扇形 8 SL TP 24 - 交易 — 基于 24 根蜡烛的八个参数，扇形模板：

止盈 60 止损 600：

前向验证

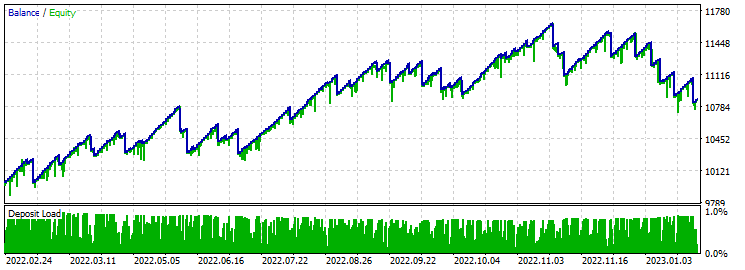
该图形非常不均匀，但结果与具有相同止盈和止损的四个参数的 EA 本质上不同。前半年后也略有下降。优化期间的平均盈利因子约为 6，这算相当多的。

止盈 230 止损 200：

前向验证

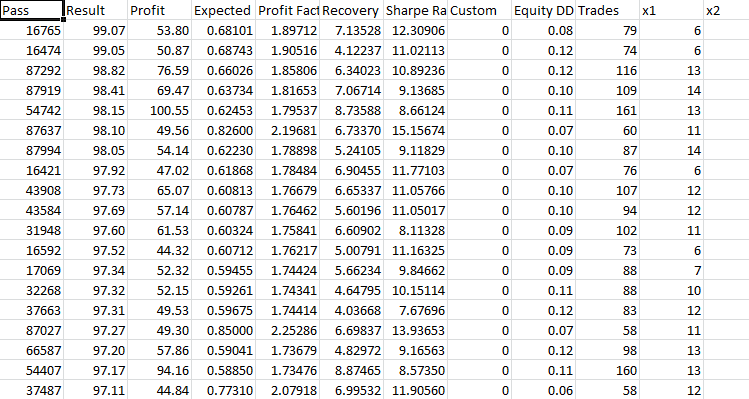
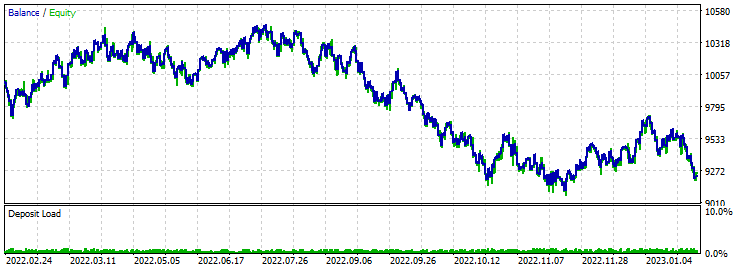
在这次前向验证测试中，我们体验到彻底的失败。我认为这是由于止盈和止损的比例是一比一。优化显示盈利因子约为 1.7，但这并没有挽救这种情况。

止盈 430 止损 200：

前向验证

这个选项也彻底失败，尽管一开始有一些抵抗。优化显示盈利因子约为 1.8，但也再次无济于事。

感知器扇形 8 SL TP 48 - 交易 — 基于 48 根蜡烛的八个参数，扇形模板：

止盈 60 止损 600：

前向验证

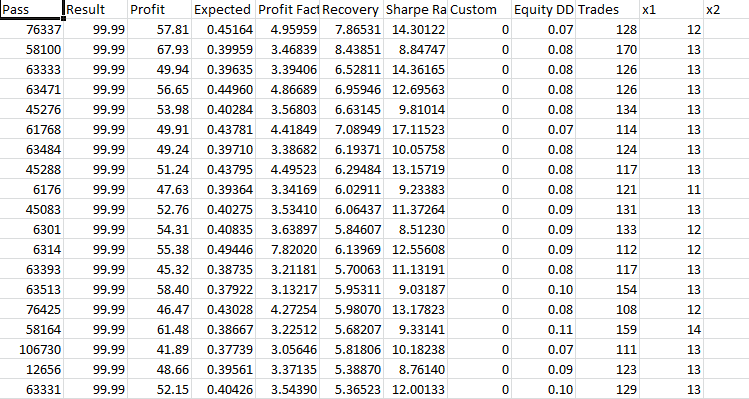
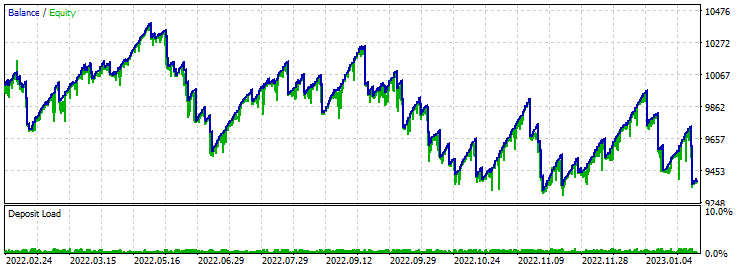
不均匀图形考虑到止盈与止损的比率，我们还是亏损了。优化显示盈利因子约为 3.5-4，但前向验证测试显示亏损。

止盈 230 止损 200：

前向验证

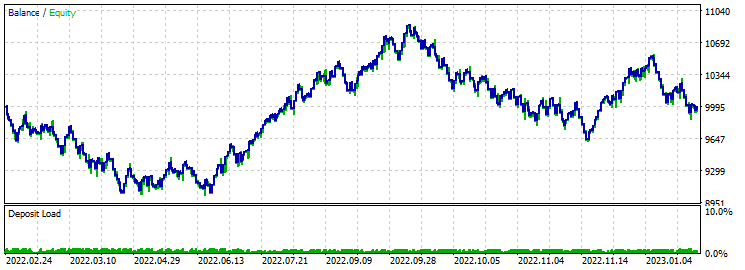
在这个版本中，我们在一个地方还遇到了波动。奇怪的是，余额的下降在测试开始时立即发生。优化显示盈利因子约为 2。

止盈 430 止损 200：

前向验证

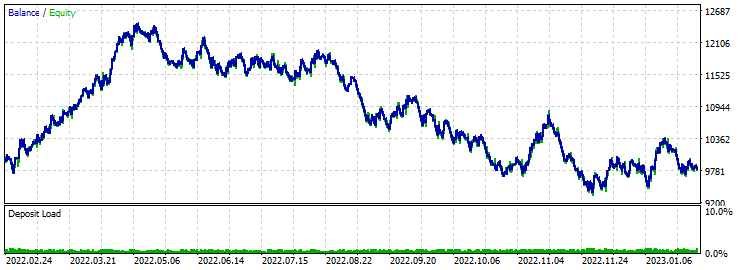
大约前 3 个月，开始时是一个非常好的开始。然后，自己就表现出缺乏新的优化。止盈与止损的比例二比一，在这么长时间里也没能挽回亏损的状况。优化时，平均盈利因子为 1.4。

3.2 基于 DeepNeuralNetwork.mqh 函数库的 EA。

4-4-3 扇形 4 SL TP 24 - 交易 — 基于 24 根蜡烛的四个参数，扇形模板：

止盈 60 止损 600：

前向验证

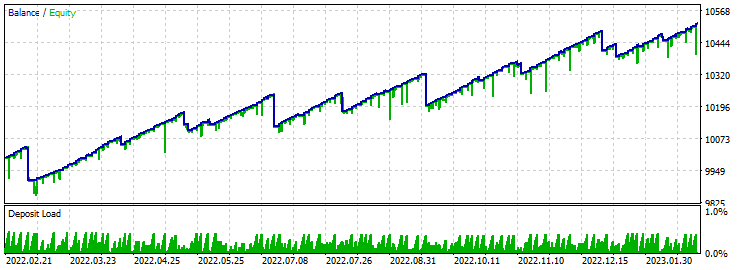
盈利因子 20 这相当多了。前向验证测试显示出积极的结果，但我们碰到大量的止损。但直至此刻，数量更多的小幅止盈挽救了这种情况。

止盈 230 止损 200：

前向验证

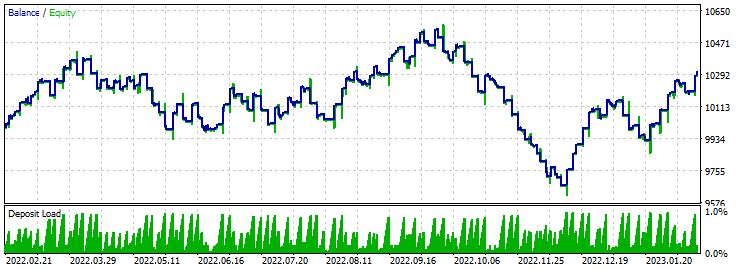
余额图在一个地方缩水。优化显示盈利因子约为 1.7。

止盈 430 止损 200：

前向验证

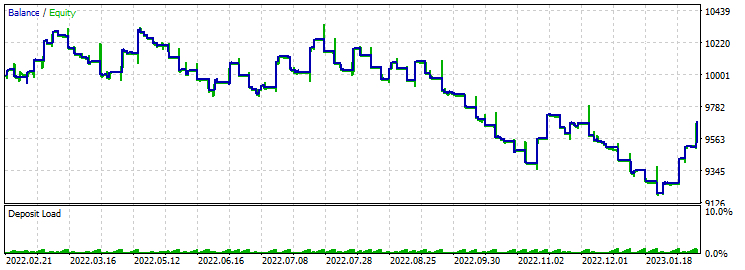
缓慢但确定下降。止盈与止损的比率并不能挽回这种状况。优化显示盈利因子约为 2。

4-4-3 扇形 4 SL TP 48 - 交易 — 基于 48 根蜡烛的四个参数，扇形模板：

止盈 60 止损 600：

前向验证

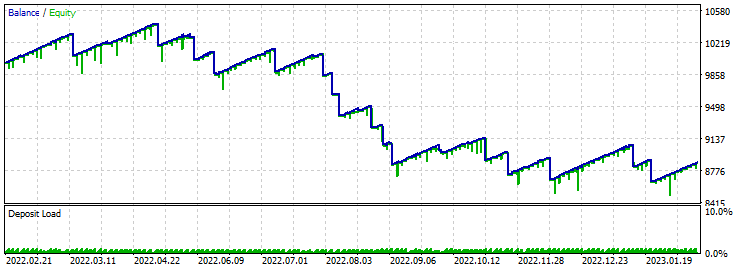
与 24 根蜡烛的相同模板相比，传递 48 根蜡烛模板也·并未显示出积极结果。显然，这样的一个模板，在如此长时间里并不能很好地与这样的止盈与止损比率配合使用。优化显示盈利因子约为 14，这是相当多的。

止盈 230 止损 200：

前向验证

优化时，我们得到的盈利因子为 2.5。正如我们所见，止盈 230 止损 200 并无帮助。我们的余额缓慢下降。

止盈 430 止损 200：

前向验证

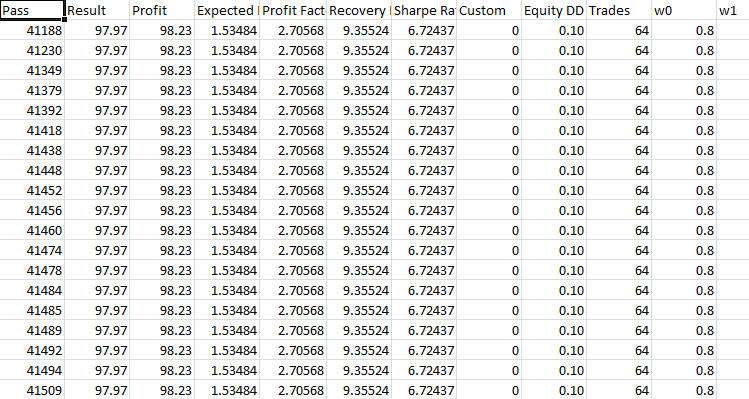
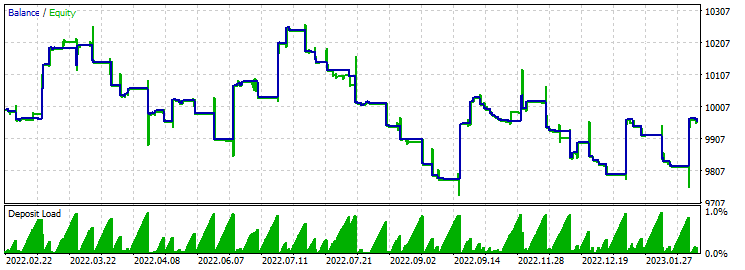
在这种情况下，我们没有任何进展。贯穿全年，余额下降和增长并存。优化时，我们得到的盈利因子为 2.7。

8-4-3 扇形 8 SL TP 24 - 交易 — 基于 24 根蜡烛的八个参数，扇形模板：

止盈 60 止损 600：

前向验证

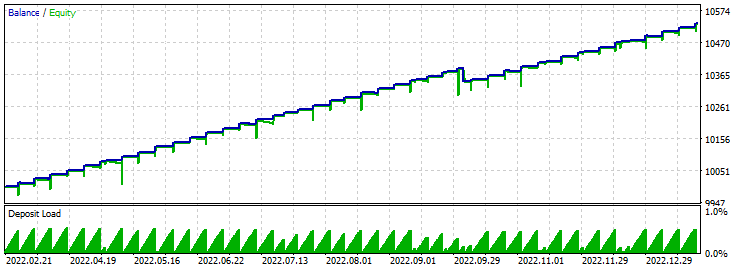
非常有趣的结果，在整个前向验证测试历史上只有一次止损。但结果仍然是随机的。优化时，盈利因子远超规模，在 29 左右。

止盈 230 止损 200：

前向验证

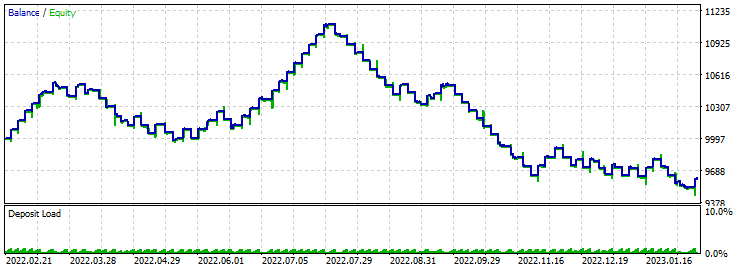
正如我们从屏幕截图中所见，再次没有进展。优化时，盈利因子处于 2.7 的水平，这在当前的止盈与止损比率下应该足够了，但事实并非如此。前六个月出现了一些涨潮。

止盈 430 止损 200：

前向验证

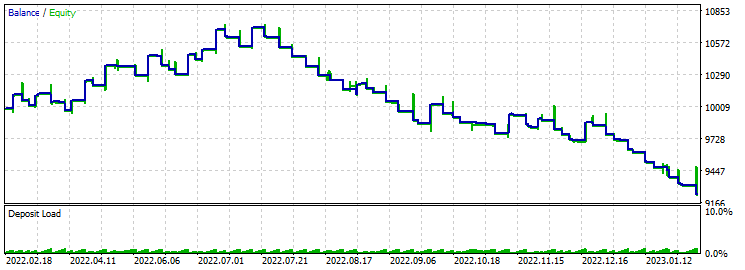
在最初的两三个月里，略有增加，然后，显然市场情况发生了变化，EA 开始资金亏损。显然，仍然需要不断优化。优化时，利润因子为 3.9。

8-4-3 扇形 8 SL TP 48 - 交易 — 基于 48 根蜡烛的八个参数，扇形模板：

止盈 60 止损 600：

前向验证

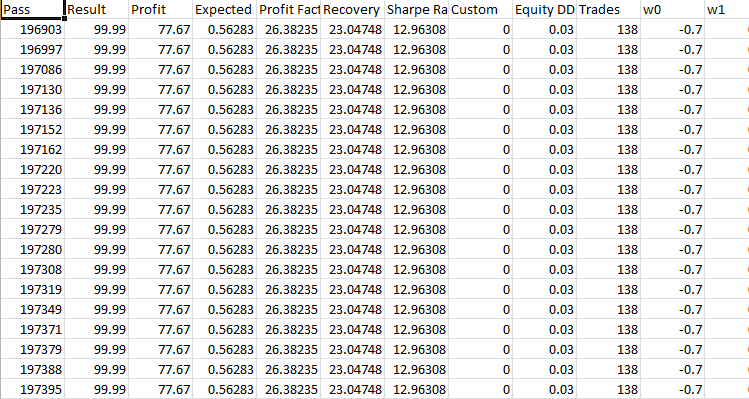
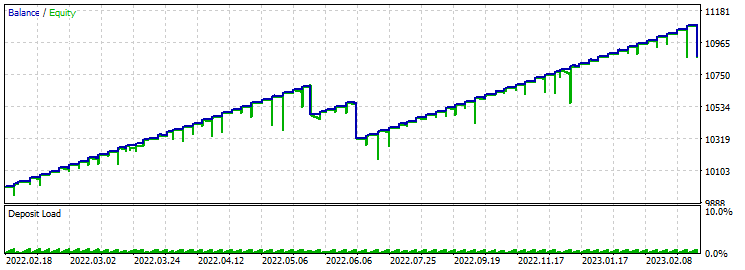
此 EA 的行为类似于 24 蜡烛形态上的前一个。更多亏损交易。优化时，盈利因子处于 26 水平。在 24 根蜡烛的情况下，它处于 29 的水平。

止盈 230 止损 200：

前向验证

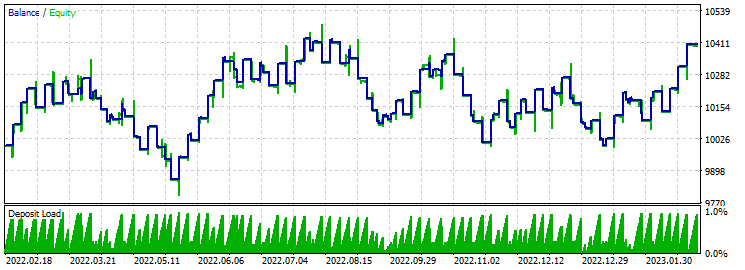
优化时，利润因子处于 3 的水平。余额保持不变。亏损与应i交替出现。

止盈 430 止损 200：

前向验证

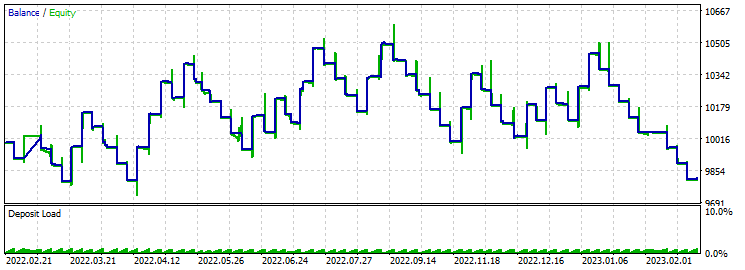
止盈是止损的两倍不会导致积极的结果。更像是，神经网络无法预测如此大的止盈。优化时，利润因子处于 3 的水平。

结束语

我们可以从所做的工作中得出积极和消极的结论。我将以小清单的形式陈列它们，以免思路错乱。

在伸缩方面，事实证明这是一个非常灵活的系统。可以应用无限数量的模板和我们传递给它们的参数。提出新的模式并观察结果，前向验证测试会得到更好的效果。
也许需要尝试具有多个感知器和不同模板的系统来判定入场信号。
计算机能力显然是不够的。需要具有大量核心的系统。理想情况下，两个 CPU 汇集总共有 16 个或更多核心。您可能知道，策略测试器仅使用物理核心，而非线程。使用 MQL5 云网络的能力可以显著提高我们的搜索效率。
传递的输入数量会显著增加感知器或神经网络的负载。将输入值四舍五入会令积极结果的数量增加大约两倍。
在选择进一步开发的系统之前，有必要检查更多将数据传递到感知器和神经网络的选项，即在一定范围内移动的指标，以及背离等有趣的现象。我想，我会在不久的将来这样做。

附件清单：

DeepNeuralNetwork - 原始函数库；
DeepNeuralNetwork2 - 4-4-3 结构神经网络的改编函数库；
DeepNeuralNetwork3 - 8-4-3 结构神经网络的改编函数库；
perceptron fan 4 SL TP 24 - opt - 基于感知器的 EA，扇形模板优化，在 24 根蜡烛上具有四个参数；
perceptron fan 4 SL TP 48 - opt - 基于感知器的 EA，扇形模板优化，在 48 根蜡烛上具有四个参数；
perceptron fan 8 SL TP 24 - opt - 基于感知器的 EA，扇形模板优化，在 24 根蜡烛上具有八个参数；
perceptron fan 8 SL TP 48 - opt - 基于感知器的 EA，扇形模板优化，在 48 根蜡烛上具有八个参数；
perceptron fan 4 SL TP 24 - trade (600 60), (200 230), (200 430) - 优化的基于感知器的 EA，扇形模板在 24 根蜡烛上具有四个参数；
perceptron fan 4 SL TP 48 - trade (600 60), (200 230), (200 430) - 优化的基于感知器的 EA，扇形模板在 48 根蜡烛上具有四个参数；
perceptron fan 8 SL TP 24 - trade (600 60), (200 230), (200 430) - 优化的基于感知器的 EA，扇形模板在 24 根蜡烛上具有八个参数；
perceptron fan 8 SL TP 48 - trade (600 60), (200 230), (200 430) - 优化的基于感知器的 EA，扇形模板在 48 根蜡烛上具有八个参数；
4-4-3 fan 4 SL TP 24 - opt - 基于函数库的 EA，扇形模板优化，在 24 根蜡烛上具有四个参数；
4-4-3 fan 4 SL TP 48 - opt - 基于函数库的 EA，扇形模板优化，在 48 根蜡烛上具有四个参数；
8-4-3 fan 4 SL TP 24 - opt - 基于函数库的 EA，扇形模板优化，在 24 根蜡烛上具有八个参数；
8-4-3 fan 4 SL TP 48 - opt - 基于函数库的 EA，扇形模板优化，在 48 根蜡烛上具有八个参数；
4-4-3 fan 4 SL TP 24 - trade (600 60), (200 230), (200 430) - 优化的基于函数库的 EA，扇形模板在 24 根蜡烛上具有四个参数；
4-4-3 fan 4 SL TP 48 - trade (600 60), (200 230), (200 430) - 优化的基于函数库的 EA，扇形模板在 48 根蜡烛上具有八个参数；
8-4-3 fan 4 SL TP 24 - trade (600 60), (200 230), (200 430) - 优化的基于函数库的 EA，扇形模板在 24 根蜡烛上具有八个参数；
8-4-3 fan 4 SL TP 48 - trade (600 60), (200 230), (200 430) - 优化的基于函数库的 EA，扇形模板在 48 根蜡烛上具有八个参数；

感谢您的关注！

本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/12202

附加的文件 |

下载ZIP

EA.zip (4191.11 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

该作者的其他文章

最近评论 | 前往讨论 (16)

Roman Poshtar | 8 4月 2023 在 18:02

Sergei Poliukhov 星期、小时
例如，从 15-17 个波动小时和数字突破三角形。
也许每月的第一个周五（非农）。还可以添加不平衡（脉冲蜡烛中间，订单块，只有那些不平衡。
例如，在强势新闻后的周五，每月的最后一天通常是令人讨厌的。或者每月的最后一天也是如此。我还注意到最后一分钟是 15、30 分钟的倍数的行为是不平衡的。

一切皆有可能。只要你愿意。感谢您的反馈。交易时段正在开发中。

Roman Poshtar | 8 4月 2023 在 18:03

Sergei Poliukhov #:
如果你是开发人员，我还可以在工作时间免费提供 mvli 供测试使用。

团队正在招募中。请发邮件至

Guilherme Mendonca | 28 4月 2023 在 03:15

你的系列文章写得很棒！

你在神经网络世界中的冒险经历似乎与我的相似。

感谢您花时间写作并与我们分享。

Roman Poshtar | 28 4月 2023 在 05:19

Guilherme Mendonca 神经网络世界的冒险经历似乎与我的相似。
感谢您花时间写作并与我们分享。

感谢您的反馈。非常高兴听到您的反馈。

Top-T | 27 6月 2023 在 20:12

嘿，罗曼，非常感谢你分享的这些文章。

我想知道你是否提供了这些值所指的解释？

字符串EURUSD[][37]=

{

{"1.71225","-1","-1","-1","0.6","-0.5","0.5","-1","-1","-1","-1","-0.3","-0.5","-0.3","0.6","0","-0.4","0.1","0.1","-0.5","0.9","-0.3","0.5","-0.4","0","0.1","0.1","-0.2","-0.8","-0.5", "0.5", "0.3", "0.8","-1","-1","-1"},
.....

在 4-4-3 扇形 4 SL TP 24 - 交易 (200 230) 脚本中。

我是否能从其他货币对中获得这些值？

先谢谢您。

Taher

数据科学和机器学习（第 12 部分）：自训练神经网络能否帮助您跑赢股市？

您是否厌倦了持续尝试预测股市？您是否希望有一个水晶球来帮助您做出更明智的投资决策？自训练神经网络可能是您一直在寻找的解决方案。在本文中，我们将探讨这些强大的算法是否可以帮助您“乘风破浪”，并跑赢股市。通过分析大量数据和识别形态，自训练神经网络通常可以做出比人类交易者更准确的预测。发现如何使用这项尖端技术来最大化您的盈利，并制定更明智的投资决策。