高度なリサンプリングと総当たり攻撃によるCatBoostモデルの選択

はじめに

前回の記事では、主要な機械学習モデルの作成手順とそのさらなる実用化についての一般的概念の提供を試みました。本稿では、ナイーブモデルから統計的に有意なモデルに切り替えたいと思います。機械学習ベースの取引システムの作成作業は簡単ではないため、最適な結果を達成するのに役立ついくつかのデータ準備の改善から始めます。さまざまなリサンプリング手法を使用して、ソースデータの表示を改善できます(訓練例)。本稿では、そのような手法の1つについて説明します。

前の記事で使用したラベルの単純な無作為抽出には、いくつかの欠点があります。

• クラスが不均衡になる可能性 - 訓練期間中に、母集団(相場履歴全体)が上下両方の動きを示唆する一方、市場が主に上昇していたと仮定します。この場合、ナイーブな抽出では、買いラベルが多くなり、売りラベルが少なくなります。したがって、あるクラスのラベルが別のクラスよりも優先されます。モデルは売り取引よりも買い取引を予測する頻度が高くなりますが、これは、新しいデータでは無効になる可能性があります。

• 機能とラベルの自己相関 - 無作為抽出が使用される場合、同じクラスのラベルは互いに続きますが、特徴自体(たとえば、増分など)はほとんど変化しません。このプロセスは、回帰モデルの訓練の例を使用して示すことができます。この場合、モデルの残差に自己相関が観察され、モデルの過大評価と過学習が発生する可能性があります。この状況を以下に示します。

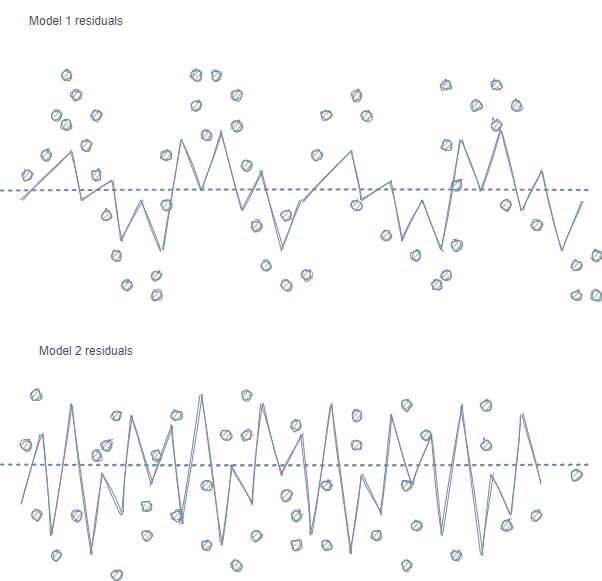
モデル1には残差の自己相関があり、特定の市場プロパティ(たとえば、訓練データのボラティリティに関連する)でのモデルの過剰適合と比較できますが、他のパターンは考慮されません。モデル2には、(平均して)同じ分散の残差があります。これは、モデルがより多くの情報をカバーしているか、他の依存関係が見つかったことを示します(隣接する抽出の相関に加えて)。

クラスが少ないため直感的ではありませんが、回帰モデルで使用される連続変数とは対照的に、分類についても同じ効果が見られます。ただし、効果は、ピアソン残差および同様の指標などを使用して測定できます。これらの依存関係(モデル1同様)は削除する必要があります。

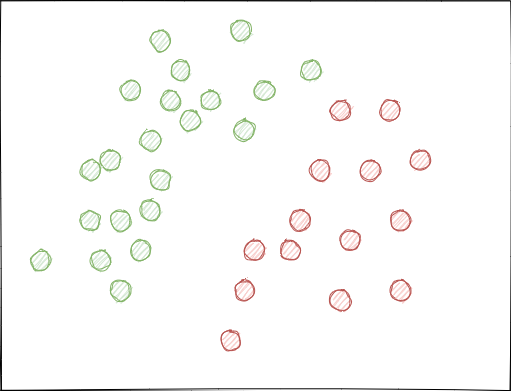
• クラスが大幅に重なり合う可能性 - 各点がクラス0または1に割り当てられている、架空の2D特徴空間(多次元空間はより複雑です)を想像してください。 

無作為抽出を使用する場合、例のセットが交差する可能性があります。これにより、異なるクラスの点間の距離(たとえば、ユークリッド距離)が減少し、同じクラスの点間の距離が増加する可能性があります。クラスを分離する多くの境界があり、訓練段階で非常に複雑なモデルが作成されます。特徴のわずかな偏差により、クラス間のモデル予測がジャンプします。新しいデータに対するモデルの安定性を損なうことになるため、この効果は排除する必要があります。

理想的には、クラスラベルは特徴空間で交差してはならず、線形(以下に示すように)または他の簡単な方法で分離される必要があります。この解決法は、新しいデータでより優れたモデルの安定性を提供します。

元のGIGOデータセットの分析

この記事では、前の部分から変更および改善された関数を使用します。データを読み込みます。

LOOK_BACK = 5
MA_PERIODS = [15, 55, 150, 250]

SYMBOL = 'EURUSD'
MARKUP = 0.00010
TIMEFRAME = mt5.TIMEFRAME_H1
START_DATE = datetime(2020, 1, 1)
TSTART_DATE = datetime(2015, 1, 1)
STOP_DATE = datetime(2021, 1, 1)

# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=10, max=25, add_noize=0)
res = tester(pr, plot=True)
pca_plot(pr)

元のデータセットの次元については特徴量が20(loock_back * len(ma_periods))またはその他の大きなものであるため、平面に表示するのはあまり便利ではありません。PCA法を使用して、5つの主成分のみを表示します。これにより、情報の損失を最小限に抑えて特徴空間を圧縮できます。

PCA(主成分分析)に精通していない場合は、Googleで検索してください。

def pca_plot(data):
    from sklearn.decomposition import PCA
    pca = PCA(n_components = 5)
    components = pd.DataFrame(pca.fit_transform(data[data.columns[1:-1]]))
    components['labels'] = data['labels'].reset_index(drop = True)
    import seaborn as sns
    g = sns.PairGrid(components, hue="labels", height=1.2)
    g.map_diag(sns.histplot)
    g.map_offdiag(sns.scatterplot)
    g.add_legend()
    plt.show()

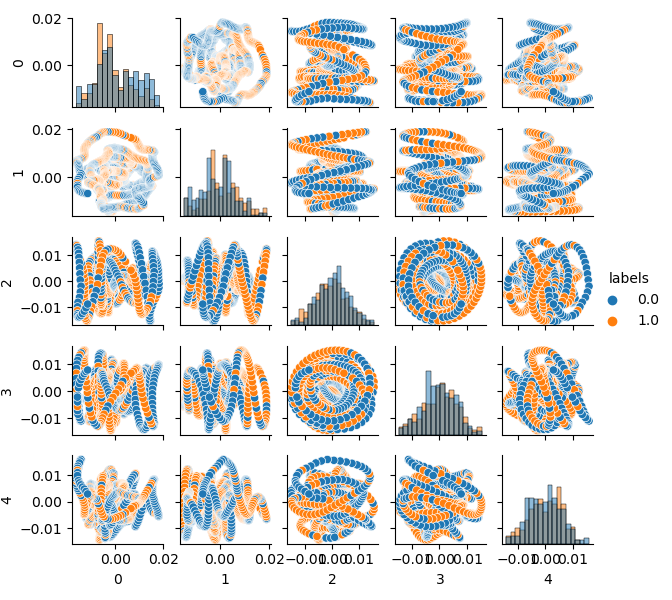
これで、各成分が他の成分に依存していることがわかります。これは、クラス0と1にラベル付けされた2D特徴空間です。成分のペアはループを形成しますが、これは通常の点群とは異なります。これは、点の自己相関が原因です。行を間引くと、リングは消えます。もう1つの事実は、クラスが強く重複していることです。エラーを最小限に抑えてラベルを分類するには、分類器は非常に複雑なモデルを作成する必要があり、多くの分割境界があります。元のデータセットは単なるガベージであると言えます。そして、ルール通り、ガベージイン—ガベージアウト(GIGO)です。GIGOの哲学を回避して研究をより意味のあるものにするために、機械学習モデル(CatBoostなど)の元のデータの表現を改善することをお勧めします。

理想的な特徴空間

特徴空間を2つのクラスに効果的に分割するために、たとえばK-means法を使用してクラスタリングを実装できます。これにより、特徴空間を理想的に分割する方法がわかります。

ソースデータセットは2つのクラスタにクラスタ化されます。 5つの主要成分が表示されます。

# perform K-means clustering over dataset
from sklearn.cluster import KMeans
pr = get_prices(look_back=LOOK_BACK)
X = pr[pr.columns[1:]]
kmeans = KMeans(n_clusters=2).fit(X)
y_kmeans = kmeans.predict(X)
pr['labels'] = y_kmeans
pca_plot(pr)

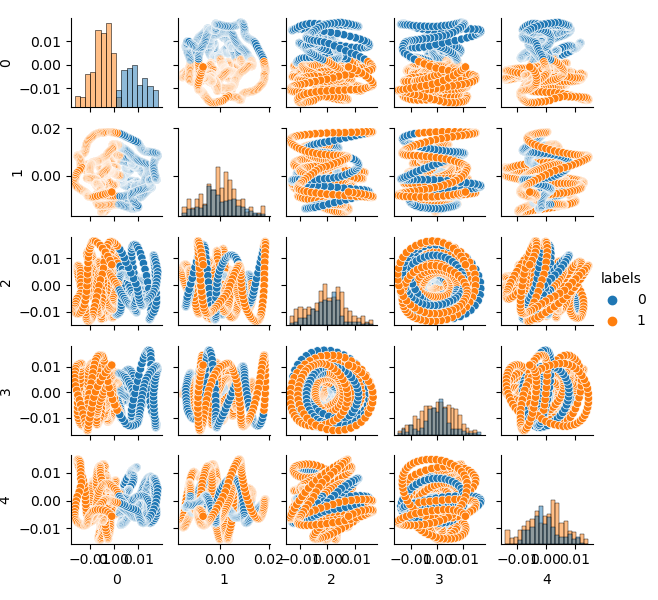
特徴空間は理想的に見えますが、クラスラベル(0、1)は明らかに収益性の高い取引に対応していません。この例は、GIGOデータセットよりも好ましい特徴空間のみを示しています。そのため、理想的なデータとガベージデータの間に妥協点を設ける必要があります。これを次におこなおうと思います。

訓練例をリサンプリングするための生成モデル

「私が自分で作れないものは、私が本当の意味で理解していないものだ。」

- リチャード・ファインマン

このセクションでは、データを「理解」し、新しいデータを再作成することを学習するモデルについて検討します。

k-meansクラスタリング手法は、比較的単純で理解しやすいものです。ただし、これにはいくつかの欠点があり、ここでは適していません。特に、この手法は確率的ではないため、多くの実際のケースではパフォーマンスが劣ります。この手法で、クラスタの最も外側の点によって決定される半径を持つ、指定された数の重心の周りに円(または超球)を配置するとします。この半径は、各クラスタの点のセットを厳密に制限します。したがって、すべてのクラスタは円と超球でのみ記述できますが、実際のクラスタは常にこの基準を満たすとは限りません(長方形または楕円の形である可能性があるため)。これにより、異なるクラスタ値が重複します。

より高度なアルゴリズムは、混合ガウスモデルです。このモデルは、データセットを最適にモデル化する多変量ガウス確率分布の混合を検索します。モデルは確率的であるため、これは、特定のクラスタとして分類されている例の確率を出力します。さらに、各クラスタは、厳密に定義された球ではなく、滑らかなガウスモデルに関連付けられています。このモデルは、円としてだけでなく、空間内で任意に方向付けられた楕円としても表すことができます。

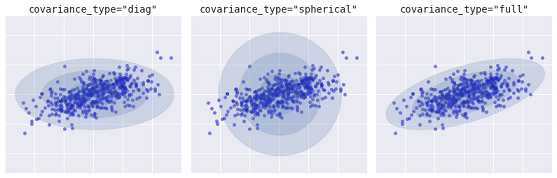
covaiance_typeに応じた、さまざまな種類の確率モデル

以下は、k-meansとGMM(ソース)によって取得されたクラスタの比較です。

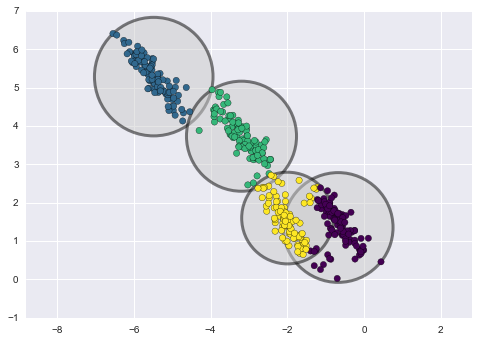
K-meansクラスタリング

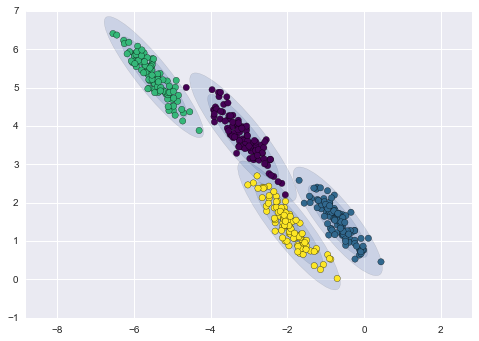
GMMクラスタリング

実際、混合ガウスモデル(GMM)アルゴリズムはクラスタライザーではありません。その主なタスクは確率密度を推定することです。このモデルのクラスタは、このデータを説明する確率分布から生成されたデータとして表されます。したがって、各クラスタの確率密度を推定した後、これらの分布から新しいデータセットを生成できます。これらのセットは元のデータと似ていますが、多少のばらつきがあり、外れ値が少なくなります。さらに、多くの場合、データセットの相関は低くなります。無作為な例を取得し、これらの例を使用してCatBoost分類器を訓練できます。 

元のデータセットの反復リサンプリングとCatBoostモデル訓練のパイプライン

まず、クラスラベルを含むソースデータをクラスタ化する必要があります。

# perform GMM clustering over dataset
from sklearn import mixture
pr_c = pr.copy()
X = pr_c[pr_c.columns[1:]]
gmm = mixture.GaussianMixture(n_components=75, covariance_type='full').fit(X)

選択できる主なパラメータはn_componentsで、経験的に75(クラスタ)に設定されました。その他のパラメータはそれほど重要ではないため、ここでは考慮しません。モデルが訓練された後、GMMモデルの多変量分布からいくつかの人工サンプルを生成し、いくつかの主要な成分を視覚化できます。

# plot resampled components
generated = gmm.sample(5000)
gen = pd.DataFrame(generated[0])
gen.rename(columns={ gen.columns[-1]: "labels" }, inplace = True)
gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
gen.loc[gen['labels'] < 0.5, 'labels'] = 0
pca_plot(gen)

ラベルもクラスタ化されているため、バイナリシリーズを表していないことに注意してください。上記のコードでは、ラベルは再び値(0; 1)に変換されます。これで、pca_plot()関数を使用して、結果の特徴空間を表示できます。

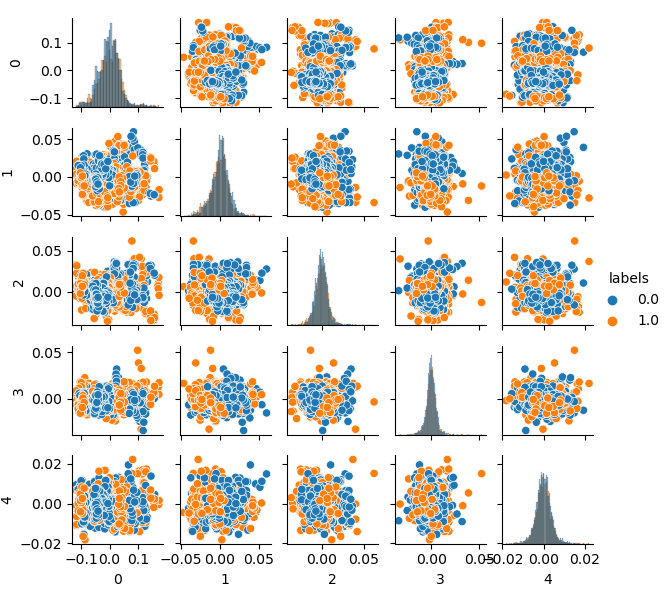
この図を前に示したGIGOデータセット図と比較すると、データループがないことがわかります。機能とラベルの相関が低くなり、学習結果にプラスの効果があるはずです。同時に、ラベルはより密なクラスタを形成する傾向があり、モデルの分割境界が少なくなって、より単純になる可能性があります。ガベージデータの問題を解消するという望ましい効果を部分的に達成しました。それにもかかわらず、データは本質的に同じです。元のデータをリサンプリングしただけです。

GMMがサンプルを無作為に生成する場合、これはデータの多元性につながります。最適なモデルは総当たり攻撃で選択できます。この目的のために、特別な総当たり攻撃関数が作成されています。

# brute force loop
def brute_force(samples = 5000):
    # sample new dataset
    generated = gmm.sample(samples)
    # make labels 
    gen = pd.DataFrame(generated[0])
    gen.rename(columns={ gen.columns[-1]: "labels" }, inplace = True)
    gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
    gen.loc[gen['labels'] < 0.5, 'labels'] = 0
    X = gen[gen.columns[:-1]]
    y = gen[gen.columns[-1]]
    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(X, y, train_size = 0.5, test_size = 0.5, shuffle=True)
    #learn with train and validation subsets
    model = CatBoostClassifier(iterations=500,
                            depth=6,
                            learning_rate=0.1,
                            custom_loss=['Accuracy'],
                            eval_metric='Accuracy',       
                            verbose=False, 
                            use_best_model=True,
                            task_type='CPU')
    model.fit(train_X, train_y, eval_set = (test_X, test_y), early_stopping_rounds=25, plot=False)
    # test on new data
    pr_tst = get_prices(TSTART_DATE, START_DATE)
    X = pr_tst[pr_tst.columns[1:]]
    X.columns = [''] * len(X.columns)

    #test the learned model
    p = model.predict_proba(X)
    p2 = [x[0]<0.5 for x in p]
    pr2 = pr_tst.iloc[:len(p2)].copy()
    pr2['labels'] = p2
    R2 = tester(pr2, MARKUP, plot=False)

    return [R2, samples, model]

コードの要点は強調表示しています。まず、GMM分布からn個の無作為な例を生成しました。次に、このデータを使用してCatBoostモデルが訓練されます。この関数は、テスターで計算されたR2スコアを返します。モデルは、訓練期間のデータだけでなく、以前のデータも使用してテストされることに注意してください。たとえば、モデルは2020年初頭からのデータで訓練され、2015年初頭からのデータを使用してテストされました。日付範囲は自由に変更できます。

指定された関数を数回呼び出し、各パスの結果をリストに保存するループを作成しましょう。

res = []
for i in range(50):  
    res.append(brute_force(10000))
    print('Iteration: ', i, 'R^2: ', res[-1][0])


res.sort()
test_model(res[-1])

次に、リストが並べ替えられ、リストの最後にあるモデルのR2スコアが最高になります。最良の結果を表示しましょう。

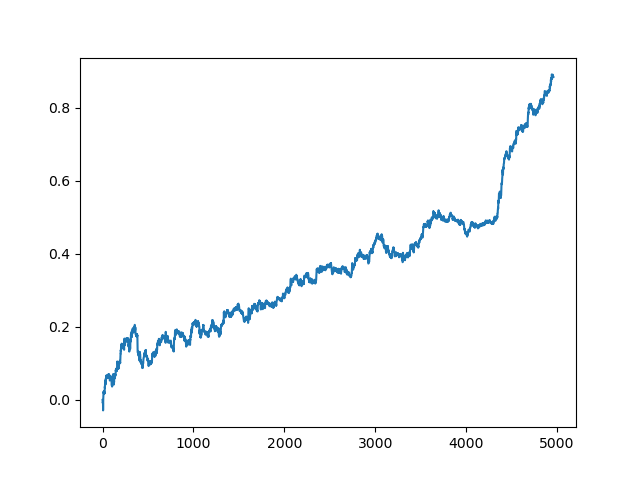
グラフの最後(右)の部分(約1000件の取引)は2020年の初めからの訓練データセットであり、残りはモデルの訓練で使用されなかった新しいデータを使用しています。モデルはR2指標に従って昇順で並べ替えられるため、以前のモデルをより低いスコアでテストできます。

test_model(res[-2])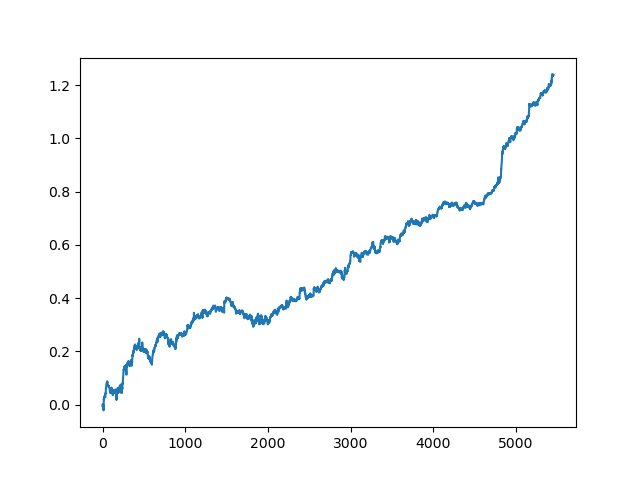

R2スコア自体も確認できます。

>>> res[-2][0]
0.9576444017048906

ご覧のとおり、モデルは1年間の訓練を受けましたが、5年間の長い期間でテストされています。次に、モデルをMQH形式にエクスポートできます。CatBoostモデルオブジェクトはネストされたリストにあり、インデックス2が付いています。最初の次元にはモデル番号が含まれています。ここでは、インデックス[-2](並び替えられたリストの最後から2番目)を使用してモデルをエクスポートします。

# export best model to mql
export_model_to_MQL_code(res[-2][2])

エクスポート後、モデルは標準のMetaTrader 5ストラテジーテスターでテストできます。カスタムテスターのスプレッドは実際よりも小さかったため、曲線はわずかに異なりますが、一般的な形状は同じです。

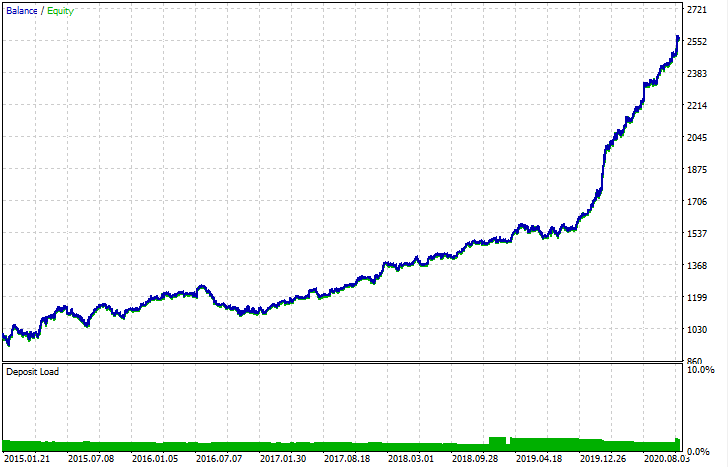
モデルの改善方法

モデルの訓練は、毎回異なる多くの無作為成分を意味します。たとえば、取引の無作為抽出、GMM訓練(ランダム性の要素もあります)、事後GMM分布からの無作為抽出、およびランダム性の要素も含むCatBoost訓練などです。したがって、プログラム全体を数回再起動して、最良の結果を得ることができます。安定したモデルが得られない場合は、LOOK_BACKパラメータと移動平均の数およびそれらの期間を調整する必要があります。また、GMMから受け取る標本の数、および訓練とテストの間隔を変更することもできます。 

変更ログとコードのリファクタリング

プログラムのPythonコードにいくつかの変更が加えられたので、説明が必要です。

平均期間が異なる移動平均のリストを設定できるようになりました。複数のMAの組み合わせは、通常、訓練結果にプラスの効果をもたらします。

MA_PERIODS = [15, 55, 150, 250]

テストプロセス、モデルの評価および選択のための設定可能な開始日を追加しました。

TSTART_DATE = datetime(2015, 1, 1)

無作為抽出機能に、いくつかの変更が加えられました。元のデータセットにノイズを追加できるようにするadd_noizeパラメータが追加されました。これは、ドローダウンを追加して取引を混合することにより、取引の理想性を低下させます。場合によっては、0.1～02のレベルでエラーを導入することにより、新しいデータでモデルを改善できます。 

スプレッドが考慮されるようになりました。スプレッドをカバーしない取引は2.0のラベルでマークされ、情報がないためデータセットから削除されます。

def add_labels(dataset, min, max, add_noize = 0.1):
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'][i]
        future_pr = dataset['close'][i + rand]

        if future_pr + MARKUP < curr_pr:
            labels.append(1.0)
        elif future_pr - MARKUP > curr_pr:
            labels.append(0.0)              
        else:
            labels.append(2.0)
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2].index).reset_index(drop=True)

    if add_noize==0:
        return dataset

    # add noize to samples
    noize_b = dataset[dataset.labels == 0]['labels'].sample(frac = add_noize)
    noize_s = dataset[dataset.labels == 1]['labels'].sample(frac = add_noize)
    noize_b = noize_b+1
    noize_s = noize_s-1
    dataset.update(noize_b)
    dataset.update(noize_s)
    return dataset

テスト関数はR 2スコアを返すようになりました。

def tester(dataset, markup = 0.0, plot = False):
    last_deal = int(2)
    last_price = 0.0
    report = [0.0]
    for i in range(dataset.shape[0]):
        pred = dataset['labels'][i]
        if last_deal == 2:
            last_price = dataset['close'][i]
            last_deal = 0 if pred <= 0.5 else 1
            continue
        if last_deal == 0 and pred > 0.5:
            last_deal = 1
            report.append(report[-1] - markup + (dataset['close'][i] - last_price))
            last_price = dataset['close'][i]
            continue
        if last_deal == 1 and pred < 0.5:
            last_deal = 0
            report.append(report[-1] - markup + (last_price - dataset['close'][i]))
            last_price = dataset['close'][i]      

    y = np.array(report).reshape(-1,1)
    X = np.arange(len(report)).reshape(-1,1)
    lr = LinearRegression()
    lr.fit(X,y)

    l = lr.coef_
    if l >= 0:
        l = 1
    else:
        l = -1

    if(plot):
        plt.plot(report)
        plt.show()

    return lr.score(X,y) * l

主要成分メソッドによるデータ視覚化のヘルパー関数を追加しました。これは、データをよりよく理解するのに役立つ場合があります。

def pca_plot(data):
    from sklearn.decomposition import PCA
    pca = PCA(n_components = 5)
    components = pd.DataFrame(pca.fit_transform(data[data.columns[1:-1]]))
    components['labels'] = data['labels'].reset_index(drop = True)
    import seaborn as sns
    g = sns.PairGrid(components, hue="labels", height=1.2)
    g.map_diag(sns.histplot)
    g.map_offdiag(sns.scatterplot)
    g.add_legend()
    plt.show()

コードパーサーが拡張されました。MQLプログラムに追加された移動平均のすべての期間が考慮され、fill_arrays関数が特徴ベクトルを形成します。

def export_model_to_MQL_code(model):
    model.save_model('catmodel.h',
           format="cpp",
           export_parameters=None,
           pool=None)

    # add variables
    code = 'int ' + 'loock_back = ' + str(LOOK_BACK) + ';\n'
    code += 'int hnd[];\n'
    code += 'int OnInit() {\n'
    code +=     'ArrayResize(hnd,' + str(len(MA_PERIODS)) + ');\n'

    count = len(MA_PERIODS) - 1
    for i in MA_PERIODS:
        code +=     'hnd[' + str(count) + ']' + ' =' + ' iMA(NULL,PERIOD_CURRENT,' + str(i) + ',0,MODE_SMA,PRICE_CLOSE);\n'
        count -= 1

    code += 'return(INIT_SUCCEEDED);\n'
    code += '}\n\n'

    # get features
    code += 'void fill_arays(int look_back, double &features[]) {\n'
    code += '   double ma[], pr[], ret[];\n'
    code += '   ArrayResize(ret,' + str(LOOK_BACK) +');\n'
    code += '   CopyClose(NULL,PERIOD_CURRENT,1,look_back,pr);\n'
    code += '   for(int i=0;i<' + str(len(MA_PERIODS)) +';i++) {\n'
    code += '       CopyBuffer(hnd[' + 'i' + '], 0, 1, look_back, ma);\n'
    code += '       for(int f=0;f<' + str(LOOK_BACK) +';f++)\n'
    code += '           ret[f] = pr[f] - ma[f];\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

終わりに

この記事では、元のデータセットをリサンプリングするために、単純な生成モデルであるGMM(混合ガウスモデル)を使用する方法の例を示しました。このモデルでは、特徴空間の特性を改善することにより、新しいデータに対するCatBoost分類器のパフォーマンスを改善できます。最適なモデルを選択するために、反復データリサンプリングを実装し、目的の結果を選択できるようにしました。

これは、ナイーブなモデルから意味のあるモデルへの一種のブレークスルーでした。取引ストラテジーの論理コンポーネントを開発するために最小限の労力を費やすことで、興味深い機械学習ベースの自動売買ロボットを手に入れることができます。