Fortschrittliches Resampling und Auswahl von CatBoost-Modellen durch die Brute-Force-Methode

Einführung

Im vorhergehenden Artikel habe ich versucht, einen allgemeinen Überblick über die wichtigsten Schritte zur Erstellung eines maschinellen Lernmodells und seine weitere praktische Anwendung zu geben. In diesem Teil möchte ich von einfachen Modellen zu statistisch signifikanten Modellen wechseln. Da die Erstellung eines auf maschinellem Lernen basierenden Handelssystems keine triviale Aufgabe ist, werden wir mit einigen Verbesserungen der Datenaufbereitung beginnen, die dazu beitragen, optimale Ergebnisse zu erzielen. Verschiedene Resampling-Techniken können verwendet werden, um die Darstellung der Quelldaten zu verbessern (Schulungsbeispiele). Eine dieser Techniken wird in diesem Artikel besprochen.

Eine einfache Zufallsstichprobe der im vorigen Artikel verwendeten Labels hat einige Nachteile:

• Die Klassen können unausgewogen sein. Nehmen wir an, dass der Markt vor allem während der Trainingsphase anstieg, während die allgemeinen Daten (die gesamte Historie der Preise) sowohl ein Auf und Ab impliziert. In diesem Fall führt eine naive Stichprobenziehung zu mehr Käufen und weniger Verkäufen. Dementsprechend werden sich Labels einer Klasse gegenüber einer anderen durchsetzen, wodurch das Modell lernen wird, Käufe öfter vorherzusagen als Verkäufe, was jedoch für neue Daten ungültig sein kann.

• Autokorrelation von Merkmalen und Labels. Bei Verwendung von Zufallsstichproben folgen die Labels derselben Klasse aufeinander, während sich die Merkmale selbst (wie z.B. Inkremente) nur unwesentlich ändern. Dieser Prozess kann am Beispiel eines Regressionsmodelltrainings gezeigt werden - in diesem Fall wird sich herausstellen, dass Autokorrelation in den Modellresiduen beobachtet wird, was zu einer möglichen Überschätzung des Modells und zu einem Übertraining führt. Diese Situation ist unten dargestellt:

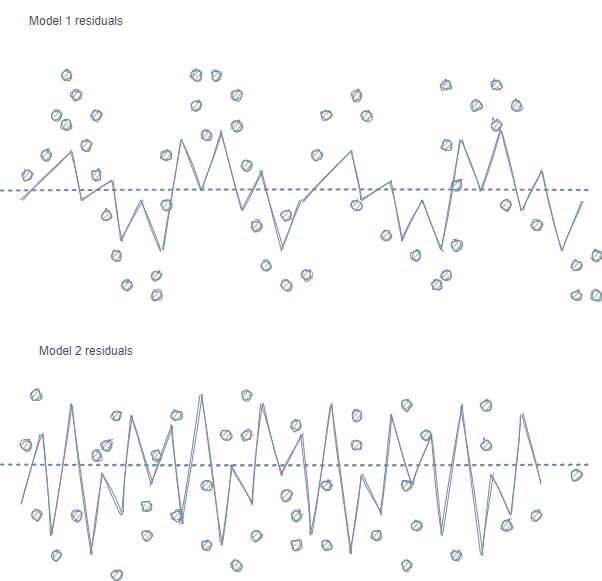
Modell 1 verfügt über eine Autokorrelation der Residuen, die mit einer Modellüberanpassung bei bestimmten Markteigenschaften verglichen werden kann (z.B. in Bezug auf die Volatilität der Trainingsdaten), während andere Muster nicht berücksichtigt werden. Modell 2 hat Residuen mit der gleichen Varianz (im Durchschnitt), was darauf hinweist, dass das Modell mehr Informationen abdeckt oder andere Abhängigkeiten gefunden wurden (zusätzlich zur Korrelation benachbarter Stichproben).

Derselbe Effekt ist auch bei der Klassifikation zu beobachten, die allerdings weniger intuitiv ist, da sie nur wenige Klassen hat, im Gegensatz zu einer kontinuierlichen Variablen, die in Regressionsmodellen verwendet wird. Dennoch kann der Effekt z.B. mit Hilfe von Pearson-Residuen und ähnlichen Metriken gemessen werden. Diese Abhängigkeiten (wie in Modell 1) sollten eliminiert werden.

• Die Klassen können sich erheblich überlappen. Stellen Sie sich einen hypothetischen 2D-Merkmalsraum vor (mehrdimensionale Räume sind komplexer), bei dem jeder Punkt der Klasse 0 oder 1 zugeordnet ist. 

Bei der Verwendung von Zufallsstichproben können sich Beispielsätze überschneiden. Dies kann zu einer Verringerung des Abstands (z.B. des euklidischen Abstands) zwischen Punkten verschiedener Klassen und zu einer Vergrößerung des Abstands zwischen Punkten derselben Klasse führen, was im Stadium des Trainings zur Erstellung eines zu komplexen Modells mit vielen Grenzen zwischen den Klassen führt. Kleine Abweichungen in den Merkmalen führen zu Sprüngen in den Modellvorhersagen von Klasse zu Klasse. Dieser Effekt ruiniert die Modellstabilität bei neuen Daten und muss beseitigt werden.

Idealerweise sollten sich die Klassenlabels im Feature-Raum nicht überschneiden und entweder linear (wie unten dargestellt) oder durch eine andere einfache Methode getrennt werden. Diese Lösung würde für eine größere Modellstabilität bei neuen Daten sorgen.

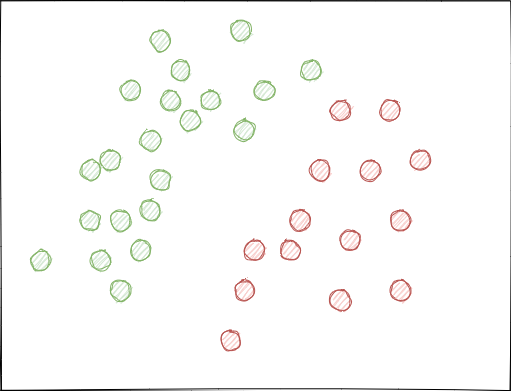
Analyse des ursprünglichen GIGO-Datensatzes

In diesem Artikel werden modifizierte und verbesserte Funktionen aus dem vorherigen Teil verwendet. Laden Sie die Daten:

LOOK_BACK = 5
MA_PERIODS = [15, 55, 150, 250]

SYMBOL = 'EURUSD'
MARKUP = 0.00010
TIMEFRAME = mt5.TIMEFRAME_H1
START_DATE = datetime(2020, 1, 1)
TSTART_DATE = datetime(2015, 1, 1)
STOP_DATE = datetime(2021, 1, 1)

# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=10, max=25, add_noize=0)
res = tester(pr, plot=True)
pca_plot(pr)

Da die Dimension des Originaldatensatzes 20 Merkmale (loock_back * len(ma_periods)) oder irgendein anderes großes Merkmal ist, ist es nicht sehr praktisch, ihn auf einer Ebene darzustellen. Lassen Sie uns die PCA-Methode verwenden und nur 5 Hauptkomponenten anzeigen, was es erlaubt, den Merkmalsraum mit dem geringsten Informationsverlust zu verdichten:

Wenn Sie mit der PCA (Principal Component Analysis) nicht vertraut sind, informieren Sie sich bitte über Google.

def pca_plot(data):
    from sklearn.decomposition import PCA
    pca = PCA(n_components = 5)
    components = pd.DataFrame(pca.fit_transform(data[data.columns[1:-1]]))
    components['labels'] = data['labels'].reset_index(drop = True)
    import seaborn as sns
    g = sns.PairGrid(components, hue="labels", height=1.2)
    g.map_diag(sns.histplot)
    g.map_offdiag(sns.scatterplot)
    g.add_legend()
    plt.show()

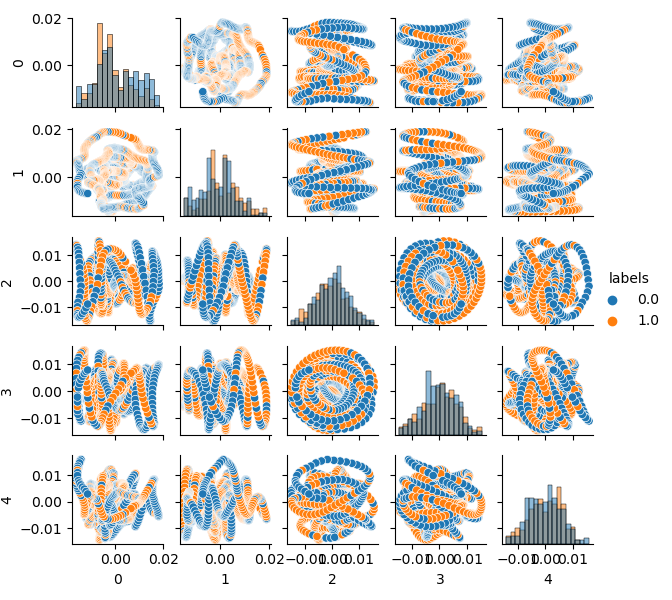
Jetzt können Sie die Abhängigkeit jeder Komponente von der anderen sehen: Dies ist der 2D-Merkmalsraum, der in die Klassen 0 und 1 eingeteilt ist. Komponentenpaare bilden Schleifen, die der üblichen Punktwolke nicht ähnlich sind. Dies wird durch die Autokorrelation der Punkte verursacht. Die Ringe verschwinden, wenn Sie die Reihe ausdünnen. Eine weitere Tatsache ist, dass sich die Klassen stark überschneiden. Um die Label mit dem geringsten Fehler zu klassifizieren, muss der Klassifikator ein sehr komplexes Modell erstellen, mit vielen Trenngrenzen. Man kann sagen, dass der Originaldatensatz einfach Müll ist, und die Regel lautet Garbage in - Garbage out (GIGO). Um die GIGO-Philosophie zu vermeiden und die Forschung sinnvoller zu gestalten, schlage ich vor, die Repräsentation der Originaldaten für ein maschinelles Lernmodell (z. B. CatBoost) zu verbessern.

Idealer Merkmalsraum

Um den Merkmalsraum effektiv in zwei Klassen aufzuteilen, können wir ein Clustering implementieren, z. B. mit der Methode k-Means. Dies soll eine Vorstellung davon geben, wie der Merkmalsraum idealerweise aufgeteilt werden könnte.

Der Quelldatensatz wird in zwei Cluster geclustert; es werden fünf Hauptkomponenten angezeigt:

# perform K-means clustering over dataset
from sklearn.cluster import KMeans
pr = get_prices(look_back=LOOK_BACK)
X = pr[pr.columns[1:]]
kmeans = KMeans(n_clusters=2).fit(X)
y_kmeans = kmeans.predict(X)
pr['labels'] = y_kmeans
pca_plot(pr)

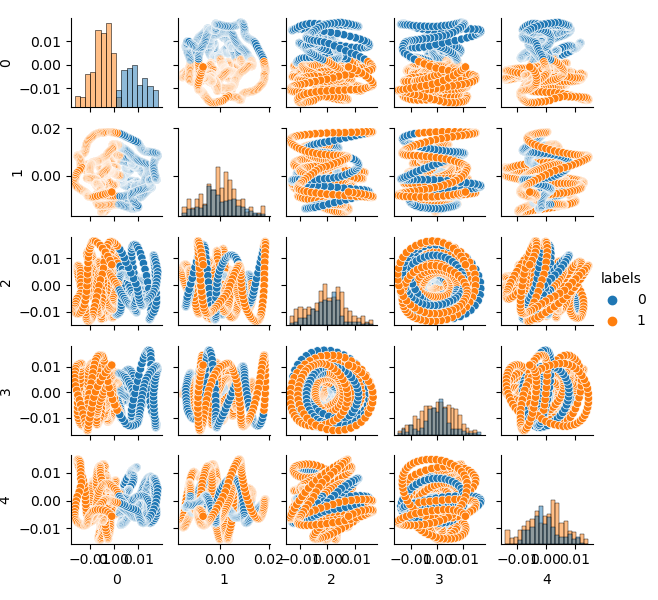
Der Merkmalsraum sieht ideal aus, aber die Klassenlabels (0, 1) entsprechen offensichtlich nicht dem profitablen Handel. Dieses Beispiel veranschaulicht nur einen bevorzugteren Merkmalsraum als der GIGO-Datensatz. Deshalb müssen wir einen Kompromiss zwischen idealen und Mülldaten schaffen. Dies werden wir als Nächstes tun.

Generatives Modell für das Resampling von Trainingsbeispielen

"Was ich nicht erschaffen kann, verstehe ich nicht."

—Richard Feynman

In diesem Abschnitt werden wir ein Modell betrachten, das lernt, Daten zu "verstehen" und neue Daten zu erzeugen.

Die k-Means Clustering-Methode ist relativ einfach und leicht zu verstehen. Sie hat jedoch eine Reihe von Nachteilen und ist für unseren Fall nicht geeignet. Insbesondere hat sie in vielen realen Fällen eine schlechte Leistung, da sie nicht probabilistisch ist. Stellen Sie sich vor, dass diese Methode Kreise (oder Hypersphären) um eine gegebene Anzahl von Zentroiden mit einem Radius platziert, der durch den äußersten Punkt des Clusters bestimmt wird. Dieser Radius schränkt die Menge der Punkte für jeden Cluster streng ein. Somit können alle Cluster nur durch Kreise und Hypersphären beschrieben werden, während reale Cluster dieses Kriterium nicht immer erfüllen (da sie länglich oder in Form von Ellipsen sein können). Dadurch kommt es zu Überschneidungen der verschiedenen Clusterwerte.

Ein fortschrittlicherer Algorithmus ist das Gaussian Mixture Model. Dieses Modell sucht nach einer Mischung aus multivariaten Gaußschen Wahrscheinlichkeitsverteilungen, die den Datensatz am besten modelliert. Da es sich um ein probabilistisches Modell handelt, werden die Wahrscheinlichkeiten für die Zuordnung eines Beispiels zu einem bestimmten Cluster ausgegeben. Außerdem ist jeder Cluster nicht mit einer streng definierten Kugel verbunden, sondern mit einem gleichmäßigen Gaußschen Modell, das nicht nur als Kreise, sondern auch als Ellipsen dargestellt werden kann, die beliebig im Raum orientiert sind.

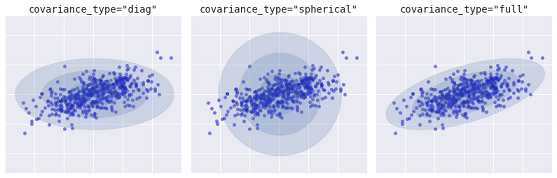
Verschiedene Arten von probabilistischen Modellen, abhängig von covaiance_type

Unten sehen Sie einen Vergleich von Clustern, die durch k-Means und GMM erhalten wurden (Quelle):

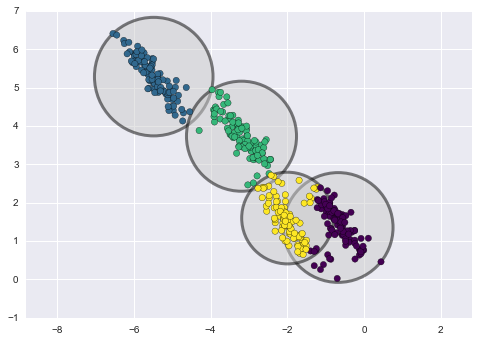
k-Means Clustering

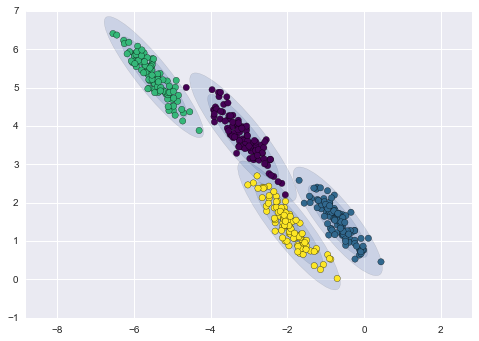
GMM Clustering

In der Tat ist der Gaussian Mixture Model (GMM)-Algorithmus nicht wirklich ein Clusterizer, da seine Hauptaufgabe darin besteht, die Wahrscheinlichkeitsdichte zu schätzen. Cluster werden in diesem Modell als Daten dargestellt, die aus Wahrscheinlichkeitsverteilungen erzeugt werden, die diese Daten beschreiben. Daher können nach der Schätzung der Wahrscheinlichkeitsdichte jedes Clusters neue Datensätze aus diesen Verteilungen generiert werden. Diese Datensätze werden den ursprünglichen Daten ähnlich sein, aber sie werden mehr oder weniger Variabilität und weniger Ausreißer haben. Außerdem werden die Datensätze in vielen Fällen weniger korreliert sein. Wir können zufällige Beispiele erhalten und dann den CatBoost-Klassifikator mit diesen Beispielen trainieren. 

Pipeline für iteratives Resampling des Originaldatensatzes und Training des CatBoost-Modells

Zunächst ist es notwendig, die Quelldaten zu clustern, einschließlich der Klassenlabels:

# perform GMM clustering over dataset
from sklearn import mixture
pr_c = pr.copy()
X = pr_c[pr_c.columns[1:]]
gmm = mixture.GaussianMixture(n_components=75, covariance_type='full').fit(X)

Der wichtigste Parameter, der gewählt werden kann, ist n_components. Er wurde empirisch auf 75 (Cluster) gesetzt. Andere Parameter sind nicht so wichtig und werden hier nicht besprochen. Nachdem das Modell trainiert ist, können wir einige künstliche Stichproben aus der multivariaten Verteilung des GMM-Modells erzeugen und mehrere Hauptkomponenten visualisieren:

# plot resampled components
generated = gmm.sample(5000)
gen = pd.DataFrame(generated[0])
gen.rename(columns={ gen.columns[-1]: "labels" }, inplace = True)
gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
gen.loc[gen['labels'] < 0.5, 'labels'] = 0
pca_plot(gen)

Bitte beachten Sie, dass auch die Labels geclustert wurden und somit keine binäre Reihe mehr darstellen. Die Labels werden im obigen Code wieder in Werte (0;1) umgewandelt. Nun kann der resultierende Merkmalsraum mit der Funktion pca_plot() dargestellt werden:

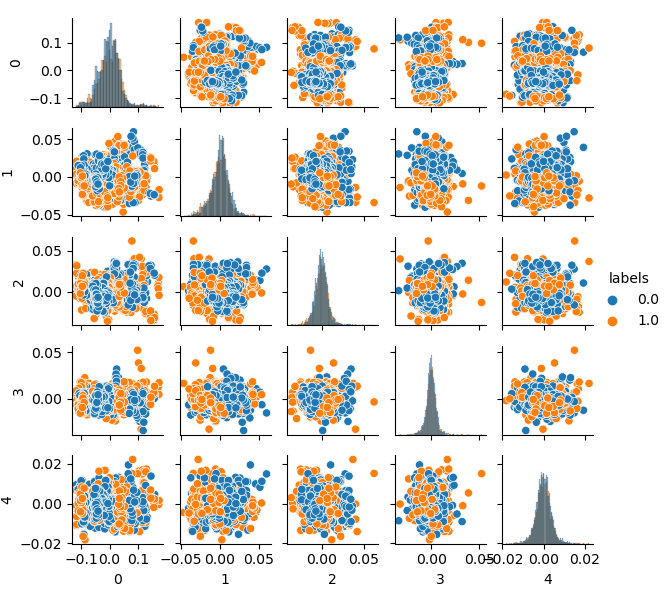
Wenn Sie dieses Diagramm mit dem früher vorgestellten Diagramm des GIGO-Datensatzes vergleichen, können Sie sehen, dass es keine Datenschleifen aufweist. Merkmale und Labels sind nun weniger korreliert, was sich positiv auf das Lernergebnis auswirken sollte. Gleichzeitig neigen die Labels manchmal dazu, dichtere Cluster zu bilden, und das Modell kann sich als einfacher erweisen, mit weniger Trennungsgrenzen. Wir haben teilweise den gewünschten Effekt erreicht, indem wir Probleme mit Mülldaten eliminiert haben. Dennoch sind die Daten im Wesentlichen die gleichen. Wir haben einfach die ursprünglichen Daten neu gesampelt.

Vorausgesetzt, dass GMM Stichproben zufällig generiert, führt dies zu einer Datenvielfalt. Das beste Modell kann mit Brute-Force ausgewählt werden. Zu diesem Zweck wurde eine spezielle Brute-Force-Funktion geschrieben:

# brute force loop
def brute_force(samples = 5000):
    # sample new dataset
    generated = gmm.sample(samples)
    # make labels 
    gen = pd.DataFrame(generated[0])
    gen.rename(columns={ gen.columns[-1]: "labels" }, inplace = True)
    gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
    gen.loc[gen['labels'] < 0.5, 'labels'] = 0
    X = gen[gen.columns[:-1]]
    y = gen[gen.columns[-1]]
    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(X, y, train_size = 0.5, test_size = 0.5, shuffle=True)
    #learn with train and validation subsets
    model = CatBoostClassifier(iterations=500,
                            depth=6,
                            learning_rate=0.1,
                            custom_loss=['Accuracy'],
                            eval_metric='Accuracy',       
                            verbose=False, 
                            use_best_model=True,
                            task_type='CPU')
    model.fit(train_X, train_y, eval_set = (test_X, test_y), early_stopping_rounds=25, plot=False)
    # test on new data
    pr_tst = get_prices(TSTART_DATE, START_DATE)
    X = pr_tst[pr_tst.columns[1:]]
    X.columns = [''] * len(X.columns)

    #test the learned model
    p = model.predict_proba(X)
    p2 = [x[0]<0.5 for x in p]
    pr2 = pr_tst.iloc[:len(p2)].copy()
    pr2['labels'] = p2
    R2 = tester(pr2, MARKUP, plot=False)

    return [R2, samples, model]

Ich habe die wichtigsten Punkte im Code hervorgehoben. Zuerst werden n zufällige Beispiele aus der GMM-Verteilung generiert. Dann wird das CatBoost-Modell mit diesen Daten trainiert. Die Funktion gibt den im Tester berechneten R^2-Wert zurück. Achten Sie darauf, dass das Modell nicht nur mit den Daten der Trainingsperiode getestet wird, sondern auch mit früheren Daten. Zum Beispiel wurde das Modell mit Daten seit Anfang 2020 trainiert und es wurde mit Daten seit Anfang 2015 getestet. Sie können die Datumsbereiche nach Belieben ändern.

Lassen Sie uns eine Schleife schreiben, die die angegebene Funktion mehrmals aufruft und die Ergebnisse jedes Durchgangs in einer Liste speichert:

res = []
for i in range(50):  
    res.append(brute_force(10000))
    print('Iteration: ', i, 'R^2: ', res[-1][0])


res.sort()
test_model(res[-1])

Dann wird die Liste sortiert und das Modell am Ende der Liste zeigt das beste R^2-Wert. Lassen wir uns das beste Ergebnis anzeigen:

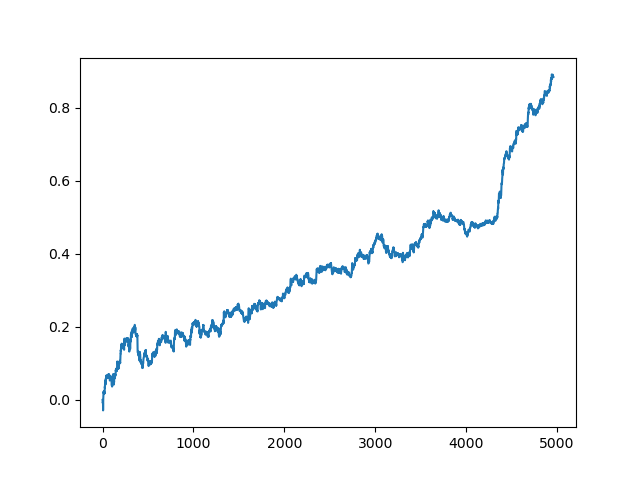
Der letzte (rechte) Teil des Graphen (ca. 1000 Deals) ist ein Trainingsdatensatz, vom Anfang des Jahres 2020, während der Rest neue Daten verwendet, die nicht beim Training des Modells verwendet wurden. Da die Modelle in aufsteigender Reihenfolge sortiert sind, entsprechend der R^2-Metrik, können wir frühere Modelle mit einer niedrigeren Punktzahl testen:

test_model(res[-2])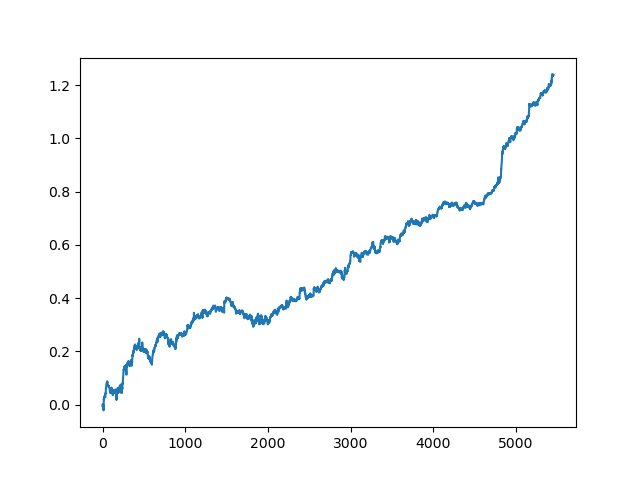

Sie können sich auch den R^2-Wert selbst ansehen:

>>> res[-2][0]
0.9576444017048906

Wie Sie sehen können, wird das Modell jetzt auf einen langen Fünfjahreszeitraum getestet, obwohl es auf einen Einjahreszeitraum trainiert wurde. Anschließend kann das Modell in das MQH-Format exportiert werden. Das CatBoost-Modellobjekt befindet sich in der verschachtelten Liste, mit dem Index 2 - die erste Dimension enthält die Modellnummern. Hier exportieren wir das Modell mit dem Index [-2] (das zweite vom Ende der sortierten Liste):

# export best model to mql
export_model_to_MQL_code(res[-2][2])

Nach dem Export kann das Modell im standardmäßigen MetaTrader 5 Strategietester getestet werden. Da der Spread im nutzerdefinierten Tester geringer war als im realen, sind die Kurven leicht unterschiedlich. Dennoch ist ihre allgemeine Form die gleiche.

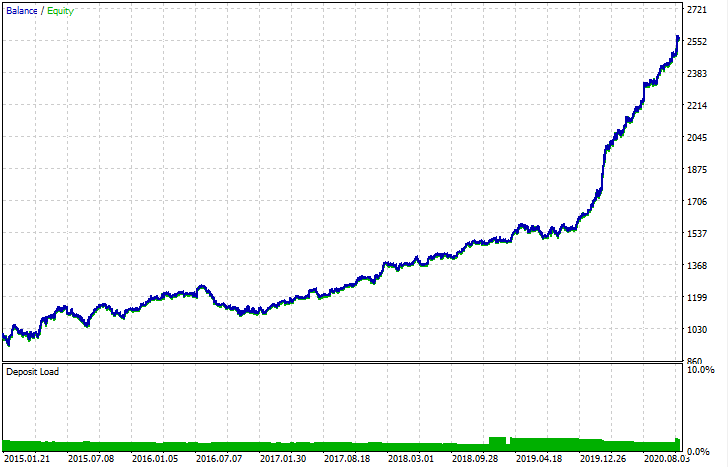
Wie können die Modelle verbessert werden?

Das Training von Modellen beinhaltet viele Zufallskomponenten, die jedes Mal anders sind. Zum Beispiel, Zufallsstichproben von Geschäften, GMM-Training (das auch ein Element der Zufälligkeit enthält), Zufallsstichproben aus der posterioren GMM-Verteilung und CatBoost-Training, das auch ein Element der Zufälligkeit enthält. Daher kann das gesamte Programm mehrmals neu gestartet werden, um das beste Ergebnis zu erhalten. Wenn kein stabiles Modell erzielt werden kann, sollten Sie den Parameter LOOK_BACK und die Anzahl der gleitenden Durchschnitte und deren Perioden anpassen. Sie können auch die Anzahl der vom GMM erhaltenen Stichproben sowie die Trainings- und Testintervalle ändern. 

Änderungsprotokoll und Code-Refactoring

Es wurden einige Änderungen am Python-Code des Programms vorgenommen. Sie erfordern einige Klarstellungen.

Jetzt kann eine Liste von gleitenden Durchschnitten mit verschiedenen Mittelungsperioden eingestellt werden. Eine Kombination von mehreren MAs wirkt sich in der Regel positiv auf die Trainingsergebnisse aus.

MA_PERIODS = [15, 55, 150, 250]

Konfigurierbares Startdatum für Testprozess, Modellbewertung und -auswahl hinzugefügt.

TSTART_DATE = datetime(2015, 1, 1)

Die Zufallsstichprobenfunktion hat eine Reihe von Änderungen erfahren. Es wurde der Parameter add_noize hinzugefügt, mit dem Sie dem Originaldatensatz Rauschen hinzufügen können. Dies macht den Handel weniger ideal, indem Drawdowns hinzugefügt und Geschäfte vermischt werden. Manchmal kann ein Modell auf neuen Daten verbessert werden, indem ein Fehler auf dem Niveau von 0,1 - 02 eingeführt wird. 

Jetzt wird der Spread berücksichtigt. Die Geschäfte, die den Spread nicht abdecken, werden mit einem Label von 2,0 markiert und dann aus dem Datensatz gelöscht, da sie nicht informativ sind.

def add_labels(dataset, min, max, add_noize = 0.1):
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'][i]
        future_pr = dataset['close'][i + rand]

        if future_pr + MARKUP < curr_pr:
            labels.append(1.0)
        elif future_pr - MARKUP > curr_pr:
            labels.append(0.0)              
        else:
            labels.append(2.0)
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2].index).reset_index(drop=True)

    if add_noize==0:
        return dataset

    # add noize to samples
    noize_b = dataset[dataset.labels == 0]['labels'].sample(frac = add_noize)
    noize_s = dataset[dataset.labels == 1]['labels'].sample(frac = add_noize)
    noize_b = noize_b+1
    noize_s = noize_s-1
    dataset.update(noize_b)
    dataset.update(noize_s)
    return dataset

Die Testfunktion gibt nun den R^2-Wert zurück:

def tester(dataset, markup = 0.0, plot = False):
    last_deal = int(2)
    last_price = 0.0
    report = [0.0]
    for i in range(dataset.shape[0]):
        pred = dataset['labels'][i]
        if last_deal == 2:
            last_price = dataset['close'][i]
            last_deal = 0 if pred <= 0.5 else 1
            continue
        if last_deal == 0 and pred > 0.5:
            last_deal = 1
            report.append(report[-1] - markup + (dataset['close'][i] - last_price))
            last_price = dataset['close'][i]
            continue
        if last_deal == 1 and pred < 0.5:
            last_deal = 0
            report.append(report[-1] - markup + (last_price - dataset['close'][i]))
            last_price = dataset['close'][i]      

    y = np.array(report).reshape(-1,1)
    X = np.arange(len(report)).reshape(-1,1)
    lr = LinearRegression()
    lr.fit(X,y)

    l = lr.coef_
    if l >= 0:
        l = 1
    else:
        l = -1

    if(plot):
        plt.plot(report)
        plt.show()

    return lr.score(X,y) * l

Es wurde eine Hilfsfunktion für die Datenvisualisierung über die Hauptkomponentenmethode hinzugefügt. Dies kann zum besseren Verständnis Ihrer Daten beitragen.

def pca_plot(data):
    from sklearn.decomposition import PCA
    pca = PCA(n_components = 5)
    components = pd.DataFrame(pca.fit_transform(data[data.columns[1:-1]]))
    components['labels'] = data['labels'].reset_index(drop = True)
    import seaborn as sns
    g = sns.PairGrid(components, hue="labels", height=1.2)
    g.map_diag(sns.histplot)
    g.map_offdiag(sns.scatterplot)
    g.add_legend()
    plt.show()

Der Code-Parser wurde erweitert. Jetzt berücksichtigt er alle Perioden der gleitenden Durchschnitte, die dem MQL-Programm hinzugefügt werden, wonach die Funktion fill_arrays einen Feature-Vektor bildet.

def export_model_to_MQL_code(model):
    model.save_model('catmodel.h',
           format="cpp",
           export_parameters=None,
           pool=None)

    # add variables
    code = 'int ' + 'loock_back = ' + str(LOOK_BACK) + ';\n'
    code += 'int hnd[];\n'
    code += 'int OnInit() {\n'
    code +=     'ArrayResize(hnd,' + str(len(MA_PERIODS)) + ');\n'

    count = len(MA_PERIODS) - 1
    for i in MA_PERIODS:
        code +=     'hnd[' + str(count) + ']' + ' =' + ' iMA(NULL,PERIOD_CURRENT,' + str(i) + ',0,MODE_SMA,PRICE_CLOSE);\n'
        count -= 1

    code += 'return(INIT_SUCCEEDED);\n'
    code += '}\n\n'

    # get features
    code += 'void fill_arays(int look_back, double &features[]) {\n'
    code += '   double ma[], pr[], ret[];\n'
    code += '   ArrayResize(ret,' + str(LOOK_BACK) +');\n'
    code += '   CopyClose(NULL,PERIOD_CURRENT,1,look_back,pr);\n'
    code += '   for(int i=0;i<' + str(len(MA_PERIODS)) +';i++) {\n'
    code += '       CopyBuffer(hnd[' + 'i' + '], 0, 1, look_back, ma);\n'
    code += '       for(int f=0;f<' + str(LOOK_BACK) +';f++)\n'
    code += '           ret[f] = pr[f] - ma[f];\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

Schlussfolgerung

Dieser Artikel demonstriert ein Beispiel für die Verwendung eines einfachen generativen Modells - GMM (Gaussian Mixture Model) für das Resampling des ursprünglichen Datensatzes. Dieses Modell ermöglicht es, die Leistung des CatBoost-Klassifikators auf neuen Daten zu verbessern, indem die Eigenschaften des Merkmalsraums verbessert werden. Zur Auswahl des besten Modells haben wir ein iteratives Daten-Resampling implementiert, mit der Möglichkeit, das gewünschte Ergebnis auszuwählen.

Dies war eine Art Durchbruch von naiven Modellen zu aussagekräftigen Modellen. Mit einem Minimum an Aufwand für die Entwicklung einer logischen Komponente einer Handelsstrategie können Sie interessante, auf maschinellem Lernen basierende Handelsroboter erhalten.