Remuestreo avanzado y selección de modelos CatBoost con el método de fuerza bruta

Introducción

En el artículo anterior, intentamos ofrecer una idea intuitiva sobre las principales etapas en la construcción de un modelo de aprendizaje automático, y también implementar este en la producción. En el presente artículo, queremos pasar de modelos ingenuos a modelos estadísticamente significativos. Como la creación de un sistema comercial de aprendizaje automático no es una tarea trivial, analizaremos una serie de mejoras en la preparación de los datos para lograr resultados óptimos. Para mejorar la presentación de los datos iniciales (ejemplos de entrenamiento), usaremos varias técnicas de remuestreo. En este artículo, analizaremos una de ellas.

En el artículo anterior, usamos el muestreo aleatorio simple de etiquetas, que tiene varias desventajas:

• Las clases pueden estar desequilibradas. Supongamos que durante el periodo de formación, el mercado ha crecido en general, mientras que la población total (la historia de cotizaciones al completo) ha acusado altibajos. En este caso, el muestreo ingenuo creará más etiquetas de compra, pero menos etiquetas de venta. En consecuencia, las etiquetas de una clase prevalecerán sobre las etiquetas de la otra, por lo que el modelo aprenderá a predecir las ofertas de compra con más frecuencia que las ofertas de venta, que no serán válidas en los datos nuevos.

• Autocorrelación de las características y etiquetas. Con el muestreo aleatorio, las etiquetas de una misma clase van una tras otra, mientras que las propias características (por ejemplo, los incrementos) cambian de manera poco significativa. Si imaginamos este proceso usando el ejemplo de entrenamiento de un modelo de regresión, observaremos una autocorrelación en los residuos del modelo, lo que provocará una posible valoración excesiva y un sobreentrenamiento del modelo, como se muestra en la siguiente imagen:

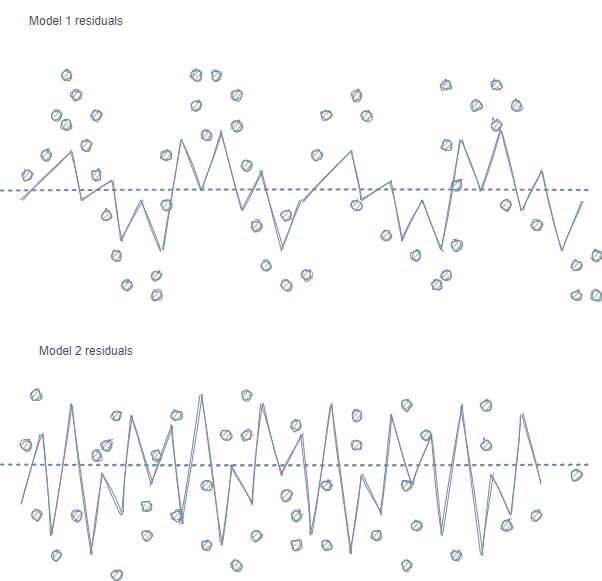
Model 1 tiene autocorrelación de residuos, lo cual se puede comparar con el sobreentrenamiento del modelo con ciertas propiedades del mercado (por ejemplo, las relacionadas con la volatilidad de los datos de entrenamiento), mientras que otros patrones no se consideran. Model 2 tiene residuos con la misma varianza (de promedio), lo cual indica que el modelo ha abarcado más información de la serie temporal o se han encontrado otras dependencias (además de la correlación de muestras colindantes).

El mismo efecto se observa también para la clasificación, aunque resulta menos intuitivo porque solo tiene unas pocas clases, en contraste con la variable continua usada en los modelos de regresión. No obstante, el efecto todavía se puede medir, por ejemplo, usando los residuos de Pearson y métricas similares. Estas dependencias (en el caso de Model 1) deben ser eliminadas.

• Las clases pueden superponerse significativamente. Imagine un espacio de características hipotético en 2D (los espacios multidimensionales son más complejos), cada punto del cual se asigna a la clase 0 o 1. 

Con el muestreo aleatorio, podría surgir (y surge) la situación cuando los conjuntos de ejemplos se cruzan. Esto puede provocar una disminución en la distancia (supongamos, de la distancia euclidiana) entre puntos de diferentes clases y a un aumento en la distancia entre puntos de la misma clase, lo cual provoca la creación de un modelo demasiado complejo en la etapa de entrenamiento, teniendo muchos límites que separan las clases. Las pequeñas desviaciones en las lecturas de las características provocan saltos en las predicciones del modelo de una clase a otra. Este efecto destruye la estabilidad del modelo con nuevos datos y debe ser combatido.

Sería deseable que las etiquetas de clase no se cruzaran en el espacio de características y se separasen, si no linealmente (como se muestra a continuación), al menos de la forma más simple. Esta solución permitiría una mayor estabilidad del modelo con nuevos datos.

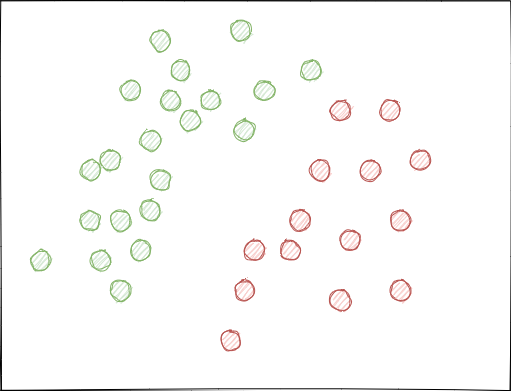
Análisis del conjunto de datos GIGO original

Este artículo usa funciones modificadas y mejoradas del artículo anterior. Vamos a cargar los datos:

LOOK_BACK = 5
MA_PERIODS = [15, 55, 150, 250]

SYMBOL = 'EURUSD'
MARKUP = 0.00010
TIMEFRAME = mt5.TIMEFRAME_H1
START_DATE = datetime(2020, 1, 1)
TSTART_DATE = datetime(2015, 1, 1)
STOP_DATE = datetime(2021, 1, 1)

# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=10, max=25, add_noize=0)
res = tester(pr, plot=True)
pca_plot(pr)

Como la dimensión del conjunto de datos original es de 20 características (loock_back * len(ma_periods)) o cualquier otra considerable, no resulta muy adecuado mostrarlo en un plano. Utilizaremos el método PCA y visualizaremos solo 5 componentes principales, lo cual nos permitirá compactar el espacio de características con la menor pérdida de información posible:

Si no está familiarizado con el PCA (principal component analysis), busque información sobre él en Google.

def pca_plot(data):
    from sklearn.decomposition import PCA
    pca = PCA(n_components = 5)
    components = pd.DataFrame(pca.fit_transform(data[data.columns[1:-1]]))
    components['labels'] = data['labels'].reset_index(drop = True)
    import seaborn as sns
    g = sns.PairGrid(components, hue="labels", height=1.2)
    g.map_diag(sns.histplot)
    g.map_offdiag(sns.scatterplot)
    g.add_legend()
    plt.show()

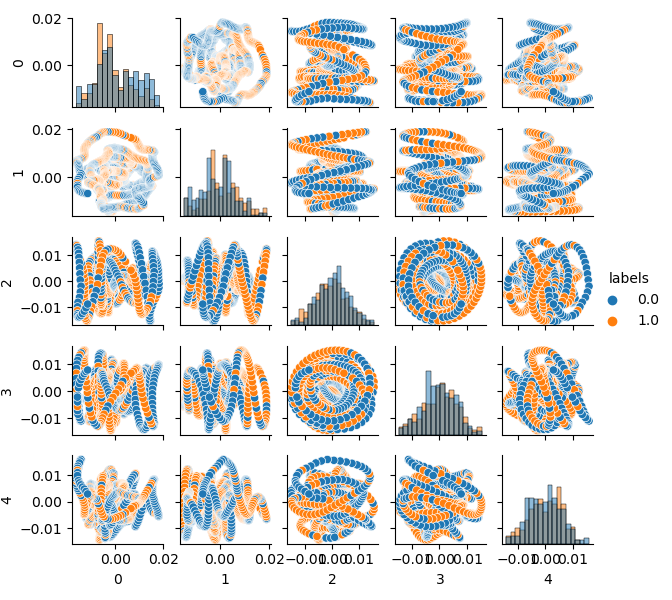
Ahora podemos ver la dependencia de cada componente respecto al otro, es decir, un espacio de características en 2D, etiquetado con las clases 0 y 1. Los pares de componentes forman bucles, a diferencia de la nube de puntos habitual. Esto se debe a la considerable autocorrelación de puntos, y si estrechamos la fila, los anillos desaparecerán. No obstante, también nos interesa que las clases se superpongan intensamente. El clasificador tendrá que crear un modelo muy complejo, con muchos límites divisorios, para poder clasificar las etiquetas con el menor error posible. Podemos afirmar con seguridad que el conjunto de datos original es simplemente basura y, como el lector ya sabrá, garbage in — garbage out (GIGO). Para no seguir la filosofía GIGO y hacer que la investigación sea más significativa, le sugerimos pensar un poco en la mejora de la presentación de los datos de entrada para un modelo de aprendizaje automático (por ejemplo, CatBoost)

El espacio de características ideal

Para dividir eficazmente el espacio de características en dos clases, podemos realizar una clusterización, por ejemplo, usando el método K-means. Esto nos dará una idea sobre cómo dividir el espacio de características de una forma ideal.

Vamos clusterizar el conjunto de datos de origen en dos grupos y a mostrar los cinco componentes principales:

# perform K-means clasterizatin over dataset
from sklearn.cluster import KMeans
pr = get_prices(look_back=LOOK_BACK)
X = pr[pr.columns[1:]]
kmeans = KMeans(n_clusters=2).fit(X)
y_kmeans = kmeans.predict(X)
pr['labels'] = y_kmeans
pca_plot(pr)

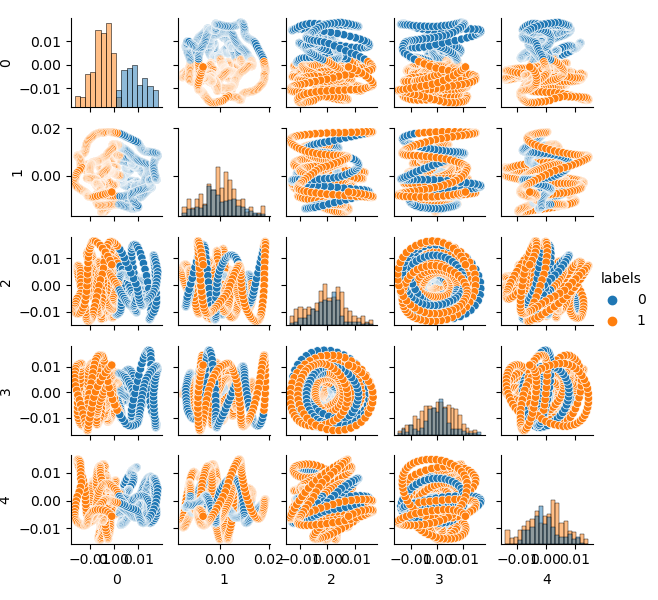
El espacio de características parece ideal, pero las etiquetas de clase (0, 1) obviamente no se corresponden con las transacciones rentables. Este ejemplo solo ilustra un espacio de características que resulta más preferible que el conjunto de datos GIGO. Por eso necesitamos crear un compromiso entre datos ideales y basura. Esto es lo que haremos a continuación.

Modelo generativo para el remuestreo de los ejemplos de entrenamiento

"Lo que no se puede crear, no se entiende".

—Richard Feynman

En este apartado, analizaremos un modelo que aprende a "comprender" los datos y recrear otros nuevos.

El método de clusterización de k-medias (k-means) es relativamente simple y fácil de entender. No obstante, posee una serie de desventajas y no resulta adecuado para nuestro caso. En particular, tiene un rendimiento deficiente en muchos casos del mundo real, porque no es probabilístico. Imaginemos que este método coloca círculos (o hiperesferas) alrededor de un número determinado de centroides con un radio que está determinado por el punto más externo del cúmulo. Este radio limita estrictamente el conjunto de puntos para cada grupo. De esta forma, todos los clústers solo podrán describirse mediante círculos e hiperesferas, mientras que los clústeres reales no siempre cumplen con este criterio (ya que pueden ser oblongos o en forma de elipses). Esto provocará la superposición de diferentes valores de los clústeres.

Un algoritmo más avanzado es el modelo de mezcla gaussiana (Gaussian mixture model). Este modelo busca la mezcla de distribuciones de probabilidad gaussianas de dimensión múltiple que mejor modele el conjunto de datos. Como el modelo es probabilístico, en la salida obtendremos las probabilidades de asignación de un ejemplo a un grupo en particular. Asimismo, cada grupo se asocia no con una esfera rígidamente definida, sino con un modelo gaussiano suave que puede representarse no solo como círculos, sino también como elipses orientadas arbitrariamente en el espacio.

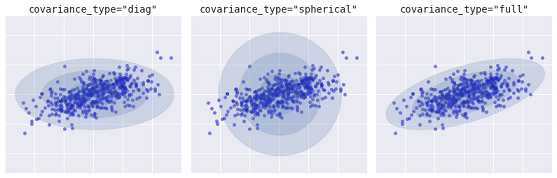
Diferentes tipos de modelos probabilísticos, dependiendo de covaiance_type

A continuación, mostramos una comparación de los clústeres obtenidos con los métodos de k-means y GMM (fuente):

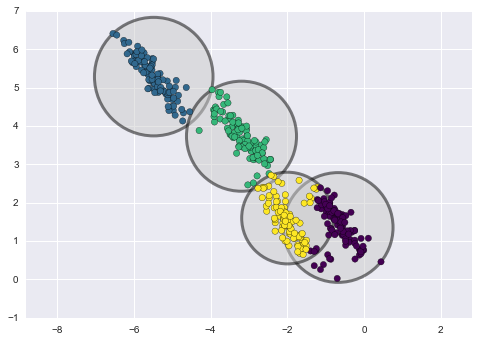
Clusterización con el método K-means

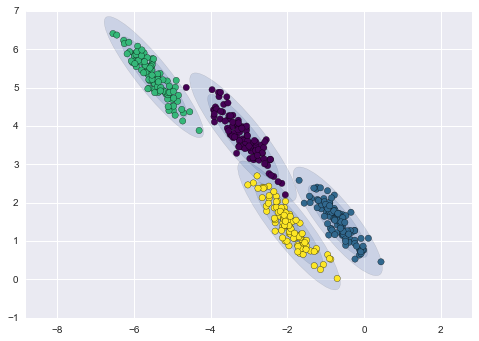
Clusterización con el método GMM

En esencia, el algoritmo del modelo de mezcla gaussiana (GMM) no es realmente un clusterizador, porque su principal tarea consiste en valorar la densidad de probabilidad. Los clústeres en este modelo se representan como datos generados a partir de distribuciones de probabilidad que describen estos datos. Por consiguiente, tras estimar la densidad de probabilidad de cada clúster, podemos generar nuevos conjuntos de datos a partir de estas distribuciones. Estos conjuntos serán plausibles, es decir, similares a los datos originales, pero tendrán más o menos variabilidad y serán menos propensos a los valores atípicos. Asimismo, en muchos casos estarán menos correlacionados. Podemos obtener más o menos ejemplos de forma aleatoria y luego entrenar el clasificador CatBoost con ellos. 

Pipeline para el remuestreo iterativo del conjunto de datos original y el entrenamiento del modelo CatBoost

En primer lugar, debemos clusterizar los datos de origen, incluidas las etiquetas de clase:

# perform GMM clasterizatin over dataset
from sklearn import mixture
pr_c = pr.copy()
X = pr_c[pr_c.columns[1:]]
gmm = mixture.GaussianMixture(n_components=75, covariance_type='full').fit(X)

El principal parámetro que podemos seleccionar es n_components, que se estableció empíricamente en 75 (grupos). Los otros parámetros no son tan importantes y no se tienen en cuenta aquí. Una vez entrenado el modelo, podemos generar algunas muestras artificiales a partir de la distribución de dimensión múltiple del modelo GMM y visualizar varios componentes principales:

# plot resampled components
generated = gmm.sample(5000)
gen = pd.DataFrame(generated[0])
gen.rename(columns={ gen.columns[-1]: "labels" }, inplace = True)
gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
gen.loc[gen['labels'] < 0.5, 'labels'] = 0
pca_plot(gen)

Debemos señalar que, como no solo las características, sino también las etiquetas han sido clusterizadas, estas últimas ahora no representan una serie binarizada. En el listado anterior, las etiquetas se vuelven a convertir a valores (0;1). Ahora podemos mostrar el espacio de características resultante utilizando la función pca_plot():

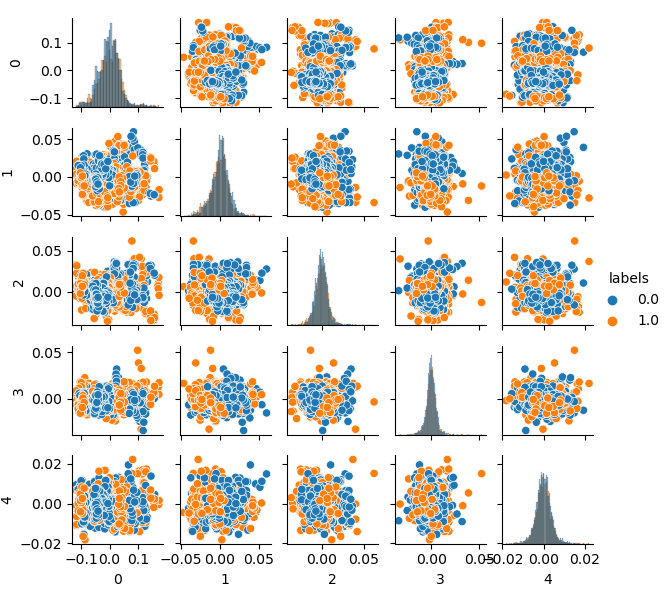
Si comparamos este diagrama con el diagrama del conjunto de datos GIGO mostrado anteriormente, podemos ver que carece de bucles de datos. Las características y las etiquetas ahora están menos correlacionadas, lo que debería tener un efecto positivo en el resultado del aprendizaje. Al mismo tiempo, las etiquetas a veces tienden a formar clústeres más densos y el modelo puede resultar más simple, con menos límites divisorios. En parte, hemos logrado el efecto necesario eliminando los problemas derivados de los datos basura. No obstante, los datos son esencialmente los mismos. Simplemente hemos realizado el remuestreo de los datos originales.

Siempre que GMM genere muestras aleatoriamente, esto redundará en el pluralismo de los datos. El mejor modelo se puede seleccionar usando la fuerza bruta. Especialmente para ello, hemos escrito una función de fuerza bruta:

# brute force loop
def brute_force(samples = 5000):
    # sample new dataset
    generated = gmm.sample(samples)
    # make labels 
    gen = pd.DataFrame(generated[0])
    gen.rename(columns={ gen.columns[-1]: "labels" }, inplace = True)
    gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
    gen.loc[gen['labels'] < 0.5, 'labels'] = 0
    X = gen[gen.columns[:-1]]
    y = gen[gen.columns[-1]]
    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(X, y, train_size = 0.5, test_size = 0.5, shuffle=True)
    #learn with train and validation subsets
    model = CatBoostClassifier(iterations=500,
                            depth=6,
                            learning_rate=0.1,
                            custom_loss=['Accuracy'],
                            eval_metric='Accuracy',       
                            verbose=False, 
                            use_best_model=True,
                            task_type='CPU')
    model.fit(train_X, train_y, eval_set = (test_X, test_y), early_stopping_rounds=25, plot=False)
    # test on new data
    pr_tst = get_prices(TSTART_DATE, START_DATE)
    X = pr_tst[pr_tst.columns[1:]]
    X.columns = [''] * len(X.columns)

    #test the learned model
    p = model.predict_proba(X)
    p2 = [x[0]<0.5 for x in p]
    pr2 = pr_tst.iloc[:len(p2)].copy()
    pr2['labels'] = p2
    R2 = tester(pr2, MARKUP, plot=False)

    return [R2, samples, model]

Hemos destacado los principales puntos a los que merece la pena prestar atención. Primero, generamos ejemplos n-aleatorios a partir de la distribución del modelo GMM. A continuación, entrenamos el modelo CatBoost con estos datos. La función retorna la valoración R^2 calculada en el simulador. Tenga en cuenta que el modelo se pone a prueba no solo con los datos del periodo de entrenamiento, sino también con los datos anteriores. Por ejemplo, el modelo se ha entrenado con datos desde principios de 2020, mientras que las pruebas se han realizado desde principios de 2015. Podrá cambiar los intervalos de fechas a su gusto.

Escribamos un ciclo que llame varias veces a la función especificada y guarde en una lista los resultados de cada pasada:

res = []
for i in range(50):  
    res.append(brute_force(10000))
    print('Iteration: ', i, 'R^2: ', res[-1][0])


res.sort()
test_model(res[-1])

Después de ello, la lista es clasificada, y el modelo que se encuentra al final de la lista tendrá la mejor valoración R^2. Mostramos el mejor resultado:

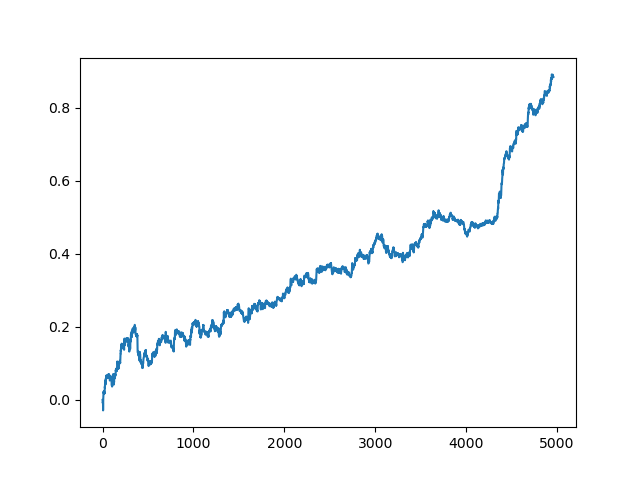
La última parte (la derecha) del gráfico (aproximadamente 1000 transacciones) es el conjunto de datos de entrenamiento de principios de 2020, mientras que el resto son los datos nuevos que no han estado implicados en el entrenamiento del modelo de ninguna manera. Como los modelos se ordenan de forma ascendente según la métrica R^2, podemos poner a prueba los anteriores modelos con una puntuación más baja:

test_model(res[-2])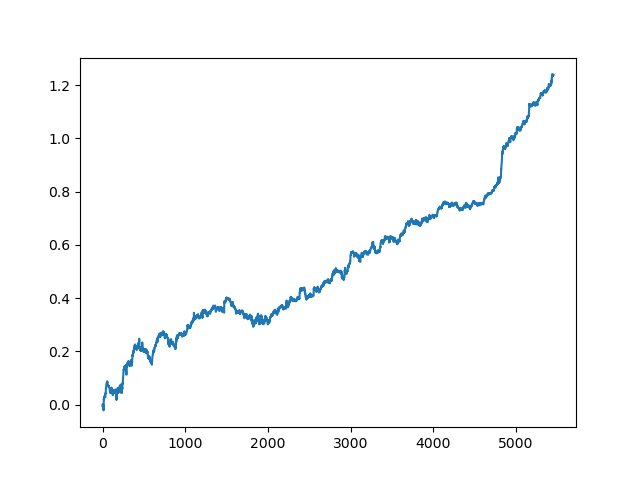

Asimismo, podemos mirar la propia valoración de R^2:

>>> res[-2][0]
0.9576444017048906

Como ve, ahora el modelo se pone a prueba con un periodo largo de cinco años, aunque se ha entrenado con un periodo de un año. Luego, el modelo se puede exportar a formato MQH. El propio objeto del modelo CatBoost se encuentra en la lista anidada con el índice 2, mientras que la primera dimensión contiene los números de los modelos. Aquí exportamos el modelo con el índice [-2] (el segundo desde el final de la lista ordenada):

# export best model to mql
export_model_to_MQL_code(res[-2][2])

Después de ser exportado, el modelo se puede poner a prueba en el simulador de estrategias estándar de MetaTrader 5. Como el spread en el simulador personalizado era inferior al real, las curvas resultan ligeramente distintas. No obstante, su forma general es la misma.

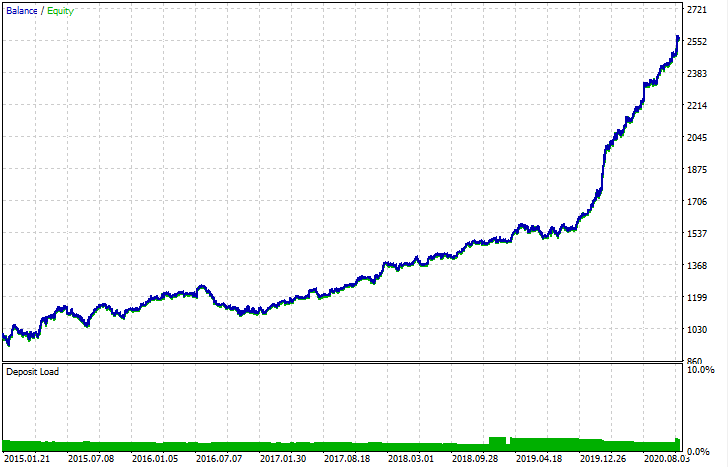
¿Cómo podemos mejorar los modelos?

Debemos entender que, al entrenar modelos, existen muchos componentes aleatorios que cambian de vez en cuando. Por ejemplo, el muestreo aleatorio de transacciones, después el entrenamiento de GMM (que también tiene un elemento de aleatoriedad), luego el muestreo aleatorio de la distribución posterior del modelo de GMM, y más tarde el entrenamiento de CatBoost, que también contiene un elemento de aleatoriedad. Por consiguiente, podemos reiniciar el programa completo varias veces para obtener el mejor resultado. Al mismo tiempo, si no podemos obtener un modelo estable, deberemos jugar con el parámetro LOOK_BACK y el número de medias móviles y sus periodos. Tiene sentido cambiar el número de muestras obtenidas del modelo GMM, y también modificar el intervalo temporal del entrenamiento y la prueba. 

Log de cambios y refactorización del código

Hemos introducido algunos cambios en el código Python del programa que requieren aclaración.

Ahora, podemos definir una lista de medias móviles con diferentes periodos de promediación. La práctica ha demostrado que la combinación de varias MA tiene un efecto positivo en el resultado del aprendizaje.

MA_PERIODS = [15, 55, 150, 250]

Hemos añadido una fecha de inicio ajustable para el proceso de prueba, la evaluación y la selección del modelo.

TSTART_DATE = datetime(2015, 1, 1)

La función de muestreo aleatorio ha sufrido una serie de cambios. Hemos añadido el parámetro add_noize, que nos permite añadir ruido al conjunto de datos original. Esto hará que el comercio resulte menos ideal al añadir reducciones y mezclar transacciones. A veces, un modelo se puede mejorar con nuevos datos introduciendo un error en el nivel de 0.1 - 02. 

Asimismo, ahora se considera el spread. Las transacciones que no cubren el spread se marcan con una etiqueta de 2.0 y luego son eliminadas del conjunto de datos, porque ya no resultan informativas.

def add_labels(dataset, min, max, add_noize = 0.1):
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'][i]
        future_pr = dataset['close'][i + rand]

        if future_pr + MARKUP < curr_pr:
            labels.append(1.0)
        elif future_pr - MARKUP > curr_pr:
            labels.append(0.0)              
        else:
            labels.append(2.0)
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(dataset[dataset.labels == 2].index).reset_index(drop=True)

    if add_noize==0:
        return dataset

    # add noize to samples
    noize_b = dataset[dataset.labels == 0]['labels'].sample(frac = add_noize)
    noize_s = dataset[dataset.labels == 1]['labels'].sample(frac = add_noize)
    noize_b = noize_b+1
    noize_s = noize_s-1
    dataset.update(noize_b)
    dataset.update(noize_s)
    return dataset

La función de prueba ahora retorna una valoración R^2:

def tester(dataset, markup = 0.0, plot = False):
    last_deal = int(2)
    last_price = 0.0
    report = [0.0]
    for i in range(dataset.shape[0]):
        pred = dataset['labels'][i]
        if last_deal == 2:
            last_price = dataset['close'][i]
            last_deal = 0 if pred <= 0.5 else 1
            continue
        if last_deal == 0 and pred > 0.5:
            last_deal = 1
            report.append(report[-1] - markup + (dataset['close'][i] - last_price))
            last_price = dataset['close'][i]
            continue
        if last_deal == 1 and pred < 0.5:
            last_deal = 0
            report.append(report[-1] - markup + (last_price - dataset['close'][i]))
            last_price = dataset['close'][i]      

    y = np.array(report).reshape(-1,1)
    X = np.arange(len(report)).reshape(-1,1)
    lr = LinearRegression()
    lr.fit(X,y)

    l = lr.coef_
    if l >= 0:
        l = 1
    else:
        l = -1

    if(plot):
        plt.plot(report)
        plt.show()

    return lr.score(X,y) * l

Hemos añadido una función auxiliar para visualizar los datos a través del método de componentes principales. En algunos casos, esto nos permite comprender mejor nuestros datos.

def pca_plot(data):
    from sklearn.decomposition import PCA
    pca = PCA(n_components = 5)
    components = pd.DataFrame(pca.fit_transform(data[data.columns[1:-1]]))
    components['labels'] = data['labels'].reset_index(drop = True)
    import seaborn as sns
    g = sns.PairGrid(components, hue="labels", height=1.2)
    g.map_diag(sns.histplot)
    g.map_offdiag(sns.scatterplot)
    g.add_legend()
    plt.show()

Hemos añadido un parser de código. Ahora se tienen en cuenta todos los periodos de la media móvil; estos se añaden al programa MQL, y después la función especial fill_arrays forma un vector de características.

def export_model_to_MQL_code(model):
    model.save_model('catmodel.h',
           format="cpp",
           export_parameters=None,
           pool=None)

    # add variables
    code = 'int ' + 'loock_back = ' + str(LOOK_BACK) + ';\n'
    code += 'int hnd[];\n'
    code += 'int OnInit() {\n'
    code +=     'ArrayResize(hnd,' + str(len(MA_PERIODS)) + ');\n'

    count = len(MA_PERIODS) - 1
    for i in MA_PERIODS:
        code +=     'hnd[' + str(count) + ']' + ' =' + ' iMA(NULL,PERIOD_CURRENT,' + str(i) + ',0,MODE_SMA,PRICE_CLOSE);\n'
        count -= 1

    code += 'return(INIT_SUCCEEDED);\n'
    code += '}\n\n'

    # get features
    code += 'void fill_arays(int look_back, double &features[]) {\n'
    code += '   double ma[], pr[], ret[];\n'
    code += '   ArrayResize(ret,' + str(LOOK_BACK) +');\n'
    code += '   CopyClose(NULL,PERIOD_CURRENT,1,look_back,pr);\n'
    code += '   for(int i=0;i<' + str(len(MA_PERIODS)) +';i++) {\n'
    code += '       CopyBuffer(hnd[' + 'i' + '], 0, 1, look_back, ma);\n'
    code += '       for(int f=0;f<' + str(LOOK_BACK) +';f++)\n'
    code += '           ret[f] = pr[f] - ma[f];\n'
    code += '       ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
    code += '   ArraySetAsSeries(features, true);\n'
    code += '}\n\n'

Conclusión

En el presente artículo, hemos mostrado un ejemplo de uso de un modelo generativo simple de GMM (modelo de mezcla gaussiana) para remuestrear el conjunto de datos original. También hemos mostrado que es posible mejorar el rendimiento del clasificador CatBoost con nuevos datos mejorando las propiedades del espacio de características. Para seleccionar el mejor modelo, hemos implementado el remuestreo iterativo del conjunto de datos, con la posibilidad de seleccionar posteriormente el resultado deseado.

Asimismo, hemos logrado implementar una especie de avance desde los modelos ingenuos hacia modelos significativos. Invirtiendo un mínimo de esfuerzo en desarrollar algún tipo de componente lógico de una estrategia comercial, podemos obtener bots interesantes basados ​​en el aprendizaje de máquinas.