
Reamostragem avançada e seleção de modelos CatBoost pelo método de força bruta
Introdução
No artigo anterior, eu tentei fornecer uma ideia geral sobre as principais etapas de criação do modelo de aprendizado de máquina e sua implementação em produção. Nesta parte, eu quero mudar dos modelos ingênuos para os modelos estatisticamente significativos. Uma vez que a criação de um sistema de negociação baseado em aprendizado de máquina não é uma tarefa trivial, nós começaremos com algumas melhorias na preparação dos dados que ajudarão a alcançar resultados ideais. Várias técnicas de reamostragem podem ser usadas para melhorar a apresentação dos dados de origem (exemplos de treinamento). Uma dessas técnicas será discutida neste artigo.
A amostra aleatória simples de rótulos usada no artigo anterior tem algumas desvantagens:
- As classes podem estar desbalanceadas. Suponha que o mercado foi de alta durante o período de treinamento, enquanto a população em geral (todo o histórico de cotações) foi de alta e baixa. Nesse caso, a amostragem ingênua criará mais rótulos de compra e menos rótulos de venda. Consequentemente, os rótulos de uma classe prevalecerão sobre a outra, pois o modelo aprenderá a prever negócios de compra com mais frequência do que negócios de venda, que não serão válidos para os novos dados.
- Autocorrelação das características e rótulos. Se a amostragem aleatória for usada, os rótulos da mesma classe seguem uns aos outros, enquanto as próprias características (como por exemplo, incrementos) mudam insignificantemente. Esse processo pode ser mostrado usando um exemplo de treinamento de um modelo de regressão - neste caso, observamos uma autocorrelação nos resíduos do modelo, o que levará a uma possível superestimação e o overfitting do modelo. Essa situação é mostrada a seguir:
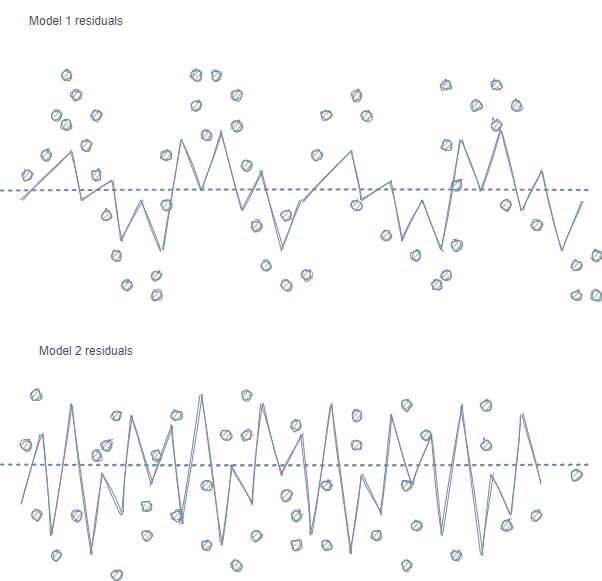
O modelo 1 tem autocorrelação de resíduos, que pode ser comparado ao overfitting do modelo em certas propriedades de mercado (por exemplo, relacionado à volatilidade dos dados de treinamento), enquanto outros padrões não são levados em consideração. O modelo 2 possui resíduos com a mesma variância (em média), o que indica que o modelo cobriu mais informações ou foram encontradas outras dependências (além da correlação de amostras vizinhas).
O mesmo efeito também é observado para a classificação, embora seja menos intuitiva por possuir poucas classes, ao contrário de uma variável contínua usada em modelos de regressão. No entanto, o efeito ainda pode ser medido, por exemplo, usando os resíduos de Pearson e métricas semelhantes. Essas dependências (como no modelo 1) devem ser eliminados.
- As classes podem se sobrepor significativamente. Imagine um espaço hipotético de características em 2D (espaços multidimensionais são mais complexos), cada ponto é atribuído à classe 0 ou 1.

Ao usar a amostragem aleatória, os conjuntos de exemplos podem se cruzar. Isso pode levar a uma diminuição da distância (digamos, distância euclidiana) entre os pontos de diferentes classes e a um aumento na distância entre os pontos de uma mesma classe, o que leva à criação de um modelo excessivamente complexo na fase de treinamento, tendo muitas fronteiras separando as classes. Pequenos desvios nas características causam saltos nas previsões do modelo de classe para classe. Este efeito destrói a estabilidade do modelo em novos dados e deve ser eliminado.
Idealmente, os rótulos de classe não devem se cruzar no espaço de características e devem ser separados linearmente (como mostrado abaixo) ou por qualquer outro método simples. Essa solução proporcionaria maior estabilidade do modelo em novos dados.
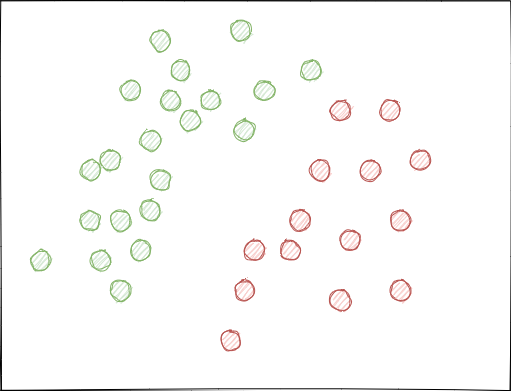
Análise do conjunto de dados GIGO original
As funções modificadas e aprimoradas da parte anterior são usadas neste artigo. Carregamos os dados:
LOOK_BACK = 5 MA_PERIODS = [15, 55, 150, 250] SYMBOL = 'EURUSD' MARKUP = 0.00010 TIMEFRAME = mt5.TIMEFRAME_H1 START_DATE = datetime(2020, 1, 1) TSTART_DATE = datetime(2015, 1, 1) STOP_DATE = datetime(2021, 1, 1) # make dataset pr = get_prices(START_DATE, STOP_DATE) pr = add_labels(pr, min=10, max=25, add_noize=0) res = tester(pr, plot=True) pca_plot(pr)
Como a dimensão do conjunto de dados original é de 20 características (loock_back * len (ma_periods)) ou qualquer outra considerável, não é muito adequado exibi-lo em um plano. Vamos usar o método PCA e exibir apenas 5 componentes principais, o que permitirá compactar o espaço do recurso com o mínimo de perda de informação:
Se você não está familiarizado com a PCA (Análise de Componentes Principais), por favor, pesquise no Google.
def pca_plot(data): from sklearn.decomposition import PCA pca = PCA(n_components = 5) components = pd.DataFrame(pca.fit_transform(data[data.columns[1:-1]])) components['labels'] = data['labels'].reset_index(drop = True) import seaborn as sns g = sns.PairGrid(components, hue="labels", height=1.2) g.map_diag(sns.histplot) g.map_offdiag(sns.scatterplot) g.add_legend() plt.show()
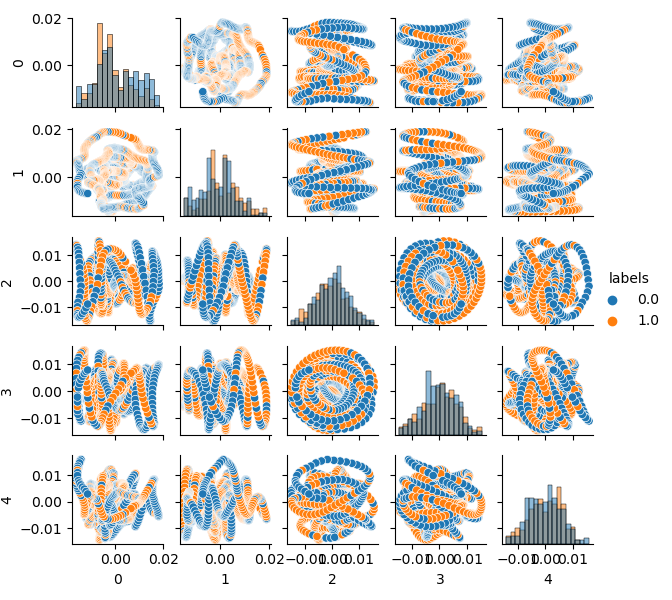
Agora você pode ver a dependência de cada componente em relação ao outro: este é o espaço de características 2D, rotulado nas classes 0 e 1. Os pares de componentes formam loops, que não são semelhantes à nuvem de pontos usual. Isso é causado pela autocorrelação de pontos. Os anéis irão desaparecer se você diminuir a linha. Outro fato é que as classes se sobrepõem fortemente. Para classificar os rótulos com o mínimo de erro, o classificador terá que criar um modelo muito complexo, com muitos cortes no espaço. Nós podemos dizer que o conjunto de dados original é apenas lixo e, como o leitor já sabe, Garbage in — Garbage out (GIGO). Para evitar a filosofia GIGO e tornar a pesquisa mais significativa, sugiro melhorar a representação dos dados originais para um modelo de aprendizado de máquina (por exemplo, CatBoost)
Espaço de características ideais
Para dividir efetivamente o espaço de características em duas classes, nós podemos implementar o agrupamento por clustering, por exemplo, usando o método K-means. Isso dará uma ideia de como o espaço de características pode ser dividido de maneira ideal.
O conjunto de dados de origem é agrupado em dois clusters; cinco componentes principais são exibidos:
# perform K-means clustering over dataset from sklearn.cluster import KMeans pr = get_prices(look_back=LOOK_BACK) X = pr[pr.columns[1:]] kmeans = KMeans(n_clusters=2).fit(X) y_kmeans = kmeans.predict(X) pr['labels'] = y_kmeans pca_plot(pr)
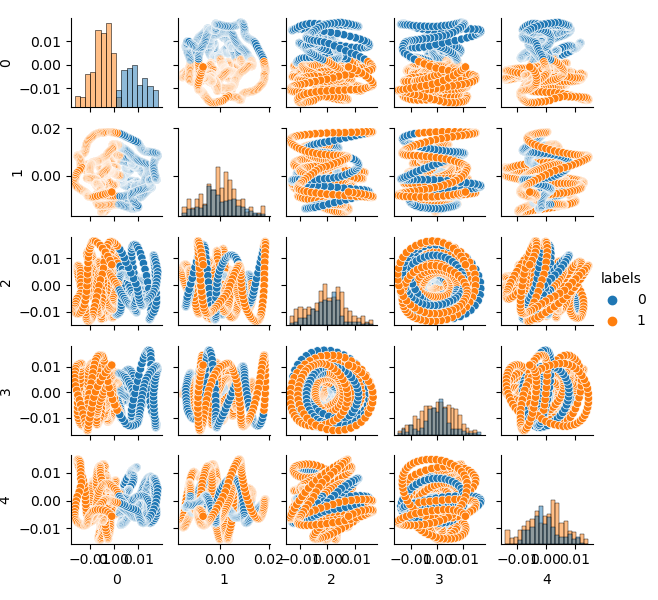
O espaço de características parece ideal, mas os rótulos de classe (0, 1) obviamente não correspondem a negociações lucrativas. Este exemplo apenas ilustra um espaço de características preferível em relação ao conjunto de dados GIGO. É por isso que nós precisamos criar um meio-termo entre os dados ideais e o lixo. Isso é o que nós vamos fazer a seguir.
Um modelo gerador para a reamostragem de exemplos de treinamento
“O que eu não consigo criar, eu não entendo.”
—Richard Feynman
Nesta seção, nós consideraremos um modelo que aprende a "entender" os dados e a recriar outros novos.
O método de agrupamento k-means é relativamente simples e fácil de entender. No entanto, ele tem várias desvantagens e não é adequado para o nosso caso. Em particular, ele tem um desempenho ruim em muitos casos do mundo real porque ele não é probabilístico. Imagine que esse método coloque círculos (ou hiperesferas) em torno de um determinado número de centroides com um raio que é determinado pelo ponto mais externo do aglomerado. Este raio limita estritamente o conjunto de pontos para cada cluster. Assim, todos os aglomerados só podem ser descritos por círculos e hiperesferas, enquanto os aglomerados reais nem sempre satisfazem este critério (visto que podem ser oblongos ou em forma de elipses). Isso causará a sobreposição de diferentes valores do cluster.
Um algoritmo mais avançado é o Modelo de Mistura Gaussiana. Este modelo procura uma mistura de distribuições multivariadas de probabilidade gaussiana que melhor modela o conjunto de dados. Como o modelo é probabilístico, isso gera as probabilidades de um exemplo ser categorizado como um cluster específico. Além disso, cada cluster está associado não a uma esfera estritamente definida, mas a um modelo gaussiano suave, que pode ser representado não apenas como círculos, mas também como elipses arbitrariamente orientadas no espaço.
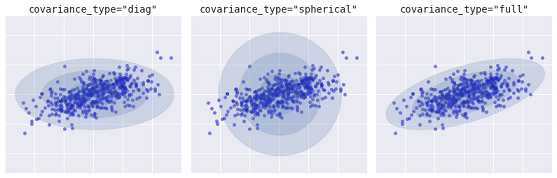
Diferentes tipos de modelos probabilísticos, dependendo do covaiance_type
Abaixo está uma comparação dos clusters obtidos pelo k-means e GMM (fonte):
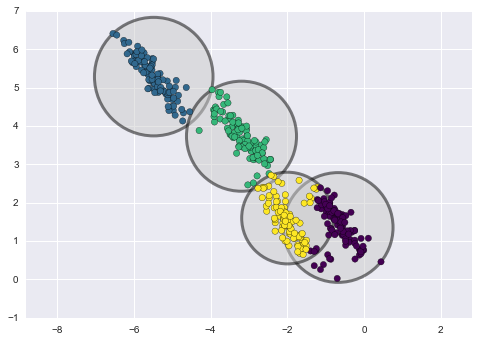
Agrupamento K-means
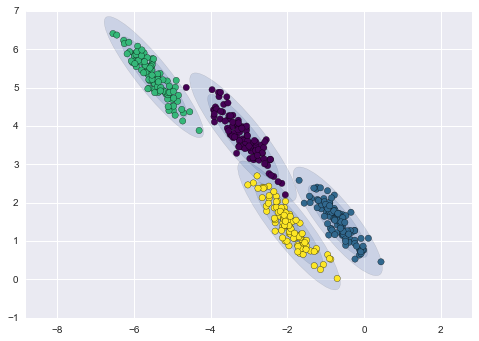
Agrupamento GMM
Na verdade, o algoritmo Gaussian Mixture Model (GMM) não é realmente um clusterizador, pois sua principal tarefa é estimar a densidade de probabilidade. Os clusters neste modelo são representados como dados gerados a partir de distribuições de probabilidade que descrevem esses dados. Assim, após estimar a densidade de probabilidade de cada cluster, novos conjuntos de dados podem ser gerados a partir dessas distribuições. Esses conjuntos serão semelhantes aos dados originais, mas têm mais ou menos variabilidade e menos outliers. Além disso, os conjuntos de dados, em muitos casos, serão menos correlacionados. Nós podemos obter exemplos aleatórios e, em seguida, treinar o classificador CatBoost usando esses exemplos.
Pipeline para reamostragem iterativa do conjunto de dados original e o treinamento do modelo CatBoost
Em primeiro lugar, é necessário agrupar os dados de origem, incluindo os rótulos de classe:
# perform GMM clustering over dataset from sklearn import mixture pr_c = pr.copy() X = pr_c[pr_c.columns[1:]] gmm = mixture.GaussianMixture(n_components=75, covariance_type='full').fit(X)
O principal parâmetro que pode ser selecionado é o n_components. Ele foi empiricamente definido para 75 (clusters). Outros parâmetros não são tão importantes e não são considerados aqui. Depois que o modelo é treinado, nós podemos gerar algumas amostras artificiais a partir da distribuição multivariada do modelo GMM e visualizar os vários componentes principais:
# plot resampled components
generated = gmm.sample(5000)
gen = pd.DataFrame(generated[0])
gen.rename(columns={ gen.columns[-1]: "labels" }, inplace = True)
gen.loc[gen['labels'] >= 0.5, 'labels'] = 1
gen.loc[gen['labels'] < 0.5, 'labels'] = 0
pca_plot(gen)
Observe que os rótulos também foram agrupados e, portanto, não representam mais uma série binária. Os rótulos são novamente convertidos em valores (0;1) no código acima. Agora, o espaço de características resultante pode ser exibido, usando a função pca_plot():
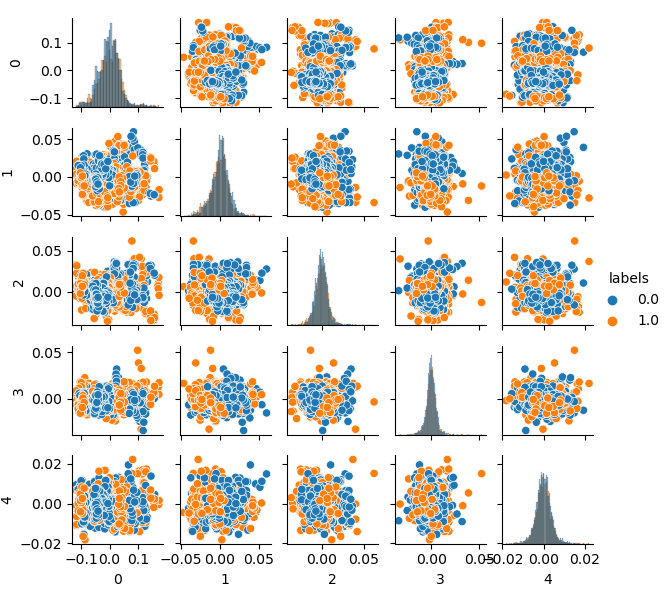
Se você comparar este diagrama com o diagrama do conjunto de dados GIGO apresentado anteriormente, poderá ver que ele não possui loops de dados. Características e rótulos tornaram-se menos correlacionados, o que deve ter um efeito positivo no resultado do aprendizado. Ao mesmo tempo, os rótulos às vezes tendem a formar clusters mais densos e o modelo pode acabar sendo mais simples, com menos cortes. Nós conseguimos parcialmente o efeito desejado ao eliminar os problemas com os dados inúteis. No entanto, os dados são essencialmente os mesmos. Nós simplesmente reamostramos os dados originais.
Desde que o GMM gere amostras aleatoriamente, isso leva ao pluralismo de dados. O melhor modelo pode ser selecionado usando força bruta. Uma função de força bruta especial foi escrita para este propósito:
# brute force loop def brute_force(samples = 5000): # sample new dataset generated = gmm.sample(samples) # make labels gen = pd.DataFrame(generated[0]) gen.rename(columns={ gen.columns[-1]: "labels" }, inplace = True) gen.loc[gen['labels'] >= 0.5, 'labels'] = 1 gen.loc[gen['labels'] < 0.5, 'labels'] = 0 X = gen[gen.columns[:-1]] y = gen[gen.columns[-1]] # train\test split train_X, test_X, train_y, test_y = train_test_split(X, y, train_size = 0.5, test_size = 0.5, shuffle=True) #learn with train and validation subsets model = CatBoostClassifier(iterations=500, depth=6, learning_rate=0.1, custom_loss=['Accuracy'], eval_metric='Accuracy', verbose=False, use_best_model=True, task_type='CPU') model.fit(train_X, train_y, eval_set = (test_X, test_y), early_stopping_rounds=25, plot=False) # test on new data pr_tst = get_prices(TSTART_DATE, START_DATE) X = pr_tst[pr_tst.columns[1:]] X.columns = [''] * len(X.columns) #test the learned model p = model.predict_proba(X) p2 = [x[0]<0.5 for x in p] pr2 = pr_tst.iloc[:len(p2)].copy() pr2['labels'] = p2 R2 = tester(pr2, MARKUP, plot=False) return [R2, samples, model]
Eu destaquei os pontos principais do código. Primeiro, ele gerou n exemplos aleatórios da distribuição GMM. Em seguida, o modelo CatBoost é treinado usando esses dados. A função retorna a pontuação R^2 calculada no testador. Observe que o modelo não é testado apenas com os dados do período de treinamento, mas também com os dados anteriores. Por exemplo, o modelo foi treinado em dados desde o início de 2020 e foi testado usando os dados desde o início de 2015. Você pode alterar os intervalos de datas como quiser.
Vamos escrever um loop que chamará a função especificada várias vezes e salvará os resultados de cada passagem em uma lista:
res = []
for i in range(50):
res.append(brute_force(10000))
print('Iteration: ', i, 'R^2: ', res[-1][0])
res.sort()
test_model(res[-1])
Em seguida, a lista é classificada e o modelo no final da lista tem a melhor pontuação R^2. Deixe-nos mostrar o melhor resultado:
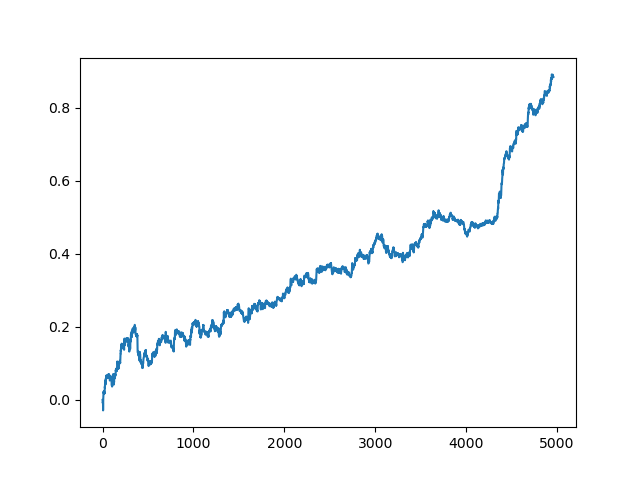
A última parte (direita) do gráfico (cerca de 1000 negócios) é um conjunto de dados de treinamento, do início de 2020, enquanto o restante usa novos dados que não foram usados no treinamento do modelo. Como os modelos são classificados em ordem crescente, de acordo com a métrica R^2, nós podemos testar os modelos anteriores com uma pontuação mais baixa:
test_model(res[-2]) 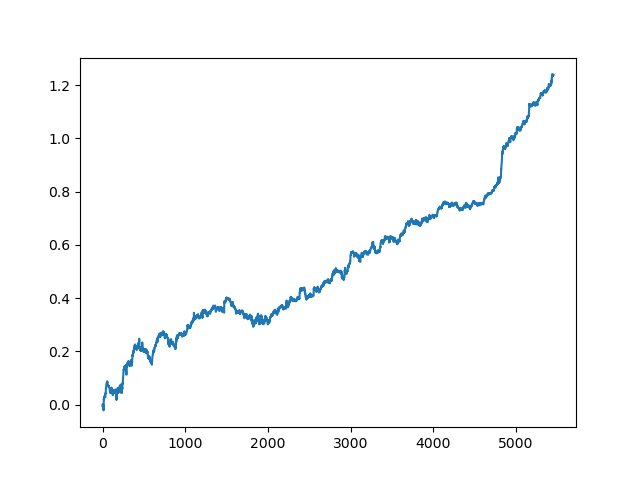
Você também pode observar a pontuação do R^2:
>>> res[-2][0] 0.9576444017048906
Como você pode ver, agora o modelo é testado em um longo período de cinco anos, embora tenha sido treinado em um período de um ano. Em seguida, o modelo pode ser exportado para o formato MQH. O objeto do modelo CatBoost está localizado na lista aninhada, com índice 2 - a primeira dimensão contém os números do modelo. Aqui, nós exportamos o modelo com o índice [-2] (o segundo do final da lista classificada):
# export best model to mql export_model_to_MQL_code(res[-2][2])
Após a exportação, o modelo pode ser testado no Testador de Estratégia padrão da MetaTrader 5. Como o spread no testador personalizado era menor do que o real, as curvas são ligeiramente diferentes. No entanto, sua forma geral é a mesma.
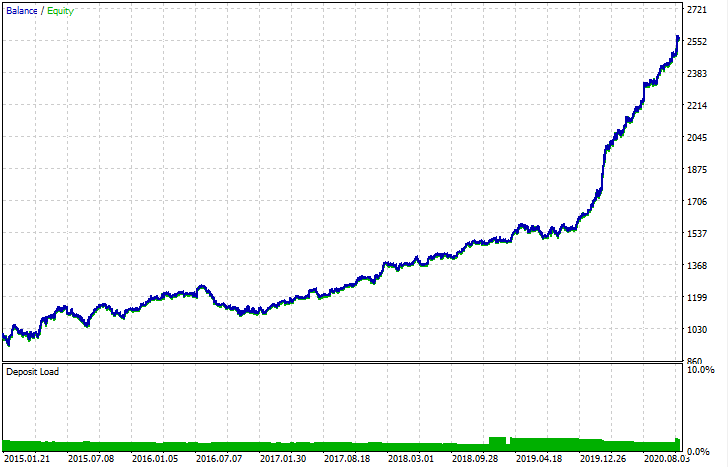
Como os modelos podem ser aprimorados?
O treinamento do modelo implica em muitos componentes aleatórios que são sempre diferentes. Por exemplo, a amostragem aleatória dos negócios, o treinamento GMM (que também tem um elemento de aleatoriedade), a amostragem aleatória da distribuição GMM posterior e o treinamento CatBoost que também contém um elemento de aleatoriedade. Portanto, todo o programa pode ser reiniciado várias vezes para obter o melhor resultado. Se um modelo estável não puder ser obtido, você deve ajustar o parâmetro LOOK_BACK e o número de médias móveis e seus períodos. Você também pode alterar o número de amostras recebidas do GMM, bem como os intervalos de treinamento e teste.
Log de alterações e refatoração do código
Algumas mudanças foram feitas no código em Python do programa. Eles requerem alguns esclarecimentos.
Agora, podemos definir uma lista de médias móveis com diferentes períodos de média. Uma combinação de várias MAs geralmente tem um efeito positivo nos resultados do treinamento.
MA_PERIODS = [15, 55, 150, 250]
Adicionado a data de início configurável para o processo de teste, avaliação e seleção do modelo.
TSTART_DATE = datetime(2015, 1, 1)
A função de amostragem aleatória sofreu uma série de mudanças. Adicionado o parâmetro add_noize, que permite adicionar o ruído ao conjunto de dados original. Isso tornará a negociação menos ideal, adicionando rebaixamentos e misturando negociações. Às vezes, um modelo pode ser aprimorado com os novos dados, introduzindo um erro no nível de 0.1-02.
Agora o spread é levado em consideração. As negociações que não cobrem o spread são marcadas com um rótulo de 2.0 e, em seguida, são excluídas do conjunto de dados por não serem informativas.
def add_labels(dataset, min, max, add_noize = 0.1): labels = [] for i in range(dataset.shape[0]-max): rand = random.randint(min, max) curr_pr = dataset['close'][i] future_pr = dataset['close'][i + rand] if future_pr + MARKUP < curr_pr: labels.append(1.0) elif future_pr - MARKUP > curr_pr: labels.append(0.0) else: labels.append(2.0) dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop(dataset[dataset.labels == 2].index).reset_index(drop=True) if add_noize==0: return dataset # add noize to samples noize_b = dataset[dataset.labels == 0]['labels'].sample(frac = add_noize) noize_s = dataset[dataset.labels == 1]['labels'].sample(frac = add_noize) noize_b = noize_b+1 noize_s = noize_s-1 dataset.update(noize_b) dataset.update(noize_s) return dataset
A função de teste agora retorna a pontuação R^2:
def tester(dataset, markup = 0.0, plot = False): last_deal = int(2) last_price = 0.0 report = [0.0] for i in range(dataset.shape[0]): pred = dataset['labels'][i] if last_deal == 2: last_price = dataset['close'][i] last_deal = 0 if pred <= 0.5 else 1 continue if last_deal == 0 and pred > 0.5: last_deal = 1 report.append(report[-1] - markup + (dataset['close'][i] - last_price)) last_price = dataset['close'][i] continue if last_deal == 1 and pred < 0.5: last_deal = 0 report.append(report[-1] - markup + (last_price - dataset['close'][i])) last_price = dataset['close'][i] y = np.array(report).reshape(-1,1) X = np.arange(len(report)).reshape(-1,1) lr = LinearRegression() lr.fit(X,y) l = lr.coef_ if l >= 0: l = 1 else: l = -1 if(plot): plt.plot(report) plt.show() return lr.score(X,y) * l
Adicionada uma função auxiliar para a visualização dos dados por meio do método do componente principal. Isso pode ajudar a entender melhor os seus dados.
def pca_plot(data): from sklearn.decomposition import PCA pca = PCA(n_components = 5) components = pd.DataFrame(pca.fit_transform(data[data.columns[1:-1]])) components['labels'] = data['labels'].reset_index(drop = True) import seaborn as sns g = sns.PairGrid(components, hue="labels", height=1.2) g.map_diag(sns.histplot) g.map_offdiag(sns.scatterplot) g.add_legend() plt.show()
O analisador de código foi estendido. Agora ele leva em consideração todos os períodos das médias móveis, que são adicionados ao programa MQL, após os quais a função fill_arrays forma um vetor de características.
def export_model_to_MQL_code(model):
model.save_model('catmodel.h',
format="cpp",
export_parameters=None,
pool=None)
# add variables
code = 'int ' + 'loock_back = ' + str(LOOK_BACK) + ';\n'
code += 'int hnd[];\n'
code += 'int OnInit() {\n'
code += 'ArrayResize(hnd,' + str(len(MA_PERIODS)) + ');\n'
count = len(MA_PERIODS) - 1
for i in MA_PERIODS:
code += 'hnd[' + str(count) + ']' + ' =' + ' iMA(NULL,PERIOD_CURRENT,' + str(i) + ',0,MODE_SMA,PRICE_CLOSE);\n'
count -= 1
code += 'return(INIT_SUCCEEDED);\n'
code += '}\n\n'
# get features
code += 'void fill_arays(int look_back, double &features[]) {\n'
code += ' double ma[], pr[], ret[];\n'
code += ' ArrayResize(ret,' + str(LOOK_BACK) +');\n'
code += ' CopyClose(NULL,PERIOD_CURRENT,1,look_back,pr);\n'
code += ' for(int i=0;i<' + str(len(MA_PERIODS)) +';i++) {\n'
code += ' CopyBuffer(hnd[' + 'i' + '], 0, 1, look_back, ma);\n'
code += ' for(int f=0;f<' + str(LOOK_BACK) +';f++)\n'
code += ' ret[f] = pr[f] - ma[f];\n'
code += ' ArrayInsert(features, ret, ArraySize(features), 0, WHOLE_ARRAY); }\n'
code += ' ArraySetAsSeries(features, true);\n'
code += '}\n\n'
Conclusão
Este artigo demonstrou um exemplo de como usar um modelo gerador simples - GMM (Gaussian Mixture Model) para reamostrar o conjunto de dados original. Este modelo permite melhorar o desempenho do classificador CatBoost em novos dados, melhorando as características do espaço de características. Para selecionar o melhor modelo, nós implementamos uma reamostragem iterativa dos dados, com a possibilidade de selecionar o resultado desejado.
Foi uma espécie de ruptura dos modelos ingênuos para os modelos significativos. Ao despender um mínimo de esforço para desenvolver um componente lógico de uma estratégia de negociação, você pode obter robôs de negociação interessantes baseados em aprendizado de máquina.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/8662
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 WebSocket para MetaTrader 5
WebSocket para MetaTrader 5
 Algoritmo de aprendizado de máquina CatBoost da Yandex sem conhecimento prévio de Python ou R
Algoritmo de aprendizado de máquina CatBoost da Yandex sem conhecimento prévio de Python ou R
 Força bruta para encontrar padrões (Parte II): Imersão
Força bruta para encontrar padrões (Parte II): Imersão
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Maxim, seria bom dar um sinal no artigo, pois ele parece ter bons resultados.
Já existem métodos mais avançados, em termos de preparação de dados, e estou trabalhando com eles.
Monitorar cada artigo não é uma opção.
É mais para fins científicos e cognitivos.