
Самооптимизация экспертов: Эволюционные и генетические алгоритмы
Содержание
- Введение
- 1. История появления эволюционных алгоритмов
- 2. Эволюционные алгоритмы (методы)
- 3. Генетические алгоритмы (ГА)
- 3.1. Область применения.
- 3.2. Решаемые задачи
- 3.3. Классический ГА
- 3.4. Стратегии поиска
- 3.5. Отличия от классического поиска оптимума
- 3.6. Терминология ГА
- 4. Преимущества ГА
- 5. Недостатки ГА
- 6. Экспериментальная часть
- 6.1. Поиск лучшей комбинации предикторов
- с использованием tabuSearch
- 6.2. Поиск лучших параметров ТС:
- 7. Пути и методы улучшения качественных показателей
- Заключение
Введение
Необходимость самооптимизации экспертов без выхода из торговли давно понята многими трейдерами. Здесь уже было опубликовано несколько статей по этой проблеме (статья1, статья2, статья3, статья4). Основой экспериментов в этих статьях служила библиотека, предложенная здесь. Однако за время, прошедшее с момента их публикации, появились новые мощные алгоритмы оптимизации и новые возможности по их применению. Кроме того, по моему мнению, эти статьи написаны программистами и предназначены для программистов.
В настоящей статье я постараюсь осветить практическое применение генетических алгоритмов (ГА) без излишнего погружения в технические детали, сугубо для трейдеров. Пользователю, коим являюсь и я, важно знать принцип работы ГА, важность и значение параметров, влияющих на качество и скорость схождения ГА и другие его утилитарные свойства. Поэтому, может быть, я и повторюсь, но всё же начну с истории возникновения ГА, продолжу его описанием и дойду до определения параметров усовершенствованных ГА. Кроме того, сравним ГА с несколькими эволюционными алгоритмами (ЭА).
1. История появления эволюционных алгоритмов
История эволюционных вычислений началась с разработки ряда различных независимых моделей. Основными из них были генетические алгоритмы и классификационные системы Голланда (Holland), опубликованные в начале 60-х годов и получившие всеобщее признание после выхода в свет книги, ставшей классикой в этой области, — "Адаптация в естественных и искусственных системах" ("Adaptation in Natural and Artifical Systems", 1975). В 70-х годах в рамках теории случайного поиска Л.А. Растригин предложил ряд алгоритмов, использующих идеи бионического поведения особей. Развитие этих идей нашло отражение в цикле работ И.Л. Букатовой по эволюционному моделированию. Развивая идеи М.Л. Цетлина о целесообразном и оптимальном поведении стохастических автоматов, Ю.И. Неймарк предложил осуществлять поиск глобального экстремума на основе коллектива независимых автоматов, моделирующих процессы развития и элиминации особей. Большой вклад в развитие эволюционного программирования внесли Фогел (Fogel) и Уолш (Walsh). Несмотря на разницу в подходах, каждая из этих "школ" взяла за основу ряд принципов, существующих в природе, и упростила их до такой степени, чтобы их можно было реализовать на компьютере.
Усилия, направленные на моделирование эволюции по аналогии с природными системами, к настоящему времени можно разбить на две большие категории.
- Системы, смоделированные на биологических принципах. Они успешно использовались для задач типа функциональной оптимизации и могут легко быть описаны на небиологическом языке.
- Системы, которые являются биологически более реалистичными, но не оказавшиеся особенно полезными в прикладном смысле. Они больше похожи на биологические системы и менее направлены (или ненаправлены вовсе). Они обладают сложным и интересным поведением, и, видимо, вскоре получат практическое применение.
Конечно, на практике мы не можем разделять эти вещи так строго. Эти категории — просто два полюса, между которыми лежат различные вычислительные системы. Ближе к первому полюсу — эволюционные алгоритмы, например, Эволюционное Программирование (Evolutionary Programming), Генетические Алгоритмы (Genetic Algorithms) и Эволюционные Стратегии (Evolution Strategies). Ближе ко второму полюсу располагаются системы, которые могут быть классифицированы как Искусственная Жизнь (Artificial Life).
2. Эволюционные алгоритмы (методы)
Эволюционные алгоритмы — направление в искусственном интеллекте (раздел эволюционного моделирования), которое использует и моделирует процессы естественного отбора. Перечислим некоторые из них:
- генетические алгоритмы — эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров;
генетическое программирование — автоматическое создание или изменение программ с помощью генетических алгоритмов;
эволюционное программирование — аналогично генетическому программированию, но структура программы постоянна, изменяются только числовые значения;
эволюционные стратегии — похожи на генетические алгоритмы, но в следующее поколение передаются только положительные мутации;
дифференциальная эволюция;
нейроэволюция — аналогична генетическому программированию, но геномы представляют собой искусственные нейронные сети, в которых происходит эволюция весов при заданной топологии сети, или, помимо эволюции весов, также производится эволюция топологии.
Все они моделируют базовые положения в теории биологической эволюции — процессы отбора, скрещивания, мутации и воспроизводства. Поведение особей определяется окружающей средой. Множество особей принято называть популяцией. Популяция эволюционирует в соответствии с правилами отбора в соответствии с целевой функцией, которая задается окружающей средой. Таким образом, каждой особи (индивидууму) в популяции назначается значение его пригодности в окружающей среде. Размножаются только наиболее пригодные особи. Рекомбинация и мутация позволяют индивидуумам изменяться и приспосабливаться к среде. Такие алгоритмы относятся к адаптивным поисковым механизмам.
Эволюционные методы (ЭМ) — приближенные (эвристические) методы решения задач оптимизации и структурного синтеза. Большинство ЭМ основано на статистическом подходе к исследованию ситуаций и итерационном приближении к искомому решению.
Эволюционные вычисления составляют один из разделов искусственного интеллекта. При построении систем ИИ по данному подходу основное внимание уделяется построению начальной модели и правилам, по которым она может изменяться (эволюционировать). При этом модель может быть составлена по самым различным методам. Например, это может быть и нейронная сеть, и набор логических правил. К основным эволюционным методам относятся методы отжига, генетические, поведения "толпы" (PSO), колонии муравьев (ACO), генетического программирования.
В отличие от точных методов математического программирования, ЭМ позволяют находить решения, близкие к оптимальным, за приемлемое время, а в отличие от других эвристических методов оптимизации, характеризуются существенно меньшей зависимостью от особенностей приложения (то есть, более универсальны) и в большинстве случаев обеспечивают лучшую степень приближения к оптимальному решению. Универсальность ЭМ определяется также применимостью к задачам с неметризуемым пространством управляемых переменных (то есть, среди управляемых переменных могут быть и лингвистические величины, в том числе и не имеющие количественного выражения).
В методе отжига (Simulated Annealing) имитируется процесс минимизации потенциальной энергии тела во время отжига деталей. В текущей точке поиска происходит изменение некоторых управляемых параметров. Новая точка принимается всегда при улучшении целевой функции и лишь с некоторой вероятностью — при ее ухудшении.
Важнейшим частным случаем ЭМ являются генетические методы и алгоритмы. Генетические алгоритмы (ГА) основаны на поиске лучших решений с помощью наследования и усиления полезных свойств множества объектов определенного приложения в процессе имитации их эволюции.
Свойства объектов представлены значениями параметров, объединяемых в запись, называемую в ЭМ хромосомой. В ГА оперируют подмножеством хромосом, называемым популяцией. Имитация генетических принципов — вероятностный выбор родителей среди членов популяции, скрещивание их хромосом, отбор потомков для включения в новые поколения объектов на основе оценки целевой функции. Этот процесс ведет к эволюционному улучшению значений целевой функции (функции полезности) от поколения к поколению.
Среди ЭМ находят применение также методы, которые, в отличие от ГА, оперируют единственной хромосомой, а не их множеством. Так, метод дискретного локального поиска (его англоязычное название Hillclimbing) основан на случайном изменении отдельных параметров (значений полей в записи или, другими словами, значений генов в хромосоме). Такие изменения называют мутациями. После очередной мутации оценивают значение функции полезности F (Fitness Function). Результат мутации сохраняется в хромосоме только если F улучшилась. При "моделировании отжига" результат мутации сохраняется с некоторой вероятностью, зависящей от полученного значения .
В методе PSO (Particles Swarm Optimization) имитируется поведение множества агентов, стремящихся согласовать свое состояние с состоянием наилучшего агента.
Метод колонии муравьев (ACO) основан на имитации поведения муравьев, минимизирующих длину своих маршрутов на пути от муравейника до источника пищи.
3. Генетические алгоритмы (ГА)
Генетические Алгоритмы — адаптивные методы поиска, которые в последнее время часто используются для решения задач функциональной оптимизации. Они основаны на генетических процессах биологических организмов: биологические популяции развиваются на протяжении нескольких поколений, подчиняясь законам естественного отбора и принципу "выживает наиболее приспособленный" (survival of the fittest), открытому Чарльзом Дарвином. Подражая этому процессу, генетические алгоритмы способны "развивать" решения реальных задач, если те соответствующим образом закодированы.
В природе особи в популяции конкурируют друг с другом за различные ресурсы — такие, например, как пища или вода. Кроме того, члены популяции одного вида часто конкурируют за привлечение брачного партнера. Особи, которые наиболее приспособлены к окружающим условиям, будут иметь относительно больше шансов воспроизвести потомков. Слабо приспособленные особи либо совсем не произведут потомства, либо оно будет немногочисленным. Это означает, что гены от хорошо адаптированных особей будут распространяться в увеличивающемся количестве потомков в каждом последующем поколении. Комбинация удачных характеристик от разных родителей иногда может приводить к появлению "суперприспособленного" потомка, чья адаптированность больше, чем у любого из его родителей. Таким образом, вид развивается, всё лучше и лучше приспосабливаясь к среде обитания.
ГА используют прямую аналогию с таким механизмом. Они работают с совокупностью "особей" — популяцией, каждая из которых представляет возможное решение данной проблемы. Каждая особь оценивается мерой ее "приспособленности" в соответствии с тем, насколько "хорошо" соответствующее ей решение задачи. Наиболее приспособленные особи получают возможность "воспроизводит" потомство с помощью "перекрестного скрещивания" с другими особями популяции. Это приводит к появлению новых особей, которые сочетают в себе некоторые характеристики, наследуемые ими от родителей. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков, так что те свойства, которыми они обладали, будут постепенно исчезать из популяции в процессе эволюции.
Так и воспроизводится вся новая популяция допустимых решений, выбирая лучших представителей предыдущего поколения, скрещивая их и получая множество новых особей. Это новое поколение содержит более высокое соотношение характеристик, которыми обладают "хорошие" члены предыдущего поколения. Таким образом, из поколения в поколение хорошие характеристики распространяются по всей популяции. Скрещивание наиболее приспособленных особей приводит к тому, что исследуются наиболее перспективные участки пространства поиска. В конечном итоге популяция будет сходиться к оптимальному решению задачи.
Имеются разные способы реализации идеи биологической эволюции в рамках ГА.
3.1. Область применения
Решаемые реальные задачи могут быть сформулированы как поиск оптимального значения, где значение — сложная функция, зависящая от некоторых входных параметров. В некоторых случаях представляет интерес найти те значения параметров, при которых достигается наилучшее точное значение функции. В других случаях точный оптимум не требуется, и решением может считаться любое значение, которое лучше некоторой заданной величины. В этом случае генетические алгоритмы часто становятся наиболее приемлемым методом для поиска "хороших" значений. Сила генетического алгоритма — в его способности манипулировать одновременно многими параметрами. Эта особенность ГА использовалась в сотнях прикладных программ, включая проектирование самолетов, настройку параметров алгоритмов и поиск устойчивых состояний систем нелинейных дифференциальных уравнений.
Однако нередки случаи, когда ГА работает не так эффективно, как ожидалось.
Предположим, есть реальная задача, сопряженная с поиском оптимального решения. Как узнать, подходит ли для этого ГА? Строго ответа на этот вопрос до настоящего времени еще не получено. Однако многие исследователи разделяют предположения о том, что ГА имеет хорошие шансы стать эффективной процедурой поиска в следующих случаях:
- если пространство поиска, которое предстоит исследовать, велико и предполагается, что оно не совершенно гладкое и унимодальное (т.е. содержит один гладкий экстремум);
- если функция приспособленности содержит шумы;
- или если задача не требует строгого нахождения глобального оптимума.
Иными словами, в ситуациях, когда нужно быстро и просто найти приемлемое "хорошее" решение (что довольно часто имеет место в реальных задачах), ГА конкурирует и превосходит другие методы, которые не используют знания о пространстве поиска.
Если же пространство поиска небольшое, то решение может быть найдено методом полного перебора, и можно быть уверенным, что наилучшее возможное решение найдено, тогда как ГА мог с большей вероятностью сойтись к локальному оптимуму, а не к глобально лучшему решению. Если пространство гладкое и унимодальное любой градиентный алгоритм (к примеру, метод скорейшего спуска) будет более эффективен, чем ГА.
Если о пространстве поиска есть некоторая дополнительная информация (как, например, пространство для хорошо известной задачи о коммивояжере), методы поиска, использующие эвристики, определяемые пространством, часто превосходят любой универсальный метод, каким является ГА. При достаточно сложном рельефе функции приспособленности методы поиска с единственным решением в каждый момент времени, такой как простой метод спуска, могли "зацикливаться" в локальном решении, однако считается, что ГА, так как они работают с целой "популяцией" решений, имеют меньше шансов сойтись к локальному оптимуму и надежно функционируют на многоэкстремальном ландшафте.
Конечно, такие предположения не предсказывают строго, когда ГА будет эффективной процедурой поиска, конкурирующей с другими процедурами. Эффективность ГА сильно зависит от таких деталей, как метод кодировки решений, операторы, настройки параметров, частный критерий успеха. Теоретическая работа, отраженная в литературе, посвященной генетическим алгоритмам, пока не дает оснований говорить о выработке каких-либо строгих механизмов для четких предсказаний.
3.2. Решаемые задачи
Генетические алгоритмы применяются для решения следующих задач:- Оптимизация функций
- Оптимизация запросов в базах данных
- Разнообразные задачи на графах (задача коммивояжёра, раскраска, нахождение паросочетаний)
- Настройка и обучение искусственной нейронной сети
- Задачи компоновки
- Составление расписаний
- Игровые стратегии
- Теория приближений
3.3. Классический ГА
Работа простого ГАПростой ГА случайным образом генерирует начальную популяцию структур. Работа ГА представляет собой итерационный процесс, который продолжается до тех пор, пока не выполнится заданное число поколений или какой-либо иной критерий остановки. На каждом поколении алгоритма реализуется отбор пропорционально приспособленности, одноточечный кроссовер и мутация.
Сначала пропорциональный отбор назначает каждой структуре вероятность Ps(i), равную отношению ее приспособленности к суммарной приспособленности популяции.
Затем происходит отбор (с замещением) всех n особей для дальнейшей генетической обработки, согласно величине Ps(i). Простейший пропорциональный отбор — рулетка (roulette-wheel selection, Goldberg, 1989c) — отбирает особей с помощью n "запусков" рулетки. Колесо рулетки содержит по одному сектору для каждого члена популяции. Размер i-ого сектора пропорционален соответствующей величине Ps(i). При таком отборе более приспособленные члены популяции с большей вероятностью будут чаще выбираться, чем особи с низкой приспособленностью.
После отбора n выбранных особей подвергаются кроссоверу (иногда называемому рекомбинацией) с заданной вероятностью Pc. n строк случайным образом разбиваются на n/2 пары. Для каждой пары с вероятностью Pc может применяться кроссовер. Соответственно, с вероятностью 1-Pc кроссовер не происходит, и неизмененные особи переходят на стадию мутации. Если кроссовер происходит, полученные потомки заменяют собой родителей и переходят к мутации.
Одноточечный кроссовер работает следующим образом. Сначала случайным образом выбирается одна из l-1 точек разрыва. (Точка разрыва — участок между соседними битами в строке.) Обе родительские структуры разрываются на два сегмента по этой точке. Затем соответствующие сегменты различных родителей склеиваются, и получаются два генотипа потомков.
После того, как закончится стадия кроссовера, выполняются операторы мутации. В каждой строке, подвергающейся мутации, каждый бит с вероятностью Pm изменяется на противоположный. Популяция, полученная после мутации, записывается поверх старой, и этим цикл одного поколения завершается. Последующие поколения обрабатываются таким же образом: отбор, кроссовер и мутация.
В настоящее время исследователи ГА предлагают множество других операторов отбора, кроссовера и мутации. Вот лишь наиболее распространенные из них. Прежде всего, турнирный отбор (Brindle, 1981; Goldberg и Deb, 1991). Турнирный отбор реализует n турниров, чтобы выбрать n особей. Каждый турнир построен на выборке k элементов из популяции и выбора лучшей особи среди них. Наиболее распространен турнирный отбор с k=2.
Элитные методы отбора (De Jong, 1975) гарантируют, что при отборе обязательно будут выживать лучший или лучшие члены популяции совокупности. Наиболее распространена процедура обязательного сохранения только одной лучшей особи, если она не прошла, как другие через процесс отбора, кроссовера и мутации. Элитизм может быть внедрен практически в любой стандартный метод отбора.
Двухточечный кроссовер (Cavicchio, 1970; Goldberg, 1989c) и равномерный кроссовер (Syswerda, 1989) — вполне достойные альтернативы одноточечному оператору. В двухточечном кроссовере выбираются две точки разрыва, и родительские хромосомы обмениваются сегментом, который находится между двумя этими точками. В равномерном кроссовере каждый бит первого родителя наследуется первым потомком с заданной вероятностью; в противном случае этот бит передается второму потомку. И наоборот.
Основные операторы генетического алгоритма
Оператор отбора (селекции)
На этом этапе отбирается оптимальная популяция для дальнейшего размножения. Обычно берут определённое число лучших по приспособленности. Имеет смысл также отбрасывать "клонов", т.е. особей с одинаковым набором генов.
Оператор скрещивания
Чаще всего скрещивание производят над двумя лучшими особями. Результатом обычно являются две особи с компонентами, взятыми от их "родителей". Цель этого оператора — распространение "хороших" генов по популяции и стягивание плотности популяции к тем областям, где она и так велика в том предположении, что "нас много там, где хорошо".
Оператор мутаций
Оператор мутаций просто меняет произвольное число элементов в особи на другие произвольные. Фактически, он является неким диссипативным элементом, с одной стороны вытягивающим из локальных экстремумов, с другой — привносящим новую информацию в популяцию.
- Инвертирует бит в случае бинарного признака.
- Изменяет на некоторую величину числовой признак (скорее всего, на ближайший).
- Заменит на другой номинальный признак.
Критерии останова
- Нахождение глобального либо субоптимального решения
- Выход на «плато»
- Исчерпание числа поколений, отпущенных на эволюцию
- Исчерпание времени, отпущенного на эволюцию
- Исчерпание заданного числа обращений к целевой функции
3.4. Стратегии поиска
Поиск — один из универсальных методов нахождения решения для случаев, когда априори не известна последовательность шагов, ведущая к оптимуму.Существуют две поисковые стратегии: эксплуатация наилучшего решения и исследование пространства решений. Градиентный метод — пример стратегии, которая выбирает наилучшее решение для возможного улучшения, игнорируя в то же время исследование всего пространства поиска. Случайный поиск — пример стратегии, которая, наоборот, исследует пространство решений, игнорируя исследование перспективных областей поискового пространства. Генетический алгоритм представляет собой класс поисковых методов общего назначения, которые комбинируют элементы обоих стратегий. Использование этих методов позволяет удерживать приемлемый баланс между исследованием и эксплуатацией наилучшего решения. В начале работы генетического алгоритма популяция случайна и имеет разнообразные элементы. Поэтому оператор скрещивания осуществляет обширное исследование пространства решений. С ростом значения функции соответствия получаемых решений оператор скрещивания обеспечивает исследование окрестностей каждого из них. Другими словами, тип поисковой стратегии (эксплуатация наилучшего решения или исследование области решений) для оператора скрещивания определяется разнообразием популяции, а не самим этим оператором.
3.5. Отличие от классического поиска оптимума
В общем случае, алгоритм решения оптимизационных проблем представляет собой последовательность вычислительных шагов, которые асимптотически сходятся к оптимальному решению. Большинство классических методов оптимизации генерируют детерминированную последовательность вычислений, основанную на градиенте или производной целевой функции более высокого порядка. Эти методы применяются к одной исходной точке поискового пространства. Затем решение постепенно улучшается в направлении наискорейшего роста или убывания целевой функции. При таком поточечном подходе существует опасность попадания в локальный оптимум.
Генетический алгоритм осуществляет одновременный поиск по многим направлениям путем использования популяции возможных решений. Переход от одной популяции к другой позволяет избежать попадания в локальный оптимум. Популяция претерпевает нечто наподобие эволюции: в каждом поколении относительно хорошие решения репродуцируются, в то время как относительно плохие отмирают. ГА используют вероятностные правила для определения репродуцируемой или уничтожаемой хромосомы, чтобы направить поиск к областям вероятного улучшения целевой функции.
В последние годы реализовано много генетических алгоритмов, и в большинстве случаев они сильно отличаются от исходного, классического. По этой причине в настоящее время под термином "генетические алгоритмы" скрывается не одна модель, а достаточно широкий класс алгоритмов, подчас мало похожих друг от друга. Исследователи экспериментировали с различными типами представлений, операторов кроссовера и мутации, специальных операторов и различных подходов к воспроизводству и отбору.
Хотя модель эволюционного развития, применяемая в ГА, сильно упрощена по сравнению со своим природным аналогом, тем не менее, ГА является достаточно мощным средством и может с успехом применяться для широкого класса прикладных задач, включая те, которые трудно, а иногда и вовсе невозможно решить другими методам. Однако, ГА, как и другие методы эволюционных вычислений, не гарантируют обнаружения глобального решения за полиномиальное время. Не гарантируют они и того, что глобальное решение вообще будет найдено. Однако генетические алгоритмы хороши для поиска "достаточно хорошего" решения задачи "достаточно быстро". Там, где задача может быть решена специальными методами, почти всегда такие методы будут эффективнее ГА и в быстродействии и в точности найденных решений. Главным же преимуществом ГА-мов является то, что они могут применяться даже на сложных задачах, там, где не существует никаких специальных методов. Даже там, где хорошо работают существующие методики, можно достигнуть улучшения сочетанием их с ГА.
3.6. Терминология ГА
Поскольку ГА происходят как из естественных наук (генетика), так и из компьютерных, то используемая терминология представляет собой сплав естественного и искусственного. Соответствие терминов, относящихся к ГА, и тех, которые относятся к решению оптимизационных проблем, приведено в табл. 1.1.
Таблица 1.
| Генетический алгоритм | Объяснение |
|---|---|
| Хромосома | Вариант решения (набор параметров) |
| Гены | Параметры, которые оптимизируются |
| Локус (положение) | Позиция гена в хромосоме |
| Аллель | Значение гена |
| Фенотип | Раскодированное решение |
| Генотип | Закодированное решение |
Классический (одноточечный) кроссинговер.
"Традиционный" генетический алгоритм использует одноточечный кроссинговер, в котором две скрещивающиеся хромосомы разрезаются один раз в соответствующей точке, после чего обмениваются полученными частями. Однако было изобретено много других различных алгоритмов с иными видами кроссинговера, часто включающих больше, чем одну точку разреза. DeJong исследовал эффективность многоточечного кроссинговера и пришел к выводу, что двухточечный кроссинговер дает улучшение, но что дальнейшее добавление точек кроссинговера редуцирует деятельность генетического алгоритма. Проблема с добавлением дополнительных точек кроссинговера состоит в том, что стандартные блоки, вероятно, будут прерваны. Однако преимущество большего количества точек кроссинговера состоит в том, что пространство состояний может быть исследовано более полно и подробно.
Двухточечный кроссинговер.
В двухточечном кроссинговере (и многоточечном кроссинговере вообще) хромосомы расцениваются как циклы, которые формируются соединением концов линейной хромосомы вместе. Для замены сегмента одного цикла сегментом другого цикла требуется выбор двух точек разреза. В этом представлении одноточечный кроссинговер может быть рассмотрен как кроссинговер с двумя точками, но с одной точкой разреза, зафиксированной в начале строки. Следовательно, двухточечный кроссинговер решает ту же самую задачу, что и одноточечный, но более полно. Хромосома, рассматриваемая как цикл, может содержать большее количество стандартных блоков, так как они могут совершить "циклический возврат" в конце строки. В настоящий момент многие исследователи соглашаются, что двухточечный кроссинговер в целом лучше, чем одноточечный.
Унифицированный (однородный) кроссинговер.
Унифицированный кроссинговер принципиально отличается от одноточечного кроссинговера. Каждый ген в потомстве создается посредством копирования соответствующего гена от одного или другого родителя, выбранного согласно случайно сгенерированной маске кроссинговера. Если в маске кроссинговера стоит 1, то ген копируется от первого родителя, если в маске стоит 0, то ген копируется от второго родителя. Для создания второго потомства процесс повторяется, но наоборот, с замененными родителями. Новая маска кроссинговера случайно генерируется для каждой пары родителей.
Дифференциальное скрещивание.
Помимо кроссовера, существуют и другие методы скрещивания. Например, для поиска минимума/максимума функции многих вещественных переменных наиболее удачным является "дифференциальное скрещивание". Вкратце опишем его суть. Пусть a и b — это два индивидуума в популяции, т.е., вещественные вектора от которых зависит наша функция. Тогда потомок c вычисляется по формуле с=a+k*(a-b), где k —это некоторый вещественный коэффициент (который может зависить от ||a-b|| — растояния между векторами).
В этой модели мутация — это добавление к индивидууму случайного вектора малой длины. Если исходная функция непрерывна, то эта модель работает хорошо. А если она еще и гладкая, то и вовсе превосходно.
Инверсия и переупорядочение.
Часто порядок генов в хромосоме является критическим для строительных блоков, позволяющих осуществлять эффективную работу алгоритма. Были предложены методы для переупорядочения позиций генов в хромосоме во время работы алгоритма. Одна из таких методик — инверсия, выполняющая реверсирование порядка генов между двумя случайно выбранными позициями в хромосоме. (Когда используются эти методы, гены должны содержать некоторую "метку", так, чтобы их можно было правильно идентифицировать независимо от их позиции в хромосоме.)
Цель переупорядочения состоит в том, чтобы попытаться найти порядок генов, который имеет лучший эволюционный потенциал. Многие исследователи использовали инверсию в своей работе, хотя кажется, что немногие попытались ее обосновать или определить ее вклад. Goldberg & Bridges анализируют оператор переупорядочения на очень маленькой задаче, показывая, что она может дать определенное преимущество, хотя они заключают, что их методы не принесли бы то же самое преимущество на больших задачах.
Переупорядочение также значительно расширяет область поиска. Мало того, что генетический алгоритм пытается находить хорошие множества значений генов, он также одновременно пробует находить их "правильное" упорядочение. Это гораздо более трудная задача для решения.
Что такое эпистаз?
Термин "эпистаз" в генетике определяется как влияние гена на пригодность индивидуума в зависимости от значения гена, присутствующего в другом месте. Иными словами, генетики используют термин "эпистаз" в смысле эффекта "переключения" или "маскирования": "Ген считают эпистатическим, когда его присутствие подавляет влияние гена в другом локусе. Эпистатические гены иногда называют ингибирующими из-за их влияния на другие гены, которые описываются как гипостаз".
В терминологии ГА это может звучать так: "Приспособленность особи зависит от взаимного расположения хромосом в генотипе".
Что такое ложный оптимум?
Одним из фундаментальных принципов генетических алгоритмов является то, что хромосомы, включенные в шаблоны, содержащиеся в глобальном оптимуме, увеличиваются по частоте. Особенно это верно для коротких шаблонов небольшого порядка, известных как строительные блоки. В конечном счете при кроссинговере эти оптимальные шаблоны сойдутся, и будет создана глобальная оптимальная хромосома. Но если шаблоны, которые не содержатся в глобальном оптимуме, будут увеличиваться по частоте быстрее, чем другие, то генетический алгоритм будет введен в заблуждение и уйдет в другую сторону от глобального оптимума, вместо того, чтобы приблизиться к нему. Это явление известно как ложный оптимум.
Ложный оптимум — частный случай эпистаза, и он был глубоко изучен Goldberg и другими. Ложный оптимум непосредственно связан с вредными влияниями эпистаза в генетических алгоритмах.
По статистике, шаблон увеличится по частоте в популяции, если его пригодность выше, чем средняя пригодность всех шаблонов в популяции. Задача обозначается как задача ложного оптимума, если средняя пригодность шаблонов, которые не содержатся в глобальном оптимуме, больше, чем средняя пригодность других шаблонов.
Задачи ложного оптимума трудны для решения. Однако, Grefenstette остроумно демонстрирует, что они возникают не всегда. После первого поколения генетический алгоритм не получает объективную выборку точек в области поиска. Поэтому он не может оценивать объективную глобальную среднюю пригодность шаблона. Он способен только получить необъективную оценку пригодности шаблона. Иногда это предубеждение помогает генетическому алгоритму сходиться (даже при том, что задача иначе могла бы иметь сильный ложный оптимум).
Что такое инбридинг, аутбридинг, селективный выбор, панмиксия?
Существует несколько подходов к выбору родительской пары. Наиболее простой из них — панмиксия. Этот подход предполагает случайный выбор родительской пары, когда обе особи, которые составят родительскую пару, случайным образом выбираются из всей популяции. В этом случае любая особь может стать членом нескольких пар. Несмотря на простоту, такой подход универсален для решения различных классов задач. Однако он достаточно критичен к численности популяции, поскольку эффективность алгоритма, реализующего такой подход, снижается с ростом численности популяции.
Селективный способ выбора особей в родительскую пару состоит в том, что "родителями" могут стать только те особи, значение приспособленности которых не меньше среднего значения приспособленности по популяции, при равной вероятности таких кандидатов составить брачную пару.
Такой подход обеспечивает более быструю сходимость алгоритма. Однако из-за быстрой сходимости селективный выбор родительской пары не подходит тогда, когда ставится задача определения нескольких экстремумов, поскольку для таких задач алгоритм, как правило, быстро сходится к одному из решений. Кроме того, для некоторого класса задач со сложным ландшафтом приспособленности быстрая сходимость может превратиться в преждевременную сходимость к квазиоптимальному решению. Этот недостаток может быть отчасти компенсирован использованием подходящего механизма отбора, который бы "тормозил" слишком быструю сходимость алгоритма.
Инбридинг представляет собой такой метод, когда первый член пары выбирается случайно, а вторым с большей вероятностью будет максимально близкая к нему особь.
При аутбридинге также используют понятие схожести особей. Однако теперь брачные пары формируют из максимально далеких особей.
Последние два способа по-разному влияют на поведение генетического алгоритма. Так, инбридинг можно охарактеризовать свойством концентрации поиска в локальных узлах, что фактически приводит к разбиению популяции на отдельные локальные группы вокруг подозрительных на экстремум участков ландшафта. Аутбридинг же направлен на предупреждение сходимости алгоритма к уже найденным решениям, заставляя алгоритм просматривать новые, неисследованные области.
Динамическая самоорганизация параметров ГА
Зачастую выбор параметров генетического алгоритма и конкретных генетических операторов производится на интуитивном уровне, поскольку пока не существует объективных доказательств преимущества тех или иных настроек и операторов. Однако не нужно забывать, что сама суть ГА заключается в динамике и "мягкости" алгоритма и производимых вычислений. Тогда почему бы не позволить алгоритму самому настраиваться во время решения задачи и адаптироваться к ней?
Проще всего организовать адаптацию применяемых операторов. Для этого встроим в алгоритм несколько (чем больше, тем лучше) различных операторов выборки (элитная, случайная, рулеточная,..), кроссинговера (одноточечный, двухточечный, унифицированный,..) и мутации (случайная одноэлементная, абсолютная,..). Установим для каждого оператора равные вероятности применения. Далее на каждом цикле алгоритма будем выбирать один из операторов каждой группы (выбор, кроссинговер, мутация) в соответствии с вероятностным распределением. При этом в полученной особи отметим, с помощью какого именно оператора она была получена. Тогда, если новое распределение вероятностей мы вычислим исходя из информации, содержащейся в популяции (вероятность применения оператора пропорциональна числу особей в популяции, полученных при помощи этого оператора), то генетический алгоритм получит механизм динамической самоадаптации.
Такой подход дает еще одно преимущество: теперь не нужно беспокоиться о применяемом генераторе случайных чисел (линейный, экспоненциальный и т.д.), поскольку алгоритм динамически изменяет характер распределения.
Метод миграции и искусственной селекции
В отличие от обыкновенных ГА, выполняется макроэволюция, т.е., создается не одна популяция, а некоторое их множество. Генетический поиск здесь осуществляется путем объединения родителей из различных популяций.
Метод прерывистого равновесия
Метод основан на палеонтологической теории прерывистого равновесия, которая описывает быструю эволюцию за счет вулканических и других изменений земной коры. Для применения данного метода в технических задачах предлагается после каждой генерации случайным образом перемешивать индивидуальности в популяции, а затем формировать новые текущие генерации. Здесь можно предложить, как аналог из живой природы, бессознательный отбор родительских пар и синтетический отбор лучших родительских пар. Далее следует случайным образом смешать результаты обоих отборов и не оставлять размер популяции постоянным, а управлять им в зависимости от наличия лучших индивидуальностей. Такая модификация метода прерывистого равновесия может позволить сократить неперспективные популяции и расширить популяции, в которых находятся лучшие особи.
Метод прерывистого равновесия — мощный стрессовый метод изменения окружающей среды, который используется для эффективного выхода из локальных ям.
4. Преимущества ГА
Есть два главных преимущества генетических алгоритмов перед классическими оптимизационными методиками.
1. ГА не имеет значительных математических требований к видам целевых функций и ограничений. Исследователь не должен упрощать модель объекта, теряя ее адекватность, и искусственно добиваясь возможности применения доступных математических методов. При этом могут использоваться самые разнообразные целевые функции и виды ограничений (линейные и нелинейные), определенные на дискретных, непрерывных и смешанных универсальных множествах.
2. При использовании классических пошаговых методик глобальный оптимум может быть найден только в том случае, когда проблема обладает свойством выпуклости. В тоже время эволюционные операции генетических алгоритмов позволяют эффективно отыскивать глобальный оптимум.
Менее глобальные, но тоже важные преимущества ГА:
большое число свободных параметров, позволяющее эффективно встраивать эвристики;
эффективное распараллеливание;
работает заведомо не хуже абсолютно случайного поиска;
связь с биологией, дающая некоторую надежду на исключительную эффективность ГА.
5. Недостатки ГА
Большое количество свободных параметров, которое превращает "работу с ГА" в "игру с ГА"
Недоказанность сходимости
В простых целевых функциях (гладкие, один экстремум и т.п.) генетика всегда проигрывает по скорости простым алгоритмам поиска
6. Экспериментальная часть
Все эксперименты мы будем проводить в среде языка R 3.2.4. Используем набор данных для обучения модели и большинство функций из предыдущей статьи.
Задачам оптимизации и математического программирования посвящен раздел депозитария CRAN, который содержит большое количество пакетов, предназначенных для их решения. Мы применим несколько различных методов ГА и ЭМ для решения задач, перечисленных ниже. Требование к моделям, которые участвуют в процессе оптимизации, только одно — быстродействие. Применять модели, которые обучаются в течение сотни секунд, нежелательно. С учетом того, что в каждом поколении будет минимум 100 особей, а популяция пройдет через ряд (от единиц до десятков) эпох, процесс оптимизации затянется на неприемлемое время. В предыдущих статьях мы применяли два вида глубоких сетей (с инициализацией SAE и RBM). Обе показали высокое быстродействие и вполне могут использоваться при генетической оптимизации.
Мы будем решать две задачи оптимизации: поиск лучшей комбинации предикторов и выбор оптимальных параметров индикаторов. Для решения первой (выбор предикторов) мы с целью осваивания новых алгоритмов применим часто упоминаемый в последнее время алгоритм XGBoost(Extreme Gradient Boosting). По упоминаниям в источниках, он показывает очень хорошие результаты в задачах классификации. Алгоритм доступен для языков R, Python, Java. В языке R этот алгоритм реализован в пакете “xgboost” v. 0.4-3.
Для решения второй задачи (выбор оптимальных параметров индикаторов) мы возьмем простейший советник MACDsample и посмотрим, что можно получить с его помощью при использовании на лету генетической оптимизации
6.1. Поиск лучшей комбинации предикторов
Для решения задачи оптимизации любым методом необходимо определить:
параметры, которые будут оптимизироваться;
критерий оптимизации — скаляр, который нужно максимизировать/минимизировать. Критерий может быть не один;
целевую (объективную, фитнес) функцию которая будет вычислять величину критерия оптимизации.
Фитнес-функция в нашем случае будет выполнять последовательно:
формирование исходного датафрейма;
разделение его на train/test;
обучение модели;
тестирование модели;
вычисление критерия оптимизации.
Критерием оптимизиции могут быть как стандартные метрики — Accuracy,Recall, Kappa, AUC, так и предложенные разработчиком. Мы будем использовать в этом качестве ошибку классификации.
Поиск лучшей комбинации предикторов будем производить с помощью пакета "tabuSearch" v.1.1, который является расширением алгоритма HillClimbing. Алгоритм TabuSearch оптимизирует двоичную строку, используя объективную функцию, определенную пользователем. В результате он выдает лучшую бинарную конфигурацию с самым высоким значением объективной функции. Мы будем использовать этот алгоритм для поиска наилучшей комбинации предикторов.
Основная функция:
tabuSearch(size = 10, iters = 100, objFunc = NULL, config = NULL, neigh = size, listSize = 9, nRestarts = 10, repeatAll = 1, verbose = FALSE)
Аргументы:
size – длина оптимизируемой бинарной конфигурации;
iters – число итераций в предварительном поиске алгоритма;
objFun – предлагаемый пользователем метод, который оценивает целевую функцию для данной двоичной строки;
config – стартовая конфигурация;
neigh – количество соседних конфигураций для проверки на каждой итерации. По умолчанию равно длине двоичной строки. Если число меньше длины строки, соседи выбираются случайным образом;
listSize – размер табу-списка;
nRestarts – максимальное количество перезапусков на интенсивном этапе поиска алгоритма;
repeatAll – количество повторений поиска;
verbose – логический, если true, печатается имя текущего этапа алгоритма, например, предварительный этап, этап интенсификации, этап диверсификации.
Напишем объективную функцию и приступим к экспериментам.
ObjFun <- function(th){
require(xgboost)
# Если в бинарной строке все ноли выходим
if (sum(th) == 0) return(0)
# имена предикторов соответствующих 1 в бинарной строке
sub <- subset[th != 0]
# Создадим структуру для обучения модели
dtrain <- xgb.DMatrix(data = x.train[ ,sub], label = y.train)
# Обучим модель
bst = xgb.train(params = par, data = dtrain, nrounds = nround, verbose = 0)
# Вычислим предсказания по тестовому набору
pred <- predict(bst, x.test[ ,sub])
# Определим ошибку предсказания
err <- mean(as.numeric(pred > 0.5) != y.test)
# Вернем критерий качества
return(1 - err)
}
Для вычислений нам нужно подготовить наборы данных для обучения и тестирования модели, а также определить параметры модели и начальную конфигурацию для оптимизации. Используем те же данные и функции, что и в предыдущей статье (EURUSD/M30, 6000 баров по состоянию на 14.02.16).
Листинг с комментариями:
#---tabuSearch---------------------- require(tabuSearch) require(magrittr) require(xgboost) # Исходный датафрейм dt <- form.data(n = 34, z = 50, len = 0) # Имена всех предикторов в исходном наборе subset <- colnames(In()) set.seed(54321, kind = "L'Ecuyer-CMRG") # Подготовим наборы для обучения и тестирования DT <- prepareTrain(x = dt[ ,subset], y = dt$y, balance = FALSE, rati = 4/5, mod = "stratified", norm = FALSE, meth = method) train <- DT$train test <- DT$test x.train <- train[ ,subset] %>% as.matrix() y.train <- train$y %>% as.numeric() %>% subtract(1) x.test <- test[ ,subset] %>% as.matrix() y.test <- test$y %>% as.numeric() %>% subtract(1) # Исходный бинарный вектор th <- rep(1,length(subset)) # Параметры модели par <- list(max.depth = 3, eta = 1, silent = 0, nthread = 2, objective = 'binary:logistic') nround = 10 # Начальная конфигурация conf <- matrix(1,1,17) res <- tabuSearch(size = 17, iters = 10, objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1) # Максимальное значение объективной функции max.obj <- max(res$eUtilityKeep) # Лучшая комбинация бинарного вектора best.comb <- which.max(res$eUtilityKeep)%>% res$configKeep[., ] # Лучший набор предикторов best.subset <- subset[best.comb != 0]
Запустим оптимизацию с десятью итерациями и посмотрим, каков максимальный критерий качества и набор предикторов.
> system.time(res <- tabuSearch(size = 17, iters = 10, + objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1)) user system elapsed 36.55 4.41 23.77 > max.obj [1] 0.8 > best.subset [1] "DX" "ADX" "oscDX" "ar" "tr" "atr" [7] "chv" "cmo" "vsig" "rsi" "slowD" "oscK" [13] "signal" "oscKST" > summary(res) Tabu Settings Type = binary configuration No of algorithm repeats = 1 No of iterations at each prelim search = 10 Total no of iterations = 30 No of unique best configurations = 23 Tabu list size = 9 Configuration length = 17 No of neighbours visited at each iteration = 17 Results: Highest value of objective fn = 0.79662 Occurs # of times = 2 Optimum number of variables = c(14, 14)
Вычисления заняли около 37 секунд при точности предсказания около 0.8 и 14 предикторах. Полученный показатель качества с параметрами по умолчанию очень хорош. Проведем тот же расчет, но со 100 итерациями.
> system.time(res <- tabuSearch(size = 17, iters = 100, + objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1)) user system elapsed 377.28 42.52 246.34 > max.obj [1] 0.8042194 > best.subset [1] "DX" "ar" "atr" "cci" "chv" "cmo" [7] "sign" "vsig" "slowD" "oscK" "SMI" "signal" >
Видим, что увеличение количеств итераций пропорционально увеличило время вычисления, чего не скажешь о точности предсказания. Оно увеличилось незначительно. Значит, улучшать качественные показатели нужно за счет настройки параметров модели.
Это не единственный алгоритм и пакет, который помогает выбрать лучший набор предикторов с помощью ГА. Вы можете использовать пакеты kofnGA, fSelector. Кроме них, в пакете "caret" функцией gafs() реализован выбор предикторов с помощью ГА.
6.2. Поиск лучших параметров ТС
1. Исходные данные для проектирования. Возьмем для примера эксперт MACDSampl.
В эксперте MACDSample реализован алгоритм, генерирующий сигналы при пересечении линий macd и signal. Используется один индикато.
MACD(x, nFast = 12, nSlow = 26, nSig = 9, maType, percent = TRUE, ...)Arguments
|
x |
Таймсерия одной переменной; как правило price, но может быть volume, и т.п. |
|
nFast |
Количество периодов для быстрой МА. |
|
nSlow |
Количество периодов для медленной МА |
|
nSig |
Количество периодов для сигнальной МА |
MaType – тип применяемой МА
percent – логическая, если true, то возвращается разница между быстрой и медленной МА в процентах, иначе — простая разница.
Функция MACD возвращает две переменных: macd — разница между быстрой МА и медленной МА, или скорость изменения расстояния между быстрой МА и медленной МА; signal — МА от этой разницы. MACD является частным случаем общего осциллятора, применяемого к цене. Он может быть использован также с любой таймсерией одной переменной. Временные периоды для MACD часто устанавливают как 26 и 12, но функция первоначально использовала экспоненциальные константы 0.075 и 0.15, которые ближе к 25.6667 и 12.3333 периодов.
Итак наша функция имеет 7 параметров с диапазонами изменений:
p1 - расчетная цена (Close, Med, Typ, WClose)
p2 - nFast (8:21)
p3 – nSlow(13:54)
p4 - nSig (3:13)
p5 - MAtypeMACD – тип МА для линии MACD
p6 - MatypeSig – тип МА для линии Signal
p7 — percent (TRUE, FALSE)
p5,p6 = Cs(SMA, EMA, DEMA, ZLEMA).
Сигналы для торговли можно генерировать различными способами:
Вариант 1
Buy = macd > signal
Sell = macd < signal
Вариант 2
Buy = diff(macd) > 0
Sell = diff(macd) <= 0
Вариант 3
Buy = diff(macd) > 0 & macd > 0
Sell = diff(macd) < 0 & macd < 0
Это еще один параметр оптимизации signal(1:3).
И, наконец, последний параметр — глубина истории оптимизации len = 300:1000 (количество последних баров на которых проводится оптимизация).
Итого имеем 9 параметров оптимизации. Я умышленно увеличил их количество, чтобы показать: параметром может стать все, что угодно (числа, строки и т. п.).
Критерий оптимизации — коэффициент качества К в пунктах (в моих предыдущих публикациях он уже был подробно описан).
Для оптимизации параметров нам нужно определить фитнес (объективную) функцию, которая будет вычислять критерий качества и выбрать программу оптимизации. Начнем с программы.
Мы будем применять надежный, быстрый, а главное — многократно проверенный на практике пакет "rgenoud". Основное его ограничение — в том, что его параметры должны быть или все целые, или все вещественные. Это мягкое ограничение, оно легко обходится. Функция genoud()комбинирует алгоритм эволюционного поиска с методами на базе производных (Newton or quasi-Newton) для решения различных оптимизационных проблем. Genoud()можно использовать для решения оптимизационных проблем, для которых производные не определяемы. Кроме того, используя опцию cluster, функция поддерживает использование нескольких компьютеров, процессоров или ядер для качественного параллельного вычисления.
genoud(fn, nvars, max = FALSE, pop.size = 1000, max.generations = 100, wait.generations = 10, hard.generation.limit = TRUE, starting.values = NULL, MemoryMatrix = TRUE, Domains = NULL, default.domains = 10, solution.tolerance = 0.001, gr = NULL, boundary.enforcement = 0, lexical = FALSE, gradient.check = TRUE, BFGS = TRUE, data.type.int = FALSE, hessian = FALSE, unif.seed = 812821, int.seed = 53058, print.level = 2, share.type = 0, instance.number = 0, output.path = "stdout", output.append = FALSE, project.path = NULL, P1 = 50, P2 = 50, P3 = 50, P4 = 50, P5 = 50, P6 = 50, P7 = 50, P8 = 50, P9 = 0, P9mix = NULL, BFGSburnin = 0, BFGSfn = NULL, BFGShelp = NULL, control = list(), optim.method = ifelse(boundary.enforcement < 2, "BFGS", "L-BFGS-B"), transform = FALSE, debug = FALSE, cluster = FALSE, balance = FALSE, ...)
Arguments
- fn – объективная функция, которая минимизируется (или максимизируется, если max = TRUE). Первым аргументом функции должен быть вектор с параметрами, с использованием которых и проводится минимизация. Функция должна возвращать скаляр (за исключением случая lexical = TRUE)
- nvars – количество параметров, которые будут выбраны для минимизируемой функции
- max = FALSE Максимизировать(TRUE) или Минимизировать(FALSE) объективную функцию
- pop.size = 1000 размер популяции. Это количество особей, которые будут использованы для решения оптимизационной проблемы. Есть несколько ограничений на то, каким может быть значение этого числа. Независимо от того, что численность популяции запрашивается у пользователя, число автоматически скорректируется, чтобы удовлетворить соответствующим ограничениям. Эти ограничения происходят от требований некоторых операторов ГА. В частности, оператор Р6 (простой кроссовер) и Р8 (эвристический кроссовер) требуют, чтобы количество особей было четным, т. е., они требуют двух родителей. Поэтому переменная pop.size должна быть четной. Если это не так, численность популяции увеличивается для удовлетворения этого ограничения.
- max.generations = 100 — Максимум Поколений. Это максимальное количество поколений, которые genoud выполнит при попытке оптимизировать функцию. Это — мягкое ограничение. Максимальный предел поколений будет действовать для genoud, только если hard.generation.limit будет установлен в TRUE, иначе два мягких триггера контролируют, когда genoud должен остановиться: wait.generations и gradient.check.
Несмотря на то, что переменная max.generations по умолчанию не ограничивает количество поколений, это, тем не менее, важно, потому что многие операторы используют его, чтобы скорректировать свое поведение. В сущности, многие операторы становятся менее случайными, поскольку количество поколений становится ближе к пределу max.generations. Если предел превышен и genoud решает продолжать работать, то он автоматически увеличивает предел max.generation.
- wait.generations = 10. Если не будет никакого улучшения целевой функции в этом количестве поколений, то genoud будет думать, что найден оптимум. Если триггер gradient.check был включен, genoud начнет считать wait.generations, только если градиенты будут в рамках solution.tolerance равны нулю. Другими переменными, управляющие завершением, являются max.generations и hard.generation.limit.
- hard.generation.limit = TRUE. Эта логическая переменная определяет, является ли переменная max.generations обязательным ограничением для genoud. При hard.generation.limit, выставленном на FALSE, genoud может превысить количество max.generations, если в любом из числе поколений (определенном в wait.generations) целевая функция улучшилась или если градиент (определенный в gradient.check) не равен нулю.
- starting.values = NULL - Вектор или матрица, содержащая значения параметров, которые genoud будет использовать при запуске. Используя эту опцию, пользователь может ввести одну или более особей в стартовую популяцию. Если предоставлена матрица , столбцы должны быть параметрами, а строки — особями. genoud в произвольном порядке создаст другие особи.
- Domains = NULL . Это — nvars *2 матрица. Для каждого параметра в первом столбце — нижняя граница, а во втором столбце — верхняя. Ни однаособь из стартовой популяции genoud не будет сгенерирована за пределами границ. Но некоторые операторы могут генерировать дочерние элементы, которые будут находиться за пределами границ, если флаг boundary.enforcement не будет включен.
- Если пользователь не обеспечит значений для Доменов, то genoud установит домены по умолчанию, используя default.domains.
- default.domains = 10. Если пользователь не хочет предоставлять матрицу Доменов, домены, тем не менее, могут быть установлены пользователем с этой простой в использовании скалярной опцией. Genoud создаст матрицу Доменов, устанавливая нижнюю границу для всех параметров, равную (-1 )* default.domains, и верхнюю границу, равную default.domains.
- solution.tolerance = 0.001. Это уровень допуска, используемый genoud. Числа с разницей solution.tolerance, как полагают, равны. Это особенно важно, когда дело доходит до оценки wait.generations и проведения gradient.check.
- gr = NULL. Функция, предоставляющая градиент для оптимизатора BFGS. Если это NULL, то вместо этого будут использоваться числовые градиенты.
- boundary.enforcement = 0. Эта переменная определяет уровень, до которого genoud подчиняется граничным ограничениям пространства поиска (ПП). Несмотря на значение этой переменной, ни у одной особи из стартовогопоколения значения параметров не будет за пределами границ ПП.
У boundary.enforcement есть три возможных значения: 0 (подходит все), 1 (частично ограничен), и 2 (никаких нарушений границы):
0: подходит все, эта опция позволяет любому из операторов создавать особи за пределами ПП. Эти особи будут включены в популяцию, если их фитнес-значения будут достаточно хороши. Границы важны только при генерации случайных особей.
1: частичное ограничение. Это позволяет операторам (особенно тем, которые используют базируемый на производной оптимизатор, BFGS), выйти за пределы ПП во время создания особи. Но когда оператор выбрал особь, это должно быть в приемлемых границах.
2: никакого нарушения границы. За пределами ПП оценки никогда не будут требоваться. В этом случае граничное ограничение также применено к алгоритму BFGS, которое препятствует тому, чтобы кандидаты отклонялись вне границ, определенных Доменами. Обратите внимание на то, что это вызывает использование L-BFGS-B алгоритма для оптимизации. Этот алгоритм требует, чтобы все подходящие значения и градиенты были определены и конечны для всех функциональных оценок. Если это вызывает ошибку, предложено, чтобы использовался алгоритм BFGS и установка boundary.enforcement=1.
- lexical = FALSE. Эта опция включает лексическую оптимизацию. Это оптимизация по нескольким критериям, при этом они определяются последовательно, в порядке, выдаваемом фитнес-функцией.Фитнес-функция, используемая с этой опцией, должна возвратить числовой вектор значений фитнеса в лексическом порядке. Эта опция может иметь значения FALSE, TRUE или целого числа, равного числу подходящих критериев, которые возвращены фитнес-функцией.
- gradient.check = TRUE. Если эта переменная равна TRUE, то genoud не начнет считать wait.generations, пока каждый градиент не будет с solution.tolerance близок к нулю. Эта переменная не имеет никакого эффекта, если предел max.generations был превышен, и hard.generation.limit опция была установлена в TRUE. Если BFGSburnin < 0, то это будет проигнорировано, если gradient.check = TRUE.
- BFGS = TRUE. Эта переменная обозначает, применять или нет квазиньютоновский оптимизатор производной (BFGS) к лучшей особи в конце каждого поколения после начального. Установка в FALSE не означает, что BFGS не будет применяться. В частности, если Вы хотите чтобы BFGS никогда не применялся, оператор Р9 (Локально-минимальный кроссовер) должен быть обнулен.
- data.type.int = FALSE. Эта опция устанавливает тип данных параметров функции, которая будет оптимизирована. Если переменная будет TRUE, то genoud будет искать решение среди целых чисел, когда оптимизирует параметры.
С целочисленными параметрами genoud никогда не использует информацию о производных. Это подразумевает, что оптимизатор BFGS никогда не используется — т.е., флаг BFGS установлен в FALSE. Это также подразумевает, что Оператор P9 (Локально-минимальный кроссовер) обнулен и что проверка градиента (как критерий сходимости) выключена. Независимо от того, во что были установлены другие опции, data.type.int имеет приоритет — т.е., если genoud сказано, что нужно искать по целочисленному пространству параметров, информация о градиенте никогда не рассматривается.
Нет опции, позволяющей смешать целочисленные параметры и с плавающей точкой. Если вы хотите смешать эти два типа, можно указать целочисленный параметр, а в объективной функции преобразовать целочисленный диапазон в диапазон с плавающей точкой. Например, вам нужно получить поисковую сетку от 0.1 до 1.1. Вы указываете genoud искать от 10 до 110, а в фитнес-функции разделяете этот параметр на 100.
- hessian = FALSE. Когда этот флаг установлен в TRUE, genoud возвратит матрицу гессиана в решении как часть его списка возврата. Пользователь может использовать эту матрицу, чтобы вычислить стандартные погрешности.
- unif.seed = 812821. Этим устанавливается seed для генератора псевдослучайного числа с плавающей точкой для использования genoud. Значение по умолчанию этого seed 81282. genoud использует свой собственный внутренний генератор псевдослучайных чисел (Tausworthe-Lewis-Payne генератор), чтобы допускать рекурсивные и параллельные вызовы к genoud.
- int.seed = 53058. Этим устанавливается seed для целочисленного генератора, используемого genoud. Значение по умолчанию этого seed 53058. genoud использует свой собственный внутренний генератор псевдослучайных чисел (Tausworthe-Lewis-Payne генератор), чтобы допускать рекурсивные и параллельные вызовы к genoud.
- print.level = 2. Эта переменная управляет уровнем печати того, что делает genoud. Есть 4 возможных уровня : 0 (минимальная печать), 1 ( нормальный), 2 (подробный) и 3 (отладка). Если будет выбран уровень 2, то genoud распечатает детали о популяции в каждом поколении.
- share.type = 0. Если share.type равен 1, то genoud при запуске проверит, существует ли файл проекта (см. project.path). Если такой файл существует, она инициализирует свою исходную популяцию, используя его. Эта опция может использоваться с lexical, но не с transform опцией.
Операторы. Genoud имеет и использует 9 операторов. Целочисленные значения, которые присвоены каждому из этих операторов (P1... P9) — веса. Genoud вычисляет сумму s = P1+P2 +... +P9. Каждому оператору присваивают вес, равный W_n = s / (P_n). Количество вызовов оператора обычно равняется c_n = W_n * pop.size.
Операторы Р6 (Простой кроссовер) и Р8 (Эвристический кроссовер) требуют четного количества особей для продолжения работы — иными словами, им нужны два родителя. Поэтому переменная pop.size и наборы операторов должны быть такими, чтобы у этих трех операторов было четное число особей. Если этого не происходит, genoud автоматически корректирует вверх численность популяции, чтобы это ограничение выполнялось.
Сильные проверки уникальности были встроены в операторы, чтобы гарантировать, что операторы произвели потомков, отличающихся от их родителей, но это не всегда происходит.
Эволюционный алгоритм в rgenoud использует девять операторов, которые перечислены ниже.
- P1 = 50 – Клонирование. Клонирующий оператор просто делает копии лучшего испытательного решения в текущемпоколении (независимый от этого оператора, rgenoud всегда сохраняет один экземпляр лучшего испытательного решения).
Универсальная мутация, граничная мутация и неоднородные мутации действуют на единственное испытательное решение.
- P2 = 50 – Универсальная мутация. Универсальная мутация изменяет один параметр в испытательном решении случайным значением, однородно распределенным на домене, определенном для параметра.
- P3 = 50 – Граничная мутация. Граничная мутация заменяет один параметр одной из границ его домена.
- P4 = 50 – Неоднородная мутация. Неоднородная мутация уменьшает один параметр к одной из границ с суммой уменьшения, уменьшающейся, когда количество поколений приближается к указанному максимальному числу поколений.
- P5 = 50 – Многогранный кроссовер. Многогранный кроссовер (вдохновленный симплексным поиском, Gill и др. 1981, p. 94–95), вычисляет испытательное решение, которое является выпуклой комбинацией стольких же испытательных решений, сколько есть параметров.
- P6 = 50 – Простой кроссовер. Простой кроссовер вычисляет два испытательных решения из двух входных испытательных решений, обменивая значения параметров между решениями после разделения решений в произвольном порядке в выбранной точке. Этот оператор может быть особенно эффективным, если упорядочивание параметров в каждом испытательном решении последовательное.
- P7 = 50 – Целая неоднородная мутация. Целая неоднородная мутация делает неоднородную мутацию для всех параметров в испытательном решении.
- P8 = 50 – Эвристический кроссовер. Эвристический кроссовер использует два испытательных решения для производства нового решения, расположенного вдоль вектора, который начинается в одном испытательном решении.
- P9 = 0 — Локально-минимальный кроссовер: BFGS. Локально-минимальный кроссовер вычисляет решение для нового рассмотрения в два шага. Сначала BFGS выполняет предварительно установленное число итераций, запускающихся с входного решения; после этого вычисляют выпуклую комбинацию входных решений, и BFGS выполняет итерации.
Замечание:
Самые важные опции, влияющие на качество, — это те, которые определяют численность популяции (pop.size) и число поколений, выполняемых алгоритмом (max.generations, wait.generations, hard.generation.limit и gradient.check). Поисковая производительность, как ожидают, улучшится, если численность популяции и число поколений, выполняемых программой, увеличатся. Эти и другие опции должны быть скорректированы для различных проблем вручную. Обратите особое внимание на области поиска (Домены и default.domains).
Линейные и нелинейные ограничения среди параметров могут быть представлены пользователями в их фитнес-функции. Например, если сумма параметров 1 и 2 должна быть меньше чем 725, это условие можно заложить в фитнес-функцию, пользователь будет максимизировать genoud, : if((parm1 + parm2)>= 725) {return (-99999999)}. В этом примере очень плохое фитнес-значение будет возвращено genoud, если линейное ограничение нарушено. Тогда genoud попытается найти значения параметров, которые удовлетворят ограничение.
Напишем нашу фитнес-функцию. Она должна вычислять:
MACD
сигналы
коэффициент качества
# фитнес функция-------------------------fitnes <- function(param, test = FALSE){
require(TTR)
require(magrittr)
# определим переменные
x <- pr[param[1]]
nFast <- param[2]
nSlow <- param[3]
nSig <- param[4]
macdType <- MaType[param[5]]
sigType <- MaType[param[6]]
percent <- per[param[7]]
len <- param[9]*100
# линейное ограничение для macd
if (nSlow <= nFast) return(-Inf)
# вычисляем macd
md <- MACD(x = x, nFast = nFast, nSlow = nSlow,
nSig = nSig, percent = TRUE,
maType = list(list(macdType),
list(macdType),
list(sigType)))
# вычисляем сигналы и сдвигаем вправо на 1 бар
sig <- signal(md, param[8]) %>% Lag()
#вычисляем баланс на истории длиной len
bal <- cumsum(tail(sig, len) * tail(price[ ,'CO'], len))
if(test)
{bal <<- cumsum(tail(sig, len) * tail(price[ ,'CO'], len))}
# вычисляем коэффициент качества(округляем до целого числа)
K <- ((tail(bal,1)/length(bal))* 10 ^ Dig) %>% floor()
# возвращаем полученный критерий оптимизации
return(unname(K))
}Ниже приведен листинг определения всех переменных и функций
require(Hmisc) # Типы средних = 4 ------------------------------------------- MaType <- Cs(SMA, EMA, DEMA, ZLEMA) require(dplyr) # Типы цен = 4 ----------------------------------------------- pr <- transmute(as.data.frame(price), Close = Close, Med = Med, Typ = (High + Low + Close)/3, WClose = (High + Low + 2*Close)/4) # как считать? per <- c(TRUE, FALSE) # Варианты сигналов = 3 -------------------------- signal <- function(x, type){ x <- na.omit(x) dx <- diff(x[ ,1]) %>% na.omit() x <- tail(x, length(dx)) switch(type, (x[ ,1] - x[ ,2]) %>% sign(), sign(dx), ifelse(sign(dx) == 1 & sign(x[ ,1]) == 1, 1, ifelse(sign(dx) == -1 & sign(x[ ,1]) == -1,-1, 0)) ) } # начальная крнфигунация-------------------------- par <- c(2, 12, 26, 9, 2, 1, 1, 3, 5) # пространство поиска------------------------------ dom <- matrix(c(1, 4, # для типов цен 8, 21, # для периода быстрой МА 13, 54, # для периода медленной МА 3, 13, # для периода сигнальной МА 1, 4, # тип МА для быстрой и медленной 1, 4, # тип МА для сигнальной 1, 2, # тип percent 1, 3, # вариант signal 3,10), # длина истории [300:1000] ncol = 2, byrow = TRUE) # создать кластер из доступных ядер процессора puskCluster<-function(){ library(doParallel) library(foreach) cores<-detectCores() cl<-makePSOCKcluster(cores) registerDoParallel(cl) #clusterSetRNGStream(cl) return(cl) }
Определим коэффициент качества с начальными (как правило, по умолчанию) параметрами
> K <- fitnes(par, test = TRUE) > K [1] 0 > plot(bal, t="l")
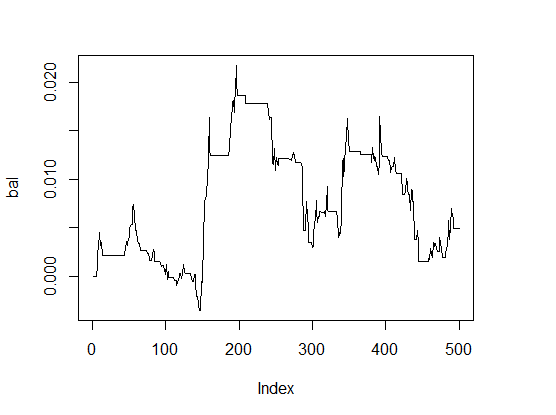
Рис.1 Баланс с параметрами по умолчанию
Результат очень плохой.
Для сравнения скорости вычисления проведем оптимизацию на одном ядре и на кластере из двух ядер процессора.
На одном ядре:
pr.max <- genoud(fitnes, nvars = 9, max = TRUE, pop.size = 500, max.generation = 300, wait.generation = 50, hard.generation.limit = FALSE, starting.values = par, Domains = dom, boundary.enforcement = 1, data.type.int = TRUE, solution.tolerance = 0.01, cluster = FALSE, print.level = 2) 'wait.generations' limit reached. No significant improvement in 50 generations. Solution Fitness Value: 1.600000e+01 Parameters at the Solution: X[ 1] : 1.000000e+00 X[ 2] : 1.400000e+01 X[ 3] : 2.600000e+01 X[ 4] : 8.000000e+00 X[ 5] : 4.000000e+00 X[ 6] : 1.000000e+00 X[ 7] : 1.000000e+00 X[ 8] : 1.000000e+00 X[ 9] : 4.000000e+00 Solution Found Generation 5 Number of Generations Run 56 Thu Mar 24 13:06:29 2016 Total run time : 0 hours 8 minutes and 13 seconds
Оптимальные параметры (генотип)
> pr.max$par [1] 1 14 26 8 4 1 1 1 4
Расшифруем (фенотип):
- тип цены pr[ ,1]= Close
- nFast = 14
- nSlow = 26
- nSig = 8
- macdType = ZLEMA
- sigType = SMA
- percent = TRUE
- signal = пересечение линий macd и signal
- длина истории = 400 баров.
Посмотрим,
как выглядит линия баланса с оптимальными
параметрами. Для этого выполним фитнес-функцию с этими параметрами и с опцией
test = TRUE.
> K.opt <- fitnes(pr.max$par, test = TRUE) > K.opt [1] 16 > plot(bal, t="l")
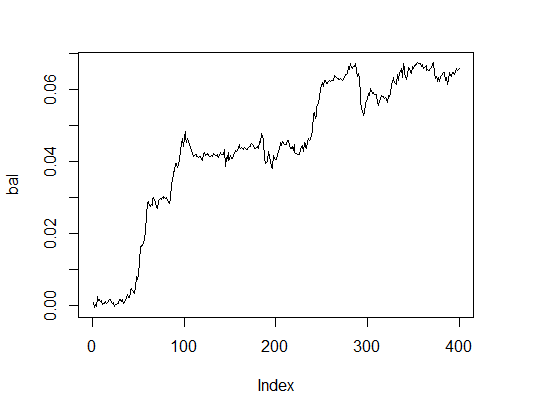
Рис.2. Баланс с оптимальными параметрами
Это вполне приемлемый результат, с которым может работать эксперт.
Выполним те же вычисления на кластере из двух ядер
# запускаем кластер
cl <- puskCluster()
# максимизация фитнес функции
# передаем каждому ядру в кластере необходимые переменные и функции
clusterExport(cl, list("price", "pr", "MaType", "par", "dom", "signal",
"fitnes", "Lag", "Dig", "per" ) )
pr.max <- genoud(fitnes, nvars = 9, max = TRUE,
pop.size = 500, max.generation = 300,
wait.generation = 50,
hard.generation.limit = FALSE,
starting.values = par, Domains = dom,
boundary.enforcement = 1,
data.type.int = TRUE,
solution.tolerance = 0.01,
cluster = cl,
print.level = 2) # только для экспериментов.
# В эксперте установить в 0
# останавливаем кластер
stopCluster(cl)
'wait.generations' limit reached.
No significant improvement in 50 generations.
Solution Fitness Value: 1.300000e+01
Parameters at the Solution:
X[ 1] : 1.000000e+00
X[ 2] : 1.900000e+01
X[ 3] : 2.000000e+01
X[ 4] : 3.000000e+00
X[ 5] : 1.000000e+00
X[ 6] : 2.000000e+00
X[ 7] : 1.000000e+00
X[ 8] : 2.000000e+00
X[ 9] : 4.000000e+00
Solution Found Generation 10
Number of Generations Run 61
Thu Mar 24 13:40:08 2016
Total run time : 0 hours 3 minutes and 34 seconds
Время гораздо лучше, однако качество немного хуже. Для решения даже такой простой задачи нужно «поиграть» с параметрами.
Вычислим cамый простой вариант
pr.max <- genoud(fitnes, nvars = 9, max = TRUE, pop.size = 500, max.generation = 100, wait.generation = 10, hard.generation.limit = TRUE, starting.values = par, Domains = dom, boundary.enforcement = 0, data.type.int = TRUE, solution.tolerance = 0.01, cluster = FALSE, print.level = 2) 'wait.generations' limit reached. No significant improvement in 10 generations. Solution Fitness Value: 1.500000e+01 Parameters at the Solution: X[ 1] : 3.000000e+00 X[ 2] : 1.100000e+01 X[ 3] : 1.300000e+01 X[ 4] : 3.000000e+00 X[ 5] : 1.000000e+00 X[ 6] : 3.000000e+00 X[ 7] : 2.000000e+00 X[ 8] : 1.000000e+00 X[ 9] : 4.000000e+00 Solution Found Generation 3 Number of Generations Run 14 Thu Mar 24 13:54:06 2016 Total run time : 0 hours 2 minutes and 32 seconds
Хороший результат. А баланс?
> k [1] 15 > plot(bal, t="l")
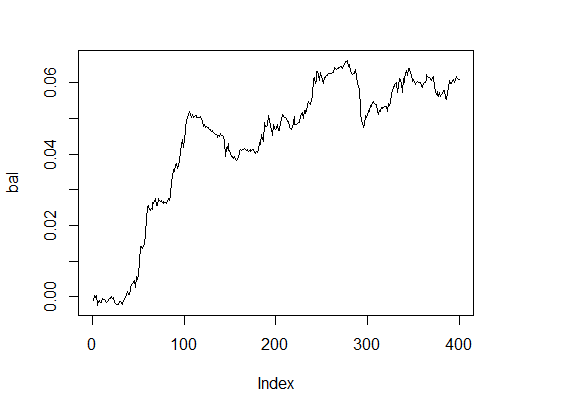
Рис.3. Баланс с оптимальными параметрами
Очень приличный результат за приемлемое время.
Для сравнения результатов генетического алгоритма с эволюционными, проведем серию экспериментов с ними. Первым испытаем алгоритм SOMA(Self-Organising Migrating Algorithm), реализованный в пакете "soma".
Самоорганизующийся миграционный алгоритм общего назначения стохастической оптимизации — подход, аналогичный генетическим алгоритмам, хотя он основан на идее серии "миграций" с помощью фиксированного набора особей, а не развития последующих поколений. Он устойчив к локальным минимумам и может быть применен к любой задаче минимизации затрат с ограниченным пространством параметров. Основная функция:
soma(costFunction, bounds, options = list(), strategy = "all2one", …) Arguments
Детали
Для настройки проведения оптимизации и критериев ее завершения доступны множество
опций.
Значения по умолчанию, используемые
здесь, рекомендованы автором
Zelinka (2004).
- pathLength: Расстояние до лидера, к которому могут мигрировать особи. Значение 1 соответствует позиции лидера, а значение больше единицы (рекомендуется) учитывает некоторое перерегулирование. По умолчанию выставлено 3.
- stepLength: Минимальный шаг, по которому оцениваются возможные шаги. Рекомендуется, чтобы длина пути не была целым кратным этого значения. Значение по умолчанию составляет 0.11.
- perturbationChance: Вероятность того, что отдельные параметры изменятся на любом данном этапе. Значение по умолчанию 0.1.
- minAbsoluteSep: Наименьшая абсолютная разница между максимальным и минимальным значениями функции стоимости. Если разница падает ниже этого минимума, то алгоритм завершается. Значение по умолчанию равно 0. Это означает, что данный критерий прекращения никогда не будет удовлетворен.
- MinRelativeSep: Наименьшая относительная разница между максимальным и минимальным значениями функции стоимости. Если разница падает ниже этого минимума, то алгоритм завершается. Значение по умолчанию составляет 0,001.
- nMigrations: Максимальное количество миграций для завершения. Значение по умолчанию 20.
- populationSize: Число особей в популяции. Рекомендуется, чтобы это значение было несколько больше, чем число оптимизируемых параметров, и оно не должно быть меньше 2. Значение по умолчанию равно 10.
Поскольку алгоритм выполняет только минимизацию, доработаем нашу фитнес-функцию для того, чтобы она выдавала значение с противоположным знаком и запустим оптимизацию.
require(soma) x <- soma(fitnes, bounds = list(min=c(1,8,13,3,1,1,1,1,3), max = c(4,21,54,13,4,4,2,3,10)), options = list(minAbsoluteSep = 3, minRelativeSep = -1, nMigrations = 20, populationSize = 20), opp = TRUE) Output level is not set; defaulting to "Info" * INFO: Starting SOMA optimisation * INFO: Relative cost separation (-2.14) is below threshold (-1) - stopping * INFO: Leader is #7, with cost -11
Лучшие параметры:
> x$population[ ,7] [1] 1.532332 15.391757 37.348099 9.860676 1.918848 [6] 2.222211 1.002087 1.182209 3.288627 Округлим > x$population[ ,7]%>% floor [1] 1 15 37 9 1 2 1 1 3
Лучшее значение фитнес-функции = 11. Это приемлемо для практического применения, но есть возможность для улучшения.
Алгоритм быстр, но нестабилен по результатам и требует тонкой настройки.
Generalized Simulated Annealing Function( Обобщенная функция симуляции отжига)
Этот алгоритм реализован в пакете «GenSA”. Эта функция может выполнять поиск глобального минимума весьма сложной нелинейной целевой функции с очень большим количеством оптимумов.
GenSA(par, fn, lower, upper, control=list(), …)
Аргументы:
- par - Начальные значения для компонентов, которые должны быть оптимизированы. По умолчанию NULL, в этом случае значения по умолчанию будут сгенерированы автоматически.
- fn - функция, которая будет минимизирована. Для минимизации функциии задается ряд параметров в виде вектора. Она должна возвращать скалярный результат.
- lower – вектор длиной length(par). Нижняя граница компонентов.
- upper - вектор длиной length(par). Верхняя граница компонентов.
- … позволяет пользователю передать дополнительные аргументы функцииfn.
- control - аргумент управления. Это список, который может быть использован для управления поведением алгоритма.
- maxit – Целое. Максимальное число итераций алгоритма.
- threshold.stop - Числовой. Программа остановится при достижении ожидаемого значения целевой функции threshold.stop. Значение по умолчанию — NULL.
- nb.stop.improvement - Целое. Программа будет остановлена, если нет каких-либо улучшений на протяжении nb.stop.improvement шагов.
- smooth - логическая. TRUE, когда целевая функция является гладкой, или почти всюду дифференцируема в области параметров; FALSE — в противном случае. Значение по умолчанию — TRUE
- max.call - Целое. Максимальное количество вызова целевой функции. По умолчанию установлено значение 1е7.
- temperature - Числовой. Начальное значение температуры.
- simple.function - Логический. TRUE означает, что целевая функция имеет лишь несколько локальных минимумов. По умолчанию установлено FALSE, что означает, что целевая функция осложнена многими локальными минимумами.
- trace.mat - Логический. По умолчанию — TRUE. Это означает, что матрица трассировки будет доступна в возвращаемом значении GenSA вызова.
Значения компонентов управления по умолчанию установлены для сложной задачи оптимизации. Для обычной задачи оптимизации со средней сложностью GenSA может найти разумное решение быстро, поэтому пользователю рекомендуется позволить GenSA остановиться раньше:
установив threshold.stop, если threshold.stop — это ожидаемое значение функции;
либо путем установки max.time, если пользователь просто хочет запустить GenSA для max.time секунд;
либо установив max.call, если пользователь просто хочет запустить GenSA в пределах max.call вызовов функций.
Для очень сложных задач оптимизации пользователю рекомендуется увеличить maxit и temperature.
Запустим оптимизацию, ограничив максимальное время исполнения 60 секундами.
require(GenSA) pr.max <- GenSA(par, fitnes, lower = c(1,8,13,3,1,1,1,1,3), upper = c(4,21,54,13,4,4,2,3,10), control = list(verbose = TRUE, simple.function = TRUE, max.time = 60), opp = TRUE)
Значение фитнес-функции и значение оптимальных параметров:
> pr.max$value * (-1) [1] 16 > par1 <- pr.max$par > par1 [1] 1.789901 14.992866 43.854988 5.714345 1.843307 [6] 1.979723 1.324855 2.639683 3.166084
Округлим:
> par1 <- pr.max$par %>% floor [1] 1 14 43 5 1 1 1 2 3
Вычислим значение фитнес-функции с этими параметрами и посмотрим на линию баланса:
> f1 <- fitnes(par1, test = TRUE) > plot(-1 * bal, t="l")
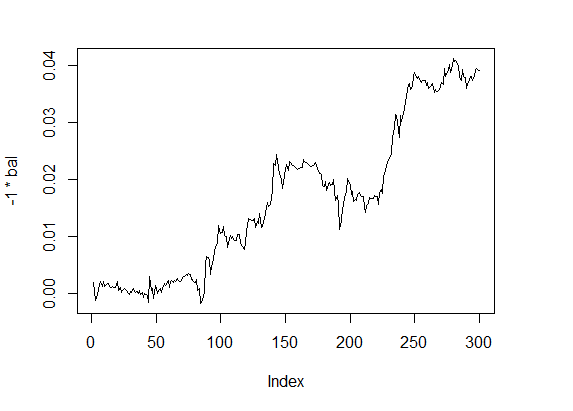
Рис.4 Баланс 4
Показатели качества — на хорошем уровне, а вычисления удивительно быстры.
Все эти и многие другие аналогичные алгоритмы (пакеты dfoptim, nlopt,CEoptim, DEoptim,RcppDE и др) оптимизируют функцию по одному критерию. Для многокритериальной оптимизации предназначен пакет mco.
7. Пути и методы улучшения качественных показателей
Проведенные нами эксперименты показали эффективность генетических алгоритмов. Для дальнейшего улучшения качественных показателей желательно выполнить дополнительные исследования с применением:
- мультикритериальной оптимизации. Например, провести оптимизацию коэффициента качества и максимальной просадки. Пакет, реализующий такую возможность, — "mco".
- попробовать реализовать динамическую самоорганизацию параметров ГА. Пакет для возможной реализации — "GA". Он предоставляет широкий выбор видов операторов селекции, кроссовера и мутации.
- экспериментально проверить возможность применения генетического программирования в торговой системе.
Заключение
Мы рассмотрели основные принципы, заложенные в эволюционных алгоритмах, их разновидности и особенности. На примере простого эксперта MACDSample мы с помощью экспериментов показали, что применение оптимизации параметров даже для такой элементарной ТС дает значительный положительный эффект.
Время выполнения оптимизации и простота в программировании позволяют производить ее во время работы эксперта без выхода из рынка. А отсутствие строгих ограничений на тип параметров оптимизации позволяют реализовать самые разнообразные виды оптимизации на различных этапах работы эксперта.
Самая важная часть работы при этом — правильно написать фитнес-функцию.
Надеюсь эта статья поможет вам понять, что это несложно, и самим попробовать внедрить оптимизацию в Ваши эксперты.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Универсальный торговый эксперт: работа с отложенными ордерами и поддержка хеджинга (часть 5)
Универсальный торговый эксперт: работа с отложенными ордерами и поддержка хеджинга (часть 5)
 Калькулятор сигналов
Калькулятор сигналов
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Ну предлагайте функции.
Подключайтесь к дискуссии. Скоро будет Ваш выход.
Это не дискуссия, это скорее "Пусть говорят" в худшем проявлении.
Рад, что раньше не заходил туда.
Пошел мыть руки.
Ужас.
Это не дискуссия, это скорее "Пусть говорят" в худшем проявлении.
Рад, что раньше не заходил туда.
Пошел мыть руки.
Ужас.
Опубликована статья Самооптимизация ЭА: генетические и эволюционные алгоритмы:
Автор: Владимир Перервенко