
Optimización propia de EA: algoritmos genéticos y evolutivos
Contenido
- Introducción
- 1. Como aparecieron los primeros algoritmos por primera vez
- 2. Algoritmos evolutivos (métodos)
- 3. Algoritmos genéticos (GA)
- 3.1. Campo de aplicación.
- 3.2. Solución de problemas
- 3.3. GA clásico
- 3.4. Estrategias de búsqueda
- 3.5. Diferencia entre la búsqueda clásica y la óptima
- 3.6. Terminología del GA
- 4. Ventajas del GA
- 5. Desventajas del GA
- 6. Parte experimental
- 6.1. Buscar la mejor combinación de predictores
- con tabuSearch
- 6.2. Buscar los mejores parámetros del TS:
- 7. Formas y métodos de mejora de las características cualitativas
- Conclusión
Introducción
Muchos traders hace tiempo que se ha dado cuenta de la necesidad de una optimización automática que no requiera que el Asesor Experto detenga el trading. Ha habido varios artículos relacionados (artículo1, Artículo2, article3, article4) publicados ya. Los experimentos en estos artículos se basan en la libreria sugerida aquí. Sin embargo, puesto que fueron publicados, han surgido nuevos algoritmos de optimización de gran alcance y nuevas formas de aplicación. Además de eso, creo que estos artículos fueron escritos por programadores y fueron pensados para programadores.
En este artículo, voy a intentar ilustrar la aplicación práctica de algoritmos genéticos (GA) sin entrar en profundidad con detalles técnicos, dirigida específicamente a traders. Para los usuarios como yo, es importante saber el principio de funcionamiento de GA, la importancia y el valor de los parámetros que afectan la calidad y velocidad de convergencia del GA y sus otras propiedades utilitarias. Por lo tanto, puedo repetirme, pero, sin embargo, se comienza con la historia de la aparición de GA, proceder a su descripción y llegar a la identificación de parámetros de la mejor GA. También, compararemos GA con algunos algoritmos evolutivos.
1. Como aparecieron los primeros algoritmos por primera vez
La historia de los cálculos evolutivos comenzó con el desarrollo de diversos modelos independientes. Principalmente eran algoritmos genéticos y sistemas de clasificación de Holanda que fueron publicados en la década de los 60s y ganó reconocimiento universal después de que el libro "Adaptación en Sistemas Naturales y Artificiales" fue lanzado en 1975, convirtiéndose en un clásico en su campo. En los años 70, en el marco de la búsqueda aleatoria, L.A. Rastrigin introdujo algunos algoritmos que utilizan ideas de comportamiento bionico. El desarrollo de estas ideas encuentran reflejo en una serie de trabajos de I.L. Bukatova sobre modelos evolutivos. Durante el desarrollo de ideas de M.L. Tsetlin sobre comportamiento recomendable y óptimo de máquinas estocásticas, Y.I. Neumark sugirió buscar extremum globales basados en un equipo independiente autómata que modela los procesos de desarrollo y eliminación de las especies. Fogel y Walsh son individuos que contribuyeron enormemente al desarrollo de la programación evolutiva. A pesar de su diferencia en los enfoques, cada una de estas "escuelas" basa su estrategia en algunos principios que existen en la naturaleza y les simplifica para que puedan ser utilizados en una computadora.
Esfuerzos encaminados a modelar la evolución por analogía con los sistemas de la naturaleza pueden dividirse en dos categorías principales.
- Sistemas de modelados basados en principios biológicos. Se han utilizado con éxito para las tareas de optimización de la función y pueden ser fácilmente descritos en lenguaje no-biológico.
- Sistemas que aparecen más realistas desde la perspectiva biológica, pero no son particularmente beneficiosos en el sentido de aplicación. Más se asemejan a los sistemas biológicos y son menos direccionales (o no direccionales en absoluto). Tienen un comportamiento complicado e interesante y, al parecer, se encuentra poco uso práctico.
Ciertamente, no podemos dividir estos aspectos tan estrictamente en la práctica. Estas categorías son en realidad dos polos donde varios sistemas informáticos se encuentran entre ellos. Más cerca del primer poste hay algoritmos evolutivos como la programación evolutiva, algoritmos genéticos y estrategias de la evolución, por ejemplo. Más cerca el segundo Polo hay sistemas que pueden clasificarse como Vida Artificial.
2. Algoritmos evolutivos (métodos)
Algoritmos evolutivos, una división de inteligencia artificial (sección del modelo evolutivo), que utiliza modelos de los procesos de selección natural. Enumeramos algunos de ellos:
- algoritmos genéticos : algoritmo de búsqueda heurística utilizada para la optimización y modelado a través de la selección aleatoria, combinaciones y variaciones de los parámetros deseados;
programación genética : creación automatizada o cambio de programas usando algoritmos genéticos;
Programación evolutiva — similar a la programación genética, pero la estructura del programa es consistente, solo los valores numéricos están sujetos a cambios;
estrategias evolutivas , se asemejan a los algoritmos genéticos, pero sólo se adminten mutaciones positivas de la siguiente generación;
evolución diferencial;
neuroevolución — similares a la programación genética, pero los genomas son unas redes neuronales artificiales donde se producen la evolución de los pesos en la topología de red especificada o además de evolución también se lleva a cabo la evolución de la topología de los pesos.
Todas las posiciones del modelo básico en la teoría de la evolución biológica, los procesos de selección, cruzamientos, mutación y reproducción. El comportamiento de las especies se determina por el medio ambiente. Múltiples especies se conocen como población. La población evoluciona según reglas de selección de acuerdo con una función objetivo por el medio ambiente. De esta manera, cada espécimen (individual) en la población tiene su valor en el medio ambiente. Sólo se multiplican las especies más adecuadas. La recombinación y mutación permiten a los individuos cambiar y adaptarse al medio ambiente. Estos algoritmos se refieren a mecanismos de búsqueda adaptativa.
Los métodos evolutivos (EM), métodos aproximados (heurísticos) de resolver tareas de optimización y síntesis de la estructura. La mayoría de los EM se basan en el enfoque estático para investigar situaciones y aproximaciones iterativas a la solución deseada.
Los cálculos evolutivos constituyen una de las secciones de la inteligencia artificial. Al crear sistemas de inteligencia artificial utilizando este enfoque, el énfasis se hace en la construcción del modelo inicial y reglas basadas en que se puede cambiar (evolucionar). Al mismo tiempo, el modelo puede crearse mediante la aplicación de diversos métodos. Por ejemplo, puede ser red neuronal o un conjunto de reglas lógicas. Recocido, los algoritmos genéticos, PSO, ACO y la programación genética se refieren a los métodos evolutivos principales.
A diferencia de los precisos métodos de programación matemática, los métodos evolutivos permiten encontrar soluciones cercanas a lo óptimo en tiempo razonable y a diferencia de otros métodos heurísticos de optimización que se caracterizan por una dependencia considerablemente menor de características de la aplicación (es decir más universal) y en la mayoría de los casos proporciona un mejor grado de aproximación a la solución óptima. La universalidad de la EM también está determinada por la aplicación a tareas de espacio de variables gestionadas no metrizables (es decir que pueden existir valores lingüísticos, que no tengan ninguna medida cuantificable entre las variables gestionadas incluidas).
En simulado templado, se imita el proceso de reducir al mínimo la energía potencial del cuerpo durante el templado de detalles. El cambio de algunos parámetros gestionados ocurre en el punto actual. Siempre es aceptado un nuevo punto cuando mejora la función de destino y, con probabilidad pequeña, cuando empeora.
El caso más importante de la EM consiste en algoritmos y métodos genéticos. Los Algoritmos Genéticos (GA) se basan en la búsqueda de las mejores soluciones utilizando herencia y el fortalecimiento de características útiles de varios objetos de una aplicación específica en el proceso de imitación de su evolución.
Las propiedades de los objetos se presentan con valores de parámetros combinados en un disco que se llama cromosoma en Subconjuntos EM. de los cromosomas llamados la población que opera en Georgia. Imitación de los principios genéticos: selección estocástica de los padres entre los miembros de la población, cruce cromosómico, la selección de niños para ser incluido en la nueva generación de objetos basados en la evaluación de la función objetivo. Este proceso conduce a la mejora evolutiva de los valores de una función objetivo (función de utilidad) de generación en generación.
También existen métodos entre EM que a diferencia de los GA operan con un solo cromosoma en lugar de múltiples cromosomas. De ssta manera, el método de búsqueda local discreto llamado Hillclimbing se basa en el cambio al azar de diferentes parámetros (valores de campos en un registro) o, en otras palabras de los genes en un cromosoma. Tales cambios se llaman mutaciones. Después de cada mutación, se evalúa la función de la aptitud. El resultado de la mutación se guarda en un cromosoma sólo si la aptitud mejoró. En el "modelado de recocido", se guarda el resultado de la mutación con cierta probabilidad que depende del valor obtenido.
En el método de Optimización de enjambre de partículas , se imita el comportamiento de varios agentes que pretenden alinear su estado con un estado del mejor agente.
El método ACO se basa en la imitación del comportamiento de las hormigas que acortar sus rutas desde una fuente de comida a su hormiguero.
3. Algoritmos genéticos (GA)
Métodos de búsqueda de adaptación Algoritmos genéticos — que se han utilizado comúnmente para resolver tareas de optimización funcional últimamente. Se basan en procesos genéticos de organismos biológicos: las poblaciones biológicas evolucionan durante varias generaciones y siguen la regla de la selección natural y el principio de supervivencia del más apto, como descubierto por Charles Darwin. Por imitación de este proceso, los algoritmos genéticos son capaces de evolución de soluciones de tareas reales, si son codificados adecuadamente.
En la naturaleza, las especies en la población compiten uno contra el otro por diversos recursos, como alimentos y agua. Además, los miembros de la población del mismo tipo con frecuencia compiten por atraer a un socio. Las especies que más se ajustan al entorno tienen mejores oportunidades de crear descendencia. La especie inferior o bien no se reproduce o tienen sólo unas pocas crías. Esto significa que los genes de especies bien adaptadas se extenderán con creciente número de descendientes en cada generación nueva. Una combinación de características de éxito de padres diferentes puede conducir a veces a descendientes "demasiado adaptados" que son más adaptables que cualquiera de sus padres. De esta manera, una especie se desarrolla y ajusta al medio ambiente aún mejor.
Algoritmos genéticos establecen una analogía con este mecanismo. Funcionan con un sistema de "especies": población, donde cada uno de ellos proporciona una posible solución de un problema. Cada especímen se evalúa con una medida de «ajuste» de acuerdo a lo "bueno" de una solución pertinente. Las especies más aptas obtienen la oportunidad de "crear" descendencia utilizando "mestizaje" con otras especies de la población. Esto conduce a la aparición de nuevas especies que combinan algunas características heredadas de sus padres. Las especies menos aptas son menos probabilidades de crear crias, por lo que las características que poseen poco a poco van a desaparecer de la población en el proceso de evolución.
Así es cómo se reproduce toda la nueva población de soluciones aceptables por la selección de los mejores representantes de una generación anterior, los cruzamientos y obtención de nuevas especies. Esta nueva generación contiene una mayor proporción de las características que los miembros «buenos» de una pandilla de generación anterior. De esta forma, las buenas características se distribuyen en toda la población de generación en generación. El cruce de las especies más aptas conduce a las zonas más de perspectiva del espacio de búsqueda que se está explorando. En última instancia, la población descenderá a la solución óptima.
Hay diferentes formas de implementación de ideas de la evolución biológica dentro del GA
3.1. Campo de aplicación
Las tareas reales resueltas pueden ser identificadas como una búsqueda del valor óptimo, donde el valor es una función compleja que depende de varios parámetros de entrada. En algunos casos, es de interés encontrar los valores de los parámetros que se utilizan para alcanzar el valor más exacto de la función. En otros casos, no es necesario precisión óptima, y cualquier valor que es mejor que un valor ajustado puede ser considerado como una solución. En este caso, los algoritmos genéticos con frecuencia se convierten en el método más adecuado para buscar valores "buenos". La fuerza de un algoritmo genético es su capacidad de manipular simultáneamente varios parámetros. Esta característica del GA fue utilizada en cientos de aplicaciones, incluyendo el diseño de aeronaves, ajuste de parámetros de algoritmos y búsqueda de condiciones estables de sistemas de ecuaciones diferenciales no lineales.
Sin embargo, hay casos en los que el GA no funciona tan eficientemente como se espera.
Vamos a suponer que existe una tarea real que implica la búsqueda de la decisión óptima. ¿Cómo saber si es conveniente para el GA? No ha habido ninguna respuesta determinante a esta pregunta hasta ahora. Sin embargo, muchos investigadores comparten el supuesto de que el GA tiene buenas posibilidades de convertirse en un proceso de búsqueda eficiente en los siguientes casos:
- Si el campo de búsqueda a ser investigado es grande, y se supone que no es completamente liso y unimodal (es decir, contiene un extremo liso);
- Si la función de la aptitud contiene ruido;
- o si una tarea no requiere una determinación estricta del óptimo global.
En otras palabras, en situaciones cuando es necesario encontrar la solución "buena" aceptable (que es algo común con tareas reales), GA compite y supera a otros métodos que no aplican el conocimiento de la zona de búsqueda.
Si el área es pequeña, entonces puede encontrar solución mediante la búsqueda exhaustiva, y puede estar a seguro de que se encuentra la mejor solución posible, mientras que GA se haría probablemente a converger en un óptimo local, en lugar de una solución global mejor. Si el espacio es liso y unimodal, entonces cualquier algoritmo de gradiente (por ejemplo, el método de descenso más empinado) será más eficaz que GA
Si hay alguna información adicional sobre el área de búsqueda (por ejemplo, el área de un conocido "problema del vendedor ambulante"), los métodos de búsqueda que utilizan heurística determinada por el área, con frecuencia superan cualquier método universal que es lo que es el GA. Teniendo en cuenta una estructura relativamente compleja de la función de la aptitud, los métodos de búsqueda con una única solución en el momento, como un simple método de la pendiente, podría "quedar atrapado en" una solución local. Sin embargo, se considera que los algoritmos genéticos tienen menos posibilidades para converger en un óptimo local y con seguridad la función en un paisaje multi-extremado, ya que operan con toda la "población" de soluciones.
Ciertamente, tales supuestos estrictamente no predicen cuando GA será un procedimiento de búsqueda eficiente compitiendo con otros procedimientos. La eficacia de GA altamente depende de detalles como el método de codificación de soluciones, parámetros, operadores, parcial criterio de éxito. El trabajo teórico que se documenta en la literatura sobre algoritmos genéticos hasta el momento no da motivos de discutir el desarrollo de mecanismos estrictos de predicciones precisas.
3.2. Solución de problemas
Los algoritmos genéticos se aplican para resolver las siguientes tareas:- Optimización de funciones
- Optimización de las solicitudes de bases de datos
- Diversas tareas en los gráficos (problemas de viajantes, colorear, encontrar pares)
- Establecimiento y entrenamiento de redes neuronales artificiales
- Tareas de diseño
- Creación de horarios
- Estrategias de juego
- Teoría de la aproximación
3.3. GA clásico
Operación de GA simpleEl GA simple genera aleatoriamente la población inicial de las estructuras. la operativa GA es un proceso de iteración que continúa hasta que es aplicado el número de generaciones obtenido o cualquier otro criterio de terminación. La selección proporcional de aptitud, se implementa un solo punto de cruce y mutación en cada generación del algoritmo.
En primer lugar, la selección proporcional designa a cada estructura la probabilidad de Ps(i) que es igual al ratio dentre su aptitud a la aptitud total de la población.
Entonces seleccionan a todas las n especies (con reemplazo) para el mamejo de más datos genéticos según el valor de Ps(i). La selección proporcional más simple es una selección de la rueda de la ruleta, Goldberg, 1989 c) — las especies se seleccionan con n "vueltas" de una ruleta. La rueda de la ruleta contiene un sector para cada miembro de la población. El tamaño del i-ésimo sector es proporcional al valor correspondiente al Ps(i). En esta selección, los miembros más aptos de la población son más propensos de ser seleccionados de entre las especies menos aptas.
Después de la selección, las n especies seleccionadas están sujetas al cruce (a veces llamado recombinación) con una probabilidad de ajuste del Pc. n cadenas al azar se dividen en n/2 pares. Para cada par con probabilidad Pc, puede ser aplicado el cruce. En consecuencia, el cruce no ocurre con probabilidad 1-Pc, y las especies constante pasan a la etapa de mutación. Si hay un cruce, las crias obtenidas reemplazan a sus padres y proceden a la mutación.
Un punto de cruce funciona como sigue. En primer lugar, uno de los puntos de interrupción l-1 se seleccionaron al azar. (Punto de quiebre es un área entre bytes adyacentes en un string). Las estructuras de ambos padres se dividen en dos segmentos partiendo de este punto. Luego, se ligan los segmentos correspondientes de diferentes padres, y se crean dos genotipos de los niños.
Después de la etapa de transición, se realizan las operaciones de mutación . Cada byte con la probabilidad Pm se cambia al contrario en cada cadena que está sujeta a mutación. La población obtenida después de la mutación sobrescribe la antigua población, y así es como termina un bucle de una generación. Las generaciones siguientes se tratan del mismo modo: selección, cruce y mutación.
Las investigaciones con GA actualmente ofrecen un montón de otras operaciones de selección, cruce y mutación. A continuación se muestran los más comunes. En primer lugar, selección de torneo (Brindle, 1981; Goldberg y Deb, 1991). Implementa n torneos para seleccionar n especies. Cada torneo se basa en la selección de k elementos de la población y la selección del especímen mejor entre todos. La selección de torneo con k = 2 es la más común.
Métodos de selección élite (De Jong, 1975) garantiza que va a sobrevivir durante la selección de los mejores miembros de la población. El proceso más común es una retención obligatoria de un solo especímen mejor, si no pasa por el proceso de selección, el cruce y mutación como el resto. El Elitismo puede integrarse en cualquier método de selección estándar.
El cruce de dos puntos (Cavicchio, 1970; Goldberg, 1989c) y el cruce uniforme (Syswerda, 1989), son alternativas decentes para el operador con un punto. Hay dos puntos de interrupción en el cruce de dos puntos, y los cromosomas padres intercambian un segmento que está entre estos dos puntos. En un cruce uniforme, cada byte del primer padre se hereda con el primer niño con un conjunto de probabilidades, de lo contrario, este byte es transferido al segundo niño. Y viceversa.
Principales operadores del algoritmo genético
Operador de selección
En esta etapa, la población óptima se selecciona para su posterior reproducción más. Normalmente se toma el número específico de los más aptos. Tiene sentido dejar caer los "clones", es decir, especies con el mismo conjunto de genes.
Operador de cruce
El mestizaje se realiza más a menudo, sobre las dos mejores especies. Los resultados generalmente son dos especies con componentes de sus "padres". El objetivo de este operador es distribuir genes "buenos" a través de la población y para ajustar la densidad de población hacia zonas donde es alta ya.
Operación de mutación
La operador de mutación simplemente cambia el número arbitrario de elementos en un especímen a otros números arbitrarios. De hecho, es un elemento disipativo que tira del anclaje local por un lado y añade nueva información a la población por otro lado.
- En el caso de una señal binaria, se invierte un byte
- Cambia el signo numérico a un valor determinado (probablemente, el valor más cercano).
- Reemplaza a otro signo nominal.
Criterio de Stop
- Solución global o subóptima
- Salida a "llanuras"...
- Agotar el número de generaciones para evolucionar
- Agotar el tiempo restante para evolucionar
- Agotar al número de llamadas a la función del destino especificado
3.4. Estrategias de búsqueda
La búsqueda es uno de formas universales de encontrar soluciones para los casos en que no se conoce la secuencia de pasos que conducen a lo óptimo.Hay dos estrategias de búsqueda: explotación de la mejor solución y estudiar el espacio de soluciones. Un método gradiente es un ejemplo de una estrategia que selecciona la mejor solución para una posible mejora, haciendo caso omiso de la investigación de la zona de toda búsqueda. Una búsqueda al azar es un ejemplo de una estrategia que, por el contrario, estudia el área de soluciones mientras se ignoran las investigaciones de los campos de la perspectiva de la zona de búsqueda. Un algoritmo genético es una clase de métodos de búsqueda de una función general que combinan elementos de ambas estrategias. La aplicación de estos métodos permite mantener el equilibrio aceptable entre la investigación y explotación de la mejor solución. En el inicio del funcionamiento del algoritmo genético, la población es aleatoria y tiene diversos elementos. Por lo tanto, el operador de cruce lleva a cabo una amplia investigación del área de solución. Con el aumento de la función de la aptitud de las soluciones obtenidas, el operador de cruce permite investigar cada uno de su entorno. En otras palabras, el tipo de estrategia de búsqueda (explotación de la mejor solución o investigación del área de solución) para el operador de cruce está definido con una diversidad de población, en lugar del operador en sí mismo.
3.5. Diferencia de la clásica búsqueda de lo óptimo
En general, el algoritmo de resolución de problemas de optimización es una secuencia de pasos de cálculo que convergen asintóticamente a la solución óptima. La mayoría de los métodos de optimización clásica genera una determinada secuencia de cálculos que se basa en un gradiente o un derivado de una función objetivo de un rango más alto. Estos métodos se aplican a un punto de salida única de una zona de búsqueda. Entonces la decisión es mejorada gradualmente hacia el más rápido aumento o disminución de la función de destino. Con este planteamiento detallado, existe el riesgo de golpear lo óptimo local.
Un algoritmo genético realiza una búsqueda simultánea en varias direcciones mediante el uso de la población de posibles soluciones. La conmutación de una población a otra evita golpear el óptimo local. La Población sufre algo similar con la evolución: soluciones relativamente buenas se reproducen en cada generación, mientras que los relativamente malos mueren se van. Los algoritmos genéticos utilizan reglas de probabilidad para identificar una reproducción o un cromosoma destruido para dirigir la búsqueda a las áreas de posible mejora de la función objetivo.
Muchos algoritmos genéticos se implementaron en los últimos años, y en la mayoría de los casos difieren drásticamente de los del algoritmo clásico inicial. Y esta es la razón por qué en vez de un modelo, hay una amplia gama de clases de algoritmo que llevan poca semejanza con los demás bajo el término "algoritmos genéticos". Los investigadores experimentaron con varios tipos de vistas, los operadores de cruce y mutaciones, operadores especiales y diversos enfoques para la reproducción y selección.
Aunque el modelo de desarrollo evolutivo aplicado en GA es mayoritariamnete simplificado en comparación con su análogo de la naturaleza, sin embargo, GA es una poderosa herramienta y puede ser aplicado con éxito para una amplia clase de tareas, incluidas las que son difíciles y a veces imposible de resolver utilizando otros métodos. Sin embargo, GA junto con otros métodos de cálculo evolutivo, no puede garantizar la búsqueda de una solución global en tiempo polinómico. Tampoco puede garantizar que se encontrará incluso una solución global. Sin embargo, los algoritmos genéticos son buenos buscando "relativamente buena" solución "relativamente rápida". Casi siempre estos métodos serán más eficaces que GA en velocidad y exactitud que las soluciones encontradas, donde pueden utilizarse métodos especiales para encontrar una solución. La principal ventaja del GAs es que se puede aplicar incluso para tareas complicadas, si no existen métodos especiales. Incluso donde existen métodos de trabajo buenos, el GA puede utilizarse para mejorar.
3.6. Terminología del GA
Desde que GA se deriva de la ciencia natural (genética) y Ciencias de la computación, la terminología aplicada es una mezcla de compuestos naturales y artificiales. Los términos refiridos a GA y la solución de problemas de optimización se proporcionan en la tabla. 1.1.
Tabla 1.
| Algoritmo genético | Explicación |
|---|---|
| Cromosoma | Posible solución (conjunto de parámetros) |
| Genes | Parámetros que están optimizados |
| Locus (localización) | Posición de un gen en un cromosoma |
| Alelo | Valor del gen |
| Fenotipo | Solución sin codificar |
| Genotipo | Solución codificada |
Clásico (un punto) sobre cruces.
El algoritmo "Tradicional" genético utiliza un cruce de un punto donde los dos cromosomas se cortan una vez en un punto específico, y las piezas obtenidas se intercambian luego. También se descubrieron otros algoritmos distintos con otros tipos de cruce incluyendo con frecuencia más de un punto de corte. DeJong ha investigado la eficacia de un multi-acentuado cruce y llegó a la conclusión de que dos puntos de cruce muestran mejora, pero más adición de puntos de sobre cruce reduce la actividad de un algoritmo genético. El problema de añadir puntos de sobre cruces es que los bloques estándar probablemente serán interrumpidos. Sin embargo, la ventaja de varios puntos de sobre crossing es que el área de los astados se pueden investigar con más detalle.
Dos puntos que cruzan.
Cruzando dos puntos (y varios puntos de cruce generalmente) los cromosomas se consideran como bucles formados al conectar juntos los extremos de los cromosomas lineales. Para cambiar un segmento de un ciclo a un segmento de otro ciclo, se requiere una selección de dos puntos de corte. En esta presentación, un cruce de un punto se puede considerar como un cruce con dos puntos, pero con un punto de corte fijo al principio de la cadena. Por lo tanto, un punto doble de sobre cruce soluciona la misma tarea que un cruce de un punto, pero de una manera más completa. Un cromosoma que se considera como un ciclo puede contener un montón de bloques estándar, porque pueden realizar un "retorno cíclico" al final de la cadena. Muchos investigadores actualmente están de acuerdo en que, en general, el cruce de dos puntos es mejor que un cruce de un punto.
Unificación (homogéneo) de sobre cruces.
La unificación de sobre cruces es fundamentalmente diferente de un cruce de un punto. En una generación, cada gen se crea copiando un gen relevante de uno de los progenitores u otro que se seleccionó de acuerdo con la máscara de cruce generada aleatoriamente. Si una máscara de cruce tiene 1, se copia un gen del primer progenitor, si es 0, entonces se copia un gen del segundo progenitor. Con el fin de crear una segunda generación, se repite el proceso, pero al revés, con los progenitores intercambiados. Una nueva máscara de cruce se genera aleatoriamente para cada par de progenitores.
Cruce diferencial.
Aparte de este cruce, hay otros métodos de cruce. Por ejemplo, para buscar una función de mínimos y máximos de muchas variables físicas, el "cruce diferencial" es la más acertado. Describiremos su concepto brevemente Supongamos que a y b son dos individuos en una población, es decir vectores físicos de los que depende de nuestra función. Entonces un hojo (c) se calcula mediante la fórmula с=a+k*(a-b), donde k, es una cierta relación física (que puede depender de || a b || — una distancia entre vectores).
La mutación en este modelo es una adición a un vector de longitud corto aleatorio individual. Si la función de salida es continua, entonces el modelo funciona bien. Es aún mejor si es suave.
Inversión y reordenamiento.
El orden de los genes en un cromosoma es a menudo crítico para los bloques de construcción que permiten realizar una operación eficiente del algoritmo. Durante la operación del algoritmo, se sugirieron métodos para reordenar las posiciones de los genes en un cromosoma. Uno de tales métodos es la inversión que se invierte el orden de los genes entre dos posiciones seleccionadas al azar en un cromosoma. (Cuando se utilizan estos métodos, los genes necesitan tener cierta "marca", por lo que podrían ser identificados correctamente a pesar de su posición en un cromosoma.)
El objetivo del reordenamiento es tratar de encontrar el orden de los genes que tengan el mejor potencial evolutivo. Muchos investigadores han aplicado la inversión en su trabajo, aunque parece que pocos han tratado de justificarla o evaluar su contribución. Goldberg y Bridges analizan el operador de reordenamiento en una tarea muy pequeña, mostrando que se puede dar una cierta ventaja, sin embargo, concluyen que sus métodos no tienen la misma ventaja con tareas grandes.
El reordenamiento también aumenta considerablemente el área de búsqueda. No sólo trata que un algoritmo genético encontre buenos conjuntos de valores de los genes, a la vez también intenta encontrar su orden "correcto". Se trata de un reto mayor a resolver.
¿Qué es la epistasis?
El término "epistasis" en genética se determina como la influencia de un gen en la aptitud de un individuo dependiendo del valor de un gen presente en otro lugar. En otras palabras, los genetistas utilizan el término "epistasis" en términos de un efecto de "switch" o "enmascarado": "un gen se considera epistáticas cuando su presencia suprime la influencia de un gen en otro lugar. Los genes epistáticos a veces se llaman inhibidores debido a su influencia en otros genes que se describen como hipóstasis.
En la terminología de GA puede sonar como: "La aptitud de un espécimen depende de la posición de los cromosomas en un genotipo".
¿Qué es un óptimo falso?
Uno de los principios fundamentales de los algoritmos genéticos es que los cromosomas en plantillas contenidas en grado óptimo global aumentan en frecuencia. Esto es especialmente adecuado para plantillas cortas de pequeño orden, conocido como bloques de construcción. En última instancia, estas plantillas óptimas se reunirán en el cruce, y se creará un cromosoma óptimo global. Pero si las plantillas que no se encuentran en un óptimo global aumentan en frecuencia más rápidamente que otros, entonces se engaña a un algoritmo genético y se le desvia desde el óptimo global, a lugar cercano. Este fenómeno se conoce como óptimo falso.
El Óptimo falso es un caso particular de epistasis y se analizó profundamente por Goldberg y otros. El Óptimo falso está directamente relacionado con el impacto negativo del epistasis en algoritmos genéticos.
Estadísticamente, la plantilla se incrementará con la frecuencia en la población, si su aptitud es mayor que la aptitud promedio de todas las plantillas en una población. La tarea está marcada como una tarea óptima falsa, si la aptitud promedio de las plantillas que no se encuentran en un óptimo global es más que la aptitud promedio de otras plantillas. Las tareas óptimas falsas son complejas. Sin embargo, Grefenstette ingeniosamente demuestra que no siempre hay complicaciones. Después de la primera generación, un algoritmo genético no obtiene una selección objetiva de los puntos en la zona de búsqueda. Por lo tanto no puede evaluar objetivamente una aptitud promedio global de una plantilla. Sólo es capaz de obtener una evaluación sesgada de una adecuación de la plantilla. A veces este prejuicio ayuda un algoritmo genético a que coincida (incluso si una tarea, por lo contrario, podría ser un óptimo falso más fuerte).
¿Qué es endogamia, exogamia, elección selectiva, panmixia?
Existen varios enfoques para seleccionar un par de progenitores. El más simple de todos ellos es la panmixia. Este enfoque implica una selección al azar de un par de progenitores cuando ambas especies de un par son seleccionadas al azar de toda la población. En este caso, cualquier specipem puede convertirse en un miembro de varios pares. A pesar de la sencillez, este enfoque es universal para la solución de diversas tareas. Sin embargo, es relativamente importante para un número de población, ya que la eficiencia del algoritmo que implementa este acercamiento disminuye con un aumento de la población.
Con un método selectivo de elegir especies para un par de progenitores, sólo aquellas especies cuya aptitud está por encima de la aptitud promedio en una población pueden llegar a ser "padres", en igual probabilidad de esos candidatos para hacer un par.
Este enfoque permite una convergencia más rápida del algoritmo. Sin embargo, debido a una convergencia rápida, una elección selectiva de un par de progenitores no es adecuada cuando deben definirse algunos extremos, porque el algoritmo llega rápidamente a una de las soluciones con tales tareas. Además, para algunas clases de tareas con un complicado paisaje de aptitud, la convergencia rápida puede convertir una convergencia prematura en una solución casi óptima. Esta desventaja puede ser parcialmente compensada con un uso de un mecanismo de selección conveniente que "frenaría" la convergencia de un algoritmo demasiado rápido.
Endogamia es un método cuando el primer miembro de un par es al azar, y el segundo especimen es seleccionado por ser tan cercano como sea posible del primer miembro.
El concepto de similitud de especies se aplica también para la exogamia. Ahora, sin embargo, se forman pares de especies que son lo más lejos posible.
Los dos últimos métodos diferentemente influyen en el comportamiento de un algoritmo genético. Por lo tanto, la endogamia puede caracterizarse por la propiedad de concentrar la búsqueda en nodos locales, que, de hecho, conduce a dividir una población en distintos grupos locales alrededor de las áreas sospechosas del extremo del paisaje. La exogamia está dirigida a prevenir la convergencia del algoritmo para encontrar ya soluciones por forzar el algoritmo de búsqueda a través de nuevas áreas que quedan por explorar.
Autoorganitzación dinámica de parámetros del GA
Con frecuencia, la selección de parámetros de un algoritmo genético y operadores genéticos específicos se realiza utilizando la intuición, puesto que no existe evidencia objetiva que algunos ajustes y los operadores son más ventajosos. Sin embargo, no debemos olvidar que el punto del GA se encuentra en la dinámica, el algoritmo "suavidad" y cálculos realizados. Entonces ¿por qué no dejar que el algoritmo se configure a sí mismo a la hora de resolver una tarea y adaptarse a él?
La forma más fácil es organizar la adaptación de los operadores aplicados. Para ello, construimos algunos (cuanto más mejor) varios operadores de selección (elite, al azar, ruleta,..), cruzando (un punto, dos puntos, unificado,..) y mutación (al azar un elemento, absoluta,..) en el algoritmo. Vamos a establecer probabilidades iguales de aplicación para cada operador. En cada lazo del algoritmo, seleccionamos un operador para cada grupo (opción, cruzando, mutación) según distribución posible. Se marca en el especimen obtenido del operador que fue recibido. Entonces, si hay una nueva distribución de probabilidades se calculan basándose en información contenida en la población (probabilidad de aplicar el operador es proporcional al número de especies en una población con este operador), a continuación, un algoritmo genético recibe un mecanismo de una adaptación dinámica.
Este enfoque ofrece otra ventaja: ahora, no hay que preocuparse por el generador aplicado de figuras al azar (lineales, exponenciales, etc.), ya que el algoritmo dinámicamente cambia el modo de distribución.
Método de migración y selección artificial
A diferencia de un GA regular, la macro evolución se realiza, es decir, no sólo una, sino que se crean varias poblaciones. Se realiza una búsqueda genética aquí uniendo progenitores de distintas poblaciones.
Método de equilibrio interrumpido
El método se basa en la teoría paleontológica del equilibrio interrumpido que describe una evolución rápida a través cambios volcánicos y otros cambios de la corteza terrestre. Para aplicar este método en tareas técnicas, se aconseja mezclar aleatoriamente individuos de una población tras cada generación y luego formar nuevas generaciones actuales. Como con la fauna, aquí se pueden sugerir la selección inconsciente de pares de progenitores y una sintética selección de pares de progenitores. Entonces, los resultados de ambas selecciones deben mezclarse al azar, y en lugar de mantener el tamaño de la población constante, deben gestionarse dependiendo de la presencia de mejores individuos. Dicha modificación de los métodos de equilibrio interrumpido puede reducir las poblaciones poco sólidas y aumentar las poblaciones con las mejores especies.
El método de equilibrio interrumpido es un método de estrés de gran alcance para cambiar el ambiente que se utiliza para la salida eficiente de pozos locales.
4. Ventajas del GA
Hay dos ventajas principales de los algoritmos genéticos sobre métodos de optimización clásica.
1. GA tiene ningún requisito matemático considerable de los tipos de funciones objetivo y restricciones. Un investigador no debería simplificar el objeto del modelo perderdiendo la adecuación y garantizando artificialmente la aplicación de los métodos matemáticos disponibles. Las más diversas funciones de destino y tipos de restricción (lineales y no lineal) que se definen discretamente, sin interrupciones y se puede utilizar uno mixto universal.
2. Cuando se usan métodos clásicos paso a paso, el óptimo global se puede encontrar sólo cuando un problema tiene una propiedad de convexidad. Al mismo tiempo, operaciones evolutivas de algoritmos genéticos permiten buscar una óptima global eficiente.
Menos graves, pero todavía importantes ventajas de GA:
un gran número de parámetros libres que permiten construir heurística eficaz;
paralelización eficiente;
trabajos tan buenos como una búsqueda al azar;
la conexión con la biología da algo de esperanza para el excepcional rendimiento del GA.
5. Desventajas del GA
Múltiples parámetros libres que hacen del "funcionamiento con GA" un "juego con GA"
Falta de apoyo evidente para la convergencia
En funciones de objetivo genético simple (liso, una extrema y etc.), siempre pierde en velocidad contra los algoritmos de búsqueda simple
6. Parte experimental
Todos los experimentos se realizarán en el entorno de lenguajes R 3.2.4. Utilizamos un conjunto de datos para la formación de un modelo y la mayoría de funciones desde el artículo anterior.
La Sección depositaria CRAN que contiene un gran número de paquetes dedicados, destinada a tareas de programación matemáticas y optimización. Vamos a aplicar varios métodos diferentes de GA y EM para la solución de las tareas mencionadas. Hay sólo un requisito para los modelos que participan en el proceso de optimización: velocidad. No es aconsejable aplicar métodos que entrenan en cien segundos. En consideración que en cada generación habrá un mínimo de 100 especies y la población pasará por varias (de unidad a decenas) épocas, el proceso de optimización se extenderá con un tiempo inaceptable. En los artículos anteriores se aplicaron dos tipos de redes profundas (con inicialización RBM y SAE). Ambos han demostrado alta velocidad y bien pueden ser usados para una optimización genética.
Vamos a resolver dos tareas de optimización: la búsqueda de la mejor combinación de predictores y la selección de parámetros óptimos de los indicadores. Vamos a aplicar el XGBoost (impulsar el gradiente extremo) algoritmo que se utiliza a menudo para resolver la primera tarea (selección del predictor) para aprender nuevos algoritmos. Como se menciona en las fuentes, muestran muy buenos resultados en tareas de clasificación. El algoritmo está disponible para lenguajes R, Python, Java. En lenguaje R, este algoritmo está implementado en el paquete v "xgboost" . 0.4-3.
Para resolver la segunda tarea (selección de parámetros óptimos de los indicadores), vamos a utilizar un EA con el más simple MACDsample y ver lo que se puede obtener con su ayuda cuando se usa la optimización genética sobre el flujo.
6.1. Buscar la mejor combinación de predictores
Es importante definir lo siguiente para resolver la tarea de optimización:
parámetros que se optimizarán;
criterio de optimización — escala que deben ser maximizada/minimizada. Puede haber más de un criterio;
función objetivo (objetivo, aptitud) que calcula el valor del criterio de optimización.
La función de aptitud en nuestro caso se implementará constantemente como sigue:
formando la estructura de datos iniciales;
dividiéndolo en un tren de pruebaa;
formación del modelo;
prueba el modelo;
calcular el criterio de optimización.
El criterio de optimización puede ser de métricas estándar como precisión, memoria, Kappa, AUC, así como los proporcionados por un desarrollador. Utilizamos un error de clasificación en esta capacidad.
Se realizará la búsqueda de la mejor combinación de predictores con el paquete "tabuSearch « v.1.1 que es una extensión del algoritmo de HillClimbing . El algoritmo de TabuSearch optimiza una cadena binaria mediante el uso de una función objetivo identificada por un usuario. Como resultado, da la mejor configuración binaria con el valor más alto de la función objetivo. Vamos a utilizar este algoritmo para buscar la mejor combinación de la quiniela.
La función principal:
tabuSearch(size = 10, iters = 100, objFunc = NULL, config = NULL, neigh = size, listSize = 9, nRestarts = 10, repeatAll = 1, verbose = FALSE)
Argumentos:
size – longitud de la configuración binaria optimizada;
iters – número de iteraciones en la búsqueda de algoritmo preliminar;
objFun – un método sugerido por el usuario que evalúa la función objetivo para la cadena binaria especificada;
config – configuración de arranque;
iters – número de configuraciones adyacentes para la comprobación en cada iteración. Por defecto, es igual a la longitud de la cadena binaria. Si un número es menor que la longitud de la cadena, los vecinos se seleccionan aleatoriamente;
listSize – tamaño de la lista tabú;
nRestart s -tiempos máximos de reinicio en la etapa intensiva de búsqueda de algoritmos;
repeatAll – número de repeticiones de búsqueda;
verbose , lógico es true, que se imprime el nombre de la actual fase del algoritmo, por ejemplo, una etapa preliminar, etapa de intensificación, etapa de diversificación.
Vamos a escribir una función objetivo y proceder a experimentar.
ObjFun <- function(th){
require(xgboost)
# Salir si son todos ceros en la cadena binaria en
if (sum(th) == 0) return(0)
# nombres de predictores que corresponden a 1 en la cadena binaria
sub <- subset[th != 0]
# Crear la estructura para la formación de un modelo
dtrain <- xgb.DMatrix(data = x.train[ ,sub], label = y.train)
# entrenear un modelo
bst = xgb.train(params = par, data = dtrain, nrounds = nround, verbose = 0)
# Calcular pronósticos con el conjunto del texto
pred <- predict(bst, x.test[ ,sub])
# Calcular el error de pronóstico
err <- mean(as.numeric(pred > 0.5) != y.test)
# Devuelve el criterio de calidad
return(1 - err)
}
Para los cálculos debemos preparar conjuntos de datos para entrenamiento y pruebas del modelo y también para definir los parámetros del modelo y la configuración inicial de la optimización. Utilizamos los mismos datos y funciones a partir del artículo anterior (EURUSD/M30, 6000 barras como en 14.02.16).
Listado con comentarios:
#---tabuSearch---------------------- require(tabuSearch) require(magrittr) require(xgboost) # Salida dataframe dt <- form.data(n = 34, z = 50, len = 0) # Nombres de los predictores en el conjunto inicial subset <- colnames(In()) set.seed(54321, kind = "L'Ecuyer-CMRG") # Preparar conjuntos de entrenamiento y ensayo DT <- prepareTrain(x = dt[ ,subset], y = dt$y, balance = FALSE, rati = 4/5, mod = "stratified", norm = FALSE, meth = method) train <- DT$train test <- DT$test x.train <- train[ ,subset] %>% as.matrix() y.train <- train$y %>% as.numeric() %>% subtract(1) x.test <- test[ ,subset] %>% as.matrix() y.test <- test$y %>% as.numeric() %>% subtract(1) # Vector binario inicial th <- rep(1,length(subset)) # Modelo de parámetros par <- list(max.depth = 3, eta = 1, silent = 0, nthread = 2, objective = 'binary:logistic') nround = 10 # Configuración inicial conf <- matrix(1,1,17) res <- tabuSearch(size = 17, iters = 10, objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1) # Máximo valor de la función objetivo max.obj <- max(res$eUtilityKeep) # La mejor combinación del vector binario best.comb <- which.max(res$eUtilityKeep)%>% res$configKeep[., ] # El mejor conjunto de predictores best.subset <- subset[best.comb != 0]
Iniciar optimización con diez iteraciones y ver lo que es el conjunto de criterio y predictor de máxima calidad.
> system.time(res <- tabuSearch(size = 17, iters = 10, + objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1)) sistema de usuario transcurrido 36.55 4.41 23.77 > max.obj [1] 0.8 > best.subset [1] "DX" "ADX" "oscDX" "ar" "tr" "atr" [7] "chv" "cmo" "vsig" "rsi" "slowD" "oscK" [13] "signal" "oscKST" > summary(res) Configuración Tabu Type = configuración binaria Se repite el num de algoritmo = 1 Num de iteraciones en cada búsqueda prelim = 10 Total num de iteraciones = 30 Num de únicas configuraciones mejores = 23 Tamaño de la lista Tabu = 9 Longitud de configuración = 17 Num de vecinos en cada iteración = 17 Resultados: Highest valor objetivo fn = 0.79662 Occurs # veces = 2 Número óptimo de variables = c(14, 14)
Los cálculos tomaron aproximadamente 37 segundos con una precisión de la predicción de alrededor de 0,8 y 14 predictores. El indicador de calidad obtenido con la configuración predeterminada es muy bueno. Vamos a hacer otro cálculo, pero con 100 iteraciones.
> system.time(res <- tabuSearch(size = 17, iters = 100, + objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1)) sistema de usuario transcurrido 377.28 42.52 246.34 > max.obj [1] 0.8042194 > best.subset [1] "DX" "ar" "atr" "cci" "chv" "cmo" [7] "sign" "vsig" "slowD" "oscK" "SMI" "signal" >
Vemos que el aumento de las iteraciones ha aumentado proporcionalmente el tiempo de cálculo, a diferencia de la precisión del pronóstico. Ha aumentado sólo ligeramente. Esto significa que los indicadores deben mejorarse a través de la configuración de parámetros del modelo de calidad.
Este no es el único algoritmo y paquete que ayuda a seleccionar el mejor conjunto de predictores con GA Usted puede utilizar el kofnGA, paquetes del fSelector. Aparte de aquellos, una selección de predictores es implementada por la función gafs() del paquete de "cursor" con GA
6.2. Busca los mejores parámetros del ТС
1. Salida de datos para la proyección. Usaremos el EA MACDSampl como ejemplo.
En el EA MACDSample, se lleva a cabo un algoritmo que genera las señales al cruzar el macd y las secuencias de señal Se utiliza un indicador.
MACD(x, nFast = 12, nSlow = 26, nSig = 9, maType, percent = TRUE, ...)Argumentos
|
x |
Timeseries de una variable; normalmente es el precio, pero puede ser el volumen etc. |
|
nFast |
Número de períodos para MA rápida. |
|
nSlow |
Número de períodos para MA lenta |
|
nSig |
Número de períodos para la señal del MA |
MaType – tipo de MA aplicada
percent – lógica si true, entonces devuelve la diferencia entre la MA rápida y lenta en porcentaje, de lo contrario, diferencia simple.
La función MACD devuelve dos variables: macd — diferencia entre la MA rápida y la МА lenta o velocidad de cambio de la distancia entre la МА rápida y МА lenta; señal , МА de esta diferencia. MACD es un caso particular de un oscilador común aplicado al precio. Puede también ser utilizado con cualquier serie de una variable. Con frecuencia se establecen periodos para MACD como 26 y 12, pero inicialmente utiliza la función exponencial constante 0.075 y 0.15 más cercanos a los períodos 25.6667 y 12.3333.
Por lo tanto, nuestra función tiene 7 parámetros con una rango de cambio:
p1 — precio calculado (Close, Med, Typ, WClose)
p2 — nFast (8:21)
p3 — nSlow(13:54)
p4 — nSig (3:13)
p5 — MAtypeMACD – tipo de МА para el string MACD
p6 — MatypeSig – tipo de МА para el string de Señal
p7 — porcentage (TRUE, FALSE)
p5,p6 = Cs(SMA, EMA, DEMA, ZLEMA).
Las señales de Trading pueden generarse de diferentes maneras:
Opción 1
Buy = macd > signal
Sell = macd < signal
Opción 2
Buy = diff(macd) > 0
Sell = diff(macd) <= 0
Opción 3
Buy = diff(macd) > 0 & macd > 0
Sell = diff(macd) < 0 & macd < 0
Este es otro parámetro de optimización signal(1:3).
Y, finalmente, el último parámetro, profundidad del historial de optimización len = 300:1000 (el número de barras pasadas donde se realiza la optimización).
En total tenemos 9 parámetros de optimización. He aumentado su número a propósito para demostrar que nada puede utilizarse como un parámetro (figuras y strinfs).
El criterio de optimización — relación calidad К en puntos (en mis publicaciones anteriores ya fue bien descrito).
Para la optimización de los parámetros que necesitamos para identificar una función de aptitud (objetivo) seleccionaremos el programa de optimización y calculamos el criterio de calidad. Vamos a comenzar con el programa.
Se aplicará seguro, rápido y, lo más importante, las repetidamente probadas del paquete ''rgenoud « . Su principal restricción implica todos los parámetros para que todos sean integer o physical. Esta es una restricción suave, y suavemente pasa por alto. La función genoud() combina el algoritmo de búsqueda evolutiva con métodos sobre la base de derivado (Newton o quasi-Newton) para resolver distintos problemas de optimización. Genoud() puede utilizarse para resolver problemas de optimización de derivados que no están definidos. Además, utilizando la opción de cluster, la función apoya el uso de varios equipos, procesadores y núcleos de cálculo paralelos cualitativo.
genoud(fn, nvars, max = FALSE, pop.size = 1000, max.generations = 100, wait.generations = 10, hard.generation.limit = TRUE, starting.values = NULL, MemoryMatrix = TRUE, Domains = NULL, default.domains = 10, solution.tolerance = 0.001, gr = NULL, boundary.enforcement = 0, lexical = FALSE, gradient.check = TRUE, BFGS = TRUE, data.type.int = FALSE, hessian = FALSE, unif.seed = 812821, int.seed = 53058, print.level = 2, share.type = 0, instance.number = 0, output.path = "stdout", output.append = FALSE, project.path = NULL, P1 = 50, P2 = 50, P3 = 50, P4 = 50, P5 = 50, P6 = 50, P7 = 50, P8 = 50, P9 = 0, P9mix = NULL, BFGSburnin = 0, BFGSfn = NULL, BFGShelp = NULL, control = list(), optim.method = ifelse(boundary.enforcement < 2, "BFGS", "L-BFGS-B"), transform = FALSE, debug = FALSE, cluster = FALSE, balance = FALSE, ...)
Argumentos
- fn -función objetivo que se minimiza (o maximiza si max = TRUE). El primer argumento de la función debe ser un vector de parámetros que se utilizan para minimizar. La función debe devolver el escalar (excepto cuando lexical = TRUE)
- nvars – cantidad de parámetros que serán seleccionados para una función reducida al mínimo
- max = FALSE maximiza (TRUE) o minimiza (FALSE) la función objetivo
- pop.Size = tamaño 1000 de población. Se trata de un número de especies que se utilizarán para resolver problemas de optimización. Hay algunas restricciones con respecto al valor de esta figura. A pesar del número de población que se solicita de un usuario, la cifra se corrige automáticamente para satisfacer las restricciones pertinentes. Estas restricciones se derivan de las exigencias de algunos operadores de GA. En particular, el operador Р6 (cruce simple) y Р8 (cruce heurístico) requieren un número de especies uniformes, es decir, piden a ambos progenitores. Por lo tanto, incluso la variable pop.size debe estar. Si no es así, entonces se incrementa la población para satisfacer estas restricciones.
- max.generations = 100 — generaciones máximas. Se trata de un número máximo de generaciones que genoud actuará en el intento de optimizar la función. Se trata de una restricción leve. Las generaciones máximas actuarán de genoud, sólo si hard.generation.limit se establece en TRUE, de lo contrario dos disparadores suaves de control cuándo se debe dejar genoud : wait.generations y gradient.check.
A pesar de que la variable max.generations no limite el número de generaciones por defecto, sin embargo es importante porque muchos operadores lo utilizan para corregir su comportamiento. De hecho, muchos operadores se convierten en menos al azar, puesto que el número de generaciones se convierten más cercanos del límite de max.generations . Si se supera el límite y genoud decide proceder con la operación automáticamente aumenta el límite de max.generation.
- wait.generations = 10. Si la función objetivo no mejora en este número de generaciones, entonces genoud piensa que se encuentra el óptimo. Si estaba habilitado el gatillo gradient.check, genoud se iniciará el cálculo wait.generations sólo si los gradientes dentro de solution.tolerance son iguales a cero. Otras variables que gestionan la terminación son max.generations y hard.generation.limit.
- hard.generation.limit = TRUE. Esta variable lógica determina si la variable max.generations es una restricción obligatoria de genoud. Cuando hard.generation.limit se muestra en FALSE, genoud puede exceder la cantidad de max.generations, si la función objetivo fue mejorada en cualquier número de generaciones (determinada en wait.generations), o si no son iguales cero gradientes (determinada en gradient.check).
- Starting.Values = NULL, vector o matriz que contiene los valores de los parámetros que genoud utilizará al comienzo. Mediante esta opción, un usuario puede escribir una o más especies en la población de partida. Si se proporciona una matriz, entonces las columnas deben ser parámetros y cadenas, especies. genoud creará otras especies en un orden aleatorio.
- Domains = NULL . Esto es nvars *2 matriz. Para cada parámetro en la primera columna, frontera inferior, segunda columna, frontera superior. Ninguna especie degenoud a partir de población no generará más allá de las fronteras. Pero algunos operadores pueden generar elementos subsidiarios que se colocarán más allá de las fronteras, si no se activa la bandera boundary.enforcement.
- Si un usuario no proporciona valores para los dominios, entonces genoud establece dominios predeterminados a través de default.domains.
- default.domains = 10. Si un usuario no desea proporcionar una matriz de dominios, después, sin embargo, los dominios se pueden fijar por un usuario con esta opción escalable fácil de usar. Genoud va a crear la matriz de dominio estableciendo una frontera inferior para todos los parámetros que es igual a (-1) * default.domainsy una frontera superior que es igual a default.domains.
- solution.tolerance = 0.001. Este es un nivel de seguridad utilizado en Reber. Figuras con la diferencia de solution.tolerance, como lo sugiere, son iguales. Esto es particularmente importante cuando llega a la evaluación de wait.generations y realiza gradient.check.
- gr = NULL. Función que proporciona un gradiente para optimizar BFGS. Si es NULL, entonces los gradientes numéricos se utilizará en su lugar.
- boundary.enforcement = 0. Esta variable determina el nivel hasta que genoud está sujeto a restricciones de límite de la zona de búsqueda. A pesar del valor de esta variable, ninguna de las especies de la generación inicial tendrán los valores de los parámetros más allá de los límites de la zona de búsqueda.
boundary.enforcement tiene tres valores posibles: 0 (todo adecuado), 1 (restricción parcial) y 2 (no violaciones de límites):
0: todo conveniente, esta opción permite a cualquier operador crear especies más allá de la zona de búsqueda. Estas especies se incluirán en una población, si sus valores de las aptitudes son suficientemente buenas. Los Internos son importantes sólo cuando la generación de especies es al azar.
1: restricción parcial. Esto permite a los operadores (especialmente aquellos que utilizan el optimizador basado en un derivado, BFGS), ir más allá de los límites de la zona de búsqueda durante la creación de un espécimen. Pero cuando un operador selecciona una muestra, debe ser dentro de límites razonables.
2: no hay violación de límites. Más allá de la zona de búsqueda, las evaluaciones nunca será necesarias. En este caso, la restricción de los límites también se aplica al algoritmo BFGS que impide que a los candidatos desviarsa más allá de los límites determinados por dominios. Por favor prestar atención a lo que provoca el uso del algoritmo L-BFGS-B para la optimización. Este algoritmo requiere que todos los valores adecuados y gradientes sean determinados y finalmente para todas las evaluaciones funcionales. Si esta causa de error, se aconseja utilizar algoritmo BFGS y el ajuste de boundary.enforcement=1.
- lexical = FALSE. Esta opción incluye optimización léxica. Esto es una optimización por varios criterios, y se determina secuencialmente en la orden dada por la función de la aptitud. La función de la aptitud con esta opción debe devolver el vector numérico de valores de aptitud en el orden léxico. Esta opción puede tener FALSE, TRUE o número entero de valores que es igual al número de criterios adecuados devueltos por la función de la aptitud.
- gradient.check = TRUE. Si esta variable es igual a TRUE, genoud no arranca contando wait.generations, hasta que cada gradiente no sea cercano a cero con solution.tolerance. Esta variable no tiene ningún efecto si se supera el límite de max.generations, y la opción hard.generation.limit se establece en TRUE. Si BFGSburnin < 0, entonces esto será ignorado, si gradient.check = TRUE.
- BFGS = TRUE. Si el optimizador derivado de quasi-Newton (BFGS), esta preguntas variables deben aplicarse hacia el mejor ejemplar al final de todas las generaciones después de la inicial. El ajuste en FALSE no significa que no se aplican BFGS. En particular, si se desea que nunca se aplique BFGS, el operador de Р9 (cruce mínimo local) debe ser restablecido.
- data.type.int = FALSE. Esta opción establece el tipo de datos de parámetros de la función optimizada. Si la variable es TRUE, entonces >genoud buscará solución entre números enteros cuando se optimizan los parámetros.
Con los parámetros del número entero, >genoud nunca utiliza información sobre derivados. Esto implica que nunca se utiliza el optimizador BFGS — es decir, la bandera BFGS se establece en FALSE. Esto también implica que el operador de P9 (cruce mínimo local) se reinicie, y la comprobación de un gradiente (como un criterio de convergencia) está deshabilitada. A pesar de que se incorporaban otras opciones, data.type.int tiene una prioridad, es decir, si >genoud indica que la búsqueda debe realizarse por el área entera de parámetros, la información sobre el gradiente no se considera.
No hay ninguna opción que permite mezclar parámetros enteros con un punto flotante. Si desea mezclar estos dos tipos, entonces se puede indicar un parámetro entero y la gama del número entero puede ser transformada a la gama con un punto flotante en la función objetivo. Por ejemplo, usted necesita obtener la red de búsqueda de 0.1 a 1.1. Indicar genoud a la búsqueda de 10 a 110 y luego divida este parámetro por 100 en la función de la aptitud.
- hessian = FALSE. Cuando esta bandera se establece en TRUE, Reber devuelve la matriz del Hessian en una solución como parte de su lista de vuelta. Un usuario puede utilizar esta matriz para calcular errores estándar.
- unif.seed = 812821. Esto establece la seed para un generador de una pseudo figura aleatoria con un punto flotante para utilizar genoud. El valor por defecto de esta seed es 81282. genoud utiliza su generador interno personal de pseudo figuras al azar (generador de Tausworthe-Lewis-Payne) para permitir las llamadas recursivas y paralelas a genoud.
- int.seed = 53058. Esto fija la v para un generador de número entero que utiliza genoud. El valor predeterminado de la seed es 53058. genoud utiliza su generador interno personal de pseudo figuras al azar (generador de Tausworthe-Lewis-Payne) para permitir las llamadas recursivas y paralelas a genoud.
- print.level = 2. Esta variable maneja el nivel de impresión de lo que genoud hace. Hay 4 niveles posibles: 0 (mínima impresión), 1 (normal), 2 (detallado) y 3 (depuración). Si se selecciona el nivel 2, genoud mostrará detalles sobre la población en cada generación.
- share.type = 0. Si share.type es igual a 1, entonces genoud comprobará al principio si existe el archivo del proyecto (ver project.path). Si este archivo existe, inicializa su población de partida utilizandolo. Esta opción puede utilizarse con lexical, pero no con la opción de transform .
Los operadores. Genoud tiene y utiliza los 9 operadores. Los pesos son valores enteros que se asignan a cada uno de estos operadores (P1... P9). Genoud calcula el total s = P1 + P2 +... + P9. Los pesos igual a W_n = s / (P_n) son asignados a cada operador. El número de llamadas de operador normalmente es igual a c_n = W_n * pop.size.
Los operadores Р6 (cruce Simple) y Р8 (cruce heurístico) requieren un número de especies para proceder con la operación, en otras palabras requieren de dos progenitores. Por lo tanto, la variable pop.size y los sistemas de los operadores deben ser específicos para asegurarse de que estos tres operadores tienen un número de especies. Si no sucede, genoud automáticamente aumenta la población, para cumplir con esta restricción.
Se construlleron fuertes controles de singularidad en los operadores para garantizar que los operadores producen a hojos que son diferentes de sus progenitores, pero no siempre ocurre.
Los algoritmos evolutivos en rgenoud utilizan nueve operadores que se mencionan a continuación.
- P1 = 50 – Cloning. Operador Cloning simplemente hace copias de la mejor solución en la generación actual (independiente de este operador, rgenoud siempre guarda una muestra de la mejor solución).
Mutación universal, mutación límite y mutación heterogénea afectan la única solución de prueba.
- P2 = 50 – Mutación universal. Mutación universal cambia un parámetro en la solución de prueba con un valor aleatorio uniformemente distribuido en un dominio definido por el parámetro.
- P3 = 50 – Mutación límite. Mutación límite cambia un parámetro con una de las fronteras de su dominio.
- P4 = 50 – Mutación heterogénea. Mutación Heterogénea disminuye un parámetro a una de las fronteras con un total de disminución disminuyendo cuando el número de generaciones se acerca al número máximo indicado de generaciones.
- P5 = 50 – Cruce multifacético. Cruce Multifacético (inspirado por la simple búsqueda, Gill y otros. 1981, p. 94 – 95), calcula la solución de prueba que tiene como parámetros una combinación de convexidad de la misma cantidad de soluciones de ensayo.
- P6 = 50 – Cruce simple. Cruce Simple calcula dos soluciones de prueba de dos soluciones de entrada, cambiando los valores de los parámetros entre las soluciones después de dividir aleatoriamente soluciones en un punto seleccionado. Este operador puede ser especialmente eficaz si la matriz de parámetros en cada solución de ensayo es secuencial.
- P7 = 50 – Mutación heterogénea entera. Mutación heterogénea entera hace mutación heterogénea de todos los parámetros en la solución de la prueba.
- P8 = 50 – Cruce heurístico. Cruce Heurístico utiliza dos soluciones de prueba para una nueva solución que se encuentra a lo largo del vector que comienza en una solución.
- P9 = 0 — Cruce mínimo local: BFGS. Cruce Local mínimo calcula una solución para una nueva consideración en dos pasos. Primera BFGS realiza un número preliminar de iteraciones de la solución de entrada; Después se calcula la combinación de convexidad de soluciones de entrada y se repite BFGS.
Observaciones:
Las opciones más importantes los afectan a la calidad son los que definen el tamaño de la población (pop.size) y el número de generaciones realizado por el algoritmo (max.generations, wait.generations, hard.generation.limit y gradient.check). El rendimiento de la búsqueda, como se esperaba, se mejora si el tamaño de la población. y aumentará el número de generaciones realizado por el programa. Estas y otras opciones se deben corregir para los diversos problemas manualmente. Preste más atención en las áreas de búsqueda (dominios y default.domains).
Se pueden presentar restricciones lineales y no lineales entre los parámetros por los usuarios en sus funciones de aptitud. Por ejemplo, si el total de los parámetros 1 y 2 está por debajo de 725, a continuación, esta condición puede ser embebida en la función de la aptitud, un usuario maximizará genoud,: Si ((parm1 + parm2) > = 725) {vuelta (-99999999)}. En este ejemplo, se devolverá un valor de condición física muy malo a genoud, si se viola una restricción lineal. Luego genoud intenta encontrar valores de parámetros que satisfagan la restricción.
Escribiremos la función de la aptitud. Deben ser capaces de calcular:
MACD
Señales
Ratio de calidad
# función de aptitud -------------------------aptitud <- function(param, test = FALSE){
require(TTR)
require(magrittr)
# definición de variables
x <- pr[param[1]]
nFast <- param[2]
nSlow <- param[3]
nSig <- param[4]
macdType <- MaType[param[5]]
sigType <- MaType[param[6]]
percent <- per[param[7]]
len <- param[9]*100
# restricción lineal para MACD
if (nSlow <= nFast) return(-Inf)
# Cálculo del macd
md <- MACD(x = x, nFast = nFast, nSlow = nSlow,
nSig = nSig, percent = TRUE,
maType = list(list(macdType),
list(macdType),
list(sigType)))
# calcular señales y shift a la derecha de 1 barra
sig <- signal(md, param[8]) %>% Lag()
#calcular el balance del historial con longitud len
bal <- cumsum(tail(sig, len) * tail(price[ ,'CO'], len))
if(test)
{bal <<- cumsum(tail(sig, len) * tail(price[ ,'CO'], len))}
# calcula ratio de calidad (redondeado a entero to integer)
K <- ((tail(bal,1)/length(bal))* 10 ^ Dig) %>% floor()
# volver al criterio de optimización obtenida
return(unname(K))
}
A continuación un listado para calcular todas las variables y funciones
require(Hmisc) # Tipo de la media = 4 ------------------------------------------- MaType <- Cs(SMA, EMA, DEMA, ZLEMA) require(dplyr) # Tipos de precios = 4 ----------------------------------------------- pr <- transmute(as.data.frame(price), Close = Close, Med = Med, Typ = (High + Low + Close)/3, WClose = (High + Low + 2*Close)/4) # ¿Cómo calcular? per <- c(TRUE, FALSE) # Tipos de señales = 3 -------------------------- signal <- function(x, type){ x <- na.omit(x) dx <- diff(x[ ,1]) %>% na.omit() x <- tail(x, length(dx)) switch(type, (x[ ,1] - x[ ,2]) %>% sign(), sign(dx), ifelse(sign(dx) == 1 & sign(x[ ,1]) == 1, 1, ifelse(sign(dx) == -1 & sign(x[ ,1]) == -1,-1, 0)) ) } # configuración inicial--------------------------- par <- c(2, 12, 26, 9, 2, 1, 1, 3, 5) # área de búsqueda-------------------------------------- dom <- matrix(c(1, 4, # for types of prices 8, 21, # para el periodo de la МА rápida 13, 54, # para periodo de la MA lenta 3, 13, # para la señal del periodo de la MA 1, 4, # tipo de la МА type rápida o lenta 1, 4, # tipo de señal de la MA 1, 2, # tipo porcentaje 1, 3, # opciones de la señal 3,10), # longitud del historial [300:1000] ncol = 2, byrow = TRUE) # crear un clúster de núcleos disponibles de procesamiento puskCluster<-function(){ library(doParallel) library(foreach) cores<-detectCores() cl<-makePSOCKcluster(cores) registerDoParallel(cl) #clusterSetRNGStream(cl) return(cl) }
Definir ratio de calidad con parámetros iniciales (generalmente por defecto)
> K <- fitnes(par, test = TRUE) > K [1] 0 > plot(bal, t="l")
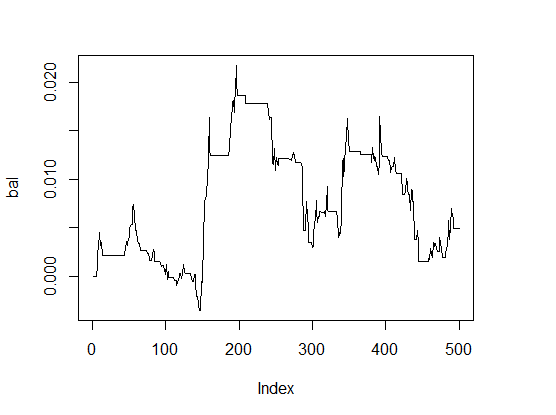
Fig.1 Balance con parámetros por defecto
Los resultados son muy malos.
Para comparar la velocidad de cálculo, vamos a realizar la optimización con un núcleo y con el clúster de dos núcleos de procesamiento.
Sobre un nucleo:
pr.max <- genoud(fitnes, nvars = 9, max = TRUE, pop.size = 500, max.generation = 300, wait.generation = 50, hard.generation.limit = FALSE, starting.values = par, Domains = dom, boundary.enforcement = 1, data.type.int = TRUE, solution.tolerance = 0.01, cluster = FALSE, print.level = 2) 'wait.generations' limit reached. No mejoría significativa en 50 generaciones. Valor de aptitud la la solución: 1.600000e + 01 Parámetros de la solución: X[ 1] : 1.000000e+00 X[ 2] : 1.400000e+01 X[ 3] : 2.600000e+01 X[ 4] : 8.000000e+00 X[ 5] : 4.000000e+00 X[ 6] : 1.000000e+00 X[ 7] : 1.000000e+00 X[ 8] : 1.000000e+00 X[ 9] : 4.000000e+00 Solución encontrada de generación 5 Número de generaciones ejecutadas 56 Thu Mar 24 13:06:29 2016 Duración total: 0 horas 8 minutos y 13 segundos
Parámetros óptimos (henotype)
> pr.max$par [1] 1 14 26 8 4 1 1 1 4
Nos descifra (fenotipo):
- price type pr[ ,1]= Close
- nFast = 14
- nSlow = 26
- nSig = 8
- macdType = ZLEMA
- sigType = SMA
- percent = TRUE
- señal = intersección de las líneas macd y las lineas de señal
- longitud del historial = 400 barras.
Vamos a ver cómo aparece la línea de balance con parámetros óptimos. Para ello vamos a realizar una función de aptitud con estos parámetros y con la prueba de opción verdadera =.
> K.opt <- fitnes(pr.max$par, test = TRUE) > K.opt [1] 16 > plot(bal, t="l")
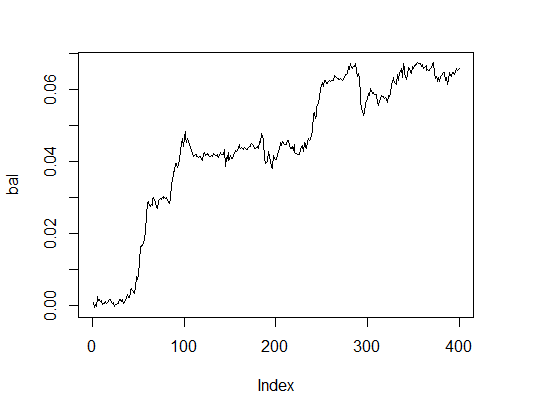
Fig.2. Balance con parámetros óptimos
Este es un resultado aceptable con el que un asesor experto puede funcionar.
Vamos a calcular el mismo en el clúster que contiene dos núcleos
# iniciar el cluster
cl <- puskCluster()
# maximizar la función de aptitud
# enviar variables necesarias y funciones a cada núcleo del cluster
clusterExport(cl, list("price", "pr", "MaType", "par", "dom", "signal",
"fitnes", "Lag", "Dig", "per" ) )
pr.max <- genoud(fitnes, nvars = 9, max = TRUE,
pop.size = 500, max.generation = 300,
wait.generation = 50,
hard.generation.limit = FALSE,
starting.values = par, Domains = dom,
boundary.enforcement = 1,
data.type.int = TRUE,
solution.tolerance = 0.01,
cluster = cl,
print.level = 2) # only for experiments.
# Establecer 0 en EA
# parar el cluster
stopCluster(cl)
'wait.generations' limit reached.
No mejoría significativa en 50 generaciones.
Valor de aptitud de la solución: 1.300000e+01
Parámetros de la solución:
X[ 1] : 1.000000e+00
X[ 2] : 1.900000e+01
X[ 3] : 2.000000e+01
X[ 4] : 3.000000e+00
X[ 5] : 1.000000e+00
X[ 6] : 2.000000e+00
X[ 7] : 1.000000e+00
X[ 8] : 2.000000e+00
X[ 9] : 4.000000e+00
Solución encontrada generación 10
Número de generaciones ejecutar 61
Thu Mar 24 13:40:08 2016
Duración total: 0 horas 3 minutos y 34 segundos
El tiempo parece mucho mejor, pero la calidad es ligeramente inferior. Para solucionar esto una tarea sencilla, es importante para "jugar" con los parámetros.
Calcularemos la opción más simple
pr.max <- genoud(fitnes, nvars = 9, max = TRUE, pop.size = 500, max.generation = 100, wait.generation = 10, hard.generation.limit = TRUE, starting.values = par, Domains = dom, boundary.enforcement = 0, data.type.int = TRUE, solution.tolerance = 0.01, cluster = FALSE, print.level = 2) 'wait.generations' limit reached. Ninguna mejora significativa en 10 generaciones. Valor de aptitud de la solución: 1.500000e + 01 Parámetros de la solución: X[ 1] : 3.000000e+00 X[ 2] : 1.100000e+01 X[ 3] : 1.300000e+01 X[ 4] : 3.000000e+00 X[ 5] : 1.000000e+00 X[ 6] : 3.000000e+00 X[ 7] : 2.000000e+00 X[ 8] : 1.000000e+00 X[ 9] : 4.000000e+00 Solución encontrada generación 3 Número de generaciones ejecuta 14 Thu Mar 24 13:54:06 2016 Duración total: 0 horas 2 minutos y 32 segundos
Esto muestra un buen resultado. ¿Y que hay balance?
> k [1] 15 > plot(bal, t="l")
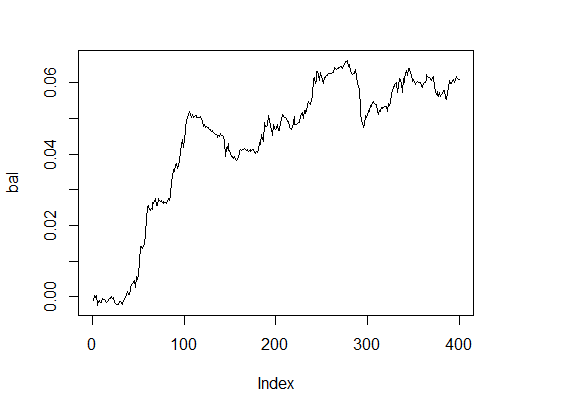
Fig.3. Balance con parámetros óptimos
Resultado muy decente dentro de un tiempo razonable.
Vamos a realizar algunos experimentos para comparar resultados de algoritmos genéticos con algoritmos evolutivos. En primer lugar, vamos a probar SOMA(Self-Organising Migrating Algorithm) implementado en el paquete de "soma".
Algoritmo general de migración de auto-organización de optimización estocástica, enfoque similar al algoritmo genético, aunque se basa en el concepto de series de "migración" con un conjunto fijo de especies, en lugar de desarrollo de más generaciones. Es resistente a mínimos locales y puede ser aplicada a cualquier tarea de minimizar gastos con área limitada de parámetros. La función principal:
soma(costFunction, bounds, options = list(), strategy = "all2one", …) Argumentos
Detalles
Hay múltiples opciones para la configuración de optimización y criterios de su terminación. Los valores por defecto utilizados aquí son recomendados por el autor Zelinka (2004).
- pathLength : Distancia hasta el líder de las especies que pueden migrar. Valor 1 corresponde a la posición de liderazgo y valor superior a 1 (recomendado) considera cierta re-regulación. 3 se indica por defecto.
- stepLength: Paso mínimo utilizado para evaluar posibles medidas. Se recomienda que la longitud del camino no sea un número entero múltiplo de este valor. El valor predeterminado es 0.11.
- perturbationChance: Probabilidad de que seleccionado parámetros vaya a cambiar en cualquier momento dado. Default value 0.1.
- minAbsoluteSep: El menos absoluto de la diferencia entre los valores máximos y mínimos de la función de precio. Si la diferencia está por debajo de este mínimo, se termina el algoritmo. Valor predeterminado es 0. Esto significa que este criterio de terminación nunca estará satisfecho.
- MinRelativeSep: La diferencia menos relativa entre los valores máximo y mínimo de la función de precio. Si la diferencia está por debajo de este mínimo, se termina el algoritmo. Default value is 0,001.
- nMigrations: Número máximo de migraciones para la terminación. El valor predeterminado es 20.
- populationSize: Número de especies en la población. Se recomienda que este valor es ligeramente mayor que el número de parámetros optimizados, y no debería ser inferior a 2. Valor por defecto es igual a 10.
Dado que el algoritmo realiza la minimización sólo, vamos a revisar nuestra función de fitness por lo que le proporciona valor de signo opuesto e iniciar optimización.
require(soma) x <- soma(fitnes, bounds = list(min=c(1,8,13,3,1,1,1,1,3), max = c(4,21,54,13,4,4,2,3,10)), options = list(minAbsoluteSep = 3, minRelativeSep = -1, nMigrations = 20, populationSize = 20), opp = TRUE) Output level is not set; defaulting to "Info" * INFO: Starting SOMA optimisation * INFO: Relative cost separation (-2.14) is below threshold (-1) - stopping * INFO: Leader is #7, with cost -11
Best parameters:
> x$population[ ,7] [1] 1.532332 15.391757 37.348099 9.860676 1.918848 [6] 2.222211 1.002087 1.182209 3.288627 Redondo a > x$population[ ,7]%>% floor [1] 1 15 37 9 1 2 1 1 3
Mejor valor en la función de aptitud = 11. Esto es aceptable para el uso práctico, pero hay espacio para mejorar.
El algoritmo es rápido pero inestable en los resultados y requiere la puesta a punto.
Función generalizada de recocido simulada
Este algoritmo está implementado en la «GenSA "paquete. Esta función puede realizar la búsqueda de un mínimo global con una función objetivo no lineal compleja con un gran número de óptimos.
GenSA(par, fn, lower, upper, control=list(), …)
Argumentos:
- par — Valores iniciales para los componentes que deben ser optimizados. NULL es por defecto, y en este caso, los valores por defecto se generarán automáticamente.
- fn , función que será mínima. Se establecen algunos parámetros del vector para reducir al mínimo de la función. Debe devolver un resultado escalar.
- lower – vector with length(par) length. Frontera inferior de componentes.
- upper — vector with length(par) length. Frontera superior de componentes.
- … permite al usuario enviar argumentos adicionales de la función fn.
- control : controlar el argumento. Esta es una lista que puede utilizar para administrar el comportamiento del algoritmo.
- maxit – Integer. Número máximo de iteraciones del algoritmo.
- THRESHOLD.Stop — Numérico.. El programa terminará con el valor esperado de la función de destino threshold.stop . Valor por defecto : NULL.
- nb.stop.improvement — Integer. El programa terminará si no hay ninguna mejora a lo largo de los pasos nb.stop.improvement.
- smooth — logical. Cierto, cuando la función objetivo es liso o diferenciados en el área de parámetros casi por todas partes; lo contrario es FALSE. Valor por defecto — TRUE
- max.call — Integer. Número máximo de llamadas de la función objetivo. El valor predeterminado es 1е7.
- temperature — Numerical. Valor inicial de temperatura.
- simple.function — Logical. TRUE significa que la función objetivo tiene sólo unos mínimos locales. FALSE está activada por defecto, que significa que la función objetivo SE complica con muchos mínimos locales.
- trace.mat — Logical. TRUE por defecto. Esto significa que la matriz de seguimiento estarán disponibles en el valor devuelto de la llamada de GenSA.
Los valores de los componentes de control se establecen por defecto para una tarea de optimización compleja. Para una tarea de optimización regular con complejidad media que Gensa puede encontrar rápidamente una solución razonable, por lo tanto es recomendable para un usuario deje GenSA terminar antes:
mediante el establecimiento de threshold.stop, si threshold.stop es un valor esperado de la función;
o terminando max.time, si un usuario quiere simplemente ejecutar GenSA durante max.time segundos;
o estableciendo max.call, si un usuario quiere simplemente ejecutar GenSA en max.call llamadas de funciones.
Para las tareas de optimización muy complejas, un usuario debe aumentar maxit y temperature.
Vamos a ejecutar la optimización limitando el tiempo máximo de funcionamiento en 60 segundos.
require(GenSA) pr.max <- GenSA(par, fitnes, lower = c(1,8,13,3,1,1,1,1,3), upper = c(4,21,54,13,4,4,2,3,10), control = list(verbose = TRUE, simple.function = TRUE, max.time = 60), opp = TRUE)
Valor de la función de la aptitud y valor de los parámetros óptimos:
> pr.max$value * (-1) [1] 16 > par1 <- pr.max$par > par1 [1] 1.789901 14.992866 43.854988 5.714345 1.843307 [6] 1.979723 1.324855 2.639683 3.166084
Redondear:
> par1 <- pr.max$par %>% floor [1] 1 14 43 5 1 1 1 2 3
Calcular el valor de la función de la aptitud con estos parámetros y ver la línea de balance:
> f1 <- fitnes(par1, test = TRUE) > plot(-1 * bal, t="l")
Fig.4 Balance 4
Indicadores de calidad, en un buen nivel, y los cálculos son sorprendentemente rápidos.
Estos y muchos algoritmos similares (paquetes dfoptim, nlopt, CEoptim, DEoptim, RcppDE etc.) optimizan la función de un criterio. Para la optimización de múltiples criterios, el el paquete destinado es el mco.
7. Formas y métodos de mejora de las características cualitativas
Los experimentos demostraron la eficiencia de los algoritmos genéticos. Para una mejora de los indicadores cualitativos se recomienda realizar investigaciones adicionales con el uso de:
- optimización multicriterio. Por ejemplo, para realizar la optimización de la ración de la calidad y su aspiración máxima. El paquete "mco" implementa tal oportunidad.
- tratar de implementar un autoorganitzación dinámica de parámetros de GA. El paquete de aplicación posible: "GA". Ofrece una amplia gama de operadores de selección, cruce y mutación.
- para probar la posibilidad de aplicar una programación genética en el sistema de comercio.
Conclusión
Se ha considerado establecer los principios básicos en algoritmos evolutivos, sus diferentes tipos y características. Usando un simple asesor experto de MACDSample hemos utilizado los experimentos para demostrar que aplicando la optimización de parámetros para tal elemental TC tiene un considerable efecto positivo.
El momento de realizar la simplicidad y optimización en programación permiten realizar durante la operación del EA sin entrada en el mercado. Y la falta de restricciones estrictas sobre el tipo de parámetros de optimización permiten aplicar los más diversos tipos de optimización en diversas etapas de la operación EA.
La parte más importante del trabajo es escribir correctamente la función de la aptitud.
Espero que este artículo ayude a entender que no es difícil, así que puedes intentar tu mismo aplicar optimización de tus asesores expertos.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/2225
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Experto comercial universal: Trabajando con trailing-stops personalizados (parte 6)
Experto comercial universal: Trabajando con trailing-stops personalizados (parte 6)
 Interfaces gráficas VI: Controles "Slider" y "Slider doble" (Capítulo 2)
Interfaces gráficas VI: Controles "Slider" y "Slider doble" (Capítulo 2)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Sugiere características.
Únete a la discusión. Pronto te irás.
No es una discusión, es más como "Déjalos hablar" en su peor momento.
Me alegro de no haber ido antes.
Voy a lavarme las manos.
Es horrible.
No es una discusión, es más bien un "Que hablen ellos" en el peor de los casos.
Me alegro de no haber ido antes.
Voy a lavarme las manos.
Eso es terrible.
Artículo publicado Uno mismo-optimización de EA: algoritmos genéticos y evolutivos:
Autor: Vladimir Perervenko