Глубокие нейросети (Часть III). Выбор примеров и уменьшение размерности

Содержание

• Введение
• 1. Выбор примеров
  
• 2. Уменьшение размерности
  
• 2.1. Анализ главных компонент (PCA)
• 2.2. Анализ независимых компонент (ICA)
• 2.3. Вероятностный метод главных компонент (PPCA)
• 2.4. Автоэнкодер (нелинейный PCA)
  
• 2.5. Инверсный нелинейный PCA (NLPCA)
• 3. Разделение набора на выборки train/valid/test
• Заключение
• Приложение

Введение

Это третья (и последняя) статья, описывающая самый ответственный этап работы с глубокими нейросетями — подготовку данных. Мы рассмотрим два очень важных метода подготовки данных — удаление шумовых примеров и уменьшение размерности входов. Описание методов будет проиллюстрировано подробными примерами и наглядными графиками.

1. Выбор примеров

В задачах классификации к шумовым примерам относится неправильная разметка учебных примеров. Как известно, это крайне нежелательная особенность данных. Для решения этой проблемы будем использовать пакет NoiseFilterR, в котором R-реализованы классические и современные фильтры шумовых помех.

В последние годы Data Mining (анализ данных) сталкивается со все более сложными проблемами с точки зрения характера имеющихся данных. Не только объемы данных, но и их несовершенство и разнообразные формы предоставляют исследователям множество различных сценариев. Следовательно, предварительная обработка данных стала важной частью процесса KDD (Knowledge Discovery from Databases). В свою очередь, разработка связанного с ней программного обеспечения предоставляет практикам адекватные инструменты для работы.

Предварительная обработка данных нужна, чтобы последующие алгоритмы обучения смогли извлечь из выборки максимум знаний. Это один из самых трудозатратных шагов во всем процессе KDD. Предварительная обработка данных разделяется на подзадачи: например, это выбор предикторов или устранение недостающих значений и шумных данных. Выбор предикторов направлен на извлечение самых важных атрибутов для этапа обучения, что уменьшает сложность моделей и время вычислений. Обработка недостающих значений необходима для хранения как можно большего количества данных. И, наконец, шумные данные — это либо неправильные, либо сильно выбивающиеся из общего распределения значения.

Для решения всех этих задач уже есть доступное программное обеспечение. Например, инструмент KEEL (RKEEL) содержит широкий набор алгоритмов предварительной обработки данных, который охватывает все вышеупомянутые темы. Есть и  другие популярные решения: такие как WEKA (RWEKA) или RapidMiner для выбора предикторов. Помимо них, существует ряд универсальных программных комплексов Data Mining, таких как R, KNIME или Python.

Что касается статистического программного обеспечения R, в Репозитории всеобъемлющей архивной сети (CRAN) есть множество пакетов для решения задач предварительной обработки.

В реальных наборах данных обычно есть несовершенства и шум. Этот шум отрицательно влияет на процесс обучения классификаторов, что, в свою очередь, снижает точность прогнозов, переусложняет модели и увеличивает время вычислений.

В специализированной литературе по классифицированию обычно выделяются два различных типа шума: шум атрибутов и шум разметки (он же — шум класса). Первый относится к несовершенствам в атрибутах набора учебных данных, второй — к ошибкам в методах классификации. В пакете NoiseFiltersR основное внимание уделяется именно разметочному шуму, самому пагубному, поскольку качество разметки имеет важное значение для обучения классификаторов.

Описаны два основных подхода к решению проблемы шума разметки. Подробнее с ними можно познакомиться в недавней работе Бенуа Френэ и Мишеля Верлейсена.

• Это, с одной стороны, подход уровня алгоритма, когда проблема решается путем создания надежного алгоритма классификации, на котором наличие шума слабо отражается. Каждый алгоритм при этом будет специфическим, неуниверсальным решением.
  
• С другой стороны, подход уровня данных (фильтры) — попытка разработать стратегии для очистки набора данных, которая будет проводиться перед обучением классификатора. Пакет NoiseFiltersR следует второму подходу, так как это позволяет предварительно обработать данные только один раз, а после этого менять классификаторы для обработки по мере своей фантазии.

Из устойчивых к шуму классификаторов можно упомянуть С4.5 и J48, Jrip (WEKA).

Проведем эксперимент. Возьмем три набора данных: DT (сырой набор, не прошедший никакой предобработки), DTn (только нормализованный набор сырых данных), DTTanh.n (без выбросов, тангенс-трансформированные и нормализованные) и, конечно, только train. Обработаем их функцией ORBoostFilter(), которая представляет собой фильтр для удаления выбросов. Посмотрим, как изменилось распределение после такой обработки.

evalq({
  #-----DT---------------------
  out11 <- ORBoostFilter(Class~., data = DT$train, N = 10, useDecisionStump = TRUE)
  DT$train_clean1 <- out11$cleanData
  #----------DTTanh.n------------------------
  out1 <- ORBoostFilter(Class~., data = DTTanh.n$train, N = 10, useDecisionStump = TRUE)
  DTTanh.n$train_clean1 <- out1$cleanData
  #-----------DTn--------------------------------
  out12 <- ORBoostFilter(Class~., data = DTn$train, N = 10, useDecisionStump = TRUE)
  DTn$train_clean1 <- out12$cleanData
},
env)
#---Ris1-----------------
require(funModeling)
evalq({
  par(mfrow = c(1,3))
  par(las = 1)
  boxplot(DT$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
          main = "DT$train_clean1")
  boxplot(DTn$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
          main = "DTn$train_clean1")
  boxplot(DTTanh.n$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
          main = "DTTanh.n$train_clean1")
  par(mfrow = c(1,1))
}, env)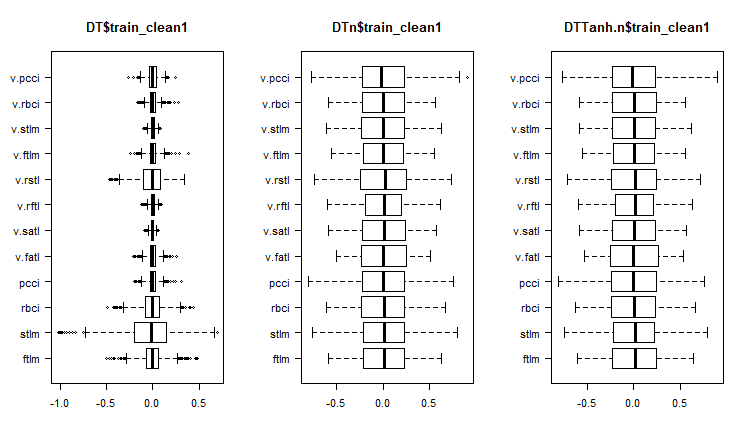

Рис. 1. Распределение предикторов в наборах после удаления шумовых примеров

Посмотрим вариацию и ковариацию предикторов в этих же наборах:

#----Ris2------------------
require(GGally)
evalq(ggpairs(DT$train_clean1 %>% select(-Data), 
              columns = c(1:6, 13), 
              mapping = aes(color = Class),
              title = "DT$train_clean1/1"), 
      env)

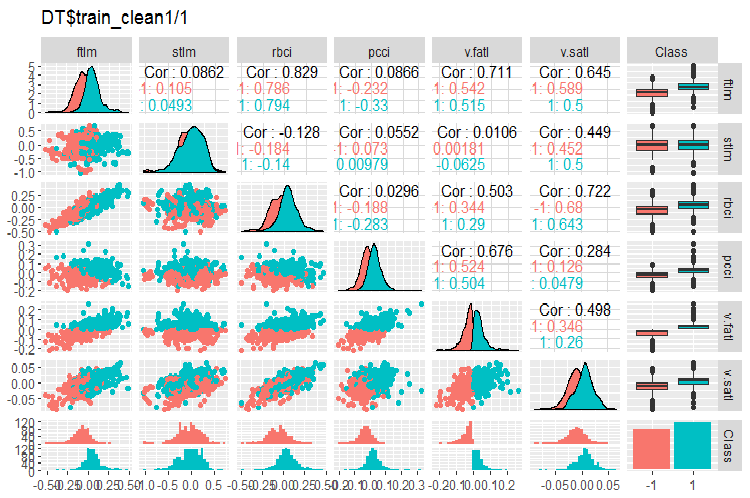
Рис. 2. Вариация и ковариация в наборе DT$train_clean1/1 после удаления шумовых примеров

#-----Ris3---
evalq(ggpairs(DT$train_clean1 %>% select(-Data), 
              columns = 7:13, 
              mapping = aes(color = Class),
              title = "DT$train_clean1/2"), 
      env)

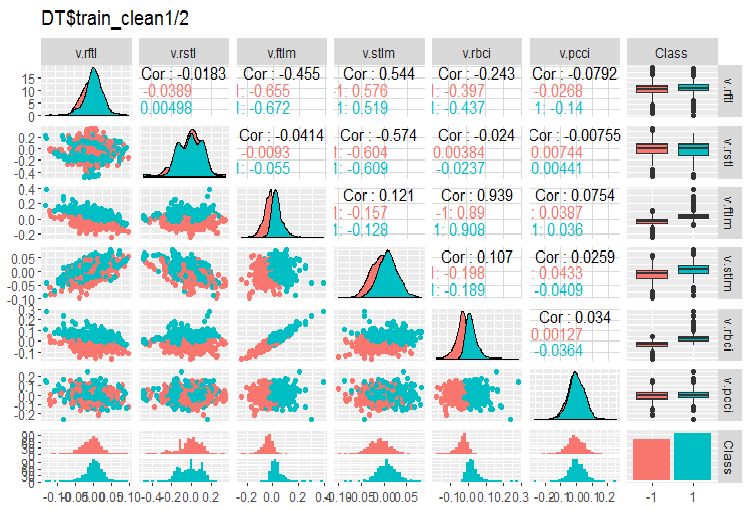
Рис. 3. Вариация и ковариация в наборе DT$train_clean1/2 после удаления шумовых примеров

Сколько примеров из DT$train было удалено?

> env$out11$remIdx %>% length()
[1] 658

Это около 30%. Есть два варианта дальнейших действий. Первый — удалить шумовые примеры из обучающего набора и передать его модели для обучения.  Второй — переразметить их новой меткой класса и обучить модель на полном train наборе, но с одним дополнительным уровнем целевой. При таком большом количестве шумовых примеров второй вариант может быть предпочтительным. Нужно проверить это экспериментом.

Что мы видим на графиках распределения переменных без шумовых?

1. Очень четкое разделение распределения предикторов по целевой. Скорее всего, это значительно повысит точность обучаемой модели.
2. Практически удалены выбросы.

Точно так же очистим фильтром наборы DTn$train DTTanh.n$train. И здесь мы с удивлением обнаружим, что шумовых переменных почти столько же, как и в первом случае.

c(env$out1$remIdx %>% length(), env$out12$remIdx %>% length())
[1] 652 653

То есть, никакие преобразования не делают шумовые примеры полезными? Это интересно.

Давайте посмотрим на вариацию и ковариацию набора DTTanh.n$train после удаления шумовых переменных.

#----Ris4-----------------------
evalq(ggpairs(DTTanh.n$train_clean1, columns = 1:13, 
              mapping = aes(color = Class),
              upper = "blank",
              title = "DTTanh.n$train_clean_all"), 
      env)

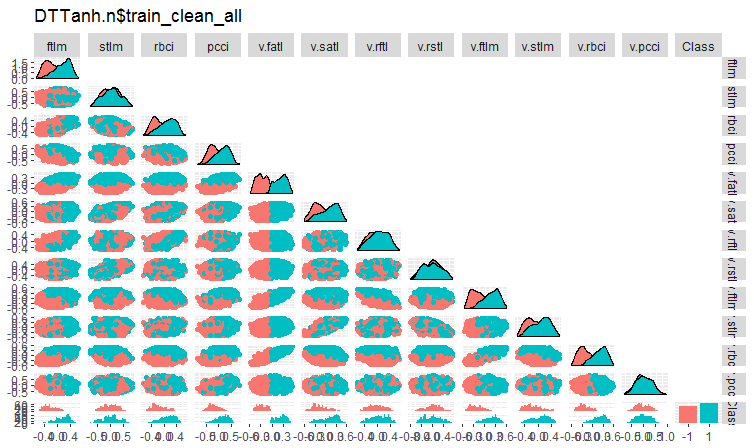
Рис. 4. Вариация и ковариация в наборе DTTanh.n$train_clean после удаления шумовых примеров.

Очень интересная ковариация всех переменных с переменной v.fatl. Визуально мы можем предварительно определить иррелевантные к целевой предикторы — это stlm, v.rftl, v.rstl, v.pcci. Ниже мы проверим это предположение другими методами и на другом наборе.

И тот же график для DTn$train_clean1:

#-------ris5----------
require(GGally)
evalq(ggpairs(DTn$train_clean1 %>% select(-Data), 
              columns = 1:13, 
              mapping = aes(color = Class),
              upper = "blank",
              title = "DTn$train_clean1_all"), 
      env)

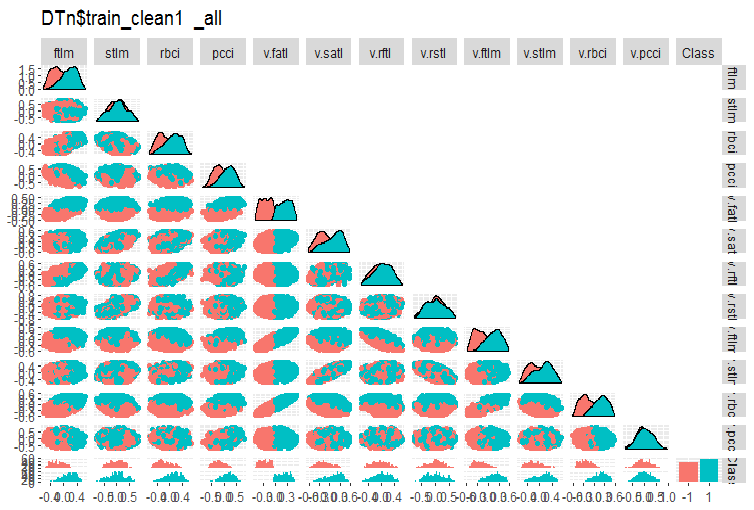
Рис. 5. Вариация и ковариация в наборе DTn$train_clean после удаления шумовых примеров.

Здесь мы видим, что вариация тех же предикторов (stlm, v.rftl, v.rstl, v.pcci) не разделяется по уровням целевой. Что делать с шумовыми переменными, решает сам разработчик, по результатам экспериментов с обучением конкретной модели.

Теперь рассмотрим, как изменилась важность предикторов в этих наборах после удаления шумовых примеров.

#--------Ris6---------------------------
require(smbinning)
par(mfrow = c(1,3))
evalq({
  df <- renamepr(DT$train_clean1) %>% targ.int
  sumivt.dt = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.dt, cex = 0.8)
  rm(df)
}, 
env)
evalq({
  df <- renamepr(DTTanh.n$train_clean1) %>% targ.int
  sumivt.tanh.n = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.tanh.n, cex = 0.8)
  rm(df)
}, 
env)
evalq({
  df <- renamepr(DTn$train_clean1) %>% targ.int
  sumivt.dtn = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.dtn, cex = 0.8)
  rm(df)
}, 
env)
par(mfrow = c(1, 1))

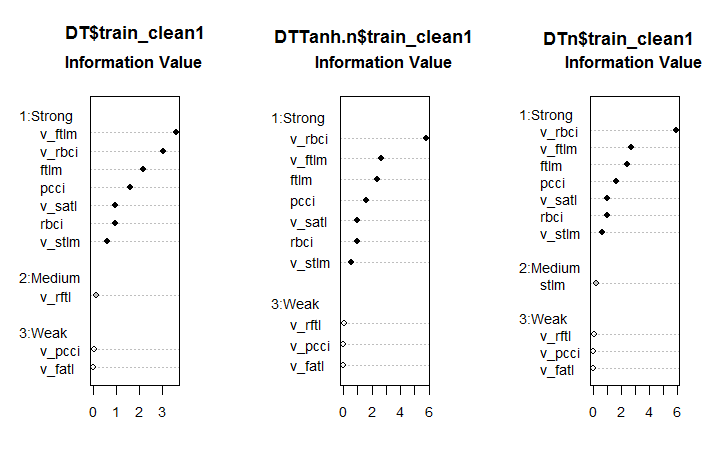
Рис. 6. Важность предикторов в трех наборах

Результат, прямо скажем, неожиданный. Переменная v.fatl оказалась самой слабой из слабых!

Семь сильных предикторов во всех наборах одинаковы. В первом и третьем появляется по одному предиктору средней силы. Ранее предварительно определенные как иррелевантные (stlm, v.rftl, v.rstl, v.pcci) подтверждаются и этим расчетом. Все эти выкладки нужно проверять экспериментами с конкретной моделью.

В пакете NoiseFilterR есть более десятка других фильтров для определения шумовых примеров. Экспериментируйте!

2. Уменьшение размерности

Уменьшение размерности — преобразование исходных данных с большой размерностью в новое представление меньшей размерности, сохраняющее основную информацию. В идеальном случае размерность преобразованного представления соответствует внутренней размерности данных. Внутренняя размерность данных — минимальное число переменных, необходимое, чтобы выразить все возможные свойства данных. Традиционно, для уменьшения размерности используются алгоритмы, такие как Principal Component Analisys (PCA), Independent Component Analisys (ICA), Singular Value Decomposition (SVD) и другие.

Уменьшение размерности помогает смягчить влияние так называемого проклятия размерности и других нежелательных свойств пространств большой размерности. В задаче описания данных оно преследует следующие цели.

• Сокращение вычислительных затрат при обработке данных
• Борьба с переобучением. Чем меньше количество признаков, тем меньше нужно объектов для уверенного восстановления скрытых зависимостей в данных и тем больше качество восстановления подобных зависимостей
• Сжатие данных для более эффективного хранения информации. В этом случае, помимо преобразования X → T, нужна еще и возможность осуществлять обратное преобразование T → X
• Визуализация данных. Проектирование выборки на двух-/трехмерное пространство позволяет графически представить выборку
• Извлечение новых признаков. Новые признаки, полученные в результате преобразования X → T, могут оказывать значимый вклад при последующем решении задач распознавания (например, как метод главных компонент)

Заметим, что все бегло описанные далее методы уменьшения размерности относятся к классу методов обучения без учителя, т.е. в качестве исходной информации выступает только признаковое описание объектов X (предикторы).

2.1. PCA, Анализ главных компонент

Анализ главных компонент (Principal Component Analysis, PCA) — простейший метод уменьшения размерности данных. Его идеи высказывались еще в 19 веке. Идея метода — найти в исходном пространстве гиперплоскость заданной размерности и спроецировать выборку на эту гиперплоскость. При этом выбирается та гиперплоскость, ошибка проецирования данных на которую минимальна в смысле суммы квадратов отклонений.

Размерность редуцированного пространства d  пользователь может задать заранее. Это значение легко выбрать, если перед нами стоит задача визуализации данных (d = 2 или d = 3) или задача вложения выборки в заданный объем памяти. Однако во многих других случаях выбор d далеко не очевиден из априорных предположений.

Есть простой эвристический прием выбора величины d для метода главных компонент. Одна из особенностей метода главных компонент — то, что все редуцированные пространства для d = 1, 2, . . . вложены друг в друга. Так, один раз рассчитав все собственные векторы и собственные значения матрицы ковариации, мы получим редуцированное пространство для любого значения d. Поэтому, чтобы выбрать значение d, можно отобразить на графике собственные значения в порядке убывания и выбрать порог отсечения так, чтобы справа остались значения, незначимо отличные от нуля. Другой способ предполагает выбор порога так, чтобы справа оставался определенный процент от общей площади под кривой (например, 5% или 1%).

Упрощенно PCA можно считать предварительным подавлением шумовых предикторов при значительном их количестве (>50).

2.2. ICA, Анализ независимых компонент

Анализ независимых компонент, в отличие от PCA — предмет довольно недавний, но быстро набирающий популярность в различных областях исследования данных.

В отличие от анализа основных компонентов, преобразования ICA предполагают наличие модели. Наиболее распространенная модель — предположение о том, что переменные P измеряются из линейного преобразования p независимых переменных. Цель ICA — восстановить исходные независимые переменные. Большинство алгоритмов ICA сначала включают отбеливание данных, а затем их вращение таким образом, чтобы сделать результирующие компоненты максимально независимыми. Когда компоненты производятся последовательно, это обычно подразумевает поиск «большей» негауссовской проекции, которая не связана с ранее выделенными проекциями.

Метод независимых компонент получил широкое распространение при обработке сигналов. Эта техника пытается линейно преобразовать исходные данные в новые компоненты, которые будут максимально независимы друг от друга в статистическом смысле. Независимые компоненты не обязательно ортогональны друг другу, но их статистическая независимость — даже еще более строгое условие, чем статистическая некоррелированность, которая используется в PCA.

Методы PCA и ICA реализованы в пакете caret функцией preProcess(), в которой можно указать либо конкретное количество главных компонент, либо кумулятивный процент рассеивания, охватываемый PCA. Выполняется в два этапа: сначала на train выборке вычисляются необходимые параметры, а затем, используя predict(), выполняют преобразование выборок train/val/test и всех новых данных, поступающих в последующем.

Таблица 1. Сравнительные характеристики PCA и ICA

Метод	Преимущества	Недостатки	Особенности	Результат, получаемый в общем случае	Способ вычисления новых главных компонентов
PCA	Простота выполнения  расчетов	Линейность преобразований Высокая чувствительность к выбросам Не принимают NA в данных	Неединственность решения (вращательная неопределенность. При каждом новом расчете  на основании одного обучающего набора мы будем получать различные главные компоненты.	Т — матрица счетов (scores) размерностью  [I x A] (собственно главные компоненты) P — матрица нагрузок (loadings) размерностью [J x A]. Матрица перехода из пространства Х[ ,J] в PCA[ ,A] E — матрица остатков размерностью [I x J]	Tnew = Xnew * P
ICA	Простота выполнения расчетов	Принудительная стандартизация данных Линейность преобразований Высокая чувствительность к выбросам не принимают NA в данных Применим при количестве компонент 2 — 5	При большой разнице размерностей входного набора и независимых компонентов применяют последовательно PCA -> ICA.	W — матрица разделения K — матрица предотбеливания	Snew =scale( Xnew )* W * K

Проведем небольшой эксперимент. Загрузим в Rstudio снимок результатов вычисления скриптов первой части статьи Part_1.Rda. Напомним содержание окружения env:

> ls(env)
 [1] "cap1"         "cap2"         "Close"        "Data"         "dataSet"     
 [6] "dataSetCap"   "dataSetClean" "dataSetOut"   "High"         "i"           
[11] "k"            "k.cap"        "k.out"        "lof.x"        "lof.x.cap"   
[16] "Low"          "lower"        "med"          "Open"         "out.ftlm"    
[21] "out.ftlm1"    "pr"           "pre.outl"     "preProClean"  "Rlof.x"      
[26] "Rlof.x.cap"   "sk"           "sk.cap"       "sk.out"       "test"        
[31] "test.out"     "train"        "train.out"    "upper"        "Volume"      
[36] "x"            "x.cap"        "x.out" 

Возьмем выборку x.cap  c импутированными выбросами и вычислим ее главные и независимые компоненты с помощью функции preProcess::caret. Для PCA и ICA явно укажем количество компонент. Для ICA не будем указывать способ нормализации.

require(caret)
evalq({
  prePCA <- preProcess(x.cap, 
                       pcaComp = 5,
                       method = Hmisc::Cs(center, scale, pca))
  preICA <- preProcess(x.cap,
                       n.comp = 3, 
                       method = "ica")
}, env)

Посмотрим параметры трансформации:

> str(env$prePCA)
List of 20
 $ dim              : int [1:2] 7906 11
 $ bc               : NULL
 $ yj               : NULL
 $ et               : NULL
 $ invHyperbolicSine: NULL
 $ mean             : Named num [1:11] -0.001042 -0.003567 -0.000155 -0.000104 -0.000267 ...
  ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
 $ std              : Named num [1:11] 0.091 0.237 0.1023 0.0377 0.0356 ...
  ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
 $ ranges           : NULL
 $ rotation         : num [1:11, 1:5] -0.428 -0.091 -0.437 -0.107 -0.32 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  .. ..$ : chr [1:5] "PC1" "PC2" "PC3" "PC4" ...
 $ method           :List of 4
  ..$ center: chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ scale : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ pca   : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ ignore: chr(0) 
 $ thresh           : num 0.95
 $ pcaComp          : num 5
 $ numComp          : num 5
 $ ica              : NULL
 $ wildcards        :List of 2
  ..$ PCA: chr(0) 
  ..$ ICA: chr(0) 
 $ k                : num 5
 $ knnSummary       :function (x, ...)  
 $ bagImp           : NULL
 $ median           : NULL
 $ data             : NULL
 - attr(*, "class")= chr "preProcess"

Нам важны три слота: prePCA$mean и prePCA$std (параметры нормализации) и prePCA$rotation (матрица вращения, нагрузок).

> str(env$preICA)
List of 20
 $ dim              : int [1:2] 7906 11
 $ bc               : NULL
 $ yj               : NULL
 $ et               : NULL
 $ invHyperbolicSine: NULL
 $ mean             : Named num [1:11] -0.001042 -0.003567 -0.000155 -0.000104 -0.000267 ...
  ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
 $ std              : Named num [1:11] 0.091 0.237 0.1023 0.0377 0.0356 ...
  ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
 $ ranges           : NULL
 $ rotation         : NULL
 $ method           :List of 4
  ..$ ica   : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ center: chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ scale : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ ignore: chr(0) 
 $ thresh           : num 0.95
 $ pcaComp          : NULL
 $ numComp          : NULL
 $ ica              :List of 3
  ..$ row.norm: logi FALSE
  ..$ K       : num [1:11, 1:3] -0.214 -0.0455 -0.2185 -0.0534 -0.1604 ...
  ..$ W       : num [1:3, 1:3] -0.587 0.77 -0.25 -0.734 -0.636 ...
 $ wildcards        :List of 2
  ..$ PCA: chr(0) 
  ..$ ICA: chr(0) 
 $ k                : num 5
 $ knnSummary       :function (x, ...)  
 $ bagImp           : NULL
 $ median           : NULL
 $ data             : NULL
 - attr(*, "class")= chr "preProcess"

Здесь те же $mean и $std и две матрицы $K и $W. Пакет caret для вычисления ICA, в свою очередь, использует пакет fastICA, алгоритм которого следующий:

• исходная матрица центрируется (возможно нормирование строк), получаем матрицу Х
• затем матрица Х проецируется на направления главных компонент, получаем PCA = X * K
• после этого, умножив PCA на unmixing матрицу, получим независимые компоненты ICA = X * K * W

Вычислим PCA и ICA двумя способами, используя функцию predict::caret и параметры, полученные функцией preProcess.

require(magrittr)
evalq({
  pca <- predict(prePCA, x.cap)
  ica <- predict(preICA, x.cap)
  pca1 <- ((x.cap %>% scale(prePCA$mean, prePCA$std)) %*% 
                   prePCA$rotation) 
  ica1 <- ((x.cap %>% scale(preICA$mean, preICA$std)) %*% 
                   preICA$ica$K) %*% preICA$ica$W
  colnames(ica1) <- colnames(ica1, do.NULL = FALSE, prefix = 'ICA')
    
},env)
evalq(all_equal(pca, pca1), env)
# [1] TRUE
evalq(all_equal(ica, ica1), env)
# [1] TRUE

Результат идентичен, что понятно.

Более надежный способ вычисления PCA — использование пакета pcaPP,  более точно определяющего главные компоненты.

Пакет fastICA содержит много дополнительных возможностей и параметров для более гибкого и полного вычисления независимых компонент. Я бы рекомендовал пользоваться им, а не функцией в caret.

2.3 Вероятностный метод главных компонент (PPCA)

Для метода главных компонент можно сформулировать вероятностную модель (probabilistic PCA, PPCA). Переформулирование метода в вероятностных терминах дает целый ряд преимуществ.

• Возможность использования ЕМ-алгоритма для поиска решения. Для PCA ЕМ-алгоритм — более вычислительно эффективная процедура в ситуациях, когда d ≪ D
• Корректная обработка пропущенных значений. Они просто добавляются в список скрытых переменных вероятностной модели, для которой затем применяется соответствующий ЕМ-алгоритм
• Возможность перехода к модели смеси вероятностных распределений, которая значительно расширяет область применимости метода
• Возможность использования т.н. байесовского подхода для решения задач выбора моделей. В частности, здесь можно построить теоретически обоснованную схему выбора размерности редуцированного пространства d  (см.[24, 25])
• Возможность генерирования новых объектов из вероятностной модели
• Для задач классификации — возможность моделировать распределения отдельных классов объектов для дальнейшего использования в схемах классификации
• Значение функции правдоподобия — универсальный критерий, позволяющий сравнивать различные вероятностные модели между собой. В частности, с помощью значения правдоподобия можно легко определять выбросы в данных.

Как и классическая модель PCA, вероятностная модель PCA инвариантна относительно выбора базиса в гиперплоскости.

В отличие от классической модели PCA, в которой восстанавливается только гиперплоскость, наилучшим образом объясняющая данные, вероятностная модель восстанавливает всю модель изменчивости данных. В частности, она описывает дисперсию данных по всем направлениям. Поэтому решение включает в себя не только направляющие базисные вектора гиперплоскости, задаваемые собственными векторами матрицы ковариаций, но также и длины этих базисных векторов.

Для использования РРСА и других нелинейных методов получения главных компонент можно использовать очень серьезный пакет pcaMethods.

Пакет pcaMethods предоставляет набор различных реализаций PCA, а также инструменты для перекрестной проверки и визуализации результатов. Методы в основном позволяют применять PCA к неполным данным, а значит, их можно использовать для оценки недостающих значений (NA). Пакет находится в репозитории Bioconductor и устанавливается так:

source("https://bioconductor.org/biocLite.R")
biocLite("pcaMethods")
library(pcaMethods)

Все методы пакета возвращают общий класс pcaRes, который содержит результат. Это гарантирует максимальную гибкость для пользователя. Оберточная функция pca() предоставляет доступ ко всем желаемым типам РСА через строку наименования. Перечень алгоритмов с кратким описанием:

• svdPCA — оберточная функция для стандартной prcomp.
• svdImpute — реализация алгоритма для импутации NA. Толерантен к большому количеству NA (>10%).
  
• Probabilistic PCA (ppca) — PPCA толерантна к количеству NA между 10% и 15%.
• Bayesian PCA (bpca) — подобно вероятностному PCA, использует EM-подход вместе с байесовской моделью для расчета вероятности восстановления значения. Алгоритм толерантен относительно большого количества недостающих данных (> 10%). Счета и нагрузки, полученные этим методом, немного отличаются от полученных с помощью обычного РСА. Это связано с тем, что BPCA был разработан специально для оценки недостающих значений и основывается на вариационном байесовском фреймворке (VBF) с автоматическим определением релевантности (ARD). Алгоритм не форсирует ортогональность между нагрузками. Более того, авторы документа BPCA обнаружили, что включение критерия ортогональности ухудшило прогнозы.
• Inverse non-linear PCA (NLPCA) особенно подходит для данных из экспериментов, в которых связь предикторов и целевой нелинейна. NLPCA основана на тренировке декодирующей части автоассоциативной нейронной сети (автоэнкодера). Нагрузки можно увидеть в скрытом слое нейросети. Отсутствующие значения в данных обучения просто игнорируются при вычислении ошибки во время обратного распространения. Таким образом, NLPCA может использоваться для обработки недостающих значений так же, как и для обычного РСА. Единственное различие — в том, что нагрузки P теперь представлены нейронной сетью. Ниже мы отдельно и более детально исследуем этот вариант понижения размерности в разделе "Автоэнкодер".
• Nipals PCA —  нелинейная оценка по итерационным частичным наименьшим квадратам. Это алгоритм в корне регрессии PLS, который может выполнять PCA с отсутствующими значениями, просто оставляя их вне соответствующих внутренних продуктов. Он терпим к небольшим количествам (как правило, не более 5%) недостающих данных.
• Local least squares (LLS) imputation — алгоритм/функция llsImpute() для оценки отсутствующих значений, основанный на линейной комбинации k ближайших соседей неполной переменной . Расстояние между переменными определяется как абсолютное значение Pearson, Spearman или Kendall-коэффициентов корреляции. Оптимальная линейная комбинация находится путем решения локальной задачи наименьших квадратов.

В текущей реализации предоставлены два немного разных способа оценки пропущенных значений. Первый — это ограничение поиска соседей в подмножестве полных переменных. Такой способ предпочтителен, когда неопределенных переменных относительно немного. Во втором способе в качестве кандидатов рассматриваются все переменные. Здесь отсутствующие значения сначала заменяются средним значением столбцов. Затем метод выполняет итерацию, используя текущую оценку как вход для регрессии LLS до тех пор, пока изменения между новой и старой оценкой падают ниже определенного порога (0,001).

К сожалению тема статьи и ее объем не позволяют более подробно остановиться на всех предложенных алгоритмах этого замечательного пакета. Мы рассмотрим только NLPCA в сравнении с автоэнкодером ниже.

2.4. Автоэнкодер

Автоассоциативные сети получили практическое применение с началом использования глубоких нейросетей. В одной из моих предыдущих статей мы рассматривали подробно структуру и особенности обучения автоэнкодеров (АЕ), сложенных автоэнкодеров (Stacked AE), ограниченной машины Больцмана (RBM) и т.д.

Напомню, автоэнкодер — это нейросеть с одним или несколькими скрытыми слоями, у которых количество нейронов входного слоя равно количеству нейронов выходного слоя. Основная задача АЕ — как можно точнее воспроизвести входные данные. Для обучения АЕ применяются те же методы обучения, регуляризации и активации нейронов, что и для обычных нейросетей. Построить модель АЕ можно с использованием любого пакета построения NN, который позволяет извлекать матрицу весов скрытых слоев. Будем использовать пакет autoencoder. В качестве примера напомню возможные структуры АЕ:

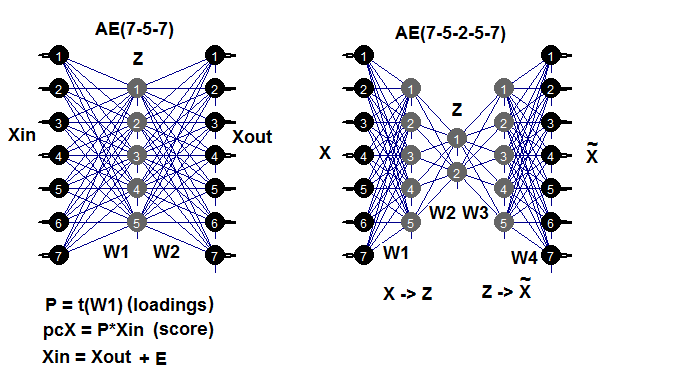
Рис. 7. Структурная схема автоэнкодеров (трех- и пятислойных)

Матрица весов W1 между первым (входным) и скрытым слоем и есть получаемая после обучения нагрузка. После проецирования (умножения) входной матрицы Xin на нагрузку Р мы получаем редуцированную матрицу (собственно, главные компоненты). Такой же результат мы можем получить, используя predict(). Эта функция позволяет получить выход либо скрытого слоя (при hidden.output = TRUE), либо выходного слоя автоэнкодера (при hidden.output = FALSE).

После обучения AE мы можем извлечь из модели матрицу весов W1 и ошибку восстановления при обучении. Если же мы подали и тестовый набор, то из модели мы можем получить и ошибку тестирования. Ошибка обучения зависит от параметров АЕ и (очень сильно) от соотношения n.hidden/n.in. Чем оно меньше, тем больше ошибка восстановления. Если наша задача — получить большое уменьшение размерности, можно сложить два АЕ последовательно. Например, при 12 входах мы можем обучить модель 12-7-12, сделать predict() со скрытого слоя и подать его на автоэнкодер 7-3-7. Получим редукцию 12 -> 3. Экспериментируйте!

Отдельно отмечу, что хотя в пакете и анонсирована возможность создать и обучить многослойный АЕ, мне это не удалось.

Проведем эксперимент. У Вас уже загружен Part_1.RData с результатами расчета первой части статьи. Последовательность вычисления (коротко):

• из выборки dataSet создаем выборки train/val/test, получаем лист DT;
• импутируем выбросы, получаем лист DTcap;
• нормализуем наши выборки последовательно методами c("center", "scale", "spatialSign"). Возможны и другие варианты трансформации и нормализации, которые мы рассматривали раньше;
• обучаем модель автоэнкодера с тремя нейронами в скрытом слое. Вы можете исследовать другие варианты. С увеличением количества скрытых нейронов уменьшается ошибка восстановления;
• используя обученную модель и predict(), получаем результат со скрытого слоя, т.е собственно редуцированную матрицу (РСА). Добавим к ней целевую;
• построим графики вариации и ковариации редуцированных выборок train/val/test/.
  

require(FCNN4R)
require(deepnet)
require(darch)
require(tidyverse)
require(magrittr)
#----Clean---------------------
require(caret)
require(pipeR)
evalq(
  {
    train = 1:2000
    val = 2001:3000
    test = 3001:4000
    DT <- list()
    dataSet %>%
      preProcess(., method = c("zv", "nzv", "conditionalX")) %>%
      predict(., dataSet) %>%
      na.omit -> dataSetClean
    list(train = dataSetClean[train, ], 
         val = dataSetClean[val, ], 
         test = dataSetClean[test, ]) -> DT
    rm(dataSetClean, train, val, test)
  }, 
  env)
#------outlier-------------
require(foreach)
evalq({
  DTcap <- list()
  foreach(i = 1:3) %do% {
    DT[[i]] %>% 
      select(-c(Data, Class)) %>%
      as.data.frame() -> x
    if (i == 1) {
      foreach(i = 1:ncol(x), .combine = "cbind") %do% {
        prep.outlier(x[ ,i]) %>% unlist()
      } -> pre.outl
      colnames(pre.outl) <- colnames(x)
    } 
    foreach(i = 1:ncol(x), .combine = "cbind") %do% {
      stopifnot(exists("pre.outl", envir = env))
      lower = pre.outl['lower.25%', i] 
      upper = pre.outl['upper.75%', i]
      med = pre.outl['med', i]
      cap1 = pre.outl['cap1.5%', i] 
      cap2 = pre.outl['cap2.95%', i] 
      treatOutlier(x = x[ ,i], impute = T, fill = T, 
                   lower = lower, upper = upper, 
                   med = med, cap1 = cap1, cap2 = cap2) 
    } %>% as.data.frame() -> x.cap
    colnames(x.cap) <- colnames(x)
    return(x.cap)
  } -> DTcap
  foreach(i = 1:3) %do% {
    cbind(DTcap[[i]], Class = DT[[i]]$Class)
  } -> DTcap
  DTcap$train <- DTcap[[1]]
  DTcap$val <- DTcap[[2]]
  DTcap$test <- DTcap[[3]]
  rm(lower, upper, med, cap1, cap2, x.cap, x)
}, env)
#------normalize-----------
evalq(
  {
    method <- c("center", "scale", "spatialSign") #, "expoTrans") #"YeoJohnson", 
                                                 # "spatialSign"
    preProcess(DTcap$train, method = method) -> preproc 
    list(train = predict(preproc, DTcap$train), 
         val = predict(preproc, DTcap$val),
         test = predict(preproc, DTcap$test)
    ) -> DTcap.n
    #foreach(i = 1:3) %do% {
    #  cbind(DTcap.n[[i]], Class = DT[[i]]$Class)
    #} -> DTcap.n
  }, 
  env) 
#----train-------
require(autoencoder)
evalq({
  train <-  DTcap.n$train %>% select(-Class) %>% as.matrix()
  val <-  DTcap.n$val %>% select(-Class) %>% as.matrix()
  test <-  DTcap.n$test %>% select(-Class) %>% as.matrix()
  ## Set up the autoencoder architecture:
  nl = 3                    ## number of layers (default is 3: input, hidden, output)
  unit.type = "tanh"        ## specify the network unit type, i.e., the unit's 
   ## activation function ("logistic" or "tanh")
  N.input = ncol(train)   ## number of units (neurons) in the input layer (one unit per pixel)
  N.hidden = 3              ## number of units in the hidden layer
  lambda = 0.0002           ## weight decay parameter     
  beta = 0                  ## weight of sparsity penalty term 
  rho = 0.01                ## desired sparsity parameter
  epsilon <- 0.001          ## a small parameter for initialization of weights 
   ## as small gaussian random numbers sampled from N(0,epsilon^2)
  max.iterations = 3000     ## number of iterations in optimizer
   ## Train the autoencoder on training.matrix using BFGS 
 ##optimization method 
  AE_13 <- autoencode(X.train = train, X.test = val,
                      nl = nl, N.hidden = N.hidden, 
                      unit.type = unit.type,
                      lambda = lambda,
                      beta = beta,
                      rho = rho,
                      epsilon = epsilon,
                      optim.method = "BFGS", #"BFGS", "L-BFGS-B", "CG"
                      max.iterations = max.iterations,
                      rescale.flag = FALSE, 
                      rescaling.offset = 0.001)}, env)
## Report mean squared error for training and test sets:
#cat("autoencode(): mean squared error for training set: ",
#    round(env$AE_13$mean.error.training.set,3),"\n")
## Extract weights W and biases b from autoencoder.object:
#evalq(P <- AE_13$W, env)
#-----predict-----------
evalq({
  #Train <- predict(AE_13, X.input = train, hidden.output = FALSE) 
  pcTrain <- predict(AE_13, X.input = train, hidden.output = TRUE)$X.output %>%
    tbl_df %>% cbind(., Class = DTcap.n$train$Class)
  #Val <- predict(AE_13, X.input = val, hidden.output = FALSE) 
  pcVal <- predict(AE_13, X.input = val, hidden.output = TRUE)$X.output %>%
    tbl_df %>% cbind(., Class = DTcap.n$val$Class)
  #Test <- predict(AE_13, X.input = test, hidden.output = FALSE) 
  pcTest <- predict(AE_13, X.input = test, hidden.output = TRUE)$X.output %>%
    tbl_df %>% cbind(., Class = DTcap.n$test$Class)
}, env)
#-----graph---------------
require(GGally)
evalq({
  ggpairs(pcTrain,columns = 1:ncol(pcTrain), 
          mapping = aes(color = Class),
          title = "pcTrain")}, 
  env)
evalq({
  ggpairs(pcVal,columns = 1:ncol(pcVal), 
          mapping = aes(color = Class),
          title = "pcVal")}, 
  env)
evalq({
  ggpairs(pcTest,columns = 1:ncol(pcTest), 
          mapping = aes(color = Class),
          title = "pcTest")}, 
  env)

Посмотрим графики 

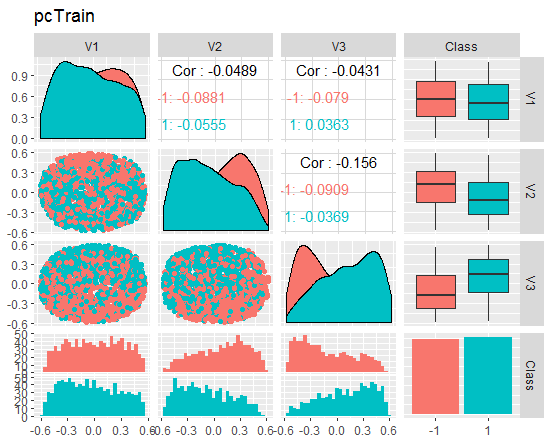
Рис. 8. Вариация и ковариация редуцированного набора train

 

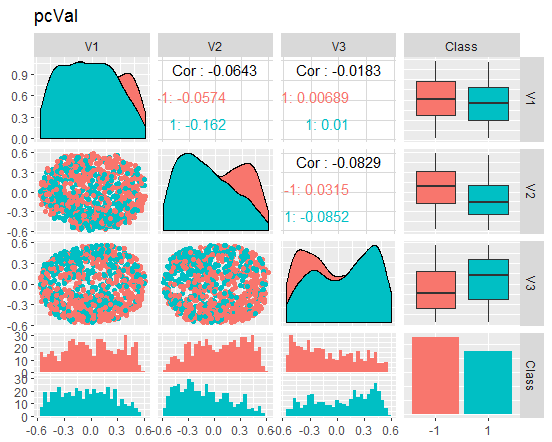
Рис. 9. Вариация и ковариация редуцированного набора val

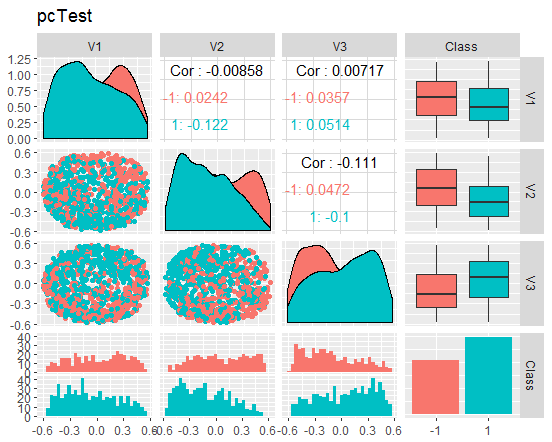
Рис. 10. Вариация и ковариация редуцированного набора test

Что можно сказать по графикам?  Мы видим, что "главные компоненты" (V1, V2, V3) хорошо разделяемы по уровням целевой, а распределения в наборах train/val/test "плывут". Можно было бы отсеять шумовые примеры и посмотреть, насколько улучшится картина. Оставляю эту идею читателю для самостоятельного рассмотрения.

Небольшое отступление: NLPCA

Чтобы осмысленно разлагать данные по главным компонентам, важно различать приложения чистого уменьшения размерности от приложений, где первичный интерес представляет идентификация и распознавание уникальных и значимых компонентов, обычно называемая экстракцией признаков (feature extraction).

В приложениях для чистого уменьшения размерности с четким акцентом на подавление шума и сжатие данных требуется только подпространство с высокой описательной емкостью. Способы того, как отдельные компоненты образуют это подпространство, не ограничиваются и, следовательно, не обязательно должны быть уникальными. Единственное требование состоит в том, чтобы подпространство объясняло максимальную информацию в смысле квадрата ошибки (MSE). Поскольку отдельные компоненты, которые охватывают это подпространство, одинаково обрабатываются алгоритмом без какого-либо конкретного порядка или дифференциального взвешивания, это называется симметричным типом обучения. Оно включает в себя нелинейный PCA, выполняемый стандартной автоассоциативной нейронной сетью (автоэнкодер), которая поэтому называется s-NLPCA. В предыдущем разделе мы рассматривали этот вариант.

Напротив, иерархический нелинейный PCA (h-NLPCA) обеспечивает не только оптимальное нелинейное подпространство, охватываемое компонентами, но также ограничивает нелинейные компоненты одинаковым иерархическим порядком, как линейные компоненты в стандартном PCA. Иерархия в этом контексте объясняется двумя важными свойствами: масштабируемостью и стабильностью. Масштабируемость означает, что первые n компонентов объясняют максимальную дисперсию, которая может быть покрыта n-мерным подпространством. Стабильность означает, что i-я компонента n-компонентного решения идентична i-му компоненту m-компонентного решения.

Иерархический порядок дает некоррелированные компоненты. Нелинейность также означает, что h-NLPCA способен устранить сложные нелинейные корреляции между компонентами. Это помогает отфильтровать полезные и значимые компоненты. Кроме того, путем масштабирования нелинейной некоррелированной компоненты к единичной дисперсии мы получаем комплексное нелинейное отбеливание (сферическое преобразование). Это полезная предварительная обработка для таких приложений, как регрессия, классификация или слепое разделение источников. Поскольку нелинейное отбеливание устраняет нелинейности в данных, впоследствии применяемые методы могут быть линейными. Это особенно важно для ICA, который может быть расширен до нелинейного подхода с использованием этого нелинейного отбеливания.

Как мы можем добиться иерархического порядка? Наивный подход в простой сортировке симметрично обработанных компонент по дисперсии не дает требуемого иерархического порядка — ни линейно, ни нелинейно. В принципе, достичь иерархичности можно двумя взаимосвязанными способами: либо ограничением на дисперсию в пространстве компонентов, либо ограничением квадрата ошибки реконструкции в исходном пространстве. Подобно линейному PCA, i-й компонент будет вынужден учитывать i-ю самую высокую дисперсию.

Но нелинейно такое ограничение может быть неэффективным или не единичным без дополнительных ограничений. Напротив, ошибка восстановления может контролироваться намного лучше, поскольку является абсолютной величиной, инвариантной к любому масштабированию в преобразовании. Поэтому иерархическое ограничение ошибки — гораздо более эффективный метод. В простом линейном случае мы можем достичь иерархического упорядочивания компонентов путем последовательного (дефляционного) подхода, в котором компоненты последовательно извлекаются один за другим на оставшейся дисперсии, заданной квадратичной ошибкой предыдущих. Однако это не работает в нелинейном случае, ни последовательно, ни одновременно путем обучения нескольких сетей параллельно. Оставшаяся дисперсия не может быть интерпретирована квадратом ошибки, независимо от нелинейного преобразования. Решение состоит в использовании только одной сети с иерархией подсетей. Это позволяет нам сформулировать иерархию непосредственно в функции ошибки.

2.5. Инверсный нелинейный PCA

В этом разделе нелинейный PCA будет решать обратную задачу. В то время как проблема прямого характера состоит в прогнозировании выхода с заданного входа, обратная задача — это оценка входа, который наилучшим образом соответствует заданному результату. Поскольку нам неизвестны ни модель, ни процесс генерации данных, перед нами так называемая слепая обратная задача.

Простой линейный PCA можно рассматривать одинаково хорошо как в прямой, так и в обратной задаче, в зависимости от того, предсказываются ли желаемые компоненты в качестве выходов или оцениваются как входные данные по соответствующему алгоритму. Автоассоциативная сеть (АЕ) одновременно моделирует как прямую, так и обратную модели.

Прямая модель задается первой частью АЕ, функцией извлечения Fextr: X → Z. Обратная модель задается второй частью, функцией генерации Fgen: Z → X. Первая модель более подходит для линейного PCA, и менее — для нелинейного PCA. Это происходит, потому что она может быть функционально очень сложной или даже трудноразрешимой из-за проблемы отображения «один ко многим». Две идентичных выборки X могут соответствовать разным значениям компонентов Z.

Для инверсной нелинейной РСА требуется только вторая часть автоассоциативной сети (рис.11), что иллюстрируется сетью 3-7-12. Эта часть генерации представляет собой обратное отображение Fgen, которое генерирует или реконструирует образцы больших размеров Х из их представлений Z более низких размерностей. Эти значения компонентов Z теперь являются неизвестными входами, которые можно оценить, распространяя частичные ошибки σ обратно на входной слой Z.

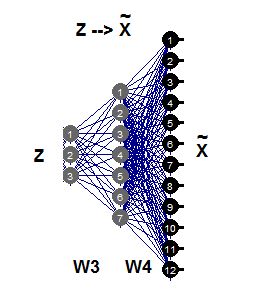
Рис. 11. Инверсная нелинейная модель РСА

Давайте сравним результаты, полученные с помощью АЕ и через функцию nlpca::pcaMethods. Эта функция была кратко представлена выше. Теперь на тех же данных и с теми же исходными требованиями редукции 12->3 выполним расчет и сравним результаты.

Для этого возьмем выборку DTcap.n$train, удалим из нее целевую Class и конвертируем ее в матрицу, после чего центрируем выборку. Структуру нейросети зададим как c(3,8,12), остальные параметры  можно увидеть в скрипте ниже. После получения результата выделим главные компоненты (scores), пристыкуем к ним целевую и построим график.

Отдельно предупрежу, что алгоритм очень медленный, и каждый новый запуск дает новый, отличный от предыдущего результат.

require(pcaMethods)
evalq({
  DTcap.n$train %>% tbl_df %>%
    select(-Class) %>% as.matrix() %>%
    prep(scale = "none", center = TRUE) -> train
  resNLPCA <- pca(train, 
                  method = "nlpca", weightDecay = 0.01,
                  unitsPerLayer = c(3, 8, 12),
                  center = TRUE, scale = "none",# c("none", "pareto", "vector", "uv")
                  nPcs = 3, completeObs = FALSE, 
                  subset = NULL, cv = "none", # "none""q2"), ...) 
                  maxSteps = 1100)
  rm(train)},
  env)
#--------
evalq(
   pcTrain <- resNLPCA@scores %>% tbl_df %>% 
           cbind(., Class = DTcap.n$train$Class)
, env)
#------graph-------
require(GGally)
evalq({
  ggpairs(pcTrain,columns = 1:ncol(pcTrain), 
          mapping = aes(color = Class),
          title = "pcTrain -> NLPCA(3-8-12) wd = 0.01")}, 
  env)
#----------

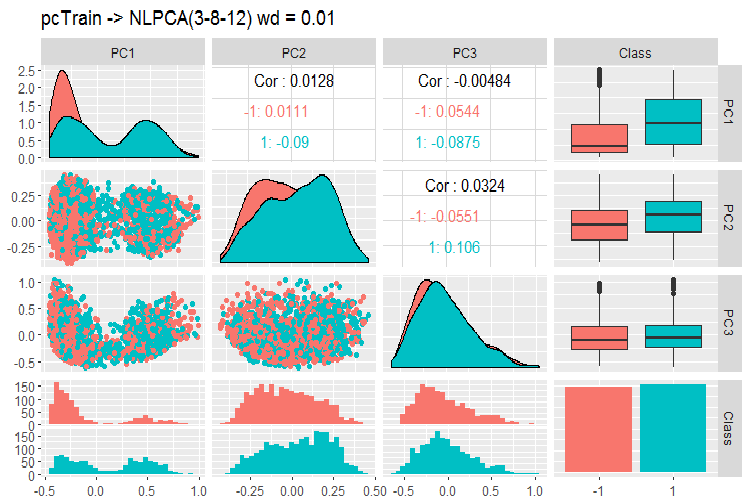
Рис. 12. Вариация и ковариация главных компонент полученных с помощью NLPCA

Что мы видим на графике? Главные компоненты хорошо разделяются по уровням целевой, имеют очень низкую корреляцию, и третья компонента выглядит лишней. Посмотрим общую информацию по модели.

> print(env$resNLPCA)
nlpca calculated PCA
Importance of component(s):
                 PC1    PC2     PC3
R2            0.3769 0.2718 0.09731
Cumulative R2 0.3769 0.6487 0.74599
12      Variables
2000    Samples
0       NAs ( 0 %)
3       Calculated component(s)
Data was mean centered before running PCA 
Data was NOT scaled before running PCA 
Scores structure:
[1] 2000    3
Loadings structure:
Inverse hierarchical neural network architecture
3 8 12 
Functions in layers
linr tanh linr 
hierarchic layer: 1 
hierarchic coefficients: 1 1 1 0.01 
scaling factor: 0.3260982 

Есть одна проблема: результат не возвращает матрицы весов W3 и W4. Иными словами, у нас нет нагрузки P, и мы не можем получить главные компоненты S (scores) на тестовом и валидационном наборах. Та же проблема и в двух других неплохих методах редукции размерности — tSNE, ICS. Конечно, применив несложную умственную гимнастику, мы можем решить эти задачи, но по этому сомнительному пути с неясным исходом лучше не ходить.

В пакете предложены еще два метода — вероятностный и байесовский РСА. Они работают быстро и возвращают нагрузки, что позволяет легко получить главные компоненты на val/test наборах. Приведу пример только для PPCA.

#=======PPCA===================
evalq({
  DTcap.n$train %>% tbl_df %>%
    select(-Class) %>% as.matrix() -> train
  DTcap.n$val %>% tbl_df %>%
    select(-Class) %>% as.matrix() -> val
  DTcap.n$test %>% tbl_df %>%
    select(-Class) %>% as.matrix() -> test
  resPPCA <- pca(train, method = "ppca",
                  center = TRUE, scale = "none",# c("none", "pareto", "vector", "uv")
                  nPcs = 3, completeObs = FALSE, 
                  subset = NULL, cv = "none", # "none""q2"), ...) 
                  maxIterations = 3000)
  },
  env)
#-----------
>print(env$resPPCA)
ppca calculated PCA
Importance of component(s):
 PC1 PC2 PC3
R2 0.2873 0.2499 0.1881
Cumulative R2 0.2873 0.5372 0.7253
12 	Variables
2000 	Samples
0 	NAs ( 0 %)
3 	Calculated component(s)
Data was mean centered before running PCA 
Data was NOT scaled before running PCA 
Scores structure:
[1] 2000 3
Loadings structure:
[1] 12 3

Построим график нагрузок и счетов для компонент 1 и 2:

slplot(env$resPPCA, pcs = c(1,2), 
       lcex = 0.9, sub = "Probabilistic PCA")

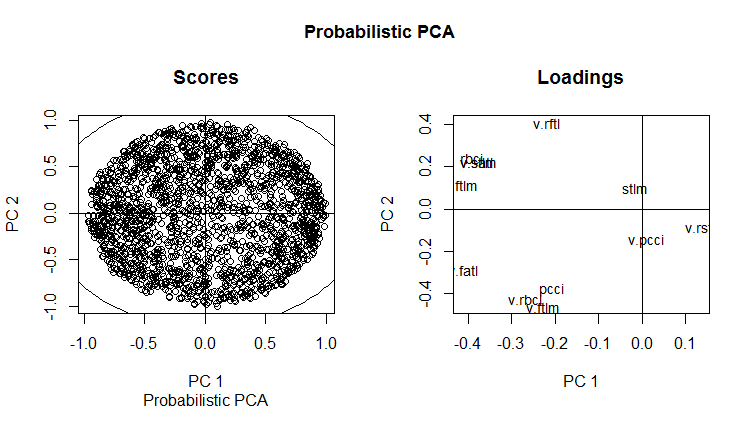
Рис. 13. РС1 и РС2 вероятностного РСА (loadings and scores)

Графики вариации и ковариации главных компонент выборок PPCA train/val/test приведены ниже. Скрипты смотрите на GitHub.

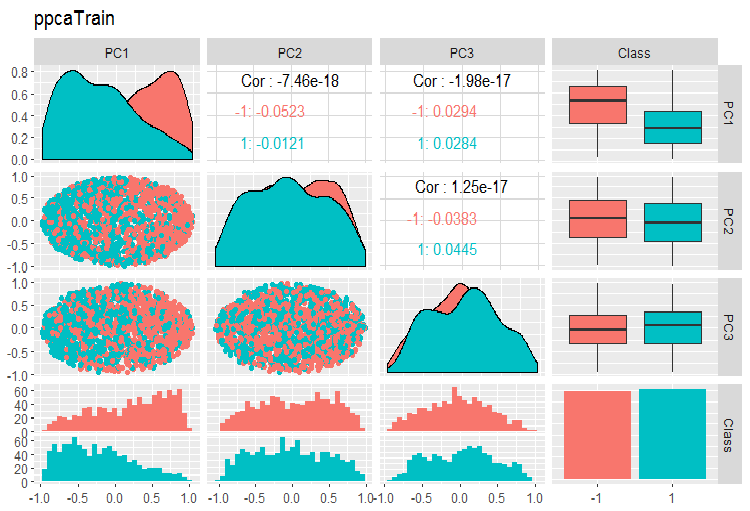
Рис. 14. Вариация и ковариация главных компонент выборки train полученных с помощью PPCA

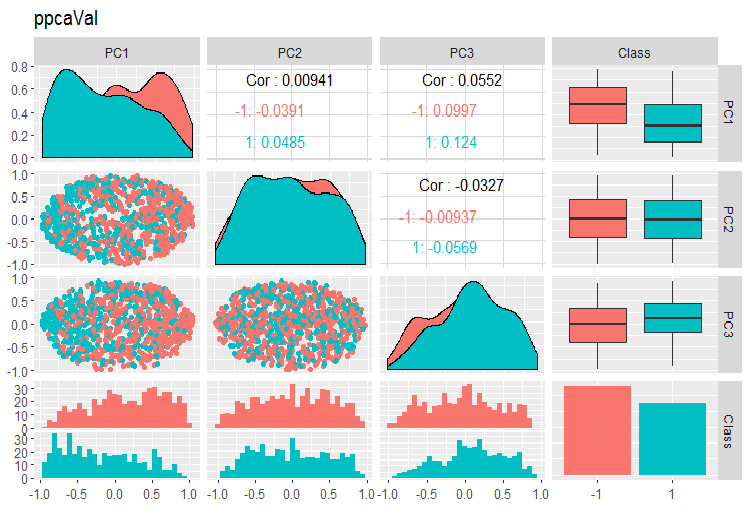
Рис. 15. Вариация и ковариация главных компонент выборки val полученных с помощью PPCA

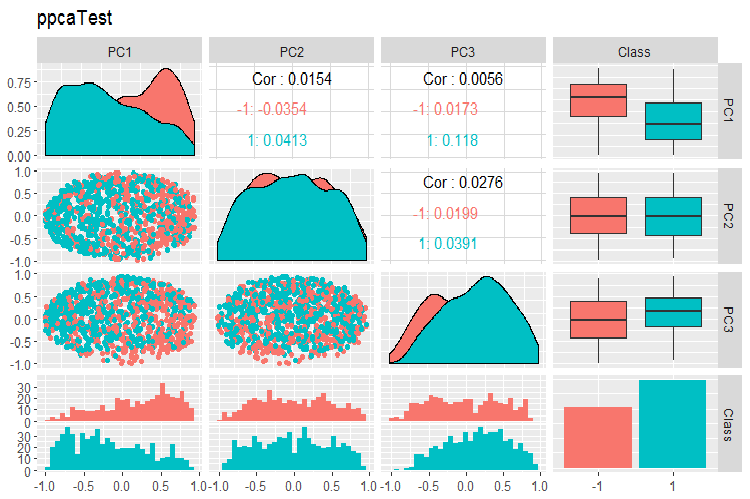
Рис. 16. Вариация и ковариация главных компонент выборки test полученных с помощью PPCA

Не могу сказать, что разделение по уровням целевой у главных компонент, полученных с помощью PPCA, лучше или качественней такой же редукции с помощью автоэнкодера, рассматривавшегося выше. Преимущество PPCA и BPCA — в скорости и простоте. Качество каждый раз нужно проверять конкретной моделью классификации.

3.Разделение набора на train/valid/test

В этой части все остается так же, как было описано в предыдущих статьях. При обучении — train/valid/test, скользящее окно, растущее окно, реже —  bootstrap. При выборе модели — кроссвалидация. Открытым вопросом остается определение достаточного размера этих выборок.

Отдельно обращаю ваше внимание на интересное утверждение фирмы Win Wector LLC об использовании выборок train при препроцессинговых трансформациях. Они утверждают, что если мы на обучающем наборе определили главные компоненты, то обучать модель нужно на главных компонентах, полученных на валидационном наборе. Т.е. использовать для обучения модели уже использованную выборку нельзя. Мы сможем это проверить при обучении нейросети.

Заключение

В трех частях статьи мы рассмотрели почти все этапы подготовки данных для использования их в обучении глубоких нейросетей. Как видим это сложный, трудозатратный и наукоёмкий этап. Но без понимания и умения правильно подготовить данные все последующие этапы и действия бессмыслены.

Без визуального контроля всех расчетов на этапе подготовки данных  невозможно получить хороший результат. Для нетерпеливых и ленивых разработаны пакеты "preprocomb" и "metaheur" которые могут автоматически подобрать (по Вашему выбору) наиболее подходящие этапы предподготовки.

Приложение

Скрипты, использованные в статье, выложены на GitHub/Part_III.