
Selbstoptimierung der Experten: evolutionäre und genetische Algorithmen
Inhalt
- Einführung
- 1. Die Geschichte der evolutionären Algorithmen
- 2. Evolutionäre Algorithmen (Methoden)
- 3. Genetische Algorithmen (GA)
- 3.1. Anwendungsgebiet
- 3.2. Aufgaben
- 3.3. Klassische GA
- 3.4. Suchstrategien
- 3.5. Der Unterschied von der klassischen Suche nach dem Optimum
- 3.6. Terminologie GA
- 4. GA Vorteile
- 5. GAs Nachteile
- 6. Experimentelles Teil
- 6.1. Die Suchen nach den besten Kombinationen von Prädiktoren
- mit der Verwendung tabuSearch
- 6.2. Suche nach den besten Parametern TS:
- 7. Die Mittel und Wege, um die Qualität der Indikatoren zu verbessern
- Fazit
Einführung
Die Notwendigkeit für die Selbstoptimierung der Experten ohne das Handeln zu verlassen, ist schon seit lange klar für viele Händler. Ich habe schon hier ein Paar Artikel über dieses Problem veröffentlicht (Artikel1, Artikel2, Artikel3, Artikel4). Die Basis für die Experimente in diesen Artikeln war die Bibliothek, die hier vorgeschlagen wurde. Doch seitdem, als sie veröffentlicht wurden, kamen neue in der Leistung stärkere Optimierungsalgorithmen und neue Möglichkeiten für ihre Anwendung. Darüber hinaus wurden meiner Meinung nach diese Artikel von Programmierern geschrieben und sind für Programmierer vorgesehen.
In diesem Artikel werde ich versuchen, die praktische Anwendung der genetischen Algorithmen (GA) ohne übermäßige technische Details zu erklären, vor allem für Händler. Dem Benutzer, der bin ich auch, ist es wichtig, das Arbeitsprinzip GA zu wissen, die Bedeutung und der Wert der Parameter, die die Qualität und die Geschwindigkeit der Konvergenz von GA und seinen anderen nützlichen Funktionen beeinflussen. Von daher, wahrscheinlich wiederhole ich es, aber beginne mit der Geschichte der Entstehung GA, weiterhin setzte ich es mit seiner Beschreibung fort, und ich werde auch die Parameter der verbesserten GA aufführen. Darüber hinaus werden wir GA mit mehreren evolutionären Algorithmen (EA) vergleichen.
1. Die Geschichte der evolutionären Algorithmen
Die Geschichte der evolutionären Berechnungen begann mit der Entwicklung einer Reihe von verschiedenen unabhängigen Modellen. Die wichtigsten sind von ihnen die genetischen Algorithmen und klassifizierenden Holland-Systeme (Holland), die an anfangs 60er Jahren veröffentlicht wurden und wurden allgemein nach der Veröffentlichung des Buches anerkannt, das Klassik in diesem Bereich geworden ist, - "Adaptation in Natural and Artifical Systems", 1975. In 70 Jahren im Rahmen einer Zufallssuchtheorie L.A. Rastrigin schlug eine Reihe von Algorithmen vor, die Ideen des bionischen Verhaltens von Individuen verwenden. Die weitere Entwicklung dieser Ideen wurde in Werken von I.L. Bukatov über die evolutionäre Modellierung gefunden. Während der Entwicklung der Idee von M.L. Tsetlin über die Machbarkeit und optimales Verhalten von stochastischen Automaten hat Y.I. Neumark die Suche nach globalen Extremumen durch die Kollektiv von unabhängigen Automaten vorgeschlagen, die den Prozess der Entwicklung und Elimination von Individuen simulieren. Ein großer Beitrag zur Entwicklung der evolutionären Programmierung haben Fogel und Walsh gemacht. Trotz des Unterschieds in Ansätzen hat jede von diesen "Schulen" eine Reihe von Prinzipien als Grundlage genommen, die in der Natur vorkommen und sie so weit vereinfachten, damit sie auf einem Computer realisiert werden könnten.
Die Bemühungen in der Modellierung der Evolution sind ähnlich mit natürlichen Systemen, sie können in zwei großen Kategorien geteilt werden.
- Die Systeme, die nach biologischen Prinzipien modelliert wurden. Sie wurden erfolgreich bei Aufgaben wie funktionelle Optimierung angewendet und können leicht unter nicht-biologische Sprache beschrieben werden.
- Die Systeme, die biologisch realistischer sind, aber nicht besonders anwendbar sind. Sie sind ähnlich mit biologischen Systemen und weniger konzentriert (oder nenapravleny überhaupt). Sie haben ein komplexes und interessantes Verhalten, und offenbar werden bald praktisch angewendet.
Natürlich, können wir in der Praxis diese Sachen nicht so deutlich trennen. Diese Kategorien - nur die beiden Pole, zwischen denen eine Vielzahl von Computersystemen liegt. Näher zum ersten Pol - evolutionäre Algorithmen, wie evolutionäre Programmierung (Evolutionary Programming), Genetische Algorithmen (Genetic Algorithms) und Evolutionsstrategien (Evolution Strategies). Näher zum zweiten Pol sind Systeme, die als künstliches Leben (Artificial Life) eingestuft werden können.
2. Evolutionäre Algorithmen (Methoden)
Evolutionäre Algorithmen — in Richtung der künstlichen Intelligenz (der Abschnitt evolutionäre Modellierung), die die Modelle und Prozesse der natürlichen Selektion verwendet. Hier sind einige von ihnen:
- Genetische Algorithmen — eine heuristischer Suchalgorithmus wird zur Lösung der Optimierung und Simulation durch zufällige Auswahl, Kombination und Variation der gewünschten Parameter verwendet;
Genetische Programmierung — automatische Erstellung oder Änderung der Programmen unter Verwendung der genetischen Algorithmen;
Evolutionäre Programmierung — ist wie die genetische Programmierung, aber die Struktur des Programms ist konstant, nur numerische Werte werden sich ändern;
evolutionäre Strategien — ähnlich mit den genetischen Algorithmen, aber in die nächste Generation werden nur positive Mutationen fort gegeben;
Differentiale Evolution;
neuroevolution — ist wie genetische Programmierung, aber Genome sind künstliche neuronale Netze, in denen die Evolution der Gewichte bei der gegebenen Netzwerktopologie stattfindet, oder zusätzlich zu der Evolution der Gewichte auch die Evolution der Topologie erzeugt wird.
Sie modellieren alle die grundlegenden Bestimmungen der Theorie der biologischen Evolution - die Selektionsprozesse, Kreuzung, Mutation und Reproduktion. Das Verhalten der Individuen wird durch die Umgebung bestimmt. Eine Menge der Individuen wird als eine Population genannt. Die Population entwickelt sich in Übereinstimmung mit den Auswahlsregeln in Übereinstimmung mit der Zielfunktion, die durch die Umgebung festgelegt wird. Somit wird jedem einzelnen Individuen in einer Population der Wert seiner Tauglichkeit in der Umgebung zugeordnet. Nur geeignete Individuen werden sich fortsetzen. Die Rekombination und Mutation ermöglicht jedem Einzelnen für die Umwelt zu verändern und anzupassen. Solche Algorithmen zeichnen sich durch adaptive Suchmechanismen.
Evolutionäre Methoden (EM) - ungefähre (Heuristik) Methoden zur Lösung der Optimierungsproblemen und strukturellen Synthese. Die meisten EM basieren auf einem statistischen Ansatz für die Untersuchung Situationen und iterative Annäherung zur gewünschten Lösung.
Evolutionäre Berechnungen bilden einen der Abschnitte der künstlichen Intelligenz. Beim Aufbau der AI-Systeme, nach diesem Ansatz wird Aufmerksamkeit auf den Aufbau des Ausgangsmodells und die Regeln gegeben, nach denen sie sich ändern kann (sich entwickeln). Dabei kann dieses Modell nach verschiedenen Verfahren formuliert werden. Beispielsweise kann es auch ein neuronales Netzwerk sein, und ein Satz von logischen Regeln. Zu wichtigsten evolutionären Methoden gehören Glühtechniken, genetische Verhalten der "Masse" (PSO), Ameisenkolonien (ACO), genetischer Programmierung.
Im Gegensatz zu den genauen Methoden der mathematischen Programmierung erlauben EM die Lösungen in einer akzeptablen Zeit zu finden, die optimal nahe sind, und im Vergleich zu den anderen heuristischen Optimierungsverfahren gekennzeichnet sich durch wesentlich weniger Abhängigkeit von der jeweiligen Anwendung (dh vielseitiger) und in den meisten Fällen durch eine bessere Annäherung zur optimalen Lösung. Die Vielseitigkeit einer EM wird durch Anwendbarkeit auf Probleme mit nicht metrisierbar Raum der gesteuerten Variablen definiert(das heißt, unter linguistischen Werte können auch die gesteuerten Variablen sein, einschließlich ohne Quantifizierung).
In Glühtechniken (Simulated Annealing) wird der Prozess der potentiellen Minimierung der Energie des Körperteiles während der Heizung des Details simuliert. Im aktuellen Suchpunkt findet eine Änderung einiger Steuereinstellungen statt. Der neue Punkt wird immer bei der Verbesserung der objektiven Funktionen genommen und manchmal bei der Wahrscheinlichkeit - wenn es verschlimmert.
Ein wichtiger Spezialfall der EM sind genetische Methoden und Algorithmen. Genetische Algorithmen (GA) basieren sich auf den besten Lösungen durch Vererbung und Verstärkung der nützlichen Eigenschaften der Objekte, die zur bestimmten Anwendung in der Simulation der Evolution gehören.
Die Eigenschaften der Objekte werden durch die Werte der Parameter dargestellt, kombiniert in einem Datensatz im EM-Chromosom. Der GA arbeiten auf einer Teilmenge von Chromosomen, die als Population genannt werden. Die Imitation der genetischen Prinzipien - die probabilistische Wahl der Eltern unter den Mitgliedern der Population, kreuzen ihre Chromosomen, die Auswahl der Nachkommen für die Aufnahme zur neuen Generation von Objekten, die auf der Auswertung der Zielfunktion basiert sind. Dieser Prozess führt zu einer evolutionären Verbesserung des Zielfunktionswertes (Nutzenfunktion) von Generation zur Generation.
Unter EM werden auch die Methoden verwendet, die im Gegensatz zu GA nur mit einem Chromosom arbeiten, anstatt mit mehreren. So ist die Methode der diskreten lokalen Suche (sein englischer Name Hillclimbing), basierend auf zufällige Variationen der einzelnen Parameter (Werte der Felder im Datensatz, oder mit anderen Worten, die Werte der Gene in einem Chromosom). Diese Veränderungen werden Mutationen genannt. Nach einer weiteren Mutation wird der Wert der Nutzenfunktion F (Fitness Function) eingeschätzt. Das Mutationsergebnis wird in den Chromosomen gespeichert, nur wenn F sich verbessert hat. Bei "Simulation Annealing" wird das Ergebnis einer Mutation mit einer gewissen Wahrscheinlichkeit gespeichert, die vom erhaltenen Wert abhängig sein wird.
In der Methode PSO (Particles Swarm Optimization) simuliert das Verhalten einer Menge der Agenten, die seinen Zustand mit dem Zustand des besten Agenten in Einklang bringen.
Die Ameisenkolonie Methode (ACO), basierend auf das Verhalten der Ameisen, die die Länge ihrer Routen auf dem Weg aus dem Nest bis zu einer Nahrungsquelle minimieren.
3. Genetische Algorithmen (GA)
Genetische Algorithmen — sind adaptive Suchtechniken, die in letzter Zeit häufig zur Lösung der Funktionsoptimierung eingesetzt werden. Sie basieren sich auf die genetischen Prozesse der biologischen Organismen: biologische Populationen entwickeln sich über mehrere Generationen, die unter den Gesetzen der natürlichen Selektion und dem Prinzip des "überlebt der am besten anpassungsfähiger" (survival of the fittest), das Charles Darwin erfunden hat. Nachahmen diesem Prozess können genetische Algorithmen die Lösungen für reale Probleme entwickeln, wenn sie entsprechend codiert sind.
In der Natur einer Population konkurrieren Individuen miteinander für eine Vielzahl von Ressourcen - wie beispielsweise Lebensmittel oder Wasser. Darüber hinaus die Mitglieder der Population einer Art konkurrieren oft um einen Ehepartner. Die Tiere, die am besten anpassungsfähig für die Umgebungsbedingungen sind, werden relativ mehr Nachkommen reproduzieren. Die wenig anpassender Individuen werden entweder keine Nachkommen produzieren, oder die werden weniger sein. Dies bedeutet, dass die Gene von gut angepassten Arten in einer zunehmenden Anzahl von Kindern in jeder Generation verteilt werden. Die Kombination der guten Eigenschaften von verschiedenen Eltern können manchmal zum Auftreten von "superanpassungsfähiger" Nachkommen führen, deren Anpassungsfähig größer ist als bei jedem seinen Eltern. Dadurch entwickelt sich die ganze Art besser zur Anpassung auf die Umwelt.
GA verwendet eine direkte Analogie mit dem Mechanismus. Sie arbeiten mit einer Reihe von "Individuen" - mit einer Population, von denen jede eine mögliche Lösung für dieses Problem darstellt. Jedes Individuum wird nach seiner "Anpassungsfähigkeit" eingeschätzt, je nachdem wie "gut" die Lösung des Problems entsprechend ist. Am wenigsten angepasste Individuen haben dann die Möglichkeit, den Nachkommen durch die Kreuzung mit anderen Populationen zu bekommen. Das führt zur Entstehung der neuen Individuen, die einige von Eltern geerbte Eigenschaften haben. Am wenigsten angepassten Individuen sind mit weniger Wahrscheinlichkeit in der Lage, den Nachkommen zu reproduzieren, so dass die Eigenschaften, die sie besitzen, werden allmählich von der Population im Verlauf der Evolution verschwinden.
So wird eine Population von möglichen Lösungen reproduziert, es werden die besten Vertreter der vorherigen Generation ausgewählt, sie kreuzen und viele neue Arten bekommen. Diese neue Generation enthält ein höheres Verhältnis der Eigenschaften, die "gute" Mitglieder der vorherigen Generation haben. So werden von Generation zur Generation die guten Eigenschaften in der Population verteilt. Die Kreuzung der Anpassungsfähigen Individuen führen dazu, dass die am meisten Perspektive Bereiche des Suchraums geforscht werden. Schließlich wird die Population zur optimalen Lösung der Aufgabe kommen.
Es gibt unterschiedliche Methoden der Realisierung der Idee von der biologischen Evolution im Rahmen GA.
3.1. Anwendungsgebiet
Die echten lösbaren Probleme können wie die Suche nach dem optimalen Wert formuliert werden, wo der Wert - eine komplexe Funktion ist, die von bestimmten Eingabeparametern abhängig ist. In einigen Fällen ist es interessant, die Werte der Parameter zu finden, bei den die besten aktuellen Werte der Funktion erreicht werden. In anderen Fällen wird das genaue Optimum nicht erforderlich, und als Lösung kann jeder Wert angesehen werden, der besser als vorbestimmter Wert ist. In diesem Fall werden genetische Algorithmen oft die am besten geeignete Methode für die Suche der "guten" Werte sein. Die Stärke eines genetischen Algorithmus - liegt an seiner Fähigkeit, mehrere Parameter zugleich zu manipulieren. Diese Besonderheit des GAs wurde in Hunderten von Anwendungen verwendet, einschließlich der Konstruktion von Flugzeugen, die Einstellungen der Konfigurationsparameter und Algorithmen zur Suche von stabilen Zuständen der Systeme von nichtlinearen Differentialgleichungen.
Es gibt jedoch Fälle, wenn ein GA funktioniert nicht so wirksam, wie erwartet.
Angenommen gibt es eine echte Problem, die mit der Suche nach optimalen Lösungen verbunden ist. Wie kann man erfahren, ob es für den GA geeignet ist? Eine genaue Antwort auf diese Frage gibt es bisher nicht. Allerdings haben viele Forscher die Annahme, dass der GA eine gute Chance hat, ein effektives Suchverfahren in folgenden Fällen zu werden:
- wenn der Suchraum, der geforscht werden soll, groß ist, und es wird angenommen, dass es nicht vollständig glatt und unimodal ist (dh enthält eine glatte Extremem);
- wenn die Anpassung-Funktion Geräusche hat;
- oder wenn die Aufgabe keine strenge Feststellung eines globalen Optimums erfordern.
Mit anderen Worten, in Situationen, in denen Sie eine geeignete "gute" Lösung finden müssen (was der Fall in realen Anwendungen recht häufig vorkommt), konkurriert GA und übertrifft andere Methoden, die keine Kenntnisse über den Raum bei der Suche nutzen.
Wenn der Suchraum klein ist, kann die Lösung durch ganze Suchmethode gefunden werden, und Sie können sicher sein, dass die bestmögliche Lösung gefunden wird, während der GA eher zu einem lokalen Optimum konvergieren könnte und nicht zur globalen besten Lösung. Wenn der Raum glatt und unimodal zu einem Gradientenalgorithmus ist, (beispielsweise das Verfahren des steilsten Abfalls) wird es wirksamer als GA.
Wenn es über den Suchraum einige zusätzliche Informationen gibt (wie zB der Raum für einen bekannten Travelling salesman problem), werden Suchmethoden, die vom Raum definierten Heuristik verwenden, oft besser als jede universelle Methode sein, was GA ist. Bei einer ziemlich komplexen Gelände der Anpassungsmethode mit einer einzigartigen Lösung zu jedem Zeitpunkt, wie eine einfache Methode des Abstiegs verfügt, kann es in der lokalen Entscheidung "hängen bleiben", aber es wird angenommen, dass GA, weil sie mit der ganzen "Population" von Lösungen arbeiten, haben wenige Chance zu einem lokalen Optimum zu konvergieren und funktionieren zuverlässig bei einer viel extremigen Landschaft.
Natürlich sind diese Annahmen nicht genau vorhersagbar, wann GA eine effektive Suchmethode sein wird, die mit anderen Methoden konkurrieren wird. Die Effizienz des GAs hängt stark von Details ab, wie die Kodierungsmethode, Operatoren, Anwendungseinstellungen, ein besonderes Kriterium für den Erfolg. Die theoretische Arbeit, die in der Literatur über genetischen Algorithmen durchgeführt wurde, gibt es solange keine Gründe, über die Entwicklung der strengen Mechanismen für präzise Vorhersagen zu sprechen.
3.2. Aufgaben
Genetische Algorithmen werden für die folgenden Aufgaben verwendet:- Optimierungsfunktionen
- Die Aufrufoptimierung in der Datenbank
- Eine Vielfalt der Problemen auf Graphen (Travelling Salesman Problem, Färbung, die passenden finden)
- Einstellung und Ausbildung eines künstlichen neuronalen Netzes
- Layout-Probleme
- Ablaufplanung
- Spielstrategien
- Approximationstheorie
3.3. Klassische GA
Die Arbeit eines einfachen GAsEin einfacher GA generiert zufällig die anfängliche Populationsstrukturen. Die Arbeit des GAs ist ein iterativer Prozess, der so weit fortgesetzt wird, bis es eine vorbestimmte Anzahl von Generationen ausgeführt wird, oder ein anderes Abbruchkriterium. In jeder Generation des Algorithmus wird die Auswahl der proportionalen Anpassung realisiert, ein Einzelpunkt-Crossover und eine Mutation.
Zunächst weist die proportionale Auswahl jeder Struktur die Wahrscheinlichkeit Ps (i) zu, die gleich dem Verhältnis seiner Anpassungsfähigkeit zu der gesamten Anpassungsfähigkeit der Population ist.
Dann wird die Auswahl (mit Ersatz) allen n-Individuen für die weitere genetische Verarbeitung entsprechend dem Wert Ps(i) durchgeführt. Eine einfache proportionale Auswahl - Roulette (roulette-wheel selection, Goldberg, 1989c) - wählt Individuen durch n-Zahl von "starten" der Roulette aus. Das Roulette-Rad enthält einen Sektor für jeden Mitglied der Population. Die Größe des i-ten Sektors ist proportional zu dem entsprechenden Wert Ps(i). Bei einer solchen Auswahl werden mehr angepassten Mitglieder der Population häufiger als Personen mit niedriger Anpassungsfähigkeit ausgewählt.
Nach der Auswahl n werden Individuen durch Crossover (manchmal nennt man das als Rekombination) mit einer gegebenen Wahrscheinlichkeit Pc bearbeitet. n Zeilen werden zufällig in n / 2 Paare aufgeteilt. Für jedes Paar mit Wahrscheinlichkeit Pc werden Crossover verwendet. Dementsprechend wird Crossover mit einer Wahrscheinlichkeit 1-Pc nicht stattfinden und die nicht geänderte Individuen gehen zur Mutation. Wenn der Crossover auftritt, die erhaltenden Nachkommen ersetzen Eltern und gehen zur Mutation.
Ein-Punkt-Crossover arbeitet auf folgende Weise. Zuerst wird eine von l-1 Bruchstellen zufällig ausgewählt. (Bruchstellen - Der Abschnitt zwischen benachbarten Bits in einer Zeile) Beide Elternstrukturen werden durch den Punkt in zwei Segmenten aufgeteilt. Dann werden die entsprechenden Segmente der verschiedenen Eltern zusammengeklebt, und daraus kommen zwei Genotype der Nachkommen.
Nach dem Abschluss der Crossoversphasen werden Mutationen-Operatoren durchgeführt. In jeder Zeile, die Mutationen erlebt haben, wird sich jeder Bit mit der Wahrscheinlichkeit Pm umgekehrt ändern. Die Population, die nach der Mutation erhalten wurde, wird über die alte geschrieben, damit beendet dieser Generation-Zyklus. Die nachfolgenden Generationen werden auf die gleiche Weise verarbeitet: Selektion, Crossover und Mutation.
Derzeit schlagen GA-Forscher viele andere Operatoren der Selektionen, Kreuzung und Mutation vor. Hier sind die häufigsten von ihnen. Vor allem, ist die Turnierauswahl (Brindle, 1981; Goldberg und Deb, 1991). Die Turnierauswahl realisiert n-Turnieren, um n Individuen auszuwählen. Jedes Turnier wird auf einer Stichprobe von k-Elementen der Population gebaut und auf die Auswahl der besten Individuen unter ihnen. Die häufigste Turnierauswahl ist mit k = 2 verbreitet.
Die elite Selektionsmethoden (De Jong, 1975) garantieren, dass bei der Auswahl notwendigerweise die beste oder die bessere Mitglieder der Population überleben. Die verbreitete Methode vermutet die obligatorische Speicherung nur eines besten Individuens, wenn es nicht durch erlebt hat, wie andere durch einen Prozess der Selektion, Crossover und Mutation. Die Elitizm kann in jedem Standard-Auswahlsmethode hingeführt werden.
Zwei-Punkte-Crossover (Cavicchio, 1970; Goldberg, 1989c) und gleichmäßiger Crossover (Syswerda, 1989) — sind durchaus gute Alternative für einen Ein-Punkt-Operator. Im Zwei-Punkt-Crossover werden zwei Bruchstellen ausgewählt, und die elterliche Chromosomen tauschen mit Segmenten aus, das zwischen diesen beiden Punkten sind. Im gleichmäßigen Crossover wird jedes Bit des ersten Elternteils vom ersten Nachkommen mit einer bestimmten Wahrscheinlichkeit geerbt; andernfalls wird dieses Bit von dem zweiten Nachkommen geerbt. Und umgekehrt.
Die wichtigsten Operatoren des genetischen Algorithmus
Der Operator des Auswahls (Selektion)
In diesem Stadium wird die optimale Population für die weitere Vermehrung ausgewählt. Normalerweise wird es eine bestimmte Anzahl der besten Anpassungsfähigen genommen. Es ist auch sinnvoll, die "Klone", also Individuen mit dem gleichen Satz von Genen zu verwerfen.
Crossovers Operator
Häufiger werden zwei besten Individuen gekreuzt. Das Ergebnis ist in der Regel zwei Individuen mit den getroffenen Komponenten von ihren "Eltern". Das Ziel des Operators - die Verteilung der "guten" Gene durch die Population und eine Kontraktion der Populationsdichte in Bereichen, in denen es bereits groß ist, die Annahme lautet, "wir sind da viel, wo es gut geht.".
Mutations-Operator
Der Mutationsoperator ersetzt einfach die willkürliche Zähle der Elementen um die anderen willkürlich Zähle. In der Tat ist es eine Art eines ableitenden Elementes, das einerseits aus den lokalen Extremums gezogen wird, auf der anderen - das die neuen Informationen zur Population einführt.
- Es invertiert die Bits bei einem binären Attributs.
- Es ändert im Wert eines numerischen Attributs (höchstwahrscheinlich für die nächste).
- Ersetzt um ein anderes Attribut.
Abbruchkriterien
- Die Suche nach globaler oder suboptimaler Lösung
- Der Anschluss zum «Plato»
- Die Erschöpfung der Anzahl der Generationen, die für die Evolution vorgegeben wurden
- Die Erschöpfung der Zeit, die für die Evolution vorgegeben wurde
- Die Erschöpfung einer vorbestimmten Anzahl von Anrufen zur zweckbestimmten Funktion
3.4. Suchstrategien
Die Suche - eine der universellen Rechnungs-Methoden der Lösungen, falls es überhaupt keine bekannte Reihe von Schritten gibt, die zum Optimum führt.Es gibt zwei Suchstrategien: die Verwendung der besten Lösung und die Untersuchung des Lösungsraums. Die Gradient-Methode - ein Beispiel einer Strategie, die die beste Lösung für die mögliche Verbesserung auswählt, dabei ignoriert es die Forschung aller Suchraum. Die Zufallssuche - ein Beispiel einer Strategie, die im Gegenteil ist, forscht den Lösungsraum, dabei ignoriert die Forschung der vielversprechenden Bereichen des Suchraums. Der genetische Algorithmus stellt eine Allzweck-Suchklasse Methoden dar, welche die Elemente beider Strategien kombinieren. Die Verwendung dieser Methoden ermöglicht eine gute Balance zwischen der Forschung und der Nutzung der besten Lösung zu halten. Am Anfang des genetischen Algorithmus ist die Population zufällig und hat eine Vielzahl von Elementen. Von daher führt der Kreuzungsoperator eine umfangreiche Forschung des Lösungsraumes durch. Mit der Zunahme der Funktionawerten wird der Kreuzungsoperator die Entsprechung der erhaltenden Lösungen mit der Forschung der Bereiche bei jedem von ihnen sicherstellen. Mit anderen Worten, die Art der Suchstrategie (die Nutzung der besten Lösung oder die Forschung des Lösungsraums), für den Kreuzungsoperator wird durch die Vielfalt der Population bestimmt, und nicht von diesem Operator selbst.
3.5. Der Unterschied von der klassischen Suche nach dem Optimum
Im Allgemeinen, der Lösungsalgorithmus der Optimierungsprobleme ist eine Reihe von Rechnungsschritten, die asymptotisch zur optimalen Lösung konvergieren. Die meisten klassischen Optimierungsmethoden erzeugen eine deterministische Reihe von Berechnungen, die auf dem Gradient oder auf dem Derivat der objektiven Funktion einer höheren Ordnung basierend sind. Diese Methoden werden auf einen Startpunkt des Suchraums verwendet. Dann wird die Lösung nach und nach in die Richtung der steigenden Zunahme oder Abnahme der Zielfunktion verbessern. Bei diesem Ansatz besteht die Gefahr in einem lokalen Optimum zu geraten.
Der genetische Algorithmus führt die gleichzeitige Suche in vielen Richtungen durch die Verwendung einer Population von möglichen Lösungen. Der Übergang von einer Population zur anderen ermöglicht zu vermeiden, in einem lokalen Optimum zu geraten. Die Population erlebt so etwas wie Evolution: in jeder Generation werden relativ gute Lösungen reproduziert, zugleich die relativ schlechte Lösungen sterben. Der GA verwendet die probabilistischen Regeln für die Bestimmung des reproduzierbaren oder vernichteten Chromosoms, um die Suche zu Bereichen der wahrscheinlichsten Verbesserung der Zielfunktion zurichten.
In den letzten Jahren wurden viele genetische Algorithmen realisiert, und meistens sind sie ziemlich unterschiedlich von anfangs klassischem Modell. Aus diesem Grund versteckt sich derzeit nicht nur ein Modell unter dem Begriff "genetische Algorithmen", sondern eine ziemlich große Klasse von Algorithmen, und manchmal sind sie wenig ähnlich mit einander. Die Forscher experimentierten mit verschiedenen Arten von Darstellungen, Crossoversoperatoren und Mutation, spezielle Operatoren und der verschiedenen Ansätze zur Auswahl und Wiedergabe.
Obwohl das Modell der evolutionären Entwicklung, die in GA verwendet wird, ist stark im Vergleich mit seinem natürlichen Analogon vereinfacht, jedoch ist GA ein recht mächtiges Werkzeug und kann für eine Vielzahl von Anwendungen erfolgreich eingesetzt werden, auch für solche, die schwer und manchmal sogar unmöglich für andere Methoden ist. Allerdings ist GA, sowie andere Methoden der evolutionären Berechnungen garantieren nicht, globale Lösungen in polynomieller Zeit zu finden. Sie garantieren auch nicht, dass eine globale Lösung überhaupt gefunden wird. Allerdings sind genetische Algorithmen gut für die Suche "genügend gute" Lösung des Problems "ziemlich schnell". Dort, wo die Aufgabe durch spezielle Methoden gelöst werden kann, werden solche Methoden fast immer wirksamer als GA und auch schneller und genauer bei den erhaltenen Lösungen. Der Hauptvorteil der GAs ist es, dass sie auch für komplexe Aufgaben eingesetzt werden können, wo es keine speziellen Methoden gibt. Selbst dort, wo existierende Methoden gut funktionieren, ist es möglich, Verbesserungen mit einer Kombination von GA zu erreichen.
3.6. Terminologie GA
Da der GA aus der Naturwissenschaften (Genetik) stammt und sowie vom Computer, ist der verwendete Begriff eine Mischung von der Natur und Kunst. Die Entsprechung der Begriffe, die GA betreffen, und deren Lösung für Optimierungsprobleme ist, werden in der Tabelle angegeben. 1.1.
Tabelle 1.
| Genetischer Algorithmus | Erklärung |
|---|---|
| Chromosom | Eine mögliche Lösung (ein Satz von Parametern) |
| Gene | Die Parameter, die optimiert werden |
| Lokus (Position) | Die Genepositionen in Chromosomen |
| Allel | Der Wert des Gens |
| Phänotyp | die abcodierte Lösung |
| Genotyp | die codierte Lösung |
Der klassische (Ein-Punkt) Crossover.
Der "Traditionelle" genetische Algorithmus verwendet einen Ein-Punkt-Crossover, bei dem zwei kreuzbaren Chromosomen an der entsprechenden Stelle einmal geschnitten werden und dann tauschen mit erhaltenden Teilen aus. Es wurde jedoch viele andere verschiedene Algorithmen mit anderen Typen von Crossover erfunden, die oft mehr als einen Schnittpunkt umfassen. DeJong suchte die Wirksamkeit eines mit mehreren Punkten Crossover und beschlossen, dass der Zwei-Punkt-Crossover eine Verbesserung gibt, aber dass die weitere Zugabe der Kreuzungspunkte die Aktivität des genetischen Algorithmus verringert. Das Problem mit dem Hinzufügen der zusätzlichen Punkte des Crossovers liegt daran, dass die standarte Blöcke wahrscheinlich unterbrochen werden. Jedoch besteht der Vorteil von mehreren Crossoversspunkte daran, dass der Zustandsraum im Detail und ausführlicher untersucht werden kann.
Zwei-Punkt-Crossover.
In einem Zwei-Punkt-Crossover (und generell auch in einem Mehr-Punkte-Crossover) werden Chromosomen als Loops betrachtet, die miteinander durch Verbindung der Enden von linearen Chromosomen gebildet werden. Um ein Segment eines Loops mit einem Segment von einem anderen Loop zu ersetzen, wird eine Auswahl von zwei Schnittpunkten erfordert. In dieser Ansicht können Ein-Punkt-Crossover als Crossover mit zwei Punkten in Betracht gezogen werden, aber mit einem Schnittpunkt, der am Anfang der Zeile festgelegt ist. Von daher löst ein Zwei-Punkt-Crossover das gleiche Problem wie Ein-Punkt-Crossover, aber vollständiger. Die Chromosome, die als Loop betrachtet wird, kann mehr standarte Blöcke enthalten, da sie einen "Loop-Rückkehr" am Ende der Zeile machen können. Derzeit sind viele Forscher damit einig, dass die Zwei-Punkt-Crossover generell besser sind als Ein-Punkt-Crossover.
Der unverifizierte (homogen) Crossover.
Der unverifizierte Crossover unterscheidet sich grundsätzlich von Ein-Punkt-Crossover. Jedes Gen in der Nachkommenschaft wird durch Kopieren des entsprechenden Gens aus einem oder anderem Elternteil erzeugt, das entsprechend einer zufällig erzeugten Maske des Crossovers ausgewählt wird. Wenn in der Maske des Crossovers 1 steht, wird das Gen aus dem ersten Eltern kopiert, wenn die Maske auf 0 gesetzt ist, wird das Gen von dem zweiten Eltern kopiert. Um den zweiten Nachwuchs zu erzeugen, wird der Prozess wiederholt, aber schon mit den ersetzten Eltern. Die neue Maske des Crossovers wird für jeden Satz von Eltern zufällig generiert.
Die differentiale Kreuzung.
Zusätzlich zu dem Crossover gibt es andere Methoden der Kreuzung. Zum
Beispiel für die Suche des Minimum / Maximum der Funktion von mehreren
realen Variablen ist das beste die "differentielle Kreuzung".
Beschreiben wir Sie kurz. Es seien a und b — es sind zwei Individuen in
der Population, also von deren realen Vektoren unsere Funktion abhängig
ist. Dann der Nachkommen c wird durch die Formel c=a+k*(a-b) berechnet,
wobei k ein bestimmter Koeffizient ist (das von ||a-b|| abhängig sein
kann - die Abstände zwischen Vektoren).
In diesem Modell wird die
Mutation - ist eine Ergänzung zum Individuum des Zufallsvektors einer
kurzen Länge. Wenn die Anfangsfunktion ununterbrechbar ist, dann
funktioniert dieses Modell gut. Und wenn sie auch glatt ist, dann ist es
ausgezeichnet.
Inversion und Umordnung.
Oft ist die Reihenfolge
der Gene im Chromosom sind kritisch für die Baublöcke, welche die
effiziente Arbeit des Algorithmus ermöglichen. Es wurden Methoden zur
Umordnung der Gene in den Chromosom-Positionen während der Arbeit des
Algorithmus vorgeschlagen. Eine dieser Methoden - ist eine Inversion,
die Umkehrung der Reihenfolge von Genen zwischen zwei zufälligen
ausgewählten Stellen im Chromosom führt. (Wenn diese Methoden verwendet
werden, müssen die Gene ein bestimmtes "Zeichen" enthalten, so dass sie
korrekt und unabhängig von ihrer Position im Chromosom identifiziert
werden könnten.)
Der Zweck der Umordnung ist, versuchen die
Reihenfolge der Gene zu finden, die die höchste Entwicklungspotential
hat. Viele Forscher haben eine Inversion in ihrer Arbeit verwendet,
obwohl es scheint, dass nur wenige von ihnen haben versucht, sie zu
beweisen oder ihren Beitrag zu bestimmen. Goldberg & Brücken
analysieren den Operator für die Unordnung auf einer sehr kleinen
Aufgabe, und zeigen, dass Sie einen bestimmten Vorteil geben kann,
obwohl sie beschließen, dass ihre Methoden nicht den gleichen Vorteil
auf große Aufgaben ergeben würden.
Die Umordnung erweitert auch stark
den Umfang der Suche. Der genetische Algorithmus versucht nicht nur die
guten Werte vieler Gene zu finden, es versucht auch zugleich ihre
"richtige" Ordnung zu finden. Es ist eine viel schwierige Aufgabe zu
lösen.
Was ist eine Epistasis?
Der Begriff "epistasis" wird als genetischer Einfluß auf die
Tauglichkeit des Individuums abhängig vom Gen-Wert definiert, der
anderswo in vorhanden ist. Mit anderen Worten Genetikern verwenden den
Begriff "epistasis" im Sinne der Wirkung der "Umschaltung" oder
"Maskieren": " Das Gen wird epistatisch berücksichtigt, wenn seine
Anwesenheit den Einfluss des Gens in einem anderen Locus unterdrückt.
Manchmal werden epistatische Gene wegen ihrem Einfluss auf andere Gene
als inhiberen genannt, die wie Hypostase beschrieben werden".
In der
Terminologie GA kann dies auch klingen: "Die Anpassungsfähigkeit eines
Individuums hängt von der relativen Position der Chromosomen in der
Geneanlage ab".
Was ist ein falsches Optimum?
Eines der grundlegenden Prinzipien der genetischen Algorithmen ist,
dass die Chromosomen, die zu den Vorlagen hinzugefügt sind, die im
globalen Optimum enthalten sind, erhöhen sich in der Frequenz. Dies gilt
insbesondere für kleine kurze Vorlagen, die als Baublöcke bekannt
sind. Letztendlich werden beim Crossover die optimale Vorlage
zusammenlaufen, und es wird ein globales optimales Chromosom erzeugt.
Aber wenn die Vorlagen, die nicht im globalen Optimum enthalten sind,
werden sich in der Frequenz schneller erhöhen, als andere, dann wird der
genetische Algorithmus geirrt und der geht auf die andere Seite des
globalen Optimums, anstatt sich zu ihm zu nähern. Dieses Phänomen ist
als fehlerhaftes Optimum bekannt.
Ein falsches Optimum - ist ein
Spezialfall von epistasis, und er war tief von Goldberg und anderen
geforscht. Ein falsches Optimum ist direkt mit den schädlichen Wirkungen
von epistasis in genetischen Algorithmen verbunden.
Statistisch
erhöht sich die Vorlage in der Frequenz der Population, wenn ihre
Tauglichkeit höher ist als die durchschnittliche Tauglichkeit aller
Vorlagen in der Population. Die Aufgabe wird als die Aufgabe des
fehlerhaften Optimums bezeichnet, wenn die durchschnittliche
Tauglichkeit von Vorlagen, die nicht in dem globalen Optimum enthalten
sind, mehr als die durchschnittliche Tauglichkeit anderer Vorlagen ist.
Die
Aufgaben des fehlerhaften Optimums sind schwierig zu lösen. Allerdings
zeigt Grefenstette genial, dass sie nicht immer auftreten. Nach der
ersten Generation erhält der genetische Algorithmus keine objektive
Probenpunkte im Suchbereich. Von daher kann er nicht die objektive
globale durchschnittliche Tauglichkeit der Vorlage einschätzen. Er kann
nur eine voreingenommene Einschätzung der Tauglichkeit der Vorlage
erhalten. Manchmal hilft es, damit die genetischen Algorithmen
zusammenfallen (auch wenn die Aufgabe sonst ein starkes falsches Optimum
hätte).
Was ist inbreeding, outbreeding, selektive Auswahl, Panmixie?
Es gibt mehrere Ansätze zur Auswahl eines Elternpaars. Die einfachste von ihnen - ist die Panmixie.
Dieser Ansatz beinhaltet die zufällige Auswahl der Elternpaare, wenn
die beide Individuum, die ein Elternpaar bilden, werden zufällig aus der
gesamten Population ausgewählt. In diesem Fall kann jedes Individuum,
ein Mitglieder in mehreren Paaren werden. Trotz seiner Einfachheit ist
dieser Ansatz vielseitig für verschiedene Klassen von Aufgaben. Der ist
jedoch ziemlich kritisch für die Populationsgröße, weil die Wirksamkeit
des Algorithmus, der diesen Ansatz realisiert, mit zunehmender
Populationsgröße abnimmt.
Die selektive Methode der
Individuumsauswahl bei der Elternpaar besteht darin, dass "Eltern" nur
die Individuen sein können, deren Anpassungsfähigkeit nicht geringer als
die durchschnittliche Anpassungsfähigkeit der Population ist, mit der
gleichen Wahrscheinlichkeit bei solchen Kandidaten ein Paar zu machen.
Dieser
Ansatz bietet eine schnellere Konvergenz des Algorithmus an. Jedoch
aufgrund der schnellen Konvergenz der selektiven Auswahl eines
Elternpaars ist es nicht geeignet, wenn die Aufgabe für die Bestimmung
der Anzahl der Extremen entsteht, da der Algorithmus für solche Aufgaben
in der Regel schnell auf eine der Lösungen kommt. Darüber hinaus, für
eine bestimmte Klasse von Problemen mit schwierigem Gelände der
Anpassungsfähigkeit schnelle Konvergenz kann eine vorzeitige Konvergenz
zu quasi-optimaler Lösung werden. Dieser Nachteil kann teilweise durch
einen geeigneten Auswahlmechanismus kompensiert werden, das eine zu
schnellen Konvergenz des Algorithmus "bremsen" würde.
Inbreeding ist
eine Methode, bei der das erste Element des Paars zufällig ausgewählt
wird, und das zweite wird höchstwahrscheinlich nahe stehende zum
Individuum sein.
Bei outbreeding verwendet man auch den Begriff der
Ähnlichkeit der Individuen. Doch jetzt werden Paare aus am maximal
entfernten Individuen gebildet.
Die letzten beiden Methoden haben
unterschiedliche Auswirkungen auf genetisches Algorithmus-Verhalten. So
kann Inbreeding durch die Eigenschaft der Konzentration der Suche in
lokalen Knoten gekennzeichnet sein, die tatsächlich auf die Teilung der
Population in verschiedene lokale Gruppen um den verdächtigen
Extremum-Gebiete führen. Outbreeding richtet sich an die Warnung der
Konvergenz des Algorithmus zu bereits gefundenen Lösungen, so dass
Algorithmus neu unerforschte Gebiete durchsehen wird.
Dynamische Selbstorganisation der GA-Parameter
Oft wird die Wahl der Parameter des genetischen Algorithmus und der
spezifischen genetischen Operatoren auf einer intuitiven Ebene
durchgeführt, denn es gibt bisher keinen Hinweis auf die Vorteile der
verschiedenen Einstellungen und Operator. Wir sollten jedoch nicht
vergessen, dass das Wesen des GAs an der Dynamik und "Weichheit" des
Algorithmus und Berechnungen liegt. Warum erlauben wir dann nicht, dem
Algorithmus sich selbst bei der Lösungssuche des Problems einzustellen
und sich anzupassen?
Der einfachste Weg ist es, die Anpassung der
verwendeten Operatoren zu organisieren. Dafür fügen wir in diesem
Algorithmus mehrere (je mehr, desto besser) verschiedene
Auswahl-Operatoren (Elite, zufällig, Roulette, ..), Crossover
(Ein-Punkt, Zwei-Punkt, standardisierte, ..) und Mutation (zufällige
Ein-Element, absolut, ..) ein. Stellen wir für jeden Operator gleiche
Verwendungswahrscheinlichkeiten ein. Als nächstes werden wir in jedem
Loop des Algorithmus einen der Operatoren jeder Gruppe (Bereich
Crossover, Mutation) in Übereinstimmung mit der
Verteilungswahrscheinlichkeit auswählen. Zugleich bemerken wir an dem
erhaltenden Individuum, mit Hilfe von welchem Operator er empfangen
wurde. Dann, wenn wir die neu Verteilungswahrscheinlichkeit auf der
Basis von den enthaltenen Informationen in der Population berechnen (die
Wahrscheinlichkeit, dass der Operator die Anzahl der Individuen in
einer Population proportional verwendet,die durch diesen Operator
erhalten wurden), empfängt der genetische Algorithmus ein
selbstpassendes dynamisches Mechanismus.
Dieser Ansatz bietet einen
weiteren Vorteil an: jetzt braucht man keine Sorgen mehr um den
geltenden Zufallszahlengenerator zu machen (linear, exponentiell, etc.),
da der Algorithmus dynamisch den Charakter der Verteilung verändert.
Die Migrationsmethode und künstliche Selektion
Im Gegensatz zu gewöhnlichen GAn, wird die Makroevolution durchgeführt, das heißt, es wird nicht nur eine Population erstellt, sondern viele von ihnen. Die genetische Suche wird durch Kombinieren der Eltern aus verschiedenen Populationen durchgeführt.
Methode des unterbrochenen Gleichgewichts
Die Methode basiert sich auf der fossilen Theorie des unterbrochenen
Gleichgewichts, die die schnelle Entwicklung durch vulkanische und
andere Veränderungen in der Erdkruste beschreibt. Zur Verwendung dieser
Methode in technischen Problemen wird angeboten, die Individualitäten in
der Population nach jeder Erzeugung zufälligerweise mischen und dann
neue aktuelle Generationen erzeugen. Hier kann Analogon von der Natur
anbieten, eine unbewusste Auswahl von Elternpaaren und synthetische
Auswahl der besten Elternpaare. Die Ergebnisse beider Auswählen müssen
weiter zufällig gemischt werden und keine permanente Populationsgröße
inzwischen lassen, sondern steuern sie nach der Verfügbarkeit des besten
Individuens. Eine solche Modifikation der Methode unterbrochenen
Gleichgewichts kann aussichtslose Population verringern sowie die
Population zu erweitern, die die besten Exemplare sind.
Die Methode
des unterbrochenen Gleichgewichtes — die mächtige Streßmethode der
Veränderung der Umwelt, die für den wirkungsvollen Ausgang aus den
lokalen Gruben verwendet wird.
4. GA Vorteile
Es gibt zwei Haupt-Vorteile der genetischen Algorithmen vor klassischen optimierten Methoden.
1. Der GA hat keine bedeutenden mathematischen Forderungen zu den Arten der zweckbestimmten Funktionen und der Beschränkungen. Der Forscher soll das Modell des Objektes nicht vereinfachen, dabei ihre Angemessenheit verlieren, und absichtlich nach der Möglichkeit der Anwendung der zugänglichen mathematischen Methoden jagen. Dabei können die vielfältigsten zweckbestimmten Funktionen und die Arten der Beschränkungen (linear und nichtlinear) verwendet werden, die auf diskreten, ununterbrochenen und gemischten universellen Mengen bestimmt sind.
2. Unter Anwendung von den klassischen schrittweisen Methoden kann das globale Optimum nur in diesem Fall gefunden werden, wenn das Problem die Eigenschaft der Rundung verfügt. Zugleich ermöglichen die Evolutionsoperationen der genetischen Algorithmen effektiv das globale Optimum zu finden.
Weniger globaler, aber auch die wichtigen Vorteile des GAs sind:
Die große Zahl der freien Parameter, die wirkungsvoll die Heuristik zum Einfügen anbieten;
das wirkungsvolle Entparallelern;
Arbeitet wesentlich nicht schlechter als eine absolut zufällige Suche;
Die Verbindung mit der Biologie, die einige Hoffnung auf die ausschließliche Effektivität des GAs gibt.
5. GAs Nachteile
Die große Menge der freien Parameter, die "die Arbeit mit GA" in "das Spiel mit GA umwandeln"
Die Unbewiesenheit der Konvergenz
In den einfachen zweckbestimmten Funktionen (glatt, ein Extremem u.s.w) verliert die Genetik immer nach der Geschwindigkeit von einfachen Suchalgorithmen
6. Experimentelles Teil
Wir werden alle Experimente im Kreis der Sprache R 3.2.4 leiten. Wir verwenden den Datensatz für die Ausbildung des Modells und der Mehrheit der Funktionen aus dem vorhergehenden Artikel.
Den Aufgaben der Optimierung und des mathematischen Programmierens ist der Teil des Depositars CRAN gewidmet, der die große Menge der Pakete enthält, die für ihre Lösung vorgesehen sind . Wir werden einige verschiedene Methoden des GAs und EMs für die Lösung der Aufgaben verwenden, die unten hingebracht sind. Die Forderung zu den Modellen, die im Prozess der Optimierung teilnehmen, ist nur eine — die Schnelligkeit. Die Modelle verwenden, die im Laufe von Hundert Sekunden ausgebildet werden, ist unerwünscht. Unter Berücksichtigung, dass es mindestens 100 Individuen in jeder Generation werden, und die Population wird durch die Reihe (von einer bis zu Dutzenden) der Epochen gehen, der Prozess der Optimierung wird auf die unannehmbare Zeit dauern. In den vorhergehenden Artikeln verwendeten wir zwei Arten der tiefen Netze (mit der Initialization SSAE und RBM). Beider haben die hohe Schnelligkeit vorgeführt und können vollkommen bei der genetischen Optimierung verwendet werden.
Wir werden zwei Aufgaben der Optimierung lösen: die Suche der besten Kombination der Prädiktoren und die Auswahl der optimalen Parameter der Indikatoren. Für die Lösung der ersten Aufgabe (die Auswahl der Prädiktoren) werden wir zwecks der Annahme der neuen Algorithmen den oft in letzter Zeit erwähnten Algorithmus XGBoost(Extreme Gradient Boosting) verwenden. Nach den Erwähnungen in den Quellen, führt er die sehr guten Ergebnisse in den Aufgaben der Klassifikation vor. Der Algorithmus ist für die Sprachen R, Python, Java verfügbar. In der Sprache R wurde dieser Algorithmus im Paket “xgboost” v realisiert. 0.4-3.
Für die Lösung der zweiten Aufgabe (die Auswahl der optimalen Parameter der Indikatoren) werden wir den einfachen EA MACDsample nehmen und wir schauen, was man mit seiner Hilfe bei der schnellen Nutzung der genetischen Optimierung 6.1 bekommen kann
6.1. Die Suchen nach den besten Kombinationen von Prädiktoren
Für die Lösung der Optimierungsaufgabe mit einer beliebigen Methode muss man bestimmen:
die Parameter, die optimiert werden;
das Kriterium der Optimierung — der Skalar, den man maksimisieren/minimisieren muss. Es können mehrere Kriterien sein;
die zweckbestimmte (objektiv, die Fitness) Funktion, die die Größe des Kriteriums der Optimierung berechnen wird.
Die Fitness-Funktion für unseren Fall wird es konsequent erfüllen:
die Bildung der Anfangs-Dataframe;
seine Teilung auf train/test; train/test;
die Ausbildung des Modells;
Der Test des Modells;
die Berechnung der Kriteriumsoptimierung.
Eine Kriteriumsoptimierung können wie die standardmäßigen Metriken — Accuracy, Recall, Kappa, AUC, sowie auch die vom Hersteller angebotene sein. Wir werden in dieser Qualität den Fehler der Klassifikation verwenden.
Die Suche nach der besten Kombination der Prädiktor werden wir mit Hilfe des Paketes "tabuSearch" v.1.1 durchführen, der eine Erweiterung des Algorithmus HillClimbing ist. Der Algorithmus TabuSearch optimiert die binäre Zeile, durch die Verwendung der objektiven Funktion, die vom Benutzer bestimmt ist. Daraufhin gibt er die beste binäre Konfiguration mit dem höchsten Wert der objektiven Funktion aus. Wir werden diesen Algorithmus für die Suche der besten Kombination der Prädiktoren verwenden.
Die Hauptfunktion:
tabuSearch(size = 10, iters = 100, objFunc = NULL, config = NULL, neigh = size, listSize = 9, nRestarts = 10, repeatAll = 1, verbose = FALSE)
Argumente:
size – die Länge der optimierten binären Konfiguration;
iters – die Zahl der Iterationen in der vorläufigen Suche des Algorithmus;
objFun – die vom Benutzer angebotene Methode, die die zweckbestimmte Funktion für die vorliegende binäre Zeile bewertet;
config – die Startkonfiguration;
neigh – die Zahl der benachbarten Konfigurationen für die Prüfung auf jede Iteration. Die ist der Länge der binären Zeile standardmäßig gleich. Wenn die Zahl weniger als die Länge der Zeile ist, werden die Nachbarn in der zufälligen Weise ausgesucht;
listSize – der Umfang der Tabus-Liste;
nRestarts – die maximale Anzahl des Neustarts in der intensiven Etappe der Suche nach dem Algorithmus;
repeatAll – die Anzahl der Wiederholungen der Suche;
verbose – die logische, wenn es true ist, wird der aktuelle Name der Etappe des Algorithmus gedruckt, zum Beispiel, eine Voretappe, eine Identifikation-Etappe, eine Diversifikation-Etappe.
Schreiben wir eine objektive Funktion und fangen an, zu experimentieren.
ObjFun <- function(th){
require(xgboost)
# Wenn es in der binären Zeile alle 0 sind, dann verlassen
if (sum(th) == 0) return(0)
# die Namen der Prädiktoren, die 1 in der binären Zeile entsprechen
sub <- subset[th != 0]
# Erstellen wir eine Struktur der Ausbildung des Modells
dtrain <- xgb.DMatrix(data = x.train[ ,sub], label = y.train)
# Bilden wir das Modell aus
bst = xgb.train(params = par, data = dtrain, nrounds = nround, verbose = 0)
# Berechnen wir die Vorhersage über dem Testsatz
pred <- predict(bst, x.test[ ,sub])
# Finden wir den Fehler der Vorhersage raus
err <- mean(as.numeric(pred > 0.5) != y.test)
# Setzen wir die Qualitätskriterien zurück
return(1 - err)
}Für die Rechnung brauchen wir den Satz aus Daten vorbereiten, die für die Ausbildung und den Test gebraucht werden, auch müssen wir noch die Parameter des Modells und die Startkonfiguration für die Optimierung bestimmen. Verwenden wir die gleichen Daten und Funktionen, die im vorherigen Artikel waren(EURUSD/M30, 6000 Bars am 14.02.16).
Die Liste mit Kommentaren:
#---tabuSearch---------------------- require(tabuSearch) require(magrittr) require(xgboost) # die Anfangs-Dataframe dt <- form.data(n = 34, z = 50, len = 0) # die Namen aller Prädiktoren im Anfangssatz subset <- colnames(In()) set.seed(54321, kind = "L'Ecuyer-CMRG") # Lass uns die Sätze für die Ausbildung und den Test vorbereiten DT <- prepareTrain(x = dt[ ,subset], y = dt$y, balance = FALSE, rati = 4/5, mod = "stratified", norm = FALSE, meth = method) train <- DT$train test <- DT$test x.train <- train[ ,subset] %>% as.matrix() y.train <- train$y %>% as.numeric() %>% subtract(1) x.test <- test[ ,subset] %>% as.matrix() y.test <- test$y %>% as.numeric() %>% subtract(1) # der Anfangs Binärvektor th <- rep(1,length(subset)) # Modell-Parameter par <- list(max.depth = 3, eta = 1, silent = 0, nthread = 2, objective = 'binary:logistic') nround = 10 # Startkonfiguration conf <- matrix(1,1,17) res <- tabuSearch(size = 17, iters = 10, objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1) # Maximalwert der objektiven Funktion max.obj <- max(res$eUtilityKeep) # die beste Kombination des Binärvektors best.comb <- which.max(res$eUtilityKeep)%>% res$configKeep[., ] # Der beste Satz der Prädiktoren best.subset <- subset[best.comb != 0]
Starten wir die Optimierung mit 10 Iterationen und schauen wir, was für ein maximales Qualitätskriterium ist und der Satz der Prädiktoren.
> system.time(res <- tabuSearch(size = 17, iters = 10, + objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1)) user system elapsed 36.55 4.41 23.77 > max.obj [1] 0.8 > best.subset [1] "DX" "ADX" "oscDX" "ar" "tr" "atr" [7] "chv" "cmo" "vsig" "rsi" "slowD" "oscK" [13] "signal" "oscKST" > summary(res) Tabu Settings Type = binary configuration No of algorithm repeats = 1 No of iterations at each prelim search = 10 Total no of iterations = 30 No of unique best configurations = 23 Tabu list size = 9 Configuration length = 17 No of neighbours visited at each iteration = 17 Results: Highest value of objective fn = 0.79662 Occurs # of times = 2 Optimum number of variables = c(14, 14)
Die Berechnungen haben ungefähr 37 Sekunden bei der Genauigkeit der Vorhersage daneben 0.8 und 14 Prädiktoren gedauert. Die erhaltene Qualität mit den standardmäßigen Parametern ist sehr gut. Wir werden die gleiche Berechnung, aber mit 100 Iterationen durchführen.
> system.time(res <- tabuSearch(size = 17, iters = 100, + objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1)) user system elapsed 377.28 42.52 246.34 > max.obj [1] 0.8042194 > best.subset [1] "DX" "ar" "atr" "cci" "chv" "cmo" [7] "sign" "vsig" "slowD" "oscK" "SMI" "signal" >
Wir sehen, dass die Vergrößerung der Zahlen der Iterationen die Zeit der Berechnung proportional vergrössert hat, was man über die Genauigkeit der Vorhersage nicht sagen kann. Es hat unbedeutend zugenommen. Bedeutet dies, die Qualitätskennziffern verbessern, muss man auf Kosten von der Einstellung der Parameter des Modells.
Es ist nicht der einzige Algorithmus und das Paket, der hilft, den besten Satz der Prädiktoren mit Hilfe des GAs zu wählen. Sie können die Pakete kofnGA, fSelector verwenden. Außer ihnen, im Paket "caret" der Funktion gafs() wurde die Auswahl der Prädiktoren mit Hilfe des GAs realisiert.
6.2. Die Suche nach den besten Parametern TS
1. Die Anfangs-Daten für die Projektierung. Wir werden als Beispiel den Experte MACDSampl nehmen.
Im Experten MACDSample wurde der Algorithmus realisiert, der die Signale bei der Kreuzung der Linien macd und signal generiert. Ein wird ein Indikator verwendet.
ArgumenteMACD(x, nFast = 12, nSlow = 26, nSig = 9, maType, percent = TRUE, ...)
|
x |
Die Timeserie einer Variable; ist in der Regel price, kann aber auch volume, sein u.s.w |
|
nFast |
Die Zahl der Perioden für schnell MA. |
|
nSlow |
Die Zahl der Perioden für langsam MA |
|
nSig |
Die Zahl der Perioden für signal MA |
MaType – der verwendete Typ MA
percent – logische, wenn es true ist, dann setzt den Unterschied zwischen schnellen und langsamen MA prozentual zurück, sonst — der einfache Unterschied.
Die Funktion MACD setzt zwei Variabele zurück: macd — der Unterschied zwischen schnellem MA und langsamen MA, oder die Veränderung der Geschwindigkeit des Abstands zwischen schnellem MA und langsamen MA; signal — — MA von diesem Unterschied. MACD ist ein Sonderfall des Allgemeinen des Oszillators, der zum Preis verwendet wird. Er kann auch mit jeder Timeserie einer Variablen verwendet werden. Die vorübergehenden Perioden für MACD stellen oft 26 und 12 ein, aber die Funktion verwendete am Anfang die exponenten Konstanten 0.075 und 0.15, die zu Perioden 25.6667 und 12.3333 näher ist.
Also hat unsere Funktion 7 Parameter mit den Umfängen der Veränderungen:
p1 - Der Rechenpreis (Close, Med, Typ, WClose)
p2 - nFast (8:21)
p3 – nSlow(13:54)
p4 - nSig (3:13)
p5 - MAtypeMACD – der Typ MA für die Linie MACD
p6 - MatypeSig – der Typ MA für die Signal
p7 — percent (TRUE, FALSE)
p5,p6 = Cs(SMA, EMA, DEMA, ZLEMA).
Die Signale für das Handeln kann man in verschiedenen Weisen generieren:
Die Variante 1
Buy = macd > signal
Sell = macd < signal
Die Variante 2
Buy = diff(macd) > 0
Sell = diff(macd) <= 0
Variante 3
Buy = diff(macd) > 0 & macd > 0
Sell = diff(macd) < 0 & macd < 0
Es ist noch ein Parameter der Optimierung signal(1:3).
Und endlich der letzte Parameter — die Tiefe der Optimierungsgeschichte len = 300:1000 (die Zahl der letzten Bars auf den die Optimierung durchgeführt wird).
Insgesamt haben wir 9 Optimierungsparameter. Ich habe absichtlich ihre Anzahl verringert, damit Sie sehen: alles kann ein Parameter werden, alles mögliches (Zähle, Zeile u.s.w).
Die Optimierungskriterium — die Qualitätskoeffizient K in Punkten (in meinen vorherigen Artikeln wurde er bereits erwähnt).
Um die Parameter zu optimieren, müssen wir die Fitness(objektive) Funktion herausfinden, die die Qualitätskriterien rechnen wird und das Optimierungsprogramm auswählen. Wir beginnen mit dem Programm.
Wir werden ein zuverlässiges schnelles und hauptsächlich — mehrmals in der Praxis überprüftes Paket "rgenoud". Seine Hauptbeschränkung besteht darin, dass seine Parameter entweder alle ganz oder real sein müssen. Das ist eine lockere Beschränkung und die wird leicht umgegangen. Die Funktion genoud() kombiniert den Algorithmen der evolutionären Suche mit den Methoden, die auf Derivats basierend sind(Newton or quasi-Newton) , um die verschiedene Aufgaben zu lösen. Genoud() kann für die Lösung der optimierten Probleme verwendet werden, für die die Derivats nicht bestimmt werden können. Außerdem kann die Funktion durch die Verwendung der Option cluster, ein paar Computer, Prozezern für die parallele Rechnung halten.
genoud(fn, nvars, max = FALSE, pop.size = 1000, max.generations = 100, wait.generations = 10, hard.generation.limit = TRUE, starting.values = NULL, MemoryMatrix = TRUE, Domains = NULL, default.domains = 10, solution.tolerance = 0.001, gr = NULL, boundary.enforcement = 0, lexical = FALSE, gradient.check = TRUE, BFGS = TRUE, data.type.int = FALSE, hessian = FALSE, unif.seed = 812821, int.seed = 53058, print.level = 2, share.type = 0, instance.number = 0, output.path = "stdout", output.append = FALSE, project.path = NULL, P1 = 50, P2 = 50, P3 = 50, P4 = 50, P5 = 50, P6 = 50, P7 = 50, P8 = 50, P9 = 0, P9mix = NULL, BFGSburnin = 0, BFGSfn = NULL, BFGShelp = NULL, control = list(), optim.method = ifelse(boundary.enforcement < 2, "BFGS", "L-BFGS-B"), transform = FALSE, debug = FALSE, cluster = FALSE, balance = FALSE, ...)
Argumente
- fn – die objektive Funktion, die minimalisiert wird (oder maximiert, wenn max = TRUE ist). Der erste Argument der Funktion muss der Vektor mit Parametern sein, mir deren Verwendung die Minimierung stattfinden muss. Die Funktion muss den Skalar zurücksetzen (ausnahmsweise lexical = TRUE)
- nvars – die Anzahl der Parameter, die für die minimierte Funktion ausgesucht werden
- max = FALSE Maksimisiern(TRUE) oder minimieren(FALSE) der objektiven Funktion
- pop.size = 1000 Die Größe der Population. Das ist die Anzahl der Individuen, die für die Lösung der optimierten Probleme verwendet werden. Es gibt ein paar Beschränkungen, wie diese Zahl sein kann. Unabhängig davon, dass die Anzahl der Population von Benutzern eingestellt wird, wird die automatisch korrigiert, um die entsprechenden Beschränkungen zu erfüllen. Diese Beschränkungen entstehen von Forderungen der einigen Operatoren des GAs. Einschließlich ist es der Operator P6 (einfacher Crossover) und P8 (heuristischer Crossover) fordern, damit die Anzahl der Individuen gerade wäre, d.h, sie fordern zwei Eltern. Deshalb muss die Variable pop.size gerade sein. Ansonsten wird die Anzahl der Population für die Erfüllung der Beschränkung vergrößern.
- max.generations = 100 — das Maximum der Generationen. Die maximale Anzahl der Generationen, die genoud beim Versuch der Funktionsoptimierung erfüllen muss. Das ist eine lockere Beschränkung. Die maximale Grenze der Generationen wird für den genoud gelten, nur wenn hard.generation.limit in TRUE installiert wird, sonst zwei lockere Trigger kontrollieren, wann genoud angehalten werden muss: wait.generations und gradient.check.
Obwohl Variable max.generations die Zahl der Generationen standardmäßig nicht beschränkt, ist es nichtsdestoweniger wichtig, weil viele Operatoren es verwenden, um das Verhalten zu korrigieren. Eigentlich, viele Operatoren werden weniger zufällig, da die Zahl der Generationen zur Grenze max.generations näher sein wird. Wenn die Grenze übertreten ist und genoud entscheidet sich die Arbeit fortzusetzen, so vergrößert er die Grenze max.generation automatisch.
- wait.generations = 10. Wenn keine Verbesserung der zweckbestimmten Funktion in dieser Zahl der Generationen wird, so wird genoud denken, dass das Optimum gefunden ist. Wenn der Trigger gradient.check angemacht ist, beginnt genoud wait.generations zu zählen, nur wenn die Gradienten in den Rahmen solution.tolerance der Null gleich sein werden. Die andere Variablen, die das Herunterfahren kontrollieren, sind max.generations und hard.generation.limit.
- hard.generation.limit = TRUE. Diese logische Variable bestimmt, ob die Variable max.generations eine förderliche Beschränkung für genoud ist. Bei hard.generation.limit, ausgestellte auf FALSE, genoud kann die Zahl max.generations übertreten, wenn sich in jeder der Zahl der max.generations (bestimmt in wait.generations) die zweckbestimmte Funktion verbessert hat oder wenn der Gradient (bestimmt in gradient.check) der Null nicht gleich ist.
- starting.values = NULL - der Vektor oder die Matrix, die die Werte der Parameter enthält, die genoud beim Start verwenden wird. Durch die Verwendung dieser Option kann der Benutzer ein oder mehrere Individuen in die Startpopulation einführen. Wenn die Matrix dargestellt ist, sollen Spalten die Parameter sein, und die Zeile — die Individuen sein. genoud in einer willkürlichen Ordnung wird andere Individuen erstellen.
- Domains = NULL . Das ist — nvars *2 Matrix. Für jedenParameter in der ersten Spalte - die untere Grenze, und in der zweiten Spalte - die obere. KeinIndividuum aus derAnfangs Population genoud wird außerhalb der Grenzengeneriert. Aber einige Operatoren können die Tochterelemente generieren, die sich außerhalb der Grenzen befinden werden, wenn die Fahne boundary.enforcement nicht angemacht sein wird.
- Wenn der Benutzer die Werte für die Domänen nicht gewährleisten wird, so wird genoud die Domänen standardmäßig einstellen, durch die Verwendung default.domains.
- default.domains = 10. Wenn der Benutzer die Matrix der Domänen nicht darstellen will, können die Domänen vom Benutzer durch die einfache in der Nutzung Skalaroption eingestellt werden. Genoud wird die Matrix der Domänen erstellen, die die untere Grenze für alle Parameter einsetzt, welchegleich (-1 )* default.domains ist, und dieobere Grenze, gleich default.domains.
- solution.tolerance = 0.001. Das ist der Level der Zulassung, die genoud verwendet. Die Zahlen mit dem Unterschied solution.tolerance, wie man ahnt, sind gleich. Das ist sehr wichtig, wenn es um die Einschätzung wait.generations geht und dsa Verhalten gradient.check.
- gr = NULL. Die Funktion, die den Gradient für den Optimisator BFGS ist. wenn es NULL ist, dann wird statt dies die zahlige Gradiente verwendet.
- boundary.enforcement = 0. Diese Variable findet den Level raus, bis zum genoud wird von grenzen Beschränkungen der Raumsuche (RS) geführt. Trotz dem Wert dieser Variable, bei kei nemIndividuum aus der AnfangsGeneration der Werte Parameter nicht außerhalb dieser Grenzen sein werden RS.
bei boundary.enforcement gibt es drei möglichen Werte: 0 (passt zu allen), 1 (teilweisebeschränkt), und 2 (keine Verstöße der Grenzen):
0: passt alles, die Option ermöglicht jedem aus den Operatoren die Individuen außerhalb der Grenzen RS zu erstellen. Diese Individuen werden zur Popukation hinzugefügt, wenn ihr Fitness-Werte ausreichend gut sein werden. Die Grenzen sind wichtig nur bei der Erzeugung der zufälligen Individuen.
1: Teilweise Beschränkung. Dies ermöglicht den Operatoren (besonderes den, die auf dem Derivaten basierenden Optimisator, BFGS verwenden), außer der Grenzen RS während der Erstellung des Individuums auszugehen. Aber wenn der Operator das Individuum ausgesucht hat, muss es in angemessenen Grenzen sein.
2: keine nVerstoß der Grenze. Ausser Grenzen RS die Einschätzungen werden nicht gefordert. In diesem Fall die grenzwährtige Beschränkung ist auch bezüglich des Algorithmus BFGS verwendbar, der vorbeugt, damit Kandidaten sich abweichen außer der Grenzen, die von Dömenen bestimmt wurden. Bitte beachten Sie darauf, dass dies die Verwendung des Algorithmus L-BFGS-B für die Optimierung verursacht. Dieser Algorithmus fordert, damit alle passende Werte und Gradienten bestimmt werden und endgültig für alle funktionale Einschätzungen. Wenn das einen Fehler verursacht, ist es geplant, dass der Algorithmus BFGS verwendet wirdund die Einstellung boundary.enforcement=1.
- lexical = FALSE. Diese Option hat eine lektionische Optimierung. Diese Optimierung nach einigen Kriterien, dabei werden sie nacheinander in einer Reihe bestimmt, die von der Fitness-Funktion gegeben wird.die FitnessFunktion, die mit dieser Option verwendet wird, muss den zahligen Vektor des Fitnesswertes in lektionischer Reihe zurücksetzen. Diese Option kann den Wert haben FALSE, TRUE oder eine ganze Zahl, die gleich der Anzahl der Kriterien ist, die von der Fitness-Funktion zurückgesetzt ist.
- gradient.check = TRUE. wenn diese Variable gleich TRUE ist, dann genoud wird wait.generations nicht zählen, solange jeder Gradient mit solution.tolerance in der Nähe von Null sein wird. Diese Variable hat keinen Effekt, wenn die Grenze max.generations überschritten war, und hard.generation.limit die Option wurde in TRUE gesetzt. Wenn BFGSburnin < 0 ist, dann wird es ignoriert, wenn gradient.check = TRUE ist.
- BFGS = TRUE. Diese Variable bedeutet, verwenden oder nicht den quasi-Nuton Optimisator des Derivats (BFGS) zum besten Individuum am Ende jeder Generation nach dem Anfang. Die Einstellung in FALSE bedeutet nicht, dass BFGS nicht verwendet wird. Zum Beispiel, wenn Sie wollen, damit BFGS nie verwendet wird, der Operator P9 (lokal-minimale Crossover) muss auf Null gesetzt werden.
- data.type.int = FALSE. Diese Option setzt den Daten-Typ der Funktionsparameter ein. Wenn die Variable TRUE sein wird, dann wird genoud, die Lösund unter ganzen Zahlen suchen, wenn Parameter optimiert werden.
Mit Parametern der ganzen Zahlen genoud wird nie die Information über Derivats verwendet. Das bedeutet, dass der Optimisator BFGS nie verwendet wird — d.h., dir Fahne BFGS in FALSE festgesetzt ist. Das bedeutet auch, dass der Operator P9 (lokal-minimale Crossover) auf 0 gesetzt ist und die Überprüfung des Gradients (wie ein Konvergenz-Kriterium) ausgemacht ist. Unabhängig davon, weswegen andere Optionen eingesetzt wurden, data.type.int hat die Priorität — d.h., wenn genoud gesagt ist, dass es gesucht, nach ganzzahlen Raum der Parameter werden muss, die Information über die Gradient nicht betrachtet wird.
Esgibtkeine Option, die die ganzzahlen Parameter mit einem gleitenden Punkt zur Verbindung ermöglicht. wenn Sie diese zwei Typen verbinden wollen, dann können Sie auf einen ganzzahlen Parameter hinweisen, und in die objektive Funktion die ganzzahlen Grenzen mit dem gleitenden Punkt umwandeln. Zum Beispiel brauchen Sie das Such-Netz von 0.1 bis 1.1. zu erhalten Sie geben genoud von 10 bis 110 suchen, und in der Fitness-Funktion wird dieser Parameter um 100 geteilt.
- hessian = FALSE. Wenn die Fahne in TRUE eingesetzt ist, dann genoud setzt die Matrix Gessian in der Lösung, als einer seine Teil der Backliste zurück. Der Benutzer kann die Matrix benutzen, um die standarte Fehler herauszufinden.
- unif.seed = 812821. Der stellt seed für den Generator der quasi zufällige Zahl mit dem gleitenden Punkt für die Verwendung genoud. Der standardmäßige Wert dieses seed ist 81282. genoud verwendet seinen inneren Generator quasi zufälligen Zahlen (Tausworthe-Lewis-Payne Generator), um die Rekursiven und Parallele Aufrufe zu genoud zuzulassen.
- int.seed = 53058. Derr stellt seed für ganz zahlen Generator, den verwendet genoud. Der standardmäßige Wert seed 53058. genoud verwendet seinen inneren Generator quasi zufälligen Zahlen (Tausworthe-Lewis-Payne Generator), um die Rekursiven und Parallele Aufrufe zu genoud zuzulassen.
- print.level = 2. Diese Variable steuert den Level des Drucks, was genoud macht. Es gibt 4 möglichen Levels: 0 (minimales Drucken), 1 ( normales), 2 (genaueres) und 3 (probe). Wenn der Level 2 ausgewählt wird, dann druckt genoud die Details über die Population in jeder Generation.
- share.type = 0. Wennshare.type gleich 1 ist, dann überprüft genoud beim Start, ob die Datei des Projektes gibt (siehe. project.path). Wenn die Datei gibt, sie initialisiert ihre Anfangs-Population, durch deren Verwendung. Diese Option kann mit lexical verwendet werden, aber nicht mit der Option transform.
Operatoren. Genoud haben un verwenden 9 Operatoren. Die ganzzahlen Werte, die jedem von diesen Operatoren zugewiesen sind (P1... P9) — Gewicht. Genoud rechnet die Summe s = P1+P2 +... +P9. Jedem Operator wird ein Gewicht zugewiesen, das W_n = s / (P_n) gleich ist. Die Anzahl der Aufrufen des Operators ist c_n = W_n * pop.size gleich.
Operatoren P6 (einfacher Crossover) und P8 (heuristischer Crossover) fordern, damit die Anzahl der Individuen gerade wäre, d.h, sie fordern zwei Eltern. Deshalb muss die Variable pop.size und die Sätze der Operatoren solche sein,damit bei diesen Operatoren die Anzahl der Individuen gerade wäre. Wenn das nicht stattfindet, genoud automatisch korrigiert die obere Grenze der Anzahl der Population, damit die Grenze funktioniert.
Die strenge Überprüfungen der Besonderheiten wurden in Operatoren eingefügt, um zu garantieren, dass Operatoren die Nachkommen erzeugt haben, die von Eltern unterschiedlicher sind, aber dies passiert nicht immer.
Der evolutionäre Algorithmus rgenoud verwendet 9 Operatoren, die unten aufgezählt sind.
- P1 = 50 – klonen. Der Klone-Operator macht einfach die Kopie der besten experimentierten Lösung in der vorübergehendenGeneration (der davon unabhängige Operator, rgenoud speichert immer eine Kopie von der besten experimentierten Lösung).
Die universelle Mutation, die grenzwärtige Mutation und ungleichmäßige Mutation wirkt auf eine einzige experimentierte Lösung.
- P2 = 50 – Die universelle Mutation. Die universelle Mutation ändert einen Parameter mit einem zufälligen Wert in der experimentierten Lösung, der gleichmäßig auf der Domen verteilt ist, und für den Parameter bestimmt.
- P3 = 50 – die grenzwärtige Mutation. die grenzwärtige Mutation ersetzt einen Parameter, der aus einer der Domensgrenzen ist.
- P4 = 50 – ungleichmäßige Mutation. ungleichmäßige Mutation verringert einen Parameter zu einer der Grenze durch die Verringerung-Summe, wenn die Anzahl der Generationen sich zur maximalen Anzahl der Generationen nähert.
- P5 = 50 – Vielseitige Crossover. Vielseitige Crossover (der von der Simpleks-Suche, Gill u.s.w. kommt 1981, r. 94–95), findet die experimentierte Lösung heraus, die die gerundete Kombination aller solchen experimentierten Lösungen ist, wie viele Parameter da gibt.
- P6 = 50 – einfacher Crossover. einfacher Crossover berechnet 2 experimentierte Lösungen aus 2 eingangs experimentierte Lösungen, dabei tauscht die Werte der Parameter zwischen Lösungen nach der Trennung der Lösungen in der willkürlichen Reihe am ausgesuchten Punkt . Dieser Operator kann besonders effektiv sein, wenn die Anordnung der Parameter in jeder experimentierten Lösung nacheinander ist.
- P7 = 50 – Die ganze ungleichmäßige Mutation. Die ganze ungleichmäßige Mutation macht die ungleichmäßige Mutation für alle Parameter in der experimentierten Lösung.
- P8 = 50 – heuristischer Crossover. heuristisc her Crossover verwendet 2 experimentierten Lösungen für die Erzeugung einer neuen Lösung, die entlang des Vektors ist, welche in einer experimentierten Lösung beginnt.
- P9 = 0 — lokal-minimale Crossover: BFGS. lokal-minimale Crossover berechnet die Lösung für eine neue Betrachtung in zwei Schritten. Am Anfang BFGS erledigt die vorhereingestellten Iteration-Zähle, die von der Eingangslösung gestartet werden; danach wird die gerundete Kombination der Eingangslösungen gerechnet und schließlich BFGS erledigt Iteration.
Hinweise:
Die wichtigsten Optionen, die die Qualität beeinflussen, — sind diejenige, die die Anzahl der Population bestimmen (pop.size) und die Anzahl der Generationen, welche vom Algorithmen (max.generations, wait.generations, hard.generation.limit und gradient.check) erledigt werden. Die Suche-Leistung, wie erwartet, wird verbessert, wenn die Anzahl der Population und die Anzahl der Generationen, die vom Programm ausgeführt werden, werden sich vergrößern. Die und andere Optionen müssen für verschiedene Probleme manuell korrigiert werden. Bitte beachten Sie auf die Suchbereiche (Domen und default.domains).
Lineale und nicht lineale Beschränkungen unter Parameter können von Benutzern in ihren Fitness-Funktionen dargestellt werden. Zum Beispiel, wenn die Summe der Parameter 1 und 2 weniger als 725 sein muss, dann kann die Bedingung in einer Fitness-Funktion eingebaut werden kann, Benutzer wird genoud, : if((parm1 + parm2)>= 725) {return (-99999999)} maximieren. In diesem Beispiel wird der schlechte Fitness-Wert auf genoud zurückgesetzt, wenn die lineale Beschränkung verstoßen wurde. Dann genoud versucht die Parameterwerte zu finden, die die Beschränkung entsprechen.
Schreiben wir unsere Fitness-Funktion. Sie muss berechnen:
MACD
Signale
Qualitätskoeffizient
# Fitness-Funktion-------------------------fitnes <- function(param, test = FALSE){
require(TTR)
require(magrittr)
# Definieren wir Variablen
x <- pr[param[1]]
nFast <- param[2]
nSlow <- param[3]
nSig <- param[4]
macdType <- MaType[param[5]]
sigType <- MaType[param[6]]
percent <- per[param[7]]
len <- param[9]*100
# Die lineale Beschränkung für macd
if (nSlow <= nFast) return(-Inf)
# berechnen wir macd
md <- MACD(x = x, nFast = nFast, nSlow = nSlow,
nSig = nSig, percent = TRUE,
maType = list(list(macdType),
list(macdType),
list(sigType)))
# berechnen wir Signale und schieben wir es auf rechts um 1 Bar
sig <- signal(md, param[8]) %>% Lag()
#berechnen wir die Balance auf der History mit der Lange len
bal <- cumsum(tail(sig, len) * tail(price[ ,'CO'], len))
if(test)
{bal <<- cumsum(tail(sig, len) * tail(price[ ,'CO'], len))}
# Berechnen wir den Qualitätskoeffizient (runden wir es bis zu einer ganz Zahl)
K <- ((tail(bal,1)/length(bal))* 10 ^ Dig) %>% floor()
# Setzen wir die erhaltende Kriteriumsoptimierung zurück
return(unname(K))
}
Unten zeigen wir die Bestimmungsliste aller Variablen und Funktionen
require(Hmisc) # Der Typ der Mittelwerte = 4 ------------------------------------------- MaType <- Cs(SMA, EMA, DEMA, ZLEMA) require(dplyr) # Der Typ der Preise = 4 ----------------------------------------------- pr <- transmute(as.data.frame(price), Close = Close, Med = Med, Typ = (High + Low + Close)/3, WClose = (High + Low + 2*Close)/4) # Wie soll man zählen? per <- c(TRUE, FALSE) # Signal-Varianten = 3 -------------------------- signal <- function(x, type){ x <- na.omit(x) dx <- diff(x[ ,1]) %>% na.omit() x <- tail(x, length(dx)) switch(type, (x[ ,1] - x[ ,2]) %>% sign(), sign(dx), ifelse(sign(dx) == 1 & sign(x[ ,1]) == 1, 1, ifelse(sign(dx) == -1 & sign(x[ ,1]) == -1,-1, 0)) ) } # die Startkonfiguration-------------------------- par <- c(2, 12, 26, 9, 2, 1, 1, 3, 5) # der Suchraum------------------------------ dom <- matrix(c(1, 4, # für Typs der Preise 8, 21, # für die Periode des schnellen MAs 13, 54, # für die Periode des langsamen MAs 3, 13, # für die Periode des Signal-MA 1, 4, # der Typ des MAs für die schnelle und langsame 1, 4, # der Typ des MAs für signal 1, 2, # Der Typ percent 1, 3, # Die Variante signal 3,10), # Die Lange der History [300:1000] ncol = 2, byrow = TRUE) # Die Erstellung des Clusters aus erreichbaren Kern-Prozezern puskCluster<-function(){ library(doParallel) library(foreach) cores<-detectCores() cl<-makePSOCKcluster(cores) registerDoParallel(cl) #clusterSetRNGStream(cl) return(cl) }
Bestimmen wir den Qualitätskoeffizient mit den Anfangsparametern (in der Regel standardmäßig)
> K <- fitnes(par, test = TRUE) > K [1] 0 > plot(bal, t="l")
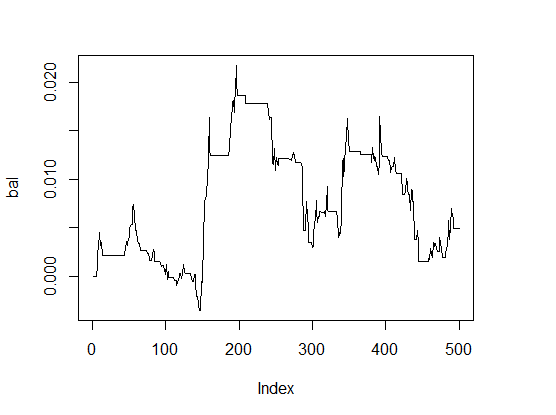
Abb.1 Die Balance mit den standardmäßigen Parametern
Ein sehr schlechtes Ergebnis.
Für den Vergleich der Geschwindigkeit der Berechnungen führen wir die Optimierung auf einem Kern und auf einem Cluster aus zwei Kern-Prozezern.
Auf einem Kern:
pr.max <- genoud(fitnes, nvars = 9, max = TRUE, pop.size = 500, max.generation = 300, wait.generation = 50, hard.generation.limit = FALSE, starting.values = par, Domains = dom, boundary.enforcement = 1, data.type.int = TRUE, solution.tolerance = 0.01, cluster = FALSE, print.level = 2) 'wait.generations' limit reached. No significant improvement in 50 generations. Solution Fitness Value: 1.600000e+01 Parameters at the Solution: X[ 1] : 1.000000e+00 X[ 2] : 1.400000e+01 X[ 3] : 2.600000e+01 X[ 4] : 8.000000e+00 X[ 5] : 4.000000e+00 X[ 6] : 1.000000e+00 X[ 7] : 1.000000e+00 X[ 8] : 1.000000e+00 X[ 9] : 4.000000e+00 Solution Found Generation 5 Number of Generations Run 56 Thu Mar 24 13:06:29 2016 Total run time : 0 hours 8 minutes and 13 seconds
Die passenden Parameter (Genotyp)
> pr.max$par [1] 1 14 26 8 4 1 1 1 4
Entcoden wir (Phänotyp):
- Der Typ des Preises pr[ ,1]= Close
- nFast = 14
- nSlow = 26
- nSig = 8
- macdType = ZLEMA
- sigType = SMA
- percent = TRUE
- signal = Die Kreuzung der Linie macd und signal
- Die Lange der History = 400 Bars.
Schauen wir, wie die Linie der Balance mit optimalen Parametern
aussieht. Dafür führen wir die Fitness-Funktion mit diesen Parametern
und der Option test = TRUE.aus
> K.opt <- fitnes(pr.max$par, test = TRUE) > K.opt [1] 16 > plot(bal, t="l")
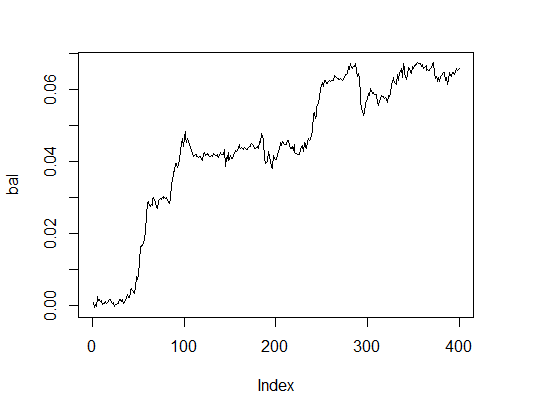
Abb.2. Balance mit optimalen Parametern
Das ist ein geeignetes Ergebnis, mir dem der Experte arbeiten kann.
Machen wir die gleichen Berechnungen auf Cluster aus zwei Kernen
# Starten wir den Cluster
cl <- puskCluster()
# Maximieren der Fitness-Funktion
# Übertragen jedem Kern im Cluster die notwendigen Variablen und Funktionen
clusterExport(cl, list("price", "pr", "MaType", "par", "dom", "signal",
"fitnes", "Lag", "Dig", "per" ) )
pr.max <- genoud(fitnes, nvars = 9, max = TRUE,
pop.size = 500, max.generation = 300,
wait.generation = 50,
hard.generation.limit = FALSE,
starting.values = par, Domains = dom,
boundary.enforcement = 1,
data.type.int = TRUE,
solution.tolerance = 0.01,
cluster = cl,
print.level = 2) # nur für die Experimenten.
# Im Experten setzen wir 0
# Halten wir den Cluster an
stopCluster(cl)
'wait.generations' limit reached.
No significant improvement in 50 generations.
Solution Fitness Value: 1.300000e+01
Parameters at the Solution:
X[ 1] : 1.000000e+00
X[ 2] : 1.900000e+01
X[ 3] : 2.000000e+01
X[ 4] : 3.000000e+00
X[ 5] : 1.000000e+00
X[ 6] : 2.000000e+00
X[ 7] : 1.000000e+00
X[ 8] : 2.000000e+00
X[ 9] : 4.000000e+00
Solution Found Generation 10
Number of Generations Run 61
Thu Mar 24 13:40:08 2016
Total run time : 0 hours 3 minutes and 34 secondsDie Zeit ist nun viel besser, allerdings die Qualität etwas schlechter. Für die Lösung einer solchen einfachen Aufgabe muss man mit Parametern spielen.
Finden wir die einfachste Variante heraus
pr.max <- genoud(fitnes, nvars = 9, max = TRUE, pop.size = 500, max.generation = 100, wait.generation = 10, hard.generation.limit = TRUE, starting.values = par, Domains = dom, boundary.enforcement = 0, data.type.int = TRUE, solution.tolerance = 0.01, cluster = FALSE, print.level = 2) 'wait.generations' limit reached. No significant improvement in 10 generations. Solution Fitness Value: 1.500000e+01 Parameters at the Solution: X[ 1] : 3.000000e+00 X[ 2] : 1.100000e+01 X[ 3] : 1.300000e+01 X[ 4] : 3.000000e+00 X[ 5] : 1.000000e+00 X[ 6] : 3.000000e+00 X[ 7] : 2.000000e+00 X[ 8] : 1.000000e+00 X[ 9] : 4.000000e+00 Solution Found Generation 3 Number of Generations Run 14 Thu Mar 24 13:54:06 2016 Total run time : 0 hours 2 minutes and 32 seconds
Ein gutes Ergebnis. Und die Balance?
> k [1] 15 > plot(bal, t="l")
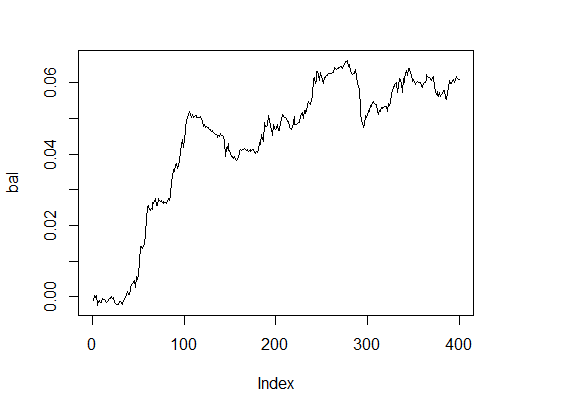
Abb.3. Balance mit optimalen Parametern
Ein sehr anständiges Ergebnis für die annehmbare Zeit.
Für den Vergleich der Ergebnisse des genetischen Algorithmus mit evolutions-, werden wir eine Serie der Experimente mit ihnen leiten. Als erste experimentieren wir den Algorithmus SOMA(Self-Organising Migrating Algorithm), der im Paket "soma" realisiert ist.
Der selbstorganisierte Migrationsalgorithmus der allgemeinen Festsetzung Stochastik Optimierung — der Ansatz, ähnlich den genetischen Algorithmen , obwohl er auf die Idee einer Serie "der Migrationen" mit Hilfe des fixierten Satzes der Individuen, und nicht derEntwicklung der nachfolgenden Generationen gegründet ist. Er ist zu lokalen Minima standfest und kann zu einer beliebigen Aufgabe der Minimierung der Aufwände mit dem begrenzten Raum der Parameter verwendet werden. Die Hauptfunktion:
soma(costFunction, bounds, options = list(), strategy = "all2one", …)
Arguments
Details
Für die Einstellung der
Optimierungsdurchführung und der Kriterien ihrer Vollendung gibt es eine
Menge der Optionen zugänglich. Die standardmäßige Werte, die hier vom Autor Zelinka (2004) empfohlen sind.
- pathLength: Der Abstand bis zum Führer, zu dem die Individuen migrieren können. Der Wert 1 entspricht der Position des Führers, und der Wert mehr als 1 (empfohlen) berücksichtigt einige Neueinstellungen. Standardmäßig setzen wir 3.
- stepLength: der Minimale Schritt, nach dem die möglichen Schritte bewertet werden. Es ist empfehlenswert, damit die Länge des Weges ganz divisibel dieses Wertes nicht wäre. Der standardmäßige Wert beträgt 0.11.
- perturbationChance: die Wahrscheinlichkeit, dass die abgesonderten Parameter auf einer beliebigen gegebenen Etappe verändert werden. Der standardmäßige Wert 0.1.
- minAbsoluteSep: die Kleinste absolute Differenz zwischen maximalen und minimalen von Werten der Funktion des Preises. Wenn die Differenz niedriger als dieses Minimum fällt, so endet der Algorithmus. Der standardmäßige Wert ist 0. Das bedeutet, dass dieses Kriterium des Abbruchs nie erfüllt wird.
- MinRelativeSep: die Kleinste relative Differenz zwischen maximalen und minimalen von Werten der Funktion des Preises. Wenn die Differenz niedriger als dieses Minimum fällt, so endet der Algorithmus. Der standardmäßige Wert beträgt 0,001.
- nMigrations: das Maximum der Migrationen für die Vollendung. Der standardmäßige Wert 20.
- populationSize: die Zahl der Individuen in der Population. Es ist empfehlenswert, dass dieser Wert etwas grösser wird, als die Zahl der optimierten Parameter, und nicht weniger als 2. Der standardmäßige Wert ist 10.
Da der Algorithmus nur die Minimierung erledigt, werden wir unsere Fitness-Funktion ausarbeiten, damit sie den Wert mit dem entgegengesetzten Zeichen ausgebe und starten wir die Optimierung.
require(soma) x <- soma(fitnes, bounds = list(min=c(1,8,13,3,1,1,1,1,3), max = c(4,21,54,13,4,4,2,3,10)), options = list(minAbsoluteSep = 3, minRelativeSep = -1, nMigrations = 20, populationSize = 20), opp = TRUE) Output level is not set; defaulting to "Info" * INFO: Starting SOMA optimisation * INFO: Relative cost separation (-2.14) is below threshold (-1) - stopping * INFO: Leader is #7, with cost -11
Beste Parameter:
> x$population[ ,7] [1] 1.532332 15.391757 37.348099 9.860676 1.918848 [6] 2.222211 1.002087 1.182209 3.288627 Runden wir ab > x$population[ ,7]%>% floor [1] 1 15 37 9 1 2 1 1 3
Der beste Wert der Fitness-Funktion = 11. Das ist annehmbar für die praktische Verwendung, aber es gibt eine Möglichkeit für die Verbesserung.
Der Algorithmus ist schnell, aber nicht stabil nach Ergebnissen und fordert eine feine Einstellung.
Generalized Simulated Annealing Function (Die verallgemeinerte Funktion der Heizung-Simulation)
dieser Algorithmus wurde im Paket «GenSA” realisiert. Diese Funktion kann die Suche nach globalen Minimums durch eine ziemlich schwere nicht lineale Funktionmit vielen Optimums durchführen.
GenSA(par, fn, lower, upper, control=list(), …)
die Argumente:
- par - Die Anfangswerte für Komponenten, die optimiert werden müssen. Standardmäßig NULL, in diesem Fall werden die Werte standardmäßig, automatisch generiert.
- fn - Die Funktion, die minimalisiert wird. Für die Minimierung der Funktion wird eine Reihe der Parameter in der Art von einem Vektor gegeben. Ser setzt dasSkalar Ergebnis zurück.
- lower – der Vektor mit der Lange length(par). Die untere Grenze der Komponenten.
- upper - der Vektor mit der Lange length(par). Die obere Grenze der Komponenten.
- … Die ermöglicht dem Benutzer die zusätzlichen Argumente der Funktion übergebenfn.
- control - Der Argument der Steuerung. Das ist die Liste, die für die Steuerung des Argumentsverhaltens verwendet werden kann.
- maxit – die maximale Zahl der Iterationen des Algorithmus.
- threshold.stop - Zahlen. Das Programm macht Schluss, wenn die erwarteten Werte der ganzen Funktionen threshold.stop erreicht werden. Der standardmäßige Wert — NULL.
- nb.stop.improvement - ganze. Das Programm wird beendet, wenn es keine Verbesserungen im Laufe der nb.stop.improvement Schritte nicht gäben.
- smooth - logische. TRUE, wenn die die zweckbestimmte Funktion gleitend ist, oder überall differenzierbar im Bereich der Parameter ist; FALSE — ansonsten. Der standardmäßige Wert — TRUE
- max.call - ganze. Die maximale Anzahl der Anrufen zur zweckbestimmten Funktion. Standardmäßig setzen wir den Wert 1e7.
- temperature - Zahlen. Der Anfangswert der Temperaturen.
- verbose - logische. TRUE heißt des, dass Nachrichten vom Algorithmen gezeigt werden. Standardmäßig — FALSE
- simple.function - logische. TRUE heißt des, dass die die zweckbestimmte Funktion nur ein paar lokalen Minimus hat. Standartmäßig wurde FALSE gesetzt, heißt des, dass die die zweckbestimmte Funktion mit vielen lokalen Minimus belastet ist.
- trace.mat - logische. Standardmäßig — TRUE. Das heißt, dass die Trace-Matrix im zurückgesetzten Wert des GenSA-Aufrufs erreichbar sein wird.
Der Wert der Steuerungskomponenten wurden standardmäßig für die schwere Optimierungsaufgabe gesetzt. Für eine einfache Aufgabe der Optimierung mit einer durchschnittlichen Schwierigkeit kann GenSA ein vernünftige Lösung schnell finden, deswegen soll GenSA vom Benuzer schneller zum Stopp gehen:
durch die Einsetzung von threshold.stop, wenn threshold.stop — ein erwarteter Wert der Funktion ist;
oder durch die Einsetzung von max.time, wenn der Benutzer GenSA einfach für max.time Sek starten will;
oder durch die Einsetzung von max.call, wenn der Benutzer GenSA einfach in Rahmen max.call der Funktion-Aufrufen starten will.
Für die sehr schweren Optimierungsaufgaben ist es dem Benutzer empfohlen, die maxit und temperature zu vergrößern.
Starten wir die Optimierung, durch die Beschränkung der maximalen Ausführungszeit mit 60 Sek.
require(GenSA) pr.max <- GenSA(par, fitnes, lower = c(1,8,13,3,1,1,1,1,3), upper = c(4,21,54,13,4,4,2,3,10), control = list(verbose = TRUE, simple.function = TRUE, max.time = 60), opp = TRUE)
Der Wert der Fitness-Funktion und der Wert der optimalen Parameter:
> pr.max$value * (-1) [1] 16 > par1 <- pr.max$par > par1 [1] 1.789901 14.992866 43.854988 5.714345 1.843307 [6] 1.979723 1.324855 2.639683 3.166084
Wir runden es ab:
> par1 <- pr.max$par %>% floor [1] 1 14 43 5 1 1 1 2 3
Berechnen wir den Wert der Fitness-Funktion mit diesen Parametern und schauen wir auf die Balance-Linie:
> f1 <- fitnes(par1, test = TRUE) > plot(-1 * bal, t="l")
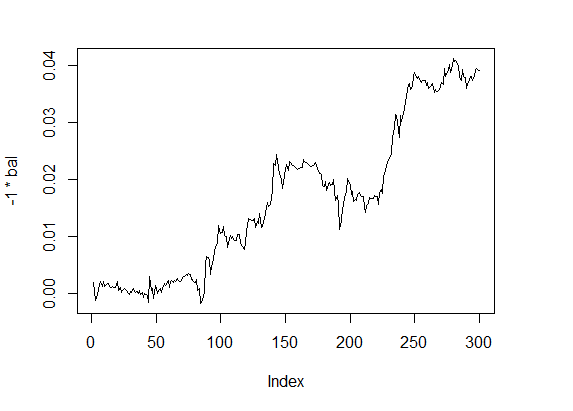
Abb.4. Balance 4
Die Werte der Qualität - ist am guten Level, und die Berechnungen sind erstaunlicherweise schnell.
Alle diese und andere ähnliche Algorithmen (Paketen dfoptim, nlopt,CEoptim, DEoptim,RcppDE und andere) optimieren die Funktion nach einem Kriterium. Für die Optimierung aus mehreren Kriterien ist das Paket mco. vorgesehen
7. Die Mittel und Wege, um die Qualität der Indikatoren zu verbessern
Die von uns geleiteten Experimente haben die Effektivität der genetischen Algorithmen vorgeführt. Für die weitere Verbesserung der Qualitätskennziffern wäre es wünschenswert, die zusätzlichen Forschungen unter Ausnutzung zu erledigen:
- die Optimierung aus mehreren Kriterien. Zum Beispiel, die Optimierung des Qualitätskoeffizienten und der maximalen Drawdown zu leiten. Das Paket, das solche Möglichkeit realisiert, — "mco".
- Versuchen, die dynamische Selbstorganisation der Parameter des GAs zu realisieren. Das Paket für die mögliche Realisation — "GA". Er stellt die breite Auswahl der Arten der Selektionsoperatoren, Crossovers und der Mutation frei.
- Überprüft experimental die Möglichkeit der Anwendung des genetischen Programmierens im Handelssystem.
Fazit
Wir haben die Hauptprinzipien, die in den Evolutionsalgorithmen versetzt sind, ihre Arten und die Besonderheiten betrachtet. Auf dem Beispiel des einfachen Experten MACDSample haben wir mit Hilfe der Experimente vorgeführt, dass die Anwendung der Optimierung der Parameter sogar für ein solches elementares Handelnsystem eine bedeutende positive Wirkung gibt.
Die Zeit der Ausführung der Optimierung und die Einfachheit im Programmieren ermöglichen ihn in die Arbeitszeit des Experten ohne Ausgang aus dem Markt auszuführen. Und die Abwesenheit der strengen Beschränkungen auf die Art der Parameter der Optimierung ermöglichen die vielfältigsten Arten der Optimierung in verschiedenen Arbeitsstufen des Experten zu realisieren.
Der wichtigste Teil der Arbeit ist es dabei — richtig, die Fitness-Funktion zu schreiben.
Ich hoffe, dass dieser Artikel Ihnen helfen wird zu verstehen, dass es nicht kompliziert ist, und dass Sie selbst versuchen, Ihre Expert Advisors zu optimieren.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/2225
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Wie man die Signale mit Hilfe vom Berater nach seinen Regeln kopieren soll?
Wie man die Signale mit Hilfe vom Berater nach seinen Regeln kopieren soll?
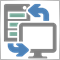 Arbeiten mit Sockets in MQL, oder Wie man ein Signalprovider wird
Arbeiten mit Sockets in MQL, oder Wie man ein Signalprovider wird
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Nun, schlagen Sie Funktionen vor.
Beteiligen Sie sich an der Diskussion. Sie werden bald wieder draußen sein.
Das ist keine Diskussion, das ist eher ein "Lass sie reden" in seiner schlimmsten Form.
Ich bin froh, dass ich da nicht schon früher hingegangen bin.
Ich gehe mir die Hände waschen.
Es ist furchtbar.
Das ist keine Diskussion, das ist eher ein "Lass sie reden" in seiner schlimmsten Form.
Ich bin froh, dass ich da nicht schon früher hingegangen bin.
Ich gehe mir die Hände waschen.
Das ist ja furchtbar.
Veröffentlichter Artikel Selbstoptimierung von EA: genetische und evolutionäre Algorithmen:
Autor: Vladimir Perervenko