
Глубокие нейросети (Часть VIII). Повышение качества классификации bagging-ансамблей
Содержание
- Введение
- Подготовка исходных данных
- Обработка шумовых примеров в поднаборе pretrain
- Обучение ансамблей нейросетевых классификаторов на обесшумленных исходных данных и вычисление непрерывных предсказаний нейросетей на тестовых поднаборах
- Определение порогов для полученных непрерывных предсказаний, перевод их в метки классов и вычисление метрик нейросетей
- Тестирование ансамблей
- Оптимизация гиперпараметров нейросетевых классификаторов ансамблей
- Оптимизация гиперпараметров постпроцессинга
- Объединение нескольких лучших ансамблей в суперансамбль и их выходов
- Анализ результатов экспериментов
- Заключение
- Приложение
Введение
В предыдущих двух статьях (1, 2) мы создавали ансамбль нейросетевых классификаторов ELM. Тогда мы говорили о том, как можно улучшить качество классификации. Среди многих возможных направлений я выбрал два: снизить влияние шумовых примеров и выбрать оптимальный порог, по которому непрерывные предсказания нейросетей ансамбля переводятся в метки классов. В этой статье предлагаю экспериментально проверить, как влияют на качество классификации:
- методы обесшумливания данных,
- типы порогов,
- оптимизация гиперпараметров нейросетей ансамбля и постпроцессинга.
Затем сравним качество классификации, которое получается при усреднении и при простом голосовании суперансамбля, составленного из лучших ансамблей по итогам оптимизации. Все вычисления проводятся в среде R 3.4.4.
1. Подготовка исходных данных
Для подготовки исходных данных будем использовать ранее описанные скрипты.
В первом блоке (Library) загружаем необходимые функции и библиотеки.
Во втором блоке (prepare), используя переданные из терминала котировки с временными метками, вычисляем значения индикаторов (в нашем случае это цифровые фильтры) и дополнительные переменные на базе OHLC. Объединяем этот набор данных в dataframe dt. Затем определяем параметры выбросов в этих данных и импутируем их. Потом определяем параметры нормализации и нормализуем данные. Получаем результирующий набор исходных данных DTcap.n.
В третьем блоке (Data X1) формируем два набора:
- data1 — содержит все 13 индикаторов с временными метками Data и целевой Class;
- X1 — тот же набор предикторов, но без временной метки. Целевая переведена в числовое значение (0, 1).
В четвертом блоке (Data X2) также формируем два набора:
- data2 — содержит 7 предикторов и временную метку (Data, CO, HO, LO, HL, dC, dH, dL);
- Х2 — те же предикторы но без временной метки.
#--1--Library------------- patch <- "C:/Users/Vladimir/Documents/Market/Statya_DARCH2/PartVIII/PartVIII/" source(file = paste0(patch,"importar.R")) source(file = paste0(patch,"Library.R")) source(file = paste0(patch,"FunPrepareData_VII.R")) source(file = paste0(patch,"FUN_Stacking_VIII.R")) import_fun(NoiseFiltersR, GE, noise) #--2-prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt$features, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) meth <- qc(expoTrans, range)# "spatialSign" "expoTrans" "range" "spatialSign", preproc <- PreNorm(DTcap$pretrain, meth = meth, rang = c(-0.95, 0.95)) DTcap.n <- NormData(DTcap, preproc = preproc) }, env) #--3-Data X1------------- evalq({ subset <- qc(pretrain, train, test, test1) foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, ftlm, stlm, rbci, pcci, fars, v.fatl, v.satl, v.rftl, v.rstl,v.ftlm, v.stlm, v.rbci, v.pcci, Class)} -> data1 names(data1) <- subset X1 <- vector(mode = "list", 4) foreach(i = 1:length(X1)) %do% { data1[[i]] %>% dp$select(-c(Data, Class)) %>% as.data.frame() -> x data1[[i]]$Class %>% as.numeric() %>% subtract(1) -> y list(x = x, y = y)} -> X1 names(X1) <- subset }, env) #--4-Data-X2------------- evalq({ foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, CO, HO, LO, HL, dC, dH, dL)} -> data2 names(data2) <- subset X2 <- vector(mode = "list", 4) foreach(i = 1:length(X2)) %do% { data2[[i]] %>% dp$select(-Data) %>% as.data.frame() -> x DT[[i]]$dz -> y list(x = x, y = y)} -> X2 names(X2) <- subset rm(dt, DT, pre.outl, DTcap, meth, preproc) }, env)
В пятом блоке (bestF) упорядочиваем предикторы набора Х1 по возрастанию их информационной важности (orderX1). Из них отбираем те, у которых коэффициент больше 0.5 (featureX1). Распечатаем коэффициенты и имена отобранных предикторов.
#--5--bestF----------------------------------- #require(clusterSim) evalq({ orderF(x = X1$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") -> rx1 rx1$stopri[ ,1] -> orderX1 featureX1 <- dp$filter(rx1$stopri %>% as.data.frame(), rx1$stopri[ ,2] > 0.5) %>% dp$select(V1) %>% unlist() %>% unname() }, env) print(env$rx1$stopri) [,1] [,2] [1,] 6 1.0423206 [2,] 12 1.0229287 [3,] 7 0.9614459 [4,] 10 0.9526798 [5,] 5 0.8884596 [6,] 1 0.8055126 [7,] 3 0.7959655 [8,] 11 0.7594309 [9,] 8 0.6960105 [10,] 2 0.6626440 [11,] 4 0.4905196 [12,] 9 0.3554887 [13,] 13 0.2269289 colnames(env$X1$pretrain$x)[env$featureX1] [1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars" "ftlm" "rbci" "v.stlm" "v.rftl" [10] "stlm"
Те же вычисления проведем и для второго набора данных Х2. Получим orderX2 и featureX2.
evalq({
orderF(x = X2$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> rx2
rx2$stopri[ ,1] -> orderX2
featureX2 <- dp$filter(rx2$stopri %>% as.data.frame(), rx2$stopri[ ,2] > 0.5) %>%
dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx2$stopri)
[,1] [,2]
[1,] 1 1.6650259
[2,] 5 1.6636689
[3,] 3 0.7751799
[4,] 2 0.7751351
[5,] 6 0.5692846
[6,] 7 0.5496889
[7,] 4 0.4970882
colnames(env$X2$pretrain$x)[env$featureX2]
[1] "CO" "dC" "LO" "HO" "dH" "dL" На этом подготовка исходных данных для экспериментов закончена. Мы подготовили два набора данных X1/data1, X2/data2 и ранжированные по важности предикторы orderX1, orderX2. Все вышеприведенные скрипты находятся в файле Prepare_VIII.R.
2. Обработка шумовых примеров в поднаборе pretrain
Многие авторы статей, в том числе и я, посвящали свои публикации отсеву шумовых предикторов. Здесь я предлагаю исследовать другую, не менее важную, но менее используемую возможность — определение и обработку шумовых примеров в наборах данных. Так почему же некоторые примеры в наборах данных считаются шумовыми и какими методами можно их обрабатывать? Попробую пояснить.
Итак, перед нами стоит задача классификации, и мы имеем обучающий набор предикторов и целевую. Мы считаем, что целевая хорошо соответствует внутренней структуре обучающего набора. Но в реальности структура данных набора предикторов гораздо сложнее предлагаемой структуры целевой. Получается, что в наборе есть примеры, хорошо соответствующие целевой, а есть — совсем не соответствующие, и они сильно искажают модель при обучении. В итоге это приводит к снижению качества классификации модели. Я уже рассматривал подробно подходы к определению и обработке шумовых примеров. Здесь мы проверим, как влияют на качество классификации ансамбля три метода обработки:
- исправление ошибочно размеченных примеров;
- удаление их из набора;
- выделение их в отдельный класс.
Определять и обрабатывать шумовые примеры будем с использованием функции NoiseFiltersR::GE(). Она ищет шумовые примеры и изменяет их метки (исправляет ошибочную разметку). Примеры, которые невозможно переразметить, удаляются. Выявленные шумовые примеры можно также удалить из набора самостоятельно или выделить их в отдельный класс, присвоив им новую метку. Все вычисления производим на поднаборе pretrain, поскольку на нем будут обучаться ансамбли. Посмотрим на результат работы функции:
#---------------------------
import_fun(NoiseFiltersR, GE, noise)
#-----------------------
evalq({
out <- noise(x = data1[[1]] %>% dp$select(-Data))
summary(out, explicit = TRUE)
}, env)
Filter GE applied to dataset
Call:
GE(x = data1[[1]] %>% dp$select(-Data))
Parameters:
k: 5
kk: 3
Results:
Number of removed instances: 0 (0 %)
Number of repaired instances: 819 (20.46988 %)
Explicit indexes for removed instances:
....... Структура выхода функции out:
> str(env$out) List of 7 $ cleanData :'data.frame': 4001 obs. of 14 variables: ..$ ftlm : num [1:4001] 0.293 0.492 0.47 0.518 0.395 ... ..$ stlm : num [1:4001] 0.204 0.185 0.161 0.153 0.142 ... ..$ rbci : num [1:4001] -0.0434 0.1156 0.1501 0.25 0.248 ... ..$ pcci : num [1:4001] -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... ..$ fars : num [1:4001] 0.208 0.255 0.246 0.279 0.267 ... ..$ v.fatl: num [1:4001] 0.4963 0.4635 0.0842 0.3707 0.0542 ... ..$ v.satl: num [1:4001] -0.0146 0.0248 -0.0353 0.1797 0.1205 ... ..$ v.rftl: num [1:4001] -0.2695 -0.0809 0.1752 0.3637 0.5305 ... ..$ v.rstl: num [1:4001] 0.398 0.362 0.386 0.374 0.357 ... ..$ v.ftlm: num [1:4001] 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... ..$ v.stlm: num [1:4001] -0.275 -0.226 -0.285 -0.11 -0.148 ... ..$ v.rbci: num [1:4001] 0.5374 0.4811 0.0978 0.2992 -0.0141 ... ..$ v.pcci: num [1:4001] -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ... $ remIdx : int(0) $ repIdx : int [1:819] 16 27 30 31 32 34 36 38 46 58 ... $ repLab : Factor w/ 2 levels "-1","1": 2 2 2 1 1 2 2 2 1 1 ... $ parameters:List of 2 ..$ k : num 5 ..$ kk: num 3 $ call : language GE(x = data1[[1]] %>% dp$select(-Data)) $ extraInf : NULL - attr(*, "class")= chr "filter"
Здесь:
- out$cleanData — это набор данных после исправления разметки шумовых примеров,
- out$remIdx — индексы удаленных примеров (в нашем примере их нет),
- out$repIdx — индексы примеров, целевая которых была переразмечена,
- out$repLab — новые метки этих шумовых примеров. Таким образом, используя out$repIdx, мы можем их удалить из набора или присвоить им новую метку.
Определив индексы шумовых примеров, подготовим четыре набора данных для обучения ансамблей, объединенных в структуру denoiseX1pretrain.
- denoiseX1pretrain$origin — оригинальный набор предобучения;
- denoiseX1pretrain$repaired — набор данных, в котором исправлена разметка шумовых примеров;
- denoiseX1pretrain$removed — набор данных, в котором удалены шумовые примеры;
- denoiseX1pretrain$relabeled — набор данных, в котором шумовым примерам присвоена новая метка (т.е. наша целевая теперь имеет три класса).
#--2-Data Xrepair-------------
#library(NoiseFiltersR)
evalq({
out <- noise(x = data1$pretrain %>% dp$select(-Data))
Yrelab <- X1$pretrain$y
Yrelab[out$repIdx] <- 2L
X1rem <- data1$pretrain[-out$repIdx, ] %>% dp$select(-Data)
denoiseX1pretrain <- list(origin = list(x = X1$pretrain$x, y = X1$pretrain$y),
repaired = list(x = X1$pretrain$x, y = out$cleanData$Class %>%
as.numeric() %>% subtract(1)),
removed = list(x = X1rem %>% dp$select(-Class),
y = X1rem$Class %>% as.numeric() %>% subtract(1)),
relabeled = list(x = X1$pretrain$x, y = Yrelab))
rm(out, Yrelab, X1rem)
}, env) В поднаборах denoiseX1pretrain$origin|repaired|relabeled предикторы х идентичны, а вот целевая у всех наборов разная. Посмотрим на их структуру:
#------------------------- env$denoiseX1pretrain$repaired$x %>% str() 'data.frame': 4001 obs. of 13 variables: $ ftlm : num 0.293 0.492 0.47 0.518 0.395 ... $ stlm : num 0.204 0.185 0.161 0.153 0.142 ... $ rbci : num -0.0434 0.1156 0.1501 0.25 0.248 ... $ pcci : num -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... $ fars : num 0.208 0.255 0.246 0.279 0.267 ... $ v.fatl: num 0.4963 0.4635 0.0842 0.3707 0.0542 ... $ v.satl: num -0.0146 0.0248 -0.0353 0.1797 0.1205 ... $ v.rftl: num -0.2695 -0.0809 0.1752 0.3637 0.5305 ... $ v.rstl: num 0.398 0.362 0.386 0.374 0.357 ... $ v.ftlm: num 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... $ v.stlm: num -0.275 -0.226 -0.285 -0.11 -0.148 ... $ v.rbci: num 0.5374 0.4811 0.0978 0.2992 -0.0141 ... $ v.pcci: num -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... env$denoiseX1pretrain$relabeled$x %>% str() 'data.frame': 4001 obs. of 13 variables: $ ftlm : num 0.293 0.492 0.47 0.518 0.395 ... $ stlm : num 0.204 0.185 0.161 0.153 0.142 ... $ rbci : num -0.0434 0.1156 0.1501 0.25 0.248 ... $ pcci : num -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... $ fars : num 0.208 0.255 0.246 0.279 0.267 ... $ v.fatl: num 0.4963 0.4635 0.0842 0.3707 0.0542 ... $ v.satl: num -0.0146 0.0248 -0.0353 0.1797 0.1205 ... $ v.rftl: num -0.2695 -0.0809 0.1752 0.3637 0.5305 ... $ v.rstl: num 0.398 0.362 0.386 0.374 0.357 ... $ v.ftlm: num 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... $ v.stlm: num -0.275 -0.226 -0.285 -0.11 -0.148 ... $ v.rbci: num 0.5374 0.4811 0.0978 0.2992 -0.0141 ... $ v.pcci: num -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... env$denoiseX1pretrain$repaired$y %>% table() . 0 1 1888 2113 env$denoiseX1pretrain$removed$y %>% table() . 0 1 1509 1673 env$denoiseX1pretrain$relabeled$y %>% table() . 0 1 2 1509 1673 819
Поскольку в наборе denoiseX1pretrain$removed изменилось количество примеров, проверим, как изменилась значимость предикторов:
evalq({
orderF(x = denoiseX1pretrain$removed$x %>% as.matrix(),
type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> rx1rem
rx1rem$stopri[ ,1] -> orderX1rem
featureX1rem <- dp$filter(rx1rem$stopri %>% as.data.frame(),
rx1rem$stopri[ ,2] > 0.5) %>%
dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx1rem$stopri)
[,1] [,2]
[1,] 6 1.0790642
[2,] 12 1.0320772
[3,] 7 0.9629750
[4,] 10 0.9515987
[5,] 5 0.8426669
[6,] 1 0.8138830
[7,] 3 0.7934568
[8,] 11 0.7682185
[9,] 8 0.6720211
[10,] 2 0.6355753
[11,] 4 0.5159589
[12,] 9 0.3670544
[13,] 13 0.2170575
colnames(env$X1$pretrain$x)[env$featureX1rem]
[1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars" "ftlm" "rbci" "v.stlm" "v.rftl"
[10] "stlm" "pcci" Изменился порядок и состав лучших предикторов. Это нужно будет учитывать при обучении ансамблей.
Итак, у наc готовы 4 поднабора: denoiseX1pretrain$origin, repaired, removed, relabeled. На них будем обучать ансамбли ELM. Скрипты для обесшумливания данных находятся в файле Denoise.R. Структура исходных данных Х1 и denoiseX1pretrain выглядит так:

Рис. 1. Структура исходных данных.
3. Обучение ансамблей нейросетевых классификаторов на обесшумленных исходных данных и вычисление непрерывных предсказаний нейросетей на тестовых поднаборах
Напишем функцию обучения ансамбля и получения предсказаний, которые в дальнейшем будут входными данными для обучающегося объединителя в stacking-ансамбле.
Мы уже проводили такие вычисления в предыдущей статье, поэтому я не буду останавливаться на подробностях. Если кратко, то:
- в блоке 1 (Input) определяем константы,
- в блоке 2 (createEns) определяем функцию CreateEns(), которая создает ансамбль индивидульных нейросетевых классификаторов с постоянными параметрами и воспроизводимой инициализацией,
- в блоке 3 (GetInputData) функция GetInputData() вычисляет предсказания трех поднаборов Х1$ train/test/test1 ансамблем Ens.
#--1--Input------------- evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear n <- 500 r = 7L SEED <- 12345 #--2-createENS---------------------- createEns <- function(r = 7L, nh = 5L, fact = 7L, X, Y){ Xtrain <- X[ , featureX1] k <- 1 rng <- RNGseq(n, SEED) #---creste Ensemble--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Y[idx], nhid = nh, actfun = Fact[fact]) } return(Ens) } #--3-GetInputData -FUN----------- GetInputData <- function(Ens, X, Y){ #---predict-InputPretrain-------------- Xtrain <- X[ ,featureX1] k <- 1 rng <- RNGseq(n, SEED) #---create Ensemble--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr k <- k + 1 predict(Ens[[i]], newdata = Xtrain[-idx, ]) } %>% unname() -> InputPretrain #---predict-InputTrain-- Xtest <- X1$train$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> InputTrain #[ ,n] #---predict--InputTest---- Xtest1 <- X1$test$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest1) } -> InputTest #[ ,n] #---predict--InputTest1---- Xtest2 <- X1$test1$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest2) } -> InputTest1 #[ ,n] #---res------------------------- return(list(InputPretrain = InputPretrain, InputTrain = InputTrain, InputTest = InputTest, InputTest1 = InputTest1)) } }, env)
У нас уже есть набор denoiseX1pretrain с четырьмя группами данных для обучения ансамблей: оригинальный (origin), с исправленной разметкой (repaired), с удаленными (removed) и переразмеченными (relabeled) шумовыми примерами. Обучая ансамбль на каждой из этих групп данных, мы получим четыре ансамбля. Используя эти ансамбли с функцией GetInputData(), получим четыре группы предсказаний в трех поднаборах: train, test и test1. Ниже приведены скрипты отдельно для каждого ансамбля в развернутом виде (только для отладки и упрощения понимания).
#---4--createEns--origin-------------- evalq({ Ens.origin <- vector(mode = "list", n) res.origin <- vector("list", 4) x <- denoiseX1pretrain$origin$x %>% as.matrix() y <- denoiseX1pretrain$origin$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.origin GetInputData(Ens = Ens.origin, X = x, Y = y) -> res.origin }, env) #---4--createEns--repaired-------------- evalq({ Ens.repaired <- vector(mode = "list", n) res.repaired <- vector("list", 4) x <- denoiseX1pretrain$repaired$x %>% as.matrix() y <- denoiseX1pretrain$repaired$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.repaired GetInputData(Ens = Ens.repaired, X = x, Y = y) -> res.repaired }, env) #---4--createEns--removed-------------- evalq({ Ens.removed <- vector(mode = "list", n) res.removed <- vector("list", 4) x <- denoiseX1pretrain$removed$x %>% as.matrix() y <- denoiseX1pretrain$removed$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.removed GetInputData(Ens = Ens.removed, X = x, Y = y) -> res.removed }, env) #---4--createEns--relabeled-------------- evalq({ Ens.relab <- vector(mode = "list", n) res.relab <- vector("list", 4) x <- denoiseX1pretrain$relabeled$x %>% as.matrix() y <- denoiseX1pretrain$relabeled$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.relab GetInputData(Ens = Ens.relab, X = x, Y = y) -> res.relab }, env)
Структура результатов предсказания ансамблей приведена ниже:
> env$res.origin %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 0.747 0.774 0.733 0.642 0.28 ... $ InputTrain : num [1:1001, 1:500] 0.742 0.727 0.731 0.66 0.642 ... $ InputTest : num [1:501, 1:500] 0.466 0.446 0.493 0.594 0.501 ... $ InputTest1 : num [1:251, 1:500] 0.093 0.101 0.391 0.547 0.416 ... > env$res.repaired %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 0.815 0.869 0.856 0.719 0.296 ... $ InputTrain : num [1:1001, 1:500] 0.871 0.932 0.889 0.75 0.737 ... $ InputTest : num [1:501, 1:500] 0.551 0.488 0.516 0.629 0.455 ... $ InputTest1 : num [1:251, 1:500] -0.00444 0.00877 0.35583 0.54344 0.40121 ... > env$res.removed %>% str() List of 4 $ InputPretrain: num [1:955, 1:500] 0.68 0.424 0.846 0.153 0.242 ... $ InputTrain : num [1:1001, 1:500] 0.864 0.981 0.784 0.624 0.713 ... $ InputTest : num [1:501, 1:500] 0.755 0.514 0.439 0.515 0.156 ... $ InputTest1 : num [1:251, 1:500] 0.105 0.108 0.511 0.622 0.339 ... > env$res.relab %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 1.11 1.148 1.12 1.07 0.551 ... $ InputTrain : num [1:1001, 1:500] 1.043 0.954 1.088 1.117 1.094 ... $ InputTest : num [1:501, 1:500] 0.76 0.744 0.809 0.933 0.891 ... $ InputTest1 : num [1:251, 1:500] 0.176 0.19 0.615 0.851 0.66 ...
Посмотрим, как выглядит распределение этих выходов/входов. Смотрим 10 первых выходов наборов InputTrain[ ,1:10]:
#------Ris InputTrain------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$res.origin$InputTrain[ ,1:10], horizontal = T, main = "res.origin$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTrain[ ,1:10], horizontal = T, main = "res.repaired$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTrain[ ,1:10], horizontal = T, main = "res.removed$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTrain[ ,1:10], horizontal = T, main = "res.relab$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
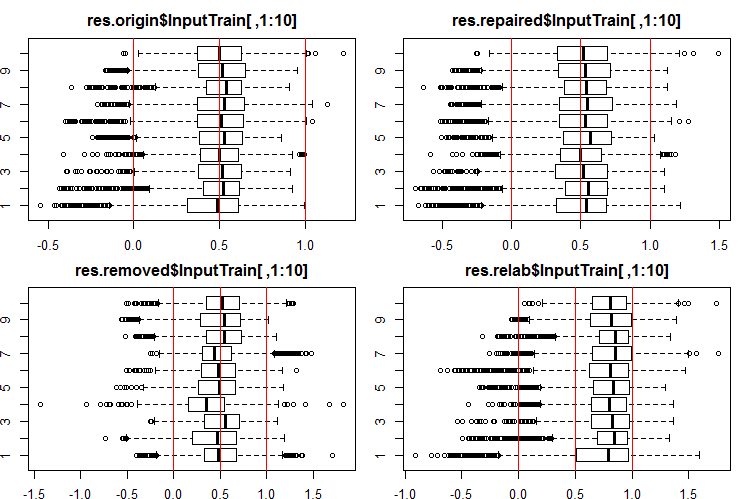
Рис. 2. Распределение предсказаний выходов InputTrain четырьмя различными ансамблями.
Смотрим 10 первых выходов наборов InputTest[ ,1:10]:
#------Ris InputTest------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2), las = 1) boxplot(env$res.origin$InputTest[ ,1:10], horizontal = T, main = "res.origin$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTest[ ,1:10], horizontal = T, main = "res.repaired$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTest[ ,1:10], horizontal = T, main = "res.removed$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTest[ ,1:10], horizontal = T, main = "res.relab$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
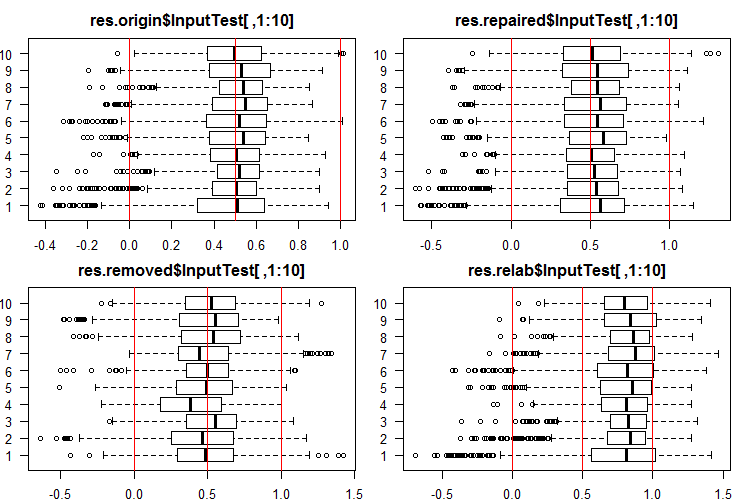
Рис. 3. Распределение предсказаний выходов InputTest четырьмя различными ансамблями.
Смотрим 10 первых выходов наборов InputTest1[ ,1:10]:
#------Ris InputTest1------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$res.origin$InputTest1[ ,1:10], horizontal = T, main = "res.origin$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTest1[ ,1:10], horizontal = T, main = "res.repaired$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTest1[ ,1:10], horizontal = T, main = "res.removed$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTest1[ ,1:10], horizontal = T, main = "res.relab$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
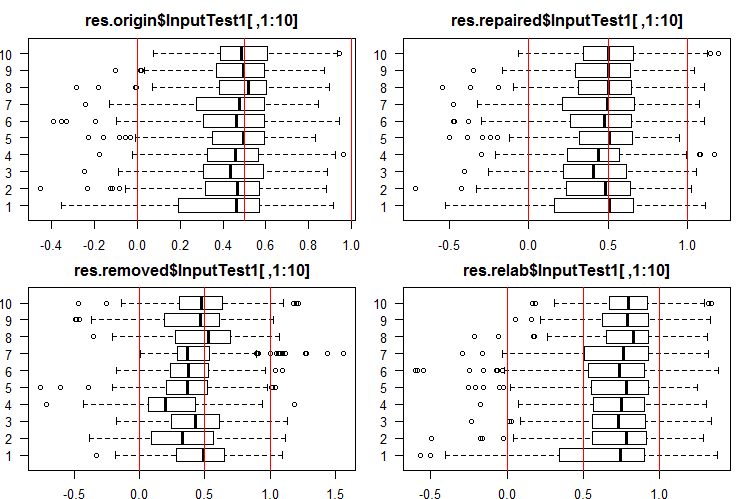
Рис. 4. Распределение предсказаний выходов InputTest1 четырьмя различными ансамблями.
Распределение всех предсказаний сильно отличается от распределений, полученных на данных, нормированных методом SpatialSign в предыдущих моих экспериментах. Можете поэкспериметрировать с различными методами нормирования самостоятельно.
Вычислив предикт поднаборов X1$train/test/test1 каждым ансамблем, получим четыре группы данных — res.origin, res.repaired, res.removed и res.relab, распределение которых мы видим на рисунках 2 — 4.
Определим качество классификации каждого ансамбля, переведя непрерывные предсказания в метки классов.
4. Определение порогов для полученных непрерывных предсказаний, перевод их в метки классов и вычисление метрик нейросетей
Чтобы переводить непрерывные предсказания в метки классов, используют один или несколько порогов деления на эти классы. Непрерывные предсказания наборов InputTrain, полученные от пятой нейросети всех ансамблей, выглядят так:
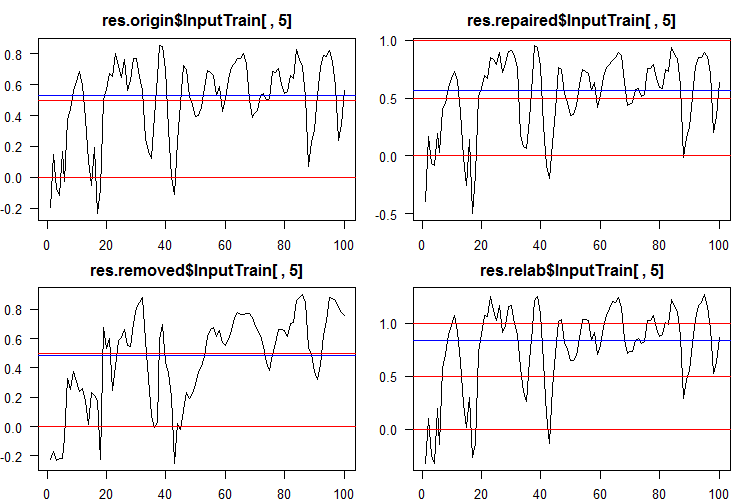
Рис. 5 Непрерывные предсказания пятой нейросети различных ансамблей.
Как видим, графики непрерывного предсказания моделей origin, repaired, relabeled похожи по форме, но имеют различный диапазон. Значительно отличается по форме линия предсказания модели removed.
Для упрощения последующих вычислений соберем в одну структуру predX1 все модели и их предсказания. Для этого напишем компактную функцию, которая повторит все вычисления в цикле. Вот скрипт и рисунок структуры predX1:
library("doFuture")
#---predX1------------------
evalq({
group <- qc(origin, repaired, removed, relabeled)
predX1 <- vector("list", 4)
foreach(i = 1:4, .packages = "elmNN") %do% {
x <- denoiseX1pretrain[[i]]$x %>% as.matrix()
y <- denoiseX1pretrain[[i]]$y
SEED = 12345
createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> ens
GetInputData(Ens = ens, X = x, Y = y) -> pred
return(list(ensemble = ens, pred = pred))
} -> predX1
names(predX1) <- group
}, env) 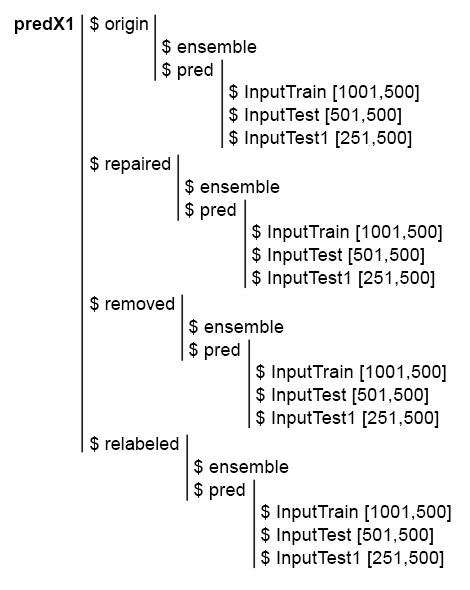
Рис. 6. Структура набора predX1
Мы помним: чтобы получить метрики качества предсказания ансамбля, нужно выполнить две операции : обрезку и усреднение (или простое голосование). Для обрезки нам нужно перевести выходы всех нейросетей ансамбля из непрерывной формы в метки класса. Затем определим метрики каждой нейросети и выберем какое-то их количество с наилучшими показателями. Потом усредняем непрерывные предсказания этих лучших нейросетей и получаем непрерывное усредненное предсказание ансамбля. Еще раз определяем порог, переводим усредненное предсказание в метки классов и вычисляем окончательные показатели качества классификации ансамбля.
Таким образом, нам дважды нужно преобразовывать непрерывное предсказание в метки классов. Пороги преобразования на этих двух этапах могут быть и одинаковыми, и различными. Какие варианты порогов мы можем использовать?
- Порог, принимаемый по умолчанию. В нашем случае он равен 0.5.
- Порог, равный медиане. Я думаю, что он более надежен. Но медиану мы можем определить только на валидационном поднаборе, а применить — только при тестировании последующих поднаборов. Например, на поднаборе InputTrain мы определяем пороги, которые будем использовать на поднаборах InputTest и InputTest1.
- Порог, оптимизированный по различным критериям. Например, это могут быть минимальная ошибка классификации, максимальная точность "1", или "0" и т.д. Оптимальные пороги определяем всегда на поднаборе InputTrain, а используем — на поднаборах InputTest и InputTest1.
- При усреднении выходов лучших нейросетей ансамбля можно использовать калибровку. Некоторые авторы пишут, что усреднять можно только хорошо откалиброванные выходы. В наши задачи проверка этого утверждения не входит.
Определять оптимальный порог будем с помощью функции InformationValue::optimalCutoff(). Она подробно описана в пакете.
Для определения порогов по пп.1 и 2 нам не нужны дополнительные вычисления. Для вычисления оптимальных порогов по п.3 напишем функцию GetThreshold().
#--function------------------------- evalq({ import_fun("InformationValue", optimalCutoff, CutOff) import_fun("InformationValue", youdensIndex, th_youdens) GetThreshold <- function(X, Y, type){ switch(type, half = 0.5, med = median(X), mce = CutOff(Y, X, "misclasserror"), both = CutOff(Y, X,"Both"), ones = CutOff(Y, X, "Ones"), zeros = CutOff(Y, X, "Zeros") ) } }, env)
Будем вычислять только первые четыре типа порогов, описанных в этой функции (half, med, mce, both). Первые два — это половинный и медианный пороги. Порог mce обеспечивает минимальную ошибку классификации, порог both — максимальное значение коэффициента youdensIndex = (sensitivity + specificity —1). Порядок вычислений будет таким:
1. В наборе predX1 отдельно в каждой группе данных (origin, repaired, removed и relabeled) вычисляем четыре типа порогов для каждой из 500 нейросетей ансамбля на поднаборе InputTrain.
2. Затем, используя эти пороги, переводим непрерывные предсказания всех нейросетей ансамблей во всех поднаборах (train|test|test1) в классы и определяем средние величины F1. Получим четыре группы метрик, по три поднабора в каждой. Ниже приведен пошагово расписанный скрипт для группы origin.
Определяем 4 типа порогов на поднаборе predX1$origin$pred$InputTrain:
#--threshold--train--origin--------
evalq({
Ytest = X1$train$y
Ytest1 = X1$test$y
Ytest2 = X1$test1$y
testX1 <- vector("list", 4)
names(testX1) <- group
type <- qc(half, med, mce, both)
registerDoFuture()
cl <- makeCluster(4)
plan(cluster, workers = cl)
foreach(i = 1:4, .combine = "cbind") %dopar% {# type
foreach(j = 1:500, .combine = "c") %do% {
GetThreshold(predX1$origin$pred$InputTrain[ ,j], Ytest, type[i])
}
} -> testX1$origin$Threshold
stopCluster(cl)
dimnames(testX1$origin$Threshold) <- list(NULL,type)
}, env) Мы используем два вложенных цикла в каждом вычислении. Во внешнем цикле выбираем тип порога, создаем кластер и распараллеливаем вычисления на 4 ядра. Во внутреннем цикле идем по предсказаниям InputTrain каждой из 500 нейросетей, входящих в ансамбль. Для каждой определяем 4 типа порогов. Структура полученных данных будет такой:
> env$testX1$origin$Threshold %>% str() num [1:500, 1:4] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ... - attr(*, "dimnames")=List of 2 ..$ : NULL ..$ : chr [1:4] "half" "med" "mce" "both" > env$testX1$origin$Threshold %>% head() half med mce both [1,] 0.5 0.5033552 0.3725180 0.5125180 [2,] 0.5 0.4918041 0.5118821 0.5118821 [3,] 0.5 0.5005034 0.5394191 0.5394191 [4,] 0.5 0.5138439 0.4764055 0.5164055 [5,] 0.5 0.5241393 0.5165478 0.5165478 [6,] 0.5 0.4673319 0.4508287 0.4608287
Используя полученные пороги, переведем непрерывные предсказания группы origin поднаборов train, test и test1 в метки классов и вычислим метрики (mean(F1)).
#--train--------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {# type
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTrain[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTrainScore
dimnames(testX1$origin$InputTrainScore)[[2]] <- type
}, env)
#--test-----------------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {# type
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTest[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTestScore
dimnames(testX1$origin$InputTestScore)[[2]] <- type
}, env)
#--test1-----------------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTest1[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTest1Score
dimnames(testX1$origin$InputTest1Score)[[2]] <- type
}, env) Посмотрим на распределение метрик в группе origin и трех ее поднаборах. Скрипт ниже для группы origin:
k <- 1L #origin # k <- 2L #repaired # k <- 3L #removed # k <- 4L #relabeling par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$testX1[[k]]$Threshold, horizontal = F, main = paste0(env$group[k],"$$Threshold"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F, main = paste0(env$group[k],"$$InputTrainScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTestScore, horizontal = F, main = paste0(env$group[k],"$$InputTestScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F, main = paste0(env$group[k],"$$InputTest1Score"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) par(mfrow = c(1, 1))
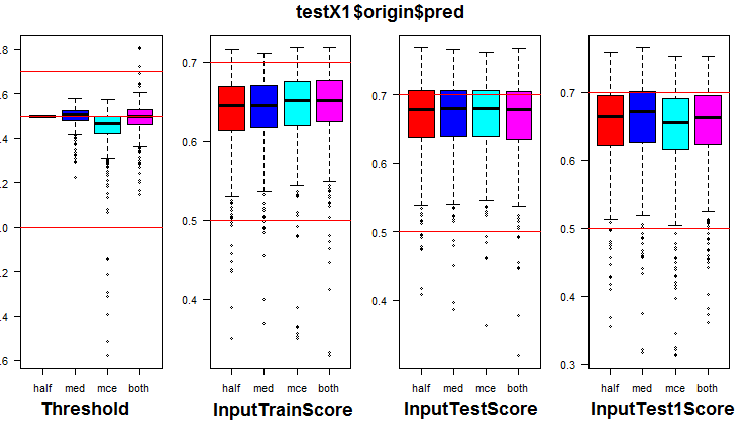
Рис. 7. Распределение порогов и метрик в группе origin
Визуализация показала, что использование в качестве порога "med" на данных группы origin не дает видимого улучшения качества по сравнению с порогом в "half".
Вычислим все 4 типа порогов во всех группах (будьте готовы к тому, что это занимает довольно много времени и памяти).
library("doFuture") #--threshold--train--------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) Ytest = X1$train$y Ytest1 = X1$test$y Ytest2 = X1$test1$y registerDoFuture() cl <- makeCluster(4) plan(cluster, workers = cl) while (k <= 4) { # group foreach(i = 1:4, .combine = "cbind") %dopar% {# type foreach(j = 1:500, .combine = "c") %do% { GetThreshold(predX1[[k]]$pred$InputTrain[ ,j], Ytest, type[i]) } } -> testX1[[k]]$Threshold dimnames(testX1[[k]]$Threshold) <- list(NULL,type) k <- k + 1 } stopCluster(cl) }, env)
Используя полученные пороги, вычислим метрики во всех группах и поднаборах:
#--train-------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTrain[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTrainScore dimnames(testX1[[k]]$InputTrainScore)[[2]] <- type k <- k + 1 } }, env) #--test----------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTest[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTestScore dimnames(testX1[[k]]$InputTestScore)[[2]] <- type k <- k + 1 } }, env) #--test1----------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTest1[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTest1Score dimnames(testX1[[k]]$InputTest1Score)[[2]] <- type k <- k + 1 } }, env)
В каждую группу данных мы добавили метрики каждой из 500 нейросетей ансамбля с четырьмя различными порогами на трех поднаборах.
Посмотрим, как распределены метрики в каждой группе и поднаборе. Я привожу скрипт для поднабора repaired. Для остальных групп он аналогичен, изменяется только номер группы. Графики всех групп сведу в один для наглядности.
# k <- 1L #origin k <- 2L #repaired # k <- 3L #removed # k <- 4L #relabeling par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$testX1[[k]]$Threshold, horizontal = F, main = paste0(env$group[k],"$$Threshold"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F, main = paste0(env$group[k],"$$InputTrainScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTestScore, horizontal = F, main = paste0(env$group[k],"$$InputTestScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F, main = paste0(env$group[k],"$$InputTest1Score"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) par(mfrow = c(1, 1))
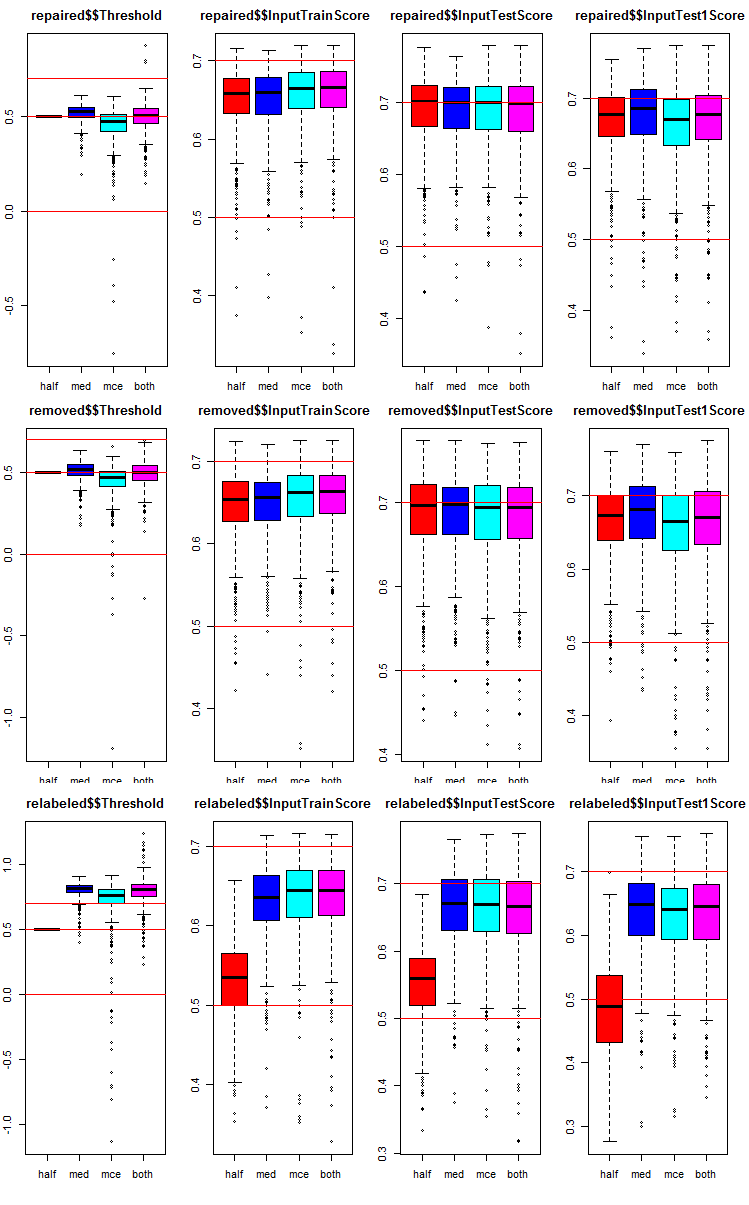
Рис. 8. Графики распределения метрик предсказаний каждой нейросети ансамбля в трех группах данных с тремя поднаборами и четырьмя различными порогами.
Общее во всех группах:
- метрики первого тестового поднабора (InputTestScore) гораздо лучше метрик валидационного (InputTrainScore);
- метрики второго тестового поднабора (InputTest1Score) заметно хуже первого тестового;
- порог типа "half" на всех поднаборах, за исключением relabeled, показывает результаты не хуже остальных.
5. Тестирование ансамблей
5.1.Определяем 7 нейросетей с лучшими метриками в каждом ансамбле и в каждой группе данных в поднаборе InputTrain
Выполняем обрезку. Нам нужно в каждой группе данных набора testX1 выбрать 7 значений InputTrainScore с наибольшими величинами среднего F1. Их индексы и будут индексами лучших нейросетей в ансамбле. Скрипт приводится ниже, вы можете найти его в файле Test.R.
#--bestNN---------------------------------------- evalq({ nb <- 3L k <- 1L while (k <= 4) { foreach(j = 1:4, .combine = "cbind") %do% { testX1[[k]]$InputTrainScore[ ,j] %>% order(decreasing = TRUE) %>% head(2*nb + 1) } -> testX1[[k]]$bestNN dimnames(testX1[[k]]$bestNN) <- list(NULL, type) k <- k + 1 } }, env)
Мы получили индексы нейросетей с наилучшими показателями в четырех группах данных (origin, repaired, removed, relabeled). Посмотрим на них и сравним, насколько отличаются эти лучшие нейросети в зависимости от группы данных и типа порога.
> env$testX1$origin$bestNN half med mce both [1,] 415 75 415 415 [2,] 191 190 220 220 [3,] 469 220 191 191 [4,] 220 469 469 469 [5,] 265 287 57 444 [6,] 393 227 393 57 [7,] 75 322 444 393 > env$testX1$repaired$bestNN half med mce both [1,] 393 393 154 154 [2,] 415 92 205 205 [3,] 205 154 220 220 [4,] 462 190 393 393 [5,] 435 392 287 287 [6,] 392 220 90 90 [7,] 265 287 415 415 > env$testX1$removed$bestNN half med mce both [1,] 283 130 283 283 [2,] 207 110 300 300 [3,] 308 308 110 110 [4,] 159 134 192 130 [5,] 382 207 207 192 [6,] 192 283 130 308 [7,] 130 114 134 207 env$testX1$relabeled$bestNN half med mce both [1,] 234 205 205 205 [2,] 69 287 469 469 [3,] 137 191 287 287 [4,] 269 57 191 191 [5,] 344 469 415 415 [6,] 164 75 444 444 [7,] 184 220 57 57
Можно заметить, что индексы нейросетей с типами порогов "mce" и "both" очень часто совпадают.
5.2. Усредняем непрерывные предсказания этих 7 лучших нейросетей.
Выбрав предсказания 7 лучших нейросетей, усредним их в каждой группе данных, в поднаборах InputTrain, InputTest, InputTest1 и по каждому типу порогов. Скрипт для обработки поднабора InputTrain в 4 группах:
#--Averaging--train------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTrain[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$TrainYpred dimnames(testX1[[k]]$TrainYpred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env)
Посмотрим на структуру и статистические показатели полученных усредненых непрерывных предсказаний в группе данных repaired:
> env$testX1$repaired$TrainYpred %>% str() num [1:1001, 1:4] 0.849 0.978 0.918 0.785 0.814 ... - attr(*, "dimnames")=List of 2 ..$ : NULL ..$ : chr [1:4] "Y.aver_half" "Y.aver_med" "Y.aver_mce" "Y.aver_both" > env$testX1$repaired$TrainYpred %>% summary() Y.aver_half Y.aver_med Y.aver_mce Y.aver_both Min. :-0.2202 Min. :-0.4021 Min. :-0.4106 Min. :-0.4106 1st Qu.: 0.3348 1st Qu.: 0.3530 1st Qu.: 0.3512 1st Qu.: 0.3512 Median : 0.5323 Median : 0.5462 Median : 0.5462 Median : 0.5462 Mean : 0.5172 Mean : 0.5010 Mean : 0.5012 Mean : 0.5012 3rd Qu.: 0.7227 3rd Qu.: 0.7153 3rd Qu.: 0.7111 3rd Qu.: 0.7111 Max. : 1.1874 Max. : 1.0813 Max. : 1.1039 Max. : 1.1039
И здесь тоже статистика двух последних типов порогов идентична. Вот скрипты для двух оставшихся поднаборов InputTest, InputTest1:
#--Averaging--test------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTest[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$TestYpred dimnames(testX1[[k]]$TestYpred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env) #--Averaging--test1------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTest1[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$Test1Ypred dimnames(testX1[[k]]$Test1Ypred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env)
Посмотрим статистику поднабора InputTest группы данных repaired:
> env$testX1$repaired$TestYpred %>% summary() Y.aver_half Y.aver_med Y.aver_mce Y.aver_both Min. :-0.1524 Min. :-0.5055 Min. :-0.5044 Min. :-0.5044 1st Qu.: 0.2888 1st Qu.: 0.3276 1st Qu.: 0.3122 1st Qu.: 0.3122 Median : 0.5177 Median : 0.5231 Median : 0.5134 Median : 0.5134 Mean : 0.5114 Mean : 0.4976 Mean : 0.4946 Mean : 0.4946 3rd Qu.: 0.7466 3rd Qu.: 0.7116 3rd Qu.: 0.7149 3rd Qu.: 0.7149 Max. : 1.1978 Max. : 1.0428 Max. : 1.0722 Max. : 1.0722
И здесь тоже статистика двух последних двух типов порогов идентична.
5.3. Определяем пороги для усредненных непрерывных предсказаний
Теперь у нас есть усредненные предсказания каждого ансамбля. Их нужно перевести в метки классов и определить окончательные метрики качества для всех групп данных и типов порогов. Для этого, по аналогии с предыдущими расчетами, определим лучшие пороги, используя при этом только поднаборы InputTrain. Скрипт, приведенный ниже, вычисляет пороги в каждой группе и в каждом поднаборе:
#-th_aver------------------------------ evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) Ytest = X1$train$y Ytest1 = X1$test$y Ytest2 = X1$test1$y while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold GetThreshold(testX1[[k]]$TrainYpred[ ,j], Ytest, type[i]) } } -> testX1[[k]]$th_aver dimnames(testX1[[k]]$th_aver) <- list(type, colnames(testX1[[k]]$TrainYpred)) k <- k + 1 } }, env)
5.4. Переводим усредненные непрерывные предсказания ансамблей в метки классов и вычисляем метрики ансамблей на поднаборах InputTrain, InputTest и InputTest1 всех групп данных.
Имея вычисленные выше пороги th_aver, определяем метрики:
#---Metrics--train------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$TrainScore dimnames(testX1[[k]]$TrainScore) <- list(type, colnames(testX1[[k]]$TrainYpred)) k <- k + 1 } }, env) #---Metrics--test------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest1, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$TestScore dimnames(testX1[[k]]$TestScore) <- list(type, colnames(testX1[[k]]$TestYpred)) k <- k + 1 } }, env) #---Metrics--test1------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest2, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$Test1Score dimnames(testX1[[k]]$Test1Score) <- list(type, colnames(testX1[[k]]$Test1Ypred)) k <- k + 1 } }, env)
Сделаем сводную таблицу и проанализируем полученные метрики. Начнем с группы origin (в ней шумовые примеры никак не обрабатывались). Нам важны показатели TestScore и Test1Score. Показатели поднабора TestTrain индикативны, они нужны для сравнения с тестовыми:
> env$testX1$origin$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.711 0.708 0.712 0.712 med 0.711 0.713 0.707 0.707 mce 0.712 0.704 0.717 0.717 both 0.711 0.706 0.717 0.717 > env$testX1$origin$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.750 0.738 0.745 0.745 med 0.748 0.742 0.746 0.746 mce 0.742 0.720 0.747 0.747 both 0.748 0.730 0.747 0.747 > env$testX1$origin$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.735 0.732 0.716 0.716 med 0.733 0.753 0.745 0.745 mce 0.735 0.717 0.716 0.716 both 0.733 0.750 0.716 0.716
Что мы видим в предложенной таблице?
Наилучший результат 0.750 в TestScore показал вариант с порогом "half" в обоих преобразованиях (и при обрезке, и при усреднении). Однако в поднаборе Test1Score качество падает до 0.735.
Более стабильный результат в обоих поднаборах ~0.745 показывают варианты порогов при обрезке (med, mce, both) и med при усреднении.
Смотрим следующую группы данных — repaired (с исправленной разметкой шумовых примеров):
> env$testX1$repaired$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.713 0.711 0.717 0.717 med 0.709 0.709 0.713 0.713 mce 0.728 0.714 0.709 0.709 both 0.728 0.711 0.717 0.717 > env$testX1$repaired$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.759 0.761 0.756 0.756 med 0.754 0.748 0.747 0.747 mce 0.758 0.755 0.743 0.743 both 0.758 0.732 0.754 0.754 > env$testX1$repaired$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.719 0.744 0.724 0.724 med 0.738 0.748 0.744 0.744 mce 0.697 0.720 0.677 0.677 both 0.697 0.743 0.731 0.731
Лучший результат, который мы видим в таблице, — это 0.759 в комбинации half/half. Более стабильный результат в обоих поднаборах ~0.750 показывают варианты порогов при обрезке (half, med, mce, both) и med при усреднении.
Смотрим следующую группы данных — removed (с удаленными из набора шумовыми примерами):
> env$testX1$removed$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.713 0.720 0.724 0.718 med 0.715 0.717 0.715 0.717 mce 0.721 0.722 0.725 0.723 both 0.721 0.720 0.725 0.723 > env$testX1$removed$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.761 0.769 0.761 0.751 med 0.752 0.749 0.760 0.752 mce 0.749 0.755 0.753 0.737 both 0.749 0.736 0.753 0.760 > env$testX1$removed$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.712 0.732 0.716 0.720 med 0.729 0.748 0.740 0.736 mce 0.685 0.724 0.721 0.685 both 0.685 0.755 0.721 0.733
Анализируем таблицу. Наилучший результат 0.769 в TestScore показал вариант с порогами med/half. Однако в поднаборе Test1Score качество падает до 0.732. Для поднабора TestScore лучшее сочетание порогов при обрезке (half, med, mce, both) и half при усреднении дает наилучшие показатели из всех групп.
Смотрим последнюю группу данных — relabeled ( с выделением шумовых примеров в отдельный класс):
> env$testX1$relabeled$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.672 0.559 0.529 0.529 med 0.715 0.715 0.711 0.711 mce 0.712 0.715 0.717 0.717 both 0.710 0.718 0.720 0.720 > env$testX1$relabeled$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.719 0.572 0.555 0.555 med 0.736 0.748 0.746 0.746 mce 0.739 0.747 0.745 0.745 both 0.710 0.756 0.754 0.754 > env$testX1$relabeled$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.664 0.498 0.466 0.466 med 0.721 0.748 0.740 0.740 mce 0.739 0.732 0.716 0.716 both 0.734 0.737 0.735 0.735
Лучшие для этой группы результаты дает комбинация порогов: при обрезке (med, mce, both) и both или med при усреднении.
Имейте в виду, что у вас могут получиться значения, отличающиеся от моих.
Ниже на рисунке показана структура данных testX1 после всех вышеприведенных вычислений:

Рис. 9. Структура данных testX1.
6. Оптимизация гиперпараметров нейросетевых классификаторов ансамблей
Все предыдущие вычисления мы проводили на ансамблях с одинаковыми гиперпараметрами нейросетей, установленными на личном опыте. Как известно, гиперпараметры нейросетей, как и других моделей, для получения лучших результатов нужно оптимизировать под конкретный набор данных. Для обучения мы используем обесшумленные данные, которые разделены на 4 группы (origin, repaired, removed и relabeled). Поэтому нам нужно получить оптимальные гиперпараметры нейросетей ансамбля именно для этих наборов. В предыдущей статье мы подробно рассматривали все вопросы, связанные с байесовской оптимизацией, поэтому я не буду останавливаться на деталях.
Оптимизировать будем 4 гиперпараметра нейросетей:
- количество предикторов — numFeature = c(3L, 13L) в диапазоне от 3 до 13;
- доля примеров используемая при обучении — r = c(1L, 10L) в диапазоне от 10 % до 100%;
- количество нейронов в скрытом слое — nh = c(1L, 51L) в диапазоне от 1 до 51;
- тип активационной функции — fact = c(1L, 10L) индекс в списке функций активации Fact.
Установим константы:
##===OPTIM=============================== evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear bonds <- list( numFeature = c(3L, 13L), r = c(1L, 10L), nh = c(1L, 51L), fact = c(1L, 10L) ) }, env)
Напишем фитнес-функцию, которая будет возвращать показатель качества Score = meаn(F1) и предсказание ансамбля в метках классов. Обрезку (выбор лучших нейросетей в ансамбле) и усреднение непрерывных предсказаний будем проводить используя одинаковый порог = 0.5. Выше мы убедились, что это очень неплохой вариант — по крайней мере, для первого приближения. Вот как выглядит скрипт:
#---Fitnes -FUN----------- evalq({ n <- 500 numEns <- 3 # SEED <- c(12345, 1235809) fitnes <- function(numFeature, r, nh, fact){ bestF <- orderX %>% head(numFeature) k <- 1 rng <- RNGseq(n, SEED) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } #---predict--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest[ , bestF]) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
Закомментированная переменная SEED имеет два значения. Это нужно для экспериментальной проверки влияния на результат этого параметра. Я проводил оптимизацию с одинаковыми исходными данными и параметрами, но с двумя различными значениями SEED. Лучший результат показал SEED = 1235809. В скриптах ниже я буду использовать именно это значение. Но полученные гиперпараметры и показатели качества классификации я приведу для обоих значений SEED. Вы можете поэкспериментировать и с другими значениями.
Проверим, работает ли фитнес-функция, сколько времени занимает один проход ее вычисления и каков результат:
evalq({
Ytrain <- X1$pretrain$y
Ytest <- X1$train$y
Ytest1 <- X1$test$y
Xtrain <- X1$pretrain$x
Xtest <- X1$train$x
Xtest1 <- X1$test$x
orderX <- orderX1
SEED <- 1235809
system.time(
res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2)
)
}, env)
user system elapsed
5.89 0.00 5.99
env$res$Score
[1] 0.741 Ниже скрипт отимизации гиперпараметров нейросетей последовательно для каждой группы обесшумленных данных. Используем 20 точек начальной случайной инициализации и 20 последующих итераций.
#---Optim Ensemble----- library(rBayesianOptimization) evalq({ Ytest <- X1$train$y Ytest1 <- X1$test$y Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 OPT_Res <- vector("list", 4) foreach(i = 1:4) %do% { Xtrain <- denoiseX1pretrain[[i]]$x Ytrain <- denoiseX1pretrain[[i]]$y BayesianOptimization(fitnes, bounds = bonds, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100, control = c(100, 50, 8)) } -> OPT_Res1 group <- qc(origin, repaired, removed, relabeled) names(OPT_Res1) <- group }, env)
Запустив скрипт на выполнение, запаситесь терпением примерно на полчаса (это зависит от вашего железа). Упорядочим полученные значения Score по убыванию и отберем по три лучших. Значения этих показателей присвоим переменной best.res (для SEED = 12345) и best.res1 (для SEED = 1235809 ).
#---OptPar------
evalq({
foreach(i = 1:4) %do% {
OPT_Res[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
} -> best.res
names(best.res) <- group
}, env)
evalq({
foreach(i = 1:4) %do% {
OPT_Res1[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
} -> best.res1
names(best.res1) <- group
}, env) Смотрим на показатели best.res:
env$best.res # $origin # Round numFeature r nh fact Value # 1 39 10 7 20 2 0.769 # 2 12 6 4 38 2 0.766 # 3 38 4 3 15 2 0.766 # # $repaired # Round numFeature r nh fact Value # 1 5 10 5 20 7 0.767 # 2 7 5 2 36 9 0.766 # 3 28 5 10 6 8 0.766 # # $removed # Round numFeature r nh fact Value # 1 1 11 6 44 9 0.764 # 2 8 8 6 26 7 0.764 # 3 19 12 1 40 5 0.763 # # $relabeled # Round numFeature r nh fact Value # 1 24 9 10 1 10 0.746 # 2 7 9 9 2 8 0.745 # 3 32 4 1 1 10 0.738
То же для показателей best.res1:
> env$best.res1 $origin Round numFeature r nh fact Value 1 19 8 3 41 2 0.777 2 32 8 1 33 2 0.777 3 23 6 1 35 1 0.770 $repaired Round numFeature r nh fact Value 1 26 9 4 17 3 0.772 2 33 11 9 30 9 0.771 3 38 5 4 17 2 0.770 $removed Round numFeature r nh fact Value 1 30 5 4 17 2 0.770 2 8 8 2 13 6 0.769 3 32 5 3 22 7 0.766 $relabeled Round numFeature r nh fact Value 1 34 12 5 8 9 0.777 2 33 9 5 4 9 0.763 3 36 12 7 4 9 0.760
Как видим, эти результаты выглядят уже лучше. Вы можете вывести для сравнения не три первых результата, а десять: различия будут еще заметней.
Каждый запуск оптимизации будет давать разные значения гиперпараметров и результаты. Оптимизировать гиперпараметры можно с различными значениями начальной установки ГСЧ, а также с конкретной начальной инициализацией.
Соберем лучшие гиперпараметры нейросетей ансамблей для 4 групп данных. Они понадобятся нам для создания ансамблей с оптимальными гиперпараметрами.
#---best.param-------------------
evalq({
foreach(i = 1:4, .combine = "rbind") %do% {
OPT_Res1[[i]]$Best_Par %>% unname()
} -> best.par1
dimnames(best.par1) <- list(group, qc(numFeature, r, nh, fact))
}, env) Сами гиперпараметры:
> env$best.par1 numFeature r nh fact origin 8 3 41 2 repaired 9 4 17 3 removed 5 4 17 2 relabeled 12 5 8 9
Все скрипты из этого раздела вы найдете в файле Optim_VIII.R.
7. Оптимизация гиперпараметров постпроцессинга (пороги обрезки и усреднения)
Оптимизация гиперпараметров нейросетей дает небольшое улучшение качества классификации. Выше мы уже убедились, что комбинация типов порогов при обрезке и усреднении сильнее влияет на качество классификации.
Мы уже оптимизировали гиперпараметры при постоянном сочетании порогов half/half. Возможно, это сочетание неоптимально. Повторим оптимизацию с двумя дополнительными оптимизируемыми параметрами th1 = с(1L, 2L)) — тип порога при обрезке ансамбля (выбор лучших нейросетей) и th2 = c(1L, 4L) —тип порогов при переводе усредненного предсказания ансамбля в метки классов. Определим константы и диапазон значений отимизируемых гиперпараметров.
##===OPTIM=============================== evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear bonds_m <- list( numFeature = c(3L, 13L), r = c(1L, 10L), nh = c(1L, 51L), fact = c(1L, 10L), th1 = c(1L, 2L), th2 = c(1L, 4L) ) }, env)
Перейдем к фитнес-функции. Я ее немного изменил: добавил два формальных параметра th1, th2. В теле функции в блоке best вычисляем порог в зависимости от th1. В блоке test-average определяем порог с помощью функции GetThreshold() в зависимости от типа порога th2.
#---Fitnes -FUN----------- evalq({ n <- 500L numEns <- 3L # SEED <- c(12345, 1235809) fitnes_m <- function(numFeature, r, nh, fact, th1, th2){ bestF <- orderX %>% head(numFeature) k <- 1L rng <- RNGseq(n, SEED) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } #---predict--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest[ , bestF]) } -> y.pr #[ ,n] #---best--- ifelse(th1 == 1L, 0.5, median(y.pr)) -> th foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > th, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>% divide_by(length(bestNN)) -> ensPred th <- GetThreshold(ensPred, Yts$Ytest1, type[th2]) ifelse(ensPred > th, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
Проверим, сколько времени занимает одна итерация этой фитнес-функции и работает ли она:
#---res fitnes------- evalq({ Ytrain <- X1$pretrain$y Ytest <- X1$train$y Ytest1 <- X1$test$y Xtrain <- X1$pretrain$x Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 th1 <- 1 th2 <- 4 system.time( res_m <- fitnes_m(numFeature = 10, r = 7, nh = 5, fact = 2, th1, th2) ) }, env) user system elapsed 6.13 0.04 6.32 > env$res_m$Score [1] 0.748
Время выполнения функции изменилось незначительно. После этого запускаем оптимизацию и ждем результата:
#---Optim Ensemble----- library(rBayesianOptimization) evalq({ Ytest <- X1$train$y Ytest1 <- X1$test$y Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 OPT_Res1 <- vector("list", 4) foreach(i = 1:4) %do% { Xtrain <- denoiseX1pretrain[[i]]$x Ytrain <- denoiseX1pretrain[[i]]$y BayesianOptimization(fitnes_m, bounds = bonds_m, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100) #, control = c(100, 50, 8)) } -> OPT_Res_m group <- qc(origin, repaired, removed, relabeled) names(OPT_Res_m) <- group }, env)
Выделим 10 лучших гиперпараметров, полученных для каждой группы данных:
#---OptPar------
evalq({
foreach(i = 1:4) %do% {
OPT_Res_m[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(10)
} -> best.res_m
names(best.res_m) <- group
}, env)
$origin
Round numFeature r nh fact th1 th2 Value
1 19 8 3 41 2 2 4 0.778
2 25 6 8 51 8 2 4 0.778
3 39 9 1 22 1 2 4 0.777
4 32 8 1 21 2 2 4 0.772
5 10 6 5 32 3 1 3 0.769
6 22 7 2 30 9 1 4 0.769
7 28 6 10 25 5 1 4 0.769
8 30 7 9 33 2 2 4 0.768
9 40 9 2 48 10 2 4 0.768
10 23 9 1 2 10 2 4 0.767
$repaired
Round numFeature r nh fact th1 th2 Value
1 39 7 8 39 8 1 4 0.782
2 2 5 8 50 3 2 3 0.775
3 3 12 6 7 8 1 1 0.769
4 24 5 10 45 5 2 3 0.769
5 10 7 8 40 2 1 4 0.768
6 13 5 8 40 2 2 4 0.768
7 9 6 9 13 2 2 3 0.766
8 19 5 7 46 6 2 1 0.765
9 40 9 8 50 6 1 4 0.764
10 20 9 3 28 9 1 3 0.763
$removed
Round numFeature r nh fact th1 th2 Value
1 40 7 2 39 8 1 3 0.786
2 13 5 3 48 3 2 3 0.776
3 8 5 6 18 1 1 1 0.772
4 5 5 10 24 3 1 3 0.771
5 29 13 7 1 1 1 4 0.771
6 9 7 3 25 7 1 4 0.770
7 17 9 2 17 1 1 4 0.770
8 19 7 7 25 2 1 3 0.768
9 4 10 6 19 7 1 3 0.765
10 2 4 4 47 7 2 3 0.764
$relabeled
Round numFeature r nh fact th1 th2 Value
1 7 8 1 13 1 2 4 0.778
2 26 8 1 19 6 2 4 0.768
3 3 6 3 45 4 2 2 0.766
4 20 6 2 40 10 2 2 0.766
5 13 4 3 18 2 2 3 0.762
6 10 10 6 4 8 1 3 0.761
7 31 11 10 16 1 2 4 0.760
8 15 13 7 7 1 2 3 0.759
9 5 7 3 20 2 1 4 0.758
10 9 9 3 22 8 2 3 0.758 Мы видим незначительное улучшение качества. Лучшие гиперпараметры для каждой группы данных сильно отличаются от гиперпараметров, полученных при предыдущей оптимизации без учета различной комбинации порогов. Лучшие показатели качества мы наблюдаем для групп данных с переразмеченными (repaired ) и с удаленными (removed) шумовыми примерами.
#---best.param------------------- evalq({ foreach(i = 1:4, .combine = "rbind") %do% { OPT_Res_m[[i]]$Best_Par %>% unname() } -> best.par_m dimnames(best.par_m) <- list(group, qc(numFeature, r, nh, fact, th1, th2)) }, env) # > env$best.par_m------------------------ # numFeature r nh fact th1 th2 # origin 8 3 41 2 2 4 # repaired 7 8 39 8 1 4 # removed 7 2 39 8 1 3 # relabeled 8 1 13 1 2 4
Скрипты из этого раздела вы можете найти в файле Optim_mVIII.R
8. Объединение нескольких лучших ансамблей в суперансамбль и их выходов
Объединим несколько лучших ансамблей в суперансамбль, а их выходы — каскадно, голосованием простым большинством.
Для начала объединим результаты нескольких лучших ансамблей, полученных при оптимизации. После оптимизации функция возвращает не только лучшие гиперпараметры, но и историю предсказаний в метках классов на всех итерациях. Сформируем суперансамбль из 5 лучших ансамблей в каждой группе данных, и путем простого голосования большинством проверим, улучшатся ли в этом варианте показатели качества классификации.
Последовательность вычислений следующая:
- в цикле идем последовательно по 4 группам данных;
- определяем индексы 5 лучших предсказаний в каждой группе данных;
- объединяем предсказания с этими индексами в датафрейм;
- изменяем во всех предсказаниях метку класса "0" на "-1";
- суммируем построчно эти предсказания;
- переведем эти суммарные значения в метки класса (-1, 0, 1) при условии: если значение больше 3, то класс = 1; если меньше -3, то класс = -1; иначе значение класса = 0
Вот так выглядит скрипт, который выполняет эти вычисления:
#--Index-best-------------------
evalq({
prVot <- vector("list", 4)
foreach(i = 1:4) %do% { #group
best.res_m[[i]]$Round %>% head(5) -> ind
OPT_Res_m[[i]]$Pred %>% dp$select(ind) ->.;
apply(., 2, function(.) ifelse(. == 0, -1, 1)) ->.;
apply(., 1, function(x) sum(x)) ->.;
ifelse(. > 3, 1, ifelse(. < -3, -1, 0))
} -> prVot
names(prVot) <- group
}, env) У нас появился дополнительный, третий класс "0". Если "-1" — это "Sell", "1" — это "Buy" то "0" — это "не знаю". Как реагировать эксперту на этот сигнал, решать пользователю. Можно быть вне рынка, а можно быть в рынке и ничего не делать, ждать нового сигнала к действию. Модели поведения нужно выстраивать и проверять при тестировании эксперта.
Для получения метрик нам нужно:
- в цикле пройтись последовательно по каждой группе данных;
- в актуальном значении целевой Ytest1 заменить метку класса "0" на метку "-1";
- объединить в датафрейм актульную и предсказанную целевую prVot, полученную выше;
- удалить из датафрейма строки, где значение prVot = 0;
- вычислить метрики.
Вычисляем и смотрим результат.
evalq({
foreach(i = 1:4) %do% { #group
Ytest1 ->.;
ifelse(. == 0, -1, 1) ->.;
cbind(actual = ., pred = prVot[[i]]) %>% as.data.frame() ->.;
dp$filter(., pred != 0) -> tabl
Eval(tabl$actual, tabl$pred)
} -> Score
names(Score) <- group
}, env)
env$Score
$origin
$origin$metrics
Accuracy Precision Recall F1
-1 0.806 0.809 0.762 0.785
1 0.806 0.804 0.845 0.824
$origin$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 157 49
1 37 201
Accuracy : 0.8063
95% CI : (0.7664, 0.842)
No Information Rate : 0.5631
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6091
Mcnemar's Test P-Value : 0.2356
Sensitivity : 0.8093
Specificity : 0.8040
Pos Pred Value : 0.7621
Neg Pred Value : 0.8445
Prevalence : 0.4369
Detection Rate : 0.3536
Detection Prevalence : 0.4640
Balanced Accuracy : 0.8066
'Positive' Class : -1
$repaired
$repaired$metrics
Accuracy Precision Recall F1
-1 0.82 0.826 0.770 0.797
1 0.82 0.816 0.863 0.839
$repaired$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 147 44
1 31 195
Accuracy : 0.8201
95% CI : (0.7798, 0.8558)
No Information Rate : 0.5731
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6358
Mcnemar's Test P-Value : 0.1659
Sensitivity : 0.8258
Specificity : 0.8159
Pos Pred Value : 0.7696
Neg Pred Value : 0.8628
Prevalence : 0.4269
Detection Rate : 0.3525
Detection Prevalence : 0.4580
Balanced Accuracy : 0.8209
'Positive' Class : -1
$removed
$removed$metrics
Accuracy Precision Recall F1
-1 0.819 0.843 0.740 0.788
1 0.819 0.802 0.885 0.841
$removed$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 145 51
1 27 207
Accuracy : 0.8186
95% CI : (0.7789, 0.8539)
No Information Rate : 0.6
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.6307
Mcnemar's Test P-Value : 0.009208
Sensitivity : 0.8430
Specificity : 0.8023
Pos Pred Value : 0.7398
Neg Pred Value : 0.8846
Prevalence : 0.4000
Detection Rate : 0.3372
Detection Prevalence : 0.4558
Balanced Accuracy : 0.8227
'Positive' Class : -1
$relabeled
$relabeled$metrics
Accuracy Precision Recall F1
-1 0.815 0.809 0.801 0.805
1 0.815 0.820 0.828 0.824
$relabeled$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 157 39
1 37 178
Accuracy : 0.8151
95% CI : (0.7741, 0.8515)
No Information Rate : 0.528
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6292
Mcnemar's Test P-Value : 0.9087
Sensitivity : 0.8093
Specificity : 0.8203
Pos Pred Value : 0.8010
Neg Pred Value : 0.8279
Prevalence : 0.4720
Detection Rate : 0.3820
Detection Prevalence : 0.4769
Balanced Accuracy : 0.8148
'Positive' Class : -1
#--------------------------------------- Во всех группах качество значительно улучшилось. Лучшие показатели Balanced Accuracy получены в группах removed (0.8227) и repaired (0.8209)
Давайте объединим и групповые предсказания простым голосованием. Выполним каскадное объединение:
- в цикле идем по всем группам данных;
- определяем индексы проходов с лучшими результатами;
- выбираем предсказания этих лучших проходов;
- заменяем в каждом столбце метку класса "0" на метку "-1";
- суммируем построчно предсказания в группе.
Посмотрим получившийся результат:
#--Index-best-------------------
evalq({
foreach(i = 1:4, .combine = "+") %do% { #group
best.res_m[[i]]$Round %>% head(5) -> ind
OPT_Res_m[[i]]$Pred %>% dp$select(ind) ->.;
apply(., 2, function(x) ifelse(x == 0, -1, 1)) ->.;
apply(., 1, function(x) sum(x))
} -> prVotSum
}, env)
> env$prVotSum %>% table()
.
-20 -18 -16 -14 -12 -10 -8 -6 -4 -2 0 2 4 6 8 10 12 14 16 18 20
166 12 4 6 7 6 5 3 6 1 4 4 5 6 5 10 7 3 8 24 209 Оставляем только самые большие значения голосования и вычисляем метрики:
evalq({
pred <- {prVotSum ->.;
ifelse(. > 18, 1, ifelse(. < -18, -1, 0))}
Ytest1 ->.;
ifelse(. == 0, -1, 1) ->.;
cbind(actual = ., pred = pred) %>% as.data.frame() ->.;
dp$filter(., pred != 0) -> tabl
Eval(tabl$actual, tabl$pred) -> ScoreSum
}, env)
env$ScoreSum
> env$ScoreSum
$metrics
Accuracy Precision Recall F1
-1 0.835 0.849 0.792 0.820
1 0.835 0.823 0.873 0.847
$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 141 37
1 25 172
Accuracy : 0.8347
95% CI : (0.7931, 0.8708)
No Information Rate : 0.5573
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6674
Mcnemar's Test P-Value : 0.1624
Sensitivity : 0.8494
Specificity : 0.8230
Pos Pred Value : 0.7921
Neg Pred Value : 0.8731
Prevalence : 0.4427
Detection Rate : 0.3760
Detection Prevalence : 0.4747
Balanced Accuracy : 0.8362
'Positive' Class : -1 Получился очень хороший показатель Balanced Accuracy = 0.8362.
Скрипты, описанные в этом разделе, вы можете найти в файле Voting.R
Но нельзя забывать об одном нюансе. При оптимизации гиперпараметров мы задействовали тестовый набор InputTest. Это значит, что мы можем начать работать со следующего тестового набора InputTest1. Скорее всего, каскадное объединение ансамблей будет давать такой же положительный эффект и без оптимизации гиперпараметров. Проверим это на полученных нами ранее результатах усреднения.
Объединим усредненные выходы ансамблей,полученные в п.5.2.
Повторим вычисления, описанные в п.5.4, с одним изменением. При переводе непрерывного усредненного предсказания в метки классов этими метками будут [-1, 0, 1]. Последовательность вычисления в каждом поднаборе train/test/test1:
- последовательно в цикле проходим по 4 группам данных;
- по 4 типам порогов обрезки;
- по 4 типам порогов усреднения;
- переводим непрерывное усредненное предсказание ансамбля в метки классов [-1, 1];
- суммируем их по 4 типам порогов усреднения;
- переразмечаем просуммированное новыми метками [-1, 0, 1];
- добавляем в структуру VotAver полученный результат.
#---train------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) VotAver <- vector("list", 4) names(VotAver) <- group while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Train.clVoting dimnames(VotAver[[k]]$Train.clVoting) <- list(NULL, type) k <- k + 1 } }, env) #---test------------------------------ evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Test.clVoting dimnames(VotAver[[k]]$Test.clVoting) <- list(NULL, type) k <- k + 1 } }, env) #---test1------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Test1.clVoting dimnames(VotAver[[k]]$Test1.clVoting) <- list(NULL, type) k <- k + 1 } }, env)
Определив переразмеченные усредненные предсказания в поднаборах и группах, вычислим их метрики. Последовательность расчетов:
- в цикле проходим по группам;
- в цикле идем по 4 типам порогов усреднения;
- изменяем в актуальном предсказании метку класса "0" на "-1";
- объединяем в датафрейм актуальное и переразмеченное предсказание;
- удаляем из датафрейма строки, в которых предсказание равно 0;
- вычисляем метрики и добавляем их в структуру VotAver.
#---Metrics--train------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Train.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$TrainScoreVot names(VotAver[[k]]$TrainScoreVot) <- type k <- k + 1 } }, env) #---Metrics--test------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest1 ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$TestScoreVot names(VotAver[[k]]$TestScoreVot) <- type k <- k + 1 } }, env) #---Metrics--test1------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest2 ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test1.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$Test1ScoreVot names(VotAver[[k]]$Test1ScoreVot) <- type k <- k + 1 } }, env)
Соберем данные в читабельный вид и посмотрим на них:
#----TrainScoreVot-------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$TrainScoreVot %>% unlist() %>% unname()
} -> TrainScoreVot
dimnames(TrainScoreVot) <- list(group, type)
}, env)
> env$TrainScoreVot
half med mce both
origin 0.738 0.750 0.742 0.752
repaired 0.741 0.743 0.741 0.741
removed 0.748 0.755 0.755 0.755
relabeled 0.717 0.741 0.740 0.758
#-----TestScoreVot----------------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$TestScoreVot %>% unlist() %>% unname()
} -> TestScoreVot
dimnames(TestScoreVot) <- list(group, type)
}, env)
> env$TestScoreVot
half med mce both
origin 0.774 0.789 0.797 0.804
repaired 0.777 0.788 0.778 0.778
removed 0.801 0.808 0.809 0.809
relabeled 0.773 0.789 0.802 0.816
#----Test1ScoreVot--------------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$Test1ScoreVot %>% unlist() %>% unname()
} -> Test1ScoreVot
dimnames(Test1ScoreVot) <- list(group, type)
}, env)
> env$Test1ScoreVot
half med mce both
origin 0.737 0.757 0.757 0.755
repaired 0.756 0.743 0.754 0.754
removed 0.759 0.757 0.745 0.745
relabeled 0.734 0.705 0.697 0.713
Лучшие результаты были показаны на тестовом поднаборе в группе данных removed, с вариантом обработки шумовых примеров.
Еще раз объединим результаты в каждом поднаборе каждой группы данных по типам усреднения.
#==Variant-2========================================== #--TrainScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Train.clVoting ->.; apply(., 1, function(x) sum(x)) ->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Train.clVotingSum ifelse(Ytest == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Train.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$TrainScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env) #--TestScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Test.clVoting ->.; apply(., 1, function(x) sum(x))->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test.clVotingSum ifelse(Ytest1 == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$TestScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env) #--Test1ScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Test1.clVoting ->.; apply(., 1, function(x) sum(x))->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test1.clVotingSum ifelse(Ytest2 == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test1.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$Test1ScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env)
Соберем в читаемый вид результаты.
evalq({
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$TrainScoreVotSum %>% unlist() %>% unname()
} -> TrainScoreVotSum
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$TestScoreVotSum %>% unlist() %>% unname()
} -> TestScoreVotSum
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$Test1ScoreVotSum %>% unlist() %>% unname()
} -> Test1ScoreVotSum
ScoreVotSum <- cbind(TrainScoreVotSum, TestScoreVotSum, Test1ScoreVotSum)
dimnames(ScoreVotSum ) <- list(group, qc(TrainScoreVotSum, TestScoreVotSum,
Test1ScoreVotSum))
}, env)
> env$ScoreVotSum
TrainScoreVotSum TestScoreVotSum Test1ScoreVotSum
origin 0.763 0.807 0.762
repaired 0.752 0.802 0.748
removed 0.761 0.810 0.765
relabeled 0.766 0.825 (!!) 0.711 Рассматриваем результаты тестового поднабора. Лучший результат неожиданно оказался у метода relabeled. Результаты во всех группах намного лучше полученных в п.5.4. Каскадный метод обединения выходов ансамблей голосованием простым большинством дает улучшение качества классификации (Accuracy) от 5% до 7%.
Скрипты из этого раздела находятся в файле Voting_aver.R. Структура полученных данных приведена на рисунке ниже:

Рис. 10. Структура данных VotAver.
На рисунке ниже дана упрощенная схема всех вычислений: указаны этапы, применяемые скрипты и структуры данных.
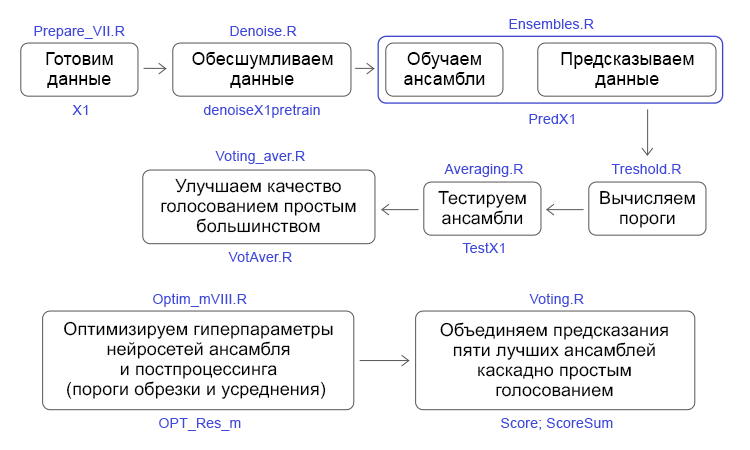
Рис. 11. Структура и последовательность основных вычислений в статье.
8. Анализ результатов экспериментов
Мы обработали шумовые примеры в исходных наборах данных в поднаборах pretrain (!) тремя способами:
- переразметили "ошибочно" размеченные данные без изменения количества классов (repaired);
- убрали из поднабора "шумовые" примеры (removed);
- выделили "шумовые" примеры в отдельный класс (relabeled).
Получены 4 группы данных (origin, repaired, removed, relabeled) в структуре denoiseX1pretrain. Обучаем на них ансамбль из 500 нейросетевых классификаторов ELM. Получаем четыре ансамбля. Рассчитаем непрерывные предсказания трех поднаборов Х1$train/test/test1 этими 4 ансамблями и соберем их в структуру predX1.
Затем рассчитаем 4 типа порогов для непрерывных предсказаний каждой из 500 нейросетей каждого ансамбля на поднаборе InputTrain (!). Используя эти пороги, переводим непрерывные предсказания в метки классов (0, 1). Вычисляем метрики (mean(F1)) для каждой нейросети ансамблей и собираем их в структуре testX1$$(InputTrainScore|InputTestScore|InputTest1Score). Визуализация распределения метрик в 4 группах данных и 3 поднаборах показывает:
- во-первых, метрики на первом тестовом поднаборе выше, чем на InputTrainScore во всех группах;
- во-вторых, в группах repaired и removed метрики визуально выше, чем в двух других.
Теперь выбираем 7 лучших нейросетей с наибольшими значениями mean(F1) в каждом ансамбле и усредняем их непрерывные предсказания. Добавим их значения в структуру testX1$$(TrainYpred|TestYpred|Test1Ypred). Вычислив пороги th_aver на поднаборе TrainYpred, определяем метрики всех усредненных непрерывных предсказаний и добавляем их в структуру testX1$$(TrainScore|TestScore|Test1Score). Теперь их можно проанализировать.
При различном сочетании порогов обрезки и усреднения в различных группах данных получаем метрики в диапазоне 0.75 — 0.77. Наилучший результат был получен в группе removed с удаленными "шумовыми" примерами.
Оптимизация гиперпараметров нейросетей ансамблей дает стабильное повышение метрик во всех группах до 0.77+.
Оптимизация гиперпараметров нейросетей и порогов постпроцессинга (обрезки и усреднения) дает стабильно высокий результат во всех группах с обработанными "шумовыми" примерами в районе 0.78+.
Создадим из нескольких ансамблей с оптимальными гиперпараметрами суперансамбль, возьмем предсказания этих ансамблей и объединим их голосованием простым большинством в каждой группе данных. В результате получим метрики в группах repaired и removed в диапазоне 0.82+. Объединив и эти предсказания суперансамблей простым голосованием, получим окончательное значение метрики 0.836. Таким образом, каскадное объединение предсказаний простым голосованием дает повышение качества на 6-7%.
Проверим это утверждение на полученных ранее усредненных предсказаниях ансамблей. Повторив вычисления и преобразования в группах, получим в группе removed поднабора Test метрики 0.8+. Продолжив каскадное объединение, получим метрики со значениями 0,8+ в поднаборе Test во всех группах данных.
Можно сделать вывод о том, что каскадное объединение предсказаний ансамблей простым голосованием действительно значительно улучшает качество классификации.
Заключение
В статье мы рассмотрели три метода повышения качества bagging-ансамблей, а также оптимизацию гиперпараметров нейросетей ансамблей и постпроцессинга. По результатам экспериментов можно сделать следующие выводы:
- обработка шумовых примеров методами repaired и removed улучшает качество классификации ансамблей;
- выбор типа порогов обрезки и усреднения, а также их комбинация значительно влияют на качество классификации;
- объединение нескольких ансамблей в суперансамбль с каскадным объединением их предсказаний проcтым голосованием дает наибольшее увеличение качества классификации;
- оптимизация гиперпараметров нейросетей ансамблей и постпроцессинга незначительно улучшают показатели качества классификации. Целесообразно проводить первую оптимизацию на новых данных, а затем повторять ее периодически при снижении качества. Периодичность определяется опытным путем.
Приложения
В GitHub/PartVIII находятся следующие файлы:
- Importar.R — функции импорта пакетов.
- Library.R — необходимые библиотеки.
- FunPrepareData_VII.R — функции подготовки исходных данных.
- FunStacking_VIII.R — функции создания и тестирования ансамбля.
- Prepare_VIII.R — функции и скрипты подготовки исходных данных для обучаемых объединителей.
- Denoise.R — скрипты обработки шумовых примеров
- Ensemles.R — скрипты создания ансамблей
- Threshold.R — скрипты определения порогов
- Test.R - скрипты тестирования ансамблей
- Averaging.R - скрипты усреднения непрерывных выходов ансамблей
- Voting_aver.R - объединение усредненых выходов каскадно простым голосованием
- Optim_VIII.R - скипты оптимизации гиперпараметров нейросетей
- Optim_mVIII.R - скипты оптимизации гиперпараметров нейросетей и постпроцессинга
- Voting.R - каскадное объединение выходов суперансамбля простым голосованием
- SessionInfo_VII.txt — перечень пакетов, использованных в скриптах статьи.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Графический конструктор стратегий. Создание торговых роботов без программирования
Графический конструктор стратегий. Создание торговых роботов без программирования
 Интеграция эксперта на MQL и базы данных (SQL Server, .NET и C#)
Интеграция эксперта на MQL и базы данных (SQL Server, .NET и C#)
 Написание биржевых индикаторов с контролем объема на примере индикатора дельты
Написание биржевых индикаторов с контролем объема на примере индикатора дельты
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Выбрав 7 лучших ансамблей и классифицировав их[=1,0,1], я хотел бы извлечь данные для обучения на модели Keras, но не могу найти нужные кадры данных.
На рисунке 11 показана структурная схема вычислений. Над каждым этапом находится название скрипта. Под каждым этапом - название результирующей структуры данных. Какие данные вы хотите использовать?
Если вы хотите использовать усредненные непрерывные предсказания семи лучших ансамблей, то они имеют структуру
k = c(origin/repaired/removed/relabeled)
j = c( half, mean, med, both)
Если вам нужны предсказания семи лучших в двоичной форме, то они находятся в структуре
Здравствуйте еще раз,
Я получаю следующие ошибки, которые я не могу решить - любые советы?
Ошибка 1: "in { : task 1 failed - "object 'History' not found"", когда я запускаю следующий сегмент кода:
#---OptPar------ evalq({ foreach(i = 1:4) %do% { OPT_Res[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3) } -> best.res names(best.res) <- group }, env) evalq({ foreach(i = 1:4) %do% { OPT_Res1[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3) } -> best.res1 names(best.res1) <- group }, env)Не уверен, где создается объект History, и вообще не смог найти его в репозитории github в различных .R файлах для этой статьи.
Ошибка 2: "Yts" не найден, когда я выполняю следующий сегмент кода:
Также не уверен, когда/как создается "Yts".
Я думаю, что обе эти проблемы могут быть решены с помощью фрагмента кода, который может отсутствовать в репо на github?
Буду признателен за любую помощь, которую вы можете предоставить, заранее спасибо.