Глубокие нейросети (Часть IV). Создание, обучение и тестирование модели нейросети
10 384
27
Оглавление
- Введение
- 1. Краткое описание возможностей пакета
- 1.1. Функции начальной инициализации нейронов
- 1.2. Функции активации нейронов
- 1.3. Методы обучения
- 1.4. Методы регуляризации и стабилизации
- 1.5. Методы и параметры обучения RBM
- 1.6. Методы и параметры обучения DNN
- 2. Проверка качества работы DNN в зависимости от применяемых параметров
- 2.1. Эксперименты
- 2.1.1. Входные данные (подготовка)
- 2.1.2. Базовая модель сравнения
- 2.1.3. Структура DNN
- 2.1.4. Варианты обучения
- 2.2. Анализ результатов
- Заключение
- Приложения
Введение
Основные направления исследования и применения
В настоящее время в исследовании и применении глубоких нейросетей образовались два основных течения. Они различаются подходом к начальной инициализации весов нейронов в скрытых слоях.
Подход № 1. Нейросети чрезвычайно чувствительны к способу начальной инициализации нейронов в скрытых слоях, особенно при увеличении количества скрытых слоев (выше 3). Первым решить эту проблему попытался профессор G.Hynton. Суть его предложения: инициировать веса нейронов в скрытых слоях весами, полученными при обучении без учителя автоассоциативных сетей, составленных из RBM (ограниченная машина Больцмана) или AE (автоэнкодера). Эти Stacked RBM (SRBM) и Stacked AE (SAE) обучаются на большом массиве неразмеченных данных. Цель такого обучения — выявить скрытые структуры (представления, образы) и зависимости в данных. Инициализация нейронов MLP весами, полученными при претренинге, помещает MLP в пространство решений, наиболее приближенное к оптимальному. Это дает возможность при последующей тонкой настройке (обучении) MLP уменьшить количество размеченных данных и эпох обучения. Для многих областей практического применения (особенно при обработке "больших данных") это критически важные преимущества.
Подход № 2: Другая группа ученых под руководством Иешуа Бенджио разработала специфические методы начальной инициализации скрытых нейронов, специальные функции активации, методы стабилизации и обучения. Успехи в этом направлении связаны с бурным развитием глубоких сверточных и рекуррентных нейросетей (DCNN, RNN). Такие нейросети показали максимальную эффективность в распознавании изображений, анализе и классификации текстов и переводе живой речи с одного языка на другой. Идеи и методы, разработанные для этих нейросетей, с успехом стали применяться и для MLP.
Сегодня оба направления активно используются на практике. Однако нейросети с претренингом требуют меньше примеров для обучения и вычислительных ресурсов при практически равных результатах. Это важное преимущество. Я сторонник направления глубоких нейросетей с предобучением. По моему мнению, будущее — за обучением без учителя.
Пакеты в языке R, позволяющие разрабатывать и практически использовать DNN
Для создания и использования DNN с различным уровнем сложности и возможностей в языке R разработан ряд пакетов.
Пакеты позволяющие создавать, обучать и тестировать DNN с претренингом:
- deepnet — простой, не обремененный множеством параметров и настроек пакет. Позволяет создавать как нейросети с предобучением SAE, так и SRBM. В предыдущей статье мы рассматривали практическую реализацию экспертов с применением этого пакета. Применение RBM для претренинга дает менее стабильные результаты. Пакет предназначен для первоначального ознакомления с темой и изучения особенностей работы таких нейросетей. При правильном подходе вполне может использоваться в экспертах. RcppDL — версия этого пакета (немного урезанная ) на С++.
- darch v.0.12 — сложный, гибкий, имеющий множество параметров, режимов и настроек пакет (рекомендованные значения по умолчанию установлены). Позволяет построить и настроить нейросеть любой сложности и конфигурации. Для претренинга используется SRBM. Пакет предназначен для подготовленных пользователей. Ниже мы детально поговорим о его возможностях.
Пакеты позволяющие создавать, обучать и тестировать DNN без претренинга:
- H2O — пакет для обработки "больших данных" (>1M строк и >1K колонок). Используемая в нем глубокая нейросеть имеет развитую систему регуляризации. Возможности для нашей области применения избыточны, но это не запрещает нам его применять.
- mxnet позволяет создавать не только MLP, но и сложные рекуррентные сети, сверточные и LSTM нейросети. Пакет имеет API для нескольких языков, в том числе для R и Python. Идеология пакета сильно отличается от вышеперечисленных. Это обусловлено тем, что разработчики в основном писали пакеты для Python. Пакет mxnet для R облегчен и имеет чуть меньшую функциональность, по сравнению с пакетом для Python. Но это не умаляет его достоинств.
В среде Python тема глубоких и рекуррентных сетей широко разработана. Есть много интересных пакетов для построения таких типов нейросетей, которых в R просто нет. Вот пакеты в R, которые позволяют исполнять программы/модули, написанные на Python:
- PythonInR и reticulate — два пакета, дающие возможность исполнять любой код Python в R. Для этого нужно иметь инсталлированный на вашем компьютере Python 2/3.
- kerasr — R-интерфейс к популярной библиотеке глубокого обучения keras.
- tensorflow — пакет, предоставляющий доступ к полному TensorFow API в среде R.
Недавно компания Microsoft выложила библиотеку cntk v.2.1(Computatinal Network Toolkit) GitHub, и теперь она может использоваться как backend для Keras, с которым R "дружит". Желательно протестировать ее в наших задачах.
Не отстает и Яндекс: в open source выложена его собственная библиотека CatBoost. С ее помощью можно эффективно обучать модели на разнородных данных, в том числе таких, которые трудно представить в виде чисел (например, виды облаков или категории товаров). Исходный код, документация, бенчмарки и необходимые инструменты уже опубликованы на GitHub под лицензией Apache 2.0. Несмотря на то, что это не нейросети а бустинговые деревья, тест-драйв алгоритма желательно провести, тем более, что в нем реализован API из R.
1. Краткое описание возможностей пакета
Пакет darch ver. 0.12.0 предоставляет широкий круг функций, позволяющих не просто создать и обучить модель, но буквально по кирпичикам сложить и настроить её под Ваши предпочтения. По сравнению с предыдущей версией пакета (0.10.0), которую мы рассматривали в предыдущей статье, произошли значительные изменения. Добавлены новые функции активации, инициализации и стабилизации, но главное — все сведено в одну функцию darch(), которая одновременно является и конструктором. Поддерживается использование графических карт. После обучения модели функция возвращает объект класса DArch. Структура объекта представлена на рис.1. Функции predict() и darchTest() возвращают предсказание по новым данным или метрики классификации.
Рис.1. Структура объекта DArch
Все параметры имеют значения по умолчанию, как правило, неоптимальные. Всё это море параметров можно объединить в три группы: общие, для RBM, для NN. Ниже рассмотрим некоторые из них подробнее.
| Функции | Виды |
|---|---|
| Функции инициализации |
|
| Функции активации |
|
| Функции обучения |
|
| Уровень обучения |
|
| Функции стабилизации |
|
| Момент |
|
| Условия остановки |
|
Глубокая нейросеть состоит из n-го количества RBM (n = layers -1), сложенных в автоассоциативную сеть (SRBM), и собственно нейросети MLP с количеством слоев layers. Послойное предобучение RBM проводится на неразмеченных данных без учителя. Тонкое обучение нейросети проводится с учителем на размеченных данных.
Разделение этих стадий обучения с помощью параметров дает нам возможность использовать различные по объему (но не по структуре!) данные или получить несколько различных тонко обученных моделей на базе одного предобучения. Кроме того, если данные для предобучения и тонкой настройки одинаковы, возможно провести обучение одним ходом без разделения на две стадии. Можно пропустить предобучение (rbm.numEpochs = 0; darch.numEpochs = 10)) и использовать только многослойную нейросеть или, наоборот, обучить только RBM (rbm.numEpochs = 10; darch.numEpochs = 0). При этом у нас есть доступ ко всем внутренним параметрам.
Обученную нейросеть можно в последующем дообучать на новых данных неограниченное количество раз. Очень немногие модели предоставляют такую возможность. Структурная схема глубокой нейросети, инициализируемой сложенными ограниченными машинами Больцмана (DNRBM), приведена на рис.2.
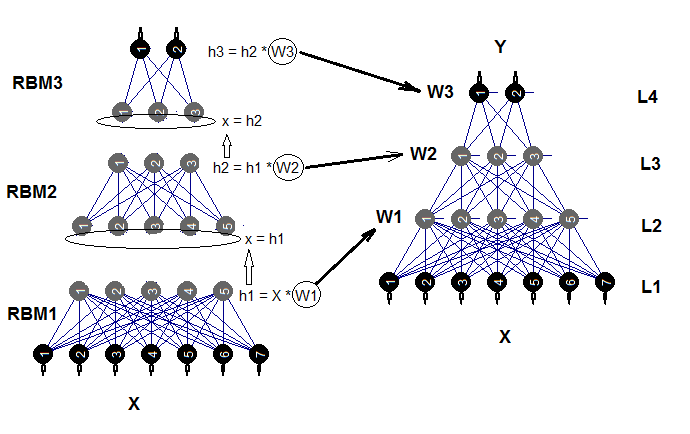
Рис.2. Структурная схема DNSRBM
1.1. Функции начальной инициализации нейронов
В пакете использованы две основных функции инициализации нейронов.
- generateWeightsUniform() использует функцию runif(n, min, max) и реализована так:
> generateWeightsUniform function (numUnits1, numUnits2, weights.min = getParameter(".weights.min", -0.1, ...), weights.max = getParameter(".weights.max", 0.1, ...), ...) { matrix(runif(numUnits1 * numUnits2, weights.min, weights.max), nrow = numUnits1, ncol = numUnits2) } <environment: namespace:darch>
Здесь numUnits1 — количество нейронов в предыдущем слое, а numUnits2 — количество нейронов в текущем слое.
- generateWeightsNormal() использует функцию rnorm(n, mean, sd) и реализована в пакете так:
> generateWeightsNormal function (numUnits1, numUnits2, weights.mean = getParameter(".weights.mean", 0, ...), weights.sd = getParameter(".weights.sd", 0.01, ...), ...) { matrix(rnorm(numUnits1 * numUnits2, weights.mean, weights.sd), nrow = numUnits1, ncol = numUnits2) } <environment: namespace:darch>
Остальные четыре функции используют эти две, но определяют min, max, mean и sd специфическими формулами. С ними вы можете познакомиться, вызвав в терминале имя функции без скобок.
1.2. Функции активации нейронов
Наряду со стандартными функциями активациями, пакет предлагает широкий набор новых. Вот некоторые из них:
x <- seq(-5, 5, 0.1) par(mfrow = c(2,3)) plot(x, y = 1/(1 + exp(-x)), t = "l", main = "sigmoid") abline(v = 0, col = 2) plot(x, y = tanh(x), t = "l", main = "tanh") abline(v = 0, h = 0, col = 2) plot(x, y = log(1 + exp(x)), t = "l", main = "softplus"); abline(v = 0, col = 2) plot(x, y = ifelse(x > 0, x ,exp(x) - 1), t = "l", main = "ELU") abline(h = 0, v = 0, col = 2) plot(x, y = ifelse(x > 0, x , 0), t = "l", main = "ReLU") abline(h = 0, v = 0, col = 2) par(mfrow = c(1,1))
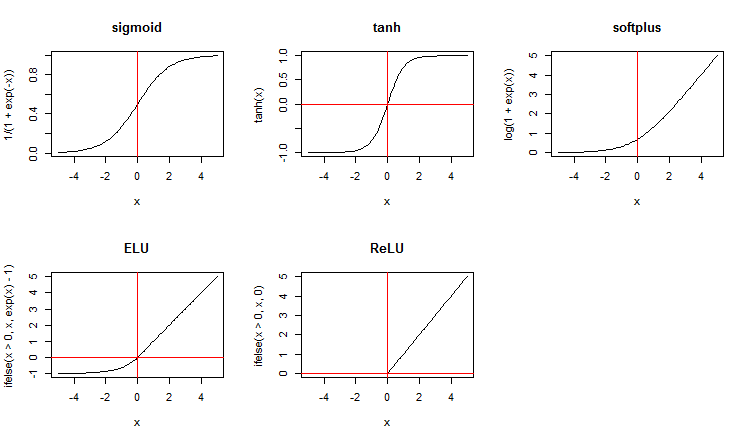
Рис.3. Функции активации нейронов
Рассмотрим отдельно функцию активации — maxout. Функция пришла из сверточных сетей. Скрытый слой нейросети разделяется на модули размером poolSize. Количество нейронов в скрытом слое должно быть кратным размеру пула. При обучении из пула выбирается нейрон с максимальной активацией и подается на выход. Функция активации нейронов в пуле задается отдельно. Проще говоря, это сдвоенный слой (сверточный + maxpooling) с ограниченными возможностями по шагу фильтра. По данным в публикациях показывает хорошие результаты в паре с dropout. На рис. 4. схематически показан скрытый слой с 8 нейронами и двумя размерами пула.
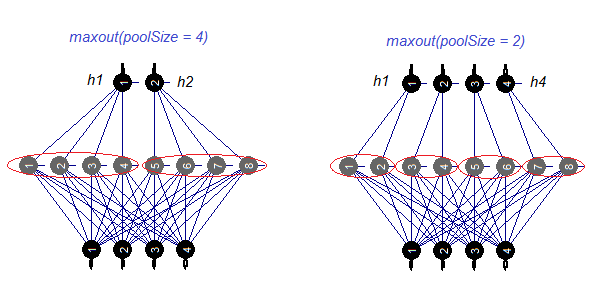
Рис.4. Функция активации maxout
1.3. Методы обучения
К сожалению, в пакете представлены только два метода обучения — backpropagation и rprop базовой и улучшенной версии с обновлением весов при обратном распространении и без него. Предусмотрена возможность изменения уровня обучения с помощью множителя bp.learnRateScale.
1.4. Методы регуляризации и стабилизации
- dropout — отсев (обнуление веса) части нейронов скрытого слоя при обучении. Нейроны обнуляются в случайном порядке, относительное количество нейронов, подлежащих отсеву, задается параметром darch.dropout. Уровень отсева в каждом скрытом слое может быть различным. Маску отсева можно генерировать для каждой мини-выборки (batch) или для каждой эпохи.
- dropconnect — отключение связи между частью нейронов текущего слоя с нейронами предыдущего слоя. Связи обрезаются в случайном порядке, относительное количество связей, подлежащих обрезанию, задается тем же параметром darch.dropout (как правило, не более 0.5). По некоторым публикациям показывает результат лучше, чем dropout.
- dither — способ предотвращения переобучения путем размыва (dithering) входных данных.
- weightDecay — вес каждого нейрона будет умножен на (1 — weightDecay) перед обновлением.
- normalizeWeights — нормализовать входящий вектор весов нейронов с возможным ограничением сверху (L2 norm)
Первые три метода применяются только раздельно.
1.5. Методы и параметры обучения RBM
Есть два способа обучения SRBM: обучать RBM по одному за rbm.numEpochs или поочередно тренировать каждый RBM по одной эпохе за раз. Выбор одного из этих способов обеспечивается параметром rbm.consecutive: TRUE или default — первый способ, FALSE — второй. На рис.5 представлена схема обучения в двух вариантах. С помощью параметра rbm.lastLayer мы можем указать, на каком слое SRBM нужно остановить предобучение. Если 0 — обучаем все слои, если (-1) — верхний слой не обучаем. Это имеет смысл, поскольку верхний слой нейросети нужно обучать отдельно и более длительно. Остальные параметры понятны без дополнительных пояснений.
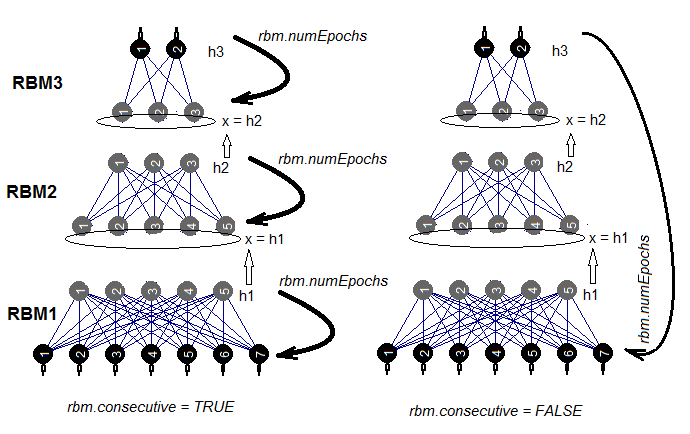
Рис.5. Два метода обучения SRBM
1.6. Методы и параметры обучения DNN
DNN можно обучать двумя способами: с претренингом и без него. Эти два способа кардинально отличаются по используемым параметрам. Так, для обучения с претренингом нет никакого смысла использовать специфические способы инициализации и регуляризации. Более того, их применение может ухудшить результат. Дело в том, что после претренинга веса нейронов скрытых слоев будут помещены в область, близкую к оптимальным значениям, и им понадобится совсем небольшая тонкая настройка. И напротив, чтобы получить такой же результат, при обучении без претренинга нужно будет использовать все доступные способы инициализации и регуляризации. Как правило, обучение по этому способу занимает больше времени.
Итак, нас интересует обучение с претренингом. Как правило, оно делится на 2 этапа.
- Обучение SRBM на большом наборе неразмеченных данных. Параметры претренинга задаем отдельно. В результате получаем нейросеть, иницированную весами SRBM. Затем обучаем верхний слой нейросети на размеченных данных со своими параметрами обучения. В результате получаем нейросеть с обученным верхним слоем и инициированными весами в нижних слоях. Сохраним ее как самостоятельный объект для использования в дальнейшем.
- На втором этапе тонкой настройки применяем совсем немного размеченных примеров, низкий уровень обучения и небольшое количество эпох обучения для всех слоев нейросети — тонко отшлифуем сеть. Обученная нейросеть готова.
Возможность разделения этапов претренинга, тонкого тренинга и последующих дообучений дает невероятную гибкость в построении алгоритмов обучения не только одной DNN, но и, что более важно, в обучении комитетов DNN. На рис.6. представлена несколько вариантов обучения DNN и комитетов DNN.
- Вариант а: при тонкой настройке сохраняем DNN через каждые n эпох. Таким образом получим ряд DNN с различной степенью обучения. Мы можем в последующем использовать каждую из них в отдельности или в составе комитета. Недостаток этого варианта состоит в том, что все DNN обучаются на одних и тех же данных, ведь параметры обучения у них всех одинаковы.
- Вариант б: инициированную DNN параллельно тонко настраиваем с различными наборами данных (скользящее окно, растущее окно и т.п.) и различными параметрами. Получим комитет DNN, который будет выдавать менее коррелированные предсказания, чем по варианту а.
- Вариант в: инициированную DNN последовательно тонко настраиваем с различными наборами данных и различными параметрами, сохраняя промежуточные модели. Это и есть дообучение, которое можно проводить постоянно по мере поступления достаточной порции новых данных.
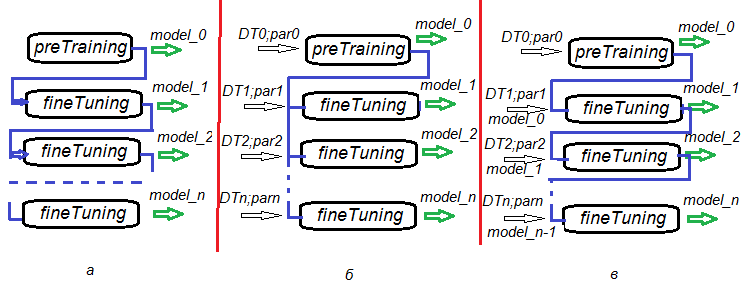
Рис.6. Варианты обучения DNN
2. Проверка качества работы DNN в зависимости от применяемых параметров.
2.1. Эксперименты
2.1.1. Входные данные (подготовка)
Будем использовать данные и функции из предыдущих частей статьи (1, 2, 3) . В них мы довольно подробно рассмотрели различные варианты предподготовки данных. Поэтому здесь я совсем коротко обозначу этапы предподготовки, которые мы будем выполнять. Исходные данные — OHLCV, те же, что и раньше. Входные данные — цифровые фильтры, выходные — ZigZag. Можно использовать функции и снимок рабочего пространства Cotir.RData.
Этапы подготовки данных, которые будут выполняться укрупнены в отдельные функции:
- PrepareData() — создаем начальный набор данных dataSet, очищаем его от NA;
- SplitData() — разделяем начальный набор dataSet на поднаборы pretrain, train, val, test;
- CappingData() — определяем и импутируем выбросы во всех поднаборах.
Во избежание загромождения статьи листинг этих функций приводить не буду. Их можно скачать с GitHub; кроме того, они подробно разобраны в предыдущих частях. Результаты выполнения рассмотрим ниже. Также не будем рассматривать все способы трансформации при препроцессинге. Многие из них широко известны и широко используются. Остановимся на менее известном и реже применяемом — это дискретизация (с учителем и без). Во второй части статьи были рассмотрены два пакета дискретизации с учителем (discretization и smbinning). В них используются различные алгоритмы для дискретизации.
Рассмотрим разные методы разделения непрерывных переменных на диапазоны, а также то, как использовать эти дискретизированные переменные в моделях.
Что такое биннинг?
Биннинг — это термин, используемый при моделировании баллов (scoring modeling). Также в машинном обучении он известен как Discretization, процесс преобразования непрерывной переменной в конечное число интервалов (диапазонов). Это помогает лучше понять его распределение и связь с двоичной целевой переменной. Диапазоны (bins), созданные в процессе, могут стать атрибутами предсказательной характеристики для использования в моделях.
Почему биннинг?
Несмотря на сдержанное отношение к биннингу, у него есть и неоспоримые преимущества.
- Он позволяет применять пропущенные данные (NA) и другие специальные вычисления (например, деленные на ноль) для включения в модель.
- Он контролирует или смягчает воздействие выбросов на модель.
- Он решает проблему наличия разных масштабов среди предикторов, делая весовые коэффициенты в конечной модели сопоставимыми.
Дискретизация без учителя
Unsupervised Discretization делит непрерывную функцию на диапазоны без учета любой другой информации. Это раздел с двумя опциями: интервалы равной длины и интервалы равной частоты.
| Опция | Цель | Пример | Недостаток |
|---|---|---|---|
| Интервалы равной длины | Понять распределение переменной | Классическая гистограмма, чьи бункеры имеют равную длину, которые могут быть рассчитаны с использованием разных правил (Sturges, Rice и т.д.) | Количество записей в бункере может быть слишком малым для проведения корректного расчета |
| Интервалы равной частоты | Проанализировать взаимосвязь с бинарной целевой переменной с помощью таких показателей, как bad rate | Quartilies или Percentiles | Выбранные точки отсечения не могут максимизировать разницу между диапазонами при сопоставлении с целевой переменной |
Дискретизация с учителем
Дискретизация с учителем делит непрерывную переменную на диапазоны (бины), отображаемые на целевую переменную. Основная идея состоит в том, чтобы найти такие точки разделения, которые максимизируют разницу между группами.
Сегодня с помощью различных алгоритмов, таких например как ChiMerge или Recursive Partitioning, аналитики могут быстро найти оптимальные точки за секунды и оценить взаимосвязь с целевой переменной, используя такие показатели, как вес фактических данных (Weight of Evidence, WoE) и информационная ценность (Information Value, IV).
WoE может использоваться как инструмент для трансформации предикторов на этапе препроцессинга для алгоритмов обучения с учителем. При дискретизации предикторов мы можем заменить их на новые номинальные переменные либо на значения их WoE. Второй вариант интересен тем, что позволяет уйти от преобразования номинальных переменных (факторов) в dummy, что дает, по некоторым данным, значимый прирост в качестве классификации.
WOE и IV играют две разные роли при анализе данных:
- WOE описывает взаимосвязь между предсказательной переменной и бинарной целевой переменной.
- IV измеряет силу этих отношений.
Разберем, что такое WOE и IV, в картинках и формулах. Вспомним график переменной v.fatl, разбитой на 10 равночастотных участков из второй части статьи.
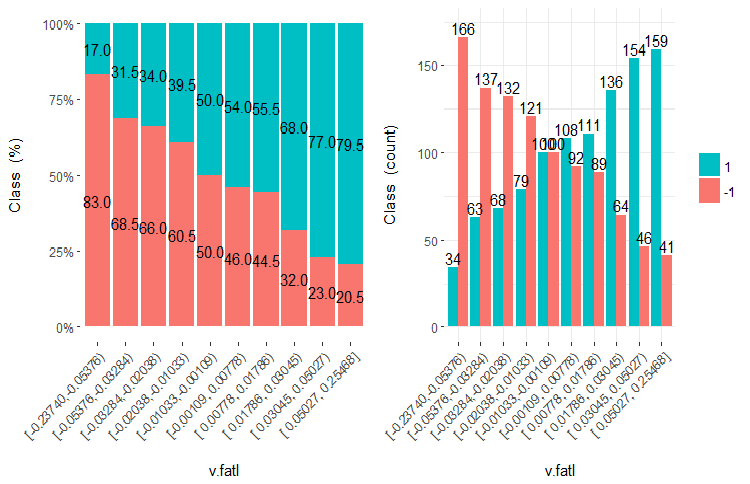
Рис.7. Переменная v.fatl, разбитая на 10 равночастотных участков
Предсказательная способность данных (WOE)
Как можно видеть, в каждом диапазоне есть примеры, которые попадают как в класс "1", так и в класс "-1". Предсказательная способность диапазонов WoEi вычисляется по формуле
WoEi = ln(Gi/Bi)*100
где:
Gi — относительная частота "хороших" (в нашем случае "хорошие" = "1") примеров в каждом диапазоне переменной;
Bi — относительная частота "плохих" (в нашем случае "плохие" = "-1") примеров в каждом диапазоне переменной.
Если WoEi = 1 , т.е. "хороших" и "плохих" примеров в этом диапазоне приблизительно равное количество, то предсказательная способность этого диапазона равна 0. Если "хороших" больше, то WOE >0 и наоборот.
Информационное значение (IV)
Самая распространенная мера определения значимости переменных и измерения разницы в распределении "хороших" и "плохих" примеров. Информационное значение определяется по формуле:
IV = ∑ (Gi – Bi) ln (Gi/Bi)
Информационное значение переменной равно сумме всех диапазонов переменной. По грубому правилу значения данного коэффициента трактуются следующим образом:
- менее 0,02 — статистически незначимая переменная;
- 0,02 – 0,1 — статистически малозначимая переменная;
- 0,1 – 0,3 — статистически значимая переменная;
- 0,3 и более — статистически сильная переменная.
Дальше, используя различные алгоритмы и критерии оптимизации, диапазоны объединяют/разъединяют, чтобы получить максимальную разницу этого критерия между диапазонами. Например, пакет smbinning использует Recursive Partitioning для категоризации числовых переменных и IV для определения оптимальных точек разделения, а пакет discretization решает эту задачу с помощью ChiMerge и MDL. Нужно также помнить, что точки разделения мы получаем на обучающем наборе, а валидационный и тестовый набор разделяем с их использованием.
Существует несколько пакетов, которые позволяют тем или иным способом дискретизировать числовые переменные. Это discretization, smbinning, Information, InformationValue и woebinning. С учетом того, что нам нужно не только дискретизировать обучающий набор, но и затем, используя эту информацию, разделить валидационный и тестовый наборы, а также очень желательно иметь визуальный контроль за результатами, я остановился на пакете woebinning.
Пакет автоматически разбивает числовые переменные и факторы с увязкой к бинарной целевой. Предусмотрены два подхода:
- реализация мелкой и грубой классификации последовательно объединяет гранулярные классы и уровни;
- древовидный подход итеративно сегментирует исходные диапазоны через двоичные расщепления.
Обе процедуры сливают разделенные диапазоны на основе аналогичных значений WOE и останавливаются на основе критериев, основанных на IV. Пакет может использоваться с одиночными переменными или целым фреймом данных. Он обеспечивает гибкие инструменты для изучения различных решений для биннинга и для их развертывания на новых данных.
Приступим к расчетам. В наше рабочее пространство уже загружены котировки из терминала (или снимок рабочего пространства Cotir.RData из GitHub). Последовательность вычислений и результат:
- PrepareData() — создаем начальный набор данных dt[7906, 14], очищаем его от NA. Набор включает временную метку Data, входные переменные(12) и целевую Class(фактор с двумя уровнями "-1" и "+1").
- SplitData() — разделяем начальный набор dt[] на поднаборы pretrain, train, val, test в соотношении 2000/1000/500/500, объединив их в датафрейм DT[4, 4000, 14].
- CappingData() — определяем и импутируем выбросы во всех поднаборах, получаем набор DTcap[4, 4000, 14]. Несмотря на то, что дискретизация терпимо относится к выбросам, мы их все же импутируем. Вы можете поэкспериментировать и без этого этапа. Напоминаю, параметры выбросов (pre.outl) определяем на поднаборе pretrain. Выборки train/val/test обрабатываем, используя эти параметры.
- NormData() — нормируем набор, используя метод spatialSing из пакета caret. Как и при импутации выбросов параметры нормализации (preproc) определяем на поднаборе pretrain. Выборки train/val/test обрабатываем используя эти параметры. Получаем DTcap.n[4, 4000, 14].
- DiscretizeData() — определяем параметры дискретизации (preCut), качество переменных и их диапазонов в смысле WOE и IV.
evalq({
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DT <- SplitData(dt, 2000, 1000, 500,500)
pre.outl <- PreOutlier(DT$pretrain)
DTcap <- CappingData(DT, impute = T, fill = T, dither = F,
pre.outl = pre.outl)
preproc <- PreNorm(DTcap, meth = meth)
DTcap.n <- NormData(DTcap, preproc = preproc)
preCut <- PreDiscret(DTcap.n)
}, env) Сведем данные дискретизации по всем переменным в таблицу и посмотрим на них:
evalq(tabulate.binning <- woe.binning.table(preCut), env) > env$tabulate.binning $`WOE Table for v.fatl` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.3904381926 154 7.7% 130 24 13.2% 2.4% 15.6% 171.3 0.185 2 <= -0.03713814085 769 38.5% 498 271 50.4% 26.8% 35.2% 63.2 0.149 3 <= 0.1130198981 308 15.4% 141 167 14.3% 16.5% 54.2% -14.5 0.003 4 <= Inf 769 38.5% 219 550 22.2% 54.3% 71.5% -89.7 0.289 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.626 $`WOE Table for ftlm` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.2344708291 462 23.1% 333 129 33.7% 12.7% 27.9% 97.2 0.204 2 <= -0.01368798447 461 23.1% 268 193 27.1% 19.1% 41.9% 35.2 0.028 3 <= 0.1789073635 461 23.1% 210 251 21.3% 24.8% 54.4% -15.4 0.005 4 <= Inf 616 30.8% 177 439 17.9% 43.4% 71.3% -88.4 0.225 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.463 $`WOE Table for rbci` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.1718377948 616 30.8% 421 195 42.6% 19.3% 31.7% 79.4 0.185 2 <= -0.09060410462 153 7.6% 86 67 8.7% 6.6% 43.8% 27.4 0.006 3 <= 0.3208178176 923 46.2% 391 532 39.6% 52.6% 57.6% -28.4 0.037 4 <= Inf 308 15.4% 90 218 9.1% 21.5% 70.8% -86.1 0.107 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.335 $`WOE Table for v.rbci` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.1837437563 616 30.8% 406 210 41.1% 20.8% 34.1% 68.3 0.139 2 <= 0.03581374495 461 23.1% 253 208 25.6% 20.6% 45.1% 22.0 0.011 3 <= 0.2503922644 461 23.1% 194 267 19.6% 26.4% 57.9% -29.5 0.020 4 <= Inf 462 23.1% 135 327 13.7% 32.3% 70.8% -86.1 0.161 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.331 $`WOE Table for v.satl` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.01840058612 923 46.2% 585 338 59.2% 33.4% 36.6% 57.3 0.148 2 <= 0.3247097195 769 38.5% 316 453 32.0% 44.8% 58.9% -33.6 0.043 3 <= 0.4003869443 154 7.7% 32 122 3.2% 12.1% 79.2% -131.4 0.116 4 <= Inf 154 7.7% 55 99 5.6% 9.8% 64.3% -56.4 0.024 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.330 $`WOE Table for v.stlm` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.4030051922 154 7.7% 118 36 11.9% 3.6% 23.4% 121.1 0.102 2 <= -0.1867821117 462 23.1% 282 180 28.5% 17.8% 39.0% 47.3 0.051 3 <= 0.1141896118 615 30.8% 301 314 30.5% 31.0% 51.1% -1.8 0.000 4 <= Inf 769 38.5% 287 482 29.0% 47.6% 62.7% -49.4 0.092 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.244 $`WOE Table for pcci` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.1738420887 616 30.8% 397 219 40.2% 21.6% 35.6% 61.9 0.115 2 <= -0.03163945242 307 15.3% 165 142 16.7% 14.0% 46.3% 17.4 0.005 3 <= 0.2553612644 615 30.8% 270 345 27.3% 34.1% 56.1% -22.1 0.015 4 <= Inf 462 23.1% 156 306 15.8% 30.2% 66.2% -65.0 0.094 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.228 $`WOE Table for v.ftlm` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.03697698898 923 46.2% 555 368 56.2% 36.4% 39.9% 43.5 0.086 2 <= 0.2437475615 615 30.8% 279 336 28.2% 33.2% 54.6% -16.2 0.008 3 <= Inf 462 23.1% 154 308 15.6% 30.4% 66.7% -66.9 0.099 5 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.194 $`WOE Table for v.rftl` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.1578370554 616 30.8% 372 244 37.7% 24.1% 39.6% 44.6 0.060 2 <= 0.1880959621 768 38.4% 384 384 38.9% 37.9% 50.0% 2.4 0.000 3 <= 0.3289762494 308 15.4% 129 179 13.1% 17.7% 58.1% -30.4 0.014 4 <= Inf 308 15.4% 103 205 10.4% 20.3% 66.6% -66.4 0.065 6 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.140 $`WOE Table for stlm` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.4586732186 154 7.7% 60 94 6.1% 9.3% 61.0% -42.5 0.014 2 <= -0.1688696056 462 23.1% 266 196 26.9% 19.4% 42.4% 32.9 0.025 3 <= 0.2631157075 922 46.1% 440 482 44.5% 47.6% 52.3% -6.7 0.002 4 <= 0.3592235072 154 7.7% 97 57 9.8% 5.6% 37.0% 55.6 0.023 5 <= 0.4846279843 154 7.7% 81 73 8.2% 7.2% 47.4% 12.8 0.001 6 <= Inf 154 7.7% 44 110 4.5% 10.9% 71.4% -89.2 0.057 8 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.122 $`WOE Table for v.rstl` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.4541701981 154 7.7% 94 60 9.5% 5.9% 39.0% 47.3 0.017 2 <= -0.3526306487 154 7.7% 62 92 6.3% 9.1% 59.7% -37.1 0.010 3 <= -0.2496412214 154 7.7% 53 101 5.4% 10.0% 65.6% -62.1 0.029 4 <= -0.08554320418 307 15.3% 142 165 14.4% 16.3% 53.7% -12.6 0.002 5 <= 0.360854678 923 46.2% 491 432 49.7% 42.7% 46.8% 15.2 0.011 6 <= Inf 308 15.4% 146 162 14.8% 16.0% 52.6% -8.0 0.001 8 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.070 $`WOE Table for v.pcci` Final.Bin Total.Count Total.Distr. 0.Count 1.Count 0.Distr. 1.Distr. 1.Rate WOE IV 1 <= -0.4410911486 154 7.7% 92 62 9.3% 6.1% 40.3% 41.9 0.013 2 <= -0.03637567714 769 38.5% 400 369 40.5% 36.5% 48.0% 10.5 0.004 3 <= 0.1801156117 461 23.1% 206 255 20.9% 25.2% 55.3% -18.9 0.008 4 <= 0.2480148615 154 7.7% 84 70 8.5% 6.9% 45.5% 20.6 0.003 5 <= 0.3348752487 154 7.7% 67 87 6.8% 8.6% 56.5% -23.7 0.004 6 <= 0.4397404288 154 7.7% 76 78 7.7% 7.7% 50.6% -0.2 0.000 7 <= Inf 154 7.7% 63 91 6.4% 9.0% 59.1% -34.4 0.009 9 Total 2000 100.0% 988 1012 100.0% 100.0% 50.6% NA 0.042
В таблице для каждой переменной приведены значения:
- Final.Bin — границы диапазонов;
- Total.Count — общее количество примеров в диапазоне;
- Total.Distr — относительное количество примеров;
- 0.Count — количество примеров, относящихся к классу "0";
- 1.Count — количество примеров, относящихся к классу "1";
- 0.Distr — относительное количество примеров, относящихся к классу "0";
- 1.Distr — относительное количество примеров относящихся к классу "1";
- 1.Rate — процентное отношение количества примеров класса "1" к количеству примеров класса "0";
- WOE — предсказательная способность диапазонов;
- IV — статистическая значимость диапазонов (нарастающим итогом!).
Графически это будет наглядней. Выведем графики WOE всех переменных в порядке возрастания их IV на основании этой таблицы:
> evalq(woe.binning.plot(preCut), env)
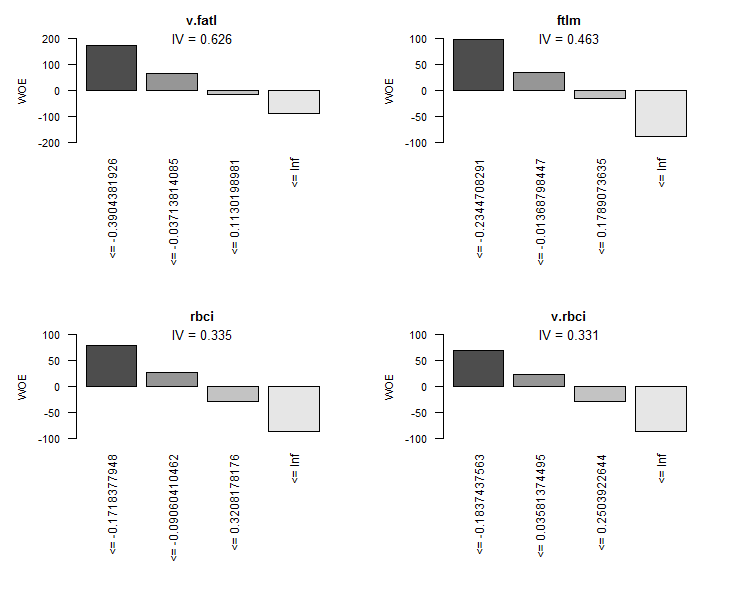
Рис.8. WOE первых 4 лучших переменных
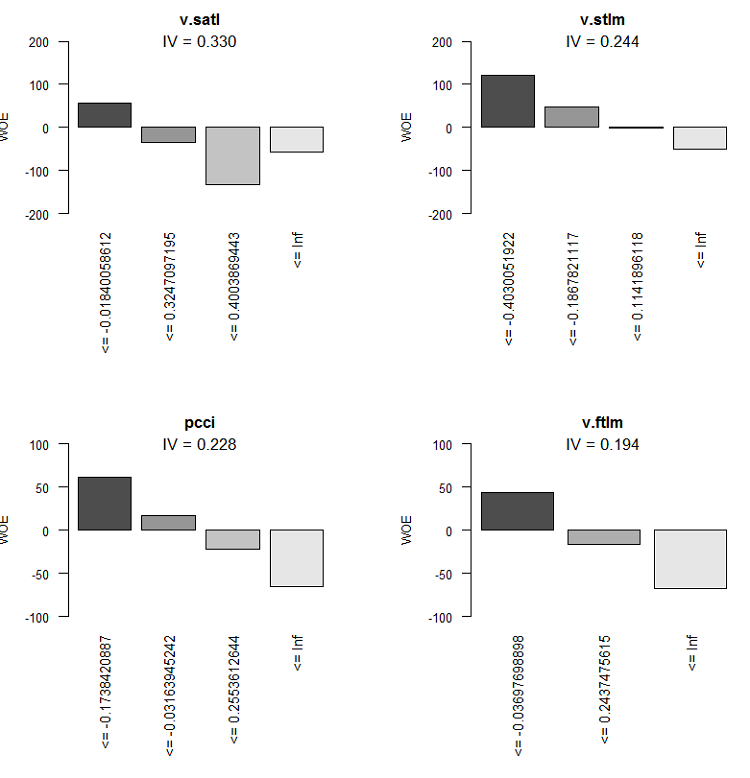
Рис.9. WOE переменных 5-8
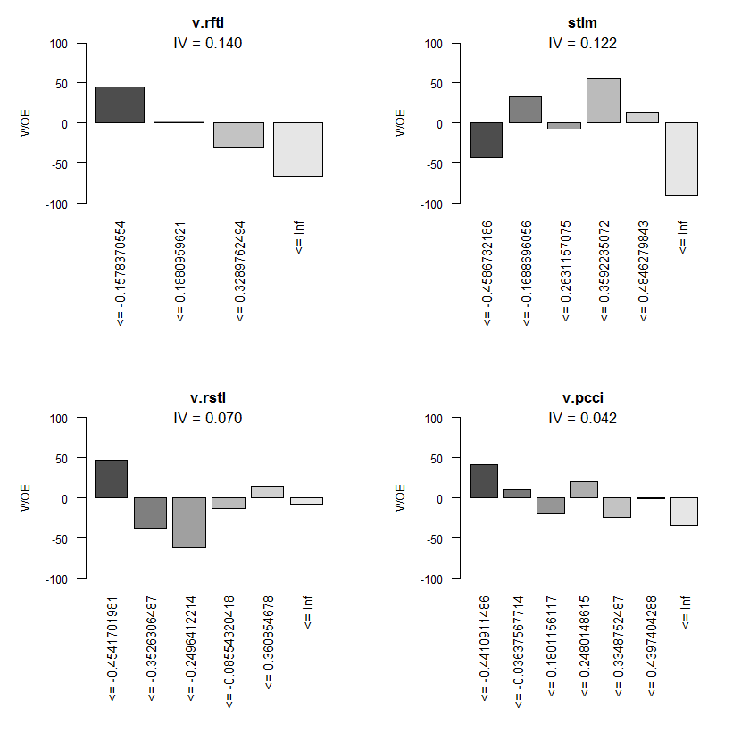
Рис.10. WOE входных переменных 9-12
Ну и график суммарного ранжирования переменных по их информационной значимости IV.
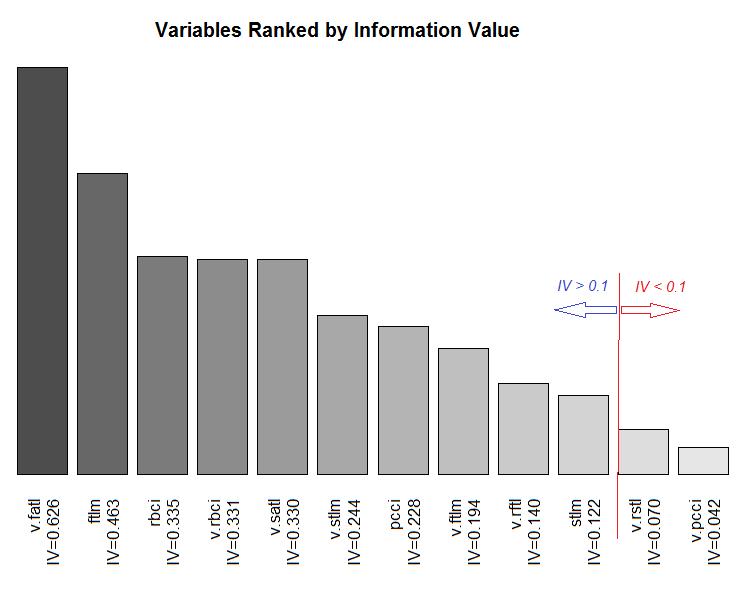
Рис.11. Ранжирование переменных по их информационному значению IV
Две малозначимые переменные — v.rstl и v.pcci, имеющие IV < 0.1, мы в дальнейшем не будем использовать. Из графиков мы видим, что из 10 значимых переменных только две — v.satl и stlm — имеют нелинейную связь с целевой, остальные связаны с ней линейно.
Для дальнейших экспериментов нам необходимо создать три набора :
- DTbin — набор данных, в котором непрерывные числовые предикторы преобразованы в факторы с количеством уровней, равным количеству диапазонов, на которые они разбиты;
- DTdum — набор данных, в котором предикторы-факторы набора DTbin преобразованы в dummy-двоичные переменные;
- DTwoe — набор данных, в котором предикторы-факторы преобразованы в числовые переменные путем замены их уровней значениями WOE этих уровней.
Первый набор DTbin нам нужен для обучения и получения метрик базовой модели. Второй и третий наборы будем использовать для обучения DNN и для сравнения эффективности этих двух методов трансформации.
В пакете woebinning есть функция woe.binning.deploy(), которая поможет нам относительно просто решить эту задачу. В функцию нужно передать:
- датафрейм с предикторами и целевой, причем целевая должна иметь значение 0 или 1;
- параметры дискретизации, полученные на предыдущем этапе (preCut);
- имена переменных, которые нужно категоризировать. Если категоризировать надо все переменные, то просто укажем имя датафрейма;
- указать, с каким минимальным IV не категоризировать переменные;
- указать, какие дополнительные переменные (кроме категоризированных) мы хотим получить. Два варианта — "woe" и "dum".
Функция возвращает датафрейм, содержащий исходные переменные, категоризированные переменные и дополнительные переменные (если они были заказаны). Имена вновь созданных переменных создаются путем добавлением к имени исходной переменной соответствующего префикса или суффикса. Так, префиксы всех дополнительных переменных — "dum" или "woe", а категоризированным переменным добавляют суффикс "binned". Напишем функцию DiscretizeData(), которая, используя woe.binning.deploy(), будет трансформировать исходный набор данных.
DiscretizeData <- function(X, preCut, var){ require(foreach) require(woeBinning) DTd <- list() foreach(i = 1:length(X)) %do% { X[[i]] %>% select(-Data) %>% targ.int() %>% woe.binning.deploy(preCut, min.iv.total = 0.1, add.woe.or.dum.var = var) -> res return(res) } -> DTd list(pretrain = DTd[[1]] , train = DTd[[2]] , val = DTd[[3]] , test = DTd[[4]] ) -> DTd return(DTd) }
Входные параметры функции: исходные данные (list X) со слотами pretrain/train/val/test, параметры дискретизации preCut, тип дополнительной переменной (string var).
Функция уберет из каждого слота переменную "Data" и заменит целевую-фактор "Class" на численную целевую "Cl". После этого она подаст на вход функции woe.binning.deploy(), во входных параметрах которой мы дополнительно укажем минимальный IV = 0.1 для включения переменных в выходной набор. На выходе получим лист с теми же слотами pretrain/train/val/test, но в каждом слоте к исходным переменным будут добавлены категоризированные и, если закажем, дополнительные. Вычислим необходимые нам наборы и добавим к ним "сырые" данные из набора DTcap.n.
evalq({
require(dplyr)
require(foreach)
DTbin = DiscretizeData(DTcap.n, preCut = preCut, var = "")
DTwoe = DiscretizeData(DTcap.n, preCut = preCut, var = "woe")
DTdum = DiscretizeData(DTcap.n, preCut = preCut, var = "dum")
X.woe <- list()
X.bin <- list()
X.dum <- list()
foreach(i = 1:length(DTcap.n)) %do% {
DTbin[[i]] %>% select(contains("binned")) -> X.bin[[i]]
DTdum[[i]] %>% select(starts_with("dum")) -> X.dum[[i]]
DTwoe[[i]] %>% select(starts_with("woe")) %>%
divide_by(100) -> X.woe[[i]]
return(list(bin = X.bin[[i]], woe = X.woe[[i]],
dum = X.dum[[i]], raw = DTcap.n[[i]]))
} -> DTcut
list(pretrain = DTcut[[1]],
train = DTcut[[2]],
val = DTcut[[3]],
test = DTcut[[4]] ) -> DTcut
rm(DTwoe, DTdum, X.woe, X.bin, X.dum)
},
env) Поскольку WOE мы получаем в процентах, то разделив на 100, мы получим значения переменных, которые можно будет подавать на входы нейросети без дополнительной нормализации. Посмотрим на структуру полученного слота, например, DTcut$val.
> env$DTcut$val %>% str() List of 4 $ bin:'data.frame': 501 obs. of 10 variables: ..$ v.fatl.binned: Factor w/ 5 levels "(-Inf,-0.3904381926]",..: 1 1 3 2 4 3 4 4 4 4 ... ..$ ftlm.binned : Factor w/ 5 levels "(-Inf,-0.2344708291]",..: 2 1 1 1 2 2 3 4 4 4 ... ..$ rbci.binned : Factor w/ 5 levels "(-Inf,-0.1718377948]",..: 2 1 2 1 2 3 3 3 4 4 ... ..$ v.rbci.binned: Factor w/ 5 levels "(-Inf,-0.1837437563]",..: 1 1 3 2 4 3 4 4 4 4 ... ..$ v.satl.binned: Factor w/ 5 levels "(-Inf,-0.01840058612]",..: 1 1 1 1 1 1 1 1 1 2 ... ..$ v.stlm.binned: Factor w/ 5 levels "(-Inf,-0.4030051922]",..: 2 2 3 2 3 2 3 3 4 4 ... ..$ pcci.binned : Factor w/ 5 levels "(-Inf,-0.1738420887]",..: 1 1 4 2 4 2 4 2 2 3 ... ..$ v.ftlm.binned: Factor w/ 4 levels "(-Inf,-0.03697698898]",..: 1 1 3 2 3 2 3 3 2 2 ... ..$ v.rftl.binned: Factor w/ 5 levels "(-Inf,-0.1578370554]",..: 2 1 1 1 1 1 1 2 2 2 ... ..$ stlm.binned : Factor w/ 7 levels "(-Inf,-0.4586732186]",..: 2 2 2 2 1 1 1 1 1 2 ... $ woe:'data.frame': 501 obs. of 10 variables: ..$ woe.v.fatl.binned: num [1:501] 1.713 1.713 -0.145 0.632 -0.897 ... ..$ woe.ftlm.binned : num [1:501] 0.352 0.972 0.972 0.972 0.352 ... ..$ woe.rbci.binned : num [1:501] 0.274 0.794 0.274 0.794 0.274 ... ..$ woe.v.rbci.binned: num [1:501] 0.683 0.683 -0.295 0.22 -0.861 ... ..$ woe.v.satl.binned: num [1:501] 0.573 0.573 0.573 0.573 0.573 ... ..$ woe.v.stlm.binned: num [1:501] 0.473 0.473 -0.0183 0.473 -0.0183 ... ..$ woe.pcci.binned : num [1:501] 0.619 0.619 -0.65 0.174 -0.65 ... ..$ woe.v.ftlm.binned: num [1:501] 0.435 0.435 -0.669 -0.162 -0.669 ... ..$ woe.v.rftl.binned: num [1:501] 0.024 0.446 0.446 0.446 0.446 ... ..$ woe.stlm.binned : num [1:501] 0.329 0.329 0.329 0.329 -0.425 ... $ dum:'data.frame': 501 obs. of 41 variables: ..$ dum.v.fatl.-Inf.-0.3904381926.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.v.fatl.-0.03713814085.0.1130198981.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.v.fatl.-0.3904381926.-0.03713814085.binned: num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.v.fatl.0.1130198981.Inf.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.ftlm.-0.2344708291.-0.01368798447.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.ftlm.-Inf.-0.2344708291.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.ftlm.-0.01368798447.0.1789073635.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.ftlm.0.1789073635.Inf.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ....................................................................................... ..$ dum.stlm.-Inf.-0.4586732186.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.stlm.-0.1688696056.0.2631157075.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.stlm.0.2631157075.0.3592235072.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.stlm.0.3592235072.0.4846279843.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... ..$ dum.stlm.0.4846279843.Inf.binned : num [1:501] 0 0 0 0 0 0 0 0 0 0 ... $ raw:'data.frame': 501 obs. of 14 variables: ..$ Data : POSIXct[1:501], format: "2017-02-23 15:30:00" "2017-02-23 15:45:00" ... ..$ ftlm : num [1:501] -0.223 -0.374 -0.262 -0.31 -0.201 ... ..$ stlm : num [1:501] -0.189 -0.257 -0.271 -0.389 -0.473 ... ..$ rbci : num [1:501] -0.0945 -0.1925 -0.1348 -0.1801 -0.1192 ... ..$ pcci : num [1:501] -0.5714 -0.2602 0.4459 -0.0478 0.2596 ... ..$ v.fatl: num [1:501] -0.426 -0.3977 0.0936 -0.1512 0.1178 ... ..$ v.satl: num [1:501] -0.35 -0.392 -0.177 -0.356 -0.316 ... ..$ v.rftl: num [1:501] -0.0547 -0.2065 -0.3253 -0.4185 -0.4589 ... ..$ v.rstl: num [1:501] 0.0153 -0.0273 -0.0636 -0.1281 -0.15 ... ..$ v.ftlm: num [1:501] -0.321 -0.217 0.253 0.101 0.345 ... ..$ v.stlm: num [1:501] -0.288 -0.3 -0.109 -0.219 -0.176 ... ..$ v.rbci: num [1:501] -0.2923 -0.2403 0.1909 0.0116 0.2868 ... ..$ v.pcci: num [1:501] -0.0298 0.3738 0.6153 -0.5643 0.2742 ... ..$ Class : Factor w/ 2 levels "-1","1": 1 1 1 1 2 2 2 2 2 1 ...
Как видим, в слоте bin 10 переменных-факторов с различным количеством уровней и суффиксом "binned". Слот woe содержит 10 переменных, у которых уровни факторных заменены на их WOE (имеют префикс "woe"). В слоте dum 41 числовая переменная dummy со значением (0, 1), которые получены из факторных путем кодирования один к одному (имеют префикс "dum"). В слоте raw, 14 переменных: Data — timestamp, Class — целевая-фактор и 12 числовых предикторов.
Мы получили все данные, которые понадобятся нам для дальнейших экспериментов. В окружении env к этому моменту уже должны находиться объекты, перечисленные ниже. Сохраним рабочую область с этими объектами в файл PartIV.RData.
> ls(env) [1] "Close" "Data" "dt" "DT" "DTbin" "DTcap" "DTcap.n" "DTcut" "High" [10] "i" "Low" "Open" "pre.outl" "preCut" "preproc" "Volume"
2.1.2. Базовая модель сравнения
В качестве базовой модели будем использовать, простую, надежную и легко интерпретируемую модель OneR, реализованную в одноименном пакете OneR. Детали об алгоритме можно прочесть в описании пакета. Модель работает только с интервальными данными, но в пакете есть вспомогательные функции, которые могут дискретизировать числовые переменные различными способами. Поскольку мы уже преобразовали предикторы в факторы, они нам не понадобятся.
Теперь поясню расчет, приведенный ниже. Создаем наборы train/val/test, извлекая из DTcut соответствующие слоты и пристыковывая к ним целевую Class. Обучаем модель на наборе train.
> evalq({
+ require(OneR)
+ require(dplyr)
+ require(magrittr)
+ train <- cbind(DTcut$train$bin, Class = DTcut$train$raw$Class) %>% as.data.frame()
+ val <- cbind(DTcut$val$bin, Class = DTcut$val$raw$Class) %>% as.data.frame()
+ test <- cbind(DTcut$test$bin, Class = DTcut$test$raw$Class) %>% as.data.frame()
+ model <- OneR(data = train, formula = NULL, ties.method = "chisq", #c("first","chisq"
+ verbose = TRUE) #FALSE, TRUE
+ }, env)
Loading required package: OneR
Attribute Accuracy
1 * v.satl.binned 63.14%
2 v.fatl.binned 62.64%
3 ftlm.binned 62.54%
4 pcci.binned 61.44%
5 v.rftl.binned 59.74%
6 v.rbci.binned 58.94%
7 rbci.binned 58.64%
8 stlm.binned 58.04%
9 v.stlm.binned 57.54%
10 v.ftlm.binned 56.14%
---
Chosen attribute due to accuracy
and ties method (if applicable): '*'
Warning message:
In OneR(data = train, formula = NULL, ties.method = "chisq", verbose = TRUE) :
data contains unused factor levels Модель выбрала переменную v.satl.binned с базовой точностью 63.14% как основу для построения правил. Посмотрим общую информацию по модели: > summary(env$model) Call: OneR(data = train, formula = NULL, ties.method = "chisq", verbose = FALSE) Rules: If v.satl.binned = (-Inf,-0.01840058612] then Class = -1 If v.satl.binned = (-0.01840058612,0.3247097195] then Class = 1 If v.satl.binned = (0.3247097195,0.4003869443] then Class = 1 If v.satl.binned = (0.4003869443, Inf] then Class = 1 Accuracy: 632 of 1001 instances classified correctly (63.14%) Contingency table: v.satl.binned Class (-Inf,-0.01840058612] (-0.01840058612,0.3247097195] (0.3247097195,0.4003869443] (0.4003869443, Inf] Sum -1 * 325 161 28 37 551 1 143 * 229 * 35 * 43 450 Sum 468 390 63 80 1001 --- Maximum in each column: '*' Pearson's Chi-squared test: X-squared = 74.429, df = 3, p-value = 4.803e-16
Графическое представление результата обучения:
plot(env$model)
Рис.12. Распределение категорий переменной v.satl.binned по классам в модели
Точность предсказания при обучении не очень высока. Посмотрим, какую точность покажет модель на валидационном наборе:
> evalq(res.val <- eval_model(predict(model, val %>% as.data.frame()), val$Class), + env) Confusion matrix (absolute): Actual Prediction -1 1 Sum -1 106 87 193 1 100 208 308 Sum 206 295 501 Confusion matrix (relative): Actual Prediction -1 1 Sum -1 0.21 0.17 0.39 1 0.20 0.42 0.61 Sum 0.41 0.59 1.00 Accuracy: 0.6267 (314/501) Error rate: 0.3733 (187/501) Error rate reduction (vs. base rate): 0.0922 (p-value = 0.04597)
и на тестовом наборе:
> evalq(res.test <- eval_model(predict(model, test %>% as.data.frame()), test$Class), + env) Confusion matrix (absolute): Actual Prediction -1 1 Sum -1 130 102 232 1 76 193 269 Sum 206 295 501 Confusion matrix (relative): Actual Prediction -1 1 Sum -1 0.26 0.20 0.46 1 0.15 0.39 0.54 Sum 0.41 0.59 1.00 Accuracy: 0.6447 (323/501) Error rate: 0.3553 (178/501) Error rate reduction (vs. base rate): 0.1359 (p-value = 0.005976)
Результаты получились не самые обнадеживающие. Error rate reduction показывает, как увеличилась точность по отношению к базовому (0.5) уровню. Низкое p-значение (< 0.05) свидетельствует о том, что модель действительно способна давать прогнозы лучше базового уровня. Точность тестового набора 0.6447 (323/501), который отстоит от обучающего дальше чем валидационный, выше чем у него. Этот показатель и будет ориентиром для сравнения с результатами предсказания наших будущих моделей.
2.1.3. Структура DNN
Для обучения и тестирования будем использовать три набора данных:
- DTcut$$raw — 12 входных переменных (выбросы импутированы и нормализованы).
- DTcut$$dum — 41 двоичная переменная.
- DTcut$$woe — 10 числовых переменных.
Со всеми наборами применяем целевую переменную Class = фактор с двумя уровнями. Структура нейросетей:
- DNNraw - layers = c(12, 16, 8(2), 2), функции активации c(tanh, maxout(lin), softmax)
- DNNwoe - layers = c(10, 16, 8(2), 2), функции активации c(tanh, maxout(lin), softmax)
- DNNdum - layers = c(41, 50, 8(2), 2), функции активации c(ReLU, maxout(ReLU), softmax)
На рисунке ниже приведена структура нейросети DNNwoe. Нейросеть состоит из входного, двух скрытых и выходного слоя. Две остальных ( DNNdum, DNNraw) имеют аналогичную структуру, но отличаются количеством нейронов в слоях и функциями активации.
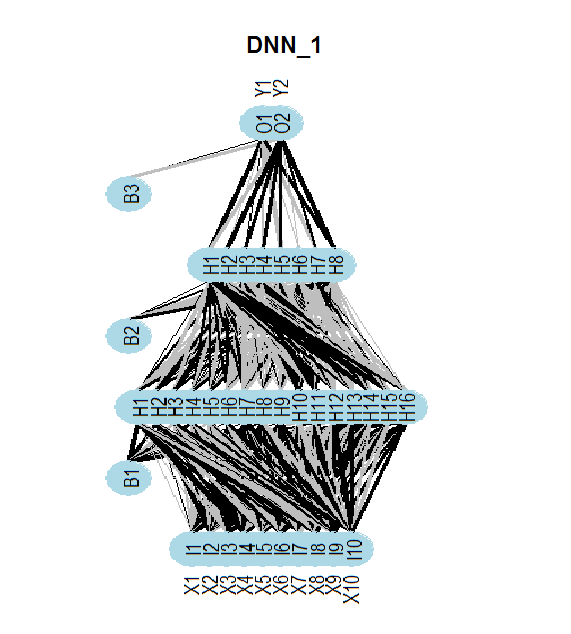
Рис.13. Структура нейросети DNNwoe
2.1.4. Варианты обучения
С претренингом
Обучение будем проводить в два этапа:
- претренинг SRBM набором /pretrain и последующее обучение только верхнего слоя DNN, валидация набором train, параметры — par_0;
- тонкое обучение всей сети наборами train/val и параметрами par_1.
Промежуточные модели тонкого обучения можем сохранять, но можем и опустить сохранение. Лучшая модель по итогам окончательного обучения сохраняется. Параметры этих двух этапов должны содержать:
- par_0 — общие параметры нейросети, параметры обучения RBM и параметры обучения верхнего слоя DNN;
- par_1 — параметры обучения всех слоев DNN.
Все параметры DArch имеют значения по умолчанию. Но если нам нужны определенные параметры на определенном этапе обучения, мы можем их задать списком, и они перезапишут параметры по умолчанию. После первого этапа обучения мы получим структуру DArch c параметрами и результатами обучения (ошибка обучения, тестирования и др.), а также нейросеть, инициированную весами обученной SRBM. Для выполнения второго этапа обучения нам нужно подать структуру DArch, полученную на первом этапе, и список параметров для этого этапа обучения. И, конечно, нам понадобятся обучающий и валидационный наборы.
Рассмотрим параметры, необходимые для первого этапа обучения (претренинг SRBM и обучение верхнего слоя нейросети) и выполним его:
##=====CODE I etap=========================== evalq({ require(darch) require(dplyr) require(magrittr) Ln <- c(0, 16, 8, 0)# // количество входных и выходных нейронов определится автоматически из набора данных nEp_0 <- 25 #------------------ par_0 <- list( layers = Ln, # // вынесем этот параметр за список (для простоты манипулирования) seed = 54321,# // если хотим получать при инициализации идентичные данные logLevel = 5, # // какой уровень вывода информации нам нужен # params RBM======================== rbm.consecutive = F, # each RBM is trained one epoch at a time rbm.numEpochs = nEp_0, rbm.batchSize = 50, rbm.allData = TRUE, rbm.lastLayer = -1, # // верхний слой SRBM не обучать rbm.learnRate = 0.3, rbm.unitFunction = "tanhUnitRbm", # params NN ======================== darch.batchSize = 50, darch.numEpochs = nEp_0,# // вынесем этот параметр за список для простоты манипулирования darch.trainLayers = c(F,F,T), #обучать //только верхний слой darch.unitFunction = c("tanhUnit","maxoutUnit", "softmaxUnit"), bp.learnRate = 0.5, bp.learnRateScale = 1, darch.weightDecay = 0.0002, darch.dither = F, darch.dropout = c(0.1,0.2,0.1), darch.fineTuneFunction = backpropagation, #rpropagation normalizeWeights = T, normalizeWeightsBound = 1, darch.weightUpdateFunction = c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate"), darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2, darch.maxout.unitFunction = "linearUnit") #--------------------------- DNN_default <- darch(darch = NULL, paramsList = par_0, x = DTcut$pretrain$woe %>% as.data.frame(), y = DTcut$pretrain$raw$Class %>% as.data.frame(), xValid = DTcut$train$woe %>% as.data.frame(), yValid = DTcut$train$raw$Class %>% as.data.frame() ) }, env)Результат по окончанию первого этапа обучения:
........................... INFO [2017-09-11 14:12:19] Classification error on Train set (best model): 31.95% (639/2000) INFO [2017-09-11 14:12:19] Train set (best model) Cross Entropy error: 1.233 INFO [2017-09-11 14:12:19] Classification error on Validation set (best model): 35.86% (359/1001) INFO [2017-09-11 14:12:19] Validation set (best model) Cross Entropy error: 1.306 INFO [2017-09-11 14:12:19] Best model was found after epoch 3 INFO [2017-09-11 14:12:19] Final 0.632 validation Cross Entropy error: 1.279 INFO [2017-09-11 14:12:19] Final 0.632 validation classification error: 34.42% INFO [2017-09-11 14:12:19] Fine-tuning finished after 5.975 secs
Второй этап обучения всей нейросети:
##=====CODE II etap=========================== evalq({ require(darch) require(dplyr) require(magrittr) nEp_1 <- 100 bp.learnRate <- 1 par_1 <- list( layers = Ln, seed = 54321, logLevel = 5, rbm.numEpochs = 0,# SRBM не обучаем! darch.batchSize = 50, darch.numEpochs = nEp_1, darch.trainLayers = c(T,T,T), #TRUE, darch.unitFunction = c("tanhUnit","maxoutUnit", "softmaxUnit"), bp.learnRate = bp.learnRate, bp.learnRateScale = 1, darch.weightDecay = 0.0002, darch.dither = F, darch.dropout = c(0.1,0.2,0.1), darch.fineTuneFunction = backpropagation, #rpropagation backpropagation normalizeWeights = T, normalizeWeightsBound = 1, darch.weightUpdateFunction = c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate"), darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2, darch.maxout.unitFunction = exponentialLinearUnit, darch.elu.alpha = 2) #------------------------------ DNN_1 <- darch( darch = DNN_default, paramsList = par_1, x = DTcut$train$woe %>% as.data.frame(), y = DTcut$train$raw$Class %>% as.data.frame(), xValid = DTcut$val$woe %>% as.data.frame(), yValid = DTcut$val$raw$Class %>% as.data.frame() ) }, env)
Результат второго этапа обучения:
........................... INFO [2017-09-11 15:48:37] Finished epoch 100 of 100 after 0.279 secs (3666 patterns/sec) INFO [2017-09-11 15:48:37] Classification error on Train set (best model): 31.97% (320/1001) INFO [2017-09-11 15:48:37] Train set (best model) Cross Entropy error: 1.225 INFO [2017-09-11 15:48:37] Classification error on Validation set (best model): 31.14% (156/501) INFO [2017-09-11 15:48:37] Validation set (best model) Cross Entropy error: 1.190 INFO [2017-09-11 15:48:37] Best model was found after epoch 96 INFO [2017-09-11 15:48:37] Final 0.632 validation Cross Entropy error: 1.203 INFO [2017-09-11 15:48:37] Final 0.632 validation classification error: 31.44% INFO [2017-09-11 15:48:37] Fine-tuning finished after 37.22 secs
График изменения ошибки предсказания в процессе обучения на втором этапе:
plot(env$DNN_1, y = "raw")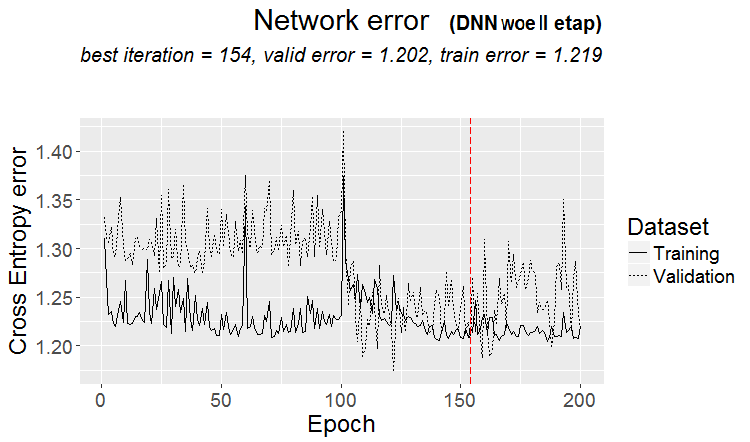 
Рис.14. Изменение ошибки классификации на втором этапе обучения
Посмотрим на ошибку классификации окончательной модели на тестовом наборе:
#-----------
evalq({
xValid = DTcut$test$woe %>% as.data.frame()
yValid = DTcut$test$raw$Class %>% as.vector()
Ypredict <- predict(DNN_1, newdata = xValid, type = "class")
numIncorrect <- sum(Ypredict != yValid)
cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (",
round(numIncorrect/nrow(xValid)*100, 2), "%)\n"))
caret::confusionMatrix(yValid, Ypredict)
}, env)
Incorrect classifications on all examples: 166 (33.13%)
Confusion Matrix and Statistics
Reference
Prediction -1 1
-1 129 77
1 89 206
Accuracy : 0.6687
95% CI : (0.6255, 0.7098)
No Information Rate : 0.5649
P-Value [Acc > NIR] : 1.307e-06
Kappa : 0.3217
Mcnemar's Test P-Value : 0.3932
Sensitivity : 0.5917
Specificity : 0.7279
Pos Pred Value : 0.6262
Neg Pred Value : 0.6983
Prevalence : 0.4351
Detection Rate : 0.2575
Detection Prevalence : 0.4112
Balanced Accuracy : 0.6598
'Positive' Class : -1
#---------------------------------------- Точность на этом наборе данных (woe) и с этими, далеко не оптимальными, параметрами немного выше базовой модели. Есть значительный потенциал к ее увеличению путем оптимизации гиперпараметров DNN. При повторении вычислений полученные данные могут не совпадать с приведенными в статье.
Для дальнейших вычислений с другими наборами данных сведем наши скрипты в компактную форму. Напишем функцию обучения для набора woe:
#------------------- DNN.train.woe <- function(param, X){ require(darch) require(magrittr) darch( darch = NULL, paramsList = param[[1]], x = X[[1]]$woe %>% as.data.frame(), y = X[[1]]$raw$Class %>% as.data.frame(), xValid = X[[2]]$woe %>% as.data.frame(), yValid = X[[2]]$raw$Class %>% as.data.frame() ) %>% darch( ., paramsList = param[[2]], x = X[[2]]$woe %>% as.data.frame(), y = X[[2]]$raw$Class %>% as.data.frame(), xValid = X[[3]]$woe %>% as.data.frame(), yValid = X[[3]]$raw$Class %>% as.data.frame() ) -> Darch return(Darch) }
Повторим расчеты для набора DTcut$$woe в компактном виде:
evalq({
require(darch)
require(magrittr)
Ln <- c(0, 16, 8, 0)
nEp_0 <- 25
nEp_1 <- 25
rbm.learnRate = c(0.5,0.3,0.1)
bp.learnRate <- c(0.5,0.3,0.1)
list(par_0, par_1) %>% DNN.train.woe(DTcut) -> Dnn.woe
xValid = DTcut$test$woe %>% as.data.frame()
yValid = DTcut$test$raw$Class %>% as.vector()
Ypredict <- predict(Dnn.woe, newdata = xValid, type = "class")
numIncorrect <- sum(Ypredict != yValid)
cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (",
round(numIncorrect/nrow(xValid)*100, 2), "%)\n"))
caret::confusionMatrix(yValid, Ypredict) -> cM.woe
}, env) Выполним расчет для набора DTcut$$raw:
#-------------------------
DNN.train.raw <- function(param, X){
require(darch)
require(magrittr)
darch( darch = NULL, paramsList = param[[1]],
x = X[[1]]$raw %>% tbl_df %>% select(-c(Data, Class)),
y = X[[1]]$raw$Class %>% as.data.frame(),
xValid = X[[2]]$raw %>% tbl_df %>% select(-c(Data, Class)),
yValid = X[[2]]$raw$Class %>% as.data.frame()
) %>%
darch( ., paramsList = param[[2]],
x = X[[2]]$raw %>% tbl_df %>% select(-c(Data, Class)),
y = X[[2]]$raw$Class %>% as.data.frame(),
xValid = X[[3]]$raw %>% tbl_df %>% select(-c(Data, Class)),
yValid = X[[3]]$raw$Class %>% as.data.frame()
) -> Darch
return(Darch)
}
#-------------------------------
evalq({
require(darch)
require(magrittr)
Ln <- c(0, 16, 8, 0)
nEp_0 <- 25
nEp_1 <- 25
rbm.learnRate = c(0.5,0.3,0.1)
bp.learnRate <- c(0.5,0.3,0.1)
list(par_0, par_1) %>% DNN.train.raw(DTcut) -> Dnn.raw
xValid = DTcut$test$raw %>% tbl_df %>% select(-c(Data, Class))
yValid = DTcut$test$raw$Class %>% as.vector()
Ypredict <- predict(Dnn.raw, newdata = xValid, type = "class")
numIncorrect <- sum(Ypredict != yValid)
cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (",
round(numIncorrect/nrow(xValid)*100, 2), "%)\n"))
caret::confusionMatrix(yValid, Ypredict) -> cM.raw
}, env)
#---------------------------- Смотрим результат и график изменения ошибки классификации для этого набора:
> env$cM.raw
Confusion Matrix and Statistics
Reference
Prediction -1 1
-1 133 73
1 86 209
Accuracy : 0.6826
95% CI : (0.6399, 0.7232)
No Information Rate : 0.5629
P-Value [Acc > NIR] : 2.667e-08
Kappa : 0.3508
Mcnemar's Test P-Value : 0.3413
Sensitivity : 0.6073
Specificity : 0.7411
Pos Pred Value : 0.6456
Neg Pred Value : 0.7085
Prevalence : 0.4371
Detection Rate : 0.2655
Detection Prevalence : 0.4112
Balanced Accuracy : 0.6742
'Positive' Class : -1
#-------------------------------------- plot(env$Dnn.raw, y = "raw")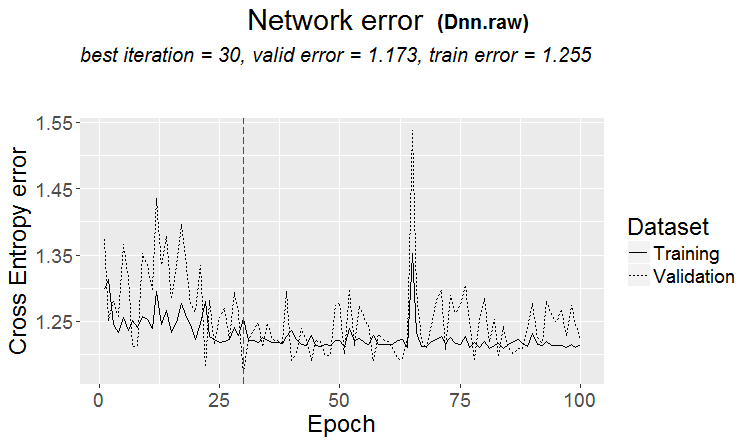 
Рис.15. Изменение ошибки классификации на втором этапе обучения
Обучить нейросеть с данными DTcut$$dum мне не удалось. Читатель может попробовать сделать это самостоятельно: например, попробовать подать на вход данные DTcut$$bin и в параметрах обучения предусмотреть перевод предикторов в dummy.
Обучение без претренинга
Проведем эксперимент с обучением нейросети без претренинга с теми же данными (woe, raw) на выборках pretrain/train/val. Посмотрим результат.
#-------WOE---------------- evalq({ require(darch) require(magrittr) Ln <- c(0, 16, 8, 0) nEp_1 <- 100 bp.learnRate <- c(0.5,0.7,0.1) #--param---------------- par_1 <- list( layers = Ln, seed = 54321, logLevel = 5, rbm.numEpochs = 0,# SRBM не обучаем! darch.batchSize = 50, darch.numEpochs = nEp_1, darch.trainLayers = c(T,T,T), #TRUE, darch.unitFunction = c("tanhUnit","maxoutUnit", "softmaxUnit"), bp.learnRate = bp.learnRate, bp.learnRateScale = 1, darch.weightDecay = 0.0002, darch.dither = F, darch.dropout = c(0.0,0.2,0.1), darch.fineTuneFunction = backpropagation, #rpropagation backpropagation normalizeWeights = T, normalizeWeightsBound = 1, darch.weightUpdateFunction = c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate"), darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2, darch.maxout.unitFunction = exponentialLinearUnit, darch.elu.alpha = 2) #--train--------------------------- darch( darch = NULL, paramsList = par_1, x = DTcut[[1]]$woe %>% as.data.frame(), y = DTcut[[1]]$raw$Class %>% as.data.frame(), xValid = DTcut[[2]]$woe %>% as.data.frame(), yValid = DTcut[[2]]$raw$Class %>% as.data.frame() ) -> Dnn.woe.I #---test-------------------------- xValid = DTcut$val$woe %>% as.data.frame() yValid = DTcut$val$raw$Class %>% as.vector() Ypredict <- predict(Dnn.woe.I, newdata = xValid, type = "class") numIncorrect <- sum(Ypredict != yValid) cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (", round(numIncorrect/nrow(xValid)*100, 2), "%)\n")) caret::confusionMatrix(yValid, Ypredict) -> cM.woe.I }, env) #---------Ris16------------------------------------ plot(env$Dnn.woe.I, type = "class") env$cM.woe.I
Метрики:
....................................................... INFO [2017-09-14 10:38:01] Classification error on Train set (best model): 28.7% (574/2000) INFO [2017-09-14 10:38:01] Train set (best model) Cross Entropy error: 1.140 INFO [2017-09-14 10:38:02] Classification error on Validation set (best model): 35.86% (359/1001) INFO [2017-09-14 10:38:02] Validation set (best model) Cross Entropy error: 1.299 INFO [2017-09-14 10:38:02] Best model was found after epoch 67 INFO [2017-09-14 10:38:02] Final 0.632 validation Cross Entropy error: 1.241 INFO [2017-09-14 10:38:02] Final 0.632 validation classification error: 33.23% INFO [2017-09-14 10:38:02] Fine-tuning finished after 37.13 secs Incorrect classifications on all examples: 150 (29.94%) > env$cM.woe.I Confusion Matrix and Statistics Reference Prediction -1 1 -1 144 62 1 88 207 Accuracy : 0.7006 95% CI : (0.6584, 0.7404) No Information Rate : 0.5369 P-Value [Acc > NIR] : 5.393e-14 Kappa : 0.3932 Mcnemar's Test P-Value : 0.04123 Sensitivity : 0.6207 Specificity : 0.7695 Pos Pred Value : 0.6990 Neg Pred Value : 0.7017 Prevalence : 0.4631 Detection Rate : 0.2874 Detection Prevalence : 0.4112 Balanced Accuracy : 0.6951 'Positive' Class : -1
График изменения ошибки классификации при обучении:
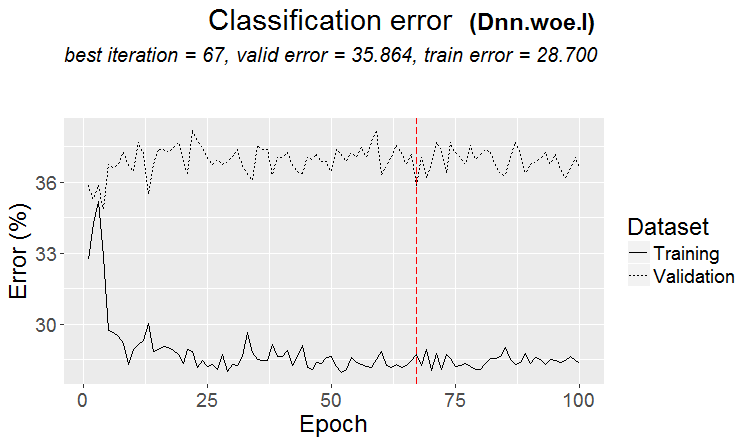
Рис.16. Изменение ошибки классификации без претренинга с набором $woe
То же для набора /raw:
evalq({
require(darch)
require(magrittr)
Ln <- c(0, 16, 8, 0)
nEp_1 <- 100
bp.learnRate <- c(0.5,0.7,0.1)
#--param-----------------------------
par_1 <- list(
layers = Ln,
seed = 54321,
logLevel = 5,
rbm.numEpochs = 0,# SRBM не обучаем!
darch.batchSize = 50,
darch.numEpochs = nEp_1,
darch.trainLayers = c(T,T,T), #TRUE,
darch.unitFunction = c("tanhUnit","maxoutUnit", "softmaxUnit"),
bp.learnRate = bp.learnRate,
bp.learnRateScale = 1,
darch.weightDecay = 0.0002,
darch.dither = F,
darch.dropout = c(0.1,0.2,0.1),
darch.fineTuneFunction = backpropagation, #rpropagation backpropagation
normalizeWeights = T,
normalizeWeightsBound = 1,
darch.weightUpdateFunction = c("weightDecayWeightUpdate",
"maxoutWeightUpdate",
"weightDecayWeightUpdate"),
darch.dropout.oneMaskPerEpoch = T,
darch.maxout.poolSize = 2,
darch.maxout.unitFunction = exponentialLinearUnit,
darch.elu.alpha = 2)
#---train------------------------------
darch( darch = NULL, paramsList = par_1,
x = DTcut[[1]]$raw %>% tbl_df %>% select(-c(Data, Class)) ,
y = DTcut[[1]]$raw$Class %>% as.vector(),
xValid = DTcut[[2]]$raw %>% tbl_df %>% select(-c(Data, Class)) ,
yValid = DTcut[[2]]$raw$Class %>% as.vector()
) -> Dnn.raw.I
#---test--------------------------------
xValid = DTcut[[3]]$raw %>% tbl_df %>% select(-c(Data, Class))
yValid = DTcut[[3]]$raw$Class %>% as.vector()
Ypredict <- predict(Dnn.raw.I, newdata = xValid, type = "class")
numIncorrect <- sum(Ypredict != yValid)
cat(paste0("Incorrect classifications on all examples: ", numIncorrect, " (",
round(numIncorrect/nrow(xValid)*100, 2), "%)\n"))
caret::confusionMatrix(yValid, Ypredict) -> cM.raw.I
}, env)
#---------Ris17----------------------------------
env$cM.raw.I
plot(env$Dnn.raw.I, type = "class") Метрики:
INFO [2017-09-14 11:06:13] Classification error on Train set (best model): 30.75% (615/2000) INFO [2017-09-14 11:06:13] Train set (best model) Cross Entropy error: 1.189 INFO [2017-09-14 11:06:13] Classification error on Validation set (best model): 33.67% (337/1001) INFO [2017-09-14 11:06:13] Validation set (best model) Cross Entropy error: 1.236 INFO [2017-09-14 11:06:13] Best model was found after epoch 45 INFO [2017-09-14 11:06:13] Final 0.632 validation Cross Entropy error: 1.219 INFO [2017-09-14 11:06:13] Final 0.632 validation classification error: 32.59% INFO [2017-09-14 11:06:13] Fine-tuning finished after 35.47 secs Incorrect classifications on all examples: 161 (32.14%) > #---------Ris17---------------------------------- > env$cM.raw.I Confusion Matrix and Statistics Reference Prediction -1 1 -1 140 66 1 95 200 Accuracy : 0.6786 95% CI : (0.6358, 0.7194) No Information Rate : 0.5309 P-Value [Acc > NIR] : 1.283e-11 Kappa : 0.3501 Mcnemar's Test P-Value : 0.02733 Sensitivity : 0.5957 Specificity : 0.7519 Pos Pred Value : 0.6796 Neg Pred Value : 0.6780 Prevalence : 0.4691 Detection Rate : 0.2794 Detection Prevalence : 0.4112 Balanced Accuracy : 0.6738 'Positive' Class : -1
График изменения ошибки классификации:
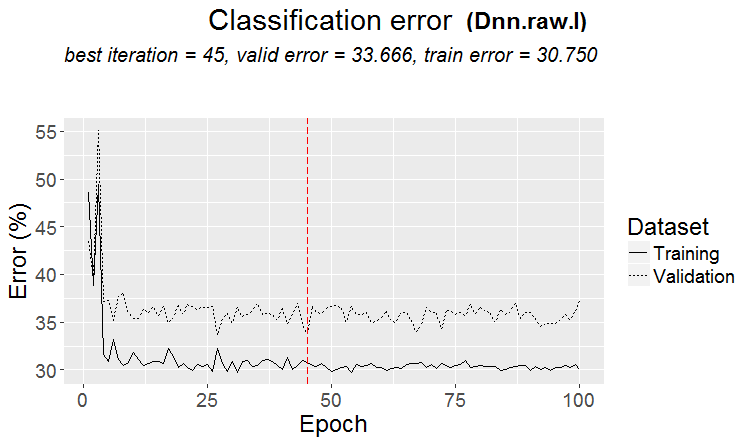
Рис.17. Изменение ошибки классификации без претренинга с набором $raw
2.2. Анализ результатов
Сведем результаты наших экспериментов в таблицу:
| Вид обучения | Набор /woe | Набор /raw |
|---|---|---|
| С претренингом | 0.6687 (0.6255 - 0.7098) | 0.6826(0.6399 - 0.7232) |
| Без претренинга | 0.7006(0.6589 - 0.7404) | 0.6786(0.6359 - 0.7194) |
Ошибка классификации с претренингом у обоих наборов приблизительно одинакова и находится в пределах 30+/-4%. При обучении без претренинга, несмотря на более низкую ошибку, по графику ее изменения явно видно переобучение (ошибка на валидационном и тестовом наборах значительно превышает ошибку обучения). Поэтому в дальнейших экспериментах будем использовать обучение с претренингом.
Результат ненамного выше показателей базовой модели, но у нас есть возможность улучшить показатели, оптимизировав некоторые гиперпараметры. Этим мы займемся в следующей статье.
Заключение
Несмотря на ограничения (например, только два базовых метода обучения), пакет darch позволяет создавать разнообразные по структуре и параметрам нейросети. Его можно считать хорошим инструментом для глубокого изучения нейросетей.
Невысокие показатели DNN объясняются главным образом тем, что мы используем параметры по умолчанию или близкие к ним. Использование набора /woe не показало преимущества перед /raw. Поэтому в следующей статье мы:
- оптимизируем часть гиперпараметров нашей ранее созданной DNN.woe;
- создадим DNN, используя библиотеку TensorFlow, протестируем ее и сравним результаты с DNN (darch);
- создадим ансамбль нейросетей различного вида (bagging, stacking) и посмотрим, насколько это повышает качество предсказания.
Приложения
В GitHub/PartIV находятся:
- FunPrepareData.R — функции, использующиеся при подготовке данных
- RunPrepareData.R — скрипты для подготовки данных
- Experiment.R — скрипты для проведения экспериментов
- Part_IV.RData — снимок рабочей области со всеми объектами, полученными после этапа подготовки данных
- SessionInfo.txt — информация об использованном ПО
- Darch_default.txt — перечень параметров структуры DArch со значениями по умолчанию
Новый подход к интерпретации классической и обратной дивергенции
Нечеткая логика в торговых стратегиях
Сравнение различных типов скользящих средних в торговле
Треугольный арбитраж
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Еще вопрос появился )
В статье от 2014 года вы использовали для запуска эксперта на разных окнах разные порты подключения к R, через svSocket.
Сейчас это нужно тоже делать?
С последних статьях это не используется. Запускал эксперта на разных окнах (на одном символе, но с разными параметрами эксперта), он вызывает разные потоки RTerm, судя по результатам - вроде бы обращается каждый к своему. Но есть сомнение - вдруг надо все таки разделить по портам?
Добрый день.
Я в дороге, поэтому коротко.
В первых статьях я использовал вариант клиент-сервер. Интересный вариант, но сейчас появились новые решения. Поэтому ничего разделять не нужно. Каждый процесс Rterm работает в своей песочнице.
Удачи
Добрый день.
Я в дороге, поэтому коротко.
В первых статьях я использовал вариант клиент-сервер. Интересный вариант, но сейчас появились новые решения. Поэтому ничего разделять не нужно. Каждый процесс Rterm работает в своей песочнице.
Удачи
Уважаемый добрый день, интересна статья новая ваша 4, у меня есть вопрос, реализовать советник можете по этой статье которая описана, естественно оплата будет, тех задание все дам, щас ищу именно нейронку обучения под цели, если да отпишите в ЛС там поговорим. Если Вы таким не занимаетесь то может подскажите к кому обратится для реализации советника под МТ5 нужна
非常感谢你的系列文章，我一直在跟踪学习，可是因为我知识结构的局限，理解这些文章不是件容易的事情。即使这样，还是希望能不断看到您的新文章，期待您发表新文章！谢谢！
А результат торговый у Вас получился?
Все вернулись к машкам. А это уже другая тема.