Глубокие нейросети (Часть V). Байесовская оптимизация гиперпараметров DNN
7 660
22
Содержание
- Введение
- 1. Определение оптимальных гиперпараметров DNN (darch)
- Формирование исходных наборов данных
- Удаление статистически незначимых предикторов
- Определение гиперпараметров DNN для оптимизации и границ их изменений
- Определение функций претренинга и тонкой настройки DNN
- Определение фитнес-функции для оптимизации
- Вычисление оптимальных параметров DNN
- 2. Обучение и тестирование DNN с оптимальными параметрами
- 3. Анализ результатов тестирования DNN с оптимальными параметрами
- 4. Форвард-тест моделей с оптимальными параметрами
- Заключение
- Приложение
Введение
В предыдущей статье этого цикла мы обучили базовую модель и модель DNN с параметрами по умолчанию. Качество классификации нашей модели получилось неудовлетворительное. Что же можно сделать для повышения качества классификации?
- Оптимизировать гиперпараметры DNN
- Усилить регуляризацию DNN
- Увеличить количество примеров для обучения
- Изменить структуру нейросети
В этой и следующих статьях предлагаю рассмотреть все перечисленные возможности усиления имеющейся DNN. Начнем с оптимизации гиперпараметров сети.
1. Определение оптимальных гиперпараметров DNN
Гиперпараметры нейросети в общем случае можно разделить на две группы : глобальные и локальные (узловые). К глобальным гиперпараметрам относятся количество скрытых слоев, количество нейронов в каждом слое, уровень обучения и момент, инициализация весов нейронов. Локальные гиперпараметры — тип слоя, функция активации, dropout/dropconect и другие параметры регуляризации.
Структура оптимизации гиперпараметров представлена на рисунке:
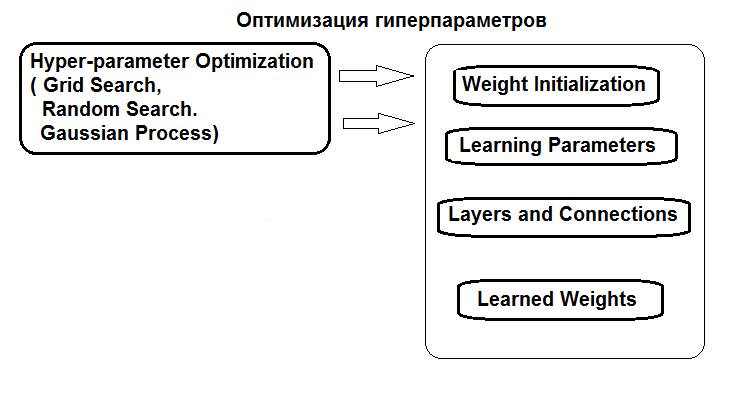
Рис.1. Структура гиперпараметров нейросети и способы оптимизации
Оптимизировать гиперпараметры можно тремя способами:
- Сеточный поиск: для каждого гиперпараметра задается вектор с несколькими фиксированными значениями. Затем, используя функцию caret::train() либо собственный скрипт, обучают модель на всех комбинациях значений гиперпараметров. После этого выбирают модель с лучшими показателями качества классификации. Ее параметры и будут приняты как оптимальные. Недостаток этого способа — в том, что задав сетку значений, мы с большой вероятностью пропустим оптимум.
- Генетическая оптимизация: стохастический поиск лучших параметров с использованием генетических алгоритмов. Ранее мы довольно подробно рассматривали несколько алгоритмов генетической оптимизации. Поэтому не будем повторяться.
- И, наконец, байесовская оптимизация. Ее мы и используем в этой статье.
Байесовский подход включает в себя гауссовские процессы и МСМС. Будем использовать пакет rBayesianOptimization (version 1.1.0). Теория применяемых методов широко представлена в литературе и приведена, например, в этой статье.
Для проведения байесовской оптимизации нам необходимо:
- определить фитнес-функцию;
- определить перечень и границы изменения гиперпараметров.
Фитнес-функция (ФФ) должна возвращать показатель качества (критерий оптимизации, скаляр) который при оптимизации должен быть максимизирован, и предсказанные значения целевой. ФФ будет возвращать значение mean(F1) — это среднее значение F1 для двух классов. Модель DNN обучаем с претеренингом.
Формирование исходных наборов данных
Для проведения экспериментов будем использовать новую версию MRO 3.4.2. В ней реализованы несколько новых пакетов, которые мы ранее не использовали.
Запускаем RStudio, загружаем из GitHub/Part_I файл Cotir.RData, содержащий котировки, полученные из терминала, и файл FunPrepareData.R с функциями подготовки данных из GitHub/Part_IV.
Ранее мы определили, что набор данных с импутированными выбросами и нормализованными данными позволяет получить лучшие результаты при обучении с претренингом. Вы можете проверить и другие варианты препроцессинга, которые мы рассматривали ранее.
При разделении на pretrain/train/val/test-разделы используем первую возможность улучшения качества классификации — увеличим количество примеров для обучения. В разделе pretrain количество примеров увеличим до 4000.
#----Prepare------------- library(anytime) library(rowr) library(darch) library(rBayesianOptimization) library(foreach) library(magrittr) #source(file = "FunPrepareData.R") #source(file = "FUN_Optim.R") #---prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 100, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) }, env)
Изменяя параметр start в функции SplitData(), мы можем получать наборы, сдвинутые вправо на величину start. Это позволит нам в будущем проверить качество на разных участках диапазона цен и определить, как оно изменяется на истории.
Удаление статистически незначимых предикторов
Уберем две статистически незначимые переменные c(v.rstl, v.pcci). Их мы определили в предыдущей статье этой серии.
##---Data DT-------------- require(foreach) evalq({ foreach(i = 1:4) %do% { DTcap.n[[i]] %>% dplyr::select(-c(v.rstl, v.pcci)) } -> DT list(pretrain = DT[[1]], train = DT[[2]], val = DT[[3]], test = DT[[4]]) -> DT }, env)
Создадим наборы данных (pretrain/train/test/test1) для претренинга, тонкой настройки и тестирования, собранные в список X.
#-----Data X------------------
evalq({
list(
pretrain = list(
x = DT$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$pretrain$Class %>% as.data.frame()
),
train = list(
x = DT$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$train$Class %>% as.data.frame()
),
test = list(
x = DT$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$val$Class %>% as.data.frame()
),
test1 = list(
x = DT$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$test$Class %>% as.vector()
)
) -> X
}, env) Наборы для проведения экспериментов готовы.
Нам нужна функция, вычисляющая метрики по результатам тестирования. Значение mean(F1) мы будем использовать как критерий оптимизации (максимизации). Загрузим эту функцию в окружение env.
evalq( #input actual & predicted vectors or actual vs predicted confusion matrix # https://github.com/saidbleik/Evaluation/blob/master/eval.R Evaluate <- function(actual=NULL, predicted=NULL, cm=NULL){ if (is.null(cm)) { actual = actual[!is.na(actual)] predicted = predicted[!is.na(predicted)] f = factor(union(unique(actual), unique(predicted))) actual = factor(actual, levels = levels(f)) predicted = factor(predicted, levels = levels(f)) cm = as.matrix(table(Actual = actual, Predicted = predicted)) } n = sum(cm) # number of instances nc = nrow(cm) # number of classes diag = diag(cm) # number of correctly classified instances per class rowsums = apply(cm, 1, sum) # number of instances per class colsums = apply(cm, 2, sum) # number of predictions per class p = rowsums / n # distribution of instances over the classes q = colsums / n # distribution of instances over the predicted classes #accuracy accuracy = sum(diag) / n #per class recall = diag / rowsums precision = diag / colsums f1 = 2 * precision * recall / (precision + recall) #macro macroPrecision = mean(precision) macroRecall = mean(recall) macroF1 = mean(f1) #1-vs-all matrix oneVsAll = lapply(1:nc, function(i){ v = c(cm[i,i], rowsums[i] - cm[i,i], colsums[i] - cm[i,i], n - rowsums[i] - colsums[i] + cm[i,i]); return(matrix(v, nrow = 2, byrow = T))}) s = matrix(0, nrow = 2, ncol = 2) for (i in 1:nc) {s = s + oneVsAll[[i]]} #avg accuracy avgAccuracy = sum(diag(s))/sum(s) #micro microPrf = (diag(s) / apply(s,1, sum))[1]; #majority class mcIndex = which(rowsums == max(rowsums))[1] # majority-class index mcAccuracy = as.numeric(p[mcIndex]) mcRecall = 0*p; mcRecall[mcIndex] = 1 mcPrecision = 0*p; mcPrecision[mcIndex] = p[mcIndex] mcF1 = 0*p; mcF1[mcIndex] = 2 * mcPrecision[mcIndex] / (mcPrecision[mcIndex] + 1) #random accuracy expAccuracy = sum(p*q) #kappa kappa = (accuracy - expAccuracy) / (1 - expAccuracy) #random guess rgAccuracy = 1 / nc rgPrecision = p rgRecall = 0*p + 1 / nc rgF1 = 2 * p / (nc * p + 1) #rnd weighted rwgAccurcy = sum(p^2) rwgPrecision = p rwgRecall = p rwgF1 = p classNames = names(diag) if (is.null(classNames)) classNames = paste("C",(1:nc),sep = "") return(list( ConfusionMatrix = cm, Metrics = data.frame( Class = classNames, Accuracy = accuracy, Precision = precision, Recall = recall, F1 = f1, MacroAvgPrecision = macroPrecision, MacroAvgRecall = macroRecall, MacroAvgF1 = macroF1, AvgAccuracy = avgAccuracy, MicroAvgPrecision = microPrf, MicroAvgRecall = microPrf, MicroAvgF1 = microPrf, MajorityClassAccuracy = mcAccuracy, MajorityClassPrecision = mcPrecision, MajorityClassRecall = mcRecall, MajorityClassF1 = mcF1, Kappa = kappa, RandomGuessAccuracy = rgAccuracy, RandomGuessPrecision = rgPrecision, RandomGuessRecall = rgRecall, RandomGuessF1 = rgF1, RandomWeightedGuessAccurcy = rwgAccurcy, RandomWeightedGuessPrecision = rwgPrecision, RandomWeightedGuessRecall = rwgRecall, RandomWeightedGuessWeightedF1 = rwgF1))) }, env) #-------------------------
Функция возвращает широкий спектр метрик, из которых сейчас нам понадобится только значение F1.
Будем использовать нейросеть с двумя скрытыми слоями, как и в предыдущей части статьи. Обучение DNN будем проводить в два этапа, с претренингом. Возможные варианты при этом:
- Претренинг:
- обучаем только SRBM;
- обучаем SRBM + верхний слой нейросети.
- Тонкое обучение:
- используем метод обучения backpropagation;
- используем метод обучения rpropagation.
Каждый из этих четырех вариантов обучения имеет различный набор гиперпараметров для оптимизации.
Определение гиперпараметров для оптимизации
Определим перечень гиперпараметров, значения которых мы предполагаем оптимизировать, и границы их изменения:
- n1, n2 — количество нейронов в каждом скрытом слое. Диапазон изменений — от 1 до 25. Перед подачей в модель параметр умножается на 2, поскольку нам нужно число, кратное 2 (poolSize). Это требуется для активационной функции maxout.
- fact1, fact2 — индексы активационной функции для каждого скрытого слоя, выбранные из перечня активационных функций, заданных вектором Fact <- c("tanhUnit","maxoutUnit","softplusUnit", "sigmoidUnit"). Вы можете добавить и другие функции.
- dr1, dr2 — величина отсева в каждом слое, диапазон — от 0 до 0.5.
- Lr.rbm — уровень обучения StackedRBM, диапазон — от 0.01 до 1.0 на этапе претренинга.
- Lr.top — уровень обучения верхнего слоя нейросети на этапе претренинга, диапазон от 0.01 до 1.0. При претренинге без обучения верхнего слоя нейросети этот параметр не нужен.
- Lr.fine — уровень обучения нейросети на этапе тонкой настройки при использовании backpropagation, диапазон от 0.01 до 1.0. При использовании rpropagation этот параметр не нужен.
Подробное описание всех параметров приведено в предыдущей статье и в описании пакета. Напомню, что все параметры функции darch() имеют значения по умолчанию. Их можно разделить на несколько групп.
- Глобальные параметры. Используются и при претренинге, и при тонкой настройке.
- Параметры препроцессинга данных. Используются возможности caret::preProcess().
- Параметры для SRBM. Используются только при претренинге.
- Параметры NN. Используются как при претренинге, так и при тонкой настройке, но могут иметь различные значения для каждого из этапов.
Значение параметров по умолчанию можно изменить, задав список с их новыми значениями или вписав их в функцию darch() явно. Кратко поясню гиперпараметры, которые будем оптимизировать.
Вначале задаем глобальные параметры DNN, общие для pretrain/train этапов.
Ln <- c(0, 2*n1, 2*n2, 0) — вектор, указывающий, что мы создаем 4-слойную нейросеть с двумя скрытыми слоями. Количество нейронов во входном и выходном слоях определяется из входных данных, можно его не указывать явно. В скрытых слоях количество нейронов 2*n1 и 2*n2, соответственно.
Далее определяем уровни обучения для RBM (Lr.rbm), для верхнего слоя DNN при претренинге Lr.top. и для всех слоев при тонкой настройке Lr.fine.
fact1/fact2 — указывают индекс активационной функции для каждого скрытого слоя из перечня активационных функций, заданного вектором Fact. В выходном слое применяем функцию softmax.
dr1/dr2 — уровень отсева в каждом скрытом слое.
darch.trainLayers — указывает, какие слои обучать при претренинге, а какие — при тонкой настройке.
Пропишем гиперпараметры и границы их изменения для каждого из 4 вариантов обучения/оптимизации. Кроме того, вынесем параметры Bs.rbm = 100 (rbm.batchSize) и Bs.nn = 50 (darch.batchSize) для удобства при поиске лучших вариантов обучения. При их уменьшении качество классификации улучшается, но значительно возрастает время оптимизации.
#-2---------------------- evalq({ #--InitParams--------------------- Fact <- c("tanhUnit","maxoutUnit","softplusUnit", "sigmoidUnit") wUpd <- c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate", "weightDecayWeightUpdate") #---SRBM + RP---------------- bonds1 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0)#, ) #---SRBM + BP---------------- bonds2 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.fine = c(0.01, 1.0) ) #---SRBM + upperLayer + BP---- bonds3 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.top = c(0.01, 1.0), Lr.fine = c(0.01, 1.0) ) #---SRBM + upperLayer + RP----- bonds4 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.top = c(0.01, 1.0) ) Bs.rbm <- 100L Bs.nn <- 50L },envir = env)
Определяем функции претренинга и тонкой настройки
Обучать DNN будем по четырем вариантам. Все необходимые функции для этого есть в скрипте FUN_Optim.R, который нужно загрузить до начала вычислений с Git/PartV.
Функции претренинга и тонкой настройки для каждого из вариантов:
- pretrainSRBM(Ln, fact1, fact2, dr1, dr2, Lr.rbm ) — претрениг только SRBM
- pretrainSRBM_topLayer(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) — претренинг SRBM + upper Layer (backpropagation)
- fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) — тонкая настройка DNN с использованием rpropagation
- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) — тонкая настройка DNN с использованием backpropagation
Чтобы не загромождать статью листингами однообразных функций, рассмотрим подробно только вариант с претренингом (SRBM + topLayer) + RP(тонкая настройка rpropagation). В моих многочисленных экспериментах этот вариант в большинстве случаев показывал лучший результат. Функции для остальных вариантов аналогичны.
# SRBM + upper Layer (backpropagation) pretrainSRBM_topLayer <- function(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) # SRBM + upper Layer (backpropagation) { darch( x = X$pretrain$x, y = X$pretrain$y, xValid = X$train$x, yValid = X$train$y, #=====constant====================================== layers = Ln, paramsList = list(), darch = NULL, shuffleTrainData = T, seed = 54321, logLevel = "WARN", #FATAL, ERROR, WARN, DEBUG, and TRACE. #--optimization parameters---------------------------------- darch.unitFunction = c(Fact[fact1], Fact[fact2], "softmaxUnit"), darch.weightUpdateFunction = c(wUpd[fact1], wUpd[fact2], "weightDecayWeightUpdate"), rbm.learnRate = Lr.rbm, bp.learnRate = Lr.top, darch.dropout = c(0, dr1, dr2), #=== params RBM ============== rbm.numEpochs = 30L, rbm.allData = T, rbm.batchSize = Bs.rbm, rbm.consecutive = F, rbm.errorFunction = mseError, #rmseError rbm.finalMomentum = 0.9, rbm.initialMomentum = 0.5, rbm.momentumRampLength = 1, rbm.lastLayer = -1, rbm.learnRateScale = 1, rbm.numCD = 1L, rbm.unitFunction = tanhUnitRbm, rbm.updateFunction = rbmUpdate, rbm.weightDecay = 2e-04, #=== parameters NN ======================== darch.numEpochs = 30L, darch.batchSize = Bs.nn, darch.trainLayers = c(FALSE, FALSE,TRUE ), darch.fineTuneFunction = "backpropagation", #rpropagation bp.learnRateScale = 1, #0.99 #--weight----------------- generateWeightsFunction = generateWeightsGlorotUniform, # generateWeightsUniform (default), # generateWeightsGlorotUniform, # generateWeightsHeUniform. # generateWeightsNormal, # generateWeightsGlorotNormal, # generateWeightsHeNormal, darch.weightDecay = 2e-04, normalizeWeights = T, normalizeWeightsBound = 15, #--parameters regularization----------- darch.dither = F, darch.dropout.dropConnect = F, darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2L, darch.maxout.unitFunction = "exponentialLinearUnit", darch.elu.alpha = 2, darch.returnBestModel = T #darch.returnBestModel.validationErrorFactor = 0, ) }
В качестве валидационного набора в этой функции мы используем значения из набора X$train.
Функция тонкой настройки с использованием rpropagation. Этой функции, кроме параметров, передаем предварительно обученную при претренинге структуру Dnn.
fineTuneRP <- function(Ln, fact1, fact2, dr1, dr2, Dnn) # rpropagation { darch( x = X$train$x, y = X$train$y, #xValid = X$test$x, yValid = X$test$y, xValid = X$test$x %>% head(250), yValid = X$test$y %>% head(250), #=====constant====================================== layers = Ln, paramsList = list(), darch = Dnn, shuffleTrainData = T, seed = 54321, logLevel = "WARN", #FATAL, ERROR, WARN, DEBUG, and TRACE. rbm.numEpochs = 0L, #--optimization parameters---------------------------------- darch.unitFunction = c(Fact[fact1], Fact[fact2], "softmaxUnit"), darch.weightUpdateFunction = c(wUpd[fact1], wUpd[fact2], "weightDecayWeightUpdate"), darch.dropout = c(0, dr1, dr2), #=== parameters NN ======================== darch.numEpochs = 50L, darch.batchSize = Bs.nn, darch.trainLayers = c(TRUE,TRUE, TRUE), darch.fineTuneFunction = "rpropagation", #"rpropagation" "backpropagation" #=== params RPROP ====== rprop.decFact = 0.5, rprop.incFact = 1.2, rprop.initDelta = 1/80, rprop.maxDelta = 50, rprop.method = "iRprop+", rprop.minDelta = 1e-06, #--weight----------------- darch.weightDecay = 2e-04, normalizeWeights = T, normalizeWeightsBound = 15, #--parameters regularization----------- darch.dither = F, darch.dropout.dropConnect = F, darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2L, darch.maxout.unitFunction = "exponentialLinearUnit", darch.elu.alpha = 2, darch.returnBestModel = T #darch.returnBestModel.validationErrorFactor = 0, ) }
Здесь в качестве валидационного набора используем первые 250 значений набора X$test. Все функции для всех вариантов обучения должны быть загружены в окружение env.
Определение фитнес-функции
Используя две эти функции, напишем фитнес-функцию, необходимую нам для оптимизации гиперпараметров. Она возвращает значение критерия оптимизации Score = mean(F1), которое нужно максимизировать, и предсказанные значения целевой Ypred.
#---SRBM + upperLayer + RP---- fitnes4.DNN <- function(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) { Ln <- c(0, 2*n1, 2*n2, 0) #-- pretrainSRBM_topLayer(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) -> Dnn fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) -> Dnn predict(Dnn, newdata = X$test$x %>% tail(250) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(250) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics$F1 %>% mean() return(list(Score = Score, Pred = Ypred) }
Определяем оптимальные параметры DNN
Функцию оптимизации BayesianOptimization() запускаем с использованием 10 начальных точек в пространстве гиперпараметров, полученных случайным путем. Несмотря на то, что расчет распараллеливается на все ядра процессора (Intel MKL), он все равно занимает значительное время и зависит от количества итераций и размера batchsize. Для экономии времени начнем с 10 итераций. В дальнейшем, если результаты будут неудовлетворительными, можно будет продолжить оптимизацию, использовав в качестве начальных оптимальные значения предыдущего прогона оптимизации.
Вариант обучения SRBM + RP
#---SRBM + RP---------------- evalq( OPT_Res1 <- BayesianOptimization(fitnes1.DNN, bounds = bonds1, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) Best Parameters Found: Round = 7 n1 = 22.0000 n2 = 2.0000 fact1 = 3.0000 fact2 = 2.0000 dr1 = 0.4114 dr2 = 0.4818 Lr.rbm = 0.7889 Value = 0.7531
Посмотрим, какие варианты оптимальных параметров и F1 мы получили. Функция BayesianOptimization() возвращает ряд значений: лучшие значения параметров — Best_Par, лучшее значение критерия оптимизации при этих оптимальных параметрах — Best_Value, историю оптимизации — History, и полученные предсказания при оптимизации после всех итераций — Pred. Посмотрим историю оптимизации, предварительно упорядочив ее по убыванию по значению Value.
evalq({
OPT_Res1 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init1
best.init1
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Value
1 22 2 3 2 0.41136623 0.48175897 0.78886312 0.7531204
2 23 8 4 2 0.16814464 0.16221565 0.08381839 0.7485614
3 19 17 3 3 0.17274258 0.46809117 0.72698789 0.7485614
4 25 25 4 2 0.30039573 0.26894463 0.11226139 0.7473266
5 11 24 3 2 0.31564303 0.11091751 0.40387209 0.7462520
6 1 6 3 4 0.36876218 0.17403265 0.90387675 0.7450260
7 25 25 3 1 0.06872059 0.42459582 0.40072731 0.7447972
8 1 25 4 1 0.24871843 0.18593687 0.31920691 0.7445628
9 18 1 4 3 0.49846810 0.38517469 0.51115471 0.7423566
10 13 25 4 1 0.37052548 0.07603925 0.87100360 0.7402597 Это хороший результат. Сделаем еще один прогон оптимизации, но для инициализации 10 начальных точек в пространстве гиперпараметров будем использовать лучшие значения предыдущего прогона best_init1.
evalq( OPT_Res1.1 <- BayesianOptimization(fitnes1.DNN, bounds = bonds1, init_grid_dt = best.init1, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) Best Parameters Found: Round = 1 n1 = 4.0000 n2 = 1.0000 fact1 = 1.0000 fact2 = 4.0000 dr1 = 0.1870 dr2 = 0.0000 Lr.rbm = 0.9728 Value = 0.7608
Посмотрим 10 лучших результатов этого прогона.
evalq({
OPT_Res1.1 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init1
best.init1
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Value
1 4 1 1 4 0.18701522 2.220446e-16 0.9728164 0.7607811
2 3 24 1 4 0.12698982 1.024231e-01 0.5540933 0.7549180
3 5 5 1 3 0.07366640 2.630144e-01 0.2156837 0.7542661
4 1 18 1 4 0.41907554 4.641130e-02 0.6092082 0.7509800
5 1 23 1 4 0.25279461 1.365197e-01 0.2957633 0.7504026
6 4 25 4 1 0.09500347 3.083338e-01 0.2522729 0.7488496
7 17 3 3 3 0.36117416 3.162195e-01 0.4214501 0.7458489
8 13 4 3 3 0.22496776 1.481455e-01 0.4448280 0.7437376
9 21 24 1 3 0.36154287 1.335931e-01 0.6749752 0.7435897
10 5 11 3 3 0.29627244 3.425604e-01 0.1251956 0.7423566 Улучшился не только лучший результат, но и качественный состав 10 лучших, повысились показатели Value. Можно повторить оптимизацию несколько раз, выбирая разные начальные точки (например, попробовать оптимизировать на худших 10 значениях, и т.д.).
Для этого варианта обучения принимаем следующие лучшие гиперпараметры:
> env$OPT_Res1.1$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm 4.0000 1.0000 1.0000 4.0000 0.1870 0.0000 0.9728
Расшифруем их. Получили следующие оптимальные параметры:
- количество нейронов первого скрытого слоя - 2*n1 = 8
- количество нейронов второго скрытого слоя - 2*n2 = 2
- функция активации первого скрытого слоя Fact[fact1] ="tanhdUnit"
- функция активации второго скрытого слоя Fact[fact2] = "sigmoidUnit"
- уровень отсева первого скрытого слоя dr1 = 0.187
- уровень отсева второго скрытого слоя dr2 = 0.0
- уровень обучения SRBM при претренинге Lr.rbm = 0.9729
Кроме того, что был получен в целом хороший результат, сложилась еще и интересная структура DNN (10-8-2-2).
Вариант обучения SRBM + BP
#---SRBM + BP---------------- evalq( OPT_Res2 <- BayesianOptimization(fitnes2.DNN, bounds = bonds2, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)
Посмотрим 10 лучших значений:
> evalq({
+ OPT_Res2 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
+ dplyr::select(-Round) -> best.init2
+ best.init2
+ }, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.fine Value
1 23 24 2 1 0.45133494 0.14589979 0.89897498 0.2325569 0.7612619
2 3 24 4 3 0.07673542 0.42267387 0.59938522 0.4376796 0.7551184
3 15 13 4 1 0.32812018 0.45708556 0.09472489 0.8220925 0.7516732
4 7 18 3 1 0.15980725 0.12045896 0.82638047 0.2752569 0.7473167
5 7 23 3 3 0.37716019 0.23287775 0.61652190 0.9749432 0.7440724
6 21 23 3 1 0.22184400 0.08634275 0.08049532 0.3349808 0.7440647
7 23 8 3 4 0.26182910 0.11339229 0.31787446 0.9639373 0.7429621
8 5 2 1 1 0.25633998 0.27587931 0.17733507 0.4987357 0.7429471
9 1 24 1 2 0.12937722 0.22952235 0.19549144 0.6538553 0.7426660
10 18 8 4 1 0.44986721 0.28928018 0.12523905 0.2441150 0.7384895 Результат хороший, дополнительная оптимизация не требуется.
Лучшие гиперпараметры для этого варианта:
> env$OPT_Res2$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.fine 23.0000 24.0000 2.0000 1.0000 0.4513 0.1459 0.8990 0.2326
Вариант обучения SRBM + upperLayer + BP
#---SRBM + upperLayer + BP---- evalq( OPT_Res3 <- BayesianOptimization(fitnes3.DNN, bounds = bonds3, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)Best Parameters Found: Round = 20 n1 = 24.0000 n2 = 5.0000 fact1 = 1.0000 fact2 = 2.0000 dr1 = 0.4060 dr2 = 0.2790 Lr.rbm = 0.9586 Lr.top = 0.8047 Lr.fine = 0.8687 Value = 0.7697
Посмотрим 10 лучших значений:
evalq({
OPT_Res3 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init3
best.init3
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Lr.fine Value
1 24 5 1 2 0.40597650 0.27897269 0.9585567 0.8046758 0.86871454 0.7696970
2 24 13 1 1 0.02456308 0.08652276 0.9807432 0.8033236 0.87293155 0.7603146
3 7 8 3 3 0.24115850 0.42538540 0.5970306 0.2897183 0.64518524 0.7543239
4 9 15 3 3 0.14951302 0.04013773 0.3734516 0.2499858 0.14993060 0.7521897
5 4 20 3 3 0.45660260 0.12858958 0.8280872 0.1998107 0.08997839 0.7505357
6 21 6 3 1 0.38742051 0.12644262 0.5145560 0.3599426 0.24159111 0.7403176
7 22 3 1 1 0.13356602 0.12940396 0.1188595 0.8979277 0.84890568 0.7369316
8 7 18 3 4 0.44786101 0.33788727 0.4302948 0.2660965 0.75709349 0.7357294
9 25 13 2 1 0.02456308 0.08652276 0.9908265 0.8065841 0.87293155 0.7353894
10 24 17 1 1 0.23273972 0.01572794 0.9193522 0.6654211 0.26861297 0.7346243 Результат хороший, дополнительная оптимизация не требуется.
Лучшие гиперпараметры для этого варианта обучения:
> env$OPT_Res3$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Lr.fine 24.0000 5.0000 1.0000 2.0000 0.4060 0.2790 0.9586 0.8047 0.8687
Вариант обучения SRBM + upperLayer + RP
#---SRBM + upperLayer + RP---- evalq( OPT_Res4 <- BayesianOptimization(fitnes4.DNN, bounds = bonds4, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)Best Parameters Found: Round = 15 n1 = 23.0000 n2 = 7.0000 fact1 = 3.0000 fact2 = 1.0000 dr1 = 0.3482 dr2 = 0.4726 Lr.rbm = 0.0213 Lr.top = 0.5748 Value = 0.7625
10 лучших вариантов гиперпараметров:
evalq({
OPT_Res4 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init4
best.init4
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Value
1 23 7 3 1 0.34823851 0.4726219 0.02129964 0.57482890 0.7625131
2 24 13 3 1 0.38677878 0.1006743 0.72237324 0.42955366 0.7560023
3 1 1 4 3 0.17036760 0.1465872 0.40598393 0.06420964 0.7554773
4 23 7 3 1 0.34471936 0.4726219 0.02129964 0.57405944 0.7536946
5 19 16 3 3 0.25563914 0.1349885 0.83913339 0.77474220 0.7516732
6 8 12 3 1 0.23000115 0.2758919 0.54359416 0.46533472 0.7475112
7 10 8 3 1 0.23661048 0.4030048 0.15234740 0.27667214 0.7458489
8 6 19 1 2 0.18992796 0.4779443 0.98278107 0.84591090 0.7391758
9 11 10 1 2 0.47157135 0.2730922 0.86300945 0.80325083 0.7369316
10 18 21 2 1 0.05182149 0.3503253 0.55296502 0.86458533 0.7359324 Результат хороший, дополнительная оптимизация не требуется.
Принимаем лучшие гиперпараметры для этого варианта обучения:
> env$OPT_Res4$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top 23.0000 7.0000 3.0000 1.0000 0.3482 0.4726 0.0213 0.5748
Обучение и тестирование DNN с оптимальными параметрами
Рассмотрим метрики, полученные при тестировании вариантов.
Вариант SRBM + RP
Для тестирования DNN с оптимальными параметрами напишем специальную функцию. Покажем ее здесь, только для этого варианта обучения. Для остальных вариантов она аналогична.
#---SRBM + RP---------------- test1.DNN <- function(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm) { Ln <- c(0, 2*n1, 2*n2, 0) #-- pretrainSRBM(Ln, fact1, fact2, dr1, dr2, Lr.rbm) -> Dnn fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(250) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(250) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) return(list(Score = Score, Pred = Ypred, Dnn = Dnn, Dnn.opt = Dnn.opt)) }
Параметры функции test1.DNN() — оптимальные гиперпараметры, которые мы получили ранее. Далее мы делаем претренинг функцией pretrainSRBM(), получаем предобученную DNN, которую затем подаем функции тонкой настройки fineTuneRP() и получаем обученную Dnn.opt. Используя эту Dnn.opt и последние 250 значений набора X$test, получаем предсказанные значения целевой Ypred. Используя предсказанные Ypred и актуальные значения целевой yTest, с помощью функции Evaluate() вычисляем ряд метрик. Здесь возможны варианты с выбором метрики. Как результат, функция выдаст список следующих объектов: Score — метрики тестирования, Pred — предсказанные значения целевой, Dnn — предобученная DNN, Dnn.opt — полностью обученная DNN.
Тестируем и смотрим результат с гиперпараметрами, полученными после дополнительной оптимизации:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res1.1$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Ln <- c(0, 2*n1, 2*n2, 0)
#---train/test--------
Res1 <- test1.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
}, env)
env$Res1$Score
Accuracy Precision Recall F1
-1 0.74 0.718 0.724 0.721
1 0.74 0.759 0.754 0.757 Результат хуже, чем после первой оптимизации, есть явный признак переобучения. Тестируем с первоначальными значениями гиперпараметров:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res1$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Ln <- c(0, 2*n1, 2*n2, 0)
#---train/test--------
Res1 <- test1.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
}, env)
env$Res1$Score
Accuracy Precision Recall F1
-1 0.756 0.757 0.698 0.726
1 0.756 0.755 0.806 0.780 Результат хороший. Посмотрим график истории обучения:
plot(env$Res1$Dnn.opt, type = "class")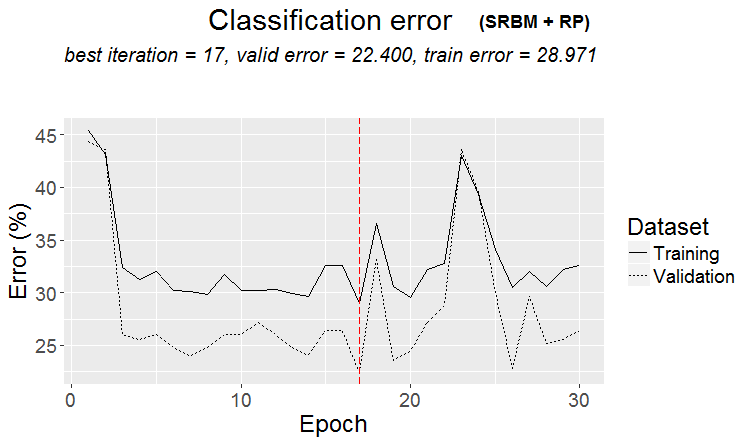 
Рис.2 История обучения DNN по варианту SRBM + RP
Как видно из рисунка, ошибка на валидационном наборе меньше ошибки на обучающем. Это говорит о том, что наша модель не переобучена и обладает хорошей обобщающей способностью. Красная вертикальная черта указывает результаты модели, признанной лучшей и вернувшейся как результат после обучения.
Для остальных трех вариантов обучения приведу только результаты вычислений и графики истории без подробных пояснений. Все вычисляется аналогично.
Вариант SRBM + BP
Тестируем:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res2$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]; Lr.fine = best.par[8]
Ln <- c(0, 2*n1, 2*n2, 0)
#----train/test-------
Res2 <- test2.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine)
}, env)
env$Res2$Score
Accuracy Precision Recall F1
-1 0.768 0.815 0.647 0.721
1 0.768 0.741 0.873 0.801 Можно сказать, что результат отличный. Посмотрим историю обучения:
plot(env$Res2$Dnn.opt, type = "class")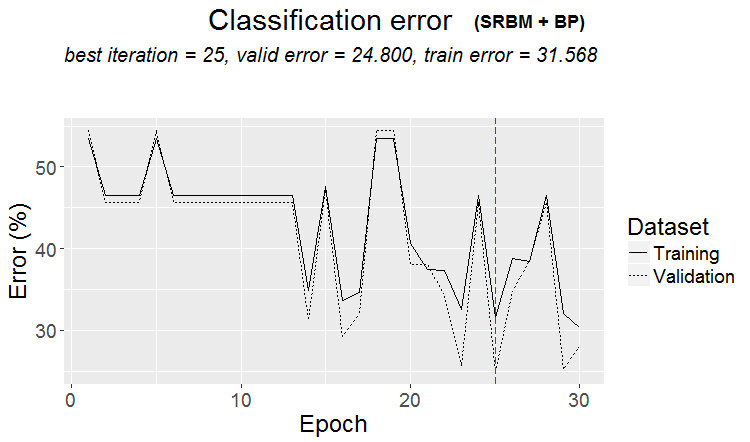 
Рис.3 История обучения DNN по варианту SRBM + ВP
Вариант SRBM + upperLayer + BP
Тестируем:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res3$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Lr.top = best.par[8]
Lr.fine = best.par[9]
Ln <- c(0, 2*n1, 2*n2, 0)
#----train/test-------
Res3 <- test3.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top, Lr.fine)
}, env)
env$Res3$Score
Accuracy Precision Recall F1
-1 0.772 0.771 0.724 0.747
1 0.772 0.773 0.813 0.793 Отличный результат. Обратите внимание, что использование в качестве критерия оптимизации среднего значения F1 дает одинаковое качество для обоих классов, несмотря на дисбаланс между ними.
График истории обучения:
plot(env$Res3$Dnn.opt, type = "class")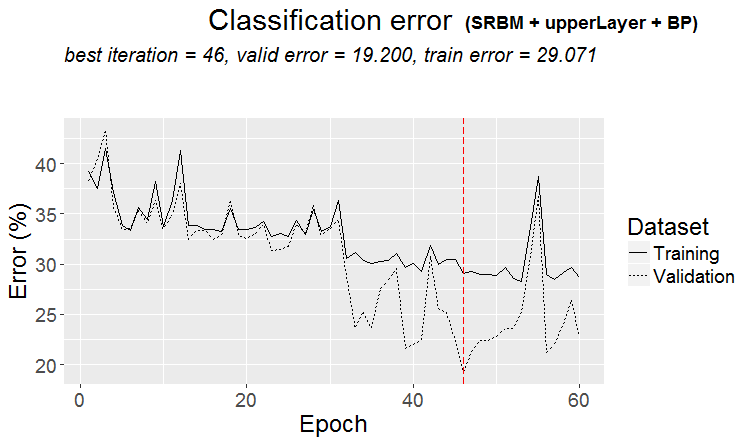 
Рис. 4. История обучения DNN по варианту SRBM + upperLayer + BP
Вариант SRBM + upperLayer + RP
Тестируем:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res4$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Lr.top = best.par[8]
Ln <- c(0, 2*n1, 2*n2, 0)
#----train/test-------
Res4 <- test4.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top)
}, env)
env$Res4$Score
Accuracy Precision Recall F1
-1 0.768 0.802 0.664 0.726
1 0.768 0.747 0.858 0.799 Очень хороший результат. Смотрим график истории обучения:
plot(env$Res4$Dnn.opt, type = "class")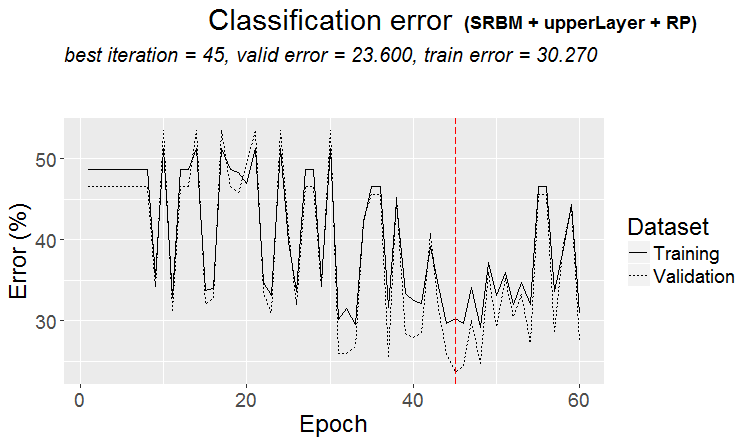 
Рис. 5. История обучения DNN по варианту SRBM + upperLayer + RP
Анализ результатов тестирования DNN с оптимальными параметрами
Результаты обучения и тестирования моделей DNN, обученных по различным вариантам с оптимизированными значениями гиперпараметров, дает хорошие результаты с точностью 75 (+/-5)%. Ошибка классификации в 25% стабильна, не зависит от способа обучения и говорит о том, что структура данных не совпадает со структурой целевой в четверти случаев. Такой же результат мы наблюдали, когда исследовали наличие шумовых примеров в исходном наборе данных. Там их количество тоже составляло около 25% и не зависело от способов трансформации предикторов. Это нормально. Вопрос: как улучшить прогноз без переобучения модели? Я вижу несколько вариантов:
- использовать ансамбль нейросетей из лучших моделей, обученных по 4 вариантам;
- использовать ансамбли нейросетей из 10 лучших моделей, полученных при оптимизации по каждому варианту обучения;
- переразметить шумовые примеры в обучающем наборе в дополнительный класс "0" и по этой целевой (с тремя классами с("-1", "0", "1")) обучить модель DNN;
- переразметить ошибочно классифицированные примеры дополнительным классом "0" и по этой целевой ( с тремя классами с("-1", "0", "1")) обучить модель DNN.
Создание, обучение и использование ансамблей мы рассмотрим подробно в следующей статье этой серии.
Эксперимент с переразметкой (relabel) шумовых примеров заслуживает отдельного исследования и выходит за рамки нашей статьи. Идея проста. С помощью функции ORBoostFilter::NoiseFiltersR, которую мы рассматривали в предыдущей части, определяем шумовые примеры в обучающем и валидационном наборах одновременно. В целевой соответствующие этим примерам значения классов ("-1"/"1") заменяем на класс "0". Т.е. в нашей целевой будет три класса. Так мы попробуем научить модель не классифицировать шумовые примеры, которые, как правило, и дают ошибку классификации. При этом будем исходить из посылки, что упущенная выгода — это не убытки.
Форвард-тест моделей с оптимальными параметрами
Давайте проверим, как долго оптимальные параметры DNN будут давать приемлемые по качеству результаты на тестах "будущих" значений котировок. Тест проведем в окружении, оставшемся после предыдущих оптимизаций и тестирования следующим образом.
Скользящим окном шириной 1350 баров, train = 1000, test = 350 (для валидации первые 250 примеров, для тестирования — последние 100 примеров) c шагом 100 пройдем по данным после первых (4000 + 100) баров, использованных для претренинга. Сделаем 10 шагов "вперед". На каждом шаге будем обучать и тестировать две модели:
- одну — с использованием предобученной DNN, т.е. будем выполнять тонкую настройку на новом диапазоне на каждом шаге;
- вторую — дообучив полученную после оптимизации на этапе тонкой настройки DNN.opt на новом диапазоне.
#---prepare----
evalq({
step <- 1:10
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DTforv <- foreach(i = step, .packages = "dplyr" ) %do% {
SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>%
CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>%
NormData(., preproc = preproc) -> DTn
foreach(i = 1:4) %do% {
DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
} -> DTn
list(pretrain = DTn[[1]],
train = DTn[[2]],
val = DTn[[3]],
test = DTn[[4]]) -> DTn
list(
pretrain = list(
x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$pretrain$Class %>% as.data.frame()
),
train = list(
x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$train$Class %>% as.data.frame()
),
test = list(
x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$val$Class %>% as.data.frame()
),
test1 = list(
x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$test$Class %>% as.vector()
)
)
}
}, env) Проведем первую часть форвард-теста с использованием предобученной DNN и оптимальными гиперпараметрами, полученными по варианту обучения SRBM + upperLayer + BP.
#----#---SRBM + upperLayer + BP---- evalq({ #--BestParams-------------------------- best.par <- OPT_Res3$Best_Par %>% unname # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = best.par[1]; n2 = best.par[2] fact1 = best.par[3]; fact2 = best.par[4] dr1 = best.par[5]; dr2 = best.par[6] Lr.rbm = best.par[7] Lr.top = best.par[8] Lr.fine = best.par[9] Ln <- c(0, 2*n1, 2*n2, 0) foreach(i = step, .packages = "darch" ) %do% { DTforv[[i]] -> X if(i==1) Res3$Dnn -> Dnn #----train/test------- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(100) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) } -> Score3_dnn }, env)
Второй этап форвард-теста с использованием Dnn.opt, полученной при оптимизации:
evalq({
foreach(i = step, .packages = "darch" ) %do% {
DTforv[[i]] -> X
if(i==1) {Res3$Dnn.opt -> Dnn}
#----train/test-------
fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
yTest <- X$test$y[ ,1] %>% tail(100)
#numIncorrect <- sum(Ypred != yTest)
#Score <- 1 - round(numIncorrect/nrow(xTest), 2)
Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
round(3)
} -> Score3_dnnOpt
}, env) Сравним результаты тестирования, оформив их в таблицу:
env$Score3_dnn env$Score3_dnnOpt
| iter | Score3_dnn | Score3_dnnOpt |
|---|---|---|
| Accuracy Precision Recall F1 | Accuracy Precision Recall F1 | |
| 1 | -1 0.76 0.737 0.667 0.7 1 0.76 0.774 0.828 0.8 | -1 0.77 0.732 0.714 0.723 1 0.77 0.797 0.810 0.803 |
| 2 | -1 0.79 0.88 0.746 0.807 1 0.79 0.70 0.854 0.769 | -1 0.78 0.836 0.78 0.807 1 0.78 0.711 0.78 0.744 |
| 3 | -1 0.69 0.807 0.697 0.748 1 0.69 0.535 0.676 0.597 | -1 0.67 0.824 0.636 0.718 1 0.67 0.510 0.735 0.602 |
| 4 | -1 0.71 0.738 0.633 0.681 1 0.71 0.690 0.784 0.734 | -1 0.68 0.681 0.653 0.667 1 0.68 0.679 0.706 0.692 |
| 5 | -1 0.56 0.595 0.481 0.532 1 0.56 0.534 0.646 0.585 | -1 0.55 0.578 0.500 0.536 1 0.55 0.527 0.604 0.563 |
| 6 | -1 0.61 0.515 0.829 0.636 1 0.61 0.794 0.458 0.581 | -1 0.66 0.564 0.756 0.646 1 0.66 0.778 0.593 0.673 |
| 7 | -1 0.67 0.55 0.595 0.571 1 0.67 0.75 0.714 0.732 | -1 0.73 0.679 0.514 0.585 1 0.73 0.750 0.857 0.800 |
| 8 | -1 0.65 0.889 0.623 0.733 1 0.65 0.370 0.739 0.493 | -1 0.68 0.869 0.688 0.768 1 0.68 0.385 0.652 0.484 |
| 9 | -1 0.55 0.818 0.562 0.667 1 0.55 0.222 0.500 0.308 | -1 0.54 0.815 0.55 0.657 1 0.54 0.217 0.50 0.303 |
| 10 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
Мы видим из таблицы, что первые два шага дают хорошие результаты. Качество на первых 2 шагах по обоим вариантам фактически равное, а дальше падает. Поэтому можно говорить о том, что после оптимизации и тестирования DNN будет обеспечивать качество классификации на уровне тестового набора как минимум на 200-250 следующих барах.
Есть много других комбинаций по дообучению модели на форвард-тестах о которых мы говорили в предыдущей статье, и множество гиперпараметров, которые можно подрегулировать.
Заключение
- Пакет darch v.0.12 предоставляет доступ к огромному перечню гиперпараметров DNN, обеспечивая большие возможности по глубокой и тонкой настройке.
- Использование байесовского подхода для оптимизации гиперпараметров DNN дает широкий выбор моделей с хорошим качеством, что можно использовать для создания ансамблей.
- Оптимизация гиперпараметров DNN байесовским методом дает повышение качества классификации на 7-10%.
- Для получения наилучшего результата необходимо проводить несколько оптимизаций (10 — 20) с последующим выбором лучшего результата.
- Процесс оптимизации можно продолжать поэтапно, предоставляя в качестве начальных значений параметры, полученные в предварительных прогонах.
- Применение в DNN полученных при оптимизации гиперпараметров обеспечивает качество классификации на форвард-тесте на уровне тестового на участке с длиной, равной тестовому набору.
Для дальнейшего улучшения имеет смысл включить в перечень оптимизируемых параметров функцию обучения rpropagation в 4 вариантах, нормализацию весов нейронов в скрытых слоях normalizeWeights(TRUE, FALSE) и верхнюю границу этой нормализации normalizeWeightsBound. Можно поэкспериментировать и с другими параметрами, которые, по вашему мнению, могут влиять на качество классификации модели. Одно из главных преимуществ пакета darch как раз и состоит в том, что нам предоставлен доступ ко всем параметрам нейросети. Мы можем экспериментально определить, как влияет каждый параметр на качество классификации.
Несмотря на значительные затраты времени, применение байесовской оптимизации целесообразно.
Другой возможностью улучшить качество классификации представляется использование ансамбля нейросетей. Этот вариант усиления в различных вариантах мы рассмотрим в следующей части статьи.
Приложение
В GitHub/PartV находятся:
1. FUN_Optim.R — функции, необходимые для проведения всех вычислений, описанных в этой статье.
2. RUN_Optim.R — вычисления, проведенные в этой статье.
3. SessionInfo. txt — пакеты, использованные при вычислении.
LifeHack для трейдера: замешиваем ForEach на дефайнах (#define)
LifeHack для трейдера: готовим фастфуд из индикаторов
ZUP - зигзаг универсальный с паттернами Песавенто. Поиск паттернов
Автоматическое построение линий поддержки и сопротивления
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Для ускорения добавьте в параметры при вызове BayesianOptimization
maxit = 1 #1 вместо 100 - число повторов для GP_fit для предсказания гиперплоскости
maxit=1 через ... пердастся в GPfit::GP_fit и оптимизация будет 1 раз запускаться вместо 100.Не заметил улучшений при 100 повторах в сравнении с 1, поэтому использую 1.
Т.е.
Еще можно передать:
control = c(20*d, 10*d, 2*d);#по умолчанию - control = c(200*d, 80*d, 2*d) - из 200*d выбрать 80*d лучших и построить 2*d кластеров - где d - число оптимизируемых параметров
Да вроде и с Darch 30% при обучении и 36% на тесте получается. Доделаю советник, запущу в работу, а потом может займусь.
Хотя Darch плохо поддерживается, кое что они поправили и доработали, но в январе его из CRAN в архив отправили за неисправление ошибок (там была одна с оценкой ошибки в режиме обучения с валидацией). В мае выпустили 13 версию, но потом откатили к 12-й. Сейчас вот опять 13-я появилась - видимо доделали.
Спасибо за информацию. Попробую с Вашими параметрами.
Я давно к ним не заходил на Github. Нужно будет предложение написать. В пакете darch предусмотрено использование GPU но пакет который они используют для этого из CRAN удалили (для 3.4.4). А было бы интересно как повлияет GPU на скорость и качество.
Удачи
Еще один тормоз тут
https://github.com/yanyachen/rBayesianOptimization/blob/master/R/Utility_Max.R
Тоже ставлю maxit = 1 вместо 100.
Через ... передать нельзя, можно просто свою Utility_Max функцию в R загрузить и пользоваться исправленной версией.
Еще один тормоз тут
https://github.com/yanyachen/rBayesianOptimization/blob/master/R/Utility_Max.R
Тоже ставлю maxit = 1 вместо 100.
Через ... передать нельзя, можно просто свою Utility_Max функцию в R загрузить и пользоваться исправленной версией.
Проверил на оптимизации ансамбля нейросетей из статьи PartVI. Ни maxit, ни control не оказывают видимого влияния на время вычисления. Наибольшее влияние оказывает количество нейронов в скрытом слое. Оставил так
OPT_Res <- BayesianOptimization(fitnes, bounds = bonds, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100, control = c(100, 50, 8)) elapsed = 14.42 Round = 1 numFeature = 9.0000 r = 7.0000 nh = 36.0000 fact = 9.0000 Value = 0.7530 elapsed = 42.94 Round = 2 numFeature = 4.0000 r = 8.0000 nh = 46.0000 fact = 6.0000 Value = 0.7450 elapsed = 9.50 Round = 3 numFeature = 11.0000 r = 5.0000 nh = 19.0000 fact = 5.0000 Value = 0.7580 elapsed = 14.17 Round = 4 numFeature = 10.0000 r = 4.0000 nh = 35.0000 fact = 4.0000 Value = 0.7480 elapsed = 12.36 Round = 5 numFeature = 8.0000 r = 4.0000 nh = 23.0000 fact = 6.0000 Value = 0.7450 elapsed = 25.61 Round = 6 numFeature = 12.0000 r = 8.0000 nh = 44.0000 fact = 7.0000 Value = 0.7490 elapsed = 8.03 Round = 7 numFeature = 12.0000 r = 9.0000 nh = 9.0000 fact = 2.0000 Value = 0.7470 elapsed = 14.24 Round = 8 numFeature = 8.0000 r = 4.0000 nh = 45.0000 fact = 2.0000 Value = 0.7620 elapsed = 9.05 Round = 9 numFeature = 7.0000 r = 8.0000 nh = 20.0000 fact = 10.0000 Value = 0.7390 elapsed = 17.53 Round = 10 numFeature = 12.0000 r = 9.0000 nh = 20.0000 fact = 6.0000 Value = 0.7410 elapsed = 4.77 Round = 11 numFeature = 9.0000 r = 2.0000 nh = 7.0000 fact = 2.0000 Value = 0.7570 elapsed = 8.87 Round = 12 numFeature = 6.0000 r = 1.0000 nh = 40.0000 fact = 8.0000 Value = 0.7730 elapsed = 14.16 Round = 13 numFeature = 8.0000 r = 6.0000 nh = 41.0000 fact = 10.0000 Value = 0.7390 elapsed = 21.61 Round = 14 numFeature = 9.0000 r = 6.0000 nh = 47.0000 fact = 7.0000 Value = 0.7620 elapsed = 5.14 Round = 15 numFeature = 13.0000 r = 3.0000 nh = 3.0000 fact = 5.0000 Value = 0.7260 elapsed = 5.66 Round = 16 numFeature = 6.0000 r = 9.0000 nh = 1.0000 fact = 9.0000 Value = 0.7090 elapsed = 7.26 Round = 17 numFeature = 9.0000 r = 2.0000 nh = 25.0000 fact = 1.0000 Value = 0.7550 elapsed = 32.09 Round = 18 numFeature = 11.0000 r = 7.0000 nh = 38.0000 fact = 6.0000 Value = 0.7600 elapsed = 17.18 Round = 19 numFeature = 5.0000 r = 3.0000 nh = 46.0000 fact = 6.0000 Value = 0.7500 elapsed = 11.08 Round = 20 numFeature = 6.0000 r = 4.0000 nh = 20.0000 fact = 6.0000 Value = 0.7590 elapsed = 4.47 Round = 21 numFeature = 6.0000 r = 2.0000 nh = 4.0000 fact = 2.0000 Value = 0.7390 elapsed = 5.27 Round = 22 numFeature = 6.0000 r = 2.0000 nh = 21.0000 fact = 10.0000 Value = 0.7520 elapsed = 7.96 Round = 23 numFeature = 7.0000 r = 1.0000 nh = 41.0000 fact = 7.0000 Value = 0.7730 elapsed = 12.31 Round = 24 numFeature = 7.0000 r = 3.0000 nh = 41.0000 fact = 3.0000 Value = 0.7730 elapsed = 7.64 Round = 25 numFeature = 8.0000 r = 4.0000 nh = 16.0000 fact = 7.0000 Value = 0.7420 elapsed = 6.24 Round = 26 numFeature = 13.0000 r = 5.0000 nh = 6.0000 fact = 1.0000 Value = 0.7600 elapsed = 8.41 Round = 27 numFeature = 11.0000 r = 8.0000 nh = 8.0000 fact = 7.0000 Value = 0.7420 elapsed = 8.48 Round = 28 numFeature = 6.0000 r = 7.0000 nh = 15.0000 fact = 2.0000 Value = 0.7580 elapsed = 10.11 Round = 29 numFeature = 12.0000 r = 6.0000 nh = 17.0000 fact = 4.0000 Value = 0.7310 elapsed = 6.03 Round = 30 numFeature = 8.0000 r = 3.0000 nh = 12.0000 fact = 1.0000 Value = 0.7540 elapsed = 8.58 Round = 31 numFeature = 13.0000 r = 5.0000 nh = 18.0000 fact = 2.0000 Value = 0.7300 elapsed = 6.78 Round = 32 numFeature = 13.0000 r = 2.0000 nh = 15.0000 fact = 8.0000 Value = 0.7320 elapsed = 9.54 Round = 33 numFeature = 10.0000 r = 3.0000 nh = 37.0000 fact = 9.0000 Value = 0.7420 elapsed = 8.19 Round = 34 numFeature = 6.0000 r = 1.0000 nh = 42.0000 fact = 3.0000 Value = 0.7630 elapsed = 12.34 Round = 35 numFeature = 7.0000 r = 2.0000 nh = 43.0000 fact = 8.0000 Value = 0.7570 elapsed = 20.47 Round = 36 numFeature = 7.0000 r = 8.0000 nh = 39.0000 fact = 2.0000 Value = 0.7670 elapsed = 11.51 Round = 37 numFeature = 5.0000 r = 9.0000 nh = 18.0000 fact = 3.0000 Value = 0.7540 elapsed = 32.71 Round = 38 numFeature = 7.0000 r = 7.0000 nh = 40.0000 fact = 6.0000 Value = 0.7540 elapsed = 28.33 Round = 39 numFeature = 7.0000 r = 9.0000 nh = 38.0000 fact = 5.0000 Value = 0.7550 elapsed = 22.87 Round = 40 numFeature = 12.0000 r = 6.0000 nh = 48.0000 fact = 3.0000 Value = 0.7580 Best Parameters Found: Round = 12 numFeature = 6.0000 r = 1.0000 nh = 40.0000 fact = 8.0000 Value = 0.7730 maxit = 100, control = c(100, 50, 8))Лучших 10
Value - средний F1. Неплохие показатели.
Для ускорения вычислений нужно переписать некоторые функции пакета. Самое первое - заменить все ncol(), nrow() которых там море на dim()[1], dim()[2]. Они исполняются в десятки раз быстрее. Ну и наверное, поскольку там только матричные операции, использовать GPU (пакет gpuR ). Сам я это сделать не смогу, может предложить разработчику?
Удачи
Проверил на оптимизации ансамбля нейросетей из статьи PartVI. Ни maxit, ни control не оказывают видимого времени иполнения. Наибольшее влияние оказывает количество нейронов в скрытом слое. Оставил так
Лучших 10
Value - средний F1. Неплохие показатели.
Для ускорения вычислений нужно переписать некоторые функции пакета. Самое первое - заменить все ncol(), nrow() которых там море на dim()[1], dim()[2]. Они исполняются в десятки раз быстрее. Ну и наверное, поскольку там только матричные операции. использовать GPU (пакет gpuR ). Сам я это сделать не смогу, может предложить разработчику?
Удачи
Просто вы оптимизируете мало параметров, я штук 20 оптимизировал, и когда известных точек становится 20-40 штук, тогда расчет только GPfit занимал десятки минут, вот в таких условиях и будет видно ускорение.
А число нейронов влияет только на время расчета самой НС.
Просто вы оптимизируете мало параметров, я штук 20 оптимизировал, и когда известных точек становится 20-40 штук, тогда расчет только GPfit занимал десятки минут, вот в таких условиях и будет видно ускорение.
А число нейронов влияет только на время расчета самой НС.
Наверное так.