Глубокие нейросети (Часть VI). Ансамбль нейросетевых классификаторов: bagging

Содержание

• Введение
1. Ансамбли нейросетевых классификаторов
2. bagging
• Формирование исходных наборов данных
• Упорядочивание предикторов по информационной важности
• Создание, обучение и тестирование ансамбля классификаторов
• Объединение индивидуальных выходов классификаторов (averaging/voting)
• Обрезка ансамбля и ее методы
• Оптимизация гиперпараметров членов ансамбля. Особенности и методы
• Обучение и тестирование ансамбля с оптимальными гиперпараметрами
• Заключение
• Приложение

Введение

В предыдущей статье этой серии мы оптимизировали гиперпараметры модели DNN, обучили ее несколькими вариантами и протестировали. Качество полученной модели оказалось довольно высоким.

Также мы обсудили возможности того, как можно улучшить качество классификации. Одна из них — использовать ансамбль нейросетей. Этот вариант усиления мы и рассмотрим в настоящей статье.

1. Ансамбли нейросетевых классификаторов

Исследования показывают, что ансамбли классификаторов обычно более точны, чем индивидуальные классификаторы. Один из таких ансамблей изображен на рис.1а. В нем использованы несколько классификаторов, каждый из которых принимает решение об объекте, представленном на входе. Затем эти индивидуальные решения агрегируются в объединителе. На выходе ансамбль выдает метку класса для объекта.

Интуитивно понятно, что невозможно дать строгое определение ансамбля классификаторов. Эту общую неопределенность иллюстрируют рис.1 b-d. По своей сути, любой ансамбль сам является классификатором (рис. 1b). Составляющие его базовые классификаторы будут извлекать из потока данных сложные функции закономерностей (зачастую неявных), а объединитель станет простым классификатором, который агрегирует эти функции.

С другой стороны, ничто не мешает нам назвать ансамблем обычный стандартный нейросетевой классификатор (рисунок 1c).  Нейроны на его предпоследнем слое можно рассматривать как отдельные классификаторы. Их решения должны быть «дешифрованы» в объединителе, роль которого играет верхний слой.

И, наконец, мы можем считать функции примитивными классификаторами, а классификатор — их сложным объединителем (рисунок 1d)

Мы объединяем простые обучаемые классификаторы, чтобы получить точное классификационное решение. Но в верном ли направлении мы движемся?

В своей критической обзорной статье «Объединение нескольких классификаторов: уроки и следующие шаги", опубликованной в 2002 году, Тин Хо пишет:

"Вместо того, чтобы искать лучшие набор функций и классификатор, теперь мы ищем лучший набор классификаторов, а затем лучший метод их сочетания. Можно себе представить, что очень скоро мы будем искать лучший набор комбинационных методов, а затем лучший способ использовать их все. Если мы не рассмотрим фундаментальные проблемы, возникающие в связи с этим вызовом, мы неизбежно столкнемся с таким бесконечным повторением, затягивая все более сложные схемы и теории комбинирования и постепенно теряя из виду исходную проблему"

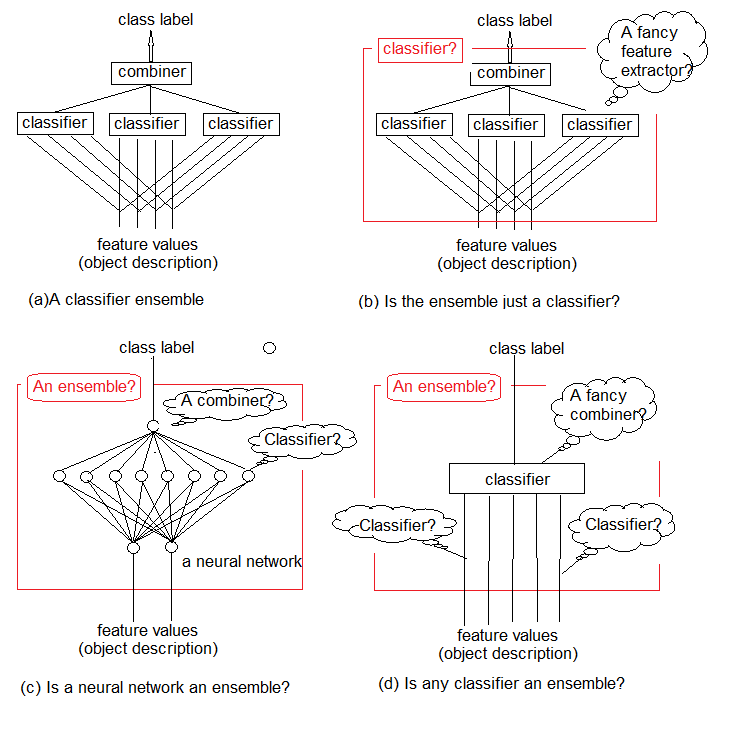
Рис.1. Что такое ансамбль классификаторов?

Известно, что классификаторы нейронных сетей — «универсальные аппроксиматоры». Это означает, что любая граница классификации, сколь бы сложной она ни была, может быть аппроксимирована конечной нейронной сетью с любой требуемой точностью. Однако это знание не дает нам способа для создания или обучения такой сети. Идея объединения классификаторов — это попытка решить проблему, составив сеть из управляемых строительных блоков.

Методы составления ансамбля — это мета-алгоритмы, которые объединяют несколько методов машинного обучения в одну прогностическую модель, чтобы:

• уменьшить дисперсию (variance) — bagging;
• уменьшить смещение (bias) — boosting;
• улучшить прогнозы — stacking.

Эти методы можно разделить на две группы:

• параллельные методы построения ансамбля, когда базовые модели генерируются параллельно (например, случайный лес). Смысл — в том, чтобы использовать независимость между базовыми моделями, а ошибку уменьшить методом усреднения. Отсюда основное требование к моделям — низкая взаимная корреляция и широкое разнообразие.
• последовательные ансамблевые методы, в которых базовые модели генерируются последовательно (например, AdaBoost, XGBoost). Основная идея здесь — использовать зависимость между базовыми моделями. Общее качество здесь можно повысить за счет присвоения более высоких весов тем примерам, которые ранее были неправильно классифицированы.

Большинство ансамблевых методов при создании однородных базовых моделей используют единый базовый алгоритм обучения. Это приводит к однородным ансамблям. Есть и методы, использующие гетерогенные модели (модели разных типов). В результате образуются гетерогенные ансамбли. Чтобы ансамбли были более точными, чем любой их отдельный член, базовые модели должны быть максимально разнообразными. Другими словами, чем больше информации поступает от базовых классификаторов, тем выше точность ансамбля.

На рис. 2 показаны 4 уровня создания ансамбля классификаторов. На каждом из них возникают вопросы, ответы на которые мы разберем ниже.

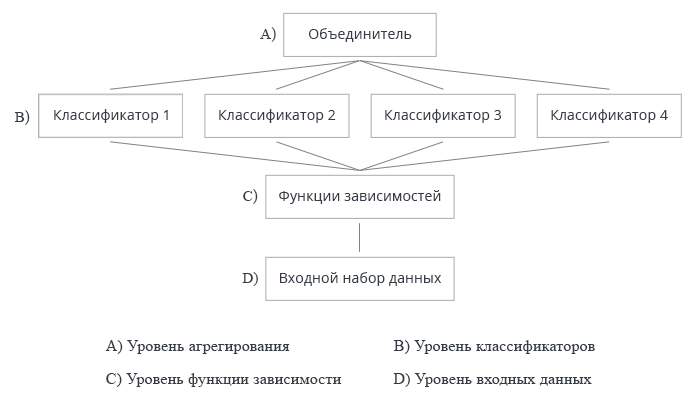
Рис.2. Четыре уровня создания ансамбля классификаторов

Поговорим об этом подробнее.

1. Объединитель

Некоторые ансамблевые методы не определяют объединитель. Но для тех методов, которые это делают, есть три типа объединителей. 

• Необучаемый (Nontrainable). Пример такого  метода — простое "большинство голосов" (majority voting).
• Обучаемый (Trainable). Эта группа включает "взвешенное большинство голосов" (weighted majority voting) и Naive Bayes, а также подход “classifier selection”, в котором решение по данному объекту принимает один классификатор ансамбля.
• Мета-классификатор (Meta classifier). Выходы базовых классификаторов рассматриваются как входные данные для нового обучаемого классификатора, который и становится объединителем. Этот подход называется «сложное обобщение», "обобщение через обучение", или просто stacking. Построение учебного набора для мета-классификатора — одна из основных проблем этого объединителя.

2. Построение ансамбля

Параллельно (независимо) или последовательно нужно обучать базовые классификаторы? Пример последовательного обучения — AdaBoost, где учебный набор каждого добавленного классификатора зависит от ансамбля, созданного до него.

3. Разнообразие

Как генерировать различия в ансамбле? Предлагаются следующие варианты.

• Манипулировать параметрами обучения. Используйте различные подходы и параметры при обучении отдельных базовых классификаторов. Например, можно инициировать веса нейронов скрытых слоев нейросети каждого базового классификатора различными случайными величинами. А можно устанавливать гиперпараметры случайным образом.
• Манипулировать выборками — брать свой образец бутстрапа из обучающего набора для каждого члена ансамбля.
• Манипулировать предикторами — для каждого базового классификатора готовить свой набор предикторов, определяемый случайным образом. Это так называемое вертикальное разбиение обучающего набора.

4. Размер ансамбля

Как определить количество классификаторов в ансамбле? Построен ли ансамбль путем одновременного обучения необходимого количества классификаторов или итеративно, путем добавления/удаления классификаторов? Возможные варианты:

• Количество зарезервировано заранее
• Количество устанавливается в ходе обучения
• Происходит перепроизводство классификаторов и последующий их выбор

5. Универсальность (относительно базового классификатора)

Некоторые ансамблевые подходы могут использоваться с любой моделью классификаторов, а другие привязаны к определенному их типу. Пример "классификатор-специфичного" ансамбля — случайный лес (Random Forest). Его базовый классификатор — решающее дерево. Итак, два варианта подходов:

• может использоваться только определенная модель базового классификатора;
• может использоваться любая модель базового классификатора.

Обучая и оптимизируя параметры ансамбля классификаторов, нужно различать оптимизацию решения и оптимизацию покрытия.

• Оптимизация принятия решений относится к выбору объединителя для фиксированного ансамбля базовых классификаторов (уровень A на рис. 2).
• Оптимизация альтернативного покрытия относится к созданию разнообразных базовых классификаторов с фиксированным объединителем (уровни B, C и D на рис.2).

Эта декомпозиция конструкции ансамбля уменьшает сложность задачи, поэтому представляется разумной.

Очень подробно и глубоко ансамблевые методы рассмотрены в книге Combining Pattern Classifiers. Methods and Algorithms, Second Edition. Ludmila Kuncheva и Ensemble Methods. Foundations and Algorithms. Рекомендую ознакомится.

2. Bagging

Название метода произошло от словосочетания Bootstrap AGGregatING. Bagging-ансамбли создаются так:

1. из обучающего набора извлекается бутстрап-выборка;
2. каждый классификатор обучается на своей выборке;
3. индивидуальные выходы от отдельных классификаторов комбинируются в одну метку класса. Если индивидуальные выходы имеют вид метки класса, то применяется голосование простым большинством. Если же на выходах классификаторов непрерывная переменная, то применяется либо усреднение, либо перевод этой переменной в метку класса и далее голосование простым большинством.
   

Вернемся к рисунку 2 и разберем все уровни создания ансамбля классификаторов в применении к методу bagging.

А: уровень агрегирования

На этом уровне происходит объединение данных, полученных от классификаторов, и агрегирование единого выхода.

Как же мы будем объединять индивидуальные выходы? Используем подход с использованием необучаемого объединителя (усреднение, простое большинство голосов).

B: уровень классификаторов

На уровне В идет вся работа с классификаторами. Вопросов здесь возникает несколько.

• Разные или одинаковые классификаторы мы используем? При подходе bagging используются одинаковые классификаторы.
• Какой классификатор принят за базовый? Мы используем ELM (Extreme Learning Machines).
  

Остановимся на этом моменте подробнее. Выбор классификатора и его обоснование — важный элемент работы. Перечислим основные требования к базовым классификаторам для качественного ансамбля. 

Во-первых, классификатор должен быть простым: применять глубокие нейросети не рекомендуется. 

Во-вторых, классификаторы должны быть разными: с разной инициализацией, параметрами обучения, обучающими наборами и т.д.

В-третьих, важна скорость классификатора: модели не должны обучаться часами.

В-четвертых, модели классификации должны быть слабыми и давать результат предсказания чуть лучше 50%.

И, наконец, в-пятых, важна нестабильность классификатора, чтобы результаты предсказания имели большой разброс.

У нас есть претендент, который соответствует всем этим требованиям. Это особый вид нейросети — ELM (экстремальные обучающие машины) были предложены в качестве альтернативных алгоритмов обучения вместо MLP. Формально это полносвязная нейронная сеть с одним скрытым слоем. Но отсутствие итерационного процесса определения весов (обучение) делает его исключительно быстрым. Он выбирает веса нейронов скрытого слоя случайным образом один раз при инициализации и затем аналитически определяет их выходной вес в соответствии с выбранной функцией активации. Подробное описание алгоритма ELM и обзор его многочисленных разновидностей вы найдете в архиве в приложении.

• Сколько классификаторов необходимо? Примем 500 с последующей обрезкой ансамбля.
  
• Используется параллельное или последовательное обучение классификаторов? Мы используем параллельное обучение, которое происходит одновременно для всех классификаторов.  
• Какими параметрами базовых классификаторов мы можем манипулировать? Количеством скрытых нейронов, функцией активации, размером выборки обучающего набора. Все эти параметры подлежат оптимизации.

С: уровень функций найденных закономерностей

• Используются все предикторы или только индивидуальные подмножества для каждого классификатора? Все классификаторы используют одно подмножество предикторов. Но количество предикторов может быть оптимизировано.
  
• Как мы выбираем/извлекаем такое подмножество? В нашем случае используются специальные алгоритмы.
  

D: уровень входных данных и манипуляций с ними

На этом уровне происходит подача исходных данных на вход нейронной сети для обучения.

Как манипулировать входными данными, чтобы обеспечить высокое разнообразие и высокую индивидуальную точность? Будем использовать бутстрап-выборки для каждого классификатора индивидуально. Размер бутстрап-выборки для всех членов ансамбля одинаков, но будет оптимизирован.

Для проведения экспериментов с ансамблями ELM у нас есть два пакета в R (elmNN, ELMR) и один пакет в Python (hpelm). Пока проверим возможности пакета elmNN, в котором реализована классическая ELM. Пакет elmNN предназначен для создания, обучения и тестирования ELM batch-методом. Таким образом, обучающая и тестовая выборки готовы до обучения и подаются модели один раз. Пакет очень простой.

Эксперимент будет состоять из следующих этапов.

1. Формирование исходных наборов данных
   
2. Упорядочивание предикторов по информационной важности
3. Обучение и тестирование ансамбля классификаторов
4. Объединение индивидуальных выходов классификаторов (averaging/voting)
   
5. Обрезка ансамбля и ее методы
6. Поиск метрик качества классификации ансамбля
7. Определение оптимальных параметров членов ансамбля. Методы
8. Обучение и тестирование ансамбля с оптимальными параметрами

Формирование исходных наборов данных

Для проведения экспериментов будем использовать последнюю версию MRO 3.4.3. В ней реализованы несколько новых для нас пакетов.

Запускаем RStudio, загружаем из GitHub/Part_I файл Cotir.RData, с котировками, полученными из терминала, и файл FunPrepareData.R с функциями подготовки данных из GitHub/Part_IV.

Ранее мы определили, что набор данных с импутированными выбросами и нормализованными данными позволяет получить лучшие результаты при обучении с претренингом. Его и будем использовать. Вы можете проверить и другие варианты препроцессинга, которые мы рассматривали ранее.

При разделении на pretrain/train/val/test-разделы используем первую возможность улучшения качества классификации — увеличим количество примеров для обучения. В разделе pretrain количество примеров увеличим до 4000.

#----Prepare-------------
library(anytime)
library(rowr)
library(elmNN)
library(rBayesianOptimization)
library(foreach)
library(magrittr)
library(clusterSim)
#source(file = "FunPrepareData.R")
#source(file = "FUN_Ensemble.R")
#---prepare----
evalq({
  dt <- PrepareData(Data, Open, High, Low, Close, Volume)
  DT <- SplitData(dt, 4000, 1000, 500, 250, start = 1)
  pre.outl <- PreOutlier(DT$pretrain)
  DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl)
  preproc <- PreNorm(DTcap, meth = meth)
  DTcap.n <- NormData(DTcap, preproc = preproc)
}, env)

Изменяя параметр start в функции SplitData(), мы можем получать наборы, сдвинутые вправо на величину start. Это позволит нам в будущем проверить качество на разных участках диапазона цен и определить, как оно изменяется на истории.

Создадим наборы данных (pretrain/train/test/test1) для обучения и тестирования, собранные в список X. Преобразуем целевую из факторной в номинальную (0,1).

#---Data X-------------
evalq({
  list(
    pretrain = list(
      x = DTcap.n$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DTcap.n$pretrain$Class %>% as.numeric() %>% subtract(1) 
    ),
    train = list(
      x = DTcap.n$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DTcap.n$train$Class %>% as.numeric() %>% subtract(1) 
    ),
    test = list(
      x = DTcap.n$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DTcap.n$val$Class %>% as.numeric() %>% subtract(1) 
    ),
    test1 = list(
      x = DTcap.n$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), 
      y = DTcap.n$test$Class %>% as.numeric() %>% subtract(1) 
    )
  ) -> X
}, env)

Упорядочивание предикторов по информационной важности

Протестируем функцию clusterSim::HINoV.Mod() (подробное описание смотрите в пакете). Она ранжирует переменные на основании кластеризации с различными дистанциями и методами. Будем использовать параметры по умолчанию. Вы можете поэкспериментировать с другими параметрами. Константа numFeature <- 10 дает возможность изменять количество лучших предикторов bestF, подаваемых модели.

require(clusterSim)
evalq({
  numFeature <- 10
  HINoV.Mod(x = X$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, 
            distance =  NULL, # "d1" - Manhattan, "d2" - Euclidean, 
            #"d3" - Chebychev (max), "d4" - squared Euclidean, 
            #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
            method = "kmeans" ,#"kmeans" (default) , "single", 
            #"ward.D", "ward.D2", "complete", "average", "mcquitty", 
            #"median", "centroid", "pam"
            Index = "cRAND") -> r
  r$stopri[ ,1] %>% head(numFeature) -> bestF
}, env)
print(env$r$stopri)
      [,1]      [,2]
 [1,]    5 0.9242887
 [2,]   11 0.8775318
 [3,]    9 0.8265240
 [4,]    3 0.6093157
 [5,]    6 0.6004115
 [6,]   10 0.5730556
 [7,]    1 0.5722479
 [8,]    7 0.4730875
 [9,]    4 0.3780357
[10,]    8 0.3181561
[11,]    2 0.2960231
[12,]   12 0.1009184

В каком порядке ранжированы предикторы, видно в листинге кода выше. Ниже показаны 10 лучших, которые мы будем использовать в дальнейшем.

> colnames(env$X$pretrain$x)[env$bestF]
 [1] "v.fatl" "v.rbci" "v.ftlm" "rbci"   "v.satl" "v.stlm" "ftlm"  
 [8] "v.rftl" "pcci"   "v.rstl"

Наборы для проведения экспериментов готовы.

Функцию Evaluate(), вычисляющую метрики по результатам тестирования, возьмем из предыдущей статьи этой серии. Значение mean(F1) будем использовать как критерий оптимизации (максимизации). Загрузим эту функцию в окружение env.

Создание, обучение и тестирование ансамбля

Обучим ансамбль нейросетей (n <- 500 шт), объединив их в Ens. Каждую нейросеть обучаем на своей выборке. Выборку формируем извлечением из обучающего набора 7/10 примеров случайным образом с замещением. Для модели нужно установить два параметра: nh — количество нейронов в скрытом слое и act — активационную функцию. Пакет предлагает следующие варианты активационных функций:

1. - sig: sigmoid
2. - sin: sine
3. - radbas: radial basis
4. - hardlim: hard-limit
5. - hardlims: symmetric hard-limit
6. - satlins: satlins
7. - tansig: tan-sigmoid
8. - tribas: triangular basis
9. - poslin: positive linear
10. - purelin: linear

Учитывая, что у нас 10 входных переменных, предварительно примем nh = 5. Функцию активации принимаем actfun = "sin". Обучается ансамбль быстро. Параметры я выбрал интуитивно, на основании опыта работы с нейросетями. Вы можете попробовать другие варианты.

#---3-----Train----------------------------
evalq({
  n <- 500
  r <- 7
  nh <- 5
  Xtrain <- X$pretrain$x[ , bestF]
  Ytrain <- X$pretrain$y 
  Ens <- foreach(i = 1:n, .packages = "elmNN") %do% {
    idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr
    elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], 
             nhid = nh, actfun = "sin")
  }
}, env)

Коротко поговорим о вычислениях в скрипте. Определяем константы n (количество нейросетей в ансамбле) и r  (размер бутстрап-выборки, подаваемой на обучение нейросети. Для каждой нейросети в ансамбле эта выборка будет различна). nh — количество нейронов в скрытом слое. Далее определяем набор входных даных Xtrain, используя основой набор X$pretrain и оставив в нем только определенные bestF предикторы.

У нас получился ансамбль Ens[[500]] из 500 индивидуальных нейросетевых классификаторов. Протестируем его на тестовом наборе Xtest, полученном из основного набора X$train с лучшими bestF предикторами. Получим в результате y.pr[1001, 500] - датафрейм из 500 непрерывных предсказательных переменных.

#---4-----predict-------------------
evalq({
  Xtest <- X$train$x[ , bestF]
  Ytest <- X$train$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
    predict(Ens[[i]], newdata = Xtest)
  } -> y.pr #[ ,n]
}, env)

Объединение индивидуальных выходов классификаторов. Методы (averaging/voting)

Базовые классификаторы ансамбля могут иметь следующие типы выходов:

• Метки классов (Class labels)
• Ранг меток классов (Ranked class labels), при классификации с количеством классов >2
• Непрерывное числовое предсказание/степень поддержки.

Наши базовые классификаторы имеют на выходе непрерывную числовую переменную (степень поддержки). Степени поддержки для данного входа Х можно интерпретировать по-разному. Это может быть достоверность предложенных меток и оценка возможных вероятностей для классов. Для нашего случая выходом будет достоверность предложенных классификационных меток.

Первый вариант объединения — усреднение: получаем среднее значение индивидуальных выходов. Затем переводим его в метки класса, при этом порог перехода принимаем равным 0.5.

Второй вариант объединения — простое голосование большинством.  Для этого  сначала каждый выход переводим из непрерывной переменной в метки класса [-1, 1] (порог перехода равен 0,5). Затем суммируем все выходы, и если результат больше 0, то присваивается класс 1, иначе — класс 0.

Используя полученные метки классов, определяем метрики (Accuracy, Precision, Recall и F1).

Обрезка ансамбля (Ensemble pruning). Методы

Мы изначально заложили избыточное количество базовых классификаторов, чтобы впоследствии выбрать из них лучшие. Для этого применяют следующие методы:

• ordering-based pruning — выбор из ансамбля, упорядоченного по определенному показателю качества:
• reduce-error pruning — упорядочиваем классификаторы по ошибке классификации и отбираем несколько лучших (с наименьшей ошибкой);
• kappa pruning — упорядочиваем члены ансамбля по показателю Kappa, отбираем необходимое количество с наименьшими показателями.
• clustering-based pruning — результаты предсказания ансамбля кластеризуем любым способом, после чего отбираем по несколько представителей из каждого кластера. Способы кластеризации:
  
• partitioning (например SOM, k-mean);
• hierarchical;
• density-based (например dbscan);
• GMM-based.
• optimization-based pruning — для выбора лучших используем эволюционные или генетические алгоритмы.

Обрезка ансамбля — это тот же выбор предикторов. Поэтому к ней применимы те же методы, что и при отборе предикторов (это мы рассматривали в предыдущих статьях серии).

В дальнейших расчетах будем использовать выбор из ансамбля, упорядоченного по ошибке классификации (reduce-error pruning).

Итого, в экспериментах будем использовать следующие методы:

• метод объединения — усреднение и голосование простым большинством;
• метрики — Accuracy, Precision, Recall и F1;
• обрезка — выбор из ансамбля, упорядоченного по ошибке классификации на базе mean(F1).

Порог перевода индивидуальных выходов из непрерывной переменной в метки классов принимаем 0.5. Предупрежу сразу: этот вариант не лучший, но самый простой. Впоследствии его можно будет улучшить.

а) Определяем лучшие индивидуальные классификаторы ансамбля

Определим mean(F1) всех 500 нейросетей, отберем несколько bestNN с лучшими показателями. Количество лучших для голосования большинством должно быть нечетным, поэтому будем определять его так: (numEns*2 + 1).

#---5-----best----------------------
evalq({
  numEns <- 3
  foreach(i = 1:n, .combine = "c") %do% {
    ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred
    Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>%
      mean() 
  } -> Score
  Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN
  Score[bestNN] %>% round(3)
}, env)
[1] 0.720 0.718 0.718 0.715 0.713 0.713 0.712

Коротко поговорим о вычислениях в скрипте. В цикле foreach() мы переводим непрерывное предсказание y.pr[ ,i] каждой нейросети в номинальное [0,1], определяем mean(F1) этого предсказания и выводим значение вектором Score[500]. Затем упорядочиваем данные этого вектора Score в убывающем порядке и определяем индексы bestNN нейросетей с лучшими (наибольшими) показателями. Выводим значение метрик этих лучших членов ансамбляScore[bestNN] округлив их до 3 знака. Как видим, индивидуальные результаты не очень высокие.

Итак, мы определили лучшие индивидуальные классификаторы в ансамбле. Давайте протестируем их на наборах X$test и X$test1, используя методы объединения: усреднение и простое большинство голосов.

б) Усреднение

#---6----test averaging(test)--------
evalq({
  n <- len(Ens)
  Xtest <- X$test$x[ , bestF]
  Ytest <- X$test$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:%
    when(i %in% bestNN) %do% {
    predict(Ens[[i]], newdata = Xtest)} %>%
    divide_by(length(bestNN)) -> ensPred
  ifelse(ensPred > 0.5, 1, 0) -> ensPred
  Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>%
    round(3)
}, env)
Accuracy Precision Recall    F1
0     0.75     0.723  0.739 0.731
1     0.75     0.774  0.760 0.767

Коротко о вычислениях в скрипте. Определяем размер ансамбля n, входные Xtest и целевую Ytest, используя основной набор X$test. Затем в цикле foreach (только когда индекс равен индексам bestNN),  вычисляем предикты этих лучших NN, суммируем их, делим на количество лучших NN. Переводим выход из непрерывной переменной в номинальную (0,1) и вычисляем метрики. Как видим, показатели качества классификации намного выше показателей индивидуальных классификаторов.

Выполним тот же тест на наборе X$test1, расположенном следом за X$test. Оценим качество.

#--6.1 ---test averaging(test1)---------
evalq({
  n <- len(Ens)
  Xtest <- X$test1$x[ , bestF]
  Ytest <- X$test1$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:%
    when(i %in% bestNN) %do% {
      predict(Ens[[i]], newdata = Xtest)} %>%
    divide_by(length(bestNN)) -> ensPred
  ifelse(ensPred > 0.5, 1, 0) -> ensPred
  Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>%
    round(3)
}, env)
Accuracy Precision Recall    F1
0    0.745     0.716  0.735 0.725
1    0.745     0.770  0.753 0.761

Качество классификации практически не изменилось и осталось достаточно высоким. Этот результат показывает, что ансамбль нейросетевых классификаторов сохраняет высокое качество классификации после обучения и обрезки на значительно более длительный период (в нашем примере 750 баров), чем DNN, полученная нами в предыдущей статье.

в) Простое большинство голосов

Определим метрики предсказания, полученные от лучших классификаторов ансамбля, но объединенных простым голосованием. Вначале переведем непрерывные предсказания лучших классификаторов в метки класса (-1/+1), затем просуммируем все метки предсказания. Если сумма больше 0, то на выходе выдаем класс 1, иначе — класс 0. Вначале протестируем всё на наборе X$test:

#--7 --test--voting(test)--------------------
evalq({
  n <- len(Ens)
  Xtest <- X$test$x[ , bestF]
  Ytest <- X$test$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% 
    when(i %in% bestNN) %do% {
    predict(Ens[[i]], newdata = Xtest)
  } %>% 
    apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>%
    apply(1, function(x) sum(x)) -> vot
  ifelse(vot > 0, 1, 0) -> ClVot
  Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>%
    round(3)
}, env)
Accuracy Precision Recall    F1
0    0.745     0.716  0.735 0.725
1    0.745     0.770  0.753 0.761

Результат практически не отличается от результата при усреднении. Проверим на наборе X$test1:

#--7.1 --test--voting(test1)--------------------
evalq({
  n <- len(Ens)
  Xtest <- X$test1$x[ , bestF]
  Ytest <- X$test1$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% 
    when(i %in% bestNN) %do% {
      predict(Ens[[i]], newdata = Xtest)
    } %>% 
    apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>%
    apply(1, function(x) sum(x)) -> vot
  ifelse(vot > 0, 1, 0) -> ClVot
  Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>%
    round(3)
}, env)
Accuracy Precision Recall    F1
0    0.761     0.787  0.775 0.781
1    0.761     0.730  0.743 0.737

Неожидано, но результат оказался лучше всех предыдущих, и это — при том, что набор X$test1 находится после X$test. 

Несмотря на то, что гиперпараметры индивидуальных классификаторов ансамбля были выбраны интуитивно и явно не являются оптимальными, мы получили высокое и стабильное качество классификации, как с использованием усреднения, так и с простым большинством.

Просуммируем все изложенное выше. Схематически весь процесс создания и тестирования ансамбля нейросетей можно условно разделить на 4 этапа:

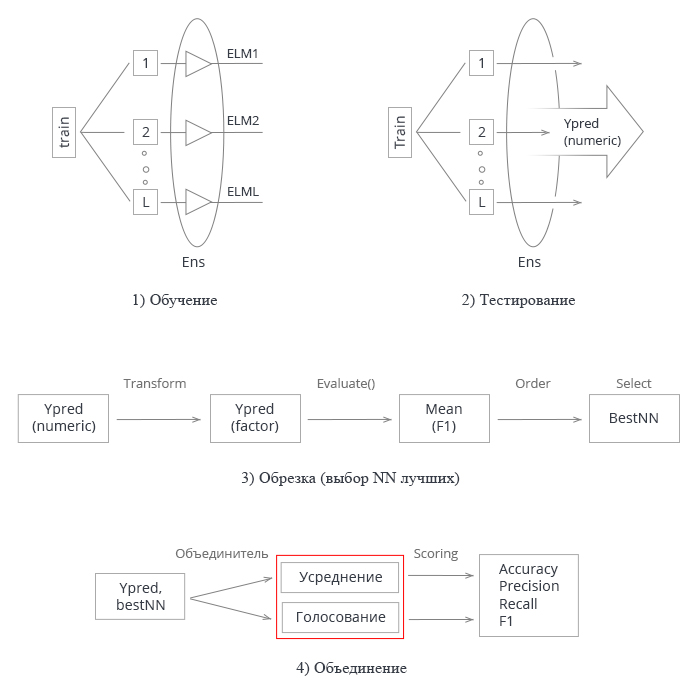
Рис.3 Структурная схема обучения и тестирования ансамбля нейросетей с объединителем averaging/voting

1. Обучение ансамбля. Обучаем L нейросетей на случайных выборках (бутстрап) из обучающего набора. Получаем ансамбль обученных нейросетей.

2. Тестируем ансамбль нейросетей на тестовом наборе. Получаем непрерывные предсказания индивидуальных классификаторов.

3. Обрезаем ансамбль, выбирая n лучших по некоторому критерию качества классификации. В нашем случае это mean(F1).

4. Используя непрерывные предсказания лучших индивидуальных классификаторов, объединяем их, используя либо усреднение, либо простое голосование большинством. После этого определяем метрики.

Два последних этапа (обрезка и объединение) имеют множество вариантов реализации. При этом успешная обрезка ансамбля (правильное определение лучших) может серьезно повысить показатели. Я имею в виду определение оптимального порога перевода непрерывного предикта в номинальный. Поэтому найти оптимальные параметры на этих этапах — трудоемкая задача. Желательно выполнять эти этапы автоматически и с лучшим результатом. Есть ли у нас возможность сделать это и улучшить полученные показатели качества ансамбля? Есть как минимум два способа сделать это, их и проверим.

• Оптимизируем гиперпараметры индивидуальных классификаторов ансамбля (байесовским оптимизатором).
• В качестве объединителя индивидуальных выходов ансамбля используем DNN. Проведем обобщение через обучение.

Определяем оптимальные параметры индивидуальных классификаторов ансамбля. Методы

Индивидуальные классификаторы в нашем ансамбле — нейросети ELM. Главная особенность ELM состоит в том, что их свойства и качество в основном зависят от случайной инициализации весов нейронов скрытого слоя. При прочих равных условиях (количество нейронов и активационная функция) каждый запуск обучения будет порождать новую нейросеть.

Для создания ансамблей эта особенность ELM просто идеальна. В ансамбле мы не только инициируем веса каждого классификатора случайными величинами, но и подаем каждому классификатору отдельную, случайным образом созданную обучающую выборку.

Но для выбора лучших гиперпараметров нейросети нам необходимо, чтобы ее качество зависело только от изменения этого гиперпараметра, и ни от чего другого. Иначе теряется смысл поиска.

Возникает противоречие: с одной стороны, нам нужен ансамбль с как можно более разнообразными членами, с другой стороны — ансамбль с разнообразными, но постоянными членами.

Возможно ли это? Покажем на примере обучения ансамбля. Нам понадобится пакет "doRNG" (Reproducible random number generation RNG). Для воспроизводимости результатов лучше проводить вычисления в одном потоке.

Новый эксперимент начнем с чистого глобального окружения. Снова загрузим котировки, нужные библиотеки, снова определим и упорядочим исходные данные и заново выберем numFeature лучших предикторов. Запустим все это одним скриптом.

#----Prepare-------------
library(anytime)
library(rowr)
library(elmNN)
library(rBayesianOptimization)
library(foreach)
library(magrittr)
library(clusterSim)
library(doRNG)
#source(file = "FunPrepareData.R")
#source(file = "FUN_Ensemble.R")
#---prepare----
evalq({
  dt <- PrepareData(Data, Open, High, Low, Close, Volume)
  DT <- SplitData(dt, 4000, 1000, 500, 250, start = 1)
  pre.outl <- PreOutlier(DT$pretrain)
  DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl)
  preproc <- PreNorm(DTcap, meth = meth)
  DTcap.n <- NormData(DTcap, preproc = preproc)
#--1-Data X-------------
  list(
    pretrain = list(
      x = DTcap.n$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DTcap.n$pretrain$Class %>% as.numeric() %>% subtract(1) 
    ),
    train = list(
      x = DTcap.n$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DTcap.n$train$Class %>% as.numeric() %>% subtract(1) 
    ),
    test = list(
      x = DTcap.n$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
      y = DTcap.n$val$Class %>% as.numeric() %>% subtract(1) 
    ),
    test1 = list(
      x = DTcap.n$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(), 
      y = DTcap.n$test$Class %>% as.numeric() %>% subtract(1) 
    )
  ) -> X
#---2--bestF-----------------------------------
#require(clusterSim)
  numFeature <- 10
  HINoV.Mod(x = X$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, 
            distance =  NULL, # "d1" - Manhattan, "d2" - Euclidean, 
            #"d3" - Chebychev (max), "d4" - squared Euclidean, 
            #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
            method = "kmeans" ,#"kmeans" (default) , "single", 
            #"ward.D", "ward.D2", "complete", "average", "mcquitty", 
            #"median", "centroid", "pam"
            Index = "cRAND") %$% stopri[ ,1] -> orderX
  orderX %>% head(numFeature) -> bestF
}, env)

Все необходимые исходные данные у нас готовы. Обучаем ансамбль нейросетей:

#---3-----Train----------------------------
evalq({
  Xtrain <- X$pretrain$x[ , bestF]
  Ytrain <- X$pretrain$y 
  setMKLthreads(1)
  n <- 500
  r <- 7
  nh <- 5
  k <- 1
  rng <- RNGseq(n, 12345)
  Ens <- foreach(i = 1:n, .packages = "elmNN") %do% {
    rngtools::setRNG(rng[[k]])
    k <- k + 1
    idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr
    elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], 
             nhid = nh, actfun = "sin")
  }
  setMKLthreads(2)
}, env)

Что происходит при исполнении? Мы определяем входные и выходные данные для обучения (Xtrain, Ytrain), устанавливаем библиотеку MKL в однопоточный режим. Инициируем некоторые константы, создаем последовательность случайных чисел rng, которыми будем инициализировать генератор случайных чисел при каждой новой итерации foreach().

После выполнения итераций не забудьте перевести MKL в многопоточный режим. В однопоточном режиме результаты вычисления получаются немного хуже.

Таким образом, мы получим ансамбль с различными индивидуальными классификаторами, но при каждом повторном запуске обучения эти классификаторы ансамбля останутся неизменными. Это легко проверить, повторив вычисления всех 4 этапов (train/predict/best/test) несколько раз. Вычисляем по порядку: train/predict/best/test_averaging/test_voting.

#---4-----predict-------------------
evalq({
  Xtest <- X$train$x[ , bestF]
  Ytest <- X$train$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
    predict(Ens[[i]], newdata = Xtest)
  } -> y.pr #[ ,n]
}, env)
#---5-----best----------------------
evalq({
  numEns <- 3
  foreach(i = 1:n, .combine = "c") %do% {
    ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred
    Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>%
      mean() 
  } -> Score
  Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN
  Score[bestNN] %>% round(3)
}, env)
# [1] 0.723 0.722 0.722 0.719 0.716 0.714 0.713
#---6----test averaging(test)--------
evalq({
  n <- len(Ens)
  Xtest <- X$test$x[ , bestF]
  Ytest <- X$test$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:%
    when(i %in% bestNN) %do% {
      predict(Ens[[i]], newdata = Xtest)} %>%
    divide_by(length(bestNN)) -> ensPred
  ifelse(ensPred > 0.5, 1, 0) -> ensPred
  Evaluate(actual = Ytest, predicted = ensPred)$Metrics[ ,2:5] %>%
    round(3)
}, env)
# Accuracy Precision Recall F1
# 0 0.75 0.711 0.770 0.739
# 1 0.75 0.790 0.734 0.761
#--7 --test--voting(test)--------------------
evalq({
  n <- len(Ens)
  Xtest <- X$test$x[ , bestF]
  Ytest <- X$test$y
  foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %:% 
    when(i %in% bestNN) %do% {
      predict(Ens[[i]], newdata = Xtest)
    } %>% 
    apply(2, function(x) ifelse(x > 0.5, 1, -1)) %>%
    apply(1, function(x) sum(x)) -> vot
  ifelse(vot > 0, 1, 0) -> ClVot
  Evaluate(actual = Ytest, predicted = ClVot)$Metrics[ ,2:5] %>%
    round(3)
}, env)
# Accuracy Precision Recall F1
# 0 0.749 0.711 0.761 0.735
# 1 0.749 0.784 0.738 0.760

И сколько бы раз мы не повторяли эти расчеты (естественно, с одними и теми же параметрами), результат будет неизменным. Это нам и нужно, чтобы оптимизировать гиперпараметры нейросетей, входящих в ансамбль.

Сначала определим перечень оптимизируемых гиперпараметров, найдем границы их изменения, а также напишем фитнес-функцию, которая должна возвращать критерий оптимизации (максимизации) и предикт ансамбля. На качество индивидуальных классификаторов влияют четыре параметра:

• количество предикторов во входных данных;
  
• размер выборки, подаваемой на обучение;
  
• количество нейронов скрытого слоя;
• активационная функция. 

Пропишем гиперпараметры и границы их изменений:

evalq({
  #type of activation function. 
  Fact <- c("sig", #: sigmoid
            "sin", #: sine
            "radbas", #: radial basis
            "hardlim", #: hard-limit
            "hardlims", #: symmetric hard-limit
            "satlins", #: satlins
            "tansig", #: tan-sigmoid
            "tribas", #: triangular basis
            "poslin", #: positive linear
            "purelin") #: linear
  bonds <- list(
    numFeature = c(3L, 12L),
    r = c(1L, 10L),
    nh <- c(1L, 50L),
    fact = c(1L, 10L)
  )
}, env)

Разберем подробнее вышеприведенный код. В нем Fact — вектор возможных функций активации. Список bonds определяет параметры, подлежащие оптимизации и их пределы изменения.

• numFeature — количество предикторов на входе, их минимум 3, максимум 12;
• r — доля обучающего набора, используемая в бутстрапе. Перед вычислением разделим его на 10.
• nh — количество нейронов скрытого слоя, их минимум 1, максимум 50.
  
• fact — индекс активационной функции в векторе Fact.

Определим фитнес-функцию.

#---Fitnes -FUN-----------
evalq({
  Ytrain <- X$pretrain$y
  Ytest <- X$train$y
  Ytest1 <- X$test$y
  n <- 500
  numEns <- 3
fitnes <- function(numFeature, r, nh, fact){
    bestF <- orderX %>% head(numFeature)
    Xtrain <- X$pretrain$x[ , bestF]
    setMKLthreads(1)
    k <- 1
    rng <- RNGseq(n, 12345)
    #---train---
    Ens <- foreach(i = 1:n, .packages = "elmNN") %do% {
      rngtools::setRNG(rng[[k]])
      idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr
      k <- k + 1
      elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], 
               nhid = nh, actfun = Fact[fact])
    }
    setMKLthreads(2)
    #---predict---
    Xtest <- X$train$x[ , bestF]
    foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
      predict(Ens[[i]], newdata = Xtest)
    } -> y.pr #[ ,n]
   #---best---
    foreach(i = 1:n, .combine = "c") %do% {
      ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred
      Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>%
        mean() 
    } -> Score
    Score %>% order(decreasing = TRUE) %>% 
      head((numEns*2 + 1)) -> bestNN
    #---test-aver--------
    Xtest1 <- X$test$x[ , bestF]
    foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:%
      when(i %in% bestNN) %do% {
        predict(Ens[[i]], newdata = Xtest1)} %>%
      divide_by(length(bestNN)) -> ensPred
    ifelse(ensPred > 0.5, 1, 0) -> ensPred
    Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>%
      mean() %>% round(3) -> Score
    return(list(Score = Score, Pred = ensPred))
   }
}, env)  

Немного поясню этот скрипт. Вынесем определение целевых (Ytrain, Ytest, Ytest1) из фитнес-функции, так как они при переборе параметров неизменны. Инициируем константы:

n — количество нейросетей в ансамбле;

numEns — количество лучших индивидуальных классификаторов (numEns*2 + 1), предикты которых мы объединяем.

Собственно, функция fitnes() имеет 4 формальных параметра, которые мы хотим оптимизировать. Далее в функции по порядку обучаем ансамбль, вычисляем predict и определяем bestNN лучших. В конце объединяем предикты этих лучших с помощью усреднения и вычисляем метрики. Функция возвращает список, содержащий критерий оптимизации Score = mean(F1) и предикт. Оптимизировать будем ансамбль, в котором использовано объединение усреднением. Фитнес-функция для оптимизации гиперпараметров ансамбля с объединением простым большинством аналогична, за исключением заключительной части. Вы сможете выполнить оптимизацию самостоятельно.

Проверим работоспособность фитнес-функции и время ее выполнения:

#----------
evalq(
  system.time(
   res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2)
  )
, env)
 user  system elapsed 
   8.65    0.19    7.86

Для получения результата на все расчеты понадобилось около 9 секунд.

> env$res$Score
[1] 0.761

Теперь можем запустить оптимизацию гиперпараметров с 10 случайными начальными точками инициализации и 20 итерациями. Смотрим лучший результат.

#------
evalq(
  OPT_Res <- BayesianOptimization(fitnes, bounds = bonds,
                                   init_grid_dt = NULL, init_points = 10, 
                                   n_iter = 20, acq = "ucb", kappa = 2.576, 
                                   eps = 0.0, verbose = TRUE)
, envir = env)
Best Parameters Found: 
  Round = 23  numFeature = 8.0000  r = 3.0000 nh = 3.0000  fact = 7.0000        Value = 0.7770

Упорядочим историю оптимизации по значению Value и выберем 10 лучших показателей:

evalq({
  OPT_Res %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
    dplyr::select(-Round) -> best.init
  best.init
}, env)
 numFeature r nh fact Value
1           8 3  3    7 0.777
2           8 1  5    7 0.767
3           8 3  2    7 0.760
4          10 7  9    8 0.759
5           8 5  4    7 0.758
6           8 2  7    8 0.756
7           8 6  9    7 0.755
8           8 3  4    8 0.754
9           9 2 13    9 0.752
10         11 2 24    4 0.751

Расшифруем получившиеся гиперпараметры лучшего результата. Количество предикторов 8, размер выборки 0.3, количество нейронов в скрытом слое 3, функция активации — "radbas". Еще раз убеждаюсь, что байесовская оптимизация дает веер разнообразных моделей, получить которые интуитивно маловероятно. Нужно повторить оптимизацию несколько раз и выбрать наилучший результат.

Итак у нас есть оптимальные гиперпараметры обучения. Протестируем ансамбль с ними.

Обучение и тестирование ансамбля с оптимальными параметрами

Протестируем ансамбль, обученный с оптимальными параметрами, которые мы получили выше, на тестовом наборе. Определим лучшие члены ансамбля, объединим их результаты усреднением и посмотрим окончательные метрики. Скрипт приведен ниже.

#--1-Train--optEns-predict--best--test-average------------------------
evalq({
  Ytrain <- X$pretrain$y
  Ytest <- X$train$y
  Ytest1 <- X$test$y
  n <- 500
  numEns <- 3
  #--BestParams--------------------------
  best.par <- OPT_Res$Best_Par %>% unname 
  numFeature <- best.par[1] # 8L
  r <- best.par[2]          # 3L
  nh <- best.par[3]         # 3L
  fact <- best.par[4]       # 7L
  bestF <- orderX %>% head(numFeature)
  Xtrain <- X$pretrain$x[ , bestF]
  setMKLthreads(1)
  k <- 1
  rng <- RNGseq(n, 12345)
  #---train---
  OptEns <- foreach(i = 1:n, .packages = "elmNN") %do% {
    rngtools::setRNG(rng[[k]])
    idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr
    k <- k + 1
    elmtrain(x = Xtrain[idx, ], y = Ytrain[idx], 
             nhid = nh, actfun = Fact[fact])
  }
  setMKLthreads(2)
  #---predict---
  Xtest <- X$train$x[ , bestF]
  foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% {
    predict(OptEns[[i]], newdata = Xtest)
  } -> y.pr #[ ,n]
  #---best---
  foreach(i = 1:n, .combine = "c") %do% {
    ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred
    Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>%
      mean() 
  } -> Score
  Score %>% order(decreasing = TRUE) %>% 
    head((numEns*2 + 1)) -> bestNN
  #---test-aver--------
  Xtest1 <- X$test$x[ , bestF]
  foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:%
    when(i %in% bestNN) %do% {
      predict(OptEns[[i]], newdata = Xtest1)} %>%
    divide_by(length(bestNN)) -> ensPred
  ifelse(ensPred > 0.5, 1, 0) -> ensPred
  Evaluate(actual = Ytest1, predicted = ensPred)$Metrics[ ,2:5] %>%
    round(3) -> OptScore
  caret::confusionMatrix(Ytest1, ensPred) -> cm
}, env)

Посмотрим результаты 7 лучших нейросетей ансамбля:

> env$Score[env$bestNN]
[1] 0.7262701 0.7220685 0.7144137 0.7129644 0.7126606 0.7101981  0.7099502

Результат после усреднения лучших нейросетей:

> env$OptScore
  Accuracy Precision Recall    F1
0    0.778     0.751  0.774 0.762
1    0.778     0.803  0.782 0.793
> env$cm
Confusion Matrix and Statistics

          Reference
Prediction   0   1
         0 178  52
         1  59 212
                                          
               Accuracy : 0.7784          
                 95% CI : (0.7395, 0.8141)
    No Information Rate : 0.5269          
    P-Value [Acc > NIR] : <2e-16          
                                          
                  Kappa : 0.5549          
 Mcnemar's Test P-Value : 0.569           
                                          
            Sensitivity : 0.7511          
            Specificity : 0.8030          
         Pos Pred Value : 0.7739          
         Neg Pred Value : 0.7823          
             Prevalence : 0.4731          
         Detection Rate : 0.3553          
   Detection Prevalence : 0.4591          
      Balanced Accuracy : 0.7770          
                                          
       'Positive' Class : 0      

Этот результат заметно лучше, чем у любой индивидуальной нейросети в ансамбле и сравним с результатами DNN с оптимальными параметрами, полученными нами в предыдущей статье этой серии.

Заключение

1. Ансамбли нейросетевых классификаторов, составленные из простых и быстрых нейросетей ELM, показывают качество классификации, сравнимое с более сложными моделями (DNN).
2. Оптимизация гиперпараметров индивидуальных классификаторов ансамбля дает повышение качества классификации до Acc = 0.77(95% CI = 0.73 - 0.81).
3. Качество классификации ансамбля с усреднением и голосованием простым большинством приблизительно одинаково.
4. Сохранение качества классификации ансамбля после обучения сохраняется на глубину более половины размера обучающего набора. В нашем случае качество сохраняется вплоть до 750 баров, что намного больше, чем тот же показатель, полученный на DNN (250 баров). 
5. Качество классификации ансамбля можно существенно повысить за счет оптимизации порога перевода непрерывной предиктовой переменной в номинальную (калибрование, оптимальный CutOff, генетический поиск).
6. Качество классификации ансамбля можно повысить и применив в качестве объединителя обучаемую модель (stacking). Это может быть нейросеть или ансамбль нейросетей. В следующей части статьи мы  проверим эти два варианта стакинга. Для построения нейросети протестируем новые возможности, предоставляемые групой библиотек TensorFlow.

Приложения

В GitHub/PartVI находятся:

1. FUN_Ensemble.R — функции, необходимые для проведения всех вычислений, описанных в этой статье.
2. RUN_Ensemble.R — скрипты для создания, обучения и тестирования ансамбля
3. Optim_Ensemble.R — скрипты для оптимизации гиперпараметров нейросетей ансамбля
4. SessionInfo_RunEns. txt — пакеты, использованные при создании и тестировании ансамбля
5. SessionInfo_OptEns. txt — пакеты, использованные при оптимизации гиперпараметров NN ансамбля
6. ELM.zip — архив статей по нейросетям ELM.