
Auto-otimização do EA: Algoritmos evolutivos e genéticos
Conteúdos
- Introdução
- 1. Como algoritmos evolutivos apareceram pela primeira vez
- 2. Algoritmos evolutivos (métodos)
- 3. Algoritmos genéticos (AG)
- 3.1. Campo de aplicação.
- 3.2. Problemas sendo resolvidos
- 3.3. AG clássico
- 3.4. Estratégias de busca
- 3.5. Diferença da pesquisa clássica de otimização
- 3.6. Terminologia do AG
- 4. Vantagens do AG
- 5. Desvantagens do AG
- 6. Parte experimental
- 6.1. Procura da melhor combinação de preditores
- com o tabuSearch
- 6.2. Procurando os melhores parâmetros:
- 7. Formas e métodos para melhorar características qualitativas
- Conclusão
Introdução
Muitos traders já perceberam que uma auto-otimização não requer um Expert Advisor para parar de negociar. Existem vários artigos relacionados já publicados (article1, article2, article3, article4). As experiências nesses artigos são baseadas na biblioteca sugerida aqui. No entanto, assim que eles forem publicados, novos algoritmos poderosos de otimização e novas maneiras de aplicá-los surgirão. Além disso, acredito que esses artigos foram escritos por programadores e foram destinados para programadores.
Neste artigo, vou tentar esclarecer a aplicação prática dos algoritmos genéticos (AG) sem me apronfundar nos detalhes técnicos, especificamente destinados a traders. Para usuários, assim como eu, é importante conhecer o princípio da operação do AG, a importância e o valor dos parâmetros que afetam a qualidade e velocidade de convergênia do AG e suas outras propriedades utilitárias. Portanto, poderia até repetir isso, mas vou começar com a aparência do histórico do AG, prosseguir com a sua descrição e começar a identificar os seus parâmetros. Além disso, vamos comparar o AG com alguns algoritmos evolutivos.
1. Como algoritmos evolutivos apareceram pela primeira vez
A história de cálculos evolutivos começaram com o desenvolvimento de vários modelos independentes. Haviam algoritmos, principalmente genéticos e sistemas de classificação de Holland que foram publicados no início dos anos 60 e ganharam reconhecimento mundial depois que o livro "Adaptation in Natural and Artifical Systems", lançado em 1975, tornou-se um clássico na sua área. Na década de 70, dentro do quadro de busca aleatória, L. A. Rastrigin introduziu alguns algoritmos que usam idéias de comportamento biônico. O desenvolvimento destas idéias foram inspiradas na série de trabalhos por I.L. Butakova sobre modelagem evolutiva. Enquanto são desenvolvidas ideias de M. L. Tsetlin sobre um comportamento aconselhável de otimização das máquinas estocásticas, Y.I. Neumark sugeriu procurar pelo extremum global baseado na equipe de autômatos independente que modelam os processos de desenvolvimento e eliminação de espécies. Fogel e Walsh são indivíduos que contribuíram grandemente para o desenvolvimento da programação evolucionária. Apesar da diferença de suas abordagens, cada uma dessas "escolas" basearam sua estratégia sobre alguns princípios que existem na natureza e simplificaram para que pudessem ser utilizados em um computador.
Os esforços focados na evolução de modelagem por analogia com os sistemas da natureza podem ser divididos em duas categorias principais.
- Sistemas modelados com base em princípios biológicos. Eles têm sido utilizados com sucesso para função de tarefas de otimização, e podem ser facilmente descritos numa linguagem não-biológica.
- Sistemas que parecem mais realista do ponto de vista biológico, mas que não são particularmente benéficos no sentido da aplicação. Eles mais se assemelham a sistemas biológicos e são menos direcionais (ou nada direcionais). Eles têm um comportamento complicado e interessante onde, em breve se achará um uso prático.
Certamente, não podemos dividir estes aspectos tão rigorosos na prática. De fato, essas categorias são dois pólos, onde vários sistemas de computadores se encontram entre eles. Mais perto do primeiro polo existem algoritmos evolucionários, tais como a Programação Evolutiva, Algoritmos Genéticos e Estratégias de Evolução, por exemplo. Mais perto do segundo polo existem sistemas que podem ser classificados como vida artificial.
2. Algoritmos evolutivos (métodos)
Algoritmos Evolutivos — uma divisão da inteligência artificial (seção de modelagem evolucionista), que usa e modela os processos de seleção natural. Listamos alguns deles:
- algoritmos genéticos - algoritmo de busca heurística utilizado para otimização e modelagem por meio de seleção aleatória, combinações e variações de parâmetros desejados;
programação genética — criação automatizada ou alteração de programas usando algoritmos genéticos;
programação evolutiva — semelhante à programação genética, mas a estrutura do programa é consistente, apenas os valores numéricos estão sujeitos a alterações;
estratégias evolutivas — assemelham-se aos algoritmos genéticos, mas apenas mutações positivas são transmitidas a próxima geração;
evolução diferencial;
neuroevolução - semelhante à programação genética, mas os genomas são redes neurais artificiais onde a evolução de pesos ocorre na topologia de rede especificada, ou além da evolução de pesos, onde a evolução da topologia também é realizada.
Todas as posições básicas do modelo na teoria da evolução biológica — processos de seleção, miscigenação, mutação e reprodução. O comportamento das espécies é determinada pelo ambiente. Várias espécies são referidas como população. A população evolui de acordo com as regras de seleção seguindo uma função da meta estabelecida pelo meio ambiente. Desta forma, cada amostra (individual) na população tem o seu valor no ambiente atribuído. Apenas as espécies mais adequadas são multiplicadas. Recombinação e mutação permitem que os indivíduos mudem e se ajustem ao ambiente. Tais algoritmos referem-se a mecanismos adaptativos de pesquisa.
Métodos Evolutivos (ME) — métodos (heurísticos) aproximados de resolução de tarefas de otimização e síntese de estrutura. A maioria dos ME são baseados na abordagem estática para investigar situações e aproximação iterativa para a solução desejada.
Cálculos evolutivos constituem uma das seções da inteligência artificial. Ao criar sistemas de inteligência artificial usando esta abordagem, a ênfase é feita sobre a construção do modelo inicial e regras com base no qual ele pode mudar (evoluir). Ao mesmo tempo, o modelo pode ser criado através da aplicação de vários métodos. Por exemplo, ele pode ser tanto da rede neural, como um conjunto de regras lógicas. Recozimento, algoritmos genéticos, PSO, ACO e programação genética estão relacionado com os principais métodos evolutivos.
Ao contrário dos métodos precisos de programação matemática, os métodos evolutivos permitem encontrar soluções próximas do ideal num prazo razoável e ao contrário de outros métodos heurísticos de otimização, eles são caracterizados por uma confiança consideravelmente menor nos recursos do aplicativo (ou seja, mais universal), na maioria dos casos proporciona um maior grau de aproximação à solução de otimização. A universalidade do ME é também determinada pela aplicabilidade de tarefas com espaço não metrizáveis de variáveis geridas (isso significa que pode haver valores linguísticos, incluindo aqueles que não têm nenhuma medida quantificável entre as variáveis geridas).
Em Simulated Annealing, o processo de minimização de energia do corpo potencial é imitado durante o tratamento térmico de detalhes. A variação de alguns parâmetros geridos tem lugar no ponto atual. Um novo ponto é sempre aceito quando a função de destino melhora e, com uma pequena probabilidade, quando se agrava.
O caso mais importante do ME envolve métodos genéticos e algoritmos. Algoritmos Genéticos (AG) são baseados na busca das melhores soluções usando a herança e o fortalecimento das características úteis de vários objetos de uma aplicação específica no processo de imitação da sua evolução.
As propriedades dos objetos são apresentadas com valores de parâmetros combinados em um registro, chamado de cromossomo no ME. Subconjuntos de cromossomos chamados de população são operados no AG. Imitação de princípios genéticos - seleção estocástica dos progenitores entre os membros da população, cruzamento cromossômico, a seleção de crianças para serem incluídas na nova geração de objetos com base na avaliação da função de destino. Este processo conduz a uma melhoria evolutiva dos valores de uma função de destino (função de utilidade) de geração em geração.
Existem também métodos entre o ME que, ao contrário do AG, operam com um único cromossomo ao invés de vários. Desta forma, um método discreto de busca local chamado Hillclimbing baseia-se na mudança aleatória de parâmetros separados (valores de campos no registro ou, em outras palavras, valores de genes no cromossomo). Tais alterações são denominadas mutações. Depois de cada mutação, a função de aptidão (fitness) é avaliada. O resultado da mutação é salvo no cromossomo somente se a aptidão foi melhorada. No "modelo de recozimento", o resultado da mutação é guardada com uma certa probabilidade que depende do valor obtido.
No método Particles Swarm Optimization (PSO), o comportamento dos vários agentes que visam alinhar o seu estado com outro estado do melhor agente é imitado.
O método Ant Colony Optimization (ACO) baseia-se na imitação do comportamento das formigas que encurtam suas rotas de uma fonte de alimento ao seu formigueiro.
3. Algoritmos genéticos (AG)
Algoritmos genéticos — métodos de pesquisa de adaptação que são comumente utilizados para resolver tarefas de otimização funcional. Eles são baseados em processos genéticos dos organismos biológicos: populações biológicas evoluem durante várias gerações e seguem a regra da seleção natural e o princípio da sobrevivência do mais apto, como descoberto por Charles Darwin. Ao imitar este processo, os algoritmos genéticos são capazes de evoluir em soluções de tarefas real, se eles são adequadamente codificados.
Na natureza, as espécies em população competem umas contra as outras para vários recursos, como comida e água. Além disso, os membros da população do mesmo tipo freqüentemente competem para atrair um parceiro. Espécies que são mais adaptadas ao ambiente têm melhores chances de criarem seus filhos. Espécies inferiores ou não se reproduzem, ou têm apenas alguns descendentes. Isso significa que os genes das espécies bem adaptadas se espalharão com o crescente número de descendentes em cada nova geração. Uma combinação de características de sucesso de diferentes progenitores às vezes pode levar a descendentes "excessivamente adaptados" que são mais adaptáveis do que qualquer um de seus pais. Desta forma, uma espécie se desenvolve e se adapta ao ambiente melhor ainda.
Algoritmos genéticos fazem uma analogia com este mecanismo. Eles operam com um conjunto de "espécies" - população onde cada uma das espécies fornece uma possível solução de um problema. Cada amostra é avaliada com uma medida de "ajuste" de acordo com a qualidade da solução relevante. As espécies mais aptas tem a oportunidade de "criar" filhotes usando a "miscigenação" com outras espécies populacionais. Isso leva ao surgimento de novas espécies que combinam algumas características herdadas de seus progenitores. As espécies menos aptas são menos propensas a criar filhos, então as características que possuem desaparecerão gradualmente da população no processo evolutivo.
Esta é a forma como toda a nova população de soluções aceitáveis será reproduzida ao selecionar os melhores representantes de uma geração anterior, através da miscigenação e obtendo novas espécies. Esta nova geração contém uma proporção mais elevada de características que os "bons" membros de uma geração anterior possuem. Desta forma, boas características são distribuídas por toda a população de geração em geração. A miscigenação das espécies mais aptas levam a maioria das áreas de perspectiva dos espaços de buscas a serem exploradas. Em última análise, a população tenderá para a solução de otimização.
Existem diferentes maneiras de implementar ideias de evolução biológica no AG.
3.1. Campo de aplicação
As tarefas reais resolvidas podem ser identificadas como uma pesquisa do valor de otimização, onde o valor é uma função complicada e depende de vários parâmetros de entrada. Em alguns casos, é interessante encontrar os valores dos parâmetros que são utilizados para atingir o valor da função mais precisa. Em outros casos, a precisão da otimização não é necessária, onde qualquer valor é melhor do que um valor de regulação a ser considerado como uma solução. Neste caso, os algoritmos genéticos freqüentemente tornam-se o método mais apropriado para a busca de "bons" valores. A força de um algoritmo genético tem a capacidade de manipular simultaneamente vários parâmetros. Esta característica do AG foi utilizada em centenas de aplicações, incluindo no designer de aeronaves, estabelecendo parâmetros de algoritmos e busca de condições estáveis dos sistemas de equações diferenciais não lineares.
No entanto, há casos em que o AG não operam de forma tão eficaz como se espera.
Vamos supor que há uma tarefa real envolvendo a busca de decisão na otimização. Como descobrir se ela é adequada no AG? Não houve nenhuma resposta rigorosa a esta questão até agora. No entanto, muitos pesquisadores partilham a suposição de que o AG tem boas chances de se tornar um procedimento eficiente de busca nos seguintes casos:
- se o campo a ser pesquisado é grande e presume-se que não é completamente suave e unimodal (isto é, contém uma suavização extrema);
- se a função de aptidão (fitness) contém ruído;
- ou se uma tarefa não exige um achado rigoroso da otimização global.
Em outras palavras, em situações onde é necessário encontrar a solução aceitável (o que é bastante comum com tarefas reais), o AG concorre e bate outros métodos que não aplicam conhecimento na área de pesquisa.
Se a área de busca é pequena, então a solução pode ser encontrada usando a busca exaustiva, e você pode ter certeza que a melhor solução possível será encontrada, enquanto é mais provável do AG convergir em otimização local, ao invés de uma melhor solução global. Se o espaço for suave e unimodal, enão qualquer algoritmo gradiente (por exemplo, o método de descida mais íngreme) será mais eficaz do que o AG.
Se houver algumas informações adicionais na área de pesquisa (por exemplo, a área do conhecido "Problema do Caixeiro Viajante"), métodos de pesquisa que utilizam as heurísticas determinadas pela área, muitas vezes superam qualquer método universal que seja o AG. Considerando uma estrutura relativamente complicada da função de aptidão (fitness), métodos de pesquisa com uma única solução no momento do tempo, como um método simples de descida, poderia "ser flagrado" como uma solução local. No entanto, considera-se que os algoritmos genéticos têm menos chances de convergirem a um local otimizado e funcionem de forma segura em paisagem multi-extrema, uma vez que operam com toda a "população" das soluções.
Certamente, tais pressupostos não preveêm estritamente quando o AG será um procedimento de busca eficiente, competindo com outros procedimentos. O parcial critério de sucesso da eficiência de um AG depende altamente de detalhes, como o método de soluções de codificação, os operadores e os parâmetros de ajuste. O trabalho teórico documentado na literatura dos algoritmos genéticos até agora não dá motivos para discutir o desenvolvimento de mecanismos estritos para previsões precisas.
3.2. Problemas sendo resolvidos
Algoritmos genéticos são aplicados para resolver as seguintes tarefas:- Otimizar funções
- Otimizar pedidos em bases de dados
- Várias tarefas nos gráficos (Problema do Caixeiro Viajante, coloração, encontrando pares)
- Definir e formação de redes neurais artificiais
- Tarefas de layout
- Criar planejamentos
- Estratégias de jogo
- Teoria da aproximação
3.3. AG clássico
Operação do AG simplesO AG simples gera aleatoriamente uma população inicial de estruturas. A operação do AG é um processo iterativo que continua até que o número definido das gerações seja alcançado ou se qualquer outro critério de terminação for aplicado. A seleção proporcional da aptidão, ponto de cruzamento único e mutação são implementados em cada geração do algoritmo.
Primeiro, a seleção proporcional nomeada para cada estrutura tem a probabilidade Ps(i) igual a razão da sua aptidão para a capacidade total da população.
Então todas as espécies "n" são selecionadas (com substituição) para obter mais dados genéticos de manuseamento, de acordo com o valor Ps(i). A seleção proporcional mais simples é uma seleção de roleta, descrita por Goldberg, 1989c) - espécies são selecionados com n "giros" de uma roleta. A roleta contém um setor para cada membro da população. O tamanho do setor i-th é proporcional ao valor correspondente Ps(i). Nesta seleção, os membros da população mais aptos são mais suscetíveis de serem selecionados do que as espécies mais fracas.
Após a seleção, as espécies "n" selecionadas estão sujeitas a um cruzamento (às vezes chamado de recombinação) com uma probabilidade Pc. Sequências "n" são divididas aleatoriamente em pares "n/2". Para cada par com probabilidade Pc, o cruzamento pode ser aplicado. Por conseguinte, o cruzamento não ocorre com uma probabilidade 1-Pc e espécies constantes prosseguem para a fase de mutação. Se existe um cruzamento, então as crianças obtidas substituem seus progenitores e prosseguem com a mutação.
Um ponto de cruzamento único opera da seguinte forma: em primeiro lugar, um dos pontos de ruptura l-1 é selecionado aleatoriamente. (Ponto de ruptura é uma área entre bytes adjacentes na string.) Ambas as estruturas parentais são divididas em dois segmentos com base nesse ponto. Então os segmentos correspondentes de diferentes progenitores estão ligados e dois genótipos de crianças são criados.
Após término da fase de cruzamento, operadores de mutação são executados. Cada byte com a probabilidade Pm é alterado ao seu oposto em cada sequência que está sujeito a mutação. A população obtida após mutação substitui a antiga população e isto é como um loop de uma geração finalizada. As gerações seguintes são tratados da mesma maneira: seleção, cruzamento e mutação.
Pesquisas de AG atualmente oferecem uma abundância de outros operadores de seleção, cruzamento e mutação. A seguir estão as mais comuns. Antes de tudo, seleção por torneio (Brindle, 1981; Goldberg и Deb, 1991). Ela implementa "n" torneios para escolha das "n" espécies. Cada torneio é construído sobre a seleção de k elementos da população e a seleção das melhores amostras entre todos. O torneio de seleção com k=2 é o mais comum.
Metodos de seleção pela elite (De Jong, 1975)garantir que os melhores membros da população vão sobreviver durante a seleção. O processo mais comum é a retenção obrigatória do melhor e único espécime, se ele não passar pelo processo de seleção, cruzamento e mutação como o resto. O elitismo pode ser integrado em praticamente qualquer método padrão de seleção.
Dois pontos de cruzamento (Cavicchio, 1970; Goldberg, 1989c) e cruzamento uniforme (Syswerda, 1989) — são alternativas decentes para o operador de um ponto. Existem dois pontos de quebra selecionados no cruzamento, onde os cromossomos parentais trocam um segmento que se encontra entre estes dois. No cruzamento uniforme, cada byte do primeiro parente é herdado na primeira criança com uma probabilidade definida, caso contrário, este byte é transferido para o segundo filho. E vice versa.
Operadores básicos do algoritmo genético
Operador de seleção
Nesta fase, a população otimizada é selecionada para posterior reprodução. O número específico do mais forte é normalmente usado. Não faz sentido usar "clones", ou seja, espécies com o mesmo conjunto de genes.
Operador de miscigenação
Na maioria das vezes, a miscigenação é realizada ao longo de duas das melhores espécies. Os resultados mais comuns são duas espécies com componentes retirados de seus "progenitores". O objetivo deste operador é distribuir "bons" genes por toda a população e apertar a densidade da população para áreas onde ela já é alta.
Operação de mutação
O operador de mutação simplesmente muda o número arbitrário de elementos numa espécime para outros números arbitrários. Na verdade, é um elemento de dissipação que extrai a partir de local extremo de um lado e acrescenta novas informações à população, para outro lado.
- No caso de um sinal binário, inverte-se um byte.
- Ele altera o sinal numérico para um determinado valor (maior probabilidade, o valor mais próximo).
- Ele substituiu por outro sinal nominal.
Critério de Finalização
- Encontrando a solução global ou subotimização
- Saída para "plateus"
- Exaurindo o número de gerações liberadas para a evolução
- Exaurindo o tempo restante para a evolução
- Exaurindo um número específico de chamadas para a função de destino
3.4. Estratégias de busca
A busca é uma das formas universais de encontrar soluções nos casos onde a sequência de passos que conduzem à otimização não são conhecidas.Há duas estratégias de pesquisa: a exploração da melhor solução e o estudo do espaço de soluções. Um método gradiente é exemplo de uma estratégia que seleciona a melhor solução para um possível aperfeiçoamento, ignorando a pesquisa de toda a área de busca. Uma pesquisa aleatória é um exemplo de uma estratégia que, pelo contrário, estuda a área de soluções, ignorando pesquisas de campos em perspectiva da área de busca. Um algoritmo genético é uma classe de métodos de busca de uma função geral que combina elementos de ambas as estratégias. A aplicação desses métodos permitirá manter o equilíbrio aceitável entre a investigação e a exploração da melhor solução. No início da operação de algoritmos genéticos, a população é aleatória e tem diversos elementos. Portanto, o operador de cruzamentos realiza uma vasta pesquisa da área de solução. Com o aumento da função de aptidão (fitness) das soluções obtidas, o operador de cruzamentos permite pesquisar cada um dos seus arredores. Em outras palavras, o tipo de estratégia de busca (exploração da melhor solução ou pesquisando a área de solução) para o operador de miscigenação é definida com uma diversidade de população, em vez do próprio operador.
3.5. Diferença da pesquisa clássica de otimização
Geralmente, o algoritmo de resolução de problemas de otimização é uma sequência de cálculo que assintoticamente convergem para a solução de otimização. A maioria dos métodos clássicos de otimização geram uma sequência determinada de cálculos que se baseia no gradiente ou na derivativa de uma função de destino da variação mais elevada. Estes métodos são aplicados a um único ponto de saída de uma área de busca. Então a decisão é melhorada gradualmente para o aumento mais rápido ou diminuição da função de destino. Com essa abordagem detalhada, existe o risco de acertar o local de otimização.
Um algoritmo genético realiza uma busca simultânea em várias direções através da utilização da população de possíveis soluções. Alternando de uma população para outra evita acertarem o local de otimização. A população sofre algo semelhante a evolução: relativamente boas soluções são produzidas a cada geração, ao passo que os relativamente maus morrem. Algoritmos genéticos usam regras de probabilidade para identificar um cromossomo reproduzido ou destruído, a fim de direcionar a pesquisa para as áreas de uma possível melhora da função de destino.
Muitos algoritmos genéticos foram implementados nos últimos anos, na maioria dos casos eles diferem drasticamente a partir do algoritmo clássico inicial. E esta é a razão pela qual, em vez de um modelo, existe uma ampla gama de classes de algoritmo que carregam pouca semelhança umas com as outras sob o termo "algoritmos genéticos". Os pesquisadores experimentaram vários tipos de pontos de vista, operadores de cruzamento e mutações, operadores especiais e diversas abordagens para reprodução e seleção.
O modelo de desenvolvimento evolutivo aplicado no AG é majoritariamente simplificado em comparação à natureza analógica, visto que o AG é uma ferramenta poderosa e pode ser aplicado com sucesso para uma ampla classe de tarefas, incluindo aquelas que são difíceis e, por vezes, impossível de resolver usando outros métodos. No entanto, juntamente com outros métodos de cálculos evolutivos, o AG não garante encontrar uma solução global ao longo do tempo polinomial. Nem se pode garantir que a solução global ainda será encontrada, mas os algoritmos genéticos são bons para a busca de uma solução "relativamente boa e rápida". Quase sempre esses métodos são mais eficazes do que o AG em velocidade e precisão das soluções encontradas, onde os métodos especiais podem ser usados para encontrar uma solução. A principal vantagem dos AGs é que eles podem ser aplicados mesmo para tarefas complicadas, na falta de outros métodos especiais. Mesmo onde os métodos existentes funcionam bem, os AGs podem ser usados para melhorar ainda mais.
3.6. Terminologia do AG
Já que o AG é derivado da ciência natural (genética) e da ciência da computação, a terminologia aplicada é uma mistura de compostos naturais e artificiais. Os termos referentes ao AG e a solução de problemas de otimização são fornecidos na tabela. 1.1.
Tabela
| Algoritmo genético | Explicação |
|---|---|
| Cromossomo | Possível solução (conjunto de parâmetros) |
| Genes | Parâmetros que são otimizados |
| Locus (localização) | Posição de um gene no cromossomo |
| Alelo | Valor do gene |
| Fenótipo | Solução codificada |
| Genótipo | Solução codificada |
Permutação (crossing over) clássica - um ponto.
O algoritmo genético "tradicional" usa a permutação (crossing over) de um ponto, onde dois cromossomos são cortados uma vez em ponto específico e as peças obtidas são trocadas depois. Outros algoritmos com outros tipos de permutaçao frequentemente inclue mais de um ponto de corte, também foram descobertos. DeJong pesquissou a eficiência de uma permutação multi-pontas e chegou a conclusão de que uma permutação de dois pontos apresenta melhoria, mas diante da adição da permutação de pontos, fica reduzida a atividade de um algoritmo genético. O problema da adição de uma permutação extra sobre os pontos é que os blocos padrões provavelmente serão interrompidos. No entanto, a vantagem da permutação de múltiplos pontos é que a área de estados pode ser pesquisada com mais detalhes.
Permutação (crossing over) de dois pontos
Na permutação de dois pontos (e permutação de múltiplos pontos generalizados), os cromossomos são considerados como anéis formados quando se conectam as extremidades dos cromossomos lineares. A fim de mudar um segmento de um ciclo a um segmento de um outro ciclo, uma seleção de dois pontos de corte é necessária. Nesta apresentação, a permutação de um ponto pode ser considerada como uma com dois pontos, mas com um ponto de corte fixado no início da cadeia. Portanto, a permutaçao (crossing over) de dois pontos resolve a mesma tarefa que um cruzamento de ponto único, mas de uma forma mais completa. Um cromossomo considerado como um ciclo pode conter uma grande quantidade de blocos padrões, porque eles podem executar um "retorno cíclico" no final da cadeia. Muitos pesquisadores atualmente concordam que, em geral, a permutação de dois pontos é melhor do que a de um ponto.
Permutação unificada (homogênea).
A permutação (crossing over) unificada é fundamentalmente diferente do cruzamento de um ponto. Cada gene numa geração é criado pela cópia de um outro relevante a partir de um parente ou outro que foi selecionado de acordo com a máscara de cruzamento gerada aleatoriamente. Se uma máscara de cruzamento tem 1, então um gene é copiado a partir de um primeiro precursor, se ele tem 0, então um gene é copiado a partir da segunda geração parental. A fim de criar uma segunda geração o processo é repetido, mas com os progenitores trocados. Uma nova máscara de permutação é gerada aleatoriamente para cada par de progenitores.
Miscigenação diferencial.
Além do cruzamento, existem outros métodos de miscigenação. Por exemplo, para procurar uma função mínima/máxima de muitas variáveis físicas, a "miscigenação diferencial" é a melhor sucedida. Vamos descrever brevemente o seu conceito. Vamos imaginar que A e B são dois indivíduos em determinada população, ou seja, vetores físicos que nossa função esta dependendo. Em seguida, uma criança (C) é calculada utilizando a fórmula C=A+k*(A-B), onde k - é uma determinada relação física (que pode depende de ||A-B|| - uma distância entre os vetores).
A mutação neste modelo é uma adição a um indivíduo de um vetor aleatório de comprimento curto. Se uma função de saída é contínua, o modelo opera bem. É ainda melhor se ele for suavisado.
Inversão e reordenação.
A ordem dos genes num cromossomo é crucial para a construção de blocos que permitem realizar uma operação eficiente do algoritmo. Durante a operação do algoritmo, foram sugeridos métodos para reordenar as posições dos genes no cromossomo. Um desses métodos é a da inversão que inverte a ordem dos genes entre duas posições selecionadas aleatoriamente num cromossomo. (Quando são utilizados estes métodos, os genes precisam ter uma certa "marca", para que possam ser identificados corretamente, independente da sua posição no cromossomo.)
O objetivo do reordenamento é tentar encontrar a ordem dos genes que possuem o melhor potencial evolutivo. Muitos pesquisadores têm aplicado a inversão no seu trabalho, embora pareça que poucos têm tentado justificar ou avaliar a sua contribuição. Goldberg & Bridges analisam o operador de reordenação numa pequena tarefa, mostrando que podem dar uma certa vantagem, no entanto concluem que os seus métodos não têm a mesma vantagem com grandes tarefas.
A reordenação também aumenta consideravelmente a área de pesquisa. Não só um algoritmo genético tenta encontrar bons valores dos conjuntos de genes, mas também tenta encontrar sua ordem "certa". Este é um desafio maior para resolver.
O que é epistasia?
O termo "epistasia" em genética representa a influência de um gene sobre a aptidão de um indivíduo dependendo do valor de um gene presente em outro lugar. Em outras palavras, os geneticistas usam o termo "epistasia" para representar o efeito de "esconder" ou "mascarar": "Um gene é considerado epistático quando a sua presença suprime a influência de um outro gene em outro lugar. Genes epistáticos são chamados às vezes de inibitórios por causa de sua influência sobre outros genes que são descritos como hipóstase.
Na terminologia AG pode soar como: "Aptidão de uma amostra depende de uma posição de cromossomos de um genótipo".
O que é uma falsa otimização?
Um dos princípios fundamentais de algoritmos genéticos é que os cromossomos incluídos nos modelos contidos na otimização global são elevados em frequência. Isto é especialmente certo para modelos curtos de pequena ordem, conhecidos como blocos de construção. Em última análise, esses modelos ideais se reunirão no cruzamento e um cromossomo de otimização global será criado. Mas se certos modelos que não estiverem contidos no otimizador global, então eles serão aumentados com uma frequência mais rápida do que outros, então um algoritmo genético será enganado e desviará da otimização global, em vez de se aproximar dela. Este fenômeno é conhecido como uma falsa otimização.
A falsa otimização é um caso particular de epistasia e foi profundamente analisada por Goldberg e outros. A falsa otimização está diretamente ligada com o impacto negativo da epistasia em algoritmos genéticos.
Estatisticamente, o modelo vai aumentar em frequência na população, se a sua aptidão é maior do que a aptidão média de todos os modelos na população. A tarefa é marcada como uma tarefa de falsa otimização, se a aptidão média dos modelos não contidas na otimização global é maior do que a média de condicionamento dos outros modelos. Tarefas de falsas otimização são complexas. No entanto, Grefenstette demonstra que nem sempre são complicadas. Depois da primeira geração, um algoritmo genético não obtém uma seleção objetiva dos pontos na área de pesquisa. Portanto, ele não pode avaliar objetivamente uma aptidão média global de um modelo, somente será capaz de obter uma avaliação tendenciosa de um modelo de aptidão. Às vezes esse viés ajuda um algoritmo genético a combinar (mesmo se uma tarefa, de alguma outra forma, tenha uma falsa otimização mais forte).
O que é a endogamia, exogamia, escolha seletiva, panmixia?
Existem várias abordagens para selecionar um par de progenitores. A mais simples de todos eles é a panmixia. Esta abordagem implica uma seleção aleatória de um par de progenitores quando ambas as espécies são selecionadas aleatoriamente a partir de toda a população. Neste caso, qualquer espécime pode se tornar um membro de diversos pares. Apesar da simplicidade, essa abordagem é universal para resolver várias tarefas. No entanto, é relativamente crítico a um número da população, uma vez que a eficiência do algoritmo que implementa esta abordagem é diminuída com o aumento da população.
Com um método seletivo de escolha da espécies quanto ao par de progenitores, apenas as espécies cuja aptidão está acima da média das aptidões na população podem se tornarem "pais", com a mesma probabilidade para tais candidatos formarem um par.
Esta abordagem permite uma convergência mais rápida do algoritmo. Devido a uma convergência rápida, uma escolha seletiva de um par de progenitores não é adequada quando algumas extremidades devem ser definidas, porque o algoritmo rapidamente chega até uma das soluções com tais tarefas. Além disso, para algumas classes de tarefas com um panorama complicado de aptidões, uma convergência rápida pode transformar-se em convergência prematura a uma solução quase-otimizada. Esta desvantagem pode ser parcialmente compensada com a utilização de um mecanismo de seleção adequado que "desaceleraria" uma rápida convergência de um algoritmo.
Endogamia é um método em que o primeiro membro de um par é aleatório e a segunda amostra é selecionada para ser a mais próxima possível do primeiro membro.
O conceito de similaridade de espécies também é aplicado para a exogamia. Agora, no entanto, os pares são formados a partir de espécies que são as mais distantes possíveis.
Os dois últimos métodos influenciam o comportamento de um algoritmo genético de forma diferente. Assim, a consanguinidade pode ser caracterizada como uma propriedade que concentra a pesquisa em nós locais, onde leva a dividir uma população em grupos locais, separados em torno de áreas extremamente suspeitas do panorama. A exogamia está destinada a impedir a convergência do algoritmo para soluções já encontradas, forçando o algoritmo de pesquisa através de novas áreas que continuam a serem exploradas.
Auto-organização dinâmica dos parâmetros do AG
Frequentemente, a seleção de parâmetros de um algoritmo genético e operadores genéticos específicos são executados utilizando a intuição, já que não há evidência objetiva de que algumas definições e os operadores são mais vantajosos, porém não devemos esquecer que o ponto do AG é dinamicamente um algoritmo de "suavidade" e os cálculos são efetuados. Então, por que não deixar o algoritmo se auto configurar ao tempo de resolver uma tarefa e se adaptar a ela?
A maneira mais fácil é organizar a adaptação dos operadores aplicados. Para este fim, vamos construir vários (quanto mais, melhor) operadores de seleção (elite, aleatório, roleta, ...), permutação (de um ponto, dois pontos, unificada, ...) e mutação (um elemento aleatório, absoluto, ...) no algoritmo. Vamos definir probabilidades iguais de aplicação para cada operador. Em cada ciclo do algoritmo, vamos selecionar um operador para cada grupo (escolha, permutação, mutação) de acordo com a eventual distribuição. Vamos marcar a espécime obtida a partir da operadora que foi recebida. Portanto, se uma nova distribuição de probabilidades for calculada com base na informação contida na população (probabilidade de aplicar o operador é proporcional a um número de espécies numa população obtida com este operador), então um algoritmo genético vai receber um mecanismo de uma dinâmica de auto-adaptação.
Esta abordagem fornece ainda outra vantagem: agora, não há necessidade de se preocupar com o gerador aplicado à figuras aleatórias (linear, exponencial, etc.), uma vez que o algoritmo muda dinamicamente o modo de distribuição.
Migração e método de seleção artificial
Ao contrário do AG regular, a macroevolução é realizada, isto é, não apenas uma, mas várias populações são criadas. Uma pesquisa genética aqui é realizada unindo os progenitores de várias populações.
Método do equilíbrio interrompido
Um método baseado na teoria paleontológica do equilíbrio interrompido que descreve uma evolução rápida através de mudanças vulcânicas e outras mudanças da crosta da Terra. A fim de aplicar este método em tarefas técnicas, é aconselhável embaralhar aleatoriamente indivíduos de uma população após cada geração e em seguida, formar novas gerações. Tal como acontece com a vida selvagem, a seleção inconsciente e uma seleção sintética de pares de progenitores pode ser sugerida aqui. Então os resultados de ambas as seções devem ser misturados aleatoriamente e, em vez de manter o tamanho da população constante, deve ser controlado em função da presença dos melhores indivíduos. Tal modificação dos métodos de equilíbrio interrompidos podem reduzir as populações pouco sólidas e aumentar as populações com as melhores espécies.
Equilíbrio interrompido é um método poderoso de pressão para mudar o ambiente que é utilizado para uma saída eficiente a partir de poços locais.
4. Vantagens do AG
Existem duas principais vantagens dos algoritmos genéticos em relação aos métodos clássicos de otimização.
1. O AG não tem requisitos matemáticos consideráveis para tipos de funções de destino e restrições. Um pesquisador não deve simplificar o objeto do modelo, perdendo adequação e assegurando artificialmente a aplicação de métodos matemáticos disponíveis. As mais diversas funções de destino e tipos de restrição (linear e não-linear) podem ser usadas, sendo definidas em conjuntos universais discretos, ininterruptos e mistos.
2. Quando utilizar métodos clássicos passo-a-passo, a otimização global somente pode ser encontrada quando um problema tem uma propriedade de convexidade. Ao mesmo tempo, as operações evolutivas de algoritmos genéticos permitem à procura da otimização global de forma eficiente.
Pequenas vantagens do AG, mas ainda importante:
um grande número de parâmetros livres permitem uma construção heurísticas eficiente;
paralelização eficiente;
funciona muito bem como uma busca aleatória;
conexão com a biologia dá alguma esperança para a eficiência excepcional do AG.
5. Desvantagens do AG
Vários parâmetros livres que transformam uma "operação com AG" num "jogo com AG"
Falta de suporte probatório para a convergência
Em funções de destino simples (suavização, um extremo e etc.), a genética sempre perde em velocidade para simples algoritmos de pesquisas
6. Parte experimental
Todos os experimentos serão realizados na linguagem ambiente R 3.2.4. Nós usamos um conjunto de dados para a formação de um modelo e maioria das funções do artigo anterior.
A seção depositária CRAN contém um grande número de pacotes voltados para otimização e tarefas de programação matemática. Vamos aplicar vários métodos do algoritmo genético (AG) e métodos evolutivos (EM) para resolver as tarefas acima mencionadas. Existe apenas um requisito para os modelos que participam do processo de otimização - velocidade. Não é aconselhável aplicar métodos que são treinados dentro de cem segundos. Considerando que, a cada geração, haverá um mínimo de 100 espécies e a população vai passar por várias épocas (em unidade de dezenas), o processo de otimização vai esticar até um tempo inaceitável. Nos artigos anteriores, aplicamos dois tipos de redes profundas (com a inicialização SAE e RBM). Ambos mostraram alta velocidade e podem muito bem serem usadas para a otimização genética.
Nós vamos resolver duas tarefas de otimização: busca da melhor combinação de indicadores e a seleção de parâmetros ideais dos indicadores. Vamos aplicar o algorítmo XGBoost(Extreme Gradiente Boosting) que é muitas vezes usado para resolver a primeira tarefa (seleção preditor), a fim de aprender novos algoritmos. Como mencionado em fontes, ele mostra resultados muito bons em tarefas de classificação. O algoritmo está disponível para as linguagens de programação R, Python, Java. Na linguagem R, este algoritmo é implementado no pacote “xgboost” v. 0.4-3.
A fim de resolver a segunda tarefa (seleção dos parâmetros ideais dos indicadores), vamos usar o mais simples Expert Advisor MACDsample e ver o que pode ser obtido com a sua ajuda ao usar a otimização genética no fluxo.
6.1. Procura da melhor combinação de preditores
É importante definir o seguinte para resolver a tarefa de otimização:
parâmetros que serão otimizados;
critério de otimização — escala que precisa ser maximizada/minimizada. Não pode haver mais do que um critério;
a função alvo (objetivo, aptidão) que irá calcular o valor de critério da otimização.
A função de aptidão (fitness) no nosso caso vai implementar de forma consistente o seguinte:
formação do quadro inicial de dados;
divisão do treinamento/teste;
treinamento do modelo;
teste do modelo;
cálculo do critério de otimização.
O critério de otimização pode ser o padrão métrico, como Accuracy, Recall, Kappa, AUC, bem como os fornecidos por um desenvolvedor. Usaremos um erro de classificação nesta capacidade.
A busca da melhor combinação dos indicadores será realizada com o pacote v.1.1 "tabuSearch", que é uma extensão do algoritmo HillClimbing. O algoritmo TabuSearch otimiza a cadeia binária usando uma função objetiva identificada por um usuário. Como resultado, apresenta a melhor configuração binária com o maior valor da função de objetivo. Iremos utilizar este algoritmo para procurar a melhor combinação do preditor.
A principal função:
tabuSearch(size = 10, iters = 100, objFunc = NULL, config = NULL, neigh = size, listSize = 9, nRestarts = 10, repeatAll = 1, verbose = FALSE)
Argumentos:
size – comprimento da configuração binária otimizada;
iters – número de iterações na pesquisa preliminar do algoritmo;
objFun – um método sugerido para um usuário que avalia a função de destino para uma cadeia binária específica;
config – iniciando a configuração;
neigh – número de configurações adjacentes para verificar cada iteração. Por padrão, é igual ao comprimento da cadeia binária. Se um número é menor do que o comprimento da string (cadeia), os vizinhos são selecionados aleatoriamente;
listSize – tamanho da lista de interdição;
nRestarts – tempo máximo de reiniciaçao na fase intensiva do algoritmo de pesquisa;
repeatAll – número de repetições da pesquisa;
verbose - lógico se for verdade, o nome do estágio do algoritmo atual é impresso, por exemplo: uma fase preliminar, estágio de intensificação, estágio de diversificação.
Vamos escrever uma função objetiva e experimentá-la.
ObjFun <- function(th){
require(xgboost)
# Sair se tudo zero na string binária
if (sum(th) == 0) return(0)
# nomes dos preditores que correspondem a 1 na cadeia binária
sub <- subset[th != 0]
# Criar estrutura para treinamento de um modelo
dtrain <- xgb.DMatrix(data = x.train[ ,sub], label = y.train)
# Treinando um modelo
bst = xgb.train(params = par, data = dtrain, nrounds = nround, verbose = 0)
# Calcula as previsões com a definição do texto
pred <- predict(bst, x.test[ ,sub])
# Calcula a previsão de erro
err <- mean(as.numeric(pred > 0.5) != y.test)
# Retorno do critério de qualidade
return(1 - err)
}
Para os cálculos devemos preparar os dados para definição do treinamento e teste do modelo, também definição ds parâmetros do modelo e da configuração inicial na otimização. Nós usamos os mesmos dados e funções a partir do artigo anterior (EURUSD/M30, 6000 barras como em 14.02.16).
Listagem com os comentários:
#---tabuSearch---------------------- require(tabuSearch) require(magrittr) require(xgboost) # Quadro dos dados de saída dt <- form.data(n = 34, z = 50, len = 0) # Nomes de todos os preditores no conjunto inicial subset <- colnames(In()) set.seed(54321, kind = "L'Ecuyer-CMRG") # Prepara a definição de treinamento e teste DT <- prepareTrain(x = dt[ ,subset], y = dt$y, balance = FALSE, rati = 4/5, mod = "stratified", norm = FALSE, meth = method) train <- DT$train test <- DT$test x.train <- train[ ,subset] %>% as.matrix() y.train <- train$y %>% as.numeric() %>% subtract(1) x.test <- test[ ,subset] %>% as.matrix() y.test <- test$y %>% as.numeric() %>% subtract(1) # Vetor binário inicial th <- rep(1,length(subset)) # Parâmetros do modelo par <- list(max.depth = 3, eta = 1, silent = 0, nthread = 2, objective = 'binary:logistic') nround = 10 # Configuraçao inicial conf <- matrix(1,1,17) res <- tabuSearch(size = 17, iters = 10, objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1) # Valor máximo da função do objeto max.obj <- max(res$eUtilityKeep) # A melhor combinação dos vetores binários best.comb <- which.max(res$eUtilityKeep)%>% res$configKeep[., ] # O melhor conjunto dos preditores best.subset <- subset[best.comb != 0]
Começamos a otimização com dez iterações e veja qual definição máxima de critérios de qualidade e preditor.
> system.time(res <- tabuSearch(size = 17, iters = 10, + objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1)) Sistema de usuário decorrido 36.55 4.41 23.77 > max.obj [1] 0.8 > best.subset [1] "DX" "ADX" "oscDX" "ar" "tr" "atr" [7] "chv" "cmo" "vsig" "rsi" "slowD" "oscK" [13] "signal" "oscKST" > summary(res) Configurações de Interdições Tipo = configuração binária Nr de repetições do algoritmo = 1 Nr de iterações em cada busca preliminar = 10 Nr total de iterações = 30 Nr das melhores configurações únicas = 23 Tamanho da lista de Interdições = 9 Comprimento da configuração = 17 Nr vizinhos que visitaram cada iteração = 17 Resultados: Maior valor do objetivo fn = 0.79662 # Tempo de ocorrências = 2 Nr de otimizaçao das variáveis = c(14, 14)
Os cálculos necessários levam aproximadamente 37 segundos com precisão de cerca de 0,8 e 14 preditores. O indicador de qualidade obtido com as configurações padrão é muito bom. Vamos fazer outro cálculo, mas com 100 iterações.
> system.time(res <- tabuSearch(size = 17, iters = 100, + objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1)) Sistema de usuário decorrido 377.28 42.52 246.34 > max.obj [1] 0.8042194 > best.subset [1] "DX" "ar" "atr" "cci" "chv" "cmo" [7] "sign" "vsig" "slowD" "oscK" "SMI" "signal" >
Vemos que o aumento de iterações aumentou proporcionalmente ao tempo de cálculo, ao contrário da precisão da previsão. Ela aumentou apenas ligeiramente. Isso significa que os indicadores de qualidade devem ser melhorados através da configuração dos parâmetros do modelo.
Este não é o único algoritmo e pacote que ajuda a selecionar a melhor configuração de preditores usando o AG. Você pode usar os pacotes kofnGA, fSelector. Para além daqueles, uma seleção de preditores é implementado pela função gafs() no pacote "caret" usando o AG.
6.2. Procurando os melhores parâmetros
1. Os dados de saída para projeção. Nós vamos usar o Expert Advisor MACDSampl como exemplo.
Neste EA, um algoritmo implementa as strings para gerar sinais no cruzamento das linhas macd e signal. Um indicador é usado.
MACD(x, nFast = 12, nSlow = 26, nSig = 9, maType, percent = TRUE, ...)Argumentos
|
x |
Timeseries de uma variável; normalmente é o preço, mas pode ser volume e etc. |
|
nFast |
Número de períodos do indicador MA rápido. |
|
nSlow |
Número de períodos do indicador MA lento |
|
nSig |
Número de períodos do sinal indicador MA |
MaType – tipo da aplicaçao do indicador MA
porcentagem - lógico se for verdade, então a diferença entre o indicador MA rápido e o lento em porcentagem é devolvido, caso contrário - a diferença é simples.
A função MACD retorna duas variáveis: macd - diferença entre o indicador MA rápido e o lento, ou a velocidade da distância da mudança entre o indicador МА rápido e o lento; sinal - indicador МА a partir desta diferença. MACD é um caso particular de oscilador comum aplicado ao preço. Ele pode também ser utilizado com qualquer série de tempo de uma variável. Os períodos de tempo para o MACD são frequentemente definidso como 26 e 12, mas a função inicou utilizando constantes exponenciais 0,075 e 0,15 que estão mais perto dos períodos 25.6667 e 12.3333.
Então, nossa função tem 7 parâmetros com variação de mudanças:
p1 — preço calculado (Close, Med, Typ, WClose)
p2 — nFast (8:21)
p3 — nSlow(13:54)
p4 — nSig (3:13)
p5 — MAtypeMACD – Tipo МА para a string MACD
p6 — MatypeSig – Tipo МА para a string Signal
p7 — percent (TRUE, FALSE)
p5,p6 = Cs(SMA, EMA, DEMA, ZLEMA).
Os sinais de negociação pode ser gerado de diversas maneiras:
Opção 1
Buy = macd > signal
Sell = macd < signal
Opção 2
Buy = diff(macd) > 0
Sell = diff(macd) <= 0
Opção 3
Buy = diff(macd) > 0 & macd > 0
Sell = diff(macd) < 0 & macd < 0
Este é outro de parâmetro de otimização signal(1:3).
E, finalmente, o parâmetro anterior - profundidade do histórico de otimização len = 300:1000 (o número das últimas barras onde a otimização é realizada).
No total, temos 9 parâmetros de otimização. Eu aumentei o número de propósito a fim de mostrar que qualquer coisa pode ser utilizada como um parâmetro (figuras, strings e etc.).
O critério de otimização - relação da qualidade K em pontos (em minhas publicações anteriores já foram exaustivamente descritas).
Para otimizar os parâmetros precisamos identificar uma função de aptidão (objetivo) que irá calcular os critérios de qualidade e a seleção do programa de otimização. Vamos começar com o programa.
Vamos aplicar o pacote "rgenoud" de forma segura, rápida e, o mais importante, testado repetidamente. Sua principal restrição implica que todos os parâmetros devem ser inteiros ou físicos. Esta é uma ligeira restrição e é suavemente contornada. A função genoud() combina o algoritmo de pesquisa evolucionário com métodos na base derivativa (Newton ou quase-Newton) para resolver vários problemas de otimização. Genoud() pode ser usado para a resolução de problemas de otimização o qual as derivativas ainda nao foram definidas. Além disso, usando a opção cluster, a função suporta o uso de vários computadores, processadores e núcleos para um cálculo paralelo qualitativo.
genoud(fn, nvars, max = FALSE, pop.size = 1000, max.generations = 100, wait.generations = 10, hard.generation.limit = TRUE, starting.values = NULL, MemoryMatrix = TRUE, Domains = NULL, default.domains = 10, solution.tolerance = 0.001, gr = NULL, boundary.enforcement = 0, lexical = FALSE, gradient.check = TRUE, BFGS = TRUE, data.type.int = FALSE, hessian = FALSE, unif.seed = 812821, int.seed = 53058, print.level = 2, share.type = 0, instance.number = 0, output.path = "stdout", output.append = FALSE, project.path = NULL, P1 = 50, P2 = 50, P3 = 50, P4 = 50, P5 = 50, P6 = 50, P7 = 50, P8 = 50, P9 = 0, P9mix = NULL, BFGSburnin = 0, BFGSfn = NULL, BFGShelp = NULL, control = list(), optim.method = ifelse(boundary.enforcement < 2, "BFGS", "L-BFGS-B"), transform = FALSE, debug = FALSE, cluster = FALSE, balance = FALSE, ...)
Argumentos
- fn – função de objetivo que é minimizada (ou maximizado se max = TRUE). O primeiro argumento da função deve ser um vetor com os parâmetros que são utilizados para minimizar. A função deve retornar como escalar (exceto quando lexical = TRUE)
- nvars – quantidade de parâmetros que serão selecionados para uma função minimizada
- max = FALSE - Objetivo da função de maximização (TRUE) ou minimização (FALSE)
- pop.size = 1000 - tamanho da população. Este é um número de espécies que serão utilizadas na resolução de problemas da otimização. Existem poucas restrições quanto ao valor desta figura. Tirando o fato que o número da população é solicitada a partir de um utilizador, a figura é automaticamente corrigida a fim de satisfazer as restrições relevantes. Estas restrições derivam dos requisitos de alguns operadores do AG. Em particular, o operador Р6 (simples cruzamento) e Р8 (cruzamento heurístico) exigem que o número de espécies sejam pares, ou seja, eles solicitam ambos os pais. Portanto, a variável pop.size deve ser par. Se não, então a população é aumentada para satisfazer estas restrições.
- max.generations = 100 — máximo de gerações. Este é um número máximo de gerações que o Genoud vai apresentar na tentativa de otimizar a função. Esta é uma limitação leve. As gerações máximas operarão para Genoud, apenas se o hard.generation.limit for definido como TRUE, caso contrário, dois gatilhos suaves irão controlar quando o genoud deve finalizar: wait.generations e gradient.check.
Apesar da variável max.generations não restringir o número de gerações por padrão, ela não é menos importante, pois muitos operadores a usam para corrigir o seu comportamento. Na verdade, muitos operadores tornam-se menos aleatórios, uma vez que o número de gerações tornam-se mais próximo dos limites do max.generations. Se o limite for excedido e o genoud decidir prosseguir com a operação, ela aumenta automaticamente o limite max.generation.
- wait.generations = 10. Se a função de destino não melhorar neste número de gerações, então o genoud vai pensar que a otimização foi encontrada. Se o gatilho gradient.check for ativado, então o genoud vai começar a calcular o wait.generations apenas se o gradiente com solution.tolerance for igual a zero. Outras variáveis que controlam a conclusão são max.generations e hard.generation.limit.
- hard.generation.limit = TRUE. Esta variável lógica determina se max.generations é uma restrição obrigatória para genoud. Quando o hard.generation.limit é exibido como FALSE, o genoud pode exceder a quantidade de max.generations, se a função de destino foi melhorada em qualquer número de gerações (determinada em wait.generations), ou se o gradiente (determinado em gradient.check) não é igual a zero.
- starting.values = NULL — vetor ou matriz que contém os valores dos parâmetros que o genoud usará no início. Ao utilizar esta opção, o usuário pode inserir uma ou mais espécies na população inicial. Se uma matriz foi fornecida, as colunas devem ser os parâmetros e strings - espécies. genoud vai criar outras espécies em ordem aleatória.
- Domains = NULL . This is nvars *2 matrix. Para cada parâmetro na primeira coluna - limite inferior; segunda coluna - limite superior. Nenhuma espécie da população inicial do genoud será gerada além dos limites. Mas alguns operadores podem gerar elementos subsidiários que serão posicionados além dos limites, se a flag boundary.enforcement não for ativada.
- Se um usuário não fornecer valores para domínios, então o genoud irá definir os domínios por padrão através do default.domains.
- default.domains = 10. Se um usuário não quiser fornecer uma matriz de domínios, então os domínios podem ser definidos por um usuário com a opção escalar. O genoud irá criar a matriz de domínio, definindo um limite inferior para todos os parâmetros que é igual a (-1)* default.domains, e um limite superior que é igual a default.domains.
- solution.tolerance = 0.001. Este é um nível de segurança utilizada em genoud. Figuras com diferenças solution.tolerance, como sugerido, são iguais. Isto é particularmente importante quando se atinge a avaliação de wait.generations e a performance gradient.check.
- gr = NULL. Função que proporciona um gradiente para otimizador BFGS.a Se for NULL, então gradientes numéricos serão utilizados.
- boundary.enforcement = 0. Esta variável determina o nível até que o genoud esteja sujeito a restrições de limite de área de pesquisa. Apesar do valor dessa variável, nenhuma das espécies a partir da geração inicial terá os valores de parâmetros além dos limites da área de busca.
boundary.enforcement tem três valores possíveis: 0 (todos adequados), 1 (restrição parcial) e 2 (sem violações dos limites):
0: todos adequados, esta opção permite que qualquer operador crie espécies além da área de pesquisa. Estas espécies serão incluídas na população, se seus valores de aptidões são suficientemente bons. Limites são importantes apenas na geração de espécies aleatórias.
1: restrição parcial. Isso permite que os operadores (especialmente aqueles que usam o otimizador baseado numa derivativa, BFGS) vão além dos limites da área de pesquisa durante a criação de um espécime. Mas quando um operador seleciona um espécime, ele deve estar dentro de limites razoáveis.
2: nenhuma violação dos limites. Além da área de pesquisa, as avaliações não serão necessárias. Neste caso, a restrição de limites é também aplicada ao algoritmo BFGS, impedindo que os candidatos desviem além dos limites determinados pelos domínios. Preste atenção, pois ele causa a utilização do algoritmo L-BFGS-B na otimização. Este algoritmo requer que todos os valores e gradientes adequados sejam determinados e finalizados em todas as avaliações funcionais. Se isto causa um erro, é aconselhável usar o algoritmo BFGS e a configuração boundary.enforcement=1.
- lexical = FALSE. Esta opção inclui uma otimização lexical. Esta é uma otimização por diversos critérios e são determinadas sequencialmente na ordem dada pela função de aptidão (fitness). Esta função usada com esta finalidade deve devolver o vetor numérico dos valores de aptidão na ordem lexical. Esta opção pode ter valores FALSE, TRUE ou inteiros que igualam o número de critérios adequados, retornados pela função de aptidão (fitness).
- gradient.check = TRUE. Se esta variável é igual a TRUE, então o genoud não vai começar a contar o wait.generations, até que cada gradiente não esteja próximo de zero com solution.tolerance. Esta variável não tem efeito se o limite de max.generations for excedido, e a opção hard.generational.limit foi definida como TRUE. Se BFGSburnin < 0, então isso vai ser ignorado, se gradient.check = TRUE.
- BFGS = TRUE. Estas perguntas variáveis do opimizador derivativo Quase-Newton(BFGS) devem ser aplicadas nas melhores amostras no fim de cada geração após a inicial. Definir comp FALSE não significa que o BFGS não será aplicado. Em particular, se você deseja que BFGS nunca seja aplicado, o operador Р9 (cruzamento mínimo local) deve ser redefinido.
- data.type.int = FALSE. Esta opção define o tipo de dados dos parâmetros da função otimizada. Se a variável for TRUE, então o genoud irá procurar uma solução entre os números inteiros quando os parâmetros são otimizados.
Com parâmetros inteiros, o genoud nunca usa informações sobre derivativos. Isso implica que o otimizador BFGS nunca é usado - ou seja, a flag BFGS é definida como FALSE. Isto também implica que o operador P9 (cruzamento mínimo local) é resetado e que a verificação de um gradiente (como critério de convergência) está desativada. Apesar de outras opções definidas, o data.type.int tem uma prioridade - isto é, se o genoud afirma que a pesquisa deve ser realizada pela área inteira dos parâmetros, informações sobre o gradiente nunca são consideradas.
Não há uma opção que permite misturar parâmetros inteiros com um ponto flutuante. Se você quiser misturar esses dois tipos, então um parâmetro inteiro pode ser indicado e a variação inteira pode ser transformada numa extensão com um ponto flutuante na função objetiva. Por exemplo, você precisa obter a rede de pesquisa 0,1-1,1. Você indica o genoud para procurar de 10 a 110 e depois divide esse parâmetro por 100 na função de aptidão (fitness).
- hessian = FALSE. Quando esta flag é definida como TRUE, o genoud retorna a matriz Hessian na solução, como parte de sua lista de retorno. Um usuário pode usar essa matriz para calcular os erros padrões.
- unif.seed = 812821. Aqui são definidas as seed para um gerador de uma figura pseudo-aleatória com um ponto flutuante, a fim de usar o genoud. O valor padrão deste seed é 81282. O genoud usa seu gerador interno pessoal dos números pseudo-aleatórios (gerador Tausworthe-Lewis-Payne) para permitir chamadas recursivas e paralelas ao genoud.
- int.seed = 53058. Isso define o seed para um gerador de número inteiro que usa o genoud. O valor padrão da seed é de 53058. O genoud usa seu gerador interno pessoal dos números pseudo-aleatórios (gerador Tausworthe-Lewis-Payne) para permitir chamadas recursivas e paralelas ao genoud.
- print.level = 2. Esta variável controla o nível de impressão que o genoud faz. Existem 4 níveis possíveis: 0 (impressão mínima), 1 (normal), 2 (detalhada) e 3 (depuração). Se o nível 2 é selecionado, então o genoud irá imprimir detalhes sobre a população em cada geração.
- share.type = 0. Se share.type for igual a 1, então o genoud irá verificar no início, se existe o arquivo do projeto (veja project.path). Se esse arquivo existir, ele usa e inicializa a sua população de saída Esta opção pode ser usada com a lexical, mas não como opção transformada.
Operadores. Genoud tem e usa 9 operadores. Os pesos são valores inteiros atribuídos a cada um desses operadores (P1 ... P9). Genoud calcula o total s = P1 + P2 + ... + P9. Pesos iguais a W_n = s / (P_n) são atribuídos a cada operador. Normalmente o operador chama o número igual a c_n = W_n * pop.size.
Operadores Р6 (cruzamento simples) e Р8 (cruzamento heurístico) requerem um número par de espécies para prosseguir com a operação - em outras palavras, eles exigem dois progenitores. Portanto, a variável pop.size e conjuntos de operadores devem ser específicos para garantir que estes três operadores tenham um número de espécies. Se isso não acontecer, o genoud automaticamente aumenta a população, a fim de atender a essa restrição.
Checagens fortes de singularidade foram construídas nos operadores para garantir que irão produzir crianças diferentes de seus pais, mas nem sempre isso ocorre.
O algoritmo evolutivo em rgenoud usa nove operadores que são mencionados abaixo.
- P1 = 50 – Clonagem. Operador de clonagem simplesmente faz cópias da melhor solução dos testes na geração atual (independentemente a partir deste operador, o rgenoud sempre salva uma amostra do melhor teste da solução).
Mutação universal, mutaçao limitada e mutação heterogênea afetam apenas as soluções do teste.
- P2 = 50 - Mutação universal. Mutação universal altera um parâmetro na solução de ensaio com um valor aleatório distribuído uniformemente sobre um domínio definido no parâmetro.
- P3 = 50 - Mutação limitada. Mutação limitada muda um parâmetro com um do limites de seu domínio.
- P4 = 50 - Mutação heterogênea. Mutação heterogênea diminui um parâmetro para um dos limites com um total de diminuição, quando o número de gerações se aproximam do número máximo indicado.
- P5 = 50 - Cruzamento multifaces. Cruzamento multifaces (inspirado pela pesquisa simplex, Gill e outras. 1981, p. 94-95), calcula uma solução de teste que tem uma combinação de convexidade com o mesmo número de soluções de teste como parâmetros.
- P6 = 50 – Cruzamento simples. O cruzamento simples calcula duas soluções a partir de dois testes de entrada, alterando os valores dos parâmetros entre as soluções, após dividir aleatoriamente as soluções no ponto selecionado. Este operador pode ser particularmente eficiente na organização dos parâmetros em cada solução de teste sequencial.
- P7 = 50 - Integral de mutação heterogênea. Integral de mutação heterogênea transforma a mutação heterozigótica em todos os parâmetros da solução de teste.
- P8 = 50 - Cruzamento heurístico. Cruzamento heurístico usa duas soluções de teste para uma nova solução localizada ao longo do vetor que começa numa única solução de teste.
- P9 = 0 - Cruzamento mínimo local: BFGS. Cruzamento mínimo local calcula solução a uma nova consideração em dois passos. Primeiro o BFGS realiza uma série de conjunto preliminares de iterações iniciados a partir da solução de entrada; em seguida, a combinação da convexidade de soluções de entrada é calculada e o BFGS é iterativo.
Observações:
As opções mais importantes que afetam a qualidade são aquelas que definem o tamanho da população (pop.size) e o número de gerações realizadas pelo algoritmo (max.generations, wait.generations, hard.generation.limit e gradient.check). A pesquisa tendo o desempenho esperado, o tamanho da população é melhorado e o número de gerações executadas pelo programa aumentarão. Estas e outras opções devem ser corrigidas manualmente para vários problemas. Por favor, preste mais atenção nas áreas de pesquisa ("domains" e "default.domains").
Linear e restrições não lineares entre os parâmetros podem ser apresentados pelos usuários em suas funções de aptidão. Por exemplo, se o total de 1 e 2 parâmetros for inferior a 725, então esta condição pode ser incorporado na função de aptidão (fitness), um usuário irá maximizar o genoud: if((parm1 + parm2)>= 725) {return (-99999999)}. Neste exemplo, um valor aptidão muito ruim será devolvido ao genoud, se uma restrição linear for violada. Então o genoud tentará encontrar valores de parâmetros que satisfaça a restrição.
Vamos escrever nossa função de aptidão (fitness). Deve poder calcular:
MACD
sinais
taxa de qualidade
# função de aptidão-------------------------fitness <- function(param, test = FALSE){
require(TTR)
require(magrittr)
# definindo variáveis
x <- pr[param[1]]
nFast <- param[2]
nSlow <- param[3]
nSig <- param[4]
macdType <- MaType[param[5]]
sigType <- MaType[param[6]]
percent <- per[param[7]]
len <- param[9]*100
# restrição linear para macd
if (nSlow <= nFast) return(-Inf)
# cálculo do macd
md <- MACD(x = x, nFast = nFast, nSlow = nSlow,
nSig = nSig, percent = TRUE,
maType = list(list(macdType),
list(macdType),
list(sigType)))
# calcular sinais e deslocamento para a barra 1 à direita
sig <- signal(md, param[8]) %>% Lag()
#calcular o saldo no histórico com comprimento "len"
bal <- cumsum(tail(sig, len) * tail(price[ ,'CO'], len))
if(test)
{bal <<- cumsum(tail(sig, len) * tail(price[ ,'CO'], len))}
# calcular razão de qualidade (arredondar para inteiros)
K <- ((tail(bal,1)/length(bal))* 10 ^ Dig) %>% floor()
# devolver o critério de otimização obtido
return(unname(K))
}
Abaixo está uma listagem de todas as variáveis e funções calculadas:
require(Hmisc) # Tipos de média = 4 ----------------------------------------------- MaType <- Cs(SMA, EMA, DEMA, ZLEMA) require(dplyr) # Tipos de preços = 4 ----------------------------------------------- pr <- transmute(as.data.frame(price), Close = Close, Med = Med, Typ = (High + Low + Close)/3, WClose = (High + Low + 2*Close)/4) # Como calcular? per <- c(TRUE, FALSE) # Tipos de sinais = 3 ---------------------------------------------- signal <- function(x, type){ x <- na.omit(x) dx <- diff(x[ ,1]) %>% na.omit() x <- tail(x, length(dx)) switch(type, (x[ ,1] - x[ ,2]) %>% sign(), sign(dx), ifelse(sign(dx) == 1 & sign(x[ ,1]) == 1, 1, ifelse(sign(dx) == -1 & sign(x[ ,1]) == -1,-1, 0)) ) } # configuração inicial---------------------------------------------- par <- c(2, 12, 26, 9, 2, 1, 1, 3, 5) # procurar área----------------------------------------------------- dom <- matrix(c(1, 4, # para tipos de preços 8, 21, # Para um período МА rápido 13, 54, # para um período МА lento 3, 13, # para sinalizar o período de direita 1, 4, # Tipo de МА rápido e lento 1, 4, # Tipo de MA para o sinal 1, 2, # tipo de porcentagem 1, 3, # opção de sinal 3,10), # comprimento do histórico [300:1000] ncol = 2, byrow = TRUE) # Criar cluster a partir de núcleos de processamento disponíveis puskCluster<-function(){ library(doParallel) library(foreach) cores<-detectCores() cl<-makePSOCKcluster(cores) registerDoParallel(cl) #clusterSetRNGStream(cl) return(cl) }
Definir relação de qualidade com parâmetros iniciais (geralmente por padrão):
> K <- fitnes(par, test = TRUE) > K [1] 0 > plot(bal, t="l")
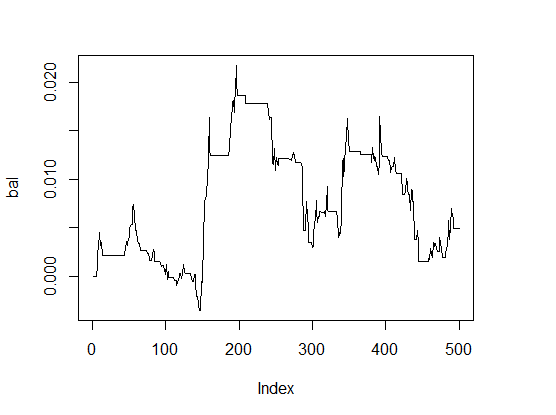
Fig.1 Saldo com os parâmetros padrão
Os resultados são muito ruins.
A fim de comparar a velocidade de cálculo, vamos executar a otimização de um núcleo e no cluster de dois núcleos de processamento.
Em um núcleo:
pr.max <- genoud(fitnes, nvars = 9, max = TRUE, pop.size = 500, max.generation = 300, wait.generation = 50, hard.generation.limit = FALSE, starting.values = par, Domains = dom, boundary.enforcement = 1, data.type.int = TRUE, solution.tolerance = 0.01, cluster = FALSE, print.level = 2) Limite 'wait.generations' alcançado. Nenhuma melhoria significativa em 50 gerações. Solução do valor "Fitness": 1.600000e+01 Parâmetros para a solução: X[ 1] : 1.000000e+00 X[ 2] : 1.400000e+01 X[ 3] : 2.600000e+01 X[ 4] : 8.000000e+00 X[ 5] : 4.000000e+00 X[ 6] : 1.000000e+00 X[ 7] : 1.000000e+00 X[ 8] : 1.000000e+00 X[ 9] : 4.000000e+00 Soluções encontradas: 5 Número de Gerações Executadas: 56 Thu Mar 24 13:06:29 2016 Tempo de execução total: 0 horas 8 minutos e 13 segundos
Parâmetros de Otimização (fenótipo)
> pr.max$par [1] 1 14 26 8 4 1 1 1 4
Decodificamos (fenótipo):
- price type pr[ ,1]= Close
- nFast = 14
- nSlow = 26
- nSig = 8
- macdType = ZLEMA
- sigType = SMA
- percent = TRUE
- sinal = intersecção do MACD e linhas de sinal
- comprimento do histórico = 400 barras.
Vamos ver como a linha de saldo aparece com os parâmetros opcionais. Para este efeito, vamos realizar uma função de aptidão (fitness) com estes parâmetros e com a opção test = TRUE.
> K.opt <- fitnes(pr.max$par, test = TRUE) > K.opt [1] 16 > plot(bal, t="l")
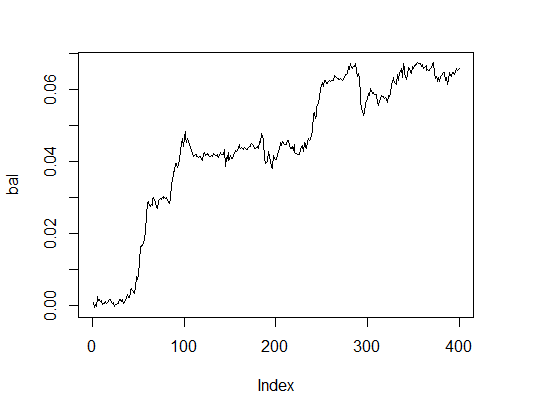
Fig.2. Balanço com parâmetros opcionais
Este é um resultado aceitável que um Expert Advisor deve operar.
Vamos calcular o mesmo no cluster que contém dois núcleos:
# Iniciar o cluster cl <- puskCluster() # Maximizar a função de aptidão (fitness) # Enviar variáveis e funções necessárias para cada núcleo do cluster clusterExport(cl, list("price", "pr", "MaType", "par", "dom", "signal", "fitnes", "Lag", "Dig", "per" ) ) pr.max <- genoud(fitnes, nvars = 9, max = TRUE, pop.size = 500, max.generation = 300, wait.generation = 50, hard.generation.limit = FALSE, starting.values = par, Domains = dom, boundary.enforcement = 1, data.type.int = TRUE, solution.tolerance = 0.01, cluster = cl, print.level = 2) # apenas para experimentos. # Definir 0 no EA # parar o cluster stopCluster(cl) Limite 'wait.generations' alcançado. Nenhuma melhoria significativa em 50 gerações. Solução do valor Fitness: 1.300000e+01 Parâmetros para a solução: X[ 1] : 1.000000e+00 X[ 2] : 1.900000e+01 X[ 3] : 2.000000e+01 X[ 4] : 3.000000e+00 X[ 5] : 1.000000e+00 X[ 6] : 2.000000e+00 X[ 7] : 1.000000e+00 X[ 8] : 2.000000e+00 X[ 9] : 4.000000e+00 Soluções encontradas:10 Número de Gerações Executadas: 61 Thu Mar 24 13:40:08 2016 Tempo de execução total: 0 horas 3 minutos e 34 segundos
O tempo parece muito melhor, mas a qualidade é ligeiramente inferior. A fim de resolver até mesmo uma tarefa tão simples, é importante "brincar" com os parâmetros.
Vamos calcular a opção mais simples:
pr.max <- genoud(fitnes, nvars = 9, max = TRUE, pop.size = 500, max.generation = 100, wait.generation = 10, hard.generation.limit = TRUE, starting.values = par, Domains = dom, boundary.enforcement = 0, data.type.int = TRUE, solution.tolerance = 0.01, cluster = FALSE, print.level = 2) Limite 'wait.generations' alcançado. Nenhuma melhoria significativa em 10 gerações. Solução do valor Fitness: 1.500000e+01 Parâmetros para a solução: X[ 1] : 3.000000e+00 X[ 2] : 1.100000e+01 X[ 3] : 1.300000e+01 X[ 4] : 3.000000e+00 X[ 5] : 1.000000e+00 X[ 6] : 3.000000e+00 X[ 7] : 2.000000e+00 X[ 8] : 1.000000e+00 X[ 9] : 4.000000e+00 Soluções encontradas: 3 Número de Gerações Executadas: 14 Thu Mar 24 13:54:06 2016 Tempo de execução total: 0 horas 2 minutos e 32 segundos
Esta amostra tem um bom resultado. E o que dizer do saldo?
> k [1] 15 > plot(bal, t="l")
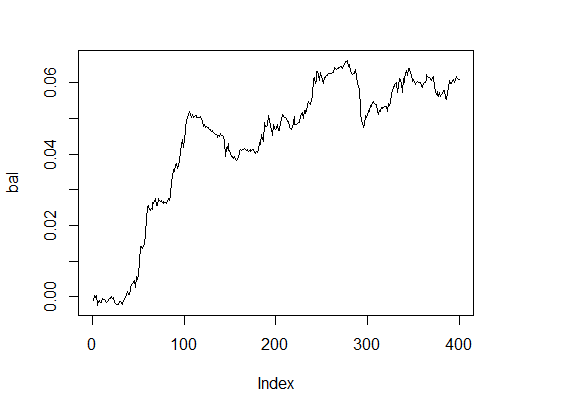
Fig.3. Balanço com parâmetros opcionais
Resultado muito decente num prazo razoável.
Vamos realizar alguns experimentos para comparar os resultados dos algoritmos genéticos com algoritmos evolucionários. Em primeiro lugar, vamos testar o SOMA (Self-Organising Migrating Algorithm) implementado no pacote "soma".
A auto-organização tem como objetivo migrar o algoritmo de otimização estocástica - abordagem semelhante ao do algoritmo genético, embora seja baseado no conceito da série "migração" com um conjunto fixo de espécies, em vez do desenvolvimento de novas gerações. É resistente as mínimas locais e pode ser aplicada a qualquer tarefa para minimizar as despesas com limitação da área dos parâmetros. A principal função:
soma(costFunction, bounds, options = list(), strategy = "all2one", …) Argumentos
Detalhes
Existem várias opções para definir a otimização e os critérios da sua conclusão. Os valores padrão usados aqui são recomendados pelo autor Zelinka (2004).
- pathLength: Distância do líder onde as espécies podem migrar. O valor 1 corresponde à posição líder e o valor acima de 1 (recomendado) considera certa nova regulação. 3 é indicado como padrão.
- stepLength: Etapa mínima utilizada para avaliar as medidas possíveis. Recomenda-se que o comprimento do percurso não seja um número inteiro múltiplo desse valor. O valor padrao é 0.11.
- perturbationChance: Probabilidade dos parâmetros selecionados serão alterados em qualquer estágio. Valor padrão 0.1.
- minAbsoluteSep: A diferença absoluta entre os valores máximos e mínimos da função de preço. Se a diferença for inferior ao mínimo, então o algoritmo é encerrado. O valor padrão é 0. Isso significa que este critério de terminação nunca ficará satisfeito.
- MinRelativeSep: A menor diferença relativa entre os valores mínimos e máximos da função de preço. Se a diferença for inferior ao mínimo, então o algoritmo é encerrado. O valor padrão é 0,001.
- nMigrations: O número máximo de migrações para a rescisão. O valor padrão é 20.
- populationSize: Número de espécies na população. Recomenda-se que este valor seja um pouco maior do que o número dos parâmetros otimizados e não deve ser inferior a 2. O valor padrão é igual a 10.
Ja que o algoritmo realiza apenas minimização, vamos rever a nossa função de aptidão (fitness) para que ela possa fornecer o valor com um sinal oposto e começar a otimização.
require(soma) x <- soma(fitnes, bounds = list(min=c(1,8,13,3,1,1,1,1,3), max = c(4,21,54,13,4,4,2,3,10)), options = list(minAbsoluteSep = 3, minRelativeSep = -1, nMigrations = 20, populationSize = 20), opp = TRUE) Nivel de saída não está definido; padronizado como "Info" * INFO: Iniciando otimização SOMA * INFO: separação custo relativo (-2.14) é abaixo do limiar (-1) - finalizando * INFO: Lider é #7, com custo de -11
Melhores parâmetros:
> x$population[ ,7] [1] 1.532332 15.391757 37.348099 9.860676 1.918848 [6] 2.222211 1.002087 1.182209 3.288627 Arredondar para > x$population[ ,7]%>% floor [1] 1 15 37 9 1 2 1 1 3
Melhor valor na função de aptidão (fitness) = 11. Isto é aceitável para a aplicação prática, mas há espaço para melhorias.
O algoritmo é rápido, mas instável em resultados e requer um ajuste fino.
Função Geral do Recozimento Simulado
Este algoritmo é implementado no pacote «GenSA”. Esta função pode executar uma busca de um mínimo global com uma função de destino não-linear complexa e com um grande número de otimizações.
GenSA(par, fn, lower, upper, control=list(), …)
Argumentos:
- par — Os valores iniciais dos componentes a serem otimizados. NULL é padrão, neste caso os valores padrão serão gerados automaticamente.
- fn — função que será minimizada. Alguns parâmetros do vetor são definidos para minimizar a função. Ela deve retornar um resultado escalar.
- lower – vetor com o comprimento length(par). Limite inferior dos componentes.
- upper — vetor com o comprimento length(par). Limite superior dos componentes.
- … permite ao usuário enviar argumentos adicionais da função fn.
- control — argumento de controle. Esta é uma lista que pode ser usada para gerenciar o comportamento do algoritmo.
- maxit – Inteiro. O número máximo de algoritmos de iteração.
- threshold.stop — Numérico. O programa terminará em cima do valor esperado da função de destino threshold.stop . Valor padrão — NULL.
- nb.stop.improvement — Inteiro. O programa será encerrado se não houver melhorias através dos passosnb.stop.improvement.
- smooth — Lógica. TRUE, quando a função de destino é suavizada ou diferenciada dentro da área de quase todos os parâmetros; caso contrário FALSE. Valor padrão — TRUE
- temperature — Numérico. Valor inicial de temperatura.
- simple.function — Lógica. TRUE significa que a função de destino tem apenas alguns locais mínimos. FALSE é definido como padrão, o que significa que a função de destino é complicada com muitos locais mínimos.
- trace.mat — Lógica. TRUE padrão. Isto significa que a matriz de rastreamento estará disponível no valor de retorno da chamada GenSan.
Os valores de componentes de controle são definidos por padrão para uma tarefa de otimização complexa. Para uma tarefa de otimização regular com média complexidade, o método GenSA pode encontrar rapidamente uma solução razoável, por isso é aconselhável a um usuário finalizar o GenSA antes:
pela definição do threshold.stop, se threshold.stop for um valor esperado da função;
ou em caso de extinção do max.time, se um usuário quer simplesmente executar o GenSA em max.time segundos;
ou definindo o max.call, se um usuário quer simplesmente executar o GenSA dentro das chamadas de funções max.call.
Para tarefas de otimização muito complexa, um usuário deve aumentar os parâmetros temperature e maxit.
Vamos executar a otimização, limitando o tempo máximo de desempenho para 60 segundos.
require(GenSA) pr.max <- GenSA(par, fitnes, lower = c(1,8,13,3,1,1,1,1,3), upper = c(4,21,54,13,4,4,2,3,10), control = list(verbose = TRUE, simple.function = TRUE, max.time = 60), opp = TRUE)
Valor da função de aptidão (fitness) e o valor dos parâmetros opcionais:
> pr.max$value * (-1) [1] 16 > par1 <- pr.max$par > par1 [1] 1.789901 14.992866 43.854988 5.714345 1.843307 [6] 1.979723 1.324855 2.639683 3.166084
Arredondar:
> par1 <- pr.max$par %>% floor [1] 1 14 43 5 1 1 1 2 3
Calcular o valor da função de aptidão (fitness) com esses parâmetros e ver a linha do saldo:
> f1 <- fitnes(par1, test = TRUE) > plot(-1 * bal, t="l")
Fig.4 Saldo 4
Os indicadores de qualidade - num bom nível e os cálculos são surpreendentemente rápidos.
Estes e muitos algoritmos similares (pacotes dfoptim, nlopt, optim, DEoptim, RcppDE etc.) otimizam a função por um critério. Para a otimização de vários critérios é destinado o pacote mco.
7. Formas e métodos para melhorar características qualitativas
Os experimentos realizados mostraram a eficiência dos algoritmos genéticos. Para uma melhoria de indicadores qualitativos, recomenda-se realizar pesquisas adicionais com aplicação da:
- Otimização multicriterial. Por exemplo, para executar a otimização da classificação de qualidade e seu rebaixamento máximo. O pacote "MCO" implementa tal oportunidade.
- Implementação de uma auto-organização dinâmica dos parâmetros do AG. O pacote para possível implementação — "AG". Ele fornece uma ampla gama de operadores para seleção, cruzamento e mutações.
- Possibilidade de testar a aplicação de uma programação genética no sistema de negociação.
Conclusão
Nós consideramos os princípios básicos estabelecidos em algoritmos evolutivos, os seus diferentes tipos e características. Usando um simples Expert Advisor MACDSample, aproveitamos as experiências para mostrar que aplicando a otimização de parâmetros para uma aplicação elementar temos um efeito positivo considerável.
Tempo de execução da otimização e a simplicidade na programação são permitidas durante a operação do EA, sem entrar no mercado. E a falta de restrições severas quanto ao tipo de parâmetros de otimização permitem implementar os tipos mais diversos em várias fases de operação do EA.
A parte mais importante do trabalho é escrever a função de aptidão (fitness) corretamente.
Espero que este artigo possa ajudá-lo a compreender que não é difícil implementar a otimização de seu Expert Advisors por conta própria.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/2225
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Interfaces Gráficas III: Grupos de Botões Simples e Multifuncionais (Capítulo 2)
Interfaces Gráficas III: Grupos de Botões Simples e Multifuncionais (Capítulo 2)
 Teste de estratégias de negociação em ticks reiais
Teste de estratégias de negociação em ticks reiais
 Interfaces Gráficas III: Botões Simples e Multifuncionais (Capítulo 1)
Interfaces Gráficas III: Botões Simples e Multifuncionais (Capítulo 1)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Bem, sugira recursos.
Participe da discussão. Em breve você estará de saída.
Não é uma discussão, é mais como "Deixe-os falar" em sua pior forma.
Ainda bem que não fui lá antes.
Vou lavar minhas mãos.
É horrível.
Não é uma discussão, é mais como "Deixe-os falar" em sua pior forma.
Fico feliz por não ter ido lá antes.
Vou lavar minhas mãos.
Isso é terrível.
Artigo publicado Auto-otimização de EA: algoritmos genéticos e evolutivos:
Autor: Vladimir Perervenko