Глубокие нейросети (Часть II). Разработка и выбор предикторов
6 828
11
Содержание
- Введение
- 1. Разработка признаков
- 2. Выбор предикторов
- Заключение
- Приложения
Введение
В предыдущей части статьи мы рассмотрели различные аспекты получения и подготовки входных данных и целевой переменной. Для воспроизведения скриптов этой статьи вам необходимо либо выполнить все скрипты первой части, либо загрузить результат вычислений первой части статьи из приложения в RStudio.
1. Разработка признаков
Разработка признаков — это наука (и искусство) извлечения дополнительной информации из имеющихся данных. Здесь наша задача — не добавить новые данные, а сделать более полезными и "говорящими" те, которые у нас уже есть. Новые возможности позволяют получить новые признаки выборки данных. Эти признаки позволяют более точно характеризовать и разделять обучающие данные, и за счет этого дают улучшенную точность модели.
Технологически процесс может быть разделен на два этапа:
- Трансформация: в зависимости от сценария, это может быть один из четырех типов преобразования: нормализация данных, устранение асимметрии переменных, устранение выбросов и дискретизация данных.
- Создание признаков: извлечение новой переменной из уже существующих называется созданием признака. Он помогает раскрыть скрытые связи набора данных.
1.1. Трансформация признаков
1.1.1. Преобразование
Что такое преобразование переменной?
В моделировании данных преобразование заключается в замене переменной функцией. Например, замена переменной x на квадратный / кубический корень или логарифм x — это трансформация (или преобразование). Иными словами, трансформация/преобразование — это процесс, который изменяет распределение или связь переменной с другими.
Перечислим ситуации, когда преобразование переменной полезно.
- Когда мы хотим изменить масштаб переменной или стандартизировать ее значения для лучшего понимания. Это преобразование необходимо, если данные имеют разные масштабы. При этом форма распределения переменной не меняется.
- Когда нужно преобразовать сложные нелинейные или криволинейные связи в линейные отношения, поскольку линейная зависимость между переменными легче воспринимается и улучшает возможности прогнозирования. Для поиска взаимосвязи между двумя непрерывными переменными в таких случаях можно использовать точечную диаграмму. Чаще всего в такой ситуации применяют логарифмическое преобразование.
- Когда несимметричное распределение необходимо перевести в симметричное для облегчения интерпретации и анализа. Некоторые методы моделирования требует нормального распределения переменных. Поэтому, когда у нас есть неравномерное распределение, мы можем использовать преобразования, которые уменьшают асимметрию. Для правого асимметричного распределения мы берем квадратный/кубический корень или логарифм переменной, а левый перекос "выправляем" квадратом/кубом или экспоненциальной переменной.
- Когда нужно преобразовать непрерывную переменную в дискретную. Метод такого преобразования — дискретизация.
Каковы общие методы преобразования переменной?
Существуют различные методы, используемые для преобразования переменных. Некоторые из них мы уже перечислили: квадратный и кубический корни, логарифмы, тригонометрические функции, сегментирование. Рассмотрим ряд методов подробно, выделив их плюсы и минусы.
- Логарифмирование: это общий метод преобразования, используемый для изменения формы распределения переменной на распределительном участке. Обычно его применяют для сокращения правой асимметрии. К нулю или отрицательным значениям логарифмирование не может быть применено.
- Квадратный/Кубический корень: оказывает значительный эффект на распределение переменной, хотя и не такой сильный, как логарифмирование. Преимущество кубического корня состоит в том, что его можно применять к нулю и отрицательным значениям. Квадратный корень может быть применен только для положительных значений и нуля.
- Дискретизация/Бининг: используется для категоризации переменных. Выполняется на исходных значениях, процентилях или частотах. Решение о методе категоризации основывается на том, какова природа данных. Мы можем проводить совместные сегментирования взаимозависимых переменных.
Любая трансформация данных приводит к изменению распределения переменных. Рассмотрим это на примерах двух методов преобразования.
Две проблемы нашего исходного набора данных — выбросы и правая асимметрия. Удаление выбросов мы уже рассмотрели. Сейчас сначала попробуем удалить/уменьшить асимметрию, а после этого уберем выбросы.
Метод 1.
Для исправления сильной правой асимметрии набора x прологарифмируем наши данные по основанию 2, а после этого уберем выбросы. Поскольку величина переменных в исходном наборе намного меньше единицы и в нем присутствуют отрицательные значения, для повышения точности будем логарифмировать переменные, добавив к ним 1. Посмотрим, как изменится скос.
evalq({x.ln <- apply(x, 2, function(x) log2(x + 1))
sk.ln <- skewness(x.ln)},
env)
> env$sk.ln
ftlm stlm rbci pcci v.fatl
Skewness -0.2715663 -2.660613 -4.484301 0.4267873 1.253008
v.satl v.rftl v.rstl v.ftlm v.stlm
Skewness 1.83489 2.065224 -0.0343451 -15.62414 0.01529019
v.pcci
Skewness 0.1811206Три переменных — stlm, rbci и v.ftlm — получили сильную левую асимметрию, три переменных — v.fatl, v.satl и v.rftl — остались с сильным правым скосом, у остальных переменных асимметрия выровнялась. Уберем и импутируем выбросы из этого набора и посмотрим, какая асимметрия и распределение переменных у нас получится:
evalq({
foreach(i = 1:ncol(x.ln), .combine = "cbind") %do% {
remove_outliers(x.ln[ ,i])
} -> x.ln.out
colnames(x.ln.out) <- colnames(x.ln)
},
env)
evalq({
foreach(i = 1:ncol(x.ln), .combine = "cbind") %do% {
capping_outliers(x.ln[ ,i])
} -> x.ln.cap
colnames(x.ln.cap) <- colnames(x.ln)
},
env)
evalq({
sk.ln.out <- skewness(x.ln.out)
sk.ln.cap <- skewness(x.ln.cap)
},
env)
> env$sk.ln.out
ftlm stlm rbci pcci
Skewness -0.119055 -0.3549119 -0.1099921 -0.01476384
v.fatl v.satl v.rftl v.rstl
Skewness -0.02896319 -0.03634833 -0.06259749 -0.2120127
v.ftlm v.stlm v.pcci
Skewness -0.05819699 -0.01661317 -0.05420077
> env$sk.ln.cap
ftlm stlm rbci pcci
Skewness -0.1814781 -0.4582045 -0.1658855 -0.02849945
v.fatl v.satl v.rftl v.rstl
Skewness -0.04336238 -0.04400781 -0.0692754 -0.2269408
v.ftlm v.stlm v.pcci
Skewness -0.06184128 -0.02856397 -0.06258243В обоих наборах (x.out и x.cap) данные почти симметричны. Распределение продемонстрировано на рисунках ниже.
par(mfrow = c(2,2)) boxplot(env$x.ln, main = "x.ln with outliers", xlab = "") boxplot(env$x.ln.out, main = "x.ln.out without outliers", xlab = "") boxplot(env$x.ln.cap, main = "x.ln.cap with imputed outliers", xlab = "") par(mfrow = c(1,1))
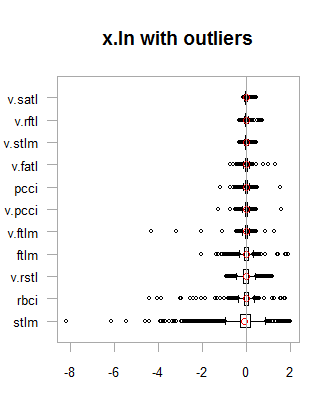
Рис.1. Логтрансформированные данные с выбросами и без
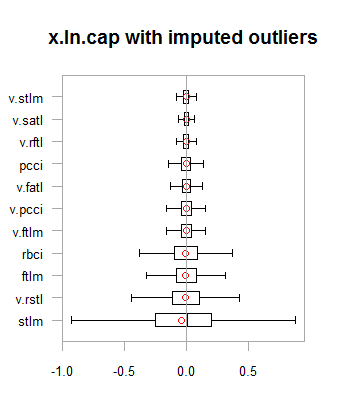
Рис.2. Логтрансформированные данные с импутированными выбросами
Результаты похожи на предыдущее преобразование, за одним исключением — диапазон изменения переменных стал шире.
Преобразуем x.ln.cap датафрейм и посмотрим вариацию и ковариацию набора:
evalq(x.ln.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetLnCap, env)
Построим графики:
require(GGally) evalq(ggpairs(dataSetLnCap, columns = 2:7, mapping = aes(color = Class), title = "PredLnCap1"), env) evalq(ggpairs(dataSetLnCap, columns = 8:13, mapping = aes(color = Class), title = "PredLnCap2"), env)
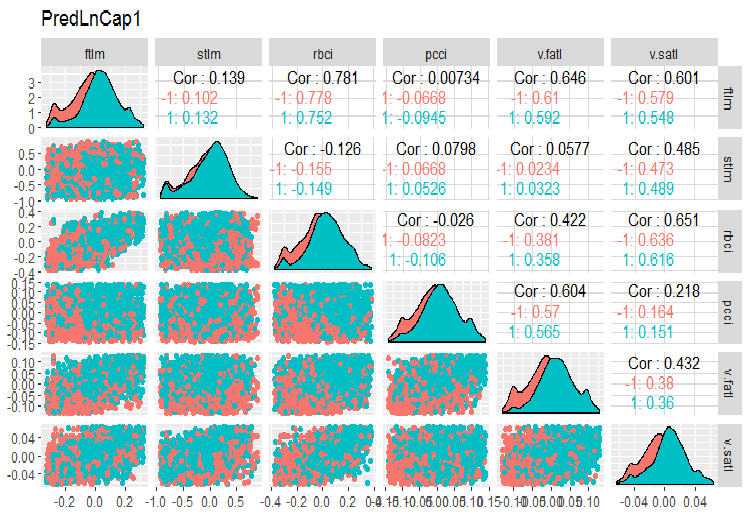
Рис.3. Параметры логтрансформированных данных, часть 1
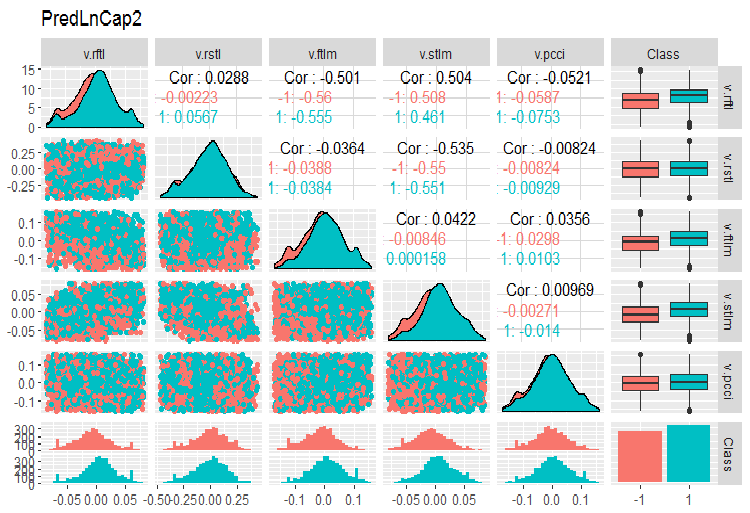
Рис. 4. Параметры логтрансформированных данных, часть 2
Метод 2.
Трансформируем данные с помощью функции sin(2*pi*x), уберем и импутируем выбросы и посмотрим на асимметрию, распределение выбросов и ковариацию трансформированных переменных на графиках.
evalq({x.sin <- apply(x, 2, function(x) sin(2*pi*x))
sk.sin <- skewness(x.sin)
},
env)
#----------
evalq({
foreach(i = 1:ncol(x.sin), .combine = "cbind") %do% {
remove_outliers(x.sin[ ,i])
} -> x.sin.out
colnames(x.sin.out) <- colnames(x.sin)
},
env)
#-----------------
evalq({
foreach(i = 1:ncol(x.sin), .combine = "cbind") %do% {
capping_outliers(x.sin[ ,i])
} -> x.sin.cap
colnames(x.sin.cap) <- colnames(x.sin)
},
env)
#-----------
evalq({
sk.sin.out <- skewness(x.sin.out)
sk.sin.cap <- skewness(x.sin.cap)
},
env) Какова асимметрия в этих трансформированных наборах?
env$sk.sin ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.0009679463 v.fatl v.satl v.rftl v.rstl Skewness 0.03280465 0.5217757 0.05611136 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.04923953 -0.2123434 0.01738377 > env$sk.sin.out ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.03532892 v.fatl v.satl v.rftl v.rstl Skewness 0.00360966 -0.02380975 -0.05336561 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.0009366441 0.01835948 0.0008843329 > env$sk.sin.cap ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.03283132 v.fatl v.satl v.rftl v.rstl Skewness 0.007588308 -0.02424707 -0.04106469 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.007003051 0.009237835 0.002101687
Как видим, при этой трансформации все наборы симметричны. Посмотрим теперь, как эти наборы выглядят:
par(mfrow = c(2, 2)) boxplot(env$x.sin, main = "x.sin with outlier") abline(h = 0, col = 2) boxplot(env$x.sin.out, main = "x.sin.out without outlier") abline(h = 0, col = 2) boxplot(env$x.sin.cap, main = "x.sin.cap with capping outlier") abline(h = 0, col = 2) par(mfrow = c(1, 1))
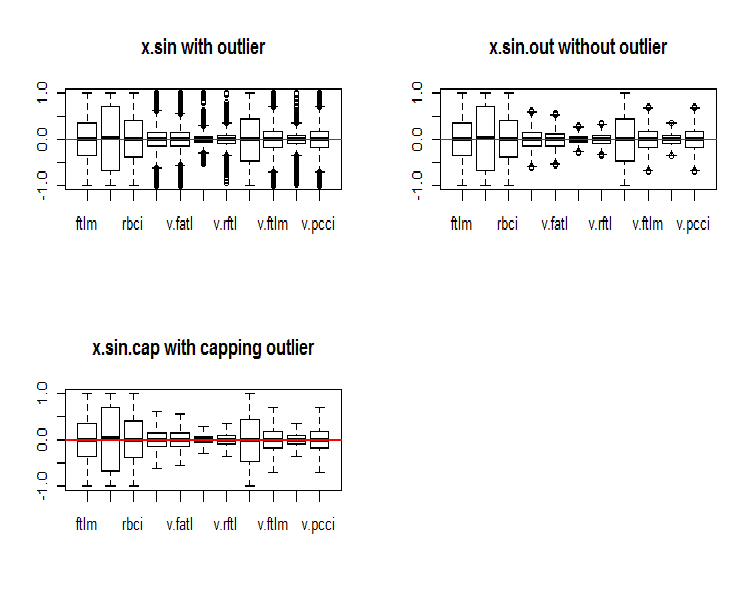
Рис.5. Набор данных, трансформированный функцией sin()
Все наборы визуально выглядят лучше, чем предыдущие (исходный и логтрансформированный).
Посмотрим, как NA распределены в переменных после удаления выбросов.
require(VIM)
evalq(a <- aggr(x.sin.out), env)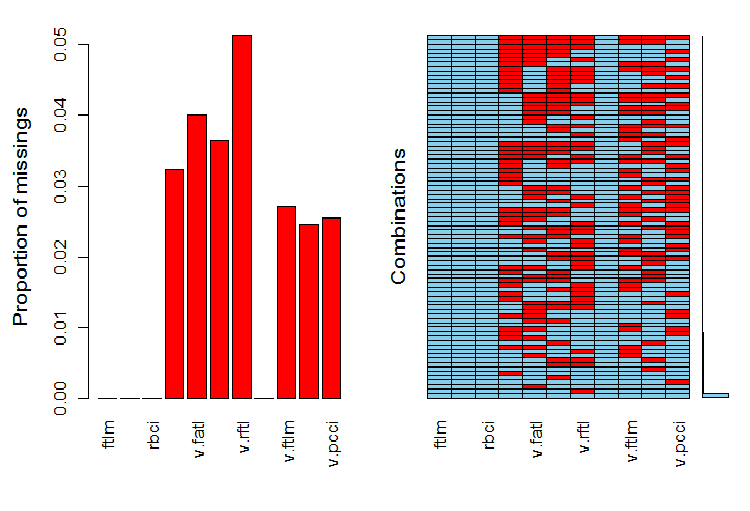 
Рис.6. Распределение NA в наборе
В левой части графика видно, сколько (относительно) неопределенных данных в каждой переменной. В правой части — комбинация примеров с различным количеством NA (снизу вверх по возрастающей). Можем посмотреть в числах:
> print(env$a) Missings in variables: Variable Count pcci 256 v.fatl 317 v.satl 289 v.rftl 406 v.ftlm 215 v.stlm 194 v.pcci 201
Как распределены NA в переменных?
par(mfrow = c(3, 4)) evalq( foreach(i = 1:ncol(x.sin.out)) %do% { barMiss(x.sin.out, pos = i, only.miss = TRUE, main = "x.sin.out without outlier") }, env ) par(mfrow = c(1, 1))
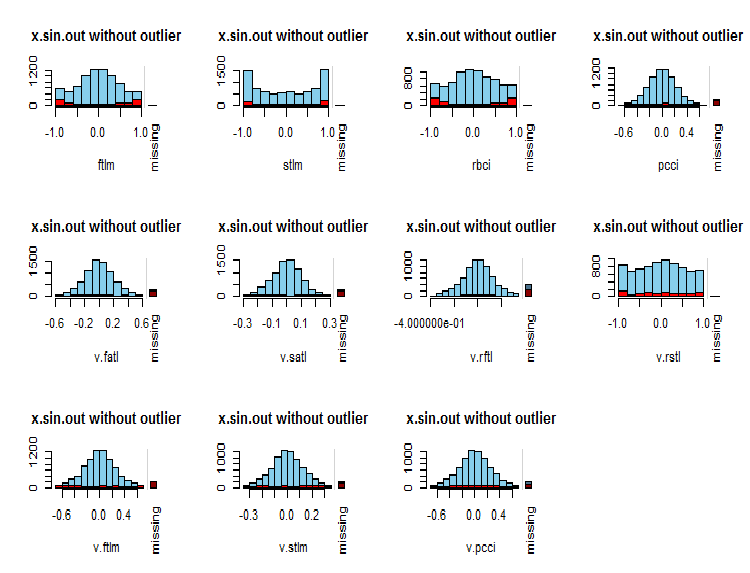
Рис.7. Распределение NA в переменных
Синим цветом показаны наблюдаемые значения переменной, красным — количество NA других переменных в различных диапазонах значений текущей. Бар справа — вклад NA текущей переменной в общее количество NA всех переменных.
В заключение посмотрим вариацию и ковариацию трансформированного набора с импутированными выбросами.
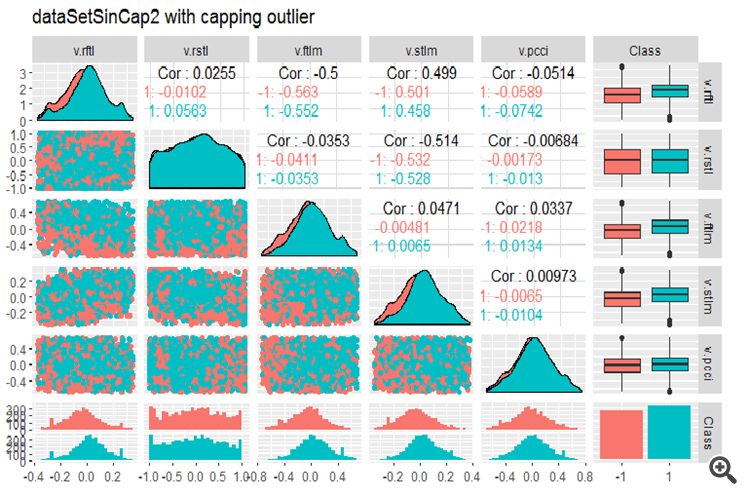
#--------------- evalq(x.sin.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetSinCap, env) require(GGally) evalq(ggpairs(dataSetSinCap, columns = 2:7, mapping = aes(color = Class), title = "dataSetSinCap1 with capping outlier "), env) evalq(ggpairs(dataSetSinCap, columns = 8:13, mapping = aes(color = Class), title = "dataSetSinCap2 with capping outlier"), env) #---------------------------
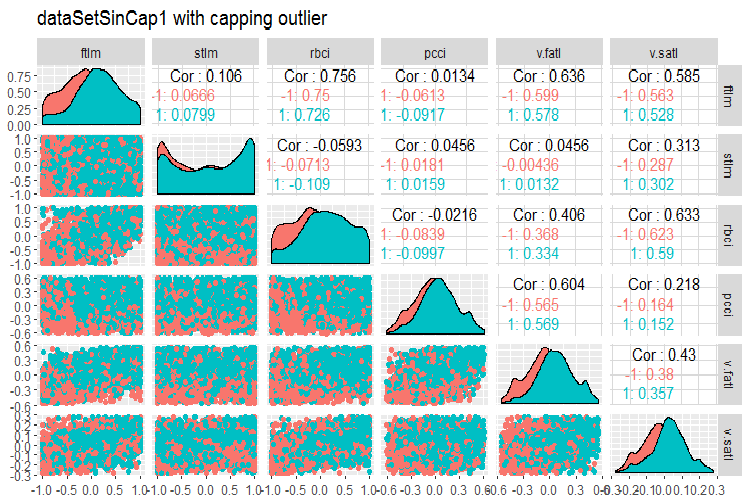
Рис.8. Параметры трансформированных sin() данных, часть 1
Рис.9. Параметры трансформированных sin() данных, часть 2
1.1.2. Нормализация
Поскольку мы готовим данные для нейросети, нужно привести переменные в диапазон { -1..+1 }. Для этого используем функцию preProcess()::caret и method = “spatialSign”. Как вариант, перед нормализацией можно центрировать и шкалировать данные. Поскольку это довольно тривиальный процесс, мы не будем останавливаться на нем подробно.
Единственное, что нужно подчеркнуть: параметры нормализации получаем на тренировочном наборе, тестовый и валидационный наборы обрабатываем с ними же.
Для использования в дальнейших экспериментах разделим наш набор, полученный в предыдущих вычислениях (dataSet без удаления высокоррелированных ) на train/test/val и приведем в диапазон (-1,+1) без стандартизации.
При нормировании со стандартизацией нужно помнить, что при определении параметров нормализации (mean/median, sd/mad) мы определяем и параметры импутации выбросов. В дальнейшем они будут использованы на train/val/test . Ранее в статье мы уже написали 2 функции: prep.outlier() и treatOutlier(), которые предназначены именно для этих целей.
Последовательность выполнения операций:
- Определение параметров выбросов в train
- Удаление выбросов в train
- Определение параметров стандартизации в train
- Импутируем выбросы в train/val/test
- Нормализация train/val/test.
Этот вариант в статье мы рассматривать не будем, вы можете ознакомиться с ним самостоятельно.
Разделяем набор на train/val/test:
evalq(
{
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
list(clean = data.frame(dataSet) %>% na.omit(),
train = clean[train, ],
val = clean[val, ],
test = clean[test, ]) -> DT
}, env) Определим параметры нормализации для набора train и нормализуем наборы train/test/val:
require(foreach)
evalq(
{
preProcess(DT$train, method = "spatialSign") -> preproc
list(train = predict(preproc, DT$train),
val = predict(preproc, DT$val),
test = predict(preproc, DT$test)
) -> DTn
},
env) Посмотрим суммарную статистику набора train:
> table.Stats(env$DTn$train %>% tk_xts()) Using column `Data` for date_var. ftlm stlm rbci pcci Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5909 -0.7624 -0.6114 -0.8086 Quartile 1 -0.2054 -0.2157 -0.2203 -0.2110 Median 0.0145 0.0246 0.0147 0.0068 Arithmetic Mean 0.0070 0.0190 0.0085 0.0028 Geometric Mean -0.0316 -0.0396 -0.0332 -0.0438 Quartile 3 0.2139 0.2462 0.2341 0.2277 Maximum 0.6314 0.8047 0.7573 0.7539 SE Mean 0.0060 0.0073 0.0063 0.0065 LCL Mean (0.95) -0.0047 0.0047 -0.0037 -0.0100 UCL Mean (0.95) 0.0188 0.0333 0.0208 0.0155 Variance 0.0719 0.1058 0.0784 0.0848 Stdev 0.2682 0.3252 0.2800 0.2912 Skewness -0.0762 -0.0221 -0.0169 -0.0272 Kurtosis -0.8759 -0.6688 -0.8782 -0.7090 v.fatl v.satl v.rftl v.rstl Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5160 -0.5943 -0.6037 -0.7591 Quartile 1 -0.2134 -0.2195 -0.1988 -0.2321 Median 0.0015 0.0301 0.0230 0.0277 Arithmetic Mean 0.0032 0.0151 0.0118 0.0177 Geometric Mean -0.0323 -0.0267 -0.0289 -0.0429 Quartile 3 0.2210 0.2467 0.2233 0.2657 Maximum 0.5093 0.5893 0.6714 0.7346 SE Mean 0.0058 0.0063 0.0062 0.0074 LCL Mean (0.95) -0.0082 0.0028 -0.0003 0.0033 UCL Mean (0.95) 0.0146 0.0274 0.0238 0.0321 Variance 0.0675 0.0783 0.0757 0.1083 Stdev 0.2599 0.2798 0.2751 0.3291 Skewness -0.0119 -0.0956 -0.0648 -0.0562 Kurtosis -1.0788 -1.0359 -0.7957 -0.7275 v.ftlm v.stlm v.rbci v.pcci Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5627 -0.6279 -0.5925 -0.7860 Quartile 1 -0.2215 -0.2363 -0.2245 -0.2256 Median -0.0018 0.0092 -0.0015 -0.0054 Arithmetic Mean -0.0037 0.0036 -0.0037 0.0013 Geometric Mean -0.0426 -0.0411 -0.0433 -0.0537 Quartile 3 0.2165 0.2372 0.2180 0.2276 Maximum 0.5577 0.6322 0.5740 0.9051 SE Mean 0.0061 0.0065 0.0061 0.0070 LCL Mean (0.95) -0.0155 -0.0091 -0.0157 -0.0124 UCL Mean (0.95) 0.0082 0.0163 0.0082 0.0150 Variance 0.0732 0.0836 0.0742 0.0975 Stdev 0.2706 0.2892 0.2724 0.3123 Skewness 0.0106 -0.0004 -0.0014 0.0232 Kurtosis -1.0040 -1.0083 -1.0043 -0.4159
Из таблицы мы видим, что переменные симметричны и имеют очень близкие параметры.
Посмотрим на распределение переменных в наборах train/val/test:
boxplot(env$DTn$train %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Train") abline(v = 0, col = 2) boxplot(env$DTn$test %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Test") abline(v = 0, col = 2) boxplot(env$DTn$val %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Val") abline(v = 0, col = 2)
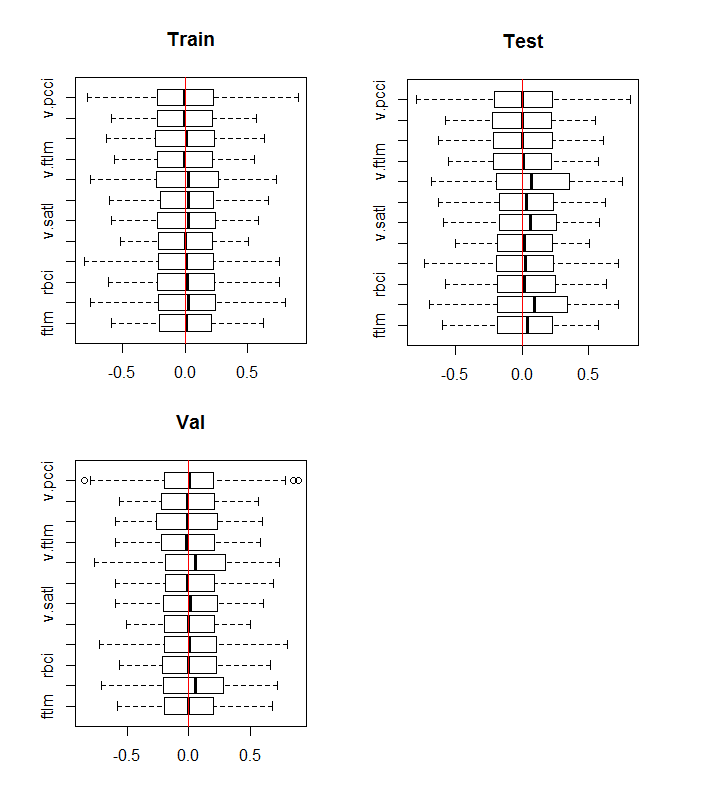
Рис.10. Распределение переменных в наборах train/val/test после нормализации
Распределение переменных во всех наборах практически одинаково. Дополнительно нужно рассмотреть корреляцию и ковариацию переменных в наборе train:
require(GGally) evalq(ggpairs(DTn$train, columns = 2:7, mapping = aes(color = Class), title = "DTn$train1 "), env) evalq(ggpairs(DTn$train, columns = 8:14, mapping = aes(color = Class), title = "DTn$train2"), env)
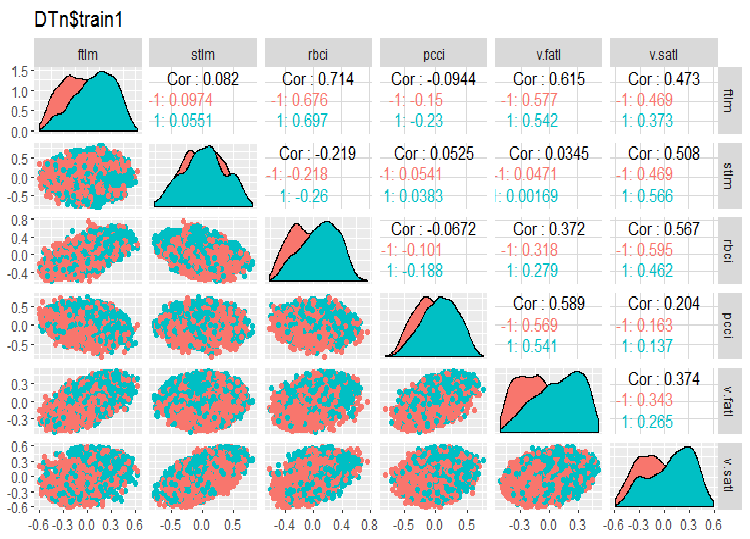
Рис.11. Вариация и ковариация набора 1 train
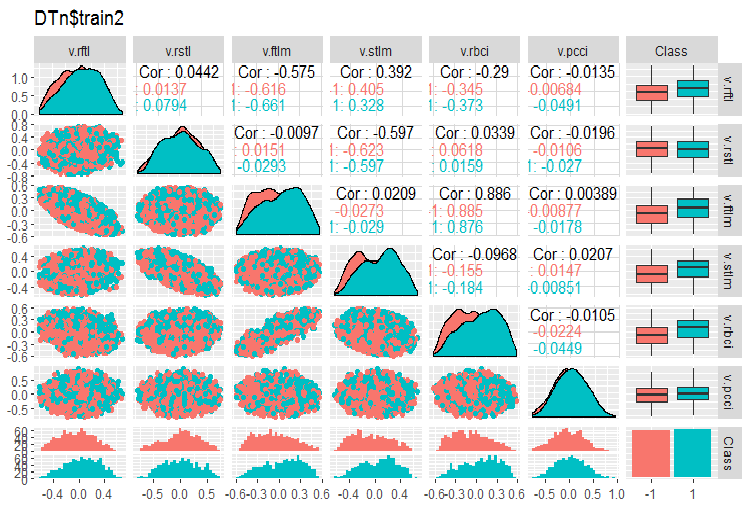
Рис.12. Вариация и ковариация набора 2 train
Высококоррелированных данных у нас нет, распределение компактное и без выбросов, данные хорошо разделяемые. На первый взгляд предварительно видны две проблемных переменных — stlm и v.rstl. В дальнейшем, когда мы будем оценивать релевантность предикторов, мы уточним это предварительное мнение. Сейчас мы можем посмотреть корреляцию этих предикторов к целевой:
> funModeling::correlation_table(env$DTn$train %>% tbl_df %>% + select(-Data), str_target = 'Class') Variable Class 1 Class 1.00 2 v.fatl 0.38 3 ftlm 0.34 4 rbci 0.28 5 v.rbci 0.28 6 v.satl 0.27 7 pcci 0.24 8 v.ftlm 0.22 9 v.stlm 0.22 10 v.rftl 0.18 11 v.pcci 0.08 12 stlm 0.03 13 v.rstl -0.01Видим, что указанные переменные находятся внизу таблицы с очень низкими показателями. Под вопросом также релевантность переменной v.pcci. Посмотрим ближе переменную v.fatl во всех наборах train/val/test:
require(ggvis) evalq( DTn$train %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$train$v.fatl"), env) evalq( DTn$val %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$val$v.fatl"), env) evalq( DTn$test %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$test$v.fatl"), env)
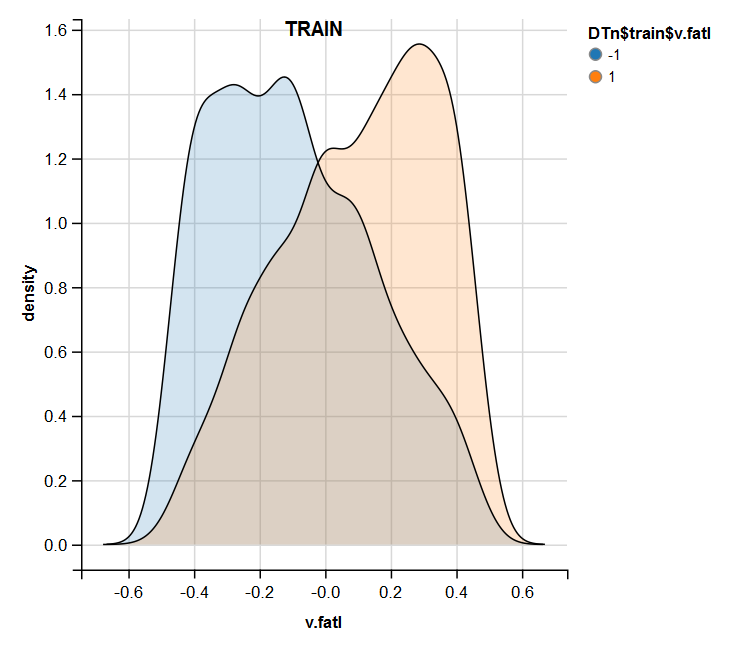
Рис.13. Распределение переменной v.fatl в наборе train после нормализации
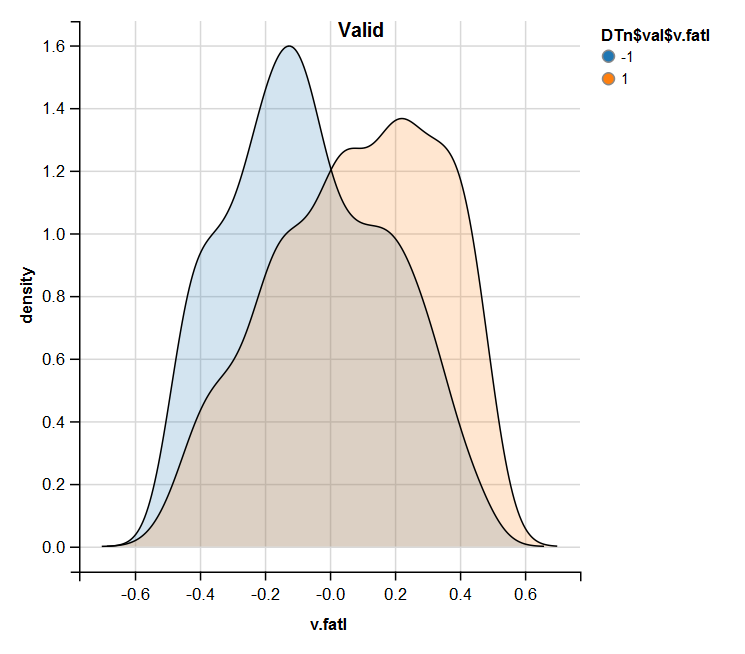
Рис.14. Распределение переменной v.fatl в наборе valid после нормализации
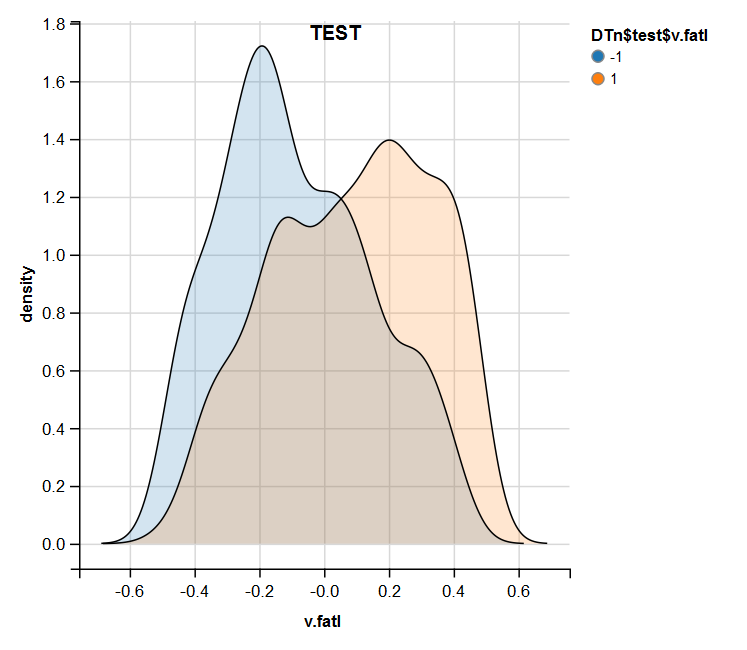
Рис.15. Распределение переменной v.fatl в наборе test после нормализации
Проведенный анализ показывает, что нормализация часто дает хорошее распределение предикторов без выбросов и высококоррелированных данных. Во многом это зависит от характера сырых данных.
1.1.3. Дискретизация
Дискретизация — процесс преобразования непрерывной переменной в дискретную, путем разделения ее значения на участки с использованием различных методов определения границ.
Можно выделить две группы методов разделения: количественный, без связи с целевой, и с учетом соответствия диапазонов целевой.
Первая группа методов практически полностью охватывается функцией cut2()::Hmisc. Можно разделить выборку на заранее заданное количество участков, с указанием конкретных границ, поквартильно, с указанием минимального количества примеров в каждом участке, на равночастотные участки.
Вторая группа методов более интересна, так как разделяет переменную на участки, связанные с уровнями целевой. Рассмотрим несколько пакетов, реализующих эти методы.
Discretization. Этот пакет представляет собой набор алгоритмов дискретизации с учителем. Он также может быть сгруппирован в терминах «сверху вниз» или «снизу вверх», реализующих алгоритмы дискретизации. Рассмотрим некоторые из них на примере нашего набора dataSet.
Проведем очистку набора (без удаления высококоррелированных), разделим на train/val/test в соотношении 2000/1000/1000.
require(discretization)
require(caret)
require(pipeR)
evalq(
{
dataSet %>%
preProcess(.,
method = c("zv", "nzv", "conditionalX")) %>%
predict(., dataSet) %>%
na.omit -> dataSetClean
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
list(train = dataSetClean[train, ],
val = dataSetClean[val, ],
test = dataSetClean[test, ]) -> DT
},
env) Будем использовать функцию mdlp()::discretization, которая описывает дискретизацию с использованием принципа минимальной длины описания. Эта функция дискретизирует непрерывные атрибуты матрицы данных с использованием критерия энтропии с минимальной длиной описания в качестве правила остановки.
evalq(
pipeline({
DT$train
select(-Data)
as.data.frame()
mdlp()}) -> mdlp.train, envir = env) Функция возвращает лист с двумя слотами: это cutp — датафрейм с точками разделения для каждой переменной и Disc.data — датафрейм с размеченными переменными.
> env$mdlp.train%>%str() List of 2 $ cutp :List of 12 ..$ : num [1:2] -0.0534 0.0278 ..$ : chr "All" ..$ : num -0.0166 ..$ : num [1:2] -0.0205 0.0493 ..$ : num [1:3] -0.0519 -0.0055 0.019 ..$ : num 0.000865 ..$ : num -0.00909 ..$ : chr "All" ..$ : num 0.0176 ..$ : num [1:2] -0.011 0.0257 ..$ : num [1:3] -0.03612 0.00385 0.03988 ..$ : chr "All" $ Disc.data:'data.frame': 2000 obs. of 13 variables: ..$ ftlm : int [1:2000] 3 3 3 3 3 2 1 1 1 1 ... ..$ stlm : int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ rbci : int [1:2000] 2 2 2 2 2 2 1 1 1 1 ... ..$ pcci : int [1:2000] 2 2 1 2 2 1 1 2 3 2 ... ..$ v.fatl: int [1:2000] 4 4 3 4 3 1 1 2 3 2 ... ..$ v.satl: int [1:2000] 1 1 1 2 2 1 1 1 1 1 ... ..$ v.rftl: int [1:2000] 1 2 2 2 2 2 2 2 1 1 ... ..$ v.rstl: int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ v.ftlm: int [1:2000] 2 2 1 1 1 1 1 1 2 1 ... ..$ v.stlm: int [1:2000] 1 1 1 2 2 1 1 1 1 1 ... ..$ v.rbci: int [1:2000] 4 4 3 3 2 1 1 2 3 2 ... ..$ v.pcci: int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ...
Что мы можем увидеть в первом слоте?
У нас есть три неразмеченных переменных, значения которых никак не связаны с целевой. Это 2,8 и 12 (stlm, v.rstl, v.pcci). Их можно удалить без потери качества набора. Кстати, эти же переменные мы определили как нерелевантные и в предыдущем разделе.
4 переменных разделены на два класса, 3 переменных — на 3 класса и две переменных — на 4 класса.
Разметим наши наборы val/test на сегменты, используя точки разделения, полученные на train. Для этого уберем из набора train переменные, которые остались неразмеченными, и сохраним набор в датафрейм train.d. Затем, используя функцию findInterval(), разметим набор test/val точками разделения, полученными ранее.
evalq(
{
mdlp.train$cutp %>%
lapply(., function(x) is.numeric(x)) %>%
unlist -> idx # bool
#----train-----------------
mdlp.train$Disc.data[ ,idx] -> train.d
#---test------------
DT$test %>%
select(-c(Data, Class)) %>%
as.data.frame() -> test.d
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {findInterval(test.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$test$Class) -> test.d
colnames(test.d) <- colnames(train.d)
#-----val-----------------
DT$val %>%
select(-c(Data, Class)) %>%
as.data.frame() -> val.d
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {findInterval(val.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$val$Class) -> val.d
colnames(val.d) <- colnames(train.d)
},env
)
Как выглядят эти наборы?
> env$train.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 3 2 2 4 1 1 2 1 4 1 2 3 2 2 4 1 2 2 1 4 1 3 3 2 1 3 1 2 1 1 3 1 4 3 2 2 4 2 2 1 2 3 1 5 3 2 2 3 2 2 1 2 2 1 6 2 2 1 1 1 2 1 1 1 -1 > env$test.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 1 1 1 2 1 1 1 1 2 -1 2 1 1 3 3 1 1 2 2 3 -1 3 1 1 2 2 1 1 1 2 2 -1 4 2 1 2 3 1 1 2 2 3 1 5 2 2 2 3 1 1 1 2 3 1 6 2 2 2 4 1 1 2 2 3 1 > env$val.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 2 2 2 2 2 2 1 2 2 1 2 2 2 2 2 2 2 1 2 2 1 3 2 2 2 3 2 2 1 2 2 1 4 2 2 2 4 2 2 2 2 3 1 5 2 2 2 3 2 2 1 2 2 1 6 2 2 2 3 2 2 2 2 2 1 > env$train.d$v.fatl %>% table() . 1 2 3 4 211 693 519 577 > env$test.d$v.fatl %>% table() . 1 2 3 4 49 376 313 262 > env$val.d$v.fatl %>% table() . 1 2 3 4 68 379 295 258
Дальнейшее использование наборов с дискретными данными зависит от используемой модели. Если это нейросеть, то нужно будет превратить предикторы в dummy-переменные. Насколько хорошо разделены классы этими переменными? Насколько хорошо они коррелируют с целевой? Визуализируем эти зависимости с помощью cross-plot()::funModeling. Cross_plot показывает, как входная переменная коррелирует с целевой переменной, получая коэффициенты правдоподобия для каждого диапазона каждого входа.
Рассмотрим три переменных — v.fatl, ftlm и v.satl, разделенных на 4, 3 и 2 диапазона соответственно. Построим графики:
evalq(
cross_plot(data = train.d,
str_input = c("v.fatl", "ftlm", "v.satl"),
str_target = "Class",
auto_binning = F,
plot_type = "both"), #'quantity' 'percentual'
env
) 
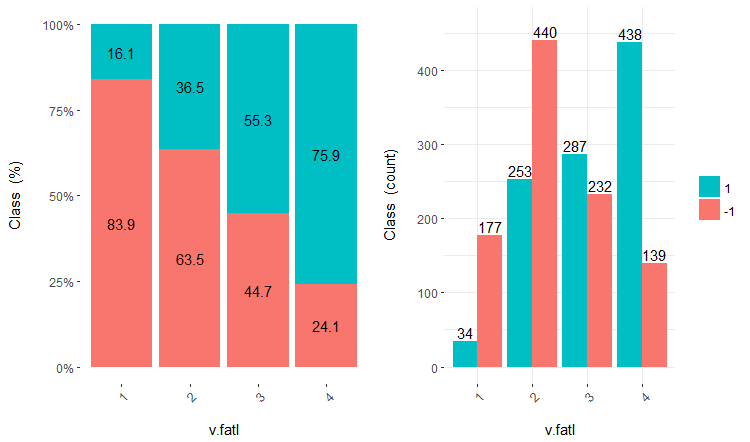
Рис.16. Cross-plot переменной v.fatl/Class
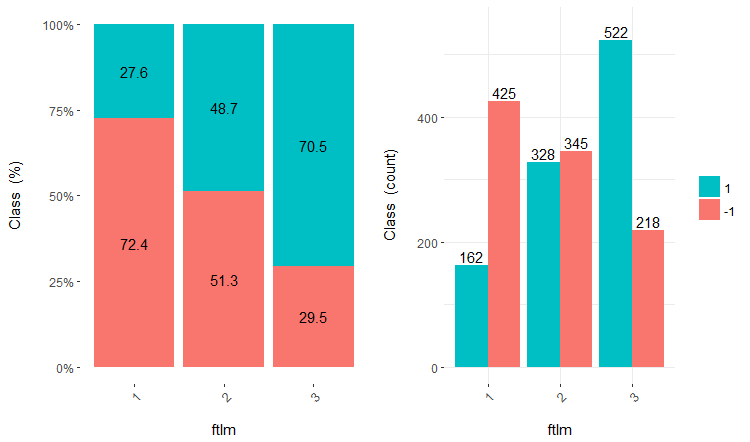
Рис.17. Cross-plot переменной ftlm/Class
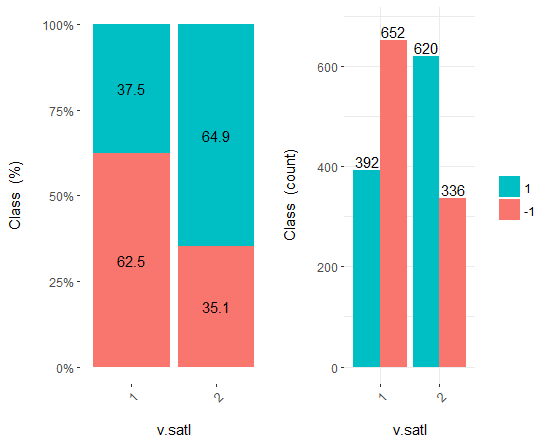
Рис.18. Cross-plot переменной v.satl/Class
Как видим, предикторы хорошо коррелированы с уровнями целевой, имеют хорошо выраженные пороги, разделяющие уровни целевой Class.
Можно просто (неоптимально) разделить предикторы на равные участки и посмотреть, как в таком случае они будут коррелировать с целевой. Возьмем три предыдущих переменных и две плохих (stlm, v.rstl) из набора train (недискретизованного). Разделим их на 10 равночастотных участков и посмотрим на cross-plot их с целевой:
evalq(
cross_plot(
DT$train %>% select(-Data) %>%
select(c(v.satl, ftlm, v.fatl, stlm, v.rstl, Class)) %>%
as.data.frame(),
str_input = Cs(v.satl, ftlm, v.fatl, stlm, v.rstl),
str_target = "Class",
auto_binning = T,
plot_type = "both"), #'quantity' 'percentual'
env
) Отрисуем пять графиков этих переменных:
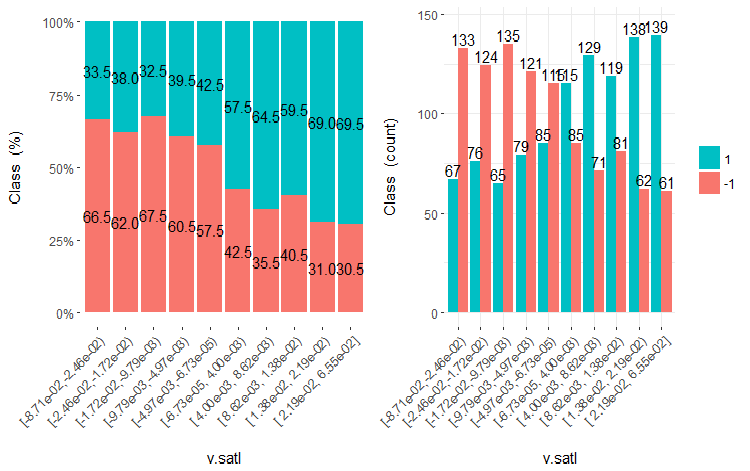
Рис.19. Cross-plot переменной v.satl (10 участков) vs Class
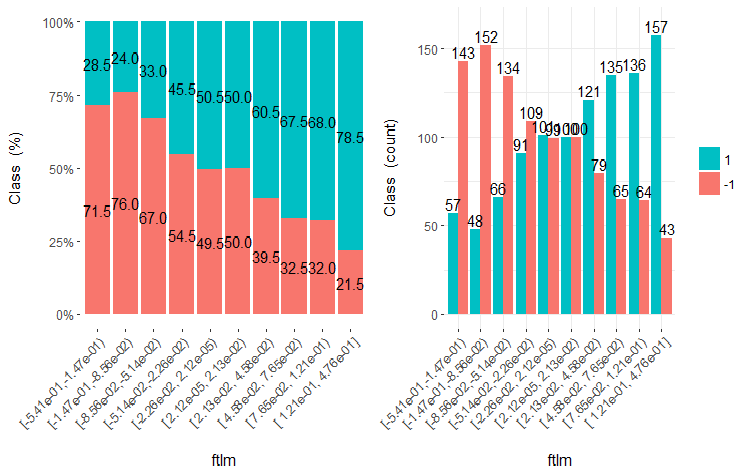
Рис.20. Cross-plot переменной ftlml (10 участков) vs Class
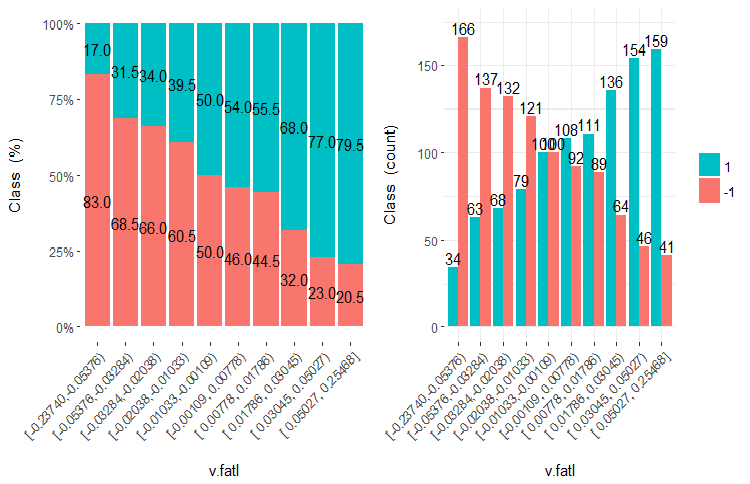
Рис.21. Cross-plot переменной v.fatl (10 участков) vs Class
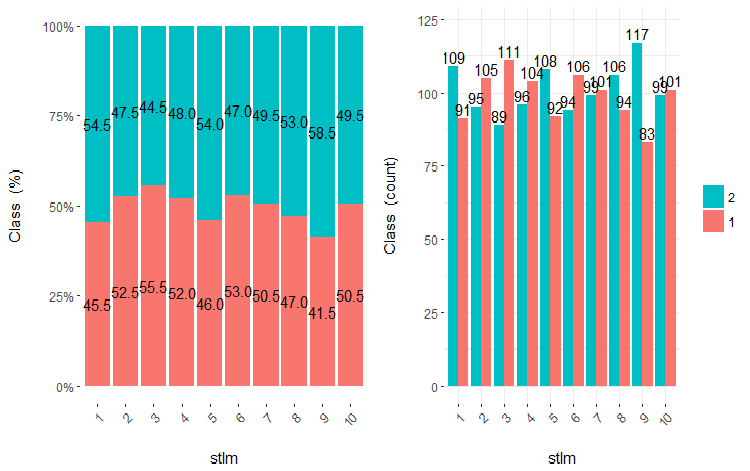
Рис.22. Cross-plot переменной stlm (10 участков) vs Class
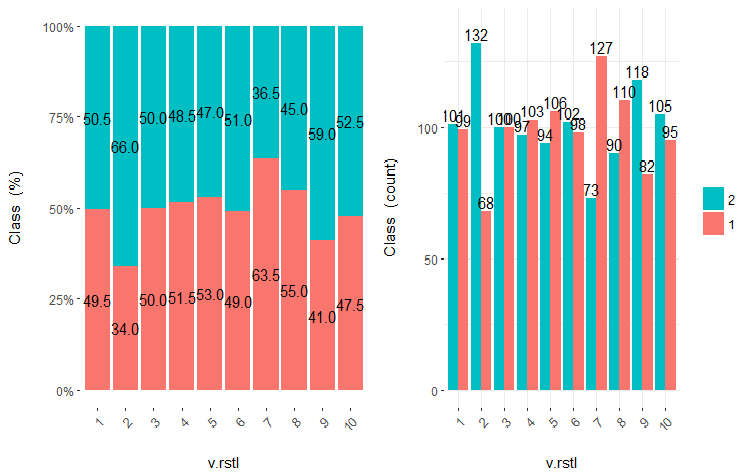
Рис.23. Cross-plot переменной v.rstl (10 участков) vs Class
Как видно из этих рисунков, и при разделении на 10 дискретных равночастотных участков переменные v.fatl, ftlm и v.satl имеют хорошо выраженный порог разделения уровней целевой. Становится понятно, почему две других переменных (stlm, v.rstl) нерелевантны. Кстати, это эффективный способ определения важности предикторов. Мы еще поговорим об этом ниже.
В заключение посмотрим, как входная переменная коррелирует с целевой переменной, сравнивая байесовским способом posterior conversion rate к целевой переменной. Полезно сравнивать категориальные ценности, которые не имеют внутреннего порядка. Для этого будем использовать функцию bayes_plot::funModeling. Возьмем переменные v.fatl, ftlm и v.satl с наборов train.d, val.d и test.d.
#------BayesTrain------------------- evalq( { bayesian_plot(train.d, input = "v.fatl", target = "Class", title = "Bayesian comparison train$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(train.d, input = "ftlm", target = "Class", title = "Bayesian comparison train$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(train.d, input = "v.satl", target = "Class", title = "Bayesian comparison train$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #------------BayesTest------------------------ evalq( { bayesian_plot(test.d, input = "v.fatl", target = "Class", title = "Bayesian comparison test$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(test.d, input = "ftlm", target = "Class", title = "Bayesian comparison test$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(test.d, input = "v.satl", target = "Class", title = "Bayesian comparison test$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #-------------BayesVal--------------------------------- evalq( { bayesian_plot(val.d, input = "v.fatl", target = "Class", title = "Bayesian comparison val$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(val.d, input = "ftlm", target = "Class", title = "Bayesian comparison val$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(val.d, input = "v.satl", target = "Class", title = "Bayesian comparison val$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #------------------------------------------
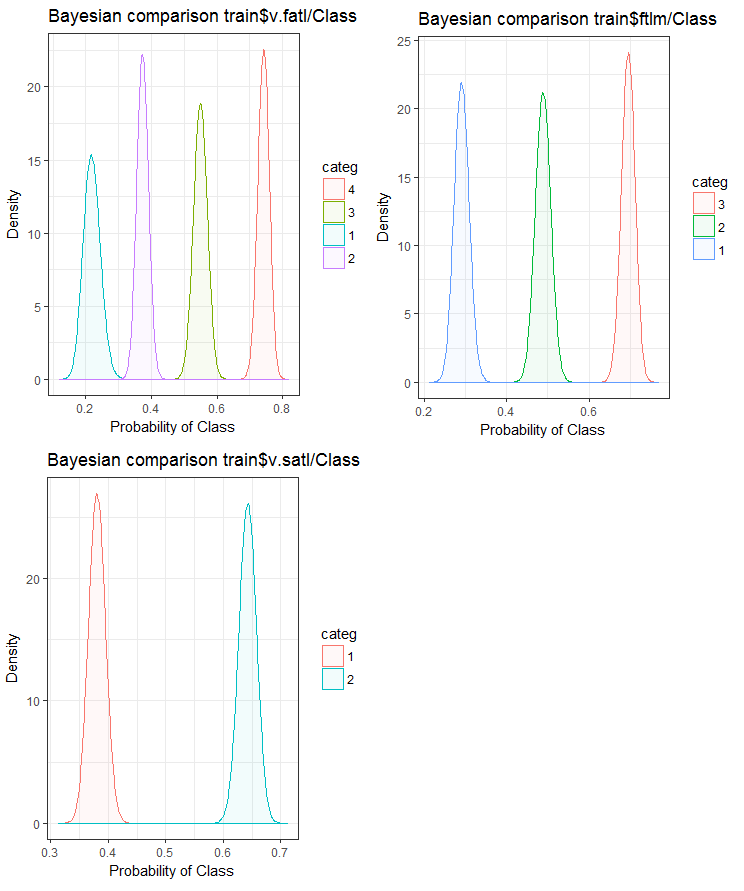
Рис.24. Байесовское сравнение переменных с целевой в наборе train
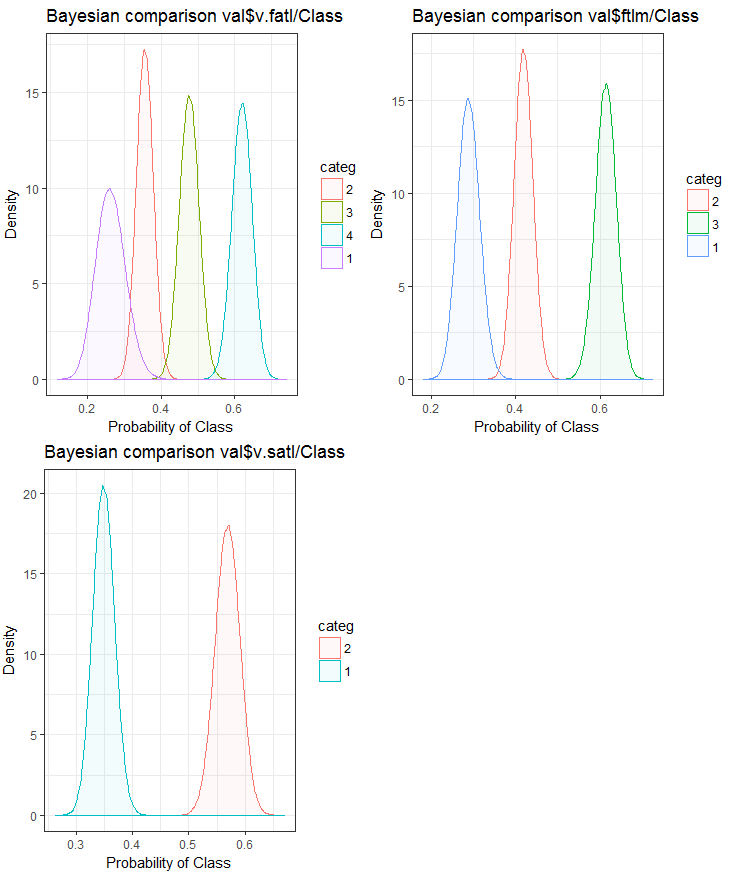
Рис.25. Байесовское сравнение переменных с целевой в наборе val
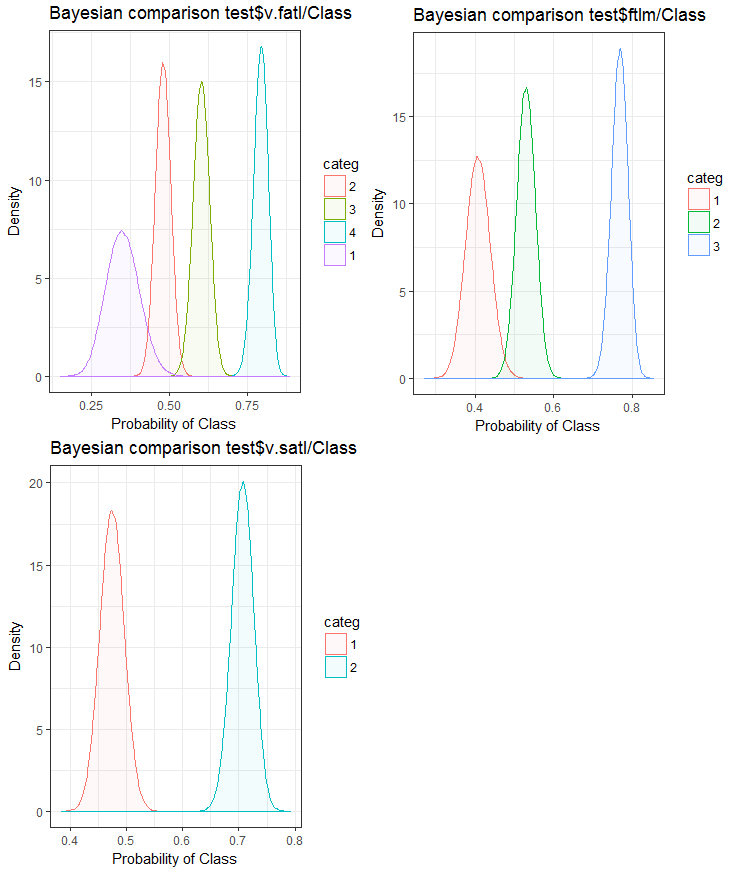
Рис.26. Байесовское сравнение переменных с целевой в наборе test
Видим, что корреляция предикторов с целевой больше дрейфует в переменной с 4 уровнями и меньше — в переменных с двумя группами. Нужно проверить в будущем, как отразится на точности модели использование только двухдиапазонных предикторов.
Эту же задачу — разбиение переменной на отрезки, оптимально соответствующие уровням целевой — можно решить и другим путем, с помощью отличного пакета smbinning. Можете проверить это самостоятельно. Напомню и о том, что в предыдущей статье рассмотрен еще один интересный метод дискретизации — с помощью пакета "RoughSets".
Дискретизация — эффективный метод трансформации предикторов. Но, к сожалению, не все модели могут работать с факторными предикторами.
1.2. Создание новых признаков
Создание переменной — это процесс создания новых переменных на основе уже существующих. Например, у нас есть дата (ДД-мм-гг) в качестве входной переменной в наборе данных. Мы можем создавать новые переменные — день, месяц, год, неделя, день недели, которые будут лучше связаны с целевой переменной. Этот шаг используется, чтобы выделить скрытые взаимосвязи в переменной.
Создание производных переменных — процесс, когда от существующей переменной создается новая с помощью набора функций или различных методов. Решение о том, какую переменную нужно создать, зависит от любопытства бизнес-аналитика, его набора гипотез и теоретической подкованности. Выбор методов тоже велик: к нашим услугам логарифмирование, сегментирование, возведение в степень и множество других способов трансформирования.
Создание фиктивных переменных — еще один популярный способ работы с переменными. Чаще всего фиктивные переменные применяются при преобразовании категориальных переменных в числовые. Категориальная переменная может принимать значения 0 и 1. Мы можем создать фиктивные переменные для более чем двух классов категориальных переменных с N или N-1 переменных.
В данной статье мы рассматриваем ситуации, с которыми сталкиваемся ежедневно в качестве аналитиков. Как же извлечь максимум информации из набора данных? Вот несколько способов.
- Использовать значения даты и времени как переменные. Можно создавать новые переменные, учитывая различия в датах и времени.
- Создать новые соотношения и пропорции: вместо того, чтобы просто держать прошлые входы и выходы в наборе данных, мы можем занести в набор их соотношения, которые могут иметь большое значение.
- Применить стандартные преобразования. Глядя на колебания и участки переменной вместе с выходом, мы можем увидеть, улучшится ли корреляция после применения базовых преобразований. Наиболее часто используемые преобразования включают log, exp, квадратичную и тригонометрическую вариации.
- Проверить переменные на сезонность и создать модель за нужный период (неделя, месяц, сессия и т.п.).
Интуитивно понятно, что в понедельник поведение рынка не такое, как в среду или четверг. То есть, день недели — важный признак. Не менее важно, в каком периоде суток находится рынок (азиатская, европейская или американская сессии). Как мы можем определить эти признаки?
Используем возможности пакета timekit. Центральная функция пакета — tk_augment_timeseries_signature(), которая добавляет к временным меткам нашего начального набора pr целый ряд временных данных, которые могут быть полезны и как дополнительные признаки, и как параметры группировки. Какие это данные?
| Index | значение индекса, который был разложен |
| Index.num | числовое значение индекса в секундах. База “1970-01-01 00:00:00” |
| diff | разница в секундах от предыдущего числового значения индекса |
| Year | год, компонента индекса |
| half | половина составляющей индекса |
| quarter | квартал, составляющая индекса |
| month | месяц, составляющая индекса с основанием 1 |
| month.xts | месяц, составляющая индекс с базой 0, так как реализовано в xts |
| month.lbl | метка месяца как упорядоченный фактор, начинающийся с января и заканчивающийся декабрем |
| day | день, составляющая индекса |
| hour | час, составляющая индекса |
| minute | минута, составляющая индекса |
| second | секунда, составляющая индекса |
| hour12 | часовая компонента в 12-часовой шкале |
| am.pm | утро (am) = 1, после полудня (pm) = 2 |
| wday | день недели с основанием 1. Воскресенье = 1, суббота = 7 |
| wday.xts | день недели с основанием 0, как реализовано в xts. Воскресенье = 0, суббота = 6 |
| wday.lbl | метка дня недели как упорядоченный фактор, начиная с воскресенья и заканчивая субботой |
| mday | день месяца |
| qday | день квартала |
| yday | день года. |
| mweek | неделя месяца |
| week | номер недели в году (начало с воскресенья) |
| week.iso | номер недели года по ISO (начало с понедельника) |
| week2 | модуль для двухнедельной частоты |
| week3 | модуль для трехнедельной частоты |
| week4 | модуль для quad-недельной частоты |
Возьмем начальный набор данных pr, усилим его функцией tk_augment_timeseries_signature(), добавим к начальному набору переменные mday, wday.lbl, hour, удалим неопределенные данные (NA) и сгруппируем данные по дням недели.
evalq(
{
tk_augment_timeseries_signature(pr) %>%
select(c(mday, wday.lbl, hour)) %>%
cbind(pr, .) -> pr.augm
pr.compl <- pr.augm[complete.cases(pr.augm), ]
pr.nest <- pr.compl %>% group_by(wday.lbl) %>% nest()
},
env)
> str(env$pr.augm)
'data.frame': 8000 obs. of 33 variables:
$ Data : POSIXct, format: "2017-01-10 11:00:00" ...
$ Open : num 123 123 123 123 123 ...
$ High : num 123 123 123 123 123 ...
$ Low : num 123 123 123 123 123 ...
$ Close : num 123 123 123 123 123 ...
$ Vol : num 3830 3360 3220 3241 3071 ...
..................................................
$ zigz : num 123 123 123 123 123 ...
$ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ...
$ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
$ mday : int 10 10 10 10 10 10 10 10 10 10 ...
$ wday.lbl: Ord.factor w/ 7 levels "Sunday"<"Monday"<..: 3 3 3 3 3 3 3 3 3 3 ...
$ hour : int 11 11 11 11 12 12 12 12 13 13 ... Тот же результат можем получить с использованием библиотеки lubridate, удалив попутно данные за субботу.
require(lubridate)
evalq({pr %>% mutate(.,
wday = wday(Data), #label = TRUE, abbr = TRUE),
day = day(Data),
hour = hour(Data)) %>%
filter(wday != "Sat") -> pr1
pr1.nest <- pr1 %>% na.omit %>%
group_by(wday) %>% nest()},
env
)
#-------
str(env$pr1)
'data.frame': 7924 obs. of 33 variables:
$ Data : POSIXct, format: "2017-01-10 11:00:00" ...
$ Open : num 123 123 123 123 123 ...
$ High : num 123 123 123 123 123 ...
$ Low : num 123 123 123 123 123 ...
$ Close : num 123 123 123 123 123 ...
$ Vol : num 3830 3360 3220 3241 3071 ...
..........................................
$ zigz : num 123 123 123 123 123 ...
$ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ...
$ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
$ wday : int 3 3 3 3 3 3 3 3 3 3 ...
$ day : int 10 10 10 10 10 10 10 10 10 10 ...
$ hour : int 11 11 11 11 12 12 12 12 13 13 ... Сгруппированные по дням недели данные выглядят так (воскресенье = 1, понедельник = 2 и т.д.):
> env$pr1.nest # A tibble: 5 × 2 wday data <int> <list> 1 4 <tibble [1,593 Ч 32]> 2 5 <tibble [1,632 Ч 32]> 3 6 <tibble [1,624 Ч 32]> 4 2 <tibble [1,448 Ч 32]> 5 3 <tibble [1,536 Ч 32]>
Из данных в основном наборе pr можно дополнительно использовать переменные dL, dH на последних 3 барах.
2. Выбор предикторов
Есть множество способов и критериев оценки важности предикторов. Некоторые из них мы уже рассматривали в предыдущих статьях. Поскольку в этой статье мы сделали упор на визуализацию, рассмотрим один визуальный и (для сравнения) один аналитический метод оценки важности предикторов.
2.1. Визуальная оценка
Используем пакет smbinning. В предыдущих разделах мы оценивали предикторы с помощью пакета funModeling и выяснили, что визуализация зависимости — это простой, надежный способ определения релевантности предикторов. Посмотрим, как покажет себя пакет smbinning с нормализованными и трансформированными данными, а также выясним, насколько преобразования предикторов влияют на их важность.
Соберем в один набор log-трансформированные, sin-трансформированные, добавим tanh-преобразованные и нормализованные данные и оценим зависимость целевой и предикторов в этих наборах.
Последовательность обработки первичного набора (приведена на ниже показанном рисунке) следующая: сырые данные dataSet очищаем (без удаления высококоррелированных) и, разделив на train/val/test, получаем набор DT. Дальше по каждому виду трансформации выполним действия по схеме. Соберем все в один скрипт:
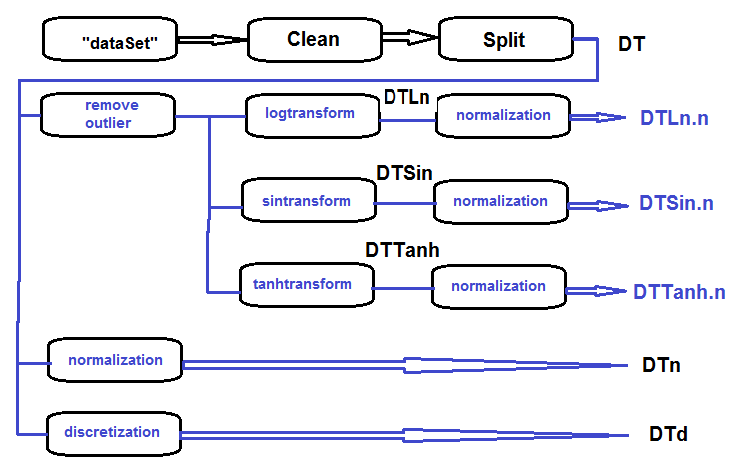
Рис.27. Структурная схема препроцессинга
Очистим набор, разделим на train/val/test и уберем ненужные данные:
#----Clean--------------------- require(caret) require(pipeR) evalq( { train = 1:2000 val = 2001:3000 test = 3001:4000 DT <- list() dataSet %>% preProcess(., method = c("zv", "nzv", "conditionalX")) %>% predict(., dataSet) %>% na.omit -> dataSetClean list(train = dataSetClean[train, ], val = dataSetClean[val, ], test = dataSetClean[test, ]) -> DT rm(dataSetClean, train, val, test) }, env)
Обработаем выбросы во всех наборах:
#------outlier-------------
evalq({
# определим новый лист для результата
DTcap <- list()
# пройдемся по трем наборам
foreach(i = 1:3) %do% {
DT[[i]] %>%
# уберем колонки c(Data, Class)
select(-c(Data, Class)) %>%
# преобразуем в data.frame и сохраним во временную переменную x
as.data.frame() -> x
if (i == 1) {
# при первом входе определеим параметры выбросов
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
prep.outlier(x[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
}
# заменим выбросы на 5/95 % и сохраним результат в x.cap
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = x[ ,i], impute = T, fill = T,
lower = lower, upper = upper,
med = med, cap1 = cap1, cap2 = cap2)
} %>% as.data.frame() -> x.cap
colnames(x.cap) <- colnames(x)
return(x.cap)
} -> Dtcap
#уберем ненужные переменные
rm(lower, upper, med, cap1, cap2, x.cap, x)
}, env) Трансформируем переменные во всех наборах Dtcap без выбросов функцией log(x+1). Получим DTLn лист с тремя наборами логарифмированных переменных.
#------logtrans------------
evalq({
DTLn <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) log2(x + 1)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTLn
},
env) Трансформируем переменные во всех наборах Dtcap без выбросов функцией sin(2*pi*x). Получим DTSin лист с тремя наборами sin-трансформированных переменных.
#------sintrans--------------
evalq({
DTSin <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) sin(2*pi*x)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTSin
},
env) Трансформируем переменные во всех наборах Dtcap без выбросов функцией tanh(x). Получим DTTanh лист с тремя наборами tanh-трансформированных переменных.
#------tanhTrans----------
evalq({
DTTanh <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) tanh(x)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTTanh
},
env) Нормализуем наборы DT, DTLn, DTSin, DTTanh.
#------normalize----------- evalq( { # определяем параметры нормализации preProcess(DT$train, method = "spatialSign") -> preproc list(train = predict(preproc, DT$train), val = predict(preproc, DT$val), test = predict(preproc, DT$test) ) -> DTn }, env) #--ln--- evalq( { preProcess(DTLn[[1]], method = "spatialSign") -> preprocLn list(train = predict(preprocLn, DTLn[[1]]), val = predict(preprocLn, DTLn[[2]]), test = predict(preprocLn, DTLn[[3]]) ) -> DTLn.n }, env) #---sin--- evalq( { preProcess(DTSin[[1]], method = "spatialSign") -> preprocSin list(train = predict(preprocSin, DTSin[[1]]), val = predict(preprocSin, DTSin[[2]]), test = predict(preprocSin, DTSin[[3]]) ) -> DTSin.n }, env) #-----tanh----------------- evalq( { preProcess(DTTanh[[1]], method = "spatialSign") -> preprocTanh list(train = predict(preprocTanh, DTTanh[[1]]), val = predict(preprocTanh, DTTanh[[2]]), test = predict(preprocTanh, DTTanh[[3]]) ) -> DTTanh.n }, env)
Дискретизируем наш набор DT с помощью функции mdlp::discretization.
##------discretize----------
#--------preCut---------------------
# определяем параметры дискретизации (cutpoint)
require(pipeR)
require(discretization)
evalq(
#require(pipeR)
# занимает некоторое время !
pipeline({
DT$train
select(-Data)
as.data.frame()
mdlp()
}) -> mdlp.train,
env)
#-------cut_opt----------
evalq(
{
DTd <- list()
mdlp.train$cutp %>%
# определяем колонки которые нужно дискретизировать
lapply(., function(x) is.numeric(x)) %>%
unlist -> idx # bool
#----train-----------------
mdlp.train$Disc.data[ ,idx] -> DTd$train
#---test------------
DT$test %>%
select(-c(Data, Class)) %>%
as.data.frame() -> test.d
# переразметим данные в соответствии с расчитанными диапазонами
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(test.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$test$Class) -> DTd$test
colnames(DTd$test) <- colnames(DTd$train)
#-----val-----------------
DT$val %>%
select(-c(Data, Class)) %>%
as.data.frame() -> val.d
# переразметим данные в соответствии с расчитанными диапазонами
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(val.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$val$Class) -> DTd$val
colnames(DTd$val) <- colnames(DTd$train)
# подчистим за собой
rm(test.d, val.d)
},
env
) Напомним, какие переменные у нас в начальном наборе DT$train:
require(funModeling)
plot_num(env$DT$train %>% select(-Data), bins = 20)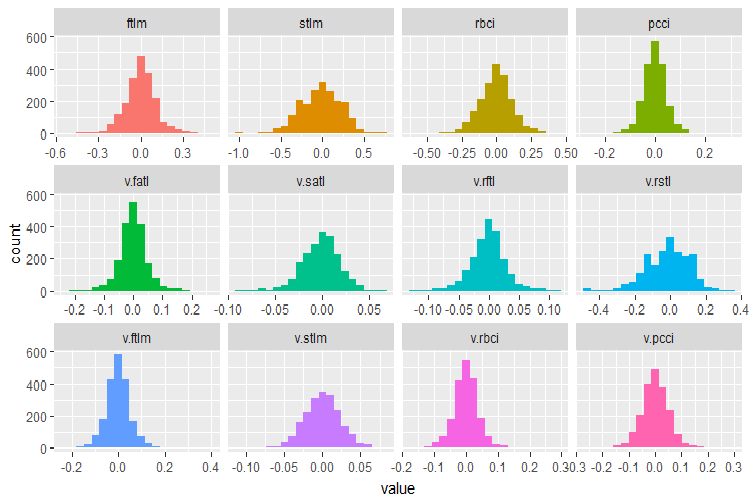 
Рис.28. Распределение переменных набора DT$train
Используем возможности пакета smbinning для определения релевантных предикторов в поднаборах train всех нормализованных наборов, полученных нами ранее (Dtn, DTLn.n, DTSin.n и DTTanh.n). Поскольку целевая в этом пакете должна быть числовой со значениями (0, 1) напишем функцию для необходимых преобразований.
#-------------------------------- require(smbinning) targ.int <- function(x){ x %>% tbl_df() %>% mutate(Cl = (as.numeric(Class) - 1) %>% as.integer()) %>% select(-Class) %>% as.data.frame() }
Кроме того, пакет не любит переменные с точкой в имени. Напишем функцию, которая переименует все переменные с точкой в переменные с нижней чертой.
renamepr <- function(X){
X %<>% rename(v_fatl = v.fatl,
v_satl = v.satl,
v_rftl = v.rftl,
v_rstl = v.rstl,
v_ftlm = v.ftlm,
v_stlm = v.stlm,
v_rbci = v.rbci,
v_pcci = v.pcci)
return(X)
} Вычислим и отрисуем графики релевантных предикторов.
par(mfrow = c(2,2)) #--Ln-------------- evalq({ df <- renamepr(DTLn.n[[1]]) %>% targ.int sumivt.ln.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.ln.n, cex = 0.7) rm(df) }, env) #---Sin----------------- evalq({ df <- renamepr(DTSin.n[[1]]) %>% targ.int sumivt.sin.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.sin.n, cex = 0.7) rm(df) }, env) #---norm------------- evalq({ df <- renamepr(DTn[[1]]) %>% targ.int sumivt.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.n, cex = 0.7) rm(df) }, env) #-----Tanh---------------- evalq({ df <- renamepr(DTTanh.n[[1]]) %>% targ.int sumivt.tanh.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.tanh.n, cex = 0.7) rm(df) }, env) par(mfrow = c(1,1))
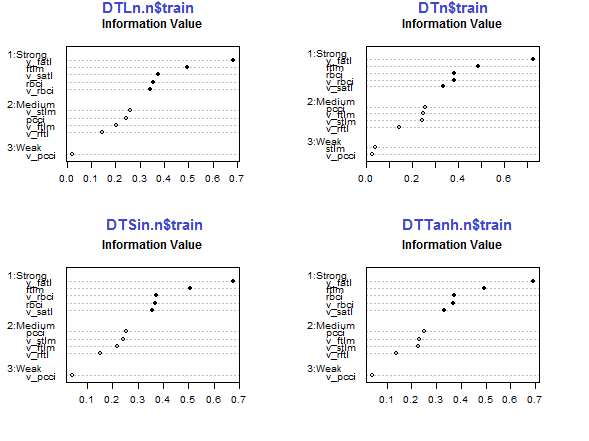
Рис.29. Важность предикторов в поднаборе train нормализованных наборов
Во всех наборах сильны пять предикторов — v_fatl, ftlm, v_satl, rbci, v_rbci, правда, в различном порядке. Средняя сила у четырех предикторов — pcci, v_ftlm, v_stlm, v_rftl. Слабые — v_pcci и stlm. Можно посмотреть по каждому набору распределение переменных в порядке их значимости:
env$sumivt.ln.n Char IV Process 5 v_fatl 0.6823 Numeric binning OK 1 ftlm 0.4926 Numeric binning OK 6 v_satl 0.3737 Numeric binning OK 3 rbci 0.3551 Numeric binning OK 11 v_rbci 0.3424 Numeric binning OK 10 v_stlm 0.2591 Numeric binning OK 4 pcci 0.2440 Numeric binning OK 9 v_ftlm 0.2023 Numeric binning OK 7 v_rftl 0.1442 Numeric binning OK 12 v_pcci 0.0222 Numeric binning OK 2 stlm NA No significant splits 8 v_rstl NA No significant splits
Последние три переменных можно спокойно отбросить. Т.е., останутся пять сильных и четыре средних. Определим имена лучших переменных (IV > 0.1).
evalq(sumivt.sin.n$Char[sumivt.sin.n$IV > 0.1] %>% na.omit %>% as.character() -> best.sin.n, env) > env$best.sin.n [1] "v_fatl" "ftlm" "rbci" "v_rbci" "v_satl" "pcci" [7] "v_ftlm" "v_stlm" "v_rftl"
Посмотрим более подробно переменные v_fatl и ftlm.
evalq({
df <- renamepr(DTTanh.n[[1]]) %>% targ.int
x = 'v_fatl'
y = 'Cl'
res <- smbinning(df = df,
y = y,
x = x)
#res$ivtable # Tabulation and Information Value
#res$iv # Information value
#res$bands # Bins or bands
#res$ctree # Decision tree from partykit
par(mfrow = c(2,2))
sub = paste0(x, " vs ", y) #rbci vs Cl"
boxplot(df[[x]]~df[[y]],
horizontal = TRUE,
frame = FALSE, col = "lightblue",
main = "Distribution")
mtext(sub,3) #ftlm
smbinning.plot(res, option = "dist",
sub = sub) #"pcci vs Cl")
smbinning.plot(res, option = "goodrate", #"badrate"
sub = sub) #"pcci vs Cl")
smbinning.plot(res, option = "WoE",
sub = sub) #"pcci vs Cl")
par(mfrow = c(1, 1))
}, env)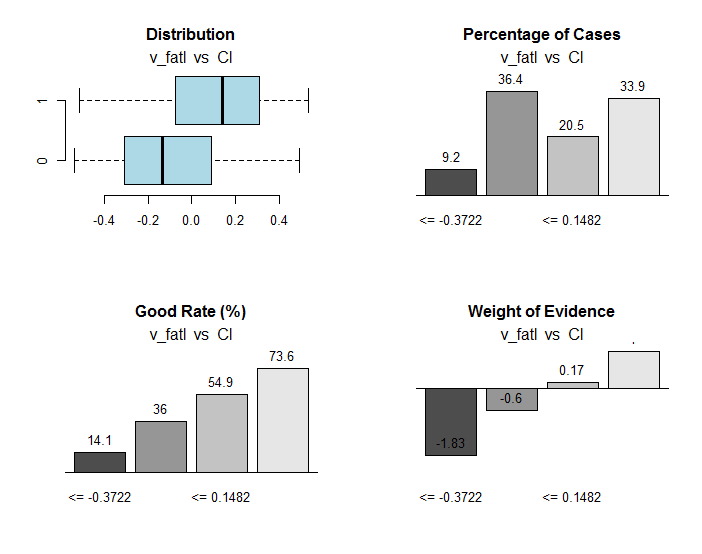 
Рис.30. Связь диапазонов переменной v_fatl с целевой Cl
В объекте res, кроме прочей полезной информации, содержатся точки раздела переменной на диапазоны, оптимально связанные с целевой. В нашем конкретном случае диапазонов 4.
> env$res$cuts [1] -0.3722 -0.0433 0.1482
Проведем аналогичный расчет для переменной ftlm и построим графики:
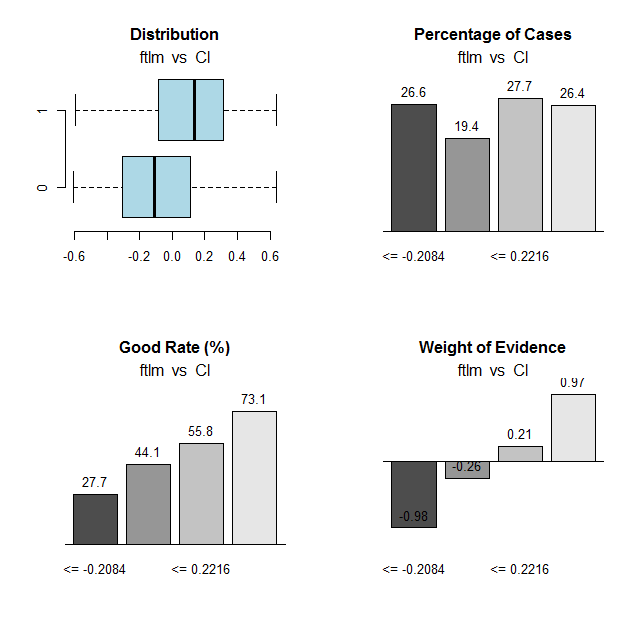
Рис.31. Связь диапазонов переменной ftlm c целевой Cl
Точки разделения диапазонов:
> env$res$cuts [1] -0.2084 -0.0150 0.2216
Имея точки разделения, мы можем дискретизировать переменные в наших наборах и посмотреть, насколько отличаются:
- важные переменные, ранее определенные с помощью функции mdlp::discretization от переменных, определенных с помощью функции smbinning::smbinning;
- разбиение переменных на диапазоны.
У нас уже есть один набор с данными, дискретизированными функцией mdlp::discretization DTd. Проделаем то же самое, но с помощью функции smbinning::smbinning и только train поднабором.
Определим параметры дискретизации:
evalq({
res <- list()
DT$train %>% renamepr() %>% targ.int() -> df
x <- colnames(df)
y <- "Cl"
foreach(i = 1:(ncol(df) - 1)) %do% {
smbinning(df, y = y, x = x[i])
} -> res
res %>% lapply(., function(x) x[1] %>% is.list) %>%
unlist -> idx
}, env) Дискретизируем поднабор DT$train:
evalq({
DT1.d <- list()
DT$train %>% renamepr() %>%
targ.int() %>% select(-Cl) -> train
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(train[ ,i],
vec = res[[i]]$cuts,
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$train$Class) -> DT1.d$train
colnames(DT1.d$train) <- colnames(train)[idx] %>%
c(., 'Class')
},
env) Определим лучшие переменные с информационной значимостью больше 0.1, упорядоченные по возрастанию:
evalq({
DT$train %>% renamepr() %>% targ.int() -> df
sumivt.dt1.d = smbinning.sumiv(df = df, y = 'Cl')
sumivt.dt1.d$Char[sumivt.dt1.d$IV > 0.1] %>%
na.omit %>% as.character() -> best.dt1.d
rm(df)
},
env) Отрисуем график разбиения переменных в наборе DTd$train:
require(funModeling) plot_num(env$DTd$train)
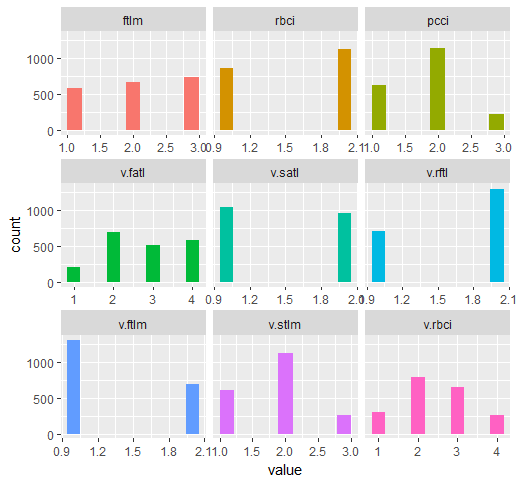
Рис.32. Переменные набора DT$ train, дискретизированные функцией mdlp
График набора DT1.d со всеми переменными и с лучшими приведен ниже.
plot_num(env$DT1.d$train)
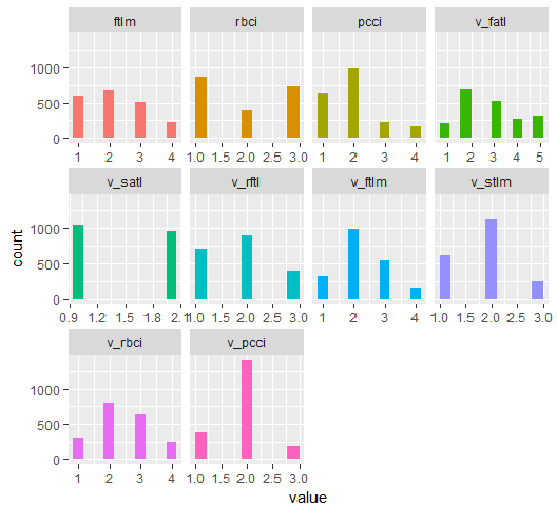
Рис.33. Переменные набора DT1 d$train, дискретизированные функцией smbinning (все)
plot_num(env$DT1.d$train[ ,env$best.dt1.d])
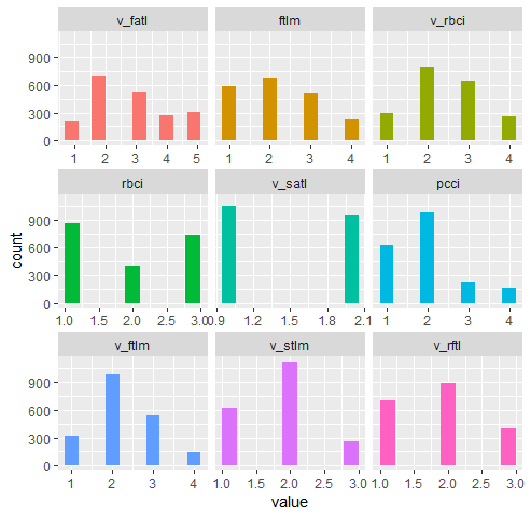
Рис.34. Переменные набора DT1.d$train, дискретизированные функцией smbinning (лучшие упорядоченные по возрастанию информационной значимости)
Что мы видим из графиков? Переменные, определенные как важные — одинаковы в обеих случаях. А вот разбиение на диапазоны отличается. Нужно проверить, какой вариант дает лучший предсказательный результат с моделью.
2.2. Аналитическая оценка
Известно много аналитических методов определения важности предикторов по самым разнообразным критериям. Некоторые из них мы рассматривали ранее. Сейчас я хочу проверить несколько необычный подход к выбору предикторов.
Используем пакет varbvs. В одноименной функции реализованы быстрые алгоритмы для установки байесовских моделей выбора переменных и вычисления коэффициентов Байеса, в которых результат (или целевая) моделируется с использованием линейной регрессии или логистической регрессии. Алгоритмы основаны на вариационных приближениях, описанных в "Масштабируемом вариационном выводе для выбора байесовских переменных в регрессии и его точности в исследованиях генетических ассоциаций" (P. Carbonetto and M. Stephens, Bayesian Analysis 7, 2012, pages 73-108). Это программное обеспечение было применено к большим наборам данных с более чем миллионом переменных и с тысячами образцов.
Функция varbvs() принимает на вход матрицу и целевую — численный вектор (0, 1). Возьмем наш набор с нормализованными данными DTTanh.n$train и проверим, какие предикторы будут определяться как важные по этому методу.
require(varbvs)
evalq({
train <- DTTanh.n$train %>% targ.int() %>% as.matrix()
fit <- varbvs(X = train[ ,-ncol(train)] ,
Z = NULL,
y = train[ ,ncol(train)] %>% as.vector(),
"binomial",
logodds = seq(-2,-0.5,0.1),
optimize.eta = T,
initialize.params = T,
verbose = T, nr = 100
)
print(summary(fit))
}, env)
Welcome to -- * *
VARBVS version 2.0.3 -- | | |
large-scale Bayesian -- || | | | || | | |
variable selection -- | || | | | | || || |||| || | ||
****************************************************************************
Copyright (C) 2012-2017 Peter Carbonetto.
See http://www.gnu.org/licenses/gpl.html for the full license.
Fitting variational approximation for Bayesian variable selection model.
family: binomial num. hyperparameter settings: 16
samples: 2000 convergence tolerance 1.0e-04
variables: 12 iid variable selection prior: yes
covariates: 0 fit prior var. of coefs (sa): yes
intercept: yes fit approx. factors (eta): yes
Finding best initialization for 16 combinations of hyperparameters.
-iteration- variational max. incl variance params
outer inner lower bound change vars sigma sa
0016 00018 -1.204193e+03 6.1e-05 0003.3 NA 3.3e+00
Computing marginal likelihood for 16 combinations of hyperparameters.
-iteration- variational max. incl variance params
outer inner lower bound change vars sigma sa
0016 00002 -1.204193e+03 3.2e-05 0003.3 NA 3.3e+00
Summary of fitted Bayesian variable selection model:
family: binomial num. hyperparameter settings: 16
samples: 2000 iid variable selection prior: yes
variables: 12 fit prior var. of coefs (sa): yes
covariates: 1 fit approx. factors (eta): yes
maximum log-likelihood lower bound: -1204.1931
Hyperparameters:
estimate Pr>0.95 candidate values
sa 3.49 [3.25,3.6] NA--NA
logodds -0.75 [-1.30,-0.50] (-2.00)--(-0.50)
Selected variables by probability cutoff:
>0.10 >0.25 >0.50 >0.75 >0.90 >0.95
3 3 3 3 3 3
Top 5 variables by inclusion probability:
index variable prob PVE coef* Pr(coef.>0.95)
1 1 ftlm 1.0000 NA 2.442 [+2.104,+2.900]
2 4 pcci 1.0000 NA 2.088 [+1.763,+2.391]
3 3 rbci 0.9558 NA 0.709 [+0.369,+1.051]
4 10 v.stlm 0.0356 NA 0.197 [-0.137,+0.529]
5 6 v.satl 0.0325 NA 0.185 [-0.136,+0.501]
*See help(varbvs) about interpreting coefficients in logistic regression. Как видим, определены пять лучших предикторов (ftlm, pcci, rbci, v.stlm, v.satl). Они входят в девятку лучших, которую мы определили раньше, но в другом порядке и с другими весами значимости. Поскольку модель у нас уже есть, давайте проверим, какое качество результата мы получим на валидационном и тестовом наборе.
Валидационный набор:
#-----------------
evalq({
val <- DTTanh.n$val %>% targ.int() %>%
as.matrix()
y = val[ ,ncol(val)] %>% as.vector()
pr <- predict(fit, X = val[ ,-ncol(val)] ,
Z = NULL)
}, env)
cm.val <- confusionMatrix(table(env$y, env$pr))
> cm.val
Confusion Matrix and Statistics
0 1
0 347 204
1 137 312
Accuracy : 0.659
95% CI : (0.6287, 0.6884)
No Information Rate : 0.516
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.3202
Mcnemar's Test P-Value : 0.0003514
Sensitivity : 0.7169
Specificity : 0.6047
Pos Pred Value : 0.6298
Neg Pred Value : 0.6949
Prevalence : 0.4840
Detection Rate : 0.3470
Detection Prevalence : 0.5510
Balanced Accuracy : 0.6608
'Positive' Class : 0 Результат, прямо скажем, не ахти. Тестовый набор:
evalq({
test <- DTTanh.n$test %>% targ.int() %>%
as.matrix()
y = test[ ,ncol(test)] %>% as.vector()
pr <- predict(fit, X = test[ ,-ncol(test)] ,
Z = NULL)
}, env)
cm.test <- confusionMatrix(table(env$y, env$pr))
> cm.test
Confusion Matrix and Statistics
0 1
0 270 140
1 186 404
Accuracy : 0.674
95% CI : (0.644, 0.703)
No Information Rate : 0.544
P-Value [Acc > NIR] : < 2e-16
Kappa : 0.3375
Mcnemar's Test P-Value : 0.01269
Sensitivity : 0.5921
Specificity : 0.7426
Pos Pred Value : 0.6585
Neg Pred Value : 0.6847
Prevalence : 0.4560
Detection Rate : 0.2700
Detection Prevalence : 0.4100
Balanced Accuracy : 0.6674
'Positive' Class : 0 Результат практически такой же. Это значит, что модель не переучена и хорошо обобщает данные.
Итак: лучшие по версии varbvs — ftlm, pcci, rbci, v.stlm, v.satl.
2.3. Нейросеть
Поскольку мы исследуем область нейросетей, проверим, какие предикторы выберет в качестве наиболее важных сама нейросеть.
Используем пакет FCNN4R, который предоставляет интерфейс для программ ядра из библиотеки FCNN C ++. FCNN основан на совершенно новом представлении искусственной нейронной сети, которое предполагает эффективность, модульность и расширяемость. FCNN4R обеспечивает стандартное обучение (backpropagation, Rprop, имитация отжига, стохастический градиент) и алгоритмы обрезки (minimum magnitude, Optimal Brain Surgeon), но прежде всего я вижу в ней эффективный вычислительный движок.
Пользователи могут легко реализовать свои алгоритмы, используя быстрые градиентные вычислительные процедуры, а также функциональность восстановления сети (удаление весов и избыточных нейронов, переупорядочивание входных данных, объединение сетей).
Сети могут быть экспортированы в функции C, чтобы интегрировать их в практически любое программное решение.
Создаем полносвязную нейросеть с двумя скрытыми слоями. Количество нейронов в каждом слое: входной = 12 (количество предикторов), выходной = 1. Инициируем нейроны случайными весами в диапазоне +/- 0.17. Установим функции активации в каждом слое нейросети (кроме входного) = c("tanh", "tanh", "sigmoid"). Подготовим наборы train/val/test.
Ниже представлен скрипт, выполняющий эту последовательность действий.
require(FCNN4R)
evalq({
mlp_net(layers = c(12, 8, 5, 1), name = "n.tanh") %>%
mlp_rnd_weights(a = 0.17) %>%
mlp_set_activation(layer = c(2, 3, 4),
activation = c("tanh", "tanh", "sigmoid"), #"threshold", "sym_threshold",
#"linear", "sigmoid", "sym_sigmoid",
#"tanh", "sigmoid_approx",
#"sym_sigmoid_approx"),
slope = 0) -> Ntanh #show()
#-------
train <- DTTanh.n$train %>% targ.int() %>% as.matrix()
test <- DTTanh.n$test %>% targ.int() %>% as.matrix()
val <- DTTanh.n$val %>% targ.int() %>% as.matrix()
}, env) Из предлагаемых методов обучения будем использовать rprop. Зададим константы: tol — уровень ошибки, при достижении которого нужно остановить обучение, max_ep — количество эпох, после выполнения которых нужно остановить обучение, l2reg — коэффициент регуляризации. Обучим модель с этими параметрами, посмотрим визуально, какую сеть и ошибку обучения мы получили.
evalq({
tol <- 1e-1
max_ep = 1000
l2reg = 0.0001
net_rp <- mlp_teach_rprop(Ntanh,
input = train[ ,-ncol(train)],
output = train[ ,ncol(train)] %>% as.matrix(),
tol_level = tol,
max_epochs = max_ep,
l2reg = l2reg,
u = 1.2, d = 0.5,
gmax = 50, gmin = 1e-06,
report_freq = 100)
}, env)
plot(env$net_rp$mse, t = "l",
main = paste0("max_epochs =", env$max_ep, " l2reg = ", env$l2reg))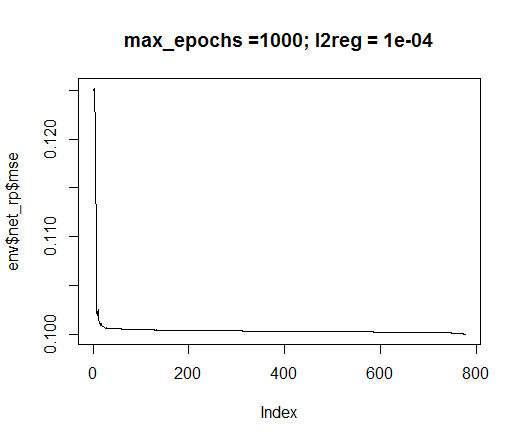 
Рис.35. Ошибка обучения нейросети
evalq(mlp_plot(net_rp$net, FALSE), envir = env)
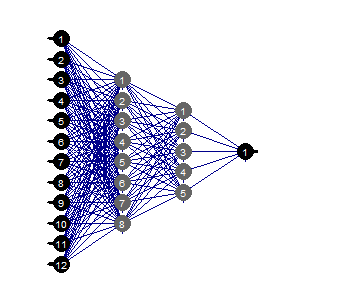
Рис.36. Структура нейросети
Обрезка (Prune)
Обрезка минимального значения — это простой в использовании алгоритм, при котором на каждом шаге отключаются веса с наименьшим абсолютным значением. Этот алгоритм требует ретрансляции сети практически на каждом шаге и дает субоптимальные результаты.
evalq({
tol <- 1e-1
max_ep = 1000
l2reg = 0.0001
mlp_prune_mag(net_rp$net,
input = train[ ,-ncol(train)],
output = train[ ,ncol(train)] %>% as.matrix(),
tol_level = tol,
max_reteach_epochs = max_ep,
report = FALSE,
plots = TRUE) -> net_rp_prune
}, env)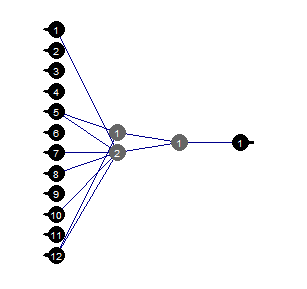 
Рис.37. Обрезанная нейросеть
Мы видим, что при конкретной структуре нейросети, начальной инициализации, функциях активации и ошибке обучения мы вполне можем обойтись сетью структуры (12, 2, 1, 1). Какие предикторы при этом выбрала нейросеть?
evalq( best <- train %>% tbl_df %>% select(c(1,5,7,8,10,12)) %>% colnames(), env) env$best [1] "ftlm" "v.fatl" "v.rftl" "v.rstl" "v.stlm" [6] "v.pcci"
Двух переменных — v.rstl и v.pcci — нет в составе лучших 9, определенных ранее.
Еще раз подчеркну: здесь показана возможность выбора важных предикторов нейросетью самостоятельно и автоматически. Но этот выбор зависит как от предикторов, так и от структуры и параметров нейросети.
Экспериментируйте!
Заключение
В следующей части статьи мы рассмотрим, как удалить шумовые примеры из набора, как уменьшить размерность входов и что это дает, а также способы разделения исходных данных на train/val/test.
Приложение
1. Скрипты FeatureTransformation.R, FeatureSelect.R, FeatureSelect_analitic.R FeatureSelect_NN.R и снимок с результатами работы скриптов первой части статьи Part_1.RData можно скачать с Git /Part_II.
Графические интерфейсы XI: Интеграция графической стандартной библиотеки (build 16)
TradeObjects: Автоматизация торговли на основе графических объектов в MetaTrader
Универсальный торговый эксперт: Индикатор CUnIndicator и работа с отложенными ордерами (часть 9)
Глубокие нейросети (Часть I). Подготовка данных
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Не лучше ли данные о часе и дне вводить в НС не одним предиктором, а отдельными по числу часов и дней?
Если одним, то вес/значимость понедельника (1) и вторника (2) будет отличаться на 100%, а четверга (4) и пятницы(5) на 20%. С часами 1,2 и 22,23 еще сильнее отличие. А переход от 5 к 1 или 23 к 1 - вообще будет огромным скачком в весе.
Т.е. будут искажения в значимости дней и часов, если они представлены одним предиктором.
5 и 24 лишних предикторов - многовато. Но т.к. последовательность дней и часов циклична, то их можно перевести в угол на окружности и поступить по аналогии с обычными углами: "Разумнее выглядит подача в качестве входных данных синуса и косинуса этого угла." Т.е. будет по 2 предиктора на часы и на дни. Идея взята отсюда http://megaobuchalka.ru/9/5905.htmlЧас суток и день(недели, месяца, года) являются номинальными переменными, не числовыми. Можно говорить только о том упорядоченны они или нет. Поэтому за предложение спасибо, но не принимается.
Использовать эти переменные как числовые ? Можно экспериментировать, но я в эту сторону не смотрю. Если у Вас есть какие то результаты, поделитесь.
Удачи
Обсуждение и вопросы по коду можно можно сделать в ветке
Удачи
why?
fervently hope your Answer！
Sir,I try to run your R code BUT the R package "funModeling" has not the "bayesian_plot()" funtion,why? Is it the package Version is not right?
why?
fervently hope your Answer！
В последних релизах пакета эту функцию убрали по неизвестным причинам. К сожалению