エキスパートアドバイザの自己最適化：進化的遺伝的アルゴリズム

目次

• 概論
• 1. 進化的アルゴリズム登場の歴史
• 2. 進化的アルゴリズム（メソッド）
• 3. 遺伝的アルゴリズム（GA）
• 3.1. 適用範囲
• 3.2. タスク
• 3.3. 古典的遺伝的アルゴリズム
• 3.4. 検索戦略
• 3.5. 古典的最適検索との違い
• 3.6. 遺伝的アルゴリズムの用語
• 4. 遺伝的アルゴリズムの特長
• 5. 遺伝的アルゴリズムの欠点
• 6. 実験
• 6.1. 予測変数の最適な組み合わせの検索
• tabuSearchの使用
• 6.2. 取引システムの最適なパラメータの検索：
• rgenoud(Genetic Optimization Using Derivatives)の使用
• SOMA( Self-Organising Migrating Algorithm)の使用
• GenSA( Generalized Simulated Annealing)の使用
• 7. 質の指標を改善する方法と手段
• まとめ

概論

取引から離れないエキスパートアドバイザの自己最適化が必要であるということは、多くのトレーダーが理解していることです。この件についてはすでにいくつかの記事が掲載されています(記事1、記事2、記事3、記事4)。これらの記事ではこちらで提供されているライブラリが実験の土台となりました。しかし、掲載時から時が経過し、新しく強力な最適化アルゴリズムや新しい適用方法が出現しました。また私が思うに、これらの記事はプログラマーによって書かれた、プログラマーの為のものだと思います。

この記事では、特にトレーダーの為に、技術的な詳細に過度に突っ込むことなく、遺伝的アルゴリズム（GA)の実用方法に焦点を当てていきたいと思っています。ユーザーにとっては私が誰であろうと、遺伝的アルゴリズムの動作原理や、遺伝的アルゴリズムの収束速度や数、またその他の実用特性に影響を与えるパラメータの値と重要性を知ることは重要です。従って、繰り返しになるかもしれませんが、遺伝的アルゴリズムの発生の歴史から始め、その説明の中で改善された遺伝的アルゴリズムのパラメータの判別までいきたいと思います。また、遺伝的アルゴリズムをいくつかの進化的アルゴリズム（EA）と比較していきます。

1. 進化的アルゴリズム登場の歴史

進化的計算の歴史は、異なる独立したモデルの一連の開発から始まりました。これらの基礎は、遺伝的アルゴリズムと、60年代の初めに発表され、この分野の古典となった本『自然と人工システムにおける適用』 ("Adaptation in Natural and Artifical Systems", 1975)が世に出ると広く好評を得た、古典的なオランダシステムです。70年代には、L.A.ラストリギンがランダム検索の枠組みの中で、生体行動の概念を使用した一連のアルゴリズムを提唱しました。これらの概念の発展は、I.L.ブカトヴァの進化的モデリングの研究の中に見ることができます。M.L.ツェトリンの確率的オートマトンの最適かつ妥当的動作のアイディアを発展させながら、U.I.ネイマークは、種の進化と淘汰のプロセスをシュミレートする、独立したオートマトンの集合体に基づく、グローバル極値の実行を提案しました。フォーゲルとウォルシュが進化的プログラミングの発展に大きく貢献しました。それぞれの『流派』が、自然界に存在する別々の原理をベースに用いたアプローチをしましたが、それでもコンピュータ上でそれらの原理を実装できるくらいのレベルまで単純化しました。

自然界のシステムに似たモデリングへの取り組みは、現在大きく分けて2つに分類することができます。

• 生物学的原則に基づいてモデル化されたシステム。これらは、機能的最適化のような問題の為に使用され、非生物学的言語で簡単に書くことができます。
• 生物学的により現実的ではあるが、その意義の中で特に有用ではないシステム。これらのシステムは生物学的システムにより似ていて、より方向性が示されていない（もしくは全く示されていない）ものです。複雑で興味深い挙動を持ち、もうすぐ実用的な適用が見込まれるものです。

勿論、これらのものを簡単に分別することはできません。これらのカテゴリーは、それらの間に様々なコンピューティングシステムがある単なる二つの極です。一つ目の極に近いのは、進化的プログラミング(Evolutionary Programming)や、遺伝的アルゴリズム(Genetic Algorithms)、進化的ストラテジー(Evolution Strategies)などの進化的アルゴリズムです。二つ目の極に近いものは、人工生命(Artificial Life)として分類することができるシステムです。

2. 進化的アルゴリズム（メソッド）

進化的アルゴリズムは、自然淘汰のプロセスをモデル化し、使用する人口知能（進化的モデリングの分野）です。これらのうちの幾つかを列挙してみましょう。

• 遺伝的アルゴリズムは、ランダム選択や求めるパラメータの組み合わせや変化によって、最適化やモデリングの課題を解決するのに使う、発見的探索アルゴリズムです。

• 遺伝的プログラミングは、遺伝的アルゴリズムを使ったプログラムの自動変更及び作成です。

• 進化的プログラミングは、遺伝的プログラミングに似ていますが、プログラムの構造は不変で、数値だけが変わります。

• 進化的ストラテジーは、遺伝的アルゴリズムに似ていますが、次世代には正突然変異のみ引き渡されます。

• 微分進化

• 進化計算（ニューロエボリューション）は、遺伝的プログラミングに似ていますが、ゲノムはネットワークトポロジー時の重みの進化の発生または、重みの進化の他にトポロジーの進化が発生する、人口ニューラルネットワークです。

これらは全て、生物学的進化理論の基本的な原理（淘汰、交叉、突然変異と再生のプロセス）をモデル化します。個体の挙動は、環境によって決まります。多くの個体は集団と呼ばれます。集団は環境によって設定される目的関数に応じた淘汰ルールに沿って進化します。このように、集団の中の各個体（個人）には、環境内でのその適応度値が割り当てられています。より適応度の高い個体のみが乗算されます。再組み換えや突然変異で、個体は変化し環境に適応することができます。このようなアルゴリズムは、適応検索エンジンに関係しています。

進化的メソッド（EM）は、最適化と構造合成のタスクを解決する為の、おおよその（ヒューリスティック）メソッドです。進化的メソッドの多くは、状況研究への統計的手法と望む解への反復近似に基づいています。

進化的計算は、人工知能分野のうちの一つを構成しています。このアプローチによる人口知能システムの構築では、初期モデルの構造と変更する（進化させる）ことができるルールに主に焦点を当てています。また、モデルは様々なメソッドごとに構築されている場合があります。例えば、これはニューラルネットワークかもしれないし、論理的規則のセットかもしれません。主要な進化的メソッドには、擬似アリーニング法や遺伝的メソッド、粒子群最適化（PSO）の挙動、蟻コロニー最適化、遺伝的プログラミングが関係しています。

数学的プログラミングの正確なメソッドとの違いは、進化的メソッドは合理的な時間内に最適に近い解を見つけることができ、アプリケーションの特徴にほんの少し依存している（つまり、より普遍的な）ことに特徴づけられる、最適化の他のヒューリスティックメソッドとは異なり、多くの場合最適解への最も良い近似度を与えます。進化的メソッドの汎用性は、制御変数の非計測領域を持つ問題への適用によっても定義されます（つまり、制御変数の中には定量化を持たないものを含む言語的数値がある）。

擬似アリーニング法(Simulated Annealing)は、詳細のアニール時に体の潜在的エネルギーの最小化プロセスをシュミレートします。現在の探索点で、いくつかの制御変数の変更が起こります。新しい点は、常に目的関数の改善時に適用され、ごく少ない確率で劣化時に適用されます。

進化的メソッドの重要で特殊なケースは、遺伝的メソッドとアルゴリズムです。遺伝的アルゴリズム（GA）は、進化のシュミレーションの過程で特定のアプリケーションの複数のオブジェクトの有用な特性の強化と継承を用いた、最良のソリューションの検索に基づいたものです。

オブジェクトのプロパティは、進化的メソッドでは染色体と呼ばれる記録に統一されるパラメータの値によって表されます。遺伝的アルゴリズムでは、集団と呼ばれる染色体の部分集合が動作します。遺伝的原則のイミテーションは、集団の構成体の中からの両親の選択、それらの染色体の交叉、目的関数の評価に基づくオブジェクトの新しい世代に入れる為の子孫の選別をします。このプロセスは、世代から世代への目的関数（効用関数）の値の進化的向上をもたらします。

遺伝的メソッドの中には、遺伝的アルゴリズムとは異なり、部分集合ではなく単一の染色体で動作するメソッド/方法があります。離散的局所探索法（英語名：Hillclimbing）は、個々のパラメータのランダムな変動（記録の中のフィールドの値、または染色体における遺伝子の値）に基づいています。このような変化は突然変異と呼ばれています。突然変異の後は、F効用関数(Fitness Function)の値が評価されます。突然変異の結果は、Fが向上した場合にのみ染色体に保存されます。『アリーニングのモデル化』時に、突然変異の結果は、得られた値に依存する一定の確率で保存されます。

PSOメソッド（Particles Swarm Optimization）では、最良のエージェントの状態で、自分の状態を調整しようとする複数のエージェントの挙動をシュミレートします。

蟻コロニー最適化法（ACO）は、巣から食物源に向かう道のりの長さを最小限に抑える蟻の行動の模倣に基づいています。

3. 遺伝的アルゴリズム（GA）

遺伝的アルゴリズムは、最近では機能的最適化の課題を解決するのに使用される適応検索法です。遺伝的アルゴリズムは、生物学的組織の遺伝的プロセスに基づいています。生物学的集団は、チャールズ・ダーウィンが発見したように、自然淘汰の法則と『適正生存』の原理に従いつつ、数世代にわたって進化します。このプロセスを模倣しながら、遺伝的アルゴリズムは、適した方法でコード化されている場合に、実際の問題の解決策を「開発」することができます。

自然界の中では集団内の個体は、例えば、食べ物や水などの様々なリソースをかけてお互いに競い合っています。また、1つの種類の集団の個体は、多くの場合、結婚相手を巡っても競い合います。環境条件に最も適している個体は、子孫を残せる可能性がより高くなります。あまりあるいは全く適応できていない個体は、子孫を残すことができないか、できたとしても少数となります。これは良く適応した個体の遺伝子が、それぞれの世代でより多くの子孫に受け継がれるということを意味します。様々な親からの良い特性の組み合わせは、時折、子孫の『最強適応』の発生をもたらすことがあり、その適応能力はその両親のどちらよりも強いものです。このように、種は発展し続け、更に更に環境に適応していきます。

遺伝的アルゴリズムは、このメカニズムの直接的アナログを使用しています。これはこの問題の重要な解答を与える集団の『個体』の総計で動作します。各個体は、課題の解答がどれだけ『良い』かによる、その『適応度』の尺度によって評価されます。最も適応した個体は、集団の他の個体の『交叉』を使用して子孫を『複製する』チャンスを獲得します。これは、両親から引き継いだいくつかの特性を自分の中に組み合わせる、新しい個体の発生をもたらします。最も適応しなかった個体が、子孫を複製できる可能性は低く、その為彼らが持っている特性は、進化の過程で集団から徐々に消えていきます。

可能なソリューションの新しい集団の全ては、前の世代の最高の代表を選択し、それらを交叉し、多くの新しい個体を得ながら生み出されていくのです。この新しい世代は、前の世代の『良い』メンバーが備える特性を持っている比率が高いです。このように、世代から世代へと良い特性は全ての集団に広がります。最も適応した個体の交叉は、探索範囲の最も有望な領域の分析につながります。最終的に集団は、課題の最適解に落ち着きます。

遺伝的アルゴリズムの枠組みの中で、生物学的進化のアイディアを実装する様々な方法があるのです。

3.1. 適用範囲

解決する実際の課題は、いくつかの入力パラメータに依存する複雑な関数の最適値の探索として表されることがあります。場合によっては、最も正確な関数の値にたどり着くパラメータ値を見つけることが重要です。他の場合では、正確な最適条件を必要とせず、いくつかの設定値よりも良い任意の値を解とみなすことができます。この場合、遺伝的アルゴリズムは、多くの場合において『良い』値の探索の為の最も適切な方法となります。遺伝的アルゴリズムの力は、同時に複数のパラメータを使用し操作する能力です。この遺伝的アルゴリズムの特徴は、飛行機の設計やアルゴリズムのパラメータの設定、非線形微分方程式系に安定状態の探索を含む数百のアプリケーションで使用されています。

しかし、遺伝的アルゴリズムが期待通りに効率的に動作しない事もあります。

最適解の探索を含む実際の課題があると仮定しましょう。遺伝的アルゴリズムがそれに適しているかを確かめるにはどうしたらいいのでしょうか？この問いへの厳密な答えは、今日に至るまでありません。しかし、多くの研究者は、遺伝的アルゴリズムは次の場合において、効果的な探索過程になる良いチャンスを持っているという仮説を共有しています。

• 調査する範囲が大きく、スムーズで単峰的ではないと予想される場合（つまり、1つの滑らかな極値を含んでいる）。
  
• 適合関数がノイズを含んでいる場合。
  
• もしくは、課題に対して厳密な大域的最適解を見つける必要がない場合。  
  

言い換えれば、迅速かつ容易に適切で『良い』解を見つける必要がある場合（実際の問題によく見受けられるもの）、遺伝的アルゴリズムは競合し、探索領域の認識を使用しない他のメソッドを凌駕します。

探索領域が小さい場合は、解は網羅的探索を使用して見つけることができ、最適解が見つかったと確信できるので、遺伝的アルゴリズムは大域的最適解ではなく、局所的最適解に収束する可能性が高いです。領域が滑らかで単峰的である場合、任意の勾配アルゴリズム（例えば、最急降下法）は遺伝的アルゴリズムよりもより効果的です。

探索領域についての幾つかの追加情報がある場合（例えば、有名な巡回セールスマン問題の領域）、決定される範囲によるヒューリスティックを使用する探索法は、しばしば遺伝的アルゴリズムのような任意の一般的メソッドを凌駕します。適応度関数が比較的複雑な時、降下法のような簡単なメソッドのような各時点の唯一の解を持つ探索法は、局所的解に『引っかかる』ことがあります。しかし、ソリューションの全『集団』で動作する為、局所最適に収束する可能性は低く、多極値で確実に機能します。

勿論、遺伝的アルゴリズムが他の手順と競合する効果的な探索手順となる場合は、このような予測は厳密ではありません。遺伝的アルゴリズムの効率は、ソリューション、演算子、設定パラメータ、成功の部分的基準の符号化に大きく依存します。遺伝的アルゴリズムに関する文献に反映された理論的研究は、正確な予測の為の厳密なメカニズムの開発についての根拠を与えるものではありません。

3.2. タスク

遺伝的アルゴリズムは、次の課題を解決する為に使用されます。

• 関数の最適化
• データベース内のリクエストの最適化
• チャート上の様々なな課題（巡回セールスマン問題、着色、マッチングの検出）
• 人口ニューラルネットワークの訓練と設定
• レイアウトタスク
• スケジュールの作成
• ゲーム戦略
• 近似理論

3.3. 古典的遺伝的アルゴリズム

単純遺伝的アルゴリズムの動作

単純遺伝的アルゴリズムは、ランダムに構造の初期集団を生成します。遺伝的アルゴリズムの動作は、世代の設定数または何らかの停止基準が実行されるまで続く、反復プロセスです。アルゴリズムの各世代で、適応度比例選択、単一の交叉と突然変異が実装されています。

初めに比例選択は、各構造に集団の全体適応度に等しい適応度の、確率Ps(i)を割り当てます。 

それから、Ps(i)値に応じた今後の遺伝的処理の為の全ての個体ｎの選択（置換を含む）が起こります。単純比例選択は、ルーレット方式(roulette-wheel selection、Goldberg、1989c)であり、ルーレットの『スピン』ｎで個体を選択します。ルーレットには、集団の個々の為のセクターが1つずつ含まれています。i番目のセクターのサイズは、対応するPs(i)値に比例します。このような淘汰では、低い適応性を持つものよりも、より高い適応性の集団のメンバーが高い確率で選択されます。

淘汰後、選択された個体のｎは、指定された確率Pcの交叉（再組み合わせ）をされます。ｎの文字列はランダムにｎ/2の組に分けられます。Pcの確率を持つ各組は交叉されます。したがって、1-Pcの確率の交叉は起こらず、変化しない個体は突然変異の段階へ進みます。交叉が起き、得られた子孫が親の代わりとなる場合、突然変異へ進みます。

一点交叉は次のように動作します。始めに、I-1のブレークポイントのうち1つがランダムに選択されます。（ブレークポイントは、文字列内の隣接するビット間の領域）両方の親構造は、このポイントで2つのセグメントに分割されます。それから、対応するそれぞれの親のセグメントがくっつき、2つの遺伝子型の子孫が生まれます。

交叉の段階が終了すると、突然変異の演算子が実行されます。突然変異される各文字列では、確率Pmの各ビットが反対に変わります。突然変異の後に生まれた集団は、古いものに上書きされ、これで一世代のループが終了します。次の世代も同じように、淘汰、交叉、突然変異によって処理されます。

現在では、遺伝的アルゴリズムの研究者は、多くの他の淘汰や交叉、突然変異の演算子を提案しています。以下は、それらのうちの最も普及しているものです。まずは、トーナメント選択(Brindle, 1981; GoldbergとDeb, 1991)です。トーナメント選択はｎの個体を選択する為に、ｎのトーナメントを実装します。各トーナメントは、集団やその中の最高の個体の選択からの要素ｋのサンプルに基づき構築されます。k=2からのトーナメント選択が最も一般的です。

エリート選択法(De Jong, 1975)は、選択時に最も優れたまたは集合の最も優れたメンバーの生き残りが保証されます。他のもののように選択や交叉、突然変異のプロセスを通過しなかった場合、1つの最も優れた個体の強制保存の処置が最も一般的です。エリート法は事実上あらゆる標準の選択法に導入されています。

二点交叉(Cavicchio, 1970; Goldberg, 1989c)と一様交叉(Syswerda, 1989)は、一点演算子の代替となるものです。二点交叉(Cavicchio, 1970; Goldberg, 1989c)と一様交叉(Syswerda, 1989)は、一点演算子の代替となるものです。一様交叉では、最初の親の各ビットは、最初の子孫によって設定された確率で継承されます。そうでない場合には、2番目の子孫に継承されます（またはその逆）。

遺伝的アルゴリズムの基本的な演算子

選択演算子

この段階では、今後の繁殖のための最適な集団が選択されます。通常は適応性の高い特定の数値を適用します。『クローン』を排除する、つまり同じ遺伝子のセットを持つ個体を排除する意味もあります。

交叉演算子

多くの場合、交叉は最高の2つの個体において行われます。通常は、彼らの『親』から得られたコンポーネントを持つ2つの個体が結果となります。通常は、彼らの『親』から得られたコンポーネントを持つ2つの個体が結果となります。

突然変異演算子

突然変異演算子は、単に個体の要素の番号を他の番号に替えます。実際には、一方では極値から引き出される散逸素子の一種であり、他方では集団に新たな情報をもたらすものです。

• これはバイナリシグナルの場合にビットを反転させます。
• 特定の値（多くの場合最も近い値）の数値符号を変更します。
• 別の名目上の記号に置き換えます。

停止基準

• グローバルまたは準最適解の発見
• 『高台』へ出た場合
• 進化する世代数の枯渇
• 進化する時間の枯渇
• 目的関数の呼び出しの指定数の枯渇

3.4. 検索戦略

検索は最適解へ導く一連の手順が不明な場合に、解決策を見つける普遍的な方法の一つです。

最適解の活用と解領域を研究する2つの検索方法があります。勾配法は、全検索領域の研究を無視して、可能な改善の為の最適解を選択するストラテジーの一例です。ランダム検索は、逆に検索領域の今後の検索領域の研究を無視して解領域を研究します。遺伝的アルゴリズムは、両方の戦略の要素を組み合わせた一般的な機能の検索方法のクラスです。これらの方法を使用することで、最適解の研究と開発の間の良好なバランスを取ることができます。遺伝的アルゴリズムの動作開始時には、集団はランダムで、様々な要素を持っています。したがって、交叉演算子は解領域の大規模な研究を行います。得られた解の適合関数の値の増加とともに、交叉演算子はそれぞれの環境の研究を開始します。言い換えれば、交叉演算子の為の検索戦略タイプ（最善の解決策または解領域の研究）は、これらの演算子自身で定義されるのではなく、集団の多様性によって定義されます。

3.5. 古典的最適解の検索との違い

一般的に、最適化問題を解くアルゴリズムは、漸近的に最適解に収束する計算ステップのシーケンスです。古典的最適化法の多くは、勾配またはより高次の目的関数の導関数に基づく計算の特定シーケンスを生成します。これらの方法は、検索領域の一つの開始点に適用されます。それから、解は徐々に目的関数の減少または最速成長の方向に改善していきます。このようなアプローチの場合、局所最適に陥る危険性があります。

遺伝的アルゴリズムは、可能な解の集団を用いて複数の方向での同時検索を実行します。一つの集団から他の集団へ移行することで、局所最適に陥るのを回避することができます。集団は各世代で比較的良い解が再生されるのに対し、良くないものは死んでゆくという進化と似たものを持っています。遺伝的アルゴリズムは、目的関数が改善される可能性の高い領域へ検索を向ける為に、再生されるまたは破壊された染色体を識別する確率的ルールを使用しています。

近年では、多くの遺伝的アルゴリズムが実装され、ほとんどの場合、それらは元の古典的なものとは大きく異なっています。そのため、現在では『遺伝的アルゴリズム』という用語には一つのモデルだけではなく、お互いにあまり似ていない広範囲のアルゴリズムクラスが含まれます。研究者らは表現の様々な種類や、交叉や突然変異の演算子、再生と選択への様々なアプローチで実験しました。

遺伝的アルゴリズムに使用される進化的発展モデルは、自然のアナログと比べて大幅に単純化され、遺伝的アルゴリズムは十分に強力なツールであり、解決が困難または他の方法では不可能なものを含む、広いクラスに正常に適用することができます。しかし、遺伝的アルゴリズムは、他の進化的計算方法のように、多項式時間にわたるグローバルな解の検出を保証するものではありません。これらもグローバルな解の検出を保証していません。しかし遺伝的アルゴリズムは、『比較的良い』解を『比較的迅速に』検索するには良いものです。特別な方法で解決されるような課題の場合には、大抵このような方法が遺伝的アルゴリズムよりも、実行速度においても検出される解の精度においてもより有効になります。遺伝的アルゴリズムの主要な利点は、特別な方法が存在しないような複雑な課題においてさえ適用することができる点です。既存の方法が良く動作している場合でも、それらと遺伝的アルゴリズムを組み合わせて改善をすることもできます。

3.6. 遺伝的アルゴリズムの用語

遺伝的アルゴリズムが自然科学（遺伝学）やコンピュータから派生している為、使用される用語は自然と人工物のブレンドになります。最適化課題の解決に関連する、遺伝的アルゴリズムに関する用語は以下の通りです。1.1.

表１

遺伝的アルゴリズム	説明
染色体	解のバリエーション（パラメータのセット）
遺伝子	最適化されたパラメータ
軌跡（場所）	染色体中の遺伝子の位置
アレル	遺伝子値
表現型	コード化されていない解
遺伝子型	コード化された解

古典的（単一）交叉

『古典的』遺伝的アルゴリズムは、2つの交叉する染色体が一度特定のポイントで切断され、その後得られた部分を交換する、単一交叉を使用しています。しかし、多くの場合に複数の切断ポイントを含む他のタイプの交叉を伴う、多くのその他のアルゴリズムが考案されました。ディヤングは、多点交叉の有効性を調べ、二点交叉は改善をもたらすが、交差点のさらなる追加は遺伝的アルゴリズムの活性を低下させると結論づけました。交叉の点を追加する問題は、標準ブロックが恐らく中断される可能性があるという点にあります。しかしながら、多点交叉の利点は、状態の領域をより完全にまた詳細に調査できることです。

二点交叉

二点交叉（そして一般的に多点交叉）では、染色体は線形染色体の端部を一緒に接合し形成されるループとして見なされます。一つのサイクルのセグメントを他のサイクルのセグメントと交換するには、二つの切断ポイントの選択する必要があります。この場合には単一交叉は二つのポイントを持つが、行頭で固定された一つの切断ポイントを持つ交叉として見なされます。したがって、二点交叉はより完全に単一交叉と同じ課題を解決します。文字列の最後で『環状的復帰』を行うことができる為、サイクルとして見なされる染色体は標準ブロックを多く含みます。現在、多くの研究者が一般的に二点交叉は単一交叉よりも優れていると同意しています。

一様（均質）交叉

一様交叉は一点交叉とは根本的に異なります。子孫における各遺伝子は、ランダムに生成された交叉マスクに応じて選択された一方または両方の親からの遺伝子のコピーによって生成されます。交叉マスクに1がある場合、遺伝子は第一の親からコピーされ、マスクに0がある場合、遺伝子は第二の親からコピーされます。第二の子孫を作成する為に、逆に置き換えられた親でプロセスを繰り返します。新しい交叉マスクは、各親のセットごとにランダムに生成されます。

差動交配

交叉に加えて、他の交配方法もあります。例えば、多くの物理的変数の最小/最大関数を見つける為には、『差動交配』が最も適しています。簡単にその概念を記述します。aとｂという二つの集団内の個体、つまり私達の関数が依存する物理的ベクトルがあるとします。その場合、子孫はс=a+k*(a-b)の式で求められ、ここでのｋはベクトル間の距離ー||a-b||に依存することがある特定の物理的比率です。
このモデルでの突然変異は、短い長さのランダムなベクトル個体への追加です。出力関数が連続である場合、このモデルは上手く機能します。それがさらに滑らかである場合は、更に良いです。

反転と並び替え

染色体中の遺伝子の順序は、多くの場合、アルゴリズムの効率的な動作を実行することを可能にするブロックを構築する為に重要なものです。アルゴリズムの動作中に、染色体における遺伝子の位置を並び替える方法が提案されました。これらの方法の一つが、染色体中の無作為に選択した二つの位置の遺伝子の順序を逆に反転させるものです。（これらの方法を使用する場合、遺伝子は染色体中の位置に拘わらずに正常に識別することができるように、特定の『マーク』を持っている必要があります。）
並べ替えの目的は、最高の進化の可能性を持つ遺伝子の順序の発見を試みることです。多くの研究者が自分の研究で反転を使用しましたが、多くがそれを証明するかそれに貢献しようとしていたように思えます。ゴールドバーグ＆ブリッジは、彼らの方法が大きな問題に対し同様の効果が得られていないと結論づけているが、特定の利点を与えることができることを示しつつ、非常に小さな問題で並び替えの演算子を分析しています。
並び替えも同様に検索範囲を大幅に拡大します。遺伝的アルゴリズムは良い遺伝子の値の集団を見つけようと試みるだけでなく、同時にそれらの『正しい』順序を見つけようとします。これは解決する為には遥かに困難な課題です。

エピスタシスとは？

遺伝学における『エピスタシス』とは、他の場所に存在する遺伝子の値に応じた、個体の適合性への遺伝子の影響として定義されています。言い換えれば、遺伝学者は『スイッチ』または『マスキング』の効果の点で、『エピスタシス』という用語を使用しています。「別の遺伝子座で遺伝子の影響を抑制する時、上位性遺伝子であると見なされます。上位性遺伝子は、時に基本原理として書かれる他の遺伝子へ影響を与えることから抑制とも抑制遺伝子とも呼ばれます。
遺伝的アルゴリズムの用語では、『個体の適合度は、遺伝子型における染色体の相対的な位置に依存する』と言えるでしょう。

偽最適とは？

遺伝的アルゴリズムの基本原理の一つは、大域的最適解に含まれるパターンに含まれる染色体の密度が増加していることです。特にこれはビルディングブロックとして知られる、小さい順序の短いパターンに当て嵌まります。最終的に、これらの最適なパターンが交叉時に出会うと、グローバルで最適な染色体が作成されます。しかし、パターンがグローバル最適に含まれておらず、他のものよりも密度が増加する場合、遺伝的アルゴリズムは、誤解に導かれグローバル最適に近づく代わりに、他の方向へと逸れてしまいます。この現象は偽最適として知られています。
偽最適とは、エピスタシスの特別な場合で、ゴールドバーグらによって深く研究されました。偽最適は直接的に遺伝的アルゴリズムにおけるエピスタシスの有害な影響と関連しています。
統計的に、集団内の全てのパターンの平均適合度平均よりも高い場合、集団内のパターンの密度は増加します。グローバル最適に含まれないパターンの平均適合度が他のパターンの平均適合度以上の場合、問題は偽最適の問題として見えてきます。
偽最適の問題は解決が困難なものです。しかし、Grefenstetteは、これらが常に起こるわけではない事を巧妙に示しています。遺伝的アルゴリズムは第一世代の後に検索範囲における点の客観的選択を取得しません。したがって、パターンの客観的なグローバル平均適合度を評価することはできません。これはパターンの適合度の非客観的評価を取得することはできます。時にこの偏見は遺伝的アルゴリズムの一致の助けとなります（問題が強い偽最適を持つ場合にも）。

近親交配、異形交配、選択的選択、任意交配とは？

親ペアの選択には、いくつかのアプローチがあります。それらのうちの最も簡単なものが、任意交配です。このアプローチは、親ペアとなる二つの個体が全集団からランダムに選択される場合に、親ペアのランダムに選択することを意味しています。この場合、どの個体もいくつかのペアのメンバーになることができます。そのシンプルさにもかかわらず、このようなアプローチには様々なクラスの問題を解決する汎用性があります。しかし、このようなアプローチを実装するアルゴリズムの有効性が集団の人口の増加に伴い下がる為、集団の人口に対して非常に重要なものです。
親ペアへの個体の選択的選択法は、集団の平均適合度数よりも低くない適合度を持つ個体だけが『親』となることができ、このような候補者の等しい確率でカップルを作成します。
このアプローチは、アルゴリズムのより迅速な収束を可能にします。しかし、迅速な収束のせいで、親ペアの選択的選択は、アルゴリズムは通常解のうちの一つに急速に収束する為、いくつかの極値を決定する課題の場合には適していません。また、適合度の難しい背景を伴う特定のクラスの課題の為に、高速収束が準最適解への早期の収束になることがあります。この欠点は、速すぎるアルゴリズムの収束に『ブレーキをかける』適切な選択メカニズムの使用によって部分的に補うことができます。
近親交配は、ペアの第一のメンバーはランダムに選ばれ、その個体に最大限に近い個体が高い確率で第二のメンバーになります。
異形交配時にも、個体の類似性の概念が使用されます。しかし、現在ではカップルは最も遠い個体から作成されます。
最後の二つの方法は遺伝的アルゴリズムの動作に対して異なる効果を持っています。従って、近親交配は事実上集団を別々のローカルグループへの分割をもたらすローカル・ノードでの検索の集中の特性によって特徴づけることができます。異形交配は、アルゴリズムに新しく未踏の領域の検索をさせつつ、すでに発見された解にアルゴリズムが収束することを予防することを目的としています。

遺伝的アルゴリズムの動的自己組織化

多くの場合、遺伝的アルゴリズムのパラメータと特定の遺伝演算子の選択は、どの設定も演算子もその長所の客観的証拠がない為、直感的なレベルで行われています。しかし、遺伝的アルゴリズムの本質自体はダイナミクスと計算値とアルゴリズムの『柔軟さ』にあることは忘れてはいけません。ではなぜ問題を解決する時やそれへの適応をアルゴリズム自体にさせないのでしょうか？
使用する演算子の適用を構成するのが最も簡単な方法です。この為に、アルゴリズムにいくつかの（なるべく多くの）異なるサンプル演算子（エリート、ランダム、ルーレットなど）や、交叉（一点、二点、一様など）、突然変異（ランダム単一要素、絶対的など）を組み込みます。各演算子に等しい適用確率を設定します。次にアルゴリズムの各サイクルで、各グループ（選択、交叉、突然変異）の演算子の中から確率分布に応じて一つを選択します。この時、取得した個体にどの演算子からそれが取得されたかをマークします。そして、新しい確率分布を集団に含まれる情報から計算する（演算子の適用確率は、この演算子を用いて得られた集団内の個体の数に比例する）場合、遺伝的アルゴリズムは動的自己適応メカニズムを取得します。
このアプローチにはもう一つ利点があります。アルゴリズムが動的に分布の特性を変更するので、適用する乱数生成器（線形、指数関数など）の心配をする必要がありません。

移行と人工選択の方法

通常の遺伝的アルゴリズムとの違いは、マクロ進化が行われ、つまり一つの集団ではなく、いくつかの集団が作成されます。ここでは遺伝的検索は異なる集団から親を組み合わせることによって行われます。

断続平衡法

この方法は、地球の地殻火山およびその他の変化を通じた、急速な進化を書いた断続平衡の古生物学的理論に基づいています。この方法を技術的問題に適用するには、各世代後にランダムな方法で集団の個体を混ぜ、それから新しい現在の世代を作成することが勧められます。ここでは、自然界のアナログのように、親ペアの無作為の選択と最高の親ペアの人口的選択をすることができます。次に、ランダムな方法で二つの選択結果を混ぜ、集団サイズを常に変更し、その管理は最高の個体の存在に応じて行われます。このような断続平衡法の修正によって、見込みがない人口を減らし、最高の個体がある集団を拡大することができます。
断続平衡法は、ローカルピットからの効率的な方策の為に使われる環境変更の強力な応力法です。

4. 遺伝的アルゴリズムの特長

古典的最適化の方法と比べて、遺伝的アルゴリズムには二つの主な特長があります。

1.遺伝的アルゴリズムは、目的関数や制約のタイプへの数学的要件を持ちません。研究者は人工的に利用可能な数学的方法の適用を確保しその妥当性を失わせて、オブジェクトのモデルを単純化するべきではありません。この時、離散、連続、混合ユニバーサルで定義される様々な目的関数や制約タイプ（線形および非線形）を使用することができます。

2. 古典的段階的方法の使用では、グローバル最適は問題が突出した特性を持つ場合にのみ見つけることができます。同時に、遺伝的アルゴリズムの進化の操作によって、グローバル最適を効果的に見つけることができます。

遺伝的アルゴリズムの比較的グローバルではないが、重要な利点：

• 効率的にヒューリスティックを構築できるようにする自由なパラメータの数が多い。

• 効率的な並列化。

• ランダム検索に劣らない動作。

• 遺伝的アルゴリズムの優れたパフォーマンスへの希望を与える生物学との関連。

5. 遺伝的アルゴリズムの欠点

• 『遺伝的アルゴリズムを使った作業』を『遺伝的アルゴリズムを使ったゲーム』に変えてしまう自由なパラメータの数の多さ。

• 収束が証明されていない。

• 単純な目的関数（平滑、1極値など）では、遺伝学は常に単純な検索アルゴリズムに速度で劣る。

6. 実験

全ての実験はR 3.2.4言語環境で行われます。モデルの訓練の為のデータセットと前の記事からの多くの関数を使用します。

最適化問題と数学的なプログラミングには、これらの問題を解決するための多くのパッケージを含む預託セクションCRANがあります。下記の問題を解決する為に、遺伝的アルゴリズムと進化的アルゴリズムの異なるメソッドをいくつか適用します。最適化プロセスに関与するモデルの要件はただ一つ実行速度だけです。数百秒間で訓練されるモデルを適用することは望ましくありません。各世代で少なくとも100の個体があり、集団がいくつかの時間を通過し（1から数十まで）、最適化プロセスが許容できない時間まで伸びることを考慮します。以前の記事では、深い二つのタイプのネットワークを使用しました（初期化SAEとRBM）。どちらも高速実行を示したので、遺伝的最適化にも使うことができます。

私達は予測変数の最適な組み合わせの発見及び指標の最適なパラメータの選択という二つの最適化問題を解決します。最初の問題（予測変数の選択）の解決の為に、新しいアルゴリズムを学ぶ目的から、最近よく耳にするアルゴリズムXGBoost(Extreme Gradient Boosting)を使用します。ソースで述べられているように、これは分類問題において非常に良い結果を示します。このアルゴリズムはR、Python、Java言語で利用できます。Ｒ言語ではこのアルゴリズムは“xgboost”v. 0.4-3パッケージで実装されています。

二つ目の問題（指標の最適なパラメータの選択）を解決する為に、最も簡単なエキスパートアドバイザーMACDsample を使用し、遺伝的最適化のフローへの使用時に何を得られるかを見てみましょう。

6.1. 予測変数の最適な組み合わせの検索

最適化問題の解決の為に、以下を定義する必要があります。

• 最適化されるパラメータ。

• 最適化基準ー最大化/最小化が必要なスカラー。基準は複数ある場合もあります。

• 最適化基準の値を計算する目的（目的、フィットネス）関数。

私達の場合には、フィットネス関数が一貫して実行します。

• 初期データ構造を形成。

• それをtrain/testに分割。

• モデルの訓練。

• モデルのテスト。

• 最適化基準の計算。

最適化基準は、精度、リコール、カッパ、AUC、そして開発者によって提供するものが標準指標としてなりえます。私達はこれに分類誤差を使用します。

HillClimbingアルゴリズムの拡張である"tabuSearch"v.1.1のパッケージを使って予測変数の最適な組み合わせを検索します。TabuSearchアルゴリズムは、ユーザーによって識別される目的関数を使用してバイナリ文字列を最適化します。その結果、目的関数の最大値を持つ最高のバイナリ設定を提供します。私達はこのアルゴリズムを、予測変数の最適な組み合わせの検索の為に使用します。

主な機能：

tabuSearch(size = 10, iters = 100, objFunc = NULL, config = NULL, neigh = size, listSize = 9, 
           nRestarts = 10, repeatAll = 1, verbose = FALSE)

引数：

size – 最適化されたバイナリ構成の長さ。

iters – 予備的検索アルゴリズムにおける反復回数。

objFun – ユーザーによって提案される当該バイナリ文字列の為の目的関数の評価方法。

config – 開始設定。

neigh – 各反復でのチェックの為の隣接する構成の数。デフォルトではバイナリ文字列と同じ長さ。数値が文字列の長さよりも小さい場合、隣接するものをランダムに選択する。

listSize – タブーリストのサイズ。

nRestarts – 検索アルゴリズムの集中的な段階での再起動の最大回数。

repeatAll – 検索を繰り返す回数。

verbose – trueの場合、例えば予備段階や強化段階、多様化段階などアルゴリズムの現段階の名前を印字する。

目的関数を記述し、実験を開始しましょう。

ObjFun <- function(th){
  require(xgboost)
  # バイナリ文字列内が全てゼロの場合終了
  if (sum(th) == 0) return(0)
  # バイナリ文字列内の1に対応する予測因子名
  sub <- subset[th != 0]
  # モデルを訓練する為の構造を作成します
  dtrain <- xgb.DMatrix(data = x.train[ ,sub], label = y.train)
  # モデルを訓練します
  bst = xgb.train(params = par, data = dtrain, nrounds = nround, verbose = 0)
  # テストセットによる予測を計算します
  pred <- predict(bst, x.test[ ,sub])
  # 予測誤差を定義します
  err <- mean(as.numeric(pred > 0.5) != y.test)
  # 品質基準を戻します
  return(1 - err) 
}

計算の為にモデルのテストと訓練の為のデータセットを準備し、モデルのパラメータと最適化の為の初期設定を定義する必要があります。以前の記事にあるデータと関数を使用しましょう（2016年2月14日時点、EURUSD/M30、6000バー）

コメントつきのリスト：

#---tabuSearch----------------------
require(tabuSearch)
require(magrittr)
require(xgboost)
# 出力データフレーム
dt <- form.data(n = 34, z = 50, len = 0)
# 初期セット内の全ての予測変数の名前 
subset <- colnames(In())
set.seed(54321, kind = "L'Ecuyer-CMRG")
# 訓練とテストの為のセットを準備します
DT <- prepareTrain(x = dt[  ,subset], 
                   y = dt$y, 
                   balance = FALSE, 
                   rati = 4/5, mod = "stratified", 
                   norm = FALSE, meth = method)
train <- DT$train
test <- DT$test
x.train <- train[  ,subset] %>% as.matrix()
y.train <- train$y %>% as.numeric() %>% subtract(1)
x.test <- test[  ,subset] %>% as.matrix()
y.test <- test$y %>% as.numeric() %>% subtract(1)
# 初期バイナリベクター
th <- rep(1,length(subset))
# モデルのパラメータ
par <- list(max.depth = 3, eta = 1, silent = 0, 
            nthread = 2, objective = 'binary:logistic')
nround = 10

# 初期設定 
conf <- matrix(1,1,17)
res <- tabuSearch(size = 17, iters = 10, 
                  objFunc = ObjFun, config = conf,
                  listSize = 9, nRestarts = 1)
# 目的関数の最大値
max.obj <- max(res$eUtilityKeep)
# バイナリベクターの最適な組み合わせ
best.comb <- which.max(res$eUtilityKeep)%>% res$configKeep[., ]
# 予測因子の最良のセット
best.subset <- subset[best.comb != 0]

10回の反復で最適化を実行し、どのような最高品質の基準と予測因子のセットとなるかを見てみましょう。

> system.time(res <- tabuSearch(size = 17, iters = 10, 
+  objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1))
   user  system elapsed 
  36.55    4.41   23.77 
> max.obj
[1] 0.8
> best.subset
 [1] "DX"     "ADX"    "oscDX"  "ar"     "tr"     "atr"   
 [7] "chv"    "cmo"    "vsig"   "rsi"    "slowD"  "oscK"  
[13] "signal" "oscKST"
> summary(res)
Tabu Settings
  Type                                       = binary configuration
  No of algorithm repeats                    = 1
  No of iterations at each prelim search     = 10
  Total no of iterations                     = 30
  No of unique best configurations           = 23
  Tabu list size                             = 9
  Configuration length                       = 17
  No of neighbours visited at each iteration = 17
Results:
  Highest value of objective fn    = 0.79662
  Occurs # of times                = 2
  Optimum number of variables      = c(14, 14)

約0.8と14の予測因子についての予測精度の計算に約37秒かかりました。得られたデフォルトによるパラメータの品質指標は非常に良いものです。100回の反復で同じ計算を行います。

> system.time(res <- tabuSearch(size = 17, iters = 100, 
+  objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1))
   user  system elapsed 
 377.28   42.52  246.34 

> max.obj
[1] 0.8042194
> best.subset
 [1] "DX"     "ar"     "atr"    "cci"    "chv"    "cmo"   
 [7] "sign"   "vsig"   "slowD"  "oscK"   "SMI"    "signal"
> 

反復回数の増加に比例して計算時間も増加し、予測の精度については何も言えません。これはわずかに増加しました。つまり、品質指標はモデルのパラメータを設定することによって改善されなければならないということを意味しています。

これは遺伝的アルゴリズムを用いた予測因子の最良のセットを選択するのに役立つ唯一のアルゴリズムとパッケージではありません。kofnGA、fSelectorのパッケージを使用することもできます。これらに加えて、"caret"パッケージでは、gafs()関数によって遺伝的アルゴリズムを使用した予測因子の選択が実装されています。

6.2. ТСの最良のパラメータを検索

1. 投影の為の初期データ。エキスパートアドバイザMACDSamplを例として取り上げます。

エキスパートアドバイザMACDSampleには、macd とsignalのラインが交差した時にシグナルを生成するアルゴリズムが実装されています。一つのインディケータを使用します。

MACD(x, nFast = 12, nSlow = 26, nSig = 9, maType, percent = TRUE, ...)

Arguments

x	一つの変数の時系列。通常はpriceだがvolumeなどもある。
nFast	高速MAの為の期間数。
nSlow	低速MAの為の期間数。
nSig	シグナルMAの為の期間数。

MaType – 使用するМАタイプ

percent – trueの場合、高速と低速MAの差をパーセンテージで返し、そうでなければシンプルな差です。

MACD関数は二つの変数を返します。（macd — 高速MAと低速MAの差もしくは高速MAと低速MAの間の距離の変化速度。signal — これらの差からのMA。）MACDは、価格に適用される一般的なオシレーターの特別なケースです。これは一つの変数のあらゆる時系列でも使用することができます。MACDの為の期間は多くの場合、26と12に設定されますが、関数は初めに25.6667と12.3333に近い0.075と0.15の指数定数を使用しました。

よって、私達の関数は変化範囲を持つ7のパラメータを持っています。

• p1 - 計算された価格(Close、Med、Typ、WClose)

• p2 - nFast (8:21)

• p3 – nSlow(13:54)

• p4 - nSig (3:13)

• p5 - MAtypeMACD – MACDラインの為のMAタイプ

• p6 - MatypeSig – Signalラインの為のMAタイプ

• p7 — percent (TRUE, FALSE)

p5,p6 = Cs(SMA, EMA, DEMA, ZLEMA).

取引の為のシグナルは、様々な方法で生成することができます。

バリエーション1

Buy = macd > signal 

Sell = macd < signal

バリエーション2

Buy = diff(macd) > 0

Sell = diff(macd) <= 0

Вариант 3

Buy = diff(macd) > 0 & macd > 0

Sell = diff(macd) < 0 & macd < 0

これはもう一つのsignal(1:3)の最適化パラメータです。

そして最後に、最後のパラメータとして、最適化履歴の深度len = 300:1000（最適化が行われる最後のバーの数）。

合計で9つの最適化パラメータがあります。私は何でも（数値、文字列など）パラメータにすることができるというのを見せる為に、意図的にその数を増やしました。

最適化基準は、ポイントでの品質係数Кです（私の以前の記事に詳細が書かれています）。

パラメータの最適化の為に、品質基準を計算し最適化プログラムを選択するフィットネス（目的）関数を定義する必要があります。プログラムから見てみましょう。

私達は信頼性が高く高速で、最も重要である繰り返しテストされた"rgenoud"のパッケージを適用します。その主な制限は、そのパラメータが全て整数または全て物理的でなければならないことにあります。これは軽度の制限で、簡単にやり過ごすことができます。genoud()関数は、様々な最適化問題を解決する為の誘導体(Newton or quasi-Newton)に基づく方法で進化的検索アルゴリズムを組み合わせます。Genoud()は誘導体が定義されていない最適化問題を解決する為に使用することができます。またcluster オプションを使用することで、関数は質の良い並列計算の為のいくつかのコンピュータ、プロセッサーまたはコアの使用をサポートしています。

genoud(fn, nvars, max = FALSE, pop.size = 1000, 
        max.generations = 100, wait.generations = 10,
      hard.generation.limit = TRUE, starting.values = NULL, MemoryMatrix = TRUE, 
      Domains = NULL, default.domains = 10, solution.tolerance = 0.001,
      gr = NULL, boundary.enforcement = 0, lexical = FALSE, gradient.check = TRUE,
      BFGS = TRUE, data.type.int = FALSE, hessian = FALSE, 
      unif.seed = 812821, int.seed = 53058,
      print.level = 2, share.type = 0, instance.number = 0, 
      output.path = "stdout", output.append = FALSE, project.path = NULL,
      P1 = 50, P2 = 50, P3 = 50, P4 = 50, P5 = 50, P6 = 50, P7 = 50, P8 = 50, 
        P9 = 0, P9mix = NULL, BFGSburnin = 0, BFGSfn = NULL, BFGShelp = NULL,
      control = list(), 
        optim.method = ifelse(boundary.enforcement < 2, "BFGS", "L-BFGS-B"), 
      transform = FALSE, debug = FALSE, cluster = FALSE, balance = FALSE, ...)

Arguments

• fn – 最小化する目的関数（またはmax = TRUEの場合に最大化する)。関数の最初の引数は、最小化する為に使用されるパラメータを持つベクトルでなければなりません。この関数はスカラーを返す必要があります（lexical = TRUEの場合を除く）。

• nvars – 最小化される関数の為に選択されるパラメータの数。

• max = FALSE 目的関数の最大化（TRUE）または最小化（FALSE）。
• pop.size = 1000 集団の規模。これは最適化問題を解く為に使用される個体の数です。この数値の意味となり得るものにはいくつかの制限があります。集合数はユーザーからの要求に関係なく、関連する制限を満たすように数は自動的に修正されます。これらの制限は、遺伝的アルゴリズムのいくつかの演算子の要件から生じます。演算子P6（単純クロスオーバー）とP8（ヒューリスティッククロスオーバー）は個体数が偶数になることを要求する、つまり二つの両親を要求します。したがって、pop.size変数は偶数でなければいけません。そうでない場合は、集団はこの制限をクリアする為に増加します。

• max.generations = 100 — 最大世代。これは関数最適化の試行時にgenoudが実行する最大世代数です。これは軽度の制限です。最大世代はhard.generation.limitがTRUEに設定された場合にのみ、genoudの為に実行し、そうでない場合はgenoudが停止しなければならない時、wait.generationsとgradient.checkの二つのソフトトリガーが制御されます。

max.generations変数がデフォルトで集団数を制限していないにも関わらず、多くの演算子が自分の動作を調整する為に使用する為、これは重要なものです。実際には、世代数がmax.generationsの制限に近づく為、多くの演算子がより少なくランダムになります。制限を超え、genoudが動作の実行を決める場合、これは自動的にmax.generationの制限を増加させます。 

• wait.generations = 10。この世代数に目的関数の改善が何もない場合、genoudは最適が検出されたと考えます。もしgradient.checkトリガーが有効になっていた場合、勾配がsolution.tolerance範囲内でゼロと等しい場合にのみgenoudはwait.generationsを計算し始めます。完了を制御する他の変数にはmax.generationsとhard.generation.limitがあります。
• hard.generation.limit = TRUE。この論理変数はmax.generations変数がgenoudの為の絶対制限であるかどうかを決定します。hard.generation.limitがFALSEの時、genoudは世代の任意の数で（wait.generationsで定義された）目的関数が改善されたまたは勾配 （gradient.checkで定義された）がゼロと等しい場合にmax.generationsの数を超えます。
• starting.values= NULL - genoudが実行時に使用されるパラメータの値が含まれているベクトルまたは行列です。このオプションを使用することで、ユーザーは1つ以上の個体を初期集団に入れることができます。行列が提供されている場合、列はパラメータで文字列は個体となります。genoudはランダムに他の個体を作成します。
• Domains = NULL。これはnvars*2行列です。各パラメータに対して、最初の列は下の線、 二つ目の列は上の線となります。genoudの初期集団から一つも制限を超えて生成されません。しかし、いくつかの演算子は、boundary.enforcementのフラグが有効になる場合に、制限を超えて配置される子孫の要素を生成することができます。
• もしユーザーがドメインの為の値を提供しない場合は、genoudはdefault.domainsを使用してデフォルトのドメインを設定します。
• default.domains = 10。もしユーザーがドメインマトリックスの提供を希望しない場合、ドメインはこの使用が簡単なスカラーオプションでユーザーによって設定することができます。Genoudは、全てのパラメータの為の下限を設定しながら、(-1)*default.domainsに等しいドメインマトリックスを作成し、上限はdefault.domainsに等しく設定します。
• solution.tolerance = 0.001。これは使用するgenoudのセキュリティレベルです。solution.toleranceの差を持つ数値は、等しいと考えられます。これはwait.generationsの評価とgradient.checkに至る時に特に重要なものです。
• gr = NULL。BFGSオプティマイザの為の勾配を提供する関数です。もしこれがNULLの場合、この代わりに数値勾配が使用されます。
• boundary.enforcement = 0。この変数はgenoudが検索範囲の制限境界に従うレベルを決定します。 この変数の値にかかわらず、初期世代のいずれの個体も検索範囲の境界を超えるパラメータ値になることはありません。

boundary.enforcementには、0 （全てに合う）、1 （部分的な制限）、2 （境界違反なし）の三つの値があります。

• 0：全てに合い、このオプションによって任意の演算子が検索範囲を超えて個体を作成することができます。そのフィットネス値が十分に良好なものである場合、これらの個体は集団に含まれます。ランダムに個体を生成する場合にのみ、境界は重要になります。

• 1：部分的制限。これによって演算子が（特に派生オプティマイザ、BFGSに基づくものを使用するものが）個体作成時に検索範囲を超えることができます。しかし、演算子が個体を選択した場合、これは許容範囲内にある必要があります。

• 2：境界の違反なし。検索範囲を超えて評価が必要になることはありません。この場合、候補がドメインによって定義された境界を超えるように逸れるのを防ぐBFGSアルゴリズムにも境界制限は適用されます。 最適化の為にL-BFGS-Bアルゴリズムが使用されることにご注意ください。このアルゴリズムは、全ての機能評価の為に全ての適切な値と勾配が定義され最終的なものであることを求めます。もしこれでエラーが発生した場合、BFGSアルゴリズムとboundary.enforcement=1の設定を使用することをお勧めします。

• lexical = FALSE。このオプションには字句の最適化が含まれています。これはいくつかの基準による最適化であり、これらは呼び出されるフィットネス関数によって定義されます。このオプションで使用されるフィットネス関数は字句順に適合値の数値ベクトルを戻す必要があります。このオプションはフィットネス関数によって戻される適切な基準の値と等しい整数、またはTRUE、FALSEの値を持っています。
• gradient.check = TRUE。もしこの変数がTRUEの場合、各勾配がsolution.toleranceとゼロに近くなるまで、genoudはwait.generationsのカウントを始めません。この変数は、max.generations制限が超えられ、hard.generation.limitオプションがTRUEに設定されている場合、何の効果もありません。BFGSburnin < 0の場合、これは無視され、gradient.check の場合はTRUEとなります。
• BFGS = TRUE。この変数は、最初の世代の後の各世代の終わりに、最良の個体に準ニュートンオプティマイザを適用するかしないかを意味しています。FALSE の設定は、BFGS が適用されないということを意味しているわけではありません。もしあなたがBFGS を適用したくない場合は、演算子Р9（ローカル最小クロスオーバー）をリセットする必要があります。
• data.type.int = FALSE。このオプションは最適化する関数のパラメータのデータタイプを設定します。もし変数がTRUEになる場合、パラメータを最適化する時にgenoudは整数の中で解を探します。

整数パラメータを使用すると、genoudはデリバティブに関する情報を使用することはありません。これはBFGSオプティマイザは使われることがない、つまりBFGSフラグがFALSEに設定されていると考えられます。これはまた、演算子P9（ローカル最小クロスオーバー）がリセットされ、勾配テスト（収束基準としての）が無効になっていると考えられます。他のオプションが設定された場所に関わらず、data.type.intが優先される、つまり、もし genoudはパラメータの整数範囲で探す必要があるとされている場合、勾配に関する情報が考慮されることはないということです。

浮動小数点と整数パラメータが混在させることができるオプションはありません。もしあなたがこれらの二つのタイプを混ぜたい場合、整数パラメータを指定することができ、目的関数で整数範囲を浮動小数点を持つ範囲に変換します。例えば、0.1から1.1までの検索ネットワークを取得する必要があります。genoudに10から110までの検索を指定し、フィットネス関数ではこのパラメータを100に分割します。

• hessian = FALSE。このフラグがTRUEである場合、genoudは解の戻りリストの一部としてヘッセ行列を返します。ユーザーは標準誤差を計算する為にこの行列を使用することができます。
• unif.seed = 812821。これはgenoudを使用する為の浮動小数点を持つ擬似乱数生成器の為のseedを設定します。このseedのデフォルトの数値は81282です。genoudはgenoudへの並列呼び出しと再帰を許可する為に、独自の内部擬似乱数生成器（Tausworthe-Lewis-Payne генератор）を使用します。
• int.seed = 53058。これはgenoudを使用する整数生成器の為のseedを設定します。このseedのデフォルトの値は53058です。genoudの並列呼び出しと再帰を許可する為に、genoudは独自の内部擬似乱数生成器(Tausworthe-Lewis-Payne генератор)を使用します。
• print.level = 2。この変数はgenoudが行う印字レベルを制御します。0（最小印字）、1（正常）、2（詳細）、3（デバッグ）の4つの値があります。2レベルが選択される場合、genoudは各世代の集団についての詳細を印字します。
• share.type = 0。もしshare.typeが1と等しい場合、genoudは実行時にプロジェクトファイルがあるかをチェックします（project.pathを参照）。このファイルがある場合、それを使用して自分の初期集団を初期化します。このオプションはtransformオプションではなく、lexicalを使用します。

演算子。Genoudは9つのパラメータを持ち使用しています。これらの演算子のそれぞれに割り当てられた整数値(P1... P9)は重みです。Genoudはs = P1+P2 +... +P9の合計を計算します。各演算子にW_n = s / (P_n)と等しい重みが割り当てられます。演算子の呼び出し数は通常c_n = W_n * pop.sizeと等しくなります。

演算子Р6（単純なクロスオーバー）とР8（ヒューリスティッククロスオーバー）は、作業を続行する為に個体の偶数の数を要求する、言い換えれば二つの親が必要です。したがって、pop.size変数と演算子のセットは、これらの三つの演算子が偶数の個体数である必要があります。もしこれが起こらない場合、genoudは、この制限が実行されるように、自動的に集団の人口上限を調整します。

常に起こるわけではないが、その親とは異なる子孫を演算子が作成するように保証する為に、独自性の強い検証が演算子に組み込まれています。

進化的アルゴリズムはrgenoudで下記の9つの演算子を使用します。

• P1 = 50 – クローニング。クローニング演算子は、単に現在の世代の最高のソリューションのコピーを作成します（この演算子にかかわらず、rgenoudは常に最高のソリューションの複製を一つ保存します）。

ユニバーサル突然変異、境界突然変異、異種の突然変異は、唯一のテストソリューションで動作します。

• P2 = 50 – ユニバーサル突然変異。ユニバーサル突然変異は、パラメータの為に定義されたドメインで均一に分布されたランダムな値でテストソリューションの一つのパラメータを変更します。

• P3 = 50 – 境界突然変異。境界突然変異は、一つのパラメータをそのドメインの境界からの一つに置き換えます。

• P4 = 50 – 異種突然変異。異種突然変異は、世代数が指定した世代最大数に近づく時、減少する減少量を持つ境界からの一つに一つのパラメータを減らします。

• P5 = 50 – 溜めんクロスオーバー。多面クロスオーバー（シンプレックス検索、ギルら、1981年、ｐ94–95）は、パラメータとしてテストソリューションと同じ数の凸部の組み合わせを持っているテストソリューションを計算します。

• P6 = 50 – 単純クロスオーバー。単純クロスオーバーは、ランダムに選択されたポイントでテストソリューションを分割した後でソリューションの間でパラメータ値を交換し、二つの入力テストソリューションから二つのテストソリューションを計算します。 この演算子は、各テストソリューションでのパラメータの配置が連続的である場合に特に効果的です。

• P7 = 50 – 完全異種突然変異。完全異種突然変異は、テストソリューションにおける全てのパラメータの為に異種突然変異を行います。

• P8 = 50 – ヒューリスティッククロスオーバー。ヒューリスティッククロスオーバーは、一つのテストソリューションで始まるベクトルに沿って配置された新しいソリューションの為の二つのテストソリューションを使用します。

• P9 = 0 —  ローカル最小クロスオーバー： BFGS。ローカル最小クロスオーバーは、2段階で新しい検証の為のソリューションを計算します。初めにBFGSは、事前に設定された入力ソリューションから実行される反復数を実行します。それから、入力ソリューションの凸部の組み合わせが計算され、BFGSが反復を行います。

備考：

品質に影響を与える最も重要なオプションは、集団の大きさ（pop.size）やアルゴリズムによって実行される世代数（max.generations、wait.generations、hard.generation.limit、gradient.check）を決定するものです。検索のパフォーマンス改善され、集団の大きさやプログラムで実行される世代数は増えることが期待されます。これらおよび他のオプションは、様々な問題の為に手動で調整する必要があります。検索範囲に特に注意を払ってください（ドメインとdefault.domains）。

パラメータ間の線形および非線形制限は、それらのフィットネス関数でユーザーによって提示することができます。例えば、1と2のパラメータの合計は、725未満である必要があり、この条件はフィットネス関数に入れることができ、ユーザーはgenoudを最大化させます（if((parm1 + parm2)>= 725) {return (-99999999)}）。この例では、線形制限が破られた場合に、genoudはとても悪い適合値を返します。したがってgenoudは、制限を満たすパラメータ値の検索を試行します。

私達のフィットネス関数を記述します。以下を計算する必要があります。

• MACD

• シグナル

• 品質指数

# フィットネス関数-------------------------fitnes <- function(param, test = FALSE){
  require(TTR)
  require(magrittr)
  # 変数を定義
  x <- pr[param[1]]
  nFast <- param[2]
  nSlow <- param[3]
  nSig <- param[4]
  macdType <- MaType[param[5]]
  sigType <- MaType[param[6]]
  percent <- per[param[7]]
  len <- param[9]*100 
  # macdの為の線形制限
  if (nSlow <= nFast) return(-Inf)
  # macdを計算します
  md <- MACD(x = x, nFast = nFast, nSlow = nSlow,
             nSig = nSig, percent = TRUE,
             maType = list(list(macdType), 
                           list(macdType),
                           list(sigType)))
  # シグナルを計算し、1バー分右にシフトします
  sig <- signal(md, param[8]) %>% Lag()
  #lenの長さ履歴でバランスを計算します
  bal <- cumsum(tail(sig, len) * tail(price[ ,'CO'], len))
  if(test)
        {bal <<- cumsum(tail(sig, len) * tail(price[ ,'CO'], len))}
  # 品質係数を計算します（整数まで四捨五入します）
  K <- ((tail(bal,1)/length(bal))* 10 ^ Dig) %>% floor()
  # 最適化基準を返します
  return(unname(K))
}

以下に、全ての変数と関数の定義がリストアップされています。

require(Hmisc)
# 平均タイプ = 4 -------------------------------------------
MaType <- Cs(SMA, EMA, DEMA, ZLEMA)
require(dplyr)
# 価格タイプ = 4 -----------------------------------------------
pr <- transmute(as.data.frame(price), Close = Close, Med = Med, 
                Typ = (High + Low + Close)/3,
                WClose = (High + Low + 2*Close)/4)
# 計算方法は？
per <- c(TRUE, FALSE)
# シグナルタイプ = 3 --------------------------
signal <- function(x, type){
  x <- na.omit(x)
  dx <- diff(x[ ,1]) %>% na.omit()
  x <- tail(x, length(dx))
  switch(type,
         (x[ ,1] - x[ ,2]) %>% sign(),
         sign(dx),
         ifelse(sign(dx) == 1 & sign(x[ ,1]) == 1, 1,
                ifelse(sign(dx) == -1 & sign(x[ ,1]) == -1,-1, 0))
  )
}
# 初期設定-------------------------- 
par <- c(2, 12, 26, 9, 2, 1, 1, 3, 5)
# 検索範囲------------------------------
dom <- matrix(c(1, 4,   # 価格タイプ用
                8, 21,  # 高速МАの期間用
                13, 54, # 低速МАの期間用
                3, 13,  # シグナルМАの期間用
                1, 4,   # 高速と低速用MAタイプ
                1, 4,   # シグナル用MAタイプ
                1, 2,   # percentタイプ
                                1, 3,   # signalタイプ
                3,10),  # 履歴の長さ[300:1000]
                                ncol = 2, byrow = TRUE)
# 利用可能なコアプロセッサからクラスターを作成します
puskCluster<-function(){
  library(doParallel)
  library(foreach)
  cores<-detectCores()
  cl<-makePSOCKcluster(cores)
  registerDoParallel(cl)
  #clusterSetRNGStream(cl)
  return(cl)
}

初期（通常デフォルト）パラメータを持つ品質係数を定義します

> K <- fitnes(par, test = TRUE)
> K
[1] 0
> plot(bal, t="l")

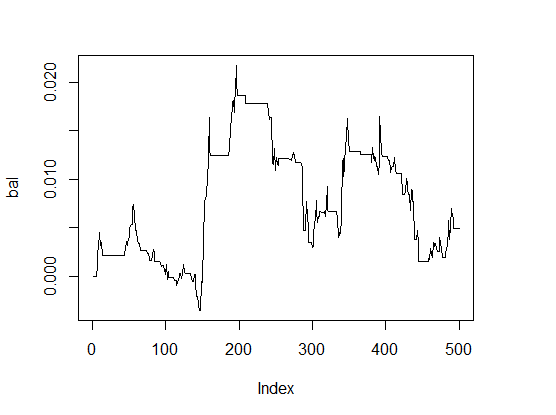
画像1　デフォルト設定のパラメータのバランス 

結果は非常に悪いです。

計算速度の比較の為にシングルコアと二つのコアプロセッサのクラスターで最適化しましょう。

シングルコア：

pr.max <- genoud(fitnes, nvars = 9, max = TRUE, 
                 pop.size = 500, max.generation = 300,
                 wait.generation = 50, 
                 hard.generation.limit = FALSE,
                 starting.values = par, Domains = dom, 
                 boundary.enforcement = 1,
                 data.type.int = TRUE,
                 solution.tolerance = 0.01,
                 cluster = FALSE,
                 print.level = 2)
'wait.generations' limit reached.
No significant improvement in 50 generations.

Solution Fitness Value: 1.600000e+01

Parameters at the Solution:
 X[ 1] :        1.000000e+00
 X[ 2] :        1.400000e+01
 X[ 3] :        2.600000e+01
 X[ 4] :        8.000000e+00
 X[ 5] :        4.000000e+00
 X[ 6] :        1.000000e+00
 X[ 7] :        1.000000e+00
 X[ 8] :        1.000000e+00
 X[ 9] :        4.000000e+00

Solution Found Generation 5
Number of Generations Run 56

Thu Mar 24 13:06:29 2016
Total run time : 0 hours 8 minutes and 13 seconds

最適なパラメータ（遺伝子型）

> pr.max$par
[1]  1 14 26  8  4  1  1  1  4

解読します（表現型）：

•   価格タイプ pr[ ,1]= Close
•   nFast = 14
•   nSlow = 26
•   nSig = 8
•   macdType = ZLEMA
•   sigType = SMA
•   percent = TRUE
•   signal = macdとsignalラインの交差
•   履歴の長さ = 400バー。

最適なパラメータを持つ残高ラインがどうなっているかを見てみましょう。この為にこれらのパラメータとtest = TRUEのオプションでフィットネス関数を実行します。

> K.opt <- fitnes(pr.max$par, test = TRUE)
> K.opt
[1] 16
> plot(bal, t="l")

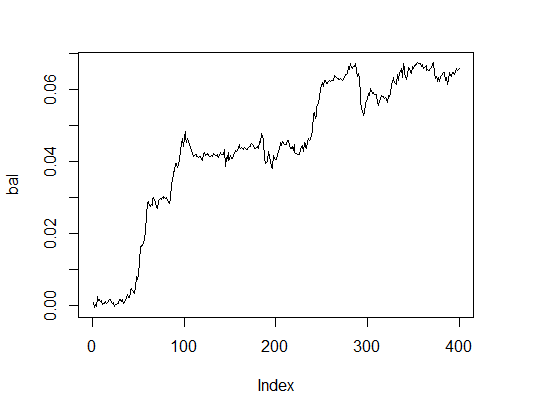
図2. 最適なパラメータのバランス 

これはエキスパートアドバイザが動作できる許容可能な結果です。

二つのコアのクラスターでの計算と同じものを実行します。

# クラスターを起動します
cl <- puskCluster()
# フィットネス関数の最大化
# クラスターの各コアに必要な変数と関数を引き渡します
clusterExport(cl, list("price", "pr", "MaType", "par", "dom", "signal", 
                                                "fitnes", "Lag", "Dig", "per" ) )
pr.max <- genoud(fitnes, nvars = 9, max = TRUE, 
                 pop.size = 500, max.generation = 300,
                 wait.generation = 50, 
                 hard.generation.limit = FALSE,
                 starting.values = par, Domains = dom, 
                 boundary.enforcement = 1,
                 data.type.int = TRUE,
                 solution.tolerance = 0.01,
                 cluster = cl,
                 print.level = 2) # エキスパートアドバイザのためのみ。 
                                            #   エキスパートアドバイザで0に設定
# クラスターを停止します
stopCluster(cl)
'wait.generations' limit reached.
No significant improvement in 50 generations.

Solution Fitness Value: 1.300000e+01

Parameters at the Solution:

 X[ 1] :        1.000000e+00
 X[ 2] :        1.900000e+01
 X[ 3] :        2.000000e+01
 X[ 4] :        3.000000e+00
 X[ 5] :        1.000000e+00
 X[ 6] :        2.000000e+00
 X[ 7] :        1.000000e+00
 X[ 8] :        2.000000e+00
 X[ 9] :        4.000000e+00

Solution Found Generation 10
Number of Generations Run 61

Thu Mar 24 13:40:08 2016
Total run time : 0 hours 3 minutes and 34 seconds

時間は遥かに良くなりましたが、品質が少し悪いです。このような単純な問題を解くにも、パラメータと『遊ばなければ』いけません。 

最も簡単なオプションを計算します

pr.max <- genoud(fitnes, nvars = 9, max = TRUE, 
                 pop.size = 500, max.generation = 100,
                 wait.generation = 10, 
                 hard.generation.limit = TRUE,
                 starting.values = par, Domains = dom, 
                 boundary.enforcement = 0,
                 data.type.int = TRUE,
                 solution.tolerance = 0.01,
                 cluster = FALSE,
                 print.level = 2)
'wait.generations' limit reached.
No significant improvement in 10 generations.

Solution Fitness Value: 1.500000e+01

Parameters at the Solution:

 X[ 1] :        3.000000e+00
 X[ 2] :        1.100000e+01
 X[ 3] :        1.300000e+01
 X[ 4] :        3.000000e+00
 X[ 5] :        1.000000e+00
 X[ 6] :        3.000000e+00
 X[ 7] :        2.000000e+00
 X[ 8] :        1.000000e+00
 X[ 9] :        4.000000e+00

Solution Found Generation 3
Number of Generations Run 14

Thu Mar 24 13:54:06 2016
Total run time : 0 hours 2 minutes and 32 seconds

良い結果です。ではバランスは？

> k
[1] 15
> plot(bal, t="l")

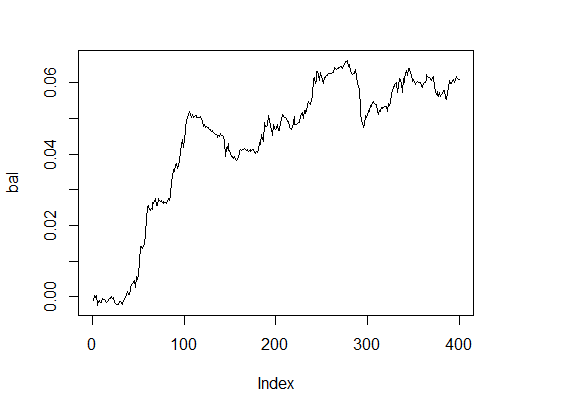
図3. 最適なパラメータのバランス

妥当な時間内で非常に良い結果です。

遺伝的アルゴリズムと進化的アルゴリズムの結果の比較の為に、これらを使用した一連の実験を行いましょう。初めに"soma"パッケージで実装されているSOMAアルゴリズム（Self-Organising Migrating Algorithm）をテストします。

一般的な自己組織移行アルゴリズム汎用的最適化は、最新世代の成長ではなく固定された個体のセットを使った『移行』の一連のアイディアに基づいているが、遺伝的アルゴリズムに似たアプローチです。これはローカル極小値に耐性があり、パラメータの範囲制限の消費を最小化する任意の課題に適用することができます。主な関数：

soma(costFunction, bounds, options = list(), strategy = "all2one", …) 

Arguments

costFunction	最初の引数としてパラメータの数値ベクトルを受け入れ、コスト値を提示する数値のスカラーを返すコスト（フィットネス）関数。
bounds	最小と最大の要素のリスト、各パラメータに上限と下限をしていする各数値ベクトル。
options	SOMAアルゴリズム自体の為のオプションリスト（下記参照）。
strategy	使用される戦略タイプ。現在、"all2one"が唯一のサポートされている数値です。
...	costFunctionの為の追加パラメータ

詳細
最適化実行設定とその終了基準の為に多くのオプションを利用できます。ここで使用するデフォルト値はZelinka(2004)
の製作者が推薦しているものです。

• pathLength: 個体が移行できるリーダーまでの距離。値1はリーダーの位置に対応し、1を超える値（推奨）はいくつかの再制御が考慮されます。デフォルトでは3です。

• stepLength: 可能なステップを評価する最小ステップ。行程の長さがこの数値の整倍数にしないことをお勧めします。デフォルト値は0.11です。

• perturbationChance: 任意の段階で個々のパラメータが変更される確率。デフォルト値は0.1です。

• minAbsoluteSep: コスト関数の最大値と最小値の間の最小絶対差。差が最小値を下回る場合は、アルゴリズムは終了します。デフォルト値は0です。これはこの停止基準が満たされないことを意味します。

• MinRelativeSep: コスト関数の最大値と最小値の間の最小相対差。差が最小値を下回る場合は、アルゴリズムは終了します。デフォルト値は0.001です。

• nMigrations: 終了の為の最大移行数。デフォルト値は20です。

• populationSize: 集団内の個体数。この値は最適化されるパラメータ数よりも少し多いことが勧められ、2以下である必要があります。デフォルト値は10です。

アルゴリズムは最小化だけ実行するので、私達のフィットネス関数が反対符号の値を与えるようにし、最適化を実行します。

require(soma)
x <- soma(fitnes, bounds = list(min=c(1,8,13,3,1,1,1,1,3), 
          max = c(4,21,54,13,4,4,2,3,10)), 
          options = list(minAbsoluteSep = 3,
                         minRelativeSep = -1,
                         nMigrations = 20,
                         populationSize = 20),
                        opp = TRUE)
Output level is not set; defaulting to "Info"
* INFO: Starting SOMA optimisation
* INFO: Relative cost separation (-2.14) is below threshold (-1) - stopping
* INFO: Leader is #7, with cost -11

最良のパラメータ：

> x$population[ ,7]
[1]  1.532332 15.391757 37.348099  9.860676  1.918848
[6]  2.222211  1.002087  1.182209  3.288627
四捨五入します
> x$population[ ,7]%>% floor
[1]  1 15 37  9  1  2  1  1  3

フィットネス関数の最良値は11です。これは実用的な適用にとって許容できるものであるが、改善の余地があります。

アルゴリズムは高速ですが、結果は不安定で微調整を必要としています。

Generalized Simulated Annealing Function（アリーニングシュミレーション一般関数）

このアルゴリズムは"GenSA"パッケージで実装されています。この関数は最適数の非常に多い複雑な非線形目的関数のグローバル最小値の検索を行うことができます。

 GenSA(par, fn, lower, upper, control=list(), …)

引数：

• par - 最適化しなければならないコンポーネントの初期値。デフォルト値はNULLで、この場合デフォルト値は自動的に生成されます。

• fn - 最小化される関数。ベクトル形式での一連のパラメータが関数の最小化の為に設定されます。これはスカラー結果を返す必要があります。

• lower – length(par)の長さのベクトル。コンポーネントの下限。

• upper - length(par)の長さのベクトル。コンポーネントの上限。

• … はユーザーがfn.関数に追加引数を引き渡すことができます。

• control - 制御引数。これはアルゴリズムの動作を管理する為に使用することができるリスト。

• maxit – 整数。アルゴリズムの反復の最大数。

• threshold.stop - 数値。プログラムはthreshold.stop目的関数の期待値に達すると停止します。デフォルト値はNULLです。

• nb.stop.improvement - 整数。nb.stop.improvementステップにおいて何の改善もない場合に、プログラムは停止します。

• smooth - ロジック。目的関数が平滑またはパラメータの範囲のどこでも微分が可能な場合はTRUE、それ以外の場合はFALSEになります。デフォルト値はTRUEです。

• max.call - 整数。目的関数の最大呼び出し数。デフォルト値は1е7です。

• max.time - 数値。最大時間（秒）。

• temperature - 数値。温度の初期値。

• visiting.param - 数値。訪問分布のパラメータ。

• acceptance.param - 数値。受け入れ分布のパラメータ。

• verbose - ロジック。TRUEは、アルゴリズムからのメッセージが表示されていることを意味します。デフォルトではFALSEです。

• simple.function - ロジック。TRUEは、目的関数がいくつかのローカル極小値を持っていることを示しています。デフォルトでは FALSEで、目的関数は多くのローカル極小値によって複雑化していることを意味しています。

• trace.mat - ロジック。デフォルトではTRUEです。これは、ルーティングマトリックスがGenSA呼び出しの戻り値で利用することができるということを示しています。

制御コンポーネントの値は、デフォルトでは難しい最適化問題の為に設定されています。平均的な難易度の通常の最適化問題には、GenSAが合理的な解決策を素早く見つけることができる為、GenSAを早く終了させることをユーザーにお勧めします。

threshold.stopが関数の期待値である場合、threshold.stopを設定します。

もしくは、max.time秒の為にユーザーが単にGenSAを実行したい場合、max.timeの設定を用います。

またはユーザーが単にmax.call関数呼び出しの範囲内でGenSAを実行したい場合、max.callを設定します。

非常に複雑な最適化問題にはユーザーにmaxitとtemperatureを増やすことをお勧めしています。

60秒の最大実行時間を制限することで、最適化を実行します。

require(GenSA)
pr.max <- GenSA(par, fitnes, lower = c(1,8,13,3,1,1,1,1,3),
            upper = c(4,21,54,13,4,4,2,3,10), 
                        control = list(verbose = TRUE, simple.function = TRUE, 
                                                        max.time = 60), opp = TRUE)

フィットネス関数値と最適化されるパラメータの値。

> pr.max$value * (-1) [1] 16
> par1 <- pr.max$par 
> par1
[1]  1.789901 14.992866 43.854988  5.714345  1.843307
[6]  1.979723  1.324855  2.639683  3.166084

四捨五入します：

> par1 <- pr.max$par %>% floor
[1]  1 14 43  5  1  1  1  2  3

これらのパラメータでフィットネス関数値を計算し、バランスラインを見てみましょう。

> f1 <- fitnes(par1, test = TRUE)
> plot(-1 * bal, t="l")

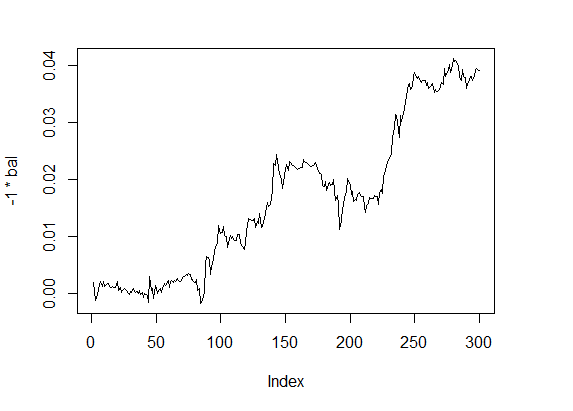
図.4　バランス4

品質指標は良いレベルで、計算は驚くほど速いです。

これらの全てとその他の多くの同様のアルゴリズム（dfoptim, nlopt,CEoptim, DEoptim,RcppDEなど）は、一つの基準で関数を最適化します。多基準最適化の為にmcoパッケージが作られています。

7. 質の指標を改善する方法と手段

私達が行った実験は、遺伝的アルゴリズムの有効性を示しました。品質指標の今後の改善の為に、適用を伴う追加研究を行うことが望ましいです。

• 多基準最適化。例えば、品質係数と最大ドローダウンを最適化します。このような機能を実装するのが"mco"パッケージです。
• 遺伝的アルゴリズムのパラメータの動的自己組織化を実装してみましょう。実装のためのパッケージは"GA"です。これは、選択、交叉、突然変異演算子の種類の幅広い選択肢を提供します。
• 取引システムに遺伝的プログラミングを適用することができるか実験的に確認をします。
  

まとめ

私達は進化的アルゴリズムにおける主要な原理と、その多様性および特徴について検証しました。実験を使用した簡単なエキスパートアドバイザMACDSampleの例では、パラメータの最適化適用は、このような初歩的な取引システムにもかなりのプラスの効果をもたらすことを示しました。 

最適化の実行時間とプログラミングの容易さが、エキスパートアドバイザの動作時に市場を離れることなくそれを実行することを可能にします。最適化パラメータのタイプに厳しい制限がないことで、エキスパートアドバイザの動作の様々な段階で、多様な種類の最適化を実装することができます。

この時最も重要な事は、フィットネス関数を正確に記述することです。

この記事が自分で自分のエキスパートアドバイザに最適化を導入することが難しいことではないということを理解するのに役立つことを願っています。