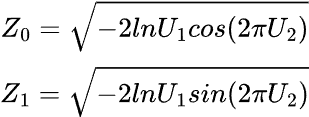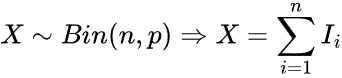MetaTrader 5 / エキスパートアドバイザー
English Deutsch
preview
データサイエンスとML（第35回）：MQL5でのNumPy活用術 - 少ないコードで複雑なアルゴリズムを構築する技法

データサイエンスとML（第35回）：MQL5でのNumPy活用術 - 少ないコードで複雑なアルゴリズムを構築する技法

MetaTrader 5 — エキスパートアドバイザー |
75 0
Omega J Msigwa
Omega J Msigwa

内容

自分ならできると信じれば、もう半分は終わったようなものだ。

-- セオドア・ルーズベルト

はじめに

どんなプログラミング言語であっても、あらゆるタスクを単独でこなせるほど万能ではありません。ほとんどの言語は、ライブラリ、フレームワーク、モジュールといった精巧に作られたツールに依存しており、これらを活用することでさまざまな課題に対応し、アイデアを現実のものにしていきます。

MQL5も例外ではありません。もともとはアルゴリズム取引を目的として設計されたMQL5は、初期の段階では主に取引操作に機能が限定されていました。前身であるMQL4は、しばしば「弱い言語」と見なされていましたが、MQL5ははるかに強力で高機能な言語です。しかし、実際に使える自動売買ロボットを構築するには、単に売買注文を出す関数を呼び出すだけでは不十分です。

金融市場の複雑さに対応するために、トレーダーたちはしばしば、機械学習や人工知能(AI)を含む高度な数学的処理を活用します。これにより、複雑な計算を効率的に処理できる最適化されたコードベースや、専門的なフレームワークの需要が高まっています。

画像出典：pexels.com

この記事の内容を完全に理解するには、PythonとNumPyの基礎知識が必要です。



なぜNumPyなのか?

MQL5で複雑な計算を扱う際、MetaQuotesが提供する優れたライブラリが多数存在します。たとえば、Fuzzy、Stat、そして強力なAlglib（MetaEditorのMQL5\Include\Math内にあります）などが挙げられます。

これらのライブラリには、複雑なエキスパートアドバイザー(EA)を少ない労力でプログラミングするのに適した関数が多数含まれています。しかし、多くの関数は柔軟性に欠けているという側面もあります。その理由は、配列やオブジェクトポインタの多用により、コードが扱いづらくなるためです。加えて、一部の関数を正しく使うには、高度な数学的知識を求められることもあります。

ですが、行列とベクトルの導入以降、MQL5はデータの格納や計算において、より柔軟で多用途な言語になりました。これらの行列・ベクトルはオブジェクト形式で扱われ、多くの数学関数が組み込まれており、従来は手作業で実装する必要があった処理も、容易におこなえるようになっています。

行列やベクトルの柔軟性のおかげで、これらをさらに拡張し、NumPy (Numerical Python)のような、さまざまな数学関数を集約したライブラリを作成することが可能になります。NumPyとは、多次元配列、マスク付き配列、行列の操作を含む高度な数学関数を提供するPythonのライブラリです。

MQL5における行列やベクトルが提供する多くの関数は、NumPyから影響を受けていると言っても過言ではありません。実際、ドキュメントを見るとそのことがよく分かり、構文も非常に似ています。


MQL5

 Python 
vector::Zeros(3);
vector::Full(10);
 
numpy.zeros(3)
numpy.full(10)

ドキュメントによれば、このようなPythonに似た構文は、「PythonからMQL5へのアルゴリズムやコードの移植を、できるだけ少ない労力でおこなえるようにするために導入されたものです。多くのデータ処理、数式、ニューラルネットワーク、機械学習タスクは、すでに用意されたPythonのメソッドやライブラリを使えば簡単に解決できます。」

これは事実ですが、MQL5の行列やベクトルが提供する関数だけでは不十分です。PythonのアルゴリズムやコードをMQL5へ移植する際に必要となる、重要な関数の多くがまだ不足しています。そこで本記事では、NumPyでよく使われる便利な関数やメソッドのいくつかを、MQL5上にPythonに近い構文で実装していきます。これにより、PythonからMQL5へのアルゴリズムの移植作業がより簡単になります。

また、Pythonの構文に近づけるため、関数名はすべて小文字で実装します。 まずは、ベクトルと行列の初期化メソッドから始めましょう。


ベクトルと行列の初期化

ベクトルや行列を扱うには、それらに値を設定して初期化するためのメソッドが必要です。以下に、そのためのいくつかの関数を紹介します。


メソッド

 説明 
template <typename T>
vector CNumpy::full(uint size, T fill_value) { return vector::Full(size, fill_value); }
template <typename T>
matrix CNumpy::full(uint rows, uint cols, T fill_value) { return matrix::Full(rows, cols, fill_value); }
  指定したサイズ（行数・列数）で、指定した値を埋めた新しいベクトルまたは行列を作成します。 
vector CNumpy::ones(uint size) { return vector::Ones(size); }
matrix CNumpy::ones(uint rows, uint cols) { return matrix::Ones(rows, cols); }
  指定したサイズのベクトル/指定した行数と列数の行列を、すべて1で埋めて新しく作成します。 
vector CNumpy::zeros(uint size) { return vector::Zeros(size); }
matrix CNumpy::zeros(uint rows, uint cols) { return matrix::Zeros(rows, cols); }
  指定したサイズのベクトル/指定した行数と列数の行列を、すべて0で埋めて作成します。 
matrix CNumpy::eye(const uint rows, const uint cols, const int ndiag=0) { return matrix::Eye(rows, cols, ndiag); }
  対角要素が1で、それ以外が0の行列を作成します。 
matrix CNumpy::identity(uint rows) { return matrix::Identity(rows, rows); }
  主対角線上に1があり、それ以外が0の正方行列を作成します。

これらのメソッドはシンプルながらも、変換やパディング、データの拡張などでよく使われるプレースホルダーとなる行列やベクトルを作成するために非常に重要です。 

使用例

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Initialization
    
    // Vectors One-dimensional
    
    Print("numpy.full: ",np.full(10, 2));
    Print("numpy.ones: ",np.ones(10));
    Print("numpy.zeros: ",np.zeros(10));
    
    // Matrices Two-Dimensional
    
    Print("numpy.full:\n",np.full(3,3, 2));
    Print("numpy.ones:\n",np.ones(3,3));
    Print("numpy.zeros:\n",np.zeros(3,3));
    Print("numpy.eye:\n",np.eye(3,3));
    Print("numpy.identity:\n",np.identity(3));
 }


数学関数

数学関数は非常に幅広いテーマであり、ベクトルや行列のために実装・説明すべき関数は多数あります。ここではその一部について取り上げます。まずは数学定数から始めましょう。

定数

数学定数は関数と同じくらい便利です。


定数

 説明

numpy.e

  オイラーの定数（自然対数の底）、ネイピア数とも呼ばれます。

numpy.euler_gamma  

  調和級数と自然対数の差の極限として定義されます。

np.inf

  

 IEEE 754浮動小数点表現における（正の）無限大

np.nan


 IEEE 754浮動小数点表現における「非数(NaN)」
np.pi
 およそ3.14159で、円周と直径の比率を表します。 

使用例

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Mathematical functions
   
    Print("numpy.e: ",np.e);
    Print("numpy.euler_gamma: ",np.euler_gamma);
    Print("numpy.inf: ",np.inf);
    Print("numpy.nan: ",np.nan);
    Print("numpy.pi: ",np.pi);
 }

関数

以下は、CNumpyクラスに含まれるいくつかの関数です。

メソッド
説明

 
vector CNumpy::add(const vector&a, const vector&b) { return a+b; };
matrix CNumpy::add(const matrix&a, const matrix&b) { return a+b; };
 2つのベクトル/行列を加算します。 
vector CNumpy::subtract(const vector&a, const vector&b) { return a-b; };
matrix CNumpy::subtract(const matrix&a, const matrix&b) { return a-b; };
 2つのベクトル/行列を減算します。 
vector CNumpy::multiply(const vector&a, const vector&b) { return a*b; };
matrix CNumpy::multiply(const matrix&a, const matrix&b) { return a*b; };
 2つのベクトル/行列を乗算します。 
vector CNumpy::divide(const vector&a, const vector&b) { return a/b; };
matrix CNumpy::divide(const matrix&a, const matrix&b) { return a/b; };
 2つのベクトル/行列を除算します。 
vector CNumpy::power(const vector&a, double n) { return MathPow(a, n); };
matrix CNumpy::power(const matrix&a, double n) { return MathPow(a, n); };
 行列/ベクトルaの全要素をn乗します。 
vector CNumpy::sqrt(const vector&a) { return MathSqrt(a); }; 
matrix CNumpy::sqrt(const matrix&a) { return MathSqrt(a); };
 ベクトル/行列aの各要素の平方根を計算します。

使用例

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Mathematical functions
   
    vector a = {1,2,3,4,5};
    vector b = {1,2,3,4,5};  
    
    Print("np.add: ",np.add(a, b));
    Print("np.subtract: ",np.subtract(a, b));
    Print("np.multiply: ",np.multiply(a, b));
    Print("np.divide: ",np.divide(a, b));  
    Print("np.power: ",np.power(a, 2));
    Print("np.sqrt: ",np.sqrt(a));
    Print("np.log: ",np.log(a));
    Print("np.log1p: ",np.log1p(a));
 }


統計関数

これらは数学関数の一種とも言えますが、基本的な算術演算とは異なり、与えられたデータから分析的な指標を提供するための関数です。機械学習の分野では、主に特徴量エンジニアリングや正規化に使われます。

以下の表は、MQL5-Numpyクラスで実装されているいくつかの関数を示しています。


メソッド

 説明 
double sum(const vector& v) { return v.Sum(); }
double sum(const matrix& m) { return m.Sum(); };
vector sum(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Sum(axis); };
  ベクトル/行列の全要素の合計を計算します。指定した軸（軸群）に沿った計算も可能です。 
double mean(const vector& v) { return v.Mean(); }
double mean(const matrix& m) { return m.Mean(); };
vector mean(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Mean(axis); };


 ベクトル/行列の要素値の算術平均を計算します。

 
double var(const vector& v) { return v.Var(); }
double var(const matrix& m) { return m.Var(); };
vector var(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Var(axis); };


 ベクトル/行列の要素値の分散を計算します。

 
double std(const vector& v) { return v.Std(); }
double std(const matrix& m) { return m.Std(); };
vector std(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Std(axis); };


 ベクトル/行列の要素値、または指定した軸に沿った要素の標準偏差を返します。

 
double median(const vector& v) { return v.Median(); }
double median(const matrix& m) { return m.Median(); };
vector median(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Median(axis); };
  

 ベクトル/行列の要素の中央値を計算します。

 
double percentile(const vector &v, int value) { return v.Percentile(value); }
double percentile(const matrix &m, int value) { return m.Percentile(value); }
vector percentile(const matrix &m, int value, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Percentile(value, axis); }

 ベクトル/行列の要素、または指定した軸に沿った要素の指定されたパーセンタイルを計算します。

 
double quantile(const vector &v, int quantile_) { return v.Quantile(quantile_); } 
double quantile(const matrix &m, int quantile_) { return m.Quantile(quantile_); }
vector quantile(const matrix &m, int quantile_, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Quantile(quantile_, axis); }
  

指定されたパーセンタイルに対応する分位点を計算します。

 
vector cumsum(const vector& v) { return v.CumSum(); };
vector cumsum(const matrix& m) { return m.CumSum(); };
matrix cumsum(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.CumSum(axis); };

ベクトル/行列の要素、または指定した軸に沿った要素の累積和を計算します。

 
vector cumprod(const vector& v) { return v.CumProd(); }
vector cumprod(const matrix& m) { return m.CumProd(); };
matrix cumprod(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.CumProd(axis); };
  

ベクトル/行列の要素、または指定した軸に沿った要素の累積積を返します。

 
double average(const vector &v, const vector &weights) { return v.Average(weights); }
double average(const matrix &m, const matrix &weights) { return m.Average(weights); }
vector average(const matrix &m, const matrix &weights, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Average(weights, axis); }


ベクトル/行列値の加重平均を計算します。

 
ulong argmax(const vector& v) { return v.ArgMax(); }
ulong argmax(const matrix& m) { return m.ArgMax(); }
vector argmax(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.ArgMax(axis); };
  

最大値のインデックスを返します。


 
ulong argmin(const vector& v) { return v.ArgMin(); }
ulong argmin(const matrix& m) { return m.ArgMin(); }
vector argmin(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.ArgMin(axis); };
 最小値のインデックスを返します。 
double min(const vector& v) { return v.Min(); }
double min(const matrix& m) { return m.Min(); }
vector min(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Min(axis); };
 ベクトル/行列、または指定した軸に沿った要素の最小値を返します。 
double max(const vector& v) { return v.Max(); }
double max(const matrix& m) { return m.Max(); }
vector max(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Max(axis); };
  ベクトル/行列、または指定した軸に沿った要素の最大値を返します。 
double prod(const vector &v, double initial=1.0) { return v.Prod(initial); }
double prod(const matrix &m, double initial) { return m.Prod(initial); }
vector prod(const matrix &m, double initial, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Prod(axis, initial); }
  

ベクトル/行列の要素の積を返します。指定した軸に沿った計算も可能です。

 
double ptp(const vector &v) { return v.Ptp(); }
double ptp(const matrix &m) { return m.Ptp(); }
vector ptp(const matrix &m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Ptp(axis); }
  

ベクトル/行列、または指定した軸に沿った要素の値の範囲（最大値 − 最小値）を返します。Ptp=Peak to peak。

これらの関数は、ドキュメントにもある通り、ベクトルや行列の組み込み統計関数をベースにしています。私が行ったのは、NumPyに似た構文を作り、それらの関数をラップしただけです。

以下にこれらの関数の使用方法の例を示します。

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {    
//--- Statistical functions
   
     vector z = {1,2,3,4,5};
    
     Print("np.sum: ", np.sum(z));
     Print("np.mean: ", np.mean(z));
     Print("np.var: ", np.var(z));
     Print("np.std: ", np.std(z));
     Print("np.median: ", np.median(z));
     Print("np.percentile: ", np.percentile(z, 75));
     Print("np.quantile: ", np.quantile(z, 75));
     Print("np.argmax: ", np.argmax(z));
     Print("np.argmin: ", np.argmin(z));
     Print("np.max: ", np.max(z));
     Print("np.min: ", np.min(z));
     Print("np.cumsum: ", np.cumsum(z));
     Print("np.cumprod: ", np.cumprod(z));
     Print("np.prod: ", np.prod(z));
     
     vector weights = {0.2,0.1,0.5,0.2,0.01};
     Print("np.average: ", np.average(z, weights));
     Print("np.ptp: ", np.ptp(z));
}


乱数生成器

NumPyには便利なサブモジュールが多数ありますが、その中の一つがrandomサブモジュールです。 

numpy.randomサブモジュールは、PCG64乱数生成器（NumPy 1.17以降）をベースにしたさまざまな乱数生成関数を提供しています。これらの多くのメソッドは、確率論や統計分布の数学的原理に基づいています。

機械学習の分野では、多くの用途で乱数を生成します。例えば、ニューラルネットワークや勾配降下法を用いたモデルの初期重みをランダムに設定したり、統計分布に従うランダムな特徴量を生成してモデルのサンプルテストデータを作成したりします。

ここで重要なのは、生成する乱数が適切な統計分布に従っていることです。これはMQL5の標準の乱数生成関数だけでは実現が難しい点です。

まずは、CNumpy.randomサブモジュールで乱数のシードを設定する方法をご紹介します。

np.random.seed(42);


一様分布 #

ある範囲（低い値と高い値の間）の一様分布に従って乱数を生成します。

式

ここでRは[0,1]の範囲から生成される乱数を表します。

 template <typename T>
 vector uniform(T low, T high, uint size=1)
  { 
    vector res = vector::Zeros(size);
    for (uint i=0; i<size; i++)
       res[i] = low + (high - low) * (rand() / double(RAND_MAX));  // Normalize rand()
    
    return res;
  }

使用法

Numpy.mqhファイル内では、CRandomという名前の構造体が別途作成されており、これがCNumpyクラスの中で呼び出されるようになっています。これにより、クラスの中から構造体を呼び出すことが可能となり、Python風の構文で使用できるようになります。

class CNumpy
  {
protected:
    
public:
                     CNumpy(void);
                    ~CNumpy(void);
                    
                    CRandom random;
  }
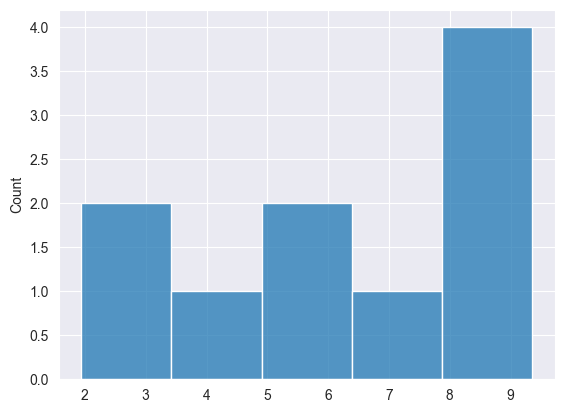
Print("np.random.uniform: ",np.random.uniform(1,10,10));

出力

2025.03.16 15:03:15.102 Numpy  np.random.uniform: [8.906552323984496,9.274605548265022,7.828760643330179,9.355082857753228,2.218420972319712,5.772331919309061,3.76067384868923,6.096438489944151,1.93908505508591,8.107272560808131]

結果を可視化して、データが均一に分布しているかどうかを確認できます。



正規分布 #

この手法は、ニューラルネットワークの重みの初期化など、多くの機械学習モデルで使用されます。

ボックス＝ミュラー法を使用して実装できます。

式

ここで

 [0,1]の範囲から生成された乱数

 vector normal(uint size, double mean=0, double std=1)
   {
       vector results = {};  // Declare the results vector
       
       // We generate two random values in each iteration of the loop
       uint n = size / 2 + size % 2;  // If the size is odd, we need one extra iteration
   
       // Loop to generate pairs of normal numbers
       for (uint i = 0; i < n; i++)
       {
           // Generate two random uniform variables
           double u1 = MathRand() / 32768.0;  // Uniform [0,1] -> (MathRand() generates values from 0 to 32767)
           double u2 = MathRand() / 32768.0;  // Uniform [0,1]
   
           // Apply the Box-Muller transform to get two normal variables
           double z1 = MathSqrt(-2 * MathLog(u1)) * MathCos(2 * M_PI * u2);
           double z2 = MathSqrt(-2 * MathLog(u1)) * MathSin(2 * M_PI * u2);
   
           // Scale to the desired mean and standard deviation, and add them to the results
           results = push_back(results, mean + std * z1);
           if ((uint)results.Size() < size)  // Only add z2 if the size is not reached yet
               results = push_back(results, mean + std * z2);
       }
       
       // Return only the exact size of the results (if it's odd, we cut off one value)
       
       results.Resize(size);
       return results;
   }

使用法

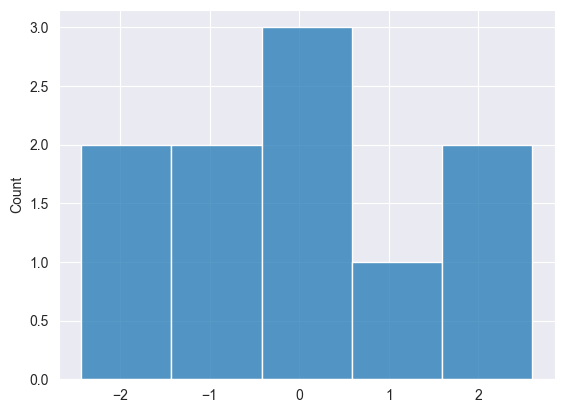
Print("np.random.normal: ",np.random.normal(10,0,1));

出力

2025.03.16 15:33:08.791 Numpy test (US Tech 100,H1)     np.random.normal: [-1.550635379340936,0.963285267506685,0.4587699653416977,-0.4813064556591148,-0.6919587880027229,1.649030932484221,-2.433415738330552,2.598464400400878,-0.2363726420659525,-0.1131299501178828]



指数分布 #

指数分布は、一定の平均率でイベントが継続的かつ独立して発生するポアソン過程（英語）におけるイベント間の時間を表す確率分布です。

以下の式で表されます。

指数分布の乱数を生成するには、逆変換サンプリング法を使用します。式は次のとおりです。

ここで

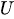  • ：0以上1未満の一様分布に従う乱数
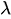  • ：発生率を示すパラメータ

 vector  exponential(uint size, double lmbda=1.0)
   {
      vector res = vector::Zeros(size);
      for (uint i=0; i<size; i++)
         res[i] = -log((rand()/RAND_MAX)) / lmbda;
          
      return res;
   }

使用法

Print("np.random.exponential: ",np.random.exponential(10));

出力

2025.03.16 15:57:36.124 Numpy test (US Tech 100,H1)     np.random.exponential: [0.4850272647406031,0.7617651806321184,1.09800210467871,2.658253432915927,0.5814831387699247,0.9920104404467721,0.7427922283035616,0.09323707153463576,0.2963563234048633,1.790326127008611]



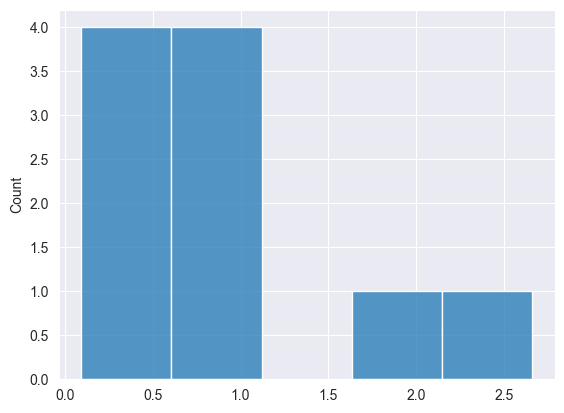
二項分布 #

これは離散確率分布であり、成功確率が一定の独立した試行を固定回数おこなったときの成功回数をモデル化したものです。

以下の式で表されます。

以下のように実装できます。

// Function to generate a single Bernoulli(p) trial
int bernoulli(double p)
  {
    return (double)rand() / RAND_MAX < p ? 1 : 0;
  }
// Function to generate Binomial(n, p) samples
vector binomial(uint size, uint n, double p)
  {
    vector res = vector::Zeros(size);
    
    for (uint i = 0; i < size; i++)
      {
        int count = 0;
        for (uint j = 0; j < n; j++)
          count += bernoulli(p); // Sum of Bernoulli trials

        res[i] = count;
      }
    
    return res;
}

使用法

Print("np.random.binomial: ",np.random.binomial(10, 5, 0.5));

出力

2025.03.16 19:35:20.346 Numpy test (US Tech 100,H1)     np.random.binomial: [2,1,2,3,2,1,1,4,0,3]



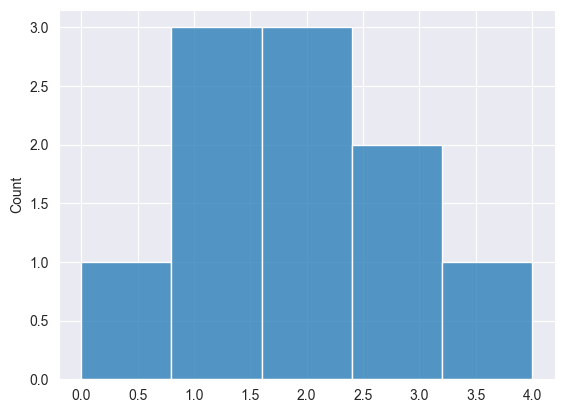
ポアソン分布 #

これは確率分布の一つで、ある一定の時間または空間内で、特定の平均発生率に基づいて、独立に発生する事象の回数を表します。また、各事象は直前の事象からの経過時間に依存せず、一定の平均頻度で発生すると仮定されています。

式

ここで

  • ：発生回数（0、1、2...）
  • ：平均発生率
  • e：ネイピア数

int poisson(double lambda)
   {
       double L = exp(-lambda);
       double p = 1.0;
       int k = 0;
   
       while (p > L)
       {
           k++;
           p *= MathRand() / 32767.0; // Normalize MathRand() to (0,1)
       }
       
       return k - 1; // Since we increment k before checking the condition
   }
// We generate a vector of Poisson-distributed values
vector poisson(double lambda, int size)
{
    vector result = vector::Zeros(size);
    for (int i = 0; i < size; i++)
        result[i] = poisson(lambda);
    
    return result;
}

使用法

Print("np.random.poisson: ",np.random.poisson(4, 10));

出力

2025.03.16 18:39:56.058 Numpy test (US Tech 100,H1)     np.random.poisson: [6,6,5,1,3,1,1,3,6,7]




シャッフル #

機械学習モデルにデータのパターンを学習させる際、データの並び順ではなく、内容そのものに含まれるパターンを学習させるために、サンプルをシャッフルすることがよくあります。

このような状況で、シャッフル機能は非常に便利です。

使用例

vector data = {1,2,3,4,5,6,7,8,9,10};
np.random.shuffle(data);

Print("Shuffled: ",data);

出力

2025.03.16 18:55:36.763 Numpy test (US Tech 100,H1)     Shuffled: [6,4,9,2,3,10,1,7,8,5]


ランダム選択 #

シャッフルと同様に、この関数は指定された1次元データをランダムにサンプリングしますが、復元抽出（重複を許可）か非復元抽出（重複なし）かを選択できるオプションがあります。

template<typename T>
vector<T> choice(const vector<T> &v, uint size, bool replace=false)

復元抽出（重複を許可）

結果として得られるシャッフル済みのベクトル/配列には、値が重複する場合があります。つまり、同じ要素が繰り返されることがあります。

vector data = {1,2,3,4,5,6,7,8,9,10};

Print("np.random.choice replace=True: ",np.random.choice(data, (uint)data.Size(), true));

出力

2025.03.16 19:11:53.520 Numpy test (US Tech 100,H1)     np.random.choice replace=True: [5,3,9,2,1,3,4,7,8,3]

非復元抽出（重複なし）

結果として得られるシャッフル済みのベクトルは、元のベクトルと同じく重複のないユニークな要素で構成されます。ただし、要素の順序だけが入れ替わります。

Print("np.random.choice replace=False: ",np.random.choice(data, (uint)data.Size(), false));

出力

2025.03.16 19:11:53.520 Numpy test (US Tech 100,H1)     np.random.choice replace=False: [8,4,3,10,5,7,1,9,6,2]

すべての関数を1か所にまとめました。

使用例

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Random numbers generating
    
    np.random.seed(42);
    
    Print("---------------------------------------:");  
    Print("np.random.uniform: ",np.random.uniform(1,10,10));
    Print("np.random.normal: ",np.random.normal(10,0,1));
    Print("np.random.exponential: ",np.random.exponential(10));
    Print("np.random.binomial: ",np.random.binomial(10, 5, 0.5));
    Print("np.random.poisson: ",np.random.poisson(4, 10));
    
    vector data = {1,2,3,4,5,6,7,8,9,10};
    //np.random.shuffle(data);
    //Print("Shuffled: ",data);
    
    Print("np.random.choice replace=True: ",np.random.choice(data, (uint)data.Size(), true));
    Print("np.random.choice replace=False: ",np.random.choice(data, (uint)data.Size(), false));
 }


高速フーリエ変換(FFT) #

高速フーリエ変換(FFT)は、離散フーリエ変換(DFT)またはその逆変換(IDFT)を効率的に計算するアルゴリズムです。フーリエ変換は、信号を元の領域（通常は時間や空間）から周波数領域へ、またはその逆に変換します。DFTは、値の列を異なる周波数成分に分解して得られます（詳細はこちら）。

この操作は多くの分野で有用です。

  1. 信号や音声処理では、時間領域の音波を周波数スペクトルに変換し、オーディオ形式のエンコードやノイズ除去に使われます。
  2. 画像圧縮や画像からのパターン認識にも用いられます。
  3. データサイエンティストは時系列データから特徴を抽出するためにFFTを活用することが多いです。

numpy.fftサブモジュールがFFT処理を担当しています。

現在のCNumpyでは、一次元の標準FFT関数のみを実装しています。

クラスに実装されている標準FFTメソッドを探る前に、まずDFTの周波数を生成する関数を理解しましょう。

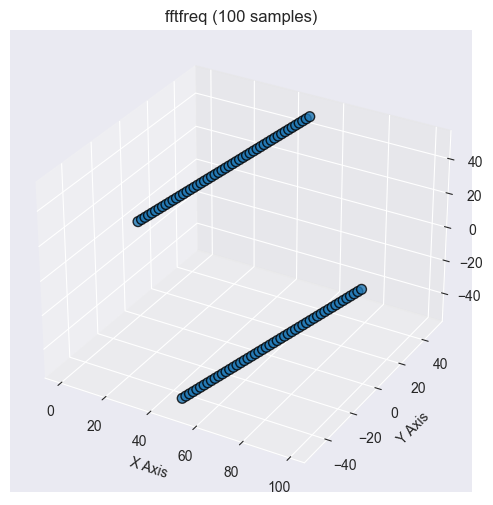
FFT周波数

信号やデータにFFTを適用すると、その出力は周波数領域のデータになります。これを解釈するためには、FFTの各要素がどの周波数に対応しているかを知る必要があります。そこでこの関数が役立ちます。

この関数は、指定されたサイズのFFTに対応する離散フーリエ変換(DFT)のサンプル周波数を返します。これにより、各FFT係数の対応周波数を判断できます。

vector fft_freq(int n, double d)

使用例

2025.03.17 11:11:10.165 Numpy test (US Tech 100,H1)     np.fft.fftfreq: [0,0.1,0.2,0.3,0.4,-0.5,-0.4,-0.3,-0.2,-0.1]



標準高速フーリエ変換 #

FFT

この関数は入力信号のFFTを計算し、信号を時間領域から周波数領域へ変換します。離散フーリエ変換(DFT)を効率的に計算するアルゴリズムです。

vector<complex> fft(const vector &x)

この関数は、ALGLIBが提供するCFastFourierTransform::FFTR1Dの上に構築されています。 詳細はALGLIBのドキュメントを参照してください。

使用例

vector signal = {0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9};
Print("np.fft.fft: ",np.fft.fft(signal));

出力

2025.03.17 11:28:16.739 Numpy test (US Tech 100,H1)     np.fft.fft: [(4.5,0),(-0.4999999999999999,1.538841768587627),(-0.4999999999999999,0.6881909602355869),(-0.5000000000000002,0.3632712640026804),(-0.5000000000000002,0.1624598481164532),(-0.5,-3.061616997868383E-16),(-0.5000000000000002,-0.1624598481164532),(-0.5000000000000002,-0.3632712640026804),(-0.4999999999999999,-0.6881909602355869),(-0.4999999999999999,-1.538841768587627)]

逆FFT

この関数は逆高速フーリエ変換(IFFT)を計算し、周波数領域のデータを時間領域に戻します。基本的に、前述のnp.fft.fftの処理を元に戻す役割を果たします。

vector ifft(const vectorc &fft_values)

使用例

vector signal = {0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9};

vectorc fft_res = np.fft.fft(signal); //perform fft
Print("np.fft.fft: ",fft_res); //fft results
Print("np.fft.ifft: ",np.fft.ifft(fft_res)); //Original signal

出力

2025.03.17 11:45:04.537 Numpy test     np.fft.fft: [(4.5,0),(-0.4999999999999999,1.538841768587627),(-0.4999999999999999,0.6881909602355869),(-0.5000000000000002,0.3632712640026804),(-0.5000000000000002,0.1624598481164532),(-0.5,-3.061616997868383E-16),(-0.5000000000000002,-0.1624598481164532),(-0.5000000000000002,-0.3632712640026804),(-0.4999999999999999,-0.6881909602355869),(-0.4999999999999999,-1.538841768587627)]
2025.03.17 11:45:04.537 Numpy test     np.fft.ifft: [-4.440892098500626e-17,0.09999999999999991,0.1999999999999999,0.2999999999999999,0.4,0.5,0.6,0.7,0.8000000000000002,0.9]


線形代数 #

線形代数は、ベクトルや行列、線形変換を扱う数学の一分野です。物理学、工学、データサイエンスなど多くの分野で基礎となっています。

NumPyは線形代数関数に特化したnp.linalgサブモジュールを提供しており、線形方程式の解法、固有値・固有ベクトルの計算など、ほぼすべての線形代数関連の関数が揃っています。

以下は、CNumpyクラスで実装されている線形代数関数の一部です。


メソッド

 説明 
matrix inv(const matrix &m)  {  return m.Inv();  }

ガウス・ジョルダンの消去法によって正方可逆行列の逆行列を計算します。

 
double det(const matrix &m)  {  return m.Det();  }

正方可逆行列の行列式を計算します。

 
matrix kron(const matrix &a, const matrix &b) { return a.Kron(b); }
matrix kron(const vector &a, const vector &b) { return a.Kron(b); }
matrix kron(const vector &a, const matrix &b) { return a.Kron(b); }
matrix kron(const matrix &a, const vector &b) { return a.Kron(b); }

2つの行列、行列とベクトル、ベクトルと行列、または2つのベクトルのクロネッカー積を計算します。

 
struct eigen_results_struct
  {
   vector eigenvalues;
   matrix eigenvectors;
  };

eigen_results_struct eig(const matrix &m) 
 {
   eigen_results_struct res;
   if (!m.Eig(res.eigenvectors, res.eigenvalues))
      printf("%s failed to calculate eigen vectors and values, error = %d",__FUNCTION__,GetLastError());
   
   return res;
 }

正方行列の固有値と右固有ベクトルを計算します。


 
double norm(const matrix &m, ENUM_MATRIX_NORM norm) {  return m.Norm(norm); }
double norm(const vector &v, ENUM_VECTOR_NORM norm) {  return v.Norm(norm); }

行列またはベクトルのノルムを返します（詳細はこちら）。

 
svd_results_struct svd(const matrix &m)
  {
    svd_results_struct res;
    if (!m.SVD(res.U, res.V, res.singular_vectors))
      printf("%s failed to calculate the SVD");
    
    return res;
  }
 特異値分解(SVD)を計算します。

 
vector solve(const matrix &a, const vector &b) { return a.Solve(b); }

線形行列方程式または線形代数方程式系を解きます。

 
vector lstsq(const matrix &a, const vector &b) { return a.LstSq(b); }

（正方行列でない場合や特異行列の場合に）線形代数方程式の最小二乗解を計算します。

 
ulong matrix_rank(const matrix &m) { return m.Rank(); }
 行列のランク（行列内の線形独立な行または列の数）を計算します。これは、線形方程式系の解空間を理解する上で重要な概念です。 
matrix cholesky(const matrix &m)
{
  vector values = eig(m).eigenvalues;
  
  for (ulong i=0; i<values.Size(); i++)
   {
    if (values[i]<=0)
       {
          printf("%s Failed Matrix is not positive definite",__FUNCTION__);
          return matrix::Zeros(0,0);
       }
   }
   
   matrix L;   
   if (!m.Cholesky(L))
      printf("%s Failed, Error = %d",__FUNCTION__, GetLastError());
      
   return L;
} 
 コレスキー分解は、正定値行列を下三角行列とその転置行列の積に分解する方法です。 
matrix matrix_power(const matrix &m, uint exponent) { return m.Power(exponent); }
 行列を特定の整数乗に累乗します。より厳密には、を計算します。ここで、は行列であり、は負でない整数です。

使用例

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {    
    //--- Linear algebra
    
    
    matrix m = {{1,1,10},
                {1,0.5,1},
                {1.5,1,0.78}};
                
    Print("np.linalg.inv:\n",np.linalg.inv(m));
    Print("np.linalg.det: ",np.linalg.det(m));
    Print("np.linalg.det: ",np.linalg.kron(m, m));
    Print("np.linalg.eigenvalues:",np.linalg.eig(m).eigenvalues," eigenvectors: ",np.linalg.eig(m).eigenvectors);
    Print("np.linalg.norm: ",np.linalg.norm(m, MATRIX_NORM_P2));
    Print("np.linalg.svd u:\n",np.linalg.svd(m).U, "\nv:\n",np.linalg.svd(m).V);
        
    
    matrix a = {{1,1,10},
                {1,0.5,1},
                {1.5,1,0.78}};
                
    vector b = {1,2,3};
    
    Print("np.linalg.solve ",np.linalg.solve(a, b));
    Print("np.linalg.lstsq: ", np.linalg.lstsq(a, b));
    Print("np.linalg.matrix_rank: ", np.linalg.matrix_rank(a));
    Print("cholesky: ", np.linalg.cholesky(a));
    Print("matrix_power:\n", np.linalg.matrix_power(a, 2));
 }


多項式（冪級数） #

numpy.polynomialサブモジュールは、多項式の作成、評価、微分、積分、操作のための強力なツール群を提供しています。これは、多項式の演算においてnumpy.poly1dを使うよりも数値的に安定しています。

PythonのNumPyライブラリにはさまざまな種類の多項式がありますが、私が実装しているCNumpy-MQL5クラスでは、現在のところ累乗基底のみを実装しています。

class CPolynomial: protected CNumpy
  {
protected:
   vector m_coeff;
      
   matrix vector21DMatrix(const vector &v)
    {
      matrix res = matrix::Zeros(v.Size(), 1);
      for (ulong r=0; r<v.Size(); r++)
         res[r][0] = v[r];
         
      return res;
    }
    
public:
                     CPolynomial(void);
                     CPolynomial(vector &coefficients); //for loading pre-trained model
                    ~CPolynomial(void);
                    
                     vector fit(const vector &x, const vector &y, int degree);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPolynomial::CPolynomial(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPolynomial::~CPolynomial(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPolynomial::CPolynomial(vector &coefficients):
m_coeff(coefficients)
 {
   
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CPolynomial::fit(const vector &x, const vector &y, int degree)
 {
   //Constructing the vandermonde matrix
   matrix X = vander(x, degree+1, true);
   
   matrix temp1 =  X.Transpose().MatMul(X);
   matrix temp2 = X.Transpose().MatMul(vector21DMatrix(y));
   
   matrix coef_m = linalg.inv(temp1).MatMul(temp2);
   
   return (this.m_coeff = flatten(coef_m));
 }

使用例

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {     
    //--- Polynomial
    
    vector X = {0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9};
    vector y = MathPow(X, 3) + 0.2 * np.random.randn(10);  // Cubic function with noise
    
    CPolynomial poly;
    
    Print("coef: ", poly.fit(X, y, 3));
 }

出力

2025.03.17 14:01:43.026 Numpy test (US Tech 100,H1)     coef: [-0.1905916844269999,2.3719065699851,-5.625684489899982,4.749058310806731]

さらに、メインのCNumpyクラスには、多項式操作に役立つユーティリティ関数があります。


関数

 説明 
vector polyadd(const vector &p, const vector &q);
 係数の次数（長さ）に合わせて2つの多項式を加算します。一方の多項式が短い場合は、加算前にゼロでパディングされます。 
vector polysub(const vector &p, const vector &q);
 2つの多項式を減算します。 
vector polymul(const vector &p, const vector &q);
 分配法則を使って2つの多項式を乗算します。多項式pの各項と多項式qの各項をすべて掛け合わせ、その結果を合計します。
 
vector polyder(const vector &p, int m=1);
 多項式pの微分を計算します。微分は、標準的な微分の法則に従って行われます。各項はからに変換されます。 
vector polyint(const vector &p, int m=1, double k=0.0)
 多項式pの積分を計算します。各項はからaltaltに変換されます。このメソッドは、定数項kを加えたm回積分も計算できます。 
double polyval(const vector &p, double x);
 多項式を特定の値xで評価します。各項はとして計算され、それらを合計します。  
struct polydiv_struct
  {
     vector quotient, 
            remainder;
  };

polydiv_struct polydiv(const vector &p, const vector &q);
 2つの多項式を除算し、商と余りを返します。

使用例

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Polynomial utils
    
    vector p = {1,-3, 2};
    vector q = {2,-4, 1};
    
    Print("polyadd: ",np.polyadd(p, q));
    Print("polysub: ",np.polysub(p, q));
    Print("polymul: ",np.polymul(p, q));
    Print("polyder:", np.polyder(p));
    Print("polyint:", np.polyint(p)); // Integral of polynomial
    Print("plyval x=2: ", np.polyval(p, 2)); // Evaluate polynomial at x = 2
    Print("polydiv:", np.polydiv(p, q).quotient," ",np.polydiv(p, q).remainder);
 }


その他（よく使われるNumPyメソッド）

すべてのNumPyメソッドを分類するのは難しいですが、以下はまだ説明していないクラス内の最も便利な関数のいくつかです。


メソッド

 説明 
vector CNumpy::arange(uint stop)
vector CNumpy::arange(int start, int stop, int step)
 最初の関数は、指定した間隔で値の範囲を持つベクトルを作成します。

2つ目のバリアントも同様ですが、値を増加させるステップ幅を考慮します。これら2つの関数は、昇順の数値ベクトルを生成するのに便利です。
 
vector CNumpy::flatten(const matrix &m)
vector CNumpy::ravel(const matrix &m) { return flatten(m); };
 2次元の行列を1次元のベクトルに変換します。

使いやすくするために、1行1列の行列をベクトルに変換する必要があることがよくあります。		 
matrix CNumpy::reshape(const vector &v,uint rows,uint cols)
  1次元ベクトルを指定した行数と列数(cols)の行列に変形します。 
matrix CNumpy::reshape(const matrix &m,uint rows,uint cols)
  2次元行列を指定した新しい形状（行数rowsと列数cols)に変形します。 
matrix CNumpy::expand_dims(const vector &v, uint axis)
  1次元ベクトルに新しい軸を追加し、実質的に行列に変換します。 
vector CNumpy::clip(const vector &v,double min,double max)
  ベクトルの値を指定した範囲（最小値と最大値の間）に収めます。これは極端な値を抑え、ベクトルを望ましい範囲内に保つのに役立ちます。 
vector CNumpy::argsort(const vector<T> &v)
  配列をソートしたときのインデックスを返します。 
vector CNumpy::sort(const vector<T> &v)
  配列を昇順にソートします。 
vector CNumpy::concat(const vector &v1, const vector &v2);
vector CNumpy::concat(const vector &v1, const vector &v2, const vector &v3);
  複数のベクトルを1つの巨大なベクトルに連結します。 
matrix CNumpy::concat(const matrix &m1, const matrix &m2, ENUM_MATRIX_AXIS axis = AXIS_VERT)
axis=0の場合、行方向に行列を連結します（つまり、行列m1とm2を縦に積み重ねます）。

axis=0の場合、列方向に行列を連結します（つまり、行列m1とm2を横に積み重ねます）。		 
matrix CNumpy::concat(const matrix &m, const vector &v, ENUM_MATRIX_AXIS axis = AXIS_VERT)
 axis=0の場合、ベクトルを新しい行として追加します（ただし、ベクトルのサイズが行列の列数と一致する場合のみ）。

axis=1の場合、ベクトルを新しい列として追加します（ただし、ベクトルのサイズが行列の行数と一致する場合のみ）。		 
matrix CNumpy::dot(const matrix& a, const matrix& b);
double CNumpy::dot(const vector& a, const vector& b);
matrix CNumpy::dot(const matrix& a, const vector& b);
 2つの行列、ベクトル、または行列とベクトルの内積を計算します。 
vector CNumpy::linspace(int start,int stop,uint num,bool endpoint=true)
  指定した範囲（startからstop）内で均等に間隔をあけた数値の配列を作成します。numは生成するサンプル数です。
endpoint（デフォルトはtrue）がtrueの場合、stopの値が含まれます。falseに設定すると、stopの値は含まれません。		 
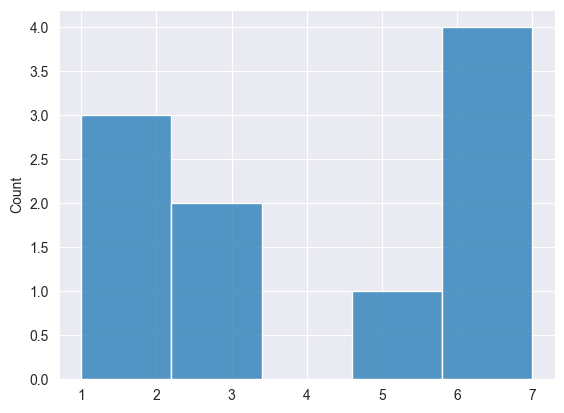
struct unique_struct
 {
   vector unique, count;
 };

unique_struct CNumpy::unique(const vector &v)
  ベクトル内の一意の項目(unique)と、その出現回数(count)を返します。

使用例

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
    //--- Common methods
    
    vector v = {1,2,3,4,5,6,7,8,9,10};  
    
    Print("------------------------------------");  
    Print("np.arange: ",np.arange(10));
    Print("np.arange: ",np.arange(1, 10, 2));
    
    matrix m = {
      {1,2,3,4,5},
      {6,7,8,9,10}
    };
      
    Print("np.flatten: ",np.flatten(m));
    Print("np.ravel: ",np.ravel(m));
    Print("np.reshape: ",np.reshape(v, 5, 2));
    Print("np.reshape: ",np.reshape(m, 2, 3));
   
    Print("np.expnad_dims: ",np.expand_dims(v, 1));
    Print("np.clip: ", np.clip(v, 3, 8));
   
    //--- Sorting
   
    Print("np.argsort: ",np.argsort(v));
    Print("np.sort: ",np.sort(v));
   
    //--- Others
    
    matrix z = {
      {1,2,3},
      {4,5,6},
      {7,8,9},
    };
      
    Print("np.concatenate: ",np.concat(v,  v));
    Print("np.concatenate:\n",np.concat(z,  z, AXIS_HORZ));
    
    vector y = {1,1,1};
    
    Print("np.concatenate:\n",np.concat(z,  y, AXIS_VERT));
    Print("np.dot: ",np.dot(v, v));
    Print("np.dot:\n",np.dot(z, z));
    Print("np.linspace: ",np.linspace(1, 10, 10, true));
    
    Print("np.unique: ",np.unique(v).unique, " count: ",np.unique(v).count);
 }

出力

NJ      0       16:34:01.702    Numpy test (US Tech 100,H1)     ------------------------------------
PL      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.arange: [0,1,2,3,4,5,6,7,8,9]
LG      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.arange: [1,3,5,7,9]
QR      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.flatten: [1,2,3,4,5,6,7,8,9,10]
QO      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.ravel: [1,2,3,4,5,6,7,8,9,10]
EF      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.reshape: [[1,2]
NL      0       16:34:01.703    Numpy test (US Tech 100,H1)      [3,4]
NK      0       16:34:01.703    Numpy test (US Tech 100,H1)      [5,6]
NQ      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8]
HF      0       16:34:01.703    Numpy test (US Tech 100,H1)      [9,10]]
HD      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.reshape: [[1,2,3]
QD      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6]]
OH      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.expnad_dims: [[1,2,3,4,5,6,7,8,9,10]]
PK      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.clip: [3,3,3,4,5,6,7,8,8,8]
FM      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.argsort: [0,1,2,3,4,5,6,7,8,9]
KD      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.sort: [1,2,3,4,5,6,7,8,9,10]
FQ      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.concatenate: [1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6,7,8,9,10]
FS      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.concatenate:
PK      0       16:34:01.703    Numpy test (US Tech 100,H1)     [[1,2,3]
DM      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6]
CJ      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8,9]
IS      0       16:34:01.703    Numpy test (US Tech 100,H1)      [1,2,3]
DH      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6]
PL      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8,9]]
FQ      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.concatenate:
CH      0       16:34:01.703    Numpy test (US Tech 100,H1)     [[1,2,3,1]
KN      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6,1]
KH      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8,9,1]]
JR      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.dot: 385.0
PK      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.dot:
JN      0       16:34:01.703    Numpy test (US Tech 100,H1)     [[30,36,42]
OH      0       16:34:01.703    Numpy test (US Tech 100,H1)      [66,81,96]
RN      0       16:34:01.703    Numpy test (US Tech 100,H1)      [102,126,150]]
RI      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.linspace: [1,2,3,4,5,6,7,8,9,10]
MQ      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.unique: [1,2,3,4,5,6,7,8,9,10] count: [1,1,1,1,1,1,1,1,1,1]


MQL5-NumPyを使って機械学習モデルをゼロから実装する

先に説明したように、NumPyライブラリはPythonで実装されている多くの機械学習モデルの基盤となっています。これは、配列・行列の操作、基本的な数学計算、さらには線形代数に対応する多数のメソッドが存在するためです。現在、MQL5においてもこれに近い機能が実現できるようになったので、簡単な機械学習モデルをゼロから実装してみましょう。

例として、線形回帰モデルを使います。

このコードはオンラインで見つけたものです。これは、学習関数で勾配降下法を使用した線形回帰モデルです。

import numpy as np
from sklearn.metrics import mean_squared_error, r2_score

class LinearRegression:
    def __init__(self, learning_rate=0.01, epochs=1000):
        self.learning_rate = learning_rate
        self.epochs = epochs
        self.weights = None
        self.bias = None

    def fit(self, X, y):
        """
        Train the Linear Regression model using Gradient Descent.
        X: Input features (numpy array of shape [n_samples, n_features])
        y: Target values (numpy array of shape [n_samples,])
        """
        n_samples, n_features = X.shape
        self.weights = np.zeros(n_features)
        self.bias = 0

        for _ in range(self.epochs):
            y_pred = np.dot(X, self.weights) + self.bias  # Predictions
            
            # Compute Gradients
            dw = (1 / n_samples) * np.dot(X.T, (y_pred - y))
            db = (1 / n_samples) * np.sum(y_pred - y)
            
            # Update Parameters
            self.weights -= self.learning_rate * dw
            self.bias -= self.learning_rate * db

    def predict(self, X):
        """
        Predict output for the given input X.
        """
        return np.dot(X, self.weights) + self.bias

# Example Usage
if __name__ == "__main__":
    # Sample Data (X: Input features, y: Target values)
    X = np.array([[1], [2], [3], [4], [5]])  # Feature
    y = np.array([2, 4, 6, 8, 10])           # Target (y = 2x)

    # Create and Train Model
    model = LinearRegression(learning_rate=0.01, epochs=1000)
    model.fit(X, y)

    # Predictions
    y_pred = model.predict(X)

    # Evaluate Model
    print("Predictions:", y_pred)
    print("MSE:", mean_squared_error(y, y_pred))
    print("R² Score:", r2_score(y, y_pred))

セル出力

Predictions: [2.06850809 4.04226297 6.01601785 7.98977273 9.96352761]
MSE: 0.0016341843485627612
R² Score: 0.9997957269564297

fit関数に注目してください。学習関数の中で、いくつかのNumPyのメソッドが使われています。私たちのCNumpyクラスにも同様の関数があるため、同じ実装をMQL5でも再現してみましょう。

#include <MALE5\Numpy\Numpy.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
    // Sample Data (X: Input features, y: Target values)
    matrix X = {{1}, {2}, {3}, {4}, {5}};
    vector y = {2, 4, 6, 8, 10};

    // Create and Train Model
    CLinearRegression model(0.01, 1000);
    model.fit(X, y);

    // Predictions
    vector y_pred = model.predict(X);

    // Evaluate Model
    Print("Predictions: ", y_pred);
    Print("MSE: ", y_pred.RegressionMetric(y, REGRESSION_MSE));
    Print("R² Score: ", y_pred.RegressionMetric(y_pred, REGRESSION_R2));
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CLinearRegression
  {
protected:

   CNumpy np;
   double m_learning_rate;
   uint m_epochs;
   vector weights;
   double bias;
   
public:
                     CLinearRegression(double learning_rate=0.01, uint epochs=1000);
                    ~CLinearRegression(void);
                    
                    void fit(const matrix &x, const vector &y);
                    vector predict(const matrix &X);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CLinearRegression::CLinearRegression(double learning_rate=0.01, uint epochs=1000):
 m_learning_rate(learning_rate),
 m_epochs(epochs)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CLinearRegression::~CLinearRegression(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CLinearRegression::fit(const matrix &x, const vector &y)
 {
   ulong n_samples = x.Rows(), n_features = x.Cols();
   this.weights = np.zeros((uint)n_features);
   this.bias = 0.0;

//---
   
   for (uint i=0; i<m_epochs; i++)
      {
        matrix temp = np.dot(x, this.weights);
        vector y_pred = np.flatten(temp) + bias;
        
        // Compute Gradients
        
        temp = np.dot(x.Transpose(), (y_pred - y));
                
        vector dw = (1.0 / (double)n_samples) * np.flatten(temp);
        double db = (1.0 / (double)n_samples) * np.sum(y_pred - y);

        // Update Parameters
        
        this.weights -= this.m_learning_rate * dw;
        this.bias -= this.m_learning_rate * db;
      }
   
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CLinearRegression::predict(const matrix &X)
 {
   matrix temp = np.dot(X, this.weights);
   
   return np.flatten(temp) + this.bias;
 }

出力

RD      0       18:15:22.911    Linear regression from scratch (US Tech 100,H1) Predictions: [2.068508094061713,4.042262972785917,6.01601785151012,7.989772730234324,9.963527608958529]
KH      0       18:15:22.911    Linear regression from scratch (US Tech 100,H1) MSE: 0.0016341843485627612
RQ      0       18:15:22.911    Linear regression from scratch (US Tech 100,H1) R² Score: 1.0

素晴らしいです。このモデルから得られた結果は、Pythonのコードと同じになりました。


次は何をする?

あなたの手元には、Pythonのプログラミング言語で数えきれないほどの機械学習や統計アルゴリズムの構築に使われてきた、強力なライブラリと多くの有用な関数群があります。つまり、Pythonでよく見るような複雑な計算を備えた高度な自動売買ロボットを作成することも、今や何も障害はありません。

とはいえ現時点では、このライブラリにはまだ多くの関数が不足しています。すべてを書くには数か月かかるので、ぜひご自身で関数を追加してみてください。中に入っている関数は、私自身が機械学習アルゴリズムをMQL5で扱う中でよく使うもの、または必要だと感じたものです。

MQL5のPythonに似たな構文は、時にややこしく感じるかもしれませんので、関数名などは自分に合ったものへ自由に変更して構いません。

では、ご健闘をお祈りします。

今後の更新にもご注目ください。こちらのGitHubリポジトリで、MQL5言語向けの機械学習アルゴリズムの開発にぜひ貢献してください。


添付ファイルの表

ファイル名 説明
Include\Numpy.mqh NumPy MQL5クローン。MQL5のすべてのNumPyメソッドを含みます。
Scripts\Linear regression from scratch.mq5 CNumpyを使用して線形回帰の例を実装したスクリプト
Scripts\Numpy test.mq5  テスト目的でNumpy.mqhからすべてのメソッドを呼び出すスクリプト

この記事で説明したすべての方法を試すための場

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/17469

添付されたファイル |
ZIPをダウンロード
attachments.zip (16 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

ディスカッションに移動
MQL5での取引戦略の自動化（第12回）：Mitigation Order Blocks (MOB)戦略の実装 MQL5での取引戦略の自動化（第12回）：Mitigation Order Blocks (MOB)戦略の実装
本記事では、スマートマネー取引向けにオーダーブロックの自動検出をおこなうMQL5取引システムを構築します。戦略のルールを明確にし、そのロジックをMQL5で実装し、さらに取引を効果的に執行するためにリスク管理も統合します。最後に、システムのパフォーマンスを評価するためにバックテストをおこない、最適な結果を得るための改良を加えます。
プライスアクション分析ツールキットの開発（第18回）：クォーターズ理論の紹介(III) - Quarters Board プライスアクション分析ツールキットの開発（第18回）：クォーターズ理論の紹介(III) - Quarters Board
この記事では、元のQuarters Scriptを改良し、「Quarters Board」というツールを導入しています。これにより、コードを編集し直すことなく、チャート上でクォーターレベルを直接オン・オフできるようになります。特定のレベルを簡単に有効化・無効化できるほか、エキスパートアドバイザー(EA)はトレンド方向に関するコメントも提供し、市場の動きをより理解しやすくします。
MQL5で自己最適化エキスパートアドバイザーを構築する（第6回）：自己適応型取引ルール(II) MQL5で自己最適化エキスパートアドバイザーを構築する（第6回）：自己適応型取引ルール(II)
本記事では、より良い売買シグナルを得るために、RSIのレベルと期間を最適化する方法を探ります。最適なRSI値を推定する手法や、グリッドサーチと統計モデルを用いた期間選定の自動化について紹介します。最後に、Pythonによる分析を活用しながら、MQL5でソリューションを実装します。私たちのアプローチは、複雑になりがちな問題をシンプルに解決することを目指した、実用的かつ分かりやすいものです。
ダーバスボックスブレイクアウト戦略における高度な機械学習技術の探究 ダーバスボックスブレイクアウト戦略における高度な機械学習技術の探究
ニコラス・ダーバスによって考案された「ダーバスボックスブレイクアウト戦略」は、株価が一定の「ボックス」レンジを上抜けたときに強い上昇モメンタムが示唆されることから、買いシグナルを見極めるためのテクニカル取引手法です。本記事では、この戦略コンセプトを例として用い、機械学習の3つの高度な技術を探っていきます。それは、取引をフィルタリングするのではなくシグナルを生成するために機械学習モデルを使用すること、離散的ではなく連続的なシグナルを用いること、異なる時間枠で学習されたモデルを使って取引を確認すること、の3点です。