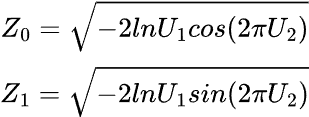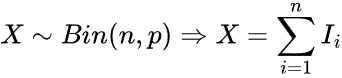MetaTrader 5 / EA交易
English Русский Deutsch 日本語
preview
数据科学和机器学习（第 35 部分）：MQL5 中的 NumPy — 用更少代码制作复杂算法的艺术

数据科学和机器学习（第 35 部分）：MQL5 中的 NumPy — 用更少代码制作复杂算法的艺术

MetaTrader 5 — EA交易 |
41 0
Omega J Msigwa
Omega J Msigwa

内容

相信您能做到，并且您行过半程

— 西奥多·罗斯福（Theodore Roosevelt）。

概述

对于我们能想到的每一项代码创建任务，没有编程语言能完全自给自足，每种编程语言都依赖于精心设计的工具，这些工具可以是函数库、框架、和模块，帮助解决某些问题，并把思路转化为现实。

MQL5 也不例外。它主要为算法交易而设计，其早期功能大多限于交易操作。不同于其前身 MQL4 — 被认为是较弱的语言 — MQL5 更强大、更有能力。然而，构建一个功能齐全的交易机器人不仅需要调用函数来下达买卖交易。

为驾驭金融市场的复杂性，交易者往往部署包括机器学习和人工智能（AI）在内的精密数学运算。而这又令优化代码函数库、及能够高效处理复杂计算的专用框架的需求增长。

图片来源：pexels.com

若要完全理解本文内容，需要具备基础的 Python 和 NumPy 知识。



为何是 NumPy？

当以 MQL5 来应对复杂计算时，MetaQuotes 为我们提供了众多优秀的函数库，诸如 Fuzzy、Stat 和强大的 Alglib（可在 MetaEditor 的 MQL5\Include\Math 目录下找到）。

这些函数库拥有许多的函数，适合以较小的工作量，来编写复杂的智能系统，但因函数库中过量用到数组和对象指针，故大多函数缺乏灵活性，更不用说有些函数需要数学知识才能正确使用。

自引入矩阵和向量以来，MQL5 语言在数据存储、及计算方面变得更加多才和灵活，这些数组均以对象形式存在，并伴随许多内置数学函数，这些都曾需要手工实现。

由于矩阵和向量的灵活性，我们能够有针对性地更大扩展它们，形成类似于已有的 NumPy（数值 Python，一款提供高级数学函数的 Python 函数库，支持多维数组、掩码数组、和矩阵）这样的各种数学函数集合。

公平地说，大多数 MQL5 提供的矩阵和向量函数都受到 NumPy 的启发，正如这篇文档中所见，语法非常相似。


MQL5

 Python 代码。 
vector::Zeros(3);
vector::Full(10);
 
numpy.zeros(3)
numpy.full(10)

根据文档，引入的这种类似语法是为了“以最小的工作量更轻松地将 Python 算法和代码翻译到 MQL5。许多数据处理任务、数学方程、神经网络、和机器学习任务，都能用现成的 Python 方法和函数库来解决。”

这确实如此，但提供的矩阵和向量函数还不够。我们还缺少众许多紧要函数，都是我们经常把这些算法和代码从 Python 翻译到 MQL5 时所需的，在本文中，我们把一些最实用的函数和方法，以非常接近的语法从 NumPy 翻译成 MQL5，令翻译 Python 编程语言算法更轻松。

为了保持语法与 Python 相似，我们将用小写字母实现函数名称。先从初始化向量和矩阵的方法开始。


向量与矩阵初始化

为了处置向量和矩阵，我们需要有初始化方法，初始化它们时填充一些数值。以下是针对该任务的一些功能。


方法

 说明 
template <typename T>
vector CNumpy::full(uint size, T fill_value) { return vector::Full(size, fill_value); }
template <typename T>
matrix CNumpy::full(uint rows, uint cols, T fill_value) { return matrix::Full(rows, cols, fill_value); }
  按给定大小/行列，构造一个新的向量/矩阵，并以一个数值填充。 
vector CNumpy::ones(uint size) { return vector::Ones(size); }
matrix CNumpy::ones(uint rows, uint cols) { return matrix::Ones(rows, cols); }
  按给定尺寸构造一个新向量，或按给定的行和列构造一个新矩阵，填充数值一 
vector CNumpy::zeros(uint size) { return vector::Zeros(size); }
matrix CNumpy::zeros(uint rows, uint cols) { return matrix::Zeros(rows, cols); }
  按一个给定大小构造向量，或给定行何列构造矩阵，填充数值零 
matrix CNumpy::eye(const uint rows, const uint cols, const int ndiag=0) { return matrix::Eye(rows, cols, ndiag); }
  构造一个矩阵，对角线上是 1，其它则是零。 
matrix CNumpy::identity(uint rows) { return matrix::Identity(rows, rows); }
  构造一个主对角线为 1 的方阵。

尽管方法简单，但对于创建占位矩阵和向量至关重要，其常用于变换、填充、和扩充。 

用法示例：

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Initialization
    
    // Vectors One-dimensional
    
    Print("numpy.full: ",np.full(10, 2));
    Print("numpy.ones: ",np.ones(10));
    Print("numpy.zeros: ",np.zeros(10));
    
    // Matrices Two-Dimensional
    
    Print("numpy.full:\n",np.full(3,3, 2));
    Print("numpy.ones:\n",np.ones(3,3));
    Print("numpy.zeros:\n",np.zeros(3,3));
    Print("numpy.eye:\n",np.eye(3,3));
    Print("numpy.identity:\n",np.identity(3));
 }


数学函数

这是一个宽泛的主题，在于向量和矩阵都需要实现和描述很多数学函数，我们于此只讨论其中的一些。从数学常数开始。

常数

数学常数和函数一样实用。


常数

 说明

numpy.e

  欧拉常数、自然对数基数、纳皮尔常数。

numpy.euler_gamma  

  定义是调和级数与自然对数之间的极限差值。

np.inf

  

 IEEE 754 浮点表示，（正）无穷大。

np.nan


 IEEE 754 浮点表示法，非数字（NaN）。
np.pi
 大约等于 3.14159，即圆周长与直径的比值。 

用法示例：

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Mathematical functions
   
    Print("numpy.e: ",np.e);
    Print("numpy.euler_gamma: ",np.euler_gamma);
    Print("numpy.inf: ",np.inf);
    Print("numpy.nan: ",np.nan);
    Print("numpy.pi: ",np.pi);
 }

函数

以下是 CNumpy 类中存在的一些函数。

方法
说明

 
vector CNumpy::add(const vector&a, const vector&b) { return a+b; };
matrix CNumpy::add(const matrix&a, const matrix&b) { return a+b; };
 两个向量/矩阵相加。 
vector CNumpy::subtract(const vector&a, const vector&b) { return a-b; };
matrix CNumpy::subtract(const matrix&a, const matrix&b) { return a-b; };
 两个向量/矩阵相减。 
vector CNumpy::multiply(const vector&a, const vector&b) { return a*b; };
matrix CNumpy::multiply(const matrix&a, const matrix&b) { return a*b; };
 两个向量/矩阵相乘。 
vector CNumpy::divide(const vector&a, const vector&b) { return a/b; };
matrix CNumpy::divide(const matrix&a, const matrix&b) { return a/b; };
 两个向量/矩阵相除 
vector CNumpy::power(const vector&a, double n) { return MathPow(a, n); };
matrix CNumpy::power(const matrix&a, double n) { return MathPow(a, n); };
 它将矩阵/向量 a 中的所有元素提升到 n 次幂。 
vector CNumpy::sqrt(const vector&a) { return MathSqrt(a); }; 
matrix CNumpy::sqrt(const matrix&a) { return MathSqrt(a); };
 计算向量/矩阵 a 中每个元素的平方根。

用法示例：

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Mathematical functions
   
    vector a = {1,2,3,4,5};
    vector b = {1,2,3,4,5};  
    
    Print("np.add: ",np.add(a, b));
    Print("np.subtract: ",np.subtract(a, b));
    Print("np.multiply: ",np.multiply(a, b));
    Print("np.divide: ",np.divide(a, b));  
    Print("np.power: ",np.power(a, 2));
    Print("np.sqrt: ",np.sqrt(a));
    Print("np.log: ",np.log(a));
    Print("np.log1p: ",np.log1p(a));
 }


统计函数

这些也可归类为数学函数，但不同于基本数学运算，这些函数有助于从给定数据中提供分析量值。在机器学习中，它们主要用于特征工程和归一化。

下表体现了 MQL5-Numpy 类中实现的一些函数。


方法

 说明 
double sum(const vector& v) { return v.Sum(); }
double sum(const matrix& m) { return m.Sum(); };
vector sum(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Sum(axis); };
  计算向量/矩阵元素的合计，也能针对给定的轴（多轴）执行。 
double mean(const vector& v) { return v.Mean(); }
double mean(const matrix& m) { return m.Mean(); };
vector mean(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Mean(axis); };


 计算向量/矩阵中元素值的算术平均值。

 
double var(const vector& v) { return v.Var(); }
double var(const matrix& m) { return m.Var(); };
vector var(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Var(axis); };


 计算矩阵/向量元素值的方差。

 
double std(const vector& v) { return v.Std(); }
double std(const matrix& m) { return m.Std(); };
vector std(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Std(axis); };


 返回向量/矩阵元素、或沿给定轴元素的标准差。

 
double median(const vector& v) { return v.Median(); }
double median(const matrix& m) { return m.Median(); };
vector median(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Median(axis); };
  

 计算向量/矩阵元素的中位数。

 
double percentile(const vector &v, int value) { return v.Percentile(value); }
double percentile(const matrix &m, int value) { return m.Percentile(value); }
vector percentile(const matrix &m, int value, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Percentile(value, axis); }

 这些函数计算向量/矩阵元素、或沿指定轴元素的指定百分位数值。

 
double quantile(const vector &v, int quantile_) { return v.Quantile(quantile_); } 
double quantile(const matrix &m, int quantile_) { return m.Quantile(quantile_); }
vector quantile(const matrix &m, int quantile_, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Quantile(quantile_, axis); }
  

它们计算矩阵/向量元素、或沿指定轴元素的指定分位数值。

 
vector cumsum(const vector& v) { return v.CumSum(); };
vector cumsum(const matrix& m) { return m.CumSum(); };
matrix cumsum(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.CumSum(axis); };

这些函数计算矩阵/向量元素的累积和，包括沿给定轴。

 
vector cumprod(const vector& v) { return v.CumProd(); }
vector cumprod(const matrix& m) { return m.CumProd(); };
matrix cumprod(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.CumProd(axis); };
  

它们返回矩阵/矢量元素的累积乘积，包括沿给定轴。

 
double average(const vector &v, const vector &weights) { return v.Average(weights); }
double average(const matrix &m, const matrix &weights) { return m.Average(weights); }
vector average(const matrix &m, const matrix &weights, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Average(weights, axis); }


计算矩阵/向量值的加权平均值。

 
ulong argmax(const vector& v) { return v.ArgMax(); }
ulong argmax(const matrix& m) { return m.ArgMax(); }
vector argmax(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.ArgMax(axis); };
  

它们返回最大值的索引。


 
ulong argmin(const vector& v) { return v.ArgMin(); }
ulong argmin(const matrix& m) { return m.ArgMin(); }
vector argmin(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.ArgMin(axis); };
 它们返回最小值的索引。 
double min(const vector& v) { return v.Min(); }
double min(const matrix& m) { return m.Min(); }
vector min(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Min(axis); };
 它们返回向量/矩阵中的最小值，包括沿指定轴。 
double max(const vector& v) { return v.Max(); }
double max(const matrix& m) { return m.Max(); }
vector max(const matrix& m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Max(axis); };
  它们返回向量/矩阵的最大值，包括沿指定轴。 
double prod(const vector &v, double initial=1.0) { return v.Prod(initial); }
double prod(const matrix &m, double initial) { return m.Prod(initial); }
vector prod(const matrix &m, double initial, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Prod(axis, initial); }
  

它们返回矩阵/矢量元素的乘积，也能针对给定轴执行。

 
double ptp(const vector &v) { return v.Ptp(); }
double ptp(const matrix &m) { return m.Ptp(); }
vector ptp(const matrix &m, ENUM_MATRIX_AXIS axis=AXIS_VERT) { return m.Ptp(axis); }
  

它们返回矩阵/向量、或给定矩阵轴的数值范围，等价于 Max() - Min()。Ptp — 峰值到峰值。

这些函数由内置的向量和矩阵统计函数驱动，正如文档中所见，我所做的全部只是创建了一个类似 NumPy 语法，并把这些函数封装。

以下是如何使用这些函数的一个示例。

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {    
//--- Statistical functions
   
     vector z = {1,2,3,4,5};
    
     Print("np.sum: ", np.sum(z));
     Print("np.mean: ", np.mean(z));
     Print("np.var: ", np.var(z));
     Print("np.std: ", np.std(z));
     Print("np.median: ", np.median(z));
     Print("np.percentile: ", np.percentile(z, 75));
     Print("np.quantile: ", np.quantile(z, 75));
     Print("np.argmax: ", np.argmax(z));
     Print("np.argmin: ", np.argmin(z));
     Print("np.max: ", np.max(z));
     Print("np.min: ", np.min(z));
     Print("np.cumsum: ", np.cumsum(z));
     Print("np.cumprod: ", np.cumprod(z));
     Print("np.prod: ", np.prod(z));
     
     vector weights = {0.2,0.1,0.5,0.2,0.01};
     Print("np.average: ", np.average(z, weights));
     Print("np.ptp: ", np.ptp(z));
}


随机数生成器

NumPy 有很多实用的子模块，其中之一就是随机子模块。 

numpy.random 子模块基于 PCG64 随机数生成器（来自 NumPy 1.17+），提供多种随机数生成函数。这些方法大多基于概率论和统计分布的数学原理。

在机器学习中，我们往往为许多用例生成随机数；我们生成随机数作为神经网络的初始起始权重，训练基于迭代梯度下降的模型，有时我们甚至遵循统计分布生成随机特征，以便为我们的模型获取样本测试数据。

至关重要的是，我们生成的随机数必须遵循统计分布，而有些用 MQL5 内置的随机数生成函数无法达成。

首先，此处是您如何为 CNumpy.random 子模块设置随机种子。

np.random.seed(42);


- 均匀分布 #

我们生成的随机数来自一些低值和高值之间的均匀分布。

公式：

其中 R 是来自 [0,1] 的随机数。

 template <typename T>
 vector uniform(T low, T high, uint size=1)
  { 
    vector res = vector::Zeros(size);
    for (uint i=0; i<size; i++)
       res[i] = low + (high - low) * (rand() / double(RAND_MAX));  // Normalize rand()
    
    return res;
  }

用法。

在 Numpy.mqh 文件中，创建了一个名为 CRandom 的独立结构，然后在 CNumpy 类内调用，这允许我们调用类内的结构，为我们给出类似 Python 的语法。

class CNumpy
  {
protected:
    
public:
                     CNumpy(void);
                    ~CNumpy(void);
                    
                    CRandom random;
  }
Print("np.random.uniform: ",np.random.uniform(1,10,10));

输出：

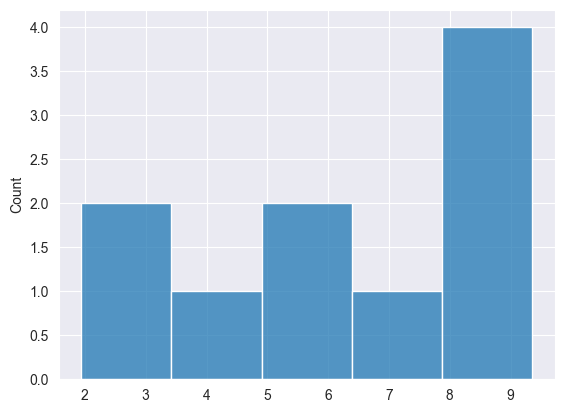
2025.03.16 15:03:15.102 Numpy  np.random.uniform: [8.906552323984496,9.274605548265022,7.828760643330179,9.355082857753228,2.218420972319712,5.772331919309061,3.76067384868923,6.096438489944151,1.93908505508591,8.107272560808131]

我们能可视化结果，看看数据是否均匀分布。



正态分布 #

在许多机器学习模型中都用到该方法，例如初始化神经网络权重。

我们可以用Box-Muller变换实现。

公式：

其中：

 随机数来自 [0,1]

 vector normal(uint size, double mean=0, double std=1)
   {
       vector results = {};  // Declare the results vector
       
       // We generate two random values in each iteration of the loop
       uint n = size / 2 + size % 2;  // If the size is odd, we need one extra iteration
   
       // Loop to generate pairs of normal numbers
       for (uint i = 0; i < n; i++)
       {
           // Generate two random uniform variables
           double u1 = MathRand() / 32768.0;  // Uniform [0,1] -> (MathRand() generates values from 0 to 32767)
           double u2 = MathRand() / 32768.0;  // Uniform [0,1]
   
           // Apply the Box-Muller transform to get two normal variables
           double z1 = MathSqrt(-2 * MathLog(u1)) * MathCos(2 * M_PI * u2);
           double z2 = MathSqrt(-2 * MathLog(u1)) * MathSin(2 * M_PI * u2);
   
           // Scale to the desired mean and standard deviation, and add them to the results
           results = push_back(results, mean + std * z1);
           if ((uint)results.Size() < size)  // Only add z2 if the size is not reached yet
               results = push_back(results, mean + std * z2);
       }
       
       // Return only the exact size of the results (if it's odd, we cut off one value)
       
       results.Resize(size);
       return results;
   }

用法。

Print("np.random.normal: ",np.random.normal(10,0,1));

输出：

2025.03.16 15:33:08.791 Numpy test (US Tech 100,H1)     np.random.normal: [-1.550635379340936,0.963285267506685,0.4587699653416977,-0.4813064556591148,-0.6919587880027229,1.649030932484221,-2.433415738330552,2.598464400400878,-0.2363726420659525,-0.1131299501178828]



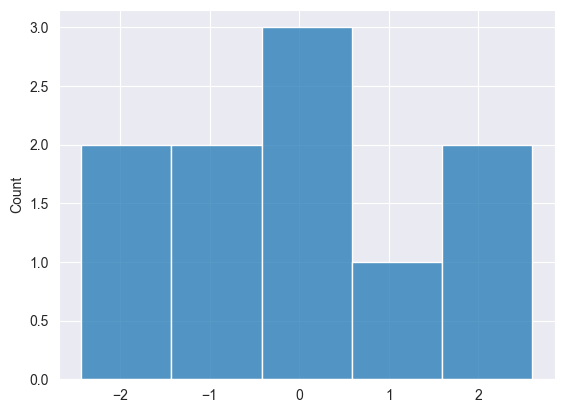
指数分布 #

指数分布是一种概率分布，描述泊松过程中事件之间的时间，其中事件以恒定的平均速率连续且独立发生。

公式给出：

为了生成指数分布随机数，我们调用逆变换抽样方法。公式：

其中：

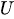  •  是介于 0 和 1 之间的均匀随机数。
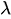  •  是速率参数。

 vector  exponential(uint size, double lmbda=1.0)
   {
      vector res = vector::Zeros(size);
      for (uint i=0; i<size; i++)
         res[i] = -log((rand()/RAND_MAX)) / lmbda;
          
      return res;
   }

用法。

Print("np.random.exponential: ",np.random.exponential(10));

输出：

2025.03.16 15:57:36.124 Numpy test (US Tech 100,H1)     np.random.exponential: [0.4850272647406031,0.7617651806321184,1.09800210467871,2.658253432915927,0.5814831387699247,0.9920104404467721,0.7427922283035616,0.09323707153463576,0.2963563234048633,1.790326127008611]



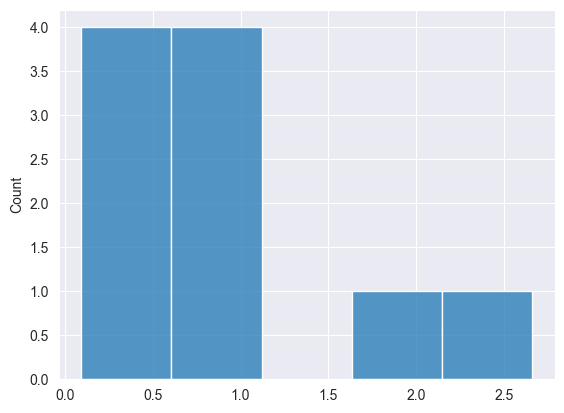
二项分布 #

这是一种离散概率分布，在固定次数的独立试验中为成功数量建模，每次都得到相同的成功概率。

公式给出。

我们能够如下实现。

// Function to generate a single Bernoulli(p) trial
int bernoulli(double p)
  {
    return (double)rand() / RAND_MAX < p ? 1 : 0;
  }
// Function to generate Binomial(n, p) samples
vector binomial(uint size, uint n, double p)
  {
    vector res = vector::Zeros(size);
    
    for (uint i = 0; i < size; i++)
      {
        int count = 0;
        for (uint j = 0; j < n; j++)
          count += bernoulli(p); // Sum of Bernoulli trials

        res[i] = count;
      }
    
    return res;
}

用法。

Print("np.random.binomial: ",np.random.binomial(10, 5, 0.5));

输出：

2025.03.16 19:35:20.346 Numpy test (US Tech 100,H1)     np.random.binomial: [2,1,2,3,2,1,1,4,0,3]



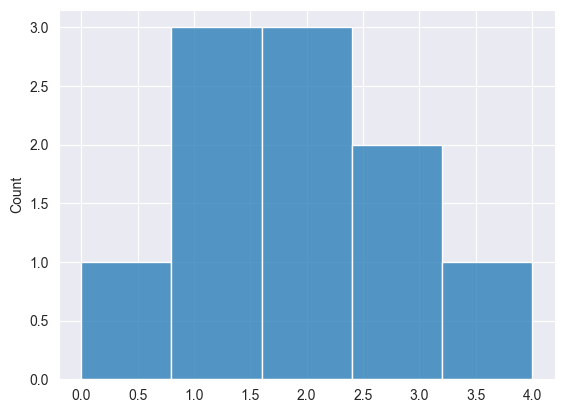
泊松分布 #

这是一种概率分布，表达在固定时间、或空间间隔内，发生给定次数事件的概率，前提是这些事件以恒定的平均速率发生，且与上次事件的发生时间无关。

公式：

其中：

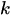  •  是发生次数 (0,1,2...)
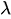  •  (lambda) 是平均发生率。
  • e 是欧拉数字。

int poisson(double lambda)
   {
       double L = exp(-lambda);
       double p = 1.0;
       int k = 0;
   
       while (p > L)
       {
           k++;
           p *= MathRand() / 32767.0; // Normalize MathRand() to (0,1)
       }
       
       return k - 1; // Since we increment k before checking the condition
   }
// We generate a vector of Poisson-distributed values
vector poisson(double lambda, int size)
{
    vector result = vector::Zeros(size);
    for (int i = 0; i < size; i++)
        result[i] = poisson(lambda);
    
    return result;
}

用法。

Print("np.random.poisson: ",np.random.poisson(4, 10));

输出：

2025.03.16 18:39:56.058 Numpy test (US Tech 100,H1)     np.random.poisson: [6,6,5,1,3,1,1,3,6,7]




洗牌 #

当训练机器学习模型来理解数据中的形态时，我们经常会对样本洗牌，帮助模型理解数据中的形态，而非数据的排列。

洗牌功能在这种状况下很便利。

用法示例：

vector data = {1,2,3,4,5,6,7,8,9,10};
np.random.shuffle(data);

Print("Shuffled: ",data);

输出：

2025.03.16 18:55:36.763 Numpy test (US Tech 100,H1)     Shuffled: [6,4,9,2,3,10,1,7,8,5]


随机选择 #

类似于洗牌，该函数从给定的一维随机采样，但有洗牌时替换或不替换的选项。

template<typename T>
vector<T> choice(const vector<T> &v, uint size, bool replace=false)

替换。

数值不会唯一，相同项能在洗牌后的结果向量/数组中重复。

vector data = {1,2,3,4,5,6,7,8,9,10};

Print("np.random.choice replace=True: ",np.random.choice(data, (uint)data.Size(), true));

输出：

2025.03.16 19:11:53.520 Numpy test (US Tech 100,H1)     np.random.choice replace=True: [5,3,9,2,1,3,4,7,8,3]

不替换。

洗牌后的结果向量就像它们在原始向量，只有唯一项，仅它们的顺序会变化。

Print("np.random.choice replace=False: ",np.random.choice(data, (uint)data.Size(), false));

输出：

2025.03.16 19:11:53.520 Numpy test (US Tech 100,H1)     np.random.choice replace=False: [8,4,3,10,5,7,1,9,6,2]

所有函数集中于一处。

用法示例：

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Random numbers generating
    
    np.random.seed(42);
    
    Print("---------------------------------------:");  
    Print("np.random.uniform: ",np.random.uniform(1,10,10));
    Print("np.random.normal: ",np.random.normal(10,0,1));
    Print("np.random.exponential: ",np.random.exponential(10));
    Print("np.random.binomial: ",np.random.binomial(10, 5, 0.5));
    Print("np.random.poisson: ",np.random.poisson(4, 10));
    
    vector data = {1,2,3,4,5,6,7,8,9,10};
    //np.random.shuffle(data);
    //Print("Shuffled: ",data);
    
    Print("np.random.choice replace=True: ",np.random.choice(data, (uint)data.Size(), true));
    Print("np.random.choice replace=False: ",np.random.choice(data, (uint)data.Size(), false));
 }


快速傅里叶变换（FFT）#

快速傅里叶变换（FFT）是一种计算序列离散傅里叶变换（DFT）、或其逆变换（IDFT）的算法。傅里叶变换将信号从原始域（通常是时间或空间），转换为频域中的表示，反之亦然。DFT 将一系列数值分解为不同频率的分量获得的，详情请阅读。

该运算在许多领域都很实用，譬如。

  1. 在信号和音频处理中，它被用来将时域声波转换为频谱。在编码音频格式和滤波噪声方面。
  2. 它也被用于图像压缩和识别图像中的形态。
  3. 数据科学家经常使用 FFT 从时间序列数据中提取特征。

numpy.fft 子模块负责处置 FFT。

就我们目前的 CNumpy，我仅实现了一维标准 FFT 函数。

我们探讨在该类中实现“标准 FFT” 方法之前，我们先来了解生成 DFT 频率的函数。

FFT 频率

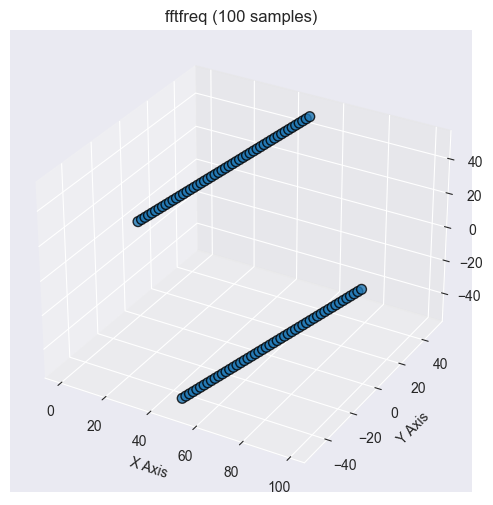
在对信号或数据执行 FFT 时，输出是频域，为了解释它，我们需要知道 FFT 中每个元素对应的频率。这就是该方法的来处。

该函数返回与给定大小 FFT 相符的离散傅里叶变换（DFT）采样频率。它有助于判定每个 FFT 系数的对应频率。

vector fft_freq(int n, double d)

用法示例：

2025.03.17 11:11:10.165 Numpy test (US Tech 100,H1)     np.fft.fftfreq: [0,0.1,0.2,0.3,0.4,-0.5,-0.4,-0.3,-0.2,-0.1]



标准快速傅里叶变换 #

FFT

该函数计算输入信号的 FFT，将其从时域转换到频域。这是一种高效计算离散傅里叶变换（DFT）的算法。

vector<complex> fft(const vector &x)

该函数基于 CFastFourierTransform::FFTR1D 的顶层构建，由 ALGLIB 提供。更多信息请参阅 ALGLIB。

用法示例：

vector signal = {0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9};
Print("np.fft.fft: ",np.fft.fft(signal));

输出。

2025.03.17 11:28:16.739 Numpy test (US Tech 100,H1)     np.fft.fft: [(4.5,0),(-0.4999999999999999,1.538841768587627),(-0.4999999999999999,0.6881909602355869),(-0.5000000000000002,0.3632712640026804),(-0.5000000000000002,0.1624598481164532),(-0.5,-3.061616997868383E-16),(-0.5000000000000002,-0.1624598481164532),(-0.5000000000000002,-0.3632712640026804),(-0.4999999999999999,-0.6881909602355869),(-0.4999999999999999,-1.538841768587627)]

逆 FFT

该函数计算逆快速傅里叶变换（IFFT），将频域数据转换回时域。它本质上是撤销之前方法的效果 np.fft.fft。

vector ifft(const vectorc &fft_values)

用法示例：

vector signal = {0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9};

vectorc fft_res = np.fft.fft(signal); //perform fft
Print("np.fft.fft: ",fft_res); //fft results
Print("np.fft.ifft: ",np.fft.ifft(fft_res)); //Original signal

输出：

2025.03.17 11:45:04.537 Numpy test     np.fft.fft: [(4.5,0),(-0.4999999999999999,1.538841768587627),(-0.4999999999999999,0.6881909602355869),(-0.5000000000000002,0.3632712640026804),(-0.5000000000000002,0.1624598481164532),(-0.5,-3.061616997868383E-16),(-0.5000000000000002,-0.1624598481164532),(-0.5000000000000002,-0.3632712640026804),(-0.4999999999999999,-0.6881909602355869),(-0.4999999999999999,-1.538841768587627)]
2025.03.17 11:45:04.537 Numpy test     np.fft.ifft: [-4.440892098500626e-17,0.09999999999999991,0.1999999999999999,0.2999999999999999,0.4,0.5,0.6,0.7,0.8000000000000002,0.9]


线性代数 #

线性代数是数学的一个分支，主要涉及向量、矩阵、和线性变换。它是物理、工程、数据科学等众多领域的基础。

NumPy 提供了 np.linalg 模块，一个专门用于线性代数函数的子模块。它几乎涵盖了线性代数的所有函数，如线性系统求解、本征值/本征向量计算、等等。

以下是 CNumpy 类中实现的一些线性代数函数。


方法

 说明 
matrix inv(const matrix &m)  {  return m.Inv();  }

通过 Jordan-Gauss 方法计算可逆方阵的乘法逆矩阵。

 
double det(const matrix &m)  {  return m.Det();  }

计算可逆方阵的行列式。

 
matrix kron(const matrix &a, const matrix &b) { return a.Kron(b); }
matrix kron(const vector &a, const vector &b) { return a.Kron(b); }
matrix kron(const vector &a, const matrix &b) { return a.Kron(b); }
matrix kron(const matrix &a, const vector &b) { return a.Kron(b); }

它们计算两个矩阵的克罗内克（Kronecker）乘积，矩阵与向量，向量与矩阵，或两个向量。

 
struct eigen_results_struct
  {
   vector eigenvalues;
   matrix eigenvectors;
  };

eigen_results_struct eig(const matrix &m) 
 {
   eigen_results_struct res;
   if (!m.Eig(res.eigenvectors, res.eigenvalues))
      printf("%s failed to calculate eigen vectors and values, error = %d",__FUNCTION__,GetLastError());
   
   return res;
 }

该函数计算方阵的特征值，和方阵的右特征向量。


 
double norm(const matrix &m, ENUM_MATRIX_NORM norm) {  return m.Norm(norm); }
double norm(const vector &v, ENUM_VECTOR_NORM norm) {  return v.Norm(norm); }

返回矩阵或向量范数，更多阅读。

 
svd_results_struct svd(const matrix &m)
  {
    svd_results_struct res;
    if (!m.SVD(res.U, res.V, res.singular_vectors))
      printf("%s failed to calculate the SVD");
    
    return res;
  }
 计算奇异值分解（SVD）。

 
vector solve(const matrix &a, const vector &b) { return a.Solve(b); }

求解一个线性矩阵方程，或线性代数方程组。

 
vector lstsq(const matrix &a, const vector &b) { return a.LstSq(b); }

计算线性代数方程的最小二乘解（针对非方阵、或退化矩阵）。

 
ulong matrix_rank(const matrix &m) { return m.Rank(); }
 该函数计算矩阵的秩，即矩阵中线性独立行或列的数量。它是理解线性方程组解空间的关键概念。 
matrix cholesky(const matrix &m)
{
  vector values = eig(m).eigenvalues;
  
  for (ulong i=0; i<values.Size(); i++)
   {
    if (values[i]<=0)
       {
          printf("%s Failed Matrix is not positive definite",__FUNCTION__);
          return matrix::Zeros(0,0);
       }
   }
   
   matrix L;   
   if (!m.Cholesky(L))
      printf("%s Failed, Error = %d",__FUNCTION__, GetLastError());
      
   return L;
} 
 Cholesky 分解用于将正定矩阵分解到一个较低的三角矩阵，及其转置。 
matrix matrix_power(const matrix &m, uint exponent) { return m.Power(exponent); }
 计算矩阵按特定整数升幂。更正式地说，它计算 ，其中 是矩阵， 是非负整数。

用法示例：

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {    
    //--- Linear algebra
    
    
    matrix m = {{1,1,10},
                {1,0.5,1},
                {1.5,1,0.78}};
                
    Print("np.linalg.inv:\n",np.linalg.inv(m));
    Print("np.linalg.det: ",np.linalg.det(m));
    Print("np.linalg.det: ",np.linalg.kron(m, m));
    Print("np.linalg.eigenvalues:",np.linalg.eig(m).eigenvalues," eigenvectors: ",np.linalg.eig(m).eigenvectors);
    Print("np.linalg.norm: ",np.linalg.norm(m, MATRIX_NORM_P2));
    Print("np.linalg.svd u:\n",np.linalg.svd(m).U, "\nv:\n",np.linalg.svd(m).V);
        
    
    matrix a = {{1,1,10},
                {1,0.5,1},
                {1.5,1,0.78}};
                
    vector b = {1,2,3};
    
    Print("np.linalg.solve ",np.linalg.solve(a, b));
    Print("np.linalg.lstsq: ", np.linalg.lstsq(a, b));
    Print("np.linalg.matrix_rank: ", np.linalg.matrix_rank(a));
    Print("cholesky: ", np.linalg.cholesky(a));
    Print("matrix_power:\n", np.linalg.matrix_power(a, 2));
 }


多项式（幂级数）#

numpy.polynomial 子模块提供了一套强大的工具，用于创建、计算、微分、积分、及操纵多项式。它比使用 numpy.poly1d 进行多项式运算时数值更稳定。

Python 编程语言的 NumPy 函数库中有不同类型的多项式，但在我们的 CNumpy-MQL5 类中，我目前已实现了一个标准幂基数（Polynomial）。

class CPolynomial: protected CNumpy
  {
protected:
   vector m_coeff;
      
   matrix vector21DMatrix(const vector &v)
    {
      matrix res = matrix::Zeros(v.Size(), 1);
      for (ulong r=0; r<v.Size(); r++)
         res[r][0] = v[r];
         
      return res;
    }
    
public:
                     CPolynomial(void);
                     CPolynomial(vector &coefficients); //for loading pre-trained model
                    ~CPolynomial(void);
                    
                     vector fit(const vector &x, const vector &y, int degree);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPolynomial::CPolynomial(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPolynomial::~CPolynomial(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CPolynomial::CPolynomial(vector &coefficients):
m_coeff(coefficients)
 {
  
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CPolynomial::fit(const vector &x, const vector &y, int degree)
 {
   //Constructing the vandermonde matrix
   matrix X = vander(x, degree+1, true);
   
   matrix temp1 =  X.Transpose().MatMul(X);
   matrix temp2 = X.Transpose().MatMul(vector21DMatrix(y));
   
   matrix coef_m = linalg.inv(temp1).MatMul(temp2);
   
   return (this.m_coeff = flatten(coef_m));
 }

用法示例：

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {     
    //--- Polynomial
    
    vector X = {0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9};
    vector y = MathPow(X, 3) + 0.2 * np.random.randn(10);  // Cubic function with noise
    
    CPolynomial poly;
    
    Print("coef: ", poly.fit(X, y, 3));
 }

输出：

2025.03.17 14:01:43.026 Numpy test (US Tech 100,H1)     coef: [-0.1905916844269999,2.3719065699851,-5.625684489899982,4.749058310806731]

此外，在主 CNumpy 类中还有辅助多项式操纵的公共函数，这些函数包括：


函数

 说明 
vector polyadd(const vector &p, const vector &q);
 两个多项式相加，系数长度基于程度对齐。如果一个多项式更短，则在执行加法前填充零值。 
vector polysub(const vector &p, const vector &q);
 两个多项式相减。 
vector polymul(const vector &p, const vector &q);
 利用分配性质将两个多项式相乘，p 的每项乘以 q 的每项，然后将结果相加。
 
vector polyder(const vector &p, int m=1);
 计算多项式 p 的导数，通过应用导数的标准规则计算。每项 变为 。 
vector polyint(const vector &p, int m=1, double k=0.0)
 计算多项式 p 的积分，每项 的积分变为 。该方法允许计算第 m 次积分，积分后加一个积分常数 k。 
double polyval(const vector &p, double x);
 将多项式的项求和，估算在特定值 x 处的多项式，其中每项 计算为 。   
struct polydiv_struct
  {
     vector quotient, 
            remainder;
  };

polydiv_struct polydiv(const vector &p, const vector &q);
 两个多项式相处，并返回商和余数。

用法示例：

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Polynomial utils
    
    vector p = {1,-3, 2};
    vector q = {2,-4, 1};
    
    Print("polyadd: ",np.polyadd(p, q));
    Print("polysub: ",np.polysub(p, q));
    Print("polymul: ",np.polymul(p, q));
    Print("polyder:", np.polyder(p));
    Print("polyint:", np.polyint(p)); // Integral of polynomial
    Print("plyval x=2: ", np.polyval(p, 2)); // Evaluate polynomial at x = 2
    Print("polydiv:", np.polydiv(p, q).quotient," ",np.polydiv(p, q).remainder);
 }


其它常用的 NumPy 方法

所有 NumPy 方法分类很困难，下面列出了一些该类中我们尚未讨论的最实用函数。


方法

 说明 
vector CNumpy::arange(uint stop)
vector CNumpy::arange(int start, int stop, int step)
 第一个函数创建一个向量，其数值范围在指定间隔内。

第二个变体做同样的事情，但参控数值递增的步长。这两个函数对于生成一个从高到低的向量非常实用。
 
vector CNumpy::flatten(const matrix &m)
vector CNumpy::ravel(const matrix &m) { return flatten(m); };
 它们将二维矩阵转换为一维向量。

我们常会遇到或许只有一行一列的矩阵，为了方便使用我们需要将其转换成向量。		 
matrix CNumpy::reshape(const vector &v,uint rows,uint cols)
  将一维向量重塑为行列矩阵（cols）。 
matrix CNumpy::reshape(const matrix &m,uint rows,uint cols)
  将二维矩阵重塑成新的形状（rows 和 cols）。 
matrix CNumpy::expand_dims(const vector &v, uint axis)
  在一维向量上加上一个新轴，效果是将其转换为一个矩阵。 
vector CNumpy::clip(const vector &v,double min,double max)
  将向量中的数值剪裁到指定范围（最小到最大值之间）内，对于减少极端值，并保持向量在期望范围内很实用。 
vector CNumpy::argsort(const vector<T> &v)
  返回数组排序的索引。 
vector CNumpy::sort(const vector<T> &v)
  数组按升序排序。 
vector CNumpy::concat(const vector &v1, const vector &v2);
vector CNumpy::concat(const vector &v1, const vector &v2, const vector &v3);
  将多个向量级联到一个庞大的向量。 
matrix CNumpy::concat(const matrix &m1, const matrix &m2, ENUM_MATRIX_AXIS axis = AXIS_VERT)
当 axis=0 时，矩阵沿行级联（将 m1 与 m2 矩阵水平堆叠）。

当 axis=1 时，矩阵沿列级联（将 m1 与 m2 矩阵垂直堆叠）。		 
matrix CNumpy::concat(const matrix &m, const vector &v, ENUM_MATRIX_AXIS axis = AXIS_VERT)
 如果 axis = 0，附加向量作为新行（仅当其大小与矩阵列数相匹配时）。

如果 axis = 1，附加向量作为新列（仅当其大小与矩阵中的行数相匹配时）。		 
matrix CNumpy::dot(const matrix& a, const matrix& b);
double CNumpy::dot(const vector& a, const vector& b);
matrix CNumpy::dot(const matrix& a, const vector& b);
 它们计算两个矩阵、向量、或矩阵与向量的点积（也称为内积）。 
vector CNumpy::linspace(int start,int stop,uint num,bool endpoint=true)
  它在指定范围（起点，终点）内创建一个均匀间距的数字数组。num = 要生成的样本数量。
endpoint (默认=true)，终点包含在内，若设为 false，则排除终点。		 
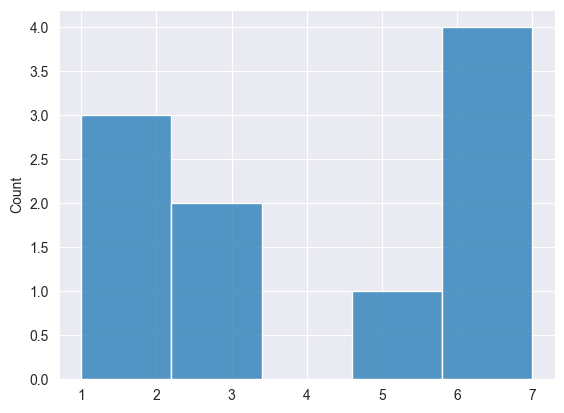
struct unique_struct
 {
   vector unique, count;
 };

unique_struct CNumpy::unique(const vector &v)
  返回向量中的唯一（unique）项，及其出现次数（count）。

用法示例：

#include <MALE5\Numpy\Numpy.mqh>
CNumpy np;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
    //--- Common methods
    
    vector v = {1,2,3,4,5,6,7,8,9,10};  
    
    Print("------------------------------------");  
    Print("np.arange: ",np.arange(10));
    Print("np.arange: ",np.arange(1, 10, 2));
    
    matrix m = {
      {1,2,3,4,5},
      {6,7,8,9,10}
    };
      
    Print("np.flatten: ",np.flatten(m));
    Print("np.ravel: ",np.ravel(m));
    Print("np.reshape: ",np.reshape(v, 5, 2));
    Print("np.reshape: ",np.reshape(m, 2, 3));
   
    Print("np.expnad_dims: ",np.expand_dims(v, 1));
    Print("np.clip: ", np.clip(v, 3, 8));
   
    //--- Sorting
   
    Print("np.argsort: ",np.argsort(v));
    Print("np.sort: ",np.sort(v));
   
    //--- Others
    
    matrix z = {
      {1,2,3},
      {4,5,6},
      {7,8,9},
    };
      
    Print("np.concatenate: ",np.concat(v,  v));
    Print("np.concatenate:\n",np.concat(z,  z, AXIS_HORZ));
    
    vector y = {1,1,1};
    
    Print("np.concatenate:\n",np.concat(z,  y, AXIS_VERT));
    Print("np.dot: ",np.dot(v, v));
    Print("np.dot:\n",np.dot(z, z));
    Print("np.linspace: ",np.linspace(1, 10, 10, true));
    
    Print("np.unique: ",np.unique(v).unique, " count: ",np.unique(v).count);
 }

输出：

NJ      0       16:34:01.702    Numpy test (US Tech 100,H1)     ------------------------------------
PL      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.arange: [0,1,2,3,4,5,6,7,8,9]
LG      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.arange: [1,3,5,7,9]
QR      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.flatten: [1,2,3,4,5,6,7,8,9,10]
QO      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.ravel: [1,2,3,4,5,6,7,8,9,10]
EF      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.reshape: [[1,2]
NL      0       16:34:01.703    Numpy test (US Tech 100,H1)      [3,4]
NK      0       16:34:01.703    Numpy test (US Tech 100,H1)      [5,6]
NQ      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8]
HF      0       16:34:01.703    Numpy test (US Tech 100,H1)      [9,10]]
HD      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.reshape: [[1,2,3]
QD      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6]]
OH      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.expnad_dims: [[1,2,3,4,5,6,7,8,9,10]]
PK      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.clip: [3,3,3,4,5,6,7,8,8,8]
FM      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.argsort: [0,1,2,3,4,5,6,7,8,9]
KD      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.sort: [1,2,3,4,5,6,7,8,9,10]
FQ      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.concatenate: [1,2,3,4,5,6,7,8,9,10,1,2,3,4,5,6,7,8,9,10]
FS      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.concatenate:
PK      0       16:34:01.703    Numpy test (US Tech 100,H1)     [[1,2,3]
DM      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6]
CJ      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8,9]
IS      0       16:34:01.703    Numpy test (US Tech 100,H1)      [1,2,3]
DH      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6]
PL      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8,9]]
FQ      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.concatenate:
CH      0       16:34:01.703    Numpy test (US Tech 100,H1)     [[1,2,3,1]
KN      0       16:34:01.703    Numpy test (US Tech 100,H1)      [4,5,6,1]
KH      0       16:34:01.703    Numpy test (US Tech 100,H1)      [7,8,9,1]]
JR      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.dot: 385.0
PK      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.dot:
JN      0       16:34:01.703    Numpy test (US Tech 100,H1)     [[30,36,42]
OH      0       16:34:01.703    Numpy test (US Tech 100,H1)      [66,81,96]
RN      0       16:34:01.703    Numpy test (US Tech 100,H1)      [102,126,150]]
RI      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.linspace: [1,2,3,4,5,6,7,8,9,10]
MQ      0       16:34:01.703    Numpy test (US Tech 100,H1)     np.unique: [1,2,3,4,5,6,7,8,9,10] count: [1,1,1,1,1,1,1,1,1,1]


从零开始利用 MQL5-NumPy 编写机器学习模型

正如我之前解释的，NumPy 函数库是众多以 Python 编程语言实现的机器学习模型的骨干，因为存在大量方法来帮助计算数组、矩阵、基础数学，甚至线性代数。既然我们已有类似的 MQL5 版本，我们就来尝试从零开始用其实现一个简单的机器学习模型。

以线性回归模型为例。

我在网上找到这段代码，它是一个线性回归模型，在其训练函数使用梯度下降。

import numpy as np
from sklearn.metrics import mean_squared_error, r2_score

class LinearRegression:
    def __init__(self, learning_rate=0.01, epochs=1000):
        self.learning_rate = learning_rate
        self.epochs = epochs
        self.weights = None
        self.bias = None

    def fit(self, X, y):
        """
        Train the Linear Regression model using Gradient Descent.
        X: Input features (numpy array of shape [n_samples, n_features])
        y: Target values (numpy array of shape [n_samples,])
        """
        n_samples, n_features = X.shape
        self.weights = np.zeros(n_features)
        self.bias = 0

        for _ in range(self.epochs):
            y_pred = np.dot(X, self.weights) + self.bias  # Predictions
            
            # Compute Gradients
            dw = (1 / n_samples) * np.dot(X.T, (y_pred - y))
            db = (1 / n_samples) * np.sum(y_pred - y)
            
            # Update Parameters
            self.weights -= self.learning_rate * dw
            self.bias -= self.learning_rate * db

    def predict(self, X):
        """
        Predict output for the given input X.
        """
        return np.dot(X, self.weights) + self.bias

# Example Usage
if __name__ == "__main__":
    # Sample Data (X: Input features, y: Target values)
    X = np.array([[1], [2], [3], [4], [5]])  # Feature
    y = np.array([2, 4, 6, 8, 10])           # Target (y = 2x)

    # Create and Train Model
    model = LinearRegression(learning_rate=0.01, epochs=1000)
    model.fit(X, y)

    # Predictions
    y_pred = model.predict(X)

    # Evaluate Model
    print("Predictions:", y_pred)
    print("MSE:", mean_squared_error(y, y_pred))
    print("R² Score:", r2_score(y, y_pred))

单元输出。

Predictions: [2.06850809 4.04226297 6.01601785 7.98977273 9.96352761]
MSE: 0.0016341843485627612
R² Score: 0.9997957269564297

注意 fit 函数，我们在训练函数里调用数个 NumPy 方法。因我们在 CNumpy 中已有同样的函数，那我们就同样实现 MQL5 版本。

#include <MALE5\Numpy\Numpy.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
    // Sample Data (X: Input features, y: Target values)
    matrix X = {{1}, {2}, {3}, {4}, {5}};
    vector y = {2, 4, 6, 8, 10};

    // Create and Train Model
    CLinearRegression model(0.01, 1000);
    model.fit(X, y);

    // Predictions
    vector y_pred = model.predict(X);

    // Evaluate Model
    Print("Predictions: ", y_pred);
    Print("MSE: ", y_pred.RegressionMetric(y, REGRESSION_MSE));
    Print("R² Score: ", y_pred.RegressionMetric(y_pred, REGRESSION_R2));
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CLinearRegression
  {
protected:

   CNumpy np;
   double m_learning_rate;
   uint m_epochs;
   vector weights;
   double bias;
   
public:
                     CLinearRegression(double learning_rate=0.01, uint epochs=1000);
                    ~CLinearRegression(void);
                    
                    void fit(const matrix &x, const vector &y);
                    vector predict(const matrix &X);
  };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CLinearRegression::CLinearRegression(double learning_rate=0.01, uint epochs=1000):
 m_learning_rate(learning_rate),
 m_epochs(epochs)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
CLinearRegression::~CLinearRegression(void)
 {
 
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CLinearRegression::fit(const matrix &x, const vector &y)
 {
   ulong n_samples = x.Rows(), n_features = x.Cols();
   this.weights = np.zeros((uint)n_features);
   this.bias = 0.0;

//---
   
   for (uint i=0; i<m_epochs; i++)
      {
        matrix temp = np.dot(x, this.weights);
        vector y_pred = np.flatten(temp) + bias;
        
        // Compute Gradients
        
        temp = np.dot(x.Transpose(), (y_pred - y));
                
        vector dw = (1.0 / (double)n_samples) * np.flatten(temp);
        double db = (1.0 / (double)n_samples) * np.sum(y_pred - y);

        // Update Parameters
        
        this.weights -= this.m_learning_rate * dw;
        this.bias -= this.m_learning_rate * db;
      }
  
 }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
vector CLinearRegression::predict(const matrix &X)
 {
   matrix temp = np.dot(X, this.weights);
   
   return np.flatten(temp) + this.bias;
 }

输出：

RD      0       18:15:22.911    Linear regression from scratch (US Tech 100,H1) Predictions: [2.068508094061713,4.042262972785917,6.01601785151012,7.989772730234324,9.963527608958529]
KH      0       18:15:22.911    Linear regression from scratch (US Tech 100,H1) MSE: 0.0016341843485627612
RQ      0       18:15:22.911    Linear regression from scratch (US Tech 100,H1) R² Score: 1.0

太棒了，我们从该模型得到的结果与 Python 代码得到的一样。


现在怎么办？

您已拥有强大的函数库，和一套宝贵的方法，这些都在由 Python 编程语言构建的无数机器学习和统计算法里运用，没什么能阻挡您开发具备复杂计算能力的复杂交易机器人，正如您经常见到的 Python 版本。

立足当下，函数库里大部分函数仍然缺失，在于我要花费数月时间才能把所有内容写下来，故欢迎您自行添加，内里的函数是我经常用到、或者打算用的，因我正在以 MQL5 进行机器学习算法工作。

Python 语法 MQL5 版本有时会让人困惑，如此无需犹豫，把函数名改成适合您的。

平安出行。

请在这个 GitHub 仓储库中为 MQL5 语言的机器学习算法开发做出贡献。


附件表

文件名 说明
Include\Numpy.mqh NumPy MQL5 克隆版，所有 MQL5 版本的 NumPy 方法都能在这个文件里找到。
Scripts\Linear regression from scratch.mq5 一个用 CNumpy 实现的线性回归示例脚本。
Scripts\Numpy test.mq5  出于测试目的，该脚本调用 Numpy.mqh 中的所有方法。

其为本文讨论的所有方法的游乐场。

本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/17469

附加的文件 |
下载ZIP
attachments.zip (16 KB)

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

该作者的其他文章

前往讨论
从基础到中级：事件（一） 从基础到中级：事件（一）
鉴于目前所展示的一切，我认为我们现在可以开始实现某种应用程序，以便直接在图表上运行某些交易品种。然而，首先我们需要讨论一个对初学者来说可能相当困惑的概念。也就是说，在 MQL5 中开发并用于在图表上显示的应用程序的创建方式与我们迄今为止看到的不同。在本文中，我们将开始更好地理解这一点。
市场模拟（第八部分）：套接字（二） 市场模拟（第八部分）：套接字（二）
用套接字实现一些实用功能怎么样？在今天的文章中，我们将开始创建一个迷你聊天室。让我们一起来看看这是怎么做到的 —— 这会非常有趣。请注意，此处提供的代码仅用于教育目的。它不应用于商业目的或现成的应用程序，因为它不提供数据传输安全性，并且可以访问通过套接字传输的内容。
MQL5 简介（第 18 部分）：沃尔夫波浪形态简介 MQL5 简介（第 18 部分）：沃尔夫波浪形态简介
本文详细解释了沃尔夫波浪形态，涵盖了看跌和看涨两种变体。它还分解了用于基于这种高级图表形态识别有效买卖设置的分步逻辑。
利用 MQL5 经济日历进行交易（第 8 部分）：通过智能事件过滤和有针对性的日志来优化新闻驱动策略的回测 利用 MQL5 经济日历进行交易（第 8 部分）：通过智能事件过滤和有针对性的日志来优化新闻驱动策略的回测
在本文中，我们利用智能事件过滤和有针对性的日志来优化我们的经济日历，以便在实时和离线模式下实现更快、更清晰的回测。我们简化了事件处理程序，并将日志集中在关键交易和仪表盘事件上，从而增强了策略的可视化效果。这些改进使得对新闻驱动型交易策略进行顺畅的测试和优化成为可能。