数据科学与机器学习（第24部分）：使用常规AI模型进行外汇时间序列预测

MetaTrader 5 — 交易 | 7 一月 2025, 09:34

353

Omega J Msigwa

内容

什么是时间序列预测?

时间序列预测是利用过去的数据来预测一系列数据点中未来值的过程。这个序列通常是按时间顺序排列的，因此得名时间序列。

时间序列数据中的核心变量

虽然我们的数据中可以有任意数量的特征变量，但任何用于时间序列分析或预测的数据都必须包含这两个变量。

时间

这是一个自变量，代表数据点被观察时的具体时间点。
目标变量

这是你想要根据过去的观察结果和其他潜在因素来预测的值。（例如，每日收盘股价，每小时温度，每分钟网站流量）。

时间序列预测的目标是利用数据中的历史模式和趋势来做出关于未来值的明智预测。

mql5时间序列预测图像

本文假设您已经对ONNX、时间序列预测和轻量梯度提升机（LightGBM）有了基本了解。如果您尚未阅读这些文章，请务必阅读以获取清晰理解。

为何及何时使用时间序列预测？

时间序列分析和预测可用于以下场景：

预测未来值
了解过去的行为（们）
基于过去的未来规划
评估当前的成果

经典与现代 vs 基于时间序列的机器学习模型

与我们之前文章中讨论的线性回归、支持向量机（SVM）、神经网络（NN）等其他经典机器学习模型不同，这些模型旨在确定特征变量之间的关系，并根据这些学习到的关系进行未来预测——时间序列模型则基于先前观察到的值来预测未来值。

这种方法上的差异意味着时间序列模型是专门设计来处理顺序数据中固有的时间依赖性和模式。时间序列预测模型，如ARIMA、SARIMA、指数平滑、循环神经网络（RNN）、长短期记忆网络（LSTM）和门控循环单元（GRU），利用历史数据来预测序列中的未来点，捕捉趋势、季节性和其他时间结构。

下面的流程图展示了用于时间序列预测的各种机器学习模型，

时间序列预测机器学习模型

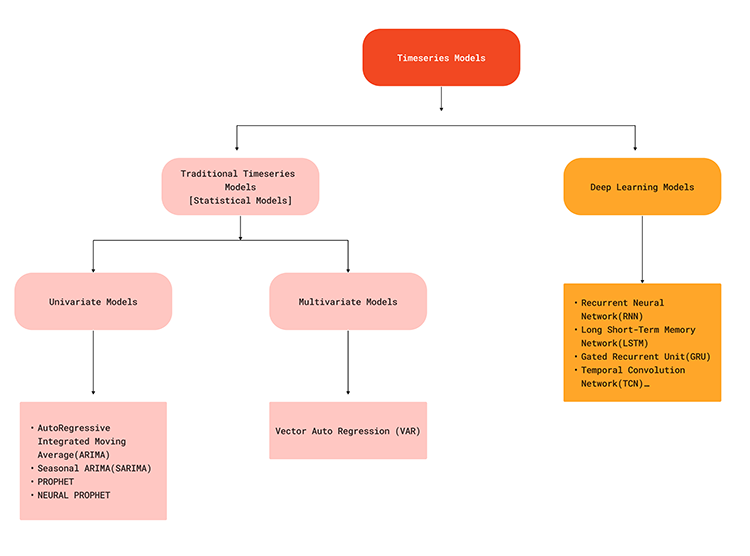
由于时间序列模型能够捕捉数据中的时间依赖性，因此在尝试对外汇市场进行预测时，它们可以提供一种现实的解决方案。我们都知道，当前市场上发生的事情可能是由于刚刚发生或过去某个时刻发生的某些因素所导致的。例如，5分钟前发布的关于EURUSD的新闻可能就是当前价格急剧变化的因素之一。为了更好地理解这一点，让我们看看时间序列预测相对于使用机器学习模型的传统预测的优势。

因素	时间序列预测	传统和现代机器学习预测
时间依赖性	能够捕捉时间模式，因为它们考虑数据点的顺序和随时间变化的依赖性。	传统机器学习模型将数据点视为独立的，这样做忽略了数据中的时间依赖性。
趋势和季节性处理	像ARIMA等一些时间序列模型具有处理趋势和季节性的内置组件。	需要手动提取和构建特征来捕捉趋势和季节性。
自相关性	像ARIMA和LSTM这样的模型可以考虑数据中的自相关性。	它们假设每个特征都是独立的，因此除非在特征中明确建模，否则它们可能无法考虑自相关性。
模型复杂性	时间序列模型是为序列数据设计的，为这类任务提供了更自然的契合。	传统模型可能需要特征工程来适当处理序列数据。这增加了过程的复杂性。
时间层次结构	可以自然地扩展到层次时间序列预测（例如，月、周）。	传统模型在没有额外工程的情况下，可能难以在多个时间尺度上进行预测。
预测性能	由于考虑了顺序，通常在时间相关任务上具有更好的预测性能。	在时间相关任务上可能表现不佳。
计算效率	时间序列模型可以高效地用新数据进行增量更新。	传统模型可能需要完整的重新训练，这对于新数据来说计算上更为密集。
可解释的趋势和季节性	像ARIMA这样的模型提供了可解释的趋势和季节性构成因素。	需要从构建的特征中额外步骤来解释趋势和季节性。

尽管默认情况下不擅长时间序列预测，但LightGBM、XGBoost、CatBoost等经典和现代机器学习模型在提供正确信息的情况下仍可用于时间序列预测。实现这一点的关键在于特征工程。

时间序列预测中的特征工程

在时间序列预测中，目标是构建新特征并准备现有特征，使它们包含时间序列的重要信息/组件，如：趋势、季节性、循环模式、平稳性、自相关和部分自相关等。

在为时间序列问题构建新特征时，您可以考虑许多方面，以下是其中一些：

01：滞后特征

在经典机器学习的数据中，我们通常收集当前条目的开盘价、最高价、最低价、收盘价以及一些其他数据。这包含每个特定条目上的当前信息，并不提供关于该特定条目之前发生了什么的信息。

通过向我们的数据引入滞后特征，我们确保捕捉到先前条目中的时间依赖性，这肯定与当前条目的价格有关。

MQL5

//--- getting Open, high, low and close prices
   
   ohlc_struct OHLC;
   
   OHLC.AddCopyRates(Symbol(), timeframe, start_bar, bars);
   time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars);
   
//--- Getting the lagged values of Open, High, low and close prices

   ohlc_struct  lag_1;
   lag_1.AddCopyRates(Symbol(), timeframe, start_bar+1, bars);
   
   ohlc_struct  lag_2;
   lag_2.AddCopyRates(Symbol(), timeframe, start_bar+2, bars);
   
   ohlc_struct  lag_3;
   lag_3.AddCopyRates(Symbol(), timeframe, start_bar+3, bars);

在上述示例中，我们仅获得了三个滞后值。由于我们是每天收集这些数据，所以在1000个数据条中，我们得到了前三天的信息。

通过将MqlRates复制到从start_bar+1开始的向量中，我们得到的bar数据会比从start_bar开始复制汇率数据早一个bar的数据。这有时可能会让人感到困惑，请参考https://www.mql5.com/en/docs/series

MQL5

input int bars = 1000;
input ENUM_TIMEFRAMES timeframe = PERIOD_D1;
input uint start_bar = 2; //StartBar|Must be >= 1

struct ohlc_struct 
{
   vector open;
   vector high;
   vector low;
   vector close;
   
   matrix MATRIX; //this stores all the vectors all-together
   
   void AddCopyRates(string symbol, ENUM_TIMEFRAMES tf, ulong start, ulong size)
    {
      open.CopyRates(symbol, tf, COPY_RATES_OPEN, start, size); 
      high.CopyRates(symbol, tf, COPY_RATES_HIGH, start, size); 
      low.CopyRates(symbol, tf, COPY_RATES_LOW, start, size); 
      close.CopyRates(symbol, tf, COPY_RATES_CLOSE, start, size); 
      
      this.MATRIX.Resize(open.Size(), 4); //we resize it to match one of the vector since all vectors are of the same size
      
      this.MATRIX.Col(open, 0);
      this.MATRIX.Col(high, 1);
      this.MATRIX.Col(low, 2);
      this.MATRIX.Col(close, 3);
    }
};

02: 滚动统计

滚动统计，如均值、标准差以及此类的其他统计量，有助于概括一个时间窗口内的最新趋势和波动性。这时，一些指标就发挥作用了，比如某一段时间的移动平均值、给定时间的标准差等。

int ma_handle = iMA(Symbol(),timeframe,30,0,MODE_SMA,PRICE_WEIGHTED); //The Moving averaege for 30 days
int stddev = iStdDev(Symbol(), timeframe, 7,0,MODE_SMA,PRICE_WEIGHTED); //The standard deviation for 7 days
   
vector SMA_BUFF, STDDEV_BUFF;
SMA_BUFF.CopyIndicatorBuffer(ma_handle,0,start_bar, bars);
STDDEV_BUFF.CopyIndicatorBuffer(stddev, 0, start_bar, bars);

这些滚动统计量提供了市场如何变化的更广泛图景，可能捕捉到在滞后特征中不明显的长期波动。

03: 日期时间特征

如前所述，时间序列数据包含时间变量，但仅有一个日期时间变量并不会有多大帮助，我们需要提取其特征。

我们知道外汇市场在特定时间展现出一些模式或以特定方式运行。例如：周五通常交易活动不多，而在有新闻事件的当天市场会波动。此外，在某些月份交易活动可能会变好或变差，同样的情况也适用于某些年份。例如：在某些国家（如美国）的选举年期间。

通过引入日期时间特征，我们明确地捕捉到了季节性模式，这将使我们的模型能够根据一年中的时间、特定的一天或月份等调整预测。

让我们在MQL5中收集日期时间特征：

vector time_vector; //we want to add time vector 
time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars); //copy the time in seconds


ulong size = time_vector.Size(); 
vector DAY(size), DAYOFWEEK(size), DAYOFYEAR(size), MONTH(size);

MqlDateTime time_struct;
string time = "";
for (ulong i=0; i<size; i++)
  {
    time = (string)datetime(time_vector[i]); //converting the data from seconds to date then to string
    TimeToStruct((datetime)StringToTime(time), time_struct); //convering the string time to date then assigning them to a structure
    
    DAY[i] = time_struct.day;
    DAYOFWEEK[i] = time_struct.day_of_week;
    DAYOFYEAR[i] = time_struct.day_of_year;
    MONTH[i] = time_struct.mon;
  }

04: 差分

对序列在季节性滞后项上进行差分可以去除数据中的季节性模式，从而实现平稳性，这通常是某些模型的要求。

让我们尝试从当前价格开始，在lag1项上进行差分。

MQL5

vector diff_lag_1_open = OHLC.open - lag_1.open;
vector diff_lag_1_high = OHLC.high - lag_1.high;
vector diff_lag_1_low = OHLC.low - lag_1.low;
vector diff_lag_1_close = OHLC.close - lag_1.close;

你可以根据需要差分任意多个滞后项，不仅仅局限于滞后1项。

到目前为止，我们已经有了26个自变量/特征，这对于我们的自变量来说已经足够了。由于我们正在解决一个回归问题，让我们收集收盘价作为我们的最终目标变量。

vector TARGET_CLOSE;
TARGET_CLOSE.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar-1, bars); //one bar forward

你可以自由地根据你的问题创建更多特征，考虑一些我们下面没有提到的其他方面。

05：外部变量（外在特征）

天气数据：尝试看看它是否有帮助。
经济指标：包括国内生产总值（GDP）、失业率等，用于金融预测。

06: 傅里叶和小波变换

使用傅里叶或小波变换来提取频域中的周期性模式和趋势。

07: 目标编码

你可以基于目标变量在不同时间段上的聚合统计量（均值、中位数）来创建特征。

最终数据集有27列：

时间序列预测数据集

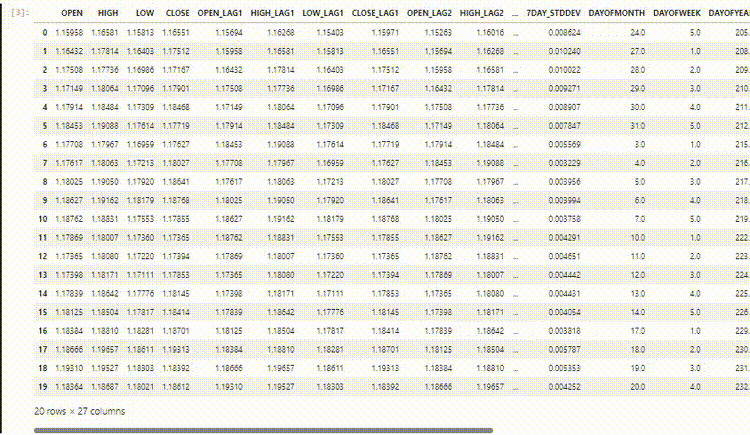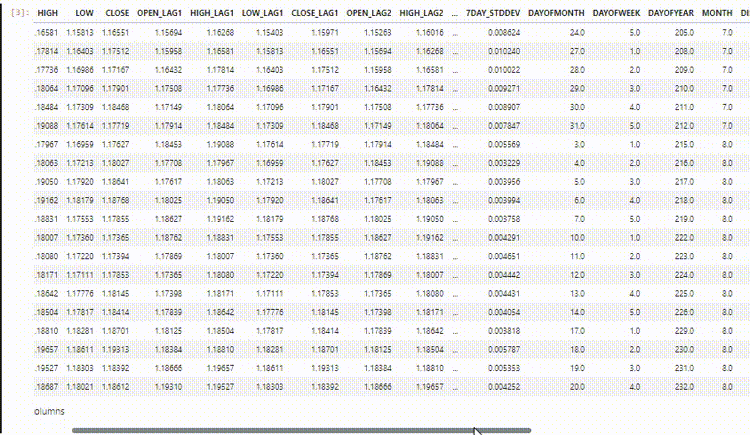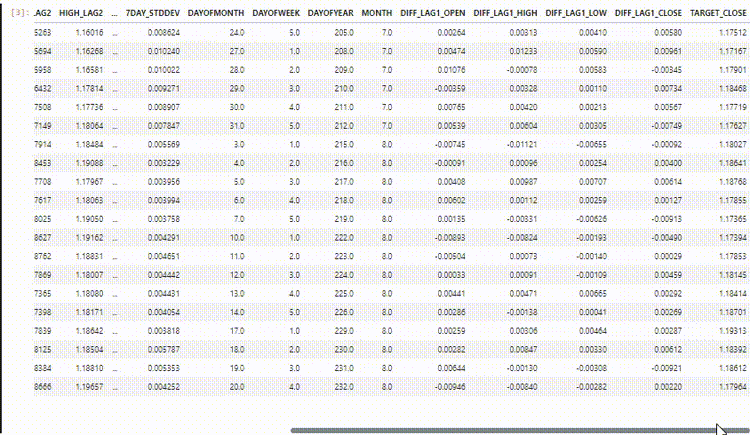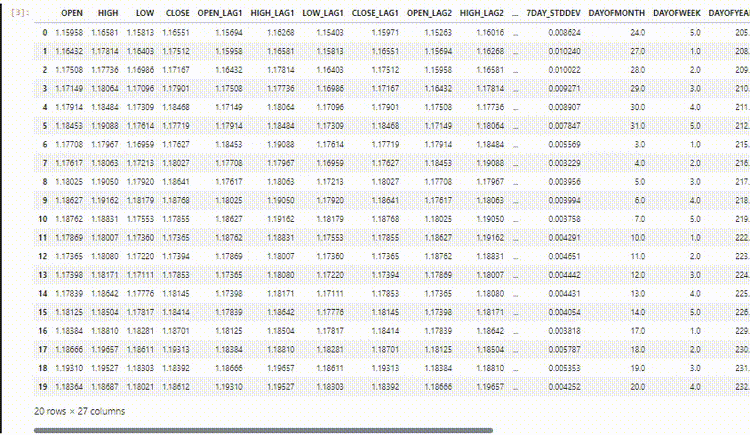
训练LightGBM回归模型

既然我们已经有了所有需要的数据，让我们转向Python方面的工作。

我们可以先从将数据分为训练样本和测试样本开始。

Python：

X = df.drop(columns=["TARGET_CLOSE"])
Y = df["TARGET_CLOSE"]

train_size = 0.7 #configure train size

train_size = round(train_size*df.shape[0])

x_train = X.iloc[:train_size,:]
x_test = X.iloc[train_size:, :]

y_train = Y.iloc[:train_size]
y_test = Y.iloc[train_size:]

print(f"x_train_size{x_train.shape}\nx_test_size{x_test.shape}\n\ny_train{y_train.shape}\ny_test{y_test.shape}")

结果

x_train_size(700, 26)
x_test_size(300, 26)

y_train(700,)
y_test(300,)

让我们将模型拟合到训练数据上。

model = lgb.LGBMRegressor(**params)
model.fit(x_train, y_train)

接下来，我们将测试训练好的模型，并绘制预测结果以及R²分数（r2_score）。

Python：

from sklearn.metrics import r2_score

test_pred = model.predict(x_test)

accuracy = r2_score(y_test, test_pred)

#showing actual test values and predictions

plt.figure(figsize=(8, 6))  
plt.plot(y_test, label='Actual Values')
plt.plot(test_pred, label='Predicted Values')
plt.xlabel('Index')
plt.ylabel('Values')
plt.title('Actual vs. Predicted Values')
plt.legend(loc="lower center")

# Add R-squared (accuracy) score in a corner
plt.text(0.05, 0.95, f"LightGBM (Accuracy): {accuracy:.4f}", ha='left', va='top', transform=plt.gca().transAxes, fontsize=10, bbox=dict(boxstyle='round', facecolor='white', alpha=0.7))

plt.grid(True)

plt.savefig("LighGBM Test plot")
plt.show()

输出

LightGBM测试绘图

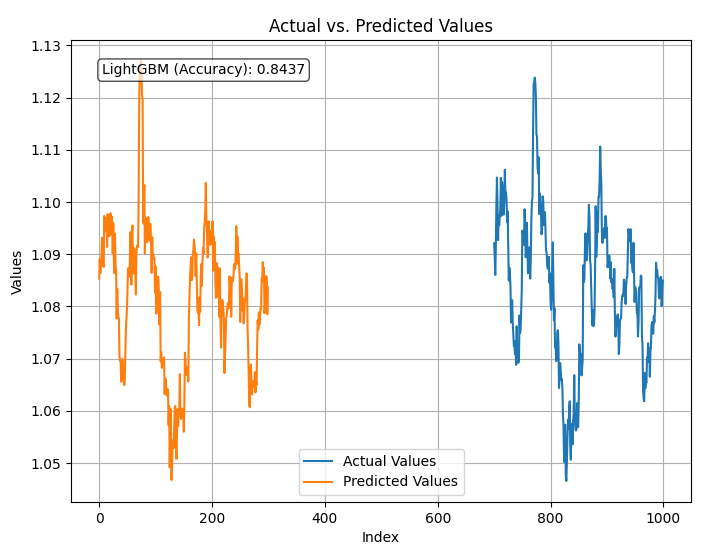
该模型在使用所给全部数据预测收盘价时的准确率为84%，这似乎是一个不错的准确率。然而，为了进行更深入的分析和模型改进，我们需要进一步检查我们的变量。

使用LightGBM内置的特征重要性绘图技术，下面是特征重要性的图表。

Python：

# Plot feature importance using Gain
lgb.plot_importance(model, importance_type="gain", figsize=(8,6), title="LightGBM Feature Importance (Gain)")

plt.tight_layout()

plt.savefig("LighGBM feature importance(Gain)")
plt.show()

输出：

时间序列OHLC（Open-High-Low-Close，即开盘价-最高价-最低价-收盘价）特征重要性

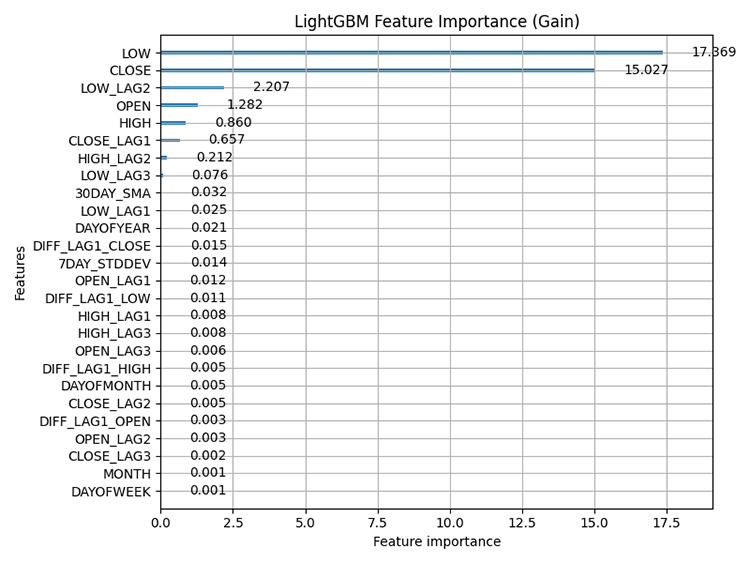
特征重要性：指的是评估数据集中每个特征（变量）对模型预测结果的相对贡献的技术。它有助于我们了解哪些特征对模型的预测结果影响最大。

重要的是要知道，基于树的方法（如LightGBM和XGBoost）计算特征重要性的方式与非基于树的方法不同。它们考虑的是特征在树中用于分裂决策的频率，以及这些分裂对最终预测的影响。

另外，你可以使用SHAP来检查特征的重要性。

Python：

explainer = shap.TreeExplainer(model)
shap_values = explainer(x_train)  

shap.summary_plot(shap_values, x_train, max_display=len(x_train.columns), show=False)  # Show all features

# Adjust layout and set figure size
plt.subplots_adjust(left=0.12, bottom=0.1, right=0.9, top=0.9)  
plt.gcf().set_size_inches(6, 8) 
plt.tight_layout()

plt.savefig("SHAP_Feature_Importance_Summary_Plot.png")
plt.show()

输出：

SHAP特征重要性在时间序列数据中的应用

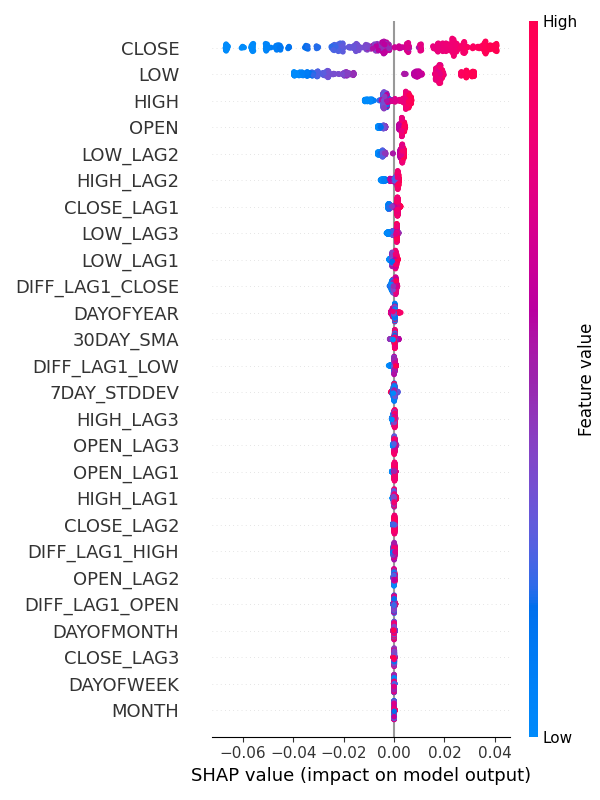
从特征重要性图中可以明显看出，像“DAYOFWEEK”（星期几）、“MONTH”（月份）、“DAYOFMONTH”（月中的日期）和“DAYOFYEAR”（年中的日期）这样用于捕捉季节性模式的变量，对模型预测的贡献最小。

奇怪的是，根据扩展迪基-富勒（Augmented Dickey-Fuller，ADF）检验的结果，所有这些变量都是平稳的。

扩展迪基-富勒（ADF）检验

这是一个统计检验，用于确定时间序列数据集是否为平稳的。平稳性是许多时间序列预测和分析方法至关重要的属性。

平稳变量或平稳数据集指的是统计属性（均值、方差、自相关）随时间保持不变的序列。以股市为例。OHLC（开盘价、最高价、最低价、收盘价）值的均值可能会随时间急剧增加或减少，使得这些值在大多数情况下是非平稳的。然而，它们的回报，如最高价和最低价之差的均值或方差，则随时间保持平稳。

我对我们拥有的整个数据集进行了这个检验。

from statsmodels.tsa.stattools import adfuller

def adf_test(series, signif=0.05):
  """
  Performs the ADF test on a pandas Series and interprets the results.

  Args:
      series: The pandas Series containing the time series data.
      signif: Significance level for the test (default: 0.05).

  Returns:
      A dictionary containing the test statistic, p-value, used lags,
      critical values, and interpretation of stationarity.
  """
  dftest = adfuller(series, autolag='AIC')
  adf_stat = dftest[0]  # Access test statistic
  pvalue = dftest[1]  # Access p-value
  usedlag = dftest[2]  # Access used lags
  critical_values = dftest[4]  # Access critical values

  interpretation = 'Stationary' if pvalue < signif else 'Non-Stationary'
  result = {'Statistic': adf_stat, 'p-value': pvalue, 'Used Lags': usedlag,
            'Critical Values': critical_values, 'Interpretation': interpretation}
  return result

for col in df.columns:
  adf_results = adf_test(df[col], signif=0.05)
  print(f"ADF Results for column {col}:\n {adf_results}")

在27个变量中，仅有9个变量被检测为平稳。这些变量是：

7DAY_STDDEV
DAYOFMONTH
DAYOFWEEK
DAYOFYEAR
MONTH
DIFF_LAG1_OPEN
DIFF_LAG1_HIGH
DIFF_LAG1_LOW
DIFF_LAG1_CLOSE

要轻松判断变量是否为平稳的，你可以简单地查看其分布图。数据如果紧密围绕均值分布，则很可能是平稳数据。

平稳vs非平稳

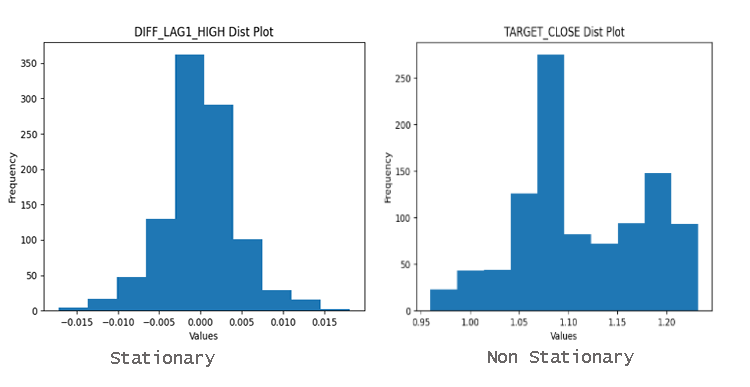
为什么平稳性很重要？

时间序列分析和预测中使用的许多统计方法都假设数据是平稳的。如果时间序列是非平稳的，这些方法可能会产生误导性或不准确的结果。

想象一下，如果股票价格持续上涨，试图预测未来的股票价格会是多么困难。时间序列模型将无法捕捉到潜在的趋势。

传统的甚至是 所谓的现代机器学习模型 ，如我们使用的LightGBM，都有能力处理特征之间的非线性关系，从而使它们受数据中平稳性的影响较小。该模型的特征重要性已经清楚地表明，对我们模型最重要的特征是非平稳的OHLC（开盘价、最高价、最低价、收盘价）变量。

然而，这并不意味着像星期几这样的变量对模型没有影响。在我看来，特征重要性只是整个故事的一部分，仍然需要领域知识。

仅仅因为这个变量的排名较低，就没有必要将其删除，因为我相信它会影响EURUSD（欧元兑美元汇率）。

预测平稳的目标变量

在时间序列预测中，平稳的目标变量可以提高许多机器学习模型的性能，因为平稳数据随时间具有恒定的（均值、方差、自相关）。正如你所知，预测市场下一个时间段的走势是困难的，但预测下一个走势的点数或点位则相对容易。

如果我们能够预测下一个时间段将产生的点数，我们就可以利用这一点来设定交易目标（止损和获利）。

为了实现这一点，我们需要找到一阶差分，即通过从下一个收盘价中减去前一个收盘价来计算。

Python：

Y = df["TARGET_CLOSE"] - df["CLOSE"] #first order differencing

通过计算下一个收盘价与前一个收盘价之间的差分，我们最终得到一个平稳变量。

adf_results = adf_test(Y,signif=0.05)

print(f"ADF Results:\n {adf_results}")

结果：

ADF Results: {'Statistic': -23.37891429248752, 'p-value': 0.0, 'Used Lags': 1, 'Critical Values': {'1%': -3.4369193380671, '5%': -2.864440383452517, '10%': -2.56831430323573}, 'Interpretation': 'Stationary'}

在将回归模型拟合到新的平稳目标变量上，并在测试数据集上评估其性能后，以下是结果。

LightGBM时间序列预测平稳目标

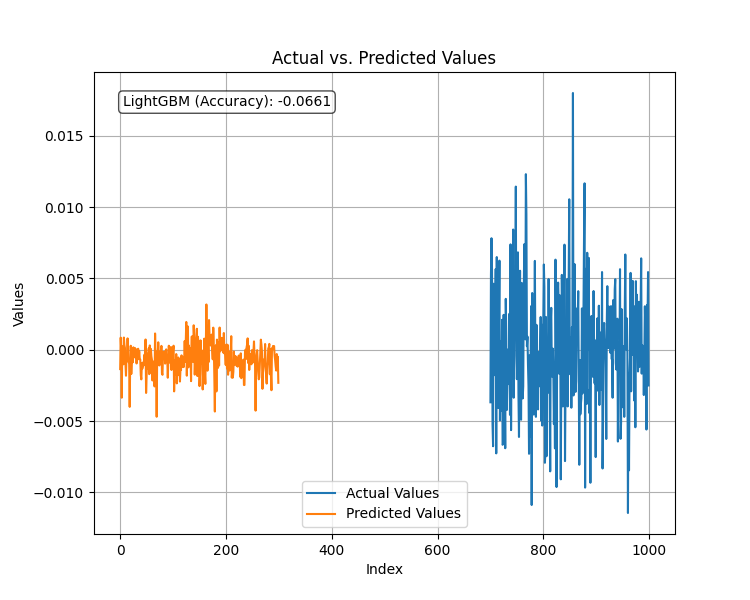
当目标变量是平稳的时，模型的性能非常糟糕。在机器学习中，这种情况可能由多种因素导致，但就目前而言，我们得出的结论是LightGBM在处理平稳目标变量时表现不佳。我们将继续使用为预测目标收盘价而生成的回归模型。

拥有一个预测连续收盘价值的回归模型并不像拥有一个预测交易信号（如买入或卖出）的模型那样有用。为了实现这一点，我们需要为预测交易信号构建另一个模型。

构建LightGBM分类模型

为了构建分类器模型，我们需要将目标变量准备为二进制目标变量，其中1表示买入信号，0表示卖出信号。

Python：

Y = []
target_open = df["TARGET_OPEN"]
target_close = df["TARGET_CLOSE"]

for i in range(len(target_open)):
    if target_close[i] > target_open[i]: # if the candle closed above where it opened thats a buy signal
        Y.append(1)
    else: #otherwise it is a sell signal
        Y.append(0)

# split Y into irrespective training and testing samples 

y_train = Y[:train_size]
y_test = Y[train_size:]

我使用Pipeline（管道）结合了StandardScaler（标准化缩放）技术对LightGBM模型进行了训练。

Python：

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

params = {
    'boosting_type': 'gbdt',  # Gradient Boosting Decision Tree
    'objective': 'binary',  # For binary classification (use 'regression' for regression tasks)
    'metric': ['auc','binary_logloss'],  # Evaluation metric
    'num_leaves': 25,  # Number of leaves in one tree
    'n_estimators' : 100, # number of trees
    'max_depth': 5,
    'learning_rate': 0.05,  # Learning rate
    'feature_fraction': 0.9  # Fraction of features to be used for each boosting round
}

pipe = Pipeline([
    ("scaler", StandardScaler()),
    ("lgbm", lgb.LGBMClassifier(**params))
])

# Fit the pipeline to the training data
pipe.fit(x_train, y_train)

测试结果的总体准确率仅为53%，这并不太令人惊讶。

分类报告：

Classification Report
               precision    recall  f1-score   support

           0       0.49      0.79      0.61       139
           1       0.62      0.30      0.40       161

    accuracy                           0.53       300
   macro avg       0.56      0.54      0.51       300
weighted avg       0.56      0.53      0.50       300

混淆矩阵

LightGBM中的混淆矩阵

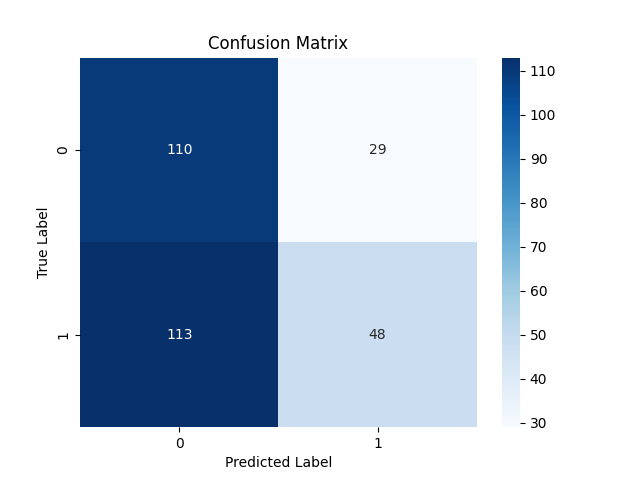
将LightGBM分类模型保存到ONNX

就像我们之前做过的那样，将LightGBM模型保存到ONNX格式是非常直接的，并且只需要几行代码。

import onnxmltools
from onnxmltools.convert import convert_lightgbm
import onnxmltools.convert.common.data_types
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx import convert_sklearn, update_registered_converter

from skl2onnx.common.shape_calculator import (
    calculate_linear_classifier_output_shapes,
)  # noqa

from onnxmltools.convert.lightgbm.operator_converters.LightGbm import (
    convert_lightgbm,
)  # noqa

# registering onnx converter

update_registered_converter(
    lgb.LGBMClassifier,
    "GBMClassifier",
    calculate_linear_classifier_output_shapes,
    convert_lightgbm,
    options={"nocl": [False], "zipmap": [True, False, "columns"]},
)

# Final LightGBM conversion to ONNX

model_onnx = convert_sklearn(
    pipe,
    "pipeline_lightgbm",
    [("input", FloatTensorType([None, x_train.shape[1]]))],
    target_opset={"": 12, "ai.onnx.ml": 2},
)

# And save.
with open("lightgbm.Timeseries Forecasting.D1.onnx", "wb") as f:
    f.write(model_onnx.SerializeToString())

将所有内容整合到EA中

既然我们已经将机器学习模型保存为ONNX格式，我们就可以直接在MetaTrader 5中的EA里嵌入它，并使用LightGBM分类器进行时间序列预测。

MQL5

#resource "\\Files\\lightgbm.Timeseries Forecasting.D1.onnx" as uchar lightgbm_onnx[] //load the saved onnx file 
#include <MALE5\LightGBM\LightGBM.mqh>
CLightGBM lgb;

利用在前文中构建的LightGBM类，我能够初始化模型并使用它进行预测。

int OnInit()
  {
//---
   
   if (!lgb.Init(lightgbm_onnx)) //Initialize the LightGBM model
     return INIT_FAILED;
   
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
    
   if (NewBar()) //Trade at the opening of a new candle
    {
     vector input_vector = input_data(); 
     long signal = lgb.predict_bin(input_vector);
     
   //---
     
      MqlTick ticks;
      SymbolInfoTick(Symbol(), ticks);
      
      if (signal==1) //if the signal is bullish
       {
          if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions
           {
             if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, ticks.bid-stoploss*Point(), ticks.ask+takeprofit*Point())) //Open a buy trade
               printf("Failed to open a buy position err=%d",GetLastError());
           }
       }
      else if (signal==0) //Bearish signal
        {
          if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions
            if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, ticks.ask+stoploss*Point(), ticks.bid-takeprofit*Point())) //open a sell trade
               printf("Failed to open a sell position err=%d",GetLastError());
        }
      else //There was an error
        return;
    }
  }

input_data() 函数负责以类似于脚本 Feature engineering Timeseries forecasting.mq5 中收集和存储在CSV文件中的数据的方式来汇总数据。

在策略测试器中测试模型。

最后，我们可以在交易环境中测试模型。由于数据是在日线时间框架上收集的，因此最好在低时间框架上进行测试，以避免在寻找新开盘时的交易信号时出现“市场已关闭的报错”。我们还可以将建模类型设置为开盘价，以加快测试速度。

测试器设置

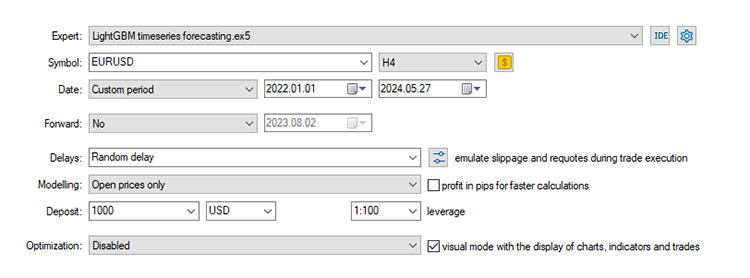
在止损为500点、止盈为700点的情况下，该EA大约有51%的时间能够做出正确的预测。

MetaTrader 5策略测试器报告

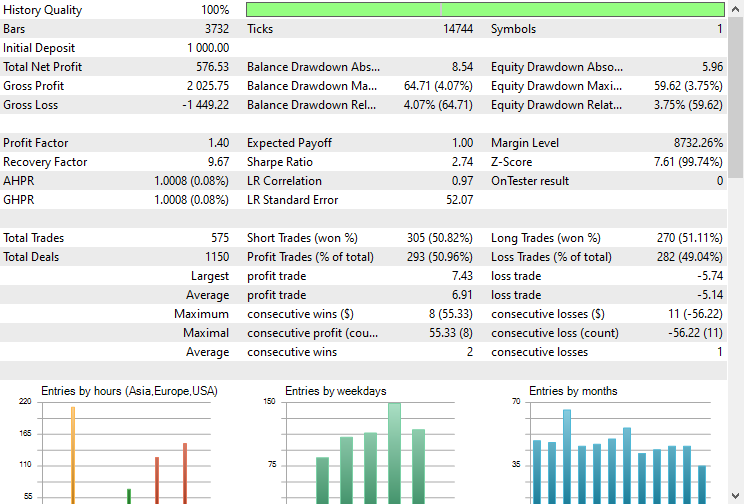
资金余额/净值曲线也同样令人印象深刻。

MetaTrader 5 测试器图表

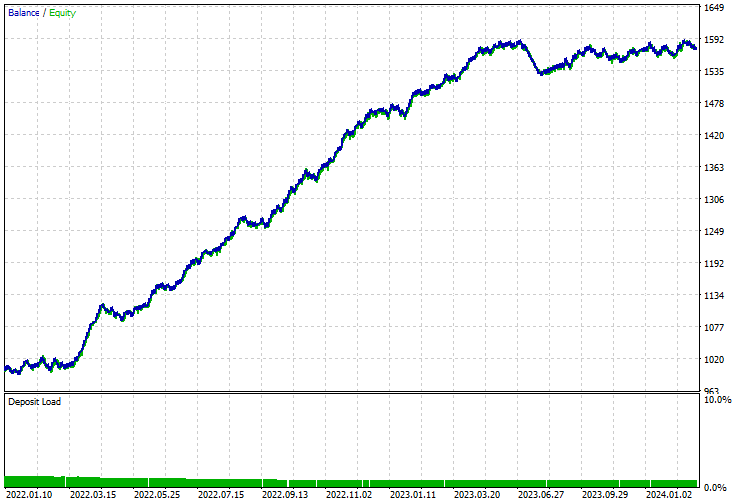
使用经典和现代机器学习模型进行时间序列预测的优势

使用非时间序列机器学习模型进行时间序列预测具有多个优势。以下是一些关键优势：

1. 特征工程的灵活性

经典机器学习模型允许进行广泛的特征工程，可以利用这一点来包含各种外部变量和派生特征。您可以利用人类智慧手动分析和整合您认为有用的所有数据，包括我们在本文中提到的滞后和滚动统计等复杂特征。

2. 处理非平稳性

您无需通过差分使序列平稳，而是可以直接将趋势和季节性作为特征包含在内，模型将毫无问题地学习这些模式。

3. 无需对数据分布做假设

许多经典时间序列模型（如ARIMA）假设数据遵循特定的统计分布。而另一方面，经典和现代机器学习模型在数据分布方面更加灵活。

决策树、随机森林和梯度提升（包括LightGBM）等模型不对数据的任何特定分布做假设。

4. 可扩展性

决策树、随机森林和梯度提升（包括LightGBM）等模型不对数据的任何特定分布做假设。

5. 复杂的交互

经典机器学习模型能够捕捉特征和目标变量之间复杂、非线性的关系。

6. 对缺失数据的鲁棒性

与传统时间序列模型相比，机器学习模型通常具有更好的处理缺失数据的机制。

7. 集成方法

您可以轻松地使用集成方法，如袋装（bagging）、提升（boosting）和堆叠（stacking），通过结合多个模型来提高预测性能和鲁棒性。

8. 易用性和集成

经典机器学习模型通常更易于使用，并配备了丰富的库和工具用于实现、可视化和评估。

Scikit-learn、LightGBM和XGBoost等库为构建、调整和评估这些模型提供了全面的工具。

总结

经典和现代机器学习模型都可以毫无问题地用于时间序列分析和预测，并且如本文所述，在拥有正确信息、调整和流程的情况下，它们的性能可以超越时间序列模型。我决定以LightGBM为例，但同样，任何经典或现代的机器学习模型，如支持向量机（SVM）、线性回归、朴素贝叶斯、XGBoost等，都可以应用。

祝好。

在GitHub的这个仓库中，本系列文章将追踪机器学习模型的发展情况，并深入讨论更多内容。

附件表格

文件名	文件类型	说明和用法
LightGBM timeseries forecasting.mq5	EA	用于加载ONNX模型并在MetaTrader 5中测试最终交易策略的自动交易系统。
lightgbm.Timeseries Forecasting.D1.onnx	ONNX	ONNX格式的LightGBM模型。
LightGBM.mqh	包含函数库	包含用于加载ONNX模型格式并将其部署到本地MQL5语言环境中的代码。
Feature engineering Timeseries forecasting.mq5	MQL5 脚本	这是一个脚本，用于收集并处理所有数据，以便进行时间序列分析和预测。
forex-timeseries-forecasting-lightgbm.ipynb	Python脚本(Jupyter Notebook)	本文中讨论的所有Python代码都可以在这个笔记本中找到。