
Машинное обучение и Data Science (Часть 03): Матричная регрессия
После долгого периода проб и ошибок, наконец, решена загадка множественной динамической регрессии... Продолжить чтение.
Если вы обратили внимание на две предыдущие статьи, то наверняка заметите, что большая проблема, с которой я столкнулся, — это программирование моделей, которые могут обрабатывать больше независимых переменных. Здесь я имею в виду динамическую обработку большего количества входных данных, потому что при создании стратегий мы имеем дело с сотнями данных. Именно поэтому нужно быть уверенным, что модели справятся с этим требованием.
Матрица
Если вы пропустили уроки математики, матрица представляет собой прямоугольный массив или таблицу чисел или других математических объектов, расположенных в строках и столбцах, которые используются для представления математического объекта или свойства такого объекта.
Например:
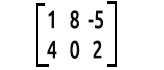
То, как мы читаем матрицы, это строки х колонки. Выше это матрица 2x3, что означает, что в ней 2 строки и 3 столбца.
Несомненно матрицы играют огромную роль в том, как современные компьютеры обрабатывают информацию и вычисляют большие числа. Основная причина заключается в том, что данные в матрице хранятся в виде массива, который компьютеры могут читать и обрабатывать. Итак, давайте посмотрим на их применение в машинном обучении.
Линейная регрессия
Матрицы позволяют выполнять вычисления линейной алгебры. Изучение матриц является большим разделом линейной алгебры. Поэтому матрицы можно использовать для создания моделей линейной регрессии.
Как мы все знаем, уравнение прямой выглядит так:
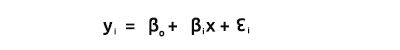
где ∈ представляет собой ошибку, а Bo и Bi — коэффициент пересечения y и коэффициент наклона, соответственно.
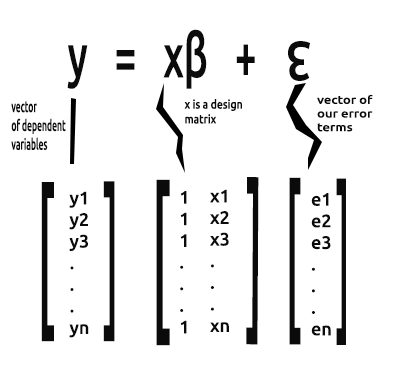
С этого момента нас будет интересовать векторная форма уравнения, вот она:
Это формула простой линейной регрессии в матричной форме.
В простой линейной модели (и других регрессионных моделях) мы обычно ищем коэффициенты наклона/обычных оценок методом наименьших квадратов.
Вектор Beta — это вектор, содержащий значения бета.
Bo и B1, как объяснялось в уравнении:
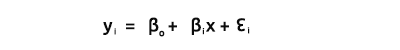
Нам нужно найти коэффициенты, поскольку они очень важны при построении модели.
Формула для оценок моделей в векторной форме:
Это очень важная формула, ее обязательно надо заучить.
Скоро мы посмотрим, как найти элементы по формуле.
Результатом произведения xTx будет симметричная матрицу, поскольку количество столбцов в xT равно количеству строк в x. Чуть позже увидим это на примере.
Как было сказано ранее,
x также называют матрицей дизайна. Вот как выглядит такая матрица:
Матрица дизайна
Как видите, в самом первом столбце мы поместили только значения 1 до конца наших строк в матричном массиве. Это первый шаг к подготовке данных для матричной регрессии. Преимущества именно этого шага вы увидите дальше по мере продвижения в вычислениях.
Этот процесс выполняем в функции Init() нашей библиотеки.
void CSimpleMatLinearRegression::Init(double &x[],double &y[], bool debugmode=true) { ArrayResize(Betas,2); //поскольку это простая линейная регрессия, у нас только две переменные x и y if (ArraySize(x) != ArraySize(y)) Alert("Обнаружено различие между количеством независимых переменных и зависимых переменных \n Расчеты могут оказаться неверными"); m_rowsize = ArraySize(x); ArrayResize(m_xvalues,m_rowsize+m_rowsize); //добавляем место размером в строку для заполненных значений ArrayFill(m_xvalues,0,m_rowsize,1); //заполняем первую строку единицами вот где выполняется операция ArrayCopy(m_xvalues,x,m_rowsize,0,WHOLE_ARRAY); //добавляем значения x в массив, начиная с места, где закончились заполненные значения ArrayCopy(m_yvalues,y); m_debug=debugmode; }
Здесь мы заполняем значения матрицы дизайна. Вывод показан ниже. Обратите внимание на строку, где заполненные значения единиц и начинаются рассчитанные значения x.
[ 0] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 21] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
........
........
[ 693] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 714] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
[ 735] 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 4173.8 4179.2 4182.7 4185.8 4180.8 4174.6 4174.9 4170.8 4182.2 4208.4 4247.1 4217.4
[ 756] 4225.9 4211.2 4244.1 4249.0 4228.3 4230.6 4235.9 4227.0 4225.0 4219.7 4216.2 4225.9 4229.9 4232.8 4226.4 4206.9 4204.6 4234.7 4240.7 4243.4 4247.7
........
........
[1449] 4436.4 4442.2 4439.5 4442.5 4436.2 4423.6 4416.8 4419.6 4427.0 4431.7 4372.7 4374.6 4357.9 4381.6 4345.8 4296.8 4321.0 4284.6 4310.9 4318.1 4328.0
[1470] 4334.0 4352.3 4350.6 4354.0 4340.1 4347.5 4361.3 4345.9 4346.5 4342.8 4351.7 4326.0 4323.2 4332.7 4352.5 4401.9 4405.2 4415.8
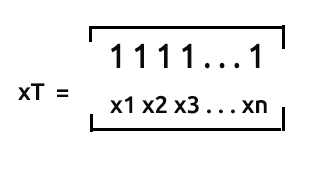
xT или транспонирование x — процесс, при котором мы в матрице меняем местами строки и столбцы.
Это означает, что если мы умножим эти две матрицы...
Мы пока пропустим процесс транспонирования матрицы, потому что благодаря тому, как мы собрали наши данные, матрица уже находится в транспонированной форме. Хотя, с другой стороны, нужно произвести обратное транспонирование значений x, чтобы их можно было умножить на уже транспонированную матрицу x.
То есть, для матрицы nx2, которая не транспонирована, массив будет выглядеть как [1 x1 1 x2 1 ... 1 xn]. Посмотрим, как это работает.
Обратное транспонирование матрицы X
Наша матрица в транспонированном виде, полученная из csv-файла, выглядит так при выводе
Транспонированная матрица
[
[ 0] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
...
...
[ 0] 4174 4179 4183 4186 4181 4175 4175 4171 4182 4208 4247 4217 4226 4211 4244 4249 4228 4231 4236 4227 4225 4220 4216 4226
...
...
[720] 4297 4321 4285 4311 4318 4328 4334 4352 4351 4354 4340 4348 4361 4346 4346 4343 4352 4326 4323 4333 4352 4402 4405 4416
]
Процесс обратного транспонирования предполагает, что мы просто меняем местами строки и столбцы — процесс, обратный транспонированию матрицы.
int tr_rows = m_rowsize, tr_cols = 1+1; //поскольку у нас есть одна независимая переменная, мы добавляем ее для пространства, созданного единицами MatrixUnTranspose(m_xvalues,tr_cols,tr_rows); Print("UnTransposed Matrix"); MatrixPrint(m_xvalues,tr_cols,tr_rows);
Здесь все становится сложнее
Мы помещаем столбцы из транспонированной матрицы туда, где должны быть строки, а строки — туда, где должны быть столбцы. Вывод после запуска этого фрагмента кода будет таким:
Обратно-транспонированная матрица [ 1 4248 1 4201 1 4352 1 4402 ... ... 1 4405 1 4416 ]
xT — это 2xn, матрица x — nx2. Итоговая матрица будет 2x2.
Итак, давайте посмотрим, как будет выглядеть произведение их умножения.
Внимание: матрицы должны быть совместимыми для умножения, т.е. количество столбцов в первой матрице должно быть равно количеству строк во второй матрице.
Правила умножения матриц можно посмотреть здесь: https://ru.wikipedia.org/wiki/%D0%A3%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BC%D0%B0%D1%82%D1%80%D0%B8%D1%86.
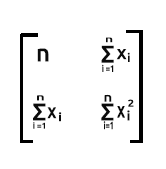
Как происходит умножение в этой матрице:
- Строка 1 помноженная на столбец 1
- Строка 1 помноженная на столбец 2
- Строка 2 помноженная на столбец 1
- Строка 2 помноженная на столбец 2
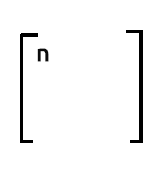
В случае наших матриц строка 1 помноженная на столбец 1 будет равна сумме произведения строки 1, которая содержит значения единицы, и произведения столбца 1, который также содержит значения единицы — это ничем не отличается от увеличения значения по одному на каждой итерации.
Обратите внимание:
Если хотите узнать количество наблюдений в вашем наборе данных, можно полагаться на число в первом столбце первой строки в выходе из хТх
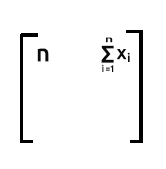
Строка 1 помноженная на столбец 2. Поскольку строка 1 содержит единицы, когда суммируем произведение строки 1 (где у нас единицы) и столбца 2 (со значениями x), на выходе мы имеем сумму элементов x, поскольку единицы никак не влияют на умножение.
Строка 2 помноженная на столбец 1. Результатом будет сумма x, поскольку опять же единицы в строке 2 не влияют на умножение со значениями x, которые находятся в столбце 1
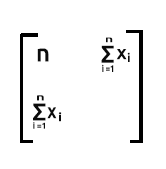
Последней частью идет сумма квадратов значений x.
Это сумма произведений строки 2, которая содержит значения x, и столбца 2, который также содержит значения x.
Таким образом, в нашем случае в результате мы получаем матрицу 2x2.
Теперь посмотрим, как это работает в реальности. Для этого используем набор данных из нашей самой первой статьи, которая была посвящена линейной регрессии: https://www.mql5.com/ru/articles/10459.
Извлечем данные и поместим их в массив x для независимой переменной и y для зависимых переменных.
//в скрипте MatrixRegTest.mq5 #include "MatrixRegression.mqh"; #include "LinearRegressionLib.mqh"; CSimpleMatLinearRegression matlr; CSimpleLinearRegression lr; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //double x[] = {651,762,856,1063,1190,1298,1421,1440,1518}; //продажи //double y[] = {23,26,30,34,43,48,52,57,58}; //деньги, потраченные на рекламу //--- double x[], y[]; string file_name = "NASDAQ_DATA.csv", delimiter = ","; lr.GetDataToArray(x,file_name,delimiter,1); lr.GetDataToArray(y,file_name,delimiter,2); }
Я импортировал сюда библиотеку CsimpleLinearRegression, которую мы создали в первой статье.
CSimpleLinearRegression lr;
Потому что эта библиотека содержит определенные функции, которые нам пригодятся, например получение данных в массивах.
Найдем xTx:
MatrixMultiply(xT,m_xvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols); Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5); //Помните? На выходе из матрицы мы получим строку 1 и столбец 2, выделенные красным
Если обратить внимание на массив хТ[], можно заметить, что мы просто скопировали значения x и сохранили их в этом массиве хТ[] просто для пояснения — как я уже говорил ранее, способ, которым мы собирали данные из нашего CSV-файла в массив с помощью функции GetDataToArray(), дает нам данные уже в транспонированном виде.
Затем умножили массив xT[] на m_xvalues[], которые теперь не транспонированы. m_xvalues — глобально определенный массив для значений x в этой библиотеке. А вот, что находится внутри функции MatrixMultiply():
void CSimpleMatLinearRegression::MatrixMultiply(double &A[],double &B[],double &output_arr[],int row1,int col1,int row2,int col2) { //--- double MultPl_Mat[]; //здесь будем хранить умножение if (col1 != row2) Alert("Matrix Multiplication Error, \n The number of columns in the first matrix is not equal to the number of rows in second matrix"); else { ArrayResize(MultPl_Mat,row1*col2); int mat1_index, mat2_index; if (col1==1) //Умножение для одномерного массива { for (int i=0; i<row1; i++) for(int k=0; k<row1; k++) { int index = k + (i*row1); MultPl_Mat[index] = A[i] * B[k]; } //Print("Matrix Multiplication output"); //ArrayPrint(MultPl_Mat); } else { //если матрица имеет более 2-х измерений for (int i=0; i<row1; i++) for (int j=0; j<col2; j++) { int index = j + (i*col2); MultPl_Mat[index] = 0; for (int k=0; k<col1; k++) { mat1_index = k + (i*row2); //k + (i*row2) mat2_index = j + (k*col2); //j + (k*col2) //Print("index out ",index," index a ",mat1_index," index b ",mat2_index); MultPl_Mat[index] += A[mat1_index] * B[mat2_index]; DBL_MAX_MIN(MultPl_Mat[index]); } //Print(index," ",MultPl_Mat[index]); } ArrayCopy(output_arr,MultPl_Mat); ArrayFree(MultPl_Mat); } } }
Честно говоря, это умножение выглядит немного запутанным, особенно когда встречаются такие вещи, как
k + (i*row2); j + (k*col2);
Но не стоит пугаться. Способ, которым мы работаем с индексами, позволяет получить индекс в определенной строке и столбце. Это было бы проще понять, если бы я использовал двумерные массивы, например, Matrix[rows][columns], в нашем случае это была бы матрица Matrix[i][k]. Но я решил не делать этого, потому что многомерные массивы имеют ограничения, поэтому мне пришлось найти другой способ. В конце статьи приложен простой код на С++, который, думаю, поможет вам понять, как я это сделал. Если же хотите узнать еще больше, рекомендую прочитать блог https://www.programiz.com/cpp-programming/examples/matrix-multiplication.
Результатом успешной работы xTx, который выведет функция MatrixPrint(), будет:
Print("xTx"); MatrixPrint(xTx,tr_cols,tr_cols,5); xTx [ 744.00000 3257845.70000 3257845.70000 14275586746.32998 ]
Как видите, первый элемент в нашем массиве хТх имеет количество наблюдений для всех данных в нашем наборе данных, поэтому очень важно заполнить матрицу дизайна значениями, равными единице, изначально на самом первом столбце.
Теперь давайте найдем обратную матрицу xTx.
Обратная матрице xTx
Чтобы найти матрицу, обратную 2x2, сначала поменяем первый и последний элемент диагонали, а затем к двум другим значениям добавляем знак минуса.
Формула показана на рисунке ниже:
Чтобы найти определитель матрицы det(xTx) = Произведение первой диагонали - Произведение второй диагонали
Вот как можно найти обратную матрицу в коде mql5:
void CSimpleMatLinearRegression::MatrixInverse(double &Matrix[],double &output_mat[]) { // Согласно матричным правилам, обратную матрицу можно найти только тогда, когда // Матрица идентична, начинается с матрицы 2x2, так что это наша отправная точка int matrix_size = ArraySize(Matrix); if (matrix_size > 4) Print("Matrix allowed using this method is a 2x2 matrix Only"); if (matrix_size==4) { MatrixtypeSquare(matrix_size); //первый шаг - поменять местами первое и последнее значение матрицы //на данный момент мы знаем, что последнее значение равно размеру массива минус один int last_mat = matrix_size-1; ArrayCopy(output_mat,Matrix); // первая диагональ output_mat[0] = Matrix[last_mat]; //меняем местами первый массив и последний output_mat[last_mat] = Matrix[0]; //меняем местами последний массив и первый double first_diagonal = output_mat[0]*output_mat[last_mat]; // вторая диагональ //добавляем знак минуса >>> output_mat[1] = - Matrix[1]; output_mat[2] = - Matrix[2]; double second_diagonal = output_mat[1]*output_mat[2]; if (m_debug) { Print("Diagonal already Swapped Matrix"); MatrixPrint(output_mat,2,2); } //формула обратной матрицы 1/det(xTx) * (xtx)-1 //определитель равен произведению первой диагонали на произведение второй диагонали double det = first_diagonal-second_diagonal; if (m_debug) Print("determinant =",det); for (int i=0; i<matrix_size; i++) { output_mat[i] = output_mat[i]*(1/det); DBL_MAX_MIN(output_mat[i]); } } }
Результат выполнения этого блока кода будет таким:
Diagonal already Swapped Matrix
[
14275586746 -3257846
-3257846 744
]
determinant =7477934261.0234375
Распечатаем обратную матрицу, чтобы посмотреть, как она выглядит.
Print("inverse xtx"); MatrixPrint(inverse_xTx,2,2,_digits); //обратная простой lr всегда будет матрицей 2x2
Вывод будет таким:
[
1.9090281 -0.0004357
-0.0004357 0.0000001
]
Теперь, когда мы нашли обратную xTx, переходим дальше.
Находим xTy
Здесь умножаем xT[] на значения y[].
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //на конце 1, потому что матрица значений y всегда будет иметь один такой столбец Print("xTy"); MatrixPrint(xTy,tr_rows,1,_digits); //снова, помните? Как мы находим выходное значение из нашей матрицы row1 x column2
Выход будет таким:
xTy
[
10550016.7000000 46241904488.2699585
]
Посмотрите на формулу:
Итак, у нас уже есть обратная xTx и xTy. Переходим к следующему шагу.
MatrixMultiply(inverse_xTx,xTy,Betas,2,2,2,1); //обратная это квадратная матрица 2x2, а xty — 2x1 Print("coefficients"); MatrixPrint(Betas,2,1,5); // для простой lr матрица с бета будет 2x1
Подробнее о том, как мы вызвали функцию.
Вывод этого фрагмента кода будет таким:
coefficients
[
-5524.40278 4.49996
]
Та-дам! Это тот же результат по нашим коэффициентам, который мы смогли получить с помощью модели в скалярной форме в Части 1 этой серии статей.
Число в первом индексе бета-массива всегда будет константой/Y-перехватом. Причина, по которой мы можем получить его изначально, заключается в том, что мы заполнили матрицу дизайна значениями единицы в первом столбце. Опять же это показывает, насколько важен весь процесс. Он оставляет в этом столбце место для y-перехвата.
Мы закончили с простой линейной регрессией. Давайте теперь посмотрим, как будет выглядеть множественная регрессия. Сейчас надо быть особенно внимательным, потому что далее будет становиться сложнее.
решение проблемы множественной динамической регрессии
Преимущество построения моделей на основе матрицы заключается в том, что их легко масштабировать без необходимости сильно изменять код, когда дело касается построения модели. Существенное изменение, которое вы заметите при множественной регрессии, заключается в том, как мы находим матрицы, потому что это самая сложная часть, на которую я потратил много времени, пытаясь ее понять. Я подробнее расскажу об этом позже, когда мы дойдем до нужного раздела. Сейчас же давайте добавим в код вещи, которые могут понадобиться в нашей библиотеке Множественной матричной регрессии.
У нас могла бы быть только одна библиотека, которая могла бы обрабатывать простую и множественную регрессию, а мы просто вводили бы аргументы функции. Но я решил создать еще один файл, чтобы объяснить, как все работает, поскольку процесс будет почти таким же. Здесь я очень надеюсь, что вы поняли расчеты, которые мы выполняли в рассмотренном выше разделе простой линейной регрессии.
Пойдем по порядку. Сначала напишем базовые вещи, которые могут пригодиться в нашей библиотеке.
class CMultipleMatLinearReg { private: int m_handle; string m_filename; string DataColumnNames[]; //сохраняем имена столбцов из csv-файла int rows_total; int x_columns_chosen; //выбранное количество столбцов x bool m_debug; double m_yvalues[]; //значения y или матрица зависимых значений double m_allxvalues[]; //все значения x матрицы дизайна string m_XColsArray[]; //сохраняем x столбцы, выбранные в Init string m_delimiter; double Betas[]; //массив для хранения коэффициентов protected: bool fileopen(); void GetAllDataToArray(double& array[]); void GetColumnDatatoArray(int from_column_number, double &toArr[]); public: CMultipleMatLinearReg(void); ~CMultipleMatLinearReg(void); void Init(int y_column, string x_columns="", string filename = NULL, string delimiter = ",", bool debugmode=true); };
А вот, что происходит внутри функции Init()
void CMultipleMatLinearReg::Init(int y_column,string x_columns="",string filename=NULL,string delimiter=",",bool debugmode=true) { //--- часть инпутов передаем в глобальные инпуты, так как они используются повторно m_filename = filename; m_debug = debugmode; m_delimiter = delimiter; //--- ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen); //--- if (m_debug) { Print("Init, number of X columns chosen =",x_columns_chosen); ArrayPrint(m_XColsArray); } //--- GetAllDataToArray(m_allxvalues); GetColumnDatatoArray(y_column,m_yvalues); // проверяем дисперсию в наборе данных, поделив общий размер строк на количество выбранных столбцов x if (rows_total % x_columns_chosen != 0) Alert("There are variance(s) in your dataset columns sizes, This may Lead to Incorrect calculations"); else { //--- заполним первую строку матрицы дизайна значениями 1 int single_rowsize = rows_total/x_columns_chosen; double Temp_x[]; //временный массив x ArrayResize(Temp_x,single_rowsize); ArrayFill(Temp_x,0,single_rowsize,1); ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //после заполнения единицами заполняем оставшиеся элементы значениями x //Print("Temp x arr size =",ArraySize(Temp_x)); ArrayCopy(m_allxvalues,Temp_x); ArrayFree(Temp_x); //нам больше не нужен этот массив int tr_cols = x_columns_chosen+1, tr_rows = single_rowsize; ArrayCopy(xT,m_allxvalues); //сохраняем транспонированные значения в глобальный массив, перед тем как транспонировать обратно MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //добавляем, чтобы оставить место для значений единицы if (m_debug) { Print("Design matrix"); MatrixPrint(m_allxvalues,tr_cols,tr_rows); } } }
Подробнее о том, что было сделано.
ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(x_columns,separator,m_XColsArray); x_columns_chosen = ArraySize(m_XColsArray); ArrayResize(DataColumnNames,x_columns_chosen);
Здесь получаем столбцы x, которые были выбраны (независимые переменные) при вызове функции инициализации в TestScript. Затем сохраняем эти столбцы в глобальном массиве m_XColsArray. Преимущество наличия столбцов в массиве в том, что скоро будем читать их, и это позволит сохранить их в правильном порядке в массиве всех значений x в матрице независимых переменных/матрице дизайна.
Также нужно убедиться, что все строки в наших наборах данных одинаковы, потому что, если есть различие хотя бы в одной строке или столбце, вычисления не будут выполнены.
if (rows_total % x_columns_chosen != 0) Alert("There are variances in your dataset columns sizes, This may Lead to Incorrect calculations");
Затем получаем все данные столбцов x в одну матрицу/матрицу дизайна/массив всех независимых переменных (выберите из этих подходящее название).
GetAllDataToArray(m_allxvalues);
Также нужно сохранить все зависимые переменные в матрице.
GetColumnDatatoArray(y_column,m_yvalues);
Это очень важный шаг, подготавливающий матрицу дизайна к расчетам. Добавляем единицы в первый столбец нашей матрицы значений x, как было сказано ранее здесь.
{
//--- заполним первую строку матрицы дизайна значениями 1
int single_rowsize = rows_total/x_columns_chosen;
double Temp_x[]; //временный массив x
ArrayResize(Temp_x,single_rowsize);
ArrayFill(Temp_x,0,single_rowsize,1);
ArrayCopy(Temp_x,m_allxvalues,single_rowsize,0,WHOLE_ARRAY); //после заполнения единицами заполняем оставшиеся элементами значениями x
//Print("Temp x arr size =",ArraySize(Temp_x));
ArrayCopy(m_allxvalues,Temp_x);
ArrayFree(Temp_x); //нам больше не нужен этот массив
int tr_cols = x_columns_chosen+1,
tr_rows = single_rowsize;
MatrixUnTranspose(m_allxvalues,tr_cols,tr_rows); //добавляем, чтобы оставить место для значений единицы
if (m_debug)
{
Print("Design matrix");
MatrixPrint(m_allxvalues,tr_cols,tr_rows);
}
}
В этот раз мы выведем нетранспонированную матрицу при инициализации библиотеки.
Это все, что нужно для функции Init. Теперь вызовем ее в нашем скрипте MultipleMatRegTestScript.mq5 (ссылка в конце статьи).
#include "multipleMatLinearReg.mqh"; CMultipleMatLinearReg matreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string filename= "NASDAQ_DATA.csv"; matreg.Init(2,"1,3,4",filename); }
После успешного запуска скрипта на выходе получим (это просто пример)
Init, number of X columns chosen =3 "1" "3" "4" All data Array Size 2232 consuming 52 bytes of memory Design matrix Array [ 1 4174 13387 35 1 4179 13397 37 1 4183 13407 38 1 4186 13417 37 ...... ...... 1 4352 14225 47 1 4402 14226 56 1 4405 14224 56 1 4416 14223 60 ]
Находим xTx
Здесь все то же, что мы делали с простой регрессией. Это тот же процесс: берем значения xT, которые представляют собой необработанные данные из файла csv, а затем умножаем их на нетранспонированную матрицу.
MatrixMultiply(xT,m_allxvalues,xTx,tr_cols,tr_rows,tr_rows,tr_cols);
Выход при печати матрицы xTx будет таким:
xTx [ 744.00 3257845.70 10572577.80 36252.20 3257845.70 14275586746.33 46332484402.07 159174265.78 10572577.80 46332484402.07 150405691938.78 515152629.66 36252.20 159174265.78 515152629.66 1910130.22 ]
Круто! Работает как надо.
Обратная матрица xTx
Это самая важная часть множественной регрессии, на которую следует обратить пристальное внимание, потому что все становится сложнее, а мы углубляемся в математику.
Когда мы искали обратную матрицу нашей xTx в предыдущей части, мы получали обратную матрицу 2x2. Но сейчас мы пойдем дальше — на этот раз мы находим обратную матрицу 4x4, потому что мы выбрали 3 столбца в качестве независимых переменных, а при добавлении значений еще одного столбца мы получаем 4 столбца. Они-то и приведут нас к матрице 4x4 при попытке найти обратную.
На этот раз нам не подходит метод, который мы использовали ранее при поиске обратного. Внимание, вопрос! Почему?
Дело в том, что поиск обратной матрице с использованием метода детерминант, который мы использовали ранее, не работает с большими матрицами. Он даже не подходит для матриц 3x3.
Разные математики предложили различные методы для нахождения обратной матрицы, один из которых является классическим сопряженным методом. Однако, согласно моему исследованию, большинство этих методов сложно написать в коде, они могут сбивать с толку. Если хотите узнать больше информации о методах и о том, как их можно запрограммировать, рекомендую почитать на этот пост в блоге: https://www.geertarien.com/blog/2017/05/15/different-methods-for-matrix-inversion/
Из всех доступных методов я выбрал исключение Гаусса-Жордана. Он мне показался надежным, простым в написании кода и легко масштабируемым. Есть отличное видео https://www.youtube.com/watch?v=YcP_KOB6KpQ, в котором хорошо объясняется метод Гаусса-Жордана. Надеюсь, оно поможет вам понять концепцию.
Хорошо, давайте напишем код метода Гаусса-Жордана. Если его трудно понять, у меня есть код этого же фрагмента на С++, ссылка на который приведена ниже, как и на мой GitHub. Возможно, больше примеров помогут понять, как все было сделано.
void CMultipleMatLinearReg::Gauss_JordanInverse(double &Matrix[],double &output_Mat[],int mat_order) { int rowsCols = mat_order; //--- Print("row cols ",rowsCols); if (mat_order <= 2) Alert("To find the Inverse of a matrix Using this method, it order has to be greater that 2 ie more than 2x2 matrix"); else { int size = (int)MathPow(mat_order,2); //поскольку массив должен быть квадратным // Создаем мультипликативную единичную матрицу int start = 0; double Identity_Mat[]; ArrayResize(Identity_Mat,size); for (int i=0; i<size; i++) { if (i==start) { Identity_Mat[i] = 1; start += rowsCols+1; } else Identity_Mat[i] = 0; } //Print("Multiplicative Indentity Matrix"); //ArrayPrint(Identity_Mat); //--- double MatnIdent[]; //исходная матрица со стороной единичной матрицы start = 0; for (int i=0; i<rowsCols; i++) //операция добавления идентичной матрицы к исходной { ArrayCopy(MatnIdent,Matrix,ArraySize(MatnIdent),start,rowsCols); //добавляем единичную матрицу в конец ArrayCopy(MatnIdent,Identity_Mat,ArraySize(MatnIdent),start,rowsCols); start += rowsCols; } //--- int diagonal_index = 0, index =0; start = 0; double ratio = 0; for (int i=0; i<rowsCols; i++) { if (MatnIdent[diagonal_index] == 0) Print("Mathematical Error, Diagonal has zero value"); for (int j=0; j<rowsCols; j++) if (i != j) //if we are not on the diagonal { /* i означает строки, а j — столбцы. При нахождении отношения строки будут постоянными, и при этом увеличиваем столбцы, которые не находятся на диагонали в приведенном выше выражении if. Это позволяет Получить доступ к значению массива на основе строк и столбцов */ int i__i = i + (i*rowsCols*2); diagonal_index = i__i; int mat_ind = (i)+(j*rowsCols*2); //row number + (column number) AKA i__j ratio = MatnIdent[mat_ind] / MatnIdent[diagonal_index]; DBL_MAX_MIN(MatnIdent[mat_ind]); DBL_MAX_MIN(MatnIdent[diagonal_index]); //printf("Numerator = %.4f denominator =%.4f ratio =%.4f ",MatnIdent[mat_ind],MatnIdent[diagonal_index],ratio); for (int k=0; k<rowsCols*2; k++) { int j_k, i_k; //первый элемент для столбца, второй для строки j_k = k + (j*(rowsCols*2)); i_k = k + (i*(rowsCols*2)); //Print("val =",MatnIdent[j_k]," val = ",MatnIdent[i_k]); //printf("\n jk val =%.4f, ratio = %.4f , ik val =%.4f ",MatnIdent[j_k], ratio, MatnIdent[i_k]); MatnIdent[j_k] = MatnIdent[j_k] - ratio*MatnIdent[i_k]; DBL_MAX_MIN(MatnIdent[j_k]); DBL_MAX_MIN(ratio*MatnIdent[i_k]); } } } // Операция строки, чтобы сделать главную диагональ равной 1 /* вернемся к нашей матрице и идентичному массиву матриц, затем выполним операции, чтобы сделать его главную диагональ равной 1 */ ArrayResize(output_Mat,size); int counter=0; for (int i=0; i<rowsCols; i++) for (int j=rowsCols; j<2*rowsCols; j++) { int i_j, i_i; i_j = j + (i*(rowsCols*2)); i_i = i + (i*(rowsCols*2)); //Print("i_j ",i_j," val = ",MatnIdent[i_j]," i_i =",i_i," val =",MatnIdent[i_i]); MatnIdent[i_j] = MatnIdent[i_j] / MatnIdent[i_i]; //printf("%d Mathematical operation =%.4f",i_j, MatnIdent[i_j]); output_Mat[counter]= MatnIdent[i_j]; //store the Inverse of Matrix in the output Array counter++; } } //--- }
Теперь вызовем функцию и выведем обратную матрицу.
double inverse_xTx[]; Gauss_JordanInverse(xTx,inverse_xTx,tr_cols); if (m_debug) { Print("xtx Inverse"); MatrixPrint(inverse_xTx,tr_cols,tr_cols,7); }
Выход будет таким:
xtx Inverse [ 3.8264763 -0.0024984 0.0004760 0.0072008 -0.0024984 0.0000024 -0.0000005 -0.0000073 0.0004760 -0.0000005 0.0000001 0.0000016 0.0072008 -0.0000073 0.0000016 0.0000290 ]
Запомните! Чтобы найти обратную матрицу, она должна быть квадратной матрицей. Именно поэтому в аргументах функций у нас есть аргумент mat_order, который равен количеству строк и столбцов.
Находим xTy
Теперь найдем матричное произведение транспонирования x и Y. Тот же процесс, что мы делали ранее.
double xTy[]; MatrixMultiply(xT,m_yvalues,xTy,tr_cols,tr_rows,tr_rows,1); //Помните! Значение 1 в конце связано с тем, что у нас есть только одна зависимая переменная y
При выводе результат будет выглядеть так:
xTy [ 10550016.70000 46241904488.26996 150084914994.69019 516408161.98000 ]
Отлично — как и ожидалось, матрица 1x4.
Посмотрите на формулу:
Теперь, когда у нас есть все необходимое для нахождения коэффициентов, перейдем к заключительной части.
MatrixMultiply(inverse_xTx,xTy,Betas,tr_cols,tr_cols,tr_cols,1); Выводом будет (и снова - помним, что первый элемент наших коэффициентов / бета-матрицы является константой или, другими словами, y-перехватом)
Coefficients Matrix [ -3670.97167 2.75527 0.37952 8.06681 ]
Отлично, теперь давайте проверим в Python, чтобы доказать, что я ошибаюсь.
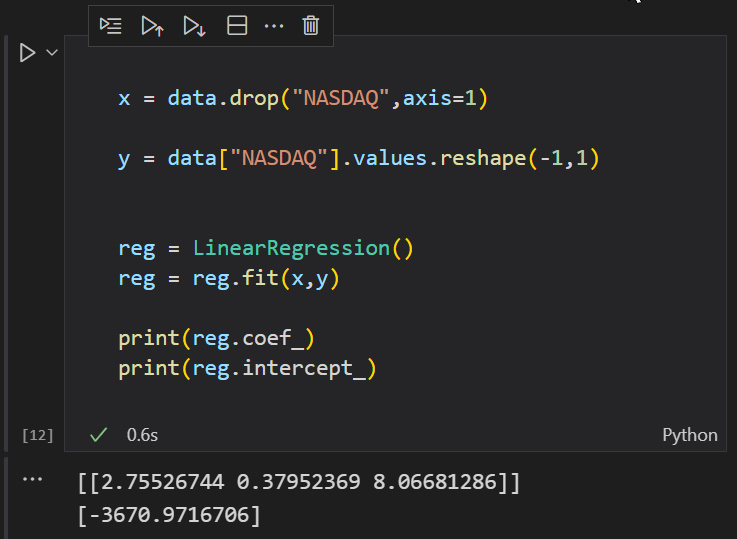
Ура!!
Теперь у нас есть несколько моделей динамической регрессии, которые наконец-то возможны в mql5. Давайте еще раз посмотрим, с чего все началось.
А начинали мы так:
matreg.Init(2,"1,3,4",filename);
Идея заключалась в том, чтобы получить строковый ввод, который позволил бы ввести неограниченное количество независимых переменных. Похоже, что в mql5 мы не можем иметь *args и *kwargs из таких языков, как Python, а они как раз позволяют вводить очень много аргументов. Поэтому единственный способ сделать это — использовать строку, а затем найти способ манипулировать массивом, чтобы один массив содержал все наши данные. А после этого уже можно найти способ манипулировать ими. Чтобы понять больше, посмотрите на мою первую неудачную попытку: https://www.mql5.com/ru/code/38894. Причина, по которой я говорю все это, заключается в том, что я верю, что кто-то может пойти по тому же пути в этом или другом проекте. Я просто объясняю, что сработало для меня, а что нет.
Заключительные мысли
Как бы круто это ни звучало, теперь у вас может быть столько независимых переменных, сколько захотите. Помните, что существует ограничение на все, что имеет слишком много независимых переменных или очень длинных столбцов наборов данных. К примеру, Вы можете столкнуться с ограничениями вычислительных мощностей компьютера. Как вы только что видели, матричные вычисления могут потребовать много время вычислений.
Добавление независимых переменных в модель множественной линейной регрессии всегда будет увеличивать величину дисперсии зависимой переменной, обычно выражаемой как R-квадрат, поэтому добавление слишком большого количества независимых переменных без какого-либо теоретического обоснования может привести к подгонке модели.
Например, если бы мы построили модель так, как делали это в первой статье из этой серии, основываясь только на двух зависимых переменных NASDAQ и независимой S&P500, наша точность могла бы быть более 95%, но это может оказаться не так, потому что теперь у нас есть 3 независимых переменных.
Всегда полезно проверить точность модели после того, как она построена. Также перед построением модели нужно проверить, существует ли корреляция между каждой независимой переменной и целью.
Всегда стройте модель на основе данных, которые имеют сильную линейную связь с вашей целевой переменной.
Спасибо за внимание! Вот ссылка на мой репозиторий в GitHub: https://github.com/MegaJoctan/MatrixRegressionMQL5.git
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/10928
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Машинное обучение и Data Science (Часть 04): Предсказание биржевого краха
Машинное обучение и Data Science (Часть 04): Предсказание биржевого краха
 Нейросети — это просто (Часть 24): Совершенствуем инструмент для Transfer Learning
Нейросети — это просто (Часть 24): Совершенствуем инструмент для Transfer Learning
 Нейросети — это просто (Часть 23): Создаём инструмент для Transfer Learning
Нейросети — это просто (Часть 23): Создаём инструмент для Transfer Learning
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования

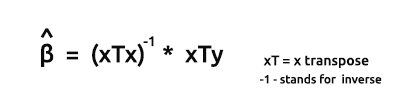
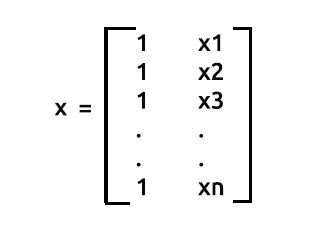
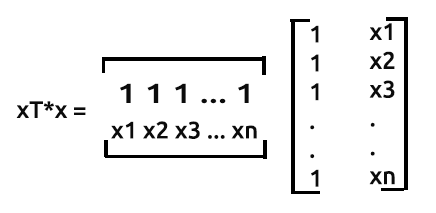

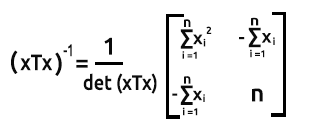
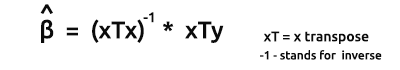
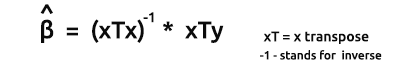
Опубликована новая статья Наука о данных и машинное обучение часть 03: Матричные регрессии:
Автор: Omega J Msigwa