Циклы и трейдинг

Введение

Основная задача, которая стоит перед трейдером — прогнозирование движения цены. Этот прогноз трейдер строит на основе той или иной модели. Одной из наиболее простых и наглядных моделей является модель циклического движения цены.

Основная идея любой циклической модели заключается в том, что различные факторы, накладываясь друг на друга, создают циклы в движении цены. Эти циклы могут отличаться друг от друга по своей продолжительности и силе. Если знать параметры этих циклов, то совершение торговых операций будет очень простым: открыть позицию buy, когда цикл достиг минимума, sell — когда цикл достиг своего максимума.

Давайте посмотрим, как можно использовать эту модель на практике.

Простой цикл

Для описания циклов, как правило, используются тригонометрические функции синус и косинус. Но цикл можно задать и по-другому — с помощью конечных разностей.

Для примера, давайте рассмотрим уравнение, в котором 2-ая разность пропорциональна значению временного ряда:

Это уравнение гармонического осциллятора. На первый взгляд, в нем нет ничего особенного. Но у этого уравнения есть одно интересное свойство. Если значение коэффициента R лежит в пределах от 0 до 4, то это уравнение может принадлежать только синусоиде. Этот коэффициент зависит от периода цикла N. То есть, его значение можно подобрать таким, чтобы уравнение реагировало только на циклы с определенной частотой:

Теперь давайте посмотрим, как это уравнение можно применять на практике. Если мы применим его к ценам p[], то нам потребуется значение уровня m, около которого происходит колебание цены.

Чтобы не рассчитывать значение этого среднего уровня, я пойду на небольшую хитрость. Давайте вспомним, что происходит с математической точки зрения, когда цикл достигает точки максимума или минимума. В эти моменты 1-ая производная меняет знак.

Вместо производной мы будем использовать 1-ую разность исходного уравнения. Вот такая нелегкая судьба трейдера — искать разности от разностей. Но такой подход значительно упрощает расчеты. Нам нужно только задать значение коэффициента R. Окончательный вид формулы будет таким:

Далее, такие формулы я буду называть формулами торгового алгоритма. На основе этой формулы мы можем создать торговую стратегию. Сначала я внесу небольшое дополнение — вместо текущей цены можно использовать любой вариант классической скользящей средней. Суть самой стратегии очень проста. Открытие и закрытие позиций происходит при изменении знака уравнения:

• с отрицательного на положительное — открыть buy, закрыть sell;
• с положительного на отрицательное — открыть sell, закрыть buy.

Изменение баланса этого советника может быть таким.

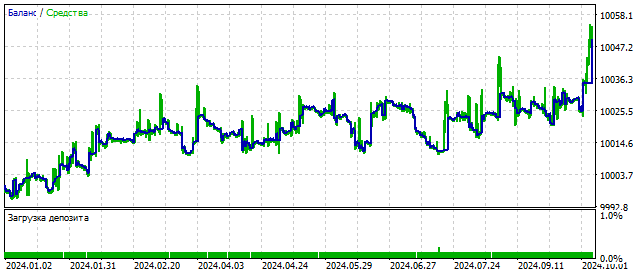
Перспективы у этой торговой стратегии есть. Но, она нуждается в доработке.

Цикл с затуханием

У стратегии, которую мы рассмотрели ранее, есть один серьезный недостаток. Этот недостаток заключается в том, что стратегия построена на предположении о том, что начавшийся цикл будет продолжаться довольно продолжительное время. В реальных условиях цикл зависит от многих внешних факторов и может разрушиться, едва начавшись.

Чтобы избавиться от этого недостатка, мы можем использовать модель гармонического осциллятора с затуханием колебаний. Уравнение такого цикла так же задается с помощью конечных разностей:

Насколько быстро затухают колебания зависит от параметра S. Чем больше его значение, тем быстрее происходит затухание. Критическое значение этого параметра можно найти по формуле:

Начиная с этого значения, движение осциллятора становится неколебательным.

Что делать с таким уравнением, мы уже знаем. Нам нужно найти его 1-ую разность, которая и будет генерировать торговые сигналы.

Благодаря добавлению нового параметра, торговая стратегия может стать более гибкой и прибыльной. Например, так выглядит изменение баланса при критическом значении S.

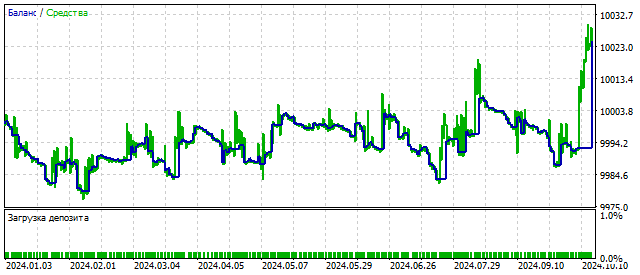
По смыслу параметр S должен быть положительным. Но это требование не является обязательным. Если мы установим отрицательное значение этого параметра, то исходное уравнение будет описывать колебания со все увеличивающейся амплитудой. Таким образом, EA может реагировать на начало цикла и, возможно, увеличить прибыльность. Результаты трейдинга в таком случае могут выглядеть так:

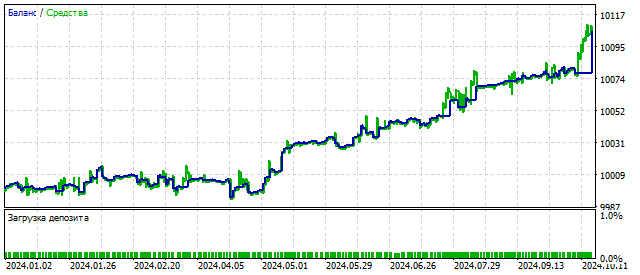
Как вы можете видеть, усложнение модели цикла может улучшить результаты трейдинга. Давайте попробуем усложнить модель еще больше.

Волны Эллиота

Волновой принцип Эллиота известен очень давно и широко используется в трейдинге. Давайте попробуем применить к волнам Эллиота циклическую модель.

Первые пять волн Эллиота можно смоделировать с помощью суммы двух синусоид с разными амплитудами и периодами:

При этом должны выполняться следующие условия:

В результате, мы можем получить примерно такую картинку:

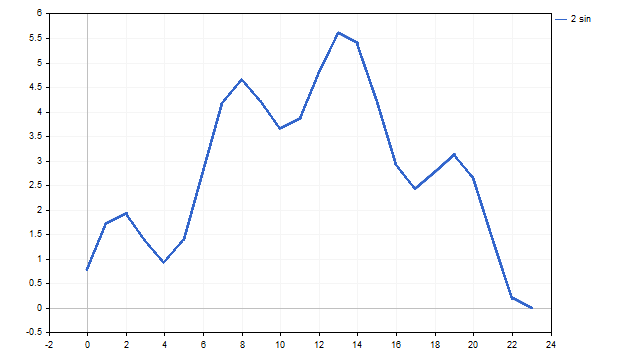
Выглядит не совсем так, как в книжках — немного угловато, но довольно похоже.

Сумму двух синусоид мы можем смоделировать с помощью конечных разностей:

Где,    — значение конечной разности порядка n, на отсчете цены с индексом i. Что нужно делать с этим уравнением мы уже знаем —находим разность от суммы разностей, и получаем торговые сигналы:

Использование суммы двух синусоид дает возможность настроить работу EA на более сложные рыночные ситуации. Использование этого торгового алгоритма может привести как к увеличению входов в рынок, так и к улучшению их прибыльности.

Вот такой результат может показать советник, построенный на волновом принципе Эллиота:

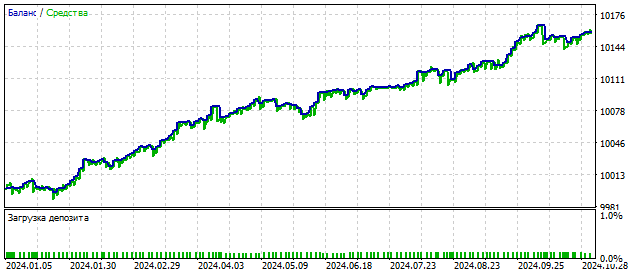
Как вы можете видеть, даже небольшое усложнение циклической модели может принести положительные результаты.

Обобщенный гармонический осциллятор

Мы с вами рассмотрели уже три модели, в основе которых лежит гармонический осциллятор. Каждая из этих моделей была построена на своих исходных предпосылках. Но в результате, мы все равно получали некоторую сумму конечных разностей.

Мы можем построить более общую модель. Суть этой модели очень проста — сначала мы берем разность заранее заданного порядка и складываем их с разностями более низких порядков, вплоть до 1-ой. При этом, каждая разность низкого порядка берется со своим весовым коэффициентом.

Для примера, я взял разность 7-го порядка. Тогда формула торгового алгоритма будет такой:

Такая модель может включать в себя самые разные сочетания циклов и их поведения. Ранее мы видели, что усложнение модели улучшает результаты трейдинга. В этом случае изменение баланса может быть таким:

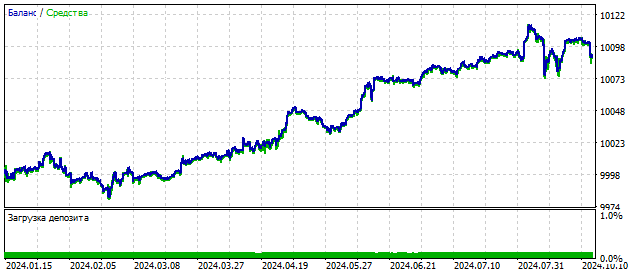
Увеличение порядка старшей разности делает модель более гибкой. Обобщенный осциллятор будет реагировать только на определенные сочетания цен. Говоря иначе, он ищет определенные паттерны. При этом вам нужно помнить — чем выше порядок осциллятора, тем реже будут встречаться именно его паттерны.

Еще одна особенность этого алгоритма заключается в том, что коэффициенты могут изменяться в очень больших пределах. Даже оценка этих пределов может быть затруднительной. С другой стороны, подбор коэффициентов позволяет настроить алгоритм таким образом, что он будет реагировать на нециклические закономерности в поведении цены.

Нелинейные осцилляторы

Линейные модели просты и интуитивно понятны. Но, поведение цены на рынке может быть и нелинейным. Например, резкое изменение цены проще описать с помощью нелинейных моделей. Основное достоинство нелинейных моделей заключается в том, что они могут описывать очень сложное поведение временного ряда. Когда вы слышите слова «хаотичность, стохастичность», то речь идет о нелинейных моделях.

Одной из простейших моделей является сигнатурный осциллятор. Его формула во многом похожа на гармонический осциллятор. А в качестве нелинейной функции используется функция знака. Формула торгового алгоритма выглядит так:

Где, sign – функция знака.

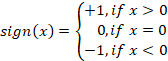
Благодаря этой функции, осциллятор может работать в 5 разных режимах. Переключение режимов зависит от движения цены. Нелинейность осциллятора дает нам надежду на то, что трейдинг с его помощью будет более гибким и устойчивым. Изменение баланса при использовании этого алгоритма может выглядеть так:

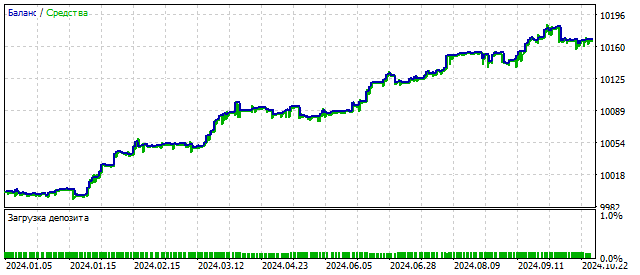
Теперь, давайте рассмотрим осциллятор с квадратичной нелинейностью. Его формула очень проста:

Для того, чтобы применить эту формулу на практике нам необходимо ее немного доработать.

В первую очередь, нам потребуется средний уровень, около которого происходит колебания цены. Напомню, что вместо реальных цен мы можем применять их сглаженное значение (SMA). Тогда средний уровень будет равен среднему значению от скользящих средних.

Рассчитать среднее от средних — на первый взгляд выглядит немного пугающе. В 1910 г. Андрей Марков опубликовал книгу «Исчисление конечных разностей». В этой работе он показал, что среднее от большого количества SMA равносильно применению LWMA ко всем значениям временного ряда. В очередной раз конечные разности упростили расчеты.

Формула торгового алгоритма квадратичного осциллятора будет такой:

Квадратичная нелинейность позволяет переключать режимы работы осциллятора более плавно, но с большим размахом. А это может улучшить результаты трейдинга.

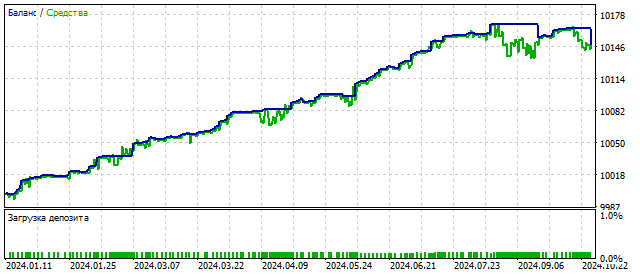
Еще одним примером квадратичной нелинейности является осциллятор Ван дер Поля. Этот осциллятор был одним из первых примеров моделирования детерминированного хаоса. Благодаря своим свойствам, уравнение Ван дер Поля нашло применение не только в теории колебаний, но и в других областях — физике, биологии и др.

Сам осциллятор Ван дер Поля представляет собой модификацию осциллятора с квадратичной нелинейностью, а формула его торгового алгоритма выглядит так:

На первый взгляд, этот осциллятор должен быть неустойчивым. На самом деле, его параметры могут изменяться в довольно большом диапазоне, не влияя на результаты торговли.

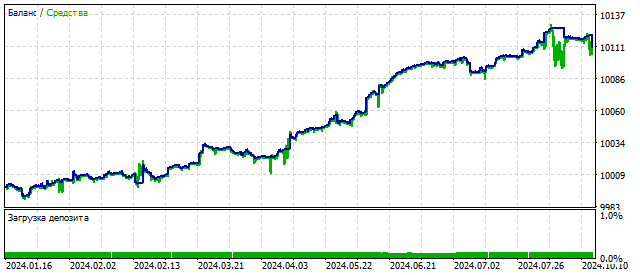
В 1918 г. Георг Дуффинг исследовал уравнение осциллятора с кубической нелинейностью. Этот осциллятор так же может моделировать хаотическое поведение цены. Но у него есть еще одна особенность — в зависимости от внешних условий и своих параметров этот осциллятор может находиться в двух стабильных состояниях.

Уравнение торгового алгоритма осциллятора Дуффинга представляет собой сумму гармонического осциллятора 3-ей степени и кубического бинома:

Результативность этого осциллятора сопоставима с другими нелинейными моделями.

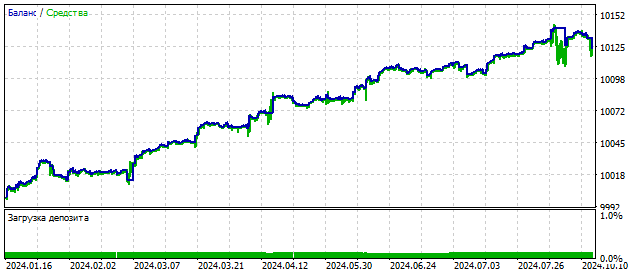
Вообще, нелинейных моделей можно создать очень много. Любая нелинейная функция может стать генератором хаоса. Нелинейность трех предыдущих осцилляторов была основана на каких-то физических принципах и представлениях. Эконофизика — направление полезное, но следовать за ним всегда и везде вовсе необязательно.

Например, я добавлю в торговый алгоритм нелинейность на основе логарифмической функции:

Вы можете мне задать вопрос: а откуда взялись эти логарифмы, исходя из каких соображений я их добавил? Мой ответ будет очень прост —мне так захотелось.

Но, если у меня будет время подумать над ответом, то он будет немного другим. Какова разность между подряд идущими ценами? Пусть, 100 пунктов. А разность логарифмов этих цен? Там кроме нулей хоть что-нибудь будет? Вот вам мой новый ответ: слева у нас обычный осциллятор, а справа — фильтр, который может повлиять на открытие позиций. И проявит себя этот фильтр только при сильном движении цены. Проверяем его работу.

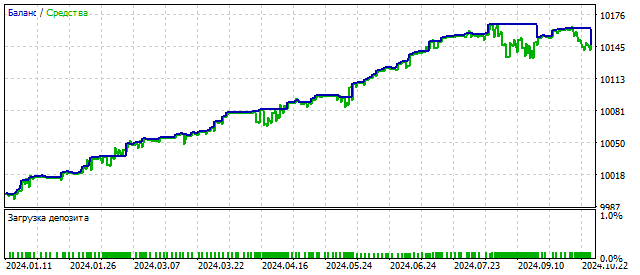
Результат похож на работу осциллятора с квадратичной нелинейностью. Фильтр работает. Но необходимо помнить, что все свои гениальнейшие идеи нужно сначала проверять в тестере. И только после этого применять их на практике.

Внешние силы

До сих пор мы рассматривали автономные осцилляторы. Представьте маятник. Он равномерно качается из стороны в сторону. Его циклы повторяются снова и снова. Почему этот маятник качается, почему он качается именно так — это вопросы, на которые мы не можем ответить. Это пример автономного осциллятора.

Теперь, толкните этот маятник. Сначала в одну сторону, потом в другую. Циклы маятника стали меняться — изменяется его мгновенная частота и амплитуда. Под воздействием внешних сил маятник перестал быть автономным.

Давайте попытаемся применить такой же подход к гармоническому осциллятору. Его формула изменится и будет выглядеть так:

Где, F[n] — какая-то внешняя сила. Что это за сила, как она действует, куда направлена — мне о ней ничего неизвестно. Я просто предполагаю, что она есть. И теперь передо мной встает вопрос: насколько оправданно такое усложнение модели? Проверяю.

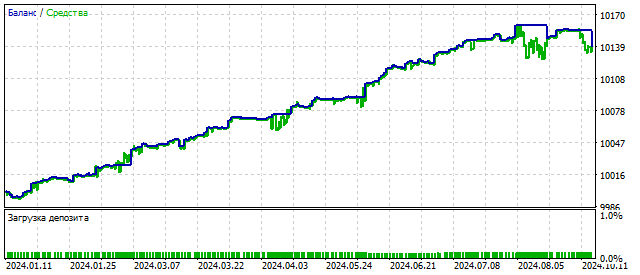
Такой результат я получил, предположив, что эта внешняя сила связана со значениями цен следующим образом:

Это предположение я сделал только по одной причине — всю статью я рассказывал о конечных разностях, и в этом случае я тоже применил коэффициенты 2-ой разности. А вы можете делать свои предположения. Например, внешняя сила может быть связана с разностью между ценами закрытия и открытия, тиковыми объемами и т.п. Вы можете добавить и элемент нелинейности:

В конце концов, эта неведомая сила может зависеть и от нескольких составляющих. Обобщайте все, что можете до тех пор, пока это возможно. Любое ваше предположение может положительно повлиять на результаты трейдинга.

Заключение

Как вы могли видеть, использование циклических моделей в трейдинге вполне оправданно. Основное преимущество таких моделей заключается в том, что у них есть сотни сочетаний параметров, которые дают устойчивый результат в течение долгого времени. Трейдеру необходимо отобрать несколько десятков вариантов, которые не коррелируют друг с другом.

В статье я затронул только несколько наиболее популярных осцилляторов. Есть еще довольно много решений, которые можно применять для построения циклических моделей (и не только их).

Тестирование EA производилось мною при следующих условиях: EURUSD, H1, 2024.01.01 - 2024.10.30

При написании статьи использовались следующие программы:

Название	Тип	Описание
Harmonic Oscillator	эксперт	iPeriod - период скользящей средней Type - тип скользящей средней R - коэффициент осциллятора, допустимое значение: 1 ... 399
Damped Harmonic Oscillator	эксперт	S - коэффициент затухания,  допустимое значение: -1000 ... +1000
scr Elliott wave	скрипт	A1, A2 - амплитуды синусоид N1, N2 - периоды синусоид Width - толщина линии Pause - задержка при показе результата Screenshot - если true, то создается картинка сохраняется в папке Files
Elliott wave	эксперт	R, S - коэффициенты осциллятора , допустимое значение: 0 ... 1000
Generalized Harmonic Oscillator	эксперт	допустимое значение коэффициентов: -1000 ... +1000
Sign Oscillator	эксперт
Quadratic Oscillator	эксперт
Van der Pol Oscillator	эксперт
Duffing Oscillator	эксперт
Log Oscillator	эксперт
Non-Autonomous Oscillator	эксперт