MetaTrader 5 / Торговые системы
English Español Deutsch 日本語 Português
preview
Машинное обучение и Data Science (Часть 15): SVM — полезный инструмент в арсенале трейдера

Машинное обучение и Data Science (Часть 15): SVM — полезный инструмент в арсенале трейдера

MetaTrader 5 — Торговые системы | 15 марта 2024, 14:47
563 0
Omega J Msigwa
Omega J Msigwa

Содержание:


    Введение

    Метод опорных векторов (Support Vector Machine, SVM) является формой машинного обучения с учителем, используемый в задачах линейной и нелинейной классификации и регрессии, а также иногда для задач обнаружения выбросов.

    В отличие от методов байесовской классификации и логистической регрессии, которые используют простые математические модели для классификации информации, SVM использует сложные функции математического обучения, направленные на поиск оптимальной гиперплоскости, разделяющей данные в N-мерном пространстве.

    Алгоритм SVM чаще используется для задач классификации. Именно такие задачи мы и будем решать в этой статье.


    Что такое гиперплоскость?

    Гиперплоскость — это линия, используемая для разделения точек данных разных классов. 

    Гиперплоскость svm (источник изображения: wikipedia.com)

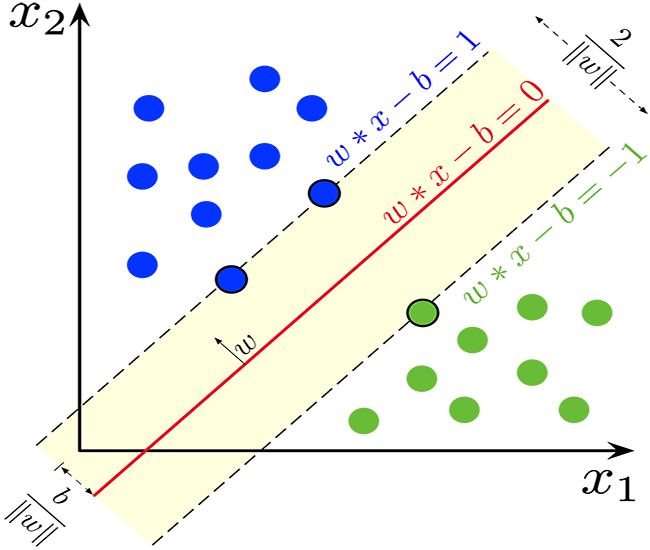
    Гиперплоскость обладает следующими свойствами:

    Размерность. В задачах бинарной классификации гиперплоскость — это (d-1)-мерное подпространство, где d — размерность пространства признаков. Например, в двумерном пространстве признаков гиперплоскость представляет собой одномерную линию.

    Математически гиперплоскость можно представить линейным уравнением вида:


     — вектор, ортогональный гиперплоскости и определяющий ее ориентацию.

     — вектор признаков.

    b — скалярный член смещения, который сдвигает гиперплоскость от начала координат.

    Разделение. Гиперплоскость делит пространство признаков на два полупространства:

    Область, где  соответствует одному классу.

    Область, где  соответствует другому классу.

    Отступ. В SVM цель состоит в том, чтобы найти гиперплоскость, которая максимизирует зазор между гиперплоскостью и ближайшими точками данных из любого класса. Эти ближайшие точки данных называются «векторами поддержки». SVM стремится найти гиперплоскость, которая обеспечивает максимальный зазор при минимизации ошибки классификации.

    Классификация. Найденную оптимальную гиперплоскость можно использовать для классификации новых точек данных. Вычислив , можно определить, на какой стороне гиперплоскости находится точка данных, и, таким образом, отнести ее к одному из двух классов.

    Концепция гиперплоскости является ключевым элементом опорных векторов, поскольку она формирует основу классификатора с максимальным зазором. Целью метода опорных векторов является поиск гиперплоскости, которая лучше всего разделяет данные, сохраняя при этом максимальный отступ между классами, что, в свою очередь, повышает обобщенность модели и ее устойчивость к невидимым данным.

    double CLinearSVM::hyperplane(vector &x)
 {
   return x.MatMul(W) - B;   
 }
    Уравнения  и  эквивалентны и описывают одну и ту же гиперплоскость. Выбор конкретного — вопрос личных предпочтений, но оба варианта алгебраически эквивалентны. В своем коде я не транспонировал матрицу x, потому что решил использовать W в качестве вектора, поэтому в этом нет необходимости.

    Как уже упоминалось, термин смещения, обозначаемый как b, является скалярным термином, поэтому для него пришлось объявить двойную переменную.

    class CLinearSVM
  {
   protected:
   
      CMatrixutils      matrix_utils;
      CMetrics          metrics;
      
      CPreprocessing<vector, matrix> *normalize_x;
      
      vector            W; //Weights vector 
      double            B; //bias term
      
      bool is_fitted_already;
      
      struct svm_config 
        {
          uint batch_size;
          double alpha;
          double lambda;
          uint epochs;
        };

   private:
      svm_config config;
  

    Здесь мы используем класса CLinearSVM. Вообще в этой статье мы рассмотрим два варианта метода опорных векторов — линейный и двойной.


    Линейный метод опорных векторов

    Линейный SVM — это тип опорных векторов, в котором используется линейное ядро, что означает, что он использует линейную границу решения для разделения точек данных. В линейном SVM вы работаете непосредственно с пространством признаков, и проблема оптимизации часто выражается в ее простой форме. Основная цель линейного SVM — найти линейную гиперплоскость, которая лучше всего разделяет данные.

    Такой тип лучше всего это работает для линейно разделимых данных.


    Двойной метод опорных векторов

    Двойная форма — это не отдельный тип метода опорных векторов, а скорее представление проблемы оптимизации SVM. Двойная форма SVM представляет собой математическую переформулировку исходной задачи оптимизации, которая позволяет использовать более эффективные методы решения. В формулу вводятся множители Лагранжа для максимизации двойной целевой функции, что эквивалентно основной задаче. Решение двойственной задачи приводит к определению опорных векторов, имеющих решающее значение для классификации.

    Такой тип лучше всего подходит для данных, которые не являются линейно разделимыми.

    Линейная и нелинейная задача

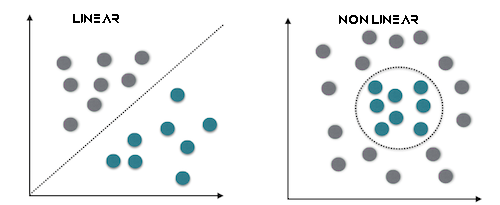
    Кроме того, можно использовать жесткие или мягкие отступы для принятия решений по классификатору SVM с использованием гиперплоскости.


    Жесткий отступ

    Если обучающие данные линейно разделимы, можно выбрать две параллельные гиперплоскости, разделяющие два класса данных так, чтобы расстояние между ними было как можно большим. Область, ограниченная этими двумя гиперплоскостями, называется отступом, а гиперплоскость с максимальным запасом — это гиперплоскость, лежащая посередине между ними. С помощью нормализованного или стандартизированного набора данных эти гиперплоскости можно описать уравнениями

     (все, что находится на этой границе или выше, относится к одному классу с меткой 1)

    и

     (все, что находится на этой границе или ниже, относится к другому классу с меткой −1).

    Расстояние между ними равно 2/||w||, и чтобы максимизировать расстояние, ||w|| должно быть минимальным. Чтобы предотвратить попадание любой точки данных в пределы поля, мы добавляем ограничение: yi(wTXi -b) >= 1, где yi = i-я строка в цели, а Xi = i-я строка в X.


    Мягкий отступ

    Для использования SVM в случаях, когда данные не являются линейно разделимыми, была введена функция шарнирных потерь.

    .

    Здесь   этой i-ая цель (т.е. в данном случае 1 или -1), а это i-ый вывод.

    Если точка данных имеет класс = 1, то потеря будет равна 0, в противном случае это будет расстояние между границей и точкой данных. Наша цель — минимизировать

      где λ — это компромисс между размером отступа, а xi находится на правильной стороне от этого отступа. Если значение λ слишком низкое, уравнение становится жестким отступом.

    Мы будем использовать жесткий отступ для класса Linear SVM. Это становится возможным благодаря функции знака, которая возвращает знак действительного числа в математической записи. Выражается как:


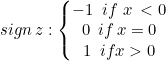
    int CLinearSVM::sign(double var)
 {   
   if (var == 0)
    return (0);
   else if (var < 0)
    return -1;
   else 
    return 1; 
 }


    Обучение модели линейного метода опорных векторов

    Процесс обучения метода опорных векторов SVM включает в себя поиск оптимальной гиперплоскости, которая разделяет данные при максимальном увеличении зазора. Зазор, или отступ — это расстояние между гиперплоскостью и ближайшими точками данных любого класса. Цель состоит в том, чтобы найти такую гиперплоскость, которая максимизирует зазор при минимизации ошибок классификации.

    Обновление весов (w):

    а. Первый член. Первый член функции потерь соответствует шарнирной потере, которая измеряет ошибку классификации. Для каждого обучающего примера i, мы рассчитываем производную функции потерь потерь относительно весов w:

    • Если 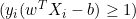, это означает, что точка данных правильно классифицирована и за пределами поля производная равна 0.
    • Если 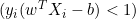, это означает, что точка данных находится внутри поля или неправильно классифицирована, производная равна .

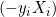    b. Второй член:

    Второй член представляет собой регуляризация. Это дает небольшой зазор и помогает предотвратить переобучение. Производная этого члена относительно весов w равна 2λw, где λ — это параметр регуляризации.

    c. Объединим производные первого и второго слагаемых,

    Обновляем веса w:

    -При веса обновляем так: , а если  , обновляем так: . Здесь α — коэффициент обучения.

    Обновление точки пересечения (b):

    а. Первый член:

    Производная функции шарнирных потерь относительно точки пересечения b вычисляется аналогично весам:

    • Если 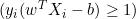, производная равна нулю.
    • Если 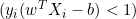, производная равна .

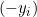    b. Второй член:

    Второй член не зависит от точки пересечения, поэтому его производная по b равна нулю. c. Обновляем точку пересечения b:

    • Если 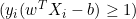, обновляем  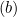так: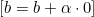 
    • Если 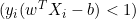, обновляем  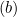так: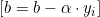

    Переменная рассогласования (ξ):

    Переменная рассогласования (ξ) позволяет некоторым точкам данных находиться внутри отступа, что означает, что они неправильно классифицированы или находятся внутри этого отступа. Условие   означает, что граница решения должна быть как минимум на ​ единиц отдалена от точки данных i.

    Таким образом, процесс обучения SVM включает в себя обновление весов и пересечения на основе шарнирной потери и члена регуляризации. Цель состоит в том, чтобы найти оптимальную гиперплоскость, которая максимизирует зазор, учитывая при этом потенциальные ошибки классификации внутри предела, допускаемые переменной рассогласования. Этот процесс обычно решается с использованием методов оптимизации. При этом векторы поддержки определяются в процессе обучения. Их цель — определить границу решения.

    void CLinearSVM::fit(matrix &x, vector &y)
 {
   matrix X = x;
   vector Y = y;
  
   ulong rows = X.Rows(),
         cols = X.Cols();
   
   if (X.Rows() != Y.Size())
      {
         Print("Support vector machine Failed | FATAL | X m_rows not same as yvector size");
         return;
      }
   
   W.Resize(cols);
   B = 0;
    
   normalize_x = new CPreprocessing<vector, matrix>(X, NORM_STANDARDIZATION); //Normalizing independent variables
     
//---

  if (rows < config.batch_size)
    {
      Print("The number of samples/rows in the dataset should be less than the batch size");
      return;
    }
   
    matrix temp_x;
    vector temp_y;
    matrix w, b;
    
    vector preds = {};
    vector loss(config.epochs);
    during_training = true;

    for (uint epoch=0; epoch<config.epochs; epoch++)
      {
        
         for (uint batch=0; batch<=(uint)MathFloor(rows/config.batch_size); batch+=config.batch_size)
           {              
              temp_x = matrix_utils.Get(X, batch, (config.batch_size+batch)-1);
              temp_y = matrix_utils.Get(Y, batch, (config.batch_size+batch)-1);
              
              #ifdef DEBUG_MODE:
                  Print("X\n",temp_x,"\ny\n",temp_y);
              #endif 
              
               for (uint sample=0; sample<temp_x.Rows(); sample++)
                  {                                        
                     // yixiw-b≥1
                     
                      if (temp_y[sample] * hyperplane(temp_x.Row(sample))  >= 1) 
                        {
                          this.W -= config.alpha * (2 * config.lambda * this.W); // w = w + α* (2λw - yixi)
                        }
                      else
                         {
                           this.W -= config.alpha * (2 * config.lambda * this.W - ( temp_x.Row(sample) * temp_y[sample] )); // w = w + α* (2λw - yixi)
                           
                           this.B -= config.alpha * temp_y[sample]; // b = b - α* (yi)
                         }  
                  }
           }
        
        //--- Print the loss at the end of an epoch
       
         is_fitted_already = true;  
         
         preds = this.predict(X);
         
         loss[epoch] = preds.Loss(Y, LOSS_BCE);
        
         printf("---> epoch [%d/%d] Loss = %f Accuracy = %f",epoch+1,config.epochs,loss[epoch],metrics.confusion_matrix(Y, preds, false));
         
        #ifdef DEBUG_MODE:  
          Print("W\n",W," B = ",B);  
        #endif   
      }
    
    during_training = false;
    
    return;
 }


    Получение прогнозов из модели линейного опорного вектора

    Чтобы получить прогнозы из нашей модели, нужно передать данные в функцию знака после того, как гиперплоскость дала результат.

    int CLinearSVM::predict(vector &x)
 { 
   if (!is_fitted_already)
     {
       Print("Err | The model is not trained, call the fit method to train the model before you can use it");
       return 1000;
     }
   
   vector temp_x = x;
   if (!during_training)
     normalize_x.Normalization(temp_x); //Normalize a new input data when we are not running the model in training 
     
   return sign(hyperplane(temp_x));
 }


    Обучение и тестирование модели линейного опорного вектора

    Нужно протестировать модель, прежде чем ее развернуть, чтобы делать какие-либо значимые прогнозы по рыночным данным. Начнем с инициализации экземпляра класса Linear SVM.

    #include <MALE5\Support Vector Machine(SVM)\svm.mqh>
CLinearSVM *svm;

input uint bars = 1000;
input uint epochs_ = 1000;
input uint batch_size_ = 64;
input double alpha__ =0.1;
input double lambda_ = 0.01;

bool train_once;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---          
    svm = new CLinearSVM(batch_size_, alpha__, epochs_, lambda_);
    train_once = false;
//---

   return(INIT_SUCCEEDED);
  }

    Мы продолжим сбор данных. Будем использовать 4 независимые переменные: RSI, HIGH BANDS BOLLINGER, LOW и MID.

    vec_.CopyIndicatorBuffer(rsi_handle, 0, 0, bars);
dataset.Col(vec_, 0);
vec_.CopyIndicatorBuffer(bb_handle, 0, 0, bars);
dataset.Col(vec_, 1);
vec_.CopyIndicatorBuffer(bb_handle, 1, 0, bars);
dataset.Col(vec_, 2);
vec_.CopyIndicatorBuffer(bb_handle, 2, 0, bars);
dataset.Col(vec_, 3);

open.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_OPEN, 0, bars);
close.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_CLOSE, 0, bars);
      
for (ulong i=0; i<vec_.Size(); i++) //preparing the independent variable
   dataset[i][4] = close[i] > open[i] ? 1 : -1; // if price closed above its opening thats bullish else bearish

    Завершаем процесс сбора данных, делим данные на обучающую и тестовую выборки.

    matrix_utils.TrainTestSplitMatrices(dataset,train_x,train_y,test_x,test_y,0.7,42); //split the data into training and testing samples


    Обучение/Подбор модели

    svm.fit(train_x, train_y);

    Результат

            0       15:15:42.394    svm test (EURUSD,H1)    ---> epoch [1/1000] Loss = 7.539322 Accuracy = 0.489000
IK      0       15:15:42.395    svm test (EURUSD,H1)    ---> epoch [2/1000] Loss = 7.499849 Accuracy = 0.491000
EG      0       15:15:42.395    svm test (EURUSD,H1)    ---> epoch [3/1000] Loss = 7.499849 Accuracy = 0.494000
....
....
GG      0       15:15:42.537    svm test (EURUSD,H1)    ---> epoch [998/1000] Loss = 6.907756 Accuracy = 0.523000
DS      0       15:15:42.537    svm test (EURUSD,H1)    ---> epoch [999/1000] Loss = 7.006438 Accuracy = 0.521000
IM      0       15:15:42.537    svm test (EURUSD,H1)    ---> epoch [1000/1000] Loss = 6.769601 Accuracy = 0.516000

    Наблюдаем за точностью модели как при обучении, так и при тестировании.

    vector train_pred = svm.predict(train_x), 
    test_pred = svm.predict(test_x);

printf("Train accuracy = %f",metrics.confusion_matrix(train_y, train_pred, true));
printf("Test accuracy = %f ",metrics.confusion_matrix(test_y, test_pred, true));

    Результат

    CH      0       15:15:42.538    svm test (EURUSD,H1)    Confusion Matrix
IQ      0       15:15:42.538    svm test (EURUSD,H1)    [[171,175]
HE      0       15:15:42.538    svm test (EURUSD,H1)     [164,190]]
DQ      0       15:15:42.538    svm test (EURUSD,H1)    
NO      0       15:15:42.538    svm test (EURUSD,H1)    Classification Report
JD      0       15:15:42.538    svm test (EURUSD,H1)    
LO      0       15:15:42.538    svm test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
JQ      0       15:15:42.538    svm test (EURUSD,H1)    -1.0    0.51     0.49     0.54       0.50     346.0
DH      0       15:15:42.538    svm test (EURUSD,H1)    1.0    0.52     0.54     0.49       0.53     354.0
HL      0       15:15:42.538    svm test (EURUSD,H1)    
FG      0       15:15:42.538    svm test (EURUSD,H1)    Accuracy                                   0.52
PP      0       15:15:42.538    svm test (EURUSD,H1)    Average   0.52    0.52    0.52      0.52    700.0
PS      0       15:15:42.538    svm test (EURUSD,H1)    W Avg     0.52    0.52    0.52      0.52    700.0
FK      0       15:15:42.538    svm test (EURUSD,H1)    Train accuracy = 0.516000

MS      0       15:15:42.538    svm test (EURUSD,H1)    Confusion Matrix
LI      0       15:15:42.538    svm test (EURUSD,H1)    [[79,74]
CM      0       15:15:42.538    svm test (EURUSD,H1)     [68,79]]
FJ      0       15:15:42.538    svm test (EURUSD,H1)    
HF      0       15:15:42.538    svm test (EURUSD,H1)    Classification Report
DM      0       15:15:42.538    svm test (EURUSD,H1)    
NH      0       15:15:42.538    svm test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
NN      0       15:15:42.538    svm test (EURUSD,H1)    -1.0    0.54     0.52     0.54       0.53     153.0
PQ      0       15:15:42.538    svm test (EURUSD,H1)    1.0    0.52     0.54     0.52       0.53     147.0
JE      0       15:15:42.538    svm test (EURUSD,H1)    
GP      0       15:15:42.538    svm test (EURUSD,H1)    Accuracy                                   0.53
RI      0       15:15:42.538    svm test (EURUSD,H1)    Average   0.53    0.53    0.53      0.53    300.0
JH      0       15:15:42.538    svm test (EURUSD,H1)    W Avg     0.53    0.53    0.53      0.53    300.0
DO      0       15:15:42.538    svm test (EURUSD,H1)    Test accuracy = 0.527000

    Модель показала точность в 53% в предсказаниях вне выборки. Кто-то может сказать, что это плохая модель, но я бы сказал, что она средняя. Такие результаты могут быть связаны с множеством факторов, включая ошибки в модели, плохую нормализацию, критерии сходимости и многое другое. Можете поэкспериментировать с параметрами и попытаться улучшить результат. Однако, вероятнее всего дело в том, что данные слишком сложны для линейной модели. В этом я почти уверен, поэтому попробуем двойной метод SVM и посмотри, покажет ли она лучшие результаты.

    Двойной метод SVM будем изучать в формате ONXX Python. Мне не удалось получить модель на MQL5, чтобы которая могла бы достаточно хорошо приблизиться к производительности и точности модели python sklearn. Именно поэтому продолжим работать над двойным методом SVM в Python. Тем не менее я приложил библиотеку Dual SVM на MQL5 в основном файле svm.mqh — он приложен к этой статье, а также доступен в моем GitHub, ссылка на который находится в конце этой статьи.

    Чтобы запустить метод двойного SVM в Python, нам нужно собрать данные и нормализовать их с помощью MQL5. Нам потребуется создать новый класс с именем CDualSVMONNX внутри файла svm.mqh. Этот класс будет отвечать за работу с моделью ONNX, полученной из Python.

    class CDualSVMONNX
  {
private:
      CPreprocessing<vectorf, matrixf> *normalize_x;
      CMatrixutils matrix_utils;
      
      struct data_struct
       {
         ulong rows,
               cols;
       } df;
      
public:  
                     CDualSVMONNX(void);
                    ~CDualSVMONNX(void);
      
                     long onnx_handle;              
                     
                     void SendDataToONNX(matrixf &data, string csv_name = "DualSVMONNX-data.csv", string csv_header="");
                     bool LoadONNX(const uchar &onnx_buff[], ENUM_ONNX_FLAGS flags=ONNX_NO_CONVERSION);
                     int Predict(vectorf &inputs);
                     vector Predict(matrixf &inputs);
  };

    Это общий обзор класса. 


    Сбор и нормализация данных

    Нам нужны данные для нашей модели, на которых можно учиться. Эти данные нужно очистить, чтобы они подходили для нашей модели SVM:

    void CDualSVMONNX::SendDataToONNX(matrixf &data, string csv_name = "DualSVMONNX-data.csv", string csv_header="")
 {
    df.cols = data.Cols();
    df.rows = data.Rows();
    
    if (df.cols == 0 || df.rows == 0)
      {
         Print(__FUNCTION__," data matrix invalid size ");
         return;
      }
    
    matrixf split_x;
    vectorf  split_y;
    
    matrix_utils.XandYSplitMatrices(data, split_x, split_y); //since we are going to be normalizing the independent variable only we need to split the data into two
    
    normalize_x = new CPreprocessing<vectorf,matrixf>(split_x, NORM_MIN_MAX_SCALER); //Normalizing Independent variable only
    
    
    matrixf new_data = split_x;
    new_data.Resize(data.Rows(), data.Cols());
    new_data.Col(split_y, data.Cols()-1);
    
    if (csv_header == "")
      {
         for (ulong i=0; i<df.cols; i++)
           csv_header += "COLUMN "+string(i+1) + (i==df.cols-1 ? "" : ","); //do not put delimiter on the last column
      }
    
//--- Save the Normalization parameters also
    
   matrixf params = {};
    
   string sep=",";
   ushort u_sep;
   string result[];
   
   u_sep=StringGetCharacter(sep,0); 
   int k=StringSplit(csv_header,u_sep,result); 
   
   ArrayRemove(result, k-1, 1); //remove the last column header since we do not have normalization parameters for the target variable  as it is not normalized
    
    normalize_x.min_max_scaler.min.Swap(params);
    matrix_utils.WriteCsv("min_max_scaler.min.csv",params,result,false,8);
    normalize_x.min_max_scaler.max.Swap(params);
    matrix_utils.WriteCsv("min_max_scaler.max.csv",params,result,false,8); 
    
//--- 
    
    matrix_utils.WriteCsv(csv_name, new_data, csv_header, false, 8); //Save dataset to a csv file 
 }

    Поскольку сбор данных для обучения необходимо выполнять один раз, используем для этого скрипт.

    Скрипт GetDataforONNX.mq5

    #include <MALE5\Support Vector Machine(SVM)\svm.mqh>

CDualSVMONNX dual_svm;

input uint bars = 1000;
input uint epochs_ = 1000;
input uint batch_size_ = 64;
input double alpha__ =0.1;
input double lambda_ = 0.01;

input int rsi_period = 13;
input int bb_period = 20;
input double bb_deviation = 2.0;

int rsi_handle, 
    bb_handle;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
  
    rsi_handle = iRSI(Symbol(),PERIOD_CURRENT,rsi_period, PRICE_CLOSE);
    bb_handle = iBands(Symbol(), PERIOD_CURRENT, bb_period,0, bb_deviation, PRICE_CLOSE);
    
//---

    matrixf data = GetTrainTestData<float>();
    dual_svm.SendDataToONNX(data,"DualSVMONNX-data.csv","rsi,bb-high,bb-low,bb-mid,target");
  }
//+------------------------------------------------------------------+
//|   Getting data for Training and Testing the model                |
//+------------------------------------------------------------------+
template <typename T>
matrix<T> GetTrainTestData()
 {
   matrix<T> data(bars, 5);
   vector<T> v; //Temporary vector for storing Indicator buffers
    
   v.CopyIndicatorBuffer(rsi_handle, 0, 0, bars);
   data.Col(v, 0);
   v.CopyIndicatorBuffer(bb_handle, 0, 0, bars);
   data.Col(v, 1);
   v.CopyIndicatorBuffer(bb_handle, 1, 0, bars);
   data.Col(v, 2);
   v.CopyIndicatorBuffer(bb_handle, 2, 0, bars);
   data.Col(v, 3);
   
   vector open, close;
   open.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_OPEN, 0, bars);
   close.CopyRates(Symbol(), PERIOD_CURRENT, COPY_RATES_CLOSE, 0, bars);
   
   for (ulong i=0; i<v.Size(); i++) //preparing the independent variable
     data[i][4] = close[i] > open[i] ? 1 : -1; // if price closed above its opening thats bullish else bearish
     
   return data;  
 }

    Результат

    В папке Files в директории MQL5 был создан файл под названием DualSVMONNX-data.csv.

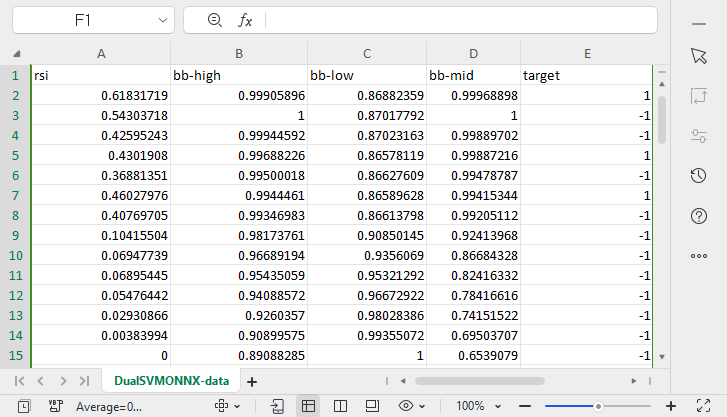
    Обратите внимание на окончание функции SendDataToONNX .

    Я также сохранил параметры нормализации.

    normalize_x.min_max_scaler.min.Swap(params);
matrix_utils.WriteCsv("min_max_scaler.min.csv",params,result,false,8);
normalize_x.min_max_scaler.max.Swap(params);
matrix_utils.WriteCsv("min_max_scaler.max.csv",params,result,false,8);

    Использованные параметры нормализации мы используем снова, чтобы получить наилучшие прогнозы от модели. Поэтому сохранение данных поможет отслеживать значения параметров нормализации. Файлы CSV будут находиться в той же папке, что и набор данных. Также мы сохраним там модель ONNX.


    Экземпляр класса DualSVMONNX. Инициализация класса

    class DualSVMONNX:
    def __init__(self, dataset, c=1.0, kernel='rbf'):
        
        data = pd.read_csv(dataset) # reading a csv file 
        np.random.seed(42)
        
        self.X = data.drop(columns=['target']).astype(np.float32) # dropping the target column from independent variable 
        self.y = data["target"].astype(int) # storing the target variable in its own vector 
        
        self.X = self.X.to_numpy()
        self.y = self.y.to_numpy()            

        # Split the data into training and testing sets
        self.X_train, self.X_test, self.y_train, self.y_test = train_test_split(self.X, self.y, test_size=0.2, random_state=42) 

        self.onnx_model_name = "DualSVMONNX" #our final onnx model file name for saving purposes really
        
        # Create a dual SVM model with a kernel
        
        self.svm_model = SVC(kernel=kernel, C=c)


    Обучение модели Dual SVM на Python

        def fit(self):
        
        self.svm_model.fit(self.X_train, self.y_train) # fitting/training the model
        
        y_preds = self.svm_model.predict(self.X_train)
        
        print("accuracy = ",accuracy_score(self.y_train, y_preds))        

    После обучения модели давайте посмотрим, какой будет точность после запуска этого фрагмента кода.

    Результат


    Мы получили точность 63%, что говорит о том, что модель SVM для классификации этой конкретной проблемы в лучшем случае является средней. Однако, проведем перекрестную проверку, чтобы понять, является ли точность такой, какой она должна быть:

            scores = cross_val_score(self.svm_model, self.X_train, self.y_train, cv=5)
        mean_cv_accuracy = np.mean(scores)

        print(f"\nscores {scores} mean_cv_accuracy {mean_cv_accuracy}")

    Результат


    Что означает такой результат перекрестной проверки? 

    При запуске модели с разными параметрами нет большой разницы между результатами. Это говорит нам о том, что наша модель находится на правильном пути. Средняя точность, которую мы смогли получить, составляет 59,875, что недалеко от полученных нами 63,3.


    Преобразование модели опорного вектора из sklearn в ONNX

        def saveONNX(self):                 
        
        initial_type = [('float_input', FloatTensorType(shape=[None, 4]))]  # None means we don't know the rows but we know the columns for sure, Remember !! we have 4 independent variables
        onnx_model = convert_sklearn(self.svm_model, initial_types=initial_type) # Convert the scikit-learn model to ONNX format

        onnx.save_model(onnx_model, dataset_path + f"\\{self.onnx_model_name}.onnx") #saving the onnx model

    Модель сохранили в каталоге MQL5/Files.

    Ниже показано, как выглядит файл ONNX при открытии в MetaEditor. Обратите внимание на разъяснение процесса. Это важно.

    Onnx-файл изнутри

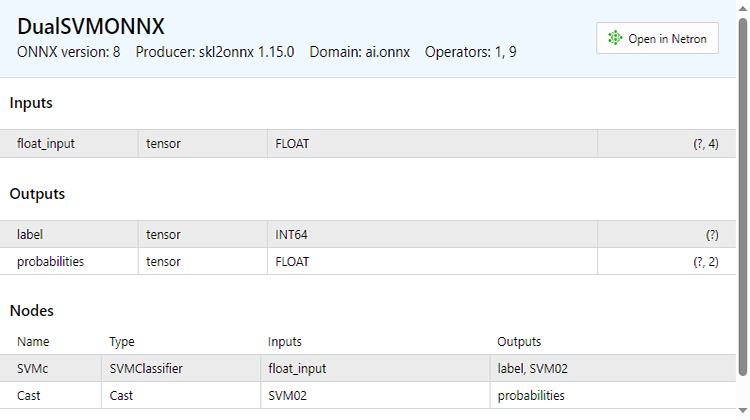
    В разделе входных параметров у нас есть float_input — параметр типа float. Далее 'tensor' означает, что нам нужно передать на вход функции OnnxRun матрицу или вектор, поскольку оба являются тензорами. В конце указано (?, 4) — размер входов, при этом ? обозначает, что количество строк неизвестно; количество столбцов равно 4. Далее идет часть Outputs.

    В нем у нас два узла — один дает предсказанные метки -1 или 1, которые в данном случае они тип INT64 или INT в mql5.

    Второй узел с вероятностями, это тензор типов float, в нем 2 столбца и неизвестное количество строк. Для извлечения значений можно использовать матрицу nx2 или просто вектор размером >= 2.

    Поскольку в выходных данных есть два узла, мы можем извлечь результаты дважды:

       long outputs_0[] = {1};
   if (!OnnxSetOutputShape(onnx_handle, 0, outputs_0)) //giving the onnx handle first node output shape
     {
       Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError());
       return false;
     }
     
   long outputs_1[] = {1,2};
   if (!OnnxSetOutputShape(onnx_handle, 1, outputs_1)) //giving the onnx handle second node output shape
     {
       Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError());
       return false;
     }

    С другой стороны, можно извлечь один входной узел.

       const long inputs[] = {1,4};
   
   if (!OnnxSetInputShape(onnx_handle, 0, inputs)) //Giving the Onnx handle the input shape
     {
       Print(__FUNCTION__," Failed to set the input shape Err=",GetLastError());
       return false;
     }  

    Этот код ONNX был получен из функции LoadONNX, показанной ниже:

    bool CDualSVMONNX::LoadONNX(const uchar &onnx_buff[], ENUM_ONNX_FLAGS flags=ONNX_NO_CONVERSION)
 {
   onnx_handle =  OnnxCreateFromBuffer(onnx_buff, flags); //creating onnx handle buffer 
   
   if (onnx_handle == INVALID_HANDLE)
    {
       Print(__FUNCTION__," OnnxCreateFromBuffer Error = ",GetLastError());
       return false;
    }
   
//---
   
   const long inputs[] = {1,4};
   
   if (!OnnxSetInputShape(onnx_handle, 0, inputs)) //Giving the Onnx handle the input shape
     {
       Print(__FUNCTION__," Failed to set the input shape Err=",GetLastError());
       return false;
     }
   
   long outputs_0[] = {1};
   if (!OnnxSetOutputShape(onnx_handle, 0, outputs_0)) //giving the onnx handle first node output shape
     {
       Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError());
       return false;
     }
     
   long outputs_1[] = {1,2};
   if (!OnnxSetOutputShape(onnx_handle, 1, outputs_1)) //giving the onnx handle second node output shape
     {
       Print(__FUNCTION__," Failed to set the output shape Err=",GetLastError());
       return false;
     }

   return true;
 }

    Посмотрите внимательно на функцию, которой, как вы могли догадаться, нам не хватает при загрузке параметров нормализации. Эти параметры очень важны для стандартизации новых входных данных, чтобы они соответствовали размерам обученных данных, с которыми модель уже знакома.

    Можно загрузить параметры из файла CSV - это работает без проблем на время реальной торговле. Однако этот метод может оказаться сложным и не всегда работать нормально в тестере стратегий. Поэтому на данный момент скопируем параметры нормализации в код нашего советника вручную. В итоге мы получим параметры нормализации внутри нашего советника. Сначала изменим функцию LoadONNX, чтобы она принимала входные векторы max и min, которые используются в Min Max Scaler.

    bool CDualSVMONNX::LoadONNX(const uchar &onnx_buff[], ENUM_ONNX_FLAGS flags, vectorf &norm_max, vectorf &norm_min)

    Окончание этой функции.

    normalize_x = new CPreprocessing<vectorf,matrixf>(norm_max, norm_min); //Load min max scaler with parameters

    Копирование и вставка параметров нормализации из файлов CSV в советники.


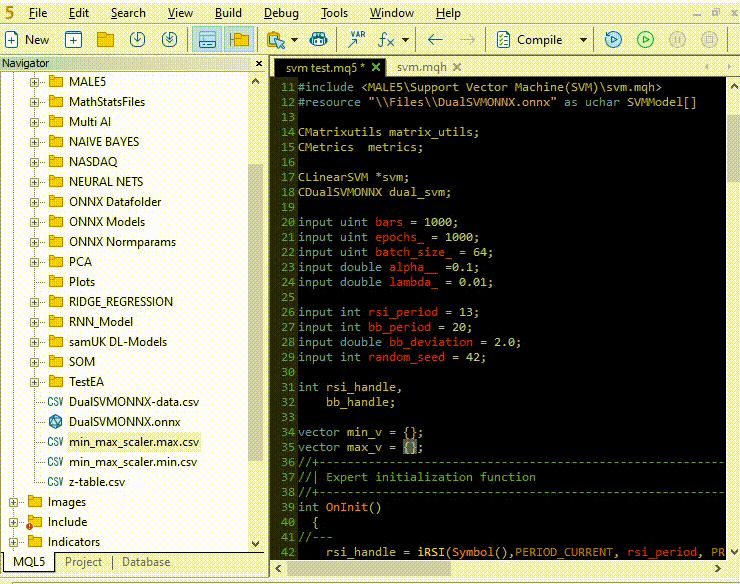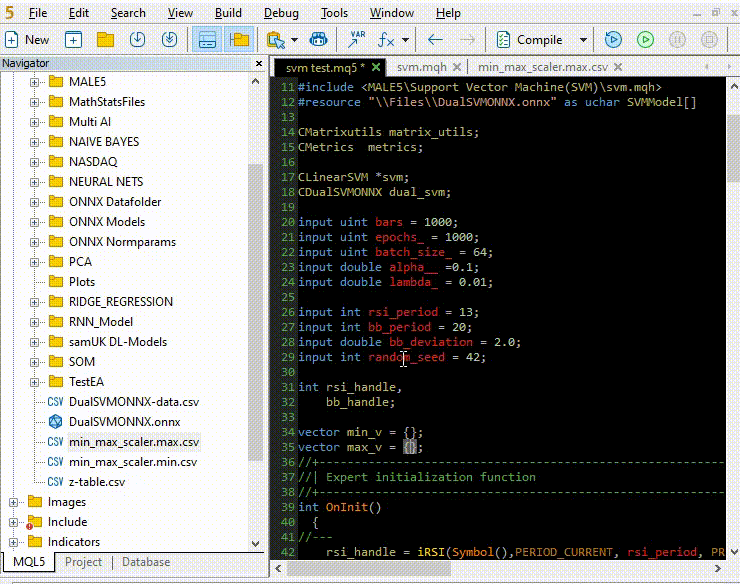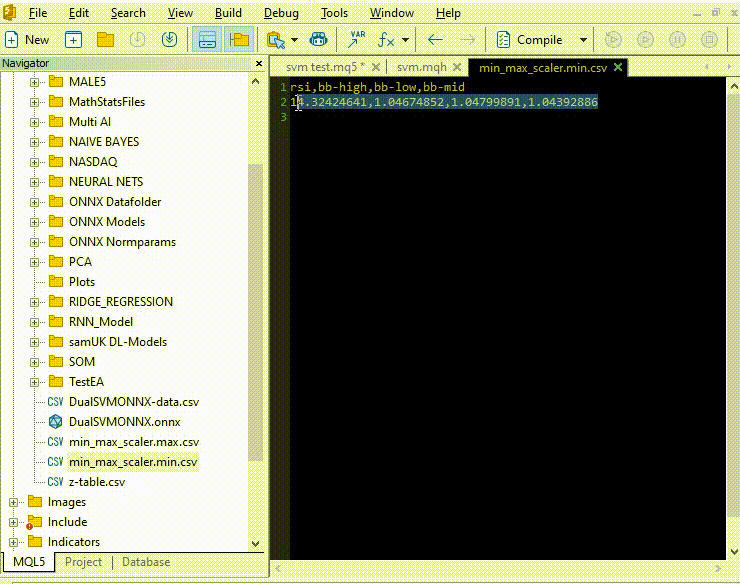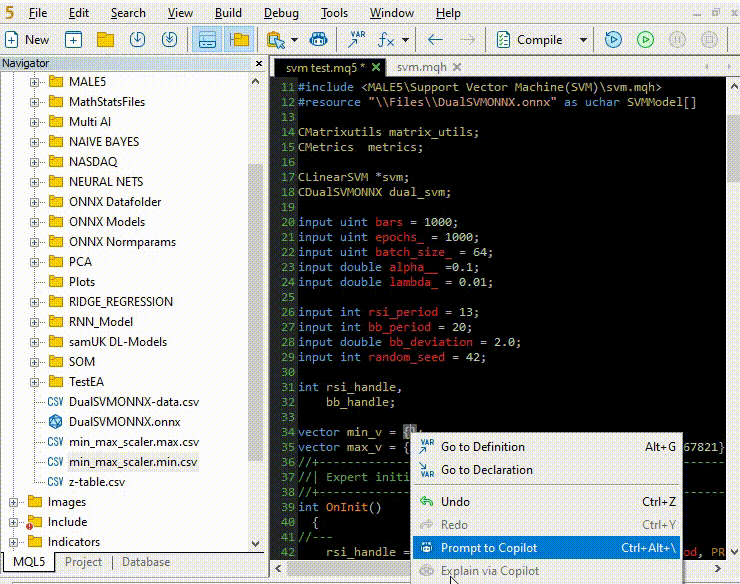
    Давайте обучим и попробуем протестировать модель так же, как мы это делали с Python. Наша цель — убедиться, что мы идем по одному и тому же пути на обоих языках.

    Функция OnInit в тестовом советнике test.mq5

    vector min_v = {14.32424641,1.04674852,1.04799891,1.04392886};
vector max_v = {86.28263092,1.07385755,1.07907069,1.07267821};
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---    
    rsi_handle = iRSI(Symbol(),PERIOD_CURRENT, rsi_period, PRICE_CLOSE);
    bb_handle = iBands(Symbol(), PERIOD_CURRENT, bb_period, 0 , bb_deviation, PRICE_CLOSE);

    
      vector y_train,
             y_test;
        
    // float values
      
      matrixf datasetf = GetTrainTestData<float>();
      matrixf x_trainf,
              x_testf;
      
      vectorf y_trainf,
              y_testf;
            
//---
      
      matrix_utils.TrainTestSplitMatrices(datasetf,x_trainf,y_trainf,x_testf,y_testf,0.8,42); //split the data into training and testing samples
      
      vectorf max_vf = {}, min_vf = {}; //convertin the parameters into float type
      max_vf.Assign(max_v); 
      min_vf.Assign(min_v);
      
      dual_svm.LoadONNX(SVMModel, ONNX_DEFAULT, max_vf, min_vf);
            
      y_train.Assign(y_trainf);
      y_test.Assign(y_testf);
      
      vector train_preds = dual_svm.Predict(x_trainf);
      vector test_preds = dual_svm.Predict(x_testf);
      
      Print("\n<<<<< Train Classification Report >>>>\n");
      metrics.confusion_matrix(y_train, train_preds);
      
      Print("\n<<<<< Test  Classification Report >>>>\n");
      metrics.confusion_matrix(y_test, test_preds);


   return(INIT_SUCCEEDED);
  }
    Результат 
    RP      0       17:08:53.068    svm test (EURUSD,H1)    <<<<< Train Classification Report >>>>
HE      0       17:08:53.068    svm test (EURUSD,H1)    
MR      0       17:08:53.068    svm test (EURUSD,H1)    Confusion Matrix
IG      0       17:08:53.068    svm test (EURUSD,H1)    [[245,148]
CO      0       17:08:53.068    svm test (EURUSD,H1)     [150,257]]
NK      0       17:08:53.068    svm test (EURUSD,H1)    
DE      0       17:08:53.068    svm test (EURUSD,H1)    Classification Report
HO      0       17:08:53.068    svm test (EURUSD,H1)    
FI      0       17:08:53.068    svm test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
ON      0       17:08:53.068    svm test (EURUSD,H1)    1.0    0.62     0.62     0.63       0.62     393.0
DP      0       17:08:53.068    svm test (EURUSD,H1)    -1.0    0.63     0.63     0.62       0.63     407.0
JG      0       17:08:53.068    svm test (EURUSD,H1)    
FR      0       17:08:53.068    svm test (EURUSD,H1)    Accuracy                                   0.63
CK      0       17:08:53.068    svm test (EURUSD,H1)    Average   0.63    0.63    0.63      0.63    800.0
KI      0       17:08:53.068    svm test (EURUSD,H1)    W Avg     0.63    0.63    0.63      0.63    800.0
PP      0       17:08:53.068    svm test (EURUSD,H1)    
DH      0       17:08:53.068    svm test (EURUSD,H1)    <<<<< Test  Classification Report >>>>
PQ      0       17:08:53.068    svm test (EURUSD,H1)    
EQ      0       17:08:53.068    svm test (EURUSD,H1)    Confusion Matrix
HJ      0       17:08:53.068    svm test (EURUSD,H1)    [[61,31]
MR      0       17:08:53.068    svm test (EURUSD,H1)     [40,68]]
NH      0       17:08:53.068    svm test (EURUSD,H1)    
DP      0       17:08:53.068    svm test (EURUSD,H1)    Classification Report
HL      0       17:08:53.068    svm test (EURUSD,H1)    
FF      0       17:08:53.068    svm test (EURUSD,H1)    _    Precision  Recall  Specificity  F1 score  Support
GJ      0       17:08:53.068    svm test (EURUSD,H1)    -1.0    0.60     0.66     0.63       0.63     92.0
PO      0       17:08:53.068    svm test (EURUSD,H1)    1.0    0.69     0.63     0.66       0.66     108.0
DD      0       17:08:53.068    svm test (EURUSD,H1)    
JO      0       17:08:53.068    svm test (EURUSD,H1)    Accuracy                                   0.65
LH      0       17:08:53.068    svm test (EURUSD,H1)    Average   0.65    0.65    0.65      0.64    200.0
CJ      0       17:08:53.068    svm test (EURUSD,H1)    W Avg     0.65    0.65    0.65      0.65    200.0

    Мы снова получили те же 63% точности, что со скриптом на Python. Разве это не чудесно?

    Вот как функция прогнозирования выглядит изнутри:

    int CDualSVMONNX::Predict(vectorf &inputs)
 {
    vectorf outputs(1); //label outputs
    vectorf x_output(2); //probabilities
    
    vectorf temp_inputs = inputs;
    
    normalize_x.Normalization(temp_inputs); //Normalize the input features
    
    if (!OnnxRun(onnx_handle, ONNX_DEFAULT, temp_inputs, outputs, x_output))
      {
         Print("Failed to get predictions from onnx Err=",GetLastError());
         return (int)outputs[0];
      }
      
   return (int)outputs[0];
 }

    Он запускает файл ONNX для получения прогнозов и возвращает целое число для прогнозируемой метки.

    Далее мы реализовали простую стратегию, чтобы протестировать обе модели метода опорных векторов в тестере стратегий. Стратегия проста: если прогнозный класс SVM == 1, открываем сделку на покупку, в противном случае, если прогнозный класс == -1, открываем сделку на продажу.

    Результаты в тестере стратегий:

    Для линейного метода опорных векторов:

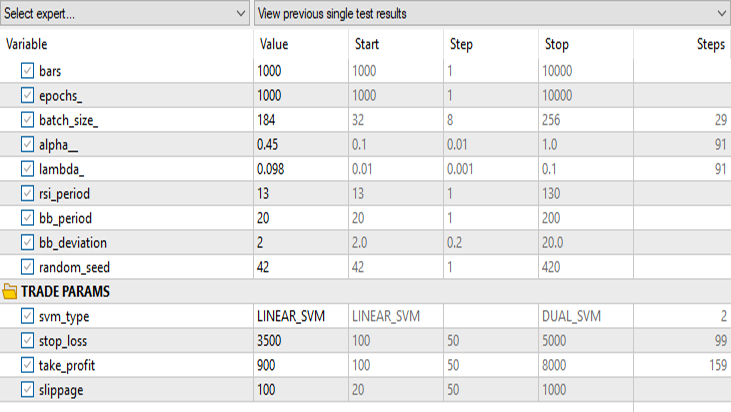
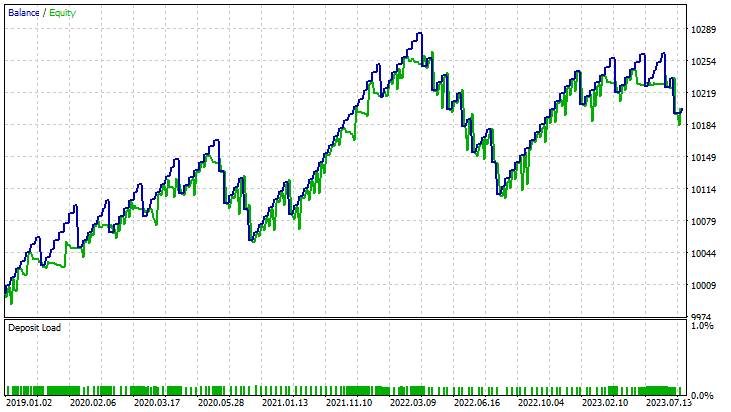
    Для двойной формулы метода опорных векторов:

    Сохраняем все те же входные данные, кроме svm_type.


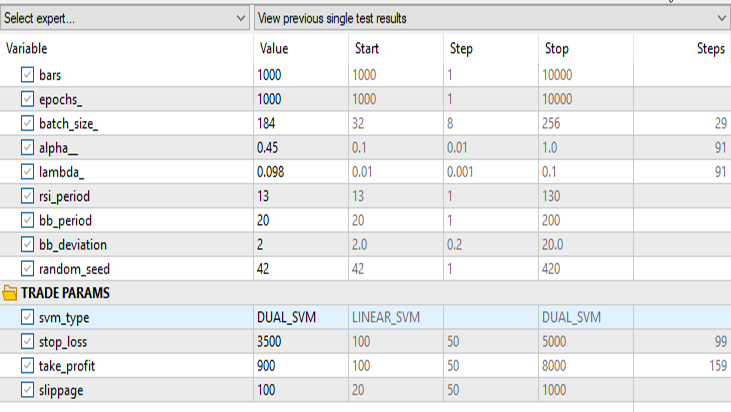
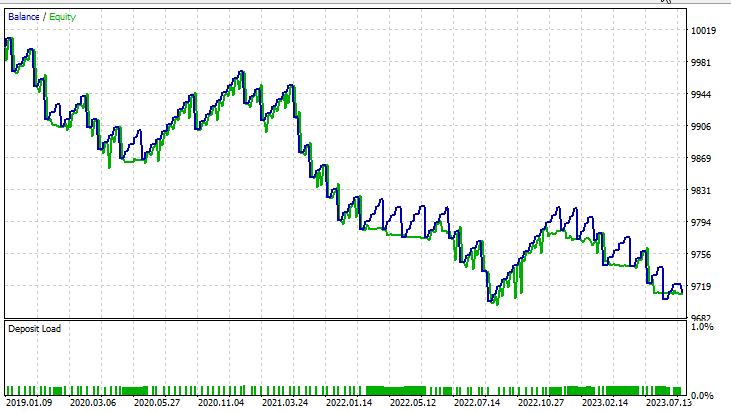
    Двойная форма SVM не очень хорошо показала себя при входных данными, которые работали для линейной SVM. Возможно, потребуется дальнейшая оптимизация и изучение того, почему модель ONNX не сходится, но это тема для другой статьи.


    Заключительные мысли

    Преимущества моделей опорных векторов SVM

    1. Эффективная работа в многомерных пространствах, т.е. метод опорных векторов подходит для работы с выборками финансовых данных с многочисленными функциями, торговыми индикаторами и рыночными переменными.
    2. Опорные вектора менее склонны к переобучению, дают более обобщенное решение, которое может лучше адаптироваться к невидимым рыночным условиям.
    3. Модели SVM обеспечивают универсальность благодаря различным функциям ядра, позволяя трейдерам экспериментировать с различными стратегиями и адаптировать модель к конкретным рыночным моделям.
    4. Методы SVM хорошо фиксируют нелинейные связи внутри данных, что является решающим аспектом при работе со сложными финансовыми рынками.

    Минусы

    1. SVM могут быть чувствительны к зашумленным данным, что влияет на их результаты и делает их более восприимчивыми к неустойчивому поведению рынка.
    2. Обучение моделей SVM может быть дорогостоящим в отношении вычислительных ресурсов, особенно при работе с большими наборами данных, что ограничивает их масштабируемость в определенных сценариях торговли в реальном времени.
    3. Опорные вектора в значительной степени полагаются на разработку функций, требуя знаний в предметной области для выбора соответствующих индикаторов и эффективной предварительной обработки данных.
    4. Как мы видели, модели на SVM показали среднюю точность до 63% при двойной форме и 59% при линейной. Хотя эти модели, возможно, и не превосходят некоторые передовые методы машинного обучения, они все же предлагают разумную отправную точку для трейдеров MQL5.

    Падение популярности

    Несмотря на успех в прошлом, в последние годы популярность SVM снизилась. Возможно, это связано со следующим:

    1. Развитие методов глубокого обучения, особенно нейронных сетей, перекрыло традиционные алгоритмы машинного обучения благодаря своей способности автоматически извлекать иерархические функции.
    2. Обширные наборы финансовых данных становятся все более доступными, поэтому модели глубокого обучения, которые успешно работают с большими объемами данных, стали более привлекательными.
    3. Появление мощного оборудования и распределенных вычислительных ресурсов сделало более возможным обучение и развертывание сложных моделей глубокого обучения.

    В заключение, хотя модели SVM, возможно, и не являются передовым решением, их использование в торговых средах MQL5 оправдано. Простота, надежность и адаптируемость делают их ценным инструментом, особенно для трейдеров с ограниченными данными или вычислительными ресурсами. Опорные вектора можно рассматривать как часть более широкого набора инструментов, потенциально дополняя их новыми подходами машинного обучения по мере развития динамики рынка.

    Спасибо за внимание.

    Файл Описание | Применение
     dual_svm.py | python script  Реализация Dual SVM на Python.
     GetDataforONNX.mq5 | mql5 script  Можно использовать для сбора, нормализации и хранения данных в файле csv, расположенном в папке MQL5/Files.
     preprocessing.mqh | mql5 include file  Содержит класс и функции для нормализации и стандартизации входных данных.
     matrix_utils.mqh | mql5 include file  Библиотека с дополнительными матричными операциями. 
     metrics.mqh | mql5 include file  Библиотека, содержащая дополнительные функции для анализа производительности моделей машинного обучения. 
     svm test.mq5 | EA  Советник для тестирования всего кода, который есть в статье.  

    Код, используемый в этой статье, также можно найти в моем репозитории в GitHub.


    Перевод с английского произведен MetaQuotes Ltd.
    Оригинальная статья: https://www.mql5.com/en/articles/13395

    Прикрепленные файлы |
    Загрузить ZIP
    code.zip (25.53 KB)
    Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

    Другие статьи автора

    Перейти к обсуждению на форуме трейдеров
    Нейросети — это просто (Часть 81): Анализ динамики данных с учетом контекста (CCMR) Нейросети — это просто (Часть 81): Анализ динамики данных с учетом контекста (CCMR)
    В предыдущих работах мы всегда оценивали текущее состояния окружающей среды. При этом динамика изменения показателей, как таковая, всегда оставалась "за кадром". В данной статье я хочу познакомить Вас с алгоритмом, который позволяет оценить непосредственное изменение данных между 2 последовательными состояниями окружающей среды.
    Создаем простой мультивалютный советник с использованием MQL5 (Часть 3): Префиксы/суффиксы символов и торговая сессия Создаем простой мультивалютный советник с использованием MQL5 (Часть 3): Префиксы/суффиксы символов и торговая сессия
    Я получил комментарии от нескольких коллег-трейдеров о том, как использовать рассматриваемый мной мультивалютный советник у брокеров, использующих префиксы и/или суффиксы с именами символов, а также о том, как реализовать в советнике торговые часовые пояса или торговые сессии.
    Опыт разработки торговой стратегии Опыт разработки торговой стратегии
    В этой статье мы сделаем попытку разработать собственную торговую стратегию. Любая торговая стратегия должна быть построена на основе какого-то статистического преимущества. Причем, это преимущество должно существовать в течение долгого времени.
    Гибридизация популяционных алгоритмов. Последовательная и параллельная схема Гибридизация популяционных алгоритмов. Последовательная и параллельная схема
    В статье мы погрузимся в мир гибридизации алгоритмов оптимизации, рассмотрев три ключевых типа: смешивание стратегий, последовательную и параллельную гибридизации. Мы проведем серию экспериментов, сочетая и тестируя соответствующие алгоритмы оптимизации.