データサイエンスと機械学習（第24回）：通常のAIモデルによるFX時系列予測

MetaTrader 5 — トレーディング | 14 8月 2024, 11:32

Omega J Msigwa

内容

時系列予測とは？

時系列予測とは、一連のデータポイントにおける将来の値を予測するために過去のデータを使用するプロセスです。このシーケンスは通常、時間順に並べられるため、時系列と呼ばれます。

時系列データの中核変数

データにはいくらでも特徴量変数を持たせることができますが、時系列分析や予測のためのデータには、必ずこの2つの変数が必要です。

時間

これは独立変数で、データポイントが観測された特定の時点を表します。
目標変数

これは、過去の観測と潜在的に他の要因に基づいて予測しようとしている値です。(例：毎日の終値、1時間ごとの気温、1分ごとのWebサイトのトラフィック）。

時系列予測の目的は、データ内の過去のパターンとトレンドを活用して、将来の値について情報に基づいた予測をおこなうことです。

mql5時系列予測画像

この記事は、読者がONNX、シリーズ予測、Light Gradient Boosting Machine(LightGBM)の基本的な理解を持っていることを前提としています。まだお読みでない方は、これらの記事をお読みください。

時系列予測はなぜ、どこで使われるのか？

時系列分析と予測は、以下のシナリオで使用することができます。

将来価値の予測
過去の行動の理解
過去に左右されかねない未来への計画
現在の業績の評価

古典的現代的機械学習モデルと時系列ベースの機械学習モデルの比較

これまでの記事で説明した線形回帰、サポートベクターマシン(SVM)、ニューラルネットワーク(NN)などの、特徴変数間の関係を決定し、学習した関係に基づいて将来の予測を行うことを目的とする古典的な機械学習モデルとは異なり、時系列モデルは、以前に観測された値に基づいて将来の値を予測します。

このアプローチの違いは、時系列モデルが逐次データに固有の時間的依存性とパターンを扱うために特別に設計されていることを意味します。ARIMA、SARIMA、指数平滑化、RNN、LSTM、GRUなどの時系列予測モデルは、過去のデータを活用して、トレンド、季節性、その他の時間的構造を捉え、系列の将来のポイントを予測します。

以下のフローチャートは、時系列予測に使用される様々な機械学習モデルを示しています。

時系列予測MLモデル

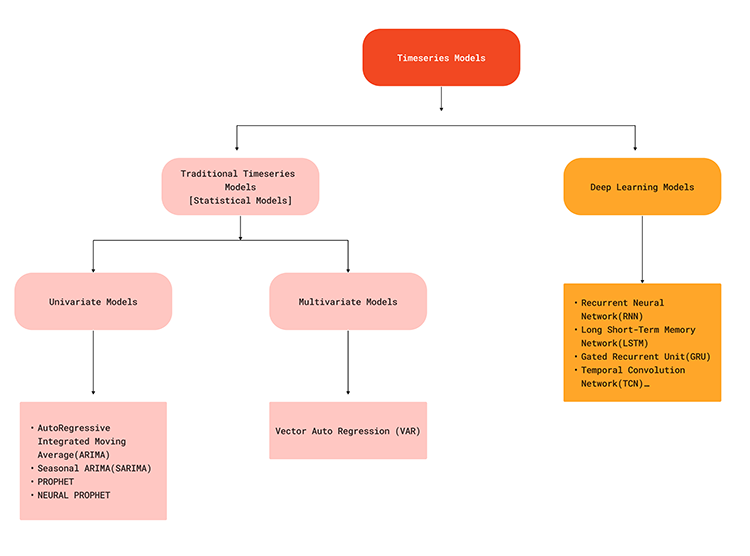
時系列モデルはデータの時間的依存関係を捉えることができるので、外国為替市場で予測を立てようとするときに現実的なソリューションを提供することができます。なぜなら、現在市場で起こっていることは、ほんの少し前に、または過去のどこかで起こった何らかの要因によるものである可能性があることは誰もが知っているからです。例えば、5分前に発表されたEURUSDのニュースが、現在、価格が急変する要因の1つかもしれません。このことをよりよく理解するために、機械学習モデルを使用した従来の予測とは対照的に、時系列予測の利点を見てみましょう。

側面	時系列予測	従来のML予測と最新のML予測
時間的依存関係	データポイントの順序や時間的な依存関係を考慮するため、時間的なパターンを捉えることができます。	従来のMLモデルはデータ点を独立したものとして扱い、その際にデータの時間的依存性を無視していました。
トレンドと季節性の取り扱い	ARIMAなどの時系列モデルには、トレンドや季節性を扱うためのコンポーネントが組み込まれています。	トレンドや季節性を把握するためには、手作業による特徴量の抽出とエンジニアリングが必要です。
自己相関	ARIMAやLSTMのようなモデルは、データの自己相関を考慮することができます。	これらはすべての特徴量が独立していると仮定しているため、特徴量で明示的にモデル化されていない限り、自己相関を考慮できない可能性があります。
モデルの複雑さ	時系列モデルは逐次データ用に設計されており、このようなタスクにより自然に適合します。	従来のモデルでは、シーケンシャルなデータを適切に扱うために特徴量エンジニアリングが必要になる場合があります。これはプロセスに複雑さを加えます。
時間的階層	階層的な時系列予測（月次、週次など）に自然に拡張できます。	従来のモデルは、追加的なエンジニアリングなしに、複数の時間スケールでの予測に苦戦する可能性があります。
予測パフォーマンス	多くの場合、順序を考慮することにより、時間に依存するタスクでより優れた予測性能が得られます。	時間に左右される仕事では、パフォーマンスが低下することがあります。
計算効率	時系列モデルは、新しいデータで効率的にインクリメンタルに更新できます。	従来のモデルは完全な再訓練が必要な場合があり、新しいデータでは計算量が多くなります。
解釈可能な傾向と季節性	ARIMAのようなモデルは、トレンドと季節性について解釈可能な要素を提供します。	設計された特徴量から傾向と季節性を解釈するには、追加のステップが必要です。

デフォルトでは時系列予測は得意ではありませんが、LightGBM、XGBoost、CatBoostなどのような古典的かつ最新の機械学習モデルがあります。適切な情報があれば、時系列予測にも使用できます。これを実現する鍵は、特徴量エンジニアリングにあります。

時系列予測のための特徴量エンジニアリング

時系列予測では、トレンド、季節性、周期性パターン、定常性、自己相関と偏自己相関などのような時系列にとって重要な情報/要素を持つように、新しい特徴量を構築し、既存の特徴量を準備することが目的です。

時系列問題に対して新しい特徴量を作成する際に考慮できる点はたくさんあります。次はそのうちのいくつかです。

01：遅延特徴量

古典的な機械学習のデータでは、現在のバーのOPEN、HIGH、LOW、CLOSEなどのデータを収集することが多いです。これは、各特定のバーにおける現在の情報を含み、その特定のバーの前に何が起こったかについての情報は提供しません。

データに遅延特徴量を導入することで、現在のバー価格に確実に関係する過去のバーからの時間的依存性を確実に捉えることができます。

MQL5

//--- getting Open, high, low and close prices
   
   ohlc_struct OHLC;
   
   OHLC.AddCopyRates(Symbol(), timeframe, start_bar, bars);
   time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars);
   
//--- Getting the lagged values of Open, High, low and close prices

   ohlc_struct  lag_1;
   lag_1.AddCopyRates(Symbol(), timeframe, start_bar+1, bars);
   
   ohlc_struct  lag_2;
   lag_2.AddCopyRates(Symbol(), timeframe, start_bar+2, bars);
   
   ohlc_struct  lag_3;
   lag_3.AddCopyRates(Symbol(), timeframe, start_bar+3, bars);

上の例では、遅延が3つしかありません。このデータを毎日収集しているため、1000本のバーについて3日前の情報を取得しています。

start_bar+1から始まるベクトルでMqlRatesをコピーすることで、start_barから始まるレートをコピーするよりも1つ前のバーを取得している。これは時々混乱を招くことがあります。https://www.mql5.com/ja/docs/seriesを参照してください。

MQL5

input int bars = 1000;
input ENUM_TIMEFRAMES timeframe = PERIOD_D1;
input uint start_bar = 2; //StartBar|Must be >= 1

struct ohlc_struct 
{
   vector open;
   vector high;
   vector low;
   vector close;
   
   matrix MATRIX; //this stores all the vectors all-together
   
   void AddCopyRates(string symbol, ENUM_TIMEFRAMES tf, ulong start, ulong size)
    {
      open.CopyRates(symbol, tf, COPY_RATES_OPEN, start, size); 
      high.CopyRates(symbol, tf, COPY_RATES_HIGH, start, size); 
      low.CopyRates(symbol, tf, COPY_RATES_LOW, start, size); 
      close.CopyRates(symbol, tf, COPY_RATES_CLOSE, start, size); 
      
      this.MATRIX.Resize(open.Size(), 4); //we resize it to match one of the vector since all vectors are of the same size
      
      this.MATRIX.Col(open, 0);
      this.MATRIX.Col(high, 1);
      this.MATRIX.Col(low, 2);
      this.MATRIX.Col(close, 3);
    }
};

02：ローリング統計

平均、標準偏差、その他のこの種の統計のようなローリング統計は、ウィンドウ内の最近のトレンドとボラティリティを要約するのに役立ちます。そこで、一定期間の移動平均や一定時間の標準偏差など、いくつかの指標が登場します。

int ma_handle = iMA(Symbol(),timeframe,30,0,MODE_SMA,PRICE_WEIGHTED); //The Moving averaege for 30 days
int stddev = iStdDev(Symbol(), timeframe, 7,0,MODE_SMA,PRICE_WEIGHTED); //The standard deviation for 7 days
   
vector SMA_BUFF, STDDEV_BUFF;
SMA_BUFF.CopyIndicatorBuffer(ma_handle,0,start_bar, bars);
STDDEV_BUFF.CopyIndicatorBuffer(stddev, 0, start_bar, bars);

このようなローリング統計は、市場がどのように変化してきたかをより広範に把握することができ、遅延特徴量では明らかにならない長期的な変動を捉えることができる可能性があります。

03：Date-Time特徴量

先に述べたように、時系列データは時間変数を持っていますが、Date-Time変数を持っているだけではあまり役に立たないので、その特徴量を抽出する必要があります。

ご存知のように、外国為替市場は特定の時間帯にいくつかのパターンを示したり、特定の行動をとったりします。例えば、金曜日は通常あまり取引がなく、その日にニュースがあると市場は不安定になります。また、月によっては取引活動が良くも悪くも変化することがあり、同じことが年にも当てはまります。例は、アメリカの選挙の年です。

Date-Time特徴量を導入することで、季節的なパターンを明示的にとらえることができ、これによって我々のモデルは、1年の時期や特定の日、月などに基づいて予測を調整することができるようになります。

MQL5でDate-Time機能を集めてみましょう。

vector time_vector; //we want to add time vector 
time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars); //copy the time in seconds


ulong size = time_vector.Size(); 
vector DAY(size), DAYOFWEEK(size), DAYOFYEAR(size), MONTH(size);

MqlDateTime time_struct;
string time = "";
for (ulong i=0; i<size; i++)
  {
    time = (string)datetime(time_vector[i]); //converting the data from seconds to date then to string
    TimeToStruct((datetime)StringToTime(time), time_struct); //convering the string time to date then assigning them to a structure
    
    DAY[i] = time_struct.day;
    DAYOFWEEK[i] = time_struct.day_of_week;
    DAYOFYEAR[i] = time_struct.day_of_year;
    MONTH[i] = time_struct.mon;
  }

04：差分化

季節ラグによって系列を差分化することで、データから季節パターンを取り除き、モデルによってはしばしば必要とされる定常性を達成します。

現在の価格からラグ1で差分をとってみましょう。

MQL5

vector diff_lag_1_open = OHLC.open - lag_1.open;
vector diff_lag_1_high = OHLC.high - lag_1.high;
vector diff_lag_1_low = OHLC.low - lag_1.low;
vector diff_lag_1_close = OHLC.close - lag_1.close;

ラグ1だけに制限されることはなく、好きなだけラグを差分化することができます。

この時点で、26の独立変数/特徴量を持っており、独立変数としては十分です。回帰問題を解こうとしているので、最終的な目標変数として終値を集めましょう。

vector TARGET_CLOSE;
TARGET_CLOSE.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar-1, bars); //one bar forward

以下で考慮していない他の面を考慮することで、ご自分の問題により多くの機能を自由に作り出してください。

05：外部変数（外生的特徴）

気象データ：役立つかどうか試してみます
経済指標：財務予測のためのGDP、失業率など

06：フーリエ変換とウェーブレット変換

フーリエ変換やウェーブレット変換を用いて、周波数領域における周期的なパターンや傾向を抽出します。

07：ターゲットエンコーディング

異なる期間における対象変数の集計統計量（平均値、中央値）に基づいて、特徴量を作成することができます。

最終的なデータセットには27の列があります。

時系列予測データセット

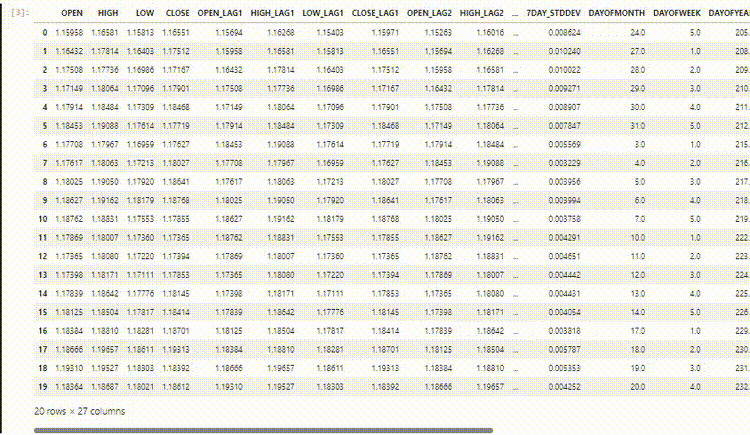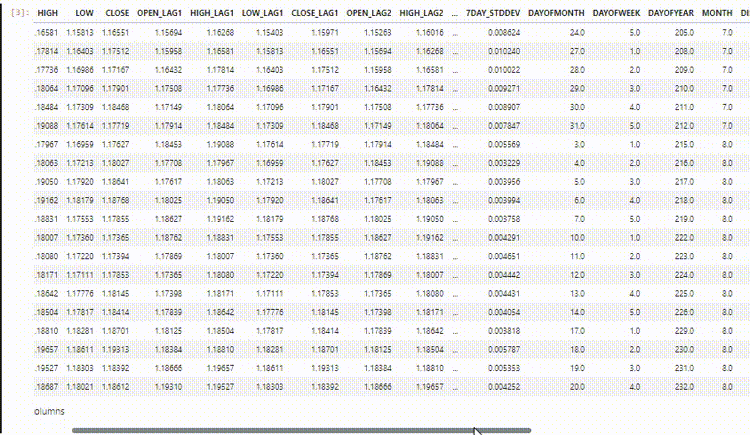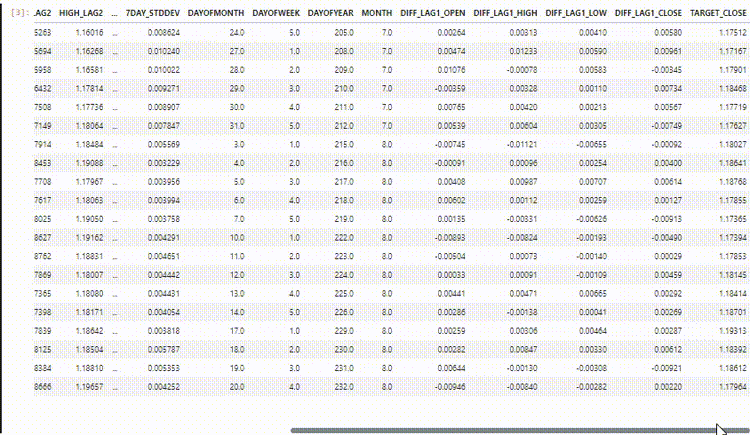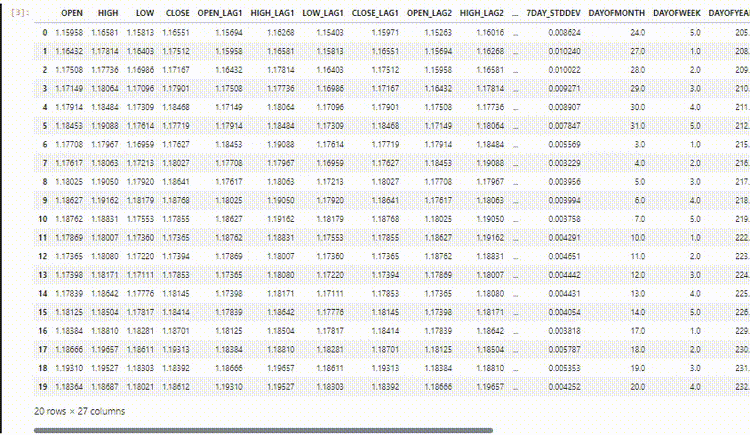
LightGBM回帰モデルの訓練

必要なデータがすべて揃ったので、Python側にシフトしてみましょう。

まず、データを訓練用サンプルとテスト用サンプルに分けることから始めよう。

Python

X = df.drop(columns=["TARGET_CLOSE"])
Y = df["TARGET_CLOSE"]

train_size = 0.7 #configure train size

train_size = round(train_size*df.shape[0])

x_train = X.iloc[:train_size,:]
x_test = X.iloc[train_size:, :]

y_train = Y.iloc[:train_size]
y_test = Y.iloc[train_size:]

print(f"x_train_size{x_train.shape}\nx_test_size{x_test.shape}\n\ny_train{y_train.shape}\ny_test{y_test.shape}")

結果

x_train_size(700, 26)
x_test_size(300, 26)

y_train(700,)
y_test(300,)

訓練データにモデルを当てはめてみましょう。

model = lgb.LGBMRegressor(**params)
model.fit(x_train, y_train)

訓練済みモデルをテストし、予測値とr2_scoreをプロットします。

Python

from sklearn.metrics import r2_score

test_pred = model.predict(x_test)

accuracy = r2_score(y_test, test_pred)

#showing actual test values and predictions

plt.figure(figsize=(8, 6))  
plt.plot(y_test, label='Actual Values')
plt.plot(test_pred, label='Predicted Values')
plt.xlabel('Index')
plt.ylabel('Values')
plt.title('Actual vs. Predicted Values')
plt.legend(loc="lower center")

# Add R-squared (accuracy) score in a corner
plt.text(0.05, 0.95, f"LightGBM (Accuracy): {accuracy:.4f}", ha='left', va='top', transform=plt.gca().transAxes, fontsize=10, bbox=dict(boxstyle='round', facecolor='white', alpha=0.7))

plt.grid(True)

plt.savefig("LighGBM Test plot")
plt.show()

結果

LightGBMテストプロット

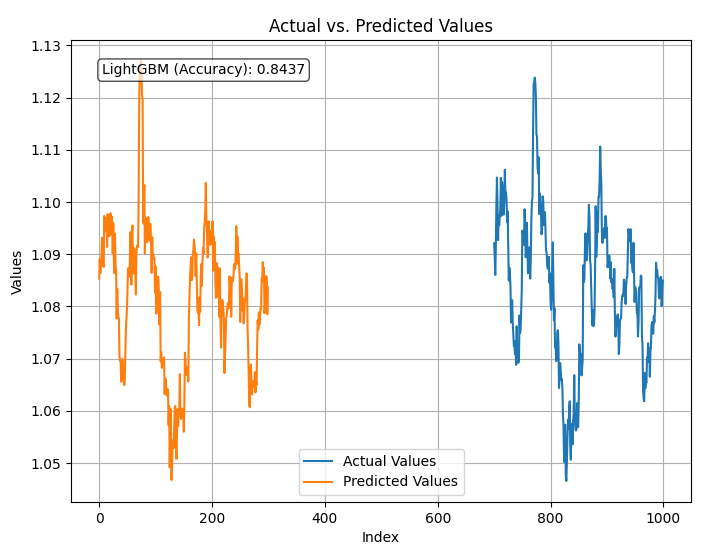
このモデルは、与えられたすべてのデータを使用して終値を84%の精度で予測しました。これは良い精度だと思われますが、さらなる分析とモデルの改良のために、変数を検討する必要があります。

組み込みの LightGBM特徴量重要度プロット手法を使用して、特徴量重要度をプロットしたものを以下に示します。

Python

# Plot feature importance using Gain
lgb.plot_importance(model, importance_type="gain", figsize=(8,6), title="LightGBM Feature Importance (Gain)")

plt.tight_layout()

plt.savefig("LighGBM feature importance(Gain)")
plt.show()

結果

時系列OHLC特徴量重要度

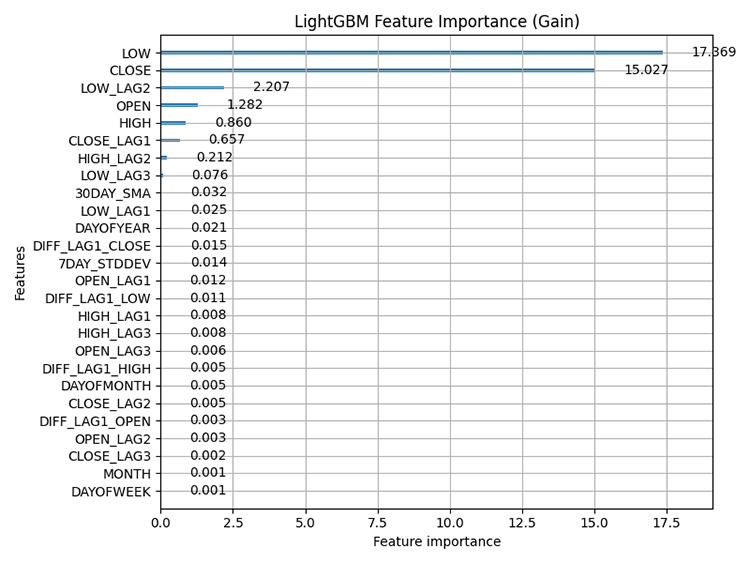
特徴量重要度：モデルによる予測に対するデータセット内の各特徴量（変数）の相対的な寄与を評価する技術を指します。これは、どの特徴がモデルの予測に最も大きな影響を与えるかを理解するのに役立ちます。

LightGBMやXGBoostのようなツリーベースの手法は、ツリーベースでないモデルとは異なる方法で特徴の重要度を計算することを知っておくことが重要です。彼らは、ある特徴がツリー内の分割決定に使用される頻度と、それらの分割が最終予測に与える影響を考慮します。

また、SHAPを使用して特徴量重要度を確認することもできます。

Python

explainer = shap.TreeExplainer(model)
shap_values = explainer(x_train)  

shap.summary_plot(shap_values, x_train, max_display=len(x_train.columns), show=False)  # Show all features

# Adjust layout and set figure size
plt.subplots_adjust(left=0.12, bottom=0.1, right=0.9, top=0.9)  
plt.gcf().set_size_inches(6, 8) 
plt.tight_layout()

plt.savefig("SHAP_Feature_Importance_Summary_Plot.png")
plt.show()

結果

SHAP特徴量重要度時系列データ

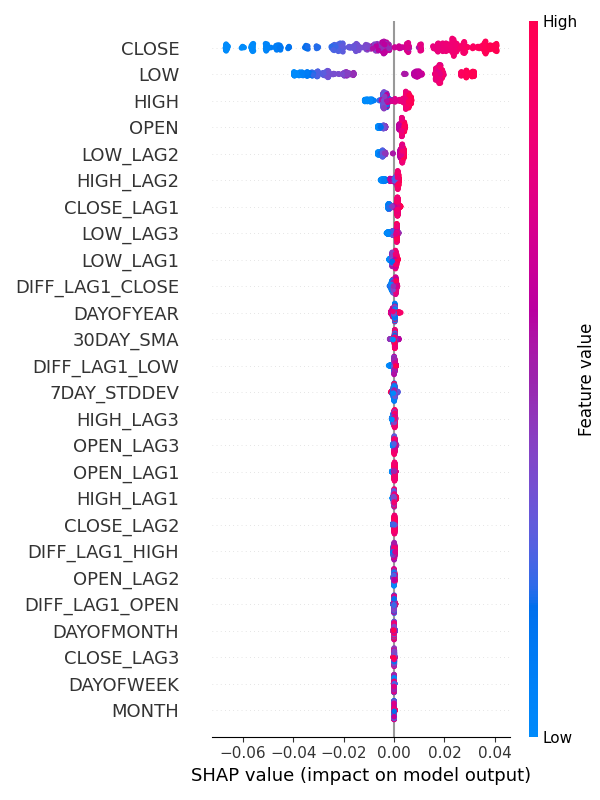
特徴量重要度プロットから、DAYOFWEK、MONTH、DAYOFMONTH、DAYOFYEARのような季節パターンを捕捉するための変数は、モデルの予測への寄与が最も少ない変数の一部であることが明らかです。

不思議なことに、拡張ディッキーフラー検定によれば、これらはすべて定常的です。

ADF （Augmented-Dickey-Fuller）検定

これは、時系列データセットが定常かどうかを判断するために使用される統計的検定です。定常性は、多くの時系列予測分析手法にとって極めて重要な性質です。

定常変数または定常データセットとは、統計的特性（平均、分散、自己相関）が時間の経過とともに一定である系列を指します。例えば、株式市場です。OHLCの平均値は時間の経過とともに大幅に増減する可能性があるため、これらの値の大部分は非定常ですが、一方で高値と安値の差の平均値や分散などのリターンは時間の経過とともに定常です。

このテストは、私たちが持っている全データセットで実行しました。

from statsmodels.tsa.stattools import adfuller

def adf_test(series, signif=0.05):
  """
  Performs the ADF test on a pandas Series and interprets the results.

  Args:
      series: The pandas Series containing the time series data.
      signif: Significance level for the test (default: 0.05).

  Returns:
      A dictionary containing the test statistic, p-value, used lags,
      critical values, and interpretation of stationarity.
  """
  dftest = adfuller(series, autolag='AIC')
  adf_stat = dftest[0]  # Access test statistic
  pvalue = dftest[1]  # Access p-value
  usedlag = dftest[2]  # Access used lags
  critical_values = dftest[4]  # Access critical values

  interpretation = 'Stationary' if pvalue < signif else 'Non-Stationary'
  result = {'Statistic': adf_stat, 'p-value': pvalue, 'Used Lags': usedlag,
            'Critical Values': critical_values, 'Interpretation': interpretation}
  return result

for col in df.columns:
  adf_results = adf_test(df[col], signif=0.05)
  print(f"ADF Results for column {col}:\n {adf_results}")

27の変数のうち、9つの変数だけが定常的に検出されました。これらの変数は以下の通りです。

7DAY_STDDEV
DAYOFMONTH
DAYOFWEK
DAYOFYEAR
MONTH
DIFF_LAG1_OPEN
DIFF_LAG1_HIGH
DIFF_LAG1_LOW
DIFF_LAG1_CLOSE

変数が定常かどうかを簡単に見つけるには、分布プロットを見ます。平均値の周りにうまく分布しているデータは、定常データである可能性が高いです。

定置と非定置

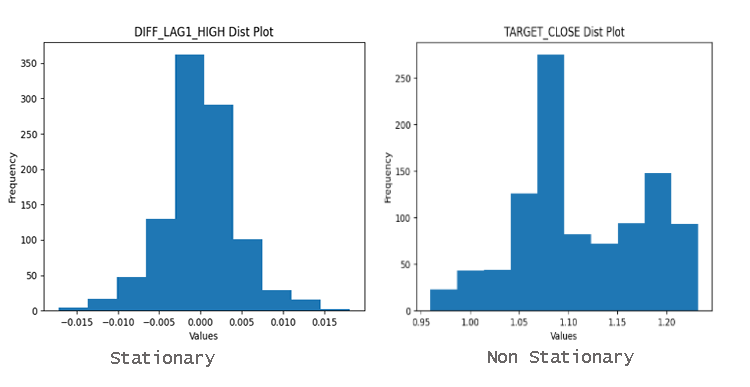
なぜ定常性が重要なのか？

時系列分析や予測で利用される多くの統計的手法は、定常性を前提としています。時系列が非定常である場合、これらの方法は誤解を招いたり、不正確な結果をもたらす可能性があります。

株価が常に上昇トレンドにある場合に、将来の株価を予測しようとすることを想像してみてください。時系列モデルでは、根本的なトレンドを捉えることはできないでしょう。

古典的な、あるいは私たちが使用したLightGBMのような最新の機械学習モデルは、特徴量間の非線形関係を処理する能力を持っているため、データに存在する定常性の影響を受けにくくなります。このモデルにおける特徴量重要性は、私たちのモデルにとって最も重要な特徴量が非定常OHLC変数であることを明確に示しています。

ただし、これは曜日などの変数がモデルに影響を与えないという意味ではありません。特徴量重要性は大きなストーリーのほんの一部に過ぎず、ドメインに関する知識が必要だと私は考えています。

この変数はEURUSDに影響すると確信しているので、ランクが低いからといって落とす必要はありません。

定常的な目標変数の予測

定常データは時間の経過とともに（平均、分散、自己相関が）一定であるため、時系列予測に関しては、定常目標変数を持つことで、多くの機械学習モデルのパフォーマンスが向上します。ご存知のように、次のローソク足で相場がどこに動くかを予測することは難しいですが、次の動きのピップスやポイントの量を予測することはそれほど難しくありません。

次のバーでどれだけのポイントが発生するかを予測できれば、それを使用して取引目標（損切りと利食い）を設定することができます。

そのためには、次の終値から前の終値を引くことで、一次差分を求める必要があります。

Python

Y = df["TARGET_CLOSE"] - df["CLOSE"] #first order differencing

次の終値とそれ以前の終値を差分することで、定常変数が出来上がります。

adf_results = adf_test(Y,signif=0.05)

print(f"ADF Results:\n {adf_results}")

結果

ADFの結果：{'Statistic': -23.37891429248752, 'p-value'：0.0, 'Used Lags':1, 'Critical Values': {'1%': -3.4369193380671, '5%': -2.864440383452517, '10%': -2.56831430323573}, 'Interpretation':'Stationary'}

新しい定常目標変数に回帰モデルをフィッティングし、テストデータセットでそのパフォーマンスを評価した結果、以下のようになりました。

Lightgbm時系列予測定常目標

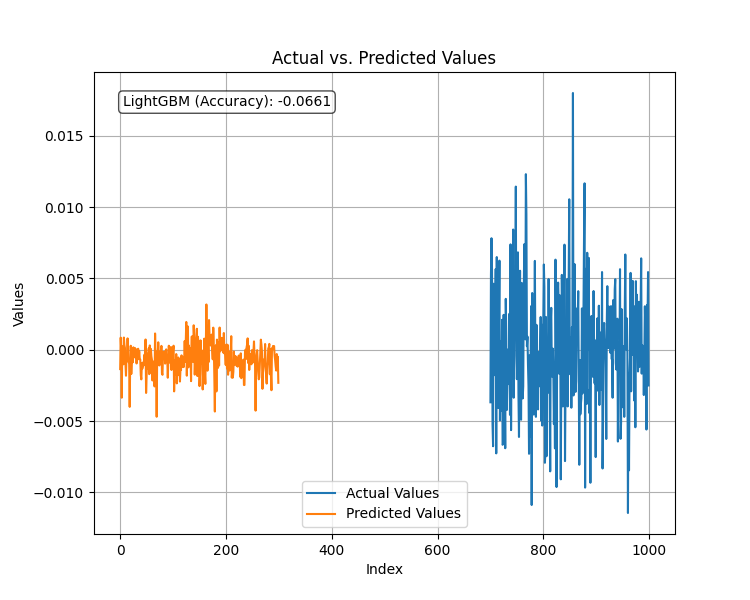
このモデルは、対象変数が定常変数であった場合、ひどいパフォーマンスを示しました。機械学習の常として、このような事態を招く要因は数多く考えられますが、今のところ、LightGBMは定常的な目標変数に対してはうまく機能しないと結論づけます。目標クローズ値を予測するために作成された回帰モデルにこだわります。

終値の連続値を予測するこの回帰モデルは、売買シグナルを予測するモデルほど有用ではありません。これを実現するには、取引シグナルを予測するための別のモデルを作成する必要があります。

LightGBM分類器モデルの構築

分類器モデルを作るには、目標変数を、1が買いシグナル、0が売りシグナルを表すバイナリ目標変数として準備する必要があります。

Python

Y = []
target_open = df["TARGET_OPEN"]
target_close = df["TARGET_CLOSE"]

for i in range(len(target_open)):
    if target_close[i] > target_open[i]: # if the candle closed above where it opened thats a buy signal
        Y.append(1)
    else: #otherwise it is a sell signal
        Y.append(0)

# split Y into irrespective training and testing samples 

y_train = Y[:train_size]
y_test = Y[train_size:]

パイプライン内のLightGBMモデルをStandardScalerの手法で訓練しました。

Python

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

params = {
    'boosting_type': 'gbdt',  # Gradient Boosting Decision Tree
    'objective': 'binary',  # For binary classification (use 'regression' for regression tasks)
    'metric': ['auc','binary_logloss'],  # Evaluation metric
    'num_leaves': 25,  # Number of leaves in one tree
    'n_estimators' : 100, # number of trees
    'max_depth': 5,
    'learning_rate': 0.05,  # Learning rate
    'feature_fraction': 0.9  # Fraction of features to be used for each boosting round
}

pipe = Pipeline([
    ("scaler", StandardScaler()),
    ("lgbm", lgb.LGBMClassifier(**params))
])

# Fit the pipeline to the training data
pipe.fit(x_train, y_train)

テスト結果は、全体の53%という驚くべきものではありませんでした。

分類報告

Classification Report
               precision    recall  f1-score   support

           0       0.49      0.79      0.61       139
           1       0.62      0.30      0.40       161

    accuracy                           0.53       300
   macro avg       0.56      0.54      0.51       300
weighted avg       0.56      0.53      0.50       300

混乱行列

混同行列lightGBM

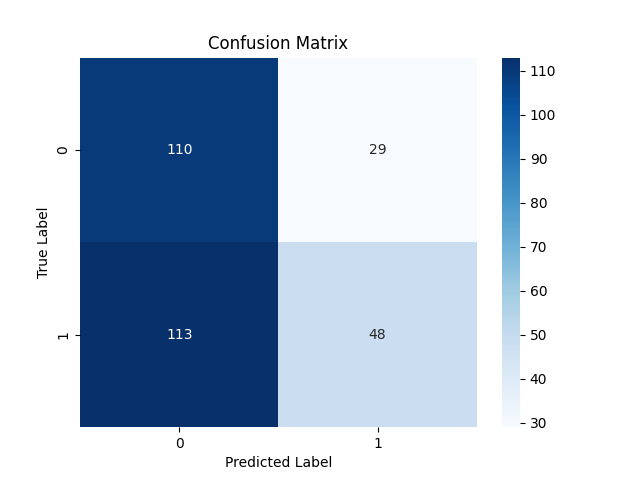
LightGBM分類器モデルのONNXへの保存

前回おこなったように、LightGBMモデルをONNXフォーマットに保存するのは簡単で、数行のコードで済みます。

import onnxmltools
from onnxmltools.convert import convert_lightgbm
import onnxmltools.convert.common.data_types
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx import convert_sklearn, update_registered_converter

from skl2onnx.common.shape_calculator import (
    calculate_linear_classifier_output_shapes,
)  # noqa

from onnxmltools.convert.lightgbm.operator_converters.LightGbm import (
    convert_lightgbm,
)  # noqa

# registering onnx converter

update_registered_converter(
    lgb.LGBMClassifier,
    "GBMClassifier",
    calculate_linear_classifier_output_shapes,
    convert_lightgbm,
    options={"nocl": [False], "zipmap": [True, False, "columns"]},
)

# Final LightGBM conversion to ONNX

model_onnx = convert_sklearn(
    pipe,
    "pipeline_lightgbm",
    [("input", FloatTensorType([None, x_train.shape[1]]))],
    target_opset={"": 12, "ai.onnx.ml": 2},
)

# And save.
with open("lightgbm.Timeseries Forecasting.D1.onnx", "wb") as f:
    f.write(model_onnx.SerializeToString())

自動売買ロボットですべてをまとめる

機械学習モデルがONNXに保存されたので、エキスパートアドバイザーに直接アタッチし、MetaTrader 5の時系列予測にLightGBM分類器を使用することができます。

MQL5

#resource "\\Files\\lightgbm.Timeseries Forecasting.D1.onnx" as uchar lightgbm_onnx[] //load the saved onnx file 
#include <MALE5\LightGBM\LightGBM.mqh>
CLightGBM lgb;

前の記事で作成したLightGBMクラスを使用して、モデルを初期化し、予測に使用することができました。

int OnInit()
  {
//---
   
   if (!lgb.Init(lightgbm_onnx)) //Initialize the LightGBM model
     return INIT_FAILED;
   
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
    
   if (NewBar()) //Trade at the opening of a new candle
    {
     vector input_vector = input_data(); 
     long signal = lgb.predict_bin(input_vector);
     
   //---
     
      MqlTick ticks;
      SymbolInfoTick(Symbol(), ticks);
      
      if (signal==1) //if the signal is bullish
       {
          if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions
           {
             if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, ticks.bid-stoploss*Point(), ticks.ask+takeprofit*Point())) //Open a buy trade
               printf("Failed to open a buy position err=%d",GetLastError());
           }
       }
      else if (signal==0) //Bearish signal
        {
          if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions
            if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, ticks.ask+stoploss*Point(), ticks.bid-takeprofit*Point())) //open a sell trade
               printf("Failed to open a sell position err=%d",GetLastError());
        }
      else //There was an error
        return;
    }
  }

input_data()関数は、Feature engineering Timeseries forecasting.mq5スクリプトでデータが収集されCSVファイルに保存された方法と同様の方法でデータを収集する役割を担っています。

ストラテジーテスターでのモデルのテスト

最後に、取引環境でモデルをテストすることができます。データは日次時間枠で収集されているため、より短い時間枠でテストすることをお勧めします。新しいバーの開始時に取引シグナルを探しているため、「市場が閉じたエラー」が発生した場合のエラーを回避するためです。また、より迅速なテストのために、モデリングタイプを始値に設定することもできます。

テスター設定

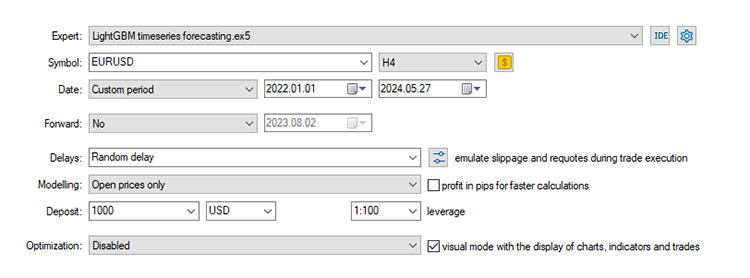
ストップロスとテイクプロフィットをそれぞれ500ポイントと700ポイントに設定した場合、EAは約5%の確率で正しい予測をおこないました。

Metatrader 5ストラテジーテスターレポート

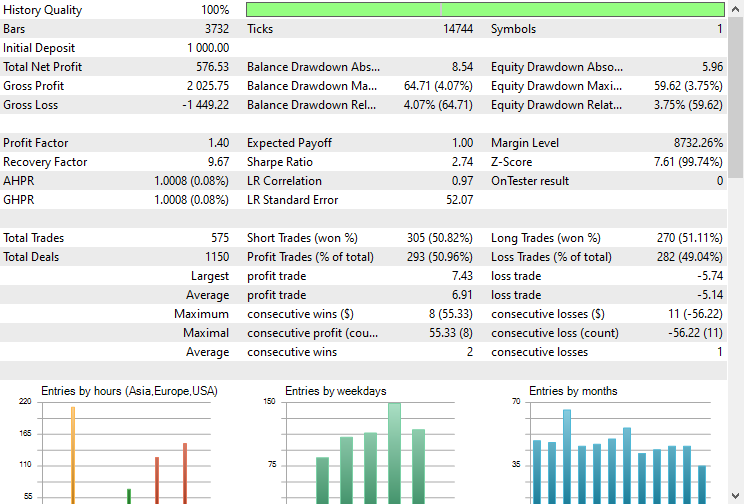
残高/エクイティ曲線も印象的でした。

Metatrader 5テスターグラフ

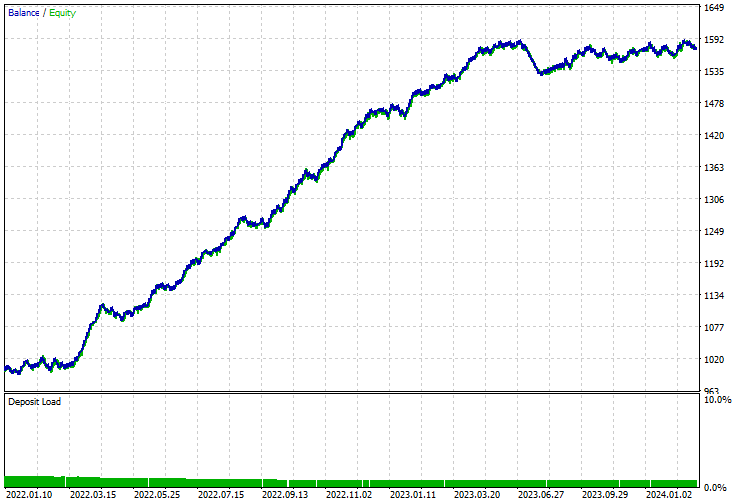
時系列予測に古典的MLモデルと最新MLモデルを使用する利点

時系列予測に非時系列機械学習モデルを用いることには、いくつかの利点があります。以下に主な利点を挙げます。

1. 特徴量エンジニアリングにおける柔軟性

古典的な機械学習モデルは、さまざまな外部変数や派生特徴を含むために活用できる、広範な特徴量エンジニアリングを可能にします。この記事でおこなったように、遅延やローリング統計のような複雑な特徴量を含め、有用と思われるすべてのデータを手作業で分析し、取り入れるために、人間の知性を使用することができます。

2. 非定常性への対応

差分化によって系列を定常化する代わりに、トレンドと季節性を直接特徴量として含めて、モデルは何の問題もなくパターンを学習するこことができます。

3. データ分布の仮定なし

多くの古典的な時系列モデル（ARIMAのような）は、データが特定の統計分布に従うことを前提としています。一方、古典的で現代的なMLモデルは、データ分布に関してより柔軟です。

決定木、ランダムフォレスト、勾配ブースティング（LightGBMを含む）などのモデルは、データの特定の分布を仮定していません。

4. スケーラビリティ

古典的なMLモデルは、より効率的に大規模なデータセットを扱うことができ、多くの場合スケールアップが容易です。

5. 複雑な相互作用

古典的なMLモデルは、特徴と対象変数の間の複雑で非線形な関係を捉えることができます。

6.欠損データに対する頑健性

機械学習モデルは、従来の時系列モデルと比較して、欠損データを扱うための優れたメカニズムを持っていることが多いです。

7.アンサンブル手法

バギング、ブースティング、スタッキングなどのアンサンブル手法を簡単に使用し、複数のモデルを組み合わせることでモデルの性能を高め、予測性能とロバスト性を向上させることができます。

8.使いやすさと統合性

古典的なMLモデルは、よりユーザーフレンドリーであることが多く、実装、可視化、評価のための広範なライブラリやツールが付属しています。

Scikit-learn、LightGBM、XGBoostなどのライブラリは、これらのモデルを構築、チューニング、評価するための包括的なツールを提供します。

結論

古典的な機械学習モデルも最新の機械学習モデルも、時系列分析や予測に問題なく使用することができ、この記事で説明したように、適切な情報、チューニング、プロセスによって、時系列モデルを凌駕することができます。例としてLightGBMを使用しましたが、SVM、線形回帰、ナイーブベイズ、XGBoostなど、古典的あるいは最新の機械学習モデルなら何でも適用できます。

では、また。

機械学習モデルの開発を追跡し、本連載で説明されている多くのことは、このGitHubレポに掲載されています。

添付ファイルの表

ファイル名	ファイルタイプ	説明と使用法
LightGBM timeseries forecasting.mq5	EA	MetaTrader 5でONNXモデルを読み込み、最終的な取引戦略をテストするための自動売買ロボット
lightgbm.Timeseries Forecasting.D1.onnx	ONNX	ONNX形式のLightGBMモデル
LightGBM.mqh	インクルード（ライブラリ）	ONNXモデル形式を読み込み、それをネイティブのMQL5言語でデプロイするためのコードで構成
Feature enginEring Timeseries forecasting.mq5	スクリプト	すべてのデータを収集し、時系列分析と予測のために設計するスクリプト
forex-timeseries-forecasting-lightgbm.ipynb	Pythonスクリプト(Jupyter Notebook)	この記事で説明するすべてのpythonコードを含むノートブック

出典と参考文献

Time Series Talk:Stationarity(https://youtu.be/oY-j2Wof51c)
Kishan Manani - Feature Engineering for Time Series Forecasting | PyData London 2022(https://www.youtube.com/watch?v=9QtL7m3YS9I)
Stock Market Prediction via Deep Learning Techniques:A Survey(https://arxiv.org/abs/2212.12717)
Challenges in Time Series Forecasting(https://www.youtube.com/watch?v=rcdDl8qf0ZA)
Stationarity and differencing(https://otexts.com/fpp2/stationarity.html)
How to perform Target/Mean Encoding for Categorical Attributes | Python (https://www.youtube.com/watch?v=nd7vc4MZQz4)

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/15013

添付されたファイル |

ZIPをダウンロード

Attachments.zip (317.52 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

LSTMニューラルネットワークを用いた時系列予測の作成：価格の正規化と時間のトークン化

この記事では、日次レンジを使用して市場データを正規化し、市場予測を強化するためにニューラルネットワークを訓練する簡単な戦略を概説します。開発されたモデルは、既存のテクニカル分析の枠組みと組み合わせて、あるいは単独で、市場全体の方向性を予測するのに役立てることができます。この記事で概説した枠組みは、テクニカルアナリストであれば、手動と自動売買の両方の戦略に適したモデルを開発するために、さらに改良を加えることができます。

Candlestick Trend Constraintモデルの構築（第5回）：通知システム（パート2）

今日は、PythonとTelegram Bot APIと連携して、MQL5のパワーを活用した MetaTrader 5指標通知のための実用的なTelegram統合について説明します。ポイントが見逃がされることがないように、すべてを詳細に説明します。このプロジェクトが終了する頃には、ご自分のプロジェクトに応用できる貴重な洞察を得ることができるでしょう。

MQL5でゾーン回復マーチンゲール戦略を開発する

この記事では、ゾーン回復取引アルゴリズムに基づくエキスパートアドバイザー(EA)の作成に向けて実施すべきステップについて、詳細な観点から論じています。これは、アルゴリズムトレーダーの時間を節約するシステムの自動化に役立ちます。

Candlestick Trend Constraintモデルの構築（第5回）：通知システム（パート1）

本連載で作成するTrend Constraint指標からのシグナル通知を受信するためのTelegramとWhatsAppの統合を説明するために、メインのMQL5コードを特定のコードスニペットに分解します。これにより、トレーダーや開発者（初心者か経験豊富かを問わず）が簡単にコンセプトを把握できるようになります。まず、MetaTrader 5の通知に関する設定と、ユーザーにとってのその意義について説明します。これは、開発者が自分のシステムにさらに応用するためのメモを事前に取るのに役立ちます。