Data Science e Machine Learning (Parte 24): Previsão de Séries Temporais no Forex Usando Modelos de IA Clássicos

Conteúdo

• O que é previsão de séries temporais?
• Por que e onde a previsão de séries temporais é usada?
• Comparação entre modelos clássicos e modernos versus modelos de ML baseados em séries temporais
• Engenharia de features para previsão de séries temporais
• Treinando o modelo regressor LightGBM
• Teste de Augmented Dickey-Fuller
• Por que a estacionaridade importa?
• Prevendo uma variável alvo estacionárias
• Construindo o modelo classificador LightGBM
• Salvando o modelo Classificador LightGBM para ONNX
• Consolidando tudo dentro de um robô de trading
• Testando o modelo no strategy tester
• Vantagens de usar modelos de ML clássicos e modernos para previsão de séries temporais
• Conclusão

O que é Previsão de Séries Temporais?

Previsão de séries temporais é o processo de usar dados passados para prever valores futuros em uma sequência de pontos de dados. Essa sequência é tipicamente ordenada pelo tempo, daí o nome série temporal.

Variáveis Centrais em Dados de Séries Temporais 

Enquanto podemos ter quantas variáveis de features quisermos em nossos dados, qualquer dado para análise ou previsão de séries temporais deve ter estas duas variáveis.

1. Tempo
   
   Esta é uma variável independente, representando os pontos específicos no tempo em que os dados foram observados.
   
   
2. Variável Alvo
   
   Este é o valor que você está tentando prever com base em observações passadas e, potencialmente, outros fatores. (por exemplo, preço de fechamento diário de ações, temperatura horária, tráfego de sites por minuto).

O objetivo da previsão de séries temporais é aproveitar os padrões históricos e tendências nos dados para fazer previsões informadas sobre valores futuros.

Este artigo assume que você tem um entendimento básico de ONNX, previsão de séries temporais, e Light Gradient Boosting Machine (LightGBM). Por favor, leia esses artigos, se ainda não leu, para fins de clareza. 

Por que e Onde a Previsão de Séries Temporais é Usada?

Análise e previsão de séries temporais podem ser usadas nos cenários abaixo:

• Previsão de valores futuros 
• Compreensão do comportamento passado
• Planejamento para o futuro, que pode depender do passado
• Avaliação de realizações atuais

Modelos Clássicos e Modernos vs. Modelos de ML Baseados em Séries Temporais

Diferentemente dos modelos clássicos de machine learning, como Regressão Linear, Máquina de Vetores de Suporte (SVM), Redes Neurais (NN) e outros que discutimos em artigos anteriores — que visam determinar relações entre variáveis de features e fazer previsões futuras com base nessas relações aprendidas — os modelos de séries temporais preveem valores futuros com base em valores observados anteriormente.

Essa diferença na abordagem significa que os modelos de séries temporais são especificamente projetados para lidar com dependências temporais e padrões inerentes a dados sequenciais. Modelos de previsão de séries temporais, como ARIMA, SARIMA, Suavização Exponencial, RNN, LSTM e GRU, aproveitam dados históricos para prever pontos futuros na série, capturando tendências, sazonalidade e outras estruturas temporais.

O fluxograma abaixo ilustra vários modelos de machine learning usados para previsão de séries temporais, 

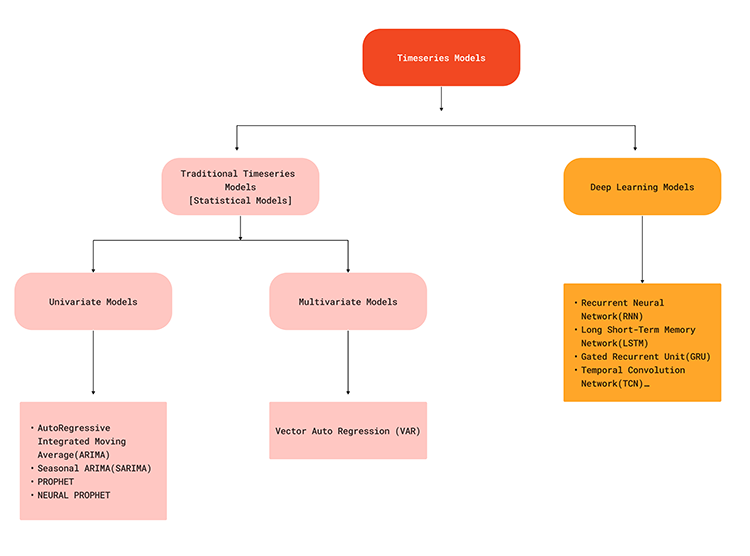
Como os modelos de séries temporais são capazes de capturar dependências temporais nos dados, eles podem oferecer uma solução realista ao tentar fazer previsões no mercado forex, pois sabemos que o que acontece atualmente no mercado pode ser devido a alguns fatores que ocorreram recentemente ou em algum momento no passado. Por exemplo, notícias divulgadas sobre o EURUSD há 5 minutos podem ser um dos fatores para uma mudança acentuada no preço atual. Para entender melhor, vamos analisar as vantagens da previsão de séries temporais em contraste com a previsão tradicional usando modelos de machine learning.

Aspecto	Previsão de Séries Temporais	Previsão de ML Tradicional e Moderna
Dependências Temporais	São capazes de capturar padrões temporais, pois consideram a ordem dos pontos de dados e dependências ao longo do tempo.	Modelos tradicionais tratam pontos de dados como independentes, ignorando as dependências temporais nos dados.
Tratamento de Tendências e Sazonalidade	Modelos de séries temporais como ARIMA e alguns outros têm componentes embutidos para lidar com tendências e sazonalidade.	Requer extração e engenharia manual de features para capturar tendências e sazonalidade.
Autocorrelação	Modelos como ARIMA e LSTMs podem considerar a autocorrelação nos dados.	Eles assumem que cada feature é independente, então podem não considerar a autocorrelação, a menos que explicitamente modelada nas features.
Complexidade do Modelo	Modelos de séries temporais são projetados para dados sequenciais, oferecendo um ajuste mais natural para tais tarefas.	Modelos tradicionais podem exigir engenharia de features para lidar adequadamente com dados sequenciais. O que adiciona complexidade ao processo.
Hierarquias Temporais	Podem ser naturalmente estendidos para previsão hierárquica de séries temporais (por exemplo, mensal, semanal).	Modelos tradicionais podem ter dificuldade em prever em múltiplas escalas temporais sem engenharia adicional.
Desempenho Preditivo	Frequentemente proporciona melhor desempenho preditivo em tarefas dependentes do tempo devido à consideração da ordem.	Pode ter desempenho inferior em tarefas dependentes do tempo.
Eficiência Computacional	Modelos de séries temporais podem ser atualizados incrementalmente com novos dados de forma eficiente.	Modelos tradicionais podem precisar de re-treinamento completo, o que é computacionalmente mais intensivo com novos dados.
Tendências e Sazonalidade Interpretáveis	Modelos como ARIMA fornecem componentes interpretáveis para tendência e sazonalidade.	Requer etapas adicionais para interpretar tendências e sazonalidade a partir de features engenheiradas.

Apesar de não serem bons em previsão de séries temporais por padrão, modelos clássicos e modernos de machine learning como LightGBM, XGBoost, CatBoost, etc. Ainda podem ser usados para previsões de séries temporais quando fornecidos com as informações corretas. A chave para alcançar isso está na engenharia de features.

Engenharia de features para previsão de séries temporais

Na previsão de séries temporais, o objetivo é construir novas features e preparar features existentes de forma que resultem em informações/componentes importantes para séries temporais, tais como: Tendência, Sazonalidade, Padrões Cíclicos, Estacionaridade, Autocorrelação e Autocorrelação Parcial, etc.

Há muitos aspectos a considerar ao criar novas features para um problema de séries temporais, abaixo estão alguns deles:

01: Features Defasadas

Nos dados para machine learning clássico, frequentemente coletamos dados como ABERTURA, MÁXIMA, MÍNIMA, FECHAMENTO e alguns outros dados no candle atual. Isso contém as informações atuais de cada candle específico e não oferece nenhuma informação sobre o que aconteceu antes desse candle específico.

Ao introduzir features defasadas em nossos dados, garantimos a captura de dependências temporais de candles anteriores, o que certamente tem relação com o preço atual.

MQL5

//--- getting Open, high, low and close prices
   
   ohlc_struct OHLC;
   
   OHLC.AddCopyRates(Symbol(), timeframe, start_bar, bars);
   time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars);
   
//--- Getting the lagged values of Open, High, low and close prices

   ohlc_struct  lag_1;
   lag_1.AddCopyRates(Symbol(), timeframe, start_bar+1, bars);
   
   ohlc_struct  lag_2;
   lag_2.AddCopyRates(Symbol(), timeframe, start_bar+2, bars);
   
   ohlc_struct  lag_3;
   lag_3.AddCopyRates(Symbol(), timeframe, start_bar+3, bars);

No exemplo acima, estamos obtendo apenas três defasagens. Como estamos coletando esses dados diariamente, estamos obtendo informações dos três dias anteriores para 1000 candles.

Ao copiar MqlRates em vetores a partir de start_bar+1, estamos obtendo um candle anterior em comparação com a cópia de taxas a partir de start_bar. Isso pode ser confuso às vezes. Consulte https://www.mql5.com/pt/docs/series para mais informações.

MQL5

input int bars = 1000;
input ENUM_TIMEFRAMES timeframe = PERIOD_D1;
input uint start_bar = 2; //StartBar|Must be >= 1

struct ohlc_struct 
{
   vector open;
   vector high;
   vector low;
   vector close;
   
   matrix MATRIX; //this stores all the vectors all-together
   
   void AddCopyRates(string symbol, ENUM_TIMEFRAMES tf, ulong start, ulong size)
    {
      open.CopyRates(symbol, tf, COPY_RATES_OPEN, start, size); 
      high.CopyRates(symbol, tf, COPY_RATES_HIGH, start, size); 
      low.CopyRates(symbol, tf, COPY_RATES_LOW, start, size); 
      close.CopyRates(symbol, tf, COPY_RATES_CLOSE, start, size); 
      
      this.MATRIX.Resize(open.Size(), 4); //we resize it to match one of the vector since all vectors are of the same size
      
      this.MATRIX.Col(open, 0);
      this.MATRIX.Col(high, 1);
      this.MATRIX.Col(low, 2);
      this.MATRIX.Col(close, 3);
    }
};

02: Estatísticas Móveis

Estatísticas móveis, como a média, desvios padrão e outras estatísticas desse tipo, ajudam a resumir as tendências recentes e a volatilidade dentro de uma janela. É aqui que alguns indicadores entram em jogo, como a média móvel para um determinado período, o desvio padrão para um determinado tempo, etc.

int ma_handle = iMA(Symbol(),timeframe,30,0,MODE_SMA,PRICE_WEIGHTED); //The Moving averaege for 30 days
int stddev = iStdDev(Symbol(), timeframe, 7,0,MODE_SMA,PRICE_WEIGHTED); //The standard deviation for 7 days
   
vector SMA_BUFF, STDDEV_BUFF;
SMA_BUFF.CopyIndicatorBuffer(ma_handle,0,start_bar, bars);
STDDEV_BUFF.CopyIndicatorBuffer(stddev, 0, start_bar, bars);

Essas estatísticas móveis fornecem uma visão mais ampla de como o mercado tem mudado, capturando potencialmente flutuações de longo prazo que não são evidentes nas features defasadas.

03: Features de Data-Hora

Como mencionado anteriormente, os dados de séries temporais possuem a variável de tempo, porém, ter apenas uma variável Data-hora não será muito útil, precisamos extrair suas features.

Como sabemos, o mercado forex exibe alguns padrões ou se comporta de certas maneiras durante tempos específicos. Por exemplo: geralmente não há muita atividade de negociação nas sextas-feiras e o mercado fica volátil quando há um evento de notícias naquele dia específico. Além disso, em alguns meses, as atividades de negociação podem mudar para melhor ou pior; o mesmo se aplica a alguns anos. Por exemplo: durante os anos de eleição em países como os EUA.

Ao introduzir as features de Data-Hora, capturamos explicitamente padrões sazonais, o que permitiria ao nosso modelo ajustar as previsões com base no período do ano, em um dia ou mês específico, etc.

Vamos coletar as features de Data-Hora no MQL5:

vector time_vector; //we want to add time vector 
time_vector.CopyRates(Symbol(), timeframe, COPY_RATES_TIME, start_bar, bars); //copy the time in seconds


ulong size = time_vector.Size(); 
vector DAY(size), DAYOFWEEK(size), DAYOFYEAR(size), MONTH(size);

MqlDateTime time_struct;
string time = "";
for (ulong i=0; i<size; i++)
  {
    time = (string)datetime(time_vector[i]); //converting the data from seconds to date then to string
    TimeToStruct((datetime)StringToTime(time), time_struct); //convering the string time to date then assigning them to a structure
    
    DAY[i] = time_struct.day;
    DAYOFWEEK[i] = time_struct.day_of_week;
    DAYOFYEAR[i] = time_struct.day_of_year;
    MONTH[i] = time_struct.mon;
  }

04: Diferenciação

Diferenciar a série em defasagens sazonais remove padrões sazonais dos dados para alcançar a estacionaridade, o que é frequentemente um requisito para alguns modelos.

Vamos tentar diferenciar em lag1 a partir dos preços atuais.

MQL5

vector diff_lag_1_open = OHLC.open - lag_1.open;
vector diff_lag_1_high = OHLC.high - lag_1.high;
vector diff_lag_1_low = OHLC.low - lag_1.low;
vector diff_lag_1_close = OHLC.close - lag_1.close;

Você pode diferenciar quantas defasagens quiser; não está restrito apenas ao lag 1.

Até este ponto, temos 26 variáveis/independentes/features que são suficientes para nossas variáveis independentes. Como estamos tentando resolver um problema de regressão, vamos coletar os preços de fechamento como nossa variável alvo final.

vector TARGET_CLOSE;
TARGET_CLOSE.CopyRates(Symbol(), timeframe, COPY_RATES_CLOSE, start_bar-1, bars); //one bar forward

Sinta-se à vontade para criar mais features para o seu problema, considerando alguns outros aspectos que não abordamos abaixo.

05: Variáveis Externas (Features Exógenas)

• Dados Climáticos: tente verificar se eles ajudam.
• Indicadores Econômicos: incluindo PIB, taxas de desemprego, etc., para previsões financeiras.

06: Transformadas de Fourier e Wavelet

Usando transformadas de Fourier ou wavelet para extrair padrões cíclicos e tendências no domínio da frequência.

07: Codificação de Alvo

Você pode criar features com base em estatísticas agregadas (média, mediana) da variável alvo em diferentes períodos de tempo.

O conjunto de dados final possui 27 colunas:

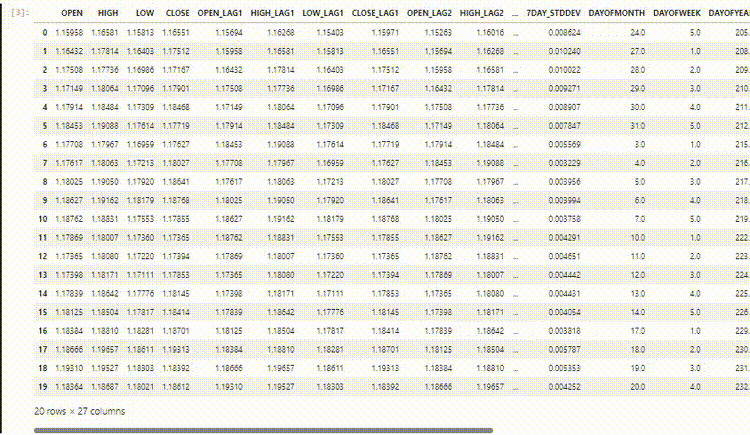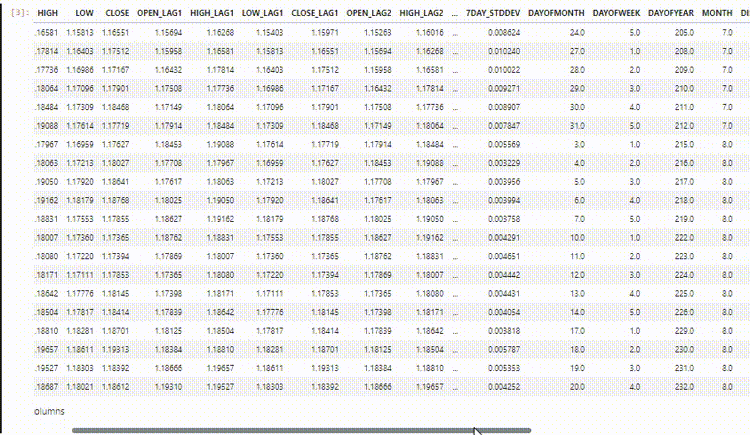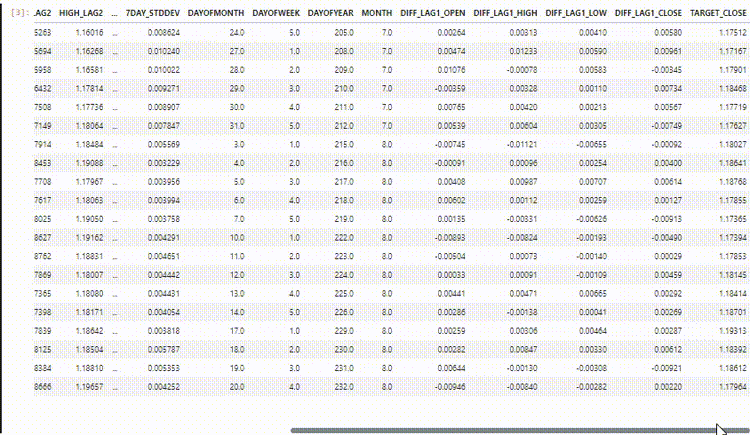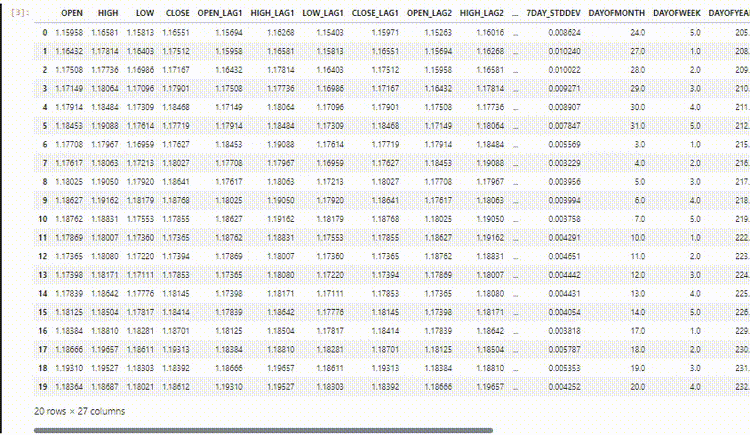
Treinando o modelo Regressor LightGBM

Agora que temos todos os dados necessários, vamos passar para a parte em Python.

Podemos começar dividindo os dados em amostras de treinamento e teste.

Python

X = df.drop(columns=["TARGET_CLOSE"])
Y = df["TARGET_CLOSE"]

train_size = 0.7 #configure train size

train_size = round(train_size*df.shape[0])

x_train = X.iloc[:train_size,:]
x_test = X.iloc[train_size:, :]

y_train = Y.iloc[:train_size]
y_test = Y.iloc[train_size:]

print(f"x_train_size{x_train.shape}\nx_test_size{x_test.shape}\n\ny_train{y_train.shape}\ny_test{y_test.shape}")

Resultados:

x_train_size(700, 26)
x_test_size(300, 26)

y_train(700,)
y_test(300,)

Vamos ajustar o modelo aos dados de treinamento.

model = lgb.LGBMRegressor(**params)
model.fit(x_train, y_train)

Vamos testar o modelo treinado e depois plotar as previsões e o r2_score.

Python

from sklearn.metrics import r2_score

test_pred = model.predict(x_test)

accuracy = r2_score(y_test, test_pred)

#showing actual test values and predictions

plt.figure(figsize=(8, 6))  
plt.plot(y_test, label='Actual Values')
plt.plot(test_pred, label='Predicted Values')
plt.xlabel('Index')
plt.ylabel('Values')
plt.title('Actual vs. Predicted Values')
plt.legend(loc="lower center")

# Add R-squared (accuracy) score in a corner
plt.text(0.05, 0.95, f"LightGBM (Accuracy): {accuracy:.4f}", ha='left', va='top', transform=plt.gca().transAxes, fontsize=10, bbox=dict(boxstyle='round', facecolor='white', alpha=0.7))

plt.grid(True)

plt.savefig("LighGBM Test plot")
plt.show()

Resultado:

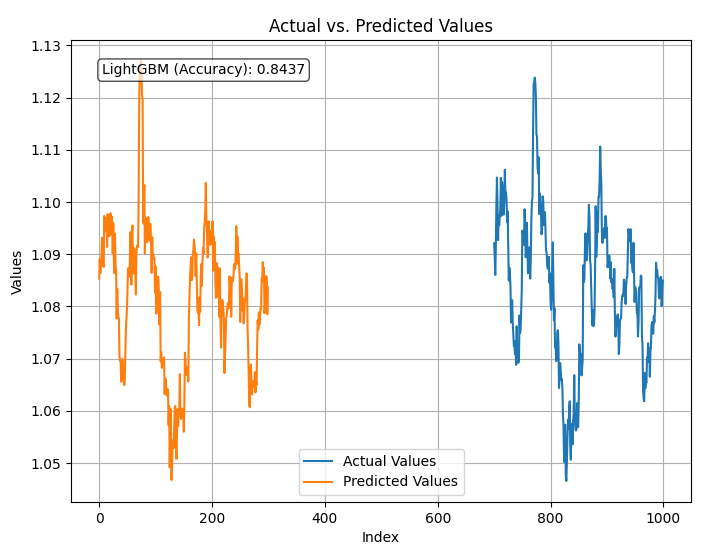
O modelo tem uma precisão de 84% na previsão dos preços de fechamento usando todos os dados fornecidos. Embora isso pareça uma boa precisão, precisamos examinar nossas variáveis para uma análise mais aprofundada e melhorias no modelo.

Usando a técnica de plotagem de importância das features integrada ao LightGBM, abaixo está o gráfico de importância das features.

Python

# Plot feature importance using Gain
lgb.plot_importance(model, importance_type="gain", figsize=(8,6), title="LightGBM Feature Importance (Gain)")

plt.tight_layout()

plt.savefig("LighGBM feature importance(Gain)")
plt.show()

Resultado:

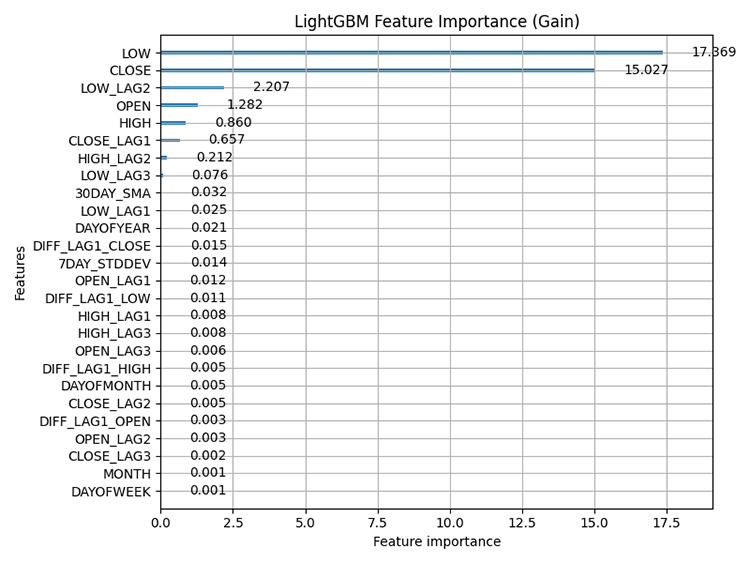
Importância das features: refere-se a técnicas que avaliam a contribuição relativa de cada feature (variável) em um conjunto de dados para as previsões feitas pelo modelo. Isso nos ajuda a entender quais features têm a maior influência nas previsões do modelo.

É importante saber que métodos baseados em árvores, como LightGBM e XGBoost, calculam a importância das features de forma diferente dos modelos não baseados em árvores. Eles consideram com que frequência uma feature é usada para decisões de divisão nas árvores e o impacto dessas divisões na previsão final.

Alternativamente, você pode usar SHAP para verificar a importância das features.

Python:

explainer = shap.TreeExplainer(model)
shap_values = explainer(x_train)  

shap.summary_plot(shap_values, x_train, max_display=len(x_train.columns), show=False)  # Show all features

# Adjust layout and set figure size
plt.subplots_adjust(left=0.12, bottom=0.1, right=0.9, top=0.9)  
plt.gcf().set_size_inches(6, 8) 
plt.tight_layout()

plt.savefig("SHAP_Feature_Importance_Summary_Plot.png")
plt.show()

Resultado:

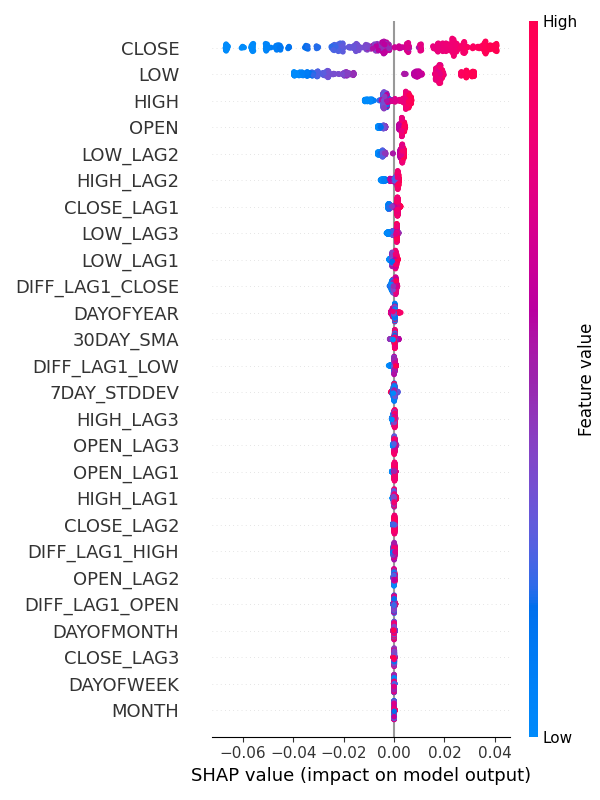
Pelos gráficos de importância das features, fica claro que as variáveis para captura de padrões sazonais, como DIASEMANA, MÊS, DIADOMÊS e DIADOANO, são algumas das que menos contribuem para as previsões do modelo.

Curiosamente, todas essas são estacionárias de acordo com o teste de Dickey-Fuller Aumentado.

  

Teste de Dickey-Fuller Aumentado (ADF)

Esse é um teste estatístico usado para determinar se um conjunto de dados de séries temporais é estacionário ou não. A estacionaridade é uma propriedade crucial para muitos métodos de previsão e análise de séries temporais.

Uma variável estacionária ou um conjunto de dados estacionário refere-se a uma série em que as propriedades estatísticas (média, variância, autocorrelação) permanecem constantes ao longo do tempo. Por exemplo, no mercado de ações. A média dos valores OHLC pode aumentar ou diminuir drasticamente ao longo do tempo, tornando esses valores não estacionários na maior parte do tempo, enquanto seus retornos, como a média ou variância da diferença entre Máxima e Mínima, são estacionários ao longo do tempo.

Eu executei este teste em todo o conjunto de dados que temos.

from statsmodels.tsa.stattools import adfuller

def adf_test(series, signif=0.05):
  """
  Performs the ADF test on a pandas Series and interprets the results.

  Args:
      series: The pandas Series containing the time series data.
      signif: Significance level for the test (default: 0.05).

  Returns:
      A dictionary containing the test statistic, p-value, used lags,
      critical values, and interpretation of stationarity.
  """
  dftest = adfuller(series, autolag='AIC')
  adf_stat = dftest[0]  # Access test statistic
  pvalue = dftest[1]  # Access p-value
  usedlag = dftest[2]  # Access used lags
  critical_values = dftest[4]  # Access critical values

  interpretation = 'Stationary' if pvalue < signif else 'Non-Stationary'
  result = {'Statistic': adf_stat, 'p-value': pvalue, 'Used Lags': usedlag,
            'Critical Values': critical_values, 'Interpretation': interpretation}
  return result

for col in df.columns:
  adf_results = adf_test(df[col], signif=0.05)
  print(f"ADF Results for column {col}:\n {adf_results}")

Das 27 variáveis, apenas 9 foram detectadas como estacionárias. Essas variáveis são: 

1. 7DAY_STDDEV
2. DAYOFMONTH
3. DAYOFWEEK
4. DAYOFYEAR
5. MONTH
6. DIFF_LAG1_OPEN
7. DIFF_LAG1_HIGH
8. DIFF_LAG1_LOW
9. DIFF_LAG1_CLOSE

Para descobrir facilmente se as variáveis são estacionárias ou não, você pode simplesmente observar o gráfico de distribuição. Dados bem distribuídos em torno da média são provavelmente estacionários.

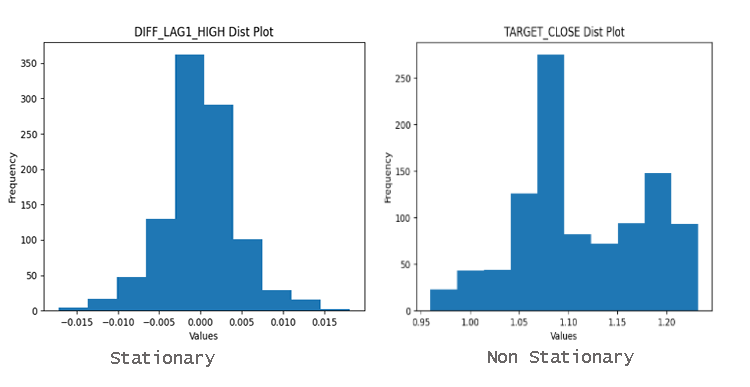
Por que a Estacionaridade é Importante?

Muitos métodos estatísticos utilizados na análise e previsão de séries temporais assumem a estacionaridade. Se uma série temporal não for estacionária, esses métodos podem produzir resultados enganosos ou imprecisos. 

Imagine tentar prever os preços futuros de ações se os preços estiverem constantemente em alta. O modelo de séries temporais não seria capaz de capturar a tendência subjacente.

Modelos clássicos ou mesmo os chamados modelos modernos de machine learning, como o LightGBM que usamos, têm a capacidade de lidar com relações não lineares entre as features, tornando-os menos afetados pela estacionaridade presente nos dados. A importância das features para este modelo demonstrou claramente que as variáveis mais importantes para o modelo são as variáveis OHLC não estacionárias.

No entanto, isso não significa que variáveis como o dia da semana não tenham impacto no modelo. A importância das features é apenas uma parte da história; conhecimento de domínio ainda é necessário na minha opinião.

Não há necessidade de remover essa variável só porque ela é classificada como menos importante, pois acredito que ela afeta o EURUSD. 

Prevendo uma variável alvo estacionária

Ter uma variável alvo estacionária melhora o desempenho de muitos modelos de machine learning quando se trata de previsão de séries temporais, pois dados estacionários têm (média, variância, autocorrelação) constantes ao longo do tempo. Como você sabe, prever para onde o mercado se moverá no próximo candle é difícil, mas prever a quantidade de pips ou pontos para o próximo movimento não é tão difícil.

Se pudermos prever a quantidade de pontos que o próximo candle gerará, podemos usar isso para definir metas de negociação (Stop loss e Take profit).

Para isso, precisamos encontrar a diferença de primeira ordem, subtraindo o preço de fechamento anterior do próximo preço de fechamento.

Python

Y = df["TARGET_CLOSE"] - df["CLOSE"] # diferença de primeira ordem 

Ao diferenciar os próximos preços de fechamento dos anteriores, obtemos uma variável estacionária.

adf_results = adf_test(Y,signif=0.05)

print(f"ADF Results:\n {adf_results}")

Resultados:

ADF Results: {'Statistic': -23.37891429248752, 'p-value': 0.0, 'Used Lags': 1, 'Critical Values': {'1%': -3.4369193380671, '5%': -2.864440383452517, '10%': -2.56831430323573}, 'Interpretation': 'Stationary'}

Após ajustar o modelo regressor para a nova variável alvo estacionária e avaliar seu desempenho no conjunto de dados de teste, o resultado foi o seguinte.

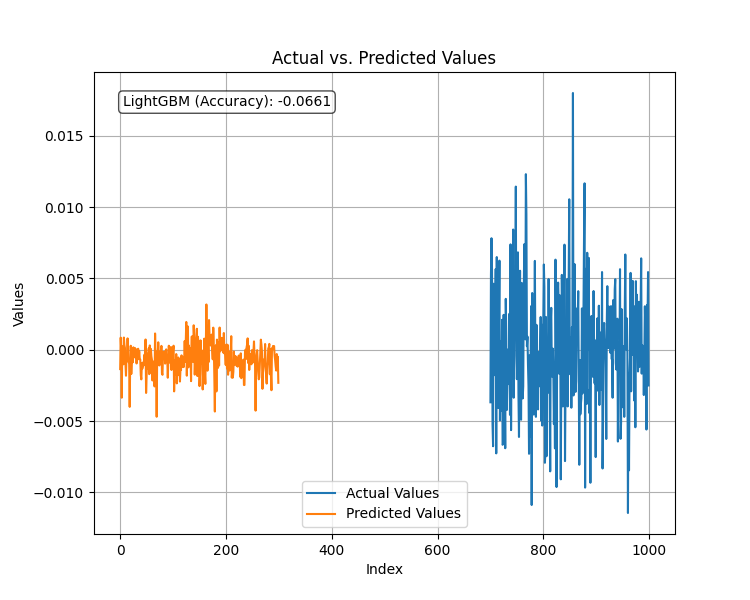
O modelo teve um desempenho ruim quando a variável alvo era estacionária. Como sempre, em machine learning, pode haver muitos fatores que levam a isso, mas por enquanto vamos concluir que o LightGBM não se sai bem com variáveis alvo estacionárias. Vamos continuar com o modelo de regressão produzido para prever os valores de fechamento alvo.

Ter este modelo de regressão que prevê valores contínuos de preço de fechamento não é tão útil quanto ter um modelo que prevê os sinais de negociação, como compra ou venda. Para conseguir isso, precisamos criar outro modelo para prever os sinais de negociação.

Construindo o modelo classificador LightGBM

Para criar um modelo classificador, precisamos preparar a variável alvo como uma variável binária onde 1 representa um sinal de compra e 0 representa um sinal de venda.

Python

Y = []
target_open = df["TARGET_OPEN"]
target_close = df["TARGET_CLOSE"]

for i in range(len(target_open)):
    if target_close[i] > target_open[i]: # if the candle closed above where it opened thats a buy signal
        Y.append(1)
    else: #otherwise it is a sell signal
        Y.append(0)

# split Y into irrespective training and testing samples 

y_train = Y[:train_size]
y_test = Y[train_size:]

Treinei o modelo LightGBM dentro de um Pipeline com a técnica StandardScaler.

Python

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

params = {
    'boosting_type': 'gbdt',  # Gradient Boosting Decision Tree
    'objective': 'binary',  # For binary classification (use 'regression' for regression tasks)
    'metric': ['auc','binary_logloss'],  # Evaluation metric
    'num_leaves': 25,  # Number of leaves in one tree
    'n_estimators' : 100, # number of trees
    'max_depth': 5,
    'learning_rate': 0.05,  # Learning rate
    'feature_fraction': 0.9  # Fraction of features to be used for each boosting round
}

pipe = Pipeline([
    ("scaler", StandardScaler()),
    ("lgbm", lgb.LGBMClassifier(**params))
])

# Fit the pipeline to the training data
pipe.fit(x_train, y_train)

Os resultados dos testes não foram surpreendentes, com uma precisão geral de 53%.

Relatório de Classificação

Classification Report
               precision    recall  f1-score   support

           0       0.49      0.79      0.61       139
           1       0.62      0.30      0.40       161

    accuracy                           0.53       300
   macro avg       0.56      0.54      0.51       300
weighted avg       0.56      0.53      0.50       300

Matriz de confusão:

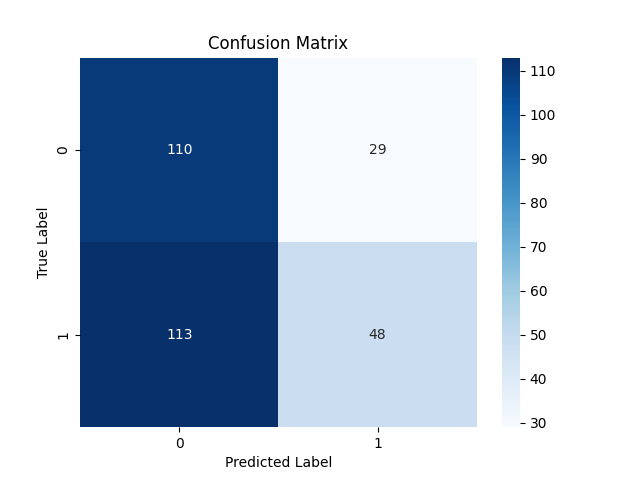
Salvando o modelo Classificador LightGBM para ONNX

Como fizemos anteriormente, salvar o modelo LightGBM no formato ONNX é simples e requer apenas algumas linhas de código.

import onnxmltools
from onnxmltools.convert import convert_lightgbm
import onnxmltools.convert.common.data_types
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx import convert_sklearn, update_registered_converter

from skl2onnx.common.shape_calculator import (
    calculate_linear_classifier_output_shapes,
)  # noqa

from onnxmltools.convert.lightgbm.operator_converters.LightGbm import (
    convert_lightgbm,
)  # noqa

# registering onnx converter

update_registered_converter(
    lgb.LGBMClassifier,
    "GBMClassifier",
    calculate_linear_classifier_output_shapes,
    convert_lightgbm,
    options={"nocl": [False], "zipmap": [True, False, "columns"]},
)

# Final LightGBM conversion to ONNX

model_onnx = convert_sklearn(
    pipe,
    "pipeline_lightgbm",
    [("input", FloatTensorType([None, x_train.shape[1]]))],
    target_opset={"": 12, "ai.onnx.ml": 2},
)

# And save.
with open("lightgbm.Timeseries Forecasting.D1.onnx", "wb") as f:
    f.write(model_onnx.SerializeToString())

Consolidando tudo dentro de um robô de trading

Agora que temos um modelo de machine learning salvo em ONNX, podemos anexá-lo diretamente a um Expert Advisor e usar o classificador LightGBM para previsões de séries temporais no MetaTrader 5.

MQL5

#resource "\\Files\\lightgbm.Timeseries Forecasting.D1.onnx" as uchar lightgbm_onnx[] //load the saved onnx file 
#include <MALE5\LightGBM\LightGBM.mqh>
CLightGBM lgb;

Usando a classe LightGBM construída no artigo anterior, consegui inicializar o modelo e usá-lo para fazer previsões.

int OnInit()
  {
//---
   
   if (!lgb.Init(lightgbm_onnx)) //Initialize the LightGBM model
     return INIT_FAILED;
   
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
    
   if (NewBar()) //Trade at the opening of a new candle
    {
     vector input_vector = input_data(); 
     long signal = lgb.predict_bin(input_vector);
     
   //---
     
      MqlTick ticks;
      SymbolInfoTick(Symbol(), ticks);
      
      if (signal==1) //if the signal is bullish
       {
          if (!PosExists(POSITION_TYPE_BUY)) //There are no buy positions
           {
             if (!m_trade.Buy(lotsize, Symbol(), ticks.ask, ticks.bid-stoploss*Point(), ticks.ask+takeprofit*Point())) //Open a buy trade
               printf("Failed to open a buy position err=%d",GetLastError());
           }
       }
      else if (signal==0) //Bearish signal
        {
          if (!PosExists(POSITION_TYPE_SELL)) //There are no Sell positions
            if (!m_trade.Sell(lotsize, Symbol(), ticks.bid, ticks.ask+stoploss*Point(), ticks.bid-takeprofit*Point())) //open a sell trade
               printf("Failed to open a sell position err=%d",GetLastError());
        }
      else //There was an error
        return;
    }
  }

A função input_data() é responsável por coletar dados de forma semelhante à maneira como os dados foram coletados e armazenados em um arquivo CSV no script Feature engineering Timeseries forecasting.mq5.

Testando o Modelo no Strategy Tester.

Finalmente, podemos testar o modelo no ambiente de negociação. Como os dados foram coletados em uma base diária, pode ser uma boa ideia testá-lo em um intervalo de tempo menor para evitar erros de "mercado fechado", já que estamos procurando sinais de negociação na abertura de um novo candle. Podemos também configurar o tipo de modelagem para preços de abertura para um teste mais rápido.

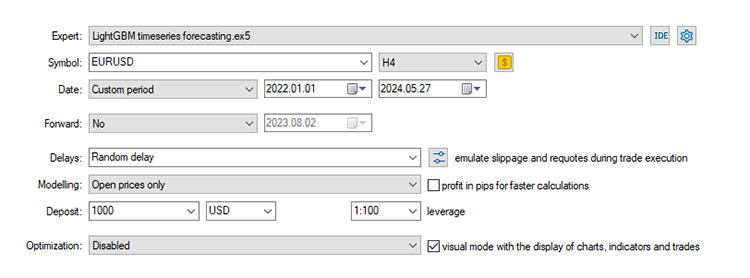
O EA fez as previsões corretas aproximadamente 51% das vezes, dado o Stop loss e Take profit de 500 e 700 pontos, respectivamente.

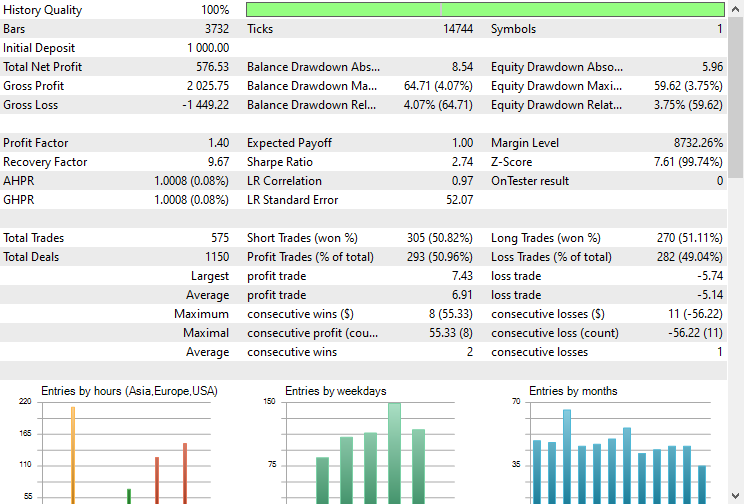
A curva de saldo/equidade foi impressionante também.

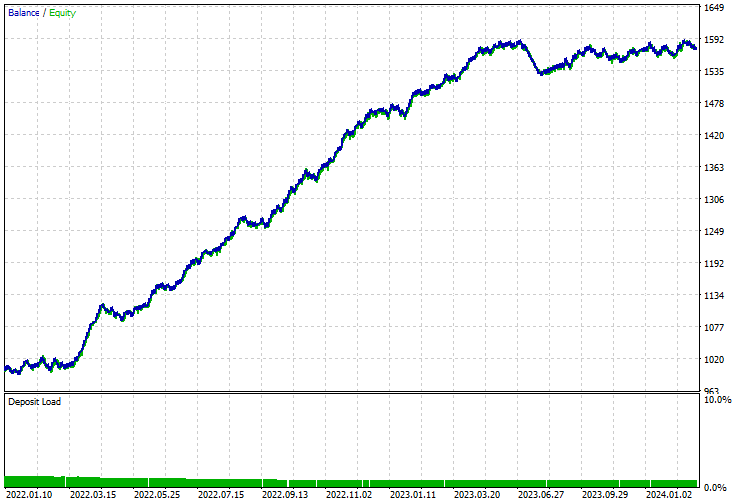
Vantagens de Usar Modelos de ML Clássicos e Modernos para Previsão de Séries Temporais

O uso de modelos de machine learning não específicos para séries temporais na previsão de séries temporais tem várias vantagens. Abaixo estão alguns benefícios principais:

1. Flexibilidade na Engenharia de Features

Modelos clássicos de machine learning permitem uma extensa engenharia de features, o que pode ser aproveitado para incluir várias variáveis externas e features derivadas. Você pode usar seu intelecto humano para analisar manualmente e incorporar todos os dados que considerar úteis, incluindo features complexas, como defasagens e estatísticas móveis, como fizemos neste post.

2. Tratamento de Não Estacionaridade

Em vez de tornar a série estacionária por meio de diferenciação, você pode incluir a tendência e a sazonalidade diretamente como features, e o modelo aprenderá os padrões sem problemas.

3. Sem Assumções Sobre a Distribuição dos Dados

Muitos modelos clássicos de séries temporais (como ARIMA) assumem que os dados seguem uma distribuição estatística específica. Modelos de ML clássicos e modernos, por outro lado, são mais flexíveis quanto à distribuição dos dados.

Modelos como árvores de decisão, florestas aleatórias e boosting de gradiente (incluindo LightGBM) não assumem nenhuma distribuição específica dos dados.

4. Escalabilidade

Modelos de ML clássicos podem lidar com grandes conjuntos de dados de forma mais eficiente e são frequentemente mais fáceis de escalar.

5. Interações Complexas

Modelos de ML clássicos podem capturar relações complexas e não lineares entre as features e a variável alvo.

6. Robustez a Dados Faltantes

Modelos de machine learning geralmente têm melhores mecanismos para lidar com dados faltantes em comparação com modelos tradicionais de séries temporais.

7. Métodos de Conjunto (Ensemble)

Você pode usar facilmente métodos de conjunto, como bagging, boosting e stacking, para melhorar o desempenho do modelo combinando múltiplos modelos para melhorar a precisão preditiva e a robustez.

8. Facilidade de Uso e Integração

Modelos de ML clássicos são frequentemente mais amigáveis ao usuário e vêm com bibliotecas e ferramentas extensas para implementação, visualização e avaliação.

Bibliotecas como Scikit-learn, LightGBM e XGBoost fornecem ferramentas abrangentes para construir, ajustar e avaliar esses modelos.

A linha de fundo

Modelos de aprendizado de máquina clássicos e modernos podem ser usados para análise e previsão de séries temporais sem problema, e eles podem superar os modelos de séries temporais com as informações, ajustes e processos corretos, conforme discutido neste artigo. Decidi usar LightGBM como exemplo; no entanto, qualquer modelo de aprendizado de máquina clássico ou moderno, como SVM, Regressão Linear, Naïve Bayes, XGBoost, etc., pode ser aplicado.

Até mais.

Acompanhe o desenvolvimento de modelos de aprendizado de máquina e muito mais discutido nesta série de artigos neste repositório GitHub.

Tabela de Anexos

Nome do Arquivo	Tipo de Arquivo	Descrição|Uso
LightGBM timeseries forecasting.mq5	Expert Advisor	Robô de negociação para carregar o modelo ONNX e testar a estratégia de negociação final no MetaTrader 5.
lightgbm.Timeseries Forecasting.D1.onnx	ONNX	Modelo LightGBM em formato ONNX.
LightGBM.mqh	Uma Inclusão (biblioteca)	Consiste no código para carregar o formato do modelo ONNX e implantá-lo na linguagem nativa MQL5.
Feature engineering Timeseries forecasting.mq5	Um Script	Este é um script onde todos os dados são coletados e preparados para a análise e previsão de séries temporais.
forex-timeseries-forecasting-lightgbm.ipynb	Python Script(Jupyter Notebook)	Todo o código Python discutido neste artigo pode ser encontrado dentro deste notebook.

Fontes e Referências:

• Time Series Talk: Stationarity(https://youtu.be/oY-j2Wof51c)
• Kishan Manani - Engenharia de Atributos para Previsão de Séries Temporais | PyData London 2022 (https://www.youtube.com/watch?v=9QtL7m3YS9I)
• Previsão do Mercado de Ações via Técnicas de Aprendizado Profundo: Uma Pesquisa (https://arxiv.org/abs/2212.12717)
• Desafios na Previsão de Séries Temporais (https://www.youtube.com/watch?v=rcdDl8qf0ZA)
• Estacionaridade e diferenciação (https://otexts.com/fpp2/stationarity.html)
• Como realizar Codificação Target/Mean para Atributos Categóricos | Python (https://www.youtube.com/watch?v=nd7vc4MZQz4)